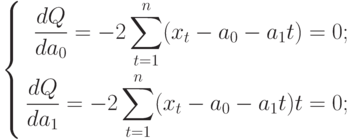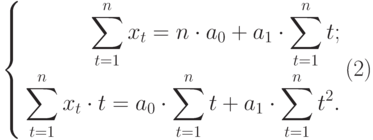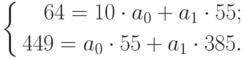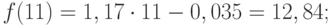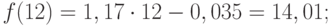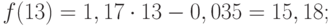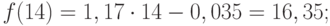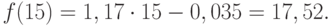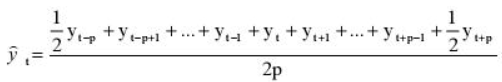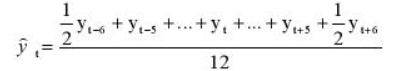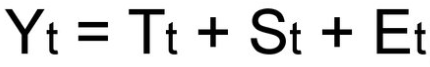Анализ временных рядов позволяет изучить показатели во времени. Временной ряд – это числовые значения статистического показателя, расположенные в хронологическом порядке.
Подобные данные распространены в самых разных сферах человеческой деятельности: ежедневные цены акций, курсов валют, ежеквартальные, годовые объемы продаж, производства и т.д. Типичный временной ряд в метеорологии, например, ежемесячный объем осадков.
Временные ряды в Excel
Если фиксировать значения какого-то процесса через определенные промежутки времени, то получатся элементы временного ряда. Их изменчивость пытаются разделить на закономерную и случайную составляющие. Закономерные изменения членов ряда, как правило, предсказуемы.
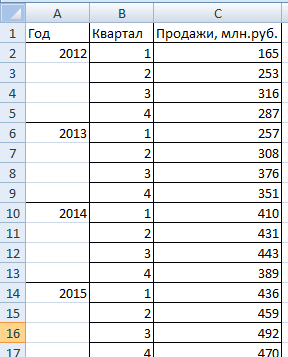
Сделаем анализ временных рядов в Excel. Пример: торговая сеть анализирует данные о продажах товаров магазинами, находящимися в городах с населением менее 50 000 человек. Период – 2012-2015 гг. Задача – выявить основную тенденцию развития.
Внесем данные о реализации в таблицу Excel:
На вкладке «Данные» нажимаем кнопку «Анализ данных». Если она не видна, заходим в меню. «Параметры Excel» — «Надстройки». Внизу нажимаем «Перейти» к «Надстройкам Excel» и выбираем «Пакет анализа».
Подключение настройки «Анализ данных» детально описано здесь.
Нужная кнопка появится на ленте.
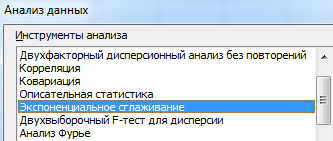
Из предлагаемого списка инструментов для статистического анализа выбираем «Экспоненциальное сглаживание». Этот метод выравнивания подходит для нашего динамического ряда, значения которого сильно колеблются.
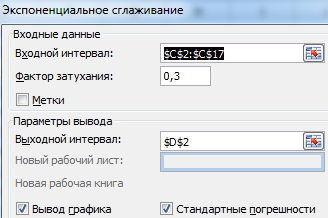
Заполняем диалоговое окно. Входной интервал – диапазон со значениями продаж. Фактор затухания – коэффициент экспоненциального сглаживания (по умолчанию – 0,3). Выходной интервал – ссылка на верхнюю левую ячейку выходного диапазона. Сюда программа поместит сглаженные уровни и размер определит самостоятельно. Ставим галочки «Вывод графика», «Стандартные погрешности».
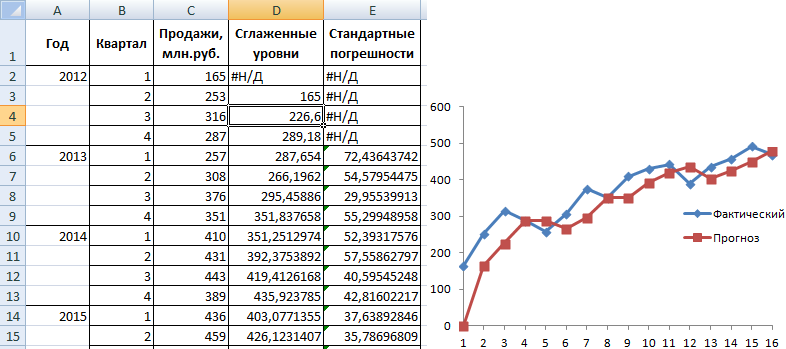
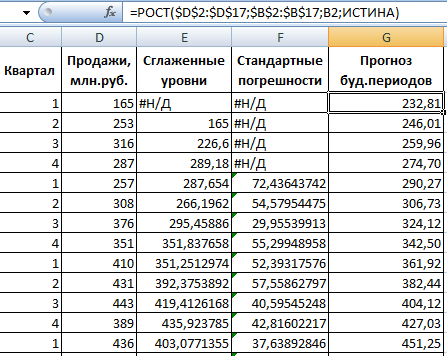
Закрываем диалоговое окно нажатием ОК. Результаты анализа:
Для расчета стандартных погрешностей Excel использует формулу: =КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; ‘диапазон прогнозных значений’)/ ‘размер окна сглаживания’). Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3).
Прогнозирование временного ряда в Excel
Составим прогноз продаж, используя данные из предыдущего примера.
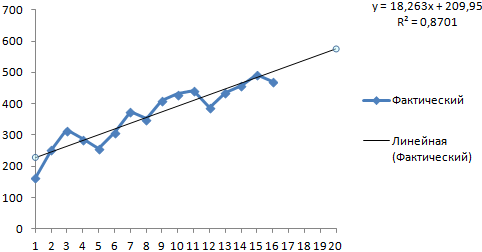
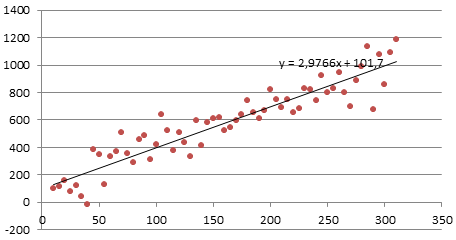
На график, отображающий фактические объемы реализации продукции, добавим линию тренда (правая кнопка по графику – «Добавить линию тренда»).
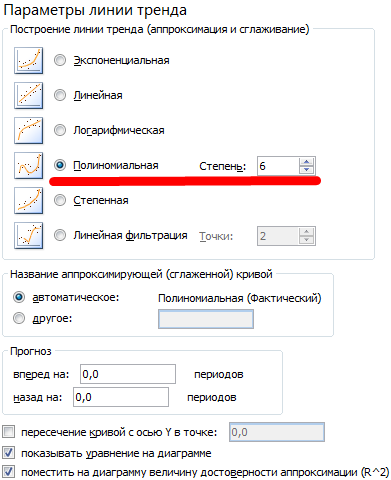
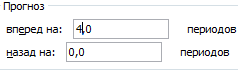
Настраиваем параметры линии тренда:
Выбираем полиномиальный тренд, что максимально сократить ошибку прогнозной модели.
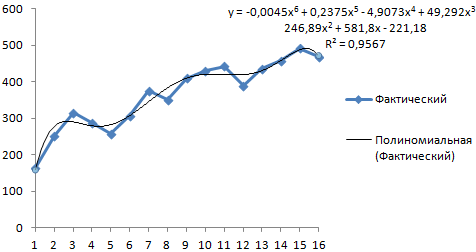
R2 = 0,9567, что означает: данное отношение объясняет 95,67% изменений объемов продаж с течением времени.
Уравнение тренда – это модель формулы для расчета прогнозных значений.
Большинство авторов для прогнозирования продаж советуют использовать линейную линию тренда. Чтобы на графике увидеть прогноз, в параметрах необходимо установить количество периодов.
Получаем достаточно оптимистичный результат:
В нашем примере все-таки экспоненциальная зависимость. Поэтому при построении линейного тренда больше ошибок и неточностей.
Для прогнозирования экспоненциальной зависимости в Excel можно использовать также функцию РОСТ.
Для линейной зависимости – ТЕНДЕНЦИЯ.
При составлении прогнозов нельзя использовать какой-то один метод: велика вероятность больших отклонений и неточностей.
history 4 июля 2021 г.
- Группы статей
В
первом разделе статьи
модели для прогнозирования временных рядов сравниваются с моделями, построение которых основано на причинно-следственных закономерностях.
Во
втором разделе
приведен краткий обзор трендов временных рядов (линейный и сезонный тренд, стационарный процесс). Для каждого тренда предложена модель для прогнозирования.
Затем даны ссылки на сайты по теории прогнозирования временных рядов и содержащие базы статистических данных.
Disclaimer:
Напоминаем, что задача сайта excel2.ru (раздел
Временные ряды
) продемонстрировать использование MS EXCEL для решения задач, связанных с прогнозированием временных рядов. Поэтому, статистические термины и определения приводятся лишь для логики изложения и демонстрации идей. Сайт не претендует на математическую строгость изложения статистики. Однако в наших статьях:
• ПОЛНОСТЬЮ описан встроенный в EXCEL инструментарий по анализу временных рядов (в составе
надстройки Пакет анализа
, различных
типов Диаграмм
(
гистограмма
,
линия тренда
) и формул);
• созданы файлы примера для построения соответствующих графиков, прогнозов и их интервалов предсказания, вычисления ошибок, генерации рядов (с
трендами
и
сезонностью
) и пр.
Модели временных рядов и модели предметной области
Напомним, что временным рядом (англ. Time Series) называют совокупность наблюдений изучаемой величины, упорядоченную по времени. Наблюдения производятся через одинаковые периоды времени. Другой информацией, кроме наблюдений, исследователь не обладает.
Основной целью исследования временного ряда является его прогнозирование – предсказание будущих значений изучаемой величины. Прогнозирование основывается только на анализе значений ряда в предыдущие периоды, точнее — на идентификации трендов ряда. Затем, после определения трендов, производится моделирование этих трендов и, наконец, с помощью этих моделей — экстраполяция на будущие периоды.
Таким образом, прогнозирование основывается на фактических данных (значениях временного ряда) и модели (
скользящее среднее
,
экспоненциальное сглаживание
,
двойное и тройное экспоненциальное сглаживание
и др.).
Примечание
: Прогнозирование методом Скользящее среднее в MS EXCEL подробно рассмотрено в
одноименной статье
.
В отличие от методов временных рядов,
где зависимости ищутся внутри самого процесса
, в «моделях предметной области» (англ. «Causal Models») кроме самих данных используют еще и законы предметной области.
Примером построения «моделей предметной области» (
моделей строящихся на основе причинно-следственных закономерностей, априорно известных независимо от имеющихся данных
) может быть промышленный процесс изготовления защитной ткани. Пусть в таком процессе известно, что прочность материала ткани зависит от температуры в реакторе, в котором производится процесс полимеризации (температура — контролируемый фактор). Однако, прочность материала является все же случайной величиной, т.к. зависит помимо температуры также и от множества других факторов (качества исходного сырья, температуры окружающей среды, номера смены, умений аппаратчика реактора и пр.). Эти другие факторы в процессе производства стараются держать постоянными (сырье проходит входной контроль и его поставщик не меняется; в помещении, где стоит реактор, поддерживается постоянная температура в течение всего года; аппаратчики проходят обучение и регулярно проводится переаттестация). Задачей статистических методов в этом случае – предсказать значение случайной величины (прочности) при заданном значении изменяемого фактора (температуры).
Обычно для описания таких процессов (зависимость случайной величины от управляемого фактора) являются предметом изучения в разделе статистики «
Регрессионный анализ
», т.к. есть основания сделать гипотезу о существовании причинно-следственной связи между управляемым фактором и прогнозируемой величиной.
Модели, строящиеся на основе причинно-следственных закономерностей, упомянуты в этой статье для того чтобы акцентировать, что их изучение предшествует теме «временные ряды». Так, часть методов, например «Регрессионный анализ» (используется
метод наименьших квадратов — МНК
), используется при анализе временных рядов, но изучаются в моделях предметной области, поэтому неподготовленным «пытливым умам» не стоит игнорировать раздел статистики «
Статистический вывод
», в котором проверяются гипотезы о
равенстве среднего значения
и строятся
доверительные интервалы для оценки среднего
, и упомянутый выше «Регрессионный анализ».
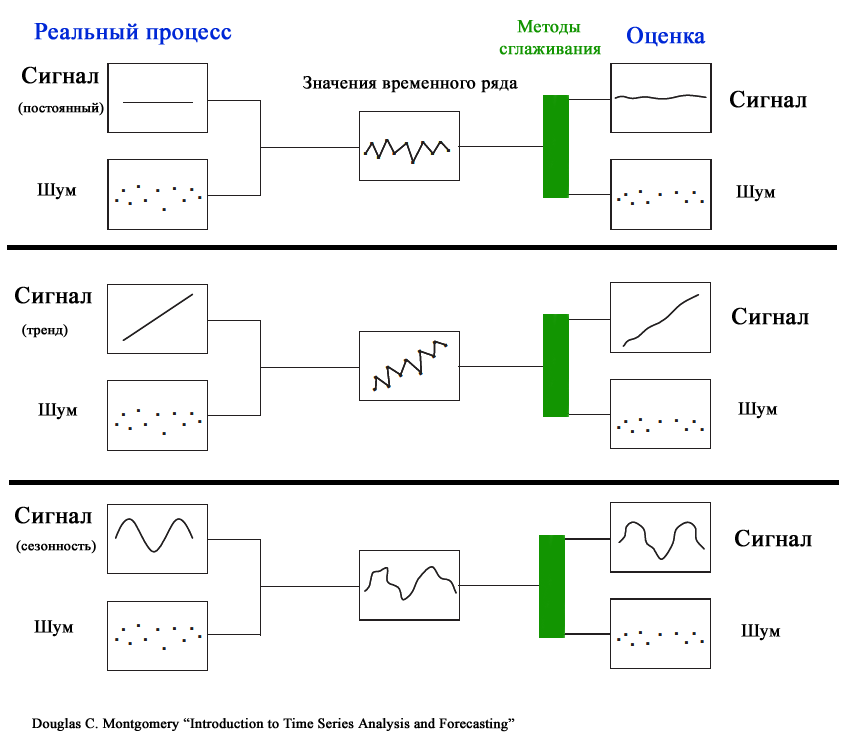
Кратко о типах процессов и моделях для их прогнозирования
Выбор подходящей модели прогнозирования делается с учетом типа моделируемого процесса (наличие трендов). Рассмотрим основные типы процессов.
1. Стационарный процесс
Стационарный процесс – это случайный процесс чьи характеристики не зависят от времени их наблюдения. Этими характеристиками являются
среднее значение
,
дисперсия
и автоковариация. В стационарном процессе не могут быть выделены предсказуемые паттерны. Соответственно ряды демонстрирующие тренд и сезонность — не стационарны. А вот ряд с цикличностью (апериодической) является стационарным, т.к. на долгосрочном временном интервале появление циклов предсказать невозможно.
Почему стационарный процесс важен? Так как стационарность подразумевает нахождение процесса в состоянии статистической стабильности, то такие временные ряды имеют постоянное среднее значение и дисперсию, которые определяются стандартным образом.
Также для стационарного процесса определяется
функция автокорреляции
– совокупность коэффициентов корреляции значений временного ряда с собственными значениями, сдвинутыми по времени на один или несколько периодов. Сдвиг на несколько временных периодов часто называется лагом (обозначается k).
Функция автокорреляции является важным источником информации о временном ряде.
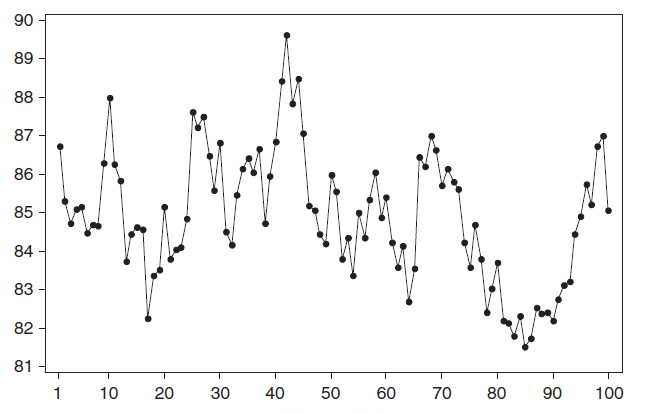
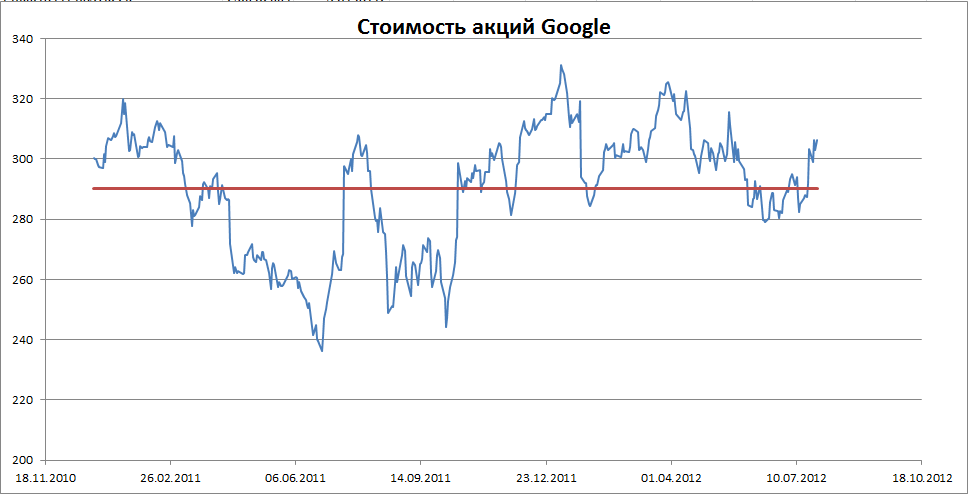
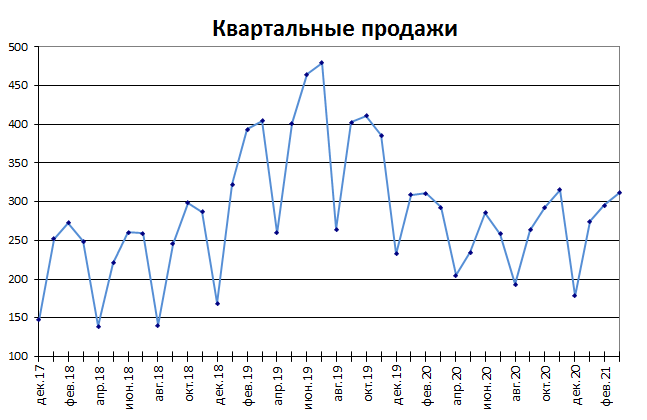
Примером стационарного процесса является колебания биржевого индекса, состоящего из стоимости акций нескольких компаний, около определённого значения (в период стабильности рынка).
Примечание
: график стоимости акций построен на реальных данных, см.
файл примера Google
.
Специальным видом стационарного процесса является белый шум. У этого процесса: среднее значений ряда равно 0, имеется конечная дисперсия и отсутствует корреляция между значениями исходного ряда и рядом сдвинутым на произвольное количество периодов (лагов). В MS EXCEL белый шум можно сгенерировать функцией СЛЧИС().
2. Линейный тренд
Некоторые процессы генерируют тренд (монотонное изменение значений ряда). Например, линейный тренд y=a*x+b, точнее y=a*t+b, где t – это время. Примером такого (не стационарного) процесса может быть монотонный рост стоимости недвижимости в некотором районе.
Для вычисления прогнозного значения можно воспользоваться методами
Регрессионного анализа
и подобрать параметры тренда: наклон и смещение по вертикали.
Примечание
: Про генерацию случайных значений, демонстрирующих линейный тренд, можно посмотреть в статье
Генерация данных для простой линейной регрессии в EXCEL
.
3. Процессы, демонстрирующие сезонность
В сезонном процессе присутствует точно или примерно фиксированный интервал изменений, например, продажи некоторых товаров имеют четко выраженный пик в ноябре-декабре каждого года в связи с праздником.
Для прогнозирования вычисляется индекс сезонности, затем ряд очищается от сезонной компоненты. Если ряд также демонстрирует тренд, то после очистки от сезонности используются методы регрессионного анализа для вычисления тренда.
Примечание
: Про генерацию случайных значений, демонстрирующих сезонность, можно посмотреть в статье Генерация сезонных трендов в EXCEL.
Часто на практике встречаются ряды, являющиеся комбинацией вышеуказанных типов тенденций.
О моделях прогнозирования
В качестве простейшей модели для прогноза можно взять последнее значение индекса. Этой модели соответствует следующий ход мысли исследователя: «Если значение индекса вчера было 306, то и завтра будет 306».
Этой модели соответствует формула Y
прогноз(t)
= Y
t-1
(прогноз в момент времени t равен значению временного ряда в момент t-1).
Другой моделью является среднее за последние несколько периодов (
скользящее среднее
). Этой модели соответствует другой ход мысли исследователя: «Если среднее значение индекса за последние n периодов было 540, то и завтра будет 540». Этой модели соответствует формула Y
прогноз(t)
=(Y
t-1
+ Y
t-2
+…+Y
t-n
)/n
Обратите внимание, что значения временного ряда берутся с одинаковым весом 1/n, то есть более ранние значения (в момент t-n) влияют на прогноз также как и недавние (в момент t-1). Конечно, в случае, если речь идет о стационарном процессе (без тренда), такая модель может быть приемлема. Чем больше количество периодов усреднения (n), тем меньше влияние каждого индивидуального наблюдения.
Третьей моделью для стационарного процесса может быть
экспоненциальное сглаживание
. В этом случае веса более ранних периодов будут меньше чем веса поздних. При этом учитываются все предыдущие наблюдения. Вес каждого последующего наблюдения больше на 1-α (Фактор затухания), где α (альфа) – это константа сглаживания (от 0 до 1).
Этой модели соответствует формула Y
прогноз(t)
=α*Y
t-1
+ α*(1-α)*Y
t-2
+ α*(1-α)2*Y
t-3
+…)
Формулу можно переписать через предыдущий прогноз Y
прогноз(t)
=α*Y
t-1
+(1- α)* Y
прогноз(t-1)
= α*(Y
t-1
— Y
прогноз(t-1)
)+Y
прогноз(t-1)
= α*(ошибка прошлого прогноза)+ прошлый прогноз
При экспоненциальном сглаживании прогнозное значение равно сумме последнего наблюдения с весом альфа и предыдущего прогноза с весом (1-альфа). Этой модели соответствует следующий ход мысли исследователя: «Вчера рано утром я предсказывал, что индекс будет равен 500, но вчера в конце дня значение индекса составило 480 (ошибка составила 20). Поэтому за основу сегодняшнего прогноза я беру вчерашний прогноз и корректирую его на величину ошибки, умноженную на альфа. Параметр альфа (константа) я найду методом экспоненциального сглаживания».
Подробнее о методе прогнозирования на основе экспоненциального сглаживания можно
найти в этой статье
.
Полезный сигнал и шум
Из-за случайного разброса, присущему временному ряду, временной ряд представляют как комбинацию двух различных компонентов: полезного сигнала и шума (ошибки). Полезный сигнал следует одному из 3-х вышеуказанных типов процессов. Сигнал может быть смоделирован и соответственно спрогнозирован. Шум представляет собой случайные ошибки (со средним значением =0, отсутствием корреляции и с фиксированной
дисперсией
).
Основной задачей моделирования идентификация полезного сигнала, имеющего определенный тренд, от непредсказуемого шума. Для этого как раз и используются Модели сглаживания.
Ссылки на источники статистических данных и обучающие материалы
Все источники англоязычные.
Сайт о применении EXCEL в статистике
Национальный Институт Стандартов и технологии
https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4.htm
Using R for Time Series Analysis
https://a-little-book-of-r-for-time-series.readthedocs.io/en/latest/src/timeseries.html#time-series-analysis
Учебник по прогнозированию временных рядов
https://otexts.com/fpp2/
Данные по болезням в Великобритании
https://ms.mcmaster.ca/~bolker/measdata.html
Курсы в Eberly College of Science (есть ссылки на базы данных)
https://online.stat.psu.edu/stat501/lesson/welcome-stat-501
https://online.stat.psu.edu/stat510/
Рассмотрим
построение модели аддитивного ряда
средствами Exel
2007 на примере изучения объемов потребления
электроэнергии (млн кВТ*ч) жителями
региона за 16 кварталов и на основании
полученной модели спрогнозируем объем
потребляемой электроэнергии на следующие
полгода. Построенный пример описан в
.
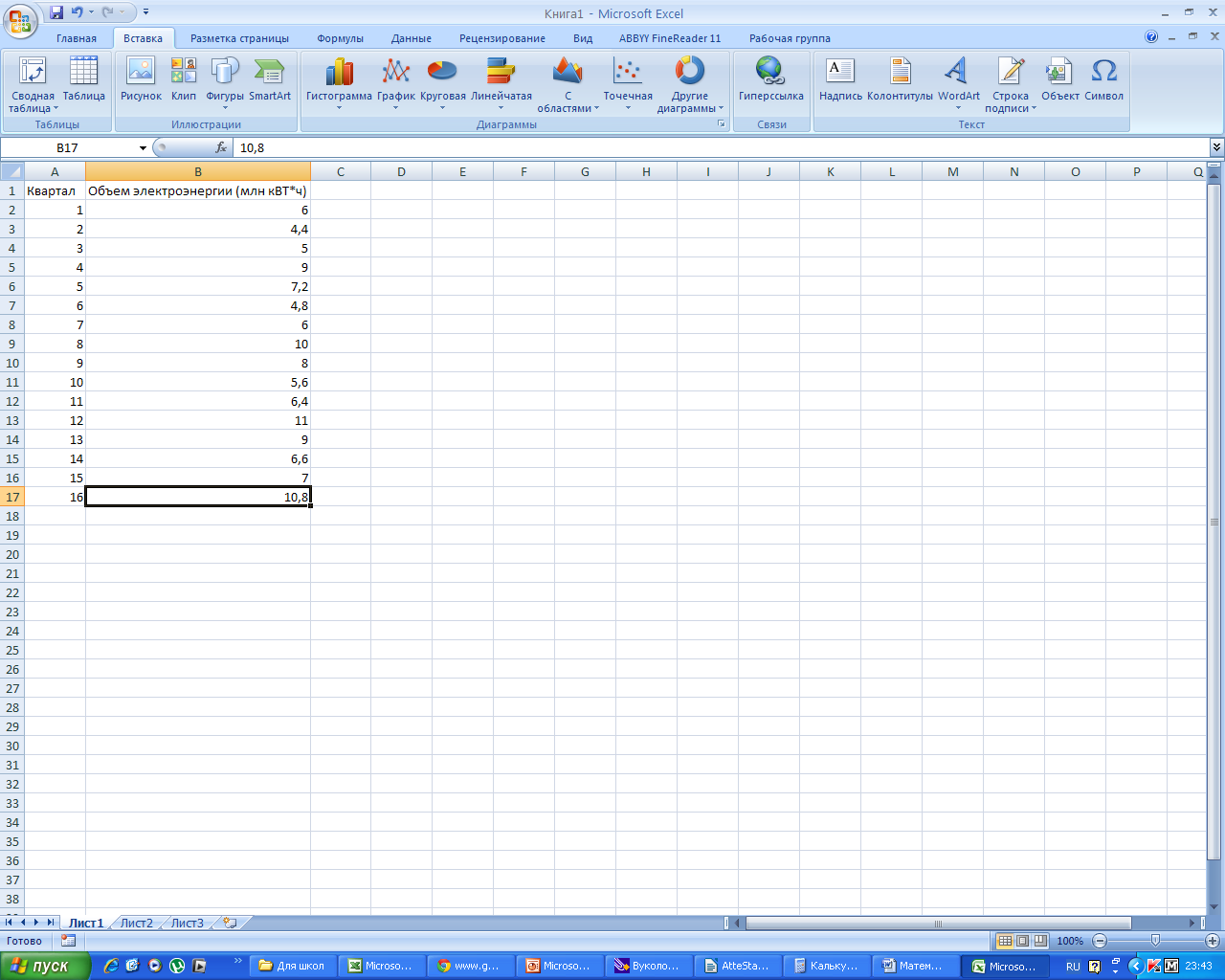
Пусть
известный объем потребляемой электроэнергии
задан таблицей 1.
Таблица
1. Потребление электроэнергии жителями
региона, млн кВТ*ч
|
№ кварт. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Объем (млн |
6,0 |
4,4 |
5,0 |
9,0 |
7,2 |
4,8 |
6,0 |
10 |
8,0 |
5,6 |
6,4 |
11 |
9,0 |
6,6 |
7,0 |
10.8 |
-
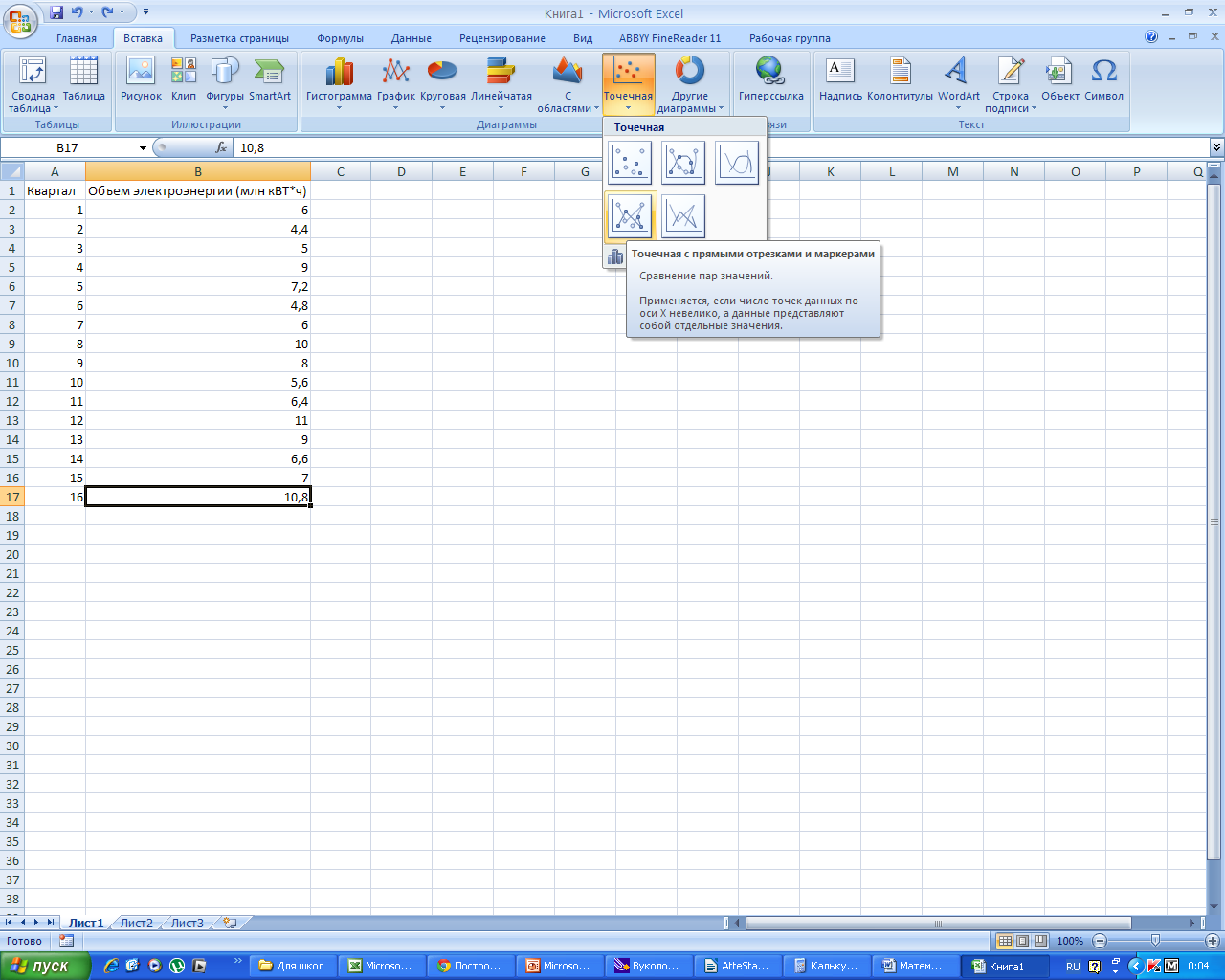
Внесем
эти данные в таблицу
-
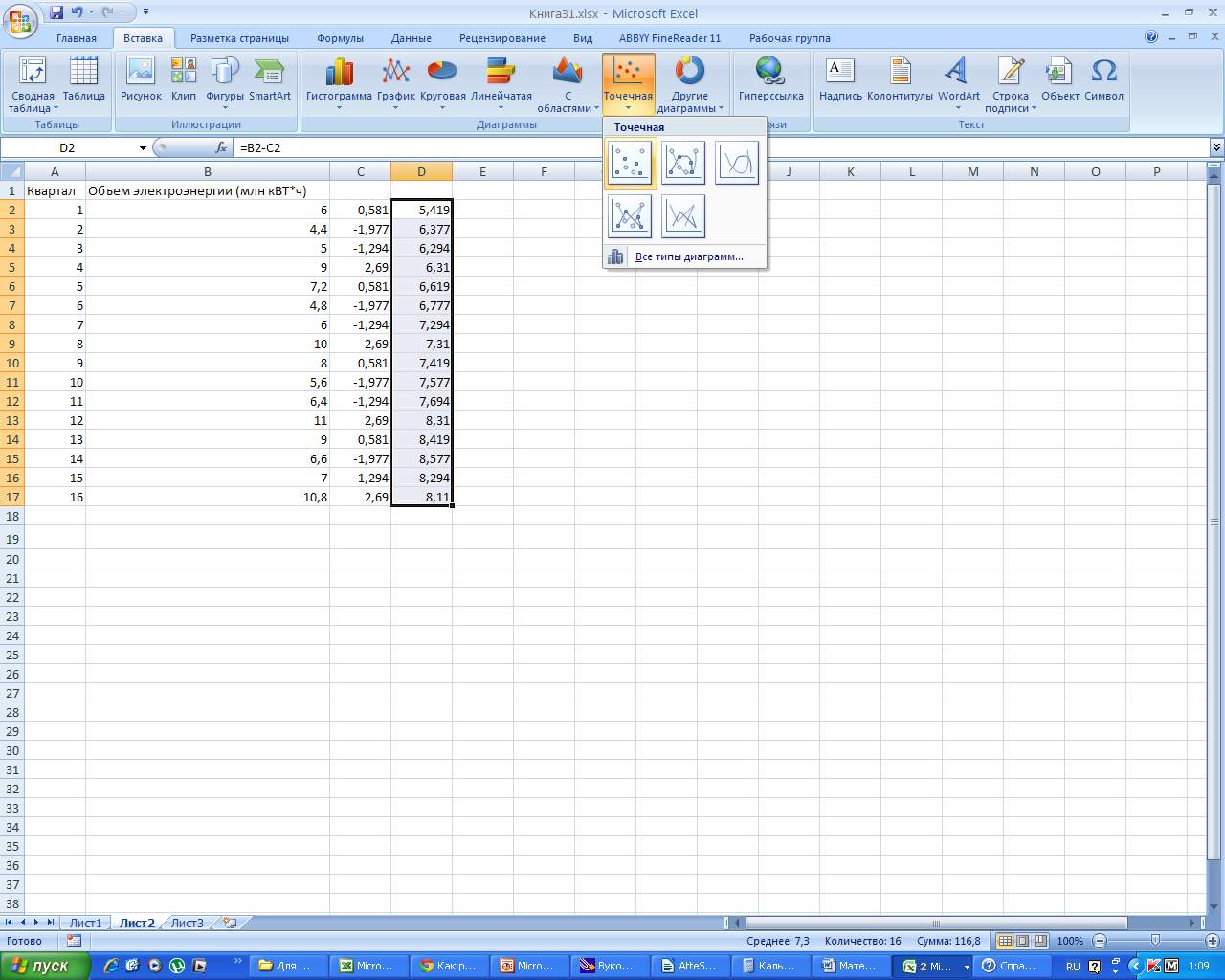
В
главном меню выбираем «ВСТАВКА»
-
В
главном меню выбираем «ТОЧЕЧНАЯ»
-
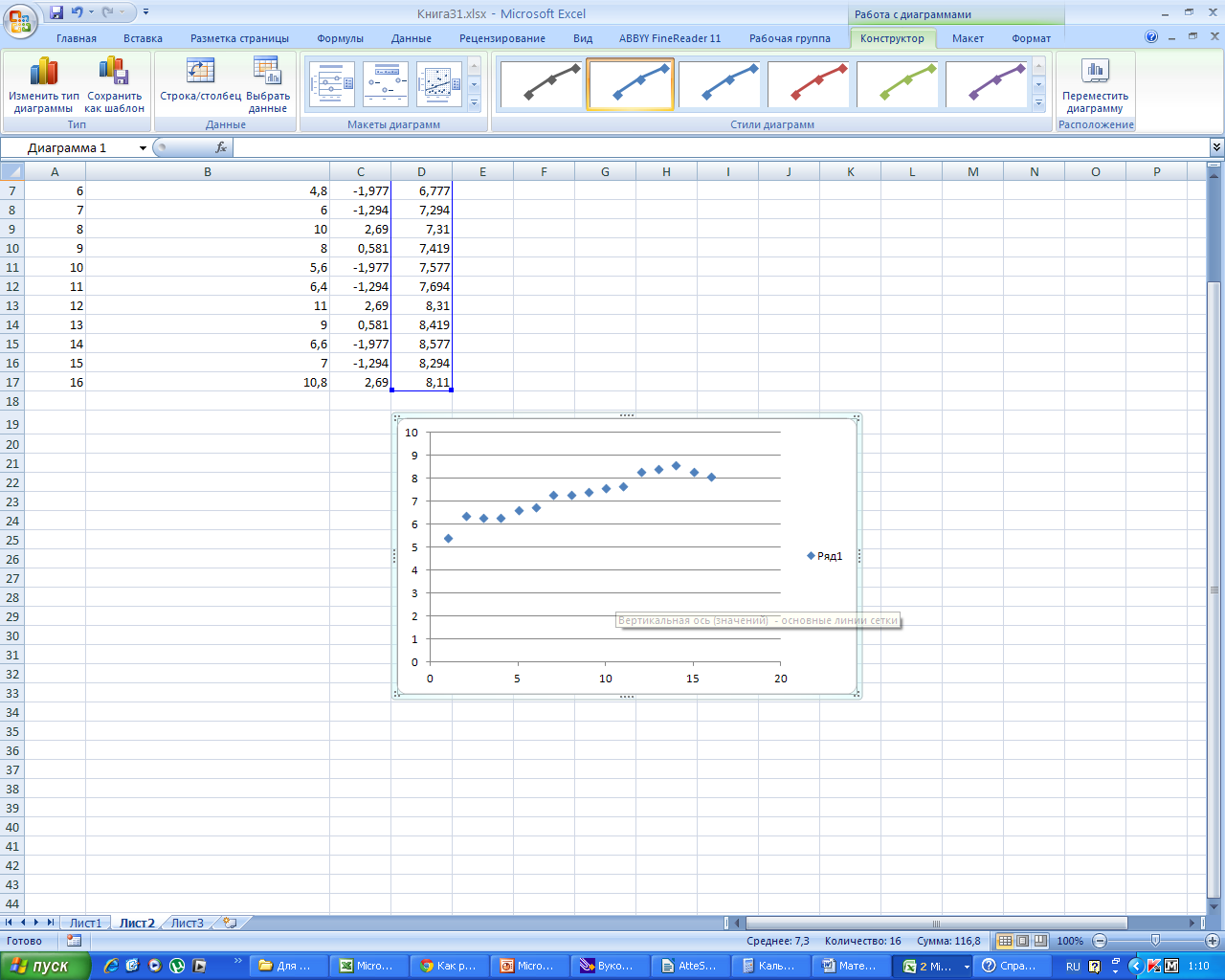
Получаем
график
-
Теперь
считаем сезонную компоненту и среднюю
ошибку аппроксимации. Для этого открываем
лист 2 и копируем в него первые два
столбца. По методике, описанной в
1рассчитаем значения сезонной компоненты.
Таблица
1- Расчет оценок сезонной компоненты в
аддитивной модели
|
Номер |
Потребление |
Итого |
Скользящая |
Центрированная |
Оценка |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
6,0 |
– |
– |
– |
– |
|
2 |
4,4 |
24,4 |
6,10 |
– |
– |
|
3 |
5,0 |
25,6 |
6,40 |
6,250 |
–1,250 |
|
4 |
9,0 |
26,0 |
6,50 |
6,450 |
2,550 |
|
5 |
7,2 |
27,0 |
6,75 |
6,625 |
0,575 |
|
6 |
4,8 |
28,0 |
7,00 |
6,875 |
–2,075 |
|
7 |
6,0 |
28,8 |
7,20 |
7,100 |
–1,100 |
|
8 |
10,0 |
29,6 |
7,40 |
7,300 |
2,700 |
|
9 |
8,0 |
30,0 |
7,50 |
7,450 |
0,550 |
|
10 |
5,6 |
31,0 |
7,75 |
7,625 |
–2,025 |
|
11 |
6,4 |
32,0 |
8,00 |
7,875 |
–1,475 |
|
12 |
11,0 |
33,0 |
8,25 |
8,125 |
2,875 |
|
13 |
9,0 |
33,6 |
8,40 |
8,325 |
0,675 |
|
14 |
6,6 |
33,4 |
8,35 |
8,375 |
–1,775 |
|
15 |
7,0 |
– |
– |
– |
– |
|
16 |
10,8 |
– |
– |
– |
– |
Таблица
расчета оценок сезонной компоненты в
аддитивной модели заполняется по
следующему правилу:
1
столбец
– известный номер квартала;
2
столбец
– известный объем потребляемой
электроэнергии(млн кВТ*ч);
3
столбец
– складываем последовательно значения
четырех ячеек 2 столбца и записываем их
на одну клетку ниже;
4
столбец
– каждое значение 3 столбца делим на 4
(период сезонных колебаний);
5
столбец
– складываем последовательно значения
двух ячеек 4 столбца, делим эту сумму на
2 и записываем на одну клетку ниже;
6
столбец
– из элементов 2 столбца вычитаем
элементы 5 столбца.
Рассчитаем
значения сезонной компоненты S
Для
этой цели составим следующую расчетную
таблицу 3, в которую последовательно
разместим данные из 6 столбца табл. 2.
Таблица
3- Расчет значений сезонной компоненты
в аддитивной модели
|
Показатель |
Год |
Номер |
|||
|
I |
II |
III |
IV |
||
|
1 |
– |
– |
–1,250 |
2,550 |
|
|
2 |
0,575 |
–2,075 |
–1,100 |
2,700 |
|
|
3 |
0,550 |
–2,025 |
–1,475 |
2,875 |
|
|
4 |
0,675 |
–1,775 |
– |
– |
|
|
Итого |
1,800 |
–5,875 |
–3,825 |
8,125 |
|
|
Средняя |
0,600 |
–1,958 |
–1,275 |
2,708 |
|
|
Скорректированная |
0,581 |
–1,977 |
–1,294 |
2,690 |
Средняя
оценка сезонной компоненты ()
рассчитывается как итого за квартал
/3.
В
аддитивных моделях с сезонной компонентой
предполагается , что сезонные воздействия
за период взаимопогашаются. Это означает,
что сумма значений сезонной компоненты
по всем кварталам должна быть равна 0.
Для
данной модели имеем 0,600+ (–1,958) + (–1,275) +
2,708 = 0,075
0.
Определим
корректирующий коэффициент k
=
0,075/4 = 0,01875.
Рассчитаем
скорректированные значения сезонной
компоненты, как разность между ее средней
оценкой и корректирующим коэффициентом
k:
k.
Проверим
условие равенства нулю суммы значений
сезонной компоненты: 0,581
– 1,977 – 1,294 + 2,690 = 0.
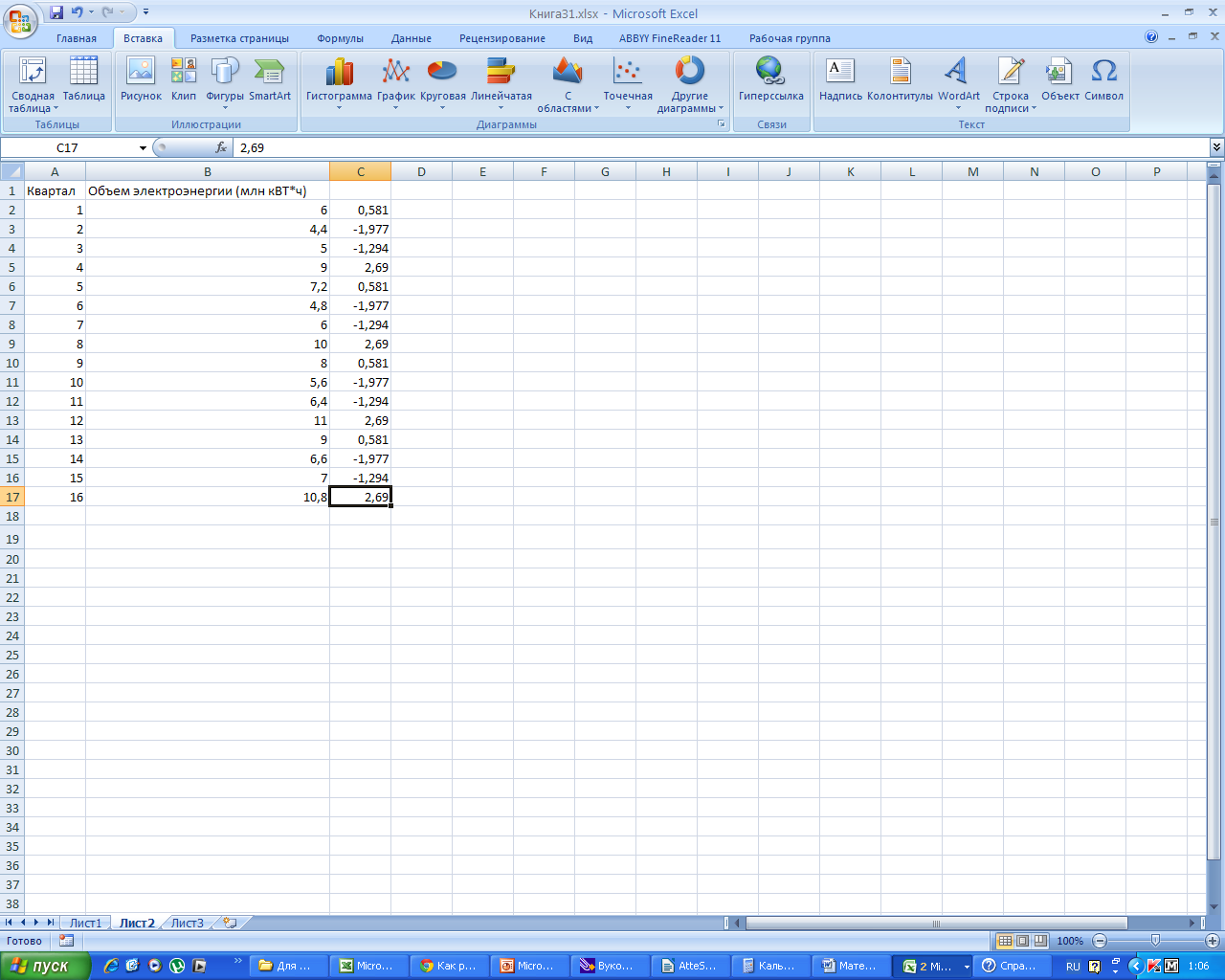
-
Подставим
значения скорректированной сезонной
компоненты в столбец С.
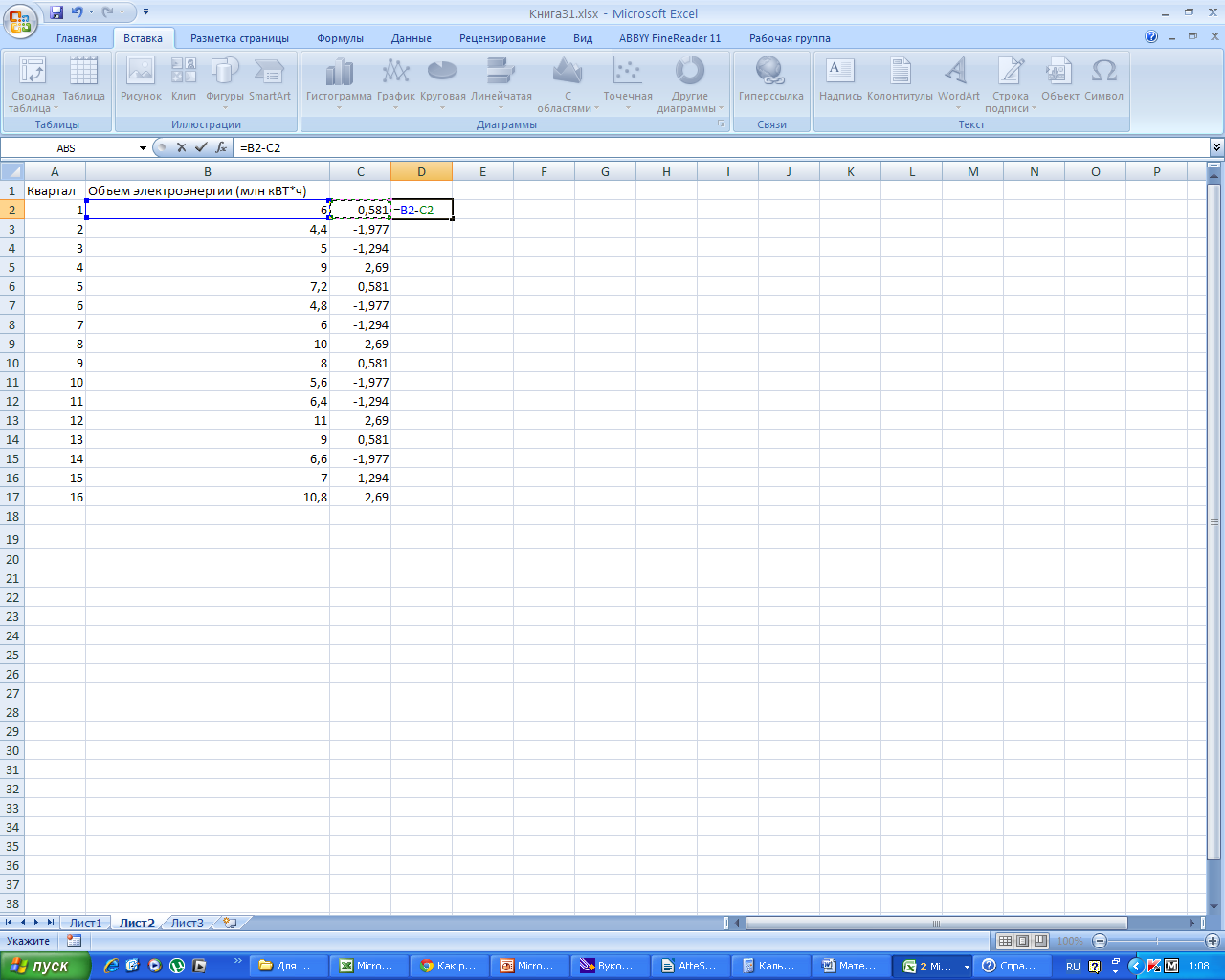
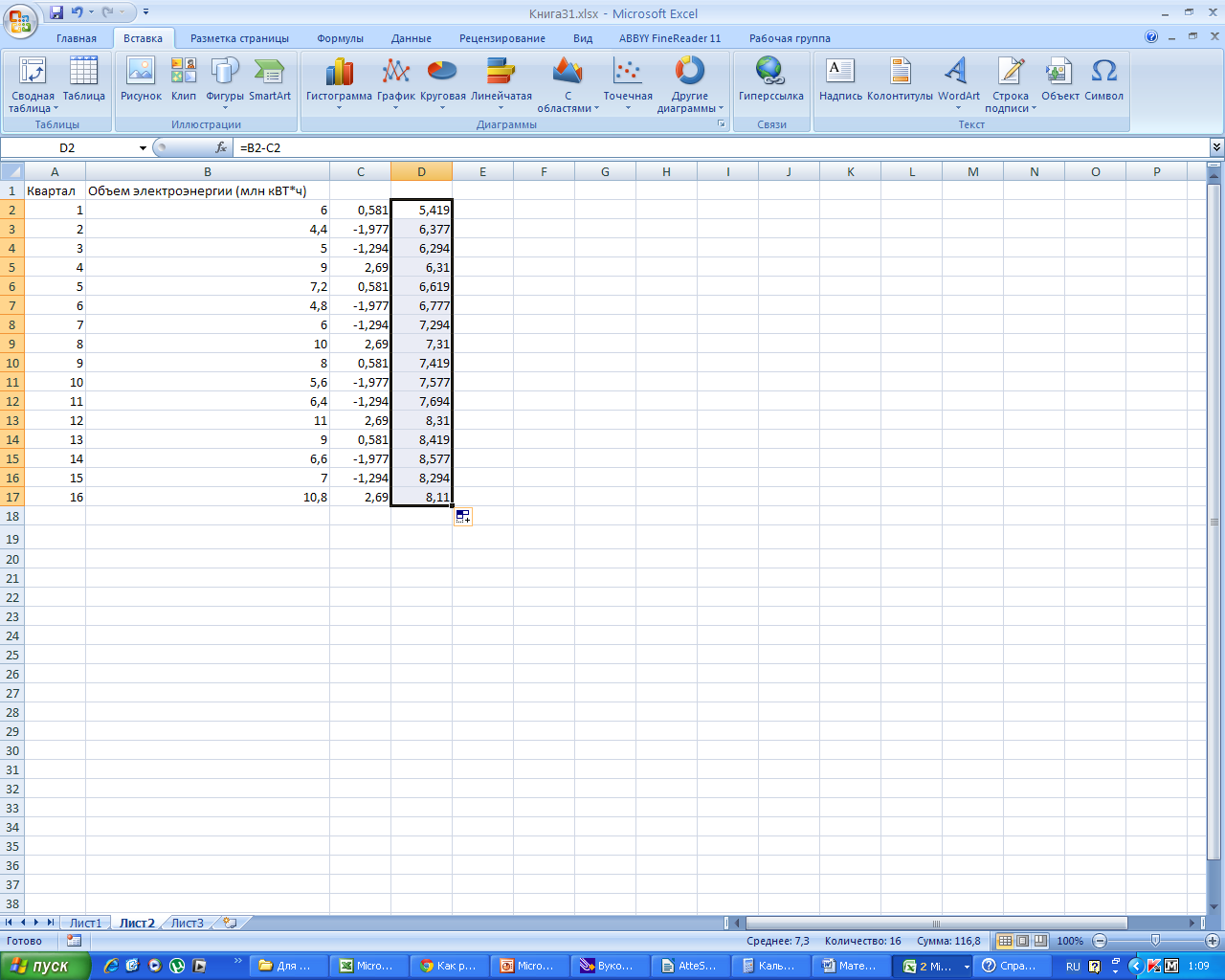
-
Заполняем
столбец D,
как разность В и С.
Получаем
-
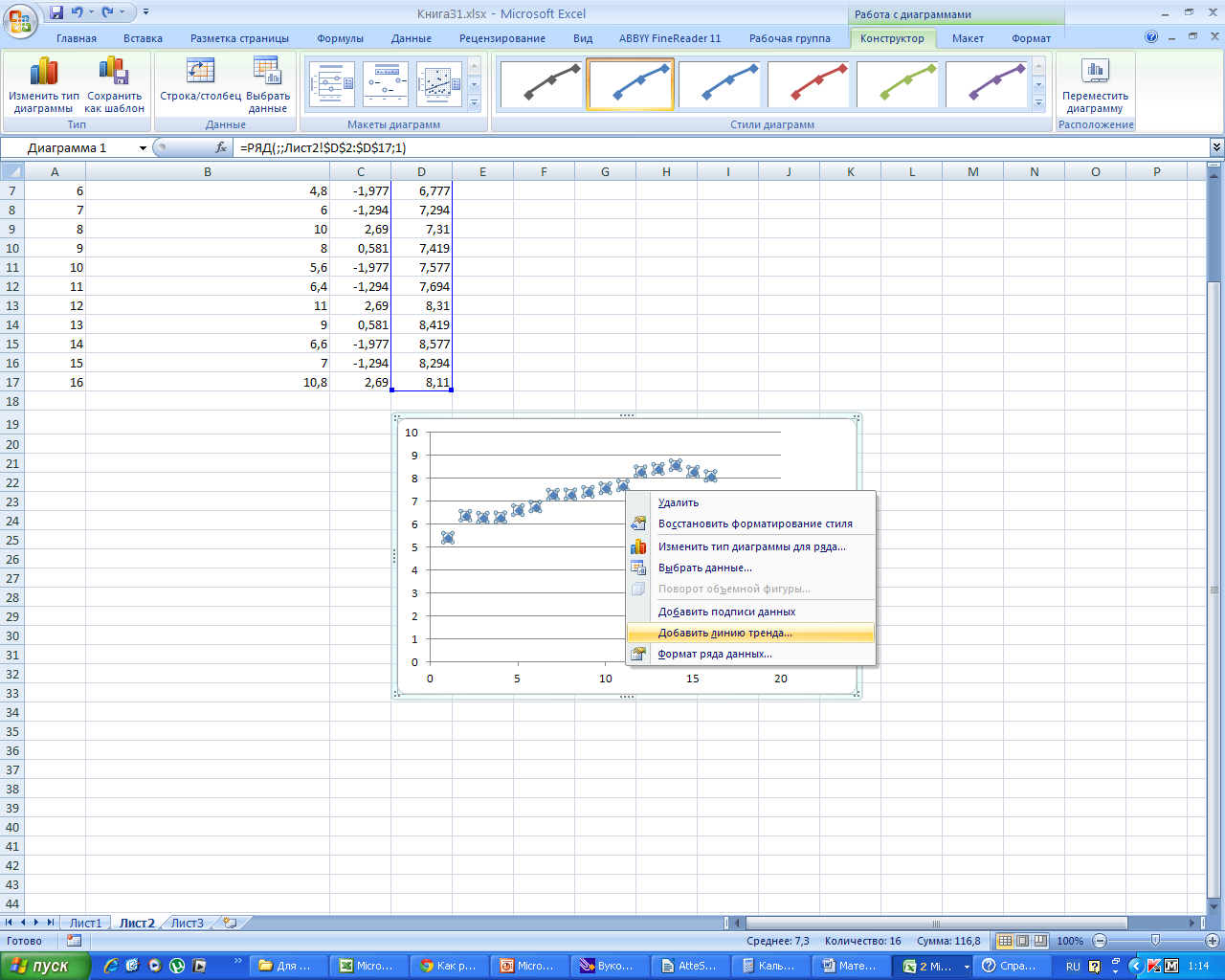
Пошагово
выбираем ту линию тренда, где наибольшее
значение имеет R2.
Для
этого ставим курсор на точки поля
корреляции и выбираем тренд, расставляя
галочки в окна, «показать уравнение на
диаграмме» и «поместить на диаграмму
величину достоверности аппроксимации».
-
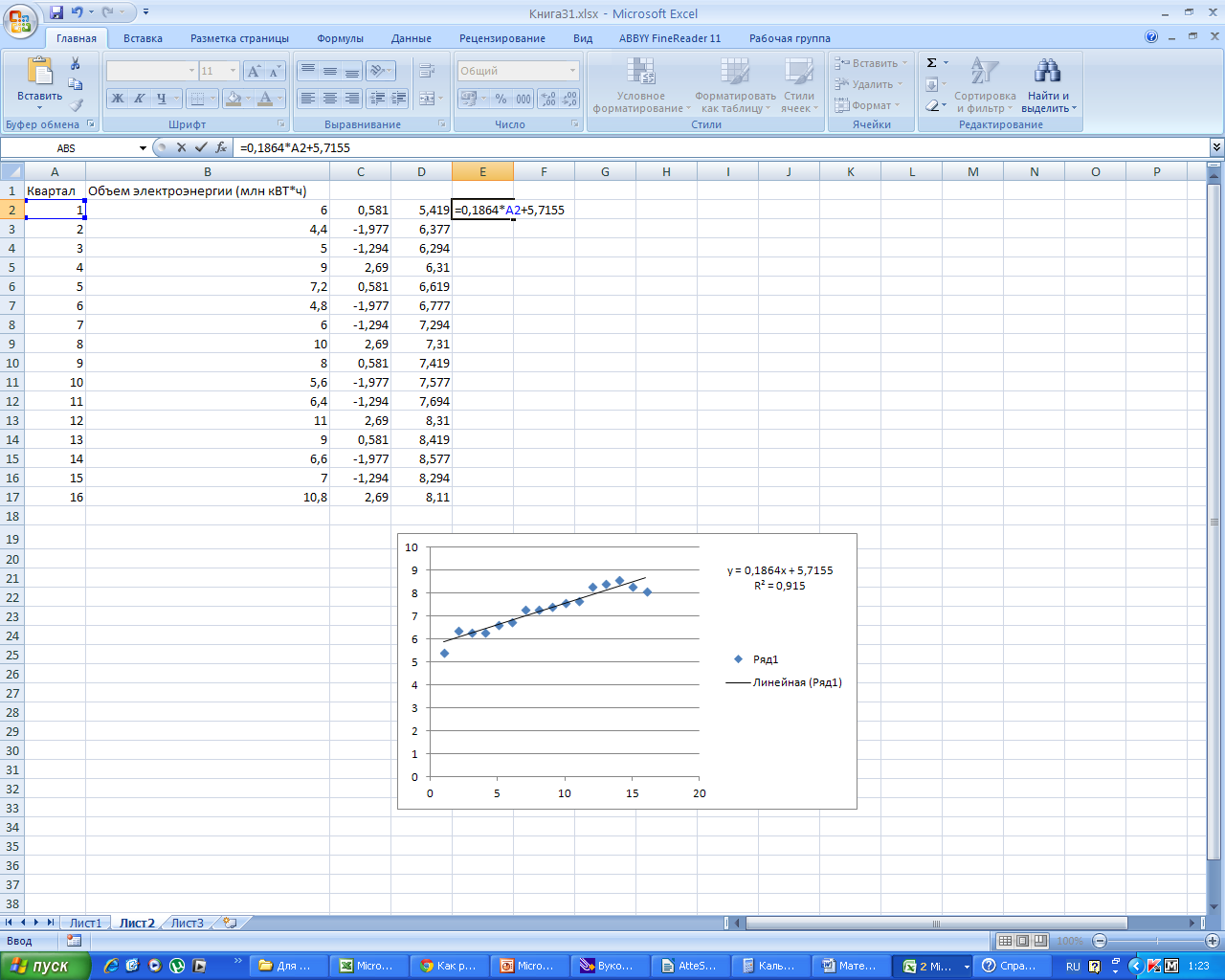
В
столбец Е вбиваем формулу для уравнения
тренда y=
0, 1864x
+ 5, 7155 и получаем расчетные значения
для тренда.
-
Заполним
столбец F,
как сумму C
и Е, и найдем ошибку аппроксимации.
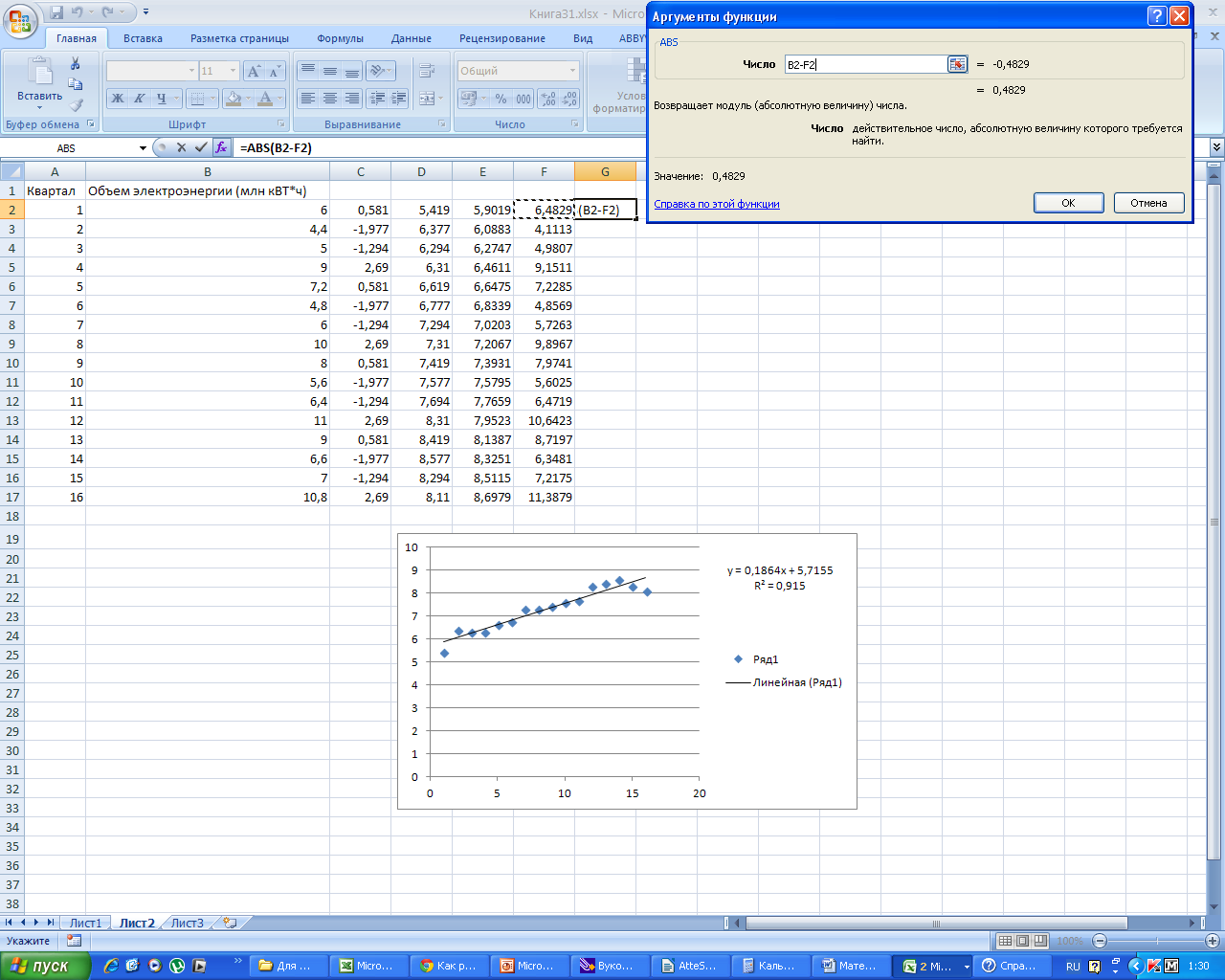
Для
нахождения ошибки аппроксимации заполним
столбец G.
Для этого в столбец G
вставляем формулу
Получаем
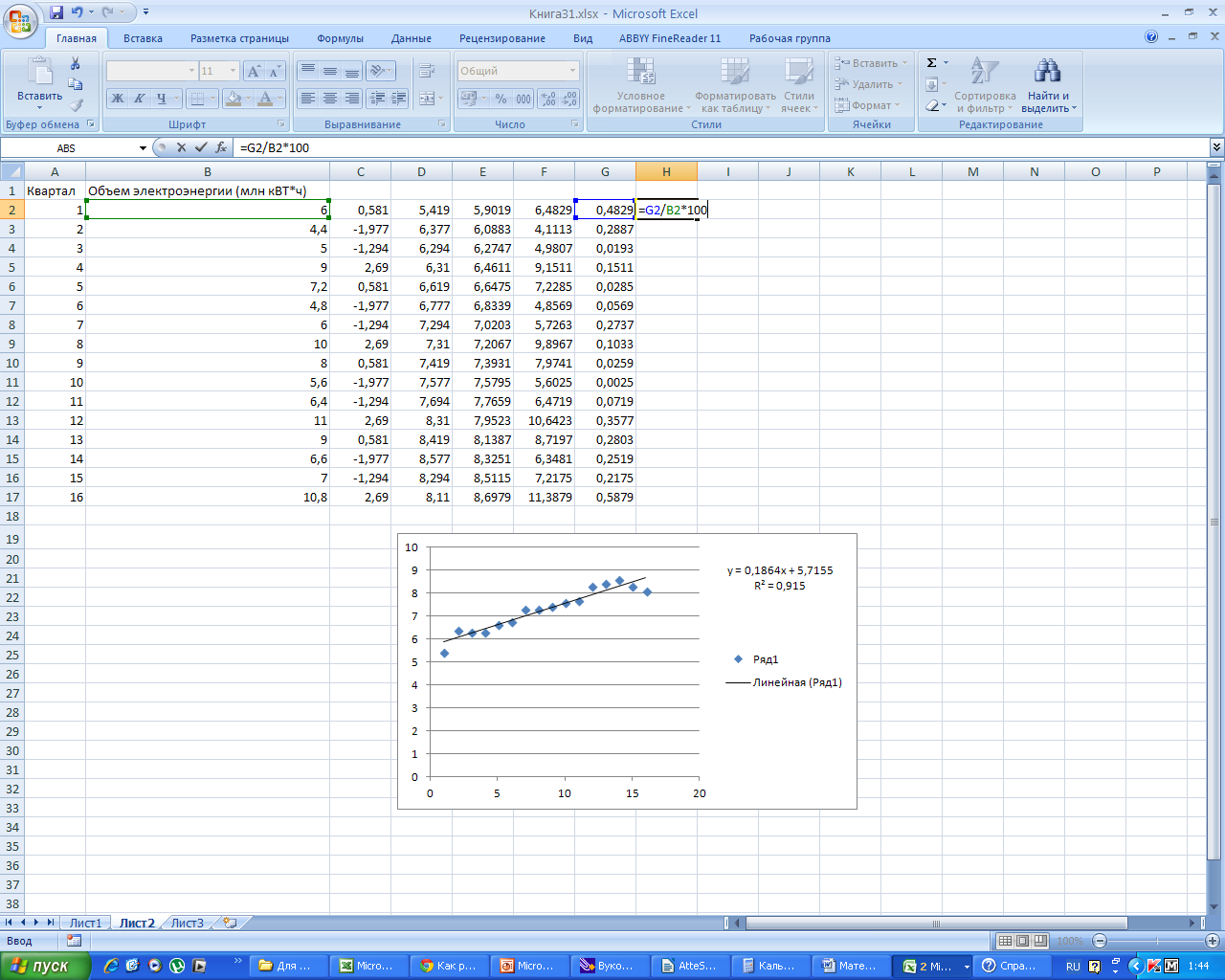
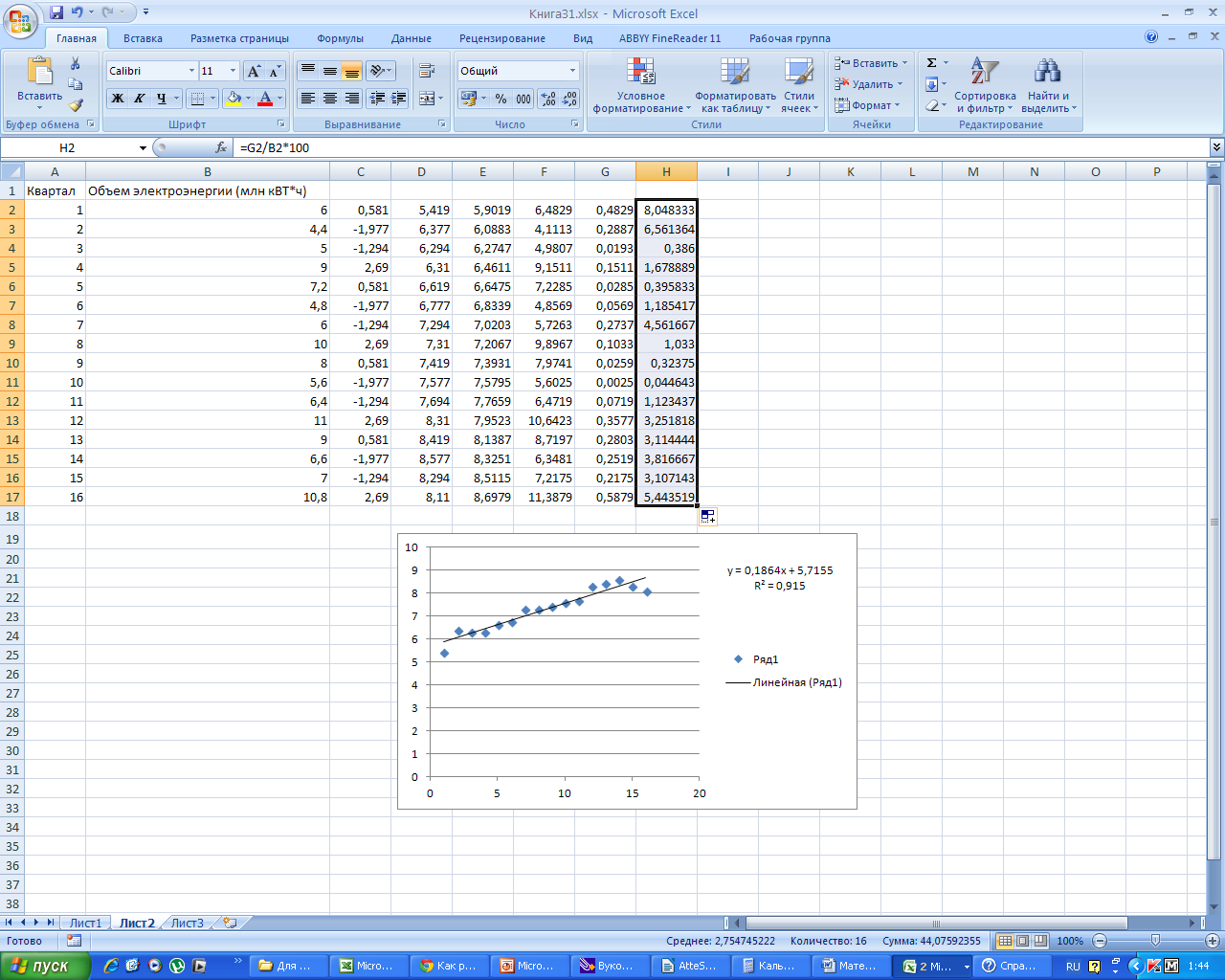
Найдем
среднюю ошибку аппроксимации, заполнив
столбец Н. Для этого разделим G
на В и умножим на 100%.
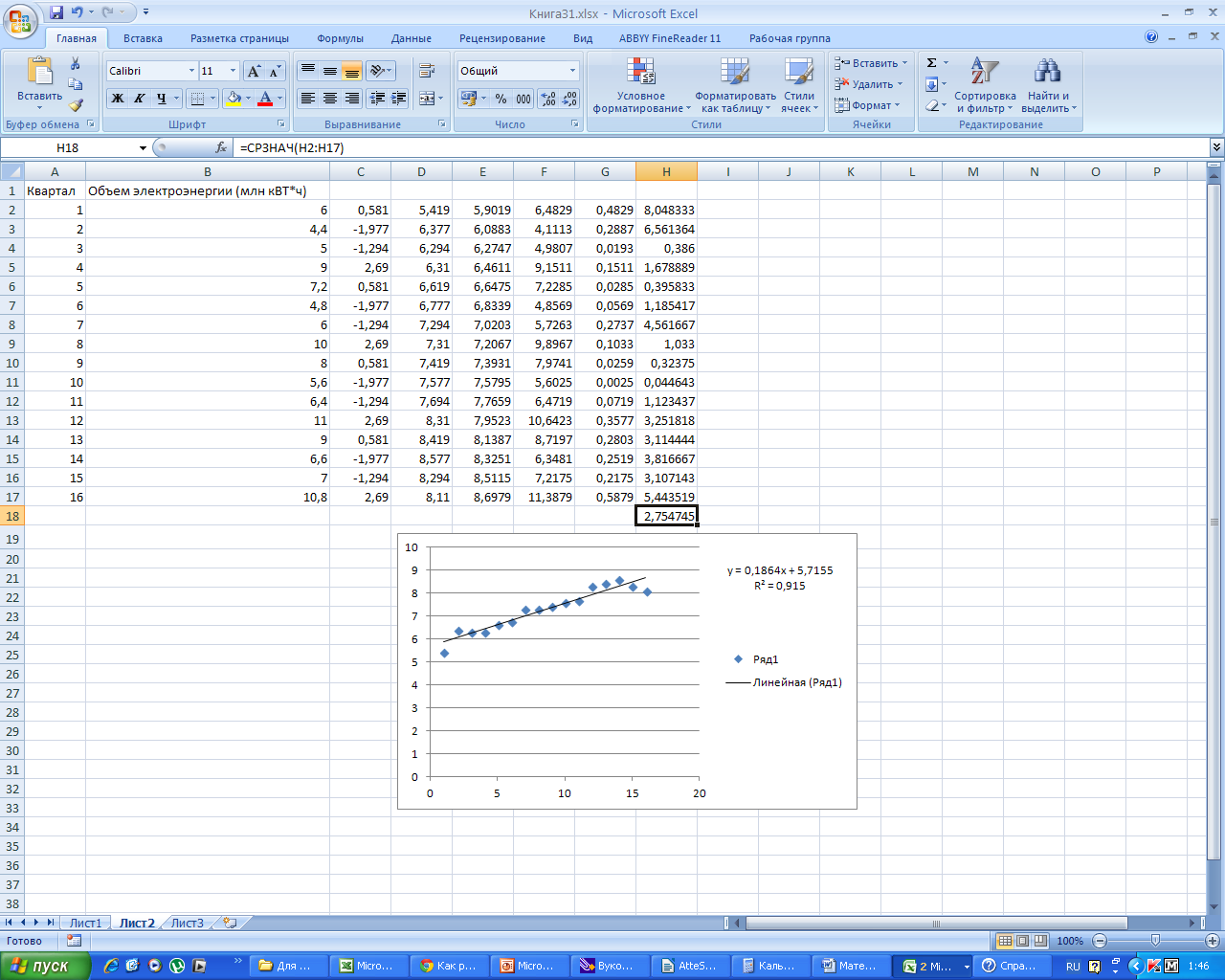
Таким
образом, заметим, что R2
= 0,915
0,75, средняя ошибка аппроксимации равна
2,75%< 3%. Значит, данная модель является
надежной.
Спрогнозируем
значения потребляемой электроэнергии
на следующий квартал. Для этого
воспользуемся вновь электронной
таблицей.
Заметим,
что полученное число 8,8843
млн. кВт/ч.
практически не отличается от полученного
ранее значения млн.
кВт/ч.
Приложение
2.
Соседние файлы в папке pravila
- #
- #
- #
- #
Аннотация:
Цель работы: научиться выполнять прогнозирование временного ряда данных с помощью средств Microsoft Excel и математически.
Содержание работы:
Анализ временных рядов.
Прогноз, характеристики и параметры прогнозирования.
Уравнение тренда временного ряда.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания с использованием средств MS Excel.
Оформить отчет, сделав выводы по заданиям.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Анализ временных рядов
Временной ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней: ряды абсолютных показателей, относительных показателей, средних величин;
- по количеству показателей, когда определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды. Временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины;
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Прогноз, характеристики и параметры прогнозирования
Прогноз (от греч. 
Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса.
Прогнозы делятся:
- по срокам: краткосрочные, среднесрочные, долгосрочные;
- по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, мировые (глобальные).
К основным методам прогнозирования относятся:
- статистические методы;
- экспертные оценки (метод Дельфи);
- моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний. Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
Прием прогнозирования – одна или несколько математических или логических операций, направленных на получение конкретного результата в процессе разработки прогноза. В качестве приема могут выступать сглаживание динамического ряда, определение компетентности эксперта, вычисление средневзвешенного значения оценок экспертов и т. д.
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования.
Методика прогнозирования – совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозирующая система – система методов и средств их реализации, функционирующая в соответствии с основными принципами прогнозирования. Средствами реализации являются экспертная группа, совокупность программ и т. д. Прогнозирующие системы могут быть автоматизированными и неавтоматизированными.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов.
Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз.
Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования.
Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Источник ошибки прогноза – фактор, способный привести к появлению ошибки прогноза. Различают источники регулярных и нерегулярных ошибок.
Верификация прогноза – оценка достоверности и точности или обоснованности прогноза.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений.
Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах.
Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия. Разработаны параметрические (обычно на основе модели нормальных ошибок) и непараметрические оценки точности прогноза и доверительные границы для него (на основе Центральной Предельной Теоремы теории вероятностей). Применяются также эвристические приемы, не основанные на вероятностно-статистической теории: метод скользящих средних, метод экспоненциального сглаживания.
Многомерная регрессия, в том числе с использованием непараметрических оценок плотности распределения – основной на настоящий момент статистический аппарат прогнозирования. Нереалистическое предположение о нормальности погрешностей измерений и отклонений от линии (поверхности) регрессии использовать не обязательно; однако для отказа от предположения нормальности необходимо опереться на иной математический аппарат, основанный на многомерной Центральной Предельной Теореме теории вероятностей, технологии линеаризации и наследования сходимости. Он позволяет проводить точечное и интервальное оценивание параметров, проверять значимость их отличия от 0 в непараметрической постановке, строить доверительные границы для прогноза.
Уравнение тренда временного ряда
Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз).
Значения временного ряда можно представить в виде: 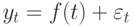

Неслучайная функция f(t) называется трендом. Тренд отражает характерное изменение (тенденцию) yt за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами (t, yt) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие.
Уравнение тренда линейного вида будем искать в виде yt=f(t), где f(t) = a0+a1(t).
Пример 1. Имеется временной ряд:
| ti | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xti | 2 | 1 | 4 | 4 | 6 | 8 | 7 | 9 | 12 | 11 |
Построим график xti во времени. Добавим на графике линию тренда исходных значений ряда. При этом, щелкнув правой кнопкой мыши по линии тренда, можно вызвать контекстное меню «Формат линии тренда», а в нем поставить флажок «показывать уравнение на диаграмме», тогда на диаграмме высветится уравнение линии тренда, вычисленное встроенными возможностями Excel.
Рис.
14.1.
Чтобы определить уравнение тренда, необходимо найти значения коэффициентов а0 и а1. Эти коэффициенты следует определять, исходя из условия минимального отклонения значений функции f(t) в точках ti от значений исходного временного ряда в тех же точках ti. Это условие можно записать в виде (на основе метода наименьших квадратов):
где n – количество значений временного ряда.
Для того, чтобы найти значения а0 и а1, необходимо иметь систему из двух уравнений. Эти уравнения можно получить, используя условие равенства нулю производной функции в точках её экстремума. В нашем случае эта функция имеет вид ![$sumlimits_{t=1}^{n}[x_{t}-a_{0}-a_{1}t]^{2}$](https://intuit.ru/sites/default/files/tex_cache/af521da64ce9abdab75d7f160f5c9bb4.png)
Полученная система может быть преобразована (математически) в систему так называемых нормальных уравнений. При этом уравнения примут вид:
Теперь необходимо решить преобразованную систему уравнений относительно а0 и а1. Однако предварительно следует составить и заполнить вспомогательную таблицу:
Подставив значения n = 10 в систему уравнений (2), получим
Решив систему уравнений относительно а0 и а1, получим а0 = -0,035, а1 = 1,17. Тогда функция тренда заданного временного ряда f(t) имеет вид:
f(t) = -0,035 + 1,17t.
Изобразим полученную функцию на графике.
Рис.
14.2.
Задание 1.
Временной ряд приведен в таблице. Используя средства MS Excel:
- построить график временного ряда;
- добавить линию тренда и ее уравнение;
- найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
- построить график временного ряда и полученной функции тренда в одной системе координат.
Варианты.
1. Реализация аспирина по аптеке (у.е.) за последние 7 недель приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 3,2 | 3,3 | 2,9 | 2,2 | 1,6 | 1,5 | 1,2 |
2. Динамика потребления молочных продуктов (у.е.) по району за последние 7 месяцев:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 30 | 29 | 27 | 24 | 25 | 24 | 23 |
3. Динамика числа работников, занятых в одной из торговых сетей города за последние 8 лет приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 280 | 361 | 384 | 452 | 433 | 401 | 512 | 497 |
4. Динамика потребления сульфаниламидных препаратов в клинике по годам (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 14 | 21 | 29 | 33 | 38 | 44 | 46 | 50 |
5. Динамика продаж однокомнатных квартир в городе за последние 8 лет (тыс. ед.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| уt | 39 | 40 | 36 | 34 | 36 | 37 | 33 | 35 |
6. Динамика потребления антибиотиков в клинике (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 10 | 17 | 18 | 13 | 17 | 21 | 25 | 29 |
7. Динамика производства хлебобулочных изделий на хлебозаводе (тонн):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 510 | 502 | 564 | 680 | 523 | 642 | 728 | 665 |
8. Динамика потребления противовирусных препаратов по аптечной сети в начале эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 36 | 42 | 34 | 38 | 12 | 32 | 26 | 20 |
9. Динамика потребления противовирусных препаратов по аптечной сети в конце эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 46 | 52 | 44 | 48 | 32 | 42 | 36 | 30 |
10. Динамика потребления витаминов по аптечной сети в весенний период (с марта по апрель) в разные годы (у.е.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 0,9 | 1,7 | 1,5 | 1,7 | 1,5 | 2,1 | 2,5 | 3,6 |
Пример 2. Используя данные примера 1, приведенного выше, вычислить точечный прогноз исходного временного ряда на 5 шагов вперед.
Исходя из условия задачи, необходимо определить точечную оценку прогноза для t = 11, 12, 13, 14, 15, где t в данном случае – шаг упреждения.
Решение.
Рассмотрим решение этой задачи средствами Microsoft Excel. При решении данной задачи следует так же, как и в примере 1, ввести исходные данные. Выделив данные, построить точечный график, щелкнув правой кнопкой мыши по ряду данных, вызвать контекстное меню и выбрать «Добавить линию тренда».
Щелкнув правой кнопкой мыши по линии тренда, вызвать контекстное меню, выбрать «Формат линии тренда», в окне Параметры линии тренда указать прогноз на 5 периодов и поставить флажок в окошке «Показывать уравнение на диаграмме (рис. 14.3
рис.
14.3.). В версии Excel ранее 2007 окно диалога представлено на рисунке 14.4
рис.
14.4.
Рис.
14.3.
Задание параметров тренда в MS Excel 2007
Рис.
14.4.
Задание параметров тренда в версии ранее MS Excel 2007
Итоговый график представлен на рисунке 14.5
рис.
14.5.
Рис.
14.5.
Значения прогноза для 11, 12, 13, 14 и 15 уровней получим, используя функцию ПРЕДСКАЗ( ). Данная функция позволяет получить значения прогноза линейного тренда. Вычисленные значения: 12,87, 14,04, 15,22, 16,39, 17,57.
Значения точечного прогноза для исходного временного ряда на 5 шагов вперед можно вычислить и с помощью уравнения функции тренда f(t), найденного по методу наименьших квадратов. Для этого в полученное для f(t) выражение необходимо подставить значения t = 11, 12, 13, 14, 15. В результате получим (эти значения следует рассчитать, сформировав формулу в табличном процессоре MS Excel):
Сравнивая результаты точечных прогнозных оценок, полученных разными способами, выявляем, что данные отличаются незначительно, таким образом, в любом из способов расчета присутствует определенная погрешность (ошибка) прогноза (
Задание 2.
Используя значения временного ряда Задания 1 согласно вашего варианта, вычислить точечный прогноз на 4 шага вперед. Продлить линию тренда на 4 прогнозных значения, вывести уравнение тренда, определить эти значения с помощью функции ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(), а также по выражению функции тренда f(t), полученному по методу наименьших квадратов в Задании 1. Сравнить полученные результаты.
В прошлой статье мы уже разобрали, что такое временной ряд и функцию тренда. Теперь подробнее разберемся с терминологией и остановимся на одной из моделей временного ряда.
Из чего состоит временной ряд
Уровни временного ряда (Yt) представляют из себя сумму двух компонент:
- Регулярную составляющую
- Случайную составляющую
В свою очередь регулярная составляющая состоит из:
- Тренда
- Сезонности
- Циклической составляющей
Однако, в модели необязательно наличие всех этих компонент сразу.
Случайная компонента отражает влияние случайных возмущений на модель, которые по отдельности имеют незначительное воздействие, но суммарно их влияние ощущается.
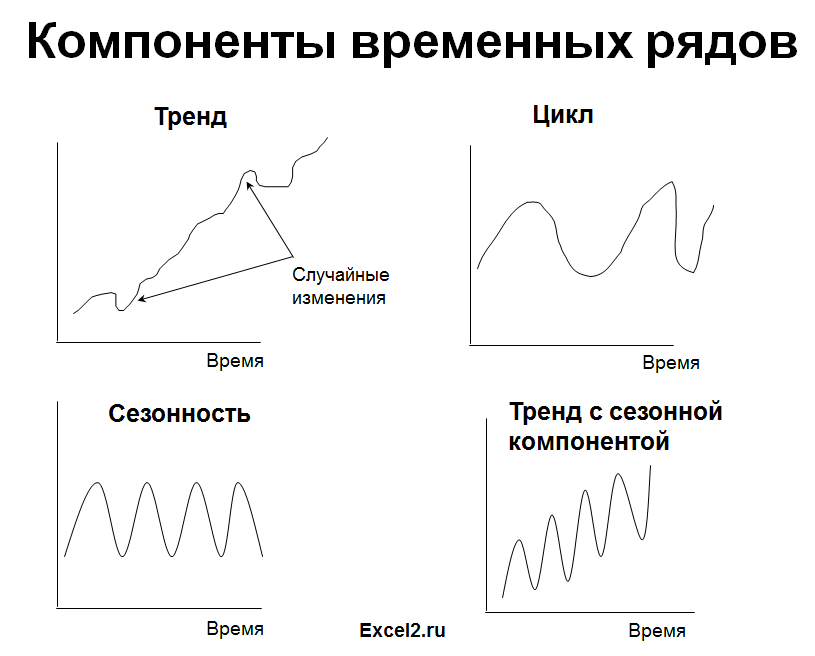
То есть, в общем случае временной ряд представляет из себя наличие четырех составляющих:
- Тренд (Tt)
- Сезонность (St)
- Цикличность (Ct)
- Случайные возмущения (Et)
Циклическая компонента, по сравнению с сезонностью, имеет более длительный эффект и меняется от цикла к циклу. Поэтому, ее обычно объединяют с трендом.
Виды моделей временного ряда
Обычно, выделяют две модели временного ряда и третью — смешанную.
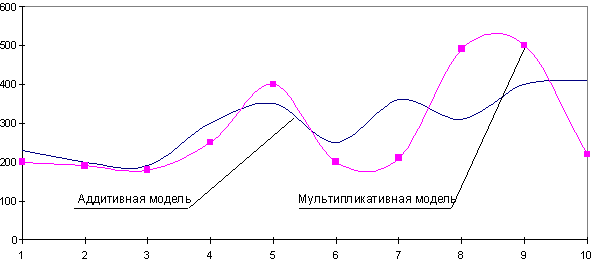
- Аддитивная модель
-
Мультипликативная модель
-
Смешанная модель
При выборе необходимой модели временного ряда смотрят на амплитуду колебаний сезонной составляющей. Если ее колебания относительно постоянны, то выбирают аддитивную модель. То есть, амплитуда колебаний примерно одинакова:
Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение этих моделей сводится к расчету тренда (Tt), сезонности (St) и случайных возмущений (Et) для каждого уровня ряда (Yt).
Алгоритм построения модели
- Выравниваем ряд с помощью скользящей средней, то есть сглаживаем ряд и отфильтровываем высокочастотные колебания.
- Рассчитываем значение сезонной компоненты St.
- Рассчитываем значения Tt с использованием полученного уравнения тренда.
- Используя полученные значения St и Tt, находим прогнозные значения уровней временного ряда.
- Оцениваем качество модели.
Реализация на практике
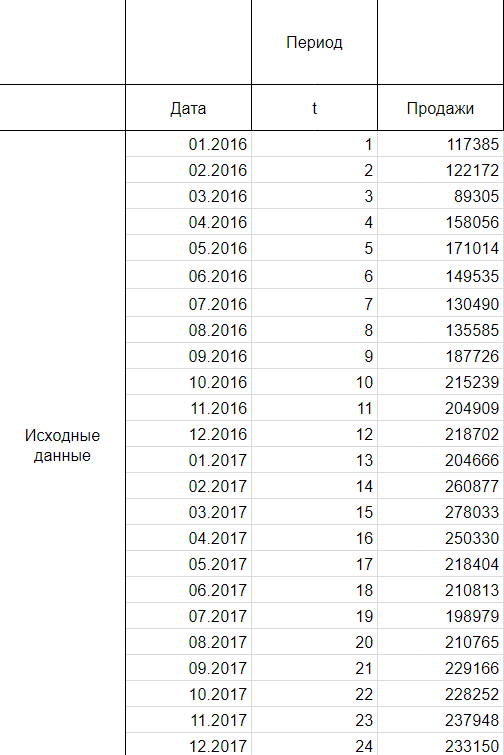
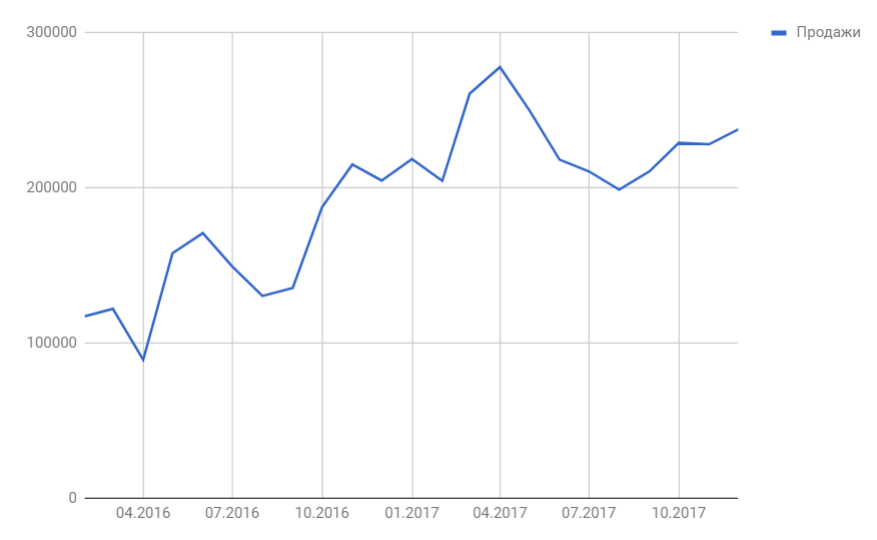
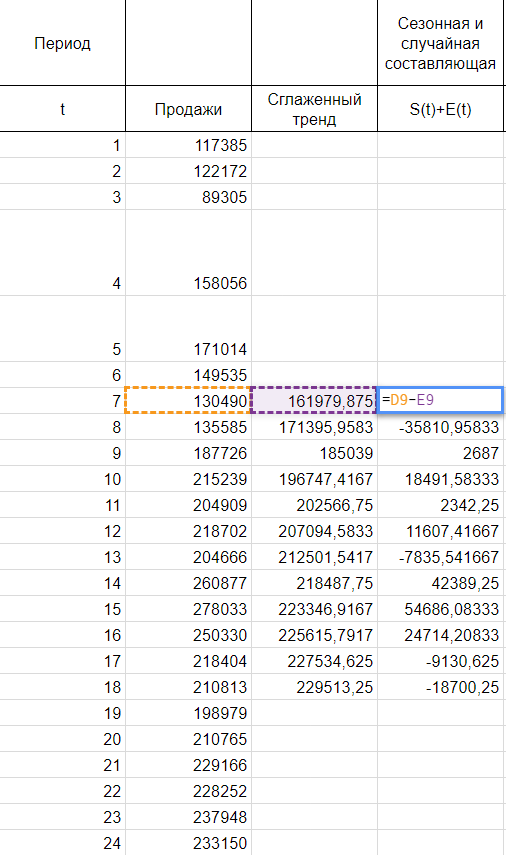
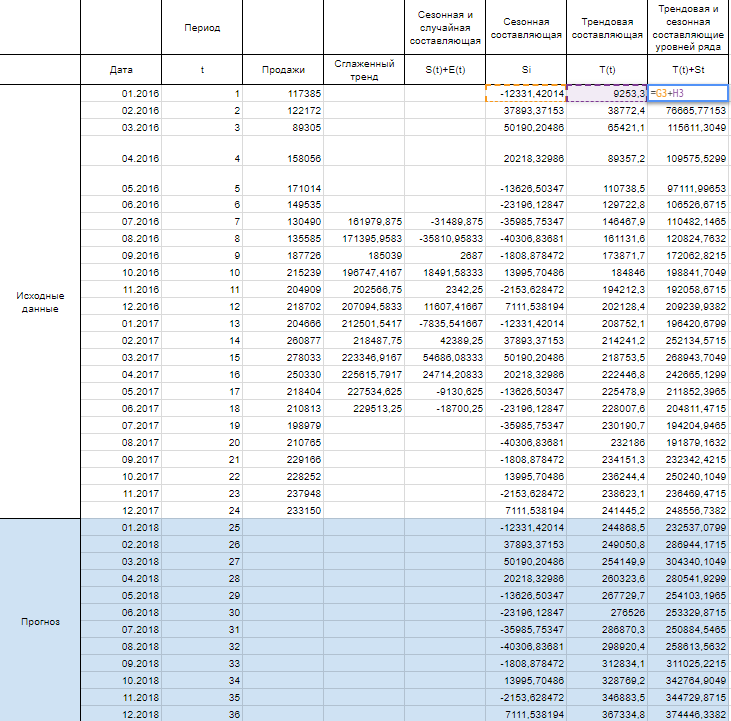
Итак, мы имеем на руках данные о продажах за 2016 и 2017 год и хотим спрогнозировать продажи на 2018 год.
Шаг 1
Следуя нашему алгоритму, мы должны сгладить временной ряд. Воспользуемся методом скользящей средней. Видим, что в каждом году есть большие пики (май-июнь 2016 и апрель 2017), поэтому возьмем период сглаживания пошире, например, месячную динамику, т.е. 12 месяцев.
Удобнее брать период сглаживания в виде нечетного числа, тогда формула для расчета уровней сглаженного ряда:
yi — фактическое значение i-го уровня ряда,
yt — значение скользящей средней в момент времени t,
2p+1 — длина интервала сглаживания.
Но так как мы решили использовать месячную динамику в виде четного числа 12, то данная формула нам не подойдет и мы воспользуемся этой:
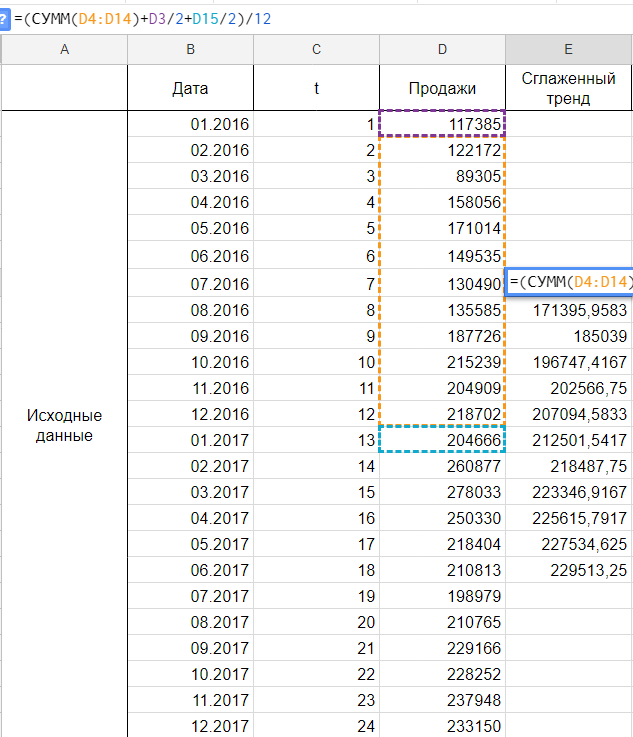
Иными словами, мы учитываем половины от крайних уровней ряда в диапазоне, в остальном формула не претерпела больше никаких изменений. Вот ее точный вид для нашей задачи:
Сглаживаем наши уровни ряда и растягиваем формулу вниз:
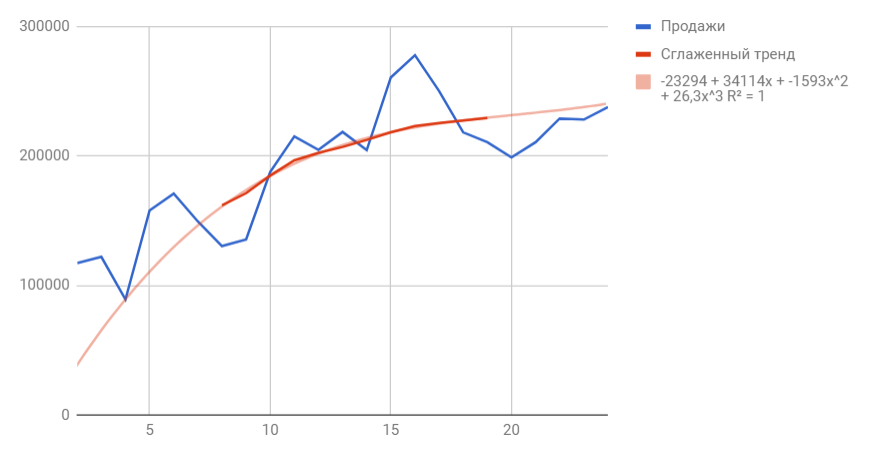
Сразу можем построить график из известных значений уровня продаж и их сглаженной. Выведем ее уравнение и значение коэффициента детерминации R^2:
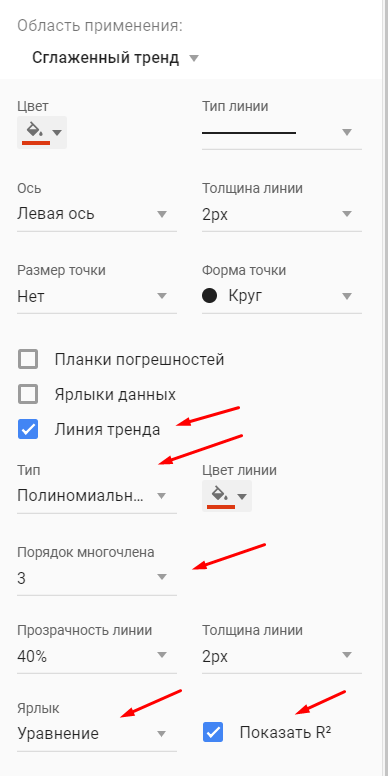
В качестве сглаженной я выбрала полином третьей степени, так как он лучше всего описывал уровни временного ряда и имел наибольший R^2.
Шаг 2
Так как мы рассматриваем аддитивную модель вида:
Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, так как Yt и Tt мы уже знаем.
Используем оценки сезонной компоненты (St+Et) для расчета значений сезонной компоненты St. Для этого найдем средние за каждый интервал (по всем годам) оценки сезонной компоненты St.
Средняя оценка сезонной компоненты находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строках без пересечений, поэтому сумма по столбцам состоит из одиночных значений, следовательно и среднее будет таким же. Если бы мы располагали периодом побольше, например с 2015, у нас бы добавилась еще одна строка и мы смогли бы полноценно найти среднее, поделив сумму на 2.
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем интервалам должна быть равна нулю. Поэтому найдя значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.
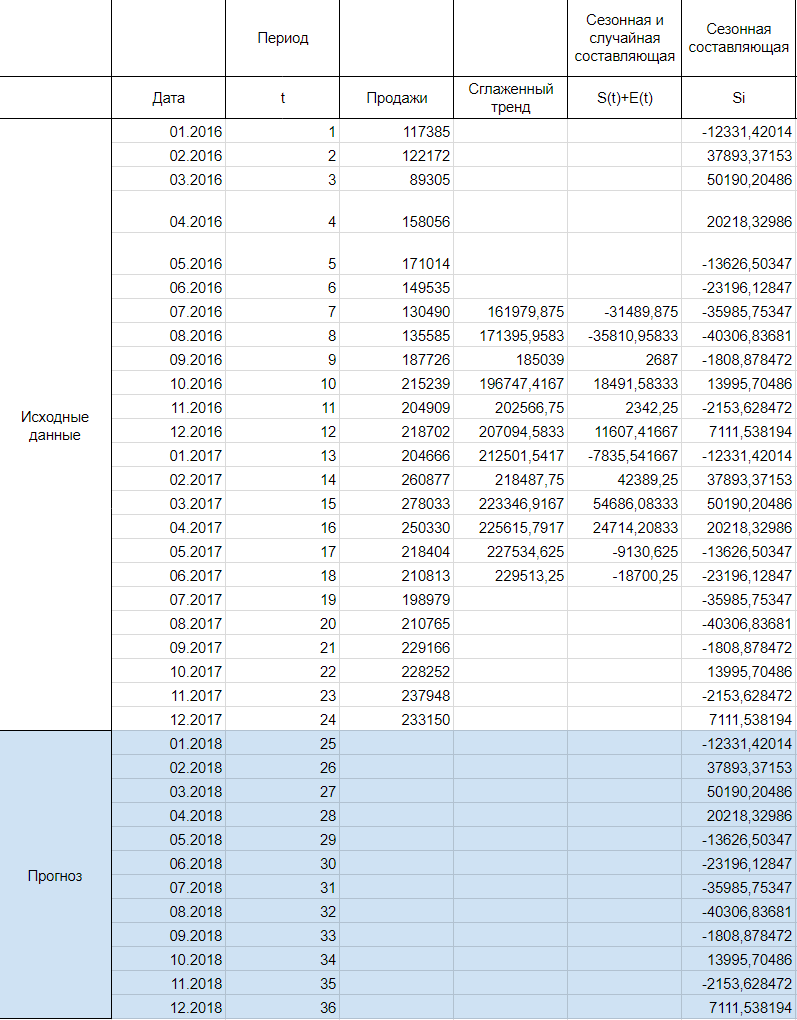
Далее, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд каждые 12 месяцев, то есть три раза:
Шаг 3
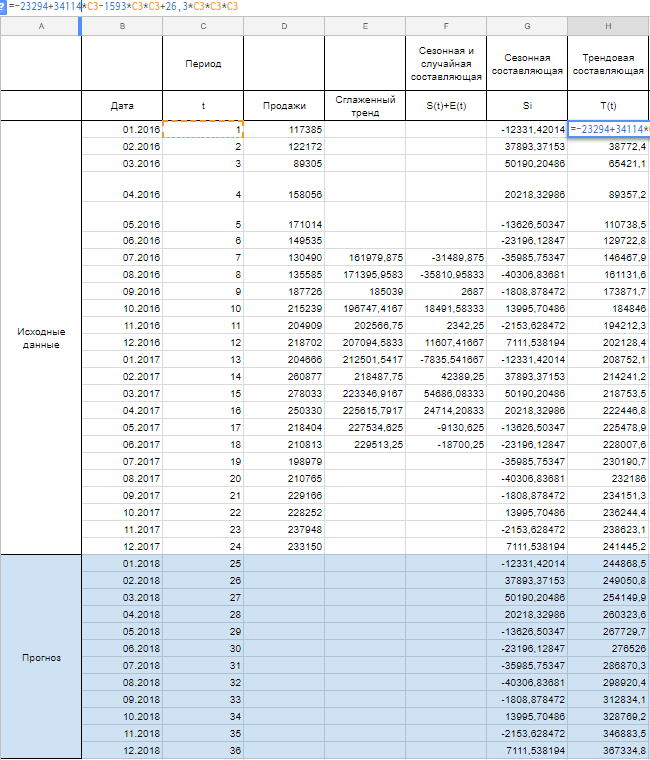
Теперь рассчитываем значения уровня тренда T(t) по тому уравнению, которое мы получили при построении сглаженного тренда на первом шаге.
T(t) = -23294+34114*t-1593*t^2+26,3*t^3
Вместо t используем значения из столбца Период из соответствующей строки.
Шаг 4
Имея рассчитанные значения S(t) и T(t) мы можем рассчитать прогнозные значения уровней ряда Y(t). Для этого накладываем уровни сезонности на тренд.
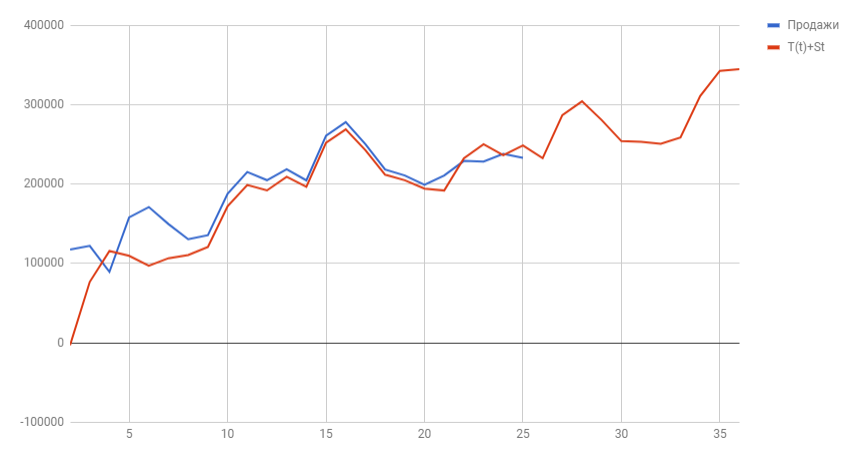
Теперь построим график известных значений Y(t) и спрогнозированных за 2018 год.
Вот мы и нашли спрогнозированные значения уровней продаж на 2018 год. Значения отражают возрастающую тенденцию и сезонные пики. Конечно, эти данные не дают 100% точности, ведь существует множество внешних воздействий, которые могут изменить направление тренда, поэтому к прогнозным значениям обычно строят доверительный интервал, это такой коридор, внутри которого могут колебаться прогнозные значения с заданной вероятностью (чаще всего выбирают 95%). Но об этом я расскажу в следующей статье.
Шаг 5
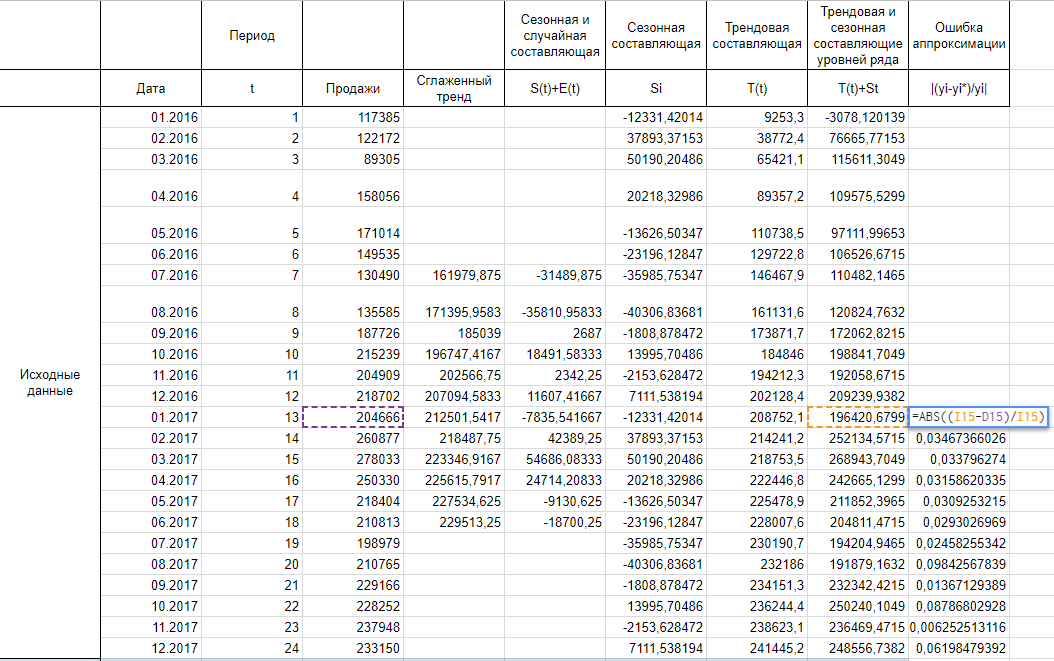
Осталось оценить точность модели. Для этого будем использовать среднюю ошибку аппроксимации, которая поможет рассчитать ошибку в относительном выражении. Иными словами, это среднее отклонение расчетных значений от фактических, которое вычисляется по формуле:
yi — спрогнозированные уровни ряда,
yi* — фактические уровни ряда,
n — количество складываемых элементов.
Модель может считаться адекватной, если:
Итак, рассчитываем ошибку аппроксимации для нашего случая. Так как в основе нашего тренда лежит полином третьей степени, прогнозные значения начинают хорошо повторять фактические значения к концу 2016 года, думаю, я думаю, поэтому корректнее было бы рассчитать ошибку аппроксимации для значений 2017 года.
Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем сделать вывод об адекватности модели.
Не забывайте, что прогнозы не бывают точными на 100%. Любые неожиданные внешние воздействия могут развернуть значения уровней ряда в неизвестном направлении 🙂
Полезные ссылки:
- Ссылка на пример Google Sheets
- Построение функции тренда в Excel. Быстрый прогноз без учета сезонности
- Бывшев В.А. Эконометрика
- Об авторе
- Свежие записи

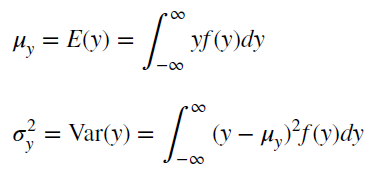
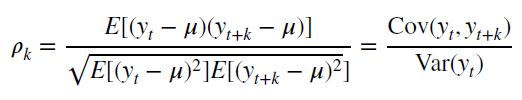












![$$sumlimits_{t=1}^{n}[x_{t}-a_{0}-a_{1}t]^{2}rightarrow mineqno(1)$$](https://intuit.ru/sites/default/files/tex_cache/56404890c825202167c4ba34001e2250.png)