Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
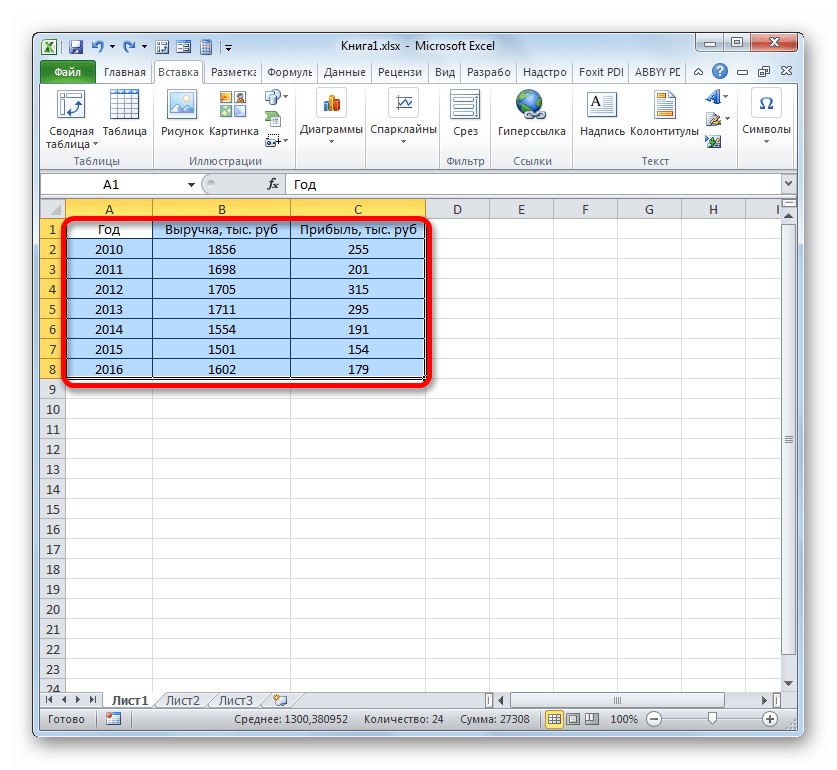
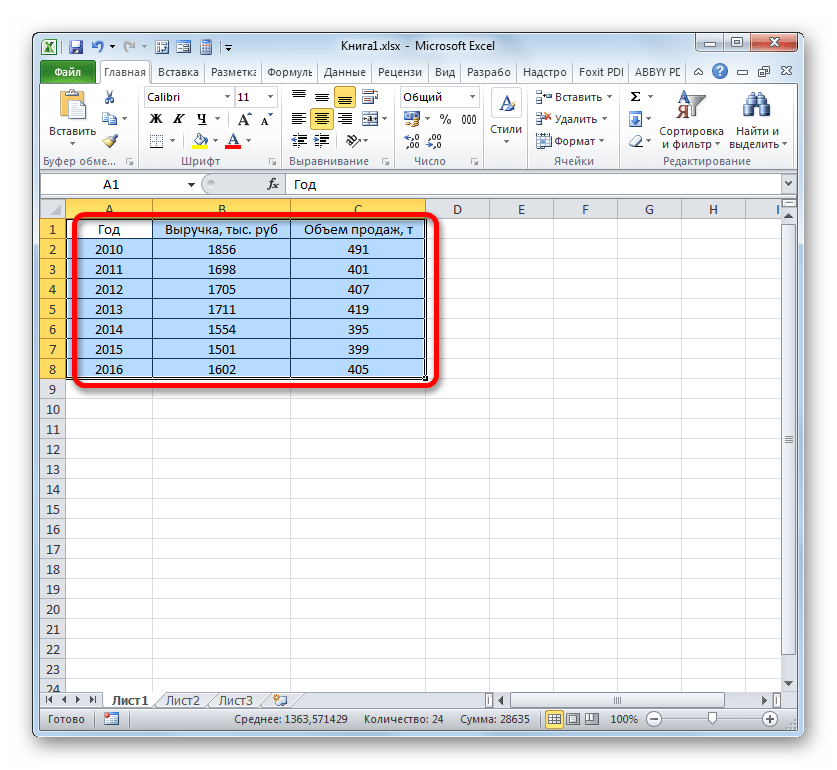
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
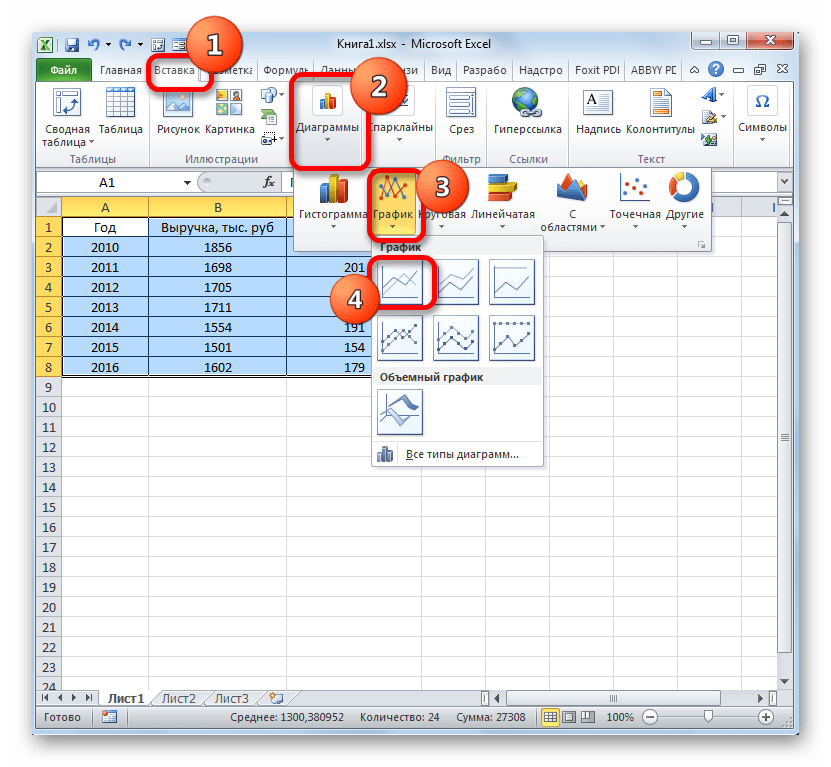
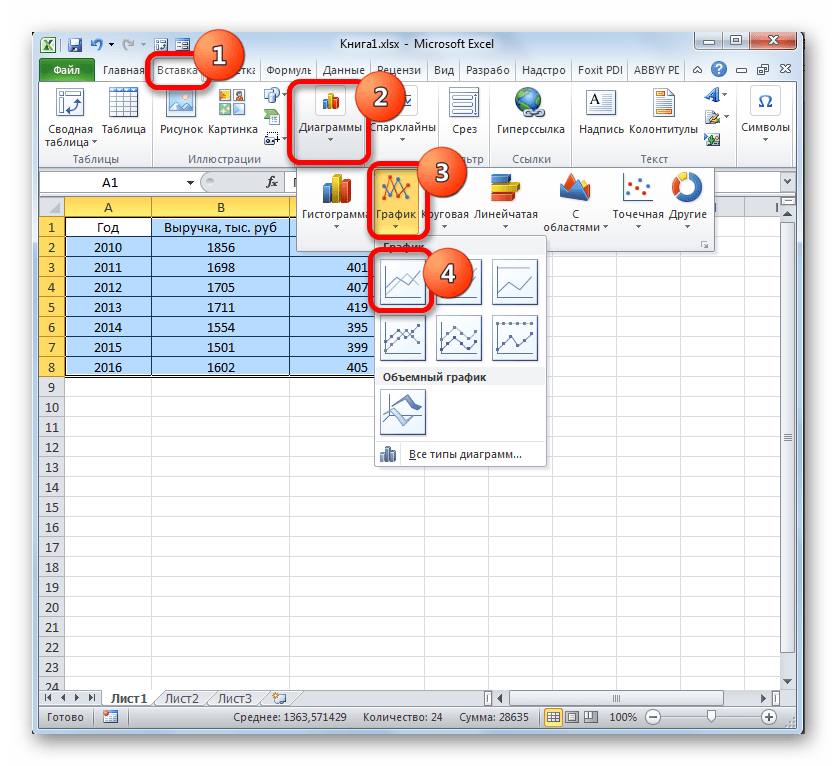
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
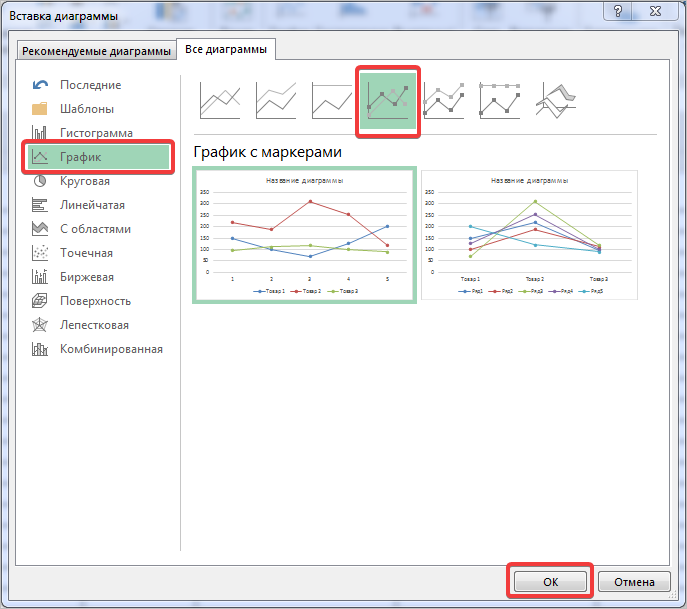
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
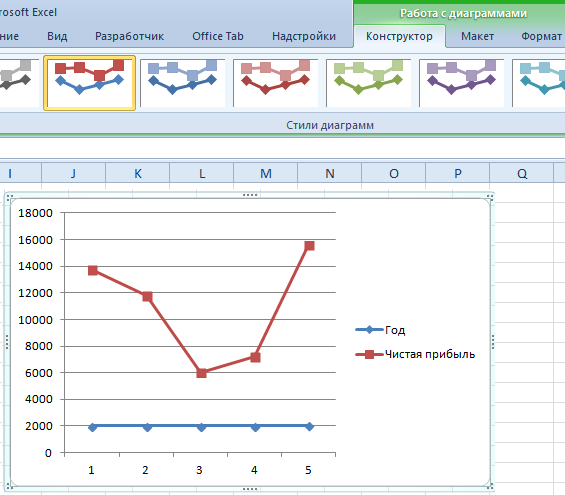
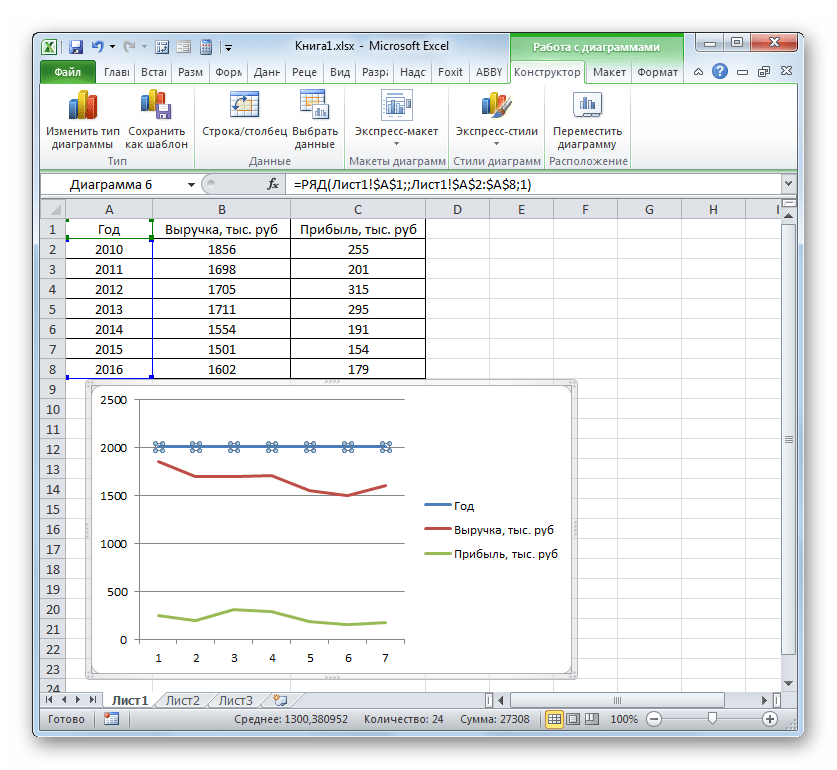
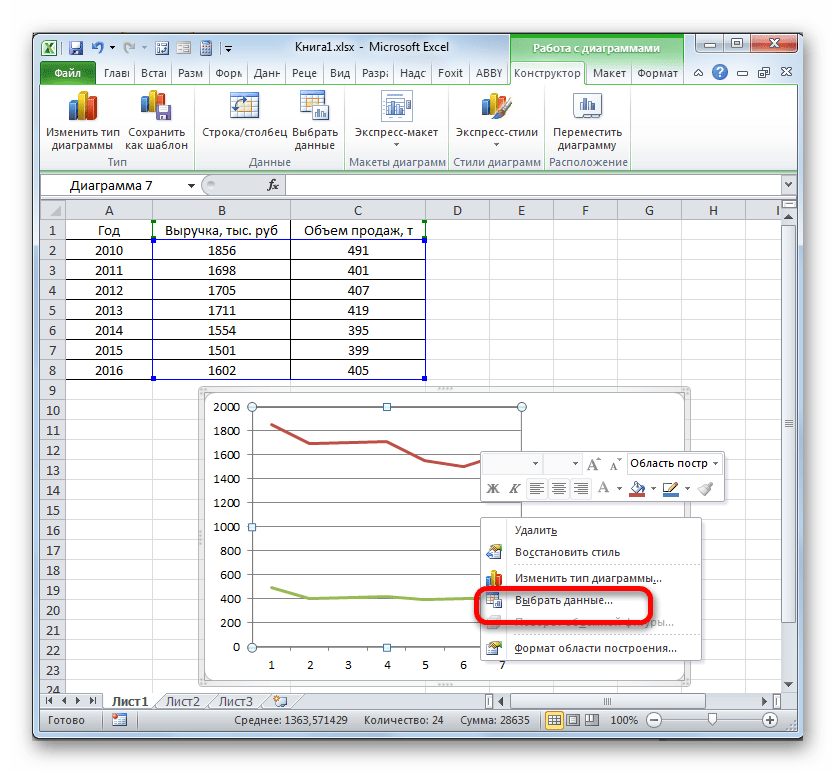
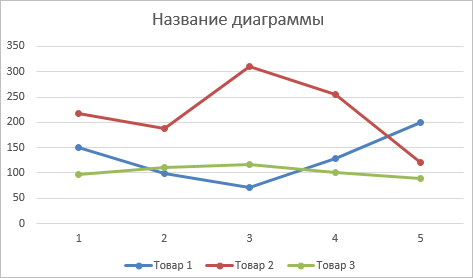
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
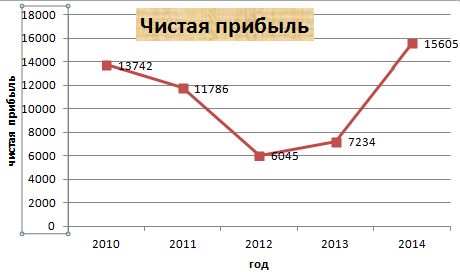
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
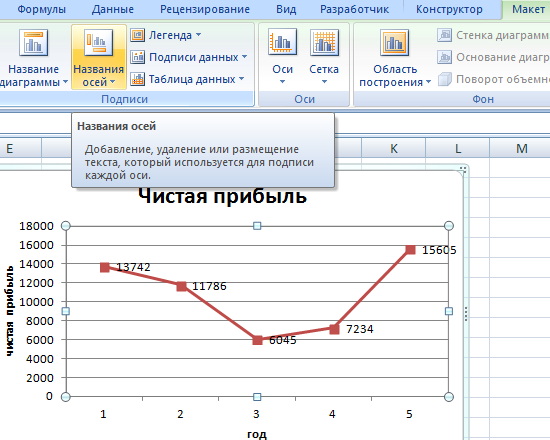
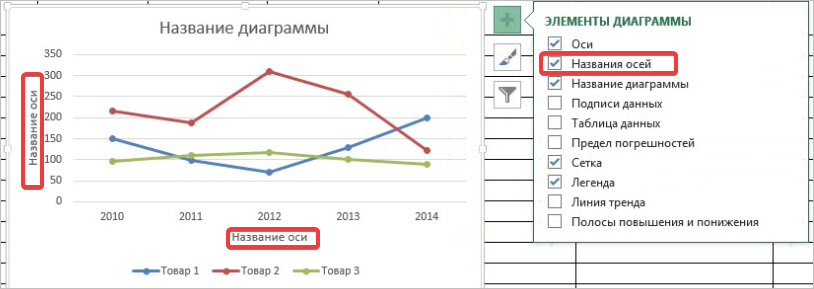
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
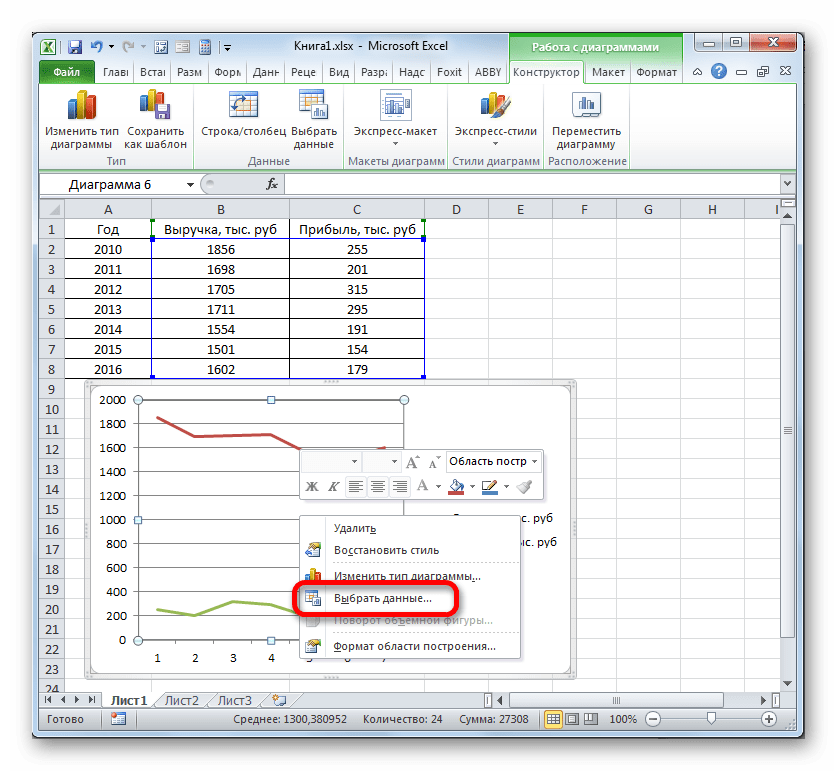
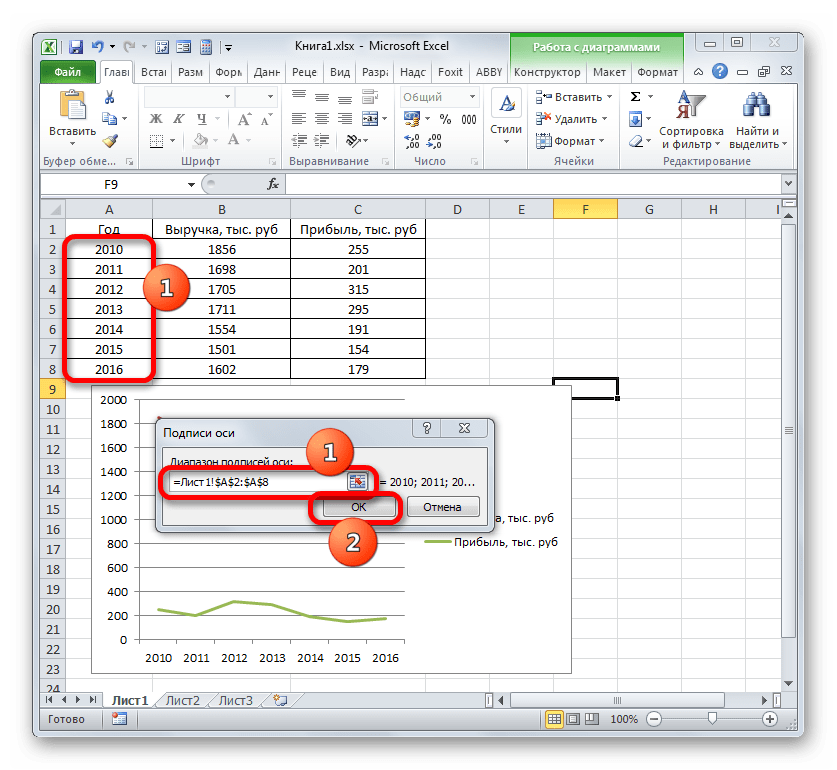
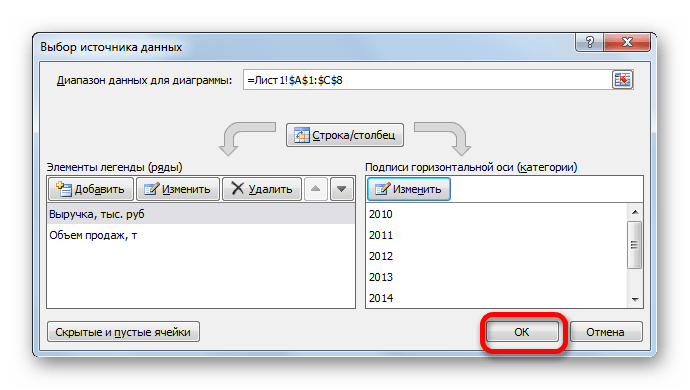
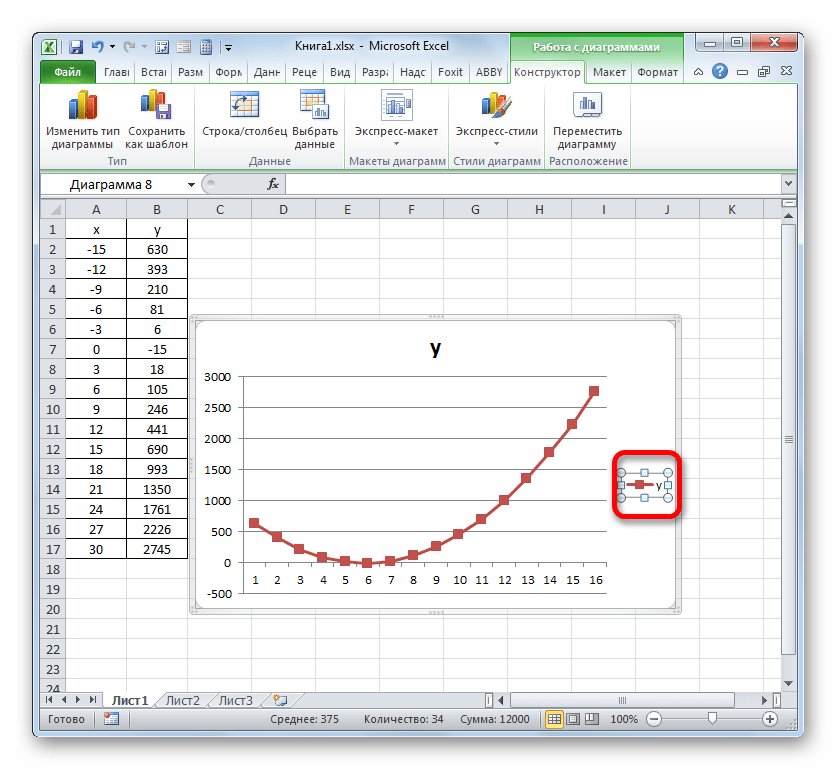
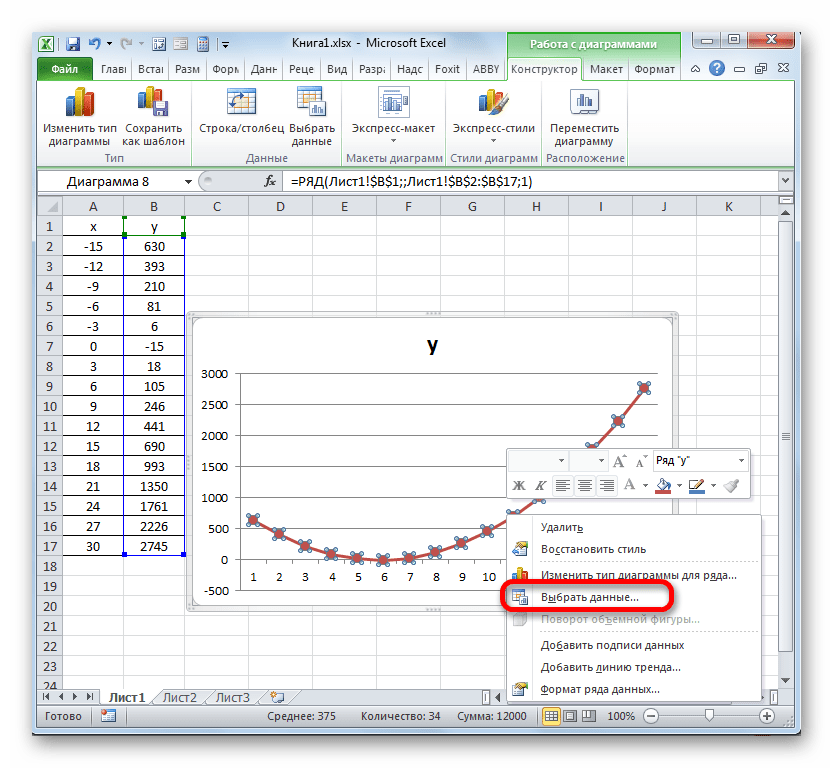
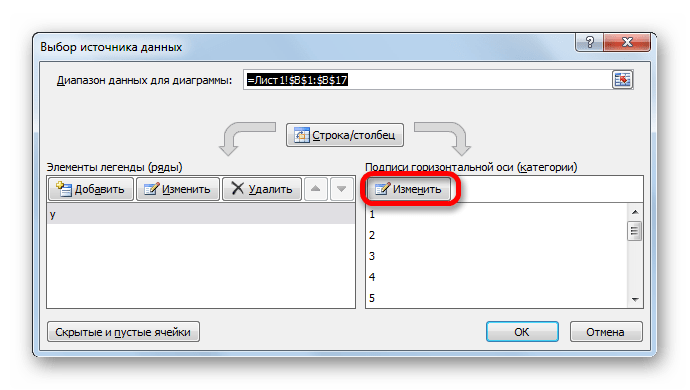
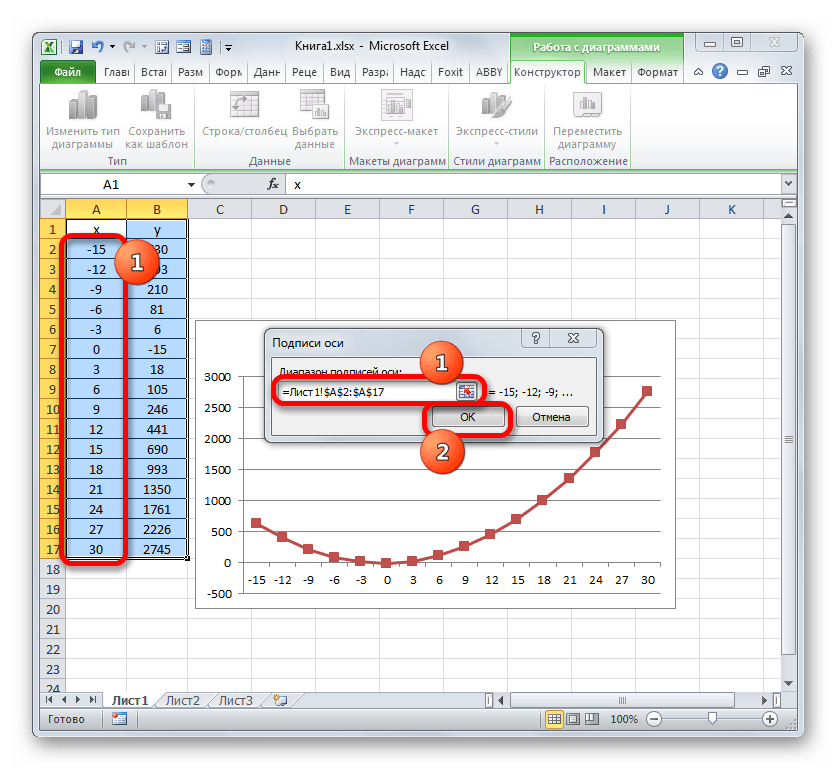
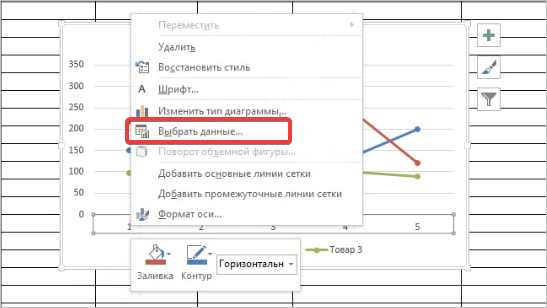
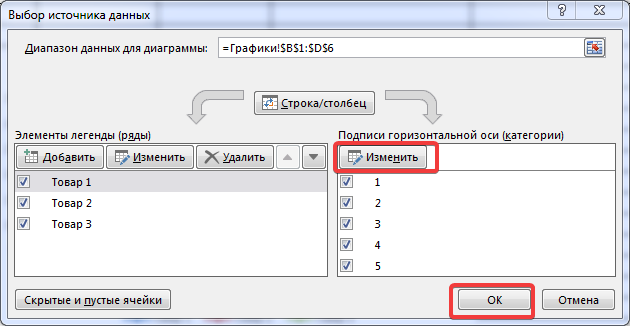
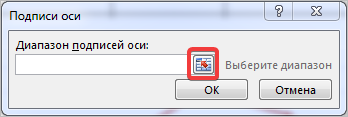
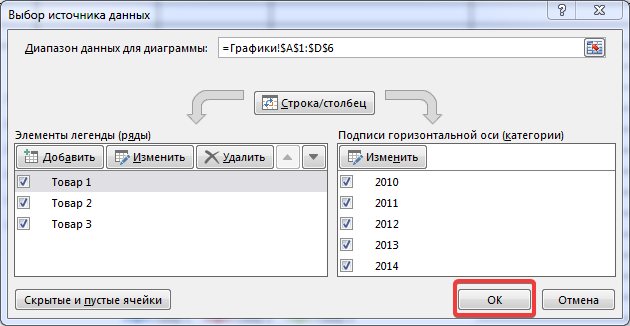
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
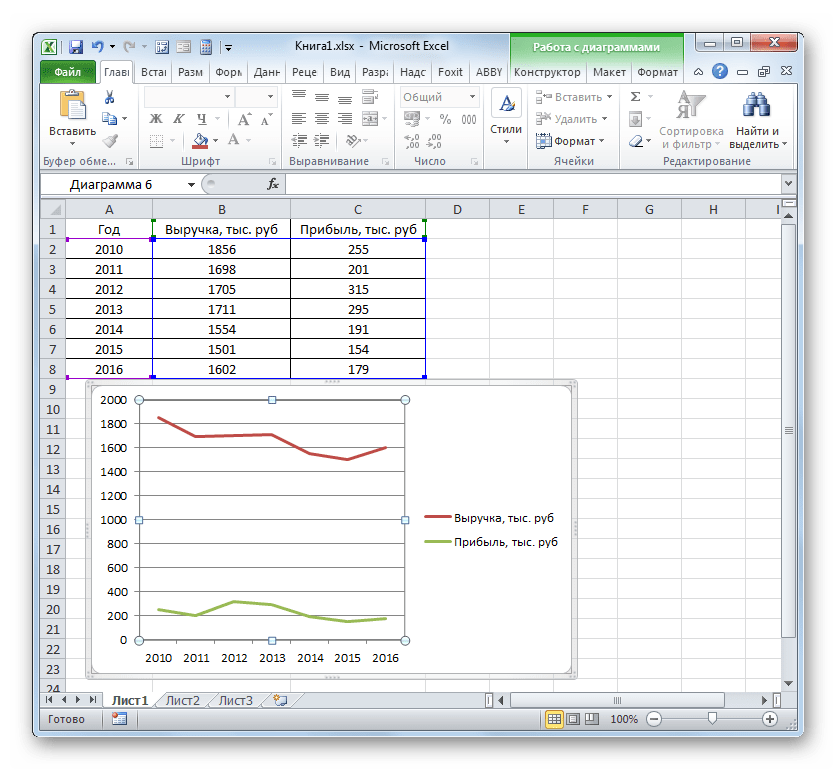
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
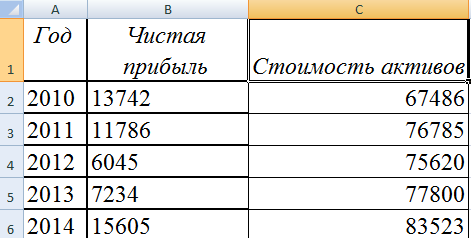
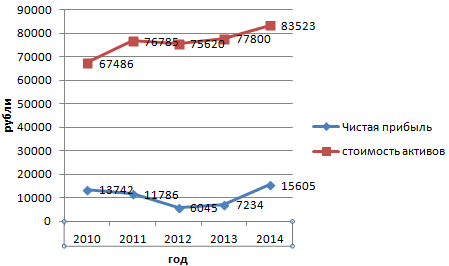
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
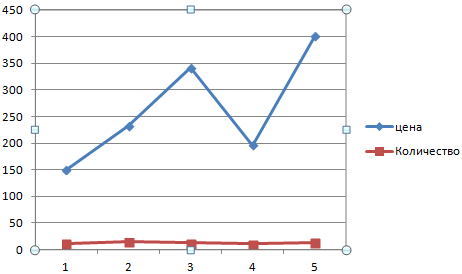
Сначала строим график так, будто у нас одинаковые единицы измерения.
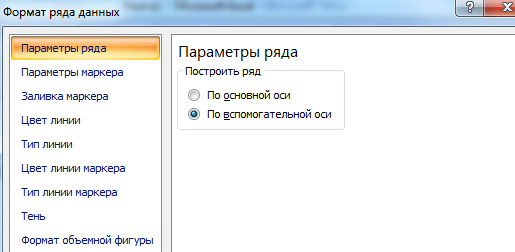
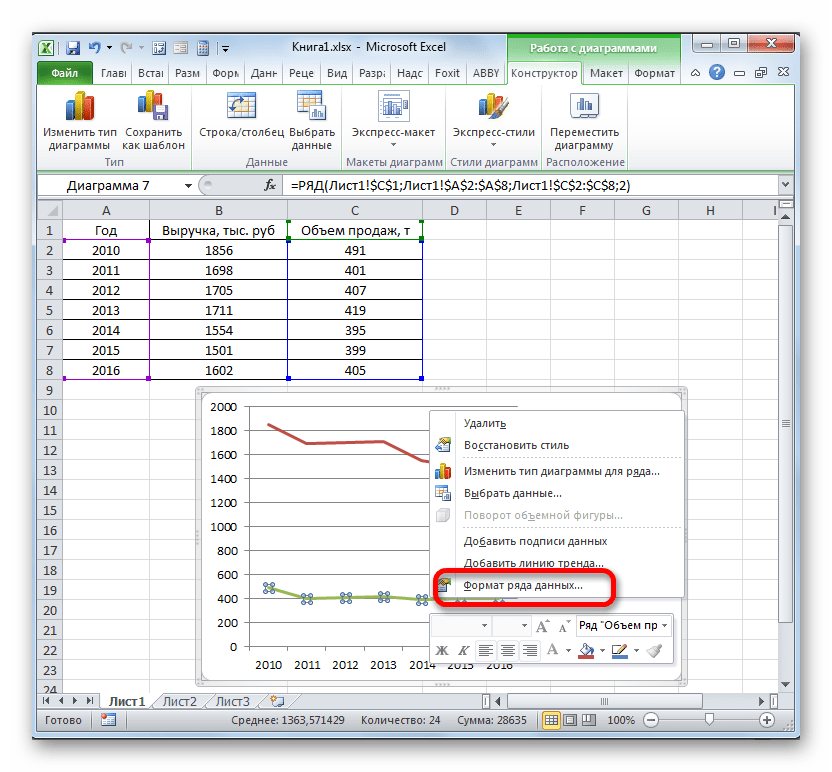
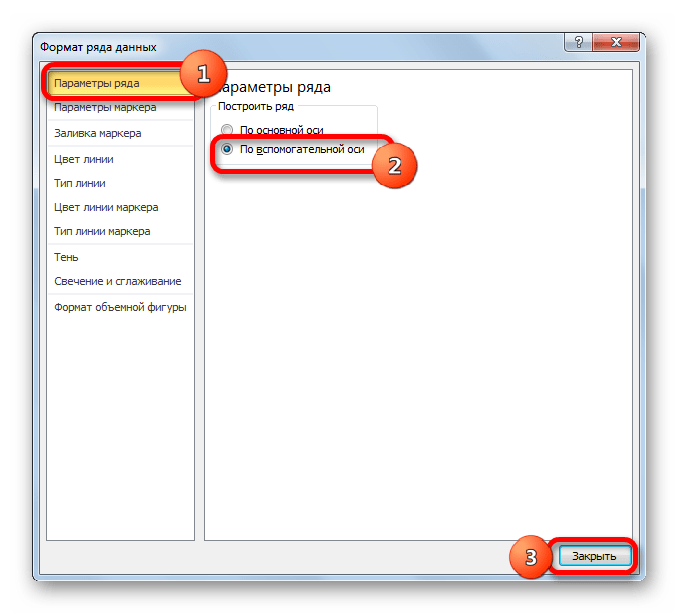
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
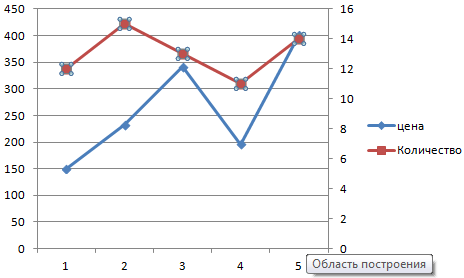
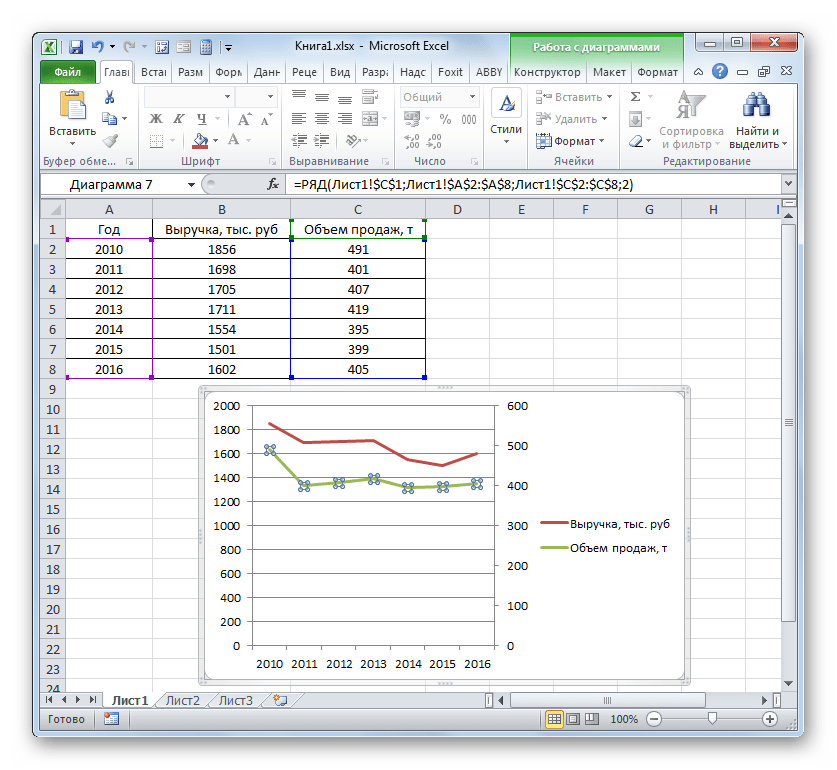
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
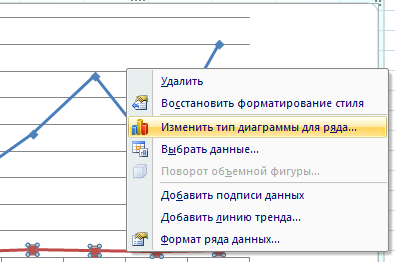
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
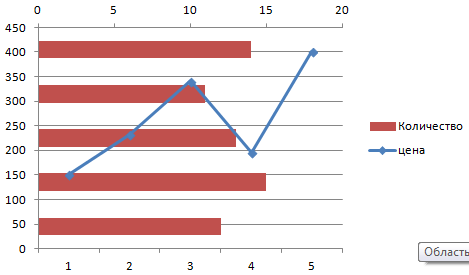
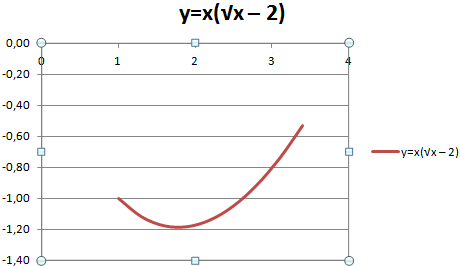
Пример: y=x(√x – 2). Шаг – 0,3.
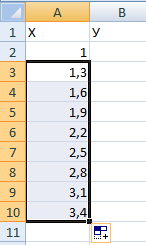
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
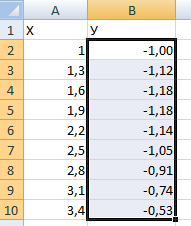
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
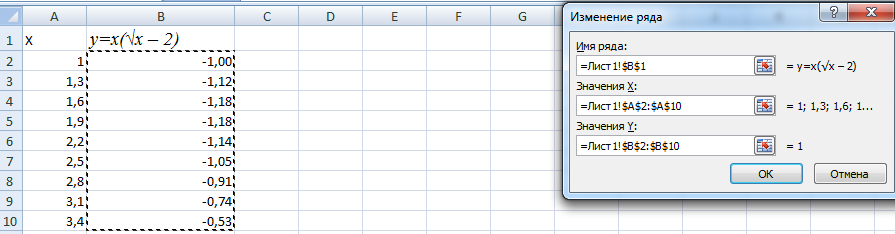
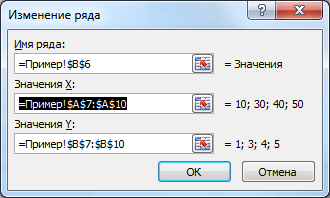
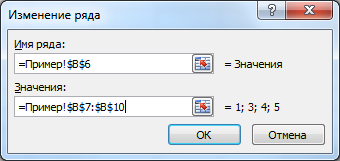
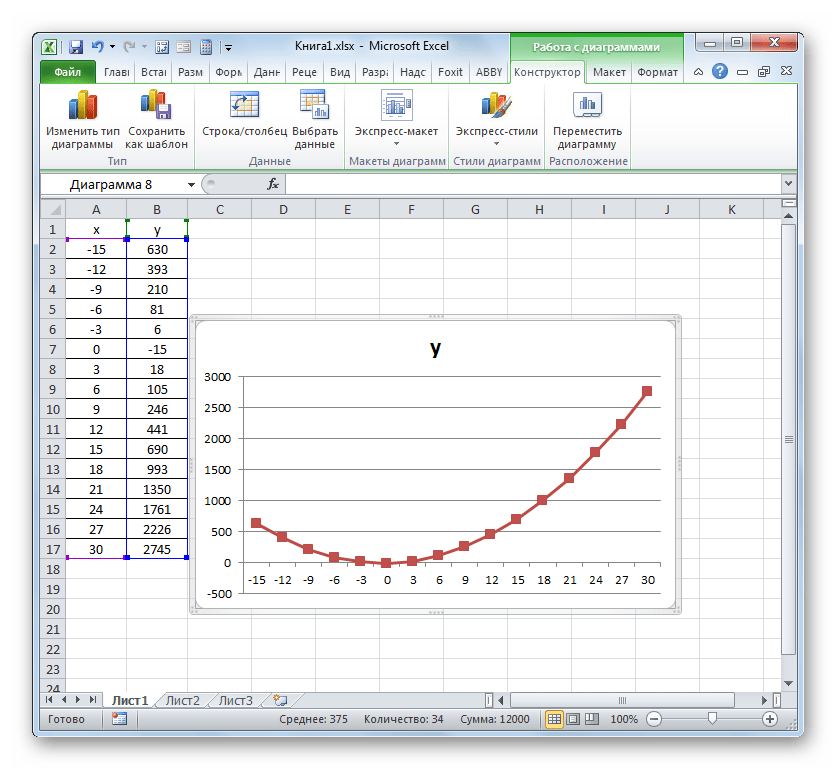
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
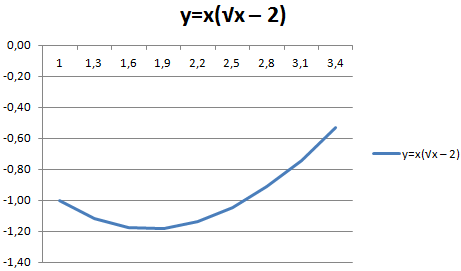
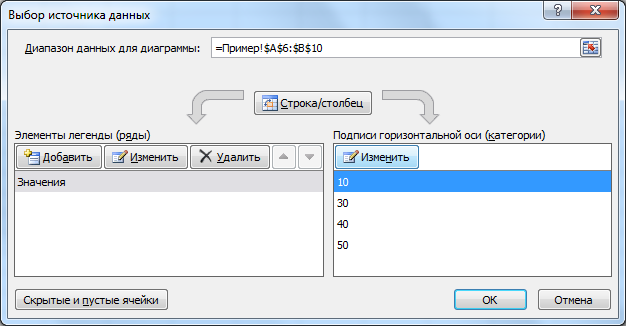
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
Наложение и комбинирование графиков
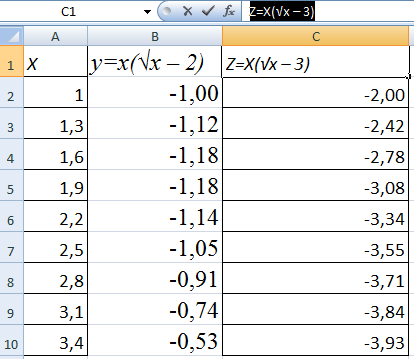
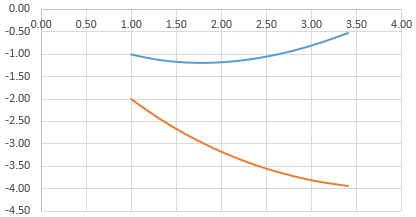
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
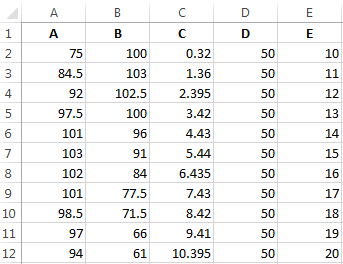
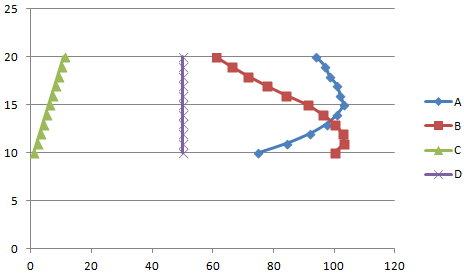
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Скачать все примеры графиков
Готовые примеры графиков и диаграмм в Excel скачать:
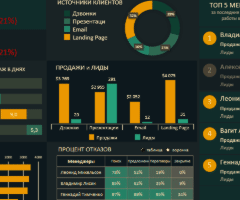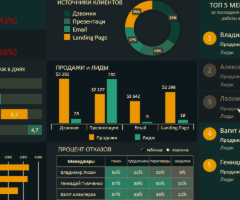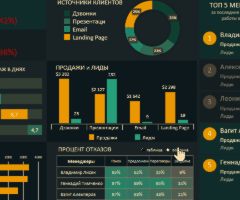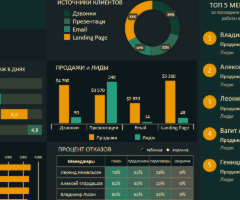
Как сделать шаблон, дашборд, диаграмму или график для создания красивого отчета удобного для визуального анализа в Excel? Выбирайте примеры диаграмм с графиками для интерактивной визуализации данных с умных таблиц Excel и используйте их для быстрого принятия правильных решений. Бесплатно скачивайте готовые шаблоны динамических диаграмм для использования их в дашбордах, отчетах или презентациях.
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Содержание
- Как по графику определить функцию в excel
- Часть 10. Подбор формул по графику. Линия тренда
- Найти функцию по ее графику (аппроксимация)
- Решение
- Как по графику в экселе определить значение точки
- Точки пересечения графиков в Excel
- Строим графики с точками пересечений
- Находим точку пересечения графиков в Excel
- Точки пересечения для трех показателей
- Особенности построения при неравномерном шаге по Х
- Построение графика функции на плоскости
- Построение плоских алгебраических кривых
- Построение диаграммы рассеяния
- Инструменты прогнозирования в Microsoft Excel
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
Как по графику определить функцию в excel
Часть 10. Подбор формул по графику. Линия тренда
Для рассмотренных выше задач удавалось построить уравнение или систему уравнений. Но во многих случаях при решении практических задач имеются лишь экспериментальные (результаты измерений, статистические, справочные, опытные) данные. По ним с определенной мерой близости пытаются восстановить эмпирическую формулу (уравнение), которая может быть использована для поиска решения, моделирования, оценки решений, прогнозов.
Процесс подбора эмпирической формулы P(x) для опытной зависимости F(x) называется аппроксимацией (сглаживанием). Для зависимостей с одним неизвестным в Excel используются графики, а для зависимостей со многими неизвестными – пары функций из группы Статистические ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ .
В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.
Степень близости подбираемой функции оценивается коэффициентом детерминации R 2 . Если нет других теоретических соображений, то выбирают функцию с коэффициентом R 2 , стремящимся к 1. Отметим, что подбор формул с использованием линии тренда позволяет установить как вид эмпирической формулы, так и определить численные значения неизвестных параметров.
Excel предоставляет 5 видов аппроксимирующих функций:
1. Линейная – y=cx+b. Это простейшая функция, отражающая рост и убывание данных с постоянной скоростью.
2. Полиномиальная – y=c0+c1x+c2x 2 +…+c6x 6 . Функция описывает попеременно возрастающие и убывающие данные. Полином 2-ой степени может иметь один экстремум (min или max), 3-ей степени – до 2-х экстремумов, 4-ой степени – до 3-х и т.д.
3. Логарифмическая – y=clnx+b. Эта функция описывает быстро возрастающие (убывающие) данные, которые затем стабилизируются.
4. Степенная – y=cx b , (х>0и y>0). Функция отражает данные с постоянно увеличивающейся (убывающей) скоростью роста.
5. Экспоненциальная – y=ce bx , (e – основание натурального логарифма). Функция описывает быстро растущие (убывающие) данные, которые затем стабилизируются.
Для всех 5-ти видов функций используется аппроксимация данных по методу наименьших квадратов (см. справку по F1 «линия тренда»).
В качестве примера рассмотрим зависимость продаж от рекламы, заданную следующими статистическими данными по некоторой фирме:
| Реклама (тыс. руб.) | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| Продажи (тыс. руб.) |
Необходимо построить функцию, наилучшим образом отражающую эту зависимость. Кроме того, необходимо оценить продажи для рекламных вложений в 6 тыс. руб.
Приступим к решению. В первую очередь введите эти данные в Excel и постройте график, как на рис. 38. Как видно, график построен на основании диапазона B2:J2. Далее, щелкнув правой кнопкой мыши по графику, добавьте линию тренда, как показано на рис. 38.
Чтобы подписать ось Х соответствующими значениями рекламы (как на рис. 38), следует в ниспадающем меню (рис. 38) выбрать пункт Исходные данные. В открывшемся одноименном окне, в закладке Ряд, в поле Подписи оси Х, укажите диапазон ячеек, где записаны значения Х (здесь $B$1:$K$1):
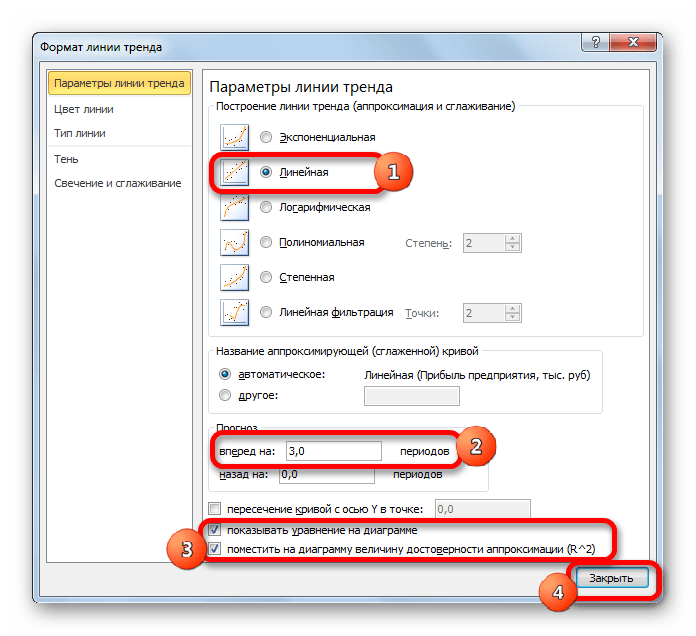
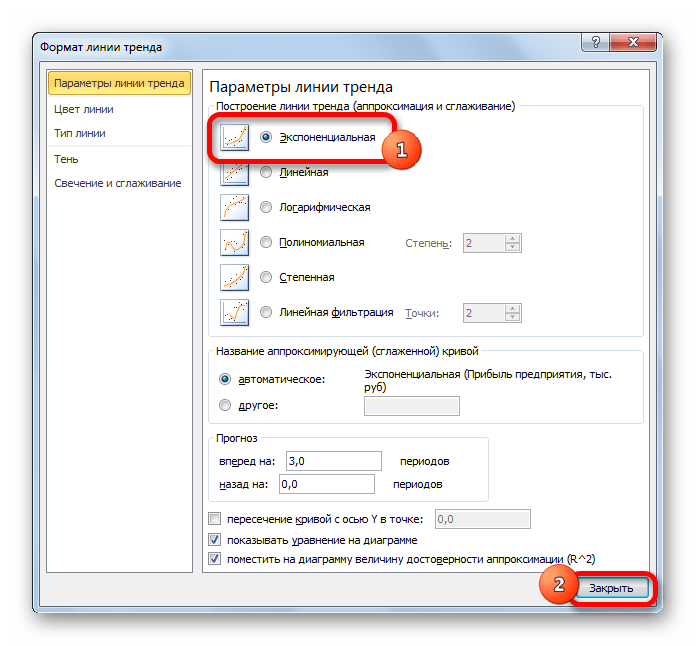
В открывшемся окне настройки (рис. 39), на закладке Тип выберите для аппроксимации логарифмическую линию тренда (по виду графика). На закладке Параметры установите флажки, отображающие на графике уравнение и коэффициент детерминации.
После нажатия ОК Вы получите результат, как на рис. 40. Коэффициент детерминации R 2 =0.9846, что является неплохой степенью близости. Для подтверждения правильности выбранной функции (поскольку других теоретических соображений нет) спрогнозируйте развитие продаж на 10 периодов вперед. Для этого щелкните правой кнопкой по линии тренда – измените формат – после этого в поле Прогноз: вперед на: установите 10 (рис. 41).
После установки прогноза Вы увидите изменение кривой графика на 10 периодов наблюдения вперед, как на рис. 42. Он с большой долей вероятности отражает дальнейшее увеличение продаж с увеличением рекламных вложений.
Вычисление по полученной формуле =237,96*LN(6)+5,9606 в Excel дает значение 432 тыс. руб.
В Excel имеется функция ПРЕДСКАЗ(), которая вычисляет будущее значение Y по существующим парам значений X и Y значениям с использованием линейной регрессии. Функция Y по возможности должна быть линейной, т.е. описываться уравнением типа c+bx. Функция предсказания для нашего примера запишется так: =ПРЕДСКАЗ(K1;B2:J2;B1:J1). Запишите – должно получится значение 643,6 тыс. руб.
Часть11. Контрольные задания
Найти функцию по ее графику (аппроксимация)
Дано:
Два параметра, зависящих друг от друга (X; Y). На их основании построен график.
Задача: найти функцию, отражающую (приблизительно) зависимость между параметрами.
Я эту задачу пытаюсь решить с помощью инструмента в экселе (построение тренда; полиноминальная линия тренда 6й степени).
Эксель подсказывает мне формулу функции, но по факту эта формула выдает не верные параметры (т.е. «Y» по данному формуле рассчитывается не правильно).
Помощь в написании контрольных, курсовых и дипломных работ здесь.
расчет.xlsx (15.9 Кб, 22 просмотров)
Аппроксимация к графику
Здравствуйте! Проблема такая, приходится работать с данными с осциллографа и с помощью программы.
Найти функцию по графику(парабола)
Нужно найти функцию по графику(только параболу), пробовал по формулам с википедии, но что то не.
Нужно найти функцию по графику
Вот собственно график и из него надо получить функцию для того чтобы написать программу на паскале.
найти функцию сигнала по графику
Доброго времени суток, как по графику сигнала найти его изображение (ну или сначала оригинал.
расчет (1).xlsx (16.1 Кб, 55 просмотров)
Сообщение было отмечено p1111 как решение
Решение
Как, оказывается, было просто.
Спасибо огромное, очень выручили.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Нужно найти функцию по графику
Здравствуйте, у меня есть данные для построения кусочка ВАХ-электрической дуги. Мне нужно найти.
Вывести функцию по графику
Процесс предполагается обратный от привычного, имея график, построить функцию. Как это сделать.
Написать функцию по графику
Помогите пожалуйста! По данному графику нужна функция (формула), чтобы я потом через if смог.
Составить функцию по графику.
Привет всем, помогите составить функцию, по графику, график приложен снизу функция в каком-то.
Источник
Как по графику в экселе определить значение точки
Точки пересечения графиков в Excel
Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.
Строим графики с точками пересечений
Имеются две функции, по которым нужно построить графики:
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:
- Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
- Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.
Находим точку пересечения графиков в Excel
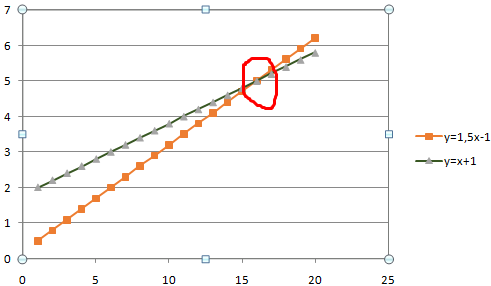
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.
Первый способ. Найти общие значения в рядах данных для указанных функций.
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.
Изменим график, добавив новые данные. Получим две пересекающиеся линии.
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».
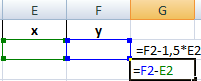
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.
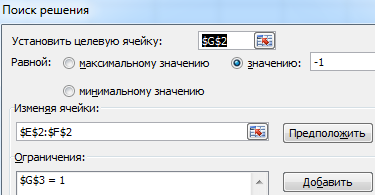
Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.
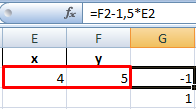
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.
Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.
Точки пересечения для трех показателей
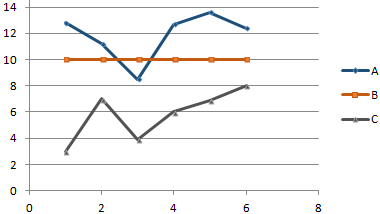
Существует три показателя, которые измерялись во времени.
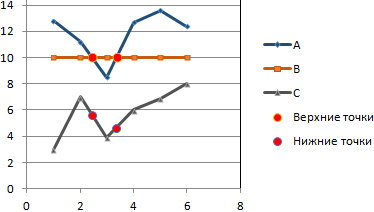
По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.
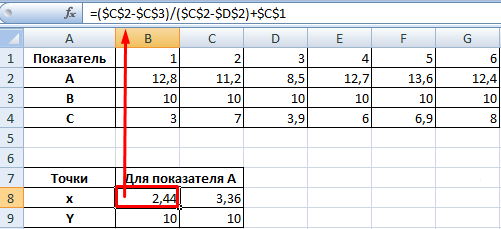
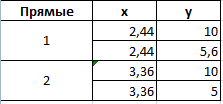
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.
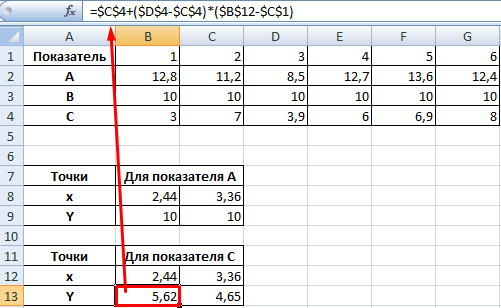
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).
Получается такой рисунок:
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:
Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.
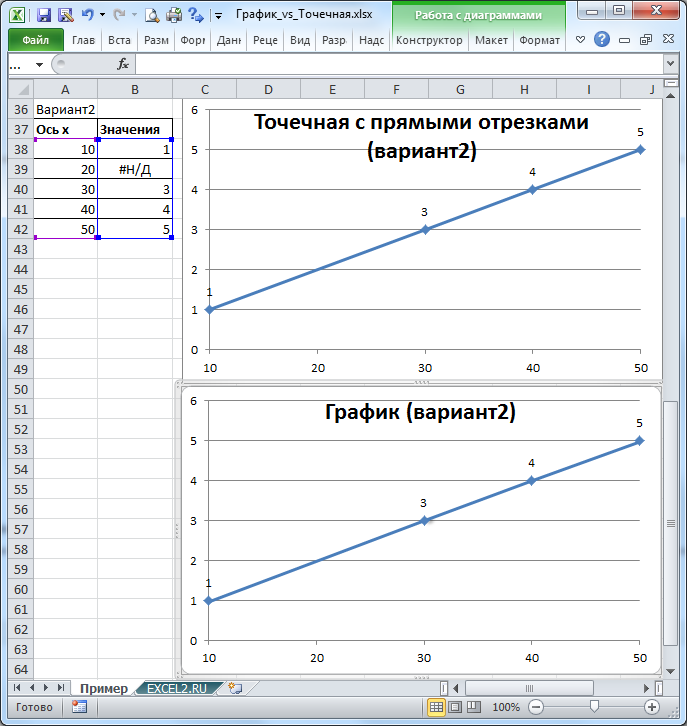
Особенности построения при неравномерном шаге по Х
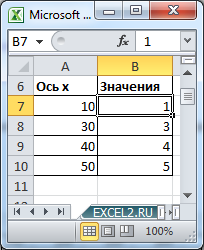
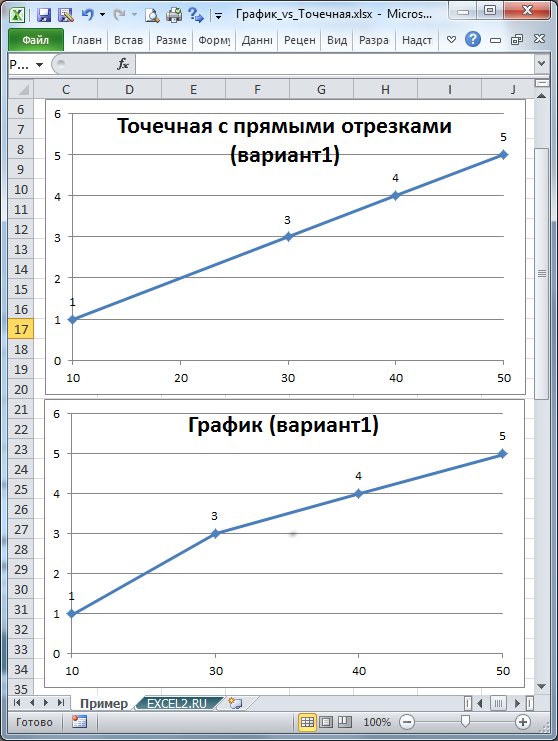
Пусть дана таблица с исходными данными (значения в исходной таблице расположены по оси Х равномерно с шагом 10, но точка с х=20 отсутствует).
Построим График и Точечную диаграмму с прямыми отрезками используя одну и туже таблицу.
Точечная диаграмма использует все данные из исходной таблицы: как значения х, так и y.
Диаграмма График откладывает значения по оси х равномерно (значения из столбца Ось х не используются для построения).
Значения из столбца Ось х используются в Диаграмме График только для подписей данных по оси х (значения из столбца Ось х никак не влияют на расположение точек). Это часто используется для гибкой настройки подписей по оси х (можно в качестве подписей указать любые, в том числе и текстовые значения).
Вывод : если значения по оси х расположены неравномерно (в исходной таблице нет точки с х=20, поэтому кривая на Диаграмме График имеет излом), то использование Точечной диаграммы предпочтительней.
В случае, если данные расположены по оси х равномерно (с определенным шагом), то можно использовать оба типа диаграммы — линии на диаграмме будут выглядеть одинаково. Но если некоторые значения по оси Х пропущены, то для настройки диаграммы типа График нужно изменить таблицу с исходными данными. Можно использовать функцию НД() см. статью Функция НД() в MS EXCEL . Эта функция позволяет сделать кривую на диаграмме График аналогичной кривой на Точечной диаграмме (вариант2).
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
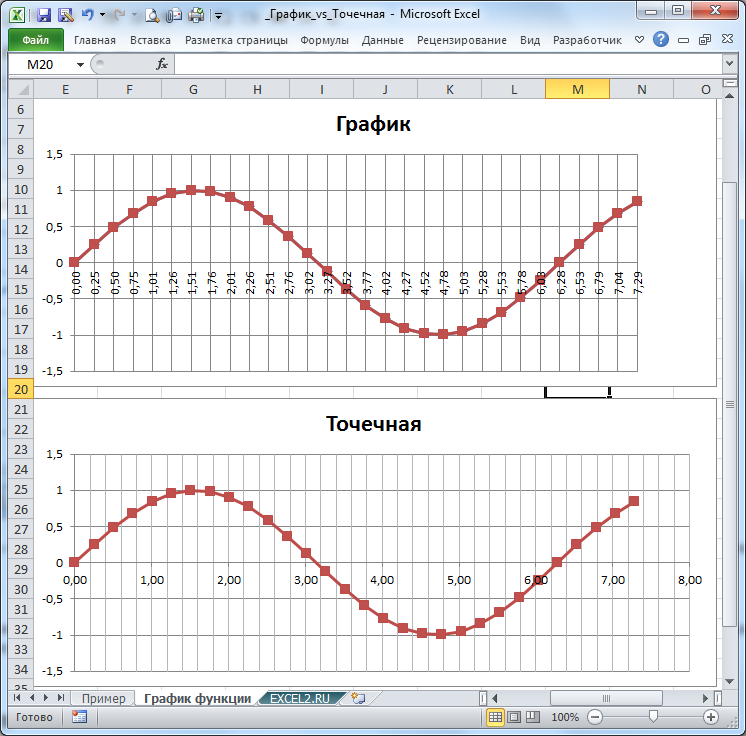
Построение графика функции на плоскости
Элементарные функции (y=sin(x), y=x 2 ) удовлетворяют условию однозначности функции: одному значению Х соответствует единственное значение Y (горизонтальная линия, параллельная оси ординат, не может пересекать график функции более чем в одной точке). Поэтому, Диаграмма типа График, как и диаграмма типа Точечная, годятся для построения графика функции на плоскости.
Построим график функции y=sin(x) с использованием обоих типов диаграмм.
- подписи Оси Х: на диаграмме График на оси Х указаны фактические значения Х (могут также быть указаны любые подписи, даже текст), а на Точечной — цены основных и промежуточных делений вычислены автоматически. Т.е. подписи на этих типах диаграмм не обязательно совпадают (но можно добиться, чтобы совпадали).
- шаг вертикальной сетки: основные линии сетки на Графике проходят строго через точки значений, а на Точечной — шаг выбирается автоматически (точно предсказать не возможно, т.к. шаг зависит от размера самой диаграммы, диапазона изменения по Х и др.)
Эти графики построены в файле примера .
Построение плоских алгебраических кривых
Кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли можно построить только с помощью диаграммы типа Точечная, т.к. эти кривые НЕ удовлетворяют условию однозначности функции: одному значению Х могут соответствовать несколько значений Y. Эти графики построены в этой статье.
Построение диаграммы рассеяния
Диаграммы рассеяния используются для анализа временных рядов и в статистическом анализе. Про построение этой диаграммы (возможно использовать только Точечную) см. эту статью.
Инструменты прогнозирования в Microsoft Excel
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
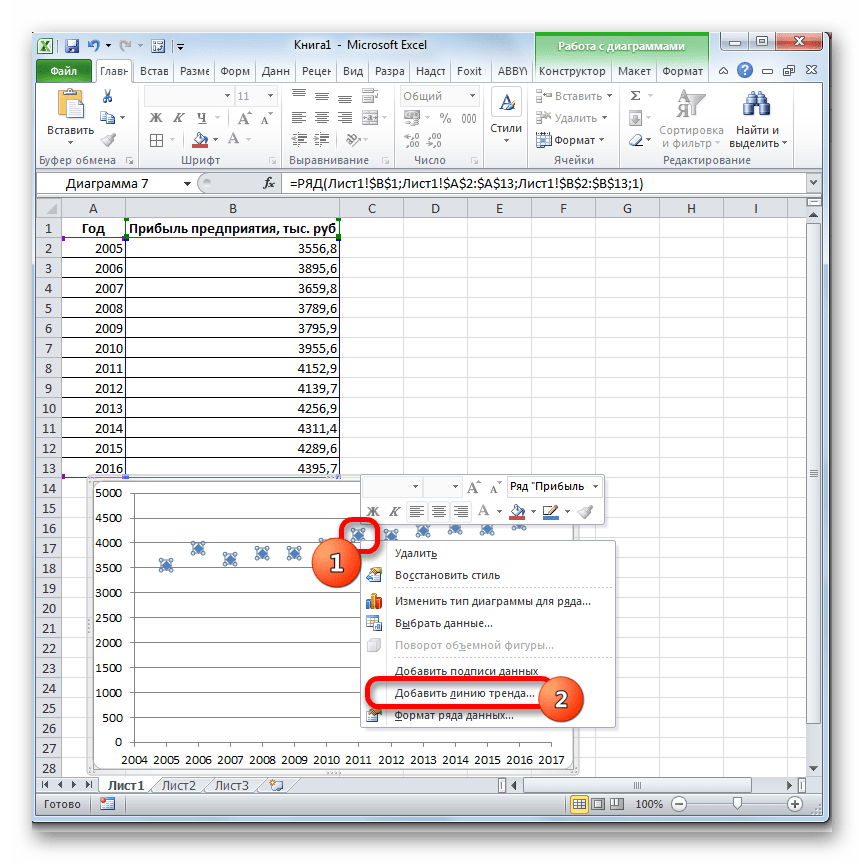
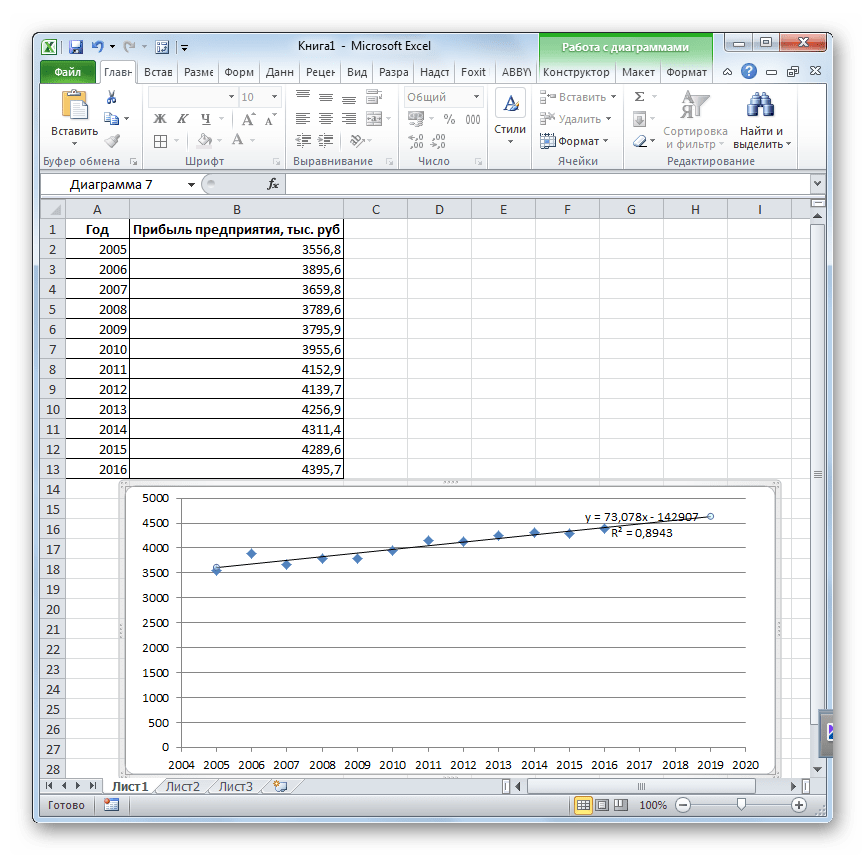
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
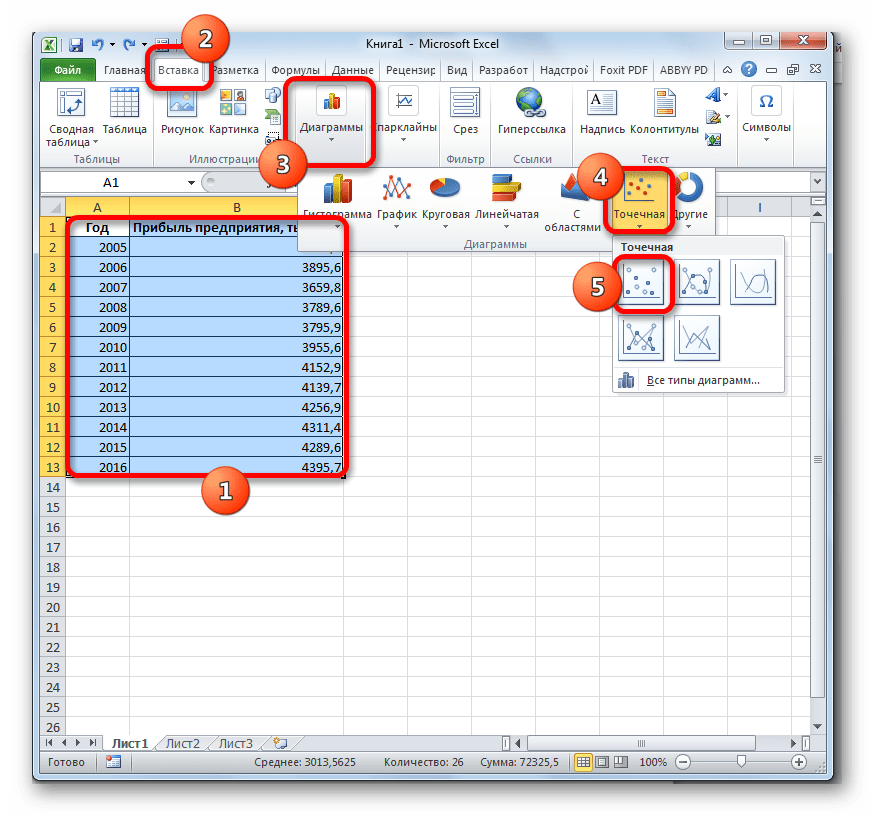
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
Давайте для начала выберем линейную аппроксимацию.
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
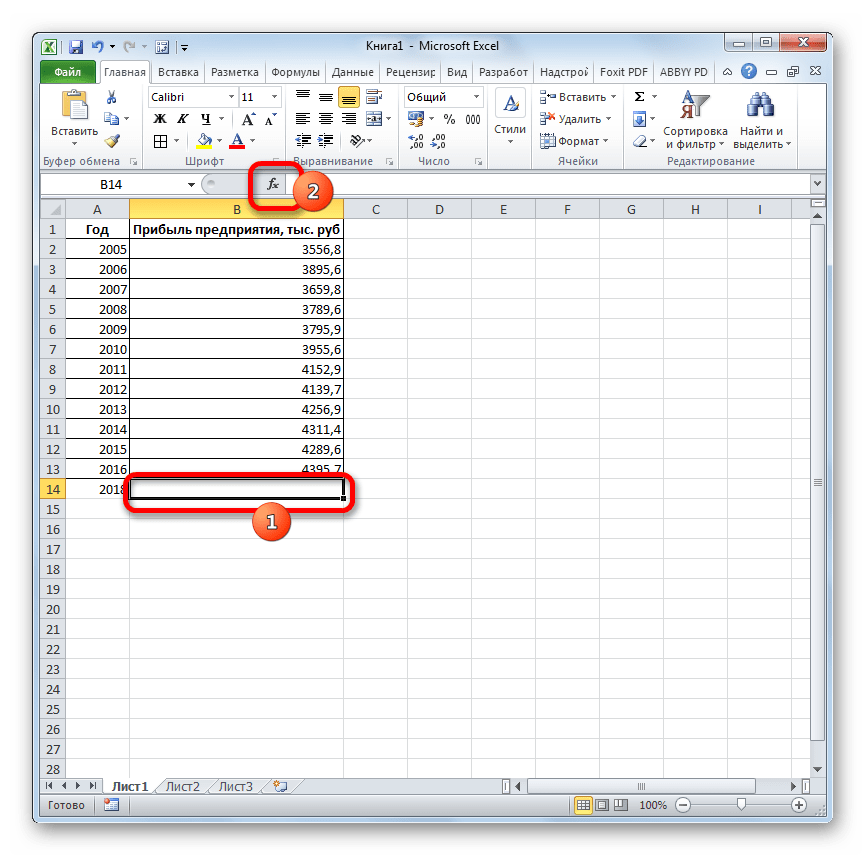
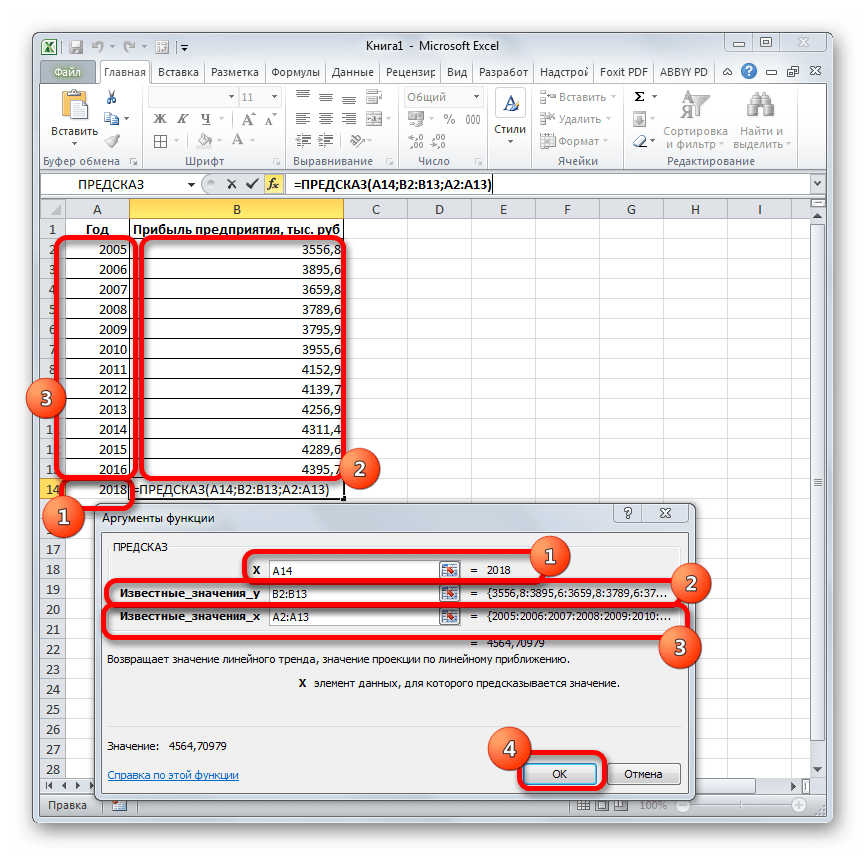
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Способ 3: оператор ТЕНДЕНЦИЯ
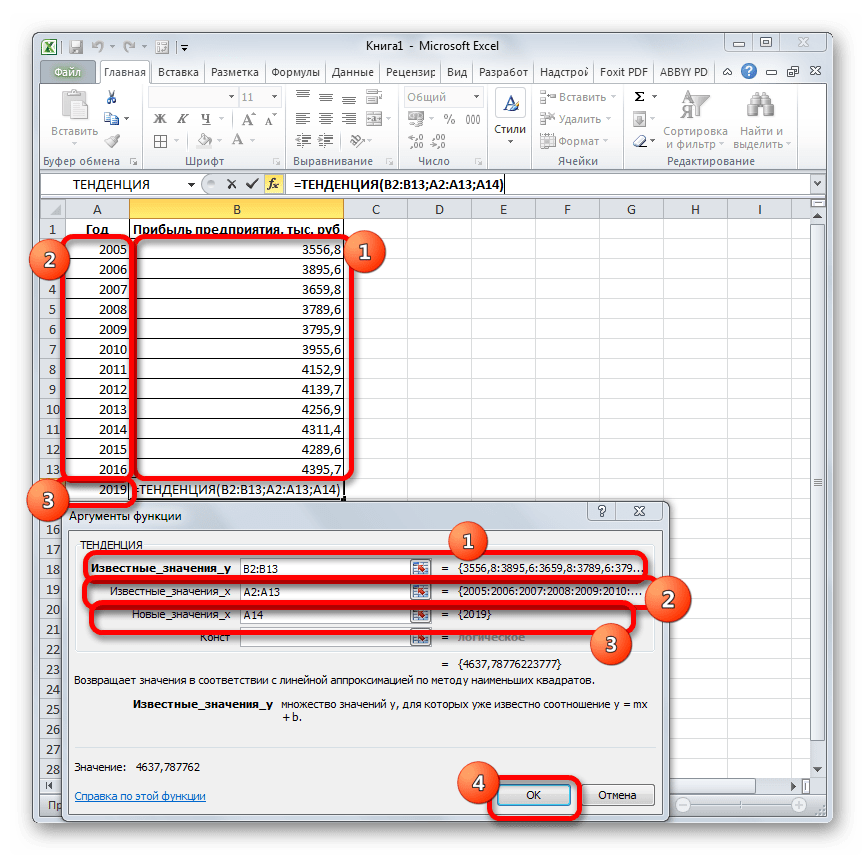
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
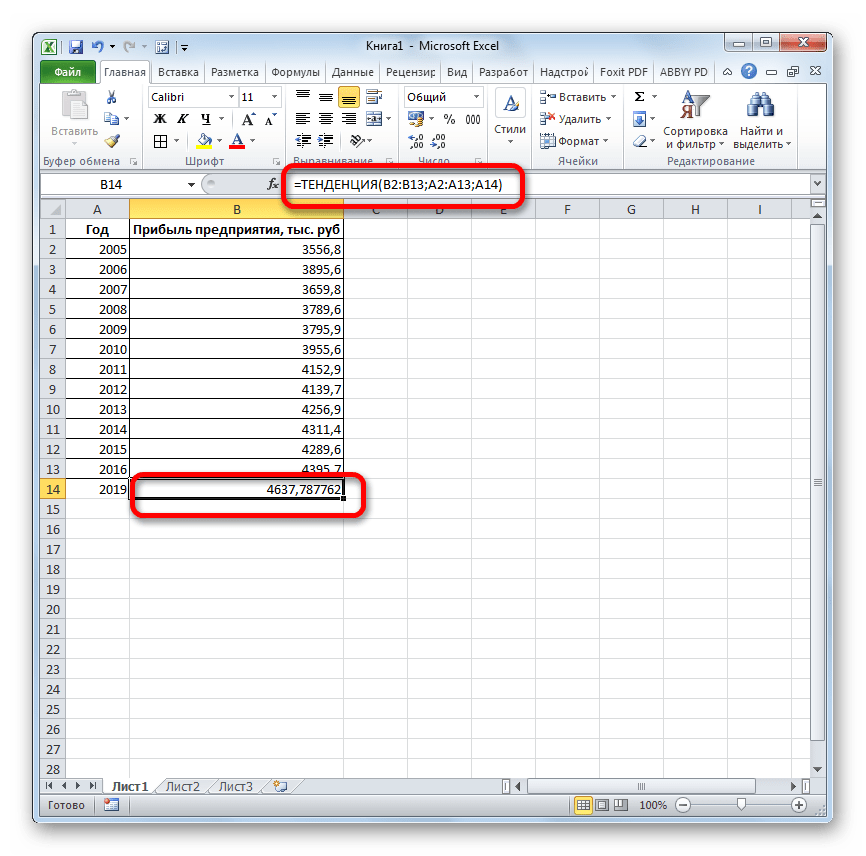
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
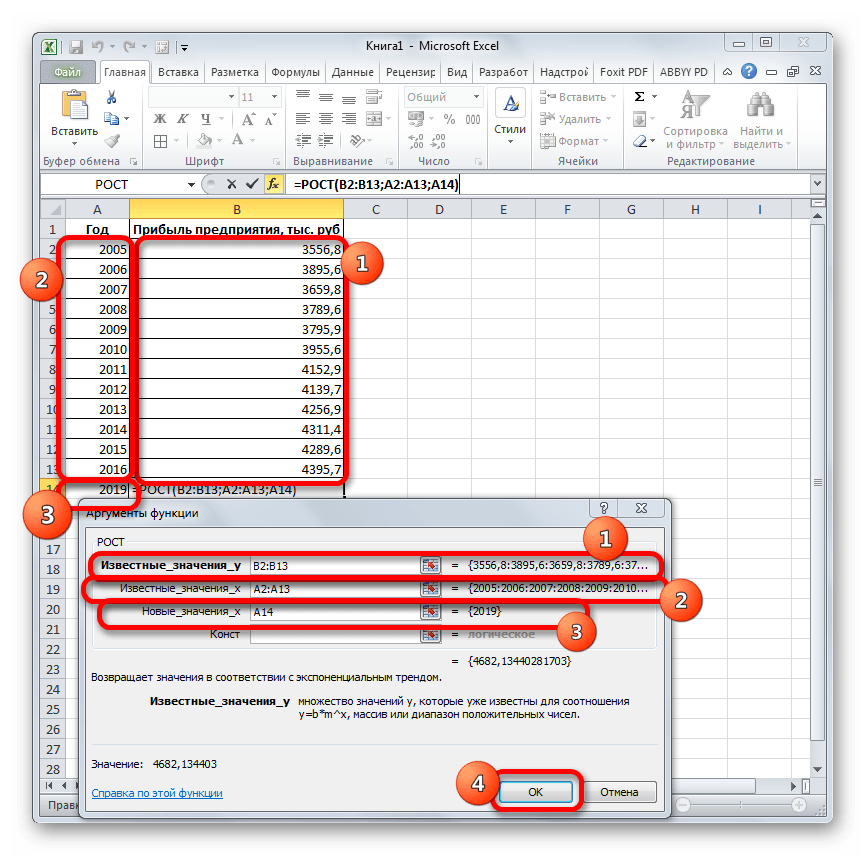
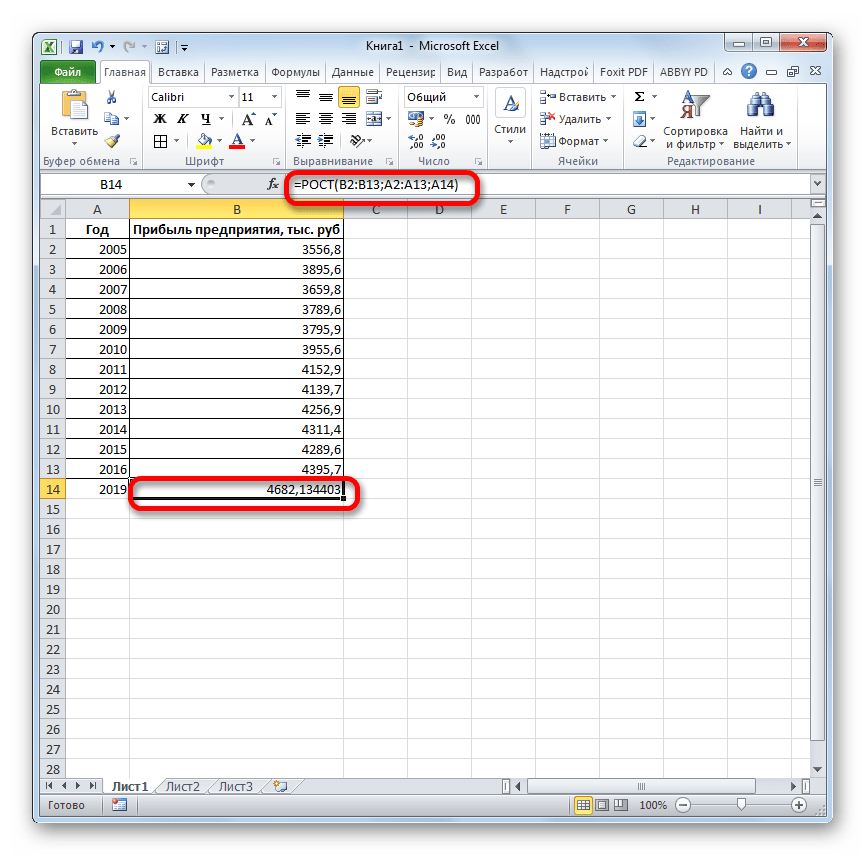
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
Способ 5: оператор ЛИНЕЙН
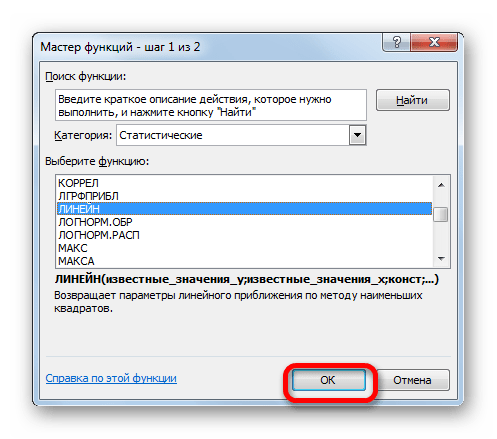
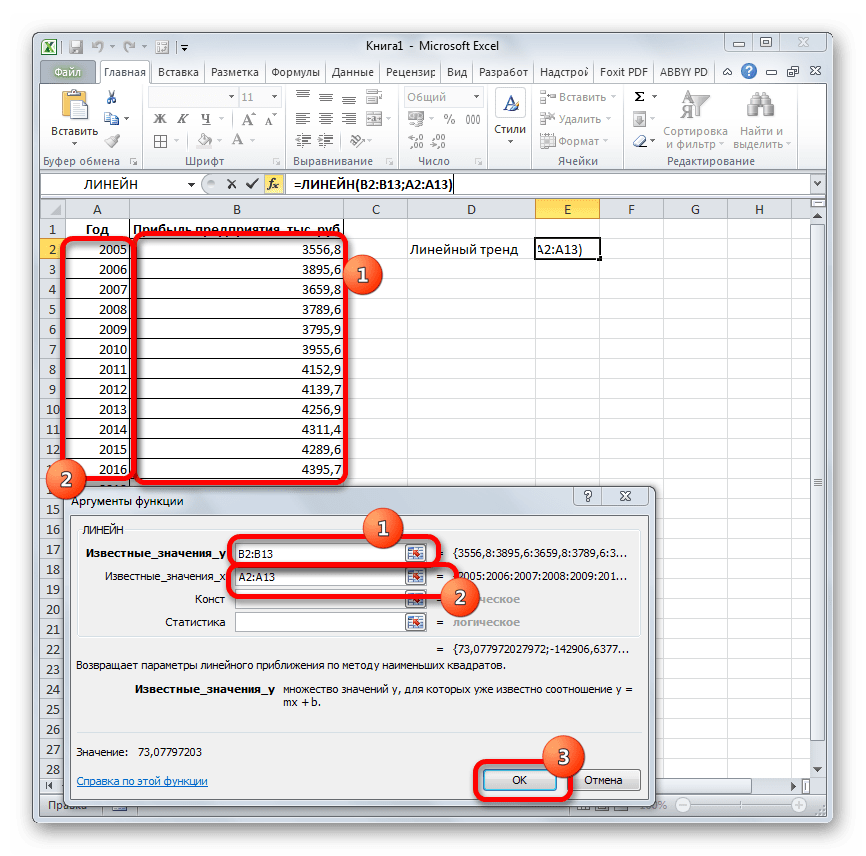
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
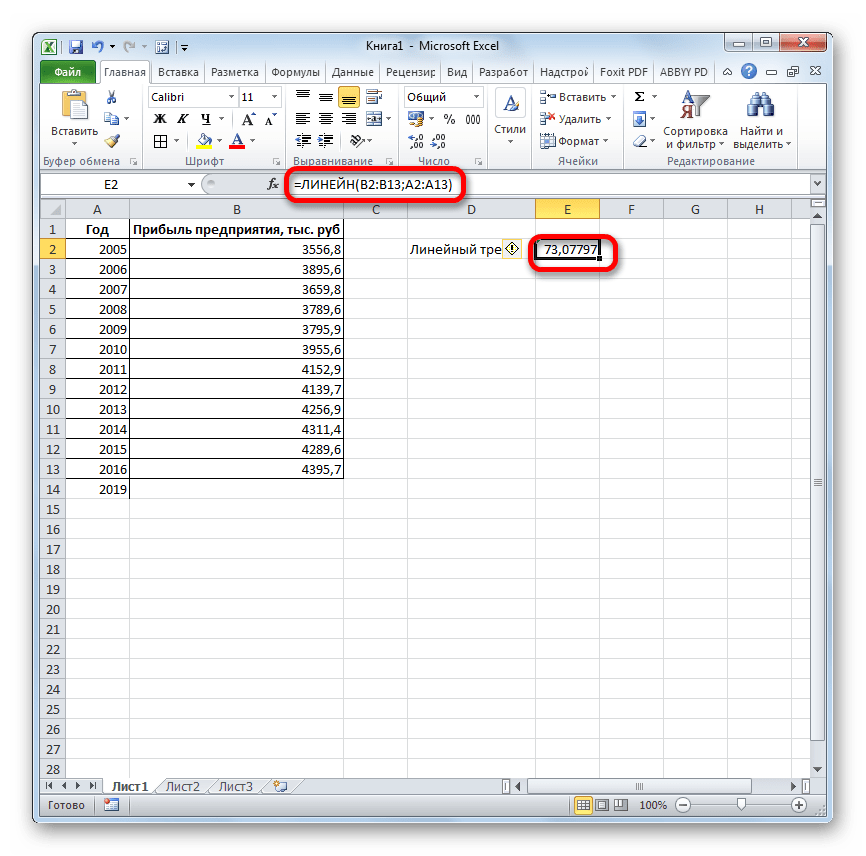
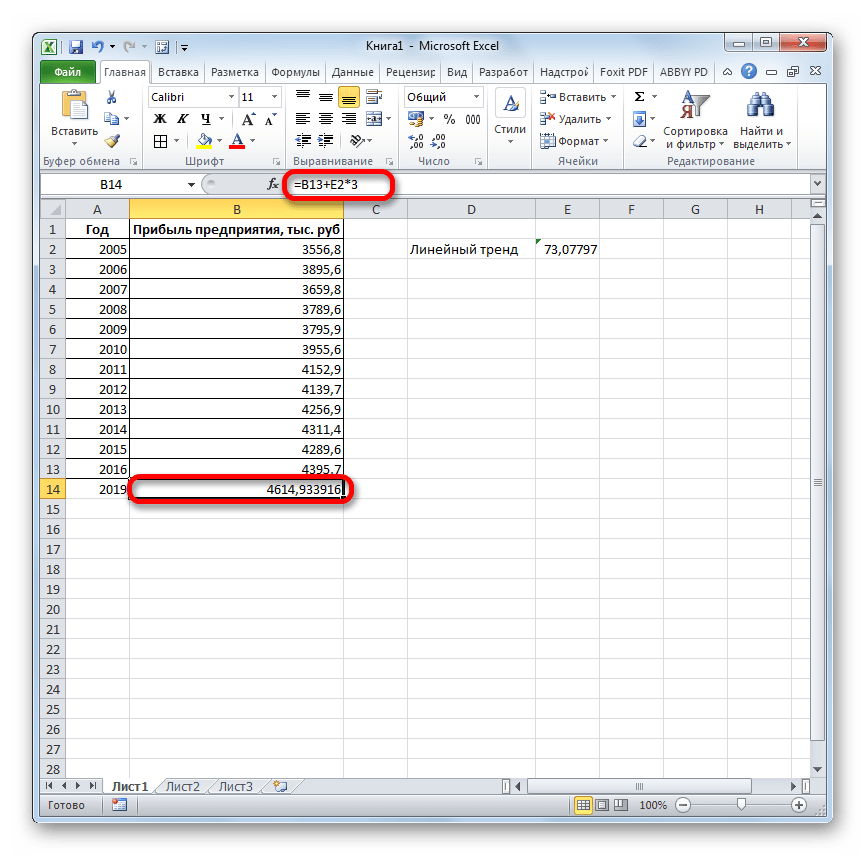
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
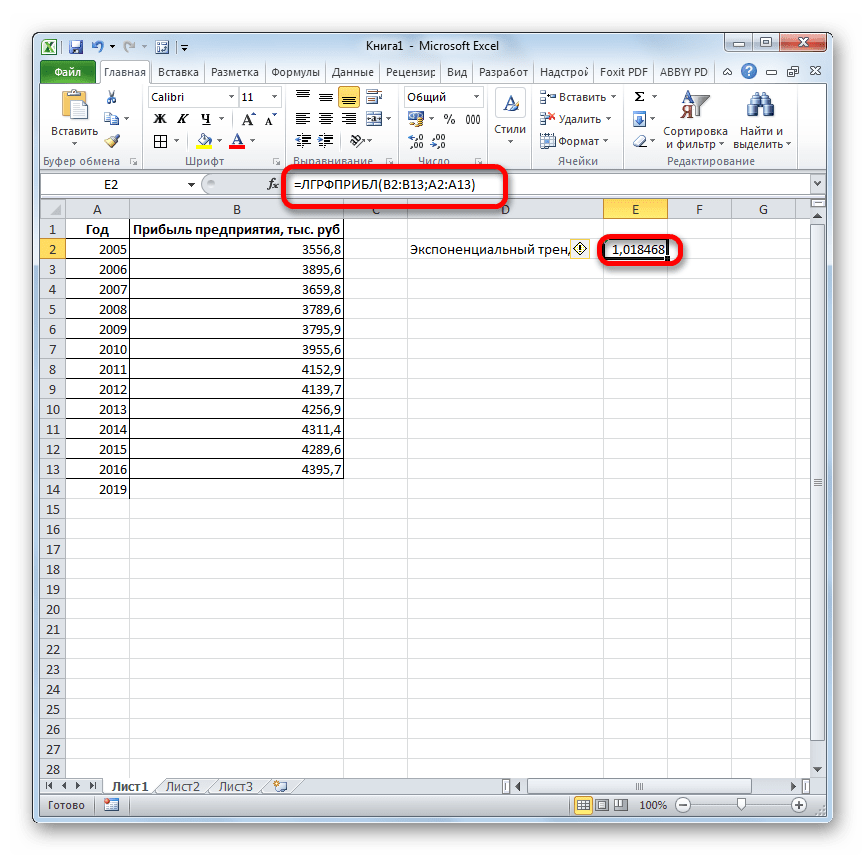
Способ 6: оператор ЛГРФПРИБЛ
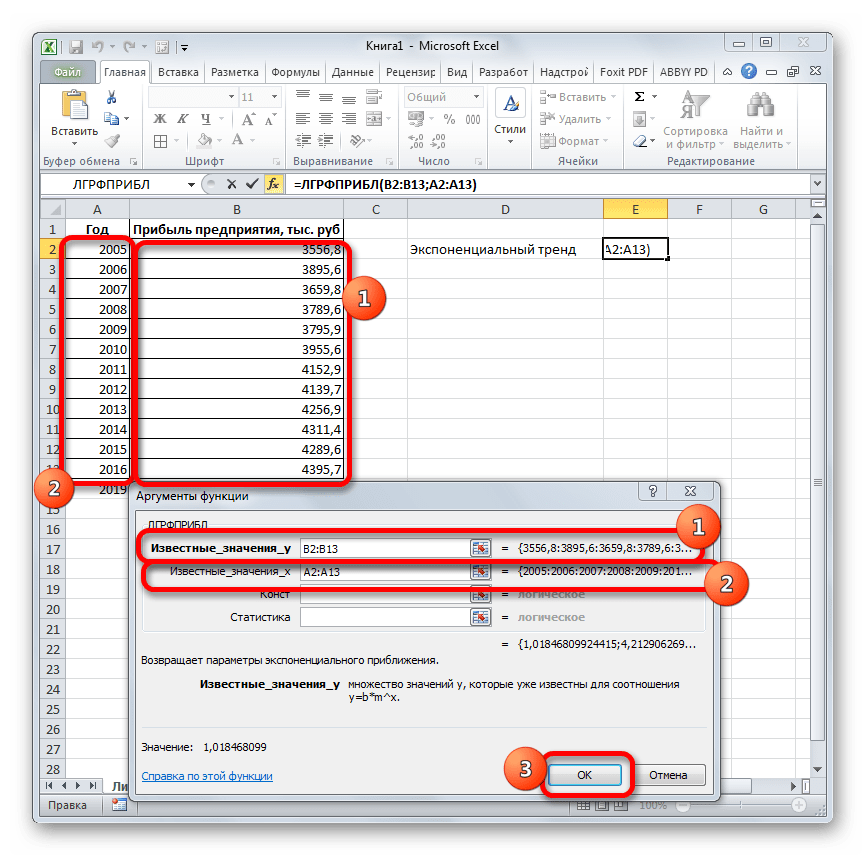
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
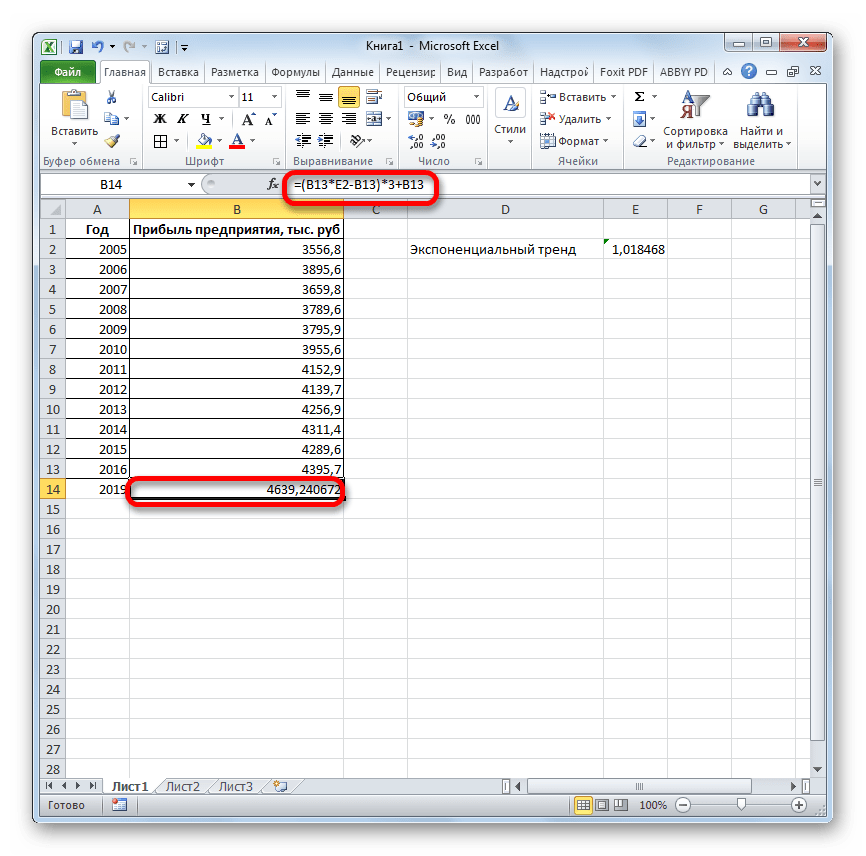
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

Источник
Содержание
- Процедура создания графика
- Способ 1: создание графика зависимости на основе данных таблицы
- Способ 2: создание графика зависимости с несколькими линиями
- Способ 3: построение графика при использовании различных единиц измерения
- Способ 4: создание графика зависимости на основе алгебраической функции
- Вопросы и ответы
Одной из типичных математических задач является построение графика зависимости. В нем отображается зависимость функции от изменения аргумента. На бумаге выполнить данную процедуру не всегда просто. Но инструменты Excel, если в должной мере овладеть ими, позволяют выполнить данную задачу точно и относительно быстро. Давайте выясним, как это можно сделать, используя различные исходные данные.
Процедура создания графика
Зависимость функции от аргумента является типичной алгебраической зависимостью. Чаще всего аргумент и значение функции принято отображать символами: соответственно «x» и «y». Нередко нужно произвести графическое отображение зависимости аргумента и функции, которые записаны в таблицу, или представлены в составе формулы. Давайте разберем конкретные примеры построения подобного графика (диаграммы) при различных заданных условиях.
Способ 1: создание графика зависимости на основе данных таблицы
Прежде всего, разберем, как создать график зависимости на основе данных, предварительно внесенных в табличный массив. Используем таблицу зависимости пройденного пути (y) от времени (x).
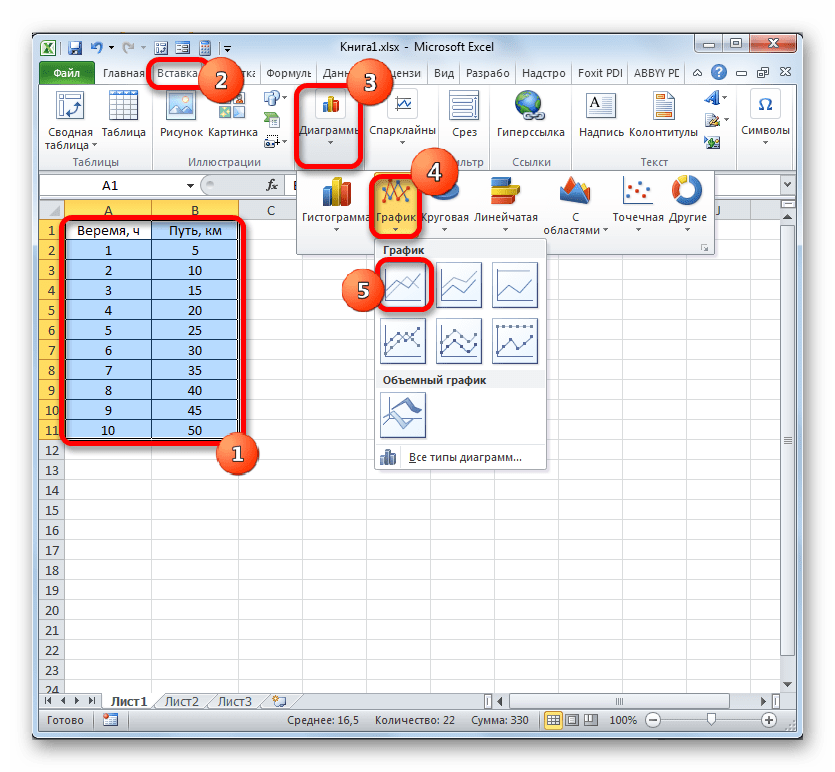
- Выделяем таблицу и переходим во вкладку «Вставка». Кликаем по кнопке «График», которая имеет локализацию в группе «Диаграммы» на ленте. Открывается выбор различных типов графиков. Для наших целей выбираем самый простой. Он располагается первым в перечне. Клацаем по нему.
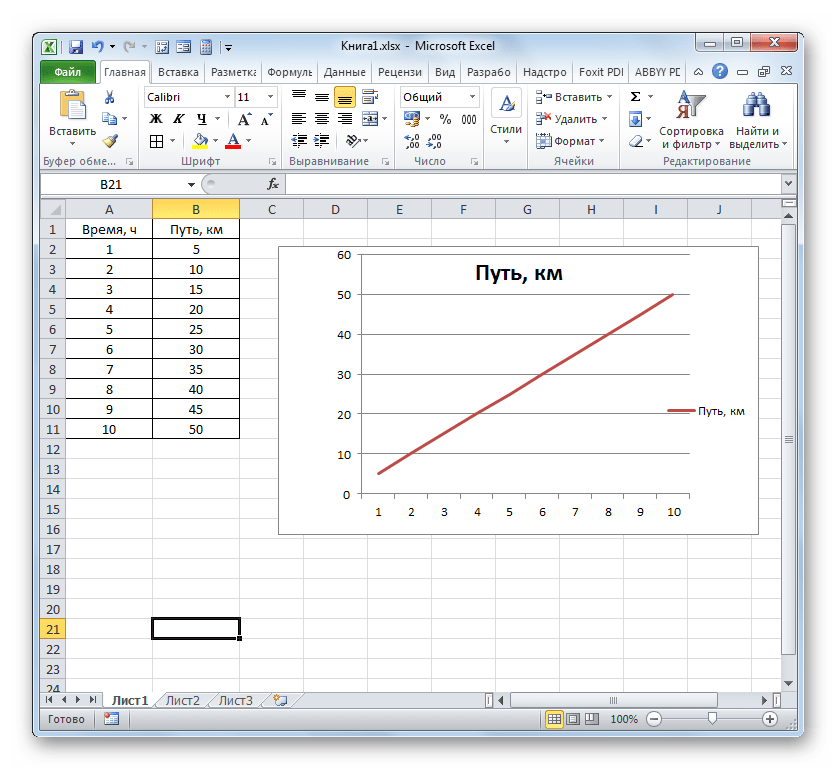
- Программа производит построение диаграммы. Но, как видим, на области построения отображается две линии, в то время, как нам нужна только одна: отображающая зависимость пути от времени. Поэтому выделяем кликом левой кнопки мыши синюю линию («Время»), так как она не соответствует поставленной задаче, и щелкаем по клавише Delete.
- Выделенная линия будет удалена.
Собственно на этом построение простейшего графика зависимости можно считать завершенным. При желании также можно отредактировать наименования диаграммы, её осей, удалить легенду и произвести некоторые другие изменения. Об этом подробнее рассказывается в отдельном уроке.
Урок: Как сделать график в Экселе
Способ 2: создание графика зависимости с несколькими линиями
Более сложный вариант построения графика зависимости представляет собой случай, когда одному аргументу соответствуют сразу две функции. В этом случае потребуется построить две линии. Для примера возьмем таблицу, в которой по годам расписана общая выручка предприятия и его чистая прибыль.
- Выделяем всю таблицу вместе с шапкой.
- Как и в предыдущем случае, жмем на кнопку «График» в разделе диаграмм. Опять выбираем самый первый вариант, представленный в открывшемся списке.
- Программа производит графическое построение согласно полученным данным. Но, как видим, в данном случае у нас имеется не только лишняя третья линия, но ещё и обозначения на горизонтальной оси координат не соответствуют тем, которые требуются, а именно порядку годов.
Сразу удалим лишнюю линию. Ею является единственная прямая на данной диаграмме — «Год». Как и в предыдущем способе, выделяем линию кликом по ней мышкой и жмем на кнопку Delete.
- Линия удалена и вместе с ней, как вы можете заметить, преобразовались значения на вертикальной панели координат. Они стали более точными. Но проблема с неправильным отображением горизонтальной оси координат все-таки остается. Для решения данной проблемы кликаем по области построения правой кнопкой мыши. В меню следует остановить выбор на позиции «Выбрать данные…».
- Открывается окошко выбора источника. В блоке «Подписи горизонтальной оси» кликаем по кнопке «Изменить».
- Открывается окошко ещё меньше предыдущего. В нём нужно указать координаты в таблице тех значений, которые должны отображаться на оси. С этой целью устанавливаем курсор в единственное поле данного окна. Затем зажимаем левую кнопку мыши и выделяем всё содержимое столбца «Год», кроме его наименования. Адрес тотчас отразится в поле, жмем «OK».
- Вернувшись в окно выбора источника данных, тоже щелкаем «OK».
- После этого оба графика, размещенные на листе, отображаются корректно.
Способ 3: построение графика при использовании различных единиц измерения
В предыдущем способе мы рассмотрели построение диаграммы с несколькими линиями на одной плоскости, но при этом все функции имели одинаковые единицы измерения (тыс. руб.). Что же делать, если нужно создать графики зависимости на основе одной таблицы, у которых единицы измерения функции отличаются? В Экселе существует выход и из этого положения.
Имеем таблицу, в которой представлены данные по объему продаж определенного товара в тоннах и по выручке от его реализации в тысячах рублей.
- Как и в предыдущих случаях выделяем все данные табличного массива вместе с шапкой.
- Клацаем по кнопке «График». Снова выбираем первый вариант построения из перечня.
- Набор графических элементов сформирован на области построения. Тем же способом, который был описан в предыдущих вариантах, убираем лишнюю линию «Год».
- Как и в предыдущем способе, нам следует на горизонтальной панели координат отобразить года. Кликаем по области построения и в списке действий выбираем вариант «Выбрать данные…».
- В новом окне совершаем щелчок по кнопке «Изменить» в блоке «Подписи» горизонтальной оси.
- В следующем окне, производя те же действия, которые были подробно описаны в предыдущем способе, вносим координаты столбца «Год» в область «Диапазон подписей оси». Щелкаем по «OK».
- При возврате в предыдущее окно также выполняем щелчок по кнопке «OK».
- Теперь нам следует решить проблему, с которой ещё не встречались в предыдущих случаях построения, а именно, проблему несоответствия единиц величин. Ведь, согласитесь, не могут располагаться на одной панели координат деления, которые одновременно обозначают и денежную сумму (тыс. рублей) и массу (тонны). Для решения данной проблемы нам потребуется произвести построение дополнительной вертикальной оси координат.
В нашем случае для обозначения выручки оставим ту вертикальную ось, которая уже имеется, а для линии «Объём продаж» создадим вспомогательную. Клацаем по данной линии правой кнопкой мышки и выбираем из перечня вариант «Формат ряда данных…».
- Запускается окно формата ряда данных. Нам нужно переместиться в раздел «Параметры ряда», если оно было открыто в другом разделе. В правой части окна расположен блок «Построить ряд». Требуется установить переключатель в позицию «По вспомогательной оси». Клацаем по наименованию «Закрыть».
- После этого вспомогательная вертикальная ось будет построена, а линия «Объём продаж» переориентируется на её координаты. Таким образом, работа над поставленной задачей успешно окончена.
Способ 4: создание графика зависимости на основе алгебраической функции
Теперь давайте рассмотрим вариант построения графика зависимости, который будет задан алгебраической функцией.
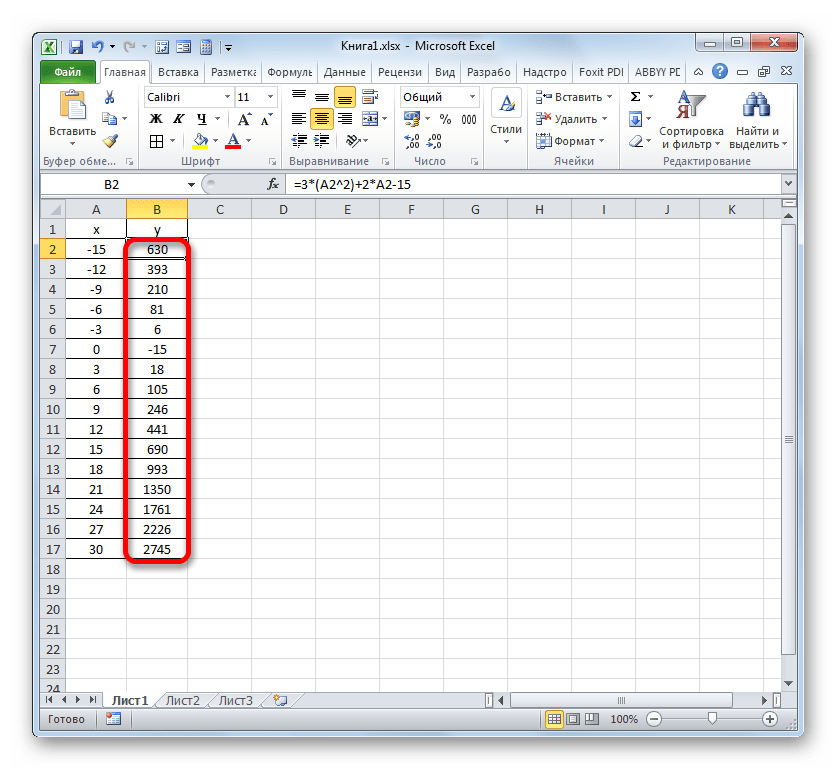
У нас имеется следующая функция: y=3x^2+2x-15. На её основе следует построить график зависимости значений y от x.
- Прежде, чем приступить к построению диаграммы, нам нужно будет составить таблицу на основе указанной функции. Значения аргумента (x) в нашей таблице будут указаны в диапазоне от -15 до +30 с шагом 3. Чтобы ускорить процедуру введения данных, прибегнем к использованию инструмента автозаполнения «Прогрессия».
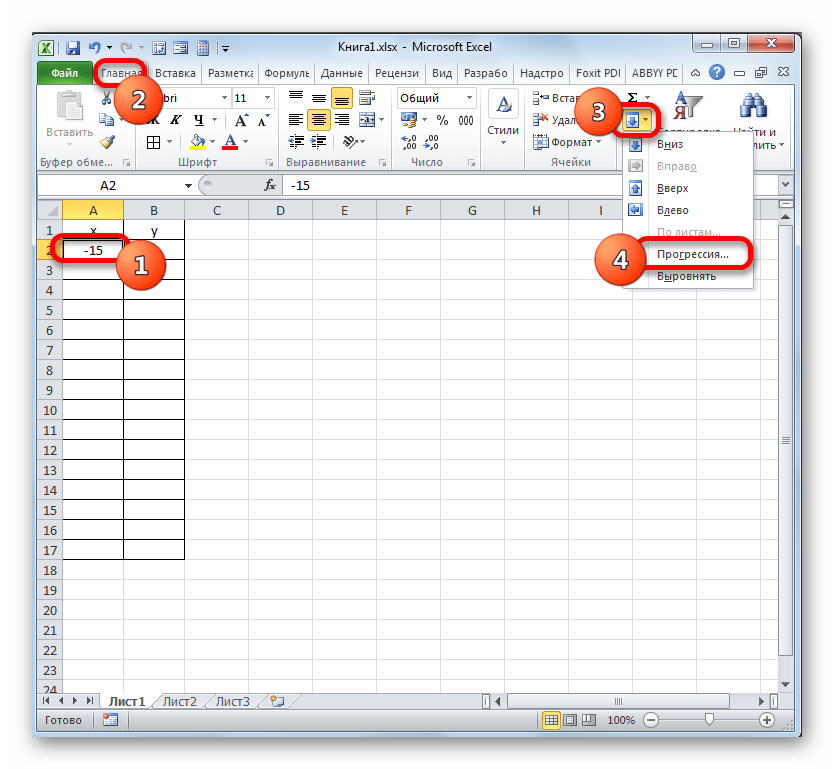
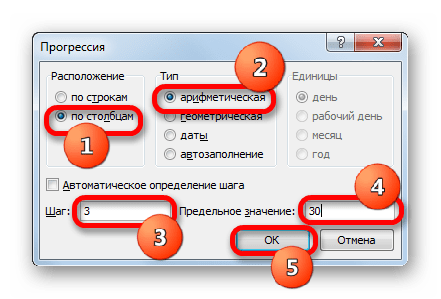
Указываем в первой ячейке столбца «X» значение «-15» и выделяем её. Во вкладке «Главная» клацаем по кнопке «Заполнить», размещенной в блоке «Редактирование». В списке выбираем вариант «Прогрессия…».
- Выполняется активация окна «Прогрессия». В блоке «Расположение» отмечаем наименование «По столбцам», так как нам необходимо заполнить именно столбец. В группе «Тип» оставляем значение «Арифметическая», которое установлено по умолчанию. В области «Шаг» следует установить значение «3». В области «Предельное значение» ставим цифру «30». Выполняем щелчок по «OK».
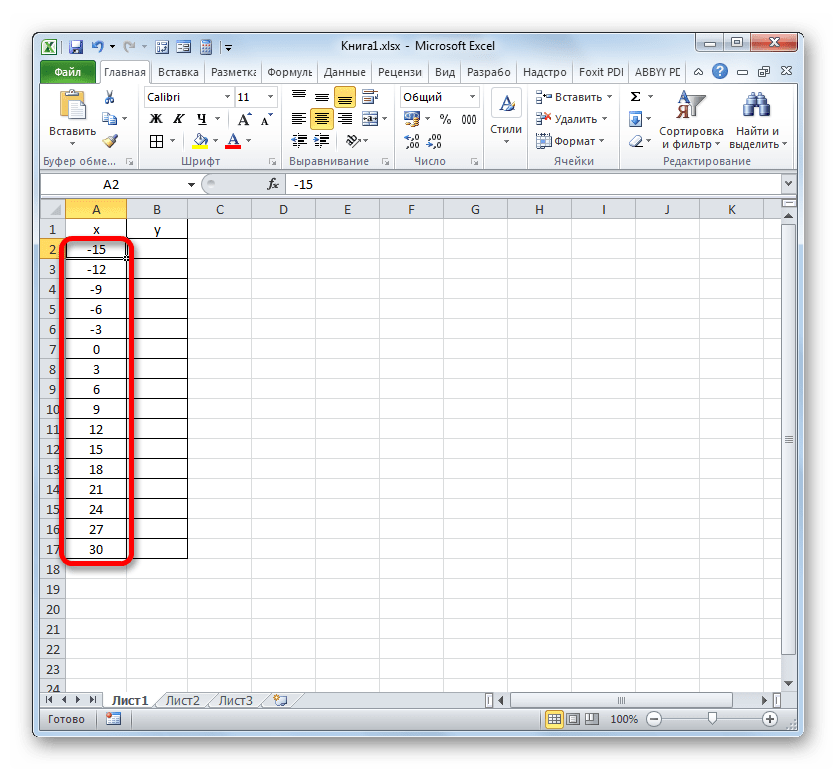
- После выполнения данного алгоритма действий весь столбец «X» будет заполнен значениями в соответствии с заданной схемой.
- Теперь нам нужно задать значения Y, которые бы соответствовали определенным значениям X. Итак, напомним, что мы имеем формулу y=3x^2+2x-15. Нужно её преобразовать в формулу Excel, в которой значения X будут заменены ссылками на ячейки таблицы, содержащие соответствующие аргументы.
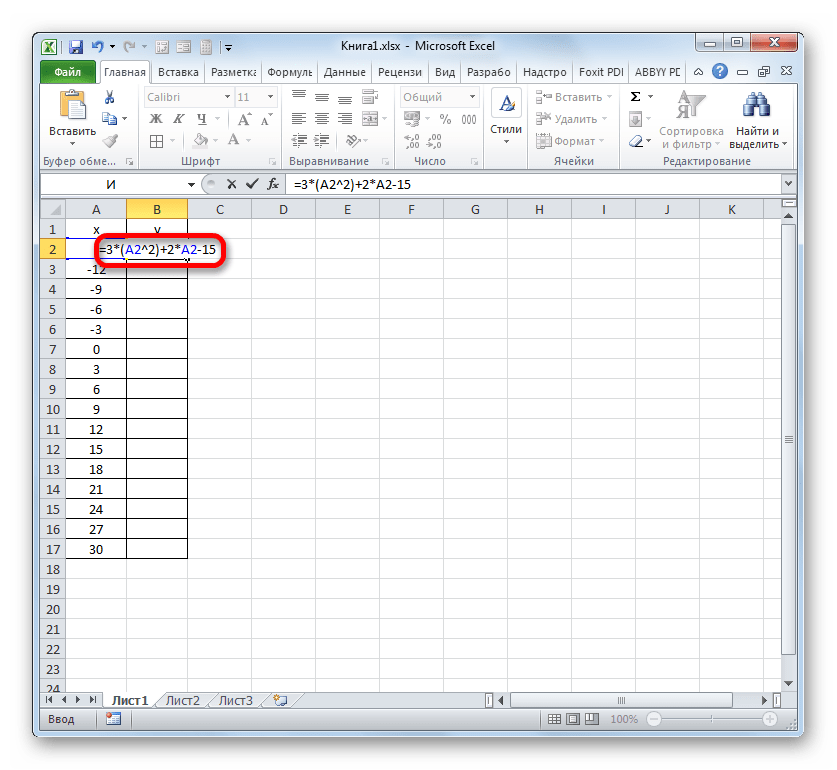
Выделяем первую ячейку в столбце «Y». Учитывая, что в нашем случае адрес первого аргумента X представлен координатами A2, то вместо представленной выше формулы получаем такое выражение:
=3*(A2^2)+2*A2-15Записываем это выражение в первую ячейку столбца «Y». Для получения результата расчета щелкаем по клавише Enter.
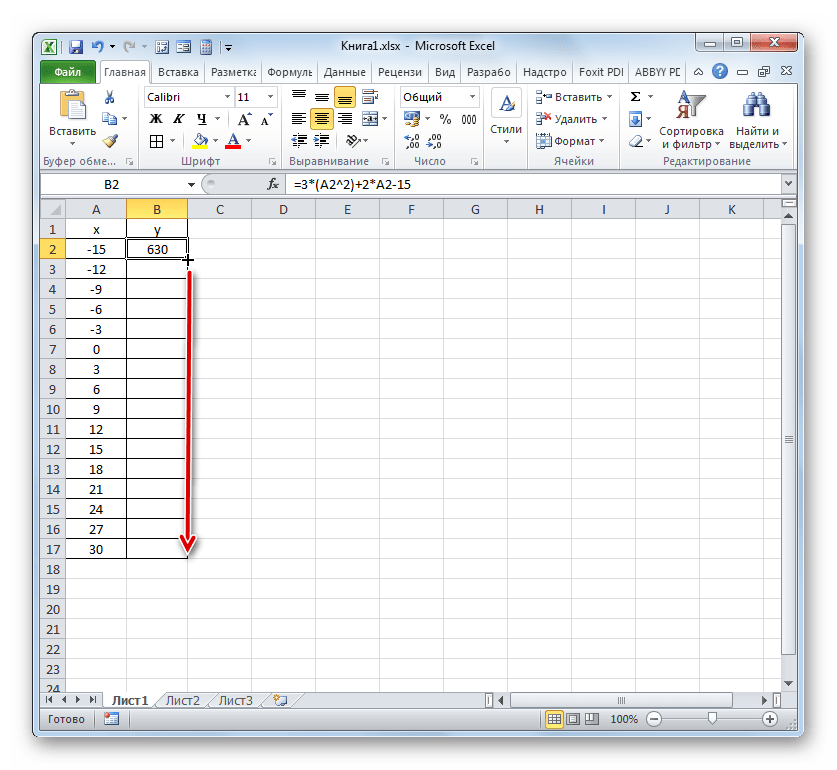
- Результат функции для первого аргумента формулы рассчитан. Но нам нужно рассчитать её значения и для других аргументов таблицы. Вводить формулу для каждого значения Y очень долгое и утомительное занятие. Намного быстрее и проще её скопировать. Эту задачу можно решить с помощью маркера заполнения и благодаря такому свойству ссылок в Excel, как их относительность. При копировании формулы на другие диапазоны Y значения X в формуле будут автоматически изменяться относительно своих первичных координат.
Наводим курсор на нижний правый край элемента, в который ранее была записана формула. При этом с курсором должно произойти преображение. Он станет черным крестиком, который носит наименование маркера заполнения. Зажимаем левую кнопку мыши и тащим этот маркер до нижних границ таблицы в столбце «Y».
- Вышеуказанное действие привело к тому, что столбец «Y» был полностью заполнен результатами расчета формулы y=3x^2+2x-15.
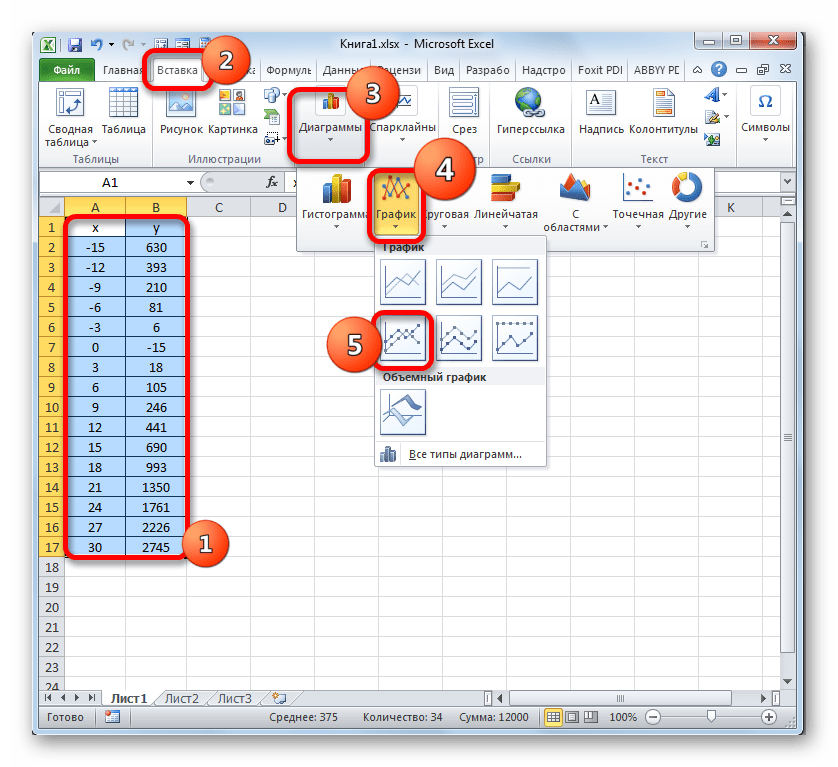
- Теперь настало время для построения непосредственно самой диаграммы. Выделяем все табличные данные. Снова во вкладке «Вставка» жмем на кнопку «График» группы «Диаграммы». В этом случае давайте из перечня вариантов выберем «График с маркерами».
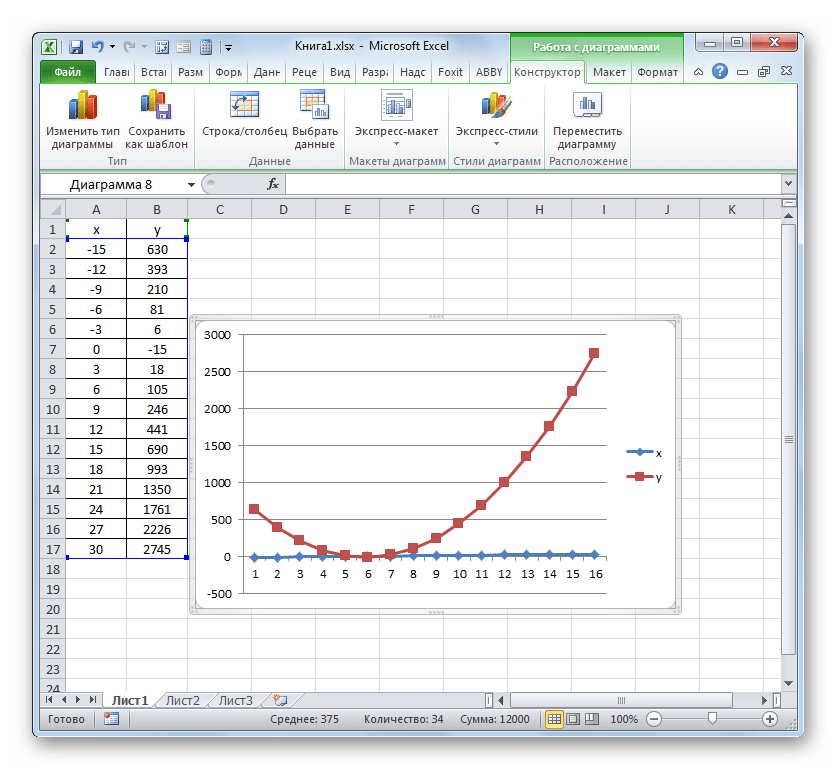
- Диаграмма с маркерами отобразится на области построения. Но, как и в предшествующих случаях, нам потребуется произвести некоторые изменения для того, чтобы она приобрела корректный вид.
- Прежде всего, удалим линию «X», которая разместилась горизонтально на отметке 0 координат. Выделяем данный объект и жмем на кнопку Delete.
- Легенда нам тоже не нужна, так как мы имеем только одну линию («Y»). Поэтому выделяем легенду и снова жмем по клавише Delete.
- Теперь нам нужно значения в горизонтальной панели координат заменить на те, которые соответствуют столбцу «X» в таблице.
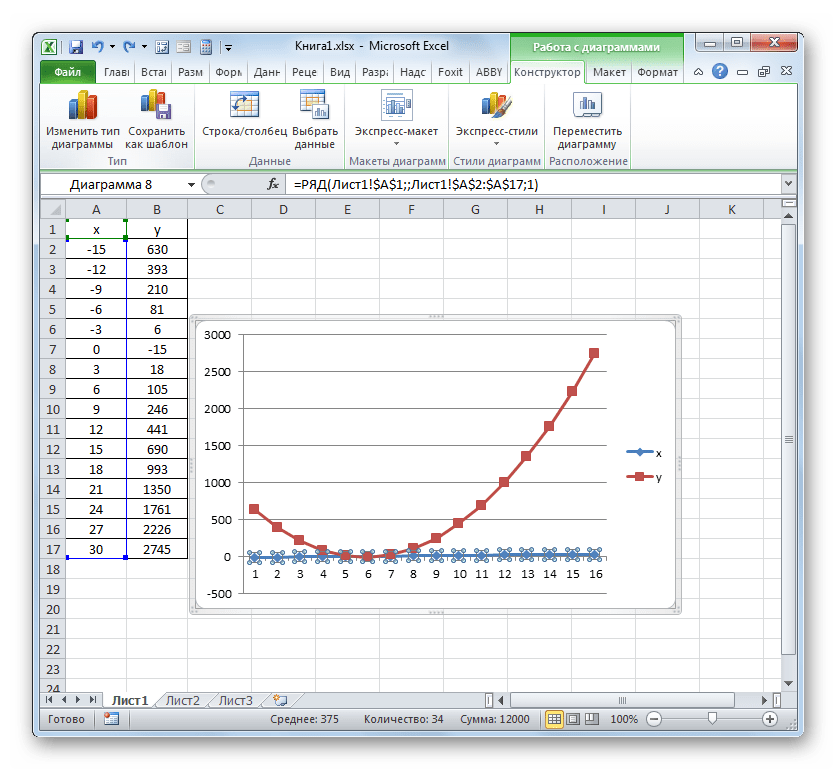
Кликом правой кнопки мыши выделяем линию диаграммы. В меню перемещаемся по значению «Выбрать данные…».
- В активировавшемся окне выбора источника клацаем по уже хорошо знакомой нам кнопке «Изменить», располагающейся в блоке «Подписи горизонтальной оси».
- Запускается окошко «Подписи оси». В области «Диапазон подписей оси» указываем координаты массива с данными столбца «X». Ставим курсор в полость поля, а затем, произведя необходимый зажим левой кнопки мыши, выделяем все значения соответствующего столбца таблицы, исключая лишь его наименование. Как только координаты отобразятся в поле, клацаем по наименованию «OK».
- Вернувшись к окну выбора источника данных, клацаем по кнопке «OK» в нём, как до этого сделали в предыдущем окне.
- После этого программа произведет редактирование ранее построенной диаграммы согласно тем изменениям, которые были произведены в настройках. График зависимости на основе алгебраической функции можно считать окончательно готовым.
Урок: Как сделать автозаполнение в Майкрософт Эксель
Как видим, с помощью программы Excel процедура построения графика зависимости значительно упрощается в сравнении с созданием его на бумаге. Результат построения можно использовать как для обучающих работ, так и непосредственно в практических целей. Конкретный вариант построения зависит от того, на основе чего строится диаграмма: табличные значения или функция. Во втором случае перед построением диаграммы придется ещё создавать таблицу с аргументами и значениями функций. Кроме того, график может быть построен, как на основе одной функции, так и нескольких.
Еще статьи по данной теме:
Помогла ли Вам статья?
Содержание
- 1 Строим графики с точками пересечений
- 2 Находим точку пересечения графиков в Excel
- 3 Точки пересечения для трех показателей
- 4 Хороший вопрос…
- 5 Скачать пример
-
- 5.0.1 ChartsIntersection.xlsx
-
- 6 Решение
- 6.1 Шаг 1
- 6.2 Шаг 2
- 6.3 Шаг 3
- 7 Пересечение двух графиков
- 8 Как найти точку пересечения графиков функций в excel
- 9 Как найти точку пересечения графиков функций в excel
- 10 Точка пересечения графиков в Excel
- 11 Пересечение двух графиков
- 12 Пересечение графика с осями координат
-
-
- 12.0.0.1 Поделиться с друзьями:
- 12.0.0.2 Поиск по сайту:
-
- 12.1 Похожие статьи:
-
- 13 Комментарии (6)
- 13.1 Добавить комментарий Отменить ответ
- 13.2 Свежие записи
- 13.3 Содержание
-
- 13.3.0.1 Обратная матрица в Excel
-
- 14 Как найти точку пересечения графиков функций в excel
- 15 Точки пересечения графиков — MS Excel
Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.
Строим графики с точками пересечений
Имеются две функции, по которым нужно построить графики:
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:
- Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
- Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.
Первый способ. Найти общие значения в рядах данных для указанных функций.
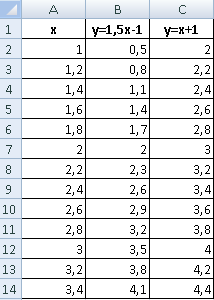
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.
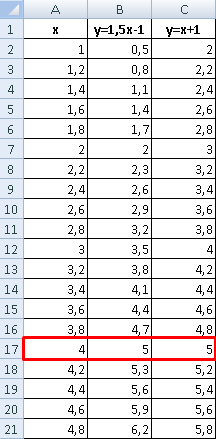
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.
Изменим график, добавив новые данные. Получим две пересекающиеся линии.
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.
Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.
Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.
Точки пересечения для трех показателей
Существует три показателя, которые измерялись во времени.
По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).
Получается такой рисунок:
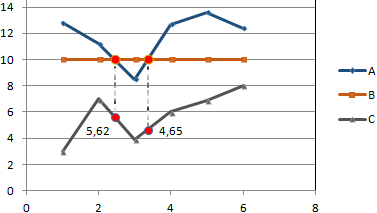
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:
Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.
Хороший вопрос…
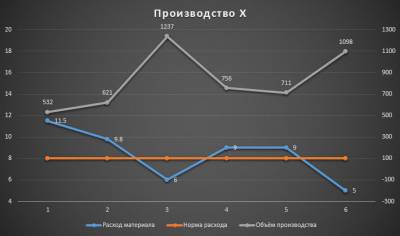
Задали мне тут недавно вопрос. Есть график, на котором имеем 3 показателя работы производства: удельный расход материала, норматив расхода и объём производства, а по горизонтальной оси временной период (недели, например).
Исходные данные выглядят так:
Удельный расход материала зависит от объёма производства. Он то выше, то ниже норматива по итогам периода и возникает естественный вопрос показать на диаграмме те моменты времени и те объёмы производства, когда линия расхода пересекает линию норматива. Может быть эта проблема и лишена какого-то великого смысла, но тем не менее вопрос был задан, значит потребность такая у людей есть.
А это наша конечная цель:
Скачать пример
ChartsIntersection.xlsx
Решение
Шаг 1
Для начала обратим внимание, что исходный тип диаграммы — График с маркерами.
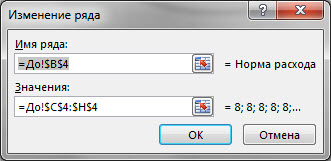
Ряды этого типа описываются так:
Заметьте, что тут нет значений координат по оси X, а есть только координаты по условной оси Y. Этим подразумевается, что условная ось X — общая для всех рядов, а также, что при их построении не используются значения, отличные от заранее фиксированного ряда оси X. Вот есть у нас периоды: 1, 2, 3 и т.д., нанесенные на ось Х, и использовать можно только их. Периода, где X=3.5 не существует для данного типа диаграммы.
Однако, нам для решения этой задачи необходимо, чтобы мы могли задавать любое значение X, в том числе промежуточные, так как наши линии как раз пересекаются где-то «между периодами». Поэтому тип диаграммы мы меняем для всех рядов с «графика с маркерами» на «точечную с прямыми отрезками и маркерами».
Следует упомянуть, что наш случай осложняется наличием двух вертикальных осей: основной и вспомогательной, так как значения расхода материала и объёма производства сильно друг от друга отличаются.
Шаг 2
Теперь нам необходимо нанести на диаграмму дополнительные ряды данных:
-
Точки пересечения линий расхода материала с нормами расхода. Таких точек у нас будет 3, исходя из условий примера. Эти точки нам необходимо будет расчитать, вспомнив школьный курс геометрии (см. лист Треугольники). В файле учебного примера на листе После в таблице N3:Q5 мы получили координаты нужных точек путем нехитрых формул. Тип диаграммы Точечная в отличие от рядов с показателями работы производства.
-
Точки пересечения найденных значений по оси X с объемом производства. Расчитывается в таблице N8:Q10 по близким формулам. Тип диаграммы Точечная.
-
Пунктирные линии, которые мы рисуем из эстетических соображений. Таблица с их координатами находится в N12:P18.
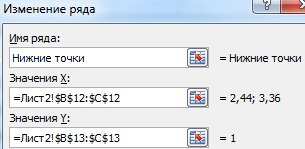
Добавляем ряды данных в соответствии с теми точками, которые мы расчитали. Щёлкните ПКМ по диаграмме и выберите «Выбрать данные…», далее воспользуйтесь кнопкой «Добавить».
Пример одного из рядов:
Шаг 3
Отформатируйте линии и маркеры новых рядов данных, так как вам необходимо. Готово! 🙂
Изучим способы поиска точек пересечения двух графиков и графика с осью координат, а также варианты их отображения в Excel.
Поиск точек пересечения графиков может применяться, к примеру, при графическом способе решения различных уравнений в математике или при поиске точки безубыточности предприятия в бизнесе.
Если графики заданы какими-либо алгебраическими функциями, то точное решение оптимальнее искать математически, приравняв функции друг к другу.
В данной статье мы разберем как найти точки пересечения для линейного графика, в котором линии имеют одинаковые координаты по оси абсцисс (горизонтальная) и различные координаты по оси ординат (вертикальная).
Как мы помним из школьного курса математики, через две любые несовпадающие точки можно провести прямую и только одну.
Поэтому зная их координаты мы можем составить уравнение прямой. Таким образом решая систему уравнений, состоящую из уравнений двух прямых, мы можем найти место пересечения:
Общий принцип поиска координат следующий: для каждых двух соседних пар точек на оси абсцисс (на рисунке x1 и x2 расположены по горизонтали) проверяется условие пересекаются ли линии, то есть выполняется ли условие y1 ≥ z1 и y2 ≤ z2, или наоборот y1 ≤ z1 и y2 ≥ z2 (на рисунке y1, y2, z1 и z2 расположены по вертикали).
Пересечение двух графиков
Предположим, что у нас имеется таблица с координатами двух линий:
Построим на основе этих данных точечную диаграмму. Выделяем диапазон данных A1:K3 и на панели вкладок выбираем Вставка -> Диаграмма -> Точечная -> Точечная с прямыми отрезками.
В итоге получаем точечную диаграмму с двумя линиями:
Как видим на диаграмме линии пересеклись в 5 местах. В общем случае подобных точек может быть сколь угодно много, поэтому вручную находить каждую из них представляется достаточно трудоемким процессом.
Чтобы упростить работу и автоматизировать расчет воспользуемся средствами Visual Basic.
Переходим в редактор VBA (в панели вкладок выбираем Разработчик -> Visual Basic или воспользуемся сочетанием клавиш Alt + F11), создаем модуль и записываем в него макрос (напротив каждой строчки даются пояснения к коду):
|
Sub IntersectionGraph() X = ActiveChart.SeriesCollection(1).XValues ‘Значение по оси X Y = ActiveChart.SeriesCollection(1).Values ‘Значения 1-ой линии по оси Y Z = ActiveChart.SeriesCollection(2).Values ‘2-ой TotalCount = ActiveChart.SeriesCollection(1).Points.Count ‘Подсчет количества точек по X Dim ArrayT1() As Double ‘Определение массива для хранения координат по X Dim ArrayT2() As Double ‘по Y ReDim ArrayT1(TotalCount) ‘Определение размера массива ReDim ArrayT2(TotalCount) k = 0 ActiveChart.SeriesCollection(1).Select For i = 1 To TotalCount — 1 ‘Цикл по всем точкам X1 = X(i) X2 = X(i + 1) Y1 = Y(i) Y2 = Y(i + 1) Z1 = Z(i) Z2 = Z(i + 1) If (Y1 >= Z1 And Y2 РЕШЕНИЕ: ||| Вариант решения 1. ||| 1) Высота, проведенная из вершины прямого угла, делит треугольник на два подобных треугольника между собой и подобных данному. Из подобия треугольников АВС и НСВ следует: В=НСА. 2) Медиана, проведенная из вершины прямого угла, равна половине. Как найти точку пересечения графиков функций в excelЭтот файлик может пригодиться для оформления задач поиска точки пересечения линейных графиков, построенных по экспериментальным данным. Графики выстраиваются по точкам эксперимента. Рассчитываются коэффициенты А и В функций, рассчитывается точка пересечения и отображается на графике. Теперь при изменении значений точка корректно отображается на графике. Нашел у Павлова пример с поиском многоточечных пересечений. Совсем немножко добавил от себя. Может тоже пригодиться для оформления лабораторных. Как найти точку пересечения графиков функций в excelТочка пересечения графиков в ExcelИзучим способы поиска Точек пересечения двух графиков и графика с осью координат, а также варианты их отображения в Excel. Если графики заданы какими-либо алгебраическими функциями, то точное решение оптимальнее искать математически, приравняв функции друг к другу. В данной статье мы разберем как Найти точки пересечения для линейного графика, в котором линии имеют одинаковые координаты по оси абсцисс (горизонтальная) и различные координаты по оси ординат (вертикальная). Как мы помним из школьного курса математики, через две любые несовпадающие точки можно провести прямую и только одну. Поэтому зная их координаты мы можем составить уравнение прямой. Таким образом решая систему уравнений, состоящую из уравнений двух прямых, мы можем найти место пересечения: Пересечение двух графиковПредположим, что у нас имеется таблица с координатами двух линий: Построим на основе этих данных точечную диаграмму. Выделяем диапазон данных A1:K3 и на панели вкладок выбираем Вставка -> Диаграмма -> Точечная -> Точечная с прямыми отрезками. В итоге получаем точечную диаграмму с двумя линиями: Как видим на диаграмме линии пересеклись в 5 местах. В общем случае подобных точек может быть сколь угодно много, поэтому вручную находить каждую из них представляется достаточно трудоемким процессом. Чтобы упростить работу и автоматизировать расчет воспользуемся средствами Visual Basic. Переходим в редактор VBA (в панели вкладок выбираем Разработчик -> Visual Basic или воспользуемся сочетанием клавиш Alt + F11), создаем модуль и записываем в него макрос (напротив каждой строчки даются пояснения к коду): Переходим обратно в Excel, нажимаем на диаграмму (для активации) и запускаем макрос: Осталось только добавить на свое усмотрение некоторые детали для улучшения визуализации и получаем итоговый вариант: Для удобства и экономии времени, определение вида и цвета отображаемой точки, формата подписи данных и прочих настроек, можно также добавить в код макроса. Пересечение графика с осями координатАналогичное решение можно применить и в случае поиска мест пересечения графика с осью абсцисс. Для этого в качестве координат одной из линий установим нулевые значения: Применяем к графику макрос и получаем: Удачи вам и до скорых встреч на страницах блога Tutorexcel. ru! Поделиться с друзьями:Поиск по сайту:Похожие статьи:Комментарии (6)Очень здорово, вопрос один. А если график 3 или более функций и можно ли как то значения автоматом в таблицу занести В случае если на графике 3 линии, то в макросе нужно будет дополнительно прописать проверки на пересечение каждой пары линий (т. е. первой и второй, первой и третьей, второй и третьей). Координаты точек пересечений хранятся в массивах ArrayT1 (ось X) и ArrayT2 (ось Y), соответственно чтобы занести эти координаты в таблицу, мы должны приравнять значения ячеек таблицы к элементам массивов. Спасибо за ответ, только если честно я конструктор, и незнаком с программированием, скажите возможно ли связаться с Вами для решения моей проблемы? Здравствуйте, помогите пожалуйста, мне нужно найти пересечение двух графиков, точки взяты произвольно, формул никаких нет. Я пробовала вставить вашу программу, но выдает ошибку Анастасия, в данной статье разбирается случай, когда графики имеют одинаковые координаты по горизонтальной оси, и разные координаты по вертикальной. В приведенном примере, в случае с красной линией, это условие не выполняется, вероятно по этой причине возникает ошибка. Добавить комментарий Отменить ответСвежие записиСодержаниеЧитайте ранее: Обратная матрица в ExcelПодробно рассмотрим особенности вычисления обратной матрицы в Excel и примеры использования функции МОБР. Как найти точку пересечения графиков функций в excelТочки пересечения графиков — MS ExcelНадо найти точки пересечения их. я сделал, но они почему то не пересекаются, может кто подсказать что я делал не так? сейчас скину формулу из ячеек Как в графике отобразить точки пересечения? А также также рядом указать сумму точки x+y как в примере. То есть пример точки 31=30+1 или. Доброго времени суток! Являюсь полным нубом относительно Excel. Задача такая: Построить графики двух уравнений и найти их точки. Здравствуйте! Помогите, пожалуйста, правильно построить графики в Excel. Вот на этом рисунке данные и графики, которые у меня получаются. Доброго времени суток. Нужна ваша помощь. Есть некие графики сделанные мною в другой программе, но потребовалась все это построить в. Помогите построить 5 графиков в одной сетке(поле) зависимость объема от обратного давления. Первый столбец — объем, он постоянен для всех. Здравствуйте, у меня есть задания которые необходимо выполнить в excele. У меня не получается выполнить задание под буквой В в первом. Да, дейстаительно они не пересекаются. Т.е. система уравнений не имеет корней. А откуда третье уравнение? Решение из маткад, у системы комплексные корни Bantline везет же вам с задачами. Krasme, я знаю, что не окружность. то я вчера где-то накосячил. Сам сегодня удивился Здравствуйте, уважаемые Специалисты! Помогите пожалуйста с совмещением двух графиков различного типа(если это конечно возможно). У меня. Помогите разобраться! Что к чему? Выделенные слова вообще могут использоваться в тексте программы? Private Sub CommandButton1_Click() . Всем привет. Как можно отобразить все значения на одном графике, а не на двух? |
Построение графиков в Excel по данным таблицы
В MS Excel есть возможность не только проводить вычисления, используя разные формулы, но и также строить на их основе различные диаграммы: гистограммы, круговые диаграммы, точечные и т.д.
В этом уроке мы разберем, для чего применяют графики.
И так, графики – это разновидность диаграммы, схожая с гистограммой. Они бывают трех видов: простой, график с накоплением и нормированный график с накоплением. Каждый из этих графиков бывает двух видов: с маркером и без. Так эти два вида строятся одинаково, рассмотрим только маркированные графики.
Коротко опишем применение каждого графика, и далее на примерах разберем более подробно, как их построить.
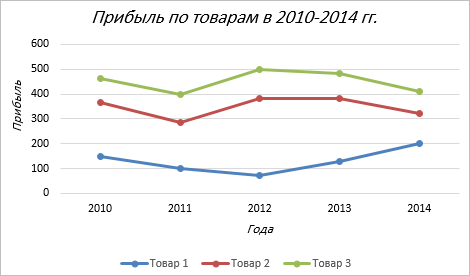
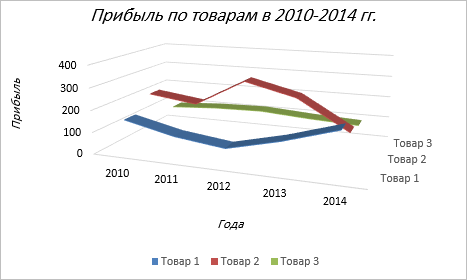
a) Простой график нужен для того, чтобы изобразить, как изменяется некое значение во времени (прибыль по месяцам; рождаемость по годам и т.д.).
b) График с накоплением показывает, как изменяется составляющая целого значения с течением времени. (Лучше использовать диаграмму с накоплением)
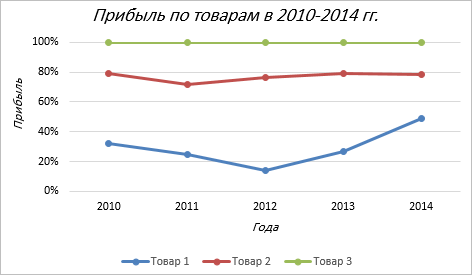
c) Нормированный график с накоплением показывает изменение доли каждого значения с течением времени.
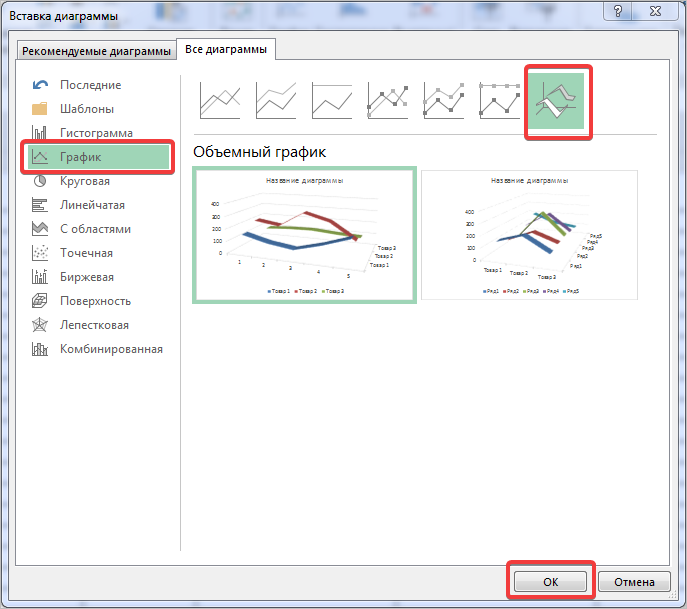
Есть еще объемный график, который схож с простым графиком. Поэтому мы покажем только его конечный вид.
Простая диаграмма
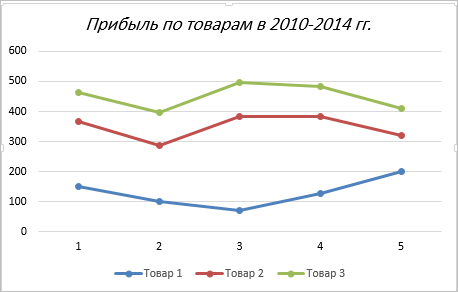
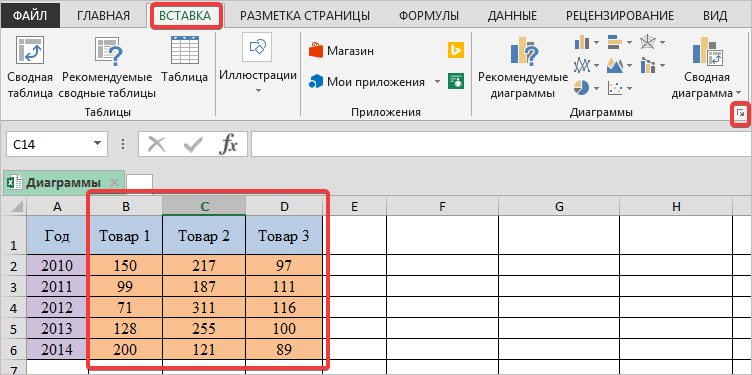
Рассмотрим простой график на примере таком примере прибыли некоторой фирмы по 3 товарам за определенный период. Для этого выделим нужные нам ячейки, как на рисунке ниже.
Теперь строим простой маркированный график. Для этого выделяем диапазон В1:D6, на главное ленте выбираем Вставка–Диаграммы (нажимаем на стрелочку справа сверху).
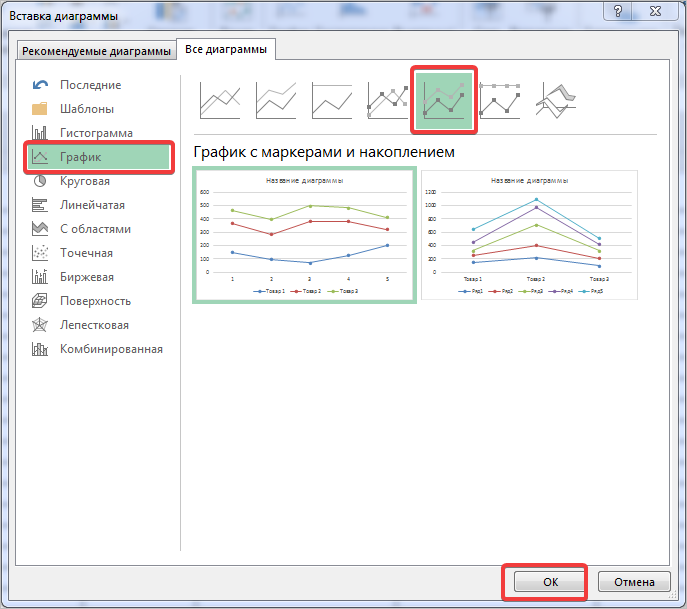
В появившемся окне выберем нужную нам диаграмму. В первом случае – простой график. Нажимаем ОК.
Выбираем график слева, т.к. он показывает изменение прибыли во времени.
Если вы все сделали правильно, то должно получиться так, как на рисунке ниже:
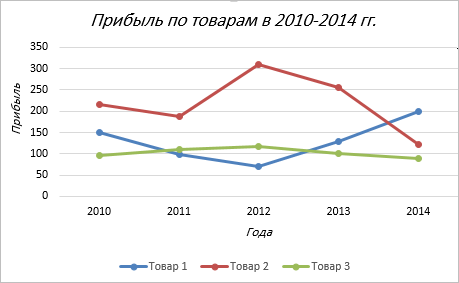
Итак, диаграмма построена, но на ней не отображаются года. Изменить название диаграммы очень просто. Нужно нажать на заголовок и ввести подходящее название. Например, Прибыль по товарам в 2010-214 гг.
Для того, чтобы года отображались на оси Х, необходимо нажать на ось правой кнопкой мыши для вызова контекстного меню и нажать Выбрать данные.
После этого появится такое окошко:
Изменяем подписи горизонтальной оси. Должно открыться такое окошко:
Нажимаем туда, где выделено красным и выбираем диапазон. В нашем случае это А2:А6. И нажимаем клавишу Enter и ОК. В результате этого должно открыться предыдущее окно, но выглядеть будет следующим образом:
Нажимаем ОК, меняем название диаграммы. Теперь она должна выглядеть так:
Осталось добавить подписи данных. В версии Excel 2013–2016 это делается очень просто. Нажимаем на плюсик справа, который вызывает различные команды и ставим галочку Название осей. Должно получиться так:
Как и в случае с названием, ставим курсор в область каждой из осей и подписываем их согласно условию. Например, ось Х – Год, ось Y – Прибыль. Должно получиться так, как на рисунке ниже:
В MS Excel версиях 2007-2010 форматировать оси, область диаграммы и т.д. с помощью дополнительной вкладки на ленте Работа с диаграммами.
График с накоплением
Строим по этим же данным график с накоплением. Повторяем все те же самые действия, как и в п.1.
Поэтому мы покажем начало, на котором видно, какой график выбираем, и конец, на котором виден результат работы.
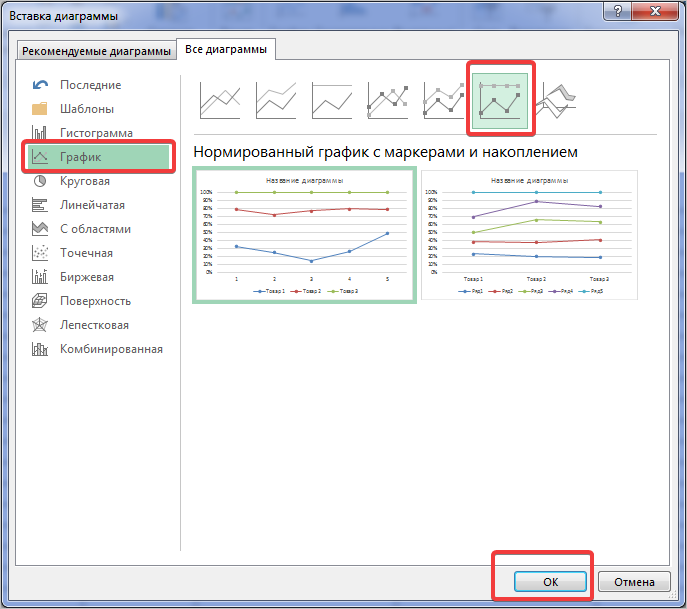
Нормированный график с накоплением
Рассмотрим третий тип графика на том же примере, выполняя все действия, как в первых двух пунктах.
Объемный график
Объемный график похож на первый с той лишь разницей, что выполнен в объеме.
В этой работе были рассмотрены различные варианты построения такой разновидности диаграмм, как графики. А также случаи их применения. Для изучения построения диаграмм в программе Эксель заходите читать статьи на Справочнике!
Тест по теме «Графики в Excel»
Как построить график в Excel с учетом погрешностей? Подобная задача нередко возникает у студента при обработке результатов лабораторных работ. Результаты представляют собой, как правило, два массива данных (в общем случае Х и Y). Пусть, для примера, имеется следующая экспериментальная зависимость:
| Х | 2,0 | 4,0 | 5,0 | 7,0 | 9,0 | 11,0 | 15,0 |
| У | 3,2 | 4,2 | 9,0 | 14,8 | 23,0 | 15,2 | 12,8 |
Требуется представить эту зависимость Y от Х графически. Получится примерно то, что представлено на рисунке.
Например, в ходе лабораторной работы студент измерял зависимость силы тока в одной из ветвей электрической цепи (в Амперах) от напряжения на том или ином ее элементе (в Вольтах). Необходимо отложить данные на графике с учетом погрешностей.
Надо сказать, что сделать построение вручную, как ни парадоксально, в данном случае даже немного проще, чем с использованием, казалось бы, такой мощной и удобной программы, как Excel . Дело в том, что, на самом деле, график, приведенный на предыдущем рисунке… построен неверно.
Почему? Ведь, вроде бы, ничего сложного нет. Нажимаем в Excel кнопку « Мастер диаграмм », Выбираем тип диаграммы – точечная . Затем нажимаем « Далее », задаем массивы для X и Y, затем опять « Далее »… — и вскоре получится то, что приведено на предыдущем рисунке.
Вроде бы, все правильно. Да только график построен строго по точкам. Видно, что зависимость немонотонная, с достаточно острым максимумом – что не всегда имеет место в реальности. Ибо в реальности подавляющее большинство зависимостей могут быть более плавными.
А вот если анализировать данные, скажем, из области психологии, физики, биологии (отчасти), а также из ряда иных отраслей, то там графики экспериментальных зависимостей, за немногим исключением, зачастую являются достаточно плавными (хотя, все относительно, конечно) .
Но, вроде бы, и здесь нет никаких проблем: следует провести линию тренда, которых Excel предлагает несколько типов. Так, можно выбрать линейный, степенной, экспоненциальный и т.д. тренд.
Можно… На примере выбранных нами данных, выбор показал, что наиболее близким для выбранной совокупности данных является параболический тренд. Отобразим его на рисунке.
Вроде бы, то, что проведено черной линией (тренд), уже гораздо ближе к истине. Правда, совсем ненамного. Фактически, проведенный тренд достаточно хорошо соответствует исходным данным только для 3, 4 и 7-й точек. Для остальных точек имеются существенные расхождения, причем ошибка доходит до 80%.
Ясно, что построенный тренд, в силу его высокой погрешности, в данном случае никак нельзя принять в качестве качественного графика, отражающего ход зависимости, выявленной экспериментально. Однако, и первоначально построенную (синюю) линию, вероятно, также нельзя принять в качестве такового, ибо, повторимся, она вообще не учитывает погрешностей.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Линия тренда регрессии лайнера на приведенном выше графике подчеркивает, что между переменными x и y существует общая восходящая взаимосвязь, несмотря на несколько падений на графике. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Чтобы отформатировать линию тренда, щелкните ее правой кнопкой мыши и выберите Формат Trendline, Это снова откроет окно Format Trendline, из которого вы можете нажать Цвет линии, Выбрать Сплошная линия и нажмите цвет поле, чтобы открыть палитру, из которой вы можете выбрать альтернативный цвет для линии тренда.
Как добавить линейную регрессию в графики Excel — Autotak
- Если частота равна нулю (т.е. происходит равномерная деформация материала), то необходимо применять установки для растяжения/сжатия, способные измерить работу, затраченную на нагрев материала в процессе деформации.
- Если говорить о частоте, когда ее значения лежат в пределах 10 Гц… 1000 Гц, то такие измерения проводятся при помощи совсем других установок, например, с использованием так называемых крутильных маятников (т.е. когда образец совершает вынужденные крутильные колебания заданной частоты).
- Если вести речь о диапазоне частот 20 кГц… 200 кГц то здесь необходимо применять ультразвуковые установки.
- Наконец, исследования при гиперзвуковых частотах (более 10 9 Гц) проводятся при помощи оптических, пьезоэлектрических методов.
Аппроксимация в Matlab по МНК осуществляется с помощью функции polyfit. Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n+1, содержащая коэффициенты аппроксимирующего полинома.
| Х | 2,0 | 4,0 | 5,0 | 7,0 | 9,0 | 11,0 | 15,0 |
| У | 3,2 | 4,2 | 9,0 | 14,8 | 23,0 | 15,2 | 12,8 |
Как добавить линию тренда в диаграмме?
- Щелкните правой кнопкой мыши по ряду данных и в контекстном меню нажмите Добавить линию тренда (Add Trendline).
- Перейдите на вкладку Параметры линии тренда (Trend/Regression Type) и выберите Линейная (Linear).
- Укажите количество периодов, включаемых в прогноз, – введите число “3” в поле Вперёд на (Forward).
Аппроксимация в Matlab по МНК осуществляется с помощью функции polyfit. Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n+1, содержащая коэффициенты аппроксимирующего полинома.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Если уравнение задано в декартовых координатах, то следует перевести его в полярные, используя формулы X R COS F , Y R SIN F. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Если уравнение задано в декартовых координатах, то следует перевести его в полярные, используя формулы: X=R*COS(F), Y=R*SIN(F). Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения кривой.
Как настроить графики в Excel: пошаговая инструкция
- Создайте диаграмму (график).
- Выделите линию функции на графике и нажмите правую кнопку мыши, выберите «Добавить линию тренда»
- Выберите тип аппроксимации во вкладке «Тип» в откурывшемся диалоговом окне «Линия тренда»
- На вкладке «Параметры» — прогностические параметры, показывать уравнение на графике или нет
Чтобы создать точечную диаграмму в Excel на устройствах Android или iOS, вам необходимо установить приложение Microsoft Excel на телефон (установить Microsoft Excel на Android или Microsoft Excel для iOS).
С несколькими кривыми
Несмотря на то, что данных будет больше, принцип построения остается прежним:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Цель работы показать алгоритм построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Цель работы – показать алгоритм построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Результаты исследования: в процессе работы я:
Как создать точечный график в Excel
- Выделить ось, для которой будет добавлена еще одна. Клацнуть по ней правой кнопкой мышки, из контекстного меню выбрать «Формат ряда данных». В новом открывшемся окне во вкладке «Параметры ряда» отметить пункт «По вспомогательной оси».
Здравствуйте! Мне нужно проанализировать ряд данных и выявить возможные зависимости, а именно: на производстве ежедневно считается дебаланс по сырью. Он может зависеть от большого количества факторов (есть данные). Как с помощью графиков выяснить какой фактор действительно влияет на дебаланс?
Простой график для одной переменной
Проще всего разобраться, как построить график в Эксель по данным таблицы, состоящей всего из двух колонок. Для наглядного примера можно взять названия месяцев и объем полученной за это время прибыли. Ряд будет только один, а осей на графике — две. Строить диаграмму можно по следующей пошаговой инструкции:
- Выделить таблицу с данными.
- Перейти на вкладку «Вставка», где можно выбирать вариант диаграммы: например, простой график функции, круговой или точечный.
- Убедиться в том, что данные в таблице были автоматически распределены так, как это было запланировано. В данном случае ошибки нет: значения указаны по оси X, даты — по OY.
Если пользователь случайно ошибся при построении графика или хочет изменить информацию, он может поменять настройки, выделив область построения диаграммы и использовав контекстное меню. Попасть в него легко с помощью клика правой кнопкой мыши. Изменению подлежат тип графика, данные для его построения, форматы сетки и каждой оси.
Перейдя в контекстном меню к пункту «Выбрать данные», можно настроить, какая информация будет отображаться. Например, для указанного примера у пользователя есть возможность выделять данные только для конкретных месяцев. Для этого достаточно убирать галочки с ненужных дат или изменить формулу в графе «Диапазон данных для диаграммы».
Стоит отметить, что построение графика по представленным в табличной форме данным обеспечит автоматическую перестройку линии при изменении информации. Например, если в показатели прибыли были внесены корректировки на основании более точных сведений, диаграмма станет другой без дополнительных действий со стороны пользователя. Точно так же изменятся и все названия, если откорректировать их на графике.
Легенду с названием графика при использовании только одного изменяющегося показателя оставлять необязательно. В современных версиях Excel имя ряда данных не будет показано на диаграмме автоматически. В более старых пакетах MS Office легенду можно удалить вручную.
Чтобы оценивать информацию на графике было проще, стоит выделить линию, в виде которой представлен ряд, и в контекстном меню указать необходимость добавления подписей. Результатом станет появление значений прямо на диаграмме — с той же точностью, с которой они указаны в таблице.
На вкладке «Конструктор» можно поменять еще больше настроек — выбрать экспресс-макет и готовый шаблон, изменить цвета и добавить дополнительные элементы графика. В том числе — подписи к осям данных, названия которых в последних версиях MS Excel вводятся вручную.
Также читайте, как сделать кнопку в Excel, чтобы быстрее перейти у нужной таблице или графику.
График с несколькими переменными
Узнав, как в Эксель нарисовать график при наличии только одного столбца со значениями, стоит перейти к решению более сложной задачи — составлению диаграмм, на которых будет несколько рядов.
Если рассматривать тот же пример, вместе с прибылью могут быть представлены еще накладные расходы. Принцип создания будет включать такие шаги:
- Выделить таблицу с данными, захватив все колонки.
- На вкладке «Вставка» выбрать тип диаграммы.
- Проверить, соответствует ли автоматически построенный программой график нужным требованиям. Если нет — изменить настройки вручную.
Для графика с двумя и большим количеством рядов данных стоит оставить «легенду» с подписями. Она позволит разобраться, каким цветом, оттенком или типом линии отмечен нужный показатель. Однако название диаграммы в этом случае придется вносить вручную — или указать в настройках, в какой ячейке таблицы расположен нужный текст.
С помощью контекстного меню на состоящем из нескольких рядов графике можно менять различные настройки, характеристики осей и линий, добавлять подписи и менять шрифты. А при изменении информации в таблице это автоматически отразится и на диаграмме. Данные, которые вводились вручную, (например, название оси или графика) придется менять тем же способом.
Добавление второй оси
Иногда информация может быть представлена в таблице так, что поместить ее на одной общей диаграмме, на первый взгляд, невозможно. Если представить, что накладные расходы указаны не в рублях, а в долларах, график получится некорректным.
Можно построить две разных диаграммы для каждого ряда данных. Или перед тем, как сделать график в Экселе, пересчитать сумму по действующем курсу — но это будет не слишком правильно, если затраты определялись именно в валюте. Решение проблемы — добавить вторую ось со своими единицами измерения.
Для этого можно выполнить такие действия:
- Построить основу — график, единицы измерения у которого одинаковые для каждого ряда.
- Выделить диаграмму и на вкладке «Конструктор» перейти к изменению ее типа.
- Выбрать вариант «Комбинированная» и второй вариант в списке — гистограмму с группировкой и график на вспомогательной оси.
- Настроить отображение — указать, для какого ряда будет построена вспомогательная ось, изменить виды диаграмм.
- Нажать «ОК» для перехода к дальнейшим настройкам.
Теперь на графике будет две отличающихся друг от друга диаграммы, каждая из которых имеет свою шкалу с отдельными единицами измерения. Можно сделать так, чтобы на экране были, например, две похожих линии, выбрав соответствующие варианты на этапе изменения типа. Хотя это будет не так удобно даже при наличии легенды.
Двойная диаграмма с разными шкалами — отличный способ, как в Экселе сделать график по таблице для двух показателей, которые нельзя сравнить друг с другом. Зато оценку их значений и изменений можно провести на одном листе. Например, чтобы выполнить работу по поиску зависимости между разными видами расходов.
Читайте также:
- 5 способов как вставить презентацию в презентацию Powerpoint
- Как очистить оперативную память смартфона на Android
Точки пересечения графиков в Excel
Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.
Строим графики с точками пересечений
Имеются две функции, по которым нужно построить графики:
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:
- Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
- Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.
Находим точку пересечения графиков в Excel
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.
Первый способ. Найти общие значения в рядах данных для указанных функций.
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.
Изменим график, добавив новые данные. Получим две пересекающиеся линии.
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.
Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.
Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.
Точки пересечения для трех показателей
Существует три показателя, которые измерялись во времени.
По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).
Получается такой рисунок:
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:
Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.
Особенности построения при неравномерном шаге по Х
Пусть дана таблица с исходными данными (значения в исходной таблице расположены по оси Х равномерно с шагом 10, но точка с х=20 отсутствует).
Построим График и Точечную диаграмму с прямыми отрезками используя одну и туже таблицу.
Точечная диаграмма использует все данные из исходной таблицы: как значения х, так и y.
Диаграмма График откладывает значения по оси х равномерно (значения из столбца Ось х не используются для построения).
Значения из столбца Ось х используются в Диаграмме График только для подписей данных по оси х (значения из столбца Ось х никак не влияют на расположение точек). Это часто используется для гибкой настройки подписей по оси х (можно в качестве подписей указать любые, в том числе и текстовые значения).
Вывод : если значения по оси х расположены неравномерно (в исходной таблице нет точки с х=20, поэтому кривая на Диаграмме График имеет излом), то использование Точечной диаграммы предпочтительней.
В случае, если данные расположены по оси х равномерно (с определенным шагом), то можно использовать оба типа диаграммы — линии на диаграмме будут выглядеть одинаково. Но если некоторые значения по оси Х пропущены, то для настройки диаграммы типа График нужно изменить таблицу с исходными данными. Можно использовать функцию НД() см. статью Функция НД() в MS EXCEL . Эта функция позволяет сделать кривую на диаграмме График аналогичной кривой на Точечной диаграмме (вариант2).
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Построение графика функции на плоскости
Элементарные функции (y=sin(x), y=x 2 ) удовлетворяют условию однозначности функции: одному значению Х соответствует единственное значение Y (горизонтальная линия, параллельная оси ординат, не может пересекать график функции более чем в одной точке). Поэтому, Диаграмма типа График, как и диаграмма типа Точечная, годятся для построения графика функции на плоскости.
Построим график функции y=sin(x) с использованием обоих типов диаграмм.
- подписи Оси Х: на диаграмме График на оси Х указаны фактические значения Х (могут также быть указаны любые подписи, даже текст), а на Точечной — цены основных и промежуточных делений вычислены автоматически. Т.е. подписи на этих типах диаграмм не обязательно совпадают (но можно добиться, чтобы совпадали).
- шаг вертикальной сетки: основные линии сетки на Графике проходят строго через точки значений, а на Точечной — шаг выбирается автоматически (точно предсказать не возможно, т.к. шаг зависит от размера самой диаграммы, диапазона изменения по Х и др.)
Эти графики построены в файле примера .
Построение плоских алгебраических кривых
Кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли можно построить только с помощью диаграммы типа Точечная, т.к. эти кривые НЕ удовлетворяют условию однозначности функции: одному значению Х могут соответствовать несколько значений Y. Эти графики построены в этой статье.
Построение диаграммы рассеяния
Диаграммы рассеяния используются для анализа временных рядов и в статистическом анализе. Про построение этой диаграммы (возможно использовать только Точечную) см. эту статью.
Инструменты прогнозирования в Microsoft Excel
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
- Линейная;
- Логарифмическая;
- Экспоненциальная;
- Степенная;
- Полиномиальная;
- Линейная фильтрация.
Давайте для начала выберем линейную аппроксимацию.
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

При создании диаграммы на листе Excel, в документе Word или презентации PowerPoint вы можете выбрать из многих вариантов. Независимо от того, будете ли вы использовать диаграмму, рекомендуемую для ваших данных, которую вы выбираете из списка всех диаграмм или одну из выбранных шаблонов диаграммы, это может помочь узнать немного больше о каждом типе диаграммы.
Щелкните здесь, чтобы приступить к созданию диаграммы.
Чтобы просмотреть описание типа диаграммы, выберите его в раскрывающемся списке.
Данные в столбцах или строках листа можно представить в виде гистограммы. В гистограмме категории обычно отображаются по горизонтальной оси (категорий), а значения — по вертикальной оси (значений), как показано в этой диаграмме:
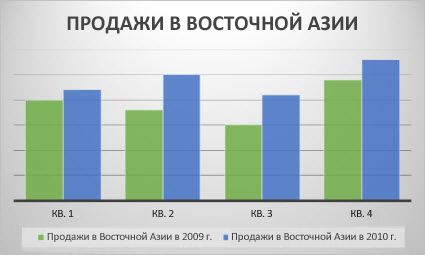
Типы гистограмм
-
Гистограмма с группировкой и объемная гистограмма с группировкой.
На гистограмме с группировкой значения выводятся в виде плоских столбцов. На объемной гистограмме с группировкой столбцы отображаются в трехмерном виде, но третья ось значений (ось глубины) не используется. Используйте этот тип диаграммы при наличии категорий, представляющих:
-
диапазоны значений (например количество элементов);
-
специфические шкалы (например шкала Ликерта с масками, такими как «Решительно за», «За», «Не знаю», «Против», «Решительно против»);
-
неупорядоченные имена (например, названия элементов, географические названия или имена людей).
-
-
Гистограмма с накоплением и объемная гистограмма с накоплением. Гистограмма с накоплением представляет значения в виде плоских столбцов с накоплением. На объемной гистограмме с группировкой столбцы с накоплением отображаются в трехмерном виде, но ось глубины не используется. Используйте этот тип диаграммы, когда есть несколько ряд данных и нужно подчеркнуть итоговое значение.
-
Нормированная гистограмма с накоплением и объемная нормированная гистограмма с накоплением. Нормированная гистограмма с накоплением представляет значения в виде плоских нормированных столбцов с накоплением для представления 100 % значений. На объемной нормированной гистограмме с группировкой столбцы отображаются в трехмерном виде, но ось глубины не используется. Используйте этот тип диаграммы, когда есть несколько рядов данных и нужно подчеркнуть их вклад в итоговое значение, особенно если итоговое значение одинаково для всех категорий.
-
Трехмерный столбец Трехмерные гистограммы используют три оси, которые можно изменить (горизонтальная ось, вертикальная ось и ось глубины), и сравнивают их точки данных по горизонтали и осям глубины. Используйте эту диаграмму, если требуется сравнить данные по категориям и рядам данных.
Данные, расположенные в столбцах или строках листа, можно представить в виде графика. На графиках данные категорий равномерно распределяются вдоль горизонтальной оси, а все значения равномерно распределяются вдоль вертикальной оси. Графики позволяют отображать непрерывное изменение данных с течением времени на оси с равномерным распределением, поэтому они идеально подходят для представления тенденций изменения данных с равными интервалами, такими как месяцы, кварталы или финансовые годы.
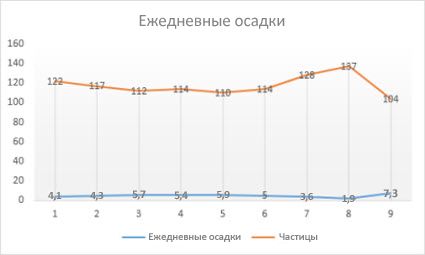
Типы графиков
-
График и график с маркерами. Графики с маркерами, отмечающими отдельные значения данных, или без маркеров можно использовать для отображения динамики изменения данных с течением времени или по категориям данных, разделенным равными интервалами, особенно когда точек данных много и порядок их представления существенен. Если категорий данных много или значения являются приблизительными, используйте график без маркеров.
-
График с накоплением и график с накоплением с маркерами. Графики с накоплением, отображаемые как с маркерами для конкретных значений данных, так и без них, могут отображать динамику изменения вклада каждого значения с течением времени или по категориям данных, разделенным равными интервалами.
-
Нормированный график с накоплением и нормированный график с накоплением с маркерами. Нормированные графики с накоплением с маркерами, отмечающими отдельные значения данных, или без маркеров могут отображать динамику вклада каждой величины в процентах с течением времени или по категориям данных, разделенным равными интервалами. Если категорий данных много или значения являются приблизительными, используйте нормированный график с накоплением без маркеров.
-
Объемный график. На объемных графиках каждая строка или столбец изображаются в виде объемной ленты. Объемный график имеет горизонтальную ось, вертикальную ось и ось глубины, которые можно изменять.
Примечания:
-
Графики лучше всего подходят для вывода нескольких рядов данных. Если нужно отобразить только один ряд данных, вместо графика рекомендуется использовать точечную диаграмму.
-
На графиках с накоплением данные суммируются, что может быть нежелательно. Увидеть накопление на графике бывает непросто, поэтому иногда вместо него стоит воспользоваться графиком другого вида либо диаграммой с областями с накоплением.
-
Данные в одном столбце или строке листа можно представить в виде круговой диаграммы. Круговая диаграмма отображает размер элементов одного ряд данных относительно суммы элементов. точки данных на круговой диаграмме выводятся как проценты от всего круга.
Круговую диаграмму рекомендуется использовать, если:
-
нужно отобразить только один ряд данных;
-
все значения ваших данных неотрицательны;
-
почти все значения данных больше нуля;
-
имеется не более семи категорий, каждой из которых соответствуют части общего круга.
Типы круговых диаграмм
-
Круговая диаграмма и объемная круговая диаграмма. Круговые диаграммы отображают вклад каждой величины в общую сумму в двухмерном или трехмерном виде. Чтобы заострить внимание на некоторых секторах, вы можете вытащить их вручную из круговой диаграммы.
-
Вторичная круговая диаграмма и вторичная гистограмма. Вторичная круговая диаграмма и вторичная гистограмма представляют собой круговые диаграммы с меньшими значениями, перенесенные на вторичную круговую диаграмму или линейчатую диаграмму с накоплением, что упрощает их просмотр.
Данные, расположенные только в столбцах или строках листа, можно представить в виде кольцевой диаграммы. Как и круговая диаграмма, кольцевая диаграмма отображает отношение частей к целому, но может содержать несколько ряд данных.
Типы кольцевых диаграмм
-
Кольцевая диаграмма На диаграммах этого типа данные отображаются в виде колец, каждое из которых представляет ряд данных. Если в метках данных отображаются проценты, каждое кольцо в сумме должно давать 100 %.
Примечание: Кольцевые диаграммы трудны для восприятия. Вместо этого можно использовать гистограммы с накоплением или линейчатую диаграмму с накоплением.
Данные в столбцах или строках листа можно представить в виде линейчатой диаграммы. Линейчатые диаграммы используют для сравнения отдельных элементов. В диаграммах этого типа категории обычно располагаются по вертикальной оси, а величины — по горизонтальной.
Линейчатые диаграммы рекомендуется использовать, если:
-
метки осей имеют большую длину;
-
выводимые значения представляют собой длительности.
Типы линейчатых диаграмм
-
Линейчатая диаграмма с группировкой и объемная линейчатая диаграмма с группировкой. На линейчатой диаграмме с группировкой значения выводятся в виде плоских столбцов. Объемная линейчатая диаграмма с группировкой отображает столбцы в трехмерном виде без использования оси глубины.
-
Линейчатая диаграмма с накоплением и объемная линейчатая диаграмма с накоплением. Линейчатая диаграмма с накоплением показывает вклад отдельных величин в общую сумму в виде плоских столбцов. В объемных линейчатых диаграммах с накоплением используются столбцы в трехмерном виде без использования оси глубины.
-
Нормированная линейчатая диаграмма с накоплением и объемная нормированная линейчатая диаграмма с накоплением. Этот тип диаграмм позволяет сравнить по категориям процентный вклад каждой величины в общую сумму. В объемных нормированных линейчатых диаграммах с накоплением отображаются столбцы в трехмерном виде без использования оси глубины.
Данные в столбцах или строках листа можно представить в виде диаграммы с областями. Диаграммы с областями могут использоваться для отображения изменений величин с течением времени и привлечения внимания к итоговому значению в соответствии с тенденцией. Отображая сумму значений рядов, такая диаграмма также наглядно показывает вклад каждого ряда.
Типы диаграмм с областями
-
Диаграмма с областями и объемная диаграмма с областями. Диаграммы с областями (в том числе объемные) отображают изменение величин с течением времени или по категориям. В объемных диаграммах с областями используются три оси (горизонтальная, вертикальная и ось глубины), которые можно изменять. Обычно вместо диаграмм с областями без накопления рекомендуется использовать графики, так как данные одного ряда могут быть скрыты за данными другого ряда.
-
Диаграмма с областями с накоплением и объемная диаграмма с областями с накоплением. Диаграммы с областями с накоплением показывают изменения вклада каждой величины с течением времени или по категориям в двухмерном виде. На объемной диаграмме с областями отображаются те же данные, но в трехмерном виде без использования оси глубины.
-
Нормированная диаграмма с областями с накоплением и объемная нормированная диаграмма с областями с накоплением. Нормированные диаграммы с областями с накоплением отображают изменения вклада каждой величины в процентах с течением времени или по категориям. На объемной нормированной диаграмме с областями отображаются те же данные, но в трехмерном виде без использования оси глубины.
Данные в столбцах и строках листа можно представить в виде точечной диаграммы. Поместите данные по оси X в одну строку или столбец, а соответствующие данные по оси Y — в соседние строки или столбцы.
Точечная диаграмма имеет две оси значений: горизонтальную (X) и вертикальную (Y). На точечной диаграмме значения «x» и «y» объединяются в одну точку данных и выводятся через неравные интервалы или кластеры. Точечные диаграммы обычно используются для отображения и сравнения числовых значений, например научных, статистических или технических данных.
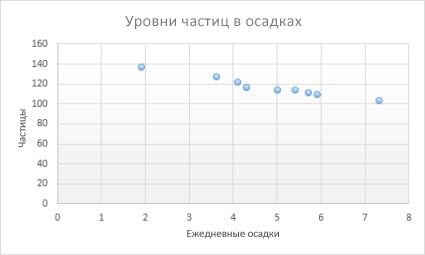
Точечные диаграммы рекомендуется использовать, если:
-
требуется изменять масштаб горизонтальной оси;
-
требуется использовать для горизонтальной оси логарифмическую шкалу;
-
значения расположены на горизонтальной оси неравномерно;
-
на горизонтальной оси имеется множество точек данных;
-
требуется настраивать независимые шкалы точечной диаграммы для отображения дополнительных сведений о данных, содержащих пары сгруппированных полей со значениями;
-
требуется отображать не различия между точками данных, а аналогии в больших наборах данных;
-
требуется сравнивать множество точек данных без учета времени; чем больше данных будет использовано для построения точечной диаграммы, тем точнее будет сравнение.
Типы точечных диаграмм
-
Точечная диаграмма. Диаграмма этого типа позволяет отображать точки данных без соединительных линий для сравнения пар значений.
-
Точечная диаграмма с плавными линиями и маркерами и точечная диаграмма с плавными линиями. На этой диаграмме точки данных соединены сглаживающими линиями. Такие линии могут отображаться с маркерами или без них. Сглаживающую кривую без маркеров следует использовать, если точек данных достаточно много.
-
Точечная с прямыми линиями и маркерами и точечная с прямыми линиями На этой диаграмме показаны линии прямого соединения между точками данных. Прямые линии могут отображаться с маркерами или без них.
Как и в точечной диаграмме, в пузырьковой диаграмме добавляется третий столбец для указания размера пузырьков, используемых для представления точек данных в рядах данных.
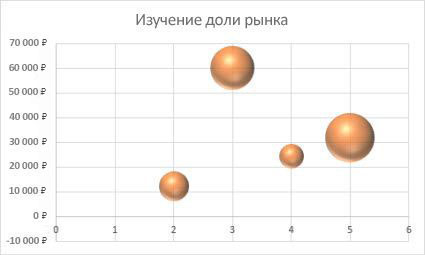
Тип пузырьковых диаграмм
-
Пузырьковая или объемная пузырьковая диаграмма. Обе эти пузырьковые диаграммы позволяют сравнивать наборы из трех значений вместо двух, отображая пузырьки в двухмерном или трехмерном виде (без использования оси глубины). Третье значение определяет размер маркера пузырька.
Данные, расположенные в столбцах или строках листа в определенном порядке, можно представить в виде биржевой диаграммы. Как следует из названия, биржевые диаграммы могут показывать изменения цен на акции. Но их также можно использовать для иллюстрации изменений других данных, таких как дневные осадки или годичные колебания температуры. Для создания биржевой диаграммы нужно правильно упорядочить данные.
Например, для создания простой биржевой диаграммы (самый высокий курс, самый низкий курс, курс закрытия) поместите данные в столбцы с заголовками «Самый высокий курс», «Самый низкий курс» и «Курс закрытия» в указанном порядке.

Типы биржевых диаграмм
-
Биржевая диаграмма (самый высокий курс, самый низкий курс, курс закрытия). В этой биржевой диаграмме используются три набора значений в следующем порядке: самый высокий курс, самый низкий курс, курс закрытия.
-
Биржевая диаграмма (курс открытия, самый высокий курс, самый низкий курс, курс закрытия). В этой биржевой диаграмме используются четыре набора значений в следующем порядке: курс открытия, самый высокий курс, самый низкий курс, курс закрытия.
-
Биржевая диаграмма (объем, самый высокий курс, самый низкий курс, курс закрытия). В этой биржевой диаграмме используются четыре набора значений в следующем порядке: объем, самый высокий курс, самый низкий курс, курс закрытия. Диаграмма такого типа отражает изменение объемов продаж на двух осях значений: одна для столбцов, в которых указан объем, а другая — для цен на акции.
-
Биржевая диаграмма (объем, курс открытия, самый высокий курс, самый низкий курс, курс закрытия). В этой биржевой диаграмме используются пять наборов значений в следующем порядке: объем, курс открытия, самый высокий курс, самый низкий курс, курс закрытия.
Данные в столбцах или строках листа можно представить в виде поверхностной диаграммы. Эта диаграмма полезна, если требуется найти оптимальные комбинации данных из двух наборов. Как на топографической карте, области, относящиеся к одинаковым диапазонам, при этом выделяются цветами и штриховкой. Вы можете создавать поверхностные диаграммы для иллюстрации категорий и наборов данных, представляющих собой числовые значения.
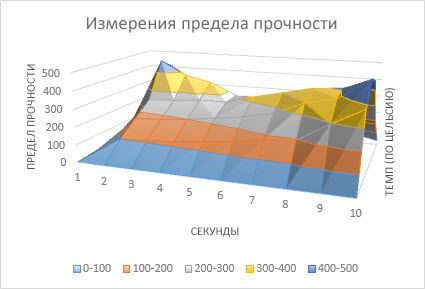
Типы поверхностных диаграмм
-
Объемная поверхностная диаграмма. На этих диаграммах данные можно представить в трехмерном виде, который можно рассматривать как резиновую пленку, натянутую на трехмерную гистограмму. Обычно такие диаграммы используются для отображения отношений между большими объемами данных, которые трудно продемонстрировать иначе. Цветные полосы на поверхности не являются рядами данных — они указывают разницу между значениями.
-
Проволочная объемная поверхностная диаграмма. Объемная поверхностная диаграмма, выводимая без цвета на поверхности, называется проволочной объемной поверхностной диаграммой. На такой диаграмме отображаются только линии. Проволочная объемная поверхностная диаграмма сложна для восприятия, но она позволяет отображать большие объемы данных намного быстрее, чем объемная поверхностная диаграмма.
-
Контурная диаграмма Контурные диаграммы являются видом сверху на поверхностные диаграммы. На них разные цвета соответствуют определенным диапазонам значений. Линии на контурной диаграмме соединяют координаты одинаковых значений, полученные интерполяцией.
-
Проволочная контурная диаграмма. Проволочные контурные диаграммы похожи на поверхностные диаграммы, если смотреть на них сверху. Они не содержат цветных полос и отображают только линии. Проволочная контурная диаграмма сложна для восприятия. Вместо нее можно использовать объемную поверхностную диаграмму.
Данные в столбцах или строках листа можно представить в виде лепестковой диаграммы. Лепестковая диаграмма позволяет сравнить агрегированные значения нескольких ряд данных.
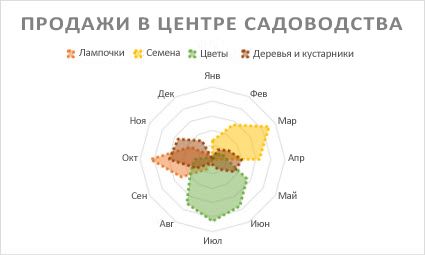
Типы лепестковых диаграмм
-
Лепестковая диаграмма и лепестковая диаграмма с маркерами. Лепестковые диаграммы отображают изменения значений относительно центральной точки с маркерами для отдельных точек данных или без них.
-
Лепестковая диаграмма с областями. На лепестковой диаграмме с областями области, заполненные рядами данных, выделены цветом.
Диаграмма «дерево» предоставляет иерархическое представление данных и простой способ сравнения различных уровней классификации. Диаграмма «дерево» отображает категории по цвету и близости и может легко отображать большой объем данных, что может быть сложно с другими типами диаграмм. Диаграмму диаграммы «дерево» можно представить, если в иерархической структуре существуют пустые (пустые) ячейки, а диаграммы диаграммы «дерево» подходят для сравнения пропорций в иерархии.
Примечание: Для диаграммы «дерево» не существует подтипов.
Диаграмма «солнечные лучи» идеально подходит для отображения иерархических данных и может отображаться, если в иерархической структуре существуют пустые (пустые) ячейки. Каждый уровень иерархии представлен одним кольцом или кругом, а ее верхом является самый близкий к центру круг. Диаграмма «солнечные лучи» без иерархических данных (один уровень категорий) похожа на кольцевую диаграмму. Однако на такой диаграмме с несколькими уровнями категорий отображается связь между внешними и внутренними кольцами. На диаграмме «солнечные лучи» наиболее эффективно показано, как одно кольцо разбивается на его части.
Примечание: Для диаграммы «солнечные лучи» не существует подтипов.
Данные, отображаемые на гистограмме, показывают частоты распределения. Каждый столбец диаграммы можно изменять для дальнейшего анализа данных.
Типы гистограмм
-
Гистограмма. Отображает распределение данных, сгруппированных в столбцы по частотам.
-
Диаграмма Парето. Это гистограмма с сортировкой, содержащая столбцы, отсортированные по убыванию, и строку, в которой представлено совокупное итоговое значение в процентах.
На линейчатой диаграмме и диаграмме усов показано распределение данных по квартилям, выделяя среднее и выбросы. Поля могут содержать линии, расширяемые вертикально под названием «усы». Эти строки указывают на вариативность за пределами верхних и нижних квартилей, и любая точка за пределами этих линий или усов считается выбросом. Используйте этот тип диаграммы, если существует несколько наборов данных, которые связаны друг с другом.
Примечание: Для диаграммы «ящик с усами» не существует подтипов.
Каскадная диаграмма показывает нарастающий финансовый итог по мере добавления или вычитания значений. Это помогает понять, как ряд положительных и отрицательных значений влияет на исходную величину. Столбцы обозначены цветом, что позволяет быстро отличить положительные значения от отрицательных.
Примечание: Для каскадных диаграмм не существует подтипов.
На воронкообразных диаграммах отображаются значения, относящиеся к разным этапам процесса.
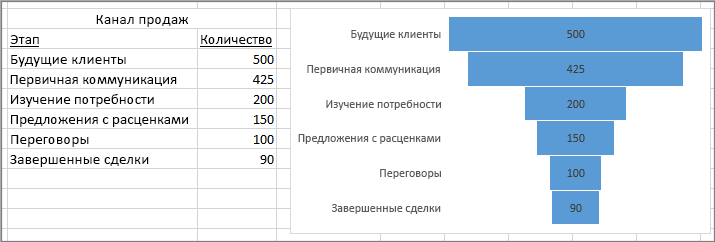
Как правило, значения постепенно уменьшаются, поэтому полосы диаграммы по виду напоминают воронку. Дополнительные сведения о воронкообразных диаграммах
Данные в столбцах и строках можно представить в виде комбинированной диаграммы. Комбинированные диаграммы объединяют диаграммы двух и более типов, чтобы улучшить читаемость данных, особенно когда они значительно отличаются друг от друга. Отображение вспомогательной оси на такой диаграмме еще больше улучшает восприятие. В данном примере для отображения количества домов, проданных с января по июнь, использовалась гистограмма, а затем для быстрого определения средней цены продажи за месяц использовался график, упрощающий восприятие.
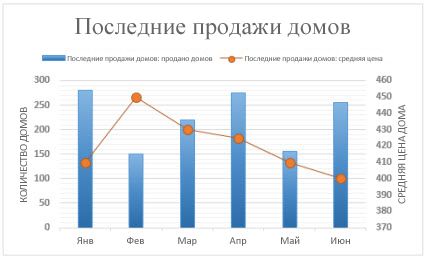
Типы комбинированных диаграмм
-
Гистограмма с группировкой — график и гистограмма с группировкой — график на вспомогательной оси. Эта диаграмма объединяет гистограмму и график (со вспомогательной осью или без нее), отображая одни ряды данных как столбцы, а другие — как линии в одной диаграмме.
-
Диаграмма с областями с накоплением — гистограмма с группировкой. Эта диаграмма объединяет диаграмму с областями с накоплением и гистограмму с группировкой, отображая одни ряды данных как области с накоплением, а другие — как столбцы в одной диаграмме.
-
Настраиваемая комбинированная диаграмма. Это возможность объединять нужные диаграммы для их отображения в одной диаграмме.
Диаграмму с картой можно использовать для сравнения значений и отображения категорий по географическим регионам. Используйте ее, если ваши данные включают географические регионы (например, сведения о странах, областях или почтовых индексах).
Например, на карте, показывающей страны по численности населения, используются значения. Значения выражают совокупную численность населения в каждой стране и отображаются с использованием спектра двухцветных градиентов. Цвет для каждого региона определяется в зависимости от того, в какую часть спектра попадает его значение относительно остальных значений.
В приведенном ниже примере карты стран по численности населения для отображения категорий используется легенда, чтобы показать группы или связи. Все точки данных представлены абсолютно разными цветами.
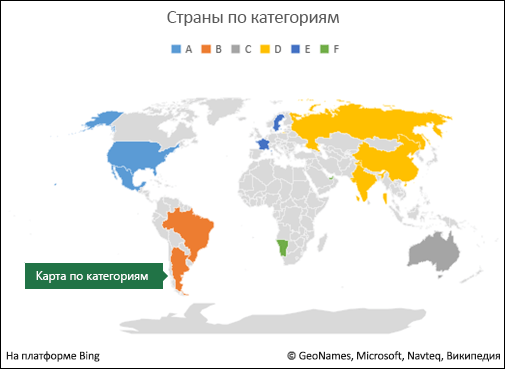
Изменение типа диаграммы
Если у вас уже есть диаграмма, а вы просто хотите изменить ее тип, выполните следующие действия:
-
Выберите диаграмму, щелкните вкладку Конструктор и выберите пункт Изменить тип диаграммы.
-
Выберите другой тип диаграммы в окне Изменение типа диаграммы.
Доступно много типов диаграмм, которые помогают отображать данные наиболее подходящим для аудитории способом. Ниже представлены некоторые примеры наиболее распространенных типов диаграмм и описаны способы их использования.
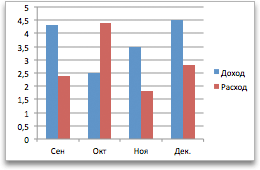
Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде гистограммы. В гистограммах категории обычно расположены вдоль горизонтальной ось, а значения — вдоль вертикальной.
Гистограммы удобны для демонстрации изменения данных с течением времени или для сравнения элементов.
Гистограммы включают в себя указанные ниже подтипы диаграмм.
-
Гистограмма с группировкой. Предназначена для сравнения значений по категориям. На гистограмме с группировкой значения отображаются в плоских вертикальных прямоугольниках. На объемной гистограмме с группировкой данные отображаются с использованием трехмерной перспективы.
-
Гистограмма с накоплением. Показывает отношение отдельных элементов к целому, отражая вклад каждого значения в итоговое по категориям. На гистограмме с накоплением значения отображаются в плоских вертикальных прямоугольниках с накоплением. На объемной гистограмме с накоплением данные отображаются с использованием трехмерной перспективы. Объемная перспектива не является объемной диаграммой в полном смысле, поскольку в ней не используется ось дополнительного значения (ось глубины).
-
Нормированная гистограмма. Отражает процентную долю каждого значения в итоговом по категориям. На нормированной гистограмме значения отображаются в плоских вертикальных прямоугольниках с нормированием. На объемной нормированной гистограмме данные отображаются с использованием трехмерной перспективы. Объемная перспектива не является объемной диаграммой в полном смысле, поскольку в ней не используется ось дополнительного значения (ось глубины).
-
Трехмерная гистограмма. Строится по трем осям, которые можно изменять (горизонтальная ось, вертикальная ось и ось глубины). Позволяет сравнивать точки данных вдоль горизонтальной оси и оси глубины.
Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде графика. На графиках можно отображать изменение непрерывных данных с течением времени с использованием общей шкалы, поэтому они идеально подходят для демонстрации тенденций в данных через равные временные интервалы. На графике данные категории равномерно распределены вдоль горизонтальной оси, а все данные значений равномерно распределены вдоль вертикальной оси.
Графики хорошо подходят для случаев, когда подписи категорий являются текстом и представляют собой значения, распределенные через равные интервалы, например месяцы, кварталы или финансовые года.
Графики включают в себя указанные ниже подтипы диаграмм.
-
График с маркерами или без них. Служит для отображения тенденций с течением времени или упорядоченных категорий, особенно если имеется много точек данных и важен порядок, в котором они представлены. Если имеется много категорий или значения являются приблизительными, используйте график без маркеров.
-
График с накоплением (с маркерами или без них). Отображает изменение вклада каждого значения в итоговое с течением времени или упорядоченные категории. Если имеется много категорий или значения являются приблизительными, используйте график с накоплением без маркеров.
-
Нормированный график с накоплением (с маркерами или без них). Отображает изменение процентной доли каждого значения в итоговом с течением времени или упорядоченные категории. Если имеется много категорий или значения являются приблизительными, используйте нормированный график с накоплением без маркеров.
-
Объемный график. Отображает каждую строку или столбец данных в виде трехмерной ленты. На объемном графике имеются горизонтальная ось, вертикальная ось и ось глубины, которые можно изменять.
Данные, упорядоченные на листе Excel в виде одного столбца или строки, можно визуально представить в виде круговой диаграммы. Круговые диаграммы отражают размер элементов одного ряд данных в пропорции к сумме элементов. Точки данных на круговой диаграмме отображаются в виде процентных долей целого круга.
Круговую диаграмму целесообразно использовать, когда нужно отобразить только один ряд данных, ни одно из значений не является отрицательным, практически отсутствуют нулевые значения, имеется не более семи категорий и они представляют собой части целого круга.
Круговые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Круговая диаграмма. Отражает вклад каждого значения в итоговое в двумерном или трехмерном формате. Сектора круговой диаграммы можно выдвинуть вручную, чтобы подчеркнуть их значимость.
-
Вторичная круговая диаграмма и вторичная гистограмма. Предназначены для отображения круговых диаграмм, часть значений которых вынесена во вторичную круговую диаграмму или в линейчатую диаграмму с накоплением. Эти типы диаграмм облегчают восприятие небольших секторов основной круговой диаграммы.
-
Кольцевая диаграмма Как и круговая диаграмма, кольцевая диаграмма показывает отношение частей к целому. Тем не менее она может содержать более одного ряда данных. Каждое кольцо в кольцевой диаграмме представляет один ряд данных. Отображает данные в виде колец, каждое из которых представляет один ряд данных. Если в метках данных отображаются процентные доли, данные каждого кольца в сумме будут составлять 100%.
Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде линейчатой диаграммы.
Линейчатые диаграммы используются для сравнения отдельных элементов.
Линейчатые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Линейчатая диаграмма с кластерией и трехмерная линейчатая диаграмма Предназначена для сравнения значений по категориям. На линейчатых диаграммах с группировкой категории, как правило, расположены по вертикальной оси, а значения — по горизонтальной оси. На объемной линейчатой диаграмме с группировкой горизонтальные прямоугольники отображаются в трехмерном формате. При этом данные на трех осях не отображаются.
-
Линейчатая диаграмма с накоплением и линейчатая диаграмма с накоплением Отражает отношение отдельных элементов к целому. На объемной линейчатой диаграмме с накоплением горизонтальные прямоугольники отображаются в трехмерном формате. При этом данные на трех осях не отображаются.
-
Линейчатая диаграмма с накоплением и линейчатая диаграмма с накоплением на 100 % в трехмерной диаграмме Отражает процентную долю каждого значения в итоговом по категориям. На объемной нормированной линейчатой диаграмме горизонтальные прямоугольники отображаются в трехмерном формате. При этом данные на трех осях не отображаются.
Данные, упорядоченные на листе Excel в виде столбцов и строк, можно визуально представить в виде точечной диаграммы. Точечная диаграмма имеет две оси значений. Один набор числовых данных отображается по горизонтальной оси (оси X), а другой — по вертикальной (оси Y). Эти значения объединены в отдельные точки данных и отображаются через неравные интервалы или группами.
Точечная диаграмма показывает отношения между численными значениями в нескольких рядах данных или отображает две группы чисел как один ряд координат x и y. Точечные диаграммы обычно используются для иллюстрации и сравнения числовых значений, например научных, статистических или технических данных.
Точечные диаграммы содержат указанные ниже подтипы диаграмм.
-
Точечная диаграмма Служит для сравнения пар значений. Если имеется много точек данных, а соединительные линии могут затруднить восприятие информации, следует использовать точечную диаграмму с маркерами данных, но без линий. Этот тип диаграммы можно также использовать, если не нужно показывать связи между точками данных.
-
Точечная диаграмма с гладкими кривыми и с гладкими кривыми и маркерами. Отображает гладкую кривую, соединяющую точки данных. Плавные линии могут отображаться с маркерами или без них. Гладкие кривые без маркеров лучше использовать, если имеется много точек данных.
-
Точечная диаграмма с прямыми отрезками и с прямыми отрезками и маркерами. Отображает прямые отрезки, соединяющие точки данных. Прямые отрезки могут отображаться с маркерами или без них.
-
Пузырьковая диаграмма (плоская и с объемным эффектом). Пузырьковая диаграмма является разновидностью точечной диаграммы с тем отличием, что размер пузырьков представляет значение третьей переменной. Позволяет сравнить наборы не из двух, а из трех значений. Третье значение определяет размер пузырька. Можно задать отображение пузырьков в двумерном формате или с эффектом объемности.
Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде диаграммы с областями. Отображение суммы построенных значений на диаграмме с областями позволяет также продемонстрировать отношение частей к целому.
Диаграммы с областями позволяют сделать акцент на амплитуде изменений с течением времени и привлечь внимание к суммарному значению по всему тренду. Например, на диаграмме с областями можно построить данные, представляющие прибыль в динамике по времени, чтобы подчеркнуть общую прибыль.
Диаграммы с областями включают в себя указанные ниже подтипы диаграмм.
-
Диаграмма с областями. Отображает изменение значений с течением времени или другие данные категории. В объемных диаграммах с областями используются три оси (горизонтальная, вертикальная и ось глубины), которые можно изменять. В общем случае следует рассмотреть вариант использования графика вместо диаграммы с областями без накопления, поскольку данные из одного ряда могут быть перекрыты данными из другого ряда.
-
Диаграмма с областями с накоплением. Отображает изменение вклада каждого значения в итоговое с течением времени или другие данные категорий. Объемная диаграмма с областями с накоплением отображается аналогичным образом, но с использованием трехмерной перспективы. Объемная перспектива не является объемной диаграммой в полном смысле, поскольку в ней не используется ось дополнительного значения (ось глубины).
-
Нормированная диаграмма с областями. Отображает изменение процентной доли каждого значения в итоговом с течением времени или другие данные категорий. Объемная нормированная диаграмма с областями отображается аналогичным образом, но с использованием трехмерной перспективы. Объемная перспектива не является объемной диаграммой в полном смысле, поскольку в ней не используется ось дополнительного значения (ось глубины).
Данные, упорядоченные на листе Excel в столбцах или строках, которые расположены в определенном порядке, можно визуально представить в виде биржевой диаграммы.
Как следует из названия, биржевые диаграммы чаще всего используются для демонстрации колебания курса акций. Тем не менее эту диаграмму можно также использовать для научных данных. Например, биржевая диаграмма подходит для отображения колебаний суточной или годовой температуры.
Биржевые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Биржевая диаграмма с высоким низким уровнем закрытия Отображает цены на акции. Для этой диаграммы требуются три ряда значений в правильном порядке: самый высокий курс, самый низкий курс и курс закрытия.
-
Биржевая диаграмма open-High-Low-Close Для этой диаграммы требуются четыре ряда значений в правильном порядке: курс открытия, самый высокий курс, самый низкий курс и курс закрытия.
-
Биржевая диаграмма volume-High-Low-Close Для этой диаграммы требуются четыре ряда значений в правильном порядке: объем, самый высокий курс, самый низкий курс и курс закрытия. На диаграмме измеряется объем с использованием двух осей значений: одна — для столбцов со значениями объема, а другая — для курса акций.
-
Биржевая диаграмма volume-Open-High-Low-Close Для этой диаграммы требуются пять рядов значений в правильном порядке: объем, курс открытия, самый высокий курс, самый низкий курс и курс закрытия.
Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде поверхностной диаграммы. Как и на топографической карте, цвета и узоры обозначают области, которые находятся в одном и том же диапазоне значений.
Поверхностная диаграмма удобна в том случае, если нужно найти оптимальную комбинацию двух наборов данных.
Поверхностные диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Объемная поверхностная диаграмма Показывает тенденции в значениях в двух измерениях в непрерывной кривой. Цветовые полосы на поверхностной диаграмме не представляют ряд данных. Они представляют разницу между значениями. На диаграммах этого типа данные можно представить в трехмерном виде, который можно рассматривать как резиновую пленку, натянутую на трехмерную гистограмму. Обычно такие диаграммы используются для отображения отношений между большими объемами данных, которые трудно продемонстрировать иначе.
-
Проволочная объемная поверхностная диаграмма. На этой диаграмме отображаются только линии. Проволочная объемная поверхностная диаграмма сложна для восприятия, но такой тип диаграмм рекомендуется использовать для быстрого отображения больших наборов данных.
-
Контурная диаграмма. Если на поверхностную диаграмму посмотреть сверху, она напоминает двумерную топографическую карту. На контурной диаграмме цветные полосы представляют конкретные диапазоны значений. Линии на контурной диаграмме связывают интерполированные точки с одинаковыми значениями.
-
Проволочная контурная диаграмма. Поверхностная диаграмма при виде сверху. Без цветных полос на поверхности контурной диаграммы отображаются только линии. Бесцветные контурные диаграммы сложны для восприятия. Вместо нее можно использовать объемную поверхностную диаграмму.
На лепестковой диаграмме каждая категория имеет свою собственную ось значений, исходящую из начала координат. Линии связывают все значения одного ряда данных.
Лепестковые диаграммы используются для сравнения совокупных значений нескольких рядов данных.
Лепестковые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Лепестковая диаграмма. Отображает изменения значений относительно начала координат.
-
Радиолокатор с маркерами Отображает изменения значений относительно центральной точки с маркерами.
-
Заполненная лепестковая диаграмма. Отображает изменения значений относительно начала координат с заливкой области, охватываемой каждым рядом данных, цветом.
Диаграмму с картой можно использовать для сравнения значений и отображения категорий по географическим регионам. Используйте ее, если ваши данные включают географические регионы (например, сведения о странах, областях или почтовых индексах).
Дополнительные сведения см. в разделе «Создание диаграммы карты».
На воронкообразных диаграммах отображаются значения на разных этапах процесса.
Как правило, значения постепенно уменьшаются, так что полосы диаграммы по виду напоминают воронку. Дополнительные сведения см. в разделе «Создание воронкообразной диаграммы».
Диаграмма «дерево» предоставляет иерархическое представление данных и простой способ сравнения различных уровней классификации. Диаграмма «дерево» отображает категории по цвету и близости и может легко отображать большой объем данных, что может быть сложно с другими типами диаграмм. Диаграмму диаграммы «дерево» можно представить, если в иерархической структуре существуют пустые (пустые) ячейки, а диаграммы диаграммы «дерево» подходят для сравнения пропорций в иерархии.
Для диаграммы «дерево» не существует подтипов.
Дополнительные сведения см. в разделе «Создание диаграммы дерева».
Диаграмма «солнечные лучи» идеально подходит для отображения иерархических данных и может отображаться, если в иерархической структуре существуют пустые (пустые) ячейки. Каждый уровень иерархии представлен одним кольцом или кругом, а ее верхом является самый близкий к центру круг. Диаграмма «солнечные лучи» без иерархических данных (один уровень категорий) похожа на кольцевую диаграмму. Однако на такой диаграмме с несколькими уровнями категорий отображается связь между внешними и внутренними кольцами. На диаграмме «солнечные лучи» наиболее эффективно показано, как одно кольцо разбивается на его части.
Для диаграммы «солнечные лучи» не существует подтипов.
Дополнительные сведения см. в разделе «Создание диаграммы солнечных лучов».
Каскадная диаграмма показывает нарастающий финансовый итог по мере добавления или вычитания значений. Это помогает понять, как ряд положительных и отрицательных значений влияет на исходную величину. Столбцы обозначены цветом, что позволяет быстро отличить положительные значения от отрицательных.
Для каскадных диаграмм не существует подтипов.
Дополнительные сведения см. в разделе «Создание каскадной диаграммы».
Данные, отображаемые на гистограмме, показывают частоты распределения. Каждый столбец диаграммы можно изменять для дальнейшего анализа данных.
Типы гистограмм
-
Гистограмма. Отображает распределение данных, сгруппированных в столбцы по частотам.
-
Диаграмма Парето. Это гистограмма с сортировкой, содержащая столбцы, отсортированные по убыванию, и строку, в которой представлено совокупное итоговое значение в процентах.
Дополнительные сведения доступны для гистограмм и диаграмм Парето .
На линейчатой диаграмме и диаграмме усов показано распределение данных по квартилям, выделяя среднее и выбросы. Поля могут содержать линии, расширяемые вертикально под названием «усы». Эти строки указывают на вариативность за пределами верхних и нижних квартилей, и любая точка за пределами этих линий или усов считается выбросом. Используйте этот тип диаграммы, если существует несколько наборов данных, которые связаны друг с другом.
Дополнительные сведения см. в разделе «Создание прямоугольника и диаграммы усов».

Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде гистограммы. В гистограммах категории обычно расположены вдоль горизонтальной ось, а значения — вдоль вертикальной.
Гистограммы удобны для демонстрации изменения данных с течением времени или для сравнения элементов.
Гистограммы включают в себя указанные ниже подтипы диаграмм.
-
Гистограмма с группировкой. Предназначена для сравнения значений по категориям. На гистограмме с группировкой значения отображаются в плоских вертикальных прямоугольниках. На объемной гистограмме с группировкой данные отображаются с использованием трехмерной перспективы.
-
Гистограмма с накоплением. Показывает отношение отдельных элементов к целому, отражая вклад каждого значения в итоговое по категориям. На гистограмме с накоплением значения отображаются в плоских вертикальных прямоугольниках с накоплением. На объемной гистограмме с накоплением данные отображаются с использованием трехмерной перспективы. Объемная перспектива не является объемной диаграммой в полном смысле, поскольку в ней не используется ось дополнительного значения (ось глубины).
-
Нормированная гистограмма. Отражает процентную долю каждого значения в итоговом по категориям. На нормированной гистограмме значения отображаются в плоских вертикальных прямоугольниках с нормированием. На объемной нормированной гистограмме данные отображаются с использованием трехмерной перспективы. Объемная перспектива не является объемной диаграммой в полном смысле, поскольку в ней не используется ось дополнительного значения (ось глубины).
-
Трехмерная гистограмма. Строится по трем осям, которые можно изменять (горизонтальная ось, вертикальная ось и ось глубины). Позволяет сравнивать точки данных вдоль горизонтальной оси и оси глубины.
-
Цилиндрические, конические и пирамидальные гистограммы. Доступны те же подтипы, что и для прямоугольных гистограмм (с группировкой, с накоплением, нормированная, включая их объемные варианты). Отображение и сравнение данных также аналогично гистограммам. Единственное отличие заключается в том, что на диаграммах этих типов вместо прямоугольников отображаются цилиндры, конусы и пирамиды.

Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде графика. На графиках можно отображать изменение непрерывных данных с течением времени с использованием общей шкалы, поэтому они идеально подходят для демонстрации тенденций в данных через равные временные интервалы. На графике данные категории равномерно распределены вдоль горизонтальной оси, а все данные значений равномерно распределены вдоль вертикальной оси.
Графики хорошо подходят для случаев, когда подписи категорий являются текстом и представляют собой значения, распределенные через равные интервалы, например месяцы, кварталы или финансовые года.
Графики включают в себя указанные ниже подтипы диаграмм.
-
График с маркерами или без них. Служит для отображения тенденций с течением времени или упорядоченных категорий, особенно если имеется много точек данных и важен порядок, в котором они представлены. Если имеется много категорий или значения являются приблизительными, используйте график без маркеров.
-
График с накоплением (с маркерами или без них). Отображает изменение вклада каждого значения в итоговое с течением времени или упорядоченные категории. Если имеется много категорий или значения являются приблизительными, используйте график с накоплением без маркеров.
-
Нормированный график с накоплением (с маркерами или без них). Отображает изменение процентной доли каждого значения в итоговом с течением времени или упорядоченные категории. Если имеется много категорий или значения являются приблизительными, используйте нормированный график с накоплением без маркеров.
-
Объемный график. Отображает каждую строку или столбец данных в виде трехмерной ленты. На объемном графике имеются горизонтальная ось, вертикальная ось и ось глубины, которые можно изменять.

Данные, упорядоченные на листе Excel в виде одного столбца или строки, можно визуально представить в виде круговой диаграммы. Круговые диаграммы отражают размер элементов одного ряд данных в пропорции к сумме элементов. Точки данных на круговой диаграмме отображаются в виде процентных долей целого круга.
Круговую диаграмму целесообразно использовать, когда нужно отобразить только один ряд данных, ни одно из значений не является отрицательным, практически отсутствуют нулевые значения, имеется не более семи категорий и они представляют собой части целого круга.
Круговые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Круговая диаграмма. Отражает вклад каждого значения в итоговое в двумерном или трехмерном формате. Сектора круговой диаграммы можно выдвинуть вручную, чтобы подчеркнуть их значимость.
-
Вторичная круговая диаграмма и вторичная гистограмма. Предназначены для отображения круговых диаграмм, часть значений которых вынесена во вторичную круговую диаграмму или в линейчатую диаграмму с накоплением. Эти типы диаграмм облегчают восприятие небольших секторов основной круговой диаграммы.
-
Разрезанная круговая диаграмма. Отражает вклад каждого значения в итоговое с выделением отдельных значений. Разрезанные круговые диаграммы можно отобразить в трехмерном формате. Можно изменить параметры разрезания диаграммы для всех или отдельных секторов. Однако переместить сектора вручную невозможно.

Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде линейчатой диаграммы.
Линейчатые диаграммы используются для сравнения отдельных элементов.
Линейчатые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Линейчатая диаграмма с группировкой. Предназначена для сравнения значений по категориям. На линейчатых диаграммах с группировкой категории, как правило, расположены по вертикальной оси, а значения — по горизонтальной оси. На объемной линейчатой диаграмме с группировкой горизонтальные прямоугольники отображаются в трехмерном формате. При этом данные на трех осях не отображаются.
-
Линейчатая диаграмма с накоплением. Отражает отношение отдельных элементов к целому. На объемной линейчатой диаграмме с накоплением горизонтальные прямоугольники отображаются в трехмерном формате. При этом данные на трех осях не отображаются.
-
Линейчатая диаграмма с накоплением и линейчатая диаграмма с накоплением на 100 % в трехмерной диаграмме Отражает процентную долю каждого значения в итоговом по категориям. На объемной нормированной линейчатой диаграмме горизонтальные прямоугольники отображаются в трехмерном формате. При этом данные на трех осях не отображаются.
-
Горизонтальные цилиндрическая, коническая и пирамидальная диаграммы. Доступны те же подтипы, что и для прямоугольных гистограмм (с группировкой, с накоплением и нормированная). Отображение и сравнение данных также аналогично гистограммам. Единственное отличие заключается в том, что на диаграммах этих типов вместо горизонтальных прямоугольников отображаются цилиндры, конусы и пирамиды.

Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде диаграммы с областями. Отображение суммы построенных значений на диаграмме с областями позволяет также продемонстрировать отношение частей к целому.
Диаграммы с областями позволяют сделать акцент на амплитуде изменений с течением времени и привлечь внимание к суммарному значению по всему тренду. Например, на диаграмме с областями можно построить данные, представляющие прибыль в динамике по времени, чтобы подчеркнуть общую прибыль.
Диаграммы с областями включают в себя указанные ниже подтипы диаграмм.
-
Диаграмма с областями. Отображает изменение значений с течением времени или другие данные категории. В объемных диаграммах с областями используются три оси (горизонтальная, вертикальная и ось глубины), которые можно изменять. В общем случае следует рассмотреть вариант использования графика вместо диаграммы с областями без накопления, поскольку данные из одного ряда могут быть перекрыты данными из другого ряда.
-
Диаграмма с областями с накоплением. Отображает изменение вклада каждого значения в итоговое с течением времени или другие данные категорий. Объемная диаграмма с областями с накоплением отображается аналогичным образом, но с использованием трехмерной перспективы. Объемная перспектива не является объемной диаграммой в полном смысле, поскольку в ней не используется ось дополнительного значения (ось глубины).
-
Нормированная диаграмма с областями. Отображает изменение процентной доли каждого значения в итоговом с течением времени или другие данные категорий. Объемная нормированная диаграмма с областями отображается аналогичным образом, но с использованием трехмерной перспективы. Объемная перспектива не является объемной диаграммой в полном смысле, поскольку в ней не используется ось дополнительного значения (ось глубины).

Данные, упорядоченные на листе Excel в виде столбцов и строк, можно визуально представить в виде точечной диаграммы. Точечная диаграмма имеет две оси значений. Один набор числовых данных отображается по горизонтальной оси (оси X), а другой — по вертикальной (оси Y). Эти значения объединены в отдельные точки данных и отображаются через неравные интервалы или группами.
Точечная диаграмма показывает отношения между численными значениями в нескольких рядах данных или отображает две группы чисел как один ряд координат x и y. Точечные диаграммы обычно используются для иллюстрации и сравнения числовых значений, например научных, статистических или технических данных.
Точечные диаграммы содержат указанные ниже подтипы диаграмм.
-
Точечная диаграмма только с маркерами. Служит для сравнения пар значений. Если имеется много точек данных, а соединительные линии могут затруднить восприятие информации, следует использовать точечную диаграмму с маркерами данных, но без линий. Этот тип диаграммы можно также использовать, если не нужно показывать связи между точками данных.
-
Точечная диаграмма с гладкими кривыми и с гладкими кривыми и маркерами. Отображает гладкую кривую, соединяющую точки данных. Плавные линии могут отображаться с маркерами или без них. Гладкие кривые без маркеров лучше использовать, если имеется много точек данных.
-
Точечная диаграмма с прямыми отрезками и с прямыми отрезками и маркерами. Отображает прямые отрезки, соединяющие точки данных. Прямые отрезки могут отображаться с маркерами или без них.
Пузырьковая диаграмма является разновидностью точечной диаграммы с тем отличием, что размер пузырьков представляет значение третьей переменной.
Пузырьковые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Пузырьковая диаграмма (плоская и с объемным эффектом). Позволяет сравнить наборы не из двух, а из трех значений. Третье значение определяет размер пузырька. Можно выбрать отображение пузырьков в плоском формате или с объемным эффектом.

Данные, упорядоченные на листе Excel в столбцах или строках, которые расположены в определенном порядке, можно визуально представить в виде биржевой диаграммы.
Как следует из названия, биржевые диаграммы чаще всего используются для демонстрации колебания курса акций. Тем не менее эту диаграмму можно также использовать для научных данных. Например, биржевая диаграмма подходит для отображения колебаний суточной или годовой температуры.
Биржевые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Биржевая диаграмма с тремя значениями (самый высокий курс, самый низкий курс, курс закрытия). Отображает цены на акции. Для этой диаграммы требуются три ряда значений в правильном порядке: самый высокий курс, самый низкий курс и курс закрытия.
-
Биржевая диаграмма с четырьмя значениями (курс открытия, самый высокий курс, самый низкий курс, курс закрытия). Для этой диаграммы требуются четыре ряда значений в правильном порядке: курс открытия, самый высокий курс, самый низкий курс и курс закрытия.
-
Биржевая диаграмма с четырьмя значениями (объем, самый высокий курс, самый низкий курс, курс закрытия). Для этой диаграммы требуются четыре ряда значений в правильном порядке: объем, самый высокий курс, самый низкий курс и курс закрытия. На диаграмме измеряется объем с использованием двух осей значений: одна — для столбцов со значениями объема, а другая — для курса акций.
-
Биржевая диаграмма с пятью значениями (объем, курс открытия, самый высокий курс, самый низкий курс, курс закрытия). Для этой диаграммы требуются пять рядов значений в правильном порядке: объем, курс открытия, самый высокий курс, самый низкий курс и курс закрытия.

Данные, упорядоченные на листе Excel в виде столбцов или строк, можно визуально представить в виде поверхностной диаграммы. Как и на топографической карте, цвета и узоры обозначают области, которые находятся в одном и том же диапазоне значений.
Поверхностная диаграмма удобна в том случае, если нужно найти оптимальную комбинацию двух наборов данных.
Поверхностные диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Объемная поверхностная диаграмма Показывает тенденции в значениях в двух измерениях в непрерывной кривой. Цветовые полосы на поверхностной диаграмме не представляют ряд данных. Они представляют разницу между значениями. На диаграммах этого типа данные можно представить в трехмерном виде, который можно рассматривать как резиновую пленку, натянутую на трехмерную гистограмму. Обычно такие диаграммы используются для отображения отношений между большими объемами данных, которые трудно продемонстрировать иначе.
-
Проволочная объемная поверхностная диаграмма. На этой диаграмме отображаются только линии. Проволочная объемная поверхностная диаграмма сложна для восприятия, но такой тип диаграмм рекомендуется использовать для быстрого отображения больших наборов данных.
-
Контурная диаграмма. Если на поверхностную диаграмму посмотреть сверху, она напоминает двумерную топографическую карту. На контурной диаграмме цветные полосы представляют конкретные диапазоны значений. Линии на контурной диаграмме связывают интерполированные точки с одинаковыми значениями.
-
Проволочная контурная диаграмма. Поверхностная диаграмма при виде сверху. Без цветных полос на поверхности контурной диаграммы отображаются только линии. Бесцветные контурные диаграммы сложны для восприятия. Вместо них можно использовать поверхностные диаграммы.
Как и круговая диаграмма, кольцевая диаграмма показывает отношение частей к целому. Тем не менее она может содержать более одного ряда данных. Каждое кольцо в кольцевой диаграмме представляет один ряд данных.
Кольцевые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Кольцевая диаграмма. Отображает данные в виде колец, каждое из которых представляет один ряд данных. Если в метках данных отображаются процентные доли, данные каждого кольца в сумме будут составлять 100%.
-
Разрезанная кольцевая диаграмма. Отражает вклад каждого значения в итоговое с выделением отдельных значений. Такие диаграммы могут содержать более одного ряда данных.

На лепестковой диаграмме каждая категория имеет свою собственную ось значений, исходящую из начала координат. Линии связывают все значения одного ряда данных.
Лепестковые диаграммы используются для сравнения совокупных значений нескольких рядов данных.
Лепестковые диаграммы включают в себя указанные ниже подтипы диаграмм.
-
Лепестковая диаграмма. Отображает изменения значений относительно начала координат.
-
Заполненная лепестковая диаграмма. Отображает изменения значений относительно начала координат с заливкой области, охватываемой каждым рядом данных, цветом.
Изменение типа диаграммы
Если у вас уже есть диаграмма, а вы просто хотите изменить ее тип, выполните следующие действия:
-
Выберите диаграмму, откройте вкладку «Конструктор диаграмм» и выберите команду «Изменить тип диаграммы».
-
Выберите новый тип диаграммы в коллекции доступных параметров.
См. также
Создание диаграммы с рекомендуемой диаграммой