|
Ард Шон Пользователь Сообщений: 132 |
Здравствуйте! Помогите разобраться, пожалуйста. 1. Возможно ли в Excel построить график с неравномерным ходом по оси абсцисс? Изменено: Ард Шон — 06.06.2013 21:45:16 |
|
Юрий М Модератор Сообщений: 60577 Контакты см. в профиле |
Даблклик по правой оси — Шкала — снимаем галку Авто с минимального значения и в поле пишем 1600. Этого хотели добиться? |
|
Шон ар Пользователь Сообщений: 132 |
Нет. То, что Вы предлагаете просто уберет ненужные значения от 0 до 1600К. Но графики останутся совмещенными своими точками в категории 1. А на деле — это распределение температур в разных сечениях изделия с разными диаметрами этих сечений, соответственно, у них у каждого своя «категория1». Мне нужно растащить эти графики по горизонтали. Изменено: Шон ар — 07.06.2013 00:30:16 |
|
Юрий М Модератор Сообщений: 60577 Контакты см. в профиле |
И здесь никому ненужное цитирование… |
|
Chonard Пользователь Сообщений: 132 |
И цитирование ни к чему и вопрос сложный. Мда… |
|
Юрий М Модератор Сообщений: 60577 Контакты см. в профиле |
|
|
Chonard Пользователь Сообщений: 132 |
Просто возвращаюсь к старому имени. Больше менять не буду. Остановлюсь на этом. 2. Есть три измерения распределения температуры по разным сечениям изделия. Диаметры этих сечений разные, соответственно, диапазон значений по оси х тоже разный и шаг может не совпадать. Можно ли совместить эти графики в одних осях? Или средствами Excel это нельзя сделать? Изменено: Chonard — 06.06.2013 22:59:50 |
|
anvg Пользователь Сообщений: 11878 Excel 2016, 365 |
Нужно построить обычную точечную диаграмму XY Прикрепленные файлы
|
|
Chonard Пользователь Сообщений: 132 |
О, спасибо! Это похоже на то, что я хотел. |
|
giveaway Пользователь Сообщений: 5 |
Каково решение данной проблемы, так и не понял? Прикрепляю свой пример. Столбец А должен быть осью Х и не просто подписи поставить равномерно, а привести ось Х в соответствующий масштаб. Потому что не может быть между делениями 1.9 и 4.5 (два первых значения) быть такое же расстояние, как между 50.2 и 65.8 (два последних значения). Это вообще возможно в графиках Excel. Ощущение, что у него по оси Х значения всегда равномерны. Изменено: giveaway — 03.12.2021 21:28:18 |
|
tutochkin Пользователь Сообщений: 559 |
giveaway, вам какой вариант нужен из двух: Вариант 2 — нелинейная ось Х как таковая Если первый — то Вам выше написали, стройте точечную диаграмму (см.первый рисунок). |
|
giveaway Пользователь Сообщений: 5 |
#12 04.12.2021 10:42:57
Благодарю,вариант 1 меня вполне устроил. |
||
|
Светлый Пользователь Сообщений: 487 |
#13 04.12.2021 17:52:54 Может, так? Прикрепленные файлы
|
Насколько я знаю по математике и статистике, чтобы разрешить такую ситуацию, мы можем подогнать уравнение к заданным данным, используя методы нескольких уравнений: В нашем случае 4 значения данных приведены так, что самое большее, мы можем соответствовать третьей степени, то есть кубическому уравнению. Таким образом, наше уравнение будет
Y = a + bX + c(X) ^ 2 + d * (X) ^ 3
Итак, есть четыре неизвестных и четыре уравнения.
Применение метода MATRIX: Y = AX, решение X = Inverse (A) * Y
Наша Y-матрица имеет порядок 4×1 = { 1,5; 3; 5,9; 11 }
Наша матрица коэффициентов А имеет порядок 4×4, приведенный ниже:
Матрица А = {1,1,1,1; 1,2,4,8; 1,4,16,64; 1,8,64,512}
X — неизвестная матрица порядка 4×1 = { a; б; с; д; }
Нашей целью является подгонка линии, а затем нанесение этих точек на X, что улучшает подгонку
ИСПОЛЬЗУЯ MMULT и MINVERSE Formula, мы получаем значения a,b,c и d.
X = MINVERSE (A) * Y
Я применил формулу. Получил константы:
а = -0,01905; b = 1,525; с = -0,00417; д = -0,00179.
Но оценки Y Использование этого уравнения дает точные значения Y, которые у нас есть, поэтому улучшения в построении графиков нет.
Так что я застрял, чтобы продолжить.
Несмотря на это, я рассказал о методе, если кто-то может дать руководство.
Благодарю.
Решение нелинейного уравнения в Excel
Разберём решение нелинейного уравнения в Excel вида:
y=4x 3 +2x–7
Ячейку A4 оставим пустой, а в ячейки B4 запишем формулу вида
Затем в Excel перейдём на вкладку Данные -> Поиск Решения
Открывается окно Параметры поиска решения. В поле оптимизировать целевую функцию выбираем ячейку B4, ставим Значения 0, ячейку переменной указываем A4, ставим галочку сделать переменные без ограничений неотрицательными, выбираем метод решения — поиск решения нелинейных задач методом ОПГ (обобщенного приведенного градиента) и жмем Найти решение
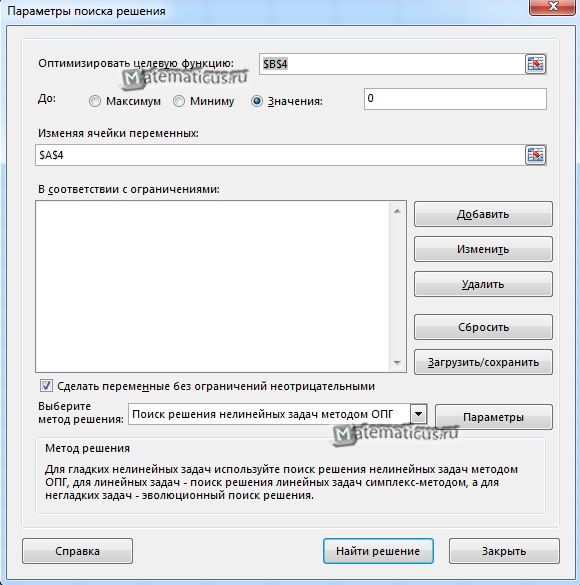
Получаем решение искомой задачи
x=1,06744215530327
Отчет результатов вычисления в Excel
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Кафедра прикладной математики и вычислительной техники
Решение нелинейных уравнений в Excel и Mathcad
к выполнению лабораторных работ
по дисциплине «Вычислительная математика»
Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с.
Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика».
Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования.
Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.
Рецензент к. ф-м. н.
Ó , составление, 2012
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
1.2 Отделение корней
1.3 Уточнение корней стандартными средствами Excel и Mathcad
1.4 Метод деления отрезка пополам
1.6 Метод Ньютона (касательных)
1.7 Комбинированный метод
1.8 Метод итераций
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
2.2 Решение систем нелинейных уравнений методом Ньютона
2.3 Решение систем нелинейных уравнений методами итераций
3 Задания к лабораторным работам
Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения
Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения
Лабораторная № 3. Решение систем нелинейных уравнений
Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем
4 Вопросы и тесты для самоконтроля
Список рекомендуемой литературы
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн.
В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью.
Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс).
1.2 Отделение корней
Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0.
Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной.
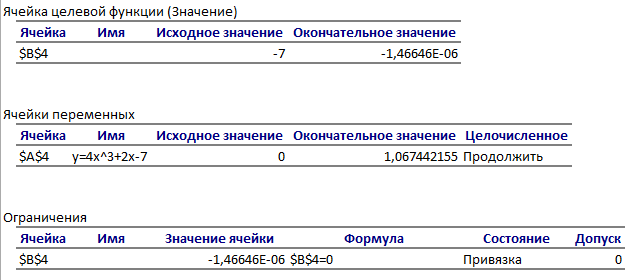
Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения».
Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения.
На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню.
Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (расположенными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.
Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения
1.3 Уточнение корней стандартными средствами Excel и Mathcad
Во всех методах уточнения корней необходимо задать начальное приближение, которое затем и будет уточняться. Если уравнение имеет несколько корней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержащий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка.
В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.
Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel
Рисунок 3 – Результаты использования средств решения уравнения в Excel
В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad
Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно.
В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет».
Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции).
1.4 Метод деления отрезка пополам
В этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге.
Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001.
Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b—a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы.
На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: Вставка

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.
Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьироваться до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться.
Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= — 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].
Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel
Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad
1.5 Метод хорд
В этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:

1.6 Метод Ньютона (касательных)
Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f»(х) > 0), или правая его граница: x0 = b (если f(b) f»(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:

Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня.
Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях.
Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции.
Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.
Точность вычислений можно оценить из соотношения
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:
где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.
Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.
Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно.
Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0.
Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя).
2.2 Решение систем нелинейных уравнений методом Ньютона
Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:
Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).

Для расчета новых приближений на шаге i+1 используется матричная формула

Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных.
Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям.
В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула

Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad.
2.3 Решение систем нелинейных уравнений методами итераций
Для реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид

Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:

Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений:
источники:
http://urok.1sept.ru/articles/564361
http://pandia.ru/text/78/157/38912.php
В диаграммах большинства типов можно скрывать и отображать оси. Чтобы упростить понимание данных диаграммы, можно также изменять их внешний вид.
Подробнее об осях
На диаграммах обычно имеется две оси, с помощью которых измеряются и систематизируются данные: вертикальная (ось значений или ось y) и горизонтальная (ось категорий или ось x). На трехмерных гистограммах, объемных конических и пирамидальных диаграммах имеется третья ось — ось глубины (ось рядов или ось z), так что данные можно строить вглубь диаграммы. На лепестковых диаграммах отсутствуют горизонтальные оси (категорий), а на круговых и кольцевых диаграммах вообще нет осей.
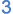
Ниже описано, что можно сделать с диаграммами, чтобы они выглядели более эффектно и лучше передавали информацию. Дополнительные сведения о том, что такое оси и что с ними можно делать, см. в разделе Все об осях.
Примечание: Следующая процедура относится к Office 2013 и более новых версий. Ищете по шагам для Office 2010?
Отображение и скрытие осей
-
Щелкните в любом месте диаграммы, на которой нужно отобразить или скрыть оси.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор и Формат.
-
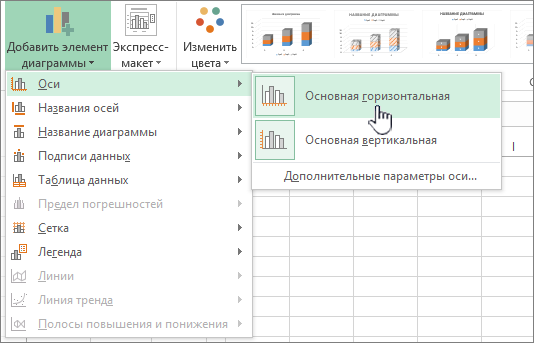
На вкладке Конструктор щелкните стрелку в поле «Добавить элемент диаграммы» и наведите указатель мыши на элемент раскрывающегося меню Оси.
-
Выберите тип оси, который вы хотите отобразить или скрыть.
Настройка делений и подписей оси
-
На диаграмме щелкните ось с делениями и подписями, которые нужно настроить, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется вкладка Работа с диаграммами с дополнительными вкладками Конструктор и Формат.
-
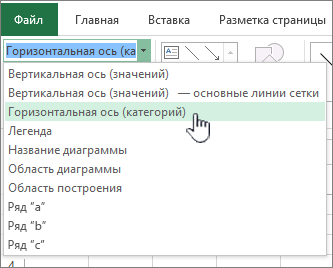
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните нужную ось.
-
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного.
-
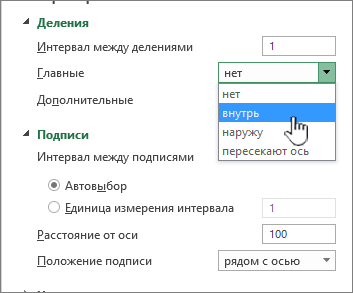
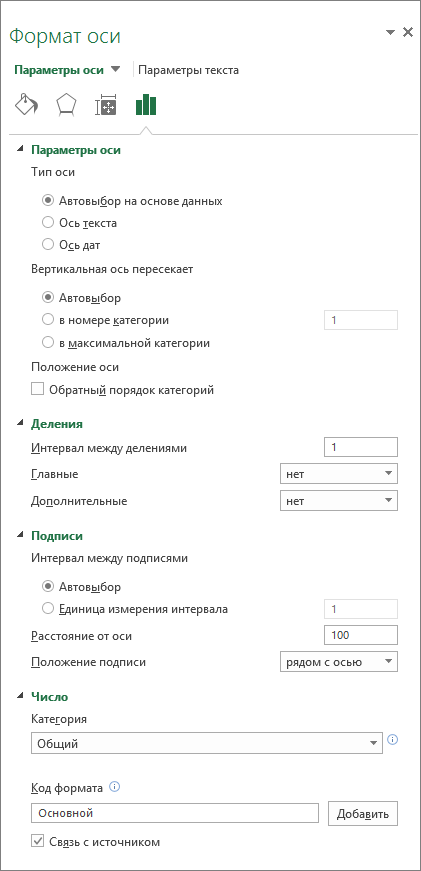
На панели «Параметры оси» в разделе Деления выполните одно или несколько из указанных ниже действий.
-
Чтобы изменить отображение основных делений, в поле Основные выберите нужное положение деления.
-
Чтобы изменить отображение промежуточных делений, в поле с раскрывающимся списком Промежуточные выберите нужное положение деления.
-
Чтобы изменить положение подписей, в разделе Подписи выберите нужный вам вариант.
Совет. Чтобы скрыть деления или их подписи, в поле Подписи оси выберите Нет.
-
Изменение количества категорий между подписями и делениями
-
На диаграмме щелкните горизонтальную ось (категорий), которую нужно изменить, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
-
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните нужную ось.
-
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного.
-
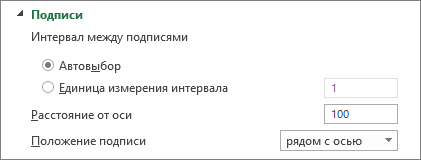
В разделе Параметры оси выполните одно или оба указанных ниже действия.
-
Чтобы изменить интервал между подписями оси, в разделе Интервал между подписями выберите Единица измерения интервала, а затем в текстовом поле введите нужное число.
Совет. Введите 1, чтобы отображалась подпись для каждой категории, 2, чтобы отображалась подпись для каждой второй категории, 3, чтобы отображалась подпись для каждой третьей категории и т. д.
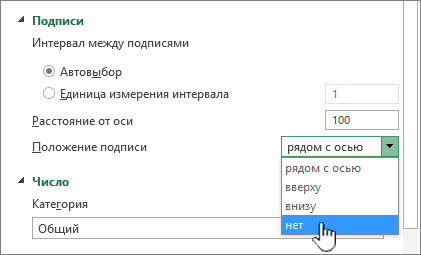
-
Чтобы изменить расположение подписей оси, в поле Расстояние до подписи от оси введите нужное число.
Совет. Чтобы расположить подписи ближе к оси, введите меньшее число. Чтобы увеличить расстояние между подписью и осью, введите большее число.
-
Изменение выравнивания и ориентации подписей
Выравнивание подписей можно изменить и на горизонтальной (категории), и на вертикальной (значения) оси. Если на диаграмме имеется многоуровневые подписи категорий, вы можете изменить выравнивание подписей всех уровней. Можно также изменить расстояние между уровнями подписей на горизонтальной оси (категорий).
-
На диаграмме щелкните ось с подписями, которые нужно иначе выровнять, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется вкладка Работа с диаграммами с дополнительными вкладками Конструктор и Формат.
-
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните нужную ось.
-
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного.
-
В диалоговом окне Формат оси щелкните Параметры текста.
-
В разделе Надпись выполните одно или несколько из указанных ниже действий.
-
В поле Вертикальное выравнивание выберите нужное положение вертикального выравнивания.
-
В поле Направление текста выберите нужную ориентацию текста.
-
В поле Другой угол выберите нужный угол поворота.
-
Совет. Вы также можете изменить горизонтальное выравнивание подписей осей, щелкнув ее и нажав кнопку «Выровнять по левую 


Изменение текста подписей категорий
Вы можете изменить текст подписей категорий на листе или прямо на диаграмме.
Изменение текста подписи категории на листе
-
На листе щелкните ячейку с текстом подписи, которую хотите изменить.
-
Введите новый текст и нажмите клавишу ВВОД.
Примечание После внесения изменений на листе диаграмма автоматически обновляется.
Изменение текста подписи на диаграмме
-
На диаграмме щелкните горизонтальную ось или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется вкладка Работа с диаграммами с дополнительными вкладками Конструктор и Формат.
-
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните горизонтальную ось (категорий).
-
-
На вкладке Конструктор в группе Данные нажмите кнопку Выбрать данные.
-
В диалоговом окне Выбор источника данных в разделе Подписи горизонтальной оси (категории) щелкните Изменить.
-
В поле Диапазон подписей оси выполните одно из указанных ниже действий.
-
Укажите диапазон на листе, который хотите использовать в качестве подписей оси категорий.
-
Введите подписи, разделяя их запятыми, например Отдел А, Отдел Б, Отдел В.
Примечание Если вы ввели текст подписи в поле Диапазон подписей оси, то текст подписи оси категорий больше не связан с ячейкой листа.
-
-
Нажмите ОК.
Изменение вида текста и чисел в подписях
Вы можете изменить формат текста подписей на оси категорий или чисел на оси значений.
Форматирование текста
-
На диаграмме щелкните правой кнопкой мыши ось с подписями, которые нужно отформатировать.
-
На панели инструментов Главная выберите нужный вам вид форматирования.
Совет. Можно также выбрать ось с подписями, а затем воспользоваться кнопками форматирования на вкладке Главная в группе Шрифт.
Форматирование чисел
-
На диаграмме щелкните ось с числами, которые нужно отформатировать, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется вкладка Работа с диаграммами с дополнительными вкладками Конструктор и Формат.
-
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните нужную ось.
-
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного.
-
В разделе «Параметры оси» щелкните Число, а затем в поле Категория выберите нужный числовой формат.
Совет. Если в выбранном числовом формате используются знаки после запятой, их количество можно указать в поле Число десятичных знаков.
-
Чтобы сохранить связь чисел с ячейками листа, установите флажок Связь с источником.
Примечание Прежде чем форматировать числа как проценты, убедитесь, что представленные на диаграмме числа были вычислены как проценты в исходных данных и отображаются в десятичном формате. Проценты вычисляются на листе с помощью выражения количество / всего = процент. Например, если вы вычисляете значение 10 / 100 = 0,1, а затем форматируете 0,1 как процент, число должно отображаться в следующем виде: 10 %.
Изменение отображения осей диаграммы в Office 2010
-
Щелкните в любом месте диаграммы, на которой нужно отобразить или скрыть оси.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
-
На вкладке Макет в группе Оси нажмите кнопку Оси.
-
Выберите тип оси, которую нужно отобразить или скрыть, а затем — нужные параметры.
-
На диаграмме щелкните ось с делениями и подписями, которые нужно настроить, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
-
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните нужную ось.
-
-
На вкладке Формат в группе Текущий фрагмент выберите элемент Формат выделенного.
-
В разделе Параметры оси выполните одно или несколько из указанных ниже действий.
-
Чтобы изменить отображение основных делений, в поле Основные выберите нужное положение деления.
-
Чтобы изменить отображение промежуточных делений, в поле с раскрывающимся списком Промежуточные выберите нужное положение деления.
-
Чтобы изменить положение подписей, в поле Подписи оси выберите нужный вариант.
Совет. Чтобы скрыть деления или их подписи, в поле Подписи оси выберите Нет.
-
-
На диаграмме щелкните горизонтальную ось (категорий), которую нужно изменить, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
-
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните нужную ось.
-
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного.
-
В разделе Параметры оси выполните одно или оба указанных ниже действия.
-
Чтобы изменить интервал между подписями оси, в разделе Интервал между подписями выберите Единица измерения интервала, а затем в текстовом поле введите нужное число.
Совет. Введите 1, чтобы отображалась подпись для каждой категории, 2, чтобы отображалась подпись для каждой второй категории, 3, чтобы отображалась подпись для каждой третьей категории и т. д.
-
Чтобы изменить расположение подписей оси, в поле Расстояние до подписи от оси введите нужное число.
Совет. Чтобы расположить подписи ближе к оси, введите меньшее число. Чтобы увеличить расстояние между подписью и осью, введите большее число.
-
Выравнивание подписей можно изменить и на горизонтальной (категории), и на вертикальной (значения) оси. Если на диаграмме имеется многоуровневые подписи категорий, вы можете изменить выравнивание подписей всех уровней. Можно также изменить расстояние между уровнями подписей на горизонтальной оси (категорий).
-
На диаграмме щелкните ось с подписями, которые нужно иначе выровнять, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
-
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните нужную ось.
-
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного.
-
В диалоговом окне Формат оси щелкните Выравнивание.
-
В разделе Разметка текста выполните одно или несколько из указанных ниже действий.
-
В поле Вертикальное выравнивание выберите нужное положение вертикального выравнивания.
-
В поле Направление текста выберите нужную ориентацию текста.
-
В поле Другой угол выберите нужный угол поворота.
-
Совет. Чтобы изменить горизонтальное выравнивание подписей осей, щелкните ее правой кнопкой мыши и выберите на мини-панели инструментов кнопку «Выровнять по левму 


Вы можете изменить текст подписей категорий на листе или прямо на диаграмме.
Изменение текста подписи категории на листе
-
На листе щелкните ячейку с текстом подписи, которую хотите изменить.
-
Введите новый текст и нажмите клавишу ВВОД.
Примечание После внесения изменений на листе диаграмма автоматически обновляется.
Изменение текста подписи на диаграмме
-
На диаграмме щелкните горизонтальную ось или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
-
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните горизонтальную ось (категорий).
-
-
На вкладке Конструктор в группе Данные нажмите кнопку Выбрать данные.
-
В диалоговом окне Выбор источника данных в разделе Подписи горизонтальной оси (категории) щелкните Изменить.
-
В поле Диапазон подписей оси выполните одно из указанных ниже действий.
-
Укажите диапазон на листе, который хотите использовать в качестве подписей оси категорий.
Совет. Вы также можете нажать кнопку «Свернуть
«, а затем выбрать диапазон, который вы хотите использовать на этом сайте. Закончив, нажмите кнопку Развернуть диалоговое окно.
-
Введите подписи, разделяя их запятыми, например Отдел А, Отдел Б, Отдел В.
Примечание Если вы ввели текст подписи в поле Диапазон подписей оси, то текст подписи оси категорий больше не связан с ячейкой листа.
-
-
Нажмите ОК.
Вы можете изменить формат текста подписей на оси категорий или чисел на оси значений.
Форматирование текста
-
На диаграмме щелкните правой кнопкой мыши ось с подписями, которые нужно отформатировать.
-
На мини-панели инструментов выберите нужные параметры форматирования.
Совет. Можно также выбрать ось с подписями, а затем воспользоваться кнопками форматирования на вкладке Главная в группе Шрифт.
Форматирование чисел
-
На диаграмме щелкните ось с числами, которые нужно отформатировать, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
-
Щелкните в любом месте диаграммы.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
-
На вкладке Формат в группе Текущий фрагмент щелкните стрелку в поле Элементы диаграммы, затем щелкните нужную ось.
-
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного.
-
Щелкните Число, а затем в поле Категория выберите нужный числовой формат.
Совет. Если в выбранном числовом формате используются знаки после запятой, их количество можно указать в поле Число десятичных знаков.
-
Чтобы сохранить связь чисел с ячейками листа, установите флажок Связь с источником.
Примечание Прежде чем форматировать числа как проценты, убедитесь, что представленные на диаграмме числа были вычислены как проценты в исходных данных и отображаются в десятичном формате. Проценты вычисляются на листе с помощью выражения количество / всего = процент. Например, если вы вычисляете значение 10 / 100 = 0,1, а затем форматируете 0,1 как процент, число должно отображаться в следующем виде: 10 %.
Добавление делений на оси
Ось можно отформатировать для отображения основных и промежуточных делений с выбранными интервалами.
-
Этот шаг относится только к Word для Mac: в меню «Вид» выберите пункт «Разметка печати».
-
Щелкните диаграмму и откройте вкладку Конструктор.
-
Щелкните «Добавить элемент диаграммы > осей > дополнительные параметры осей.)
-
В области «Формат оси» раз щелкните «Деление»,а затем выберите параметры основных и незначительных типов делений.
После добавления делеков можно изменить интервалы между ними, изменив значение в поле «Интервал между знаками».
Все об осях
На диаграммах разного типа оси могут отображаться по-разному. Например, на точечных (xy) и пузырьковых диаграммах числовые значения отображаются как по горизонтальной, так и по вертикальной оси. Примером может служить отображение количества (дюймов) осадков относительно барометрического давления. Оба элемента имеют числовые значения, и точки данных отображаются на осях x и y относительно этих значений. Для осей значений предлагается множество вариантов, например установка логарифмической шкалы в качестве масштаба.
На диаграммах других типов, таких как гистограммы, графики и диаграммы с областями, числовые значения отображаются только на вертикальной оси (значений), а текстовые классификации (или категории) — на горизонтальной. Примером может служить отображение количества (дюймов) осадков по географическим областям. В этом примере географические области являются текстовыми категориями данных, которые отображаются на горизонтальной оси (категорий). Географические области, представляющие собой текст, разносятся равномерно в отличие от значений, которые можно измерить. Учитывайте это различие при выборе типа диаграммы, поскольку возможности для осей значений и категорий различаются. В подобных случаях ось глубины (рядов) представляет собой другой вид оси категорий.
При создании диаграммы на осях по умолчанию отображаются деления и подписи. Способ их отображения можно настраивать с помощью основных и промежуточных делений и подписей. Чтобы не перегружать диаграмму, вы можете отобразить меньшее количество подписей или делений на горизонтальной оси (категорий), указав интервалы для пометки категорий или количество категорий, отображаемых между делениями.
Вы также можете изменить выравнивание и ориентацию подписей или формат отображения текста и чисел (например, для отображения чисел в виде процентов).
См. также
Добавление и удаление вспомогательной оси на диаграмме
Изменение цвета или стиля диаграммы
Создание диаграммы от начала до конца
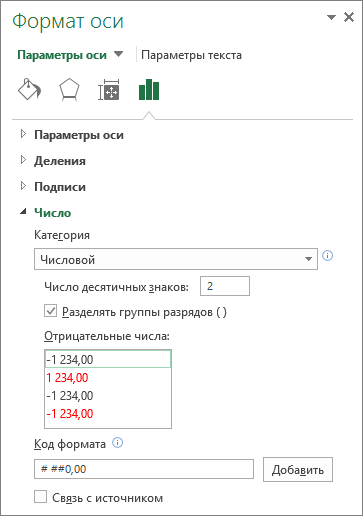
Learn how to make a scatter plot, also known as an x-y graph, where you can show the relationships between variables.
When you need to visualize the relationship between two sets of quantitative data, Microsoft Excel makes it possible for you to create an X-Y scatter graph.
For regression analysis, scatter plot graphs are the most important data visualization tool. However, you may be wondering how to make a scatter plot in Excel. Keep reading this data-based article to learn how.
Scatter Plot Excel—When You Should Use It
In Microsoft Excel, you may confuse whether an X-Y graph is a scatter plot or a line graph. Both are similar except for the data representation along the horizontal (X) axis.
A scatter chart consists of two value axes for quantitative data visualization. The horizontal (X) axis represents one set of numerical data, and the vertical (Y) axis indicates another data set.
But, the Excel line graph visualizes all category data on the horizontal (X) axis and numerical values on the vertical (Y) axis.
In Excel, you can create a scatter plot graph to visualize and compare numeric values obtained from scientific and statistical analyses. In the following scenarios, you should use a scatter plot instead of a line graph:
- To analyze if there is any correlation between two sets of quantifiable values. The appearance of the X and Y chart will be quite similar to a diagonal arrangement.
- To explore positive or negative trends in the variables.
- To scale up the horizontal (X) axis.
- To visualize outliers, clusters, non-linear trends, and linear trends in a large set of data.
- To compare large numbers of time-independent data points.
How to Make a Scatter Plot in Excel
Here are the steps to create a scatter plot using the X-Y graph template in Microsoft Excel. You can use the following data sets as an example to create a scatter plot.
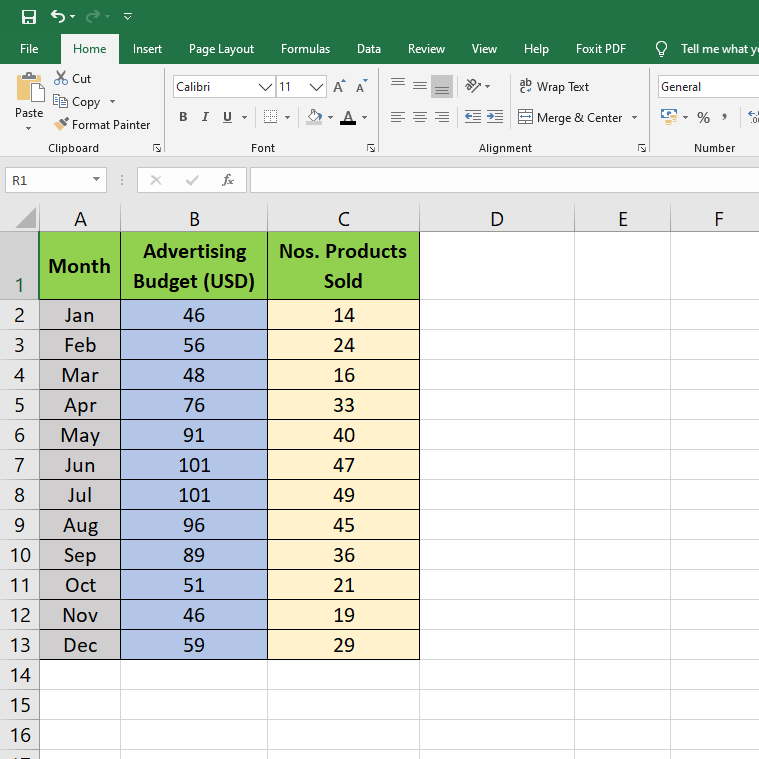
1. To start with, format the data sets to put the independent variables in the left side column and dependent variables in the right side column. In the above data sets, advertising budgets are independent variables, and items sold are dependent variables.
2. You need to select two columns in Microsoft Excel with numeric data. Make sure to include the column headers too. In this case, the range is B1:C13.
3. Now, click on the Insert tab on the Ribbon and then select the scatter plot template you like from the Charts section. For this tutorial, it is the first thumbnail which is the classic scatter chart.
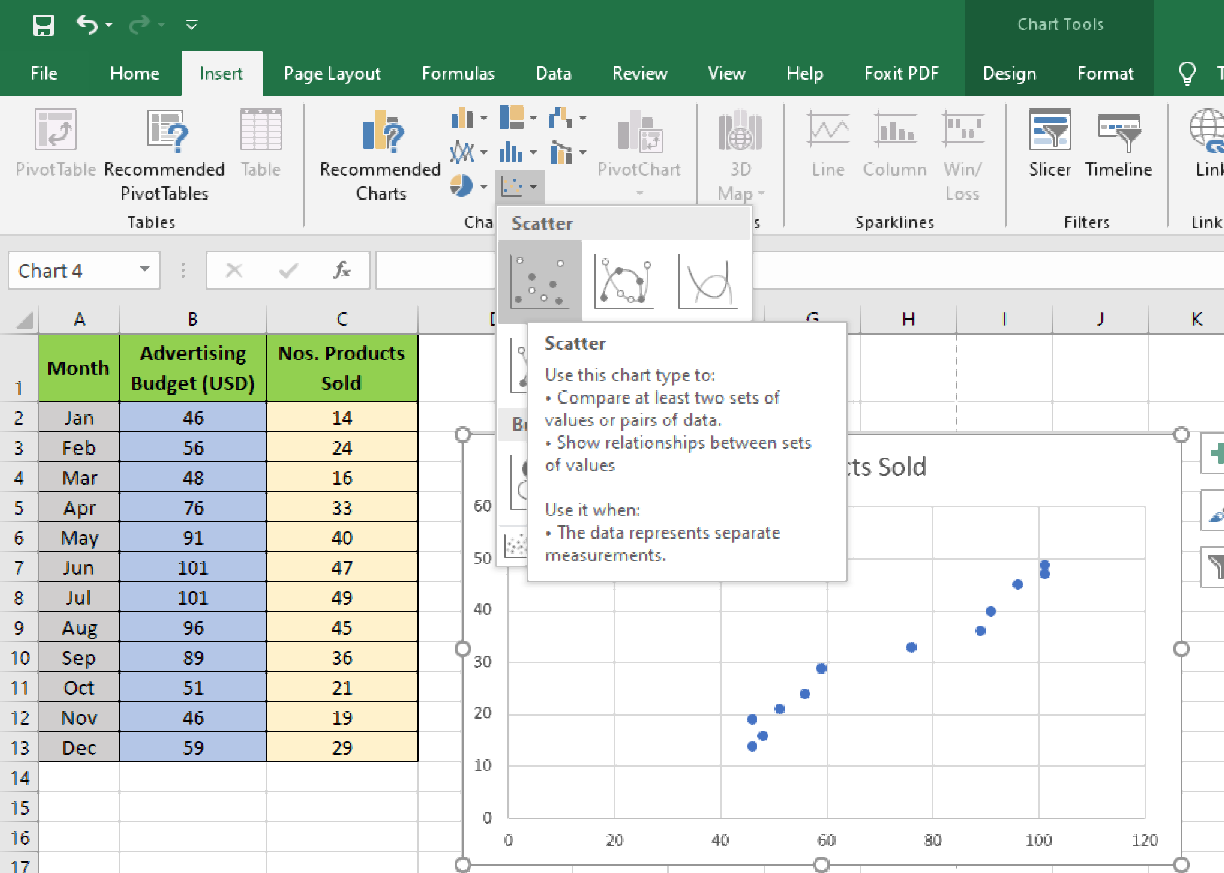
4. The classic X-Y graph scatter chart will show up in the Microsoft Excel worksheet. It is the most simple form of scatter plot graph. You can also customize to visualize the correlation clearly and professionally.
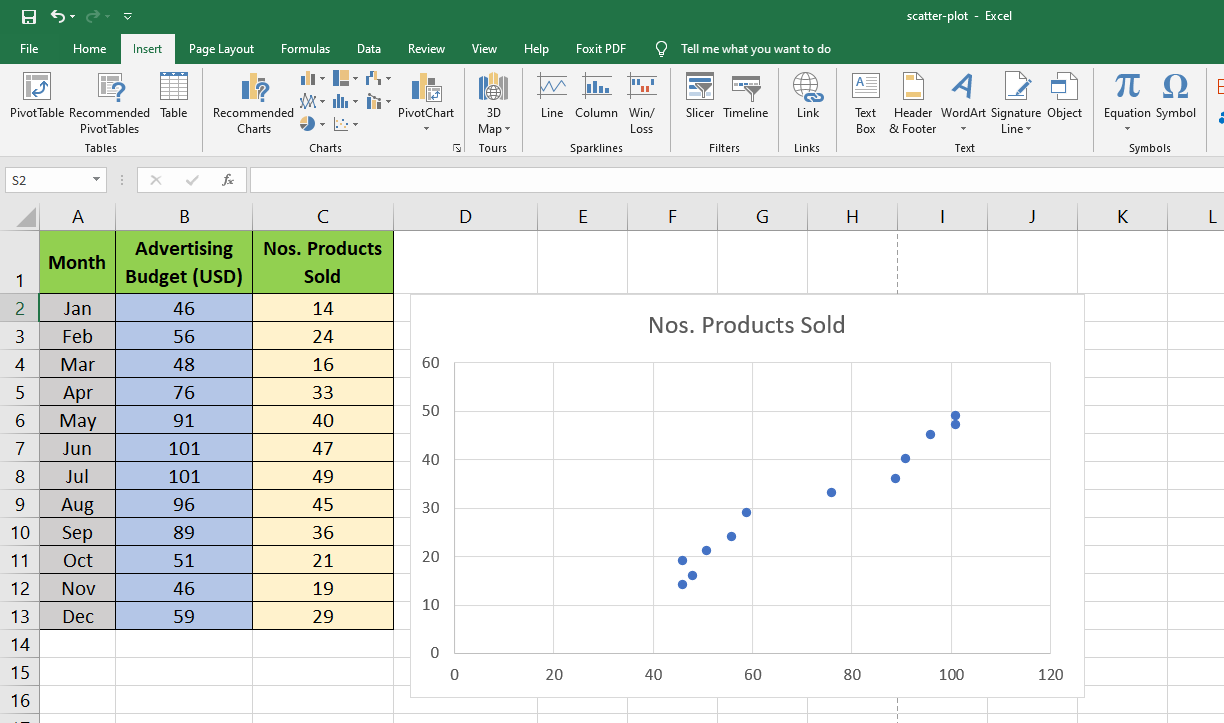
Miscellaneous Optimization for Scatter Plot Graph Visualization
Excel allows you to customize the scatter plot in a number of ways. Here are some of the possible modifications you can make:
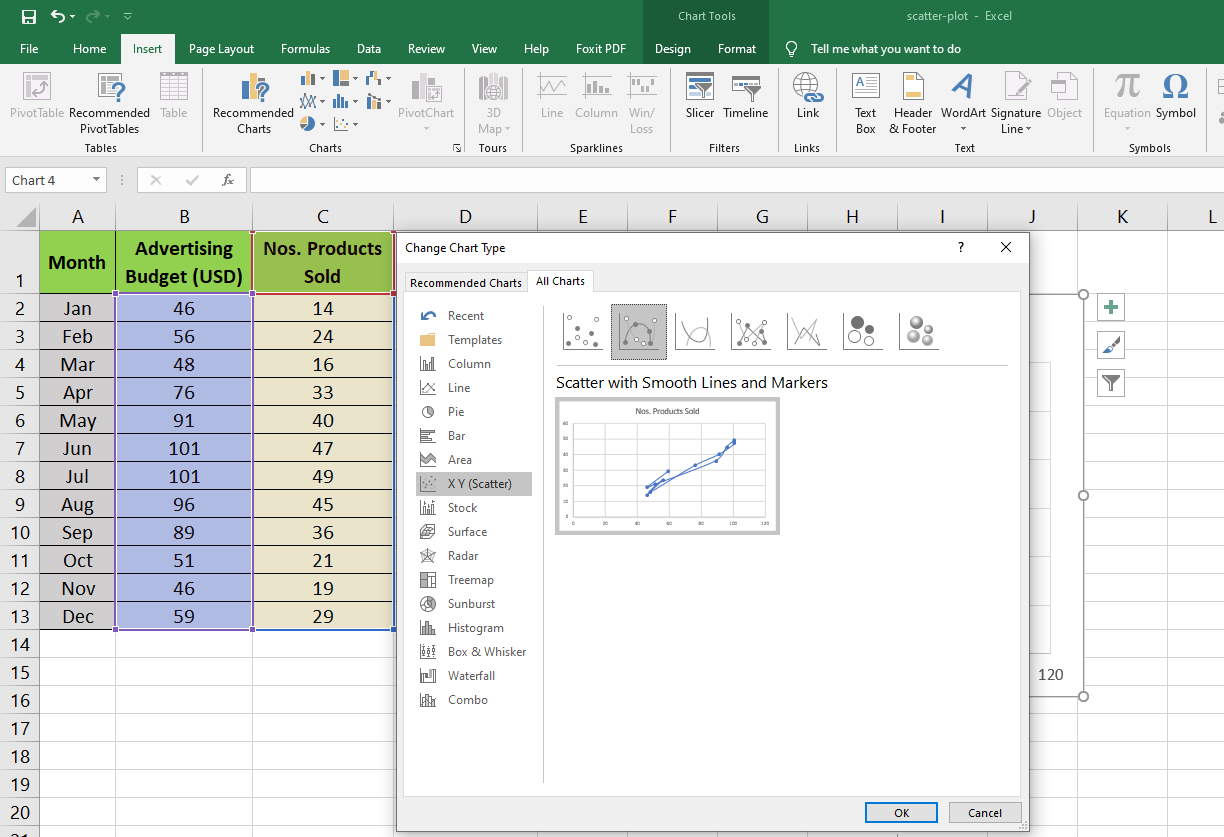
Scatter Chart Types
The X-Y scatter plot is the most common scatter plot type. Others include:
- Scatter with Smooth Lines and Markers.
- Scatter with Smooth Lines.
- Scatter with Straight Lines and Markers.
- Scatter with Straight Lines.
- Bubble X-Y scatter.
- 3-D Bubble X-Y scatter.
Customizing X-Y Graph Scatter Chart
When you create a scatter plot in Microsoft Excel, you have the freedom to customize almost every element of it. You can modify sections like axis titles, chart titles, chart colors, legends, and even hide the gridlines.
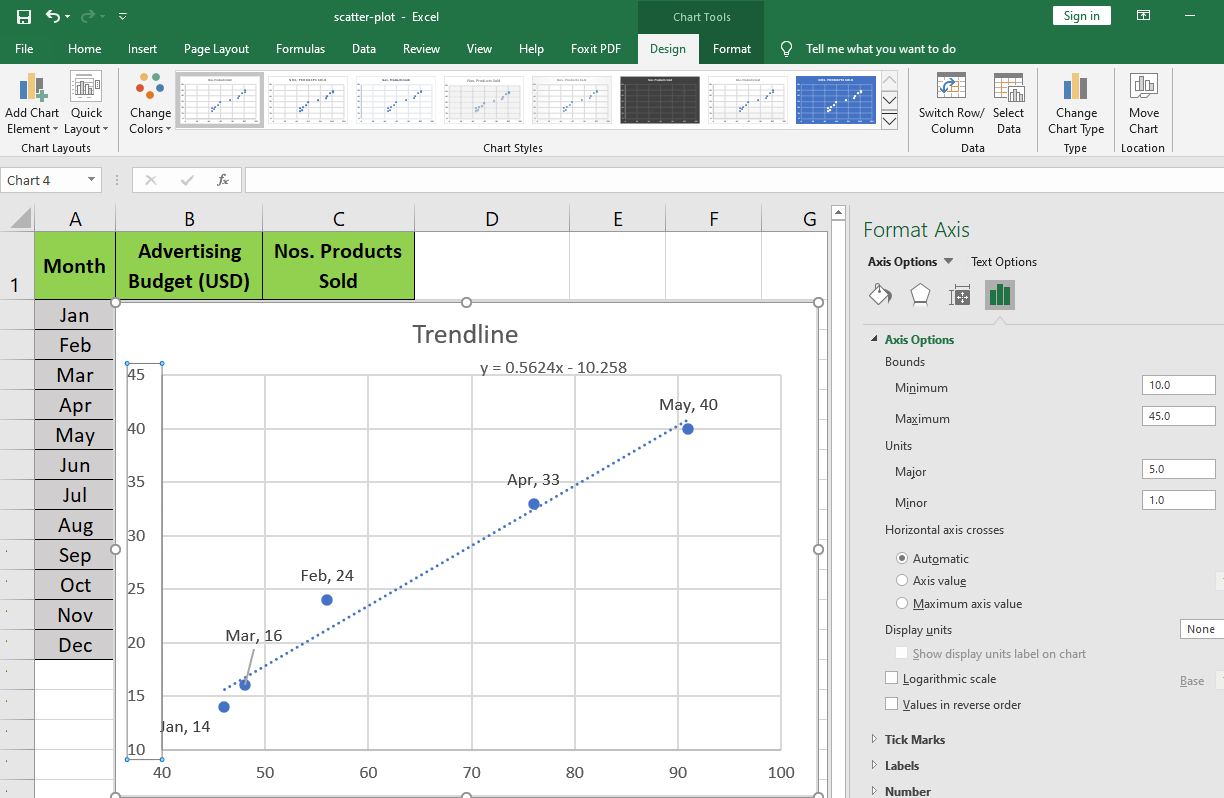
If you want to reduce the plot area, follow these steps:
- Double-click on the horizontal (X) or vertical (Y) axis to open Format Axis.
- Under the Axis Options menu, set Minimum and Maximum Bounds as per the data sets.
- The scatter plot graph will resize accordingly.
If you want to remove the gridlines, perform these steps:
- Double-click on any of the horizontal gridlines within the X-Y graph plot area.
- From the sidebar Format Major Gridlines menu, select No line.
- Now, click on any of the remaining vertical gridlines and select No line.
- Gridlines will disappear from the scatter chart.
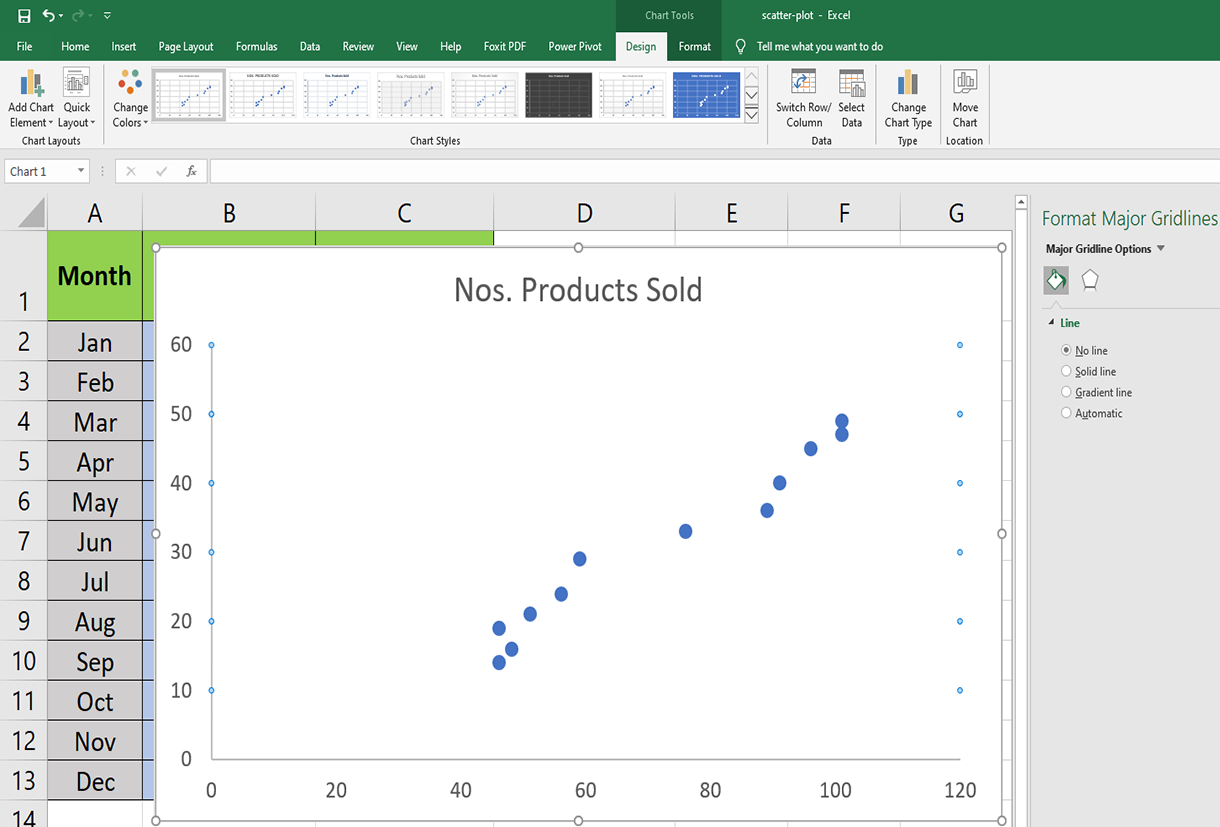
Microsoft Excel also offers professional scatter chart templates. This is how you can check those out:
- Double-click on the blank chart area.
- On the Ribbon, look for Quick Layout within the Chart Layouts section.
- Click on Quick Layout, and you will see 11 preset layouts to create a scatter plot.
- Hover the pointer on each of them to know the features and choose the one that suits your data sets.
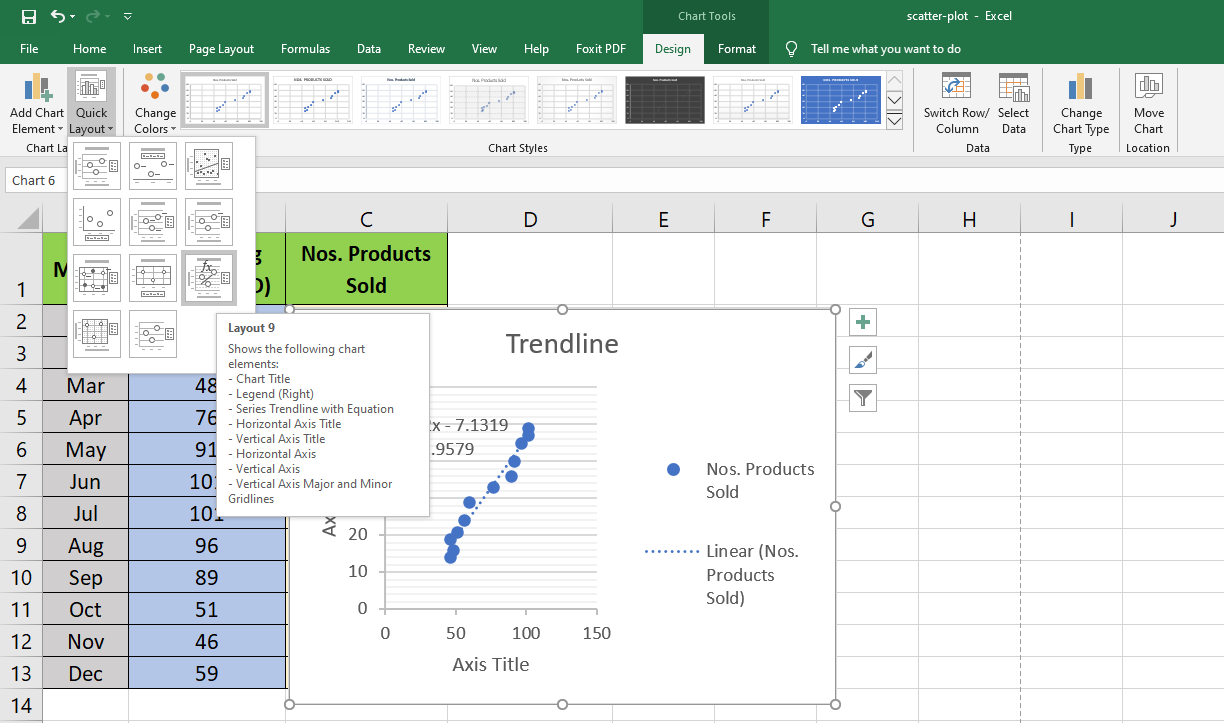
Add a professional look to your scatter graph by following these steps:
- Click on any blank space of the chart to open Chart Tools on the Ribbon.
- Under the Design tab, you will see 12 styles for the X and Y chart.
- Select any to instantly transform the classic scatter plot graph into a stylish one.
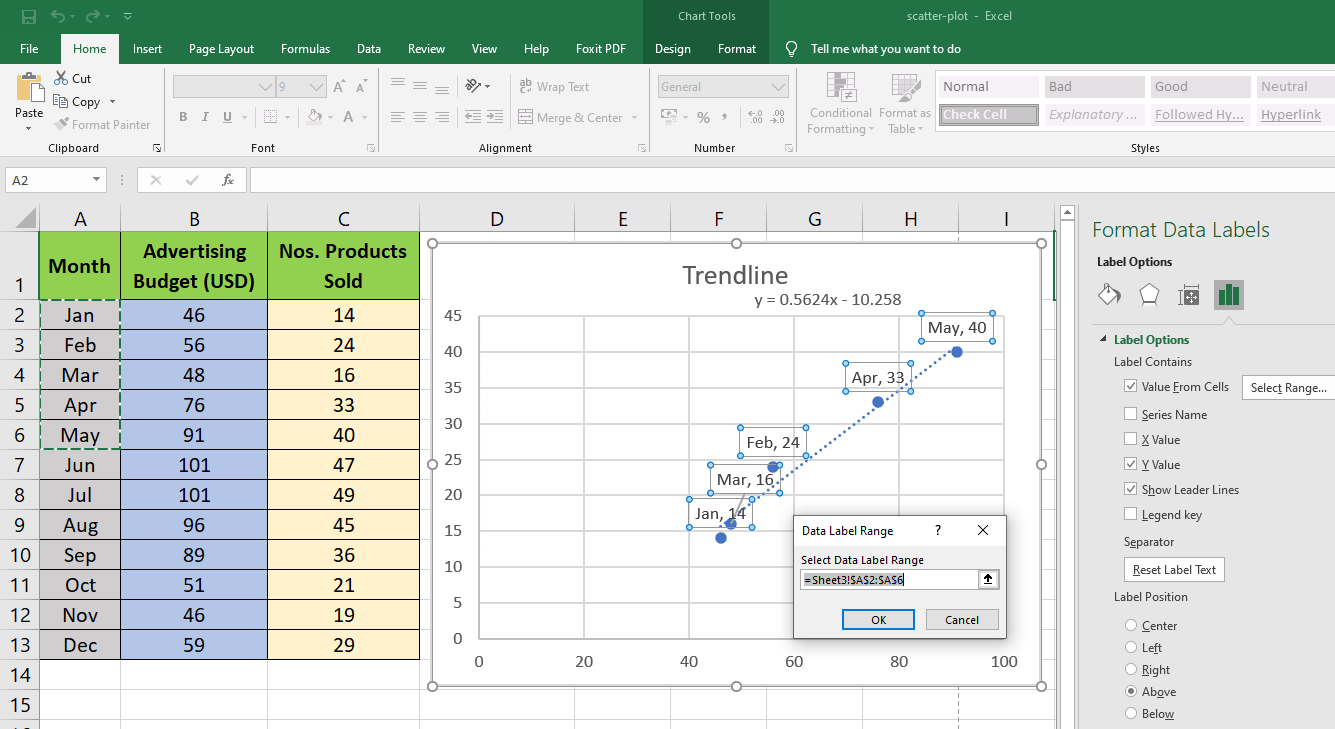
Add Labels to Scatter Plot Excel Data Points
You can label the data points in the X and Y chart in Microsoft Excel by following these steps:
- Click on any blank space of the chart and then select the Chart Elements (looks like a plus icon).
- Then select the Data Labels and click on the black arrow to open More Options.
- Now, click on More Options to open Label Options.
- Click on Select Range to define a shorter range from the data sets.
- Points will now show labels from column A2:A6.
- For a clear visualization of a label, drag the labels away as necessary.
Add a Trendline and Equation in the Scatter Plot Graph
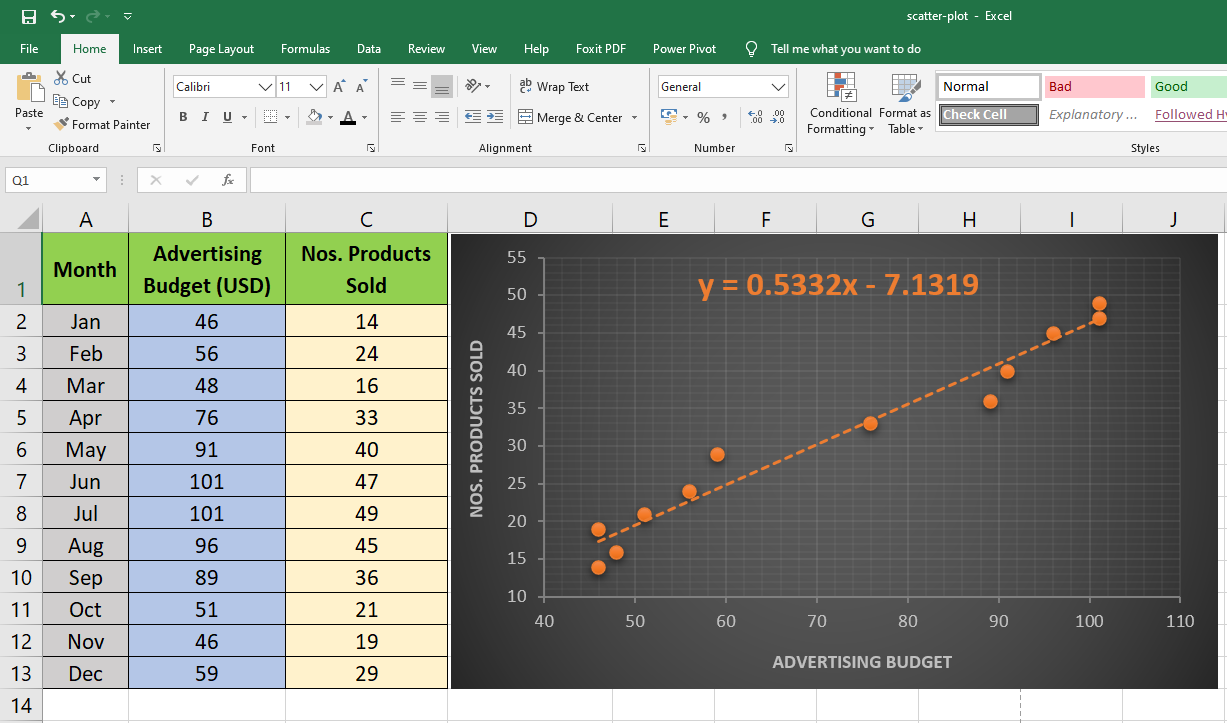
You can add a line of best fit or a Trendline in your scatter chart to visualize the relationship between variables.
- To add the Trendline, click on any blank space within the scatter graph.
- Chart Layouts section will appear on the Ribbon.
- Now click on Add Chart Element to open the drop-down menu.
- From that menu, click on Trendline and then choose the trendline style that fits the data sets.
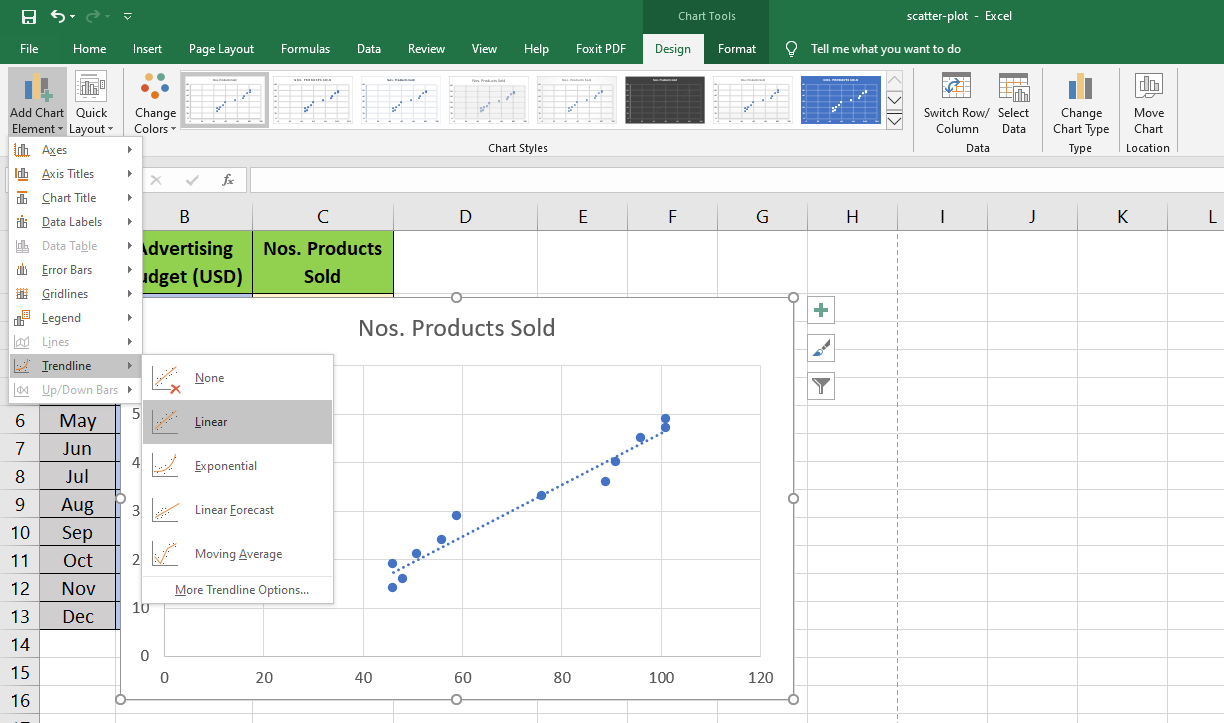
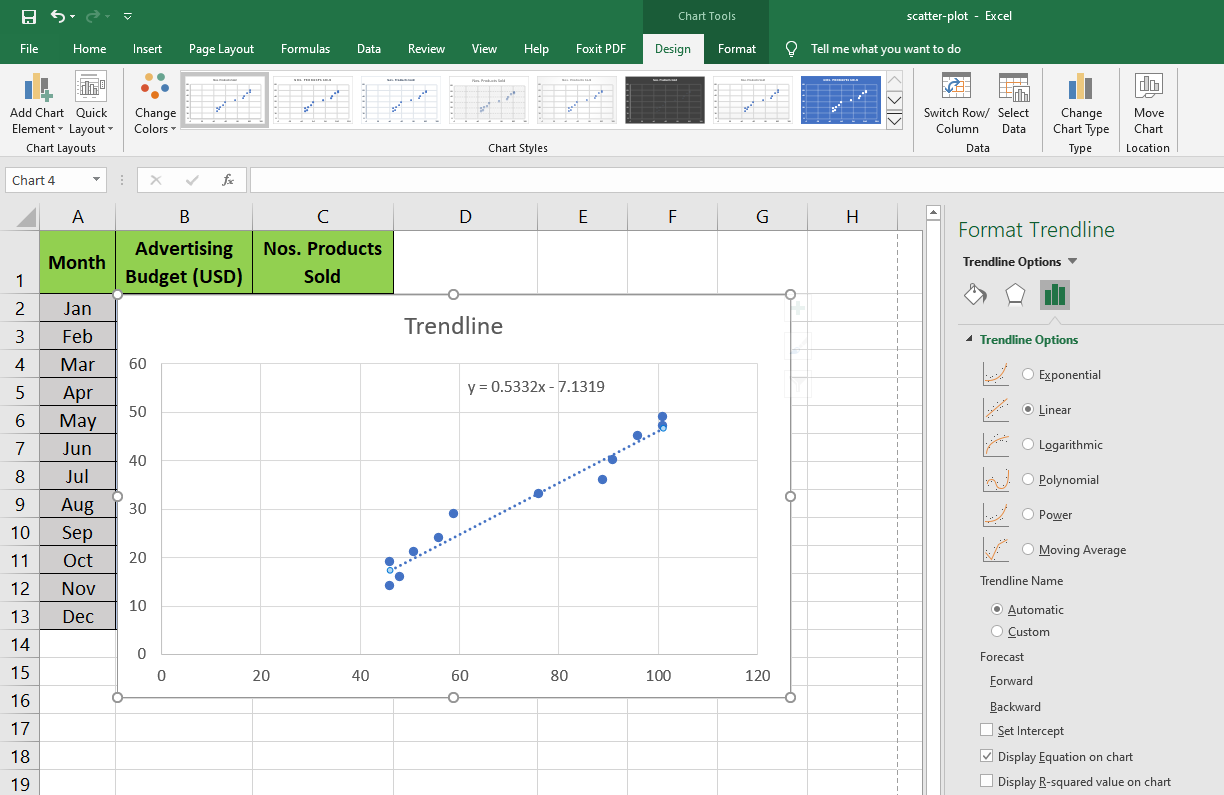
To visualize the mathematical relationship between the data variables, activate the equation display on the scatter plot graph.
- Double-click on the Trendline.
- Format Trendline sidebar will open.
- Within this sidebar, click on Trendline Options.
- Now, check the box for Display Equation on Chart.
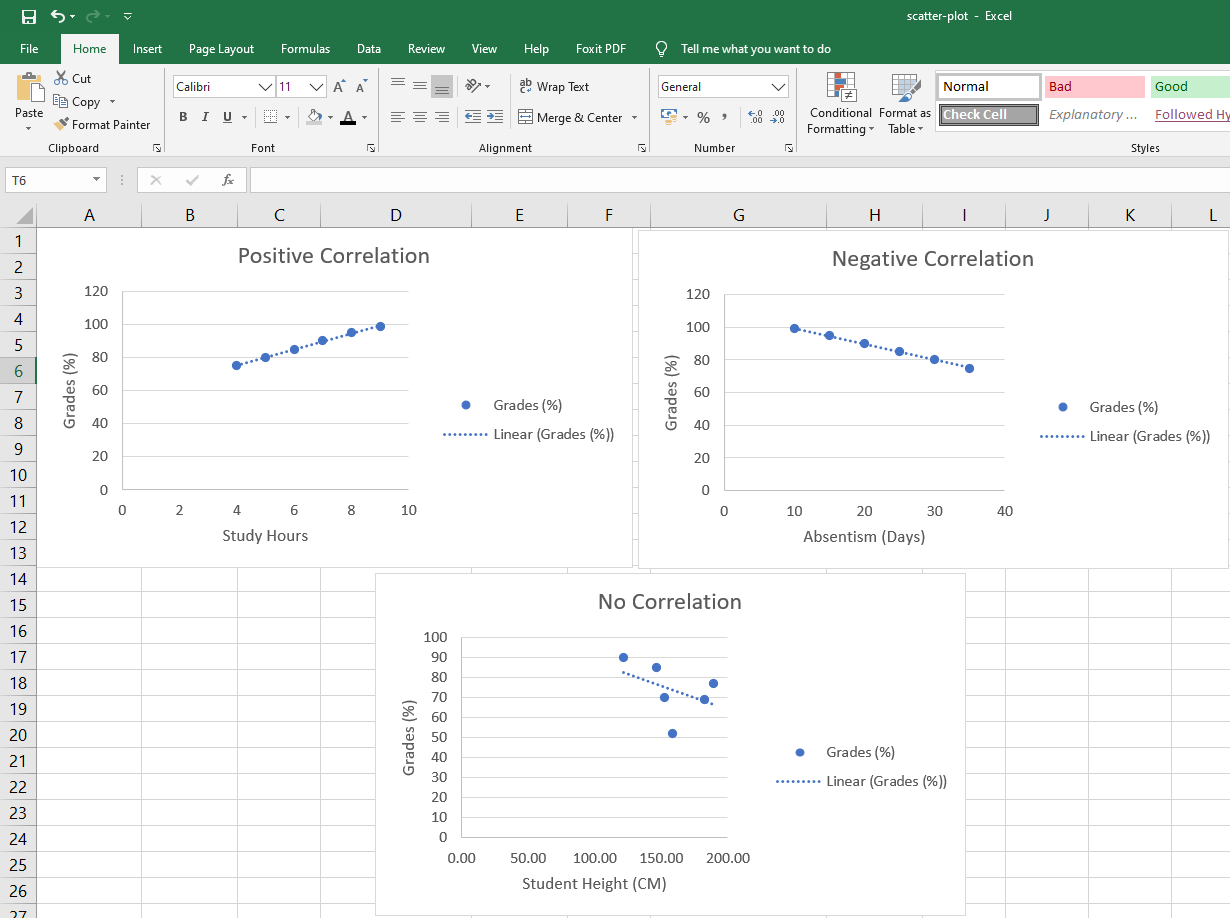
Scatter Graph and Variable Correlation
X and Y chart scatter graph can visualize three types of correlation between the variables in the data sets for meaningful data presentation. These correlations are as follows:
- Negative Correlation: In a negative correlation, the value of one variable increases while the other decreases.
- Positive Correlation: A strong example of a positive correlation is when vertical (Y) axis variables increase, the horizontal (X) axis variables increase too.
- No Correlation: There will be no correlation if dots are scattered around the whole scatter chart area.
Impress the Audience by Creating Scatter Plot in Excel
Microsoft Excel is a robust application that allows you to create the next-generation scatter plot graph. Having learned how to create a scatterplot in Excel, you can also create smart charts in the program that update automatically.

















 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):























 «, а затем выбрать диапазон, который вы хотите использовать на этом сайте. Закончив, нажмите кнопку Развернуть диалоговое окно.
«, а затем выбрать диапазон, который вы хотите использовать на этом сайте. Закончив, нажмите кнопку Развернуть диалоговое окно.