При изучении интеграла вы могли бы нарисовать построенную кривую, заштриховать область под кривой, а затем вычислить площадь участка затенения. В этой статье представлены два решения для расчета площади под кривой, построенной в Excel.
- Вычислить площадь под построенной кривой с помощью правила трапеции
- Вычислить площадь под построенной кривой с помощью линии тренда диаграммы
Вычислить площадь под построенной кривой с помощью правила трапеции
Например, вы создали построенную кривую, как показано на скриншоте ниже. Этот метод разделит область между кривой и осью x на несколько трапеций, вычислит площадь каждой трапеции по отдельности, а затем суммирует эти площади.
1. Первая трапеция находится между x = 1 и x = 2 под кривой, как показано на скриншоте ниже. Вы можете легко рассчитать его площадь по этой формуле: =(C3+C4)/2*(B4-B3).
2. Затем вы можете перетащить маркер автозаполнения ячейки формулы вниз, чтобы вычислить площади других трапеций.
Внимание: Последняя трапеция находится между x = 14 и x = 15 под кривой. Поэтому перетащите дескриптор автозаполнения на предпоследнюю ячейку, как показано ниже.
3. Теперь вычислены площади всех трапеций. Выберите пустую ячейку, введите формулу = СУММ (D3: D16) чтобы получить общую площадь под нанесенной областью.
Вычислить площадь под построенной кривой с помощью линии тренда диаграммы
Этот метод будет использовать линию тренда диаграммы, чтобы получить уравнение для построенной кривой, а затем вычислить площадь под построенной кривой с определенным интегралом уравнения.
1. Выберите построенную диаграмму и нажмите Дизайн (или Дизайн диаграммы)> Добавить элемент диаграммы > Trendline > Дополнительные параметры линии тренда. Смотрите скриншот:
2. В Форматировать линию тренда панель:
(1) В Параметры линии тренда в разделе выберите один вариант, который больше всего соответствует вашей кривой;
(2) Проверьте Отображение уравнения на диаграмме опцию.
3. Теперь уравнение добавлено в диаграмму. Скопируйте уравнение в свой рабочий лист, а затем получите определенный интеграл уравнения.
В моем случае общее уравнение по линии тренда: у = 0.0219x ^ 2 + 0.7604x + 5.1736, поэтому его определенный интеграл равен Р (х) = (0.0219 / 3) x ^ 3 + (0.7604 / 2) x ^ 2 + 5.1736x + c.
4. Теперь мы подставляем x = 1 и x = 15 к определенному интегралу и вычисляем разницу между результатами обоих вычислений. Разница представляет собой площадь под построенной кривой.
Площадь = F (15) -F (1)
Area =(0.0219/3)*15^3+(0.7604/2)*15^2+5.1736*15-(0.0219/3)*1^3-(0.7604/2)*1^2-5.1736*1
Площадь = 182.225
Статьи по теме:
Лучшие инструменты для работы в офисе
Kutools for Excel Решит большинство ваших проблем и повысит вашу производительность на 80%
- Снова использовать: Быстро вставить сложные формулы, диаграммы и все, что вы использовали раньше; Зашифровать ячейки с паролем; Создать список рассылки и отправлять электронные письма …
- Бар Супер Формулы (легко редактировать несколько строк текста и формул); Макет для чтения (легко читать и редактировать большое количество ячеек); Вставить в отфильтрованный диапазон…
- Объединить ячейки / строки / столбцы без потери данных; Разделить содержимое ячеек; Объединить повторяющиеся строки / столбцы… Предотвращение дублирования ячеек; Сравнить диапазоны…
- Выберите Дубликат или Уникальный Ряды; Выбрать пустые строки (все ячейки пустые); Супер находка и нечеткая находка во многих рабочих тетрадях; Случайный выбор …
- Точная копия Несколько ячеек без изменения ссылки на формулу; Автоматическое создание ссылок на несколько листов; Вставить пули, Флажки и многое другое …
- Извлечь текст, Добавить текст, Удалить по позиции, Удалить пробел; Создание и печать промежуточных итогов по страницам; Преобразование содержимого ячеек в комментарии…
- Суперфильтр (сохранять и применять схемы фильтров к другим листам); Расширенная сортировка по месяцам / неделям / дням, периодичности и др .; Специальный фильтр жирным, курсивом …
- Комбинируйте книги и рабочие листы; Объединить таблицы на основе ключевых столбцов; Разделить данные на несколько листов; Пакетное преобразование xls, xlsx и PDF…
- Более 300 мощных функций. Поддерживает Office/Excel 2007-2021 и 365. Поддерживает все языки. Простое развертывание на вашем предприятии или в организации. Полнофункциональная 30-дневная бесплатная пробная версия. 60-дневная гарантия возврата денег.
Вкладка Office: интерфейс с вкладками в Office и упрощение работы
- Включение редактирования и чтения с вкладками в Word, Excel, PowerPoint, Издатель, доступ, Visio и проект.
- Открывайте и создавайте несколько документов на новых вкладках одного окна, а не в новых окнах.
- Повышает вашу продуктивность на 50% и сокращает количество щелчков мышью на сотни каждый день!
Комментарии (8)
Оценок пока нет. Оцените первым!
Содержание
- Расчет. Площадь под кривой (правило трапеции) Таблицы Excel и G
- Расчет. Площадь под кривой (правило трапеции) Excel
- Начиная с вашего графика
- Начиная с вашего набора данных
- Создание формулы площади
- Конечная площадь под кривой
- Как рассчитать площадь под кривой (правило трапеции) в Google Таблицах
- Как в Excel вычислить определённый интеграл
- 1 Постановка физической задачина расчёт определённого интеграла
- 2 Геометрический смыслопределённого интеграла
- 3 Методика вычисленияопределённого интеграла
- 4 Согласованиеединиц измерения
- 5 Вычисление площадей отдельных трапеций
- 5 Определение площадипод графиком функции
- Как в excel посчитать площадь под графиком
- Вычисление интегралов в Excel
- Теория.
- Практика вычисления интегралов в Excel.
- Определение тепловой энергии.
- Общие выводы.
- Как рассчитать площадь под кривой в Excel
- Содержание:
- направления
- Использование уравнения тренда
- Приближается, если точки расположены на равном расстоянии
Расчет. Площадь под кривой (правило трапеции) Таблицы Excel и G
Расчет. Площадь под кривой (правило трапеции) Excel
Есть несколько способов рассчитать площадь под кривой, но этот пример покажет вам, как это сделать с помощью правила трапеции.
Начиная с вашего графика
Вы начнете с вашего базового графика, который показывает взаимосвязь между значениями X и Y. Цель состоит в том, чтобы найти общую площадь под кривой на графике.
Начиная с вашего набора данных
Затем у нас есть набор данных, с которым мы работаем. В этом случае месяц — это Ось X и продажи — это Ось Y.
Создание формулы площади
- Введите следующую формулу, которая является расчетом для определения площади под линией. Как показано ниже, каждая отдельная формула показывает область под графиком между точками данных. В этом случае мы набираем ((Значение Y 2) + (Значение Y 1)) / 2 * (Значение X 2 — Значение X 1)
2. Перетащите эту формулу вниз для просмотра данных. Кроме последняя точка данных
3. В пустой ячейке ниже просуммируйте все индивидуальные формулы площади, которые вы только что рассчитали, чтобы найти площадь всей кривой.
Конечная площадь под кривой
После вычисления суммы окончательная сумма покажет общую площадь под кривой. В этом случае мы получаем общую площадь 167.50.
Как рассчитать площадь под кривой (правило трапеции) в Google Таблицах
В этом случае вычисление площади под кривой с использованием правила трапеции в Google Таблицах такое же, как и в Excel. Используйте ту же формулу для значений X и Y, и вы сможете рассчитать площадь под кривой.
Источник
Как в Excel вычислить определённый интеграл
Давайте разберёмся, как вычислить определённый интеграл таблично заданной функции с помощью программы Excel из состава Microsoft Office.
1 Постановка физической задачина расчёт определённого интеграла
Допустим, у нас есть таблично заданная некоторая величина. Для примера пусть это будет накопленная доза радиации при авиаперелёте. Скажем, был такой эксперимент: человек с дозиметром летел на самолёте из пункта А в пункт Б и периодически измерял дозиметром мощность дозы (единицы измерений – микрозиверт в час, мкЗв/ч). Возможно, Вас это удивит, но при обычном перелёте на самолёте человек попадает под радиоактивное излучение, превышающее фоновый уровень до 10 раз и даже больше. Но воздействие это кратковременное, и поэтому не столь опасное. По результатам измерений у нас есть таблица вот такого формата: Время – Мощность дозы.
Таблично заданная величина для расчёта определённого интеграла
Необходимо посчитать суммарную накопленную за время полёта дозу.
2 Геометрический смыслопределённого интеграла
Как мы помним из курса школьной алгебры, определённый интеграл – это площадь под графиком измеряемой величины. Чтобы определить накопленную дозу радиации в рассматриваемом примере, нужно определить площадь фигуры под графиком таблично заданной мощности дозы. Накопленная доза радиации равна площади фигуры под графиком мощности дозы
График изменения мощности дозы во время полёта
3 Методика вычисленияопределённого интеграла
Вычислять интеграл мы будем самым простым, но довольно точным методом – методом трапеций. Напомню, площадь фигуры под графиком любой кривой можно разделить на прямоугольные трапеции. Сумма площадей этих трапеций и будет искомым значением определённого интеграла.
Площадь трапеции определяется как полусумма оснований, умноженная на высоту: Sтрап = (A + B) / 2 × h Основания в нашем случае – это табличные измеренные значения мощности дозы за 2 последовательных промежутка времени, а высота – это разница времени между двумя измерениями.
Метод трапеций для вычисления значения определённого интеграла
4 Согласованиеединиц измерения
В нашем примере измерения мощности дозы радиации даётся в мкЗв/час, а шкала времени – с точностью до минут. Мы не можем брать интеграл по времени, измеряемому в минутах, для величины, измеряемой в часах. Поэтому необходимо перевести мкЗв/час в мкЗв/мин.
Для перевода просто разделим мощность дозы в мкЗв/час построчно на количество минут в часе, т.е. на 60. Добавим ещё один столбец в нашу таблицу. На иллюстрации это столбец «D». В столбце «D» в строке 2 вписываем =С2/60 А потом с помощью маркера заполнения распространяем эту формулу на все остальные ячейки в столбце «D», (т.е. тянем мышью чёрный прямоугольник в правом нижнем углу ячейки). Таким образом, в столбце «D» у нас появятся значения мощности дозы радиации, измеряемые в микрозивертах в минуту для каждой минуты перелёта.
Согласуем единицы измерения по шкале времени и шкале мощности дозы
5 Вычисление площадей отдельных трапеций
Теперь нужно найти площади трапеций за каждый промежуток времени. В столбце «E» будем вычислять по приведённой выше формуле площади трапеций. Полусумма оснований – это половина суммы двух последовательных мощностей дозы из столбца «D». Так как данные идут с периодом 1 раз в минуту, а мы берём интеграл по времени, выраженному в минутах, то высота каждой трапеции будет равна единице (разница времени между каждыми двумя последовательными измерениями, например, 17ч31мин — 17ч30мин = 0ч1мин = 1мин).
Получаем формулу в ячейке «E3»: =1/2*(D3+D2)*1. Понятно, что «×1» в этой формуле можно не писать. И аналогично, с помощью маркера заполнения, распространяем формулу на весь столбец. Теперь в каждой ячейке столбца «Е» посчитана накопленная доза за 1 минуту полёта.
Вычисление площадей прямоугольных трапеций за каждый промежуток времени
Если бы данные шли не через 1 минуту, то нам нужно было бы написать формулу так:
=1/2*(D3+D2)*(МИНУТЫ(A3) – МИНУТЫ(A2)).
Правда при этом, если есть переход на следующий час, то получится отрицательное значение. Чтобы этого не произошло, впишем в формулу часы:
=1/2*(D3+D2)*(ЧАС(A3)*60+МИНУТЫ(A3)) – (ЧАС(A2)*60+МИНУТЫ(A2)).
Если переходим на следующие сутки, то нужно будет уже добавлять даты, и т.д.
5 Определение площадипод графиком функции
Осталось найти сумму вычисленных площадей трапеций. Можно в ячейке «F2» написать формулу: =СУММ(E:E) Это и будет сумма всех значений в столбце «E», т.е. численное значение искомого определённого интеграла. Но давайте сделаем вот что: определим накопленную дозу в разные моменты полёта. Для этого в ячейку «F4» впишем формулу =СУММ(E$3:E4) и маркером заполнения распространим на весь столбец «F».
Обозначение E$3 говорит программе Excel, что увеличивать индекс ячейки «3» в столбце «E» при переносе формулы на следующие строки не нужно. Т.е. в строке 4 формула будет определять сумму в ячейках с «Е3» по «Е4», в строке 5 – сумму с «Е3» по «Е5», в строке 6 – с «Е3» по «Е6» и т.д.
Построим график по столбцам «F» и «A». Это график изменения накопленной дозы радиации во времени. Наглядно видно монотонное увеличение накопленной дозы радиации за время полёта. Это говорит о том, что мы правильно рассчитали интеграл. И окончательное значение накопленной за двухчасовой полёт дозы радиации, которое получается в последней ячейке этого столбца, равно примерно 4,5 микрозиверт.
Вычисление суммарной площади всех трапеций, что численно равно искомому определённому интегралу
Таким образом, мы только что нашли определённый интеграл таблично заданной функции в программе Excel на реальном физическом примере. В качестве приложения к статье – файл Excel с нашим примером.
Источник
Как в excel посчитать площадь под графиком
Вычисление интегралов в Excel
При стремлении постичь нечто сложное, громоздкое, непонятное следует «разбить» его на как можно большее количество простых, мелких, понятных частей, изучить их с помощью существующих инструментов, а затем «сложить» эти результаты и получить итоговый ответ.
Формулировка в предыдущем предложении определяет сущность понятия интегрирования.
Интеграл чего-либо – это сумма всех малых частей этого чего-либо. Чем больше количество этих малых частей, тем точнее значение интеграла соответствует действительности, определяя признак изучаемого объекта.
Интегрирование применимо для изучения свойств физических и философских объектов при условии, что эти свойства остаются неизменными как для «мелкой» части, так и для всего объекта в целом.
Функция – это описание зависимости некоторого признака или свойства объекта от аргумента.
Объект – плоская фигура между графиком функции и осью абсцисс.
Признак (значение функции) – высота фигуры.
Аргумент (независимая переменная) – ширина фигуры.
Функция – описание зависимости высоты от ширины.
Определенный интеграл функции – площадь фигуры. Площадь тоже является признаком фигуры, но зависит от двух переменных – высоты и ширины – и представляет собой качественно иной новый признак.
Теория.
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.
Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.
Площадь под кривой y = f ( x ) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y =f ( x ). Суммарная площадь под графиком функции на участке от x1 до xn – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.
Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.
Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.
Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.
Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.
Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.
1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!
2. Расстояния между точками по оси x должны быть одинаковыми!
Практика вычисления интегралов в Excel.
Определенной сложностью является связать вычисление интегралов с реальными задачами из жизни. Рассмотрение примеров – лучший способ устранения подобных препятствий.
Определение тепловой энергии.
Мой знакомый из города Улан-Удэ Алексей Пыкин проводит испытания воздушных солнечных PCM-коллекторов производства КНР. Воздух из помещения подается вентилятором в коллекторы, нагревается от солнца и поступает назад в помещение. Каждую минуту измеряется и записывается температура воздуха на входе в коллекторы и на выходе при постоянном воздушном потоке. Требуется определить количество тепловой энергии полученной в течение суток.
Более подробно о преобразовании солнечной энергии в тепловую и электрическую и об экспериментах Алексея я постараюсь рассказать в отдельной статье. Следите за анонсами, многим, я думаю, это будет интересно.
Запускаем MS Excel и начинаем работу – выполняем вычисление интеграла.
1. В столбец B вписываем время проведения измерения τi .
2. В столбец C заносим температуры нагретого воздуха t2i , измеренные на выходе из коллекторов в градусах Цельсия.
3. В столбец D записываем температуры холодного воздуха t1i , поступающего на вход коллекторов.
4. В столбце E вычисляем разности температур dti на выходе и входе
5. Зная удельную теплоемкость воздуха c =1005 Дж/(кг*К) и его постоянный массовый расход (измеренная производительность вентилятора) G =0,02031 кг/с, определяем мощность установки Ni в КВт в каждый из моментов времени в столбце F
На графике ниже показана экспериментальная кривая зависимости мощности, развиваемой коллекторами, от времени.
Количество тепловой энергии, выработанной за промежуток времени – это интеграл этой функции, и значение интеграла – это заштрихованная площадь под кривой.
6. Вычисляем в ячейках столбца G площади трапеций, суммируем их и находим общее количество энергии, выработанной за день
Q =Σ Qi =10,395 КВт*час
7. Рассчитываем в ячейках столбца H элементарные площади по методу парабол, суммируем их и находим общее количество энергии по методу Симпсона
Q =Σ Qj =10,395 КВт*час
Как видим, значения не отличаются друг от друга. Оба метода демонстрируют одинаковые результаты!
Исходная таблица содержит 421 строку. Давайте уменьшим её в 30 раз и оставим всего 15 строк, увеличив тем самым интервалы между замерами с 1 минуты до 30 минут.
По методу трапеций: Q =10,220 КВт*час (-1,684%)
По методу Симпсона: Q =10,309 КВт*час (-0,827%)
Не смотря на оставшуюся неожиданно весьма высокую точность полученных результатов, метод трапеций дает в данном случае относительную ошибку в 2 раза большую, чем метод Симпсона.
Общие выводы.
Вычисление интегралов численными методами в Excel позволяет эффективно и быстро решать сложные практические задачи, обеспечивая очень высокую точность результатов.
Так как мы существуем в пространстве и времени, то и всё окружающее нас изменяется или в пространстве или во времени. Это означает, что аргументом x функций y интересующих нас процессов или объектов чаще всего являются длина или время. Например, пройденный путь – это интеграл функции скорости (аргумент – время), площадь плотины – это интеграл функции высоты (аргумент – длина), и т.д.
Понимание сути интегрального исчисления и умение использовать его на практике вооружает вас, как специалиста, мощным оружием в осознанном изучении окружающего мира!
Отзывы и комментарии к статье, уважаемые читатели, пишите в блоке, расположенном ниже статьи.
Чтобы получать информацию о выходе новых статей на блоге подпишитесь на анонсы в окне, расположенном вверху страницы или сразу после статьи. Введите адрес своей электронной почты, нажмите на кнопку «Получать анонсы статей» и подтвердите подписку кликом по ссылке в письме, которое придет к вам на указанную почту. С этого момента к вам на почтовый ящик будет пару раз в месяц приходить небольшое уведомление о появлении на моем блоге новой статьи.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
Ссылка на скачивание файла с примером: vychisleniye-integralov (xls 216,0KB).
Как рассчитать площадь под кривой в Excel
Excel может быть полезным инструментом со многими функциями для ученых, студентов, экономистов, аналитиков и многих других профессий. Одна из оригинальных функций Excel заключается в том, что он позво
Содержание:
- направления
- Использование уравнения тренда
- Приближается, если точки расположены на равном расстоянии
- чаевые
- Что вам нужно
Excel может быть полезным инструментом со многими функциями для ученых, студентов, экономистов, аналитиков и многих других профессий. Одна из оригинальных функций Excel заключается в том, что он позволяет пользователям легко анализировать и отображать большие объемы данных. Люди, обладающие знаниями в области расчета, могут использовать функцию линии тренда на графике для расчета площади под кривой. Для студентов, которые не имеют вычислительных знаний, есть другой способ приблизиться к области под кривой.
направления
Вы можете рассчитать площадь под кривой без знания расчета (Изображение калькулятора от Alhazm Salemi от Fotolia.com)
Использование уравнения тренда
Щелкните правой кнопкой мыши на кривой, где вы хотите найти область на диаграмме Excel. Нажмите на опцию, чтобы добавить линию тренда.
Выберите тип линии, которая, по вашему мнению, лучше всего соответствует кривой.
Выберите параметр для отображения уравнения в диаграмме на вкладке «Параметры».
Найдите определенный интеграл уравнения, показанного на графике в течение интервала, в котором вы хотите найти область. Значением определенного интеграла является площадь под кривой. Знание расчетов требуется для этого шага.
Приближается, если точки расположены на равном расстоянии
Соедините значения y данных, в которых вы хотите найти область. Это можно сделать, добавив значения непосредственно в диаграмму или добавив значения в ячейки на листе.
Найти расстояние между точками на оси х, если они расположены равномерно.
Умножьте сумму значений y и расстояния между значениями x. Этот продукт является приблизительной площадью под кривой.
Источник
Want to calculate the area under a plotted curve in your Excel spreadsheets to find valuable information? Here’s how you can do it.
Excel simplifies calculations with its vast arsenal of functions, but there’s no Excel function for calculating the area under a plot. However, that doesn’t mean that you can’t use Excel for calculating the area under a plot.
Excel is more than just functions, and the autofill handle alone can make calculating the area under a plot much easier. In this article, we’re going to calculate the area under a plot in Excel using mathematical formulas. Read on to learn what information the area under a plot can give you, and how to calculate it.
How to Calculate the Area Under a Plot in Excel
As a concept, the area under a plot is roughly the x-axis multiplied by the y-axis. However, there is no Excel function that calculates the area under a plot.
To calculate the area under a plot, you’ll have to separately calculate the area between every two values and then sum them to get the total area. This might sound a bit arduous, but don’t be daunted. It’s easier than it looks.
The area under a plot consists of triangles, trapezoids, and rectangles. Once you calculate the area for each of these shape types, you can use the autofill handle in Excel to automatically calculate the area of the rest of the shapes of that type.
As an example, suppose we have the speed of a car at specific times. If you create a chart for this data, the area under the plot will show the distance traveled by the car. That is because the x-axis is seconds, and the y-axis is meters per second. If you multiply these two together, you’ll get meters, or the distance traveled. Let’s get started by creating the cart.
1. Creating the Chart
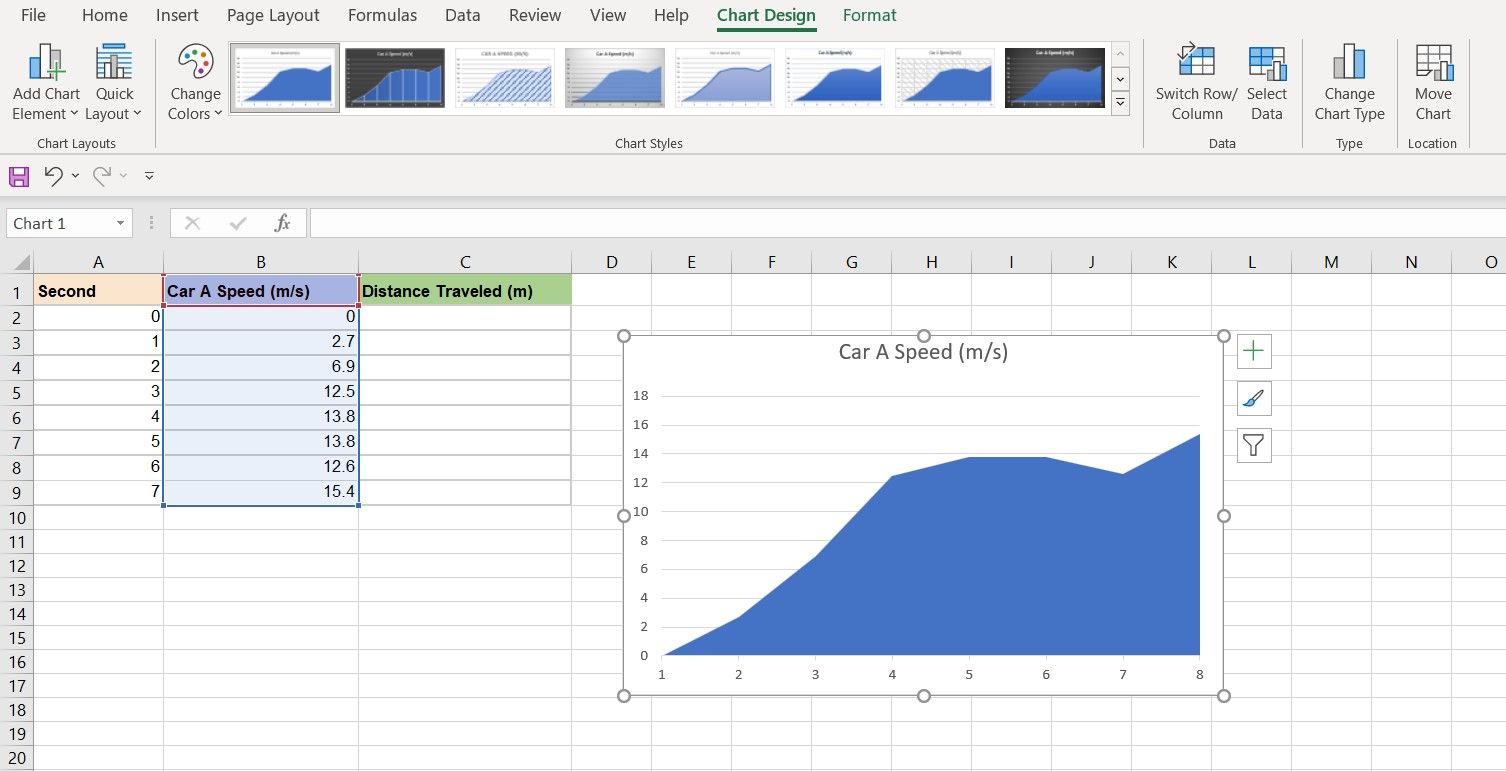
In this spreadsheet, we have the speed of a car at specific time points. The car starts moving at time zero, so its speed is 0 at that time. An area chart is the best way to see the area under a plot, so let’s make one.
- Select the data series. In this example, that will be the car speed, so we will select cells B2 to B9.
- Go to the Insert menu and then click the line chart symbol in the Charts section.
- Select 2-D Area. You have your chart now, but the X-axis isn’t quite right as it’s not set to our timeline.
- Right-click the chart and click Select Data.
- Under Horizontal Axis Labels, click Edit.
- Select the categories from your spreadsheet. That will be cells A2 to A9 for this example.
- Click OK. Now your X-axis starts from zero.
If you’re a total beginner at creating charts in Excel, you can read our guide on how to make a chart in Excel to get a quick head start.
2. Customizing the Chart
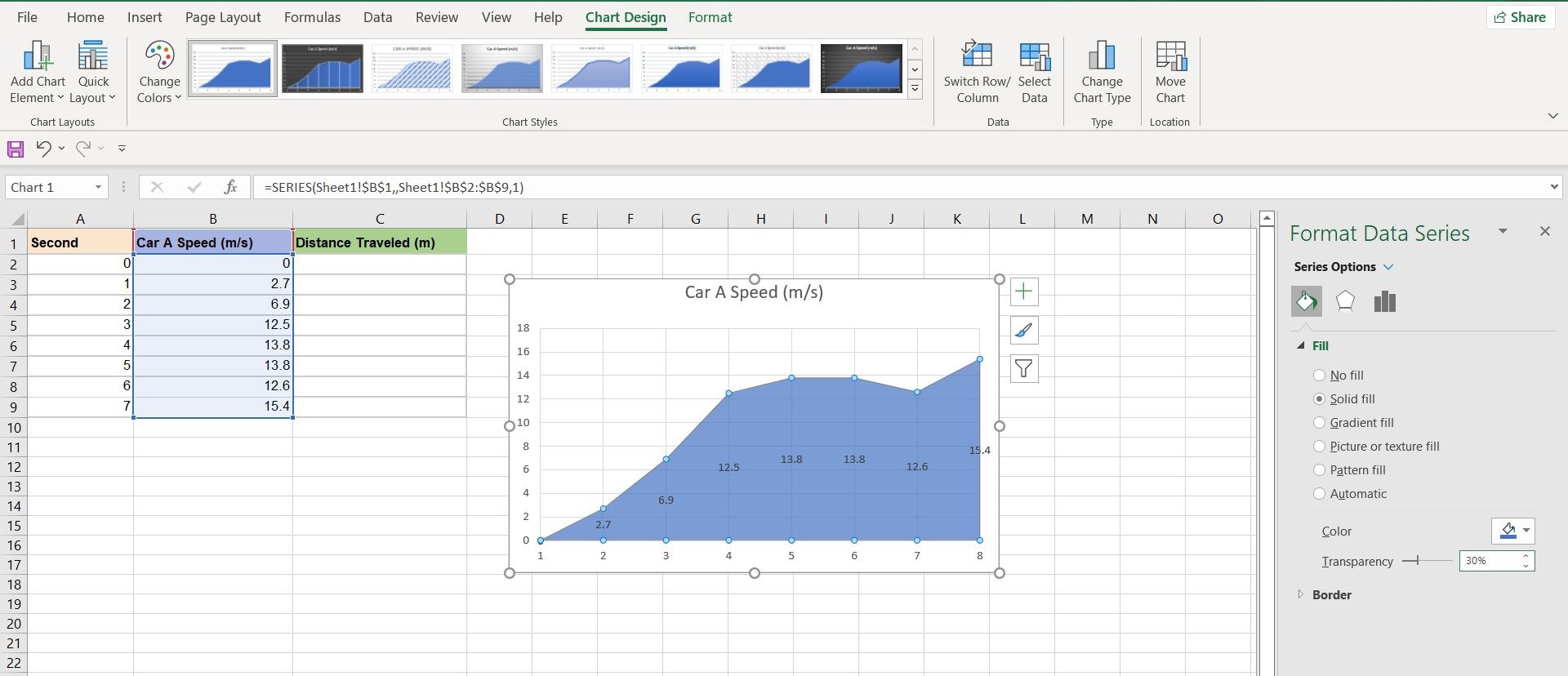
Your chart is accurate now, and it gives an okay measure of the area under the plot, but it’s still not good enough. Before getting into calculating the areas, let’s make a couple of adjustments to the chart so that the shape of the areas and their measurements are more distinctive.
- Select your chart.
- Go to the Chart Design tab from the ribbon.
- Click Add Chart Element, and then go to Gridlines.
- Select Primary Major Vertical.
Now you have vertical gridlines on your graph, which makes reading the graph easier. Unfortunately, the gridline goes behind the area, and the area isn’t transparent, so right now, you can’t see the gridlines under the plot. This can be easily fixed.
- Select your chart.
- Double-click the data series. This will open the Format Data Series bar on the right.
- In Format Data Series, under Series Options, select Fill & Line.
- Change the Fill from Automatic to Solid.
- Set the Transparency to 30%. This will let you see the gridlines.
Finally, to see the height for each input, you can add data labels to your chart.
- Select your chart.
- Go to the Chart Design tab.
- Click Add Chart Element, and then go to Data Labels.
- Select Show.
Now your area chart is ready for further analysis. With these adjustments that you just made, reading the height and the base of the different shapes in the area is much easier.
3. Calculating the Area
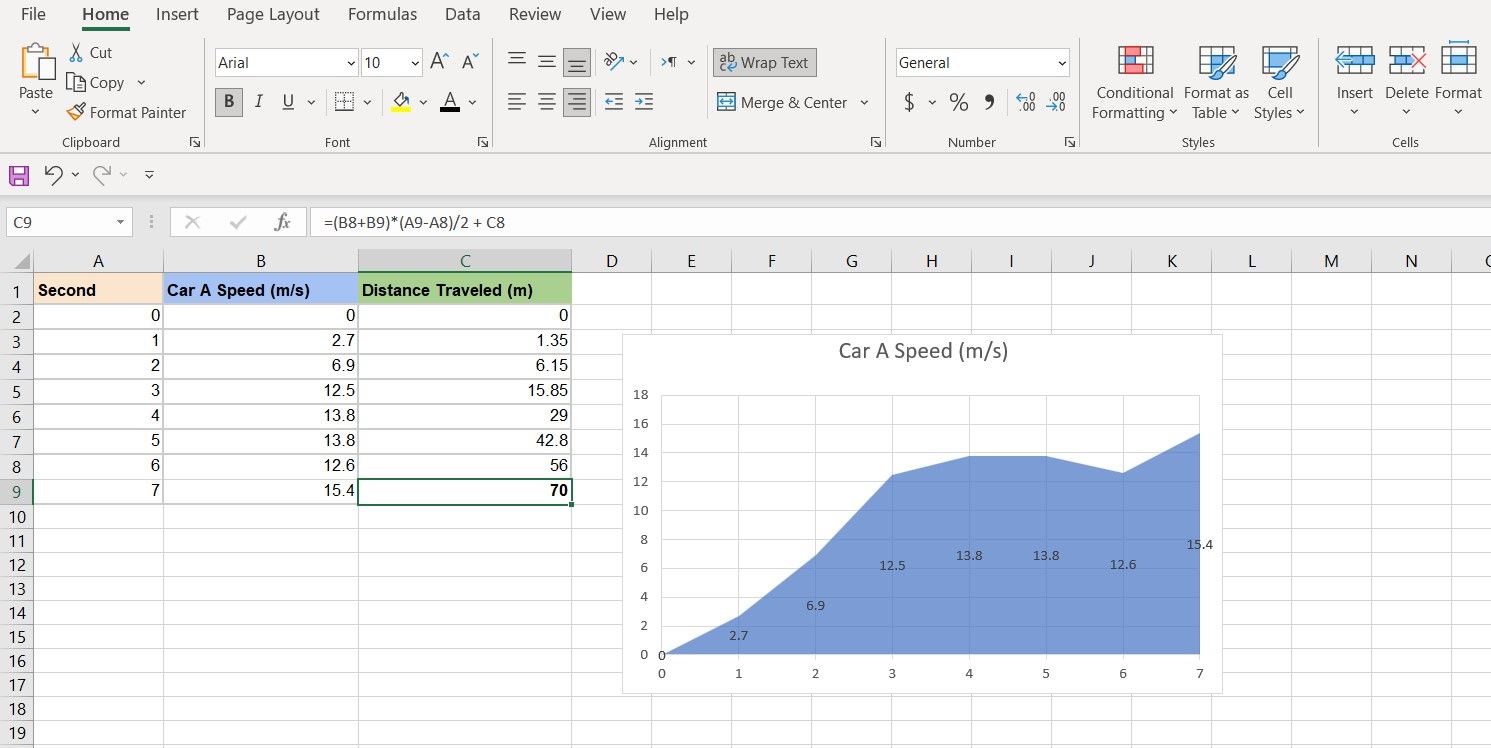
If you take a look at the example chart’s geometry, it’s actually made up of a triangle, a bunch of trapezoids, and a rectangle. So if you calculate the area for these shapes and sum them, you’ll get the total area under the plot.
Let’s write the formulas now. The first segment is going to be the area in time zero, which is naturally a zero.
- Select the cell where you want to show the area for the first segment. In this example, that will also be the distance traveled, so we’re going to use column C for this purpose.
- For the first segment, input 0. That is because the area at time zero is zero as well. Now let’s calculate the area for the next segment.
- Select the cell below, and enter the formula below in the formula bar:
=(A3-A2)*(B3)/2 + C2
This segment is a rectangle. The area of a triangle is the height multiplied by the base and then divided by two. The height of this triangle is on the X-axis and is A3-A2. The height of this triangle is on the Y-axis, and it’s B3. Once the formula calculates the area, it then sums it with the previous cell, to get the total area.
- Select the cell below and enter this formula:
=(B3+B4)*(A4-A3)/2 + C3
This time, the segment is a trapezoid. A trapezoid’s area is the sum of the two bases, multiplied by the height and then divided by two. The bases are B3 and B4, and the height is A4-A3. Again, when the formula has the area of the segment, it sums it with the previous cell to get the total area so far.
- Grab the fill handle and drop it on the cells below. This will automatically calculate the area for the cells below, since they’re all trapezoids.
If you’re wondering about the rectangle, the area for a rectangle can also be calculated using the trapezoid area formula. That is because the rectangle’s area is simply the length multiplied by the width.
If you look at a rectangle as a trapezoid, the two bases summed together make 2x widths, whereas the height is actually the length. Finally, the division by two nulls the multiplication by two, and you’ve got the rectangle’s area.
Calculate the Area Under a Plot With Excel
The area under a plot provides valuable information. Though there’s no Excel function to directly calculate this, you can still use Excel for this purpose. All you need to do is to break down the area into simpler shapes and calculate the area of those shapes.
Graphs and charts are wonderful visualizations that can make analysis and calculations much easier if you use them properly. There are lots of charts other than the area chart, and learning to use them will definitely give you an advantage in Excel.
Содержание
- Расчет. Площадь под кривой (правило трапеции) Excel
- Как рассчитать площадь под кривой (правило трапеции) в Google Таблицах
Есть несколько способов рассчитать площадь под кривой, но этот пример покажет вам, как это сделать с помощью правила трапеции.
Начиная с вашего графика
Вы начнете с вашего базового графика, который показывает взаимосвязь между значениями X и Y. Цель состоит в том, чтобы найти общую площадь под кривой на графике.
Начиная с вашего набора данных
Затем у нас есть набор данных, с которым мы работаем. В этом случае месяц — это Ось X и продажи — это Ось Y.
Создание формулы площади
- Введите следующую формулу, которая является расчетом для определения площади под линией. Как показано ниже, каждая отдельная формула показывает область под графиком между точками данных. В этом случае мы набираем ((Значение Y 2) + (Значение Y 1)) / 2 * (Значение X 2 — Значение X 1)
2. Перетащите эту формулу вниз для просмотра данных. Кроме последняя точка данных
3. В пустой ячейке ниже просуммируйте все индивидуальные формулы площади, которые вы только что рассчитали, чтобы найти площадь всей кривой.
Конечная площадь под кривой
После вычисления суммы окончательная сумма покажет общую площадь под кривой. В этом случае мы получаем общую площадь 167.50.
Как рассчитать площадь под кривой (правило трапеции) в Google Таблицах
В этом случае вычисление площади под кривой с использованием правила трапеции в Google Таблицах такое же, как и в Excel. Используйте ту же формулу для значений X и Y, и вы сможете рассчитать площадь под кривой.
Вы поможете развитию сайта, поделившись страницей с друзьями
Excel может быть полезным инструментом со многими функциями для ученых, студентов, экономистов, аналитиков и многих других профессий. Одна из оригинальных функций Excel заключается в том, что он позво
Содержание:
- направления
- Использование уравнения тренда
- Приближается, если точки расположены на равном расстоянии
- чаевые
- Что вам нужно
Excel может быть полезным инструментом со многими функциями для ученых, студентов, экономистов, аналитиков и многих других профессий. Одна из оригинальных функций Excel заключается в том, что он позволяет пользователям легко анализировать и отображать большие объемы данных. Люди, обладающие знаниями в области расчета, могут использовать функцию линии тренда на графике для расчета площади под кривой. Для студентов, которые не имеют вычислительных знаний, есть другой способ приблизиться к области под кривой.
направления
Вы можете рассчитать площадь под кривой без знания расчета (Изображение калькулятора от Alhazm Salemi от Fotolia.com)
Использование уравнения тренда
Щелкните правой кнопкой мыши на кривой, где вы хотите найти область на диаграмме Excel. Нажмите на опцию, чтобы добавить линию тренда.
Выберите тип линии, которая, по вашему мнению, лучше всего соответствует кривой.
Выберите параметр для отображения уравнения в диаграмме на вкладке «Параметры».
Найдите определенный интеграл уравнения, показанного на графике в течение интервала, в котором вы хотите найти область. Значением определенного интеграла является площадь под кривой. Знание расчетов требуется для этого шага.
Приближается, если точки расположены на равном расстоянии
Соедините значения y данных, в которых вы хотите найти область. Это можно сделать, добавив значения непосредственно в диаграмму или добавив значения в ячейки на листе.
Найти расстояние между точками на оси х, если они расположены равномерно.
Умножьте сумму значений y и расстояния между значениями x. Этот продукт является приблизительной площадью под кривой.
Вычисление интегралов в Excel
При стремлении постичь нечто сложное, громоздкое, непонятное следует «разбить» его на как можно большее количество простых, мелких, понятных частей, изучить их с помощью существующих инструментов, а затем «сложить» эти результаты и получить итоговый ответ.
Формулировка в предыдущем предложении определяет сущность понятия интегрирования.
Интеграл чего-либо – это сумма всех малых частей этого чего-либо. Чем больше количество этих малых частей, тем точнее значение интеграла соответствует действительности, определяя признак изучаемого объекта.
Интегрирование применимо для изучения свойств физических и философских объектов при условии, что эти свойства остаются неизменными как для «мелкой» части, так и для всего объекта в целом.
Функция – это описание зависимости некоторого признака или свойства объекта от аргумента.
Объект – плоская фигура между графиком функции и осью абсцисс.
Признак (значение функции) – высота фигуры.
Аргумент (независимая переменная) – ширина фигуры.
Функция – описание зависимости высоты от ширины.
Определенный интеграл функции – площадь фигуры. Площадь тоже является признаком фигуры, но зависит от двух переменных – высоты и ширины – и представляет собой качественно иной новый признак.
Теория.
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.
Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.
Площадь под кривой y = f ( x ) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y =f ( x ). Суммарная площадь под графиком функции на участке от x1 до xn – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.
Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.
Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.
Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.
Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.
Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.
1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!
2. Расстояния между точками по оси x должны быть одинаковыми!
Практика вычисления интегралов в Excel.
Определенной сложностью является связать вычисление интегралов с реальными задачами из жизни. Рассмотрение примеров – лучший способ устранения подобных препятствий.
Определение тепловой энергии.
Мой знакомый из города Улан-Удэ Алексей Пыкин проводит испытания воздушных солнечных PCM-коллекторов производства КНР. Воздух из помещения подается вентилятором в коллекторы, нагревается от солнца и поступает назад в помещение. Каждую минуту измеряется и записывается температура воздуха на входе в коллекторы и на выходе при постоянном воздушном потоке. Требуется определить количество тепловой энергии полученной в течение суток.
Более подробно о преобразовании солнечной энергии в тепловую и электрическую и об экспериментах Алексея я постараюсь рассказать в отдельной статье. Следите за анонсами, многим, я думаю, это будет интересно.
Запускаем MS Excel и начинаем работу – выполняем вычисление интеграла.
1. В столбец B вписываем время проведения измерения τi .
2. В столбец C заносим температуры нагретого воздуха t2i , измеренные на выходе из коллекторов в градусах Цельсия.
3. В столбец D записываем температуры холодного воздуха t1i , поступающего на вход коллекторов.
4. В столбце E вычисляем разности температур dti на выходе и входе
5. Зная удельную теплоемкость воздуха c =1005 Дж/(кг*К) и его постоянный массовый расход (измеренная производительность вентилятора) G =0,02031 кг/с, определяем мощность установки Ni в КВт в каждый из моментов времени в столбце F
Ni = c * G * dti
На графике ниже показана экспериментальная кривая зависимости мощности, развиваемой коллекторами, от времени.
Количество тепловой энергии, выработанной за промежуток времени – это интеграл этой функции, и значение интеграла – это заштрихованная площадь под кривой.
6. Вычисляем в ячейках столбца G площади трапеций, суммируем их и находим общее количество энергии, выработанной за день
Q =Σ Qi =10,395 КВт*час
7. Рассчитываем в ячейках столбца H элементарные площади по методу парабол, суммируем их и находим общее количество энергии по методу Симпсона
Q =Σ Qj =10,395 КВт*час
Как видим, значения не отличаются друг от друга. Оба метода демонстрируют одинаковые результаты!
Исходная таблица содержит 421 строку. Давайте уменьшим её в 30 раз и оставим всего 15 строк, увеличив тем самым интервалы между замерами с 1 минуты до 30 минут.
По методу трапеций: Q =10,220 КВт*час (-1,684%)
По методу Симпсона: Q =10,309 КВт*час (-0,827%)
Не смотря на оставшуюся неожиданно весьма высокую точность полученных результатов, метод трапеций дает в данном случае относительную ошибку в 2 раза большую, чем метод Симпсона.
Общие выводы.
Вычисление интегралов численными методами в Excel позволяет эффективно и быстро решать сложные практические задачи, обеспечивая очень высокую точность результатов.
Так как мы существуем в пространстве и времени, то и всё окружающее нас изменяется или в пространстве или во времени. Это означает, что аргументом x функций y интересующих нас процессов или объектов чаще всего являются длина или время. Например, пройденный путь – это интеграл функции скорости (аргумент – время), площадь плотины – это интеграл функции высоты (аргумент – длина), и т.д.
Понимание сути интегрального исчисления и умение использовать его на практике вооружает вас, как специалиста, мощным оружием в осознанном изучении окружающего мира!
Отзывы и комментарии к статье, уважаемые читатели, пишите в блоке, расположенном ниже статьи.
Чтобы получать информацию о выходе новых статей на блоге подпишитесь на анонсы в окне, расположенном вверху страницы или сразу после статьи. Введите адрес своей электронной почты, нажмите на кнопку «Получать анонсы статей» и подтвердите подписку кликом по ссылке в письме, которое придет к вам на указанную почту. С этого момента к вам на почтовый ящик будет пару раз в месяц приходить небольшое уведомление о появлении на моем блоге новой статьи.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
Ссылка на скачивание файла с примером: vychisleniye-integralov (xls 216,0KB).
|
Например есть два графика: 1/2*х и корень из х. Они пересекаются в точках 0 и 4. Между ними (графиками) образуется общее пространство (площадь). Как ее посчитать? Т.е. если брать математику, то это интеграл от 0 до 4 разности двух графиков. Но как это посчитать в программе |
|
|
Один из самых простых вариантов: Полученный результат: 1.333326780 |
|
|
{quote}{login=;)}{date=18.11.2008 12:21}{thema=Re: Вычислить площадь между пересечниями графиков}{post}Один из самых простых вариантов: Полученный результат: 1.333326780 а как посчитать площадь, если функции не заданы точно (тренд в Экселе с погрешностью высокой), а есть только массив точек х и у, на основе которых строятся 2 графика. |
|
|
Haken  Пользователь Сообщений: 495 |
Это смотря какой массив точек и какие графики. По одним и тем же точкам можно разные графики построить (напр. точечная/с прямыми линиями…) |
|
{quote}{login=Haken}{date=18.03.2010 11:05}{thema=}{post}Это смотря какой массив точек и какие графики. По одним и тем же точкам можно разные графики построить (напр. точечная/с прямыми линиями…){/post}{/quote} Приложила файлик! |
|
|
Haken Пользователь Сообщений: 495 |
Для Вашего случая попробовал другие виды тренда, Полиноминальная оказалась более точной. <BR>Мне выдал такую формулу: y = 9E-13×5 — 7E-10×4 + 3E-07×3 — 7E-05×2 + 0,009x + 0,064 R² = 0,999 Можете <BR>а) вставить эту формулу в данный макрос <BR>б) (тут уже математика…) если разделить график на много вертикальных полосок шириной =1, то каждая из них будет представлять собой почти трапецию (боковые линии параллельны, нижняя — прямая, верхняя — можно пренебречь и считать, что она тоже прямая на каждом отрезке. Тогда площадь каждой трапеции будет равна … не буду выводить здесь формулу, см. файл :))) <BR><STRONG>Файл удален</STRONG> — велик размер. [Модераторы] |
|
Здравствуйте, подскажите плиз как мне посчитать площадь, между пересечениями графиков, файлик приложил, нужно посути взять интеграл от первой точки пересечения до второй, но самой функции нету, есть токо набор точек… <BR><STRONG>Файл удален</STRONG> — велик размер. [Модераторы] |
|
|
UP. файл-пример в архиве, очень надо помогите плиз кто может… |
|
|
Мне выдал такую формулу: y = 9E-13×5 — 7E-10×4 + 3E-07×3 — 7E-05×2 + 0,009x + 0,064 R² = 0,999 |
|
|
sky Пользователь Сообщений: 2 |
Кусочно-линейная функция f(x) представлена в виде таблицы, состоящей из двух одинаковых по высоте столбцов чисел. В первом столбце находятся значения x, во втором — значения f. Значения x строго монотонно возрастают. Высота столбцов n заранее неизвестна, но она точно больше одного (таким образом, задан как минимум один линейный участок). Создать третий столбец высоты n, содержащий значения интеграла от f(x) по x от самого первого значения x до текущего значения x. |
|
Guest Гость |
#12 24.12.2010 00:00:30 . Прикрепленные файлы
|
Проблема собственно отображена в теме…не знаю как найти площадь под графиком (имеются только данные в таблице никаких формул). Помогите кто шарит, диплом горит 
. Решение с подсчётом квадратиков и метод трапеций(подходит только если его упростить до какой нибудь формулы) не подходит т.к графиков очень много
Эксель изощрён, но не злонамерен.
Давайте сюда экселевский файл с примером (рисунок уже видели).
Эксель изощрён, но не злонамерен.
Эксель изощрён, но не злонамерен.
спасиб братюни 
, пойду доделывать диплом…
Содержание
- направления
- Использование уравнения тренда
- Приближается, если точки расположены на равном расстоянии
- чаевые
- Что вам нужно
Excel может быть полезным инструментом со многими функциями для ученых, студентов, экономистов, аналитиков и многих других профессий. Одна из оригинальных функций Excel заключается в том, что он позволяет пользователям легко анализировать и отображать большие объемы данных. Люди, обладающие знаниями в области расчета, могут использовать функцию линии тренда на графике для расчета площади под кривой. Для студентов, которые не имеют вычислительных знаний, есть другой способ приблизиться к области под кривой.
направления
Вы можете рассчитать площадь под кривой без знания расчета (Изображение калькулятора от Alhazm Salemi от Fotolia.com)
-
Щелкните правой кнопкой мыши на кривой, где вы хотите найти область на диаграмме Excel. Нажмите на опцию, чтобы добавить линию тренда.
-
Выберите тип линии, которая, по вашему мнению, лучше всего соответствует кривой.
-
Выберите параметр для отображения уравнения в диаграмме на вкладке «Параметры».
-
Найдите определенный интеграл уравнения, показанного на графике в течение интервала, в котором вы хотите найти область. Значением определенного интеграла является площадь под кривой. Знание расчетов требуется для этого шага.
Использование уравнения тренда
-
Соедините значения y данных, в которых вы хотите найти область. Это можно сделать, добавив значения непосредственно в диаграмму или добавив значения в ячейки на листе.
-
Найти расстояние между точками на оси х, если они расположены равномерно.
-
Умножьте сумму значений y и расстояния между значениями x. Этот продукт является приблизительной площадью под кривой.
Приближается, если точки расположены на равном расстоянии
чаевые
- Попробуйте разные типы линий, чтобы увидеть, какие из них подходят лучше всего.
Что вам нужно
- калькулятор