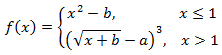history 8 января 2018 г.
- Группы статей
- Контрольные работы и задания
- Диаграммы и графики
Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.
Пусть дана система уравнений
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.
Решение (1 ряд данных)
Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.
СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .
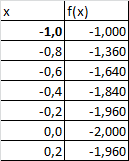
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.
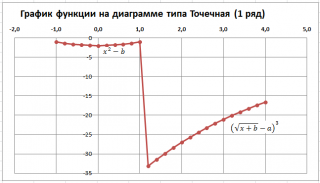
Чтобы построить диаграмму типа Точечная:
- выделите любую ячейку таблицы;
- во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .
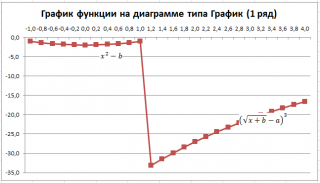
Чтобы построить диаграмму типа График:
- выделите любую столбец f(x) вместе с заголовком;
- во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .
Решение (2 ряда данных)
Создадим другую таблицу с исходными данными в файле примера, лист График :
Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.
У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
Как построить график неравенства в Excel — Вокруг-Дом — 2021
Table of Contents:
Microsoft Excel — это полезная программа, которая помогает молодым студентам изучать математику. Если вам нужно составить таблицу с неравенствами, вы можете использовать Excel, чтобы создать таблицу точек данных из уравнения, а затем использовать графический инструмент для графического отображения этого уравнения. Чтобы построить точный график, вам понадобится базовое понимание функций Excel, но даже новички найдут этот процесс довольно простым.
Научите студентов неравенствам с помощью Excel.
Шаг 1
Создайте столбец точек данных в столбце «А». Эти точки данных должны быть равномерно разнесены, но могут быть настолько маленькими или большими, насколько вы хотите, в зависимости от диапазона и области вашего графика. Если вы не уверены, обычно достаточно использовать цифры от -10 до 10.
Шаг 2
Введите уравнение неравенства в ячейку «B1» и замените «x» на «A1». Например, если ваше неравенство y
Шаг 7
Выберите опцию «2D график».
Шаг 8
Нажмите «Фигуры» над заголовком «Иллюстрации» и выберите инструмент «Свободная форма».
Шаг 9
Нарисуйте многоугольник, который проходит по краю нанесенной линии и по краям области диаграммы. Убедитесь, что он правильно расположен над или под уравнением, в зависимости от неравенства.
Шаг 10
Выберите многоугольник, нажмите на вкладку «Формат», нажмите «Форма заливки» и выберите «Дополнительные цвета заливки».
Шаг 11
Отрегулируйте цвет и прозрачность, чтобы форма четко отображалась на графике.
Решение систем уравнений в среде Microsoft Excel
обучающие:
- повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
- повторение алгоритма решения систем уравнений;
- формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;
развивающие:
- формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
воспитывающие:
- осуществление эстетического воспитания;
- воспитание аккуратности, добросовестности.
Тип урока: урок закрепления изученного материала и объяснения нового.
ХОД УРОКА
I. Организационная часть.
Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!
Ответ: “Знание – сила!”
Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)
Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).
II. Повторение пройденного материала.
Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)
Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.
III. Объяснение нового.
А. Решим систему 

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.
Запишем алгоритм решения систем уравнений графическим способом:
1. Преобразовать систему уравнений, если это необходимо.
2. Задать начальные значения для Х.
3. Найти значение первой функции при заданных Х.
4. Найти значение второй функции при тех же Х.
5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.
6. Решение системы — точка пересечения графиков функций.
7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.
Б. Решить систему уравнений 
Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:
При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения системы уравнений, используя Поиск решения
1. Преобразовать систему уравнений, если это необходимо
2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.
3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.
4. Выбрать команду Сервис – Поиск решения.
5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения
6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)
7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК
8. Решить систему уравнений, щелкнув кнопкой Выполнить
IV. Практическая работа на компьютере.
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
V. Подведение итогов.
Повторить алгоритмы решения систем уравнений
Выставить оценки за тестирование в журнал
VI. Домашнее задание.
Решить рациональным способом системы уравнений:

Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12686 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Строим график функции, заданный системой уравнений, в EXCEL
history 8 января 2018 г.
-
Группы статей
- Контрольные работы и задания
- Диаграммы и графики
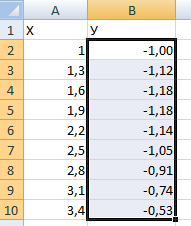
Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.
Пусть дана система уравнений
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.
Решение (1 ряд данных)
Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.
СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.
Чтобы построить диаграмму типа Точечная:
- выделите любую ячейку таблицы;
- во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .
Чтобы построить диаграмму типа График:
- выделите любую столбец f(x) вместе с заголовком;
- во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .
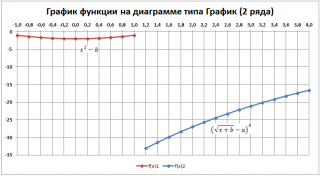
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .
Решение (2 ряда данных)
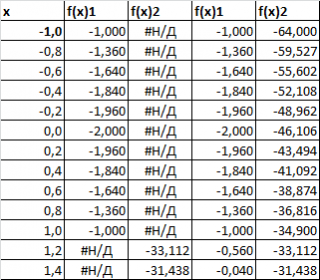
Создадим другую таблицу с исходными данными в файле примера, лист График :
Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.
У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
источники:
http://lumpics.ru/how-solve-system-equations-excel/
http://excel2.ru/articles/stroim-grafik-funkcii-zadannyy-sistemoy-uravneniy-v-ms-excel

ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств
Лабораторная работа № 3 Построение графика функции, заданной системой неравенств
Цель:
Приобрести навыки использования логической функции ЕСЛИ при вычислении таблицы значений функции, заданной системой неравенств, и построения графика
данной функции
Методические указания:
При вычислении функции используйте логическую функцию ЕСЛИ.
Логическая функция ЕСЛИ возвращает одно значение, если заданное условие при вычислении дает значение ИСТИНА, и другое значение, если ЛОЖЬ. Синтаксис функции:
=ЕСЛИ(Лог_выражение;значение_если_истина;значение_если_ложь)
Лог_выражение — это любое значение или выражение, принимающее значения ИСТИНА или ЛОЖЬ.
Значение_если_истина — это значение, которое возвращается, если лог_выражение равно ИСТИНА.
Значение_если_ложь — это значение, которое возвращается, если лог_выражение равно ЛОЖЬ.
В MS Excel 2003 до 7 функций ЕСЛИ могут быть вложены друг в друга в качестве значений аргументов значение_если_истина и значение_если_ложь для конструирования более сложных проверок. В MS Excel 2007 до 64 функций.
Ход выполнения работы:
1.Из таблицы 1 выберите варианты индивидуальных заданий в соответствии с вашим номером в журнале.
2.Откройте Excel. Назовите первый лист книги 2_№ варианта.
3.Постройте на этом листе график (Точечную диаграмму со значениями, соединенными сглаживающими линиями без маркеров) функции, заданной системой двух неравенств (таблица 2). Ход выполнения работы описан в лекции.
4.Назовите второй лист книги 3_№ варианта.
5.Постройте на этом листе график функции, заданной системой трех неравенств (таблица 3). Ход выполнения работы описан в лекции.
6.Назовите третий лист книги 4_№ варианта.
7.Постройте на этом листе график функции, заданной системой четырех неравенств (таблица 4).
8.Сохраните вашу работу под именем ЛР_4_система неравенств в свою папку.
PDF created with pdfFactory Pro trial version www.pdffactory.com

ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств
Индивидуальные задания
|
Таблица 1 |
||||||||||
|
Выбор варианта индивидуального задания в соответствии с номером в журнале |
||||||||||
|
Номер по |
Задание |
Задание |
Задание |
Номер по |
Задание |
Задание |
Задание |
|||
|
списку |
списку |
|||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
|||||
|
в журнале |
в журнале |
|||||||||
|
1. |
1 |
5 |
10 |
16. |
10 |
7 |
2 |
|||
|
2. |
2 |
6 |
11 |
17. |
11 |
8 |
3 |
|||
|
3. |
3 |
7 |
12 |
18. |
12 |
9 |
4 |
|||
|
4. |
4 |
8 |
13 |
19. |
13 |
10 |
5 |
|||
|
5. |
5 |
9 |
14 |
20. |
14 |
11 |
6 |
|||
|
6. |
6 |
10 |
15 |
21. |
15 |
12 |
7 |
|||
|
7. |
7 |
11 |
1 |
22. |
1 |
13 |
8 |
|||
|
8. |
8 |
13 |
2 |
23. |
2 |
14 |
9 |
|||
|
9. |
9 |
12 |
3 |
24. |
3 |
15 |
10 |
|||
|
10. |
10 |
14 |
4 |
25. |
4 |
1 |
11 |
|||
|
11. |
11 |
15 |
5 |
26. |
5 |
2 |
12 |
|||
|
12. |
12 |
1 |
6 |
27. |
6 |
3 |
13 |
|||
|
13. |
13 |
2 |
7 |
28. |
7 |
4 |
14 |
|||
|
14. |
14 |
3 |
8 |
29. |
8 |
5 |
15 |
|||
|
15. |
15 |
4 |
9 |
30. |
9 |
6 |
1 |
PDF created with pdfFactory Pro trial version www.pdffactory.com

ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств
Таблица 2
|
№ варианта |
y(x) |
|||||||||||||
|
1. |
y(x) = |
ìx × ln x |
x ³ 0.2 |
|||||||||||
|
í |
— 2 |
x < 0.2 |
||||||||||||
|
îx2 |
||||||||||||||
|
2. |
y(x) = |
ìx3 |
x ³ 1.0 |
|||||||||||
|
í |
x < 1.0 |
|||||||||||||
|
îx2 — 5 |
||||||||||||||
|
3. |
ìln x |
x ³ 8,0 |
||||||||||||
|
y(x) = í |
x < 8,0 |
|||||||||||||
|
î x2 |
||||||||||||||
|
4. |
ì |
1 |
x ³ 5 |
|||||||||||
|
y(x) = |
ï |
|||||||||||||
|
x |
||||||||||||||
|
í |
||||||||||||||
|
ï |
2 |
— 2x |
x < 5 |
|||||||||||
|
îx |
||||||||||||||
|
5. |
ì |
ln 3x |
x ³ 0.5 |
|||||||||||
|
y(x) = í |
4 |
—10 |
x < 0.5 |
|||||||||||
|
îx |
||||||||||||||
|
6. |
ì |
x |
3 |
x ³ 2 |
||||||||||
|
y(x) = í |
||||||||||||||
|
îx |
2 — 2 |
x < 2 |
||||||||||||
|
7. |
y(x) = |
ìx × lg x |
x ³ 0.2 |
|||||||||||
|
í |
x < 0.2 |
|||||||||||||
|
îx |
||||||||||||||
|
8. |
ì |
x |
||||||||||||
|
y(x) = íïe |
x ³ 3 |
|||||||||||||
|
ï |
3 |
— 2 |
x < 3 |
|||||||||||
|
îx |
||||||||||||||
|
9. |
ì 4x +10 |
x ³ 0 |
||||||||||||
|
y(x) = í0.5x2 — 2 |
x < 0 |
|||||||||||||
|
î |
||||||||||||||
|
10. |
ì |
3x |
x ³ 0.2 |
|||||||||||
|
y(x) = í |
x < 0.2 |
|||||||||||||
|
î— 4x2 — 2 |
||||||||||||||
|
11. |
y(x) = |
ì ln10x |
x ³ 0.2 |
|||||||||||
|
í |
x < 0.2 |
|||||||||||||
|
î— ln 5x |
||||||||||||||
|
12. |
ì0.01x — 3 |
x ³ 4 |
||||||||||||
|
y(x) = í |
2 |
— 2 |
x < 4 |
|||||||||||
|
îx |
||||||||||||||
|
13. |
ì |
2 |
||||||||||||
|
y(x) = í3x |
+ x x ³ 10 |
|||||||||||||
|
î— x2 — 2 |
x < 10 |
|||||||||||||
|
14. |
ì |
3 |
||||||||||||
|
y(x) = |
íx |
+ 4x x ³ 0 |
||||||||||||
|
î x3 — 2 |
x < 0 |
|||||||||||||
|
15. |
ì |
2 |
||||||||||||
|
y(x) = í — x |
+ 3x |
x ³ 0 |
||||||||||||
|
5x2 — 2x +10 x < 0 |
||||||||||||||
|
î |
PDF created with pdfFactory Pro trial version www.pdffactory.com
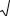
ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств
|
Таблица 3 |
|||||||||||||||
|
№ |
y(x) |
№ |
y(x) |
||||||||||||
|
варианта |
варианта |
||||||||||||||
|
1. |
9. |
ì |
|||||||||||||
|
ì x + 4 x < —1 |
1— x |
x £ 0 |
|||||||||||||
|
y(x) = |
ï |
—1 £ x < 1 |
ï |
0 < x £ 2 |
|||||||||||
|
íx2 + 2 |
y(x) = í0 |
||||||||||||||
|
ï |
2x |
x ³ 1 |
ï |
x |
— 2 |
x > 2 |
|||||||||
|
î |
î |
||||||||||||||
|
2. |
ì |
x +1 |
x £ 0 |
10. |
ì |
||||||||||
|
ï |
2 |
2x |
2 |
x £ 0 |
|||||||||||
|
y(x) = í(x +1) |
0 < x £ 2 |
ï |
|||||||||||||
|
ï |
x > 2 |
y(x) = íx |
0 < x £ 1 |
||||||||||||
|
î— x + 4 |
ï |
x > 1 |
|||||||||||||
|
î2 + x |
|||||||||||||||
|
3. |
11. |
x £ π / 2 |
|||||||||||||
|
ì x + 2 |
x £ —1 |
ìcos x |
|||||||||||||
|
y(x) = |
ïx2 +1 —1 < x £ 1 |
y(x) = ï0 |
π / 2 < x < π |
||||||||||||
|
í |
í |
||||||||||||||
|
ï |
x > 1 |
ï |
x ³ π |
||||||||||||
|
î — x + 3 |
î 2 |
||||||||||||||
|
4. |
12. |
||||||||||||||
|
ì — x |
x £ 0 |
ì x —1 |
x £ 0 |
||||||||||||
|
ï |
0 < x < 2 |
y(x) = |
ï |
0 < x < 2 |
|||||||||||
|
y(x) = í- (x —1)2 |
íx2 |
||||||||||||||
|
ï |
x — 3 |
x ³ 2 |
ï |
2x |
x ³ 2 |
||||||||||
|
î |
î |
||||||||||||||
|
5. |
13. |
||||||||||||||
|
ì- 2(x +1) |
x £ —1 |
ì x +1 |
x < 0 |
||||||||||||
|
ï |
(x |
+1)3 |
—1 < x < 0 |
y(x) = |
ï |
||||||||||
|
y(x) = í |
íx2 —1 0 £ x < 1 |
||||||||||||||
|
ï |
x |
x ³ 0 |
ï |
x ³ 1 |
|||||||||||
|
î |
î — x |
||||||||||||||
|
6. |
14. |
||||||||||||||
|
ì — x |
x £ 0 |
ì — x |
x < 0 |
||||||||||||
|
y(x) = |
ï |
x2 0 |
< x £ 2 |
y(x) = |
ï |
2 +1 0 £ x < 2 |
|||||||||
|
í |
íx |
||||||||||||||
|
ï |
x > 2 |
ï |
+1 |
x ³ 2 |
|||||||||||
|
îx +1 |
îx |
||||||||||||||
|
7. |
ì |
15. |
|||||||||||||
|
x2 +1 |
x £ 1 |
ì 2 |
x < —1 |
||||||||||||
|
y(x) = |
ï |
1 < x £ 3 |
y(x) = |
ï |
— x |
—1 £ x £ 1 |
|||||||||
|
í 2x |
í1 |
||||||||||||||
|
ï |
x > 3 |
ï |
x > 1 |
||||||||||||
|
îx + 2 |
î ln x |
||||||||||||||
|
8. |
|||||||||||||||
|
ì |
x — 3 |
x £ 0 |
|||||||||||||
|
y(x) = |
ï |
+1 |
0 < x £ 4 |
||||||||||||
|
íx |
|||||||||||||||
|
ï |
+ x |
x > 4 |
|||||||||||||
|
î 3 |
PDF created with pdfFactory Pro trial version www.pdffactory.com

ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств
Таблица 4
|
№ |
y(x) |
№ |
y(x) |
||||||||||||
|
варианта |
варианта |
||||||||||||||
|
1. |
ìcos x |
x < π |
9. |
ì |
2 |
x < —1 |
|||||||||
|
ï |
p £ x < 2p |
ïx |
—1£ x < 0 |
||||||||||||
|
ïcos5x |
ïx3 |
||||||||||||||
|
Y (x) = í |
2p £ x < 3p |
Y (x) = í |
0 £ x <1 |
||||||||||||
|
ïsin 5x |
ï— x3 |
||||||||||||||
|
ïsin2 x |
x ³ 3p |
ï |
1) |
2 |
x ³1 |
||||||||||
|
î |
î(x + |
||||||||||||||
|
2. |
ì |
2 |
x < —2 |
10. |
ì2/ x |
x < 4 |
|||||||||
|
ïx |
— 2 £ x < —1 |
ï |
4 £ x < 6 |
||||||||||||
|
ï(2x)2 |
ï5x |
||||||||||||||
|
Y (x) = í |
—1£ x <1 |
Y (x) = í |
3 |
6 £ x < 8 |
|||||||||||
|
ïsin8x |
ïx |
||||||||||||||
|
ï |
—1 |
x ³1 |
ï5 + x |
x ³ 8 |
|||||||||||
|
îx |
î |
||||||||||||||
|
3. |
ìsin x |
x < π |
11. |
ìπ |
x < π |
||||||||||
|
ï |
p £ x < 2p |
ï |
+ p/10 |
p £ x < 5 |
|||||||||||
|
ïsin 5x |
ïx |
||||||||||||||
|
Y (x) = í |
2p £ x < 3p |
Y (x) = í |
+ 15 |
5 £ x < 7.5 |
|||||||||||
|
ïcos5x |
ïx |
||||||||||||||
|
ï |
2 |
x |
x ³ 3p |
ï |
2 |
—10 |
x ³ 7.5 |
||||||||
|
îcos |
îx |
||||||||||||||
|
4. |
ì |
2 |
+ x |
x < 0 |
12. |
ì−1 |
x < −1 |
||||||||
|
ïx |
0 £ x < p/ 2 |
ï |
—1£ x <1 |
||||||||||||
|
ïsin x |
ïx |
||||||||||||||
|
Y (x) = í |
p/ 2 £ x < 3 |
Y (x) = í |
1£ x < 2 |
||||||||||||
|
ïcos x |
ï1 |
||||||||||||||
|
ï |
x ³ 3 |
ï- x2 |
x ³ 2 |
||||||||||||
|
î1/ x |
î |
||||||||||||||
|
5. |
ì2cos x |
x < π |
13. |
ì |
3 |
+ 2 |
x < —2 |
||||||||
|
ï |
ï— x |
||||||||||||||
|
ïsin x |
p £ x < 2p |
ïcos x |
— 2 £ x < 0 |
||||||||||||
|
Y (x) = í |
Y (x) = í |
0 £ x < p |
|||||||||||||
|
ï0.2 + sin 5x 2p £ x < 3p |
ïsin x |
||||||||||||||
|
ï1 |
x ³ 3p |
ï |
x ³ p |
||||||||||||
|
î |
îln x |
||||||||||||||
|
6. |
ì− 2 |
x < −10 |
14. |
ìtgx |
x < π/3 |
||||||||||
|
ï |
—10 £ x < —9 |
ï |
p/3 £ x < p |
||||||||||||
|
ï- 0.5 |
ï3x |
||||||||||||||
|
Y (x) = í |
— 9 £ x < —8 |
Y (x) = í |
p £ x <1.5p |
||||||||||||
|
ï1 |
ïsin x |
||||||||||||||
|
ï |
x ³ —8 |
ï |
2 |
x |
x ³1.5p |
||||||||||
|
î2.5 |
îcos |
||||||||||||||
|
7. |
ìx |
x < −5 |
15. |
ìsin x |
x < −π |
||||||||||
|
ï |
— 5 £ x < —3 |
ï |
2 |
+ 3 |
— p £ x < p |
||||||||||
|
ï- x |
ï- x |
||||||||||||||
|
Y (x) = í |
— 3 £ x < —1 |
Y (x) = í |
p £ x < 2p |
||||||||||||
|
ïx |
ïcos 4x |
||||||||||||||
|
ï |
x ³ —1 |
ï |
x ³ 2p |
||||||||||||
|
î— x |
î3x |
||||||||||||||
|
8. |
ì− cos x |
x < π |
|||||||||||||
|
ï |
p £ x < 2p |
||||||||||||||
|
ï- cos2x |
|||||||||||||||
|
Y (x) = í |
2p £ x < 3p |
||||||||||||||
|
ï— cos3x |
|||||||||||||||
|
ï |
x ³ 3p |
||||||||||||||
|
î— cos4x |
PDF created with pdfFactory Pro trial version www.pdffactory.com
Соседние файлы в папке Лабы
- #
- #
- #
- #
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
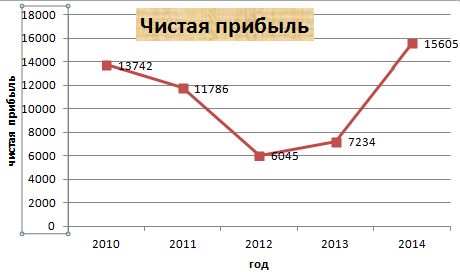
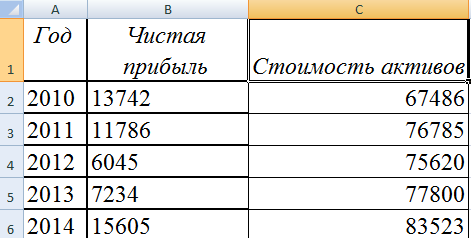
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
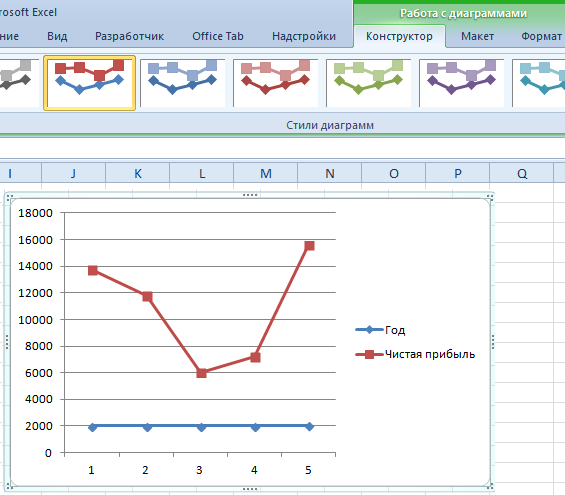
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
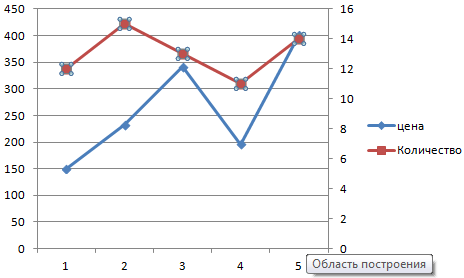
График с двумя и более кривыми
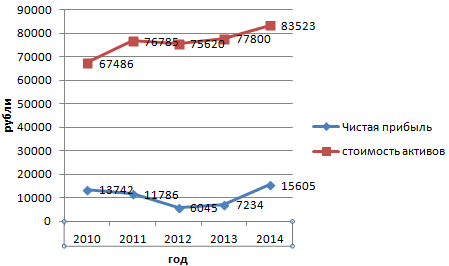
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
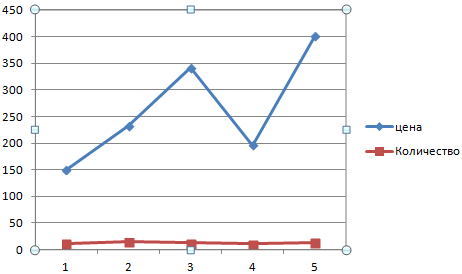
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
Сначала строим график так, будто у нас одинаковые единицы измерения.
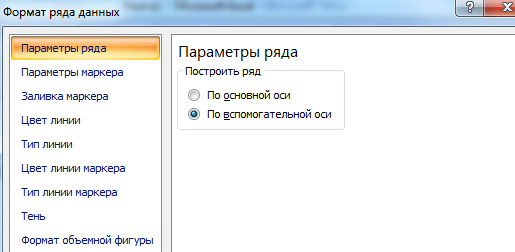
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
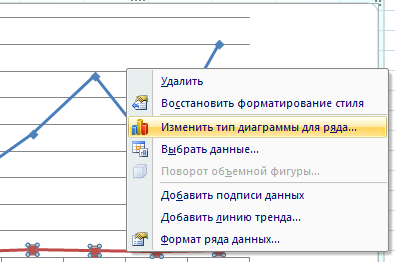
Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
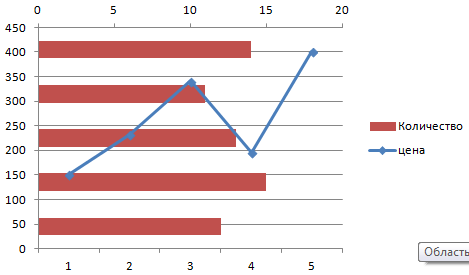
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
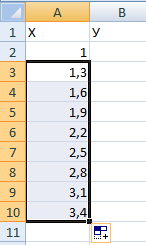
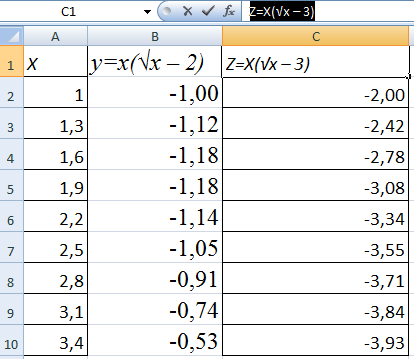
Пример: y=x(√x – 2). Шаг – 0,3.
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
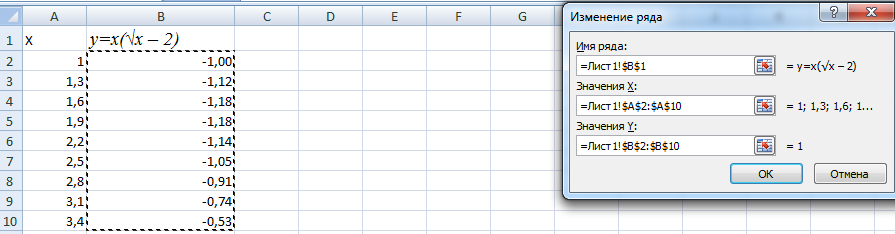
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
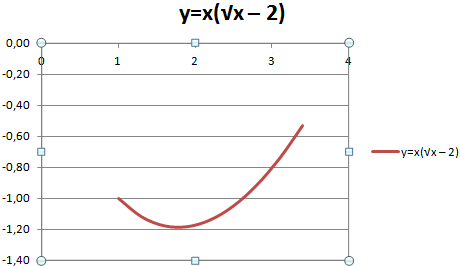
Жмем ОК и любуемся результатом.
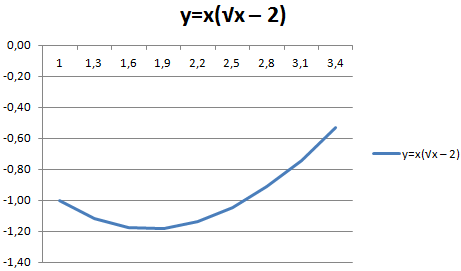
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
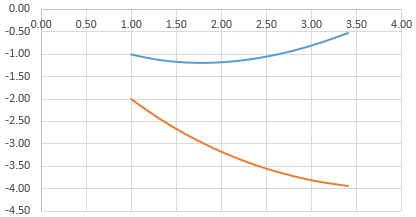
Наложение и комбинирование графиков
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
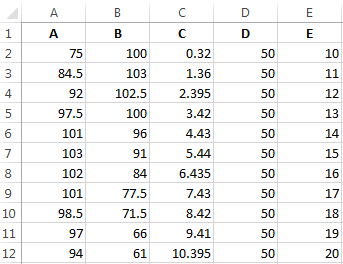
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
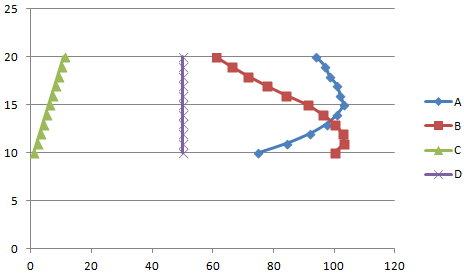
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Скачать все примеры графиков
Готовые примеры графиков и диаграмм в Excel скачать:
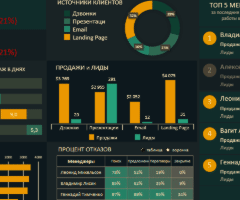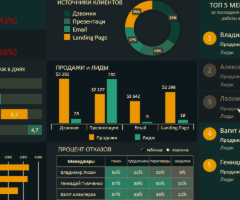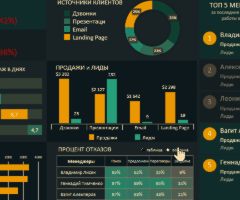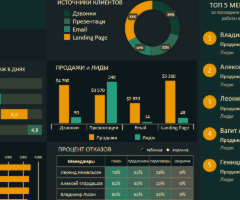
Как сделать шаблон, дашборд, диаграмму или график для создания красивого отчета удобного для визуального анализа в Excel? Выбирайте примеры диаграмм с графиками для интерактивной визуализации данных с умных таблиц Excel и используйте их для быстрого принятия правильных решений. Бесплатно скачивайте готовые шаблоны динамических диаграмм для использования их в дашбордах, отчетах или презентациях.
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Содержание
- Использование кривой Лоренца
- Построение линии равенства
- Создание кривой Лоренца
- Вопросы и ответы
Для оценки уровня неравенства между различными слоями населения общества часто используют кривую Лоренца и производный от неё показатель – коэффициент Джинни. С помощью них можно определить, насколько велик социальный разрыв в обществе между самыми богатыми и наиболее бедными слоями населения. С помощью инструментов приложения Excel можно значительно облегчить процедуру построения кривой Лоренца. Давайте, разберемся, как в среде Эксель это можно осуществить на практике.
Использование кривой Лоренца
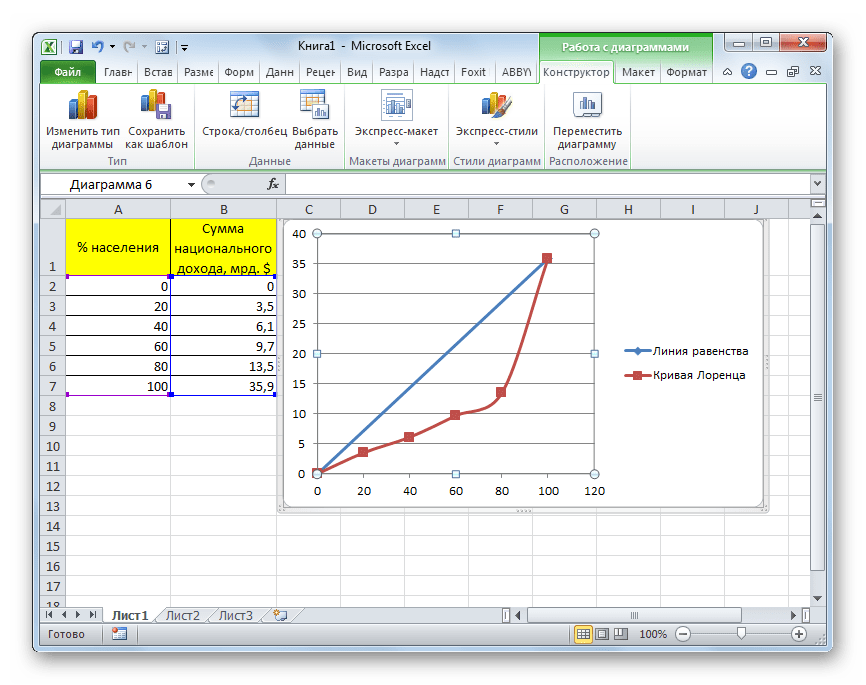
Кривая Лоренца представляет собой типичную функцию распределения, отображенную графически. По оси X данной функции располагается количество населения в процентном соотношении по нарастающей, а по оси Y — общее количество национального дохода. Собственно, сама кривая Лоренца состоит из точек, каждая из которых соответствует процентному соотношению уровня дохода определенной части общества. Чем больше изогнута линия Лоренца, тем больше в обществе уровень неравенства.
В идеальной ситуации, при которой отсутствует общественное неравенство, каждая группа населения имеет уровень дохода прямо пропорциональный её численности. Линия, характеризующая такую ситуацию, называется кривой равенства, хотя она и представляет собой прямую. Чем больше площадь фигуры, ограниченной кривой Лоренца и кривой равенства, тем выше уровень неравенства в обществе.
Кривая Лоренца может использоваться не только для определения ситуации имущественного расслоения в мире, в конкретной стране или в обществе, но и для сравнения в данном аспекте отдельных домохозяйств.
Вертикальная прямая, которая соединяет линию равенства и наиболее удаленную от неё точку кривой Лоренца, называется индексом Гувера или Робин Гуда. Данный отрезок показывает, какую величину дохода нужно перераспределить в обществе, чтобы достичь полного равенства.
Уровень неравенства в обществе определяется с помощью индекса Джинни, который может варьироваться от 0 до 1. Он ещё называется коэффициентом концентрации доходов.
Построение линии равенства
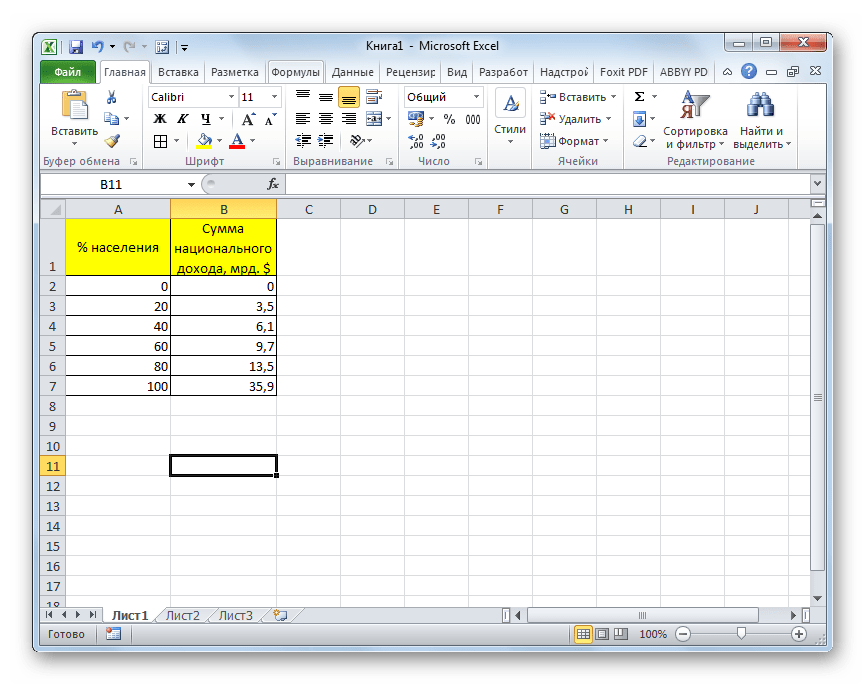
Теперь давайте на конкретном примере посмотрим, как создать линию равенства и кривую Лоренца в Экселе. Для этого используем таблицу количества населения разбитого на пять равных групп (по 20%), которые суммируются в таблице по нарастающей. Во второй колонке этой таблицы представлена величина национального дохода в процентном соотношении, которая соответствует определенной группе населения.
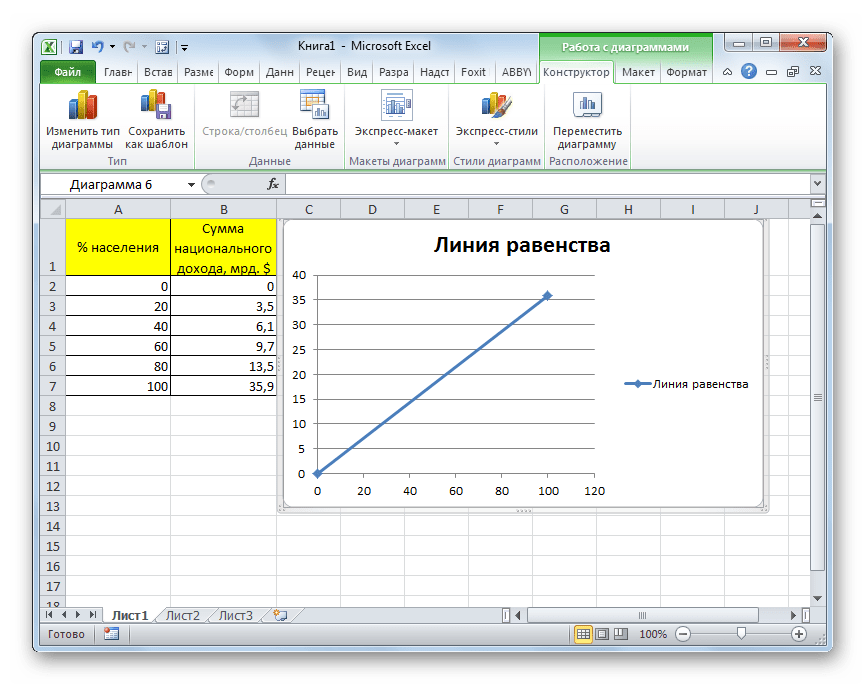
Для начала построим линию абсолютного равенства. Она будет состоять из двух точек – нулевой и точки суммарного национального дохода для 100% населения.
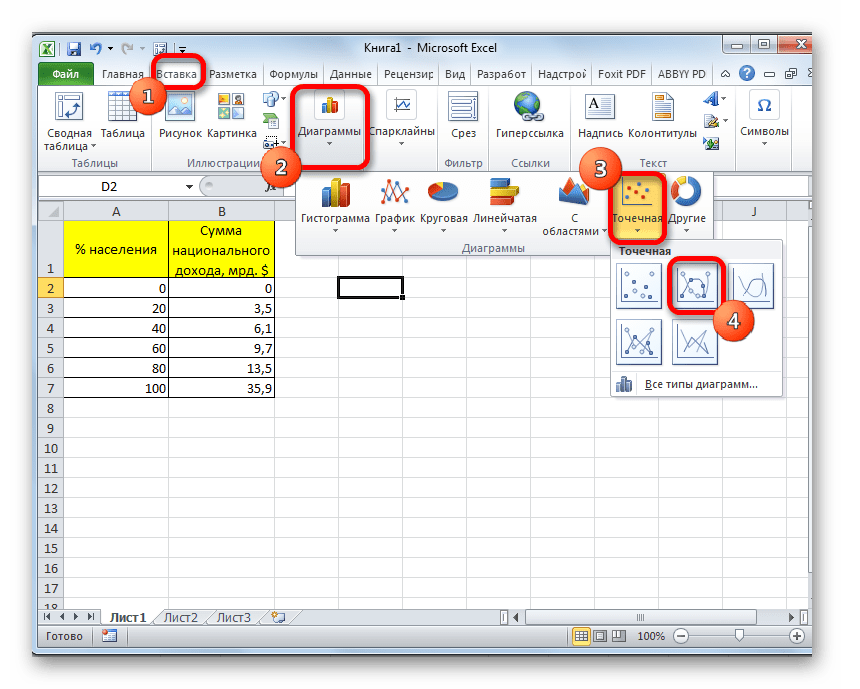
- Переходим во вкладку «Вставка». На линии в блоке инструментов «Диаграммы» жмем на кнопку «Точечная». Именно данный тип диаграмм подойдет для нашей задачи. Далее открывается список подвидов диаграмм. Выбираем «Точечная с гладкими кривыми и маркерами».
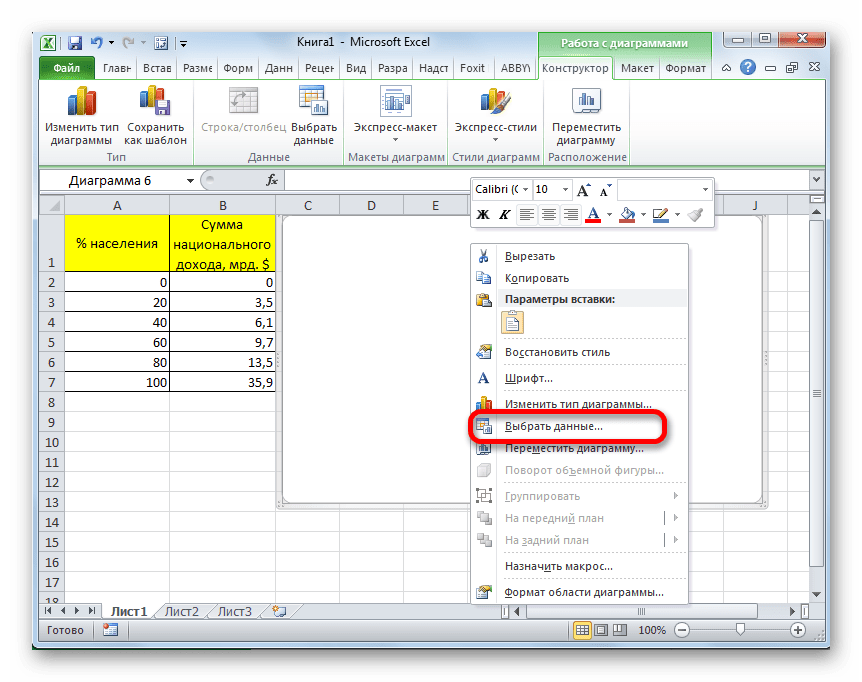
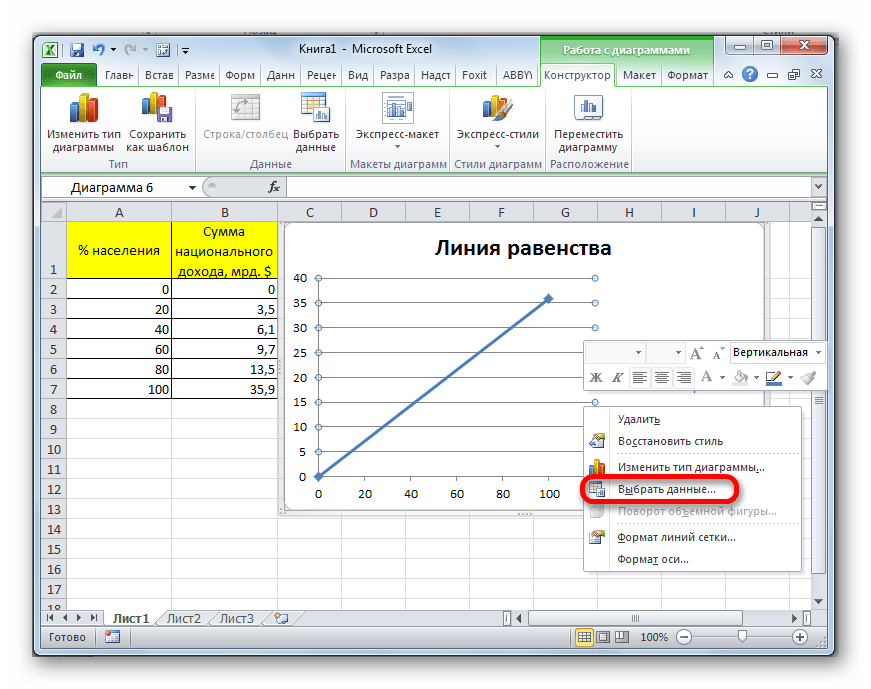
- После выполнения данного действия открывается пустая область для диаграммы. Это случилось потому, что мы не выбрали данные. Для того, чтобы внести данные и построить график, кликаем правой кнопкой мыши по пустой области. В активировавшемся контекстном меню выбираем пункт «Выбрать данные…».
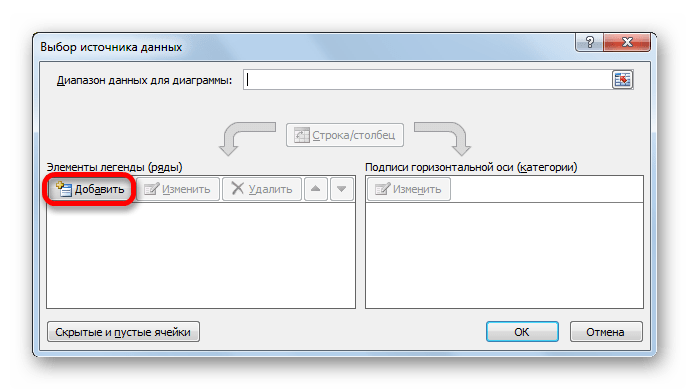
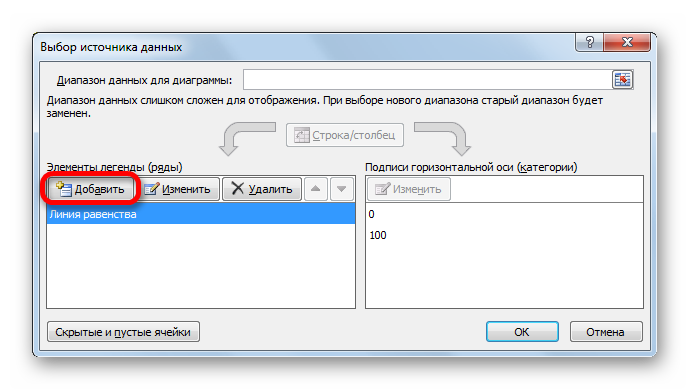
- Открывается окно выбора источника данных. В левой его части, которая называется «Элементы легенды (ряды)» жмем на кнопку «Добавить».
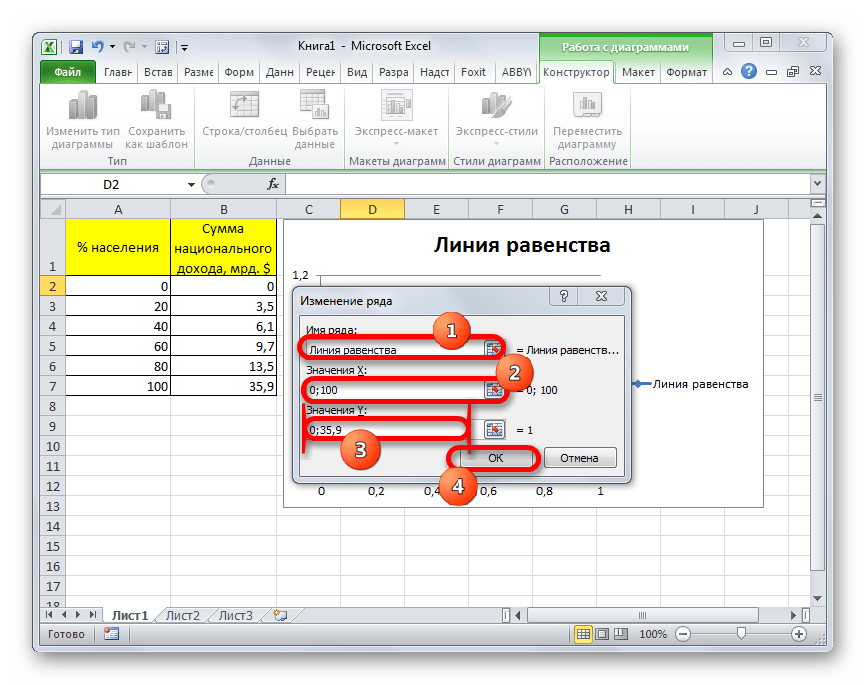
- Запускается окно изменения ряда. В поле «Имя ряда» записываем то наименование диаграммы, которое хотим ей присвоить. Оно может также располагаться на листе и в этом случае нужно указать адрес ячейки его нахождения. Но в нашем случае легче просто вписать название вручную. Дадим диаграмме наименование «Линия равенства».
В поле «Значения X» следует указать координаты точек диаграммы по оси X. Как мы помним, их будет всего две: 0 и 100. Записываем данные значения через точку с запятой в данном поле.
В поле «Значения Y» следует записать координаты точек по оси Y. Их тоже будет две: 0 и 35,9. Последняя точка, как мы можем видеть по графику, соответствует совокупному национальному доходу 100% населения. Итак, записываем значения «0;35,9» без кавычек.
После того, как все указанные данные внесены, жмем на кнопку «OK».
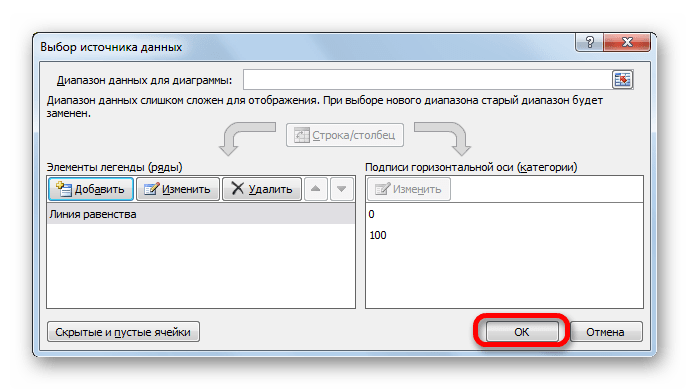
- После этого мы возвращаемся к окну выбора источника данных. В нем тоже следует нажать на кнопку «OK».
- Как видим, после вышеуказанных действий линия равенства будет построена и отобразится на листе.
Урок: Как сделать диаграмму в Экселе
Создание кривой Лоренца
Теперь нам предстоит непосредственно построить кривую Лоренца, опираясь на табличные данные.
- Кликаем правой кнопкой мыши по области диаграммы, на которой уже расположена линия равенства. В запустившемся меню снова останавливаем выбор на пункте «Выбрать данные…».
- Опять открывается окно выбора данных. Как видим, среди элементов уже представлено наименование «Линия равенства», но нам нужно внести ещё одну диаграмму. Поэтому жмем на кнопку «Добавить».
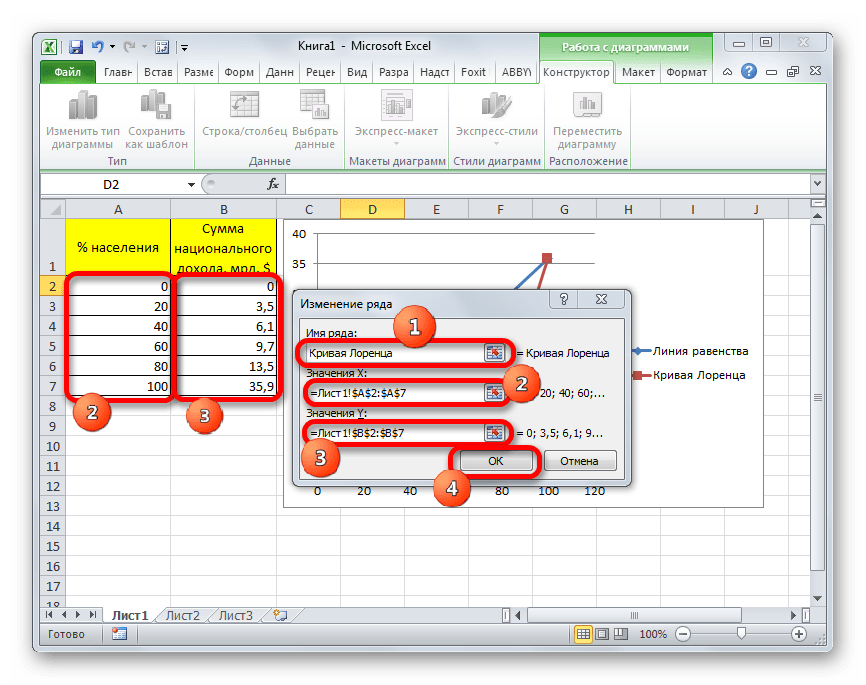
- Снова открывается окно изменения ряда. Поле «Имя ряда», как и в прошлый раз, заполняем вручную. Сюда можно вписать наименование «Кривая Лоренца».
В поле «Значения X» следует занести все данные столбца «% населения» нашей таблицы. Для этого устанавливаем курсор в область поля. Далее зажимаем левую кнопку мыши и выделяем соответствующий столбец на листе. Координаты тут же будут отображены в окне изменения ряда.
В поле «Значения Y» заносим координаты ячеек столбца «Сумма национального дохода». Делаем это по той же методике, по которой вносили данные в предыдущее поле.
После того, как все вышеуказанные данные внесены, жмем на кнопку «OK».
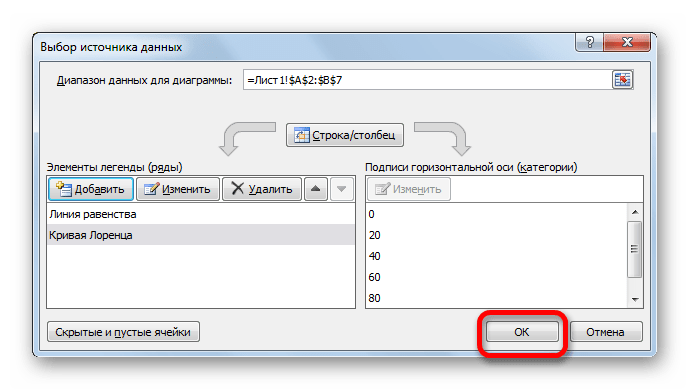
- После возврата к окну выбора источника опять жмем на кнопку «OK».
- Как видим, после выполнения вышеуказанных действий кривая Лоренца также отобразится на листе Excel.
Построение кривой Лоренца и линии равенства в Экселе производится на тех же принципах, что и построение любого другого вида диаграмм в этой программе. Поэтому для пользователей, которые овладели умением строить диаграммы и графики в Excel, данная задача не должна вызвать больших проблем.
Еще статьи по данной теме: