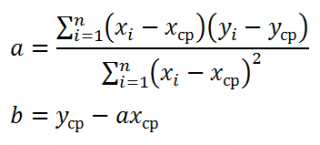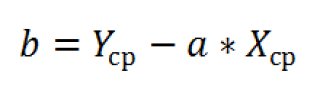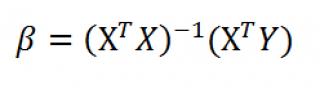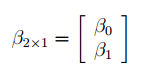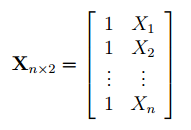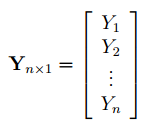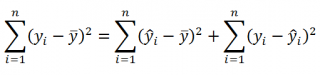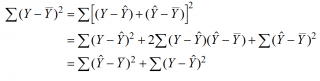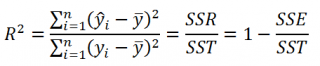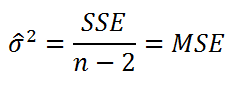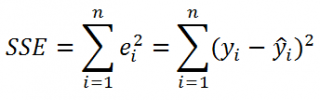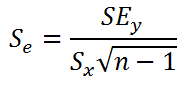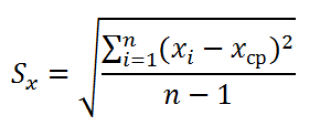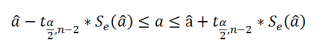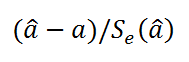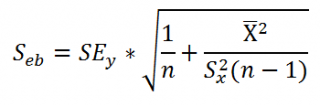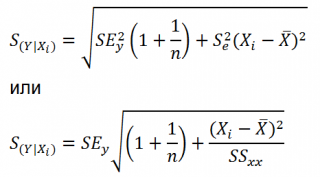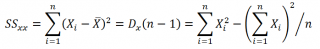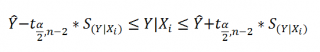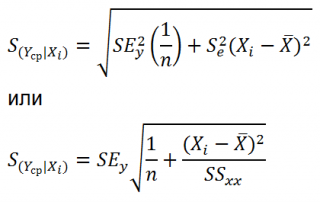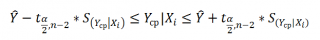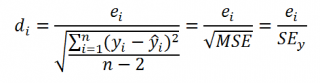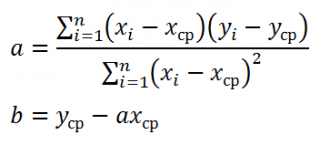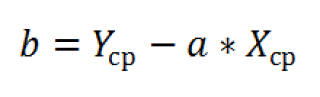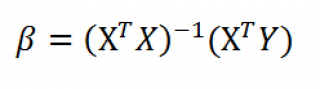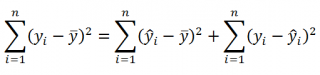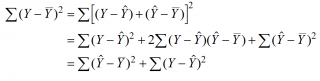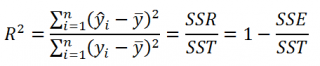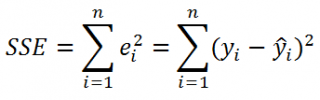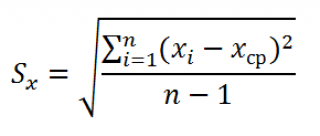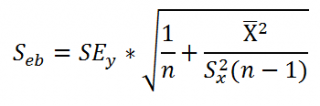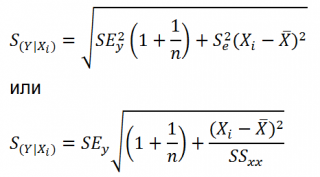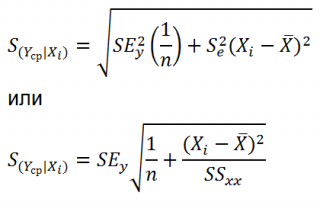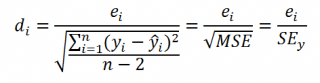17 авг. 2022 г.
читать 2 мин
Простая линия линейной регрессии представляет собой линию, которая лучше всего «соответствует» набору данных.
В этом руководстве представлен пошаговый пример того, как быстро добавить простую линию линейной регрессии на диаграмму рассеивания в Excel.
Шаг 1: Создайте данные
Во-первых, давайте создадим простой набор данных для работы:
Шаг 2: Создайте диаграмму рассеивания
Затем выделите диапазон ячеек A2:B21.На верхней ленте щелкните вкладку « ВСТАВИТЬ », затем нажмите « ВСТАВИТЬ точечную (X, Y)» или «Пузырьковую диаграмму » в группе « Диаграммы » и выберите первый вариант, чтобы создать диаграмму рассеяния:
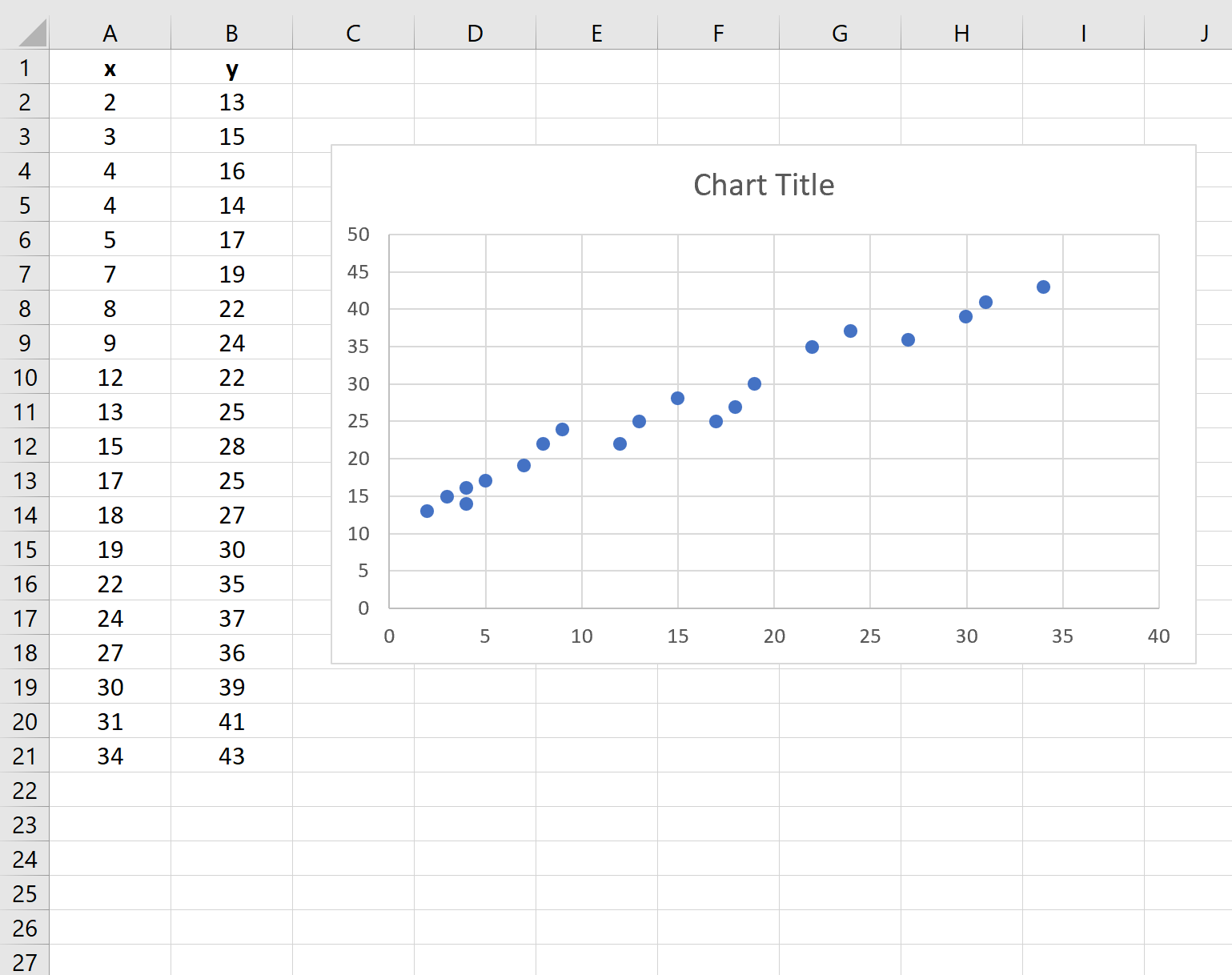
Появится следующая диаграмма рассеяния:
Шаг 3: Добавьте линию регрессии
Затем щелкните в любом месте диаграммы рассеивания. Затем щелкните знак «плюс» (+) в правом верхнем углу графика и установите флажок « Линия тренда ».
Это автоматически добавит на диаграмму рассеяния простую линию линейной регрессии:
Добавить линию регрессии в диаграмму рассеяния в Excel
Шаг 4: Добавьте уравнение линии регрессии
Вы также можете добавить уравнение линии регрессии на диаграмму, нажав Дополнительные параметры. В появившемся справа поле установите флажок рядом с Отображать уравнение на диаграмме .
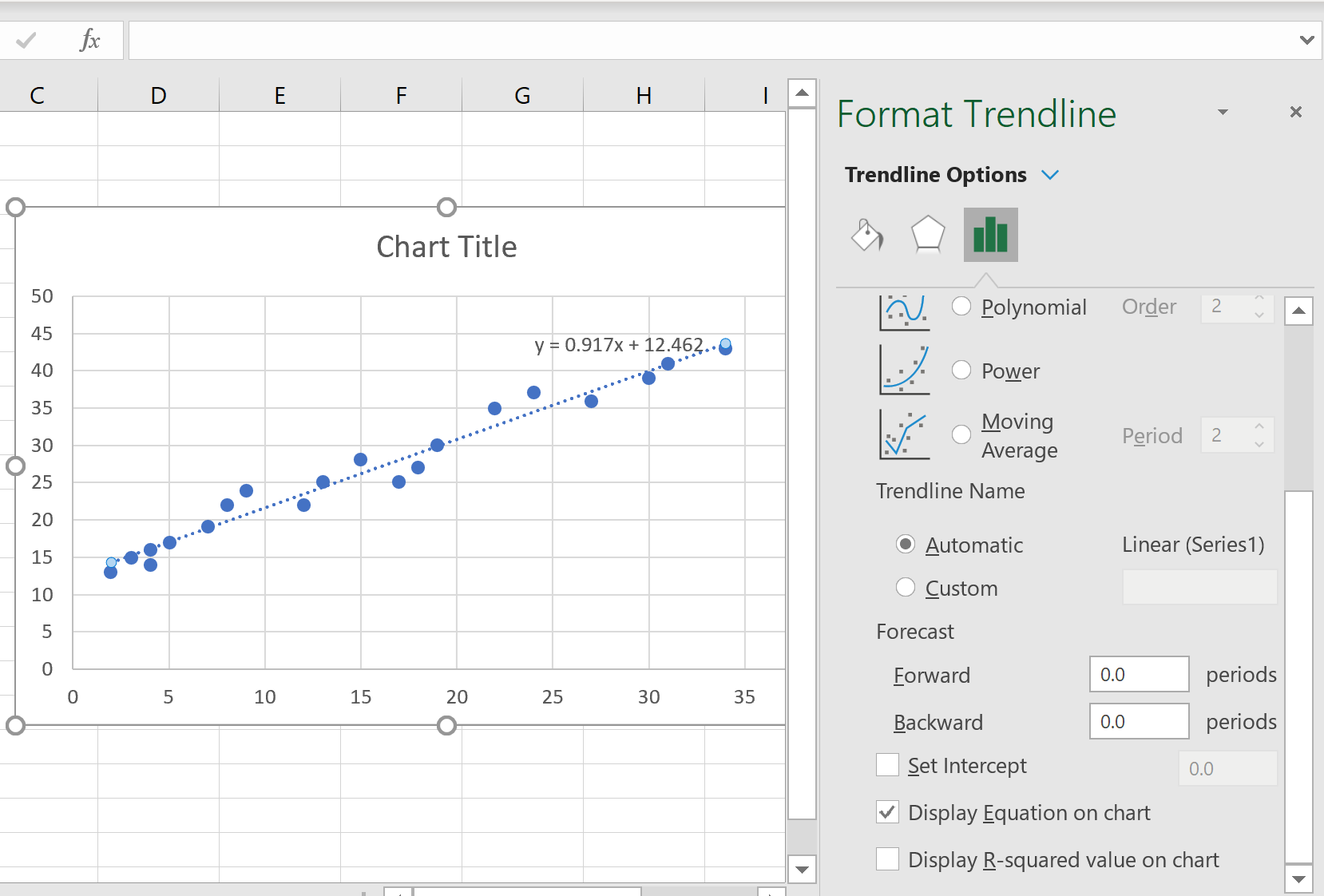
На диаграмме рассеивания автоматически появится простое уравнение линейной регрессии:
Для этого конкретного примера линия регрессии выглядит так:
у = 0,917х + 12,462
Интерпретировать это можно следующим образом:
- Для каждой дополнительной единицы увеличения переменной x среднее увеличение переменной y составляет 0,917 .
- Когда переменная x равна нулю, среднее значение переменной y равно 12,462 .
Мы также можем использовать это уравнение для оценки значения y на основе значения x.Например, когда x равно 15, ожидаемое значение y равно 26,217:
у = 0,917 * (15) + 12,462 = 26,217
Другие учебники по Excel можно найти здесь .
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
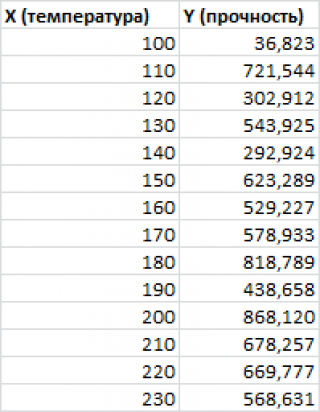
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
-
Перемещаемся во вкладку «Файл».
Переходим в раздел «Параметры».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12765 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
-
Группы статей
- Статистический анализ
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
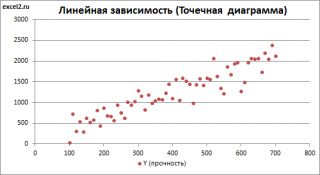
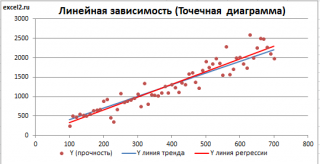
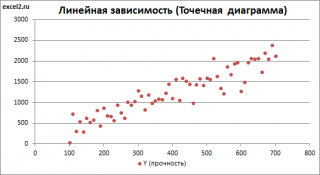
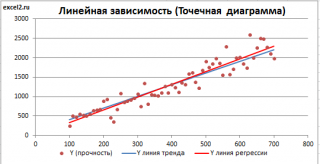
Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х i ) равному μy(i)=Е(Y i ).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.
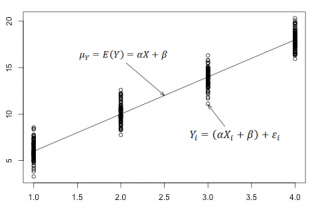
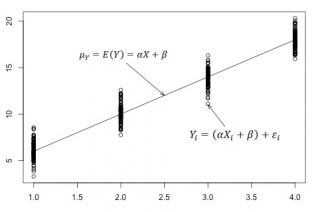
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε i была адекватной — требуется:
- Ошибки ε i должны быть независимыми переменными;
- При каждом значении Xi ошибки ε i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε i ]=0);
- При каждом значении Xi ошибки ε i должны иметь равные дисперсии (обозначим ее σ 2 ).
Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε i ).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .
Оценку параметров в MS EXCEL можно выполнить различными способами:
Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).
Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .
Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
- ввести формулу в Строке формул
- нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).
Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа <3,01279389265416;154,240057900613>. Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).
Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .
Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
Матрица Х равна:
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом Y обозначен столбец значений переменной Y.
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .
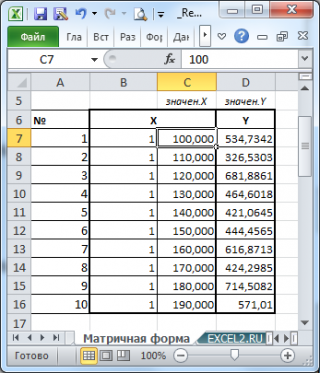
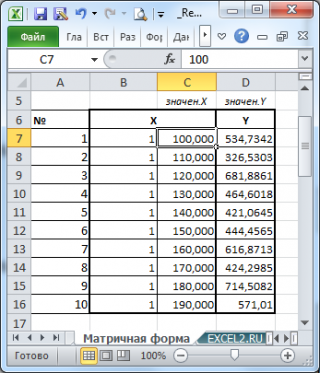
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае множественной регрессии .
Построение линии регрессии
Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).
Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .
Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .
Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
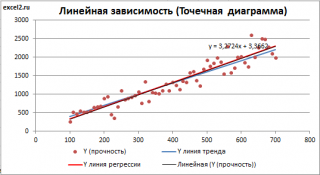
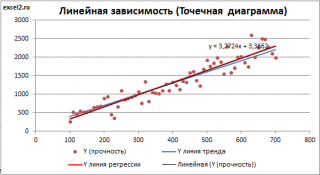
Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .
Коэффициент детерминации R 2
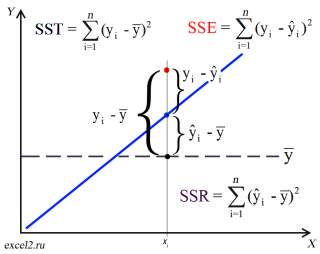
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .
После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
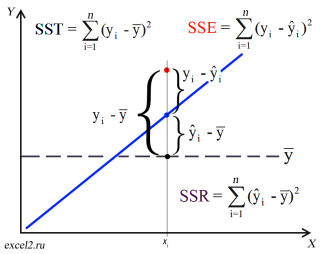
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Примечание : SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.
Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .
Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки дисперсии σ 2 используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε i =yi — ŷi ( Sum of Squared Errors ).
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .
Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).
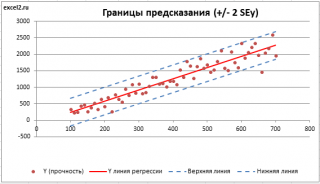
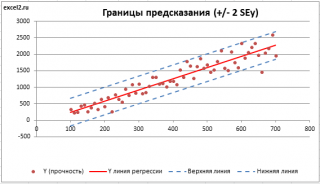
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции ЛИНЕЙН() :
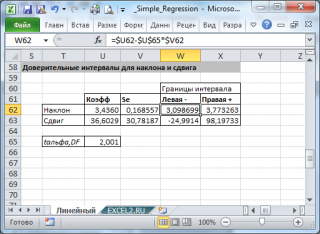
Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
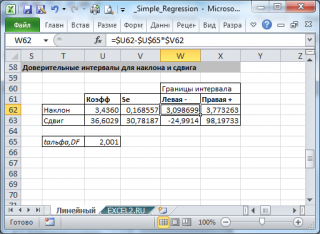
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
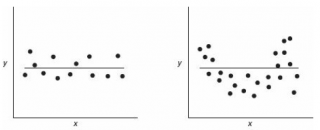
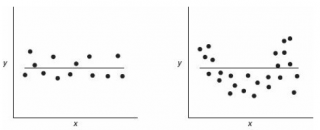
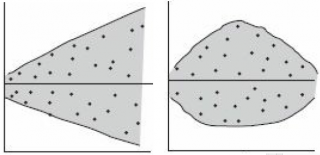
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
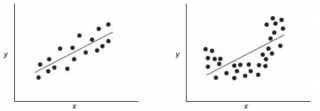
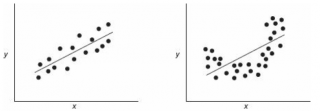
Ниже — 2 ситуации, когда нулевая гипотеза Н 0 отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
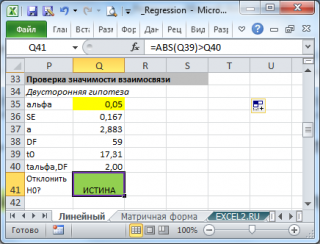
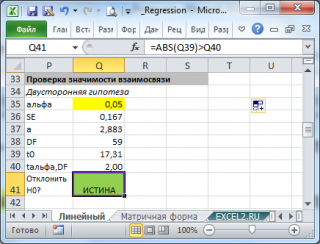
Для проверки гипотезы нам потребуется:
- Установить уровень значимости , пусть альфа=0,05;
- Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
- Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
- Вычислить значение тестовой статистики t 0 =a/S e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
- Сравнить значение тестовой статистики |t0| с пороговым значением t альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
- вычислить p-значение и сравнить его с уровнем значимости .
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
- неопределенность связанную со случайностью оценок параметров модели a и b ;
- случайность ошибки модели ε.
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.
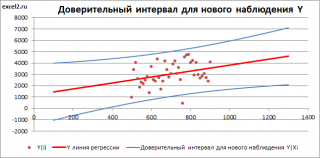
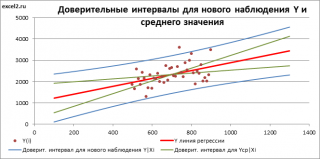
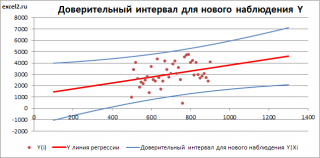
Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х ср ), то интервал будет постепенно расширяться при удалении от Х ср .
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
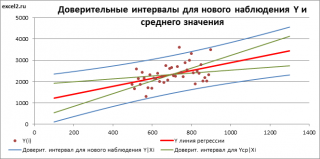
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
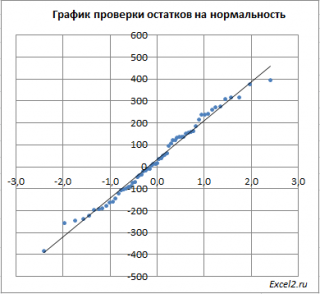
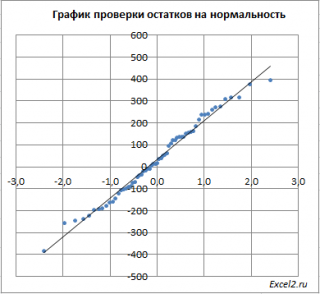
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
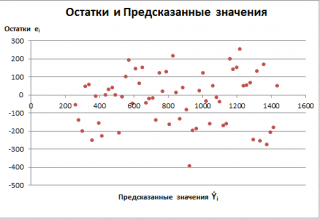
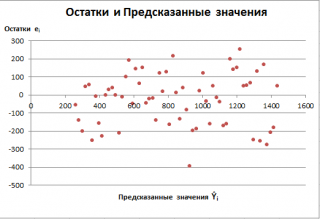
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://excel2.ru/articles/prostaya-lineynaya-regressiya-v-ms-excel
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В
MS
EXCEL
имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Статья про
Регрессионный анализ
получилась большая, поэтому ниже для удобства приведены ее разделы:
- Немного теории и основные понятия
- Предположения линейной регрессионной модели
- Задачи регрессионного анализа
- Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
- Оценка неизвестных параметров линейной модели (через статистики выборок)
- Оценка неизвестных параметров линейной модели (матричная форма)
- Построение линии регрессии
- Коэффициент детерминации
- Стандартная ошибка регрессии
- Стандартные ошибки и доверительные интервалы для наклона и сдвига
- Проверка значимости взаимосвязи переменных
- Доверительные интервалы для нового наблюдения Y и среднего значения
- Проверка адекватности линейной регрессионной модели
Примечание
: Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место
множественная регрессия
.
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание
: Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части —
оценке неизвестных параметров линейной модели
.
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем
прочность этого волокна
(Y) зависит только от
рабочей температуры процесса
в реакторе (Х), которая задается оператором.
Построим
диаграмму рассеяния
(см.
файл примера лист Линейный
), созданию которой
посвящена отдельная статья
. Вообще, построение
диаграммы рассеяния
для целей
регрессионного анализа
де-факто является стандартом.
СОВЕТ
: Подробнее о построении различных типов диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
Приведенная выше
диаграмма рассеяния
свидетельствует о возможной
линейной взаимосвязи
между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание
: Наличие даже такой очевидной
линейной взаимосвязи
не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие
причинной
взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание
: Как известно, уравнение прямой линии имеет вид
Y
=
m
*
X
+
k
, где коэффициент
m
отвечает за наклон линии (
slope
),
k
– за сдвиг линии по вертикали (
intercept
),
k
равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х (
рабочую температуру процесса
) при некотором значении Х
i
и произвести несколько наблюдений переменной Y (
прочность нити
). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого
значения
. При увеличении количества измерений, среднее этих измерений, будет стремиться к
математическому ожиданию
случайной величины Y (при Х
i
) равному μy(i)=Е(Y
i
).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела
Проверка статистических гипотез
. В статье о
проверке гипотезы о среднем значении генеральной совокупности
в качестве
нулевой
гипотезы
предполагалось равенство неизвестного значения μ заданному μ0.
В нашем случае
простой линейной регрессии
в качестве
нулевой
гипотезы
предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ
y(i)
=α* Х
i
+β. Уравнение μ
y(i)
=α* Х
i
+β можно переписать в обобщенном виде (для всех Х и μ
y
) как μ
y
=α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется
регрессионной линией генеральной совокупности
(population regression line), параметры которой (
наклон
a и
сдвиг β
) нам не известны (по аналогии с
гипотезой о среднем значении генеральной совокупности
, где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х +
β
, к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют
линейной регрессионной моделью
. Часто Х еще называют
независимой переменной
(еще
предиктором
и
регрессором
, английский термин
predictor
,
regressor
), а Y –
зависимой
(или
объясняемой
,
response
variable
). Так как
регрессор
у нас один, то такая модель называется
простой линейной регрессионной моделью
(
simple
linear
regression
model
). α часто называют
коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε
i
была адекватной — требуется:
-
Ошибки ε
i
должны быть независимыми переменными; -
При каждом значении Xi ошибки ε
i
должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε
i
]=0); -
При каждом значении Xi ошибки ε
i
должны иметь равные дисперсии (обозначим ее σ
2
).
Примечание
: Последнее условие называется
гомоскедастичность
— стабильность, гомогенность дисперсии случайной ошибки e. Т.е.
дисперсия
ошибки σ
2
не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε
i
]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε
i
]= Е[a*Xi+β]+ Е[ε
i
]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия
случайной переменной Y равна
дисперсии
ошибки ε, т.е. VAR(Y)= VAR(ε)=σ
2
. Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε
i
).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует
регрессионная линия генеральной совокупности
, т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений {X;Y}.
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно
a
и
b
. Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Таким образом:
Первая задача
регрессионного анализа
– оценка неизвестных параметров (
estimation
of
the
unknown
parameters
). Подробнее см. раздел
Оценки неизвестных параметров модели
.
Вторая задача
регрессионного анализа
–
Проверка адекватности модели
(
model
adequacy
checking
).
Примечание
: Оценки параметров модели обычно вычисляются
методом наименьших квадратов
(МНК),
которому посвящена отдельная статья
.
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры
простой линейной регрессионной модели
Y=a*X+β+ε оценим с помощью
метода наименьших квадратов
(в
статье про МНК подробно описано этот метод
).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y=
a
*X+
b
, которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание
: В статье про
метод наименьших квадратов
рассмотрены случаи аппроксимации
линейной
и
квадратичной функцией
, а также
степенной
,
логарифмической
и
экспоненциальной функцией
.
Оценку параметров в MS EXCEL можно выполнить различными способами:
-
с помощью функций
НАКЛОН()
и
ОТРЕЗОК()
; -
с помощью функции
ЛИНЕЙН()
; см. статьюФункция MS EXCEL ЛИНЕЙН()
-
формулами через статистики выборок
;
-
в матричной форме
;
-
с помощью
инструмента Регрессия надстройки Пакет Анализа
.
Сначала рассмотрим функции
НАКЛОН()
,
ОТРЕЗОК()
и
ЛИНЕЙН()
.
Пусть значения Х и Y находятся соответственно в диапазонах
C
23:
C
83
и
B
23:
B
83
(см.
файл примера
внизу статьи).
Примечание
: Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью
Генерация данных для линейной регрессии в MS EXCEL
).
В MS EXCEL наклон прямой линии
а
(
оценку
коэффициента регрессии
), можно найти по
методу МНК
с помощью функции
НАКЛОН()
, а сдвиг
b
(
оценку
постоянного члена
или
константы регрессии
), с помощью функции
ОТРЕЗОК()
. В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции
ЛИНЕЙН()
, английская версия LINEST (см.
статью об этой функции
).
Формула
=ЛИНЕЙН(C23:C83;B23:B83)
вернет наклон
а
. А формула =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)
— сдвиг
b
. Здесь требуются пояснения.
Функция
ЛИНЕЙН()
имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент
статистика
имеет значение ЛОЖЬ или опущен, то функция
ЛИНЕЙН()
возвращает только оценки параметров модели:
a
и
b
.
Примечание
: Остальные значения, возвращаемые функцией
ЛИНЕЙН()
, нам потребуются при вычислении
стандартных ошибок
и для
проверки значимости регрессии
. В этом случае аргумент
статистика
должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
-
ввести формулу в
Строке формул
-
нажать
CTRL
+
SHIFT
+
ENTER
(см. статью проформулы массива
).
Если в
Строке формул
выделить формулу =
ЛИНЕЙН(C23:C83;B23:B83)
и нажать
клавишу F9
, то мы увидим что-то типа {3,01279389265416;154,240057900613}. Это как раз значения
a
и
b
. Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу =
ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83))
. При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция
ТРАНСП()
транспонировала строку в столбец
).
Чтобы разобраться в этом подробнее необходимо ознакомиться с
формулами массива
.
Чтобы не связываться с вводом
формул массива
, можно
использовать функцию ИНДЕКС()
. Формула =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1)
или просто
ЛИНЕЙН(C23:C83;B23:B83)
вернет параметр, отвечающий за наклон линии, т.е.
а
. Формула
=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)
вернет параметр
b
.
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент
а
, можно также вычислить через
коэффициент корреляции
и
стандартные отклонения выборок
:
=
КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению
ковариации
выборок Х и Y и
дисперсии
выборки Х:
=
КОВАРИАЦИЯ.В(B23:B83;C23:C83)/ДИСП.В(B23:B83)
И, наконец, запишем еще одну формулу для нахождения сдвига
b
. Воспользуемся тем фактом, что
линия регрессии
проходит через точку
средних значений
переменных Х и Y.
Вычислив
средние значения
и подставив в формулу ранее найденный наклон
а
, получим сдвиг
b
.
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры
линии регрессии
можно найти в матричной форме (см.
файл примера лист Матричная форма
).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг
b
), β1 (наклон
a
).
Матрица Х равна:
Матрица
Х
называется
регрессионной матрицей
или
матрицей плана
. Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица
Х
T
– это
транспонированная матрица
Х
. Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом
Y
обозначен столбец значений переменной Y.
Чтобы
перемножить матрицы
используйте функцию
МУМНОЖ()
. Чтобы
найти обратную матрицу
используйте функцию
МОБР()
.
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
Записав формулу
=
МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B7:C16);(B7:C16))); МУМНОЖ(ТРАНСП(B7:C16);(D7:D16)))
и введя ее как
формулу массива
в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае
множественной регрессии
.
Построение линии регрессии
Для отображения
линии регрессии
построим сначала
диаграмму рассеяния
, на которой отобразим все точки (см.
начало статьи
).
Для построения прямой линии используйте вычисленные выше оценки параметров модели
a
и
b
(т.е. вычислите
у
по формуле
y
=
a
*
x
+
b
) или функцию
ТЕНДЕНЦИЯ()
.
Формула =
ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23)
возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца
В2
.
Примечание
:
Линию регрессии
можно также построить с помощью функции
ПРЕДСКАЗ()
. Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции
ТЕНДЕНЦИЯ()
работает только в случае одного регрессора. Функция
ТЕНДЕНЦИЯ()
может быть использована и в случае
множественной регрессии
(в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
Как видно из диаграммы выше
линия тренда
и
линия регрессии
не обязательно совпадают: отклонения точек от
линии тренда
случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии
можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента
Линия тренда.
Для этого выделите диаграмму, в меню выберите
вкладку Макет
, в
группе Анализ
нажмите
Линия тренда
, затем
Линейное приближение.
В диалоговом окне установите галочку
Показывать уравнение на диаграмме
(подробнее см. в
статье про МНК
).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами
линией регрессии,
а параметры уравнения
a
и
b
должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание:
Для того, чтобы вычисленные параметры уравнения
a
и
b
совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был
Точечная, а не График
, т.к. тип диаграммы
График
не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; … Именно эти значения и берутся при расчете параметров
линии тренда
. Убедиться в этом можно если построить диаграмму
График
(см.
файл примера
), а значения
Хнач
и
Хшаг
установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с
a
и
b
.
Коэффициент детерминации R
2
Коэффициент детерминации
R
2
показывает насколько полезна построенная нами
линейная регрессионная модель
.
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения
регрессионной модели
). Очевидно, что лучшей оценкой для yi будет
среднее значение
ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание
: Далее будет использована терминология и обозначения
дисперсионного анализа
.
После построения
регрессионной модели
для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя
регрессионную модель
мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
Доказательство:
или в других, общепринятых в зарубежной литературе, обозначениях:
SST
=
SSR
+
SSE
Что означает:
Total Sum of Squares
=
Regression Sum of Squares
+
Error Sum of Squares
Примечание
: SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность
дисперсии
(вариации) и соответственно описывают разброс (изменчивость):
Общую изменчивость
(Total variation),
Изменчивость объясненную моделью
(Explained variation) и
Необъясненную изменчивость
(Unexplained variation).
По определению
коэффициент детерминации
R
2
равен:
R
2
=
Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату
коэффициента корреляции
и в MS EXCEL его можно вычислить с помощью функции
КВПИРСОН()
или
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3)
R
2
принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии
(
Standard Error of a regression
) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение
линейной регрессионной модели
Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со
средним значением
μ и
дисперсией
σ
2
.
Оценив значение
дисперсии
σ
2
и вычислив из нее квадратный корень – получим
Стандартную ошибку регрессии.
Чем точки наблюдений на диаграмме
рассеяния
ближе находятся к прямой линии, тем меньше
Стандартная ошибка.
Примечание
:
Вспомним
, что при построении модели предполагается, что
среднее значение
ошибки ε равно 0, т.е. E[ε]=0.
Оценим
дисперсию σ
2
. Помимо вычисления
Стандартной ошибки регрессии
эта оценка нам потребуется в дальнейшем еще и при построении
доверительных интервалов
для оценки параметров регрессии
a
и
b
.
Для оценки
дисперсии
ошибки ε используем
остатки регрессии
— разности между имеющимися значениями
yi
и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки
дисперсии σ
2
используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε
i
=yi — ŷi (
Sum of Squared Errors
).
SSE часто обозначают и как SSres – сумма квадратов остатков (
Sum
of
Squared
residuals
).
Оценка
дисперсии
s
2
также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов
ошибок
или MSRES (Mean Square of Residuals), т.е. среднее квадратов
остатков
. Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание
: Напомним, что когда
мы использовали МНК
для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на
линии регрессии.
Математическое ожидание
случайной величины MSE равно
дисперсии ошибки
ε, т.е.
σ
2
.
Чтобы понять почему SSE выбрана в качестве основы для оценки
дисперсии
ошибки ε, вспомним, что
σ
2
является также
дисперсией
случайной величины Y (относительно
среднего значения
μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi =
a
* Хi +
b
(значение
уравнения регрессии
при Х= Хi), то логично использовать именно SSE в качестве основы для оценки
дисперсии
σ
2
. Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество
степеней свободы
(
df
–
degrees
of
freedom
), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае
простой линейной регрессии
число степеней свободы
равно n-2, т.к. при построении
линии регрессии
было оценено 2 параметра модели (на это было «потрачено» 2
степени свободы
).
Итак, как сказано было выше, квадратный корень из s
2
имеет специальное название
Стандартная ошибка регрессии
(
Standard Error of a regression
) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см.
этот раздел
). Если ошибки предсказания ε имеют
нормальное распределение
, то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от
линии регрессии
. SEy имеет размерность переменной Y и откладывается по вертикали. Часто на
диаграмме рассеяния
строят
границы предсказания
соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL
стандартную ошибку
SEy можно вычислить непосредственно по формуле:
=
КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)
Примечание
: Подробнее о функции
ЛИНЕЙН()
см.
эту статью
.
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе
Оценка неизвестных параметров линейной модели
мы получили точечные оценки наклона
а
и сдвига
b
. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со
средним значением
и
дисперсией
. Но, чтобы перейти от
точечных оценок
к
интервальным
, необходимо вычислить соответствующие
стандартные ошибки
(т.е.
стандартные отклонения
).
Стандартная ошибка коэффициента регрессии
a
вычисляется на основании
стандартной ошибки регрессии
по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey –
стандартная ошибка регрессии,
т.е. ошибка предсказания значения переменой Y
(
см. выше
).
В MS EXCEL
стандартную ошибку коэффициента регрессии
Se можно вычислить впрямую по вышеуказанной формуле:
=
КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;1)
Формулы приведены в
файле примера на листе Линейный
в разделе
Регрессионная статистика
.
Примечание
: Подробнее о функции
ЛИНЕЙН()
см.
эту статью
.
При построении
двухстороннего доверительного интервала
для
коэффициента регрессии
его границы определяются следующим образом:
где —
квантиль распределения Стьюдента
с n-2 степенями свободы. Величина
а
с «крышкой» является другим обозначением
наклона
а
.
Например для
уровня значимости
альфа=0,05, можно вычислить с помощью формулы
=СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является
t-распределением Стьюдента
с n-2 степенью свободы (то же справедливо и для наклона
b
).
Примечание
: Подробнее о построении
доверительных интервалов
в MS EXCEL можно прочитать в этой статье
Доверительные интервалы в MS EXCEL
.
В результате получим, что найденный
доверительный интервал
с вероятностью 95% (1-0,05) накроет истинное значение
коэффициента регрессии.
Здесь мы считаем, что
коэффициент регрессии
a
имеет
распределение Стьюдента
с n-2
степенями свободы
(n – количество наблюдений, т.е. пар Х и Y).
Примечание
: Подробнее о построении
доверительных интервалов
с использованием t-распределения см. статью про построение
доверительных интервалов
для среднего
.
Стандартная ошибка сдвига
b
вычисляется по следующей формуле:
В MS EXCEL
стандартную ошибку сдвига
Seb можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;2)
При построении
двухстороннего доверительного интервала
для
сдвига
его границы определяются аналогичным образом как для
наклона
:
b
+/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда
коэффициент регрессии
a
равен 0.
Чтобы убедиться, что вычисленная нами оценка
наклона
прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют
проверку гипотез
. В качестве
нулевой гипотезы
Н
0
принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы
Н
1
принимают, что a <>0.
Ниже на рисунках показаны 2 ситуации, когда
нулевую гипотезу
Н
0
не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом
коэффициент линейной корреляции
равен 0.
Ниже — 2 ситуации, когда
нулевая гипотеза
Н
0
отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
-
Установить
уровень значимости
, пусть альфа=0,05;
-
Рассчитать с помощью функции
ЛИНЕЙН()
стандартное отклонение
Se для
коэффициента регрессии
(см.предыдущий раздел
);
-
Рассчитать число степеней свободы: DF=n-2 или по формуле =
ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
-
Вычислить значение тестовой статистики t
0
=a/S
e
, которая имеетраспределение Стьюдента
с
числом степеней свободы
DF=n-2; -
Сравнить значение
тестовой статистики
|t0| с пороговым значением t
альфа
,n-2. Если значение
тестовой статистики
больше порогового значения, то
нулевая гипотеза
отвергается (
наклон
не может быть объяснен лишь случайностью при заданном уровне альфа) либо -
вычислить
p-значение
и сравнить его с
уровнем значимости
.
В
файле примера
приведен пример проверки гипотезы:
Изменяя
наклон
тренда k (ячейка
В8
) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание
: Проверка значимости взаимосвязи эквивалентна
проверке статистической значимости коэффициента корреляции
. В
файле примера
показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью
процедуры F-тест
.
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры
простой линейной регрессионной модели
Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ=
a
* Хi +
b
Ŷ также является точечной оценкой для
среднего значения
Yi при заданном Хi. Но, при построении
доверительных интервалов
используются различные
стандартные ошибки
.
Стандартная ошибка
нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
-
неопределенность связанную со случайностью оценок параметров модели
a
и
b
; - случайность ошибки модели ε.
Учет этих неопределенностей приводит к
стандартной ошибке
S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS
xx
– сумма квадратов отклонений от
среднего
значений переменной Х:
Примечание
: Se –
стандартная ошибка коэффициента регрессии
(
наклона
а
).
В
MS EXCEL 2010
нет функции, которая бы рассчитывала эту
стандартную ошибку
, поэтому ее необходимо рассчитывать по вышеуказанным формулам.
Доверительный интервал
или
Интервал предсказания для нового наблюдения
(Prediction Interval for a New Observation) построим по схеме показанной в разделе
Проверка значимости взаимосвязи переменных
(см.
файл примера лист Интервалы
). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х
ср
), то интервал будет постепенно расширяться при удалении от Х
ср
.
Границы
доверительного интервала
для
нового наблюдения
рассчитываются по формуле:
Аналогичным образом построим
доверительный интервал
для
среднего значения
Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае
доверительный интервал
будет уже, т.к.
средние значения
имеют меньшую изменчивость по сравнению с отдельными наблюдениями (
средние значения,
в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка
S(Yср|Xi) вычисляется по практически аналогичным формулам как и
стандартная ошибка
для нового наблюдения:
Как видно из формул,
стандартная ошибка
S(Yср|Xi) меньше
стандартной ошибки
S(Y|Xi) для индивидуального значения
.
Границы
доверительного интервала
для
среднего значения
рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел
Предположения линейной регрессионной модели
).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках
простой линейной модели
n остатков имеют только n-2 связанных с ними
степеней свободы
. Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
Чтобы проверить предположение о
нормальности распределения
ошибок строят
график проверки на нормальность
(Normal probability Plot).
В
файле примера на листе Адекватность
построен
график проверки на нормальность
. В случае
нормального распределения
значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы
генерировали с помощью тренда
, вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор
о
нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе
Стандартная ошибка регрессии
оценкой
стандартного отклонения ошибок
является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)
Иногда нормирование остатков производится на величину
стандартного отклонения
остатков (это мы увидим в статье об инструменте
Регрессия
, доступного в
надстройке MS EXCEL Пакет анализа
), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Линейная регрессия моделирует взаимосвязь между зависимыми y и независимыми x статистическими переменными данных. Другими словами, они выделяют тенденцию между двумя столбцами таблицы в электронной таблице. Например, если вы создали таблицу электронных таблиц Excel со столбцом месяца x и записали набор данных для каждого из месяцев в соседнем столбце y, линейная регрессия выделяет тренд между переменными x и y, добавляя линии тренда к графам таблиц. , Вот как вы можете добавить линейную регрессию в графики Excel.
Добавление линии тренда линейной регрессии на график
Сначала откройте пустую электронную таблицу Excel, выберите ячейку D3 и введите «Месяц» в качестве заголовка столбца, который будет переменной x. Затем щелкните ячейку E3 и введите «Значение Y» в качестве заголовка столбца переменной y. Это в основном таблица с записанным рядом значений данных за месяцы январь-май. Поэтому введите месяцы в ячейки от D4 до D8 и значения данных для них в ячейки от E4 до E8, как показано на снимке непосредственно ниже.
Теперь вы можете настроить график рассеяния для этой таблицы. Выделите все ячейки в таблице с помощью курсора. Нажмите вкладку Вставка и выберите рассеивать > Скаттер только с маркерами добавить график в электронную таблицу, как показано ниже. Кроме того, вы можете нажать горячую клавишу Alt + F1, чтобы вставить гистограмму. Затем вы должны щелкнуть правой кнопкой мыши по графику и выбрать Изменить тип диаграммы > X Y (разброс) > Скаттер только с маркерами,
Затем выберите одну из точек данных на диаграмме рассеяния и щелкните правой кнопкой мыши, чтобы открыть контекстное меню, которое включает Добавить трендлайн вариант. Выбрать Добавить трендлайн чтобы открыть окно, показанное на снимке прямо ниже. Это окно имеет пять вкладок, которые включают различные параметры форматирования для линий тренда линейной регрессии.
Сначала нажмите Параметры линии тренда и выберите тип регрессии оттуда. Вы можете выбрать экспоненциальный, линейный, логарифмический, Скользящая средняя, Сила а также многочлен Варианты типа регрессии оттуда. Выбрать линейный и нажмите близко чтобы добавить эту линию тренда на график, как показано ниже.
Линия тренда регрессии лайнера на приведенном выше графике подчеркивает, что между переменными x и y существует общая восходящая взаимосвязь, несмотря на несколько падений на графике. Обратите внимание, что линия тренда линейной регрессии не перекрывает ни одну из точек данных на графике, поэтому она не совпадает с графиком средней линии, соединяющим каждую точку.
Форматирование линии тренда линейной регрессии
Чтобы отформатировать линию тренда, щелкните ее правой кнопкой мыши и выберите Формат Trendline, Это снова откроет окно Format Trendline, из которого вы можете нажать Цвет линии, Выбрать Сплошная линия и нажмите цвет поле, чтобы открыть палитру, из которой вы можете выбрать альтернативный цвет для линии тренда.
Чтобы настроить стиль линии, перейдите на вкладку «Стиль линии». Затем вы можете настроить ширину стрелки и настроить параметры стрелки. нажмите Настройки стрелки кнопки для добавления стрелок в линию.
Добавьте эффект свечения на линию тренда, нажав пылать а также Мягкие края, Это откроет вкладку ниже, из которой вы можете добавить свечение, нажав на Пресеты кнопка. Затем выберите вариант свечения, чтобы выбрать эффект. щелчок цвет выбрать альтернативные цвета для эффекта, и вы можете перетащить Размер а также прозрачность бары для дальнейшей настройки свечения линии тренда.
Прогнозирование значений с помощью линейной регрессии
После того, как вы отформатировали линию тренда, вы также можете прогнозировать будущие значения с ней. Например, предположим, вам нужно спрогнозировать значение данных через три месяца после мая за август, которое не включено в нашу таблицу. Затем вы можете щелкнуть «Параметры линии тренда» и ввести «3» в текстовом поле «Вперед». Линия тренда линейной регрессии подчеркивает, что значение августа, вероятно, будет чуть выше 3500, как показано ниже.
Каждая линия тренда линейной регрессии имеет свое собственное уравнение и значение квадрата r, которое можно добавить на график. Нажмите на Показать уравнение на графике установите флажок, чтобы добавить уравнение на график. Это уравнение включает в себя значение наклона и перехвата.
Чтобы добавить значение квадрата r на график, щелкните Отображение значения R-квадрата на графике флажок Это добавляет г квадрат на график чуть ниже уравнения, как на снимке ниже. Вы можете перетащить поле уравнения и корреляции, чтобы изменить его положение на графике рассеяния.
Функции линейной регрессии
Excel также включает функции линейной регрессии, с помощью которых вы можете найти значения наклона, точки пересечения и r квадрата для массивов данных y и x. Выберите ячейку электронной таблицы, чтобы добавить одну из этих функций, а затем нажмите Вставить функцию кнопка. Функции линейной регрессии являются статистическими, поэтому выберите статистическая из выпадающего меню категории. Затем вы можете выбрать RSQ, SLOPE или INTERCEPT чтобы открыть их окна функций, как показано ниже.
Окна RSQ, SLOPE и INTERCEPT практически одинаковы. Они включают в себя поля Known_y и Known_x, которые можно выбрать для добавления значений переменных y и x из вашей таблицы. Обратите внимание, что ячейки должны содержать только цифры, поэтому замените месяцы в таблице соответствующими цифрами, такими как 1 для января, 2 для февраля и т. Д. Затем нажмите Хорошо закрыть окно и добавить функцию в электронную таблицу.
Так что теперь вы можете украсить свои графики электронных таблиц Excel линиями тренда линейной регрессии. Они будут выделять общие тенденции для точек данных графиков, а с помощью уравнений регрессии они также являются удобными инструментами прогнозирования.