|
Nox Пользователь Сообщений: 2 |
Здраствуйте. Не могу ни в какую понять как построить график ctg(x), нужно именно от 0 до 1020 градусов, с шагом 30. Перепробовал абсолютно всё, градусы, радианы, и так и сяк, а в результате график совсем не отвечает привычному виду котангенса. Прошу вас помочь с этим, или показать как нужно. Вот, что обычно выходит: |
|
Илья Демид Пользователь Сообщений: 320 |
#2 21.09.2017 17:16:12 Если что есть формула котангенса, по графику ищу
|
||
|
Я конечно очень извиняюсь
это нормально?) Upd. сори за 2 сообщения Таблица Брадиса Изменено: Илья Демид — 21.09.2017 17:58:51 |
|||
|
Wanschh Пользователь Сообщений: 231 |
При 180 градусах котангенса не существует, т.к. sin(180)=0, cos(180)=-1, ctg(180)=-1/0. И так далее, с периодом 180 градусов. |
|
Nox Пользователь Сообщений: 2 |
#5 21.09.2017 18:36:15 Ребята, очень вам благодарен! Спасибо, теперь буду знать, всё же и сам элементарное из тригонометрии подзабыл. Изменено: Nox — 21.09.2017 18:36:50 |

Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121), и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.
Еще одна функция – ПИ(), не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Конечно, Вы знаете эти функции:
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса).
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса).
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса).
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ.
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
Поделиться, добавить в закладки или статью
В разделе Естественные науки на вопрос Как в MS Excel можно вычислить котангенса угла? заданный автором Особняк лучший ответ это По-моему примерно так:
Угол (ы) в градусах.
Ответ от
22 ответа
Привет! Вот подборка тем с ответами на Ваш вопрос: Как в MS Excel можно вычислить котангенса угла?
Как Брадис высчитывал значения для своей знаменитой таблицы?
метки:
Тригонометрия Чему равен арктангенс (- 1/2) люди…как найти синус, косинус и катангенс, если известен тангенс?
Ответ от Простреливать
Пишешь в ячейке формулу : «=1/TAN(x)», где х-угол в радианах.Самой формулы котангенса в Excel нету
Ответ от шеврон
Например чтобы найти котангенс под углом 30 градусов, используйте следующую формулу:
=1/TAN(30*PI()/180)
Виктор
Как в MS Excel можно вычислить котангенса угла?
8месяцев назад
0 комментариев
Войдите что бы оставлять комментарии
Ответы (3)
Viktor
По-моему примерно так: Угол (ы) в градусах.
ответ написан 8месяцев назад
0 комментариев
Войдите что бы оставлять комментарии
Четвертое Измерение
Пишешь в ячейке формулу : «=1/TAN(x)», где х-угол в радианах. Самой формулы котангенса в Excel нету
ответ написан 8месяцев назад
0 комментариев
Войдите что бы оставлять комментарии
Андрей Балинов
Например чтобы найти котангенс под углом 30 градусов, используйте следующую формулу: =1/TAN(30*PI()/180)
https://support.microsoft.com/ru-ru/kb/213887
ответ написан 8месяцев назад
0 комментариев
Войдите что бы оставлять комментарии
Оставить ответ
Войдите, чтобы написать ответ
Доброго времени суток.Студент.Правила прочитал.Что бы было понятно к какой цели я иду, придётся всё-таки написать задание:
Построить график ctg(x), где x — случайные числа в диапазоне от -5 до 5.
Самую простенькую табличку делал лет 10 назад, поэтому знания по екселю у меня равны 3-м суткам штудирования в интернете.
Попытки решений:
1.=случмежду(-5;5).Делаю опускание за маленький крестик вниз на штук 30 ячеек
2.Второй столбик ввожу функцию =COT или =1/tan от каждой ячейки слева(что делал в 1 столбике)
Получаю каляку, вместо графика котангенса + получаю в некоторых ячейках ошибку с делением на ноль.
…Далее я добавлял столбик с переводом значений x(которые у меня от -5 до 5) в радианы (=РАДИАНЫ) и брал котангенс (1/tan,далее ctg)) уже от столбика с радианами.Итог — те же каляки..
…Давно позабыв геометрию и математику, которые у меня в школе были на натянутую 3-ку, я посмотрел как выглядит гипербола (Преподаватель мне сказал, что должна получится гипербола(и показал какая — 
1 столбик 1 строка 1 ячейка (далее 1ст1стр1ячейка) я поставил -5, а потом -4,6 и свёл за крестик вниз до 0,05 Т.е. я взял понравившийся мне шаг (в данном случае это 0,4) и сделал так, что бы не было деления нуля.Т.е. без функции случайных чисел.Потом перевёл получившиеся значения в радианы и взял от них ctg, вставил график и получилась гипербола.На радостях я приехал на экзамен и..завалил.Не знаю как так вышло, но преподаватель мне сказал, что график я построил совсем не тот и не так.Т.е. должен был получится такой рисунок 
У меня несколько вопросов:
1.Так нужно ли всё-таки переводить в радианы? Кто-то говорит да, кто-то говорит нет..
2.Как избежать деления на ноль в данной задаче? Или если делать всё правильно, то нуля в случ.числах вообще не должно оказаться?
А может быть, просто нужна функция генерации случайных чисел с заданным диапазоном за исключением нуля? И если такая,скажем функция есть, то верно ли будет её применить?
Насколько я теперь понял , построить такой график со случайными числами можно разными путями в екселе, по крайней мере начиная с процесса генерации случайных чисел.
Какую функцию можно применить и какие вообще функции можно использовать? Наткнулся тут на функцию нормального распределения (=нормрасп)…как ей пользоваться я так и не понял (какие значения,например в «среднее» и т.д. указывать)
Преподаватель говорил , что случайные числа нужно как-то преобразовывать, что бы получился график и ф.=случмежду тут не совсем подходит.
Ещё мне подсказали воспользоваться функцией =СЛЧИС()*(b-a)+a. Мне скинули готовое решение, где по моим (от -5 до 5) данным была строка =СЛЧИС()*(10)-5.Подставив их в формулу =СЛЧИС()*(5-(-5))+5 я получаю =СЛЧИС()*(10)+5.Т.е. получаю почему-то не -5 в конце,а +5.(Но опять же вопрос, а почему строка сама не рассчитала и не переделала из =СЛЧИС()*(5-(-5))+5 в =СЛЧИС()*(10)-5.Т.е. почему строка не считает?..(не преобразовывается)
График в итоге по присланным данным ну очень уж слабо похож на тот график который должен получится да и то это только при выборе графика точечный рисунок — точками похоже на график котангенса) а при выборе графика другого(как я всегда и делаю (точечная с гладкими кривыми в разделе диаграммы 200n -го екселя и в разделе график 2013екселя)) — всё-равно каляки.
Если кто-то знает в теории как это делается и какими функциями, то чтобы не тратить Ваше время ответьте пожалуйста хотя бы тегами,например:
=если
=случмежду
радиан
Тогда я буду хотя бы знать, что мне в задании нужен перевод в радианы и воспользоваться функцией если и случмежду.
И ещё ответьте пожалуйста какими функциями ВООБЩЕ можно оперировать в данной задаче?(В случае если она решается разными методами(функциями))
Заранее большое спасибо
Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.
Построение графиков математических функций с одной переменной
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)
Функция выражается в таком виде: у = SIN(x).
Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2).
Чтобы создать эту диаграмму, выполните следующие действия.
- Выделите диапазон
А1:В22. - Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)
Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.
Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂
Построение графиков математических функций с двумя переменными
Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)
На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.
Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными
Значения х находятся в диапазоне А2:А22, а значения у — в диапазоне B1:V1.
Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1).
Чтобы создать диаграмму, выполните приведенные ниже действия.
- Выделите диапазон
A1:V22. - Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)
Тип урока: урок обобщения и
систематизации знаний
Цели:
- научить строить графики тригонометрических
функций средствами MS Excel - закрепить навыки работы в электронных таблицах,
- углубить представления учащихся о взаимосвязи
предметов и прикладной ориентации курса
информатики.
ХОД УРОКА
Если вычислений много, а времени мало,
то доверьтесь электронным таблицам
1. Сообщение целей и задач урока
– Ребята, сегодня мы продолжим знакомиться с
возможностями электронных таблиц Excel. Давайте
вспомним, для чего предназначены электронные
таблицы? (Автоматизация расчетов).
– Что вы уже умеете делать в электронных
таблицах? (Создавать и форматировать таблицу,
работать с типами данных, решать задачи
используя относительную и абсолютную ссылки,
строить диаграммы).
– На уроках математики вы изучили
тригонометрические функции и их графики. При
построении графиков тригонометрических функций
необходимо учесть множество нюансов. Начертить
синусоиду или косинусоиду красиво – это уже
искусство, а если необходимо график растянуть,
сжать или симметрично отобразить относительно
какой-либо оси – это может вызвать затруднения. И
здесь нам на помощь нам придут электронные
таблицы MS Excel. Вы узнаете как с их помощью быстро и
красиво построить график.
Сегодня на уроке мы познакомимся с алгоритмом
построения графика тригонометрической функции.
Эпиграфом к уроку я взяла слова «Если
вычислений много, а времени мало, то доверьтесь
электронным таблицам»
2. Актуализация знаний
Фронтальный опрос (за правильный ответ даем
красную карточку)
- С чего начинается ввод формулы в ячейку? (Со
знака равенства) - На каком языке набирается формула в MS Excel? (Английском)
- Как скопировать формулу в другие ячейки?(С
помощью маркера автозаполнения) - Как изменить число десятичных знаков после
запятой в отображаемом числе? (Выделить,
Формат, Ячейки, вкладка Число, Числовой формат,
…..) - Что означает запись ###### в ячейке? (Длина
водимых данных превышает ширину ячейки) - Каким образом набирается формула, содержащая
какую-либо функцию? (Выделить ячейку, в которую
нужно вставить первое значение функции;Вставка,
Функция, выбрать Категорию и саму функцию) - Каким образом набирается формула, содержащая
сложную функцию, например, y = |x2|? (Вставляется
внешняя функция с пустым аргументом, затем левее
строки редактирования формул из раскрывающегося
списка выбирается внутренняя функция) - Как вставить какой-либо символ, например,
математический в ячейку? (Вставка, Символ, в
появившемся диалоговом окне выбрать шрифт Symbol и
нужный символ)
На прошлом уроке вы строили графики
элементарных функций. Давайте повторим алгоритм
построения графика (Учащиеся называют шаги
построения графика функции, а учитель показывает
соответствующий пункт алгоритма на доске
(используется проектор) и если необходимо
дополняет ответ учеников) (см. Приложение
1).
3. Изучение нового
С использованием презентации (см. Приложение
2) учитель рассказывает, как строится
график тригонометрической функций, а затем
выполняет его построение в электронных таблицах.
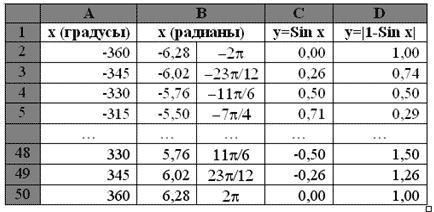
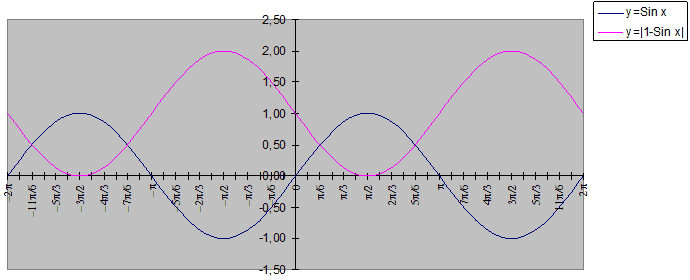
Задание. Построить в MS Excel графики
функций y = Sin x и y = |1 – sin x| на
промежутке [–360о; 360о] с шагом 15о.
Построенные графики смотри в Приложении
3
4. Закрепление полученных знаний
Каждому ученику даётся карточка с заданием и
оценочный лист, который после выполнения задания
отдается учителю (Каждый пункт в оценочном
листе является шагом построения графика
тригонометрической функции с использованием
MSExcel). Презентация находится в
сетевой папке, и любой ученик может ею
воспользоваться при выполнении своего задания.
Задание. Построить в MS Excel графики
функций на промежутке [–36о;36о] с
шагом 15о.
5. Проверка построенных графиков и разбор
нюансов
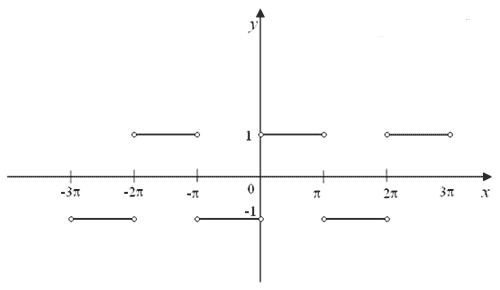
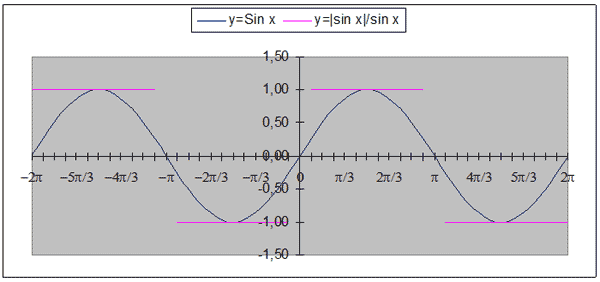
Один из учеников строил график y = |Sin x|
/ Sin x на промежутке [–360о;360о] с
шагом 15о. На доске демонстрируется этот
график и график, построенный традиционным
алгебраическим способом.
С помощью этого примера обращается внимание
учащихся, что существуют функции, графики
которых в электронных таблицах строятся неточно.
Учащихся можно попросить найти неточности в
графике, построенном с помощью MS Excel и попросить
объяснить их.
График, построенный традиционным
алгебраическим
График, построенный с использованием МS
Exel
6. Подведение итогов
Учеников просят ответить на вопросы:
- В чем достоинства и недостатки алгебраического
метода построения графиков функций и построения
графиков с использованием электронных таблиц? - Каким образом можно использовать полученные на
уроке знания в учебе?
Вывод. MS Excel облегчает построение
графиков функций, но без глубоких математических
знаний построить точные графики сложных функций
(тригонометрических функций, функций с модулем,
функций имеющих точки разрыва) невозможно.
Математика – это царица всех наук!
7. Постановка Д/З.
Построить график функции y= 1 + 0,5*ctg(X–П/4) на
промежутке [–360о;360о] с шагом 15о.
8. Рефлексия
Оцени свое настроение на уроке
Оценочный лист
|
Фамилия, имя |
Количество баллов |
| Создание заголовка таблицы |
0,2 |
| Заполнение ряда значений аргумента х в градусах |
0,1 |
| Заполнение ряда значений аргумента х в радианах (перевод градусов в радианы) |
0,5 |
| Запись формулы для вычисления значений сложной функции |
1 |
| Запись формулы для вычисления значений элементарной функции |
0,5 |
| Заполнение рядов значений функций (для обеих функций) |
0,1 |
| Установка числового формата данных |
0,2 |
| Построение графиков функций |
1 |
| Перенос оси |
0,2 |
| Подпись значений х на оси абсцисс (в градусах) |
0,2 |
| Создание ряда значений аргумента х (в радианах, например П/3) |
0,7 |
| Подпись значений х на оси абсцисс (в радианах, например П/3) |
0,5 |
|
ИТОГО |
5 |
| Если вы обращаетесь к учителю, то ставится 0 баллов |