Муниципальное автономное общеобразовательное учреждение
«Средняя общеобразовательная школа №1» г. Боровичи
Проект
«Моделирование гармонических колебаний в среде табличного процессора Microsoft Excel»
|
Подготовила: Ученица 11 «А» класса Январева Мария Руководитель: Васильева Надежда Владимировна 2021г. г. Боровичи |
|
|
Содержание Введение 1. Теоретическая часть 1.1 Гармонические колебания: понятие, основные параметры 1.2 Уравнение гармонического колебания 1.3 Табличный процессор MS Excel: понятие, основные инструменты 2. Практическая часть 2.1 Заполнение исходных параметров колебаний в таблице 2.2 Создание полосы прокрутки в MS Excel 2.3 Создание графика в MS Excel Заключение Список Литературы |
Введение
В школьной программе по предмету «физика» изучаются гармонические колебания. Однако в действительности осуществить эксперименты, в которых можно наблюдать и изучать колебательный процесс и его характеристики сложно. Microsoft Excel является отличным средством для моделирования различных динамических процессов. В этой работе с помощью функций MS Excel можно исследовать влияние параметров колебательного процесса на график колебаний.
Цель: смоделировать гармонические колебания с помощью табличного процессора Microsoft Excel.
Гипотеза: если изучить инструментарий табличного процессора Microsoft Excel, то с его помощью можно моделировать физические процессы.
Предмет: программа Microsoft Excel, как среда моделирования гармонических процессов.
Объект: График гармонических колебаний.
Задачи:
1) Изучить теоретический материал по теме Гармонические колебания.
2) Изучить теоретический материал о табличном процессоре Microsoft Excel.
3)Практически смоделировать Гармонические колебания в табличном процессоре Microsoft Excel.
1. Теоретическая часть
1.1 Гармонические колебания: понятие, основные параметры
Колебательное движение — это движение, точно или приблизительно повторяющееся через одинаковые промежутки времени, при котором тело многократно и в разных направлениях проходит положение равновесия.
Гармонические колебания – колебания, при которых физическая величина изменяется с течением времени по гармоническому закону.
Рис 1. График синусоиды
1.2 Уравнение гармонического колебания
x = a*sin*(ω*t+φ0)
- x – смещение тела
- a – амплитуда колебаний
- ω – циклическая частота колебаний
- t – время
- φ0 – начальная фаза колебаний
Период колебаний (T) – это минимальный промежуток времени, через который происходит повторение движения тела.
Τ= t / n
Начальная фаза колебания (φ0) — это фаза колебаний в начальный момент времени.
Циклическая (круговая) частота (ω) — это число колебаний тела за 2π с.
ω0 = 2π/T = 2πν
Амплитуда колебаний (a) — максимальное смещение от положения равновесия.
Это уравнение дает зависимость «x» от времени «t».
1.3 Табличный процессор MS Excel: понятие, основные инструменты
Microsoft Excel – это универсальная программа для работы с электронными таблицами, которая позволяет хранить, организовывать и анализировать информацию. В ней можно вести домашний бюджет, производить простые или сложные расчеты, организовывать дневники, составлять отчеты, строить графики, диаграммы и многое другое.
Основные инструменты MS Excel: рабочее поле, ячейка, диапазон ячеек, символьные и строковые величины, логические величины, формулы.
Рабочее поле – это экран дисплея, на котором электронная таблица предоставляется в виде прямоугольника, разделенного на строки и столбцы.
Ячейка – минимальный элемент электронной таблицы, над которым можно выполнять те или иные операции. Каждая ячейка имеет уникальное имя. Например: B2, C17, G150 и т.д.
Диапазон ячеек – его можно выделить из подряд идущих ячеек в строке, столбце или прямоугольнике. При задании диапазона указывают его начальную и конечную ячейки. Примеры диапазонов – A1:A100, B15:AZ12.
Для моделирования гармонических колебаний можно использовать:
1)Формулы
2)Полосы прокрутки
3)График
2. Практическая часть
2.1 Заполнение исходных параметров колебаний в таблице
Ячейки электронной таблицы заполнены следующим образом: в ячейке B6 — значение амплитуды (a); B8 – значение круговой частоты (ω); B10 – значение фазы колебаний (α). Каждая из этих ячеек имеет формулу: B6 (=C6/10); B8 (=C8); B10 (=C10/100). (Заменим «φ0» на «α»).
В столбце G вычисляются значения времени, возрастающие на 0,02, для этого в G4 введена формула (=G3+0,02).
В столбце H вычисляются значения X по формуле (=$B$6*SIN($B$8*G…+$B$10)) , где G меняется в зависимости от выбранной ячейки (заполняем с H3 вниз аналогичным способом). Для наглядности в ячейках G и H значения времени и координаты продолжены до 160 строчки.
В режиме отображения формул таблица выглядит следующим образом:
Рис.2. Режим отображения формул
В режиме отображения значений:
Рис.3. Режим отображения значений
2.2 Создание полосы прокрутки в MS Excel
С целью исследования влияния параметров гармонических колебаний на график колебательного процесса используем такую возможность как полосы прокрутки. Для каждой полосы прокрутки установлены максимальное и минимальное значение. Каждая полоса прокрутки привязана к соответствующей ячейке. Поправка положения ползунка на полосе прокрутки приводит к изменению значения в ячейке. Таким образом, изменяя значения амплитуды, круговой частоты и начальной фазы колебаний, можно наблюдать изменение графика.
- Через меню Разработчик (Вставить/Элементы ActiveX) выбираем элемент «Полоса прокрутки».
- Выбрав нужные ячейки, нужно вставить туда полосу прокрутки (меняем размер).
- После вставки Полосы прокрутки она становится выделенной. Если нажать на любое другое место листа, то Полоса прокрутки перестанет быть выделенной.
- Нажимаем на Полосу прокрутки правой кнопкой мыши и выбираем «Свойства».
- В свойствах меняем значения «Max» и «Min» на те, которые необходимы (на 10 и 0, соответственно).
- Чтобы привязать полосу прокрутки в строке «LinkedCell» выбираем ячейку, где будут находиться значения колебания.
- Также можно изменить цвет полосы, для этого нужно найти строчки «BackColor» и «ForeColor». «BackColor» меняет фон полосы, а «ForeColor» цвет стрелок и ползунка.
- Полоса прокрутки готова.
Полосы прокрутки находятся в ячейках D6E6, D8E8, D10E10 и привязаны к ячейкам C6, C8, C10. Полосы прокрутки меняют значения в этих ячейках от 0 до 10, так как установлено максимальное и минимальное значение.
2.3 Создание графика в MS Excel
- Выделяем таблицу от G3 и H3 до G160 и H160, и переходим во вкладку «Вставка». Нажимаем на кнопку «График» и выбираем самый простой из них (находится на первом месте).
- Программа произвела построения графика, но как видим, появилось две линии, нужно удалить одну из них (удалим линию «t»).
- Легенда тоже не нужна, так как на графике всего одна линия. Поэтому нужно удалить легенду.
- Теперь нужно значения в горизонтальной панели координат заменить на те, которые соответствуют столбцу «t» в таблице.
- Нажимаем правой кнопки мыши на график. В меню перемещаемся по значению «Выбрать данные…».
- В активировавшемся окне выбора источника нажать на правую кнопку «Изменить».
- Запускается окошко «Подписи оси». В области «Диапазон подписей оси» указываем координаты массива с данными столбца «t». Ставим курсор в полость поля, а затем, произведя необходимый зажим левой кнопки мыши, выделяем все значения соответствующего столбца таблицы, исключая лишь его наименование. Как только координаты отобразятся в поле, клацаем по наименованию «OK».
- В окне выбора источника данных нажимаем на «ОК».
- Далее выбираем «Режим Конструктора» и нажимаем на график левой кнопкой мыши. Находим и нажимаем на «Макет», переходим во вкладку «Оси». В самом низу находится «Дополнительные параметры основной горизонтальной оси…». Меняем параметры горизонтальной оси. Аналогично делаем и с вертикальной осью.
- После этого программа произведет редактирование ранее построенного графика согласно тем изменениям, которые были произведены в настройках.
Рис. 4. График колебательного процесса.
Заключение
Таким образом, данный график может применяться на уроках физики, что позволит ученикам явно проследить изменение графика колебаний при изменении различных параметров. А ученикам, увлекающимся информатикой, эта работа поможет для моделирования гармонических колебаний, поможет еще больше узнать о возможностях табличного процессора MS Excel.
Список литературы
- Мякишев Г.Я. Учебник Физики 11 класса. Гармонические колебания. Просвещение, 2010. – 399с.
2. Фаза колебаний. https://www.calc.ru/Faza-Kolebaniy.html
3. Гарнаев А.Ю. Самоучитель VBA. СПб: БХВ, Санкт Петербург, 1999.
4. Веденеева Е.А. Функции и формулы Excel 2007. Библиотека пользователя. – Санкт Петербург, 2008. –384с.
5. Полосы прокрутки. https://excel2.ru/articles/polosa-prokrutki-element-upravleniya-formy-v-ms-excel
6. График. https://exceltable.com/grafiki/grafiki-i-diagrammi-v-excel
Практическая работа Гармонические колебания.
«Построение графика функции в Excel»
-
Построить таблицу:
а) в первой строке необходимо задать аргумент функции от xn до xk с шагом h, используя автозаполнение (т.е. задаём интервал функции [-10;10] с шагом 0,5).
б) Во вторую строку вводим выражение (например: f(x)=sin x), точно также используя автозаполнение копируем его.
2. Выделить диапазон из двух строк.
3. Вкладка Вставка – панель Диаграммы – инструмент Точечная с гладкими кривыми.
Рисунок 1. Примерный график функции cos x в диапазоне [-10;10].

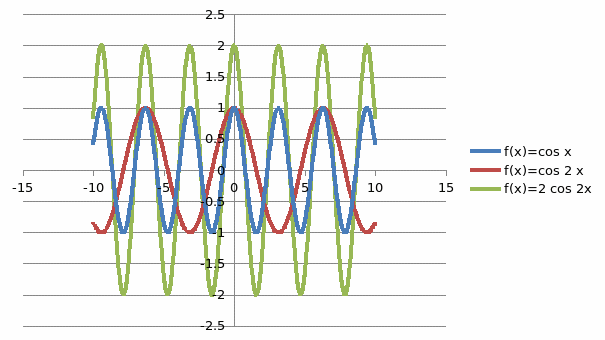
Построить диаграммы для функций:
-
f(x) = cos x;
-
f(x) = cos 2 x;
-
f(x) = 2 cos 2 x;
-
f(x) = sin x;
-
f(x) = sin 2 x;
-
f(x) = 2 sin 2 x.
Сравнить полученные графики.
Рисунок 2. Сравнение функций cos x; cos 2 x; 2 cos 2 x;
1. Моделирование гармонических колебаний в среде табличного процессора MS Excel
Работа ученицы 10 класса
МОУ СОШ пос. Мизур
Цогоевой Ирины
2. Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются
ГАРМОНИЧЕСКИМИ
КОЛЕБАНИЯМИ
x
xm
0
xm
π/2
π
3π/2
T/4
T/2
3T/4
2π
T
φ
t
3. Уравнение гармонического колебания
x = xm cos(ω0 t + φ0)
x – смещение тела
t – время
xm – амплитуда колебаний
φ0- начальная фаза колебаний
ω – циклическая частота колебаний
4. Период колебаний
X
xm
t
T
Минимальный промежуток времени, через который
происходит повторение движения тела, называется
периодом колебаний T.
= t / n
5. Амплитуда колебания
X
xm
t
xm – амплитуда колебаний, т. е. максимальное
смещение от положения равновесия
6. Частота колебаний
X
1
Т
xm
T
Физическая величина, обратная периоду колебаний,
называется частотой колебаний. Частота колебаний
показывает, сколько колебаний совершается за 1 с.
Единица частоты – герц (Гц).
7. Циклическая частота колебаний
Циклическая или круговая частота — это число
колебаний тела за 2π с.
ω0 = 2π/T = 2π
8. Исследование влияния параметров гармонических колебаний на график колебательного процесса
9. Сложение колебаний
a1
a
a2
α
0
x1
a2
α1
x2
x
x1 = а1 cos (ω1t + α)
cos (ωt + α)
x2 = a2 cos (ω2t +α)
а² = а1² + а2² + 2 а1а2 cos (α2 – α1)
X
x=a
10. Сложение колебаний в MS Excel
11. Биения
12. Информатика, физика, математика – это не скучно!
Библиографическое описание:
Бурлакова, И. О. Методика работы с динамическими графиками гармонических колебаний при показе / И. О. Бурлакова, Е. Д. Петровская. — Текст : непосредственный // Молодой ученый. — 2019. — № 51 (289). — С. 328-332. — URL: https://moluch.ru/archive/289/65650/ (дата обращения: 15.04.2023).
Статья посвящена методике работы с динамическими графиками гармонических колебаний при показе. В статье подробно описан способ работы с данным графиком.
Ключевые слова: график, «Microsoft Excel» 2010, полоса прокрутки, динамический график, гармонические колебания.
Графическое представление информации всё шире и шире используется в современном мире, поэтому умения извлекать сведения из графиков, диаграмм и таблиц необходимы как будущему учителю, так и вообще образованному человеку. Обычные статические графики, конечно, прививают некоторые необходимые навыки, но динамические позволяют делать это более наглядно и полно. [1, с.122]
В школьном курсе «Физика 9 класс» при изучении раздела «Механика» рассматриваются такие виды графиков как синусоида, прямая и др. При работе с графиками учителя могут сталкиваться с проблемой понимания учащимися влияния параметров периода и амплитуды на общий вид графика гармонических колебаний или научить учащихся извлекать из него необходимые данные. [2, с.98]
Для более быстрого понимания учениками графика и облегчения работы учителя можно использовать динамические графики. Прежде чем начать работать с графиком, стоит познакомиться с указаниями к работе с динамическими графиками, приведёнными ниже.
- При работе с файлом нельзя удалять и изменять столбцы и строки, т. к. в них содержатся данные, при исчезновении которых график не будет выполнять своей функции.
- Если необходимо, чтобы столбцы с данными не отображались, следует воспользоваться командой «Масштаб», которая находится в правом нижнем углу, нажимая на «+» происходит увеличение, при нажатии на «-» уменьшение листа, кроме этого, можно сдвинуть лист, воспользовавшись полосами прокрутки окна Excel.
- Также у каждой программы, в которой вы можете открыть данные графики, будь то Microsoft Exсel 3 или 10, существует своя специфика работ с полосой прокрутки.
В Microsoft Exсel 10 для изменения графика можно, например, использовать кнопки, которые находятся на концах полосы прокрутки, при щелчке на кнопку происходят изменения счётчика на 1 шаг. Также менять данные можно, перемещая бегунок, в этом случае график будет меняться только после того, как будет отпущена левая кнопка мыши.
При закрытии файла после работы ни в коем случае не следует сохранять изменения, даже если программа предлагает это сделать, так как может произойти сохранение разного рода ощибок.
Проверка алгоритма работы полосы прокрутки должна быть произведена до начала работы с графиком, так как в зависимости от используемой версии Microsoft Exсel алгоритм работы может быть разным.
На рисунке 1 представлен график гармонических колебаний.
График построен по функции
y=A*sin (ωt+0)
Параметры функции можно изменять при помощи трёх полос прокрутки
Амплитуду (А) от 0 до 50 см.
Период колебаний (Т) от 1 до 50 с.
Начальную фазу (0) от (–π/2) до (+π/2)
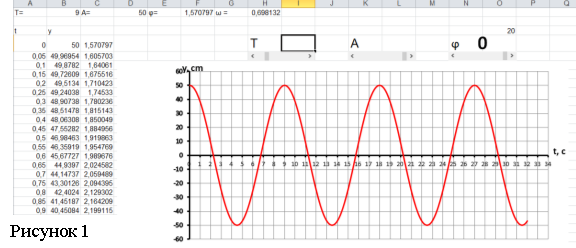
Эти возможности позволяют продемонстрировать практически все особенности гармонических колебаний.
График гармонических колебаний представляет собой зависимость смещения от времени (). Нами построен график гармонических колебаний с полосами прокрутки, с помощью которых можно изменять амплитуду, период и начальную фазу колебаний.
При изменении параметра амплитуды (А) от 0 до 50 см график будет вытягиваться или сжиматься вдоль оси y. Рассмотрим несколько примеров, где период колебаний (Т=6с) и начальная фаза (0 =1,57…) остаются неизменными, а параметр А будем менять при помощи полосы прокрутки. При демонстрации учителю стоит обратить внимание учащихся на изменение графика функции. Это можно сделать с помощью линии на графике или указки.
На рисунках 2а и 2б представлены графики, где амплитуда А= 50 см и А= 20см. Обращаем внимание учеников на то, как изменился график. Так как амплитуда — это максимальное отклонение от состояния равновесия на графике, она отображается как максимальное значение по оси y. Показываем, как изменилось значение амплитуды.
С помощью программы можно показать, как изменяется график функции при изменении периода колебаний (Т).
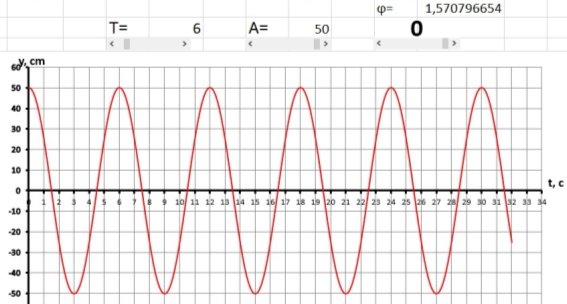
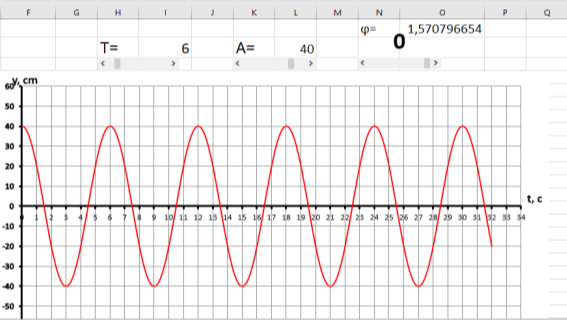
При изменении параметра период колебаний (Т) от 1 до 50 см график будет растягиваться или сжиматься вдоль оси t. Рассмотрим несколько примеров, где амплитуда (А=40см) и начальная фаза (0 =1,57…) остаются неизменными, а параметр Т меняется при помощи полосы прокрутки.
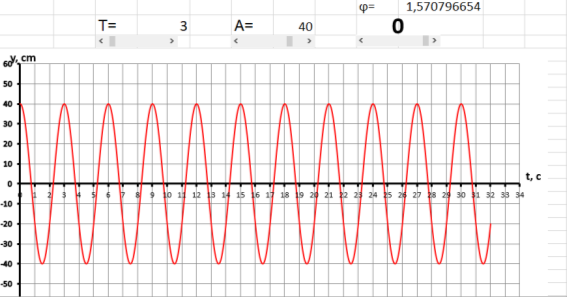
Обращаем внимание учеников на то, как изменился график. Так как период колебаний — это промежуток времени, в течение которого тело совершает одно полное колебание на графике, это можно отобразить как количество делений по оси t от одной вершины до другой. Показываем, как значение периода колебаний изменяется при Т=6см и Т=3 с. На рисунках 3а и 3б представлены графики того, как они должны выглядеть.
При помощи указки показываем момент времени, когда тело максимально отклонено. Первое максимальное отклонение t=0c, находим следующую точку, где тело максимально отклонено, это t=6c.
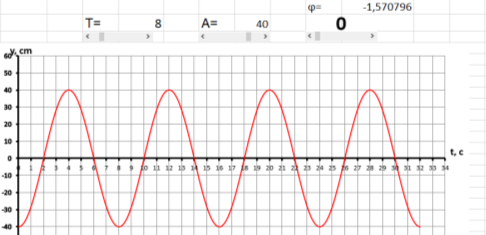
При изменении параметра начальной фазы (0) от (–π/2) до (+π/2) график будет смещаться вдоль оси t. Рассмотрим несколько примеров, где период колебаний (Т=3с) и амплитуда (А=40см) остаются неизменными, параметр начальной фазы (0) при этом будем менять с помощью полосы прокрутки. Учителю стоит обратить внимание учащихся на изменение графика функции. Это можно сделать с помощью указки.
На рисунках 4а, 4б и 4в представлены графики, где начальная фаза 0= –π/2, 0= +π/2 и 0= 0. Обращаем внимание учеников на то, как изменился график. Так как начальная фаза — это значение фазы колебаний в начальный момент t=0 с. Показываем, как меняются значения при 0= –π/2, 0= +π/2 и 0= 0.
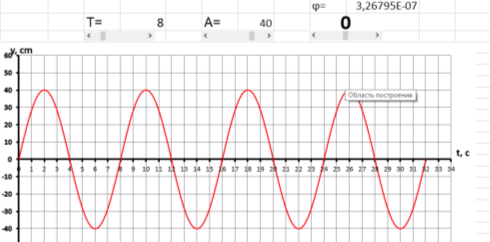
При сравнении графиков видно, что при отрицательной начальной фазе график сдвигается вправо, при положительной – влево.
При изучении гармонических колебаний, можно при помощи предлагаемой программы демонстрировать влияние амплитуды (А), периода колебаний (Т) и начальной фазу (0) на вид графика. Это поможет учащимся лучше понимать, что должно произойти при изменении того или иного параметра функции.
Литература:
- Бурлакова И. О. Правила построения графиков в пакете «Microsoft Excel» 2010/ Перспективные научные исследования: опыт, проблемы и перспективы развития. Сборник статей по материалам международной научно-практической конференции Ч-2. 2019
- Пёрышкин А. В. Физика 9 класс — М.: Дрофа, 2003. — 256 с.
Основные термины (генерируются автоматически): график, начальная фаза, период колебаний, полоса прокрутки, внимание учеников, колебание, помощь полосы прокрутки, внимание учащихся, изменение графика функции, максимальное отклонение.
Обновлено: 14.04.2023
Цель работы: знакомство с понятиями «гармонические и негармонические периодические функции» и графическим представлением звуковых колебаний; освоение построения графиков функций в электронных таблицах; получение графической иллюстрации процесса аналого-цифрового преобразования звука.
Работа носит исследовательский характер и выполняется в самостоятельном режиме.
Математическая справка. График функции Y(x) — это наглядное (графическое) отображение зависимости значения функции Y от значения аргумента x. График строится в пределах области определения функции (области изменения аргумента х) и области значений Y. Если у функции бесконечная область определения, то для построения графика выбирается тот ее отрезок, в пределах которого поведение функции наиболее характерно. График периодической функции как минимум должен отражать один период изменения значений функции.
Эксперимент 1. Моделирование гармонических колебаний
Рассмотрим метод построения графика периодической функции, описывающей гармонические колебания.
Гармоническими колебаниями называются периодические изменения со временем некоторой физической величины, описываемые функциями синуса или косинуса. Общая запись такой функции:
Человек слышит звуковые колебания, в среднем в диапазоне частот от 20 Гц до 20 кГц. Частоте 10 Гц соответствует инфразвук. Некоторые животные способны воспринимать его на слух. Если удвоить эту частоту, то будет достигнута нижняя частотная граница слышимости звука человеком. Тогда на временном интервале 0,1с. поместится два периода колебаний.
Такой эксперимент легко выполнить на уже построенной электронной таблице. Измените значение частоты в ячейке C1 на 20, после чего таблица будет автоматически пересчитана, а график примет вид, представленный на рисунке.
На интервале времени 0,1 c здесь, как и предполагалось, укладывается два периода функции. Следовательно, период колебаний равен 0,05 с.
Электронные таблицы
Задание 1 (уровень 1). Проведите несколько экспериментов с электронной таблицей для следующих значений частоты: 5 Гц, 15 Гц, 30 Гц, 40 Гц. В каждом случае определите, сколько периодов колебаний укладывается на интервале 0,1 с.
Эксперимент 2. Моделирование негармонических колебаний
В разделе математики, который называется гармоническим анализом , доказано, что любую периодическую функцию Y(t) с частотой v можно представить в виде суммы гармонических (синусоидальных) функций с частотами v, 2v, 3v, 4v . . Такие слагаемые называют гармониками , а представление функции в виде суммы гармоник называют ее гармоническим разложением :
Начальные фазы здесь равны нулю. Выполним расчеты для следующих значений параметров: v = 20 Гц, А1 = А2 = 1. Как было сделано ранее, вычисления мы будем производить на отрезке времени от 0 до 0,1 с, а шаг табулирования выберем равным 0,005.
Для получения нужной таблицы значений достаточно заменить содержимое ячейки В5 на следующую формулу:
а затем скопировать эту формулу вниз по столбцу В.
Получаемый график представлен на рисунке ниже. Из него видно, что период колебаний равен 0,05 с, т. е. периоду первой гармоники. Максимальная амплитуда колебаний увеличилась и стала равна приблизительно 1,54.
Электронные таблицы
Эксперимент 3. Моделирование аналого-цифрового преобразования
В этом эксперименте моделируется процесс аналого-цифрового преобразования (АЦП). Он включает в себя дискретизацию сигнала по времени и квантование значений амплитуды сигнала.
Дискретизация по времени определяется значением частоты дискретизации Н (Гц). Шаг по времени между двумя измерениями равен 1/ Н с.
Процесс квантования амплитуды определяется параметром глубины квантования звука b : количество уровней квантования равно 2 b . Коды, определяющие амплитуду звукового сигнала, — это целые числа в диапазоне от 0 до 2 b .
Модель процесса квантования звукового сигнала, реализованная в среде электронных таблиц, представлена на рисунке ниже.
Рассматривается гармонический сигнал с частотой v = 20 Гц (ячейка C1). Частота дискретизации АЦП Н = 200 Гц (ячейка C2).
Глубина квантования b = 8 бит (ячейка G2).
Столбец А содержит значения моментов времени измерений сигнала при реализации АЦП. В ячейке А5 записан начальный момент времени t = 0, далее время увеличивается с шагом 1/ Н с.
В ячейке А6 записана формула =A5+1/$C$2, которая далее скопирована вниз по столбцу А.
Значение амплитуды аналогового сигнала вычисляется по формуле:
Такое преобразование синусоиды переносит ее в область положительных значений Y в интервале от 0 до 1 (это сделано для упрощения описания дальнейшего процесса квантования). Соответственно, в ячейку В5 записана формула =(1+SIN(2*ПИ()*$C$1*A5))/2, которая затем скопирована вниз по столбцу В.
В столбце С получены коды измерений амплитуды сигнала, представленные целыми десятичными числами (при записи в память компьютера в ходе реального алфавитно-цифрового преобразования они переводятся в двоичную систему счисления).
В ячейку С5 помещена формула =ЦЕЛОЕ(B5*2^$G$2). Ее смысл следующий: поскольку Y лежит в диапазоне от 0 до 1, значение выражения [Y * 2 b ] будет равно целым числам в диапазоне от 0 до 2 b (квадратные скобки обозначают выделение целой части числа).
При построении диаграммы «Квантование сигнала» следует выбирать тип Гистограмма, дискретный вид которой наглядно отражает дискретный характер кода. Таблица построена в расчете на 21 измерение сигнала; при заданных значениях v и Н удалось
«оцифровать» два периода колебаний сигнала.
При изменениях трех параметров модели: v, Н и b производится автоматический пересчет таблицы. Например, если увеличить частоту дискретизации в два раза, т. е. занести в ячейку С2 число 400, то мы получим графики, представленные на рисунках ниже.
Здесь измерения произведены на одном периоде колебаний, зато дискретный код более подробно описывает колебательный процесс.
Гистограмма квантования на рисунке ниже получена для значения b = 16. На этом рисунке видно, что диапазон значений кода увеличился, следовательно, такое кодирование дает более точную информацию о величине сигнала, чем при b = 8.
Электронные таблицы
Задание 5 (уровень 1). Проведите расчеты при значениях параметров: v = 20 Гц , Н = 100 Гц, b = 8 бит. Сопоставьте полученные результаты с этими:
Задание 6 (уровень 2). Проведите численные эксперименты по кодированию негармонических колебаний. Функции, описывающие негармонические колебания, возьмите из заданий к эксперименту № 2.
Программирование на Паскале
Задание 7 (уровень 3). Составьте программу на Паскале, моделирующую процесс кодирования аналогового сигнала (без рисования графиков). Программа должна воспроизводить таблицы, которые были получены выше в среде табличного процессора.
Используемая литература:
Информатика. Углубленный уровень: практикум для 10-11 классов : в 2 ч. Ч. 1 / И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова. — М.: БИНОМ. Лаборатория знаний, 2013. — 168 с. : ил.
Тема данной исследовательской работы: Моделирование фигур Лиссажу.
Настоящее исследование посвящено актуальной проблеме изучения фигур Лиссажу в курсах физики и математики.
Фигуры Лиссажу используют для сравнения гармонических колебаний, которые изучаются в курсе физики. Но в реальности провести опыты, в которых можно наблюдать и изучать колебательный процесс и его характеристики сложно. В ходе математического и компьютерного моделирования фигур Лиссажу можно исследовать соотношение между частотами и фазами гармонических колебаний.
Цель работы: показать возможности применения математических функций среды MS Excel для моделирования некоторых физических явлений.
Достижение поставленной цели предполагает решение следующих задач:
1.Проанализировать литературу по теме исследования.
2.Раскрыть понятие фигуры Лиссажу.
3.Рассмотреть способы построения графиков в среде MS Excel.
4.Разработать модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.
Объектом исследования являются Фигуры Лиссажу. Предмет исследования: наглядное построение фигур Лиссажу. Методы исследования: для решения поставленных задач в работе используется теоретические и эмпирические методы.
1.1. Гармонические колебания
Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
Гармоническое колебание, как математическая модель участвует в множестве физических процессов, которые можно использовать для передачи информации. Многие системы совершают движение по гармоническому закону вполне естественным образом. В пример можно привести обычное раскачивание на качелях, ритмичные движения ног продолжали незатухающие колебания механического маятника, которым и являются качели.
Способы представления гармонических колебаний:[1;82-84]
2. Графическое представление (построение): Этот способ наглядно может показать вид и свойства данного явления.
- Гармоническое колебание изменяется во времени периодически. Период каждого совершённого колебания равен .
- Амплитуда (наибольшее значение) равна . Скорость изменения колебания во времени определяется круговой частотой , которая численно равна скорости изменения аргумента косинуса и измеряется в рад/с. — начальная фаза колебательного процесса. При совершении единичного гармонического колебания фаза особой роли не играет, а когда совершается несколько подобных колебаний, то даёт понять о местонахождении колебаний на оси времени друг относительно друга. Если >0, то второе колебание сдвинуто влево, т.е. опережает первое, а если <0, то ситуация обратная.
3. Векторное представление (делает очень наглядным фазовые и амплитудные соотношения между ними):
Эта формула выводится, если известна начальная фаза и амплитуда, т.е. значения при
Возьмём за гипотенузу прямоугольного треугольника, тогда будет в качестве его катета. Можно сказать, что сейчас гармоническому колебанию дали геометрическое представление. Такое представление гармонического колебания называют векторной диаграммой.
1.2 Фигуры Лиссажу
Фигуры Лиссажу — траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Эти фигуры, впервые изученные французским учёным Жюлем Антуаном Лиссажу.
Устройство для построения фигур Лиссажу — осциллограф. Изобретение относится к радиоизмерительной технике и может быть использовано для исследования параметров электрических сигналов.
Известные способы регистрации фигур Лиссажу с помощью двух координатных регистрирующих устройств позволяют производить измерения в ограниченном диапазоне частот и при отсутствии помех. Целью изобретения является создание способа регистрации фигур Лиссажу в широком диапазоне частот и при наличии помех.
Эти фигуры используют для осциллографического метода сравнения частот.
Осциллографический метод сравнениячастот:[2;97-98]
В качестве устройства сравнения частот используется осциллограф с отключённой разверткой (Развертка— это линия, которую чертит луч на экране при отсутствии исследуемого сигнала в результате действия только одного развертывающего напряжения.), таким образом информацию получают с экрана осциллографа по изображению интерференционных фигур (фигур Лиссажу).
Измеряемый сигнал подают на вход КВО (канал вертикального отклонения), а сигнал образцового генератора известной частоты — на вход КГО (канал горизонтального отклонения). Плавным изменением частоты добиваются устойчивого изображения на экране осциллографа фигур Лиссажу. В этом методе отношение частот сравниваемых сигналов определяют путём подсчета числа пересечений фигуры Лиссажу с вертикальной осью и горизонтальной осью на экране осциллографа.
Из этой формулы можно вывести измеряемую частоту,
Закон гармонического осциллятора: [3;19]
Если закон дифференцировать по времени, то найдём закон изменения скорости при гармонических колебаниях:
Так же если повторить предыдущее действие, то найдём изменения ускорения при гармонических колебаниях:
После двух дифференцирований мы получим исходное выражение:
Перенеся слагаемые в одну сторону, то получим уравнение гармонического осциллографа:
Это уравнение встречается во всех разделах физики без исключения. Это уравнение описывает эволюцию малых отклонений динамических переменных от их устойчивых значений. Но для математика это обыкновенное уравнение 2-ого порядка с постоянными коэффициентами, в это уравнение входит функция со второй производной. Решением данного уравнения являются гармонические колебания.
1.2. Анализ среды MS Excel
Microsoft Office Excel – это программа, предназначенная для работы с электронными таблицами, которая позволяет хранить, организовывать и анализировать информацию.
Excel – это универсальная программа, которая позволяет работать с различными форматами данных. В Excel можно вести домашний бюджет, производить как простые, так и очень сложные расчеты, хранить данные, организовывать различные дневники, составлять отчеты, строить графики, диаграммы и многое-многое другое.
Функции MS Excel:
1.Работа с числовыми данными. Например, составление самых различных бюджетов, начиная от домашнего, как самого простого, и, заканчивая бюджетом крупной организации.
2.Работа с текстом. Разнообразный набор инструментов для работы с текстовыми данными дает возможность представить даже самые сложные текстовые отчеты.
3.Создание графиков и диаграмм. Большое количество инструментов позволяет создавать самые различные варианты диаграмм, что дает возможность представить ваши данные наиболее ярко и выразительно.
4.Организация списков и баз данных. В Microsoft Office Excel изначально была заложена структура строк и столбцов, поэтому организовать работу со списками или создать базу данных является для Excel элементарной задачей..
2.2. Построение фигур Лиссажу средствами MS Excel
В рамках данного исследования продемонстрируем построение фигур Лиссажу в табличном процессоре MS Excel, для этого понадобятся формула:
Уравнение гармонического колебания физической величины X с циклической частотой W и амплитудой А можно записать в виде формулы:,
где F-начальная фаза. Вместо W может быть использовано 2Пи/T ,где Т-период колебаний.
Для построения фигур Лиссажу средствами MS Excel:
1.Необходимо подготовить следующую таблицу:
- Амплитуда колебаний — это наибольшее отклонение колеблющегося тела от положения равновесия.
- Циклическая частота – скалярная величина, мера частоты вращательного или колебательного движения.
- Начальная фаза – место, откуда начинается колебательный процесс в определённый момент времени (начало отсчёта).
- Время колебаний – это время колебания системы.
- Колебание Х – это колебание системы по оси OX.
- Колебание Y – это колебание системы по оси OY.
2.Столбец F начиная с ячейки F5 и далее заполнить значениями от 0,01 до 10 с шагом 0,01
(используя функцию автозаполнения)
3.В столбец G начиная с ячейки G5 и далее ввести формулу для колебания X:
4.В столбец H начиная с ячейки H5 и далее ввести формулу для колебания Y:
5.Должна получиться вот такая таблица с данными:
6.Теперь необходимо построить диаграмму по этим данным. Для этого нужно выделить два столбца со значениями колебаний X и Y. После этого нажимаем на пиктограмму мастера построения диаграмм.
7.Тип диаграммы выбираем «СТАНДАРТНЫЕ» — «ТОЧЕЧНАЯ» — «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров» Нажимаем «Далее». Переходим на вкладку «РЯД» и называем «Ряд 1» — Колебание X ,а «Ряд 2» — Колебание Y. Нажимаем «Далее» теперь надо подписать название диаграммы «Фигуры Лиссажу». Нажимаем «Далее» и выбираем расположение диаграммы в текущем листе.
8.Должно получиться следующее:
2.3 Описание применения фигур Лиссажу для сравнения гармонических колебаний
Анализ литературы показал, что фигуры Лиссажу применяются: в радиотехнике для сравнения частот, в осциллографе. Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причём период цикла вращения является величиной, обратной разности частот, например, при периоде оборота равен 2с. разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счёт кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.
Целью данной работы являлось рассказать и наглядно показать моделирование фигур Лиссажу.
В рамках исследования были решены следующие задачи:
1.Проанализированна литература по теме «Моделирование фигур Лиссажу»
2.Было раскрыты понятия: фигуры Лиссажу, гармоническое колебание, векторная диаграмма, развертка, Microsoft Office Excel, амплитуда колебаний, циклическая частота,
3.Рассмотрели способы построения графиков в среде MS Excel.
4.Разработали модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.
В столбце А набрать значения m =0, l , k =0,2, dt =0,5, x 0 =20.
В столбце В задать не менее 30-ти значений t , где to =0, a t = t + dt .
В столбце С задать модель колебаний шарика с заданными значениями t
В столбце D занести формулу скорости колебаний шарика с заданными значениями t .
В столбце Е занести формулу ускорения колебаний шарика с заданными значениями t .
Построить на одной оси графики x ( t ), v ( t ), a ( t ).
Продемонстрировать и сделать распечатки.
Провести эксперимент из заданного варианта продемонстрировать и распечатать. Оформить письменный отчет и ответить на контрольные вопросы.
Взяв три различных значения массы шарика m (от 0,1 до 0,3кг), изобразить в одной системе координат процесс колебаний шарика, к=0,1 кг/с 2 х 0 =0,5м. По графикам определить, как изменение массы влияет на амплитуду и период колебаний. Вывод записать под графиком.
Взяв три различных значения х 0 (от 0,3 до 0,5м), изобразить в одной системе координат процесс колебаний шарика k =0,2кг /с 2 , m =0,1кг. По графикам определить, как изменение первоначального отклонения шарика от положения равновесия влияет на амплитуду и период колебаний. Вывод записать под графиком.
Взяв три различных значения к (от 0,1 до 0,3 кг/с ), изобразить в одной системе координат процесс колебаний шарика, m =0,1кг х=0,4м. По графикам определить, как изменение коэффициента упругости пружины влияет на амплитуду и период колебаний. Вывод записать под графиками.
Взяв три различных значения m (от 0,2 до 0,4кг) изобразить в одной системе координат процесс колебаний скорости шарика, к=0,2кг/с 2 , х 0 =0,3м. По графику определить, как изменение массы влияет на амплитуду и период колебаний. Выводы записать под графиками.
Взяв три различных значения к (от 0,2 до 0,4кг/с ) изобразить в одной системе координат процесс колебаний скорости шарика m =0,25кг, х 0 =0,35м. По графикам определить, как изменение к влияет на амплитуду и период колебаний. Выводы записать под графиками.
6.Взяв три различных значения х 0 (от 0,4 до 0,6м) изобразить в одной
системе координат процесс колебаний скорости, m =0,35кг к=0,45кг/с 2 . Под графиком определить, как изменение х 0 влияет на амплитуду и период колебаний. Выводы записать под графиками.
7. Построить в одной системе координат процесс колебаний шарика с
тремя блоками данных:
Оборудование и материалы: МД проектор, карты с заданиями, тетради, линейки, карандаши.
Н.В. Богомолов « Практические занятия по математике», 2006г.
А.А. Дадаян « Математика», 2003г.
О.Н. Афанасьева, Я.С. Бродский « Математика для техникумов», 2001г
План занятия:
Объявление темы занятия; постановка целей;
Мотивация познавательной деятельности
Проверка опорных знаний
а) фронтальный опрос
Повторить виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях
Применение знаний к
изучению нового материала
Формирование умений и навыков построения графиков.
Построение графиков гармонических колебаний.
Закрепление умений и навыков построения графиков функций
Демонстрация лучших работ студентов.
Воспитание эстетического восприятия графических изображений;
Применение знаний к решению нестандартных задач
Показать связь математики с другими науками
Обобщение знаний, умений, навыков; оценка деятельности студентов
Инструктаж по домашнему заданию
Ход занятия:
Рождённый пустыней, колеблется звук,
Колеблется синий на нитке паук.
Колеблется воздух, прозрачен и чист,
В сияющих звездах колеблется лист.
1. Организационный момент (3 мин.)
В технике и в окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными . Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать все колебательные процессы с единой точки зрения.
Механическими колебаниями называются периодические изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальная энергия и т. п.).
Если в какой-либо точке среды, в которой близко расположенные атомы или молекулы испытывают силовое воздействие, возбужден процесс механических колебаний, то этот процесс будет с конечной скоростью, зависящей от свойств среды, распространяться от точки к точке. Так возникают механические волны . Примерами такого процесса являются звуковые волны в воздухе.
Как и колебания, волновые процессы различной физической природы (звук, электромагнитные волны, волны на поверхности жидкости и т. д.) имеют много общего. Распространение волн различной физической природы можно описывать с помощью одинаковых математических уравнений и функций. В этом проявляется единство материального мира.
2. Актуализация знаний (7 мин.)
Цель: Мотивация познавательной деятельности
Сегодня мы увидим, как с помощью математических законов и преобразований можно описывать некоторые физические явления. Например,
Что такое гармонические колебания?
Гармонические колебания – это периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса. Графиком гармонического колебания является синусоида или косинусоида , по которой можно определить все характеристики колебательного движения : амплитуду, период, частоту, начальную фазу .
Гармонические колебания играют важную роль в физике, электротехнике. Наша задача – построить графики гармонических колебаний, применив при этом все известные правила преобразований графиков без помощи трудоёмких вычислений и научиться описывать по ним колебательный процесс.
Гармонические колебания подчиняются следующему закону:
А — амплитуда, циклическая (круговая) частота,
начальная фаза колебаний, обычно
Период гармонических колебаний Т можно вычислить по формуле
Для построения графиков гармонических колебаний необходимо иметь чёткое представление о правилах построения графиков функций и их преобразованиях.
3. Проверка знаний учащихся по теме: «Преобразования графиков функций» (15 мин.)
Цель: Повторить основные виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях.
Задание 1. Сгруппируйте функции по общему признаку:
Изменение аргумента
Изменение функции
у = ctg1/3x
у = — 3cosx
Рассмотрим подробно правила построения графиков функций с изменяющимся аргументом и меняющейся функцией. (Презентация.)
4. Изучение нового материала (20 мин.) (Презентация.)
Цель: Формирование умений и навыков исследования функции, построения графиков гармонических колебаний.
Задача 1. Построить график гармонических колебаний у = 2 sin (2 x — ).
Сразу укажем на типовую ошибку в подобных задачах: осуществляют сдвиг на , а необходимо на , поэтому у = 2 sin 2( x — ).
Как построить график такого колебания? Алгоритм построения следующий:
1. у = sinx — исходная функция .
2. у = sin 2 x — сжатие в 2 раза вдоль оси Ох.
3. у = 2 sin 2 x — растяжение в 2 раза вдоль оси Оу (рис. 1).
4. у = 2 sin 2( x — ) — сдвиг на вправо по оси Оx (рис. 2).
При построении данного графика были использованы следующие виды преобразования графиков:
1. у = f ( k x ), k =2 – сжатие вдоль оси Ох
2. у = m f ( x ), m =2 — растяжение вдоль оси Ох
3. у = f ( x — x )- параллельный перенос (сдвиг) вдоль оси Ох
Задача 2. Построить графики функций и определить основные характеристики гармонического колебания:
a ) у = sin б) у = sin 3 x
a). Найдем период функции у = sin :
Период колебания Т = 6 значит, достаточно построить график на участке . Поделив этот участок на 4 равных промежутка, получим точки, которые определяют поведение графика: (рис. 3).
б) Найдем период функции у = sin 3 x :
Построим график на участке длиной в период . Поделим его на 4 равных промежутка и получим точки (рис. 4).
5. Построение графиков гармонических колебаний . Самостоятельная работа (30 мин).
Опыт – дитя мысли, мысль – дитя действий
Вениамин Дизраэли
Цель: Закрепление умений и навыков построения графиков функций
Задание учащимся:
Построить графики гармонических колебаний:
y = — sin ( x+ ).
Критерии оценки деятельности учащихся:
(1-) – удовлетворительно; (1-2) – хорошо; (1-3) – отлично.
6. Демонстрация лучших работ студентов (3 мин).
Вдохновение нужно в математике, как и в поэзии.
Цель: Воспитание эстетического восприятия графических изображений;
7. Применение знаний к решению нестандартных задач (6 мин.)
Цель: Показать связь математики с другими науками;
Задания для учащихся:
Тело движется по закону у = cos . По графику (рис.5)функции установите:
Амплитуду колебаний А ;
Ответ : А=1;
8. Итог занятия (3мин).
Дорогу осилит идущий, а математику – мыслящий.
Выполнение поставленных целей;
Приобретение навыков исследовательской работы;
Применение знаний к решению нестандартных задач;
Мы познакомились с графиками гармонических колебаний. Очевидно, что при их построении синусоида или косинусоида подверглись различным преобразованиям: сжатию, растяжению, сдвигу. Овладение этими правилами поможет при изучении других функций на последующих занятиях.
9. Домашнее задание (3 мин).
Построить график функции у = 3 cos (2 x + ) и определить основные характеристики колебательного движения.
10. Это интересно!
Биение сердца также относится к колебательному процессу. В течение минуты оно выбрасывает в аорту около 4 л крови. Сердце человека в среднем сокращается 100 тысяч раз в сутки. За 70 лет жизни оно сокращается 2 миллиарда 600 миллионов раз и перекачивает при этом 250 миллионов литров крови. Синусоидальные изменения ритмов сердца отражает кардиограф.
Читайте также:
- Как перенести файл на рабочий стол компьютера
- Санитары подземелий настройки файл
- Igc64 dll что это
- Чем отличается мультиварка от файла
- Realtek radio model rtl8188ee что это
Экспортировать графики Excel в файлы векторной графики (например, SVG)?
Как экспортировать график, сгенерированный в Excel, в редактируемый векторный графический файл, например SVG?
когда я щелкните правой кнопкой мыши на графике в Excel Сохранить как картинку. ‘option предоставляет только невекторные форматы (такие как PNG и JPG) в качестве опций.
единственный ресурс, который я нашел на этомhttp://www2b.abc.net.au/science/techtalk/newposts/790/topic790744.shtm где никто не дает реальный ответ. Так же, как и вопрос там, я не возражаю, если это многоступенчатый процесс ЭГ. В Excel -> офис -> СВГ или Excel -> СИЗО -> СВГ.
10 ответов
хотя вы действительно можете копировать — ‘ N-вставить непосредственно в InkScape, вы можете потерять некоторое форматирование в этом процессе. Экспорт в PDF гарантирует, что фон вашего файла Excel также будет сохранен. По моему опыту, работает очень хорошо.
- В Microsoft Excel, «Сохранить как PDF».
- в Inkscape «открыть PDF».
- свойства документа, разверните «изменить размер страницы для содержимого» (hiddent), нажмите кнопку.
- сохранить в SVG или расширенный мета-файл (ЭДС.)
плагины для экспорта PDF.
- 2007 надстройка Microsoft Office: Microsoft Сохранить как PDF или XPS — «FileFormatConverters.exe » (37 MB)
- дополнительная надстройка, которая создает новую опцию меню «Сохранить как pdf» в Excel — » SaveAsPDFandXPS.exe » (933 KB)
- выберите графики Microsoft Excel.
- копировать.
- Открыть Microsoft PowerPoint.
- вставить-специальный расширенный метафайл (EMF)в пустой слайд.
- сохраните слайд PowerPoint как файл » другого формата «и выберите» EMF » (расширенный Метафайл Windows).
- импорт EMF файла в InkScape и разгруппируйте объект.
- удалить все дерьмовое пустое пространство формата А4 из изображения и наслаждаться.
попробовать Gnumeric. Он поддерживает экспорт графиков в SVG изначально. Есть версия для windows, тоже. Таким образом, цепочка инструментов будет Excel -> Gnumeric -> SVG , или даже Gnumeric -> SVG без использования Excel. IMHO это самый простой способ получить график в SVG.
новые версии PowerPoint позволяют сохранять и отправлять в формате PDF. Используйте эту функцию для создания PDF-файла, затем откройте его в Inkscape и отредактируйте, разгруппировав, затем измените размер страницы на чертеже и сохраните как SVG.
используя Excel 2007 под Windows XP, я также обнаружил, что скопированные графики вставляются как растровые изображения в Inkscape. Это отличается от поведения Excel 2003 В Windows 7.
Я нашел обходной путь — если вы выберете ячейки, окружающие график (которые также будут включать график), и скопируйте, вы можете вставить векторную графику в Inkscape так же, как ожидалось. Единственным небольшим недостатком является то, что вы должны вручную удалить сетку ячеек excel, которая остается ниже вашей графика.
вы можете просто скопировать график (Ctrl-C) и вставить его в Inkscape (а затем Сохранить как SVG). Он работал для меня на Excel 2003, Inkscape (0.48.4) и Windows Vista (заимствованный компьютер), так как по крайней мере в Windows формат копирования по умолчанию кажется EMF. Но тогда я думаю, что буфер обмена OS X может обрабатывать это по-другому и копировать / вставить растровое изображение вместо этого.
чтобы избежать шага «обрезка PDF», упомянутого в нескольких ответах, вы можете поместить диаграмму на свой рабочий лист с соответствующим размером бумаги и нулевыми полями. Е. Г. в Windows версии Excel 2007:
- выберите диаграмма, из всплывающего меню выберите переместить диаграмму. / New Sheet
- на новом листе диаграммы, макет страницы / поля / пользовательские поля и ноль все
- изменить размер диаграммы до нужного размера, перетаскивая его правый нижний угол
- посмотреть результат размер Из инструментов диаграммы / формат / размер
- выберите близкий размер от макета страницы | размер, и настроить по мере необходимости
Если нет размера достаточно близко, или вы хотите быть точным, вам нужно создать пользовательский размер страницы. В отличие от Word, Excel не позволяет сделать это сам, а использует размер из драйвера принтера.
- Макет Страницы | Размер | Дополнительные Форматы Бумаги | Печать. выберите принтер, драйвер которого позволяет создавать пользовательские размеры страниц обычные драйверы PostScript или PDF
- параметры. | Передовой. | Формат Бумаги | Сохранить Пользовательский Размер Страницы
- установить размер, заботясь, чтобы получить правильные единицы измерения и поменять ширину и высоту (Excel печатает как пейзаж по умолчанию)
может быть лучше не иметь контура вокруг диаграммы в самом PDF: вы можете выбрать формат область диаграммы | цвет границы | без линии.
вот метод, использующий Excel и Powerpoint для Windows. Скопировать диаграмму в буфер обмена в Excel с помощью команды «копировать» на вкладке «Главная» ленты. Прошлое специальное в пустой слайд в Powerpoint с помощью меню вставки на ленте. Прокрутите вниз и выберите «Picture (enhanced metafile)» из выпадающего меню в диалоговом окне. Затем нажмите OK График отображается в Powerpoint. Убедитесь, что график выбран, затем выберите упорядочить > разгруппировать. Появится диалоговое окно. «Это будет импортированное изображение, а не группа. Вы хотите преобразовать его в объект Microsoft Drawing?»нажмите Да Вы почти там! Убедитесь, что grahp по-прежнему выбран. Вернуться в «упорядочить» > «разгруппировать» и нажмите кнопку Все элементы графика теперь должны быть векторными объектами Powerpoint. Ура, наслаждайся.
Векторные диаграммы
Векторные диаграммы и комплексное представление
Векторные диаграммы можно считать вариантом (и иллюстрацией) представления колебаний в виде комплексных чисел . При таком сопоставлении ось Ox соответствует оси действительных чисел, а ось Oy – оси чисто мнимых чисел (положительный единичный вектор вдоль которой есть мнимая единица ).
Тогда вектор длиной A, вращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ0 запишется как комплексное число
а его действительная часть
-есть гармоническое колебание с циклической частотой ω и начальной фазой φ0.
Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.
- Метод векторных диаграмм может излагаться отдельно в курсах электротехники или элементарной физики, если по тем или иным причинам (обычно связанным с умеренным уровнем математической подготовки учащихся и недостатком времени) надо избежать использования комплексных чисел (в явном виде) вообще.
- Метод комплексного представления (который при необходимости или желании может включать и графическое представление, что, правда, совершенно не обязательно и иногда излишне) вообще говоря более мощен, т.к. естественно включает в себя, например, составление и решение систем уравнений любой сложности, в то время как метод векторных диаграмм в чистом виде всё же ограничен задачами, подразумевающим суммирование, которое можно изобразить на одном чертеже.
- Однако метод векторных диаграмм (в чистом виде или в качестве графической составляющей метода комплексного представления) – более нагляден, а значит в некоторых случаях потенциально более надежен (позволяет до некоторой степени избежать грубых случайных ошибок, которые могут встречаться при абстрактных алгебраических вычислениях) и позволяет в некоторых случаях достичь в каком-то смысле более глубокого понимания задачи.
Разновидности векторных диаграмм
Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.
С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.
Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.
Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.
Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.
Механика; гармонический осциллятор
- Гармонический осциллятор в механике и гармонический осциллятор любой природы формально представляют точную аналогию, поэтому рассмотрим их в одном параграфе на примере механического гармонического осциллятора.
- Применение векторных диаграмм в механике сводится в основном к случаю гармонического осциллятора (в том числе имеется в виду и случай осциллятора с линейной по скорости силой трения); впрочем, векторные диаграммы могут быть до некоторой степени полезны и для исследования нескольких осцилляторов в том числе и в пределе бесконечного их количества (для колебаний или волн в распределенных системах).
- С современной точки зрения применение векторных диаграмм к гармоническому осциллятору представляет скорее только исторический и педагогический интерес, однако тем не менее в принципе они здесь вполне применимы.
- В механике применение векторных диаграмм (обычно подразумевается их применение к одномерному осциллятору) имеет ту особенность, что добавляющаяся вторая координата для превращения колебаний во вращение может иметь не только чисто формальный абстрактный смысл, но для одномерной механической системы такого сорта может быть указана механическая же двумерная система, для которой векторная диаграмма первой реализуется как вполне реальное двумерное механическое движение, и все векторы реально двумерны (а после проецирования всех их и движения точки двумерной системы на одну ось, мы получаем мгновенные значения соответствующих величин – в том числе положения – для соответствующей одномерной системы); таким образом, для механической одномерной системы возможна не только формальная математическая, но и реальная механическая модель, переводящая колебательное одномерное движение во вращательное движение в двумерном пространстве, реализующая в себе векторную диаграмму для одномерной системы.
Разберем два основных случая простого применения векторных диаграмм в механике (как замечено выше, также применимых к гармоническому осциллятору не только механической, но любой природы): осциллятор без затухания и без внешней силы и осциллятор с (линейным) затуханием (вязкостью), и внешней вынуждающей силой.
Представление синусоидальных функций в виде комплексных чисел
Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.
Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции
Данный синусоидальный сигнал можно представить в виде комплексной величины
Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.
Векторная диаграмма при последовательном соединении элементов
Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.
Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.

Составим уравнение для данной цепи по второму закону Кирхгофа :
По закону Ома падение напряжений на элементах определяется по следующим выражениям:
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.
Из курса математики известно, что j = 1∠90°, −j = 1∠−90°. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу j приводит к повороту этого вектора на 90 градусов против часовой стрелки, а умножение на −j приводит к повороту этого вектора на 90 градусов по часовой стрелке.
При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока I, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.
Падение напряжения на резисторе UR совпадает по направлению с током I (т.к. UR = I ∙ R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. UL = I ∙ jXL, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. UC = −I ∙ jXC, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелке).
Рис. 2. Векторная диаграмма напряжений при последовательном соединении элементов цепи
Векторная диаграмма при параллельном соединении элементов
Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.
Рис. 3. Параллельное соединение элементов цепи
Составим уравнение для данной цепи по первому закону Кирхгофа :
Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что 1 / j = −j:
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.
При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС E, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.
Ток в резисторе IR совпадает по направлению с ЭДС E (т.к. IR = E / R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. IL = −j ∙ E / XL, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелки). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. IC = j ∙ E / XC, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.
Рис. 4. Векторная диаграмма токов при параллельном соединении элементов цепи
Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.
Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.
Алгоритм создания лучевой векторной диаграммы в Excel
Чтобы упростить наш урок, давайте предположим, что мы говорим об отношениях не между четырнадцатью как на графике, а пока только с 4-ма людьми по имени Антон, Алиса, Борис и Белла.
Наша матрица уровня отношений и связей между ними выглядит следующим образом:
- 0 значит отсутствие отношений;
- 1 означает слабые отношения (например: Антон и Алиса просто знают друг друга);
- 2 означает крепкие отношения (например, Борис и Алиса друзья).
Как можно геометрически смоделировать визуализацию этих исходных данных? Если бы мы нарисовали отношения между этими четырьмя людьми (Антон, Алиса, Борис и Белла), это схематически выглядело бы так:
2 критерия, которые нам нужно определить:
- Расположение точек (где печатаются имена людей).
- Линии (начальная и конечная точка соединения линий).
Определение и построение точек
Сначала нам нужно построить наши точки таким образом, чтобы промежуток между каждой точкой был одинаковым. Это создаст сбалансированный график.
Какая геометрическая фигура максимально удовлетворяет нашу потребность в таких равных промежутках? Конечно же круг!
Вы можете возразить, что на готовой модели диаграммы нет фигуры круга. Да действительно нет –вот так. Нам не нужно рисовать круг. Нам просто нужно построить точки вокруг него.
Таким образом, у нас есть 4 заинтересованные стороны, нам нужно 4 точки:
- Если у нас 12 заинтересованных сторон, нам нужно 12 точек.
- Если у нас есть 20, нам нужно 20 точек.
Предполагая, что источником нашего круга является (x, y), радиус – это r, а тета – 360, деленная на количество нужных нам точек. Первая точка (x1, y1) на окружности будет в этой позиции:
- x1 = x + r * COS (тета);
- y1 = y + r * SIN (тета).
Как только все точки рассчитаны и подключены к XY-диаграмме (точечная диаграмма), давайте двигаться дальше.
Построение линий на лучевой диаграмме
Допустим, у нас в сети есть n человек. Это означает, что каждый человек может иметь максимум n -1 отношений.
Таким образом, общее количество возможных линий на нашем графике равно n * ( n -1) / 2.
Нам нужно разделить его на 2, как будто A знает B, тогда B тоже знает A. Но нам нужно нарисовать только 1 линию.
Шаблон лучевой диаграммы для анализа сетевого графика настроен для работы с 20 людьми. Его можно скачать в конце статьи и использовать как готовый аналитический инструмент визуализации данных связей. Это означает, что максимальное количество строк, которое мы можем иметь, будет равно 190.
Каждая строка требует добавления отдельной серии на график. Это означает, что нам нужно добавить 190 серий данных только для 20 человек. И это удовлетворяет только одному типу линии (пунктирная или толстая). Если нам нужны разные линии в зависимости от типа отношений, нам нужно добавить еще 190 серий.
Это больно и смешно одновременно. К счастью, выход есть!
Мы можем использовать гораздо меньшее количество серий и по-прежнему строить один и тот же график.
Допустим, у нас есть 4 человека – A,B,C и D. Ради простоты, давайте предположим, что координаты этих 4-х участников следующие:
И скажем, A имеет отношения с B, C и D.
Это означает, что нам нужно нарисовать 3 линии, от A до B, от A до C и A до D.
Теперь, вместо того, чтобы поставить 3 серии для диаграммы, что если мы поставим одну длинную серию, которая выглядит следующим образом:
Это означает, что мы просто рисуем одну длинную линию от A до B, от A до C, от A до D. Договорились, что это не прямая линия, но точечные диаграммы Excel могут нарисовать любую линию, если вы предоставите ей набор координат.
Смотрите эту иллюстрацию, чтобы понять технику:
Таким образом, вместо 190 рядов данных для диаграммы нам просто нужно 20 рядов.
На последнем графике мы имеем 40 + 2 + 1 ряд данных. Это потому что:
- 20 линий для слабых отношений (пунктирные линии);
- 20 линий для прочных отношений (толстые линии);
- 1 строка для выделения синим цветом слабых отношений выделенного участника;
- 1 строка для выделения зеленым цветом сильных отношений выделенного участника;
- 1 комплект без линий, а просто точек для подписей данных на графике.
Как сгенерировать все 20 серий данных:
Это требует следующей логики:
- разделите номер строки на 2, чтобы получить номер человека (скажем, m );
- ( Xn, Yn ), если нет отношений между n и m ;
- ( Xm, Ym ), если есть отношения.
Нам нужны формулы MOD и INDEX для выражения этой логики в Excel.
Как только все координаты линии будут рассчитаны, добавьте их к нашему точечному графику как новые ряды используя инструмент из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«КОНСТРУКТОР»-«Выбрать данные» в окне «Выбор источника данных» используйте кнопку «Добавить» для добавления всех 43-х рядов.
Реализовывать создание такой лучевой диаграммы связей будем в 3 этапа:
- Подготовка исходных данных.
- Обработка данных.
- Визуализация.
Подготовка данных для лучевой диаграммы
Как уже упоминалось выше данный шаблон будет обладать возможностью визуального построения связей до 20-ти участников (компаний, филиалов, контрагентов и т.п.). На листе книги шаблона «Данные» предоставленная таблица для заполнения входящих значений. Например, заполним ее для 14-ти участников рынка:
На этом же листе создадим дополнительную таблицу, которая представляет собой матрицу связей всех возможных участников, сгенерированную формулой:
С подготовкой данных мы закончили переходим к обработке.
Как вычислить сумму векторов?
Вектора и матрицы в электронной таблице хранятся в виде массивов.
Известно, что сумма векторов – это вектор, координаты которого равны суммам соответствующих координат исходных векторов:
Для вычисления суммы векторов нужно выполнить следующую последовательность действий:
– В диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора.
– Выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы.
– Ввести в выделенный диапазон формулу перемножения диапазонов
– Нажать комбинацию клавиш [Ctrl] + [Shift] +[Enter].
Даны два вектора:
Требуется вычислить сумму этих векторов.
– В ячейки диапазона А2:A4 введем значения координат вектора a1, а в ячейки диапазона С2:С4 – координаты вектора a2.
– Выделим ячейки диапазона, в которых будет вычисляться результирующий вектор С ( E2:E4 ) и введем в выделенный диапазон формулу:
– Нажмем комбинацию клавиш [Ctrl] + [Shift] +[Enter]. В ячейках диапазона E2:E4 будут вычислены соответствующие координаты результирующего вектора.
Сложение и вычитание векторов
Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями
Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:
Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.
Вектор Im, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).
Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):
При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.
Лучевая векторная диаграмма для визуализации связей в Excel
Как сделать в Excel отображение отношений между людьми, компаниями, филиалами и т.д. с помощью интерактивной лучевой диаграммы. Это, так называемый сетевой график, помогает нам визуализировать отношения между разными людьми в интерактивном режиме.
Как сделать лучевую векторную диаграмму связей в Excel
Сначала взглянем на то, что мы пытаемся построить и визуально оценим объем работы. Выглядит интересно? Тогда читайте дальше, чтобы узнать, как это создать.
Чтобы создать лучевую диаграмму в Excel для визуального анализа взаимоотношений в сети, нам нужно сначала понять ее различные составляющие.
Как видите, диаграмма содержит следующие части:
- Набор точек, каждая из которых представляет одну заинтересованную сторону – участники сети.
- Набор сероватых толстых сплошных и тонких пунктирных линий, представляющих все отношения между людьми. Сплошные – сильные связи (например, друзья), пунктирные – слабые связи (знакомые).
- Набор зеленых толстых и синих пунктирных линий, представляющих отношения для выбранного конкретного участника сетевой группы.
- Срез для выбора анализа участника – как панель управления лучевой диаграммой.
- Табличка со сводной статистикой выбранного человека.
Алгоритм создания лучевой векторной диаграммы в Excel
Чтобы упростить наш урок, давайте предположим, что мы говорим об отношениях не между четырнадцатью как на графике, а пока только с 4-ма людьми по имени Антон, Алиса, Борис и Белла.
Наша матрица уровня отношений и связей между ними выглядит следующим образом:
- 0 значит отсутствие отношений;
- 1 означает слабые отношения (например: Антон и Алиса просто знают друг друга);
- 2 означает крепкие отношения (например, Борис и Алиса друзья).
Как можно геометрически смоделировать визуализацию этих исходных данных? Если бы мы нарисовали отношения между этими четырьмя людьми (Антон, Алиса, Борис и Белла), это схематически выглядело бы так:
2 критерия, которые нам нужно определить:
- Расположение точек (где печатаются имена людей).
- Линии (начальная и конечная точка соединения линий).
Определение и построение точек
Сначала нам нужно построить наши точки таким образом, чтобы промежуток между каждой точкой был одинаковым. Это создаст сбалансированный график.
Какая геометрическая фигура максимально удовлетворяет нашу потребность в таких равных промежутках? Конечно же круг!
Вы можете возразить, что на готовой модели диаграммы нет фигуры круга. Да действительно нет –вот так. Нам не нужно рисовать круг. Нам просто нужно построить точки вокруг него.
Таким образом, у нас есть 4 заинтересованные стороны, нам нужно 4 точки:
- Если у нас 12 заинтересованных сторон, нам нужно 12 точек.
- Если у нас есть 20, нам нужно 20 точек.
Предполагая, что источником нашего круга является (x, y), радиус — это r, а тета — 360, деленная на количество нужных нам точек. Первая точка (x1, y1) на окружности будет в этой позиции:
- x1 = x + r * COS (тета);
- y1 = y + r * SIN (тета).
Как только все точки рассчитаны и подключены к XY-диаграмме (точечная диаграмма), давайте двигаться дальше.
Построение линий на лучевой диаграмме
Допустим, у нас в сети есть n человек. Это означает, что каждый человек может иметь максимум n -1 отношений.
Таким образом, общее количество возможных линий на нашем графике равно n * ( n -1) / 2.
Нам нужно разделить его на 2, как будто A знает B, тогда B тоже знает A. Но нам нужно нарисовать только 1 линию.
Шаблон лучевой диаграммы для анализа сетевого графика настроен для работы с 20 людьми. Его можно скачать в конце статьи и использовать как готовый аналитический инструмент визуализации данных связей. Это означает, что максимальное количество строк, которое мы можем иметь, будет равно 190.
Каждая строка требует добавления отдельной серии на график. Это означает, что нам нужно добавить 190 серий данных только для 20 человек. И это удовлетворяет только одному типу линии (пунктирная или толстая). Если нам нужны разные линии в зависимости от типа отношений, нам нужно добавить еще 190 серий.
Это больно и смешно одновременно. К счастью, выход есть!
Мы можем использовать гораздо меньшее количество серий и по-прежнему строить один и тот же график.
Допустим, у нас есть 4 человека – A,B,C и D. Ради простоты, давайте предположим, что координаты этих 4-х участников следующие:
И скажем, A имеет отношения с B, C и D.
Это означает, что нам нужно нарисовать 3 линии, от A до B, от A до C и A до D.
Теперь, вместо того, чтобы поставить 3 серии для диаграммы, что если мы поставим одну длинную серию, которая выглядит следующим образом:
Это означает, что мы просто рисуем одну длинную линию от A до B, от A до C, от A до D. Договорились, что это не прямая линия, но точечные диаграммы Excel могут нарисовать любую линию, если вы предоставите ей набор координат.
Смотрите эту иллюстрацию, чтобы понять технику:
Таким образом, вместо 190 рядов данных для диаграммы нам просто нужно 20 рядов.
На последнем графике мы имеем 40 + 2 + 1 ряд данных. Это потому что:
- 20 линий для слабых отношений (пунктирные линии);
- 20 линий для прочных отношений (толстые линии);
- 1 строка для выделения синим цветом слабых отношений выделенного участника;
- 1 строка для выделения зеленым цветом сильных отношений выделенного участника;
- 1 комплект без линий, а просто точек для подписей данных на графике.
Как сгенерировать все 20 серий данных:
Это требует следующей логики:
- разделите номер строки на 2, чтобы получить номер человека (скажем, m );
- ( Xn, Yn ), если нет отношений между n и m ;
- ( Xm, Ym ), если есть отношения.
Нам нужны формулы MOD и INDEX для выражения этой логики в Excel.
Как только все координаты линии будут рассчитаны, добавьте их к нашему точечному графику как новые ряды используя инструмент из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«КОНСТРУКТОР»-«Выбрать данные» в окне «Выбор источника данных» используйте кнопку «Добавить» для добавления всех 43-х рядов.
Реализовывать создание такой лучевой диаграммы связей будем в 3 этапа:
- Подготовка исходных данных.
- Обработка данных.
- Визуализация.
Подготовка данных для лучевой диаграммы
Как уже упоминалось выше данный шаблон будет обладать возможностью визуального построения связей до 20-ти участников (компаний, филиалов, контрагентов и т.п.). На листе книги шаблона «Данные» предоставленная таблица для заполнения входящих значений. Например, заполним ее для 14-ти участников рынка:
На этом же листе создадим дополнительную таблицу, которая представляет собой матрицу связей всех возможных участников, сгенерированную формулой:
С подготовкой данных мы закончили переходим к обработке.
Обработка данных для построения лучевой диаграммы
На следующем листе с именем «Обработка» создаем сначала 2 таблицы: одна обычная, вторая умная. Обычная таблица заполнена формулами и значениями так как показано на рисунке:
СЧЁТЗ(Данные!$B$3:$B$22);»»;ИНДЕКС(Данные!$B$3:$B$22;$B$60))’ >
- В ячейках B9 и B10 используются формулы массива поэтому при их вводе следует использовать комбинацию клавиш CTRL+SHIFT+Enter.
- Умная таблица должна быть расположена не выше 45-ой строки текущего листа Excel. Для данной таблице будет регулярно применятся фильтр, который будет скрывать часть строк листа. Нельзя допустить чтобы в эти строки попадали другие значения.
Рядом создаем еще одну таблицу для вычисления координат на основе данных первой таблицы. Для этого используется 2 формулы для значений X и Y:
Следующая таблица создана для построения координат линий – отношений на уровне знакомых. Таблица содержит 40 строк и 40 столбцов. Каждая пара столбов – это входящие данные для радов диаграммы. Все ячейки заполнены одной сложной формулой:
1);ИНДЕКС($E$3:$F$22;I$2;ОСТАТ(ЧИСЛСТОЛБ($H$2:I$2);2)+1);ИНДЕКС($E$3:$F$22;ЦЕЛОЕ($H4/2)+1;ОСТАТ(ЧИСЛСТОЛБ($H$2:I$2);2)+1))’ >
Рядом же сразу создаем аналогичным образом таблиц с координатами построения линий – отношений на уровне друзей. Все ее ячейки заполнены формулой:
2);ИНДЕКС($E$3:$F$22;AX$2;ОСТАТ(ЧИСЛСТОЛБ($AW$2:AX$2);2)+1);ИНДЕКС($E$3:$F$22;ЦЕЛОЕ($H4/2)+1;ОСТАТ(ЧИСЛСТОЛБ($AW$2:AX$2);2)+1))’ >
Эти две таблицы будут использованы для построения серых линий. А теперь создадим еще одну таблицу для построения синих и зеленых линий для выделенного участника:
В каждом столбце этой таблицы используются разные формулы:
Столбец листа CM (X-синяя):
Все с обработкой закончили! У нас есть все координаты для точек и линий. Осталось только построить лучевую диаграмму визуализировав таким образом входящие значения на листе «Данные».
Визуализация данных связей участников на лучевой диаграмме
Начнем сначала с построения серых пунктирных линий для отображения всех слабых связей между участниками. А потом сделаем те же самые действия для серых сплошных линий сильных связей. Выделите диапазон ячеек I3:J43 и выберите инструмент: «ВСТАВКА»-«Диаграммы»-«Точечная с прямыми отрезками».
Из диаграммы следует удалить: сетку, оси координат, название и легенду.
Затем из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«КОНСТРУКТОР»-«Выбрать данные» в окне «Выбор источника данных» используйте кнопку «Добавить» для добавления остальных 20-ти рядов:
Для каждой линии нужно присвоить один и тот же формат. Удобно выбирать ряды линий из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«ФОРМАТ»-«Текущий фрагмент». Из выпадающего списка выбираем необходимый нам ряд, а ниже жмем кнопку «Формат выделенного» чтобы приступить к форматированию:
Далее добавляем еще 2 ряда для выделения цветом выбранных участников. Для этого используем значения последней таблицы:
Не забудем изменить цвета линий на зеленый и синий – соответственно.
Осталось еще добавить подписи данных. Для этого используем вторую таблицу с базовыми координатами точек участников при создании еще одного ряда:
Выделяем последний ряд, щелкаем по полюсу возле диаграммы и отмечаем галочкой опцию «Подписи данных». Сам ряд лучше скрыть, убрав завивку для его линий.
Интерактивная панель управления лучевой диаграммой связей
Для создания панели управления будем использовать обычный срез для уже созданной умной таблицы. Перейдите на любую ячейку умной таблице на листе «Обработка» и выберите инструмент: «ВСТАВКА»-«Фильтры»-«Срез». В паявшемся окне укажите галочкой только на опцию «Имя».
Копируем срез и лучевую диаграмму на отельный лист «ГРАФИК» и наслаждаемся готовым результатом:
Как видно выше на рисунке было создано всего 43 ряда для лучевой диаграммы связей взаимоотношений участников рынка. Для добавления большого количества рядов на график можно создать макросы, в данном случае можно все седлать вручную.
источники:
http://exceltut.ru/vektornye-diagrammy/
http://exceltable.com/shablony-skachat/luchevaya-vektornaya-diagramma
|
Здравствуйте, дорогие форумчане, хотелось бы получить помощь по вот такому вот заданию, понимающе, отзовитесь. Заранее спасибо. Изменено: Дмитрий Сидоренко — 29.11.2021 18:25:16 |
|
|
Прошу прощения, но у вас сломались картинки |
|
|
БМВ Модератор Сообщений: 21380 Excel 2013, 2016 |
#3 29.11.2021 18:06:47
не у нас, а у вас. По вопросам из тем форума, личку не читаю. |
||
|
Тимофеев Пользователь Сообщений: 1497 |
Вид зависимости амплитуды от времени испугал сразу |
|
БМВ Модератор Сообщений: 21380 Excel 2013, 2016 |
#6 29.11.2021 18:19:55
еще лучше загружайте картинку как файл и потом кликните на результат, она будет видна как изображение в теле сообщения, но ох как везде любят снимать порчу по фотографиям…. Изменено: БМВ — 29.11.2021 18:22:12 По вопросам из тем форума, личку не читаю. |
||
|
tutochkin Пользователь Сообщений: 559 |
Так заполните табличку расчетом, а мы по ней дружно график построим.. Ведь в этом проблема, да? |
|
Проблема как раз таки в том, что я в ексель так скажем «чайник», и практически не понимаю ничего из вышесказанного. Однако преподователей не интересует, вот такая практическая работа, и так как не нашёл экспресс-курса по данной теме, обратился к данному форуму |
|
|
Тимофеев Пользователь Сообщений: 1497 |
|
|
Юрий М Модератор Сообщений: 60577 Контакты см. в профиле |
#10 29.11.2021 19:38:26
И поэтому Вы показываете картинки, а не Excel-файл? |
||
|
Ігор Гончаренко Пользователь Сообщений: 13746 |
#11 29.11.2021 20:11:35
обьявление: Дмитрий Сидоренко если у вас есть функция этих затухающих колебаний, то построить ее график — это как два пальца об асфальт Изменено: Ігор Гончаренко — 29.11.2021 20:36:09 Программисты — это люди, решающие проблемы, о существовании которых Вы не подозревали, методами, которых Вы не понимаете! |
||
|
tutochkin Пользователь Сообщений: 559 |
#12 29.11.2021 20:35:47
Итак, Вы пошли учиться, преподаватель Вам дал задание, и Вы его не хотите решить? А попробовать? Для начала с простого — построить график Y=f(x)=x… затем сложнее и … и всё. Это если Вы пошли учиться… А если нет… ну значит нет. Изменено: tutochkin — 29.11.2021 21:07:19 |
||





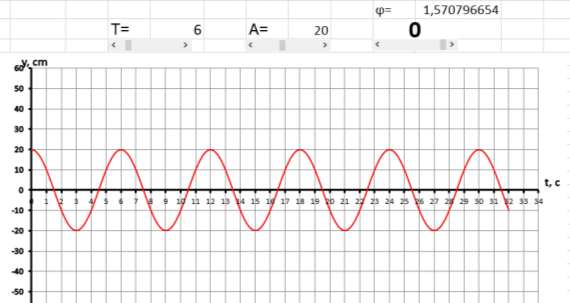

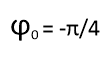
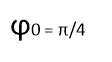
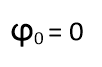
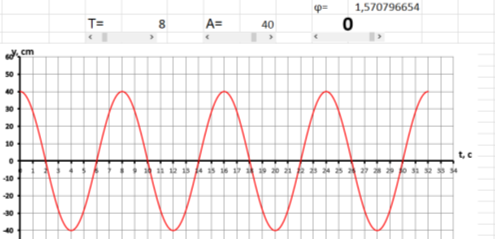

























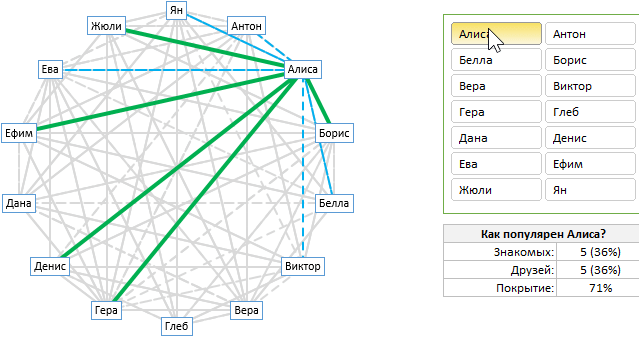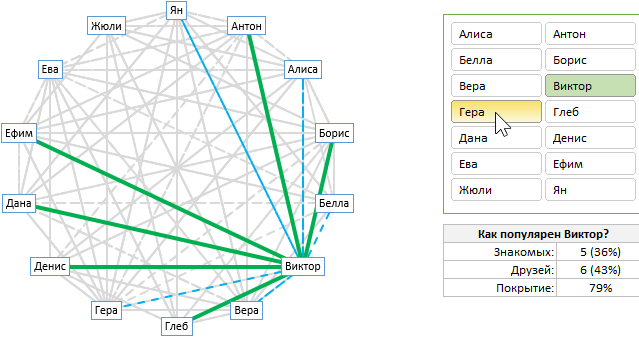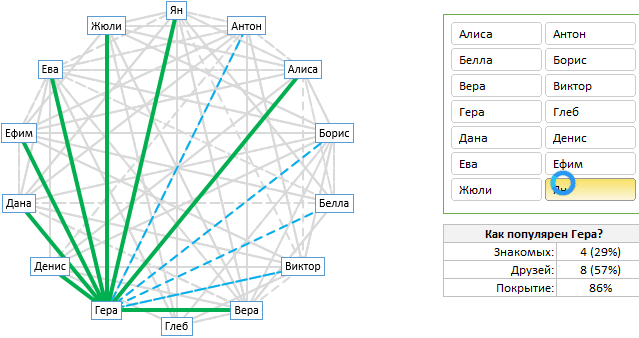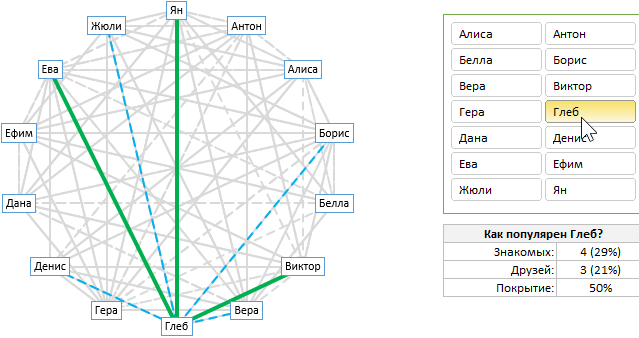
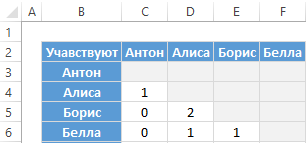
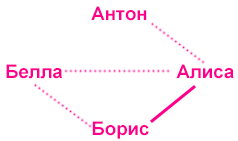
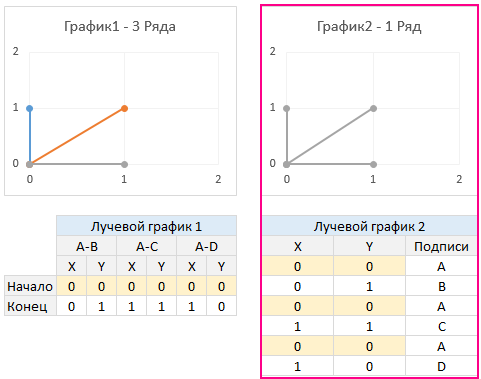
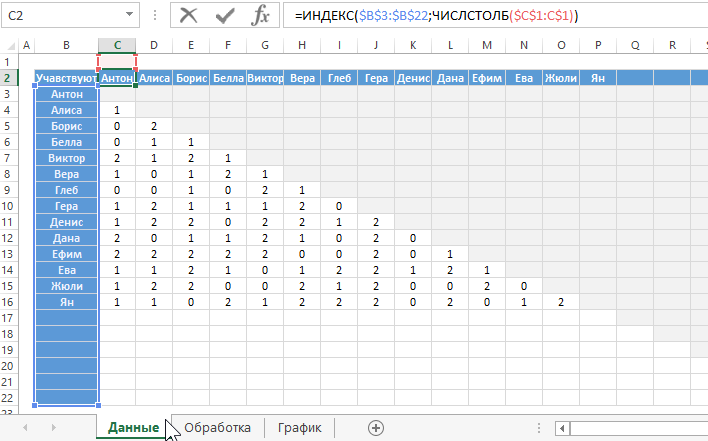
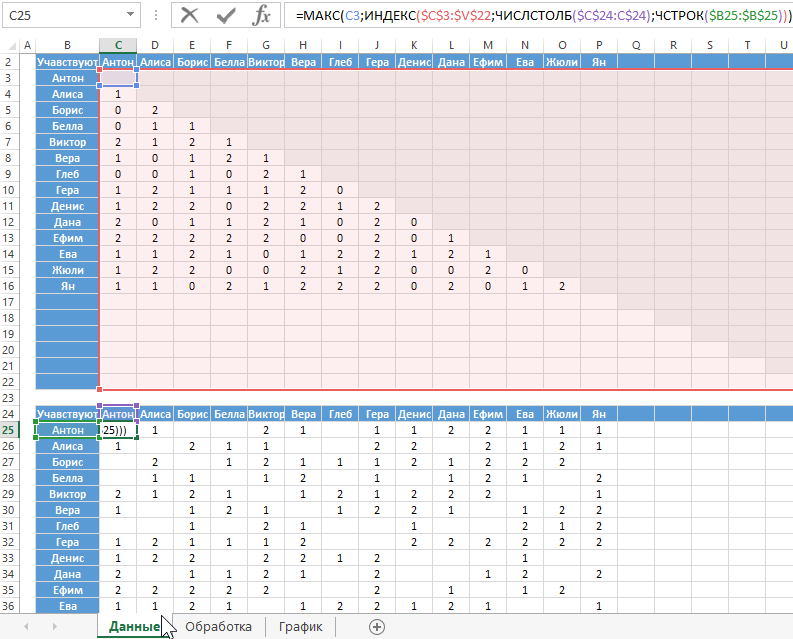
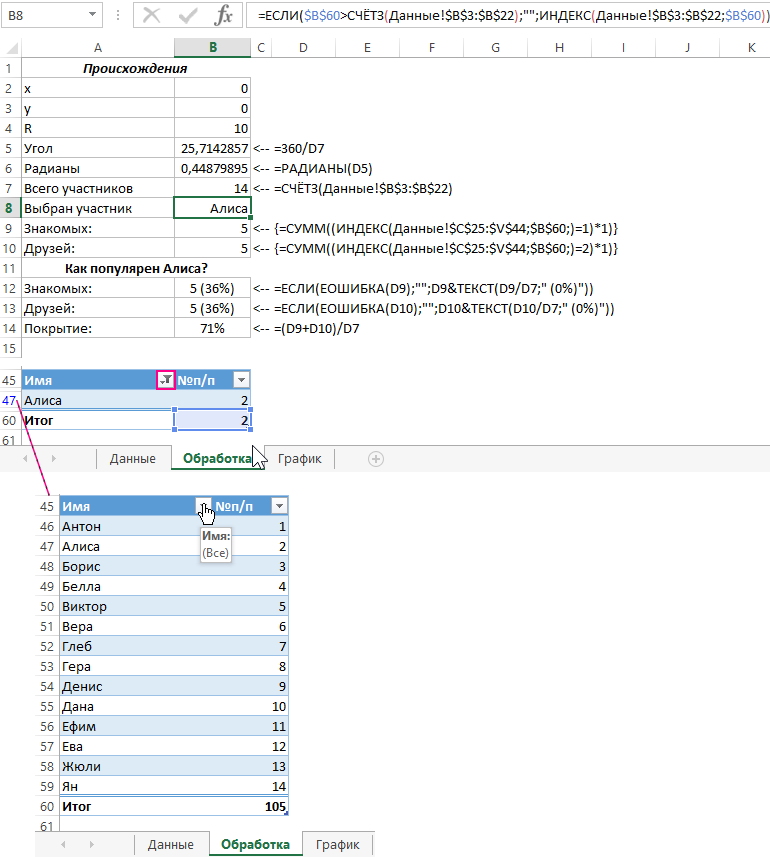
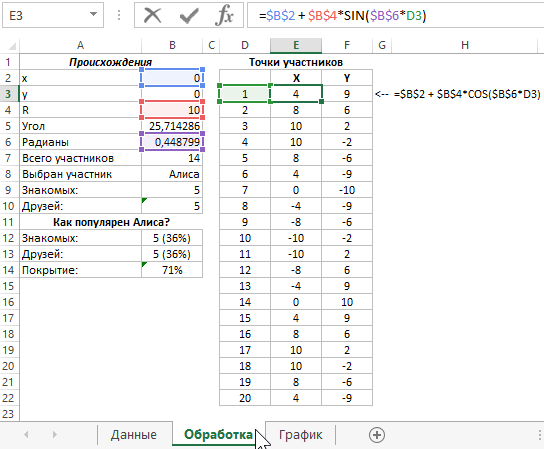
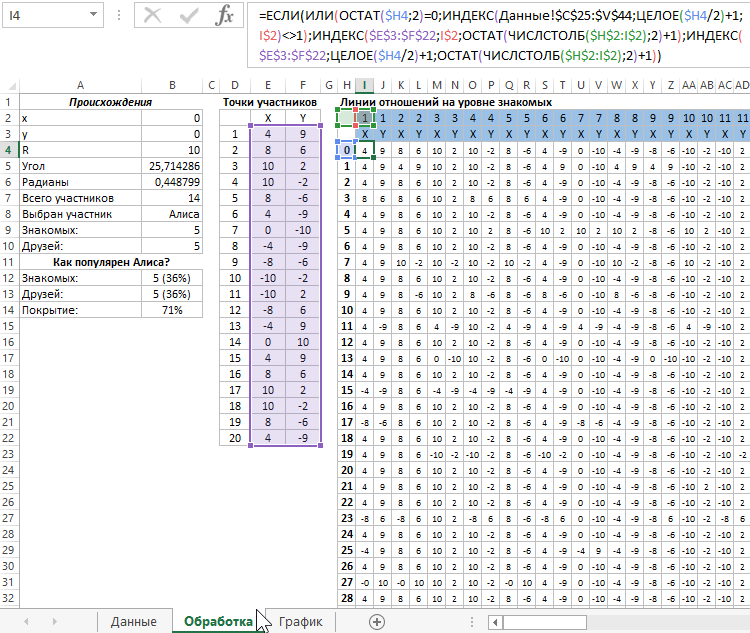
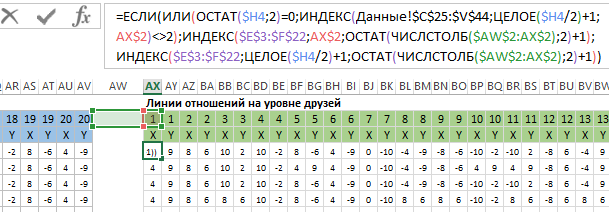
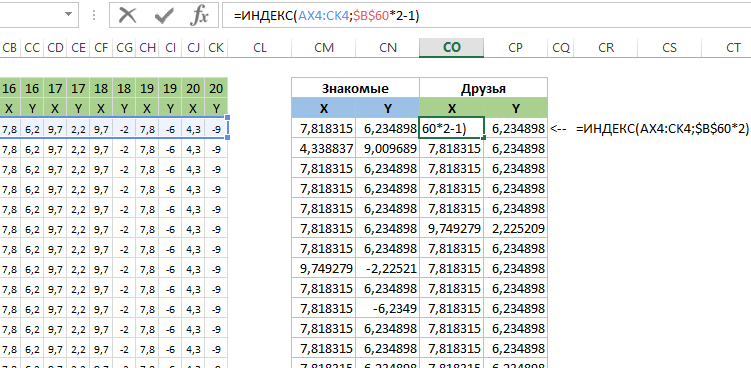
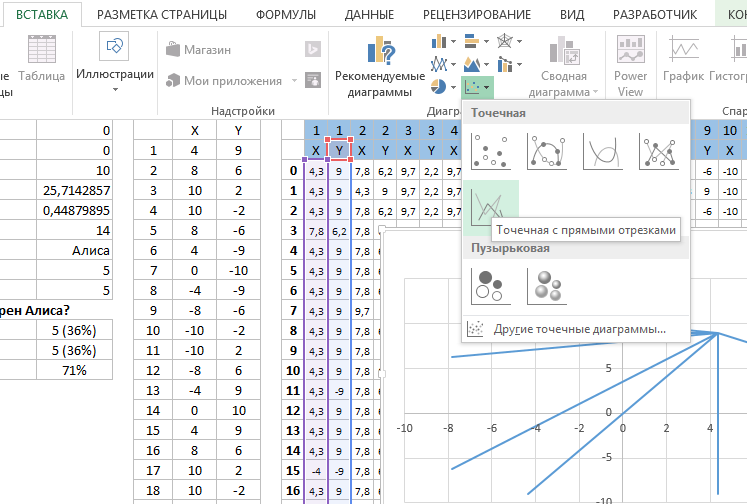
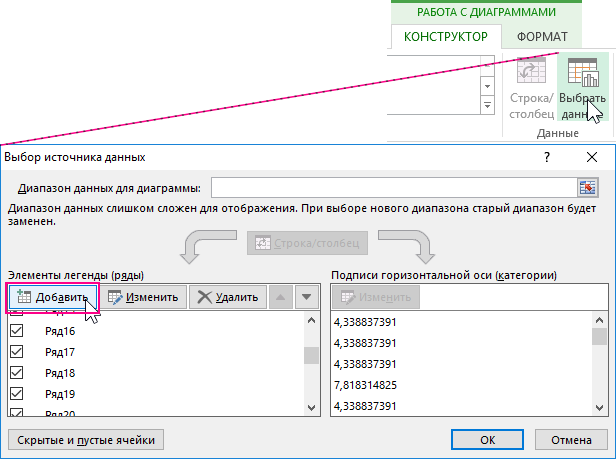
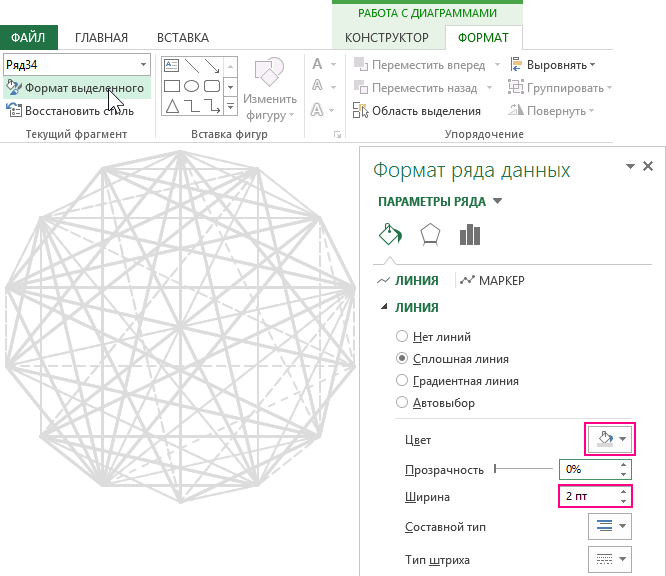
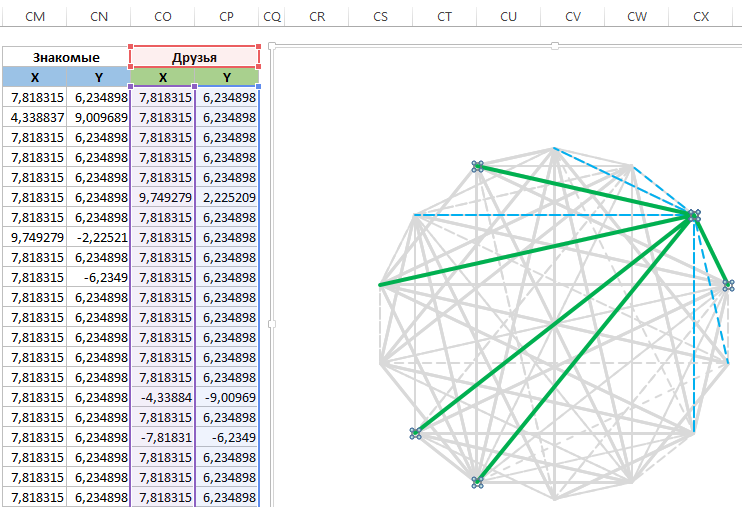

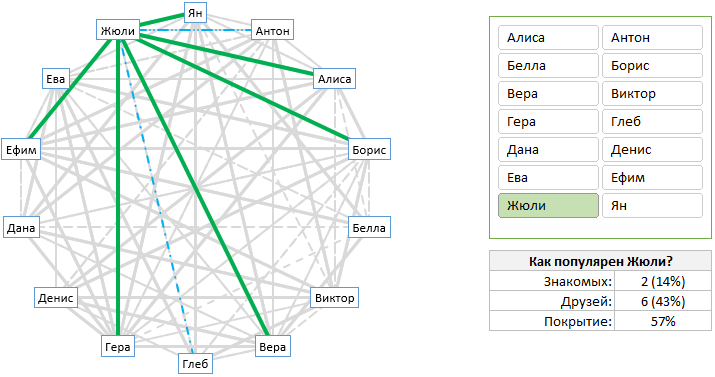
 А там указали что у вас тут даже картинка не того?
А там указали что у вас тут даже картинка не того?