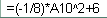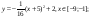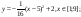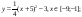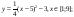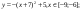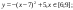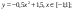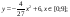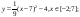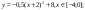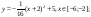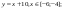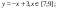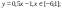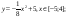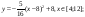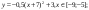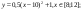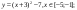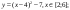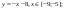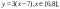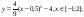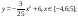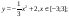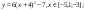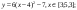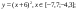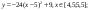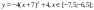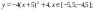Контрольная работа «Электронные
таблицы».
1.
В
электронной таблице основной элемент рабочего листа – это:
1) ячейка;
2)
строка;
3)
столбец;
4)
формула.
2.
Выберите
верное обозначение строки в электронной таблице:
1)
18D;
2)
K13;
3) 34;
4)
AB.
3.
Выберите
верный адрес ячейки в электронной таблице:
1)
11D;
2) F12;
3)
AБ3;
4)
B1A.
4.
Диапазон
— это:
1) совокупность
клеток, образующих в таблице область прямоугольной формы;
2)
все
ячейки одной строки;
3)
все
ячейки одного столбца;
4) множество
допустимых значений.
5.
Чему
будет равно значение ячейки С1, если в нее ввести формулу =СУММ(A1:A7)/2:
1.
280;
2.
140;
3.
40;
4.
35?
6.
Результатом вычислений в ячейке С1 будет:
7.
Электронную
таблицу нельзя применить для:
1)
сортировки
табличных данных;
2)
выполнения
математических и экономических расчетов;
3)
построения
графиков и диаграмм;
4) обработки
графических изображений.
8. В
электронной таблице ячейкой называют:
1.
горизонтальную
строку;
2.
вертикальный
столбец;
3.
пересечение строки и столбца;
4.
курсор
– рамку на экране.
9.Выберите верное обозначение столбца в
электронной таблице:
a.
D;
b.
F12;
c.
AБ;
d.
113.
10.В ячейке электронной таблицы не может
находиться:
a.
число;
b.
текст;
c.
лист;
d.
формула.
11. Выберите верную
запись формулы для электронной таблицы:
1.
C3+4*D4
2.
C3=C1+2*C2
3.
A5B5+23
4.
=A2*A3-A4
12 . Чему будет
равно значение ячейки С1, если в нее ввести формулу =А1+B1:
1.
20;
2.
15;
3.
10;
4.
30?
13. График функции
можно создать в Excel при помощи:
1. Строки формул;
2. Мастера Функций;
3. Мастера Шаблонов;
4. Мастера Диаграмм.
14. Гистограмма
наиболее пригодна для:
1. отображения распределений;
2. отображения динамики изменения данных;
3. сравнения различных
членов группы;
4. отображения удельных соотношений различных признаков
15. Диаграмма это:
1. карта местности;
2. форма графического представления
числовых значений, которая позволяет облегчить интерпретацию числовых данных;
3. красиво оформленная таблица;
4. обычный график.
16. Диаграмма в
электронных таблицах – это:
1. качественно оформленная числовая таблица;
2. график,
отображающий зависимость между всеми числами таблицы;
3. средство
наглядного графического изображения информации, предназначенное для сравнения
нескольких величин или нескольких значений одной величины, слежения за
изменением их значений и т. п.
4.
зависимость между числовыми значениями
17. Круговая
диаграмма – это диаграмма:
представленная в виде круга, разбитого на секторы, в которой
допускается только один ряд данных;
в которой отдельные ряды данных представлены в виде закрашенных
разными цветами областей;
в которой используется система координат с тремя координатными
осями, что позволяет получить эффект пространственного представления рядов
данных;
в которой отдельные значения представлены точками в декартовой
состеме координат.
18. В каком разделе
меню табличного процессора Excel находится Мастер Диаграмм:
1. Правка;
2. Вставка;
3. Сервис;
4. Данные.
19. Диаграмма, в которой отдельные значения
представлены точками в декартовой системе координат, называется:
1. линейчатой;
2. точечной;
3. круговой;
4. гистограммой.
20 . На основе чего
строится любая диаграмма?
а. книги Excel
б. графического файла
в. текстового файла
г. данных таблицы
21. Дана электронная таблица:
|
А |
В |
С |
D |
|
|
1 |
1 |
3 |
4 |
|
|
2 |
4 |
2 |
5 |
|
|
3 |
3 |
1 |
2 |
В ячейку D1 введена формула,
вычисляющая выражение по формуле=(A2+B1-C1).
В результате в ячейке D1 появится
значение…
1)
1
2)
2
3) 3
4) 4
22. Значение в ячейке С3 электронной таблицы
|
А |
В |
С |
|
|
1 |
3 |
9 |
=В2+$A$1 |
|
2 |
7 |
15 |
3 |
|
3 |
45 |
4 |
=C1-C2 |
равно
1)
27
2)
15
3) 34
4) 27
23. Значение С6 электронной таблицы
|
А |
В |
С |
|
|
1 |
3 |
3 |
=СУММ(В2:С3) |
|
2 |
0 |
2 |
6 |
|
3 |
=СТЕПЕНЬ(А5;2) |
5 |
3 |
|
4 |
6 |
=МАКС(В1:В3) |
7 |
|
5 |
5 |
4 |
35 |
|
6 |
=А3/В4+С1 |
равно
1) 22
2)
39
3) 26
4) 21
24. Дана электронная таблица:
|
А |
В |
С |
D |
|
|
1 |
1 |
3 |
4 |
8 |
|
2 |
3 |
2 |
5 |
|
|
3 |
7 |
1 |
2 |
Значение в ячейке С1 заменили на 7. В результате
этого значение в ячейке D1 автоматически изменилось на 11. Можно предположить
что в ячейке D1 ……
1) записана
формула В1+С1
2) при любом
изменении таблицы значение увеличивается на 3
3) записана
формула СУММ(А1:С1)
4) записана
формула СУММА(А1:А3)
25. Дан фрагмент электронной таблицы:
|
А |
В |
С |
|
|
1 |
3 |
2 |
5 |
|
2 |
7 |
1 |
|
|
3 |
4 |
4 |
Значение ячейки С1 вычисляется по формуле
=В1+$A$1
После копирования формулы значение в
ячейке С3 будет равно
1) 10
2)
6
3) 7
4) 8
26. Электронная
таблица предназначена для:
1.обработки преимущественно числовых
данных, структурированных с помощью таблиц;
1.
упорядоченного
хранения и обработки значительных массивов данных;
2.
визуализации
структурных связей между данными, представленными в таблицах;
3.
редактирования
графических представлений больших объемов информации.
27.
Документом
(объектом обработки) MS Excel является файл с произвольным именем и
1) расширением .doc
2) расширением .xls
3) расширением .bmp
28.
В
терминахMS Excel
файл называется:
1) рабочим журналом
2) рабочей страницей
3) рабочей книгой
29.
Минимальной составляющей таблицы в программе
Excel является …
1) ячейка
3) книга
2) формула
4) нет верного ответа
30.
Ниже в
табличной форме представлен фрагмент базы данных:
|
№ |
Наименование |
Цена |
Количество |
Стоимость |
|
1 |
Монитор |
7654 |
20 |
153080 |
|
2 |
Клавиатура |
1340 |
26 |
34840 |
|
3 |
Мышь |
235 |
34 |
7990 |
|
4 |
Принтер |
3770 |
8 |
22620 |
|
5 |
Колонки |
480 |
16 |
7680 |
|
6 |
Сканер |
2880 |
10 |
28800 |
На какой позиции окажется товар «Сканер»
после сортировки данной таблицы по возрастанию столбца
«Количество»?
1) 1 2) 2 3)
6 4) 5
ТЕСТ №1 «Электронные таблицы»
ВАРИАНТ 1
- Электронная таблица предназначена для:
1.обработки преимущественно числовых данных, структурированных с помощью таблиц;
- упорядоченного хранения и обработки значительных массивов данных;
- визуализации структурных связей между данными, представленными в таблицах;
- редактирования графических представлений больших объемов информации.
- В электронной таблице основной элемент рабочего листа – это:
- ячейка;
- строка;
- столбец;
- формула.
- Выберите верное обозначение строки в электронной таблице:
- 18D;
- K13;
- 34;
- AB.
- Выберите верный адрес ячейки в электронной таблице:
- 11D;
- F12;
- AБ3;
- B1A.
5. Выражение 5(A2+C3):3(2B2-3D3) в электронной таблице имеет вид:
- 5(A2+C3)/3(2B2-3D3) ;
- 5*(A2+C3)/3*(2*B2-3*D3) ;
- 5*(A2+C3)/(3*(2*B2-3*D3)) ;
- 5(A2+C3)/(3(2B2-3D3)) .
6. Активная ячейка — это ячейка:
- для записи команд;
- содержащая формулу, включающую в себя имя ячейки, в которой выполняется ввод данных;
- формула в которой содержатся ссылки на содержимое зависимой ячейки;
- в которой выполняется ввод команд.
7. Диапазон — это:
- совокупность клеток, образующих в таблице область прямоугольной формы;
- все ячейки одной строки;
- все ячейки одного столбца;
- множество допустимых значений.
8. Чему будет равно значение ячейки С1, если в нее ввести формулу =СУММ(A1:A7)/2:
- 280;
- 140;
- 40;
- 35?
9. Результатом вычислений в ячейке С1 будет:
10. Выражение 3(A1 + B1) : 5(2B1 — 3A2), записанное в соответствии с правилами, принятыми в математике, в электронной таблице имеет вид:
1. 3*(A1 + B1) / (5*(2*B1 — 3*A2))
2. 3(A1 + B1) : 5(2B1 — 3A2)
3. 3(A1 + B1) / (5(2B1 — 3A2))
4. 3(A1 + B1) / 5(2B1 — 3A2)
ТЕСТ №1 «Электронная таблица».
ВАРИАНТ 2
- Электронную таблицу нельзя применить для:
- сортировки табличных данных;
- выполнения математических и экономических расчетов;
- построения графиков и диаграмм;
- обработки графических изображений.
2. Электронная таблица представляет собой:
- совокупность нумерованных строк и поименованных буквами латинского алфавита столбцов;
- совокупность поименованных буквами латинского алфавита строк и нумерованных столбцов;
- совокупность пронумерованных строк и столбцов;
- совокупность строк и столбцов, именуемых пользователем произвольным образом.
3. Строки электронной таблицы:
- именуются пользователями произвольным образом;
- обозначаются буквами русского алфавита;
- обозначаются буквами латинского алфавита;
- нумеруются.
4. В электронной таблице ячейкой называют:
- горизонтальную строку;
- вертикальный столбец;
- пересечение строки и столбца;
- курсор – рамку на экране.
- Выберите верное обозначение столбца в электронной таблице:
- DF;
- F12;
- AБ;
- 113.
- В ячейке электронной таблицы не может находиться:
- число;
- текст;
- лист;
- формула.
7. Выберите верную запись формулы для электронной таблицы:
- C3+4*D4
- C3=C1+2*C2
- A5B5+23
- =A2*A3-A4
8. Чему будет равно значение ячейки С1, если в нее ввести формулу =А1+B1:
- 20;
- 15;
- 10;
- 30?
9. Результатом вычислений в ячейке С1 будет:
|
А |
В |
С |
|
|
1 |
5 |
= А1*2 |
=СУММ(А1:В1)*А1 |
1. 25 2. 50 3. 75 4. 100
10. Какая формула будет получена при копировании в ячейку С3, формулы из ячейки С2:
- =A1*A2+B2;
- =$A$1*$A$2+$B$2;
- =$A$1*A3+B3;
- =$A$2*A3+B3;
- =$B$2*A3+B4?
ТЕСТ №2 «Диаграммы и графики в электронных таблицах»
1. Деловая графика представляет собой:
1. совокупность графиков функций;
2. графические иллюстрации;
3. график совещания;
4. совокупность программных средств, позволяющих представить в графическом виде закономерности изменения числовых данных.
- График функции можно создать в Excel при помощи:
1. Строки формул;
2. Мастера Функций;
3. Мастера Шаблонов;
4. Мастера Диаграмм.
- Гистограмма наиболее пригодна для:
1. отображения распределений;
2. отображения динамики изменения данных;
3. сравнения различных членов группы;
4. отображения удельных соотношений различных признаков.
- Диаграмма это:
1. карта местности;
2. форма графического представления числовых значений, которая позволяет облегчить интерпретацию числовых данных;
3. красиво оформленная таблица;
4. обычный график.
- Диаграмма в электронных таблицах – это:
1. качественно оформленная числовая таблица;
2. график, отображающий зависимость между всеми числами таблицы;
3. средство наглядного графического изображения информации, предназначенное для сравнения нескольких величин или нескольких значений одной величины, слежения за изменением их значений и т. п.
4. зависимость между числовыми значениями.
- Круговая диаграмма – это диаграмма:
- представленная в виде круга, разбитого на секторы, в которой допускается только один ряд данных;
- в которой отдельные ряды данных представлены в виде закрашенных разными цветами областей;
- в которой используется система координат с тремя координатными осями, что позволяет получить эффект пространственного представления рядов данных;
- в которой отдельные значения представлены точками в декартовой состеме координат.
- В каком разделе меню табличного процессора Excel находится Мастер Диаграмм:
1. Правка;
2. Вставка;
3. Сервис;
4. Данные.
- Форма графического представления числовых значений, позволяющая облегчить восприятие и интерпретацию числовых данных, называется:
1. чертежом;
2. картой;
3. блок-схемой;
4. диаграммой.
9. Гистограмма – это диаграмма, в которой:
1. отдельные значения представлены полосами различной длины, расположенными горизонтально вдоль оси ОХ
2. отдельные значения представлены вертикальными столбцами различной высоты;
3. используется система координат с тремя координатными осями, что позволяет получить эффект пространственного представления рядов данных;
4. для представления отдельных значений используются параллелепипеды, размещенные вдоль оси ОХ.
10. Диаграмма, в которой отдельные значения представлены точками в декартовой системе координат, называется:
1. линейчатой;
2. точечной;
3. круговой;
4. гистограммой.
11. Линейчатая диаграмма – это диаграмма:
1. в которой отдельные значения представлены вертикальными столбиками различной высоты;
2. в которой отдельные значения представлены точками в декартовой системе координат;
3. в которой отдельные значения представлены полосами различной длины, расположенными горизонтально вдоль оси ОХ
4. представленная в виде круга, разбитого на секторы, и в которой допускается только один ряд данных.
12. Чтобы отформатировать какой-либо элемент диаграммы, необходимо:
1. дважды щелкнуть по нему курсором мыши;
2. выполнить команды Диаграмма, Исходные данные;
3. выполнить команды Диаграмма, Добавить данные;
4. все вышеперечисленные ответы верны.
13. На основе чего строится любая диаграмма?
а. книги Excel
б. графического файла
в. текстового файла
г. данных таблицы
14. Для сравнения нескольких величин в одной точке обычно используется:
1. линейчатая диаграмма;
2. гистограмма;
3. точечная диаграмма;
4. круговая диаграмма.
ТЕСТ №3 «Базы данных в электронных таблицах».
1. База данных — это:
- совокупность данных, организованных по определенным правилам;
- совокупность программ для хранения и обработки больших массивов информации;
- интерфейс, поддерживающий наполнение и манипулирование данными;
- определенная совокупность информации.
2. Наиболее распространенными в практике являются:
- распределенные базы данных;
- иерархические базы данных;
- сетевые базы данных;
- реляционные базы данных.
3. Таблицы в базах данных предназначены:
- для хранения данных базы;
- для отбора и обработки данных базы;
- для ввода данных базы и их просмотра;
- для автоматического выполнения группы команд;
- для выполнения сложных программных действий.
4. Для чего предназначены запросы:
- для хранения данных базы;
- для отбора и обработки данных базы;
- для ввода данных базы и их просмотра;
- для автоматического выполнения группы команд;
- для выполнения сложных программных действий;
- для вывода обработанных данных базы на принтер?
5. Для чего предназначены формы:
- для хранения данных базы;
- для отбора и обработки данных базы;
- для ввода данных базы и их просмотра;
- для автоматического выполнения группы команд;
- для выполнения сложных программных действий?
6. В каком режиме работает с базой данных пользователь:
- в проектировочном;
- в любительском;
- в заданном;
- в эксплутационном?
7. В каком диалоговом окне создают связи между полями таблиц базы данных:
- таблица связей;
- схема связей;
- схема данных;
- таблица данных?
8. Без каких объектов не может существовать база данных:
- без модулей;
- без отчетов;
- без таблиц;
- без форм;
- без макросов;
- без запросов?
9. В каких элементах таблицы хранятся данные базы:
- в полях;
- в строках;
- в столбцах;
- в записях;
- в ячейках?
10. Содержит ли какую-либо информацию таблица, в которой нет ни одной записи?
- пустая таблица не содержит ни какой информации;
- пустая таблица содержит информацию о структуре базы данных;
- пустая таблица содержит информацию о будущих записях;
- таблица без записей существовать не может.
11. Содержит ли какую-либо информацию таблица, в которой нет полей?
- содержит информацию о структуре базы данных;
- не содержит ни какой информации;
- таблица без полей существовать не может;
- содержит информацию о будущих записях.
12. Ключами поиска в системах управления базами данных (СУБД) называются:
- диапазон записей файла БД, в котором осуществляется поиск;
- логические выражения, определяющие условия поиска;
- поля, по значению которых осуществляется поиск;
- номера записей, удовлетворяющих условиям поиска;
- номер первой по порядку записи, удовлетворяющей условиям поиска?
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
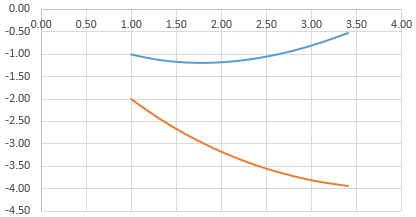
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
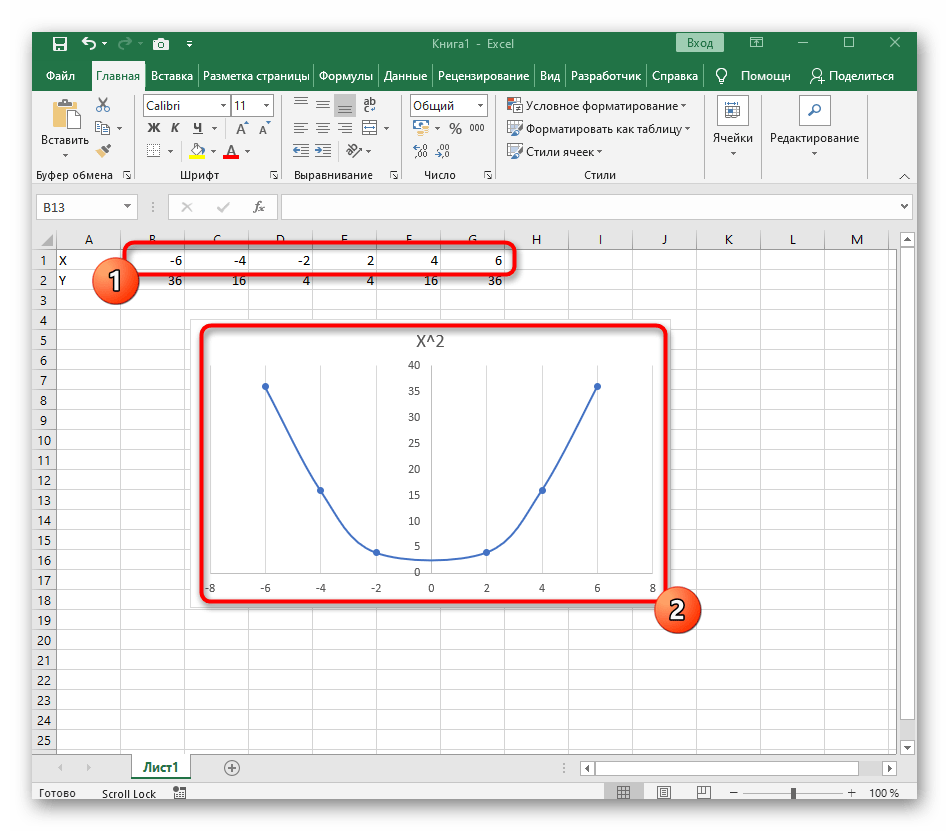
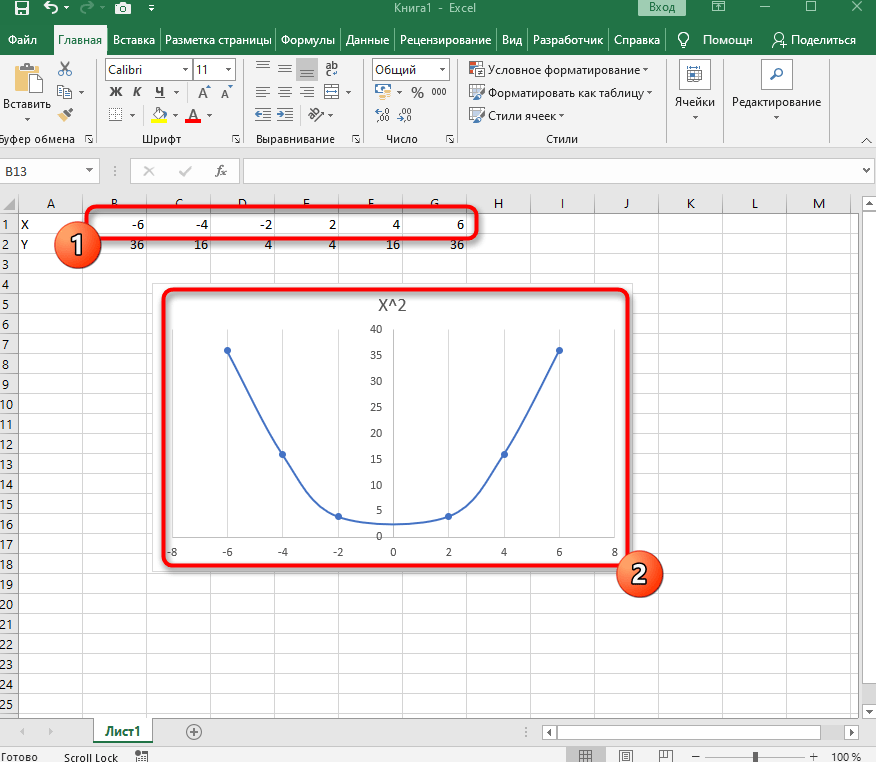
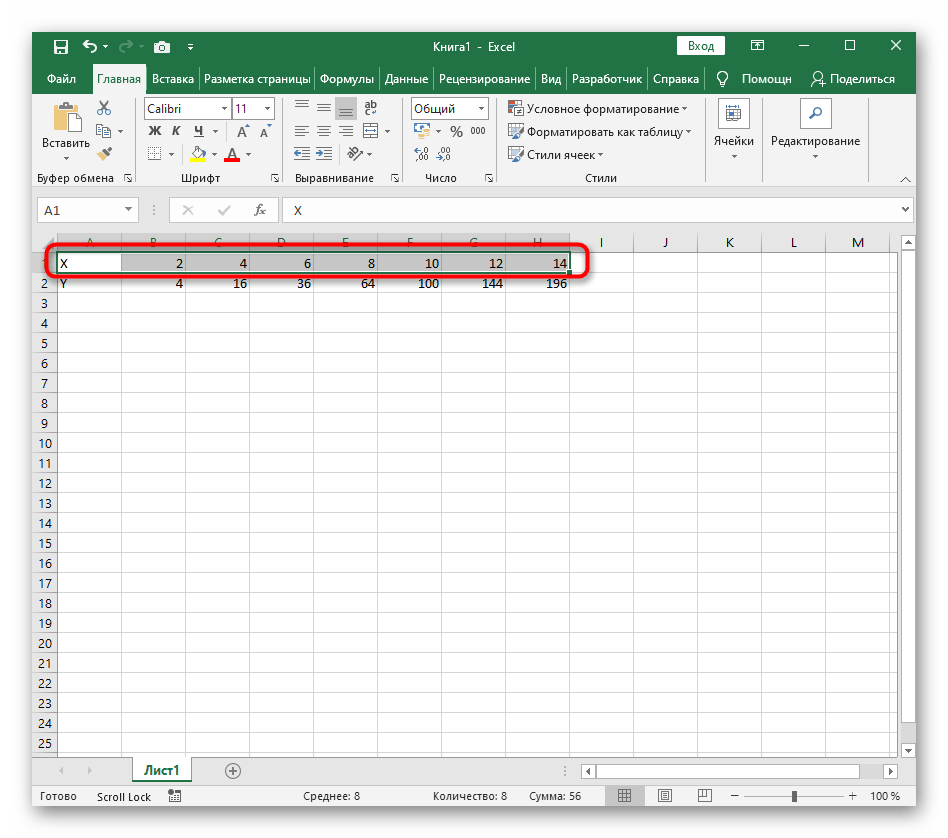
Вариант 1: График функции X^2
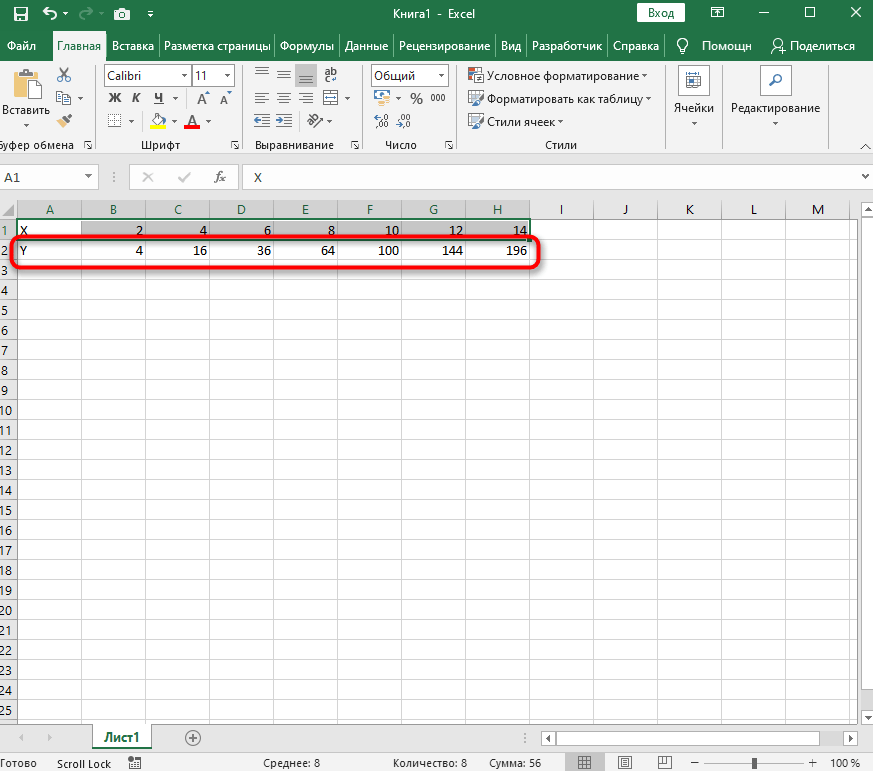
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
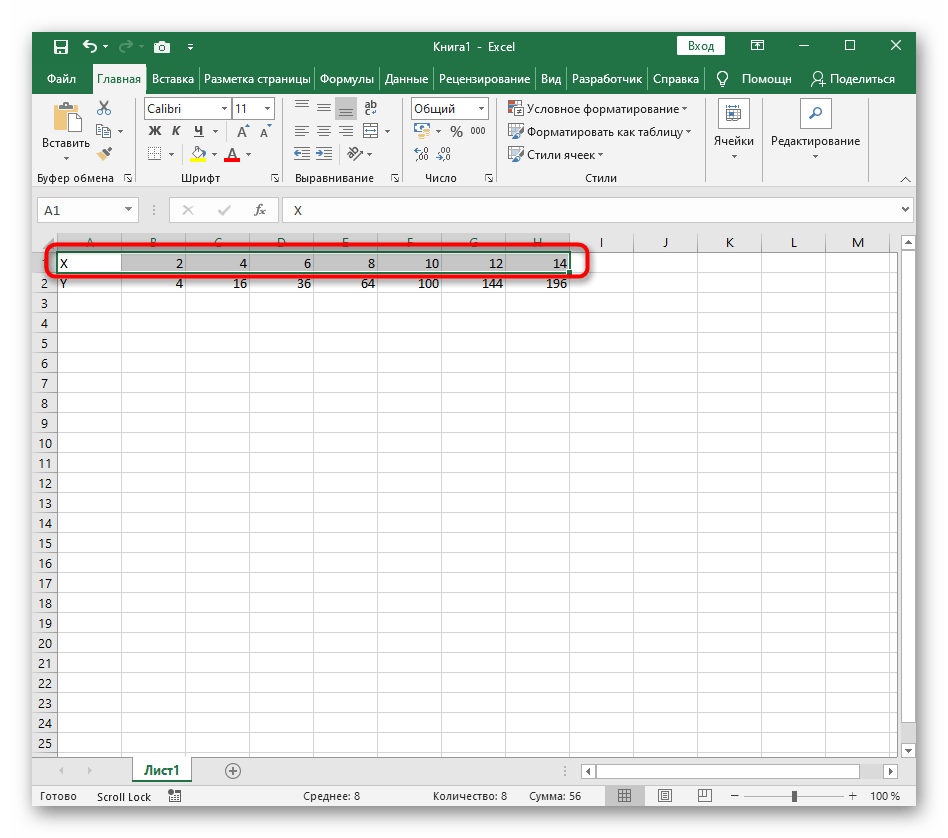
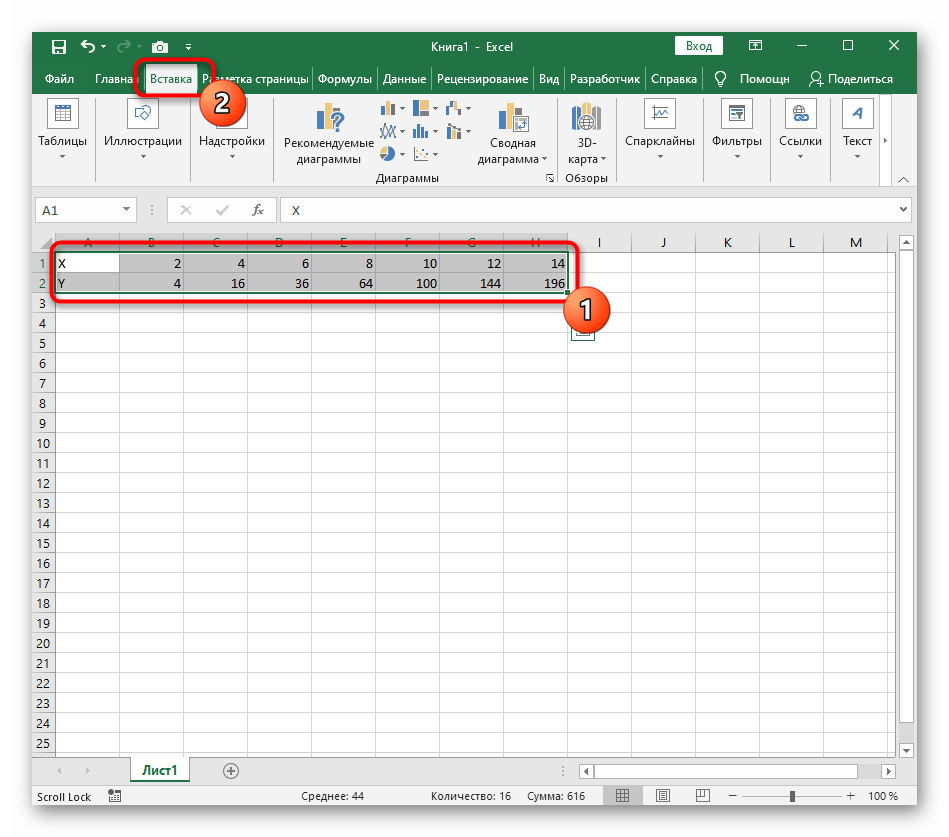
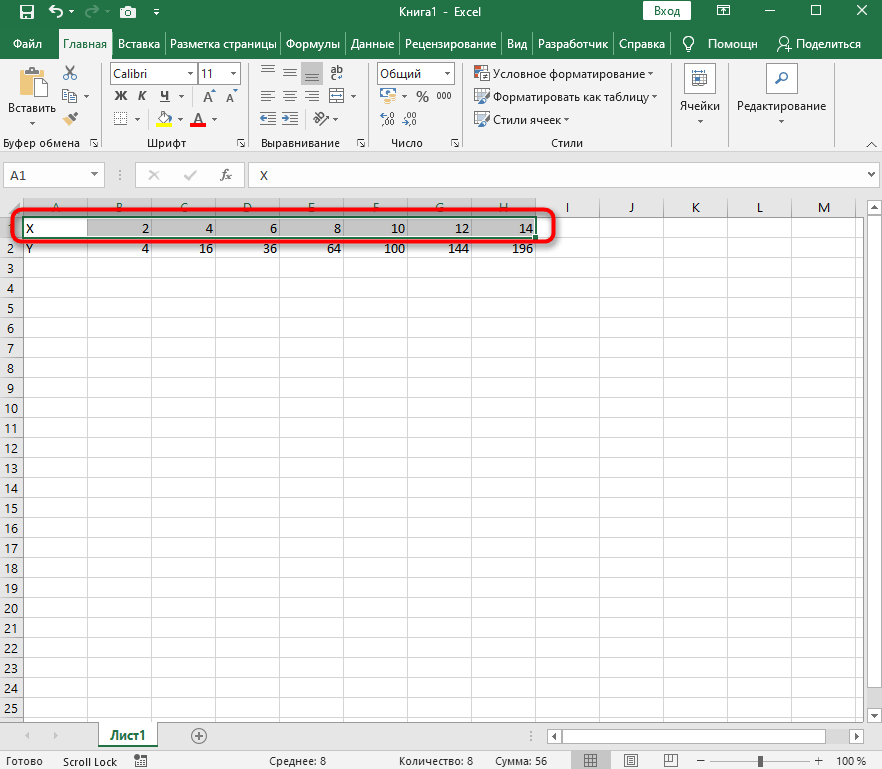
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
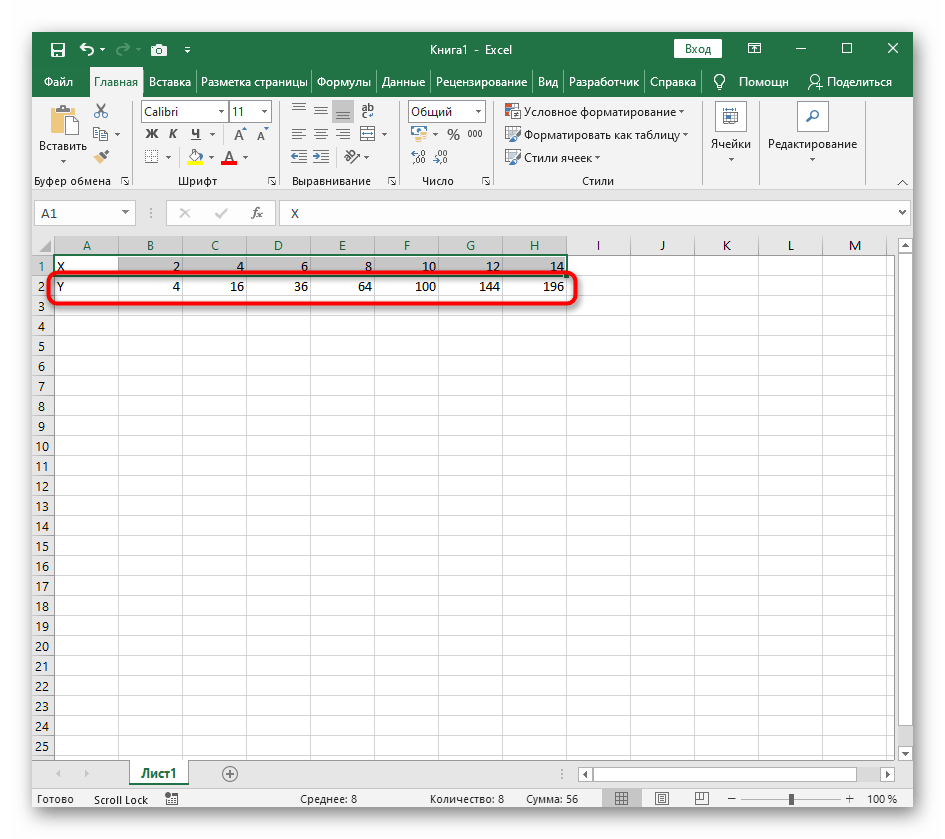
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
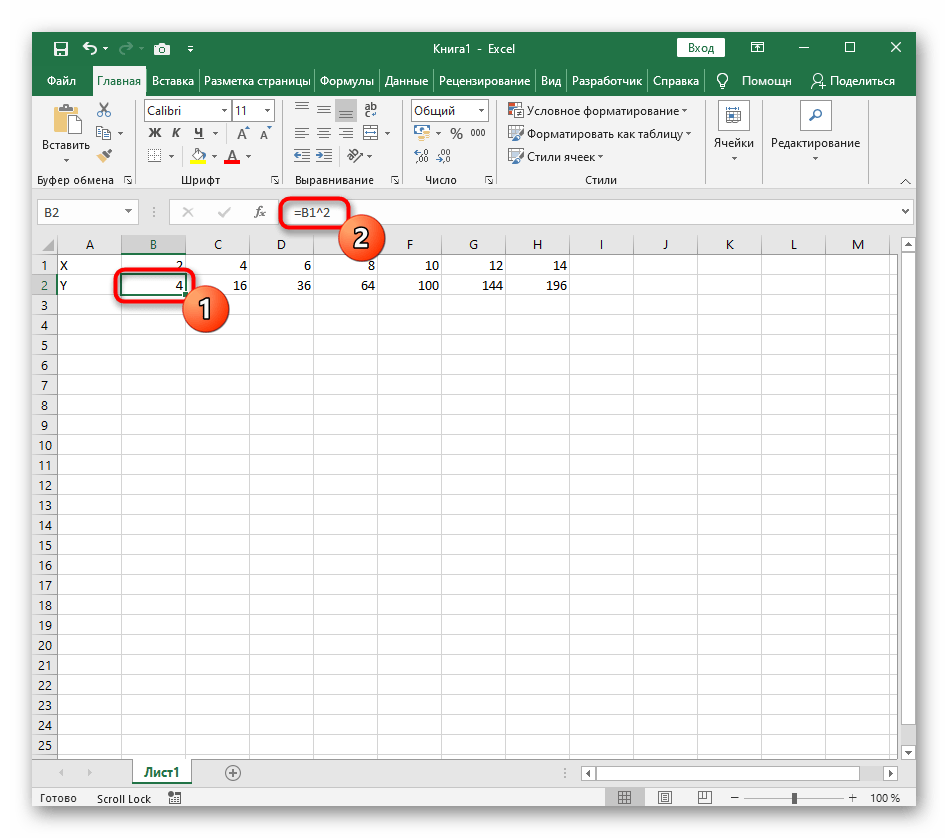
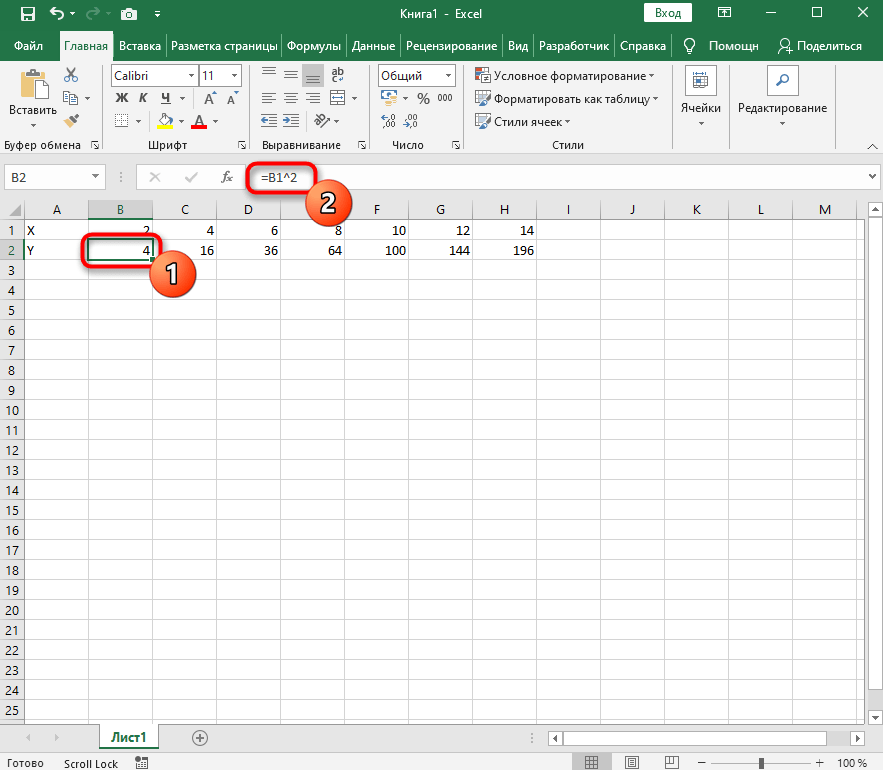
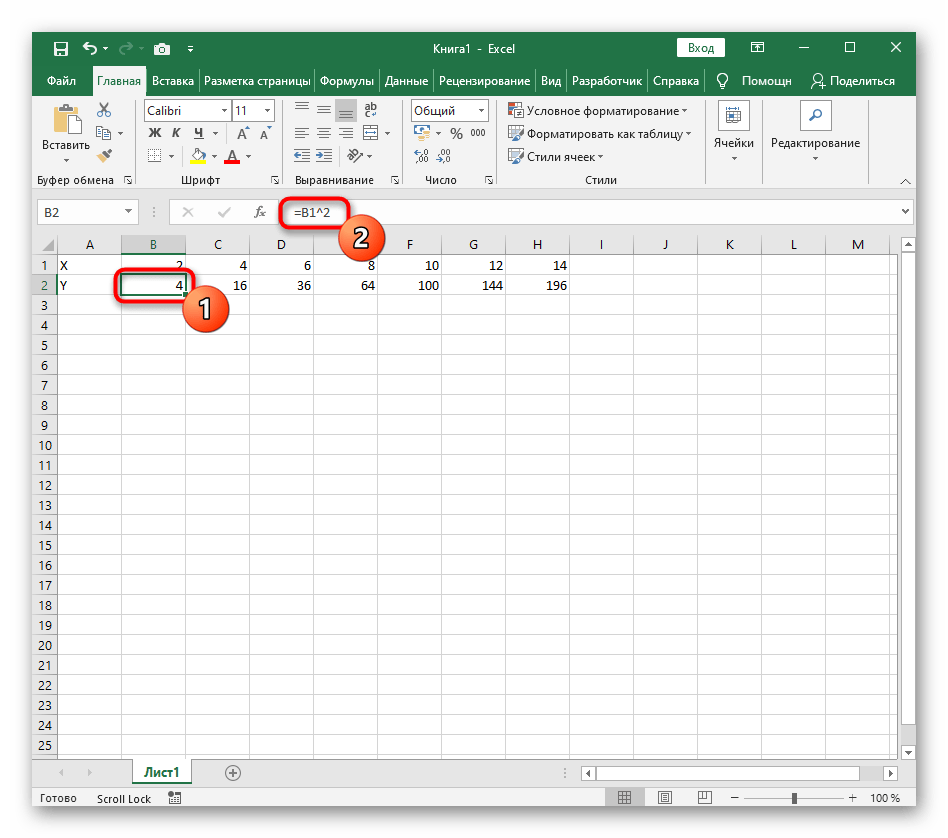
- Нажмите по первой ячейке и впишите
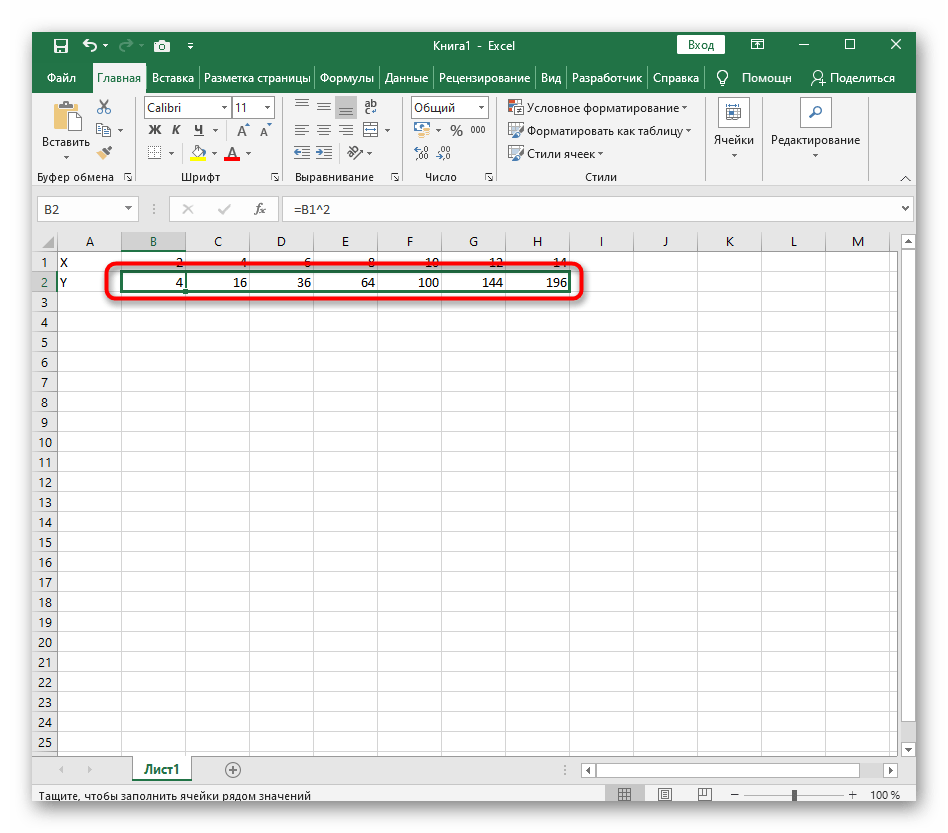
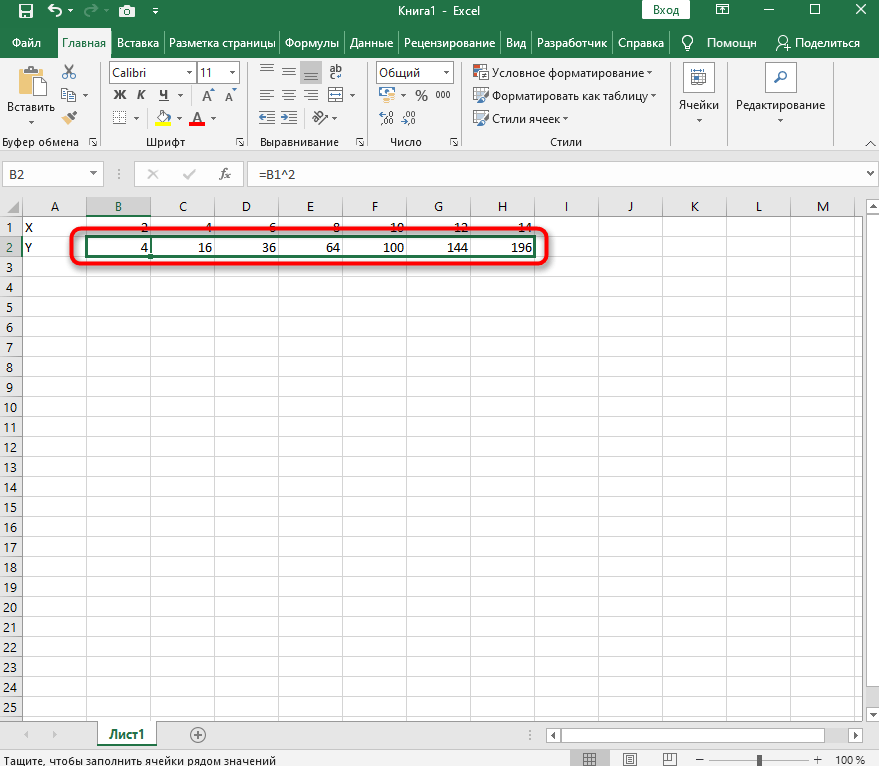
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
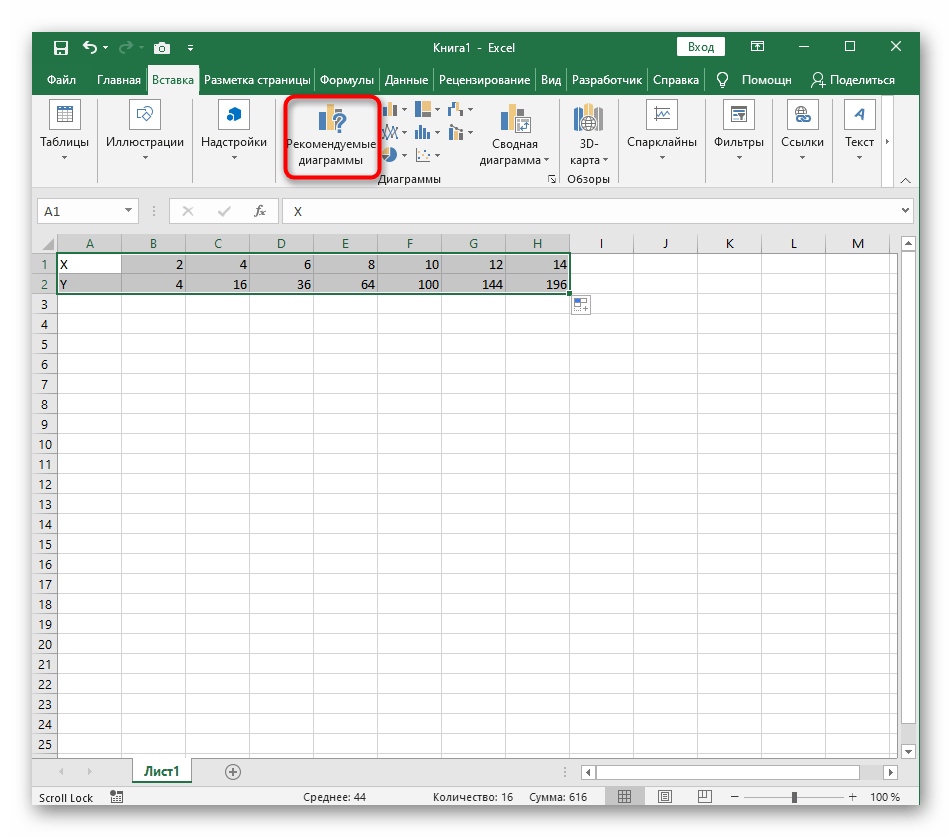
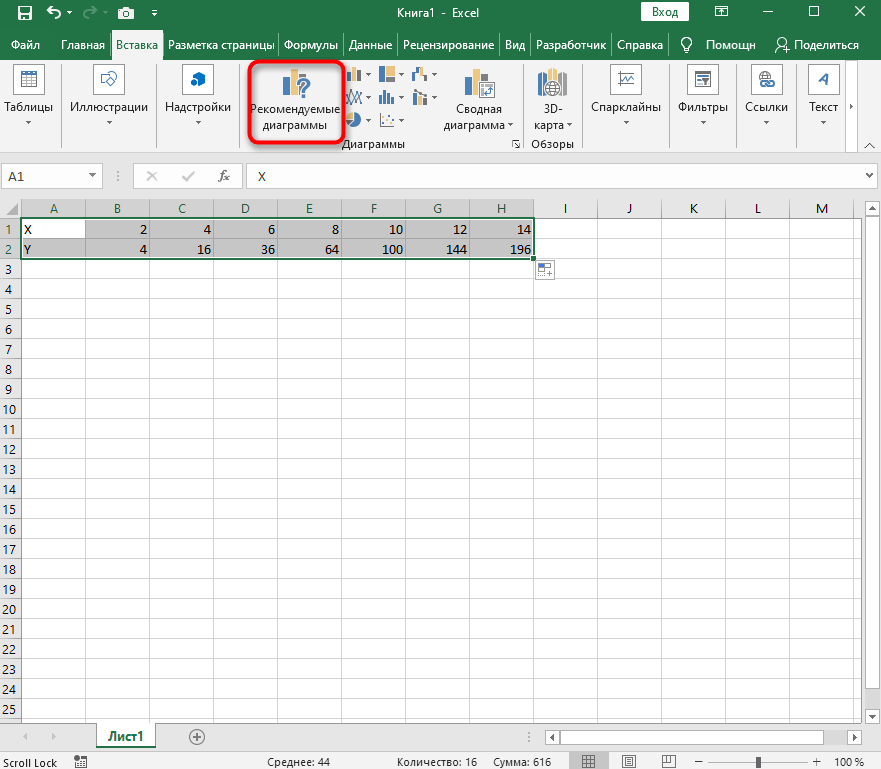
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
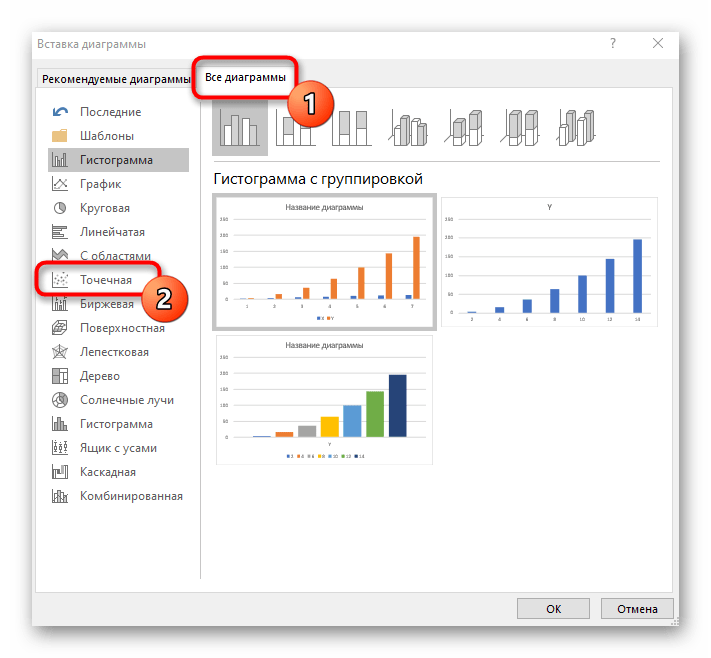
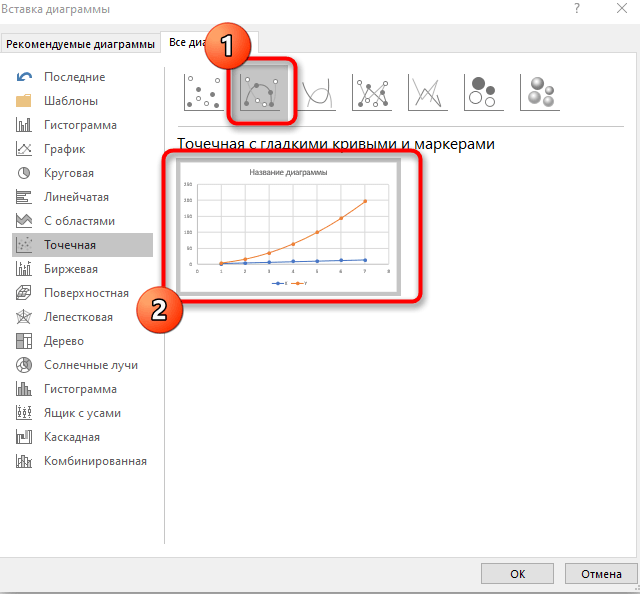
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
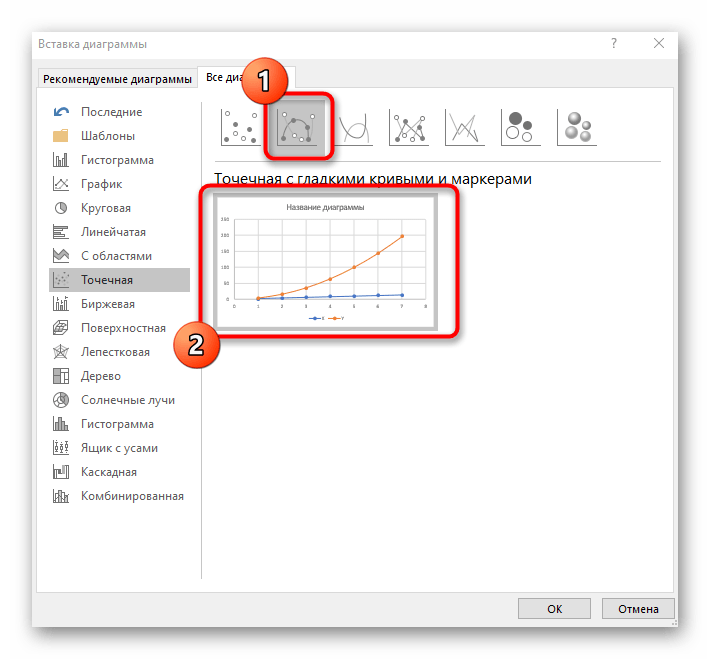
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
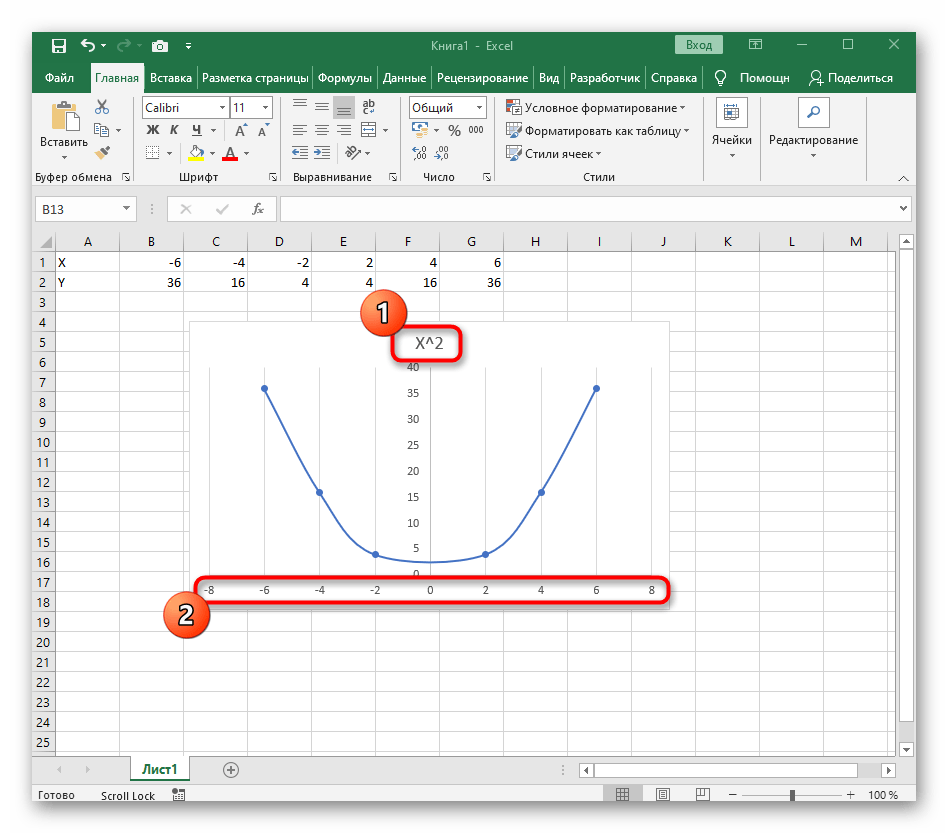
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
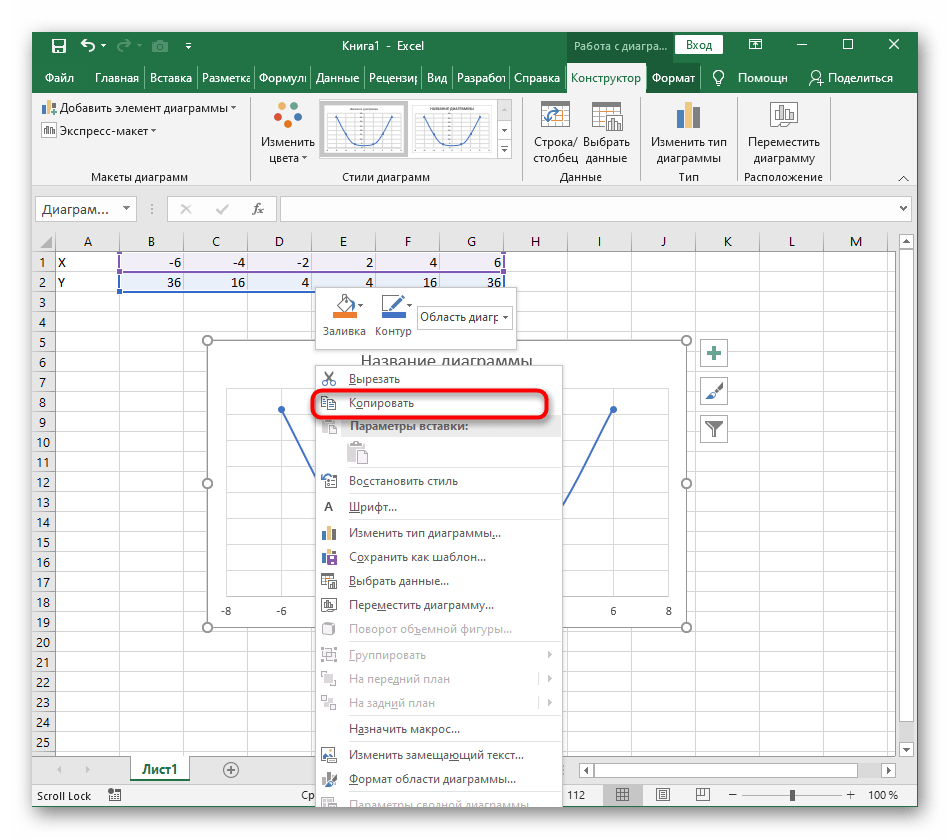
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
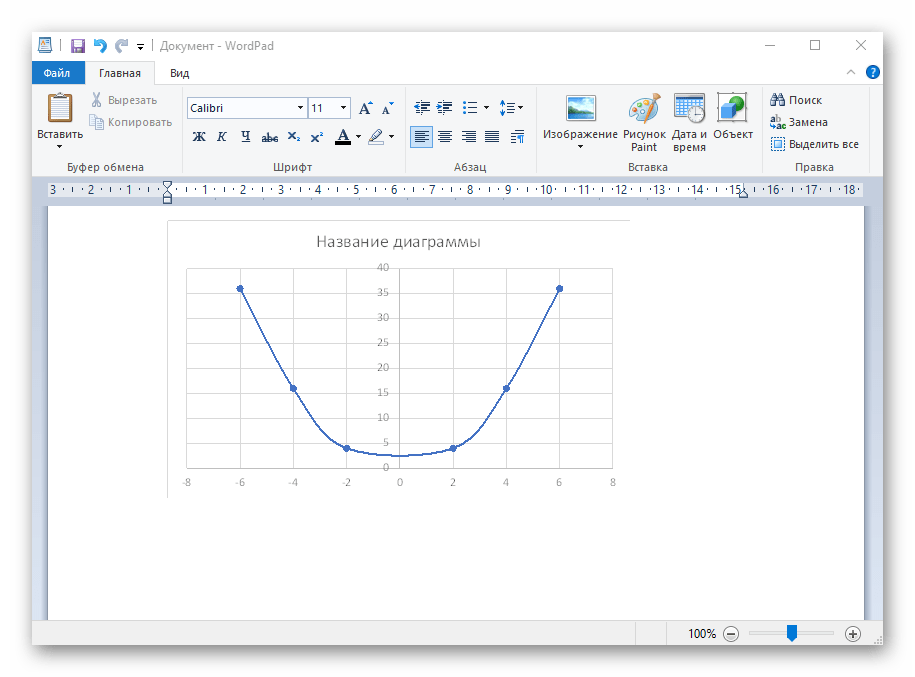
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
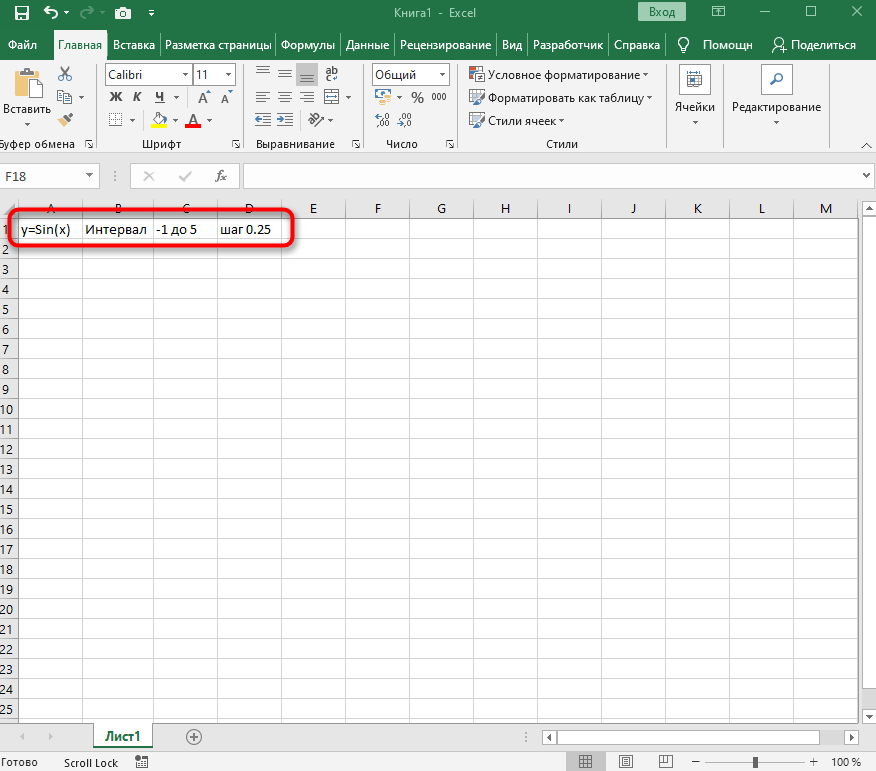
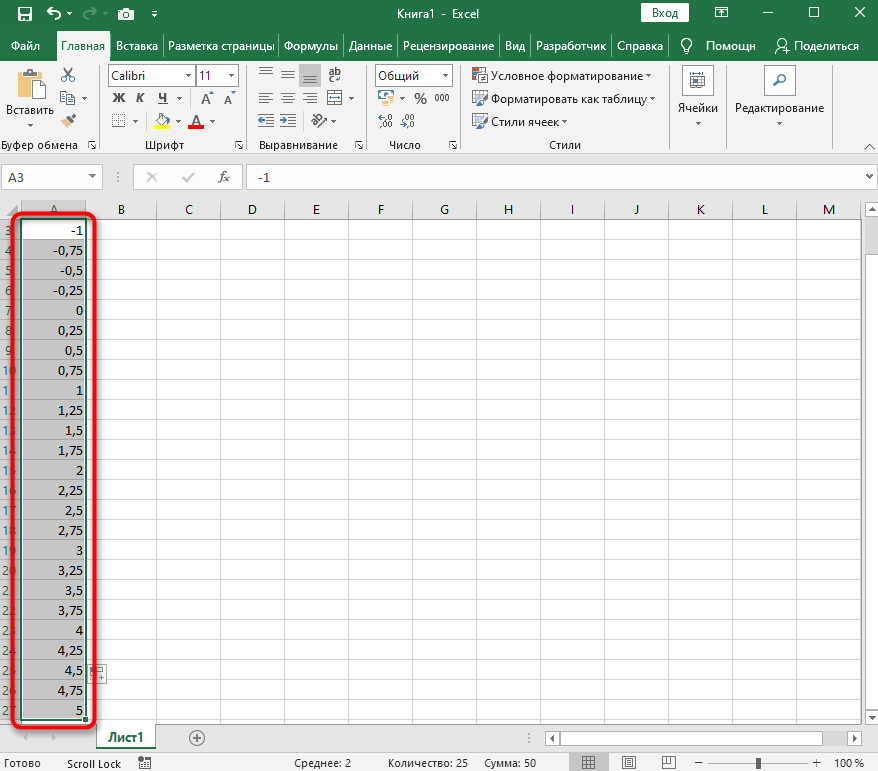
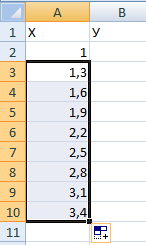
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
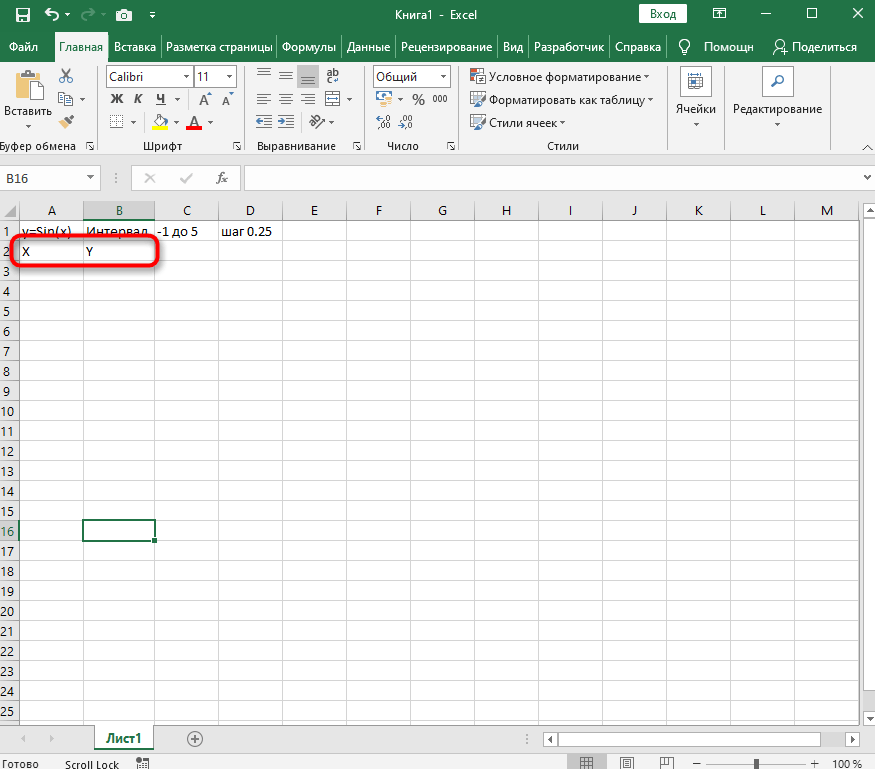
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
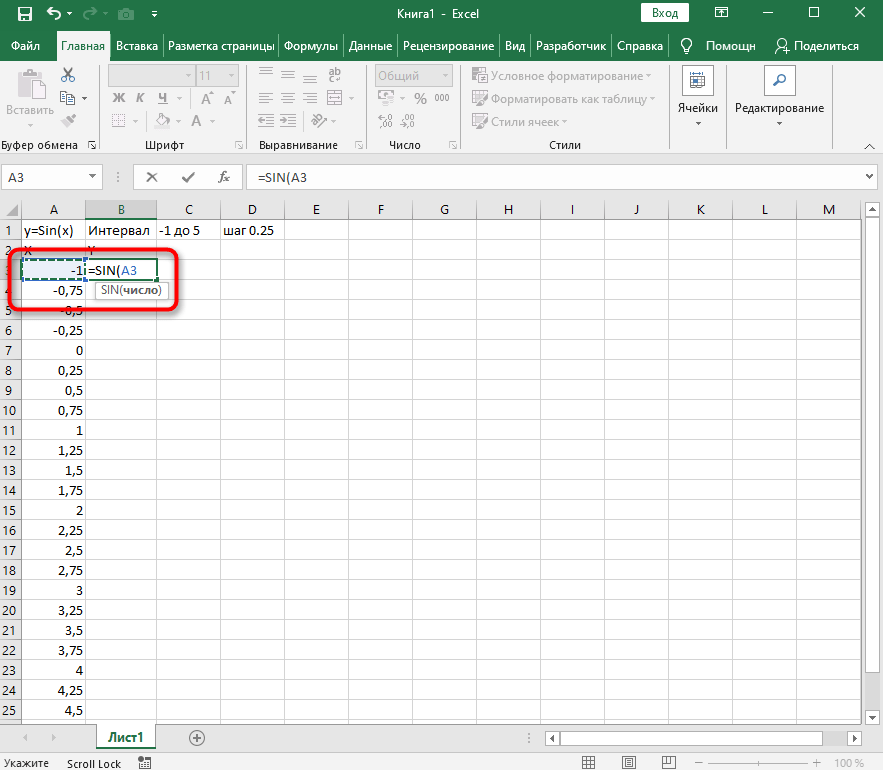
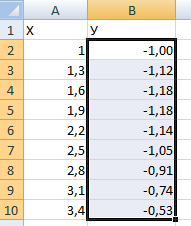
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
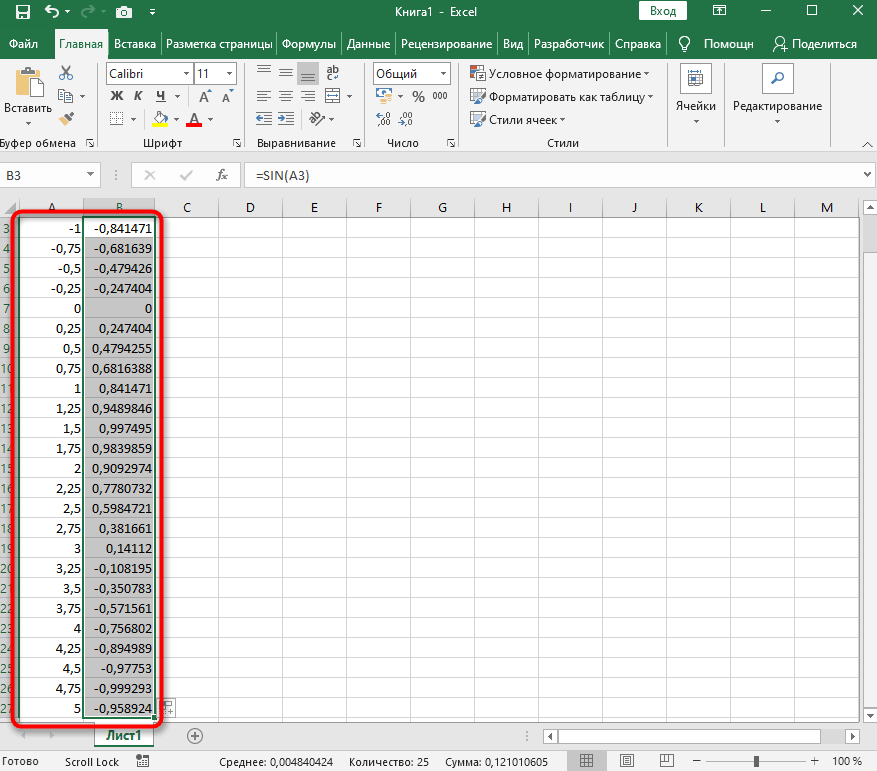
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
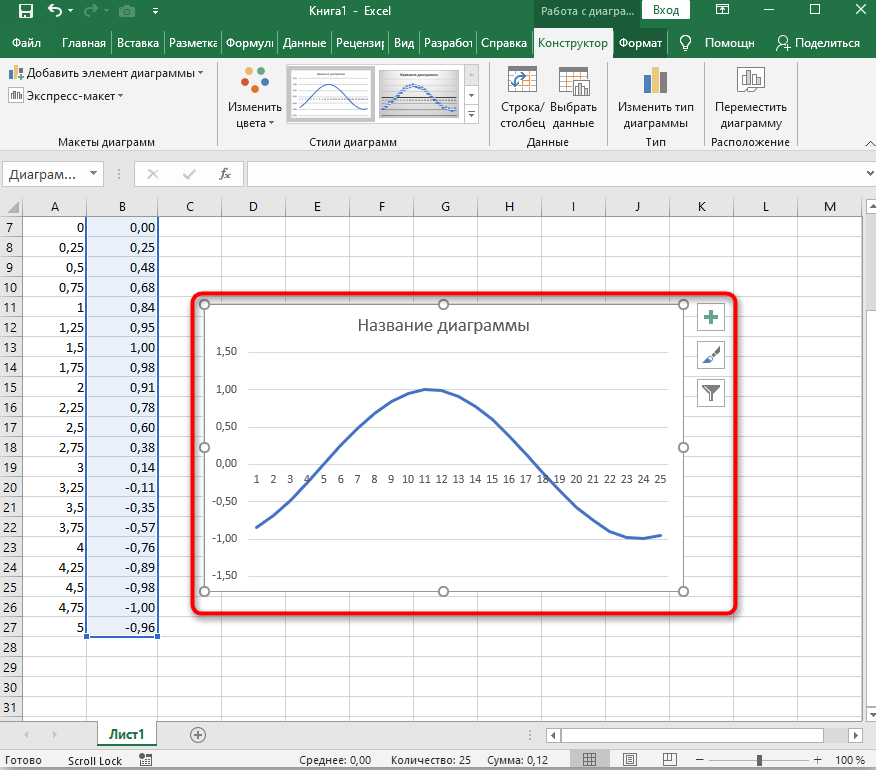
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме:
Помогла ли Вам статья?
График функции – графическое представление математического выражения, показывающее его решение. Для построения обычно используются линейные графики с точками, с чем прекрасно справляется Microsoft Excel. Кроме того, в нем еще можно выполнить автоматические расчеты, быстро подставив нужные значения.
Существует огромное количество функций, поэтому в качестве примера я разберу только две самые наглядные, чтобы вы поняли базовые правила составления подобных элементов в таблице.
Построение графиков в Excel по данным таблицы
В MS Excel есть возможность не только проводить вычисления, используя разные формулы, но и также строить на их основе различные диаграммы: гистограммы, круговые диаграммы, точечные и т.д. В этом уроке мы разберем, для чего применяют графики. И так, графики – это разновидность диаграммы, схожая с гистограммой. Они бывают трех видов: простой, график с накоплением и нормированный график с накоплением. Каждый из этих графиков бывает двух видов: с маркером и без. Так эти два вида строятся одинаково, рассмотрим только маркированные графики. Коротко опишем применение каждого графика, и далее на примерах разберем более подробно, как их построить. a) Простой график нужен для того, чтобы изобразить, как изменяется некое значение во времени (прибыль по месяцам; рождаемость по годам и т.д.). b) График с накоплением показывает, как изменяется составляющая целого значения с течением времени. (Лучше использовать диаграмму с накоплением) c) Нормированный график с накоплением показывает изменение доли каждого значения с течением времени. Есть еще объемный график, который схож с простым графиком. Поэтому мы покажем только его конечный вид.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию =SIN(, а в качестве числа укажите первое значение X.
- Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.
Мы рады, что смогли помочь Вам в решении проблемы. Помимо этой статьи, на сайте еще 12419 инструкций. Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам. Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Простая диаграмма
Рассмотрим простой график на примере таком примере прибыли некоторой фирмы по 3 товарам за определенный период. Для этого выделим нужные нам ячейки, как на рисунке ниже.
Теперь строим простой маркированный график. Для этого выделяем диапазон В1:D6, на главное ленте выбираем Вставка–Диаграммы (нажимаем на стрелочку справа сверху). В появившемся окне выберем нужную нам диаграмму. В первом случае – простой график. Нажимаем ОК.
Выбираем график слева, т.к. он показывает изменение прибыли во времени. Если вы все сделали правильно, то должно получиться так, как на рисунке ниже:
Итак, диаграмма построена, но на ней не отображаются года. Изменить название диаграммы очень просто. Нужно нажать на заголовок и ввести подходящее название. Например, Прибыль по товарам в 2010-214 гг. Для того, чтобы года отображались на оси Х, необходимо нажать на ось правой кнопкой мыши для вызова контекстного меню и нажать Выбрать данные.
После этого появится такое окошко:
Изменяем подписи горизонтальной оси. Должно открыться такое окошко:
Нажимаем туда, где выделено красным и выбираем диапазон. В нашем случае это А2:А6. И нажимаем клавишу Enter и ОК. В результате этого должно открыться предыдущее окно, но выглядеть будет следующим образом:
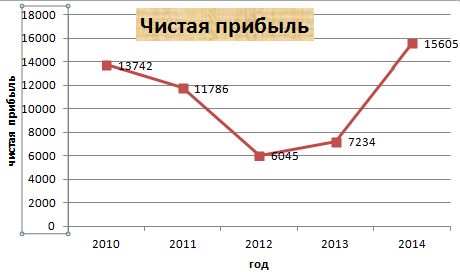
Нажимаем ОК, меняем название диаграммы. Теперь она должна выглядеть так:
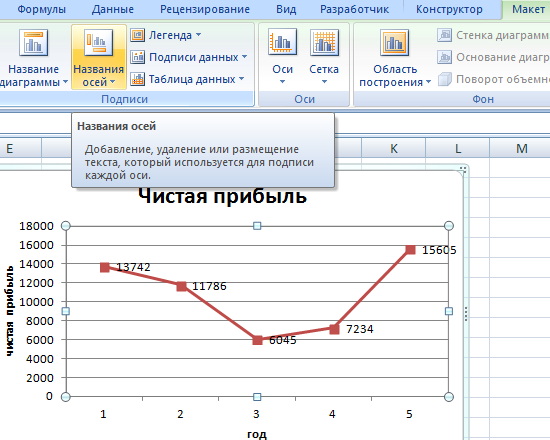
Осталось добавить подписи данных. В версии Excel 2013–2016 это делается очень просто. Нажимаем на плюсик справа, который вызывает различные команды и ставим галочку Название осей. Должно получиться так:
Как и в случае с названием, ставим курсор в область каждой из осей и подписываем их согласно условию. Например, ось Х – Год, ось Y – Прибыль. Должно получиться так, как на рисунке ниже:
В MS Excel версиях 2007-2010 форматировать оси, область диаграммы и т.д. с помощью дополнительной вкладки на ленте Работа с диаграммами.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак , который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
График с накоплением
Строим по этим же данным график с накоплением. Повторяем все те же самые действия, как и в п.1. Поэтому мы покажем начало, на котором видно, какой график выбираем, и конец, на котором виден результат работы.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Объемный график
Объемный график похож на первый с той лишь разницей, что выполнен в объеме.
В этой работе были рассмотрены различные варианты построения такой разновидности диаграмм, как графики. А также случаи их применения. Для изучения построения диаграмм в программе Эксель заходите читать статьи на Справочнике!
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
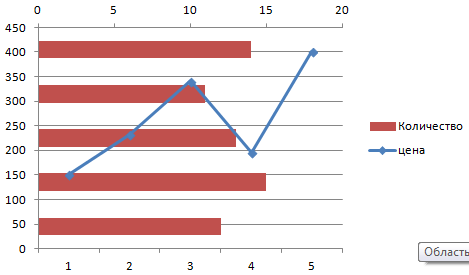
Сначала строим график так, будто у нас одинаковые единицы измерения.
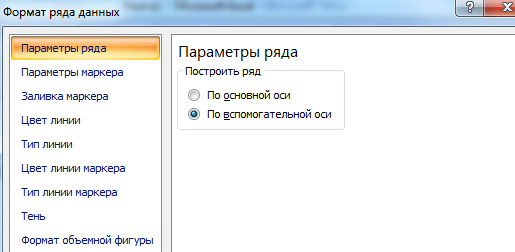
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
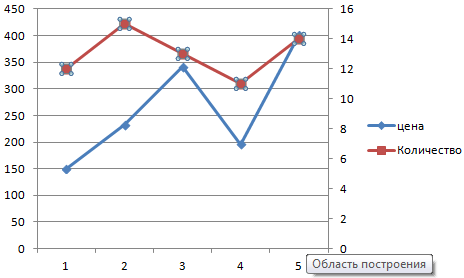
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
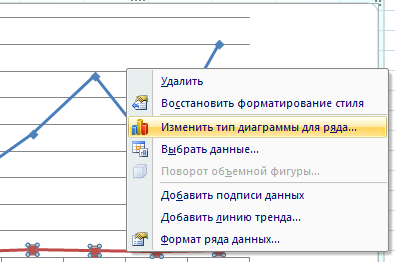
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Как добавить название в график Эксель
На примерах выше мы строили графики курсов Доллара и Евро, без заголовка сложно понять про что он и к чему относится. Чтобы решить эту проблему нам нужно:
- Нажать на графике левой клавишей мыши;
- Нажать на “зеленый крестик” в правом верхнем углу графика;
- Во всплывающем окне поставить галочку напротив пункта “Название диаграммы”:
- Над графиком появится поле с названием графика. Кликните по нему левой клавишей мыши и внесите свое название:
( 1 оценка, среднее 5 из 5 )

График функции – графическое представление математического выражения, показывающее его решение. Для построения обычно используются линейные графики с точками, с чем прекрасно справляется Microsoft Excel. Кроме того, в нем еще можно выполнить автоматические расчеты, быстро подставив нужные значения.
Существует огромное количество функций, поэтому в качестве примера я разберу только две самые наглядные, чтобы вы поняли базовые правила составления подобных элементов в таблице.
График функции F(x) = X^2
Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:
-
Создайте строку на листе в программе, вписав туда известные значения X.
-
Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.
-
Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.
-
Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.
-
Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.
-
В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.
-
Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).
Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
График функции y=sin(x)
y=sin(x) – вторая функция, которую мы возьмем за пример. Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.
-
Если вам будет проще, впишите в отдельную клетку функцию, укажите интервал и шаг. Так вы не запутаетесь при дальнейшем заполнении ячеек.
-
Добавьте два столбца, в которые будут вписаны значения каждой оси. Это нужно не только для обозначения чисел, но и для их вычисления при помощи функций программы.
-
Начните вписывать значения X с необходимым интервалом и шагом. Кстати, вы можете заполнить всего несколько полей, а затем растянуть клетки таким же образом, как было показано в предыдущем примере, чтобы они подставились автоматически до конца вашего интервала.
-
Теперь более сложное, но не страшное действие – определение значения Y. Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.
-
На следующем скриншоте вы видите результат заполнения таблицы. Используйте округление для удаления лишних знаков после запятой.
-
Вставьте обычную линейчатую диаграмму и ознакомьтесь с результатом.
На примере этих двух функций уже можно понять, как работает построение графиков в Экселе. При использовании других функций просто учитывайте особенности заполнения ячеек и не забывайте о том, что вам не нужно ничего считать, поскольку Excel все сделает за вас после указания необходимой формулы.

Наши постоянные авторы и читатели делятся лайфхаками, основанными на личном опыте. Полная свобода самовыражения.
Рекомендуем




Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке [-3;3]. Называем столбец «х», пишем первое значение «-3», второе – «-2,5». Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
В поле «Элементы легенды» кликаем на кнопочку «Добавить».
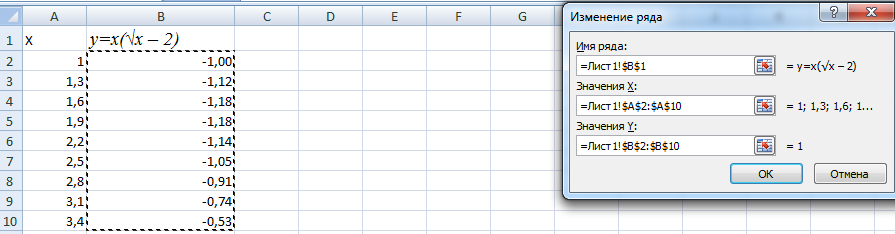
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Загрузка…
Об авторе: Олег Каминский
Вебмастер. Высшее образование по специальности «Защита информации». Создатель портала comp-profi.com. Автор большинства статей и уроков компьютерной грамотности
Содержание
- Как построить график функции в Excel
- Практическая работа построение графиков в MS Excel
- Содержимое разработки
- Варианты построения графика функции в Microsoft Excel
- Вариант 1: График функции X^2
- Вариант 2: График функции y=sin(x)
Как построить график функции в Excel
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке [-3;3]. Называем столбец «х» , пишем первое значение «-3» , второе – «-2,5» . Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у» , для удобства можно вписать всю формулу. Выделяем ячейку В2 , ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6» . Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х» , в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у» , переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная» . Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси» .
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений» , поставьте маркер в пункте «фиксированное» и впишите значение «0,5» .
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор» , «Макет» , «Формат» .
Построить график функции в Эксель можно и с помощью «Графика» . О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х» .
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные» .
В поле «Элементы легенды» кликаем на кнопочку «Добавить» .
Появится окно «Изменение ряда» . Поставьте курсор в поле «Имя ряда» и выделите ячейку С1 . Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК» .
Чтобы для первого графика в Легенде не было написано «Ряд 1» , выделите его и нажмите на кнопку «Изменить» .
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК» .
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1 , подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1» .
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Источник
Практическая работа построение графиков в MS Excel
В работе показано как с помощью графиков в Excel можно выполнить интересные рисунки
Шестакова Марина Васильевна , 21.02.2019
Содержимое разработки
Практическая работа в MS Excel по теме
ПОСТРОЕНИЕ ДИГРАММ И ГРАФИКОВ
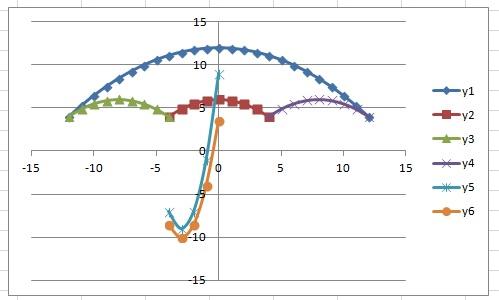
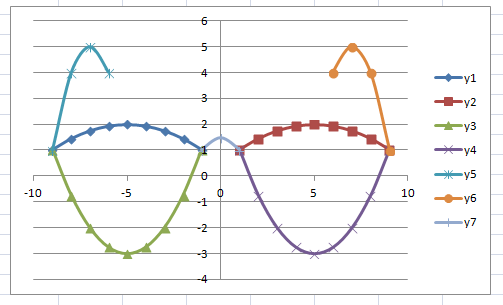
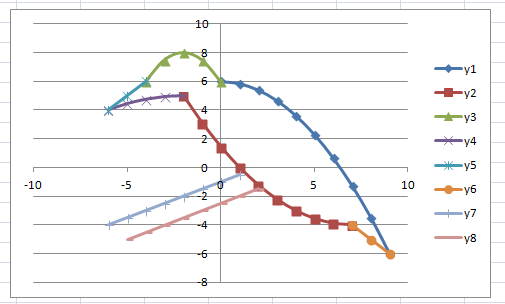
Задание: Построение рисунка «ЗОНТИК»
Приведены функции, графики которых участвуют в этом изображении:
у1= -1/18х 2 + 12, х[-12;12]
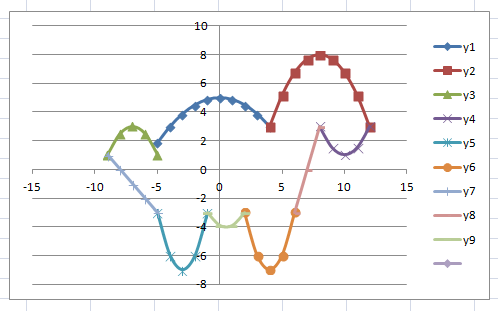
y 2= -1/8х 2 +6, х[-4;4]
y 3= -1/8( x +8) 2 + 6, х[-12; -4]
y 4= -1/8( x- 
y5= 2 ( x+3 ) 2 – 9, х[-4; 0 ]
y 6=1. 5 ( x +3) 2 – 10 , х[-4;0]
Запустить MS EXCEL
В ячейке А1 внести обозначение переменной х
Заполнить диапазон ячеек А2:А26 числами с -12 до 12.
Последовательно для каждого графика функции будем вводить формулы.
Для у1= -1/18х 2 + 12, х[-12;12]
Порядок выполнения действий:
Устанавливаем курсор в ячейку В1 и вводим у1
В ячейку В2 вводим формулу

Нажимаем Enter на клавиатуре
Автоматически происходит подсчет значения функции.
Растягиваем формулу до ячейки В26
Аналогично в ячейку С10 (т.к значение функции находим только на отрезке х[-4;4]) вводим формулу для графика функции y 2= -1/8х 2 +6.
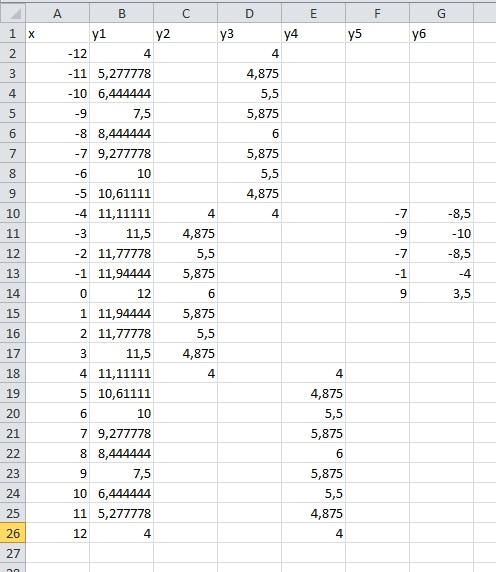
В результате должна получиться следующая ЭТ
После того, как все значения функций подсчитаны, можно строить графики этих функций.
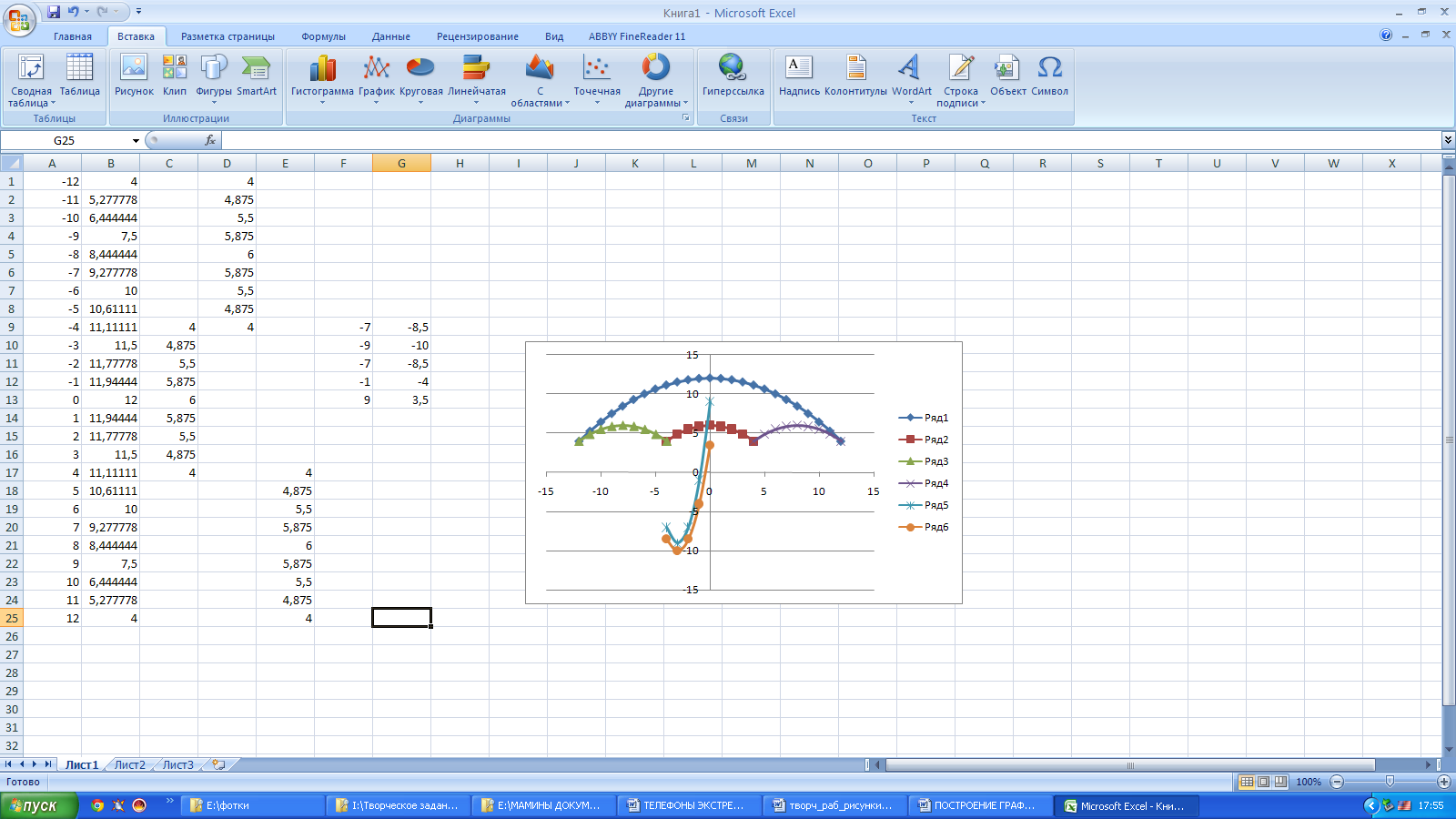
Выделяем диапазон ячеек А1: G26
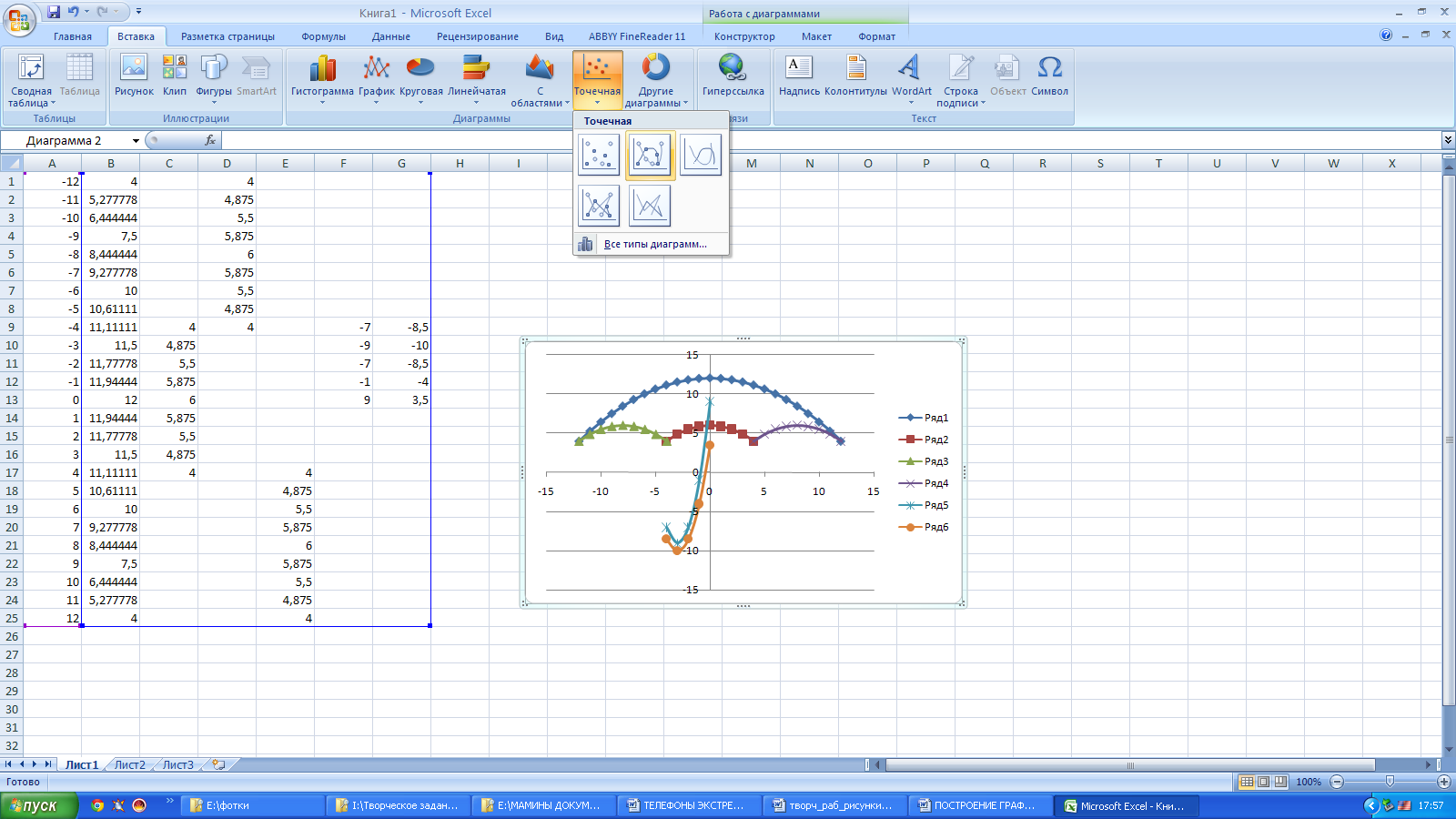
На панели инструментов выбираем меню Вставка → Диаграмма.
В окне Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok .
В результате должен получиться следующий рисунок:
Построить графики функций в одной системе координат. Получить рисунок.
1)
2)
3)
4)
5)
6)
7)
1)
2)
3)
4)
5)
6)
7)

1)
2)
3)
4)
5)
6)
7)

9)
1)
2)
3)
4)
5)
6)
7)

Источник
Варианты построения графика функции в Microsoft Excel
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
- Нажмите по первой ячейке и впишите =B1^2 , что значит автоматическое возведение указанной ячейки в квадрат.
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.











Источник
Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
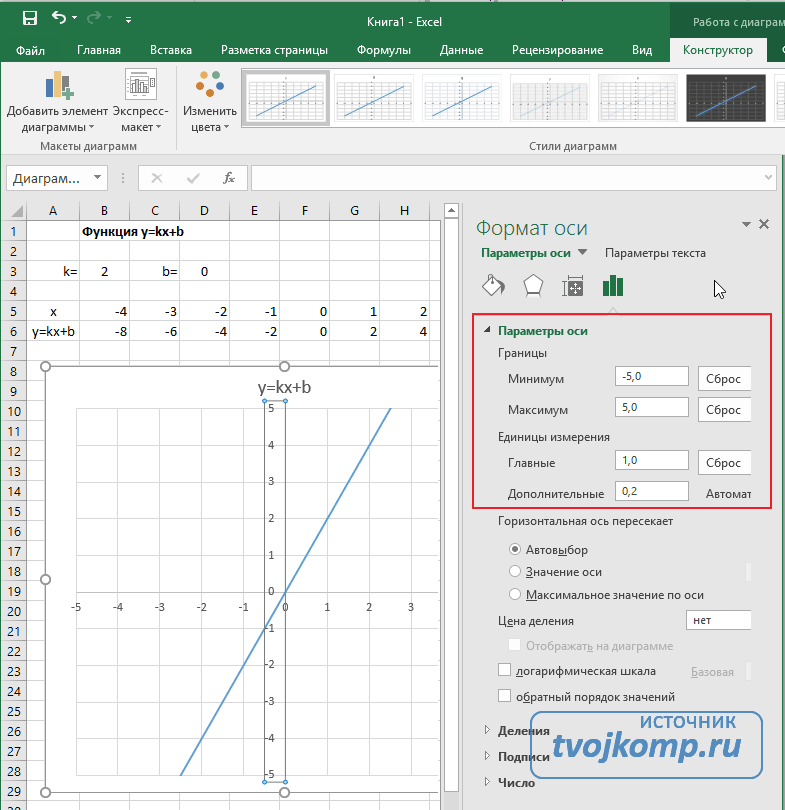
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
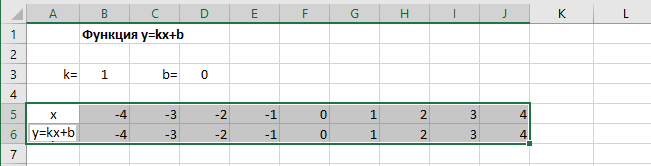
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
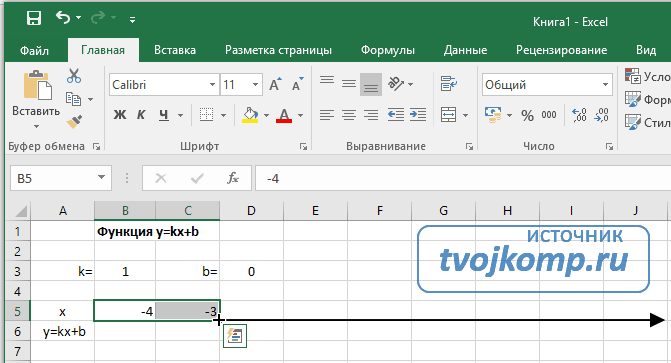
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
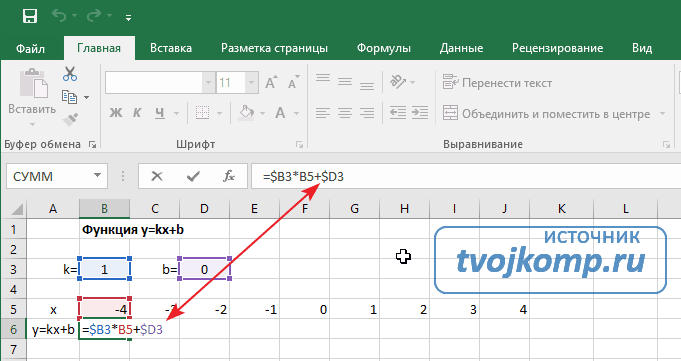
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
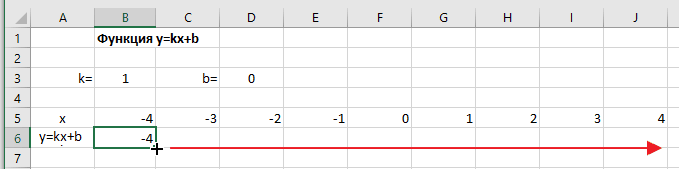
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
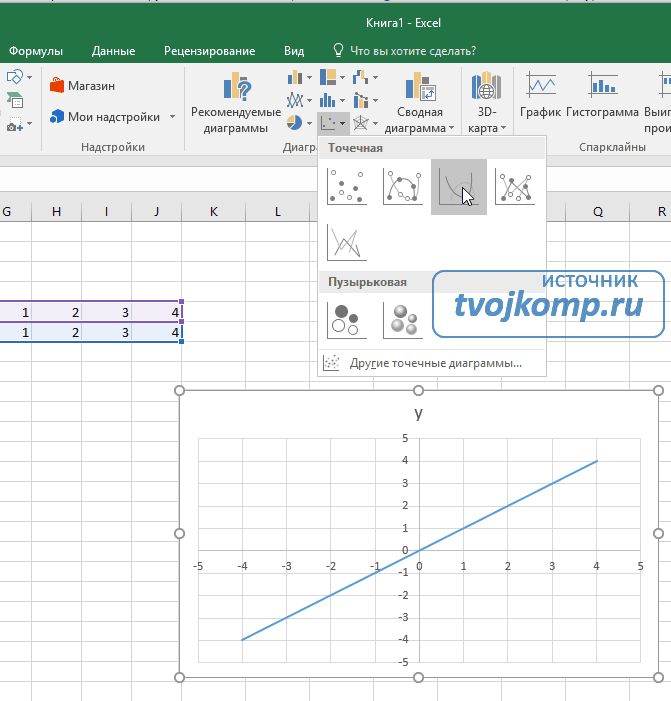
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
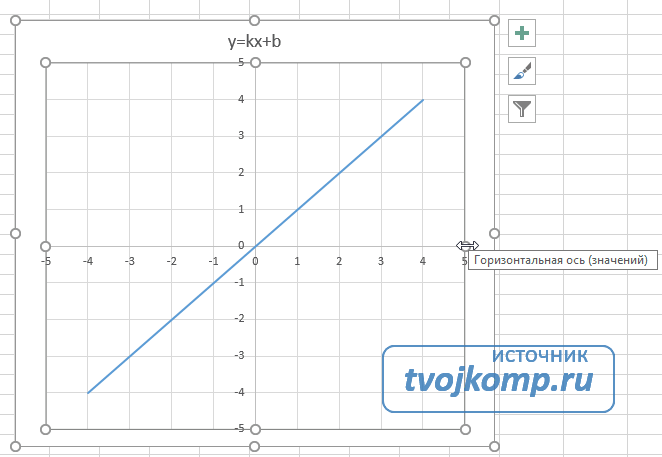
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
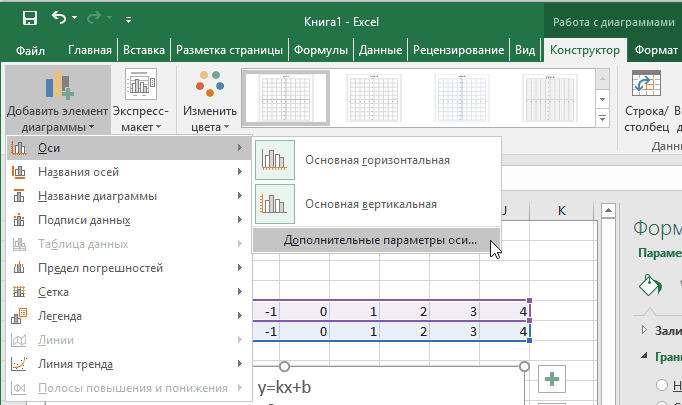
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
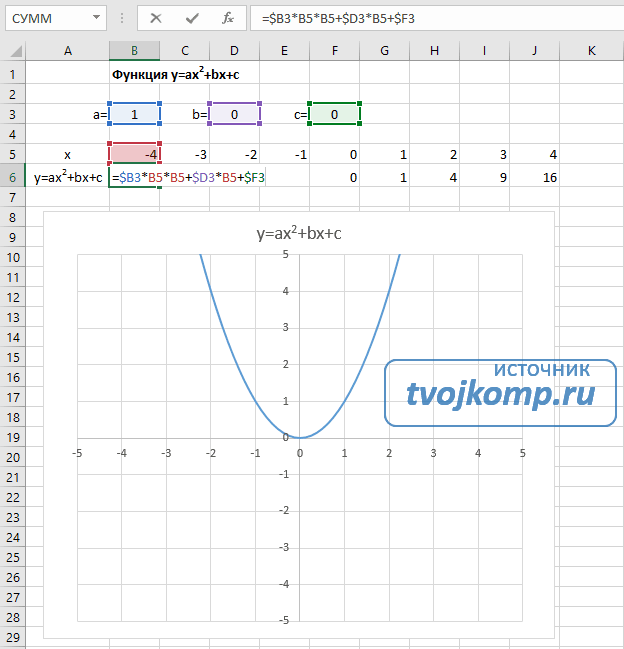
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
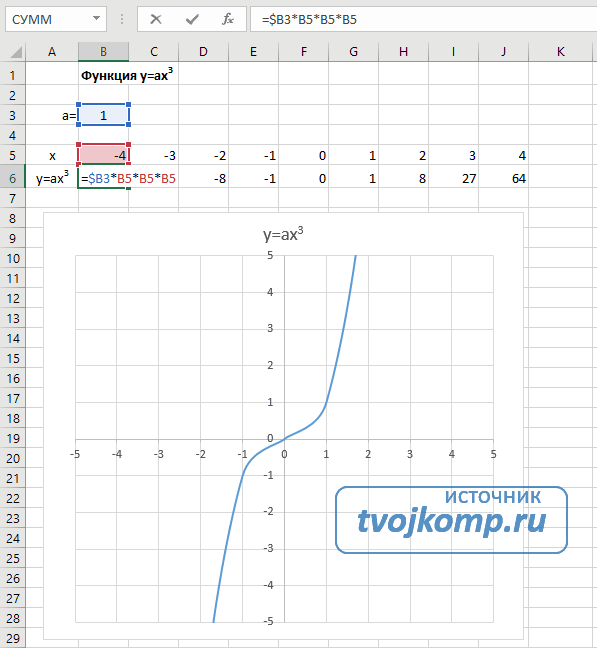
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
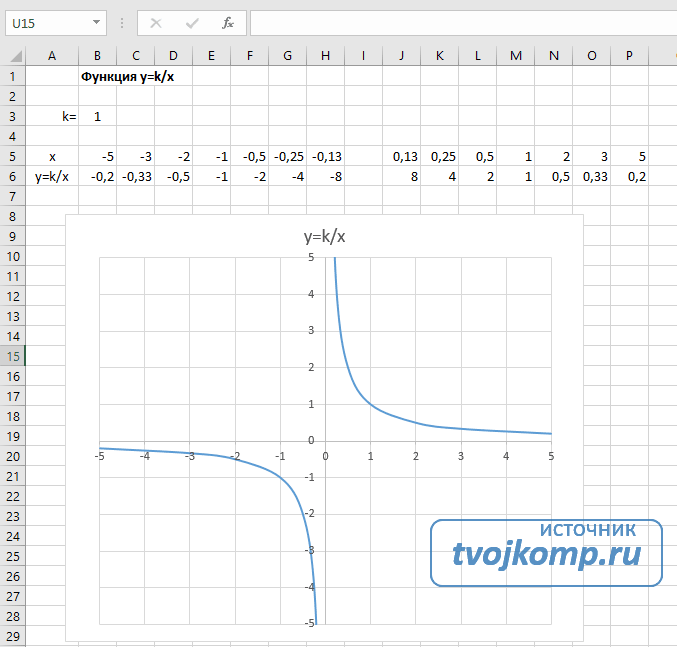
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
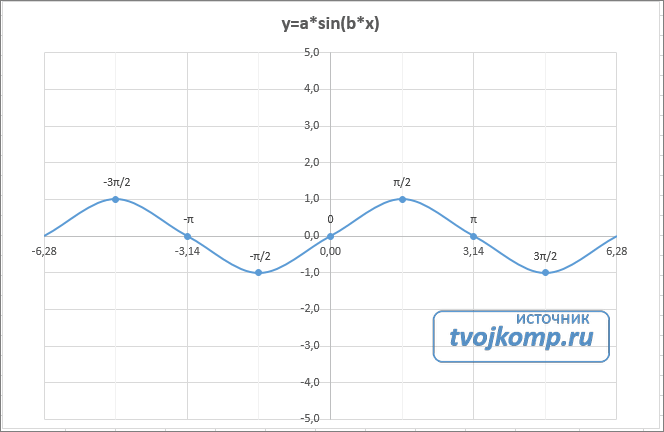
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
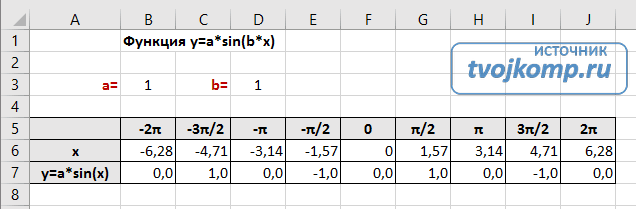
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
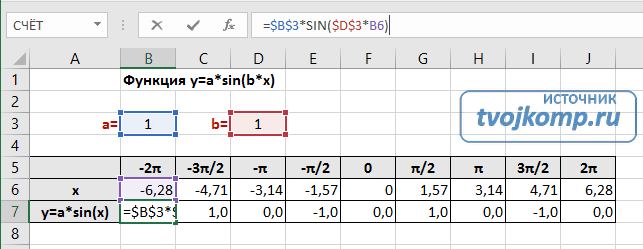
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
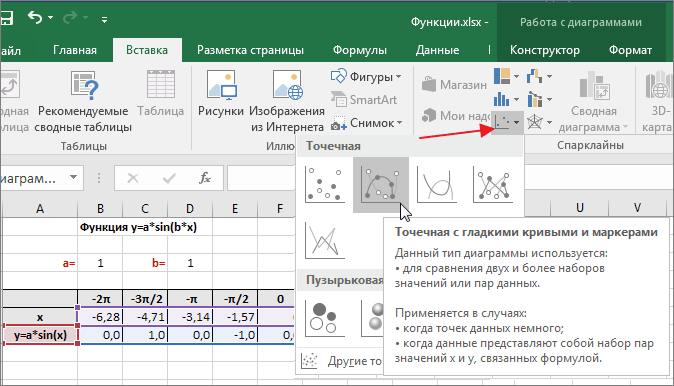
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
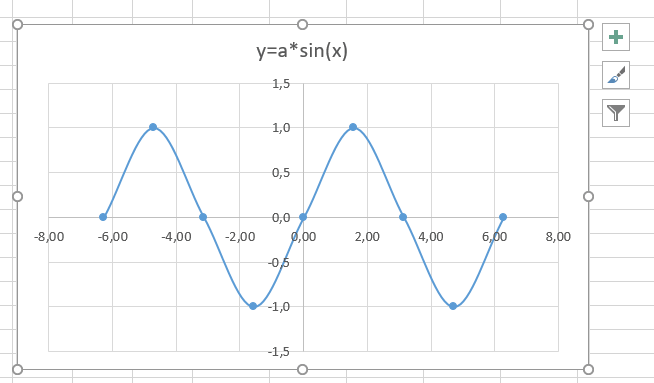
В итоге получим диаграмму.
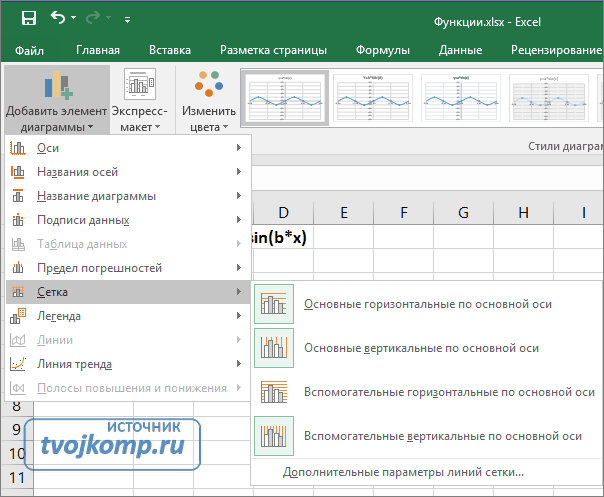
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
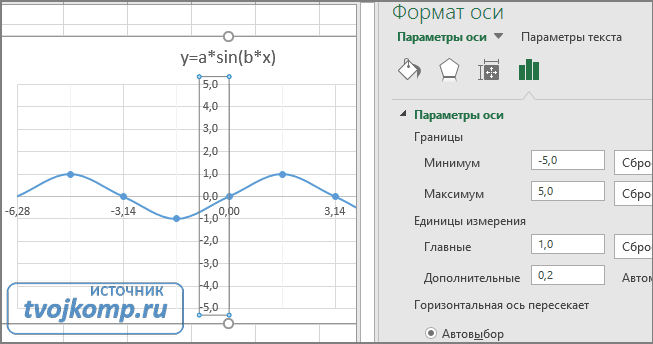
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
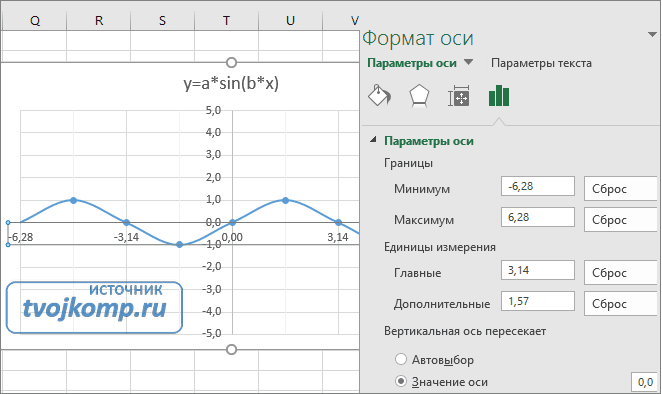
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
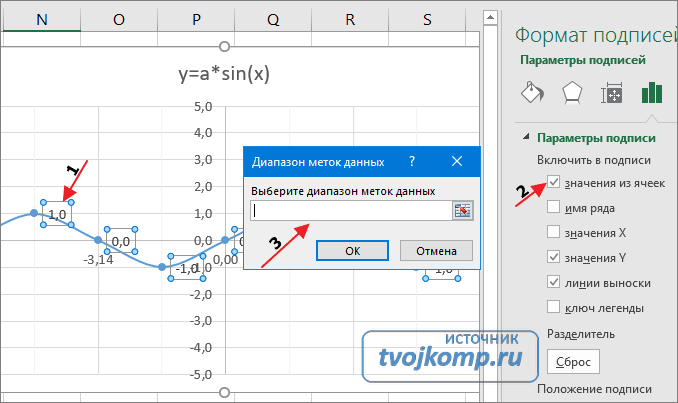
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!

Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
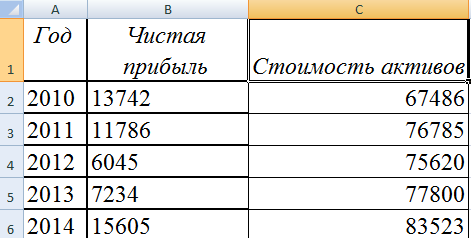
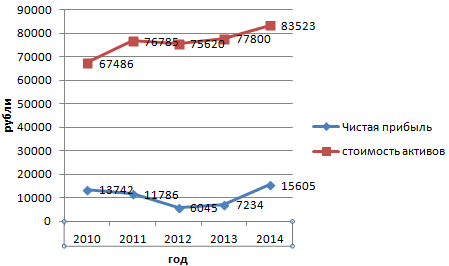
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
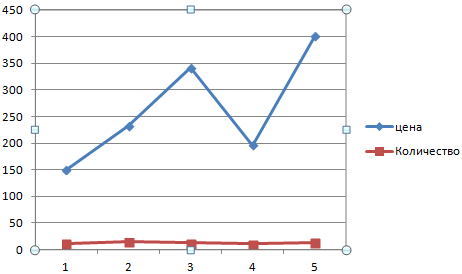
Сначала строим график так, будто у нас одинаковые единицы измерения.
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
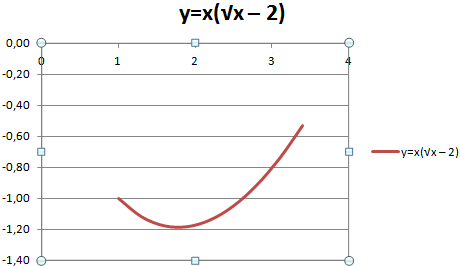
Пример: y=x(√x – 2). Шаг – 0,3.
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
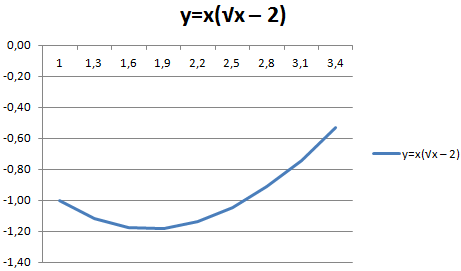
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
Наложение и комбинирование графиков
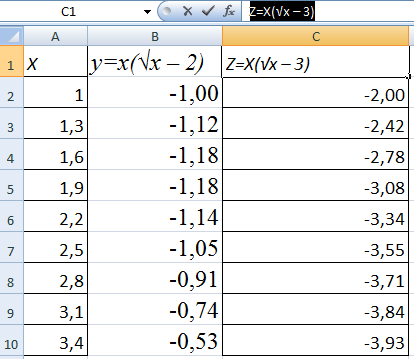
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
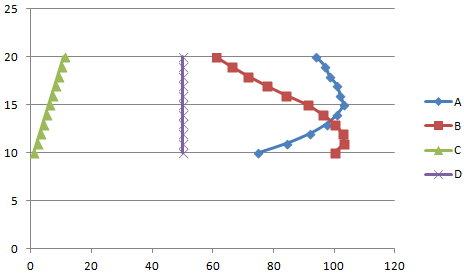
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Скачать все примеры графиков
Готовые примеры графиков и диаграмм в Excel скачать:
Как сделать шаблон, дашборд, диаграмму или график для создания красивого отчета удобного для визуального анализа в Excel? Выбирайте примеры диаграмм с графиками для интерактивной визуализации данных с умных таблиц Excel и используйте их для быстрого принятия правильных решений. Бесплатно скачивайте готовые шаблоны динамических диаграмм для использования их в дашбордах, отчетах или презентациях.
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.