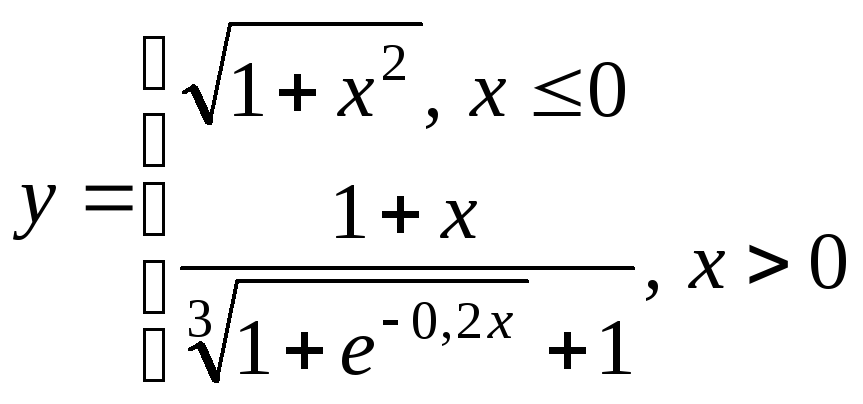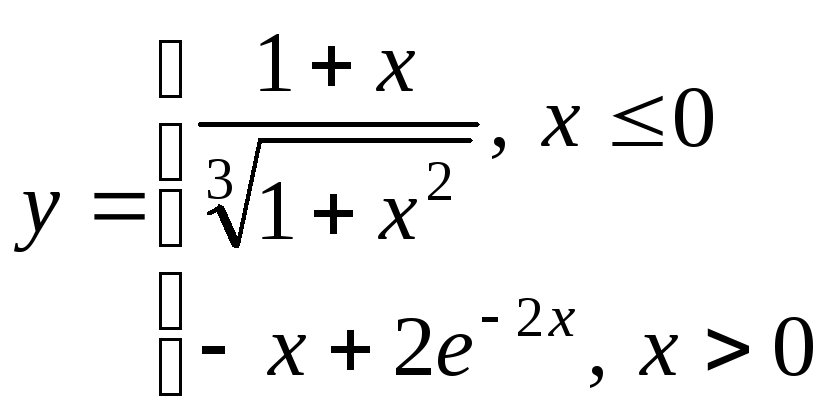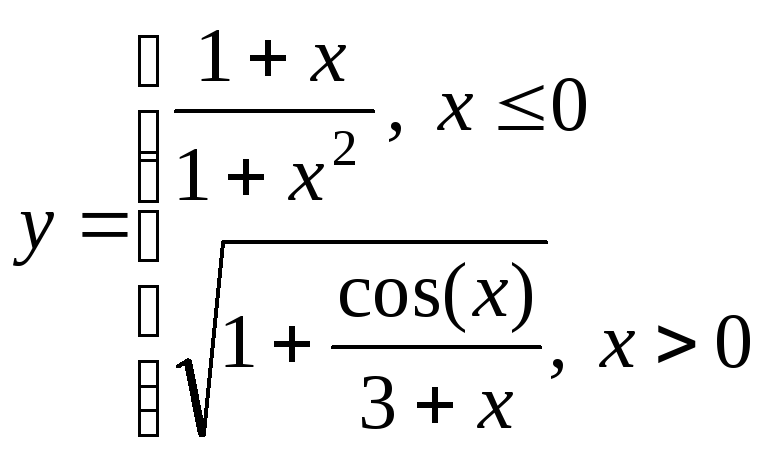Цель
работы: научиться табулировать функции
одного и двух переменных, строить графики
и поверхности, освоить работу с функцией
Excel
ЕСЛИ и логическими функциями И, ИЛИ.
С
помощью Excel можно превращать сухие и
абстрактные строки и столбцы чисел в
привлекательные и информативные графики
и диаграммы. Визуальное представление
информации облегчает ее восприятие,
помогает лучше представить поведение
функциональных зависимостей.
Построение
графиков и диаграмм осуществляется с
помощью Мастера
диаграмм.
Его вызов производится либо с помощью
команды Вставка
| Диаграмма,
либо щелчком по кнопке Мастер
диаграмм
в панели инструментов Стандартная.
Как построить
диаграмму?
Рассмотрим
таблицу 2.1, показывающую рост штатного
состава подразделений фирмы. Порядок
действий следующий.
Таблица 2.1 – Штат
фирмы «Шмидт и сыновья»
|
Подразделение |
Период |
|
|
Январь |
Октябрь |
|
|
Офис 1 |
2 |
5 |
|
Офис 2 |
7 |
9 |
-
Выделяем
необходимые табличные данные вместе
с подписями строк и столбцов. В
рассматриваемом примере можно выделить
всю таблицу, но чаще иллюстрируют лишь
некоторые строки или столбцы, содержащие
группы
данных одной размерности
(например, руб., или кг, или %). -
Нажимаем
кнопку Мастер
диаграмм
и шаг за шагом проходим все этапы
построения диаграммы.
Шаг
1.
Выбираем тип диаграммы Гистограмма
и вид диаграммы Объемная
(рис. 2.1).
Шаг
2.
Здесь указывается диапазон ячеек,
содержащих данные (рис. 2.2). Так как
таблица была заранее выделена, диапазон
уже установлен. Проверьте в окне
предварительного просмотра, как выглядит
диаграмма. Если она не соответствует
желаемому, укажите другой диапазон.
Отметьте,
как расположены данные – в столбцах
или строках. Если в строках, то подписями
оси Х
будут
Январь,
Октябрь,
а категории Офис
1
и Офис
2
уйдут в легенду диаграммы, если в
столбцах, то наоборот.
На
вкладке Ряд
можно указать другие данные для диаграммы,
а также удалить или добавить ряды.
Шаг
3.
В этом окне находится шесть вкладок
(рис. 2.3), на которых можно изменить
параметры выбранного типа диаграммы,
например, написать название диаграммы,
задать сетку, написать значения (или
проценты, доли) над столбцами диаграммы
и т.д.
Ш
4.
Здесь указывается место размещения
новой диаграммы: либо на имеющемся
листе, либо на новом листе (рис. 2.4).
После
построения диаграммы имеется возможность
изменить ее параметры. Для этого
достаточно щелкнуть правой клавишей
мыши по области построения диаграммы
и выбрать в появившемся контекстно-зависимом
меню необходимую опцию (обратите
внимание, что меню будет иметь разный
вид в зависимости от того, по какому
месту щелкнуть: или по легенде, или по
оси, или по области диаграммы и т.д.).
Существует
также удобный способ добавления новых
данных к диаграмме: выделить новые
данные в таблице и перетащить их на
диаграмму. В соответствующем виде они
появятся на поле диаграммы.
Как построить
график зависимости функции одного
переменного?
Пусть
дана таблица 2.2 зависимости цены единицы
некоторого товара от объема его продаж
(известная в экономике «кривая спроса
D-D»).
Сразу отметим: если функция задана
аналитической зависимостью y=f(x),
то нужно предварительно ее протабулировать,
то есть построить таблицу {xi
, yi},
где xi=x0
+ ih
–
узловые точки;
h
= (xn
– x0)/n
– шаг
табуляции;
i
= 0…n,
а
yi=f(xi).
Для заполнения ряда x
можно использовать режим автозаполнения
или формулу увеличения значения х
на один шаг.
Таблица 2.2 – Спрос
|
Объем продаж, |
8 |
10 |
18 |
20 |
32 |
40 |
50 |
|
Цена, руб. |
510 |
430 |
350 |
280 |
200 |
100 |
80 |
Порядок построения
графика следующий.
-
Выделяем
всю таблицу и вызываем Мастер
диаграмм. -
На
первом шаге выбираем Тип:
Точечная
и Вид:
Точечная
диаграмма со значениями, соединенными
сглаживающими линиями без маркеров.
Обращаем ваше внимание на то, что Тип:
График
не пригоден в данном случае, так как
показывает тенденции изменения данных
за равные
промежутки времени; при этом обе
группы данных (х
и у)
отображаются в виде графиков. -
На
втором шаге в окне предварительного
просмотра проверяем, правильно ли
построен график. Обратите внимание:
первая строка (или первый столбец, если
данные расположены столбцом) воспринимается
как данные оси Х,
а вторая строка (столбец) или строки
(столбцы), если они имеются, как данные
оси Y. -
Следующие
шаги
выполняются
так
же,
как
описано
выше.
Результат
приведен на рисунке 2.5.
Как
построить график зависимости функции
двух переменных?
Построим
график производственной функции
Кобба-Дугласа Y=AKL,
где А,
,
– константы, K
– объем фондов , L
–
объем трудовых ресурсов, Y
– выпуск продукции предприятием или
отраслью. Эти переменные могут выражаться
либо в стоимостном выражении, либо в
натуральном количестве.
Пусть функция
имеет вид:
Y=900K0,5L0,25
( тыс. руб.),
где
K=100
… 200 тыс. руб.;
L=30
… 50 тыс. руб.
Графическое
представление функции двух переменных
– поверхность в трехмерном пространстве.
Табулируем
функцию, располагая значения K
по горизонтали, а L
– по вертикали; тогда на пересечении
столбца со значением Ki
и строки со значением Li
будет находиться значение функции Yi
(табл. 2.3).
При
наборе формулы необходимо зафиксировать
знаком $ номер строки переменной,
изменяющейся по горизонтали (т.е. K),
и номер столбца переменной, изменяющейся
по вертикали (т.е. L).
Таблица
2.3 – Элемент листа Excel
с табулированием функции двух переменных
|
A |
B |
C |
D |
E |
|
|
… |
Значения |
Значения |
|||
|
20 |
100 |
110 |
120 |
… |
|
|
21 |
30 |
21063,1 |
22091,2 |
23073,5 |
… |
|
22 |
35 |
21890,7 |
22959,2 |
23980,1 |
… |
|
23 |
40 |
22633,8 |
23738,5 |
24794,1 |
… |
|
24 |
… |
… |
… |
… |
… |
Например, в таблице
2.3 в ячейке В21 находится формула вида
=
900*B$20^0,5*$A21^0,25
Тогда
при копировании формулы на все ячейки
таблицы смена адресов для переменных
будет проведена корректно (проверьте!).
Порядок построения
этой поверхности следующий.
-
Выделяем
всю таблицу: и значения аргументов, и
значения функции. Обратите внимание:
левая верхняя ячейка выделенной области
таблицы (у нас это ячейка А20) должна
быть пустая. -
Вызываем
Мастера
диаграмм. -
На
первом шаге выбираем Вид:
Поверхность, Тип: Поверхность. -
На
втором шаге можем предварительно
посмотреть построенную поверхность
и, при необходимости, изменить ряды
данных. -
На
третьем шаге пишем название диаграммы,
название оси Х
(категорий)
это горизонтальный ряд данных, т.е. K,
название оси Y
(рядов данных)
это вертикальный ряд данных, т.е. L,
и название оси Z
(значений) – это наша функция Y. -
На
четвертом шаге размещаем построенную
диаграмму на выбранном листе.
Обычно
после построения требуется отредактировать
диаграмму: сменить размер шрифта, фон
стенок, размещение надписей и т.д. Для
этого надо подвести стрелку к
соответствующему объекту, щелкнуть
правой клавишей мыши и из контекстно-зависимого
меню выбрать соответствующую опцию.
Пробуйте, экспериментируйте. Excel
предоставляет для этого массу возможностей!
Р
построения приведены на рисунке 2.6.
Отметим
также, что, подведя курсор к какому-нибудь
углу стенок области построения графика
(появится надпись «Углы») и «схватив»
мышью этот угол (появится тонкий крестик),
можно двигать область диаграммы,
рассматривая поверхность в различных
ракурсах.
Задания
Задание
1.
Построить диаграммы, иллюстрирующие
табличные данные из лабораторной работы
1. Тип диаграммы выбрать исходя из степени
наглядности представления информации.
Обязательно включить название, подписи
рядов данных, легенду. Поместить диаграмму
на отдельном листе.
Задание
2.
Построить графики функции одного
переменного на отрезке х[2;
2] для одного из выбранных вариантов,
приведенных ниже, при разных шагах
табуляции: 0,5; 0,2; 0,1. Сравнить вид графиков,
сделать выводы.
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
При
записи формулы использовать функцию
ЕСЛИ. Она возвращает одно значение, если
заданное условие при вычислении дает
значение ИСТИНА, и другое значение, если
ЛОЖЬ.
С
этой функции (рис. 2.7):
ЕСЛИ(условие;значение_если_истина;значение_если_ложь).
В
условии для сравнения двух значений
используются операторы сравнения: =
(равно); > (больше); < (меньше); >= (не
меньше); <= (не больше); <> (не равно).
Например, формула
=ЕСЛИ(А1>=0;КОРЕНЬ(A1);”число
отрицательное!”),
записанная
в какой-либо ячейке, помещает в нее
значение квадратного корня из числа,
находящегося в ячейке А1, при его
неотрицательном значении, и выдает
предупредительный текст в случае
отрицательного значения.
Сравнивать
можно как арифметические, так и текстовые
выражения.
Примечание.
Если
после набора формулы в одном из полей
(рис. 2.7), она вдруг окажется охваченной
двойными кавычками, т.е. интерпретирована
как текст – ищите ошибку. Это может быть
несоответствие скобок, неверно записанное
или использованное имя функции, адрес
ячейки, содержащий русские буквы,
пропущенный знак умножения и т.п.
Задание
3.
Существует гипотеза, что параметры
физической активности человека, его
умственных способностей и эмоционального
состояния можно описать периодическими
функциями вида:
,
где
t
– время (дни, отсчитываемые со дня
рождения
t0);
Ti
– периоды: Т1=23
дня для физического цикла; Т2=28
дней для эмоционального цикла; Т3=33
дня для интеллектуального цикла.
1. Построить
таблицу биоритмов на текущий месяц,
задав информацию о дате рождения, дате
начала построения графика (взяв, например,
первый день месяца), дате конца построения
графика (последний день месяца).
Для
ячеек, где будут располагаться даты,
установить формат Дата
(Формат
| Ячейки | Число | Дата).
Для подсчета прожитых лет использовать
функцию Год.
Синтаксис функции:
ГОД(дата)
Дата
– это дата, год которой необходимо
найти. Даты вводятся как текстовые
строки в двойных кавычках, например,
“31.12.03”, “7.12.2003”1.
Вариант расположения
информации на листе показан на рис. 2.8.
2. Построить
графики биоритмов.
3. Определить
«положительные и отрицательные
критические дни», т.е. точки совпадения
графиков (двойные и тройные) в положительной
или отрицательной области изменения
соответствующих функций.
Для
этого предлагается с помощью вложенных
функций ЕСЛИ
преобразовать значения функций биоритмов
в условные значки (см. рис. 2.8, столбцы
Визуальное
представление):
+ – если значения
функции положительные;
– – если значения
функции отрицательные;
*
– при совпадении двух любых функций
(можно усложнить задачу, введя разные
значки для разных комбинаций совпадений);
+!!!
– при совпадении значений всех трех
функций в положительной области;
–!!!
– при совпадении значений всех трех
функций в отрицательной области.
Сравнивать
значения рекомендуется по одному или
двум знакам после запятой (т.е. решать
задачу в некотором приближении) с
использованием функции ОТБР,
назначение которой – отсечение дробной
части числа до указанного количества
разрядов.
Формирование
условий для функций ЕСЛИ
потребует применения логических функций
И
и ИЛИ.
Функция
И
возвращает значение ИСТИНА, если все
аргументы имеют значение ИСТИНА, и
возвращает значение ЛОЖЬ, если хотя бы
один аргумент имеет значение ЛОЖЬ.
Синтаксис функции:
И(условие1;
условие2;
…).
Функция
ИЛИ
возвращает значение ИСТИНА, если хотя
бы один из аргументов имеет значение
ИСТИНА, и возвращает значение ЛОЖЬ, если
все аргументы имеют значение ЛОЖЬ.
Синтаксис функции:
ИЛИ(условие1;
условие2;
…).
В
рассматриваемой задаче условие
– это сравнение типа «равенство».
Примечание.
Задания на построение поверхности будут
предложены в лабораторных работах 3 и
4.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
11.05.2015211.06 Кб22mss_labN5.docx
Как построить график функции от двух переменных?
Графики в Excel
Как построить график функции от одной переменной?
Пусть дана таблица 1 зависимости цены единицы некоторого товара от объема его продаж (известная в экономике «кривая спроса D-D»). Сразу отметим: если функция задана аналитической зависимостью y=f(x), то нужно предварительно ее протабулировать, то есть построить таблицу <xi , yi>, где xi=x0 + i×h, h = (xn – x0)/n; i = 0…n, а yi=f(xi). Для заполнения ряда x используется режим автозаполнения.
| Объем продаж, тыс. шт. |
| Цена, руб. |
Порядок построения графика следующий.
1. Выделяем всю таблицу и вызываем Мастер диаграмм.
2. На первом шаге выбираем Тип: Точечная и Вид: Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Обращаем ваше внимание на то, что Тип: График не пригоден в данном случае, так как показывает тенденции изменения данных за равные промежутки времени; при этом обе группы данных (х и у) отображаются в виде графиков.
3. На втором шаге в окне предварительного просмотра проверяем, правильно ли построен график. Обратите внимание: первая строка (или первый столбец, если данные расположены столбцом) воспринимается как данные оси Х , а вторая строка (столбец) или строки (столбцы), если они имеются, как данные оси Y.
4. Следующие шаги выполняются так же, как описано выше.
Результат приведен на рис. 1.
Как построить график функции от двух переменных?
Построим график производственной функции Кобба-Дугласа Y=A×K a L b , где А, a, b – константы, K – объем фондов , L – объем трудовых ресурсов, Y – выпуск продукции предприятием или отраслью. Эти переменные могут выражаться либо в стоимостном выражении, либо в натуральном количестве.
Пусть функция имеет вид:
Y=900×K 0,5 L 0,25 ( тыс. руб.),
где K=100 . 200 тыс. руб.; L=30 . 50 тыс. руб.
Графическое представление функции двух переменных – поверхность в трехмерном пространстве.
Табулируем функцию, располагая значения K по горизонтали, а L – по вертикали; тогда на пересечении столбца со значением Ki и строки со значением Li будет находиться значение функции Yi .
При наборе формулы необходимо зафиксировать знаком $ номер строки переменной, изменяющейся по горизонтали (т.е. K), и номер столбца переменной, изменяющейся по вертикали (т.е. L).
Например, в таблице 2 в ячейке В21 находится формула вида
Тогда при копировании формулы на все ячейки таблицы смена адресов для переменных будет проведена корректно (проверьте!).
Элемент листа Excel с табулированием функции двух переменных
| A | B | C | D | E |
| . | Значения L | Значения К | ||
| . | ||||
| 21063,1 | 22091,2 | 23073,5 | . | |
| 21890,7 | 22959,2 | 23980,1 | . | |
| 22633,8 | 23738,5 | 24794,1 | . | |
| . | . | . | . | . |
Результаты построения приведены на рисунке 2.
Порядок построения этой поверхности следующий.
1. Выделяем всю таблицу: и значения аргументов, и значения функции. Обратите внимание: левая верхняя ячейка выделенной области таблицы (у нас это ячейка А20) должна быть пустая.
2. Вызываем Мастер диаграмм.
3. На первом шаге выбираем Вид: Поверхность, Тип: Поверхность
4. На втором шаге можем предварительно посмотреть построенную поверхность и, при необходимости, изменить ряды данных.
5. На третьем шаге пишем название диаграммы, название оси Х (категорий) — это горизонтальный ряд данных, т.е. K, название оси Y (рядов данных) — это вертикальный ряд данных, т.е. L, и название оси Z (значений) – это наша функция Y.
6. На четвертом шаге размещаем построенную диаграмму на выбранном листе.
Обычно после построения требуется отредактировать диаграмму: сменить размер шрифта, фон стенок, размещение надписей и т.д. Для этого надо подвести стрелку к соответствующему объекту, щелкнуть правой клавишей мыши и из контекстно-зависимого меню выбрать соответствующую опцию. Пробуйте, экспериментируйте. Excel предоставляет для этого массу возможностей!
Отметим еще, что, подведя курсор к какому-нибудь углу стенок области построения графика (появится надпись «Углы») и «схватив» мышью этот угол (появится тонкий крестик), можно двигать область диаграммы, рассматривая график в различных ракурсах.
Дата добавления: 2015-08-13 ; просмотров: 1919 | Нарушение авторских прав
Вычисление значений функции двух переменных
Электронные таблицы Excel
Excel – программа, предназначенная для обработки электронных таблиц.
Электронные таблицы Excel используются как средство проведения расчетов и визуализации результатов расчетов в виде таблиц и графиков.
Загрузка Excel:
Пуск ► Программы ► MS Office ► MS Excel.
После запуска MS Excel на экране появляется окно, представленное на рис. 1.
Рис.1.Окно MS Excel 2007
Документ Excel называется рабочей книгой. Рабочая книга представляет собой набор рабочих листов, каждый из которых имеет табличную структуру и может содержать одну или несколько таблиц.
По умолчанию рабочая книга имеет три рабочих листа (Лист 1, Лист 2 и Лист 3). В окне документа отображается только текущий рабочий лист, с которым и ведется работа. Число листов можно увеличить, можно изменить название листа, удалить лист, переместить лист с помощью контекстного меню (правой кнопкой мыши по ярлычку листа) и др. способов.
Ячейки и их адресация.
Электронные таблицы состоят из столбцов и строк. Столбцы озаглавлены буквами латинского алфавита и их двухбуквенными комбинациями (А, В, С,…, АА, АВ,…). Строки – пронумерованы (1, 2, 3,…).Всего рабочий лист содержит 256 столбцов и 65536 строк.
Место пересечения столбца и строки называется ячейкой. Каждая ячейка имеет свой уникальный адрес, состоящий из названия столбца и номера строки (например А1, Р45, …). Одна из ячеек всегда является активной и выделяется рамкой (рис. 1). Операция ввода и редактирования содержимого ячейки всегда проводятся в активной ячейке. В ячейку можно ввести число (целое или действительное), текст или формулу. Запись формулы в ячейку начинается с ввода знака равенства «=». Ввод данных обязательно должен завершаться нажатием клавиши ENTER.
В электронных таблицах можно работать как с отдельными ячейками, так и с группой ячеек, которые образуют диапазон (блок). В качестве диапазона может рассматриваться строка (часть строки) или столбец (часть столбца), или прямоугольник, состоящий из нескольких строк, столбцов или их частей. Диапазон задается указанием адреса первой и последней его ячеек, между которыми ставится символ двоеточие «:» (например, А4:С10, В2:В15, С1:Н1). Диапазону можно присвоить имя. Для этого необходимо выделить его на рабочем листе, а затем выполнить команду меню Вставка ► Имяи в появившемся диалоговом окне задать имя диапазона.
Формат указания адреса ячейки называется ссылкой. Ссылки на ячейки можно задавать разными способами. В пределах одного рабочего листа используются относительные, абсолютные и смешанные ссылки.
Относительные – это ссылки , которые при копировании формулы изменяются автоматически в соответствии с относительным расположением исходной ячейки и создаваемой копией. Например, А4, С10, В2 и др.
Абсолютные – это ссылки, которые не изменяются при копировании. Например, $А$4, $С$10, $В$2 и др. Если диапазону присвоено имя, то оно будет использоваться в качестве абсолютной ссылки.
Смешанные – это ссылки, в которых при копировании изменяется либо столбец, либо строка. Например, А$4, $С10, В$2 и др.
Для изменения способа адресации при записи или редактировании формулы необходимо установить указатель мыши на ссылку и нажать клавишу «F4» один или несколько раз.
Ссылки на другие листы
Различают внутренние и внешние ссылки на другие листы.
Внутренние ссылки– это ссылки на другие листы той же книги. Существует два типа внутренних ссылок:
1. Ссылки на лист с номером N. Формат ссылки ,
где Ссылка – относительная ссылка на ячейку или диапазон ячеек листа N;
2. Объемные ссылки представляют собой ссылки на ячейки диапазона листов с одинаковой структурой в книге. Формат объемной ссылки
= (‘ЛистК:ЛистМ’! ),
где – имя стандартной функции Excel, К, М – номера первого и последнего листов непрерывного диапазона в книге соответственно.
Для создания объемной ссылки необходимо выполнить следующие действия:
1. ввести в ячейку текущего листа = ;
2. отметить с помощью мыши лист К (левой кнопкой мыши по ярлычку листа с номером К) диапазона листов, а затем при нажатой клавише Shift – лист М;
3. выделить диапазон ячеек ( ) на текущем листе, и нажать клавишу Enter.
При внутренних ссылках по умолчанию используется механизм относительной адресации ячеек листа.
Объемные ссылки, как правило, используются со следующими встроенными функциями Excel: СУММ, СЧЕТ, СРЗНАЧ, МАКС, МИН, ПРОИЗВЕД и др.
Внешние ссылки – это ссылки на листы других книг. Формат внешних ссылок [КнигаК] ,
Где К – идентификатор книги.
При использовании внешних ссылок по умолчанию используется механизм абсолютной адресации на листе.
Вычисления в Excel
Вычисления в Excel осуществляются при помощи формул. Формула может содержать числовые константы, ссылки на ячейки и функции Excel, соединенные знаками арифметических операций.
Часто для табличных вычислений необходимо использовать числовые последовательности. Зададим последовательность для чисел, изменяющихся
от -4 до 4 с шагом равным 0,5. Существует три способа задания числовой последовательности с помощью автозаполнения:
Первый способ. В ячейку А1 введем начальное значение (-4). В ячейку А2 – следующее по порядку (-3,5). Выделяем ячейки А1 и А2. Указатель мыши устанавливаем на маркер заполнения и левой кнопкой мыши перемещаем его по столбцу А до значения равного 4 (рис. 2).
Рис. 2. Первый способ задания числовой последовательности
Второй способ. В ячейку А1 введем начальное значение (-4). Выделим эту ячейку. Откроем вкладку Главная ► группа Редактирование ► кнопка Заполнение (открыть) ►пункт Прогрессия. В появившемся диалоговом окне «Прогрессия» установим параметры: расположение, шаг, предельное значение (рис. 3)
Рис. 3. Второй способ задания числовой последовательности
Закрыв окно «Прогрессия» в столбце А получим все числа заданной последовательности.
Третий способ. В ячейку А1 введем начальное значение (-4). В ячейку А2 введем формулу (рис. 4). Выделим ячейку А2, установим указатель мыши на маркер заполнения и с его помощью скопируем формулу по столбцу А до значения равного 4.
Рис. 4. Третий способ задания числовой последовательность
Пользователь выбирает для себя наиболее удобный способ заполнения.
Теперь перейдем к работе с функциями Excel.
Функции — заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. В качестве аргументов используются ссылки на ячейки, формулы, или функции. В каждом конкретном случае необходимо использовать соответствующий тип аргумента. Функции позволяют выполнять как простые, так и сложные вычисления.
На рабочем листе имеется строка формул (рис. 1), предназначенная для отображения и редактирования содержимого активной ячейки. Запись формулы начинается с ввода знака равенства «=». При этом строка формул преобразуется к виду
– кнопка раскрывающегося списка недавно использованных функций, можно использовать для вставки нужной функции;
– кнопка отмены ввода формулы;
– кнопка завершения ввода формулы, аналогична действию клавиши Enter;
– кнопка вызова Мастера функций.
В самом общем смысле Мастером в Excel называется подпрограмма, нацеленная на решение определенного класса задач. Мастер ведет активный диалог с пользователем, предлагая ему вопросы, на которые он должен дать ответ, чтобы добиться желаемого результата. Помимо вопросов, Мастер предлагает варианты ответов на них.
Функции Excel предназначены для выполнения математических, статистических, финансовых и других расчетов. Методика использования функций требует соблюдения определенной технологии.
1. На рабочем листе в отдельных ячейках осуществляется подготовка (ввод) значений аргументов функции.
2. В отведенную для формулы ячейку вводится знак равенства «=». Для вставки функции вызывается Мастер функций нажатием кнопки в строке формул.
3. В появившемся диалоговом окне (рис. 5)
Рис. 5 Окно Мастера функций
в строке «Категория» выбираем нужную категорию или «Полный алфавитный перечень», в разделе «Выберите функцию» – выделяем заданную функцию и закрываем окно Мастера с помощью кнопки ОК.
4. В строке формул появляется синтаксическая форма выбранной функции (ее имя и пустые круглые скобки), а на экране – диалоговое окно «Аргументы функции» для ввода ее аргументов (рис. 6).
В строку «Число» диалогового окна можно ввести аргумент в виде ссылки на ячейку, содержащую значение аргумента, число или выражение, содержащее другие функции. При этом для вставки функции снова вызывается Мастер функций.
5. После окончания ввода аргумента, не обращая внимания на диалоговое окно «Аргументы функции», переходим в строку формул для продолжения ее ввода и т.д. Завершение ввода формулы фиксируется нажатием клавиши Enter или кнопки в строке формулы.
Рис. 6. Диалоговое окно для ввода аргументов функции
При наборе формулы необходимо помнить, что:
· Формула вводится слева направо в одну строку (не более 256 символов);
· Знаки арифметических операций («+», «-», «*», «/», «^») вводятся с клавиатуры;
· Порядок действий при вычислении формулы определяется приоритетом операций и круглыми скобками. Приоритет операций по убыванию:
1. действие в круглых скобках;
2. вычисление функций;
3. действие возведения в степень «^»;
4. умножение и деление «* и /»;
5. сложение и вычитание «+ и -».
Следовательно, если необходимо выполнить операцию низкого приоритета перед операцией более высокого приоритета, то используются круглые скобки.
Для проведения математических расчетов используются функции, относящиеся к категории «Математические». Наиболее часто встречающиеся функции приведем в таблице
| Математическая запись | Запись в синтаксисе Excel |
| SIN(число) | |
| COS(число) | |
| TAN(число) | |
| ASIN(число) | |
| ACOS(число) | |
| ATAN(число) | |
| ABS(число) | |
| EXP(число) | |
| LN(число) | |
| LOG10(число) | |
| LOG(число, основание) | |
| КОРЕНЬ(число) | |
| ПИ() |
Пример 1. Пусть необходимо вычислить значение при . В ячейку А1 введем значение 0,1 а в ячейку В1 – формулу. Результат вычисления представлен на рис. 7.
Рис. 7. Результат вычисления по формуле
Пример 2. Пусть необходимо вычислить значение при и . Ввод исходных данных и все вычисления представлены на рис. 8.
Рис. 8. Результаты вычисления по формуле
В этом примере в столбец С вводится числовая последовательность одним из способов автозаполнения, которые описаны выше. В ячейку D2 вводится формула для вычисления произведения вида
и копируется с помощью маркера заполнения по столбцу для вычисления при каждом значении k. Необходимо учесть, что для адресации значения x используется абсолютная ссылка ($A$2). В ячейку Е2 вводим формулу для вычисления произведения
Формулу для вычисления y вводим в ячейку F2
Здесь для адресации значения x используется относительная ссылка, так как вычисляется единственное значение и не копируется по столбцу.
Вычисление значений функции двух переменных
Если необходимо произвести вычисления по формуле, содержащей два аргумента, то расчет оформляется в виде таблицы. В качестве заголовков строк и столбцов такой таблицы должны выступать значения аргументов, а тело таблицы будет представлять собой набор значений функции. Таким способом можно подготовить данные для построения поверхности с помощью Мастера диаграмм. Рассмотрим вычисление функции двух переменных на примере.
Пусть необходимо вычислить значения функции двух переменных вида для , изменяющегося от -5 до 5 с шагом 2, и для , изменяющегося от 0 до 5 с шагом 1.
Построение таблицы начнем с ячейки А1, в которую введем символы x и y через несколько пробелов. Зафиксируем ввод (нажатием клавиши Enter) и выделим ее снова. Затем выполним команду меню Формат ► Ячейки ► Вкладка «Граница». Находим нужную границу. После выполнения всех операций ячейка А1 имеет вид . Теперь понятно, что заголовками строк будут значения аргумента x, а заголовками столбцов будут значения аргумента y.Далее выполняем следующие действия:
1. Введем последовательность значений x в столбец А, начиная с ячейки А2, воспользовавшись одним из способов автозаполнения;
2. Введем последовательность значений y в строку 1, начиная с ячейки В1, воспользовавшись одним из способов автозаполнения;
3. В ячейку В2 введем формулу =A2^2+B1^2. Конечно, хотелось бы, чтобы формулы в таблице появились в результате применения операции заполнения (с помощью маркера заполнения). Поскольку заполнение выполняется для строки или для столбца, то формулу в таком виде оставлять нельзя, так как при перемещении формулы относительные ссылки будут меняться. При заполнении столбцов в формуле будет меняться только номер строки, а, следовательно, и значение аргумента y, которое должно оставаться постоянным. При заполнении строк будут изменяться только столбцы, а, следовательно, и значение аргумента x, которое должно оставаться постоянным. Поэтому в ссылке А2 необходимо закрепить столбец ($A2) а, в ссылке В1 – строку (B$1). Результирующая формула будет иметь вид =$A2^2+B$1^2. Теперь можно использовать операцию заполнения.
4. Выделим ячейку В2 и с помощью маркера заполнения сначала заполним вторую строку, а затем – последний столбец. В результате получим таблицу значений функции двух переменных (рис. 9).
Рис. 9. Результаты вычислений
На рис. 9 выделена матрица значений функции двух переменных.
Создание диаграмм
Excel предоставляет пользователю широкий диапазон стандартных типов диаграмм научного и делового назначения, каждый из которых имеет несколько вариантов. Диаграммы в Excel включают много элементов, каждый из которых можно выделять и изменять отдельно. Краткие сведения об основных элементах диаграмм представлены в таблице 1.
Таблица 1. Элементы диаграммы Excel
| Название элемента | Описание |
| Ось | Линия, используемая как основа измерений для построения данных на диаграмме. Ось категорий (Х) и ось значений (У) образуют границы диаграммы и имеют шкалу для нанесения данных. Ось значений (Z) используется в трехмерных диаграммах. |
| Точка данных | Элемент данных. |
| Ряд данных | Совокупность точек данных, отображающая значения в строках или в столбцах рабочего листа. На диаграмме может быть отображен один или несколько рядов данных. |
| Легенда | Подпись, определяющая закрасу или цвета точек данных или категорий диаграммы. |
| Маркер | Элемент, который представляет точку данных на диаграмме. Вид маркера зависит от типа и вида диаграммы. Все маркеры одного ряда данных имеют одинаковую форму и цвет. |
| Область диаграммы | Вся диаграмма вместе со всеми ее элементами. |
| Область построения | В двумерной диаграмме это прямоугольная область, ограниченная двумя осями и содержащая все ряды диаграммы. В трехмерной диаграмме это область, ограниченная осями и включающая ряды данных, названия категорий, подписи делений и названия осей. |
| Формула рядов | Формула с внешними ссылками на данные определенного листа, по которым построена диаграмма. |
| Текст | Надписи (название диаграммы, значения и категории на осях) и подписи (текст, связанный с точками данных). Любой текст на диаграмме можно изменять и перемещать. |
В Excel можно построить диаграммы на рабочем листе рядом с таблицами данных или на отдельном листе. Создание диаграммы рядом с таблицами данных имеет смысл при оформлении отчетов, для демонстрации диаграмм рядом с данными, по которым они построены. Построение диаграммы на отдельном листе удобно, когда ее, например, нужно вывести на печать.
Диаграммы легко строятся с помощью Мастера диаграмм. Он руководит процессом создания диаграммы шаг за шагом и дает возможность перед завершением процесса посмотреть ее и внести необходимые изменения.
Типы диаграмм
MS Excel имеет в своем составе 11 стандартных типов диаграмм. Их названия и краткое описание приведены в таблице 2.
Таблица 2. Типы диаграмм в Excel
| Тип диаграммы | Описание |
| Гистограмма | Используется, когда нужно создать впечатление отдельных измерений, относящихся к разным интервалам времени. Категории располагаются по горизонтали, а значения – по вертикали. |
| Линейчатая | Похожа на гистограмму за исключением того, что осью категорий является вертикальная ось (У), а осью значений – горизонтальная ось (Х). Используется для сопоставления отдельных значений в определенный момент времени. |
| График | Отображает зависимость данных (ось У) от величины, которая меняется с постоянным шагом (ось Х).Используется для отображения тенденции изменения данных во времени. |
| Круговая | Используется для отображения соотношения частей и целого. Строятся только по одному ряду данных, первому в выделенном диапазоне. Эту диаграмму следует использовать, когда все компоненты в сумме составляют 100%. |
| Точечная | Используется для представления дискретных измерений по осям Х и У. Демонстрирует тенденции изменения данных при неравных интервалах времени или других интервалах измерения, отложенных по оси категорий (Х). |
| Диаграмма с областями | Используется, если необходимо проследить непрерывное изменение суммы значений всех рядов данных и вклад каждого ряда в эту сумму. |
| Кольцевая | Позволяет сравнить вклад частей в целое. В ней могут быть представлены два и более ряда данных. Каждое кольцо представляет отдельный ряд данных. |
| Лепестковая | Используется, когда нужно показать соотношения отдельных рядов данных, или одного определенного ряда данных и всех остальных рядов. |
| Поверхность | Используется для наглядного представления высоких и низких значений в наборе данных, который зависит от двух переменных. Диаграмма представляет собой поверхность, натянутую на точки. Такую диаграмму можно поворачивать и видеть ее с разных точек зрения. |
| Пузырьковая | Позволяет отобразить на плоскости набор данных из трех значений. Первые два откладываются по оси категорий (Х) и по оси значений (У). Третье значение представляется размером пузырька. |
| Биржевая | Используется для отображения изменения курса акций во времени. При формировании рядов данных для биржевой диаграммы необходимо размещать данные в последовательности, которая указывается внизу диалогового окна «Тип диаграммы», при выборе соответствующего формата диаграммы. |
| Цилиндрические, конические и пирамидальные | Объемные варианты гистограмм и линейчатых диаграмм. Эти типы объемных диаграмм не добавляют новой информации, а имеют только внешний эффект. |
Построение диаграммы
Теперь перейдем непосредственно к построению диаграммы.
1. Чтобы создать диаграмму с помощью мастера диаграмм необходимо сначала создать таблицу данных, на основе которых она будет построена.
1.1.В первом столбце должны быть представлены значения аргумента X.Используя приёмы автозаполнения ввести в диапазон А2:В630 значения от –pдо pс шагом 0,01.
1.2.Во втором столбце должны быть представлены значения функции Y=f(X).Значения Yвычислить по формуле sinХ.Для этого введем в ячейку В2 формулу =sin(A2) и скопируем ее по столбцу В.
1.3.Выделите эту таблицу.
2. Выберите команду Вставка–Диаграммы–Точечная и выберите тип диаграммы Точечная с гладкими кривыми
Редактирование и форматирование диаграммы осуществляется во вкладках Конструктор, Макет и Формат, которые отображаются при выделении области построения диаграммы.
3. Измените следующие параметры диаграммы:
3.1. Уберите легенду командой Макет–Подписи–Легенда–Нет
3.2. Введите название диаграммы «График функции y = sin x» с помощью команды Макет–Подписи–Название диаграммы––Над диаграммой;
3.3. Введите названия осей «Х» и «Y», выполнив соответственно команды Макет–Подписи–Название осей–Название основной горизонтальной оси–Название под осьюи Макет–Подписи–Название осей–Название основной вертикальной оси–Горизонтальное название
3.4. Измените расположение подписей к осям: название оси ОХ – справа от оси, название оси OY – сверху над осью. Для этого достаточно выделить подпись и перетащить ее мышью.
3.5. Измените максимальное и минимальное значения оси ОХ, выполнив команду Макет–Оси–Оси–Основная горизонтальная ось–Дополнительные параметры основной горизонтальнойоси. В появившемся диалоговом окне выберите Параметры осии установите
· фиксированное минимальное значение -3,5
· фиксированное максимальное значение 3,5
3.6. Добавьте линии сетки по оси ОХ, выполнив команды Макет–Оси–Сетка–Вертикальные линии сетки по основной оси–Основные линии сетки
3.7. Измените размер основных делений сетки по оси ОХ:
· Выделите ось ОХ на диаграмме мышью или выполним команду Макет–Текущий фрагмент и в раскрывающемся списке Элементы диаграммы выберем Горизонтальная ось (значений)
· Выполните команду Макет–Текущий фрагмент–Формат выделенного фрагмента. В появившемся диалоговом окне выберите Параметры осии установите цена основных делений 0,5
После выполнения перечисленных действий, будет построена диаграмма, вид которой представлен на рис.1. Но на ней не хватает элементов оформления. Ее необходимо отформатировать.
Когда перед пользователем стоит задача качественно оформить учебный документ, часто приходится работать с таблицами и графиками, которые строятся на ее основе. Рассмотрим несколько актуальных методик, как построить график зависимости в Excel.
Как постороить одноосевой график
Для каждого случая построения графиков существуют индивидуальные условия, но практически всегда должна быть независимая переменная функция. На практике такую обозначают символами «х» или «у».
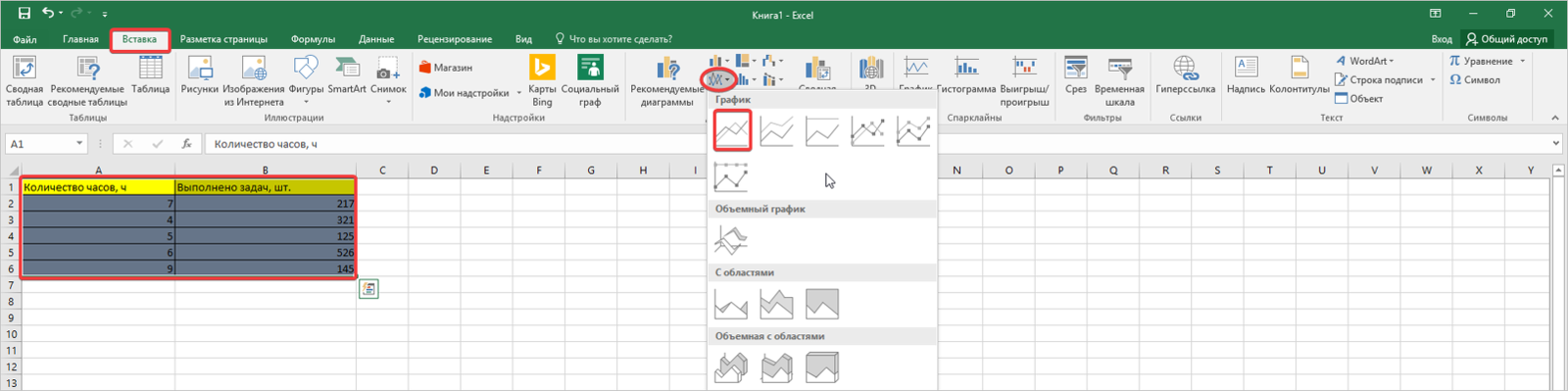
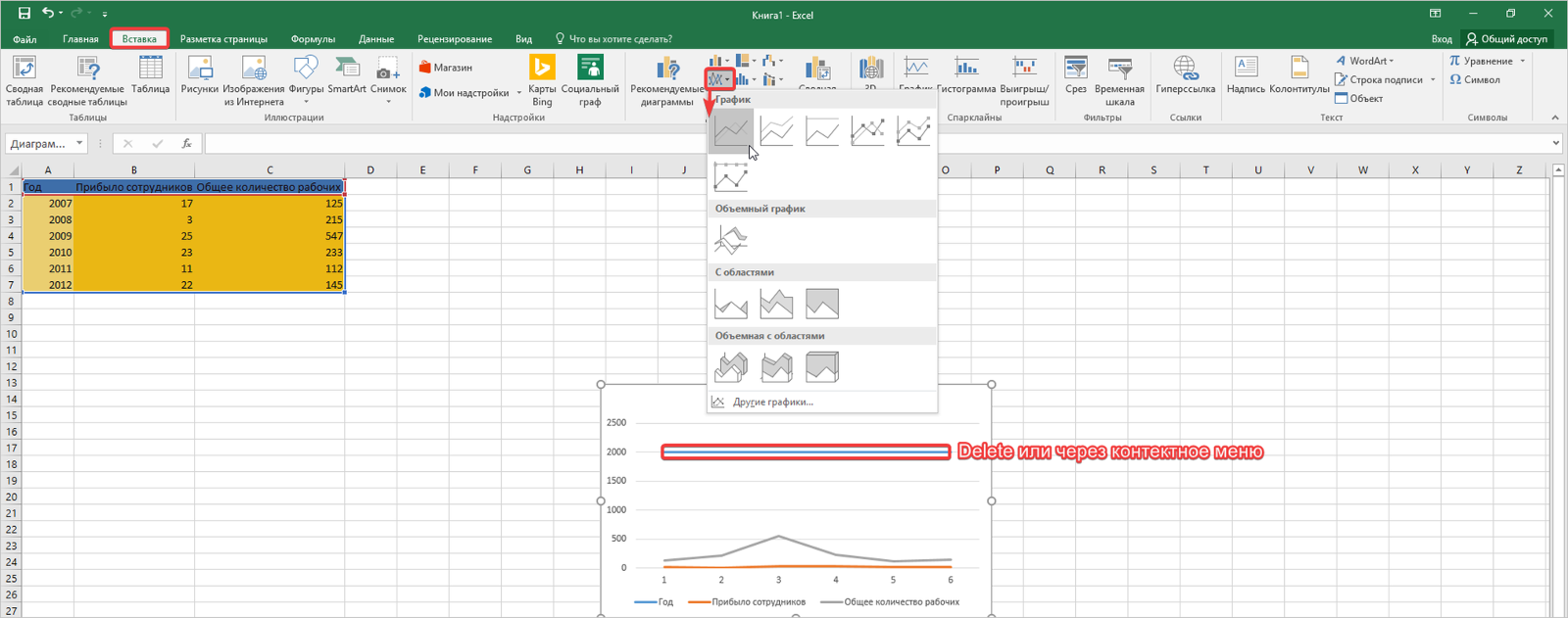
- Предположим, у нас есть таблица с двумя известными составляющими. Построим график зависимости на ее основе. Выделяем весь диапазон ячеек, которые охватывает наша таблица, затем переходим во вкладку «Вставка». Находим блок с диаграммами и нажимаем на инструмент «Вставить график». Для начала подойдёт самый простой.
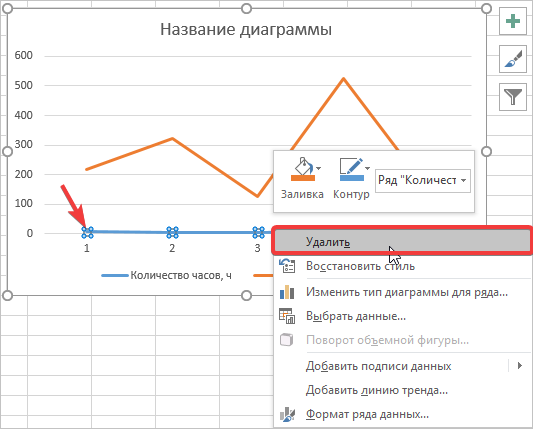
- Автоматически система произвела построение графика с ломаными линиями, однако нам понадобится лишь одна, поэтому ненужную ось (с количеством часов) можно удалить. Для этого сделаем выделяем её мышью, а затем нажмем правой кнопкой вызовем меню редактирования. Нажимаем «Удалить».
- На данном этапе можно считать первый способ построения графика завершенным. Мы удалили ось временного промежутка и получили значение, которое нас интересует: «Зависимость выполненных задач за заданное время».
Для более сложных систем зависимости можно использовать графическую диаграмму с маркерами. Она поможет более точно определить сегмент данных и выстроить аналитическую картину таблицы.
Как постороить осложненный график зависимости
При наличии двух или трех неизменных данных в таблице, график зависимости выполняет сложную функцию. Рассмотрим способ построения графика зависимости для нескольких значений:
- Выделим всю область нашей таблицы и снова запустим первый график. Перед вами появился объект, в котором одна линия, отвечающая за год, отображается некорректно. Удаляем ее, как в предыдущем способе.
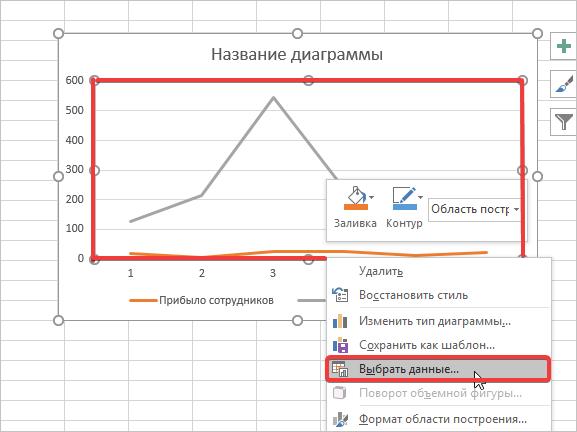
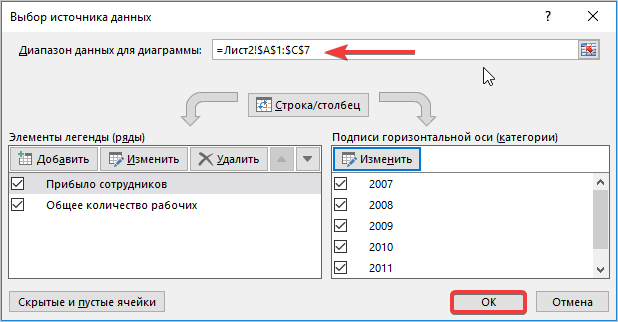
- График отобразился иначе, однако одна из линий все равно неправильно отвечает за свои функции. Для исправления этой ошибки выбираем область построения (активируем ее так, чтобы видны были элементы перемещения). Затем сделаем клик правой кнопкой мыши и нажмем на пункт «Выбрать данные».
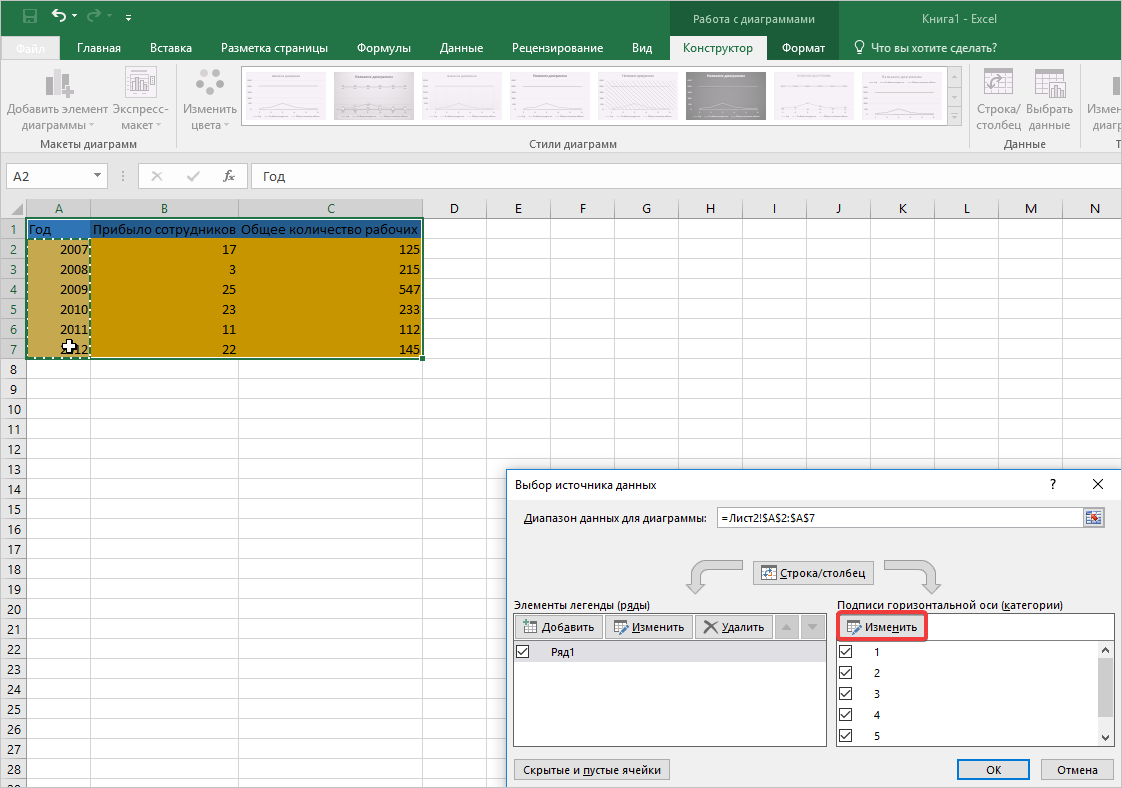
- Открывается дополнительное окно настроек. В нем находим кнопку «Изменить», после ее нажатия автоматически открывается окно поменьше.
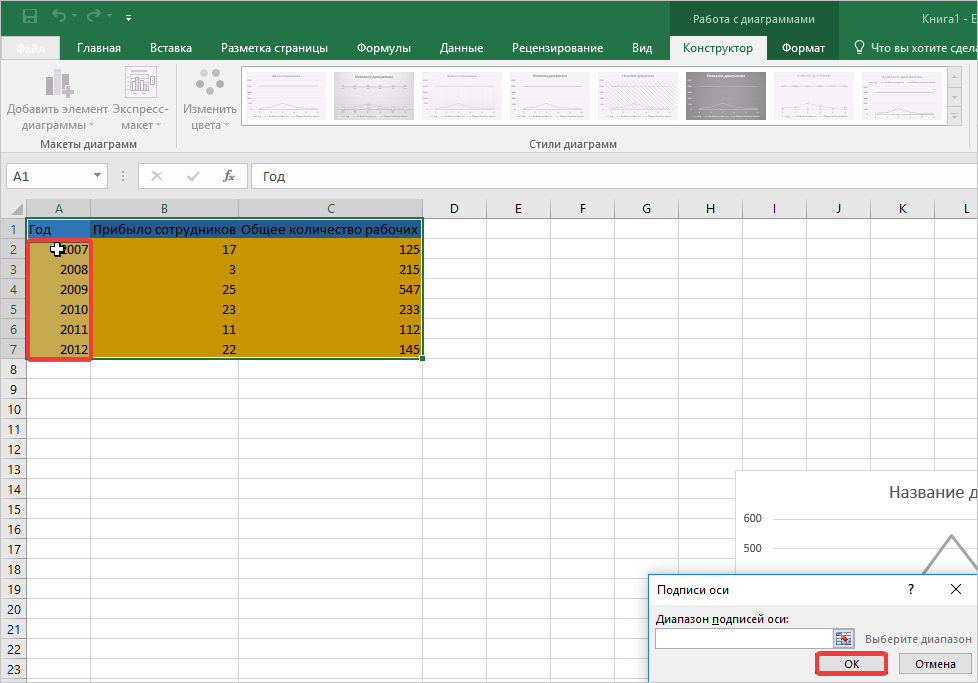
- Теперь выделяем диапазон ячеек, где отображаются года. Только не вносите в адрес заголовок этого столбца. Затем нажмите кнопку «ОК.
- Снова нажмите «ОК», чтобы сохранить изменения, внесенные в график зависимости. Обратите внимание, что адреса обрабатываемых ячеек автоматически перенеслись в поле диапазона.
После произведенных манипуляций все данные на листе получили четкую позицию, соответственно, отображаются корректно. Можно заметить, никаких сложностей с оформлением графиков зависимости нет.
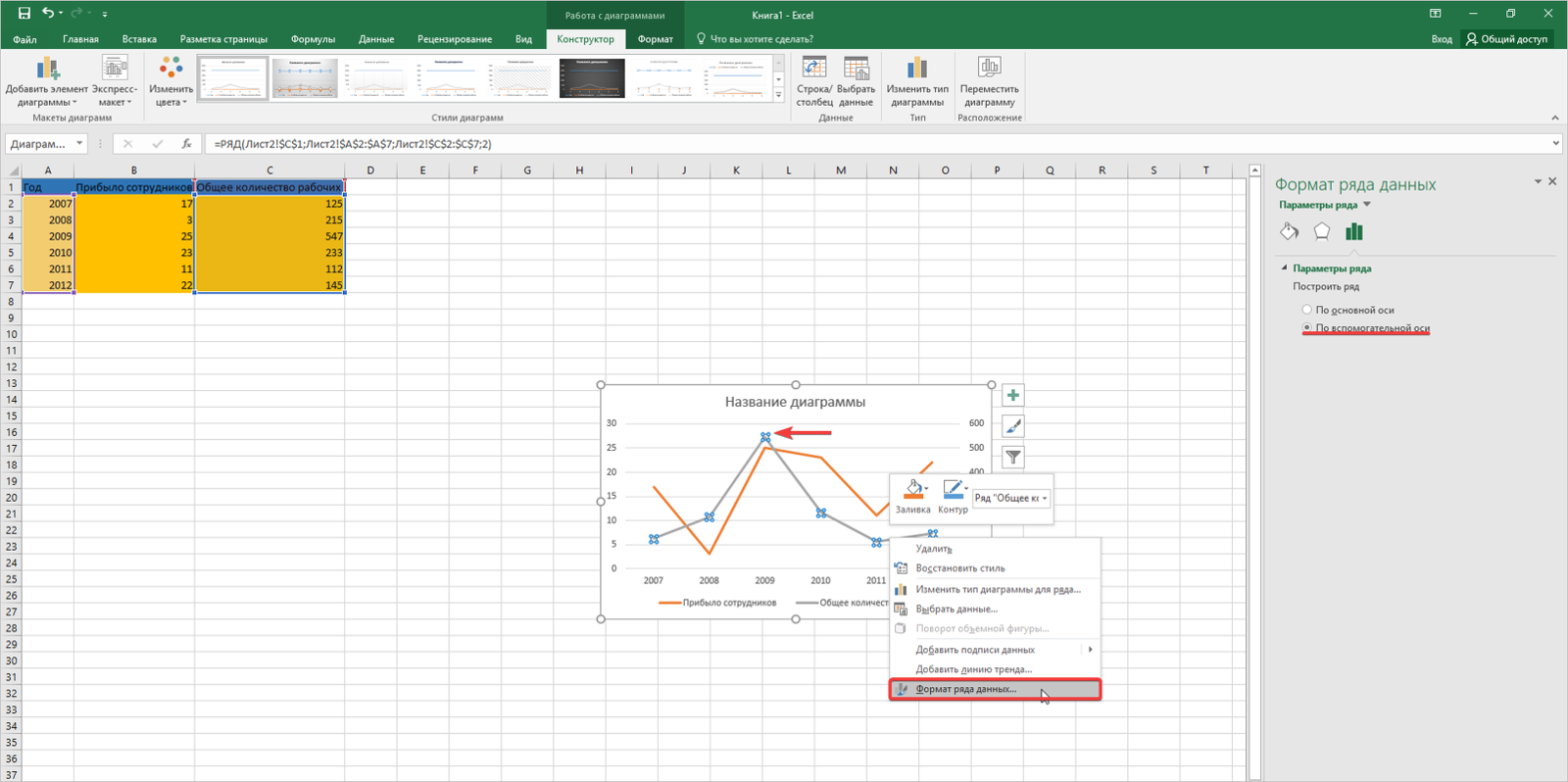
Если на графике отображается несоответствие величин, необходимо построить вспомогательную ось. Для этого нажмите на область изменения оси, а затем сделайте клик правой кнопкой мыши.
Выберите «Формат ряда данных». В окне мастера справа отметьте флажок «По вспомогательной оси». Изменения будут активированы.
Алгебраическая функция и график зависимости
Этот способ построения графика зависимости используют студенты и те, кто работают в области статистики. Прежде чем выстроить график зависимости, необходимо посчитать значение «х» и прописать его в таблице с определенным шагом.
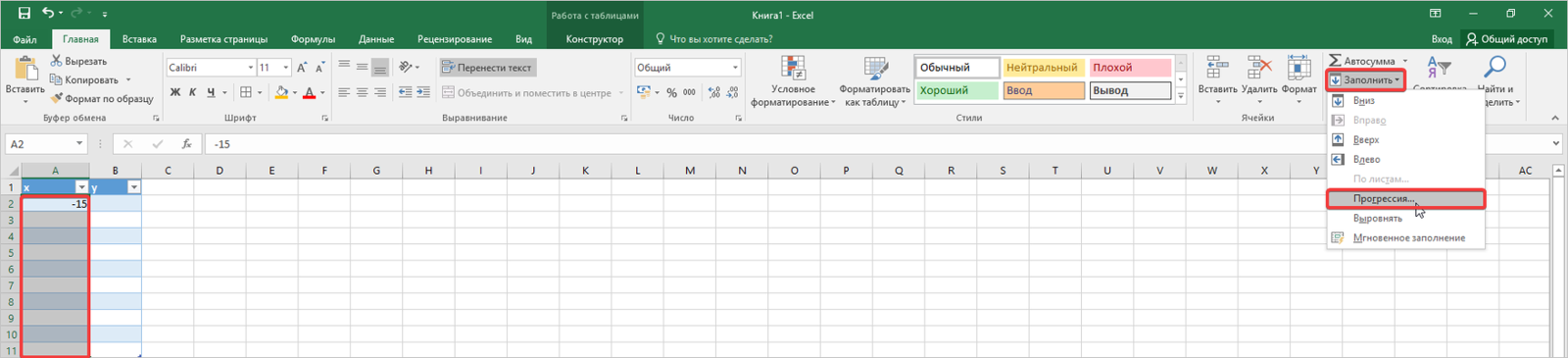
- Для начала построим таблицу и впишем в нее единственное значение. Вставляем в первую ячейку «х» число -15. Затем заполним оставшиеся данные вниз через три шага. Для этого воспользуемся автоматическим инструментом. Выделяем весь столбец «х», затем во вкладке «Главная» нажимаем на пункт «Заполнить». Высветится список, в котором выбираем «Прогрессия».
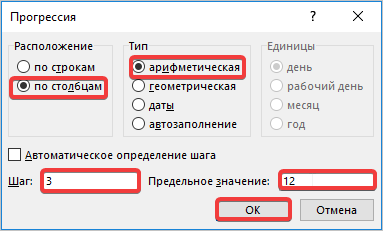
- В следующем открывшемся окне редактируем все так, как указано на фото. Обязательно проставляем величину шага «3», затем отмечаем предельное значение, в нашем случае будет число «12». Нажимаем кнопку «ОК».
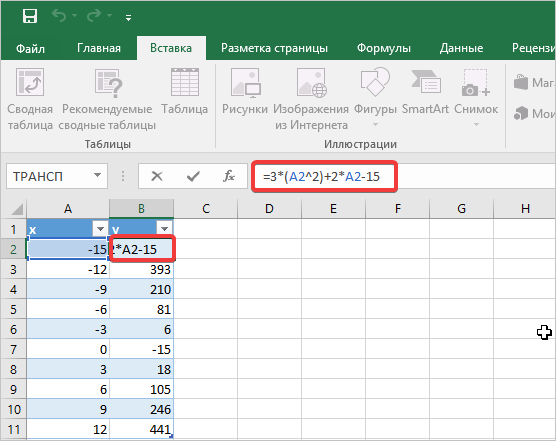
- Выполняем преобразование обычной формулы в формулу Excel. Для этого вставим нашу формулу в первую ячейку столбца «у», где вместо значения «х» пропишем адрес ячейки, в котором оно прописано. Затем в конце формулы нажимаем кнопку «Enter».
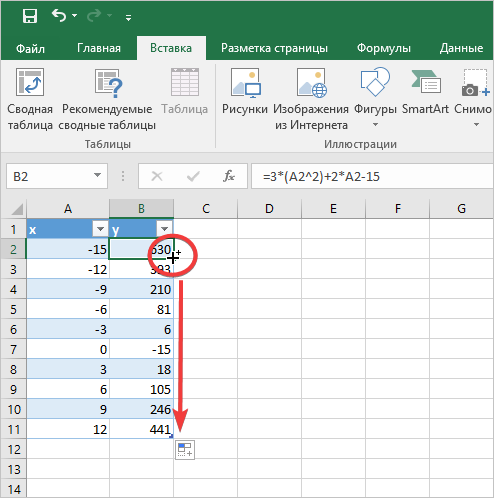
- Как вы видите, все значения автоматически посчитались для каждой отдельно взятой ячейки. Если в вашей версии Excel значения не заполнились, необходимо использовать маркер автозаполнения. Наведите на нижний угол до появления крестика. Нажмите и протяните вниз до последней ячейки.
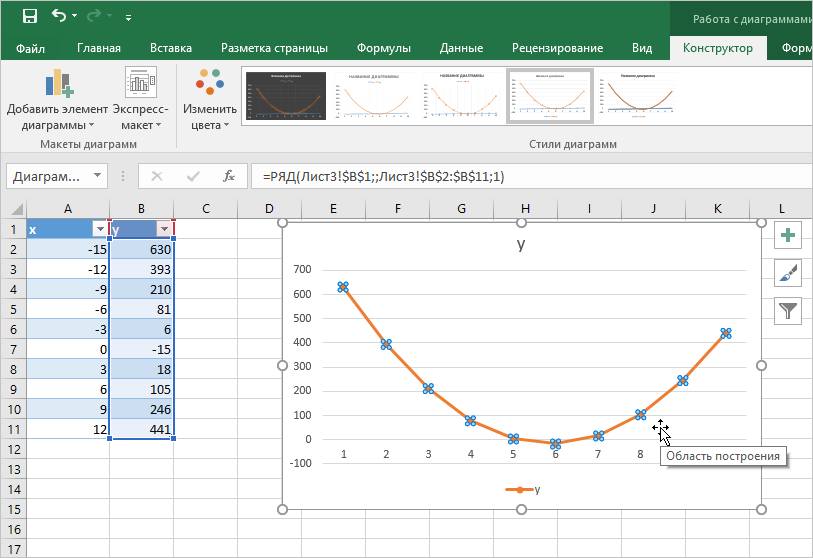
- Как в предыдущих способах, выстраиваем графики. В данном случае, необходимо выбрать маркированный объект. Обязательно удаляем лишнюю ось.
Если вам малопонятны функции Microsoft Excel, вы можете вручную прописать каждое значение выражения, однако автоматизированный процесс поможет сберечь ваше время.
Подробнее о функциях Excel и их применении читайте в инструкции Справочника.
Тест по теме «Альтернативные способы построения графика зависимости в Excel»
МОУ «Кезская средняя общеобразовательная школа №1»
Моделирование графиков функций двух
переменных
Исследовательская работа
Автор: учащийся 9а класса,
Никитин Кирилл Валентинович
Руководитель работы: учитель информатики,
Ветошкина Наталья Владимировна
п. Кез, 2011
СОДЕРЖАНИЕ
1. Содержание…………………………………………………………………..…2
2. Введение…………………………………………………………………………3
3. История……………………………………………………………………….4-5
4. Основные этапы работы
4.1. Теоретическая часть……………………………………………………6
4.2. Практическая часть…………………………………………………7-12
5. Заключение…………………………………………………………………….13
6. Приложение………………………………………………………………..14-16
7. Литература…………………………………………………………………….17
Введение
На одном из уроков алгебры мы изучали графики функций, и учитель сказал, что существуют графики функций двух переменных и их графики строятся в трехмерной системе координат. Меня заинтересовал этот факт, и я решил смоделировать графики функций двух переменных с помощью компьютера в среде Q basic и в среде электронных таблиц Excel.
Гипотеза
Многие считают графики функций не интересной теорией, основанной на сухих фактах, не представляя, какими красочными и завораживающими они могут оказаться.
Цель
Изучить теоретический материал о способах моделирования графиков функций двух переменных с помощью компьютера и составить алгоритмы их построения в разных программах.
Задачи
1) расширить понятия функции двух переменных;
2) построить с помощью компьютерных программ графики функций двух переменных;
3) рассмотреть известные графики функций двух переменных;
4) смоделировать в среде Q Basic и в электронных таблицах Excel графики функций двух переменных;
5) рассмотреть связь природы с графиками функций двух переменных.
История
Функция двух переменных:
Само слово «функция» (от латинского functio — совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673 г. в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати он его ввел с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа». В 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667 – 1748), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных». Для обозначения произвольной функции от x Бернулли применил знак j(x), называя характеристикой функции, а также буквы x или e; Лейбниц употреблял x1, x2 вместо современных f1(x), f2(x). Эйлер обозначил через f: y, f: (x + y) то, что мы ныне обозначаем через f(x), f(x+y).
История Q Basic:
QBASIC — диалект языка программирования Бейсик (BASIC), разработанный компанией Microsoft, а также среда разработки, позволяющая писать, запускать и отлаживать программы на этом языке.
Создателями языка программирования Q Basiс были John George Kemeny и Тоm Kurtz, работавшие в Дортмундском колледже в 1964 году. Свой язык они назвали по первым буквам слов «Beginner’s All-purpose Symbolic Instruction Code». Кроме того, имелась в виду ассоциация со словом «базовый». Новый язык быстро завоевал популярность благодаря своей простоте в изучении, особенно среди начинающих. Собственно, как и Pascal, Basic был предназначен для обучения студентов.
Джон Джордж Ке́мени (англ. John George Kemeny, венг. Kemény János György, 31 мая 1926, Будапешт — 26 декабря 1992, Нью-Гэмпшир,США) — американский математик и специалист по информатике. Вместе с Томасом Курцем разработал язык Бейсик (1964).[1] В 1970 году был избран 13-м президентом Дартмутского колледжа (одного из старейших и авторитетнейших университетов США) и занимал эту должность 11 лет. В этом колледже он впервые начал систематическое применение компьютеров в учебном процессе.
Джон Кемани Томас Курц
Томас Курц (Thomas Eugene Kurtz) — математик, профессор Дартмутского колледжа (США). Вместе с Джоном Кемени разработал язык программирования BASIC и сетевую систему пользования несколькими компьютерами одновременно («time sharing»). Получил научную степень в Принстонском университете в 1956 году и сразу был приглашен на Математический факультет в Дартмутский колледж.
История Excel:
Microsoft Excel (также иногда называется Microsoft Office Excel) — программа для работы с электронными таблицами, созданная корпорацией Microsoft для Microsoft Windows, Windows NT и Mac OS. Она предоставляет возможности экономико-статистических расчетов, графические инструменты и, за исключением Excel 2008 под Mac OS X. Microsoft Excel входит в состав Microsoft Office и на сегодняшний день Excel является одним из наиболее популярных приложений в мире. Первая версия Excel предназначалась для Mac и была выпущена в 1985 году, а первая версия для Windows была выпущена в ноябре 1987 года.
Теоретическая часть
Если каждой паре (x,y) значений двух, независимых друг от друга, переменных величин x и y , из некоторой области их изменений D, соответствует одно определенное значение величины z, то говорят, что z – есть функция двух независимых переменных x и y , определенная в области D (область определения функции).
С помощью графика функций двух переменных мы имеем возможность наглядно представить значения и связь трех величин в любых сферах деятельности. Также можно выявить между собой связь этих трех величин. Примеров множество: от обыкновенного прогноза погоды до математического моделирование плазмы в термоядерном ядре.
В смоделированной программе графика двух переменных в среде Q Basic используются следующие алгоритмические структуры:
1) линейная;
2) циклическая;
3) разветвляющаяся.
Вариантом циклической структуры является цикл – ДЛЯ
FOR i=i1 TO i2 STEP i3
<Тело цикла>
NEXT i
i – переменная, счетчик
i1 – первое значение которое принимает переменная i
i2 – последнее значение либо близкое к нему, не превосходящее i2
i3 – длина шага
Вариантом структуры ветвления является ветвление – ЕСЛИ
IF условие 1 OR условие 2 THEN действие 1 ELSE действие 2
Практическая часть
Часть 1: Составление графика Гиперболический параболоид в электронных таблицах Excel
- Зададим значение переменной y от -3 до 3 с шагом 0,5
- Зададим значение переменной x от -3 до 3 с шагом 0,5
- Введем в ячейку B2 адаптированную к электронным таблицам формулу гиперболического параболоида =B$1^2-$A2^2 и скопируем её в ячейки до ячейки N14
- Выделим область ячеек от B2 до N14.
- Воспроизведем следующий порядок команд: Вставка- Диаграмма, выбираем тип- Поверхность, Готово
- Удалим с графика лишнее, переместим на свободную поверхность
И вот мы получили довольно интересный рисунок, который является графиком функции двух переменных. По этому аналогу можно строить графики любых функций двух переменных (примеры в приложении). Это занимает не много времени, но выглядит очень красочно и наглядно.
Часть 2: Составление Графика функции двух переменных в среде программирования QBasic
Программа №1 «Обезьянье седло»
sx = 180
sy = 180
ratio = .6
hx = sx / 2
hy = sy / 2
s = SQR(2) / 2
aa = hx * s
SCREEN 7
FOR a = -aa TO aa + 5 * s
max = -hy
bb = aa + a — 10 * s * INT((a + ABS(a)) / (10 * s))
FOR b = -bb TO bb + s * 4 STEP 10 * s
x = s * (a + b)
y = s * (b — a)
z = b
r = SQR(x * x + y * y)
z = x * y * (x — y) * (x + y) / (1000 * r) + b
IF z < max THEN GOTO 760
max = z
u = hx + a
v = hy + z * s / ratio
IF v < 0 OR v > sy THEN GOTO 760
PSET (u, v)
760 NEXT b
NEXT a
END
Программа №2
sx = 176
sy = 160
ratio = .6
hx = sx / 2
hy = sy / 2
s = SQR(2) / 2
aa = hx * s
SCREEN 7
FOR a = -aa TO aa + 5 * s
max = -hy
bb = aa + a — 10 * s * INT((a + ABS(a)) / (10 * s))
FOR b = -bb TO bb + s * 4 STEP 10 * s
x = s * (a + b)
y = s * (b — a)
z = b
r = SQR(x * x + y * y)
z = 10 * COS(r / 5) + b
IF z < max THEN GOTO 760
max = z
u = hx + a
v = hy + z * s / ratio
IF v < 0 OR v > sy THEN GOTO 760
PSET (u, v)
760 NEXT b
NEXT a
END
Программа №3
sx = 180
sy = 180
ratio = .6
hx = sx / 2
hy = sy / 2
s = SQR(2) / 2
aa = hx * s
SCREEN 7
FOR a = -aa TO aa + 5 * s
max = -hy
bb = aa + a — 10 * s * INT((a + ABS(a)) / (10 * s))
FOR b = -bb TO bb + s * 4 STEP 10 * s
x = s * (a + b)
y = s * (b — a)
z = b
r = SQR(x * x + y * y)
z = 75 * EXP(-r * r / 600) + b
IF z < max THEN GOTO 760
max = z
u = hx + a
v = hy + z * s / ratio
IF v < 0 OR v > sy THEN GOTO 760
PSET (u, v)
760 NEXT b
NEXT a
END
Заключение
В качестве заключения был проведен опрос, в котором выяснилось, что 100% опрошенных считают, что график функции двух переменных смоделированный в среде электронных таблиц Excel выглядит понятнее и нагляднее.
Таким образом, опытным путем мы выяснили, что моделирование графиков функций двух переменных в среде электронных таблиц Excel нагляднее и проще для восприятия, чем эти же графики, но смоделированные в среде программирования Q basic.
Если учитывать по времени выполнения графиков в этих двух средах то можно уверенно сказать, что моделирование в среде электронных таблиц в 10 разы быстрее и, что немаловажно, легче.
В дальнейших исследованиях возможно построение этих графиков в других средах, или же можно построить другие графики более сложные по структуре. А также изучить вопрос о том, какие процессы описываются функциями двух переменных. Как применяются графики функций двух переменных.
Приложение
График функции Полусфера
График функции Конус
График функции Эллиптический цилиндр от 0 до 2
График функции Гиперболический цилиндр от -1 до 1
График функции Эллиптический параболоид
График функции
Литература
- Журнал «Информатика», №1, 1-15 января 2007 года, издательский дом «Первое сентября»
- «Занимательная математика и компьютер», Ч. Конёвски, издательство «Мир», 1987 год.
- «Основы Информатики и вычислительной техники», А.П. Ершова и В.М. Монахова, издательство «Просвещение», 1985 год.
- «Методические рекомендации по изучению языка программирования MSX- Бейсик», Глазов, 1988 год.
- http://ru.wikipedia.org