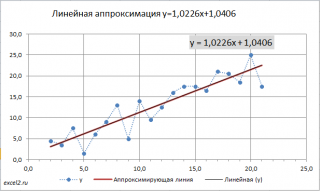
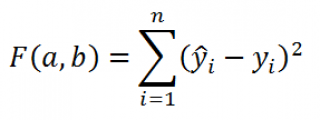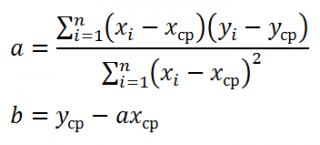Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью линейной функции
y
=
a
x
+
b
.
Метод наименьших квадратов
(англ.
Ordinary
Least
Squares
,
OLS
) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров
регрессионных моделей
по выборочным данным.
Рассмотрим приближение функциями, зависящими только от одной переменной:
- Линейная: y=ax+b (эта статья)
-
Логарифмическая
: y=a*Ln(x)+b
-
Степенная
: y=a*x
m
-
Экспоненциальная
: y=a*EXP(b*x)+с
-
Квадратичная
: y=ax
2
+bx+c
Примечание
: Случаи приближения полиномом с 3-й до 6-й степени рассмотрены в этой статье. Приближение тригонометрическим полиномом рассмотрено здесь.
Линейная зависимость
Нас интересует связь 2-х переменных
х
и
y
. Имеется предположение, что
y
зависит от
х
по линейному закону
y
=
ax
+
b
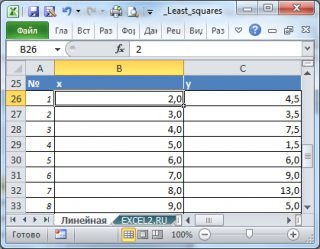
. Чтобы определить параметры этой взаимосвязи исследователь провел наблюдения: для каждого значения х
i
произведено измерение y
i
(см.
файл примера
). Соответственно, пусть имеется 20 пар значений (х
i
; y
i
).
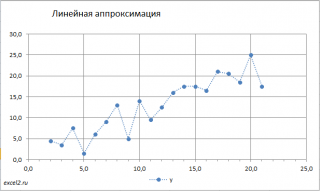
Для наглядности рекомендуется построить диаграмму рассеяния.
Примечание:
Если шаг изменения по
х
постоянен, то для построения
диаграммы рассеяния
можно использовать
тип График
, если нет, то необходимо использовать тип диаграммы
Точечная
.
Из диаграммы очевидно, что связь между переменными близка к линейной. Чтобы понять какая из множества прямых линий наиболее «правильно» описывает зависимость между переменными, необходимо определить критерий, по которому будут сравниваться линии.
В качестве такого критерия используем выражение:
где
ŷ
i
=
a
*
x
i
+
b
;
n – число пар значений (в нашем случае n=20)
Вышеуказанное выражение представляет собой сумму квадратов расстояний между наблюденными значениями y
i
и ŷ
i
и часто обозначается как SSE (
Sum
of
Squared
Errors
(
Residuals
), сумма квадратов ошибок (остатков)
)
.
Метод наименьших квадратов
заключается в подборе такой линии
ŷ
=
ax
+
b
, для которой вышеуказанное выражение принимает минимальное значение.
Примечание:
Любая линия в двухмерном пространстве однозначно определяется значениями 2-х параметров:
a
(наклон) и
b
(сдвиг).
Считается, что чем меньше сумма квадратов расстояний, тем соответствующая линия лучше аппроксимирует имеющиеся данные и может быть в дальнейшем использована для прогнозирования значений y от переменной х. Понятно, что даже если в действительности никакой взаимосвязи между переменными нет или связь нелинейная, то МНК все равно подберет «наилучшую» линию. Таким образом, МНК ничего не говорит о наличии реальной взаимосвязи переменных, метод просто позволяет подобрать такие параметры функции
a
и
b
, для которых вышеуказанное выражение минимально.
Проделав не очень сложные математические операции (подробнее см.
статью про квадратичную зависимость
), можно вычислить параметры
a
и
b
:
Как видно из формулы, параметр
a
представляет собой отношение ковариации и
дисперсии
, поэтому в MS EXCEL для вычисления параметра
а
можно использовать следующие формулы (см.
файл примера лист Линейная
):
=
КОВАР(B26:B45;C26:C45)/ ДИСП.Г(B26:B45)
или
=
КОВАРИАЦИЯ.В(B26:B45;C26:C45)/ДИСП.В(B26:B45)
Также для вычисления параметра
а
можно использовать формулу =
НАКЛОН(C26:C45;B26:B45)
. Для параметра
b
используйте формулу =
ОТРЕЗОК(C26:C45;B26:B45)
.
И наконец, функция
ЛИНЕЙН()
позволяет вычислить сразу оба параметра. Для ввода формулы
ЛИНЕЙН(C26:C45;B26:B45)
необходимо выделить в строке 2 ячейки и нажать
CTRL
+
SHIFT
+
ENTER
(см. статью про
формулы массива, возвращающими несколько значений
). В левой ячейке будет возвращено значение
а
, в правой –
b
.
Примечание
: Чтобы не связываться с вводом
формул массива
потребуется дополнительно использовать функцию
ИНДЕКС()
. Формула =
ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);1)
или просто =
ЛИНЕЙН(C26:C45;B26:B45)
вернет параметр, отвечающий за наклон линии, т.е.
а
. Формула =
ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);2)
вернет параметр, отвечающий за пересечение линии с осью Y, т.е.
b
.
Вычислив параметры, на
диаграмме рассеяния
можно построить соответствующую линию.
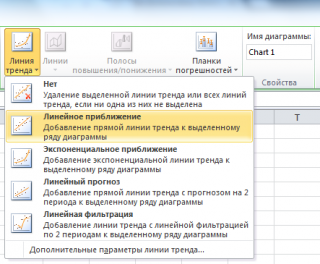
Инструмент диаграммы Линия тренда
Еще одним способом построения прямой линии по методу наименьших квадратов является инструмент диаграммы
Линия тренда
. Для этого выделите диаграмму, в меню выберите
вкладку Макет
, в
группе Анализ
нажмите
Линия тренда
, затем
Линейное приближение
.
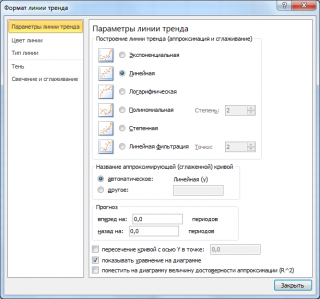
Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме.
Примечание
: Для того, чтобы параметры совпадали необходимо, чтобы тип у диаграммы был
Точечная, а не График
. Дело в том, что при построении диаграммы
График
значения по оси Х не могут быть заданы пользователем (пользователь может указать только подписи, которые не влияют на расположение точек). Вместо значений Х используется последовательность 1; 2; 3; … (для нумерации категорий). Поэтому, если строить
линию тренда
на диаграмме типа
График
, то вместо фактических значений Х будут использованы значения этой последовательности, что приведет к неверному результату (если, конечно, фактические значения Х не совпадают с последовательностью 1; 2; 3; …).
СОВЕТ
: Подробнее о построении диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
Сразу скажу могу ошибаться. Корень из r2= корреляция
Справка из Excel функции ЛИНЕЙН
Пример 4. Использование F-статистики и r2-статистики
В предыдущем примере коэффициент детерминированности r2 равен 0,99675 (см. ячейку A17 в результатах функции ЛИНЕЙН), что указывает на сильную зависимость между независимыми переменными и продажной ценой. Можно использовать F-статистику, чтобы определить, является ли этот результат (с таким высоким значением r2) случайным.
Предположим, что на самом деле взаимосвязи между переменными не существует, просто статистический анализ вывел сильную взаимозависимость по взятой равномерной выборке 11 зданий. Величина «Альфа» используется для обозначения вероятности ошибочного вывода о существовании сильная взаимозависимости.
В выходных данных функции ЛИНЕЙН величины F и df используются для оценки вероятности случайного получения наибольшего значения F. Величину F можно сравнить с критическими значениями в публикуемых таблицах F-распределения, либо для вычисления возможности случайного получения наибольшего значения F можно использовать функцию Microsoft Excel FРАСП. Соответствующее F-распределение имеет степени свободы v1 и v2. Если величина n представляет количество точек данных и аргумент конст имеет значение ИСТИНА или опущен, то v1 = n – df – 1 и v2 = df. (При конст = ЛОЖЬ v1 = n – df и v2 = df). Функция FРАСП — с синтаксисом FРАСП(F,v1,v2) — возвращает вероятность случайного получения наибольшего значения F. В примере 4 df = 6 (ячейка B18), а F = 459,753674 (ячейка A18).
Предположим, что значение «Альфа» равно 0,05, v1 = 11 – 6 – 1 = 4 и v2 = 6, а критический уровень F равен 4,53. Поскольку значение F = 459,753674 намного больше 4,53, вероятность случайного получения такого большого значения F исключительно мала (при Альфа = 0,05 гипотеза об отсутствии связи между аргументами известные_значения_y и известные_значения_x отвергается, если значение F превышает критический уровень 4,53). Использование функции Microsoft Excel FРАСП дает возможность вычислять вероятность случайного получения больших значений F. Значение вероятности FРАСП(459,753674; 4; 6) = 1,37E-7 чрезвычайно мало. Из этого можно заключить через нахождение критического уровня F в таблице или использование функции Microsoft Excel FРАСП, что уравнением регрессии можно воспользоваться для предсказания оценочной стоимости зданий под офис в данном районе. Следует учесть, что использование правильных значений v1 и v2, вычисление которых показано в предыдущем абзаце, является критически важным.
По мне так пять точек и 0,95 достаточно. Я так понимаю такие расчёты в нашей стране вряд ли кто производит.
17 авг. 2022 г.
читать 2 мин
Метод наименьших квадратов — это метод, который мы можем использовать для поиска линии регрессии, которая лучше всего соответствует заданному набору данных.
В следующем видео представлено краткое объяснение этого метода:
Чтобы использовать метод наименьших квадратов для подбора линии регрессии в Excel, мы можем использовать функцию =ЛИНЕЙН() .
В следующем пошаговом примере показано, как использовать эту функцию на практике.
Шаг 1: Создайте набор данных
Во-первых, давайте создадим следующий набор данных в Excel:
Шаг 2: Используйте метод наименьших квадратов для подбора линии регрессии
Мы можем использовать функцию =LINEST(known_ys, known_xs) , чтобы использовать метод наименьших квадратов, чтобы подобрать линию регрессии к этому набору данных:
Как только мы нажмем ENTER , появятся коэффициенты регрессионной модели:
Шаг 3: интерпретируйте результаты
Используя коэффициенты из функции =LINEST() , мы можем написать следующую подобранную линию регрессии:
у = 11,55211 + 1,07949(х)
Мы можем использовать это уравнение для оценки значения y на основе значения x.
Например, если x = 10, то мы оценили бы, что y будет равно 22,347 :
у = 11,55211 + 1,07949(10) = 22,347
Шаг 4: Нанесите результаты на график
Наконец, мы можем использовать следующие шаги для построения набора данных вместе с подобранной линией регрессии:
- Выделите ячейки A2:B16 .
- Щелкните вкладку « Вставка » на верхней ленте. Затем щелкните первый параметр диаграммы под названием « Вставить точечную (X, Y)» или «Пузырьковую диаграмму » в группе «Диаграммы».
- После того, как диаграмма появится, нажмите знак плюс «+» в правом верхнем углу. В раскрывающемся меню установите флажок рядом с линией тренда , чтобы добавить на график подобранную линию регрессии.
Дополнительные ресурсы
Как выполнить множественную линейную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Подбор кривой в Excel (с примерами)
Я с эксель вообще не дружу и понять не могу,как простейший график закончить делать.
Помогите пожалуйста(
Нужно поставить точку 0,5 на самом графике (на линии), а потом определить значение икса.
как это сделать?
Икс в данном случае будет массой металла в растворе.Нужно найти затем массовую долю металла.
Задача такая:
Для определения металла навеску образца 0,1г растворили, перевели в мерную колбу на 100 мл, провели фотометрическую реакцию, довели до метки дистиллированной водой и измерили оптическую плотность: Ах=0,5 . Для построения градуировочного графика в 5 мерных колб на 100 мл поместили стандартный раствор, содержащий: 2,00; 4,00; 6,00; 8,00; 10 мг металла, провели фотометрическую реакцию, довели до метки дистиллированной водой и измерили оптическую плотность: А1 = 0,24; А2 = 0,46; А3 = 0,72; А4 = 0,95, А5 = 1,15.
Постройте градуировочный график в координатах А — масса металла m(Me),мг в растворе, по нему найдите массу металла в растворе, затем рассчитайте массовую долю металла в образце массой m г.

Изменено 18 Июня, 2020 в 14:04 пользователем colddawm
Содержание
Взаимосвязь ВЛК и проверки стабильности ГХ
Принцип построения градуировочного графика
Пример построения градуировочного графика
Расчет сходимости и воспроизводимости результатов
Контроль стабильности градуировочных характеристик (ГХ)
Литература
Взаимосвязь процедур внутрилабораторного контроля и проверки стабильности градуировочных характеристик
Ранее считалось, что для оценки качества результатов анализа необходимо использовать процедуры внутрилабораторного контроля, которые рассчитаны на контроль показателей качества результатов анализа, получаемых в конкретной лаборатории.
Внутрилабораторный контроль включает в себя такие составляющие, как оперативный контроль процедуры выполнения анализа и контроль стабильности результатов анализа.
Следует отметить, что в некоторых методиках количественного химического анализа используют градуировочные характеристики, применение которых насчитывает более чем двухсотлетнюю историю.
Коэффициенты градуировочных характеристик периодически контролируются в рамках процедур проверки стабильности градуировочных характеристик.
Таким образом, появление процедур внутрилабораторного контроля как полноценной документированной системы контроля качества результатов анализа произошло сравнительно недавно и касается всей процедуры анализа и всех методик, выполняемых в лаборатории.
Проверка стабильности градуировочных характеристик зародилась значительно раньше, но касается не всей процедуры анализа и не всех методик, выполняемых в лаборатории.
На первый взгляд кажется, что процедуры оперативного контроля с образцом для контроля и контроля градуировочной характеристики с использованием градуировочного раствора совершенно аналогичны по технике выполнения, что обе процедуры показывают готовность методики к работе, т.е. к анализу рабочих проб. Поэтому возникает вопрос, возможно ли, для экономии времени и материальных ресурсов в лаборатории, сократить количество проводимых проверок для оценки качества результатов анализа.
Работы по контролю градуировочных характеристик можно считать одним из этапов внутрилабораторного контроля. Контроль стабильности градуировочных характеристик необходимо осуществлять, когда при выполнении измерений применяют средства измерений, установленные характеристики которого могут изменяться в течение какого-то интервала времени.
Однако следует учитывать, что контроль градуировочных характеристик гарантирует только проверку качества работы средства измерения, но не отвечает за правильность процедуры предварительной подготовки пробы к измерению и за весь ход анализа.
Для лабораторий, которые выполняют анализы на заказ или анализируют готовую продукцию, важен каждый результат анализа. Для таких лабораторий важен юридический и статусный аспект гарантии качества результатов анализа, такие лаборатории будут выполнять все требования методик анализа.
Подумать о совмещении контроля качества результатов анализа по внутрилабораторному контролю с контролем градуировочной характеристики могут лаборатории, выполняющие рутинные анализы в стабильных условиях, когда заказчика результатов анализа интересует не отдельные результаты анализа, а совокупность результатов за длительный период, исключая аварийные ситуации. К таким лабораториям можно отнести гидрометеорологические лаборатории, экологические лаборатории по контролю водных объектов, почвы, лаборатории водоканалов по контролю качества питьевой воды и другие. Полезные рекомендации по совмещению этих видов контроля приведены в МР 18.1.04-2005 «Методические рекомендации. Система контроля качества результатов анализа проб объектов окружающей среды».
Из этого документа следует, что, так как внутрилабораторный контроль стабильности результатов анализа — это более общий контроль, охватывающий всю методику в целом, то контроль стабильности градуировочной характеристики можно не проводить в тот период времени, когда ведется контроль стабильности результатов анализа.
Однако для методик по анализу газовых сред, вследствие невозможности приготовления адекватного средства контроля и разделения отобранной пробы, контроль стабильности градуировочной характеристики может являться основным видом контроля. При этом результаты контроля стабильности градуировочной характеристики следует оформлять в виде контрольных карт.
Вернуться к содержанию
Принцип построения градуировочного графика
Основой для построения градировочного графика является приготовление стандартных растворов.
Стандартные растворы необходимо готовить из аттестованных государственных образцов (ГСО). Если таковых не имеется, необходимо четко придерживаться основных требований к точности приготовления стандартных растворов:
- следует применять реактивы квалификации не ниже ч.д.а.;
- использование реактивов с просроченным сроком годности недопустимо;
- для приготовления стандартных растворов использовать только гостированную мерную посуду.
Особое внимание необходимо обратить на условия и сроки хранения: растворы с содержанием вещества 1 мг/см3 хранят 1 год, 0,1 мг/см3 – 3 месяца (если нет других указаний, а также если нет помутнения, хлопьев, осадка), растворы с меньшим содержанием применяются свежеприготовленными. Стандартные растворы фильтровать не допускается.
Для определения содержания вещества методом градуировочного графика готовят 3 серии шкал стандартов. Указания по приготовлению шкалы стандартов конкретно оговорены в каждой методике.
Внимание! При приготовлении параллельных шкал рабочие растворы готовят соответствующим разбавлением основного стандартного раствора, который готовится из одной взятой навески или ГСО.
Градуировочный график строят на миллиметровой бумаге или в электронном виде в программе Microsoft Excel, откладывая по оси абсцисс указанную в методике определения концентрацию, а по оси ординат – измеренные значения оптической плотности.
Количественное значение оптической плотности для каждой точки градуировочного графика определяется как среднее арифметическое результатов параллельных измерений 3-х шкал.
С целью уменьшения погрешности графического измерения необходимо подобрать такой масштаб графика, чтобы угол его наклона приблизительно равнялся 45°.
Градуировочный график должен нести следующую информацию:
- название определения;
- НД на метод проведения исследования;
- метод определения;
- марка спектрофотометра, его заводской номер;
- длина волны;
- длина рабочей грани кюветы;
- раствор сравнения (растворитель, нулевой раствор и т.д.), т. е. тот раствор, относительно которого снимались показания испытуемого раствора;
- дата построения;
- даты поверки;
- на графике должны присутствовать данные 3-х параллельных измерений и среднее арифметическое значение (в виде таблицы).
Градуировочный график строится один раз в год и после ремонта прибора. Оформление градуировочного графика может быть выполнено на миллиметровой бумаге или с помощью таблиц в формате xlsx если нет прибора с программным обеспечением построения градуировочных характеристик. Проверка графика должна проводиться 1 раз в квартал, если нет других указаний в методике определения (например, график на определение фтора в питьевой воде по ГОСТ 4386-89 необходимо проверять 1 раз в месяц), а также после приготовления реактивов из новой партии, поверки прибора. Проверка проводится по 3-м точкам графика – наиболее часто встречающимся в работе концентрациям. Данные проверки заносятся в Журнал проверок градуировочных графиков или наносятся на обратную сторону графика в виде таблицы.
При построении градуировочного графика должна соблюдаться прямая зависимость между оптической плотностью и концентрацией. Прямолинейность графика сохраняется только в интервале концентраций, указанных в методике. Поэтому продлевать градуировочную прямую выше последней указанной в методике точки не допустимо. Находить значение концентраций испытуемого раствора по градуировочному графику ниже первой точки графика не рекомендуется, т. к. это определение несет большую погрешность. В таком случае результат исследования следует записывать в виде «менее … мг/ дм3«.
Практическое использование градуировочных графиков в ряде случаев вносит дополнительную погрешность при определении концентрации растворов как за счет субъективного построения графической зависимости, так и за счет несоответствия графических (масштабных) погрешностей и погрешностей измерения оптических плотностей. Поэтому для получения более объективных результатов в фотометрическом анализе целесообразно построение градуировочного графика методом регрессивного анализа (уравнение регрессии).
В практике для построения градуировочных графиков и расчета коэффициентов уравнения регрессии используется метод наименьших квадратов, который имеет погрешность 1–5% при доверительной вероятности 95%. В связи с этим в фотоэлектроколориметрии при построении градуировочных графиков применяется метод наименьших квадратов.
Точная зависимость между концентрацией определяемого ингредиента (x) и оптической плотностью (y) будет выражаться уравнением:
которое называется уравнением регрессии или уравнением градуировочного графика. На градуировочном графике это уравнение представляет уравнение прямой. Первая и последняя точка отрезка есть диапазон определения, регламентируемый данной методикой.
Для расчета коэффициентов а и b уравнения (I) весь расчетный материал сводят в таблицу.
| № п/п | x | y1 | y2 | y3 | yср | xy | x2 | yрасч |
| Σn | Σx | Σy | Σ(xy) | Σx2 |
Коэффициент b рассчитывают по формуле:
| b = | n Σ(xy) − Σx Σy |
| n Σx2 − (Σx)2 |
(II)
Коэффициент a рассчитывают по формуле:
| a = | Σx2 Σy − Σx Σ(xy) |
| n Σx2 − (Σx)2 |
(III)
где
Σx — сумма концентраций определяемого ингредиента во всех стандартных растворах, начиная с первого и заканчивая последним;
Σx2 — сумма квадратов вышеуказанных концентраций;
Σ(xy) — сумма произведений концентрации определяемого ингредиента, умноженного на его оптическую плотность во всех стандартных растворах;
(Σx)2 — сумма концентраций определяемого ингредиента в вышеуказанных стандартных, возведенная в квадрат;
Σy — сумма оптических плотностей всех стандартных растворов.
Вернуться к содержанию
Пример построения градуировочного графика
Для построения градуировочного графика было приготовлено 6 стандартных растворов. Набранный после фотометрирования на фотоэлектроколориметре материал свели в таблицу:
| № п/п | x | y1 | y2 | y3 | yср | xy | x2 | yрасч | p,% | Δ,% |
| 1 | 5,0 | 0,022 | 0,021 | 0,021 | 0,0213 | 0,1065 | 25 | 0,0231 | 4,65 | -7,79 |
| 2 | 10,0 | 0,043 | 0,044 | 0,044 | 0,0437 | 0,4370 | 100 | 0,0391 | 2,30 | 11,76 |
| 3 | 30,0 | 0,096 | 0,094 | 0,095 | 0,0950 | 2,8500 | 900 | 0,1031 | 2,11 | -7,86 |
| 4 | 50,0 | 0,171 | 0,170 | 0,171 | 0,1707 | 8,5350 | 2500 | 0,1671 | 0,59 | 2,15 |
| 5 | 70,0 | 0,226 | 0,225 | 0,224 | 0,2250 | 15,7500 | 4900 | 0,2311 | 0,89 | -2,64 |
| 6 | 100,0 | 0,324 | 0,324 | 0,324 | 0,3240 | 32,4000 | 10000 | 0,3271 | 0,00 | -0,95 |
| Σn = 6 | Σx = 265 | Σy = 0,8797 | Σ(xy) = 60,0785 | Σx2 = 18425 |
Рассчитали значение коэффициентов a и b по формулам (II) и (III):
| a = | 18425 × 0,8797 − 265 × 60,0785 | = 0,0071 |
| 6 × 18425 − 2652 |
| b = | 6 × 60,0785 − 265 × 0,8797 | = 0,0032 |
| 6 × 18425 − 2652 |
Уравнение градуировочного графика (I) после подстановки в него значений коэффициентов a и b будет иметь вид:
Подставляя в это уравнение значения концентрации (5,0; 10,0; 30,0; 50,0; 70,0; 100,0) получают расчетные значения оптических плотностей yрасч (0,0231; 0,0391; 0,1031; 0,1671; 0,2311; 0,3271).
Откладывая на оси абсцисс значения концентрации, а по оси ординат расчетные значения оптических плотностей, по данному уравнению строят градуировочный график.
Полученное уравнение градуировочного графика можно использовать для обсчета результатов исследования. Для этого значение измеренной оптической плотности (y) подставляют в уравнение и рассчитывают x:
| x = | y − a | , в нашем случае | x = | y − 0,0071 |
| b | 0,0032 |
(III)
Результат, найденный по уравнению регрессии или по градуировочному графику необходимо подставить в формулу обработки результатов, приведенную в методике определения.
Вернуться к содержанию
Расчет сходимости и воспроизводимости результатов
Для контроля аналитической работы и получения более точных результатов параллельно определяют и вычисляют сходимость результатов (p, %), т.е. показатель качества измерений, отражающий близость друг к другу результатов, полученных в одинаковых условиях.
Расчет погрешности между параллельными исследованиями (y1, y2, y3) следует производить по следующей формуле:
| p = 2 | A1 − A2 | × 100% |
| A1 + A2 |
где A1 — больший результат из параллельных определений, A2 — меньший результат из параллельных определений.
Для большинства макрокомпонентов рекомендуются следующие значения сходимости:
| Cодержание, мг/дм3 | Сходимость, % |
| более 10 | до 10 |
| от 10 до 1 | от 10 до 15 |
| от 1 до 0,01 | от 15 до 25 |
| менее 0,01 | 30 |
Расчет воспроизводимости Δ,% (относительной погрешности между yср и yрасч) производится по формуле:
| Δ = | yср − yрасч | × 100% |
| yрасч |
При этом воспроизводимость результатов не должна превышать +15% (показано практикой при фотометрических измерениях с доверительной вероятностью 95%).
Выполнение измерений градуировочных характеристик (далее – ГХ) средств измерений состава и свойств веществ и материалов (далее – СИ) также возможно проводить по РМГ 54-2002 «ГСИ. Характеристики градуировочные средств измерений состава и свойств веществ и материалов. Методика выполнения измерений с использованием стандартных образцов».
Вернуться к содержанию
Контроль стабильности градуировочных характеристик (ГХ)
Периодичность контроля устанавливается в применяемой методике или на основании опыта работы лаборатории с используемым ею средством измерений.
Контроль стабильности ГХ, как правило, является вспомогательным видом контроля и вводится с целью сокращения трудоемкости процедур по контролю стабильности результатов анализа.
Контроль стабильности ГХ необходимо осуществлять, когда при выполнении измерений применяют СИ, установленные характеристики которого могут изменяться в течение короткого интервала времени. В этом случае стабильность ГХ контролируют перед каждой (очередной) серией измерений не позднее установленного интервала времени.
Если лаборатория выполняет определения содержания конкретного показателя периодически (например, один раз в неделю), то рекомендуется стабильность ГХ контролировать перед каждой серией измерений содержания этого показателя. Контроль стабильности ГХ проводят также при смене реактивов, оборудования, персонала или изменении условий проведения аналитических работ, например, при изменении условий окружающей среды, если известно, что при этом метрологические характеристики применяемого СИ могут меняться.
Стабильность ГХ контролируют:
а) с использованием одного средства контроля, если известно, что градуировочная зависимость линейна в достаточно широком диапазоне измеряемых концентраций. При этом контроль проводят либо в диапазоне наиболее часто встречающихся значений содержаний определяемого показателя в рабочих пробах, либо в середине градуировочного диапазона, если значения содержаний определяемого показателя в рабочих пробах приблизительно равно удаленно находятся от середины диапазона градуировки;
б) с использованием двух средств контроля, позволяющих контролировать точки градуировки вблизи ее начала и окончания, если известно, что начальные и конечные точки градуировки «чувствительны» (неустойчивы) к изменениям различных факторов, или если о стабильности градуировки имеется мало информации.
Если в диапазоне наиболее часто встречающихся значений содержаний определяемого показателя в рабочих пробах в применяемой методике установлены разные значения характеристик погрешности или нормативов контроля стабильности ГХ, то контроль стабильности ГХ проводят для различных диапазонов установленной ГХ.
Результаты контроля стабильности ГХ оформляют в соответствии с нормативной документацией на определяемый показатель.
Вернуться к содержанию
Литература
1. МР 18.1.04-2005 «Система контроля качества результатов анализа проб объектов окружающей среды».
2. Р 50.2.028-2003 «ГСИ. Алгоритмы построения градуировочных характеристик средств измерений».
3. РМГ 54-2002 «ГСИ. Характеристики градуировочные средств измерений состава и свойств веществ и материалов. Методика выполнения измерений с использованием стандартных образцов».
4. ГОСТ Р ИСО 11095-2007 «Статистические методы. Линейная калибровка с использованием образцов сравнения».
5. МИ 2175-91 «Градуировочные характеристики средств измерений. Методы построения. Оценивание погрешностей».
6. Терещенко А.Г., Пикула Н.П. «Внутрилабораторный контроль качества результатов химического анализа» (скачать pdf).
7. Булатов М.И., Малинкин И.П. «Практическое руководство по фотометрическим методам анализа».
8. Справочник по физико-химическим методам исследования объектов окружающей среды под редакцией Арановича Г.И.
9. Новиков Ю.В., Ласточкина К.О., Болдина З.Н. «Методы исследования качества воды водоемов».