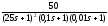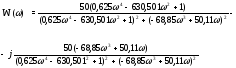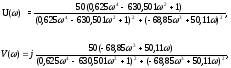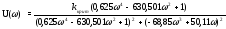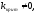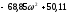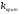Годограф михайлова в excel - Word и Excel - помощь в работе с программами

Задача
2

Условие
задания.

Пользуясь
критерием устойчивости Михайлова,
Найквиста определить устойчивость
одноконтурной системы управления,
имеющую в разомкнутом состоянии
передаточную функцию вида

в
формулу проставить значения К, а, b и с
по варианту.

W(s)
=,
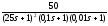
(1)

Построить
годографы Михайлова и Найквиста.
Определить
частоту среза системы.

Определить
критическое значение коэффициента
усиления системы.

Решение.

Задачи
анализа и синтеза систем управления
решаются с помощью такого мощного
математического аппарата, каким является
операционное исчисление (преобразование)
Лапласа. Задачи анализа и синтеза систем
управления решаются с помощью такого
мощного математического аппарата, каким
является операционное исчисление
(преобразование) Лапласа.
Общее
решение операторного уравнения
представляет собой сумму слагаемых,
определяемых значениями корней
характеристического полинома (многочлена):

D
(s) = d
sⁿ
d_n).

Построение
годографа Михайлова.

А)
Выписываем характеристический многочлен
для замкнутой системы, описываемой
уравнением (1)

D
(s)
= 50 + (25s+1)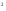(0,1s+1)(0,01s+1)
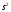
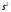
= 50+(625+50s+1)(0,001+0,11s+1)
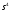
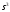
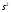
=0,625+68,85+630,501+50,11s+51.

Корни
многочлена D
(s)
могут быть: нулевыми; вещественными
(отрицательными, положительными); мнимыми
(всегда парными, сопряженными) и
комплексными сопряженными.

Б)
Преобразуем к виду s→
ωj

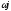
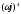
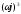
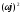
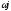
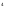
D()=0,625+68,85+630,501+50,11+51=0,625ω-68,85jω—
630,501ω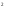+50,11jω+51

ω
– частота сигнала, j
= (1)^1/2
– мнимая
единица.
J⁴
=(-1)^4/2=1,
J³
=(-1)^3/2=-(1)^1/2=
— j,
J²
=(-1)^2/2=-1,
J
=(-1)^1/2=
j,

В)
Выделим действительную и мнимую часть.

D
= U()+jV(),
где U()
– действительная часть, а V()
– мнимая часть.

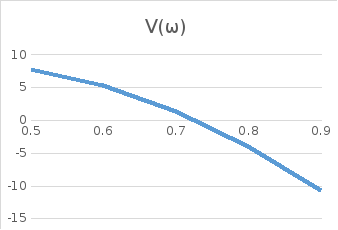
U(ω)
=0,625ω-630,501ω+51

V(ω)
=ω(50,11-68,85ω)

Г)
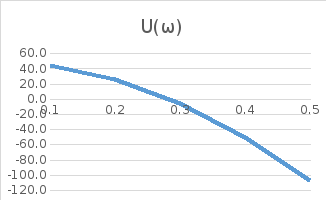
Построим годограф Михайлова.

Построим
годограф Михайлова вблизи и сдали от
нуля, для этого построем D(jw) при изменении
w от 0 до +∞. Найдем точки пересечения
U(w)
и V(w)
с осями. Решим задачу с использованием
MicrosoftExcel.

-задаем
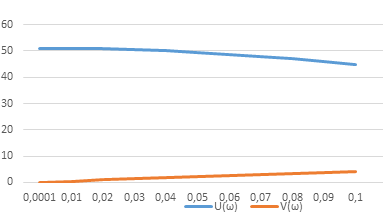
значения w в диапазоне от 0 до 0,0001 до 0,1,
рассчитаем в табл. Excel значения U(ω)
и
V(ω),
D(ω);
находим точки пересечения U(w)
и V(w)
с осями,

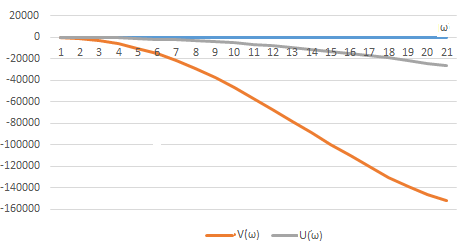
-задаем
значения w в диапазоне от 0,1 до 20, рассчитаем
в табл. Excel значения U(w)
и V(w),
D;
находим точки пересечения U(w)
и V(w)
с осями.

Таблица
2.1 – Определение действительной
и мнимой частей и самого многочлена
D(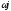)с
использованием MicrosoftExcel

ω	0,0001	0,001	0,003	0,006	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,1
U(ω)	51	51	51,0	51,0	50,9	50,7	50,4	50,0	49,4	48,7	47,9	47,0	45,9	44,7
V(ω)	0,005	0,05	0,15	0,298	0,494	0,975	1,4413	1,8942	2,333	2,7587	3,17	3,5682	3,952	4,3225
D	51,005	51,05	51,14	51,28	51,43	51,72	51,874	51,885	51,76	51,489	51,08	50,533	49,845	49,018
ω	0,1	0,2	0,3	0,5	0,7	0,8	1,0	2	5,0	7,5	10,0	12,5	15,0	20
U(ω)	44,70	25,78	-5,74	-107	-258	-352,3	-578,9	-2461	-15321	-33437	-56749	-83206	-110171	-152149
V(ω)	4,32	7,27	8,84	7,843	1,341	-3,976	-18,74	-175,2	-1471	-3497	-6384	-10131	-14740	-26538
D	49,02	33,05	3,10	-98,7	-256	-356,2	-597,6	-2636	-16792	-36934	-63133	-93337	-124911	-178687

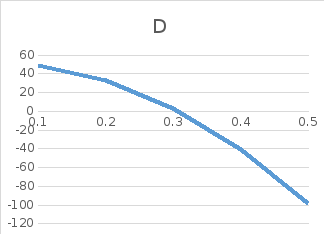
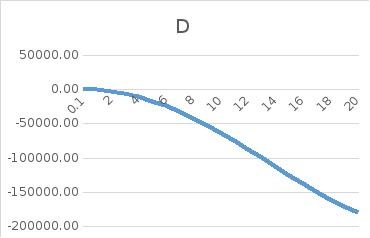
Рис.
А, Б, ….. Зависимости U(ω)
и
V(ω),
D(ω)
от ω

По
рис. А,
Б, …..находим точки пересечения U(w)
и V(w)
с осями:

при
ω
= 0 U(ω)=
…. и
V(ω)=
……

Рис.1.
Годограф Михайлова при ω = 0:000,1:0,1.

Рис.2.
Годограф Михайлова при ω = 0,1:20

Д)
Выводы об устойчивости системы по
годографу.

Устойчивость
(как понятие) любой динамической системы
определяется ее поведением после снятия
внешнего воздействия, т.е. ее свободным
движением под влиянием начальных
условий. Система является устойчивой,
если она возвращается в исходное
состояние равновесия после прекращения
действия на систему сигнала (возмущения),
выведшего ее из этого состояния.
Неустойчивая система не возвращается
в исходное состояние, а непрерывно со
временем удаляется от него.
Для
оценки устойчивости системы необходимо
исследовать свободную составляющую
решения уравнения динамики, т.е решения
уравнения:.

D
(s)
= d
sⁿ
d_n)=0.

Проверить
устойчивость системы с помощью критерия
Михайлова:

Критерий
Михайлова: Для
устойчивой АСР необходимо и достаточно,
чтобы годограф Михайлова (см. рис.1 и
рис.2), начинаясь при w = 0 на положительной
вещественной полуоси, обходил
последовательно в положительном
направлении (против часовой стрелки)
при возрастании w от 0 до ∞ n квадрантов,
где n — степень характеристического
полинома.

Из
решения видно (см. рис.1 и рис.2), что
годограф удовлетворяет следующим
условиям критерия: Начинается
на положительной вещественной полуоси
при
w = 0. Годограф
не удовлетворяет следующим условиям
критерия:
не обходит
в положительном направлении все 4
квадранта (степень полинома n=4)
при ω.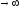

Делаем
вывод, что данная разомкнутая система
не устойчива.

Построение
годографа Найквиста.

А)
Произведем замену в формуле (1) s→
ωj

W(s)
=
=,

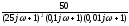
Б)
Раскроем скобки и выделим действительную
и мнимую часть в знаменателе

W()
=,

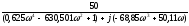
В)
Умножим на сопряженное и выделим
действительную и мнимую часть

где
U()
– действительная часть, а V()
– мнимая часть.

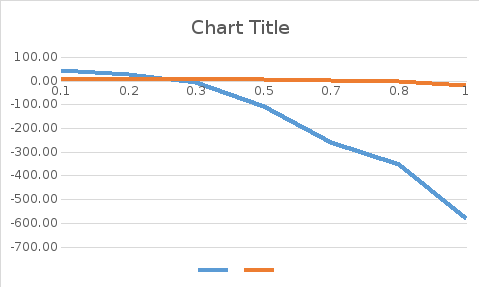
Г)
Построим годограф Найквиста: — зависимость
W()
от
.

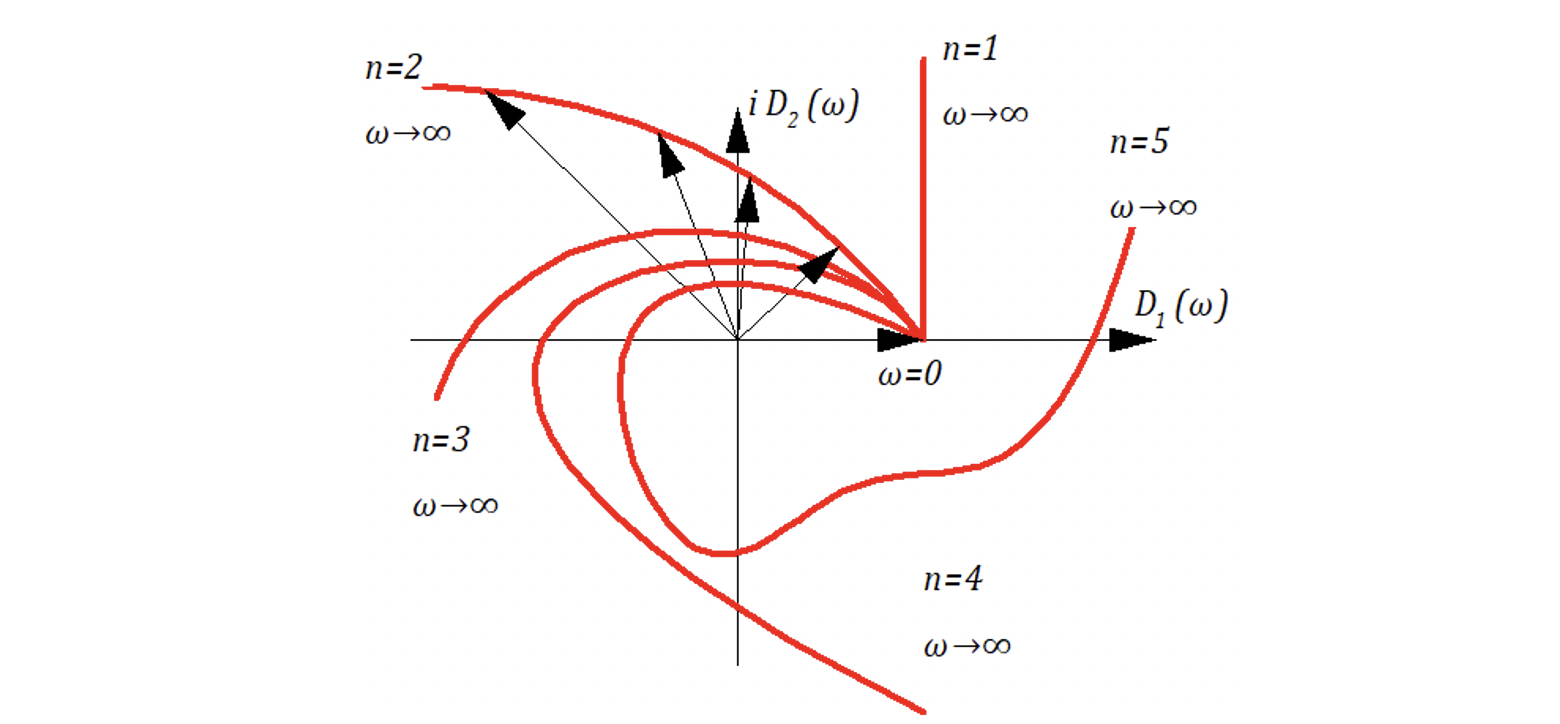
Рис.3.
Годограф Найквиста.

Д)
Проверим устойчивость системы с помощью
критерия Найквиста:

Критерий
Найквиста: Для
того чтобы система, которая в разомкнутом
состоянии была устойчива, была устойчива
и в замкнутом, необходимо, чтобы годограф
Найквиста при изменении частоты от нуля
до бесконечности не охватывал точку с
координатами (-1; j0).

Из
решения видно (см. рис.3), что годограф
удовлетворяет всем условиям критерия:

Годограф
меняет свое направление по часовой
стрелке
Годографом
не охватывается точка (-1; j0)
Делаем
вывод, что данная разомкнутая система
устойчива.

Определение
критического значения коэффициента
усиления системы.

А)
В пункте 2 уже были выделены действительная
и мнимая части

Б)
Для того, чтобы найти критическое
значение коэффициента усиления системы
необходимо приравнять мнимую часть к
нулю, а действительную к -1

=-1
(1)

=0 (2)

В)
Найдем

из второго (2) уравнения

=
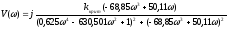
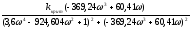
0

Числитель
должен быть равен 0.

=
0

Принимаем,
что

,
тогда

=
0

=0,853

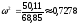
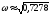
В)
Подставляем
в
первое (1) уравнение и находим

=
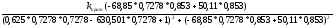
-1

Далее
произвести расчет

—
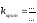
критическое значение коэффициента
усиления системы.

Литература:

1.Методы
классической и современной теории
автоматического управления. Том 1.

Анализ
и статистическая динамика систем
автоматического управления. М: Изд. МГТУ
им Баумана. 2000 г.

2.
Воронов А.А. Теория автоматического
управления. Т. 1-3, М., Наука, 1992

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

1.

Оценка устойчивости замкнутого
контура САР по критерию
Михайлова с помощью программы
Exsel» проекта
Выполнил студент группы Д-17-АиУ-1
Жидков Дмитрий Вячеславович
под руководством преподавателя
спец. дисциплин Волковой Елены
Олеговной
Eurasian Resources Group
www.eurasianresources.lu

2.

Цели и задачи проекта
Цель данной работы: исследовать, разработать,
проанализировать и оценить устойчивость замкнутого
контура САР по критерию Михайлова с помощью
программы Exsel.
Задача
— упростить расчет с помощью программы Exsel;
— повысит качество расчета;
— сократить время расчета оценки устойчивости
замкнутого контура;
— сравнить расчет по критерию Михайлова
произведенный с помощью калькулятора, с
расчетом с применением программы Exsel.
2

3.

Описание проблемы, которая решается через
проект
В этой научной работе будет проведено исследование замкнутого контура САР на
устойчивость с помощью частотного критерия Михайлова. Этот критерий гласит –
Замкнутая система устойчива если годограф вектора её характеристического
уравнения n-ой степени при изменении частоты ω от нуля до бесконечности
начинается на действительной полуоси и проходит последовательно через n
квадрантов комплексной плоскости в направлении
против часовой стрелки,
не обращаясь при этом в ноль.
Рисунок 1. Годограф Михайлова
Устойчив
не устойчив
3

4.

Решение проблемы через ваш проект
Работая в Excel можно очень быстро и удобно исследовать замкнутый
контур на устойчивость с помощью частотного критерия Михайлова.
Интерфейс excel несколько схож с интерфейсом word поэтому работа с
этой программой не вызовет затруднений. Большим преимуществом excel
является то, что в нём есть встроенный калькулятор в строке формул и
благодаря этому можно мгновенно получать нужные значения.
Начнём исследование. Для начала запишем само характеристическое уравнение.
4

5.

Используемые методы и методологии
Далее заменяем корни уравнения P на jω, переходя к комплексным числам и получая
комплексное уравнение А(jω).
Теперь, нужно составить таблицу и,
изменяя частоту ω от нуля до
бесконечности подобрать числа так,
чтобы годограф проходя по всем
четвертям, будет начинаться на
действительной положительной полуоси
и проходить последовательно через n
квадрантов
5

6.

Используемые методы и методологии
Строим годограф Михайлова по
полученным расчетным данным
Рисунок 2. Годограф Михайлова
6

7.

Используемые методы и методологии
Проводя сравнение с подобной работой, сделанной
в ручную, можно сразу определить, что на
исследование будет затрачено больше времени и
не исключены ошибки при расчетах.
Ключевое преимущество интерфейса excel в том, что
он имеет встроен калькулятор формул, что в разы
сократит время расчёта. Далее записываем в
таблицу результаты исследований.
Рисунок 3. Произведенные
расчеты ручным способом
7

8.

Результат. Экономический эффект.
Таблица 1. Результаты исследования
Доказательство преимущества расчёта точек вектора Годографа Михайлова
очевидно по результатам исследований, к тому же удобность ввода и
просмотра делает этот способ передовым.
8

9.

Заключение
Наши исследования показали:
— мы упростили расчет с помощью
программы Exsel;
— сократили время расчета оценки
устойчивости замкнутого контура;
— сравнили расчет произведенный с
помощью калькулятора, с расчетом с
применением программы Exsel;
— устранить возможность ошибки со стороны
человека (качество расчета).
9

Источник

Обновлено: 14.04.2023

S-образная кривая в Excel

Точечная диаграмма в Excel
График в Excel

Если мы используем этот тип диаграммы, должны быть данные, т. Е. Две используемые переменные должны соответствовать одному и тому же периоду времени. Эта кривая может использоваться для построения графика изменений одной переменной, связанной с другой переменной.

Кривая Excel S представлена на скриншоте ниже.

Как сделать S-образную кривую в Excel?

Ниже приведены примеры S-образной кривой в Excel.

В приведенном выше примере на графике есть небольшая S-образная кривая. Кривая будет зависеть от полученных данных.

Шаг 1: Выберите данные.

Шаг 2: Теперь перейдите на вкладку вставки и выберите линейный или точечный график в соответствии с требованиями.

В тот момент, когда мы выбираем тип диаграммы, диаграмма будет отображаться на листе. Теперь, посмотрев на график, мы можем выбрать график в соответствии с нашими требованиями.

Шаг 3: Окончательный график будет готов, и его можно будет увидеть на листе.

На этом графике присутствует небольшая кривая s. Поскольку название указывает на S-образную кривую, нет необходимости, чтобы график полностью выглядел в форме S. На графике может присутствовать небольшая кривая. Форма кривой будет зависеть от данных, которые мы берем.

В этом примере мы берем двухосный график с S-образной кривой.

Шаг 1: Выберите данные.

Шаг 2: Перейдите на вкладку «Вставка», выберите линейный график или трехмерную диаграмму рассеяния в Excel или 2d, в зависимости от требований и интересов. Теперь нажмите «ОК».

Шаг 3: На этом шаге график будет готов. Если на одной диаграмме должны отображаться 2 столбца данных, то можно использовать двойную диаграмму.

Шаг 4: После того, как диаграмма подготовлена, щелкните точку диаграммы, в которой вы хотите переместиться на вспомогательную ось. Щелкните правой кнопкой мыши, теперь выберите опцию формата данных серии.

Шаг 5: На вкладке «Ось» параметром по умолчанию будет первичная ось, теперь измените ее на вторичную ось. Работа сделана. Теперь выбранные данные будут установлены для вторичной оси.

S-образная кривая в Excel, пример №3

Шаг 1: Правильно заполните данные на листе со всеми столбцами, как показано на скриншоте ниже.

Шаг 2: Выберите данные, для которых вы хотите нарисовать S-образную кривую, как показано на снимке экрана ниже.

Шаг 3: Перейдите на вкладку «Вставка», выберите «Линейные графики» и выберите модель линейного графика, которую вы хотите использовать.

График выглядит так, как показано ниже:

Выберите диаграмму рассеяния на вкладке вставки таким же образом, как показано ниже.

Кривая отобразится автоматически, как показано на скриншоте ниже, после выбора типа диаграмм в Excel, которые мы хотим использовать.

Использование S-образной кривой в Excel

Также есть несколько формул для вычисления S-образной кривой вручную, но в Excel это очень легко сделать, так что это можно сделать в кратчайшие сроки. Ручной метод может быть выполнен путем взятия точек оси X и оси Y с графика.

Частотные критерии позволяют сравнительно легко исследовать устойчивость систем высокого порядка и дают представления о качестве процесса регулирования.

Частотные критерии используют понятие годографа, т.е. кривой в плоскости с координатами (действительная и мнимые части АФЧХ), которую описывает конец вектора при увеличении частоты от 0 до .

Значения и получают, заменив в характеристическом уравнении (2) постоянную p на переменную .

Характеристическое уравнение представляет собой полином знаменателя передаточной функции замкнутой САР, т.е.

Записать передаточные функции разомкнутой и замкнутой САР. Например: регулятор – П (пропорциональный), объект – А (апериодическое звено).

Записываем характеристическое уравнение

Критерий Михайлова

Чем дальше годограф от нуля, тем система более устойчива.

Порядок построения годографа

1. Откладывается точка при .

2. Увеличивается частота и находятся другие точки.

3. Определяются точки пересечения с осями координат, как корни уравнений: ,

Особенности годографа устойчивых систем

1. Начало в точке , .

3. Модуль вектора должен быть отличен от нуля при любых .

Если годограф проходит через начало координат, то система находится на границе устойчивости.

Найдем точки пересечения с осями координат.

С мнимой осью из уравнения

Подставив значение в мнимую часть, получим точку пересечения с (0;0,26).

С действительной осью из уравнения

. Подставив значение в действительную часть, получим точку пересечения с (0,1;0).

0,32	0,5	1,25
0,1	-0,15	-0,9	-1,46
0,26	0,4	0,8

Найдем точки пересечения с осями координат.

С мнимой осью из уравнения

Подставив значение в мнимую часть, получим точку пересечения с (0;-6,8).

С действительной осью из уравнения

Подставив значение в действительную часть, получим точки пересечения с (3,0) и (2,0)

0,5	1,73
2,75	-1
0,75	-6,8	-12

\|	следующая лекция ==>
Возможные виды корней и решения ДУ	\|	Область применения частотных критериев

Практическое построение годографа Михайлова

Для примера рассмотрим систему 4 ой степени:

Чтобы найти точки пересечения годографа с осями координат, необходимо приравнять нулю вещественную и мнимую части и найти частоты, при которых они равны нулю.

Построение годографа ведется в следующем порядке:

1. В характеристическом уравнении замкнутой системы производим замену на :

2. Из уравнения выделяем вещественную и мнимую части:

3. Приравняем нулю мнимую часть и находим частоты, при которых годограф пересекается с вещественной осью (точки 1 и 3):

4. Полученные значения частоты подставим в уравнение вещественной части, получаем точки 1 и 3:

5. Приравняем нулю уравнение вещественной части, получаем частоты, при которых годограф пересекается с мнимой осью:

Введем новую переменную и получим квадратное уравнение:

Решим квадратное уравнение:

Найдем и (только положительные значения):

6. Полученные значения частоты подставим в уравнение мнимой части и находим точки 2 и 4:

7. Задаются промежуточными частотами и частотой , для которых находят значения вещественной и мнимой части:

8. Все расчеты сводятся в таблицу:

0.23	0.46	0.68	0.89	1.2	1.51	1.6
0.74	-0.88	-1.71	-2.1	1,31
0.86	1.35	1.15	-3.84	-11.17	-14,08

9. По данным таблицы строится годограф (рисунок 1).

10. Вывод: Система устойчива, т.к. вектор годографа Михайлова начинает свое движение с положительной вещественной полуоси, вращается против часовой стрелки, нигде не обращается в ноль и обходит последовательно 4 квадранта комплексной плоскости.

Цель: формирование умения построения графической модели в Excel .

Необходимые знания и умения к данному уроку.

Учащиеся должны знать понятия моделирования, модели, формы информационных моделей. Уметь в электронной таблице Excel заполнять ячейки, работать с формулами, строить диаграммы.

Организационный момент.
Постановка задачи.
Эксперимент.
Историческая справка о циклоиде.
Практическая работа: построение графика кривой в Excel .
Повторение.
Задание на дом.

1. Организационный момент (учащиеся сидят за партами). Мы продолжаем изучение темы моделирование. Напомните, что означает моделирование, что называется моделью? Сегодня вы будете строить графическую модель, но сначала вспомним, какие графические модели нам известны? (графы, графики, чертежи, схемы и т.д.).

2. Постановка задачи. Возьмём колесо, обруч, круг. Зафиксируем точку круга. Будем катить круг по прямой. Какую кривую опишет зафиксированная точка круга? Следите внимательно за траекторией точки (в большинстве учащиеся отвечают, что точка опишет окружность , но кто-то догадается и скажет, что точка опишет дугу ).

У читель показывает на большом экране :

( нажмите кнопку «Движение» )

3. Эксперимент. Проверим наше предположение. Прикрепим к обручу или кругу кусок мела и покатим вдоль стены, мел будет вычерчивать «кругообразную» кривую, называемую циклоидой . Одному обороту обруча соответствует одна «арка» циклоиды, если обруч будет катиться дальше, то будут получаться еще и еще арки той же циклоиды.

У читель показывает на большом экране :

( нажмите кнопку «Движение» )

4. Историческая справка о циклоиде. Первым из учёных обратил внимание на циклоиду Николай Кузанский в XV веке, но серьёзное исследование этой кривой началось только в XVII веке. Название циклоида придумал Галилей (во Франции эту кривую сначала называли рулеттой). Содержательное исследование циклоиды провёл современник Галилея Мерсенн.

Паскаль писал о циклоиде: « … является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса.».

Эта кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали Декарт, Ферма, Ньютон, Лейбниц, братья Бернулли и другие корифеи науки XVII—XVIII веков.

Циклоида имеет ряд удивительных свойств:

ü «Перевёрнутая» циклоида является кривой скорейшего спуска. Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.

ü Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды, этот факт был использован Гюйгенсом для создания точных механических часов.

Координаты точки окружности в данный момент времени вычисляются по формулам:

Обратите внимание на то, как надо правильно ввести формулу (это для ячейки В2).

6. Повторение. Итак, вы сегодня построили графическую модель кривой, которую описывает некоторая точка окружности, катящейся без скольжения по неподвижной прямой.

ü Как называется эта к ривая?

ü Какие интересные свойства циклоиды вы запомнили?

ü Предположем, что катится гимнастический обруч. Внешняя и внутренняя точки обруча будут описывать одинаковые кривые?

7. Домашнее задание . Поищите в справочниках, интернете, какие существуют ещё интересные кривые. Модели каких кривых мы можем построить в электронной таблице Excel ?

Циклоида как построить в excel

Ещё раз про морковь или возвращаясь к непечатному. Доброго здоровья, Денис.

P. S. Всё вышенаписанное стоило писать месяца полтора назад. Руки дошли только сейчас, однако.

Пример №1 . На основе данных таблицы:

Денежные доходы населения

Группы по денежным доходам, %	Доля денежных доходов в группе, %
20	6
40	11.6
60	17.6
80	26.5
100	38.3

Линия фактического неравенства строится на основании данных о процентах дохода приходящихся на каждые 20 % населения.
Если нижняя первая часть населения получила 6.0% всех доходов, то графически это будет точка А. Чтобы получить точку В необходимо сложить процент дохода первых 20 % населения с процентами доходов вторых 20 % населения (6.0% + 11.6%) и т.д.

20-ти процентные группы населения	Объем денежных доходов населения, в % к итогу	Доля денежных доходов нарастающим итогом, %	Площадь треугольника	Площадь прямоугольника	Общая площадь фигуры, S_i
20	6	6	60	0	60
40	11.6	17.6	116	120	236
60	17.6	35.2	176	352	528
80	26.5	61.7	265	704	969
100	38.3	100	383	1234	1617
3410

Чтобы построить кривую Лоренца откладываем по оси Х значения 1-го столбца, а по оси Y значения 3-го столбца.

Пример №2 . Имеются следующие данные о распределении доходов населения региона по трем группам и доле населения в каждой группе:

1 группа	2 группа	3 группа
Доходы населения по группам (руб.)	5000-10000	10000-20000	20000-30000
Доля населения в группе	0,15	0,60	0,25

Определить коэффициент концентрации доходов Джинни.
Решение.
Необходимо найти доли среднего дохода на человека в каждой группе, в виде отношения среднего дохода группы к суммарному среднему доходу, и соответствующие накапливаемые частоты этих долей. Чем ближе значение коэффициента к единице, тем выше уровень дифференциации доходов.

1 группа	2 группа	3 группа	Итого
Доходы населения по группам (руб.)	5000-10000	10000-20000	20000-30000
Среднее значение дохода в группе, руб.	7500	15000	25000	47500
Доля доходов в группе, %	15,8	31,6	52,6	100,0

Далее решается через калькулятор.

Доля доходов в группе, %	Доля населения в группе
15,8	0,15
31,6	0,6
52,6	0,25

Пример №3 . Дать графическое изображение вариационного ряда, приведенного в таблице (гистограмма, полигон, кумулята). Определить средние величины (меры положения) – среднюю арифметическую, моду, медиану, вычислить квартили и показатели вариации – среднее абсолютное отклонение, дисперсию, среднее квадратическое отклонение, относительный квартильный размах, коэффициент вариации. Построить кривую (ломаную) Лоренца, вычислить коэффициент концентрации дохода (индекс Джини). Пояснить статистический, физический, экономический или иной смысл вычисленных величин.

№ группа	Среднедушевые доходы населения (тыс. руб.)	Количество насосов
1	0-30	10
2	30,1-60	14
3	60,1-90	19
4	90,1-120	25

Пример №4 . Исходные данные:

%	Доход
10	2.3
20	4.5
30	4.7
40	6
50	7.5
60	10.2
70	14.1
80	16.7
90	18.5
100	15.5

Линия фактического неравенства строится на основании данных о процентах дохода приходящихся на каждые 10% населения. Если нижняя первая часть населения получила 2.3% всех доходов то графически это будет точка А. Чтобы получить точку В необходимо сложить процент дохода первых 10% населения с процентами доходов вторых 10% населения (2.3% + 4.5%) и т.д.

%	Доход	S=S_i+S_i-1	Площадь треугольника	Площадь	Сумма
10	2.3	2.3	11.5	0	11.5
20	4.5	6.8	22.5	23	45.5
30	4.7	11.5	23.5	68	91.5
40	6	17.5	30	115	145
50	7.5	25	37.5	175	212.5
60	10.2	35.2	51	250	301
70	14.1	49.3	70.5	352	422.5
80	16.7	66	83.5	493	576.5
90	18.5	84.5	92.5	660	752.5
100	15.5	100	77.5	845	922.5
Итого	3481

Чтобы построить кривую Лоренца откладываем по оси Х откладываем значения столбца Процент (%), а по сои Y значения столбца S.

Рассчитаем коэффициенты концентрации доходов (индекс Джини)

Уровень неравенства определяется с помощью коэффициента Джини.

Он рассчитывается как отношение площади фигуры OABCDKLMNPE к площади треугольника ОEG.

Для того чтобы определить площадь фигуры, лежащей ниже кривой Лоренца, соединяем прямыми линиями точки ОА, АВ и т.д.

Опускаем перпендикуляр на ось X и находим площади фигур, лежащих ниже точек А, B , С.

Площадь S_ABB’A состоит из треугольника и прямоугольника S_BCCB’ также состоит из треугольника и прямоугольника.

Сложив все площади фигур, получим площадь фигуры S₂.

Площадь треугольника OEG находим по формуле:

1/2 *100%*100% = 5000

Отсюда индекс Джини равен:

I = 1519 / 5000 = 0.3038

Децильный коэффициент дифференциации доходов

Построение кривой Лоренца в Microsoft Excel

Для оценки уровня неравенства между различными слоями населения общества часто используют кривую Лоренца и производный от неё показатель – коэффициент Джинни. С помощью них можно определить, насколько велик социальный разрыв в обществе между самыми богатыми и наиболее бедными слоями населения. С помощью инструментов приложения Excel можно значительно облегчить процедуру построения кривой Лоренца. Давайте, разберемся, как в среде Эксель это можно осуществить на практике.

Использование кривой Лоренца

Кривая Лоренца представляет собой типичную функцию распределения, отображенную графически. По оси X данной функции располагается количество населения в процентном соотношении по нарастающей, а по оси Y — общее количество национального дохода. Собственно, сама кривая Лоренца состоит из точек, каждая из которых соответствует процентному соотношению уровня дохода определенной части общества. Чем больше изогнута линия Лоренца, тем больше в обществе уровень неравенства.

В идеальной ситуации, при которой отсутствует общественное неравенство, каждая группа населения имеет уровень дохода прямо пропорциональный её численности. Линия, характеризующая такую ситуацию, называется кривой равенства, хотя она и представляет собой прямую. Чем больше площадь фигуры, ограниченной кривой Лоренца и кривой равенства, тем выше уровень неравенства в обществе.

Кривая Лоренца может использоваться не только для определения ситуации имущественного расслоения в мире, в конкретной стране или в обществе, но и для сравнения в данном аспекте отдельных домохозяйств.

Вертикальная прямая, которая соединяет линию равенства и наиболее удаленную от неё точку кривой Лоренца, называется индексом Гувера или Робин Гуда. Данный отрезок показывает, какую величину дохода нужно перераспределить в обществе, чтобы достичь полного равенства.

Уровень неравенства в обществе определяется с помощью индекса Джинни, который может варьироваться от 0 до 1. Он ещё называется коэффициентом концентрации доходов.

Построение линии равенства

Теперь давайте на конкретном примере посмотрим, как создать линию равенства и кривую Лоренца в Экселе. Для этого используем таблицу количества населения разбитого на пять равных групп (по 20%), которые суммируются в таблице по нарастающей. Во второй колонке этой таблицы представлена величина национального дохода в процентном соотношении, которая соответствует определенной группе населения.

Для начала построим линию абсолютного равенства. Она будет состоять из двух точек – нулевой и точки суммарного национального дохода для 100% населения.

«Вставка»

«Диаграммы»

«Точечная»

«Точечная с гладкими кривыми и маркерами»

Открывается окно выбора источника данных. В левой его части, которая называется «Элементы легенды (ряды)» жмем на кнопку «Добавить».

Запускается окно изменения ряда. В поле «Имя ряда» записываем то наименование диаграммы, которое хотим ей присвоить. Оно может также располагаться на листе и в этом случае нужно указать адрес ячейки его нахождения. Но в нашем случае легче просто вписать название вручную. Дадим диаграмме наименование «Линия равенства».

В поле «Значения X» следует указать координаты точек диаграммы по оси X. Как мы помним, их будет всего две: 0 и 100. Записываем данные значения через точку с запятой в данном поле.

В поле «Значения Y» следует записать координаты точек по оси Y. Их тоже будет две: 0 и 35,9. Последняя точка, как мы можем видеть по графику, соответствует совокупному национальному доходу 100% населения. Итак, записываем значения «0;35,9» без кавычек.

После того, как все указанные данные внесены, жмем на кнопку «OK».

После этого мы возвращаемся к окну выбора источника данных. В нем тоже следует нажать на кнопку «OK».

Создание кривой Лоренца

Теперь нам предстоит непосредственно построить кривую Лоренца, опираясь на табличные данные.

«Выбрать данные…»

Опять открывается окно выбора данных. Как видим, среди элементов уже представлено наименование «Линия равенства», но нам нужно внести ещё одну диаграмму. Поэтому жмем на кнопку «Добавить».

Снова открывается окно изменения ряда. Поле «Имя ряда», как и в прошлый раз, заполняем вручную. Сюда можно вписать наименование «Кривая Лоренца».

В поле «Значения X» следует занести все данные столбца «% населения» нашей таблицы. Для этого устанавливаем курсор в область поля. Далее зажимаем левую кнопку мыши и выделяем соответствующий столбец на листе. Координаты тут же будут отображены в окне изменения ряда.

В поле «Значения Y» заносим координаты ячеек столбца «Сумма национального дохода». Делаем это по той же методике, по которой вносили данные в предыдущее поле.

После того, как все вышеуказанные данные внесены, жмем на кнопку «OK».

После возврата к окну выбора источника опять жмем на кнопку «OK».

Построение кривой Лоренца и линии равенства в Экселе производится на тех же принципах, что и построение любого другого вида диаграмм в этой программе. Поэтому для пользователей, которые овладели умением строить диаграммы и графики в Excel, данная задача не должна вызвать больших проблем.

Мы рады, что смогли помочь Вам в решении проблемы.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Читайте также:

Файлы драйвера которые нужно удалить не будут удалены так как соответствующая плата не вставлена

Имя make не распознано как имя командлета функции файла сценария или выполняемой программы

Как прошить планшет irbis tz55 через компьютер

Как из капса сделать обычный шрифт word

Как работать пиратским 1с

Источник

Порядок построения годографа

Частотные критерии устойчивости

Значения и получают, заменив в характеристическом уравнении (2) постоянную p на переменную .

Записываем характеристическое уравнение



	T	2T

Критерий Михайлова

Линейная система n-го порядка устойчива, если при изменении от 0 до годограф Михайлова — последовательно обходит n — квадрантов комплексной плоскости против часовой стрелки, начинаясь в точке на положительной вещественной полуоси и нигде не проходя через начало координат.

Чем дальше годограф от нуля, тем система более устойчива.

Порядок построения годографа

1. Откладывается точка при .

2. Увеличивается частота и находятся другие точки.

3. Определяются точки пересечения с осями координат, как корни уравнений: ,

Особенности годографа устойчивых систем

1. Начало в точке , .

2. При вектор поворачивается против часовой стрелки на угол , поочередно обходя n — квадрантов.

3. Модуль вектора должен быть отличен от нуля при любых .

Если годограф проходит через начало координат, то система находится на границе устойчивости.

Найдем точки пересечения с осями координат.

С мнимой осью из уравнения

Подставив значение в мнимую часть, получим точку пересечения с (0;0,26).

С действительной осью из уравнения

. Подставив значение в действительную часть, получим точку пересечения с (0,1;0).

0,32	0,5	1,25
0,1	-0,15	-0,9	-1,46
0,26	0,4	0,8

Найдем точки пересечения с осями координат.

С мнимой осью из уравнения

Подставив значение в мнимую часть, получим точку пересечения с (0;-6,8).

С действительной осью из уравнения

Подставив значение в действительную часть, получим точки пересечения с (3,0) и (2,0)

0,5	1,73
2,75	-1
0,75	-6,8	-12

\|	следующая лекция ==>
Возможные виды корней и решения ДУ	\|	Область применения частотных критериев

Дата добавления: 2019-10-16 ; просмотров: 5015 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Практическое построение годографа Михайлова

Для примера рассмотрим систему 4 ой степени:

Построение годографа ведется в следующем порядке:

1. В характеристическом уравнении замкнутой системы производим замену на :

2. Из уравнения выделяем вещественную и мнимую части:

— уравнение вещественной части — ;

— уравнение мнимой части — .

4. Полученные значения частоты подставим в уравнение вещественной части, получаем точки 1 и 3:

Введем новую переменную и получим квадратное уравнение:

Решим квадратное уравнение:

Найдем и (только положительные значения):

6. Полученные значения частоты подставим в уравнение мнимой части и находим точки 2 и 4:

7. Задаются промежуточными частотами и частотой , для которых находят значения вещественной и мнимой части:

8. Все расчеты сводятся в таблицу:

0.23	0.46	0.68	0.89	1.2	1.51	1.6
0.74	-0.88	-1.71	-2.1	1,31
0.86	1.35	1.15	-3.84	-11.17	-14,08

9. По данным таблицы строится годограф (рисунок 1).

10. Вывод: Система устойчива, т.к. вектор годографа Михайлова начинает свое движение с положительной вещественной полуоси, вращается против часовой стрелки, нигде не обращается в ноль и обходит последовательно 4 квадранта комплексной плоскости.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Время на прочтение
6 мин

Количество просмотров 2.7K

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица.

6.4. Частотный критерий устойчивости Михайлова

Советским ученым Михайловым в 30-тых годах впервые был предложен оригинальный критерий оценки устойчивости САР, основанный на исследовании частотных свойств полинома при подстановки вместо , где

Связь между частотными свойствами системы и передаточными функцииями более подробно описана в лекции 3. Частотные характеристики САР

$D(s)=a_0cdot s^n+a_1 cdot s^{n-1}+ cdots +a_{n-1}cdot s+ a_n mathbf{(6.4.1)}$

Подставим в формулу 6.4.1

$D(icdot omega)=D_1(omega)+icdot D_2(omega) Rightarrow mathbf{(6.4.2)}$ $Rightarrow begin{cases} D_1(omega) =a_n-a_{n-2}cdot omega^2+a_{n-4}cdot omega^4- ... \ D_2(omega) = -a_{n-3}cdot omega^3+a_{n-5}cdotomega^5-cdots end{cases} mathbf{(6.4.3)}$

Совершенно очевидно, что:

$text{если }omega rightarrow 0 Rightarrow begin{cases} D_1 rightarrow a_n \D_2 rightarrow 0 end{cases}$ $text{если }omega rightarrow 0 Rightarrow begin{cases} D_1 rightarrow pminfty \D_2 rightarrow pminfty end{cases}$

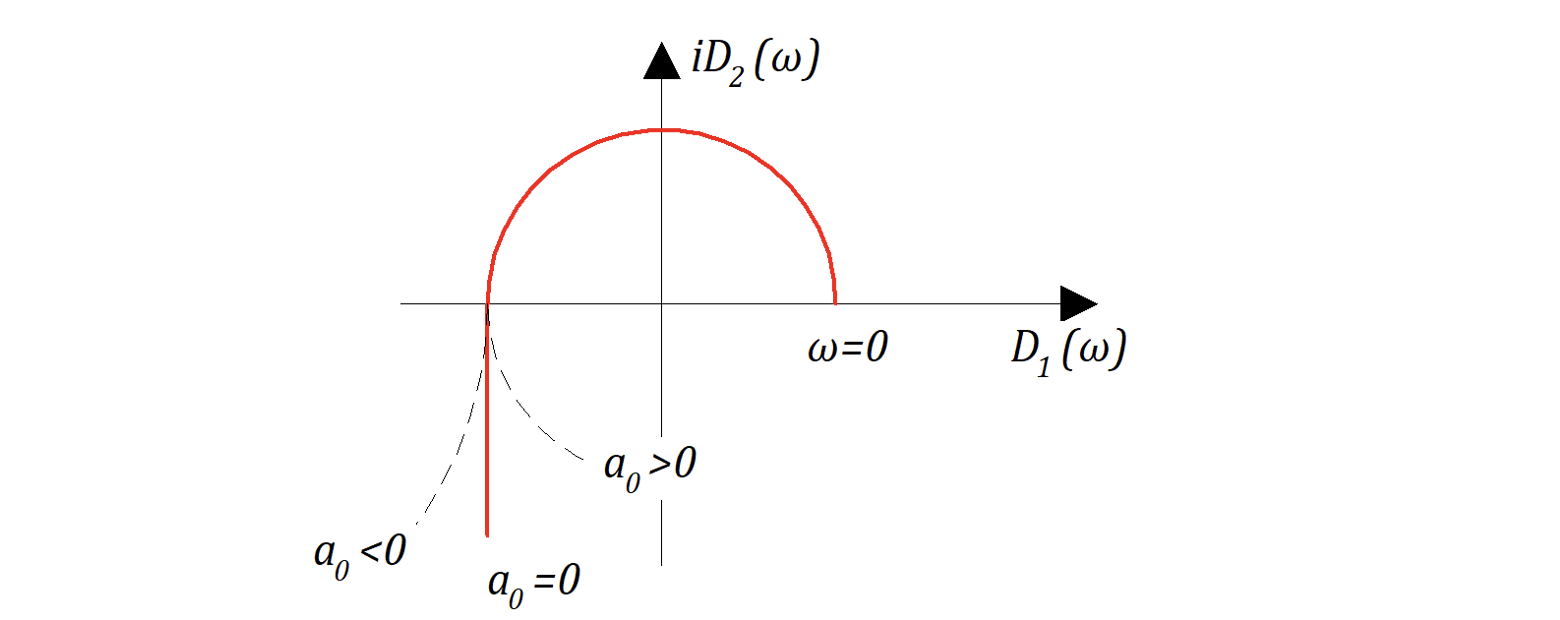
Критерий устойчивости Михайлова:

Чтобы САР (замкнутая или разомкнутая) была устойчивой, необходимо и достаточно, чтобы годограф при изменении от нуля до переходил поочередно из квадранта в квадрант против часовой стрелки, совершив при этом поворот на угол $frac{pi}{2}cdot n$ , где — степень полинома .

На рисунке 6.4.1 представлены варианты годографов для различных степеней n полинома

Рисунок 6.4.1 Годографы устойчивых систем

Если САР устойчива, то вектор при изменении от 0 до совершает поворот на угол $frac{pi}{2}cdot n$ , где n — степень полинома .

Следствием частотного критерия Михайлова является перемежаемость (чередование) нулей полиномов и в самом деле (см. рисунок 6.4.1), для кривой с последовательность пресечения осей получается как на рисунке 6.4.2

Рисунок 6.4.2. Нули полиномов

чередуются для устойчивости системы.

Если система находится на апериодической границе устойчивости (один нулевой полюс при всех остальных в левой полуплоскости), то годограф имеет следующий «примерный» вид, см. рисунок 6.4.3:

Рисунок 6.4.3 — Годограф начинается из начала координат и поочередно «проходит» все квадранты в положительном направлении (начиная со 2-го квадранта).

Если система находится на колебательной границе устойчивости (2 чисто мнимых полюса при всех остальных в левой полуплоскости), то годограф имеет вид как на рис. 6.4.4:

Рисунок 6.4.4 — Годограф

при некоторой частоте

проходит через начало координат, «перескакивая» из 2-го в 4-ый квадрант (минуя 3-ий). Частота

— частота незатухающих колебаний в такой САР.

Если САР неустойчива, годографы имеют вид как представлено на рисунке 6.4.5:

Рисунок 6.4.5. Годографы

неустойчивых систем.

Докажем ряд основных моментов в критерии Михайлова.

Представим полином в виде произведения:

$D(s)=a_0cdot(s-s_1)cdot(s-s_2)cdot...cdot(s-s_n) mathbf{(6.4.3)}$

где — полюса главной передаточной функции.

Учитывая, что любое комплексное число типа можно представить в виде: $(a+icdot b)=Acdot e^{icdot varphi},$ где – модуль, — фаза.

$D(icdot omega)=a_0cdot(icdotomega-s_1)cdot(icdotomega-s_2)cdot...cdot(icdotomega-s_n) =\=a_0cdot A_1(omega)cdot e^{icdotvarphi_1(omega)}cdot A_2(omega)cdot e^{icdotvarphi_2(omega)}cdot...cdot A_n(omega)cdot e^{icdotvarphi_n(omega)} mathbf{(6.4.4)}$

Рассмотрим изменнение фазы, при изменении от 0 до . Обозначим изменение фазы как

$Deltavarphi|_{omega=0}^{omega=infty}=Delta arg(icdot omega-s_j)|_{omega=0}^{omega=infty}=Delta arg(iomega-s_j) mathbf{(6.4.5)}$

Для устойчивой САР, все полюса D(s) лежат в левой полуплоскости. (см. предыдущию лекцию) Рассмотрим различные варианты расположения полюсов на плоскости:

1-й случай: пусть является реальным числом , например, , где , поскольку корень в левой полуплоскости.

Рассмотрим поведение вектора при изменении от нуля до бесконечности

Рисунок 6.4.6. Вектор

для реального корня

Из рисунка 6.4.6 очевидно, что

при ,

при $omegarightarrowinfty Rightarrowvarphi_1(infty)rightarrowfrac{pi}{2}$ .

$Deltavarphi|_{omega=0}^{omega=infty}=Delta arg(icdot omega+s_j)=Delta arg(alpha_1+iomega)=frac{pi}{2} mathbf{(6.4.6)}$

Т.е. при изменении от 0 до вектор, описывающий скобку повернется в положительном направлении на угол $frac{pi}{2}$ .

2-й случай: Пусть где, преобразуем скобку:

Рассмотрим изменение от до :

при — точка лежит в правом нижнем квадранте коплексной плоскости, фаза (сдвиг фазы):

$varphi_2 (0)= gamma_2=arctg(frac{alpha_2}{beta_2})$ (см. рис. 6.4.7)

при фаза (сдвиг фазы) $varphi_2(infty)rightarrow frac{pi}{2}$ (см. рис. 6.4.7)

Рисунок 6.4.7 Вектор для

для комплексного корня.

Изменение фазы:

$Delta arg(iomega-s_2)=frac{pi}{2}+gamma_2 mathbf{(6.4.7)}$

3-й случай: Пусть (полюс комплексно сопряженный со вторым вариантом). Преобразуем скобку

Рассмотрим изменение от до :

при — точка лежит в правом верхнем квадранте коплексной плоскости, фаза (сдвиг фазы):

$varphi_2 (0)= -gamma_2=-arctg(frac{alpha_2}{beta_2})$ (см. рис. 6.4.8)

при фаза (сдвиг фазы) $varphi_2(infty)rightarrow frac{pi}{2}$ (см. рис. 6.4.8)

Рисунок 6.4.8 Вектор для

для комплексного корня.

Изменение фазы:

$Delta arg(iomega-s_3)=frac{pi}{2}-gamma_2 mathbf{(6.4.8)}$

Рассмотрим изменения годографа полинома устойчивой системы c учетом изменения фазы для трех случаев полюсов рассмотрены выше.

Пусть у нас общее количество полюсов , — количество сопряженных полюсов полинома, тогда количество вещественных полюсов.

$Delta arg D(icdotomega)|_{omega=0}^{omega=infty}=sum^n_{j=1}varphi_j=sum_{j=0}^nDelta arg(iomega-s_j) =\=kcdot(frac{pi}{2}+gamma_j+frac{pi}{2}-gamma_j)+(n-k)cdot frac{pi}{2} = ncdotfrac{pi}{2}$

Покольку вещественны полюс дает $Delta arg(iomega-s_j)=frac{pi}{2}$ (cм. формулу 6.4.6), а два комплексно сопряженных корня в сумеее дают $2cdotfrac{pi}{2}$ (формулы 6.4.7 и 6.4.8)

$Delta argD(iomega)=ncdotfrac{pi}{2} mathbf{(6.4.9)}$

Это означает, что при изменении частоты от нуля до бесконечности, годограф должен поочередно пройти все квадранты в положительном направлении, если САР – устойчива.

Рассмотрим неустойчивую САР, у которой ряд полюсов полинома расположен в правой полуплоскости.

4-й случай: Пусть где — реальное число.

Преобразуем скобку подставля значения полюса .

Рассмотрим изменние вектора при изменении от 0 до. Примерный вид представлен на рисунке 6.4.9, где :

Рисунок 6.4.9 Вектор для

для комплексного корня.

Изменение фазы вектора:

при ;

при $omegarightarrowinftyRightarrow varphi_4(omega_infty)rightarrowfrac{pi}{2}$ .

Изменение фазы:

$Delta arg(iomega-s_4) =-frac{pi}{2} mathbf{(6.4.10)}$

Следовательно отрицательный реальный полюс дает вращение вектора в отрицательном направлении на угол $-frac{pi}{2}$ . Получается наличе одного реального полюса вызывает «недоповорот» вектора на угол .

Рассмотрим два варианта с коплексными полюсами лежашими в левой полуплоскости:

5-й случай: Пусть , где и преобразуем скобку для данного случая:
.

Рассмотрим изменние вектора при изменении от 0 до . Примерный вид представлен на рисунке 6.4.10, где: , $gamma_5 = arctgleft(frac{beta_5}{alpha_5}right)$

Рисунок 6.4.10 Вектор для

для комплексного корня.

Рисунок 6.4.10 Вектор длядля комплексного корня. Изменение фазы вектора:

при ;

при $omegarightarrowinftyRightarrow varphi_5(omega_infty)rightarrowfrac{pi}{2}$ .

Изменение фазы:

$Delta arg(iomega-s_5)=-frac{pi}{2}-gamma_5 mathbf{(6.4.11)}$

6-й случай: Пусть , явялется комплексно сопряженным полюсом для 5-го случая, где и преобразуем скобку для данного случая:.

Рассмотрим изменние вектора при изменении от 0 до . Примерный вид представлен на рисунке 6.4.11, где: , $gamma_5 = arctgleft(frac{beta_5}{alpha_5}right)$

Рисунок 6.4.11 Вектор для

для комплексного корня.

при ;

при $omegarightarrowinftyRightarrow varphi_6(omega_infty)rightarrow-frac{pi}{2}$ .

Изменение фазы:

$Delta arg(iomega-s_6)=-frac{pi}{2}+gamma_5 mathbf{(6.4.12)}$

При наличии двух комплексно-сопряженных корней в левой полуплоскости (варианты 5 и 6) общее изменение фазы вычисляется по формуле:

$sum_{j=5}^{j=6} Delta arg(iomega-s_6)=-frac{pi}{2}-gamma_5-frac{pi}{2}+gamma_5=-pi$

Резюмируем:

Если САР — устойчива все полюса полинома степенью лежат в левой полуплоскости, то изменение фазы годографа при изменении on 0 доописывается формулой 6.4.13:

$Delta arg D(icdot omega)=ncdotfrac{pi}{2} mathbf{(6.4.13)}$

Если один полюс полинома степенью лежит в правой полуплоскости, а остальные в левой полуплоскости, то изменение фазы годографа при изменении on 0 доописывается формулой 6.4.14:

$Delta arg D(icdot omega)=ncdotfrac{pi}{2}- pi mathbf{(6.4.14)}$

Если в правой полуплоскости расположено L полюсов полинома степенью , а остальные в левой полуплоскости, то изменение фазы годографа при изменении on 0 доописывается формулой 6.4.15:

$Delta arg D(icdot omega)=ncdotfrac{pi}{2}-Lcdot pi mathbf{(6.4.15)}$

Предельный случай

Если один из полюсов полинома явялется бесконечным (см. рисунок 6.4.12):

Рисунок. 6.4.12 Бесконечный полюс

Данный случай возникает, если годограф в этом случае ведет себя как показано на рисунке 6.4.13:

Рисунок 6.4.13 Вид годографа

c «бесконечным» корнями

Пример

Исследовать на устойчивость САР , представленную на рисунке 6.4.14 с использованием критерия Михайлова

Рисунок 6.4.14 САР для исследования

Полином

$begin{cases} D_1(omega)=1-omega^2; \ D_2(omega)=omega-2cdotomega^3.end{cases}$

Корни полинома : $omega_{1.1} =1$ ;

Корни полинома $omega_{2.1} =0, omega_{2.2}=frac{sqrt{2}}{2}$ ;

Чередования 0 для полиномов не происходит, (см. рис. 6.4.15)

Рисунок 6.4.15 Корни полиномов

Определим какие должны быть коэффициенты полинома и что бы САР была устойчивой согласно критерию Михайлов.

Для устойчивой системы, необходимо чередование корней, для нашего случа корни могут распологаться по возрастанию в следующем порядке: $omega_{2.1}<omega_{1.1}<omega_{2.2};$

Изменим коэффициент так, что-бы неравенство $omega_{2.2}>(omega_{1.1}=1)$ сталов верным. Например пусть $omega_{2.2}=2$ . Тогда решая уравнение для , при получаем коэффициент

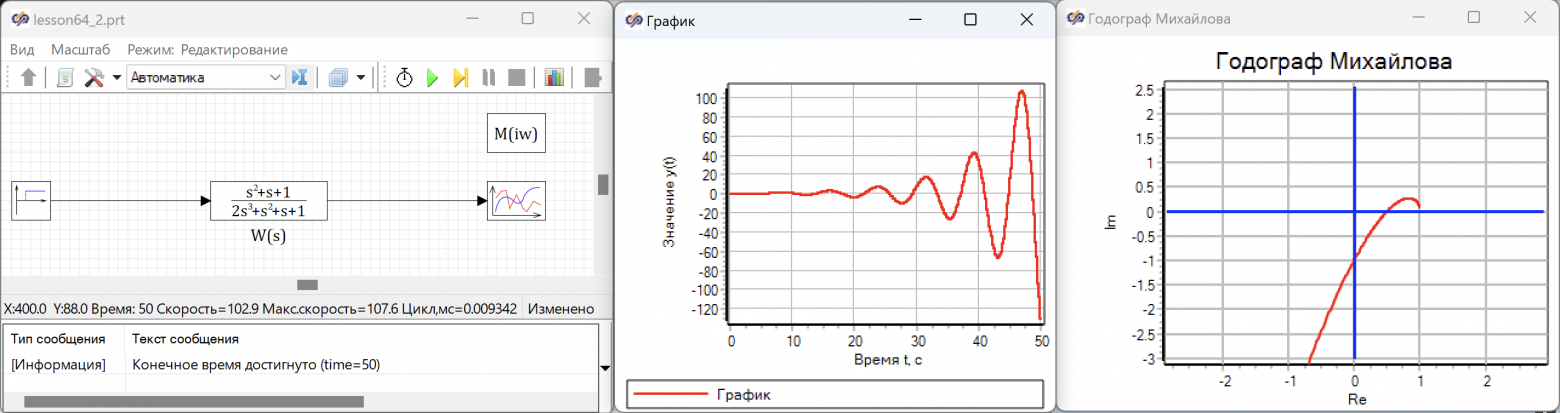
Проверим результат численным моделированием. Создадим стуркутурную схему, как показанао на рисунке 6.4.15.

Рисунок 6.4.15 Схема модели для проверки решения примера 1.

Используем блок передаточная переменная общего вида, где будем задавать, коэффициет k, из условия задачи в качестве глобальной переменной, меня которую можно изменять коэффициент числителя (см. рис. 6.4.15). Зададим в качестве тестового воздействия ступеньку на 5-й секунду, так же поместим на схему блок построения гадогрофа Михайлова. Результаты расчет приведены на рисунке 6.4.16

Рисунок 6.4.16 Расчет неустойчивой системы.

Меняя коэффициет , можно убедиться, что система остается неустойчивой, при любых значениях коэффициента меняется только амплитуда колебательного процесса. График годографа Михайлова показывает, что годограф переходит из квадранта в квандрат комплексной полсокости, по часовой стрелке (см. рис. 6.4.16).

Изменим коэффициент блока предаточной функции общего вида рассчитанные для получения чердования корней , и повторим расчет. Изменненная модель и результаты моделирования представлены нар рисунке 6.4.17

Рисунок 6.4.17 Расчет устойчивой системы.

Измененная система, оказывается устойчивой. При единичном ступенчатом воздействии она приходит в новое состояние равновесия. Точно так же, как для неустойчивой системы, для устойчивой системы коэффицент влияет только на амплитуду выхода, но не влияет на устойчивость. Для устойчиваой системы график годографа Михайлова показывает, что годограф переходит из квадранта в квандрат комплексной полсокости, против часовой стрелке (см. рис. 6.4.17).

Далее будет совсем жестко — годограф Найквиста! Не переключайтесь!

Источник