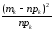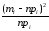Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции
ЧАСТОТА()
и диаграммы.
Гистограмма (frequency histogram) – это
столбиковая диаграмма MS EXCEL
, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).
Гистограмма поможет визуально оценить распределение набора данных, если:
- в наборе данных как минимум 50 значений;
- ширина интервалов одинакова.
Построим гистограмму для набора данных, в котором содержатся значения
непрерывной случайной величины
. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе
Гистограмма AT
в
файле примера.
Данные содержатся в диапазоне
А8:А57
.
Примечание
: Для удобства написания формул для диапазона
А8:А57
создан
Именованный диапазон
Исходные_данные.
Построение гистограммы с помощью надстройки
Пакет анализа
Вызвав диалоговое окно
надстройки Пакет анализа
, выберите пункт
Гистограмма
и нажмите ОК.
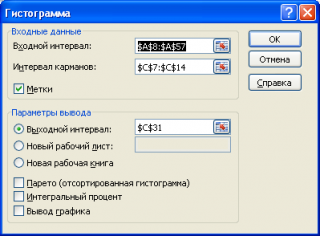
В появившемся окне необходимо как минимум указать:
входной интервал
и левую верхнюю ячейку
выходного интервала
. После нажатия кнопки
ОК
будут:
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
-
если поставлена галочка напротив пункта
Вывод графика
, то вместе с таблицей частот будет выведена гистограмма.
Перед тем как анализировать полученный результат —
отсортируйте исходный массив данных
.
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием
Еще
) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:
=(МАКС(
Исходные_данные
)-МИН(
Исходные_данные
))/7
где
Исходные_данные –
именованный диапазон
, содержащий наши данные.
Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).
Примечание
:
Похоже, что инструмент
Гистограмма
для подсчета общего количества интервалов (с учетом первого) использует формулу
=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(
Исходные_данные
)))+1
Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция
ЦЕЛОЕ()
округляет до ближайшего меньшего целого
(ЦЕЛОЕ(КОРЕНЬ(35))=5
, а
ЦЕЛОЕ(КОРЕНЬ(36))=6)
.
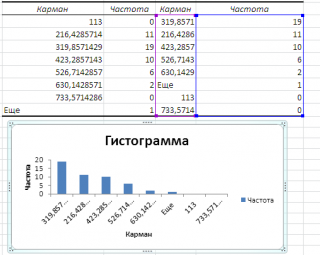
Если установить галочку напротив поля
Парето (отсортированная гистограмма)
, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.
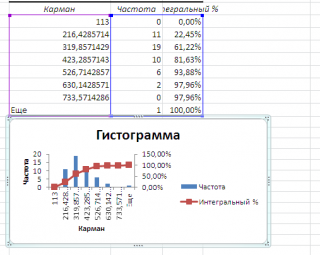
Если установить галочку напротив поля
Интегральный процент
, то к таблице с частотами будет добавлен столбец с
нарастающим итогом
в % от общего количества значений в массиве.
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля
Метка
).
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.
В результате получим практически такую же по форме
гистограмму
, что и раньше, но с более красивыми границами интервалов.
Как видно из рисунков выше, надстройка
Пакет анализа
не осуществляет никакого
дополнительного форматирования диаграммы
. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении
гистограммы
с помощью функции
ЧАСТОТА()
без использовании надстройки
Пакет анализа
.
Построение гистограммы распределения без использования надстройки Пакет анализа
Порядок действий при построении гистограммы в этом случае следующий:
- определить количество интервалов у гистограммы;
- определить ширину интервала (с учетом округления);
- определить границу первого интервала;
- сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
- построить гистограмму.
СОВЕТ
: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент
описательной статистики
, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.
В наших расчетах для определения количества интервалов мы будем пользоваться формулой
=ЦЕЛОЕ(КОРЕНЬ(n))+1
.
Примечание
: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.
Расчет ширины интервала и таблица интервалов приведены в
файле примера на листе Гистограмма
. Для вычисления количества значений, попадающих в каждый интервал, использована
формула массива
на основе функции
ЧАСТОТА()
. О вводе этой функции см. статью
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL
.
В MS EXCEL имеется диаграмма типа
Гистограмма с группировкой
, которая обычно используется для построения
Гистограмм распределения
.
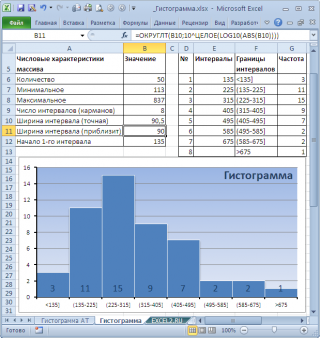
В итоге можно добиться вот такого результата.
Примечание
: О построении и настройке макета диаграмм см. статью
Основы построения диаграмм в MS EXCEL
.
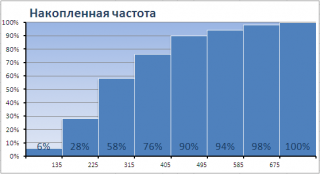
Одной из разновидностей гистограмм является
график накопленной частоты
(cumulative frequency plot).
На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.
СОВЕТ
: О построении
двумерной гистограммы
см. статью
Двумерная гистограмма в MS EXCEL
.
Примечание
: Альтернативой
графику накопленной частоты
может служить
Кривая процентилей
, которая рассмотрена в
статье про Процентили
.
Примечание
: Когда количество значений в выборке недостаточно для построения полноценной
гистограммы
может быть полезна
Блочная диаграмма
(иногда она называется
Диаграмма размаха
или
Ящик с усами
).
Содержание
- Построение гистограммы
- Способ 1: создание простой гистограммы в блоке диаграмм
- Способ 2: построение гистограммы с накоплением
- Способ 3: построение с использованием «Пакета анализа»
- Способ 4: Гистограммы при условном форматировании
- Вопросы и ответы
Гистограмма является отличным инструментом визуализации данных. Это наглядная диаграмма, с помощью которой можно сразу оценить общую ситуацию, лишь взглянув на неё, без изучения числовых данных в таблице. В Microsoft Excel есть сразу несколько инструментов предназначенных для того, чтобы построить гистограммы различного типа. Давайте взглянем на различные способы построения.
Урок: Как создать гистограмму в Microsoft Word
Построение гистограммы
Гистограмму в Экселе можно создать тремя способами:
- С помощью инструмента, который входит в группу «Диаграммы»;
- С использованием условного форматирования;
- При помощи надстройки Пакет анализа.
Она может быть оформлена, как отдельным объектом, так и при использовании условного форматирования, являясь частью ячейки.
Способ 1: создание простой гистограммы в блоке диаграмм
Обычную гистограмму проще всего сделать, воспользовавшись функцией в блоке инструментов «Диаграммы».
- Строим таблицу, в которой содержатся данные, отображаемые в будущей диаграмме. Выделяем мышкой те столбцы таблицы, которые будут отображены на осях гистограммы.
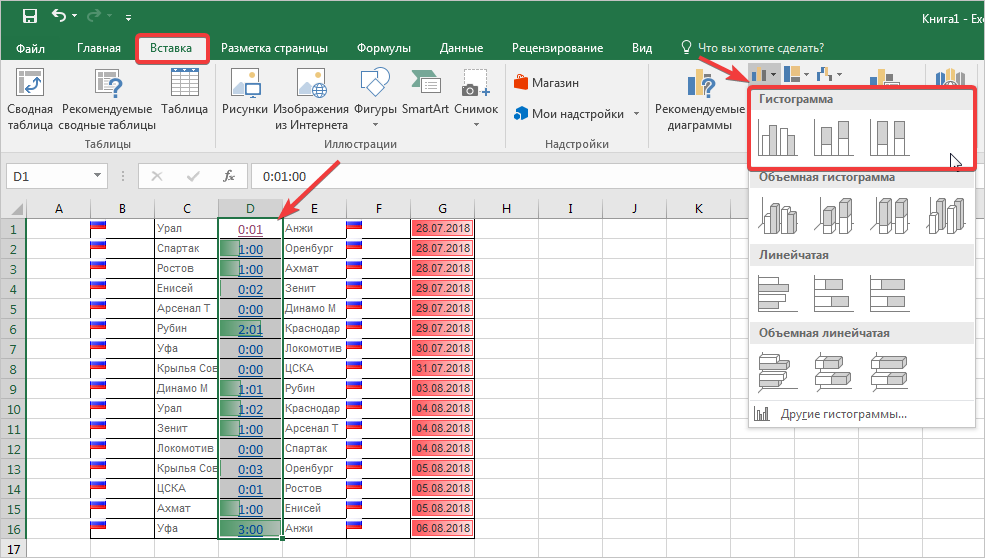
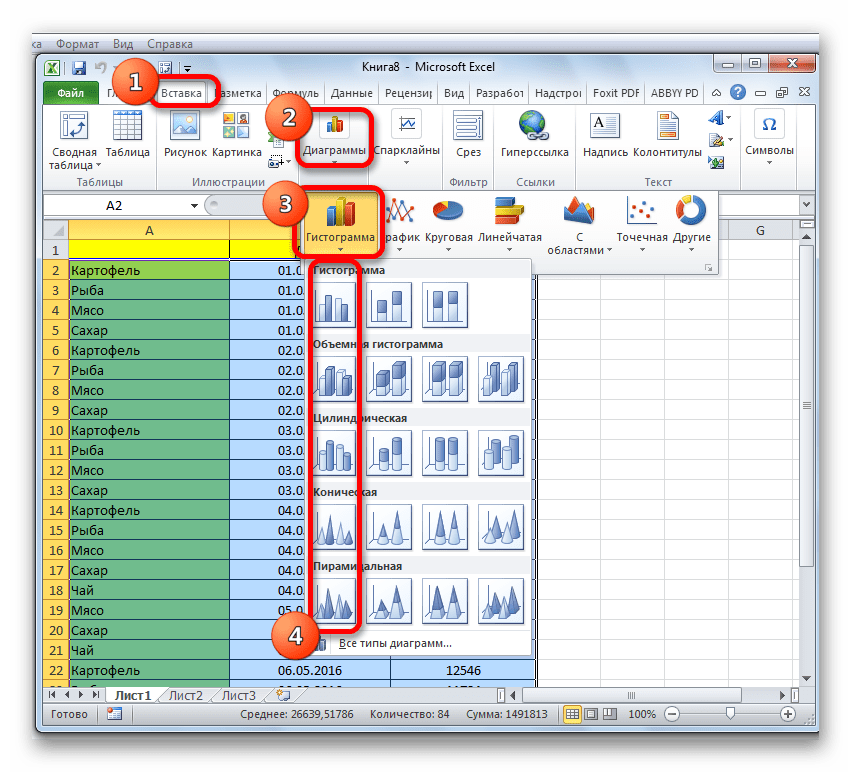
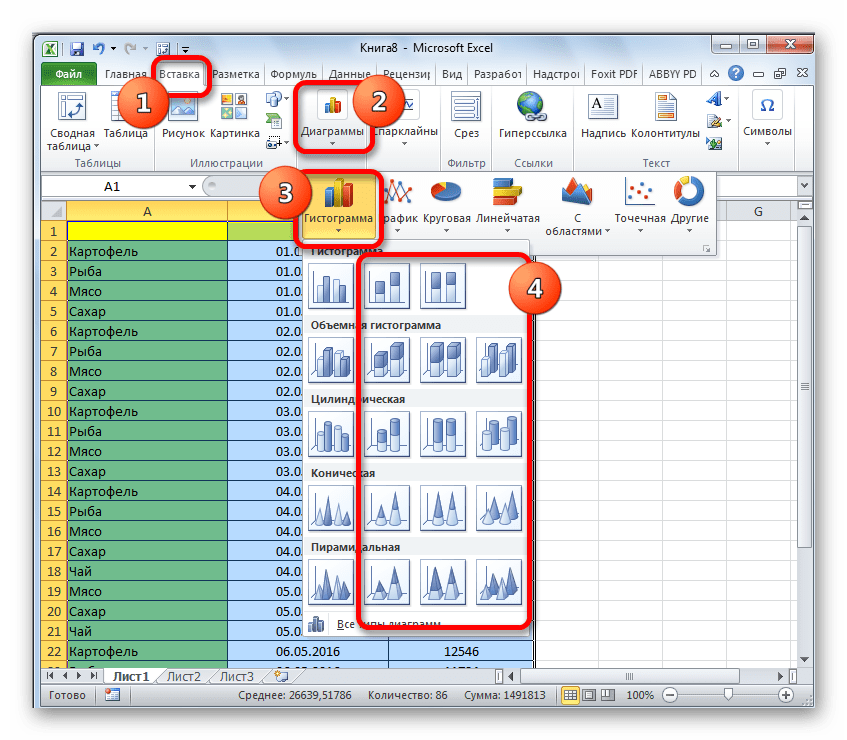
- Находясь во вкладке «Вставка» кликаем по кнопке «Гистограмма», которая расположена на ленте в блоке инструментов «Диаграммы».
- В открывшемся списке выбираем один из пяти типов простых диаграмм:
- гистограмма;
- объемная;
- цилиндрическая;
- коническая;
- пирамидальная.
Все простые диаграммы расположены с левой части списка.
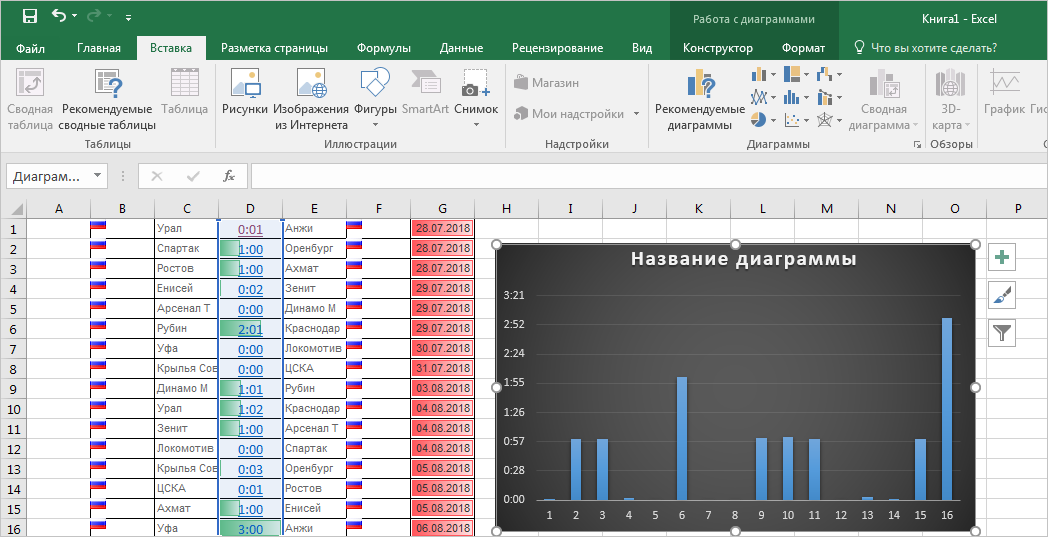
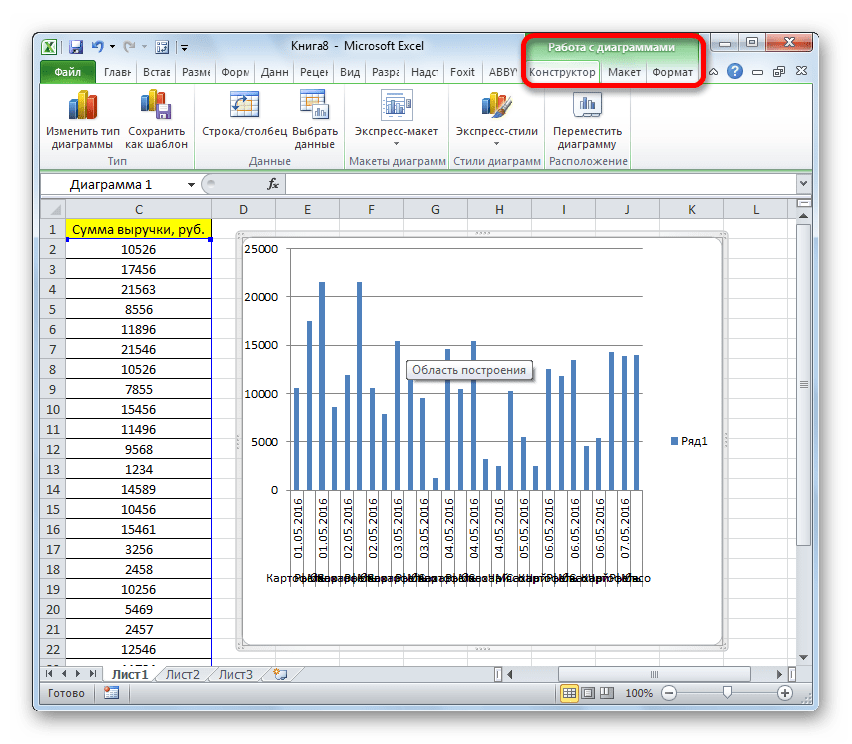
После того, как выбор сделан, на листе Excel формируется гистограмма.
- Изменять стили столбцов;
- Подписывать наименование диаграммы в целом, и отдельных её осей;
- Изменять название и удалять легенду, и т.д.
С помощью инструментов, расположенных в группе вкладок «Работа с диаграммами» можно редактировать полученный объект:
Урок: Как сделать диаграмму в Excel
Способ 2: построение гистограммы с накоплением
Гистограмма с накоплением содержит столбцы, которые включают в себя сразу несколько значений.
- Перед тем, как перейти к созданию диаграммы с накоплением, нужно удостовериться, что в крайнем левом столбце в шапке отсутствует наименование. Если наименование есть, то его следует удалить, иначе построение диаграммы не получится.
- Выделяем таблицу, на основании которой будет строиться гистограмма. Во вкладке «Вставка» кликаем по кнопке «Гистограмма». В появившемся списке диаграмм выбираем тот тип гистограммы с накоплением, который нам требуется. Все они расположены в правой части списка.
- После этих действий гистограмма появится на листе. Её можно будет отредактировать с помощью тех же инструментов, о которых шёл разговор при описании первого способа построения.
Способ 3: построение с использованием «Пакета анализа»
Для того, чтобы воспользоваться способом формирования гистограммы с помощью пакета анализа, нужно этот пакет активировать.
- Переходим во вкладку «Файл».
- Кликаем по наименованию раздела «Параметры».
- Переходим в подраздел «Надстройки».
- В блоке «Управление» переставляем переключатель в позицию «Надстройки Excel».
- В открывшемся окне около пункта «Пакет анализа» устанавливаем галочку и кликаем по кнопке «OK».
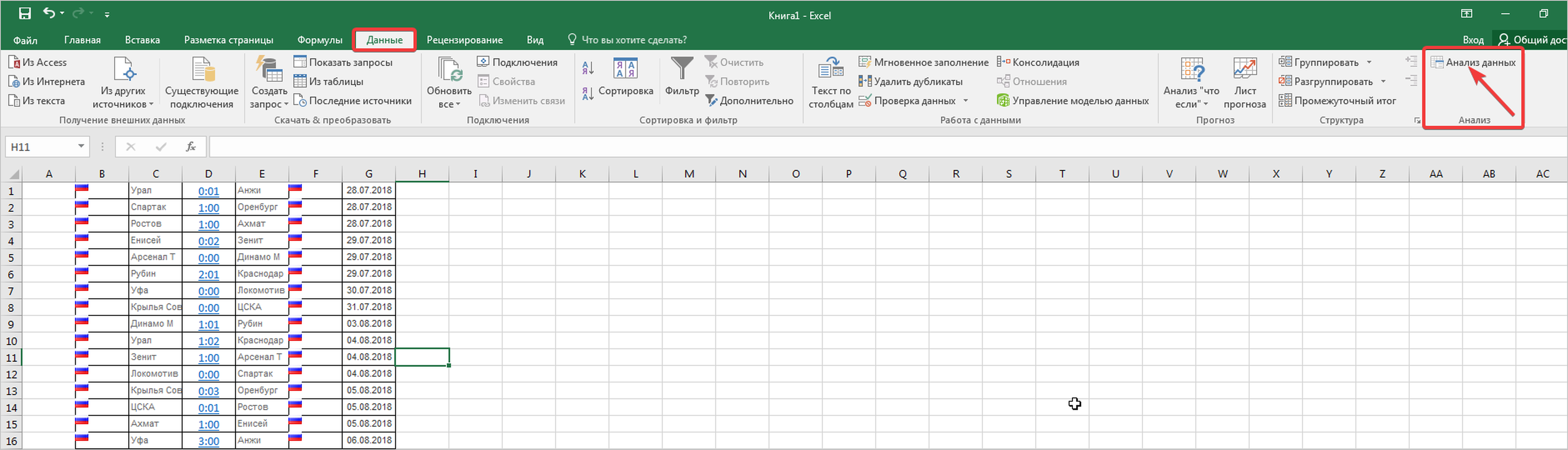
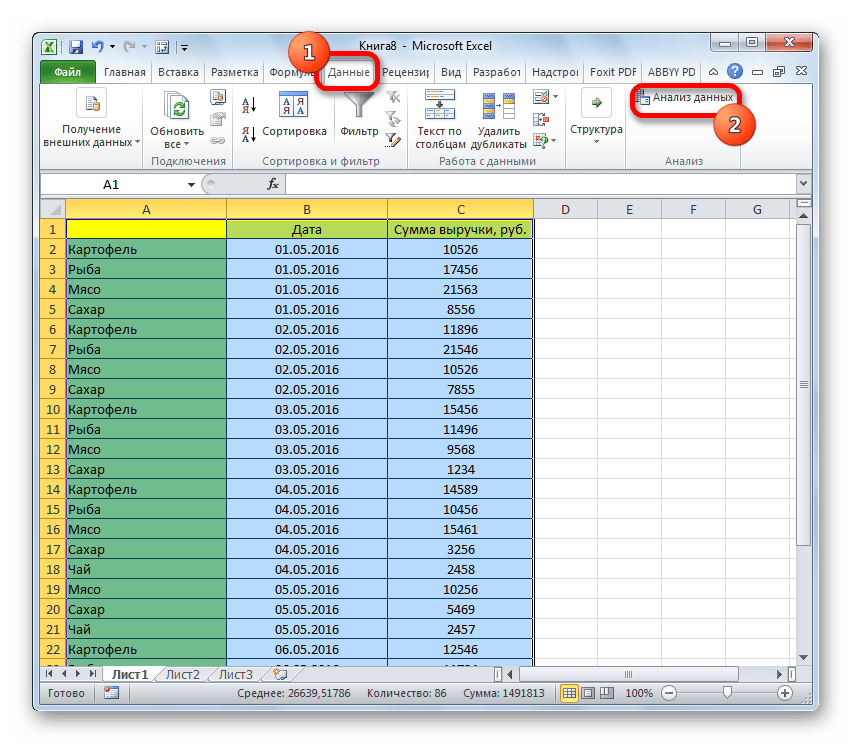
- Перемещаемся во вкладку «Данные». Жмем на кнопку, расположенную на ленте «Анализ данных».
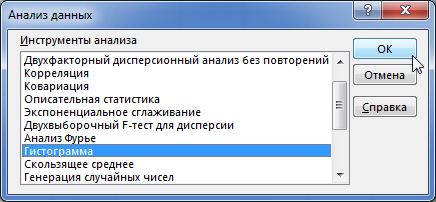
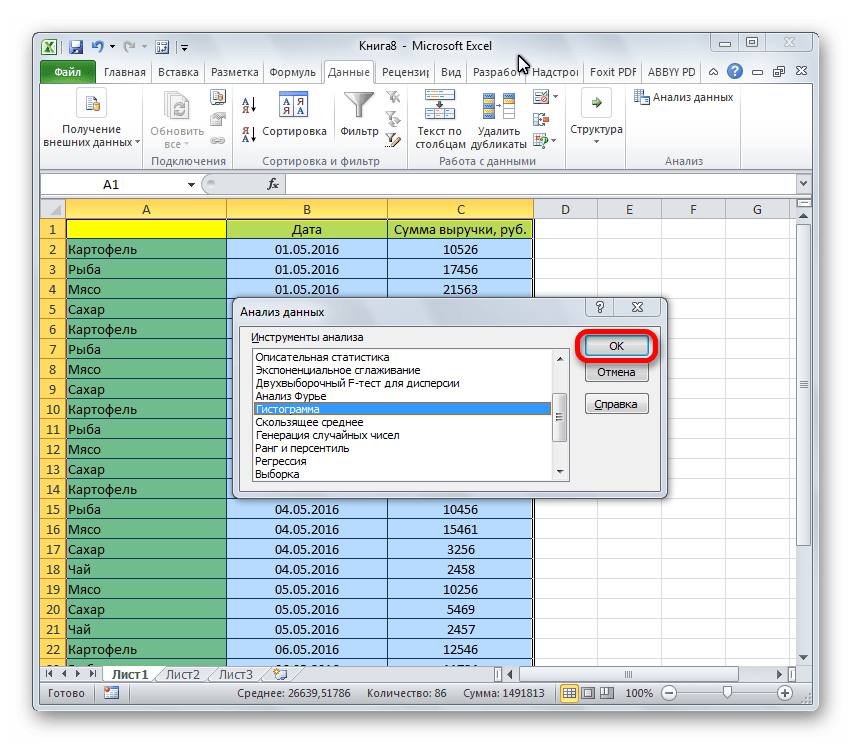
- В открывшемся небольшом окне выбираем пункт «Гистограммы». Жмем на кнопку «OK».
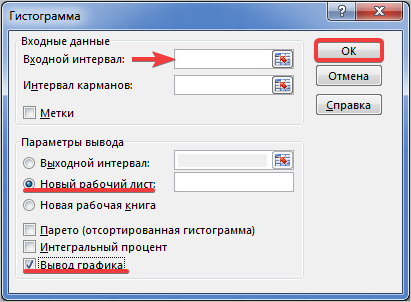
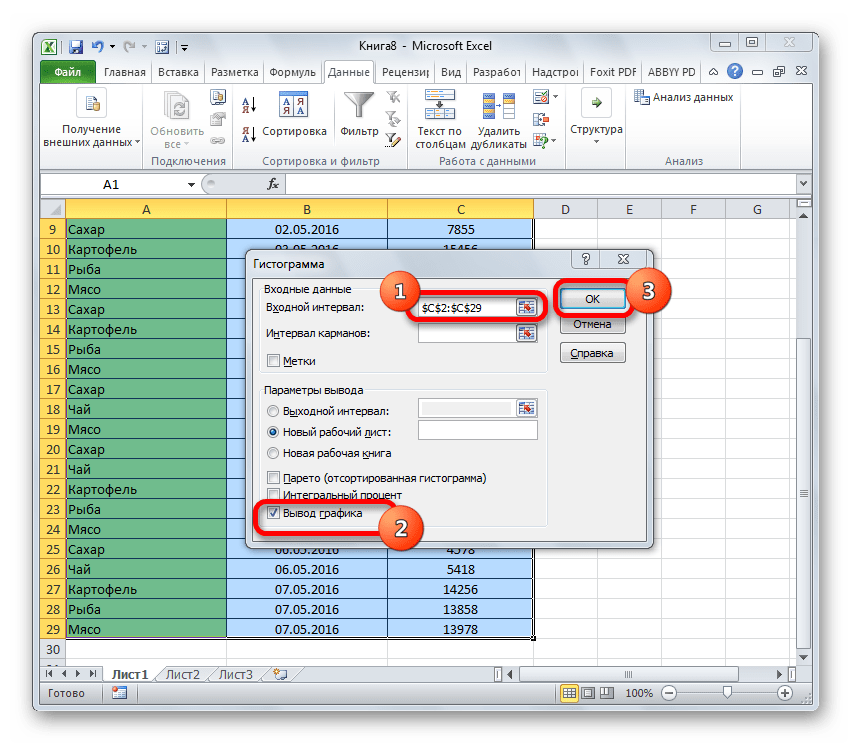
- Открывается окно настройки гистограммы. В поле «Входной интервал» вводим адрес диапазона ячеек, гистограмму которого хотим отобразить. Обязательно внизу ставим галочку около пункта «Вывод графика». В параметрах ввода можно указать, где будет выводиться гистограмма. По умолчанию — на новом листе. Можно указать, что вывод будет осуществляться на данном листе в определенных ячейках или в новой книге. После того, как все настройки введены, жмем кнопку «OK».
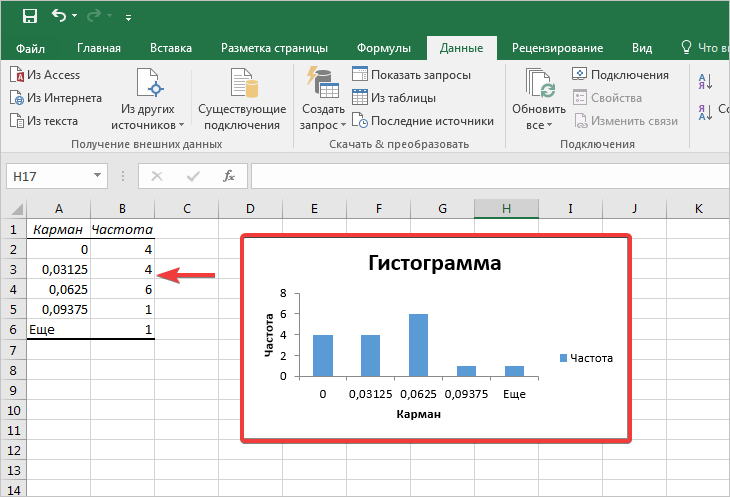
Как видим, гистограмма сформирована в указанном вами месте.
Способ 4: Гистограммы при условном форматировании
Гистограммы также можно выводить при условном форматировании ячеек.
- Выделяем ячейки с данными, которые хотим отформатировать в виде гистограммы.
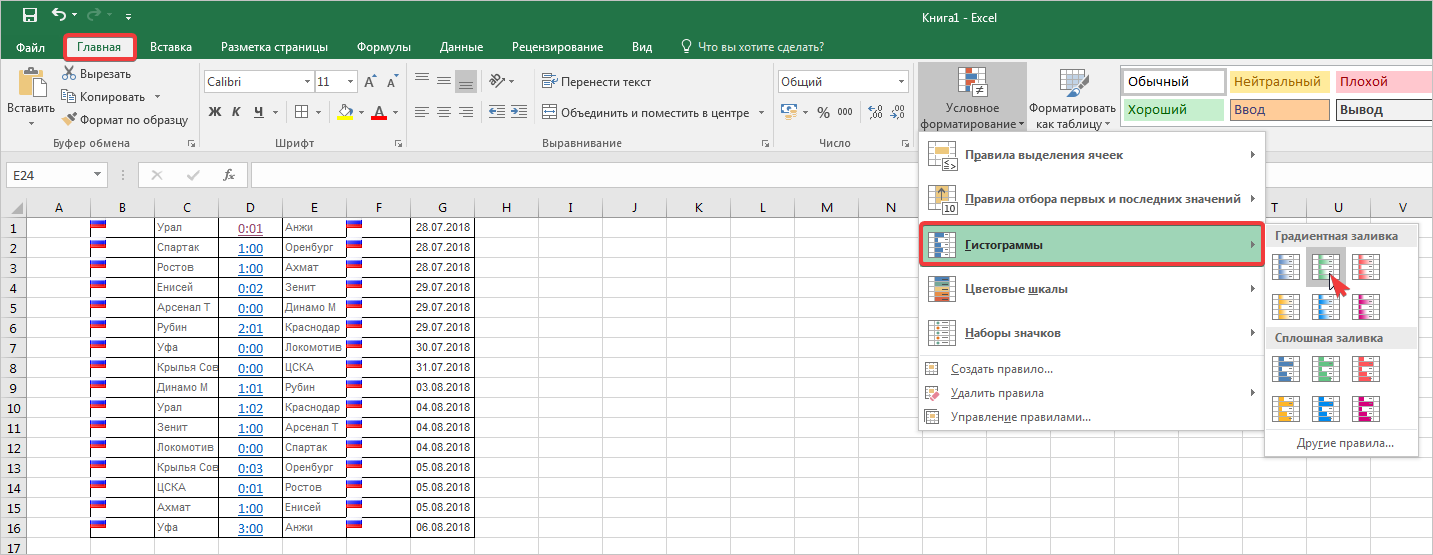
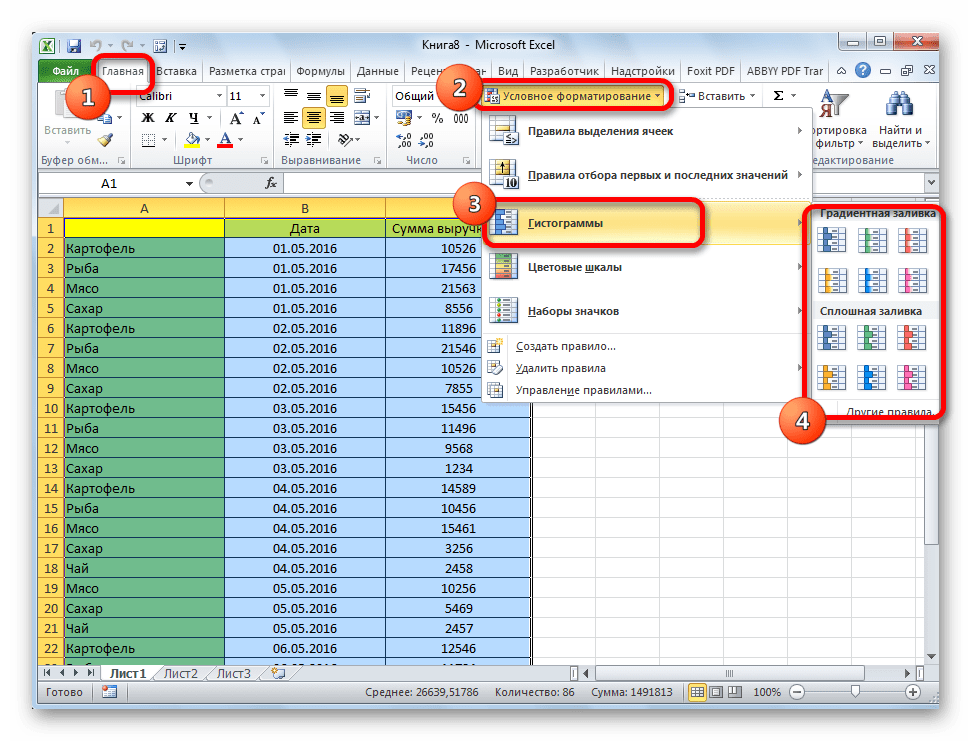
- Во вкладке «Главная» на ленте жмем на кнопку «Условное форматирование». В выпавшем меню кликаем по пункту «Гистограмма». В появившемся перечне гистограмм со сплошной и градиентной заливкой выбираем ту, которую считаем более уместной в каждом конкретном случае.
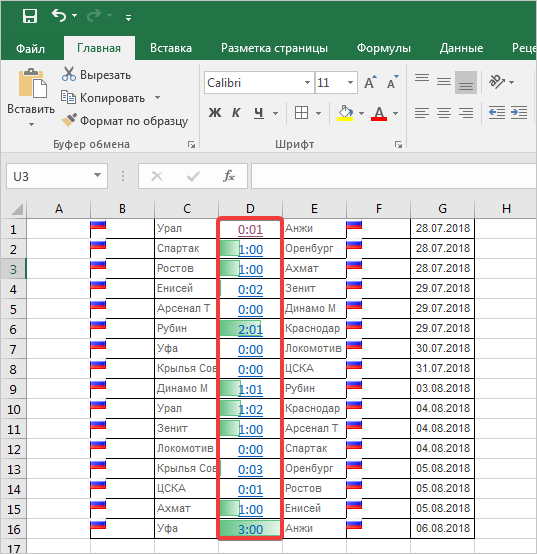
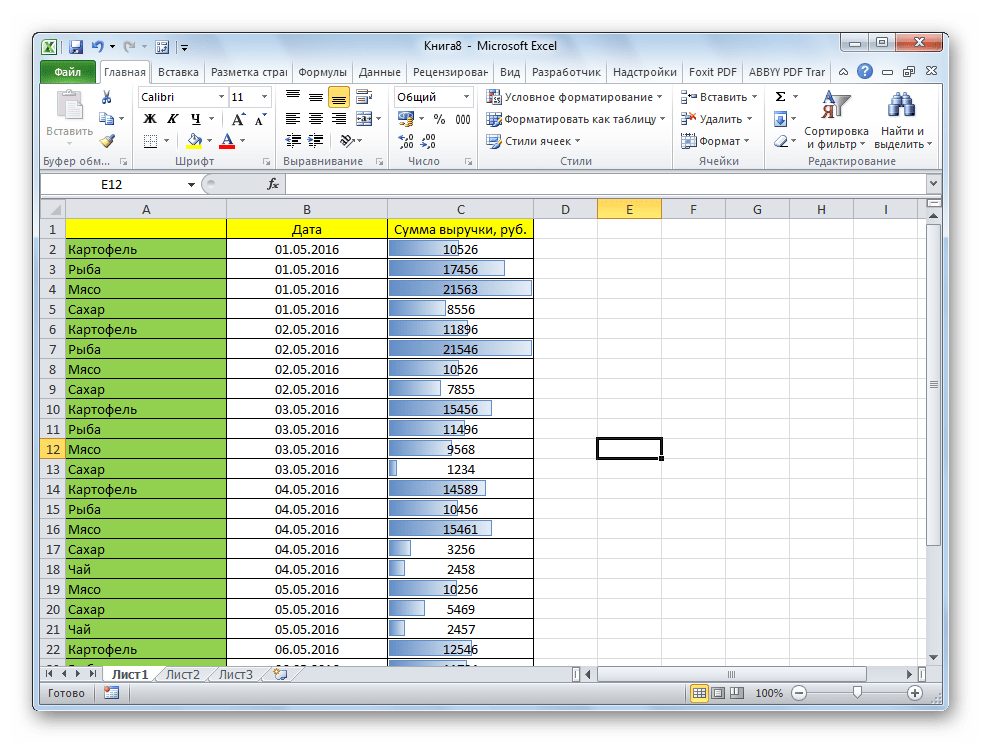
Теперь, как видим, в каждой отформатированной ячейке имеется индикатор, который в виде гистограммы характеризует количественный вес данных, находящихся в ней.
Урок: Условное форматирование в Excel
Мы смогли убедиться, что табличный процессор Excel предоставляет возможность использовать такой удобный инструмент, как гистограммы, совершенно в различном виде. Применение этой интересной функции делает анализ данных намного нагляднее.
Еще статьи по данной теме:
Помогла ли Вам статья?
Гистограмма – очень полезный инструмент, с помощью которого можно сделать демонстрируемую информацию более наглядной и простой для восприятия. Это особенно актуально, когда время на изучение данных в таблице ограничено, и нужно в сжатые сроки сформировать целостное представление о них. Давайте посмотрим, каким образом можно построить гистограмму в Эксель.
Содержание
- Строим гистограмму
- Метод 1: используем инструменты на ленте программы
- Метод 2: пользуемся надстройкой “Пакета “анализа”
- Метод 3: выполняем условное форматирование с гистограммой
- Редактирование гистограммы
- Заключение
Строим гистограмму
Для выполнения поставленной задачи в Excel можно воспользоваться разными методами:
- использовать инструменты на ленте программы;
- воспользоваться надстройкой “Пакет анализа”;
- применить условное форматирование.
Ниже мы подробнее остановимся на каждом из этих пунктов.
Метод 1: используем инструменты на ленте программы
Это, пожалуй, самый простой способ. И вот, как он реализуется:
- Открываем (или создаем) таблицу. Выделяем любым удобным способом (например, с помощью зажатой левой кнопки мыши) ячейки, на базе которых планируется построить диаграмму.
- Переходим во вкладку “Вставка”, в группе инструментов “Диаграммы” жмем кнопку “Вставить гистограмму”.
- Раскроется перечень возможных вариантов:
- гистограмма;
- объемная гистограмма;
- линейчатая;
- объемная линейчатая.
- После клика по нужному (понравившемуся) варианту, на листе появится гистограмма. В нашем случае мы выбрали самую простую.
Гистограмма с накоплением
До того, как приступить к созданию гистограммы с накоплением, проверяем, чтобы самая верхняя левая ячейка таблицы была пустой.
- Выполняем выделение таблицы, на базе которой планируем построить гистограмму. Переходим во вкладку “Вставка”, нажимаем кнопку “Вставить гистограмму” (группа “Диаграммы”) и в раскрывшемся перечне останавливаем на варианте – “Гистограмма с накоплением”.
- Гистограмма вставлена, что и требовалось.
Примечание: в гистограммах с накоплением один столбец содержит сразу несколько значений. В нашем случае – это данные по всем четырем торговым точкам за конкретную дату.
Нормированная гистограмма с накоплением
В данном случае отображается (в процентном выражении) вклад каждого значения в общем количестве.
Метод 2: пользуемся надстройкой “Пакета “анализа”
Для начала нужно включить данный пакет.
- Идем в меню “Файл”.
- В перечне слева в самом низу щелкаем по пункту “Параметры”.
- В открывшемся окне выбираем “Надстройки”. В правой части окна для параметра “Управление” ставим значение “Надстройки Excel”, после чего жмем кнопку “Перейти”.
- В появившемся окошке ставим галочку напротив надстройки “Пакет анализа” и жмем OK.
- Перейдя во вкладку “Данные” в группе инструментов “Анализ” нажимаем кнопку “Анализ данных”.
- Откроется окошко, в котором нам нужен пункт “Гистограмма“, после выбора которого щелкаем OK.
- Перед нами появится окно, в котором нужно выполнить настройки гистограммы:
- в поле “Входной интервал” указываем диапазон ячеек, по которым нужно построить гистограмму. Сделать это можно вручную, прописав адреса с помощью клавиш на клавиатуре. Также мы можем выделить нужный диапазон ячеек в самой таблице, предварительно установив курсор в поле для ввода информации.
- внизу окна ставим галочку напротив параметра “Вывод графика”.
- в группе параметров вывода можно указать, куда следует вставить созданную гистограмму. Стандартное значение – на новом листе.
- по готовности жмем кнопку OK.
- Гистограмма сформирована и добавлена на отдельном листе, как мы и хотели.
Метод 3: выполняем условное форматирование с гистограммой
Получить гистограмму можно и с помощью условного форматирования ячеек. План действий следующий:
- Для начала нужно выделить элементы, которые нужны для гистограммы.
- Находясь в главной вкладке в группе “Стили” щелкаем по кнопке “Условное форматирование”. Откроется список, в котором выбираем “Гистограмму”. Раскроется еще один перечень, где нужно определиться с вариантами заливки – градиентная или сплошная.
- В выделенных ячейках появились гистограммы, соответствующие их значениям. В нашем случае была выбрана сплошная заливка синим цветом.
Редактирование гистограммы
Вставленную на лист гистограмму можно изменить:
- Корректируем или удаляем название. Для активации режима редактирования щелкаем по названию, после чего вокруг него появится рамка. Теперь кликаем в любом месте внутри рамки и мы можем приступать к редактированию.
- Удаляем легенду (если она не нужна). Предварительно нужно ее выбрать. Первым кликом выделяем все легенды (если их несколько), вторым – конкретную легенду. Удалить легенду можно через контекстное меню, вызываемое щелчком правой кнопки мыши по ней или просто нажав клавишу Del на клавиатуре.
- Меняем положение названия гистограммы и легенды. Для этого кликаем по выбранному объекту, чтобы выделить его. Затем наводим указатель мыши на любую из появившихся границ, и когда появится характерный символ в виде стрелок в четыре стороны, зажав левую кнопку мыши перетаскиваем объект в новое место.
- Меняем размер и положение гистограммы. Чтобы изменить размер гистограммы, зажав левую кнопку мыши тянем за одну из точек, расположенных на рамке вокруг нее.
Для изменения положения выполняем те же самые действия, что и в отношении названия или легенды.
- Для более детальных настроек щелкаем по любой свободной части в области диаграммы (белые участки) и в открывшемся контекстном меню выбираем пункт “Формат области диаграммы”.
Появится вспомогательное окно, в котором мы можем настроить:
- заливку и границы;
- добавить различные эффекты;
- размеры и свойства;
- параметры текста.
- Настраиваем шкалы по осям X и Y. Щелкаем по подписям выбранной шкалы правой кнопкой мыши и в открывшемся контекстном меню выбираем “Формат оси”.
Откроется окно, в котором мы можем выполнить соответствующие настройки.
Помимо вышеперечисленного, на ленте программы во вкладке “Конструктор”, в которой мы окажемся автоматическим после создания гистограммы, мы можем сменить стиль, выбрать один из экспресс-макетов и т.д.
Также, мы можем добавить новый элемент диаграммы, щелкнув на соответствующий значок в левом верхнем углу ленты и выбрав из списка нужный пункт.
Примечание: возможных настроек и параметров, которые можно задать для гистограммы достаточно много, и каждый пользователь сможет подобрать для себя оптимальный вариант. Мы описали лишь часть основных действий и инструментов, которые могут помочь в этом.
Заключение
Программа Excel позволяет построить различные гистограммы, которые помогают лучше и быстрее освоить информацию, особенно, когда ее слишком много, а времени, наоборот, мало. Выбор конкретного вида и метода построения диаграммы зависит от того, какие цели преследует пользователь, и каким он видит конечный результат.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Если вам нужно разработать сложный статистический или инженерный анализ, вы можете сэкономить время и этапы с помощью этого средства. Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.
Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопкуАнализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».
-
Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
-
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
-
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
-
Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
-
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
-
Примечание: Чтобы включить Visual Basic для приложений (VBA) для надстройки «Надстройка анализа», вы можете загрузить надстройку VBA так же, как и надстройку «Надстройка анализа». В поле Доступные надстройки выберите «Надстройка анализа — VBA».
Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.
Однофакторный дисперсионный анализ
Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ дает проверку гипотезы о том, что каждая выборка взята из одного и того же распределения вероятности на основе альтернативной гипотезы о том, что для всех выборок распределение вероятности не одно и то же. Если есть только два примера, можно использовать функцию T.ТЕСТ. В более чем двух примерах нет удобного обобщения T.ВМЕСТОэтого можно использовать модель Anova для одного фактора.
Двухфакторный дисперсионный анализ с повторениями
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий {удобрение, температура}, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:
-
Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
-
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.
Извлечены ли шесть выборок, представляющих все пары значений {удобрение, температура}, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар {удобрение, температура} превышает влияние отдельно удобрения и отдельно температуры.
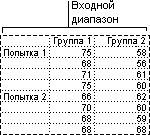
Двухфакторный дисперсионный анализ без повторений
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров {удобрение, температура} из предыдущего примера).
Функции CORREL и PEARSON вычисляют коэффициент корреляции между двумя переменными измерения, если для каждой переменной наблюдаемы измерения по каждому из N-объектов. (Любые отсутствующие наблюдения по любой теме вызывают игнорирование в анализе.) Средство анализа корреляции особенно удобно использовать, если для каждого субъекта N имеется более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение CORREL (или PEARSON),примененного к каждой из возможных пар переменных измерения.
Коэффициент корреляции, как и ковариана, — это мера степени, в которой две единицы измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц измерения, выраженных в двух переменных измерения. (Например, если двумя переменными измерения являются вес и высота, то значение коэффициента корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно от -1 до +1 включительно.
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).
Средства корреляции и коварианс могут использоваться в одном и том же параметре, если у вас есть N различных переменных измерения, наблюдаемые для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, которая показывает коэффициент корреляции или коварианс между каждой парой переменных измерения соответственно. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансы не масштабироваться. Коэффициент корреляции и коварианс — это показатели степени, в которой две переменные «различаются».
Инструмент Ковариана вычисляет значение функции КОВАРИАНА. P для каждой пары переменных измерения. (Прямое использование КОВАРИАНА. P вместо ковариана является разумной альтернативой, если есть только две переменные измерения, то есть N=2.) Запись в диагонали выходной таблицы средства Коварица в строке i, столбце i — коварианс i-й переменной измерения. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕРС.P.
Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).
Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.
Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.
Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.
С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости «Альфа». Если f > 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем дает критическое значение больше 1 для «Альфа».
Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.

Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.
Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.
Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.
Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:
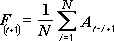
где
-
N — число предшествующих периодов, входящих в скользящее среднее;
-
A
j — фактическое значение в момент времени j; -
F
j — прогнозируемое значение в момент времени j.
Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.
Средство анализа Ранг и процентиль создает таблицу, которая содержит порядковую и процентную ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая обрабатывает связанные значения как имеющие одинаковый ранг или использует РАНГ.Функция AVG, которая возвращает средний ранг связанных значений.
Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
В средстве регрессии используется функция LINEST.
Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.
Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.
Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t < 0 «P(T <= t) одностороннее» дает вероятность того, что наблюдаемое значение t-статистики будет более отрицательным, чем t. При t >=0 «P(T <= t) одностороннее» делает возможным наблюдение значения t-статистики, которое будет более положительным, чем t. «t критическое одностороннее» дает пороговое значение, так что вероятность наблюдения значения t-статистики большего или равного «t критическое одностороннее» равно «Альфа».
«P(T <= t) двустороннее» дает вероятность наблюдения значения t-статистики, по абсолютному значению большего, чем t. «P критическое двустороннее» выдает пороговое значение, так что значение вероятности наблюдения значения t- статистики, по абсолютному значению большего, чем «P критическое двустороннее», равно «Альфа».
Парный двухвыборочный t-тест для средних
Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.
Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:
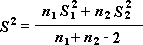
Двухвыборочный t-тест с одинаковыми дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Его называют гомике t-тестом. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения.
Двухвыборочный t-тест с различными дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных были полученными из распределения с неравными дисперсиями. Его называют гетероскестическими t-тестами. Как и в предыдущем примере с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения. Этот тест можно использовать, если в двух примерах есть отдельные объекты. Используйте тест Парный, описанный в примере, если существует один набор тем и две выборки представляют измерения по каждой теме до и после обработки.
Для определения тестовой величины t используется следующая формула.
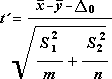
Следующая формула используется для вычисления степеней свободы (df). Так как результат вычисления обычно не является integer, значение df округлится до ближайшего другого, чтобы получить критическое значение из таблицы t. Функция Excel T .Test использует вычисляемую величину df без округлений, так как можно вычислить значение для T.ТЕСТ с неинтегрированной df. Из-за этих разных подходов к определению степеней свободы результаты T.Тест и этот t-тест будут отличаться в случае неравных дисперсий.
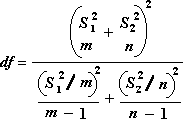
Z-тест. Средство анализа «Две выборки для середины» выполняет два примера z-теста для средств со известными дисперсиями. Этот инструмент используется для проверки гипотезы NULL о том, что между двумя значениями численности населения нет различий между односторонними или двухбокльными альтернативными гипотезами. Если дисперсии не известны, функция Z .Вместо этого следует использовать тест.
При использовании этого инструмента следует внимательно просматривать результат. «P(Z <= z) одностороннее» на самом деле есть P(Z >= ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z <= z) двустороннее» на самом деле есть P(Z >= ABS(z) или Z <= -ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. Двусторонний результат является односторонним результатом, умноженным на 2. Инструмент «z-тест» можно также применять для гипотезы об определенном ненулевом значении разницы между двумя средними генеральных совокупностей. Например, этот тест можно использовать для определения разницы выступлений на соревнованиях двух автомобилей разных марок.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Создание гистограммы в Excel 2016
Создание диаграммы Парето в Excel 2016
Загрузка средства анализа в Excel
Инженерные функции (справка)
Общие сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Поиск ошибок в формулах
Сочетания клавиш и горячие клавиши в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Нужна дополнительная помощь?
Загрузить PDF
Загрузить PDF
Гистограмма является графическим методом представления табличных данных, которые отображаются в виде прямоугольников с пропорциональными площадями. Чтобы в Excel использовать инструмент «Гистограмма», нужно ввести данные в два столбца таблицы: один столбец для входных данных, а другой для интервалов (в Excel они называются «интервалы карманов»). Входные данные – это данные, которые нужно проанализировать, а интервалы используются при получении входных данных и их анализа с помощью инструмента «Гистограмма».
Убедитесь, что надстройка установлена. Перед тем, как приступить к работе с инструментом «Гистограмма» в Microsoft Excel, убедитесь, что надстройка Analysis ToolPak готова к использованию.[1]
-
1
Откройте окно «Надстройки Excel». Это можно сделать из основного окна программы Excel.
- Нажмите «Файл» – «Параметры».
- В левой панели нажмите «Надстройки».
- В меню «Управление» выберите «Надстройки Excel». Затем нажмите «Перейти».
-
2
Отметьте надстройку Analysis ToolPak. Открыв окно «Надстройки», в разделе «Доступные надстройки» поставьте флажок у «Analysis ToolPak». Затем нажмите «OK».
- Обратите внимание, что если надстройка Analysis ToolPak на компьютере не установлена, она не отобразится в окне «Надстройки». В этом случае запустите установщик Microsoft Excel и добавьте надстройку Analysis ToolPak в список установленных элементов.
Реклама
-
1
Откройте окно «Надстройки Excel». В этом окне можно проверить, установлена ли надстройка Analysis ToolPak.
- В основном окне Excel нажмите кнопку «Microsoft Office». Затем нажмите «Параметры Excel».
- В левой панели нажмите «Надстройки».
- В меню «Управление» выберите «Надстройки Excel». Затем нажмите «Перейти».
-
2
Отметьте надстройку Analysis ToolPak. Открыв окно «Надстройки», в разделе «Доступные надстройки» поставьте флажок у «Analysis ToolPak». Затем нажмите «OK». Это приведет к активации надстройки Analysis ToolPak и инструмента «Гистограмма».[2]
Реклама
-
1
Введите данные. Сделайте это в двух смежных столбцах электронной таблицы. В первый (левый) столбец введите входные данные, а во второй (правый) – интервалы.[3]
- Входные данные – это значения (числа), которые нужно проанализировать с помощью инструмента «Гистограмма».[4]
- Интервалы используются при получении входных данных и их анализа с помощью инструмента «Гистограмма». Например, чтобы проанализировать количество выпущенных автомобилей за последние пять лет, в качестве интервалов введите числа 2012, 2013, 2014, 2015, 2016.[5]
- Входные данные – это значения (числа), которые нужно проанализировать с помощью инструмента «Гистограмма».[4]
-
2
Откройте окно «Анализ данных». Процесс открытия этого окна аналогичен во всех версиях Excel, начиная с Excel 2007. В случае более ранней версии Excel нужно выполнить немного другие действия.
- В Excel 2007/2010/2013 перейдите на вкладку «Данные» и в группе «Анализ» выберите «Анализ данных».
- В Excel 2003 и более ранних версиях откройте меню «Сервис» и выберите опцию «Анализ данных». Если в этом меню такой опции нет, установите соответствующую надстройку.
-
3
Выделите инструмент «Гистограмма». В окне «Анализ данных» выделите инструмент «Гистограмма» и нажмите «OK». Откроется окно «Гистограмма».
-
4
Укажите диапазон ячеек с входными данными и диапазон ячеек с интервалами. Например, если входные данные – это десять чисел, которые введены в столбце А (ячейки от A1 до A10), диапазон ячеек с входными данными будет таким: A1:A10. Если в столбце B введены четыре интервала (ячейки от В1 до В4), диапазон ячеек с интервалами будет таким: В1:В4.
-
5
Отметьте опцию «Вывод графика». В разделе «Параметры вывода» щелкните по «Новая рабочая книга». Затем поставьте флажок у «Вывод графика».
-
6
Нажмите «OK», чтобы закончить работу. Excel создаст новую рабочую книгу с таблицей и графиком. График представляет собой гистограмму, которая построена на основе табличных данных.[6]
Реклама
Советы
- По умолчанию вывод размещается на новом рабочем листе. Однако, вывод можно разместить на том же листе, указав выходной интервал.
- Обратите внимание, что вместе с графиком (гистограммой) создается таблица с данными.
- Откройте соответствующий сайт, чтобы скачать простой шаблон для создания гистограмм.
Реклама
Предупреждения
- Убедитесь, что гистограмма имеет смысл, прежде чем делать какие-либо выводы на ее основе.
- Уясните значение интервалов (интервалов карманов). Не перепутайте интервалы с входными данными.
Реклама
Об этой статье
Эту страницу просматривали 28 249 раз.
Была ли эта статья полезной?
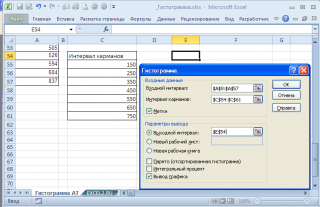
В
главном меню Excel
выбрать Данные
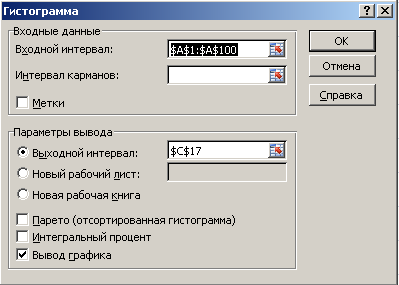
→ Анализ данных → Гистограмма → ОК.
Далее
необходимо заполнить поля ввода в
диалоговом окне Гистограмма.
Входной
интервал: 100
случайных чисел в ячейках $A$1:
$A$100;
Интервал
карманов: не
заполнять;
Выходной
интервал:
адрес ячейки, с которой начинается вывод
результатов процедуры Гистограмма;
Вывод
графика –
поставьте галочку.
Если
поле ввода Интервал
карманов не
заполняется, то процедура вычисляет
число интервалов группировки k
и границы интервалов автоматически.
Рис. 6.
Диалоговое окно Гистограмма.
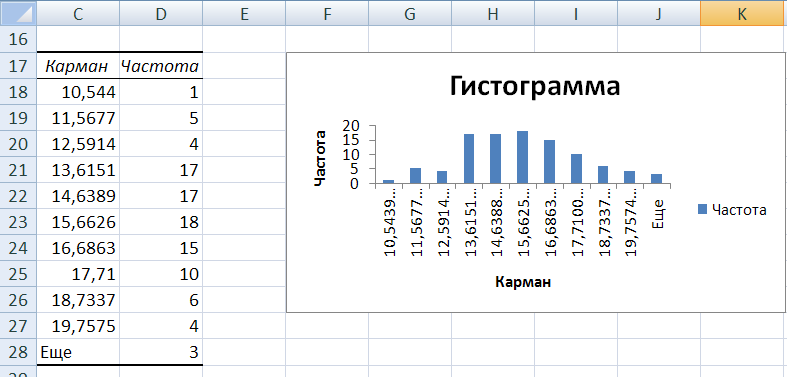
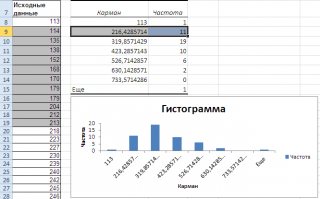
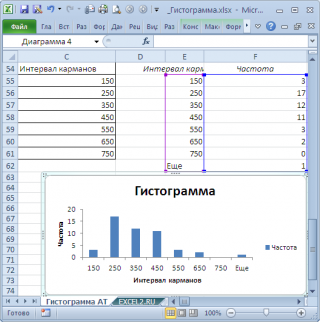
В
результате выполнения процедуры
Гистограмма
появляется таблица, содержащая границы
xi
интервалов
группировки (столбец – Карман)
и частоту попадания случайных величин
выборки mi
в i–ый
интервал (столбец
–
Частота).
Справа
от таблицы – график гистограммы.
Рис. 7. Фрагмент
листа Excel
с результатами процедуры Гистограмма
По
виду гистограммы можно предположить
(принять гипотезу) о том, что выборка
случайных чисел подчиняется нормальному
закону распределения.
Далее,
для того чтобы убедиться в правильности
выбранной гипотезы (по крайней мере
визуально) надо, первое – построить
график гипотетического нормального
закона распределения, выбрав в качестве
параметров (математического ожидания
и среднего квадратического отклонении)
их оценки (среднее и стандартное
отклонение), и совместить график
гипотетического распределения с графиком
гистограммы.
И,
второе – используя критерий согласия
Пирсона установить справедливость
выбранной гипотезы.
4. Построение теоретического закона распределения
Для
построения теоретического закона
распределения совместно с гистограммой
и проверки согласия по критерию хи-квадрат
Пирсона надо заполнить таблицу, знакомую
по лекции (см. ниже по тексту, таблица
№1). Для построения этой таблицы
надо воспользоваться таблицей карман
– частота
процедуры
Гистограмма.
xi
– границы
интервалов группировки (карманы –
получены как результат выполнения
процедуры Гистограмма);
mi
– количество
элементов выборки, попавших в i–ый
интервал (частота – получена в результате
процедуры Гистограмма);
Таблица №1
|
xi |
mi |
n∙pi |
|
|
карманы |
частота |
теоретическая |
статистика |
|
x1 |
m1 |
n∙p1 |
|
|
x2 |
m2 |
n∙p2 |
|
|
… |
… |
… |
… |
|
xk |
mk |
n∙pk |
|
|
|
Для построения
этой таблицы в Excel
к столбцам карман
– частота
процедуры
Гистограмма
надо
добавить столбцы n∙pi
и
Теоретическая
вероятность pi
попадания элементов выборки в i—ый
интервал группировки для принятой
гипотезы о нормальном распределении
генеральной совокупности
равна
pi
= P(xi-1
< X
< xi)
=
F(xi)
– F(xi-1).
n∙pi
– теоретическая (ожидаемая) частота
попадания элементов выборки в i–ый
интервал группировки для принятой
гипотезы о нормальном распределении
генеральной совокупности.
В
Excel
эту величину можно вычислить,
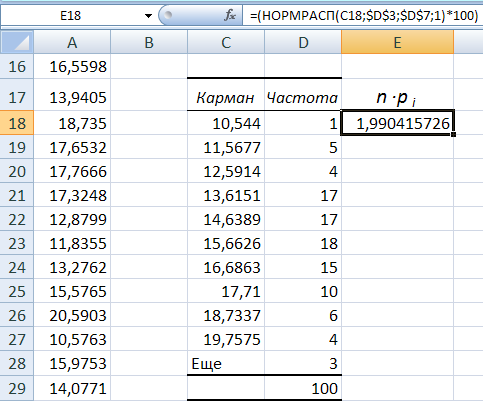
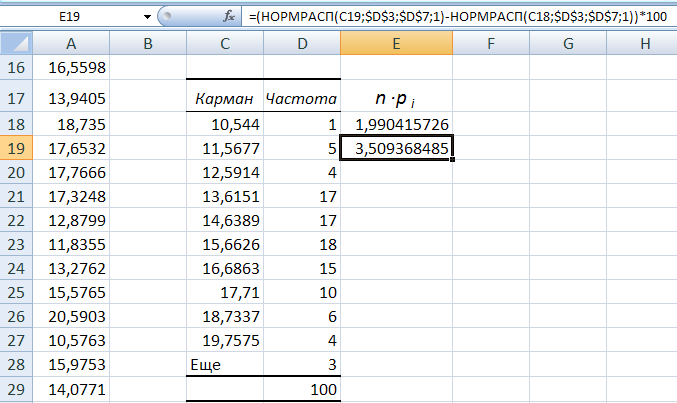
воспользовавшись функцией НОРМРАСП.
n∙pi
= (НОРМРАСП(xi;
среднее; стандартное_откл; 1) –
– НОРМРАСП(xi-1;
среднее; стандартное_откл; 1))
* n.
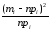
являющаяся мерой расхождения между
значениями эмпирической и теоретической
плотности распределения;
4.1.
Найдите сумму элементов выборки,
попавших в карманы
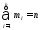
= 100), для контроля (ячейка D29,
рис. 8).
Столбцу
E18:
E28 присвойте
имя n∙pi
,
поместив
его в ячейку
E17.
В
ячейку E18
внесите
формулу для вычисления значения
функции нормального распределения
F(x1
= 10,544) = P(–
∞ < X
≤ x1),
умноженную на число наблюдений n.
В
рассматриваемом примере n
=100. В ячейку
E18
будет получено теоретическое (ожидаемое)
число значений случайной величины,
попавших в интервал
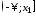
= F(x1)∙100
=НОРМРАСП(C$18$;D$3$;D$7$;1)*100
Рис.
8. В ячейке E18
результаты вычислений функции
НОРМРАСП(C$18$;D$3$;D$7$;1)*100
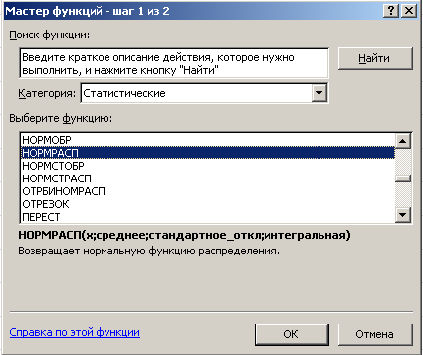
Функцию
НОРМРАСП вызывается следующим образом.
В главном меню Excel
выбирается закладка Формулы
→ Вставить функцию → в
диалоговом окне
Мастер функций – шаг 1 из 2 в
категории
Статистические → НОРМРАСП.
ОК.
Рис.
9. Окно Мастер
функций для
выбора функции НОРМРАСП из категории
Статистические.
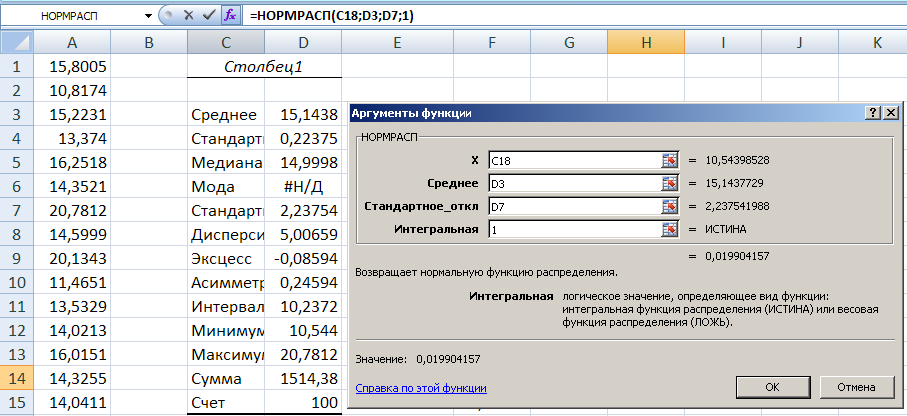
В
раскрывшемся окне Аргументы
функции
НОРМРАСП
заполните поля ввода как показано далее
на рис. 10.
Рис.
10. Окно ввода параметров для получения
функции нормального распределения
В
поле X
введите адрес ячейки, в которой находится
граница первого интервала группировки
C18
(верхняя ячейка столбца Карманы).
В
поле Среднее
введите адрес ячейки, в которой находится
среднее значение выборки, полученное
при выполнении процедуры Описательная
статистика –
D3.
В
поле Стандартное_откл
введите адрес ячейки, в которой находится
значение стандартного отклонения
выборки, полученное при выполнении
процедуры Описательная
статистика –
D7.
В
поле Интегральная
введите единица 1.
Единица
в поле
Интегральная
означает вычисление функции распределения
F(x).
ОК.
В
ячейку E19
поместите формулу для вычисления
теоретического (гипотетического) числа
случайных величин, попавших в интервал
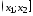
n∙p2
= n
∙
[F(x2)
– F(x1)]
= n
∙
[P(x1
< X
≤ x2)]
= n
∙
[P(10,544
< X
≤ 11,5777)],
где
p2
= F(x2)
– F(x1)
=
P(x1
< X
≤ x2)
= P(10,544
< X
≤ 11,5777)
— теоретическая вероятность попадания
нормально распределенных случайных
величин в промежуток
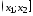
В
Excel
в строку формул необходимо поместить
формулу:
=(НОРМРАСП(C19;$D$3;$D$7;1)
– НОРМРАСП(C18;$D$3;$D$7;1))*100
Рис.
11. В ячейке E19
показаны результаты вычислений функции
=(НОРМРАСП(C19;$D$3;$D$7;1)
– НОРМРАСП(C18;$D$3;$D$7;1)) *100
Заполните
диапазон ячеек Е20:Е27
результатами вычисления этой формулы,
используя маркер заполнения.
Рис.
12. Столбец E19;E27
с результатами вычисления функции
n∙pi
= (НОРМРАСП(C32;$D$3;$D$7;1)
– НОРМРАСП(C31;$D$3;$D$7;1))
*100
В
ячейку E28
поместите формулу для вычисления
теоретического (гипотетического) числа
случайных величин, попавших в промежуток
(x10;
∞ ):
P(x10
< x
< ∞) = 1 – P(–
∞ < x
≤ x10)
= 1 – F(x10)
–
вероятность попадания нормально
распределенных случайных величин в
промежуток (x10;
∞).
В
Excel
в строку формул необходимо поместить
формулу:
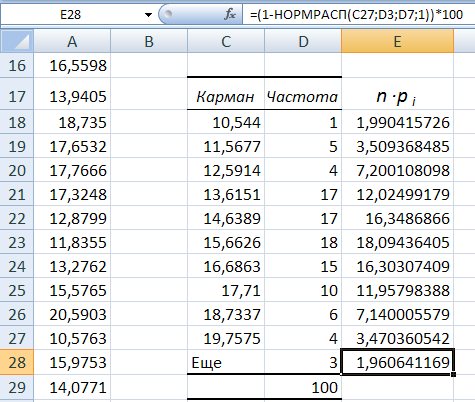
=(1
– НОРМРАСП(C27;D3;D7;1))*100
Для
этого сначала необходимо вызвать функции
НОРМРАСП и заполнить поля ввода
Рис.
13. Диалоговое окно функции НОРМРАСП с
заполненными полями ввода
Рис.
14. Столбец n∙pi
(E18;E28)
содержит результаты вычисления
теоретических значений числа случайных
величин попавших в каждый частичный
интервал (карман) n∙pi
Для
проверки правильности вычислений
просуммируйте числа в ячейках столбца
E18:E28.
В
ячейке Е29
показана сумма содержимого ячеек
Е31:Е40. Она должна быть равна n
=
100.
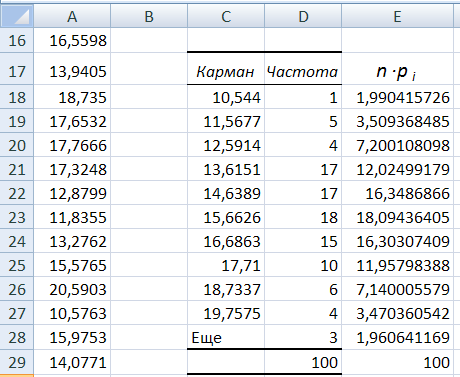
Рис.
15. Таблицы распределения эмпирических
частот mi
– столбец Частота
и теоретических частот npi
– столбец n∙pi
4.2.
В графике Гистограмма
частот добавьте
кривую нормального распределения, как
это вы умеете.
Рис.
16. Графики гистограммы эмпирических
и теоретических частот, позволяющие по
виду графиков выбрать в качестве гипотезы
H0
нормальное распределение.
Для
того чтобы сохранить графики гистограммы
эмпирических и теоретических частот
(рис. 16) необходимо скопировать таблицу
на рис. 15 Карман
– Частота
– n∙pi
в
другое место таблицы.
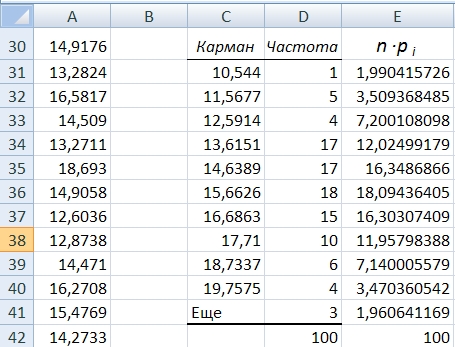
4.3.
Скопируйте таблицу Карман
– Частота –
n∙pi
в свободные
ячейки листа Excel,
для чего, верхний левый угол копии
разместите в ячейке C30,
как показано далее на рис. 8.
Рис.
17. Фрагмент листа Excel
с копией таблицы распределения
эмпирических и теоретических частот
по карманам
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
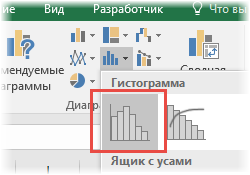
Excel 2016 обзавелся новыми типами графиков. Причем, это не какие-нибудь дизайнерские новшества, а самые настоящие статистические диаграммы.
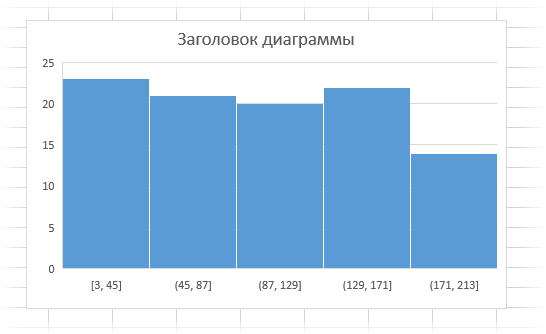
Так, «ящик с усами» применяется для анализа выборки. Диаграмма Парето пригодится при анализе вклада отдельных элементов в общую сумму. В этой заметке рассмотрим еще одну новую диаграмму из Excel 2016 – гистограмму частот.
На первый взгляд и в более ранних версиях Excel можно изобразить частоты с помощью диаграмм. Можно, но для этого предварительно необходимо числовые данные сгруппировать. То есть для каждой категории (интервала, группы, года и т.д.) нужно посчитать частоту. Теперь появилась возможность изобразить распределение данных буквально в один клик без предварительных расчетов и группировок.
Строится такая диаграмма в один клик. Выделяем ряд данных и нажимаем кнопку гистограммы частот.
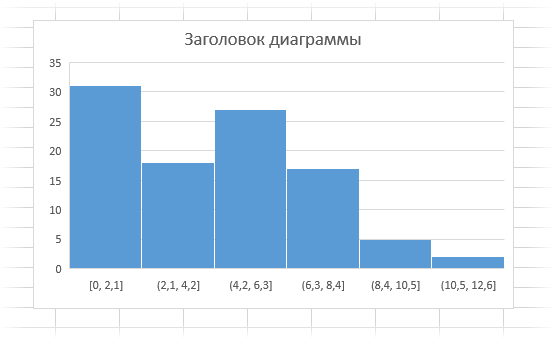
Собственно, все. Тут же появляется соответствующая диаграмма.
Возникает вопрос: как Excel делит данные на интервалы? Справка Excel говорит, что с помощью формулы.
Количество интервалов получается достаточным для того, чтобы визуально прикинуть, каков характер распределения анализируемых данных.
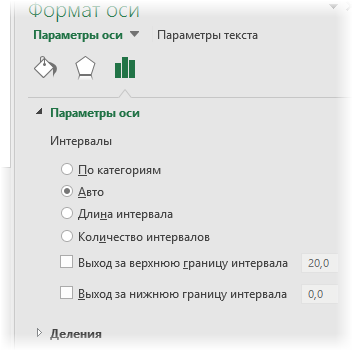
Интервалы легко перестроить под свои потребности. Можно, например, задать нижнюю и верхнюю границу, за пределами которых данные будут объединены в один интервал.
При выборе опции выхода за нижнюю и верхнюю границы, судя по той же справке, их значения рассчитываются, как расстояние ±3σ от средней арифметической.
Однако рассчитываемые автоматически значения легко изменить в окне настроек.
Это был пример, когда данные разбиваются на интервалы. Такой вариант группировки установлен по умолчанию (см. окно параметров настройки оси выше).
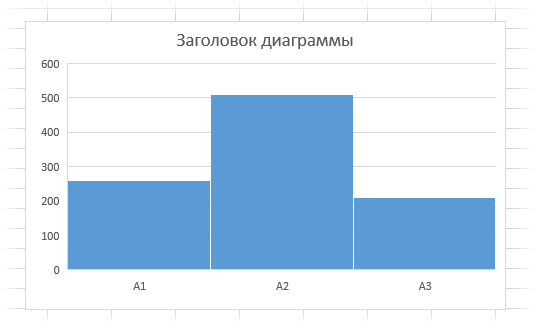
Распределение частот можно получить и по имеющимся категориям (должен быть указан соответствующий столбец). Выбираем в настройках «По категориям» и получаем новые частоты.
Проведем эксперимент. С помощью функции СЛУЧМЕЖДУ смоделируем равномерно распределенную выборку в пределах, скажем, от 0 до 200. Пусть выборка состоит из 100 значений. Теперь изобразим гистограмму частот.
Как видно, частоты примерно одинаковы.
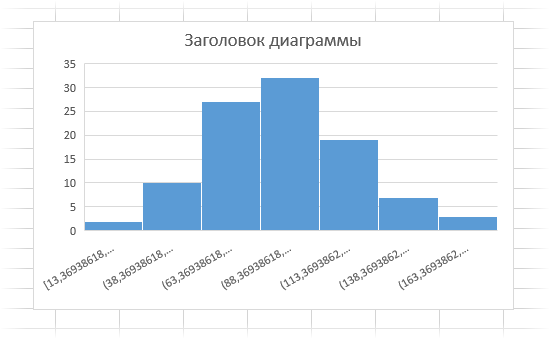
А теперь смоделируем нормальную выборку, со средней 100 и стандартным отклонением 30.
Отчетлива видна характерная конфигурация нормального распределения.
Поделиться в социальных сетях:
Числовые и табличные данные в Excel вычисляются в считанные минуты, если вы знаете, как работать с предустановленными инструментами. Однако всегда визуальное отображение какой-то информации оценивается выше, чем то, что представлено в форме обыкновенной таблицы с расчетами. Именно графическому изображению посвящена наша сегодняшняя статья, а точнее вопросу, как построить гистограмму в Excel.
Общее определение и способы построения гистограммы
Гистограмма — это один из удобных инструментов приложения Excel, при помощи которого вы можете построить индивидуальный график с любым дизайнерским оформлением. Зная принцип действия этой утилиты, пользователю удается передать всю информацию значительно быстрее и понятнее.
Графики данного типа можно построить несколькими разными способами, например:
• при помощи блока «Диаграммы»;
• посредством различного форматирования;
• используя надстройку «Пакет анализа».
Давайте рассмотрим каждый из способов подробнее с пошаговыми фотоинструкциями.
Гистограмма может оформляться как отдельный блок графических данных либо же являться частью ячейки обрабатываемой таблицы.
Применение «Пакета анализа»
Для начала убедитесь в том, что нужная таблица построена и все данные верны, только после этого можно приступать к созданию гистограммы. В противном случае вам необходимо будет редактировать сразу два объекта.
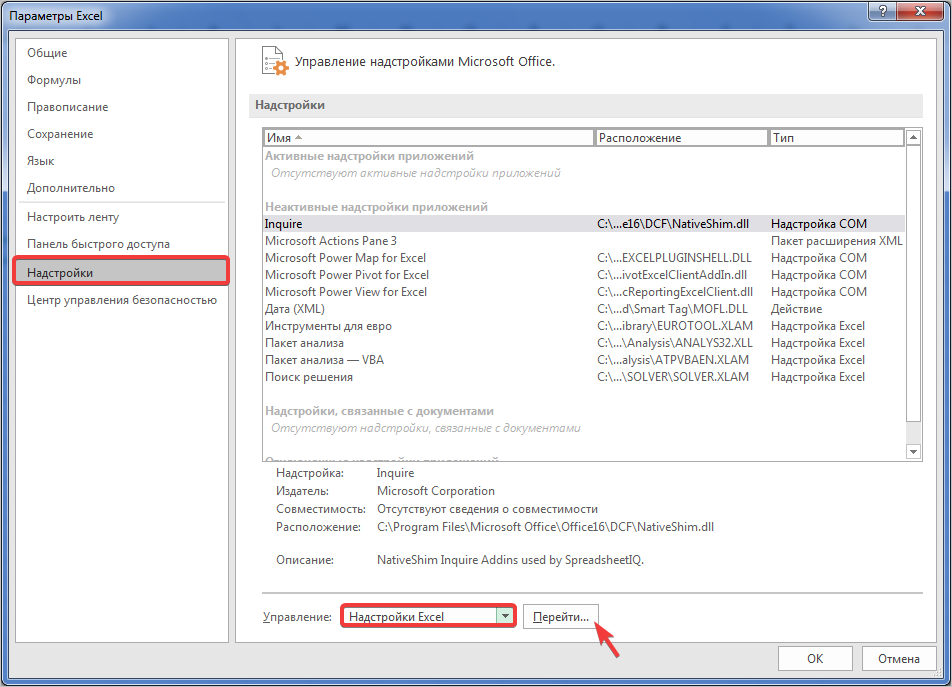
- С «Главной» вкладки переходим на вкладку «Файл». Здесь находим вкладку «Параметры».
- В появившемся окошке находим вкладку «Надстройки» и переходим по ней. Перед вами открывается новая страничка, где нужно указать способ управления «Надстройки Excel», после чего подтвердите выполненное действие нажатием на кнопку «Перейти».
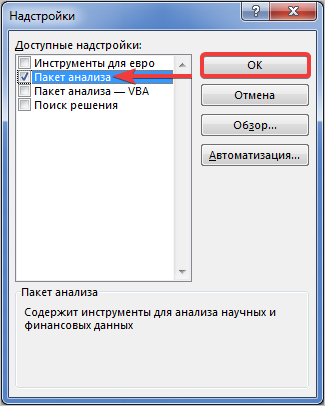
- В новом окне необходимо установить флажок «Пакет анализа» и нажать кнопку «ОК»
- Перемещаемся во вкладку «Данные», где в блоке «Анализ» видим, что появился новый инструмент «Анализ данных». Им и воспользуемся.
- Переходим в инструмент «Анализ данных», где в открывшемся окне отмечаем мышью «Гистограммы» и нажимаем кнопку «ОК».
- Снова открывается окно с меню. Здесь необходимо выбрать место расположения будущей гистограммы. Чтобы не портить внешний вид таблицы и не делать ее нагроможденной для построения графика, установим гистограмму на новом рабочем листе. Для этого отметим флажки на полях «Новый рабочий лист» и «Вывод графика». А также впишем в поле «Входной интервал» адрес ячеек или их диапазон.
- Откроется новый лист в программе Excel, где и будет построена наша гистограмма. Обратите внимание, что она устанавливается с автоматической таблицей, в которой отмечаются числовые данные.
Таким образом мы можем видеть сводные графические данные по таблице, в нашем случае это матчи по футболу российской сборной.
Условное форматирование и построение гистограмм
Также вы можете построить гистограмму непосредственно в ячейках, которые соответствуют таблице. В данном случае информация будет восприниматься проще, одновременно в числовом и графическом эквиваленте. Давайте рассмотрим пошаговый алгоритм создания такой гистограммы
- У нас уже есть таблица с данными, заходим на вкладку «Главная» и ищем блок «Стили». Здесь кликаем на «Условное форматирование». Далее выбираем пункт «Гистограммы», в котором необходимо выбрать обозначение с подходящим стилем.
- Обратите внимание на столбец, к которому была применена функция «Условное форматирование».
Вы можете строить гистограммы автоматически при помощи встроенной утилиты. При этом допускается редактировать и форматировать различным образом графический объект.
Упрощенное построение
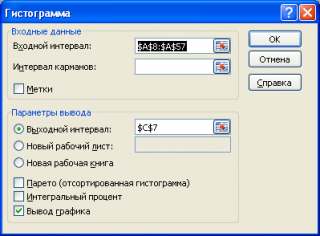
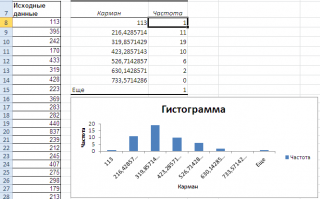
Данный метод предусматривает самое простое создание гистограммы. Вам не нужно затрагивать глубокие настройки, так как необходимый инструмент находится на рабочей панели. Итак, приступим.
- Перейдите во вкладку «Вставка», выделите диапазон ячеек, которые будут участвовать в гистограмме, затем найдите пункт «Вставить гистограмму», после чего подберите необходимый тип.
- После проделанных действий смотрите, что у вас должно получиться.
Сразу после построения гистограмма имеет стандартную заливку цветом, чтобы сделать ее более привлекательной, необходимо использовать инструменты форматирования в «Конструкторе».




























 Для изменения положения выполняем те же самые действия, что и в отношении названия или легенды.
Для изменения положения выполняем те же самые действия, что и в отношении названия или легенды. Появится вспомогательное окно, в котором мы можем настроить:
Появится вспомогательное окно, в котором мы можем настроить:

 Откроется окно, в котором мы можем выполнить соответствующие настройки.
Откроется окно, в котором мы можем выполнить соответствующие настройки.