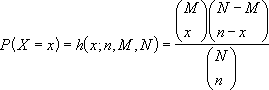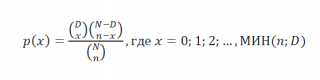Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ГИПЕРГЕОМ.РАСП в Microsoft Excel.
Возвращает гипергеометрическое распределение. Значение, возвращаемое функцией ГИПЕРГЕОМ.РАСП, — это вероятность заданного количества успехов в выборке, если заданы размер выборки, количество успехов в генеральной совокупности и размер генеральной совокупности. Функция ГИПЕРГЕОМ.РАСП используется в задачах с конечной генеральной совокупностью, где каждое наблюдение — успех или неудача, а каждое из подмножеств заданного размера выбирается с равной вероятностью.
Синтаксис
ГИПЕРГЕОМ.РАСП(число_успехов_в_выборке;размер_выборки;число_успехов_в_совокупности;размер_совокупности;интегральная)
Аргументы функции ГИПЕРГЕОМ.РАСП описаны ниже.
-
Число_успехов_в_выборке — обязательный аргумент. Количество успешных испытаний в выборке.
-
Размер_выборки — обязательный аргумент. Размер выборки.
-
Число_успехов_в_совокупности — обязательный аргумент. Количество успешных испытаний в генеральной совокупности.
-
Размер_совокупности — обязательный аргумент. Размер генеральной совокупности.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция ГИПЕРГЕОМ.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.
Замечания
-
Все аргументы усекаются до целых.
-
Если какой-либо из аргументов не является числом, hypGEOM. DIST возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если sample_s < 0 или sample_s больше, чем меньшее из number_sample или population_s, ТО HYPGEOM. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если sample_s меньше, чем большее из 0 или (number_sample — number_population + population_s), HYPGEOM. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если number_sample ≤ 0 или number_sample > number_population, hypgeOM. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если population_s ≤ 0 или population_s > number_population, hypgeOM. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если number_pop ≤ 0, перегиб. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Уравнение для гипергеометрического распределения имеет следующий вид:
где
x — число_успехов_в_выборке
n — размер_выборки
M — число_успехов_в_совокупности
N — размер_совокупности
Функция ГИПЕРГЕОМ.РАСП используется для выборок без замещения из конечной генеральной совокупности.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
Результат |
|
1 |
Число успехов в выборке |
|
|
4 |
Размер выборки |
|
|
8 |
Число успехов в совокупности |
|
|
20 |
Размер совокупности |
|
|
Формула |
Описание (результат) |
|
|
=ГИПЕРГЕОМ.РАСП(A2;A3;A4;A5;ИСТИНА) |
Интегральное гипергеометрическое распределение для выборки и совокупности, приведенных в ячейках с A2 по A5. |
0,4654 |
|
=ГИПЕРГЕОМ.РАСП(A2;A3;A4;A5;ЛОЖЬ) |
Вероятностное гипергеометрическое распределение для выборки, приведенной в ячейках с A2 по A5. |
0,3633 |
Нужна дополнительная помощь?
Рассмотрим Гипергеометрическое распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции
MS
EXCEL
ГИПЕРГЕОМ.РАСП()
построим графики функции распределения и плотности вероятности. Приведем пример аппроксимации гипергеометрического распределения биномиальным.
Определение
. Рассмотрим совокупность, состоящую из
N
элементов. Известно, что элементы в этой совокупности принадлежат разным классам, например, часть элементов зеленого цвета, другая часть – красного, третья – черного и т.д. Нас интересует только определенный класс элементов, например, только зеленые элементы. Известно, что в нашей совокупности содержится
D
элементов
интересующего нас класса (D<=N), т.е. D зеленых элементов.
Пусть из совокупности делается выборка
без возвращения
, состоящая из
n
элементов.
Гипергеометрическое распределение
(англ.
Hypergeometric distribution
) моделирует вероятность получить
x
«удачных» наблюдений в
выборке
. В нашем случае «удачным» наблюдением является наличие в нашей выборке элементов зеленого элемента.
Другими словами,
х
является случайной величиной распределенной по
гипергеометрическому закону
. Плотность
Гипергеометрического распределения
задается следующей формулой:
N — размер всей совокупности, D — число элементов, интересующего нас класса (общее число_успехов_в_совокупности), n — размер_выборки, x — число_успехов_в_выборке.
Примечание
: Запись
означает количество
Сочетаний
из N элементов по n. Для сочетаний также используют эквивалентную запись
. Подробнее о
сочетаниях
см. статью
Сочетания без повторений: Комбинаторика в MS EXCEL
.
Примечание
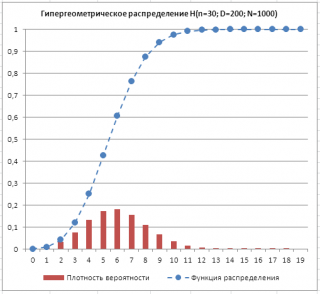
: На
диаграмме
значения
функции распределения
соединены пунктирной линией для наглядности (
функция распределения
определена только для целых х).
Примечание
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Гипергеометрическое распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
Гипергеометрического распределения
имеется функция
ГИПЕРГЕОМ.РАСП()
, английское название — HYPGEOM.DIST(), которая позволяет вычислить не только вероятность того, что в выборке будет
х
нужных нам элементов (
функцию плотности вероятности
), но и
интегральную функцию распределения
(вероятность того, что в выборке будет не меньше
x
нужных нам элементов).
До MS EXCEL 2010 в EXCEL была только функция
ГИПЕРГЕОМЕТ()
, которая позволяла вычислить только плотность вероятности.
ГИПЕРГЕОМЕТ()
оставлена в MS EXCEL 2010 только для совместимости. Для пользователей MS EXCEL 2007 и более ранних – в
файле примера
приведена формула для расчета интегральной функции распределения на основе функции
ГИПЕРГЕОМЕТ()
.
В
файле примера
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Гипергеометрическое распределение
имеет обозначение
H
(
n
;
D
;
N
)
.
Примечание
: Для построения
интегральной функции распределения
идеально подходит диаграмма типа
График
, для
плотности распределения
–
Гистограмма с группировкой
. Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
В
файле примера
приведены различные расчеты вероятности:
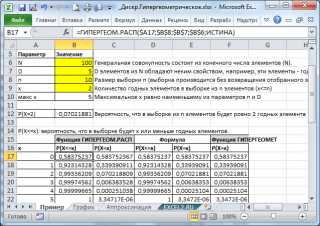
Как видно на картинке выше, для расчета предполагается, что:
-
совокупность, из которой делается выборка, состоит из 100 элементов (N, четвертый аргумент функции
ГИПЕРГЕОМ.РАСП()
). - Всего в этой совокупности содержится 5 элементов интересующего нас класса, например, «годных» элементов (D, третий аргумент функции).
-
Чтобы вычислить вероятность, того что в выборке из 10 элементов (n, второй аргумент функции) будет 2 элемента из интересующего нас класса (первый аргумент функции), нужно записать формулу:
=ГИПЕРГЕОМ.РАСП(2;10;5;100;ЛОЖЬ)
-
Последний, пятый элемент, установлен =ЛОЖЬ, т.е. возвращается значение
функции плотности распределения
.
Если значение пятого аргумента =ИСТИНА, то функция
ГИПЕРГЕОМ.РАСП()
возвращает значение
интегральной функции распределения
или просто
Функцию распределения
. В этом случае можно рассчитать вероятность того, что в выборке количество «годных элементов» будет из определенного диапазона, например, 2 или меньше (включая 0). Для этого нужно записать формулу:
=ГИПЕРГЕОМ.РАСП(2;10;5;100;ИСТИНА)
Примечание
: При нецелом значении х,
дробная часть отбрасывается
. Например, следующие формулы вернут одно и тоже значение:
ГИПЕРГЕОМ.РАСП(
2
;10;5;100;ИСТИНА) = ГИПЕРГЕОМ.РАСП(
2,9
;10;5;100;ИСТИНА)
Чтобы вычислить вероятность того, что в выборке окажется 1, 2 или 3 «годных» элемента нужно записать выражение:
=ГИПЕРГЕОМ.РАСП(3;10;5;100;ИСТИНА)- ГИПЕРГЕОМ.РАСП(0;10;5;100;ИСТИНА)
или
=ГИПЕРГЕОМ.РАСП(1;10;5;100;ЛОЖЬ)+ +ГИПЕРГЕОМ.РАСП(2;10;5;100;ЛОЖЬ)+ +ГИПЕРГЕОМ.РАСП(3;10;5;100;ЛОЖЬ)
Примечание
: В
файле примера
плотность вероятности
и
функция распределения
также вычислены с использованием определения и функции
ЧИСЛКОМБ()
.
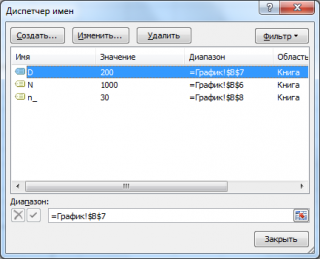
Примечание
: Для удобства написания формул в
файле примера
созданы
Имена
для параметров
Гипергеометрического распределения
: n, D и N.
Показатели распределения
В
файле примера на листе График
имеются формулы для расчета:
-
математического ожидания
=n*D/N,
-
дисперсии (квадрата стандартного отклонения)
=n*D/N*(1-D/N)*((N-n)/(N-1)),
-
моды
=(D+1)*(n+1)/(N+2)
-
коэффициента асимметрии
.
Аппроксимация Биноминальным распределением
В случае, когда размер совокупности N гораздо больше размера выборки n (т.е., N >> n или n/N<<1),
Гипергеометрическое распределение
хорошо аппроксимируется
Биномиальным распределением
с параметрами
n
(количество испытаний) и
p
= D / N (вероятность успеха в одном испытании).
Подробнее об этом приближении и об условиях, при которых допустима аппроксимация других распределений, можно прочитать в статье
Взаимосвязь некоторых распределений в MS EXCEL
.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
17 авг. 2022 г.
читать 2 мин
Гипергеометрическое распределение описывает вероятность выбора k объектов с определенным признаком за n розыгрышей без замены из конечной совокупности размера N , содержащей K объектов с этим признаком.
Если случайная величина X следует гипергеометрическому распределению, то вероятность выбора k объектов с определенным признаком может быть найдена по следующей формуле:
P(X=k) = K C k ( NK C nk ) / N C n
куда:
- N: численность населения
- K: количество объектов в популяции с определенным признаком
- n: размер выборки
- k: количество объектов в выборке с определенным признаком
- K C k : количество комбинаций K вещей, взятых k за раз
Чтобы рассчитать вероятности, связанные с гипергеометрическим распределением в Excel, мы можем использовать следующую формулу:
=HYPGEOM.DIST(sample_s, number_sample, population_s, number_pop, cumulative)
куда:
- sample_s : количество успехов в образце
- number_sample : размер выборки
- населения_с : количество успехов в популяции
- number_pop : численность населения
- cumulative : вычислять ли кумулятивную функцию распределения
Следующие примеры показывают, как использовать эту формулу на практике.
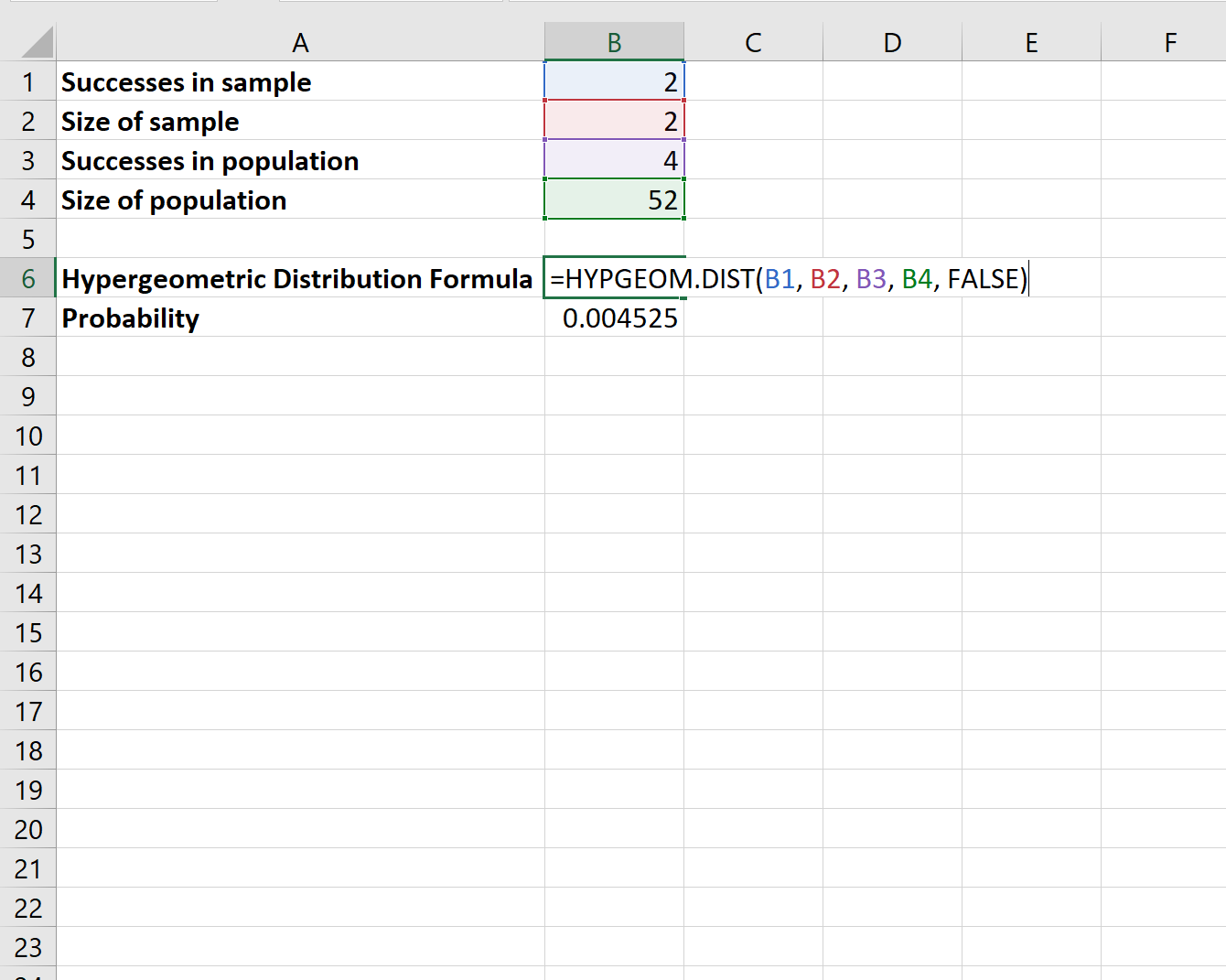
Пример 1: выбор карт из колоды
В стандартной колоде из 52 карт 4 дамы. Предположим, мы случайным образом выбираем карту из колоды, затем, без замены, случайным образом выбираем другую карту из колоды. Какова вероятность того, что обе карты дамы?
Мы можем использовать следующую формулу в Excel, чтобы вычислить вероятность того, что обе карты являются дамами:
Вероятность того, что обе карты дамы, равна.00452 .
Пример 2: Сбор шаров из урны
В урне 3 красных и 5 зеленых шаров. Вы случайным образом выбираете 4 шара. Какова вероятность того, что вы выберете ровно 2 красных шара?
Мы можем использовать следующую формулу в Excel, чтобы найти эту вероятность:
Вероятность того, что вы выберете ровно 2 красных шара, равна.428571 .
Пример 3: выбор шариков из корзины
В корзине 7 фиолетовых и 3 розовых шарика. Вы случайным образом выбираете 6 шариков. Какова вероятность того, что вы выберете ровно 3 розовых шарика?
Мы можем использовать следующую формулу в Excel, чтобы найти эту вероятность:
Вероятность того, что вы выберете ровно 3 розовых шарика, равна.16667 .
Дополнительные ресурсы
Введение в гипергеометрическое распределение
Онлайн-калькулятор гипергеометрического распределения
Наблюдения и советы этой статьи мы подготовили на основании опыта команды ГИПГЕОМ.РАСП Функция возвращает значение гипергеометрического распределения, которое является вероятностью для указанного количества успехов в выборке населения. Гипергеометрическое распределение используется для расчета вероятностей заданного количества успехов в выборке без замены из конечной совокупности.
Синтаксис
=HYPGEOM.DIST (sample_s,number_sample,population_s,number_pop,cumulative)
аргументы
- Sample_s (обязательно): Количество успехов в выборке.
- Number_sample (обязательно): размер выборки.
- Население_с (обязательно): Количество успехов в популяции.
- Number_pop (обязательно): Размер населения.
- Кумулятивный (обязательно): логическое значение, определяющее тип распределения, которое необходимо рассчитать. Это либо ИСТИНА, либо ЛОЖЬ.
Если оно равно TRUE, функция HYPGEOM.DIST возвращает кумулятивную функцию распределения, которая вычисляет вероятность не более чем n успешных попыток из заданного числа испытаний.
Если оно равно FALSE, HYPGEOM.DIST возвращает функцию плотности вероятности, которая вычисляет вероятность ровно n успешных попыток из заданного числа испытаний.
Возвращаемое значение
Наблюдения и советы этой статьи мы подготовили на основании опыта команды ГИПГЕОМ.РАСП функция возвращает числовое значение.
Примечания к функциям
- Функция HYPGEOM.DIST была недавно введена в Excel 2010, поэтому он недоступен в более ранних версиях.
- Наблюдения и советы этой статьи мы подготовили на основании опыта команды #СТОИМОСТЬ! значение ошибки возникает, если какой-либо из предоставленных аргументов не является числовым.
- Наблюдения и советы этой статьи мы подготовили на основании опыта команды #NUM! значение ошибки возникает, если возникает любая из следующих ситуаций:
- Предоставленный sample_s < 0;
- Предоставленный number_sample < 0 или > number_pop;
- Предоставленное население_s < 0 или > число_поп;
- Предоставленное число_поп ≤ 0.
- Zero (0) будет возвращено, когда предоставленное значение sample_s < (number_sample — number_population + pool_s) значение.
- Наблюдения и советы этой статьи мы подготовили на основании опыта команды уравнение для гипергеометрического распределения:
Где x означает sample_s, n означает number_sample, M означает население_s, а N означает number_pop.
Примеры
Пример первый: кумулятивная функция распределения
В данном случае у вас есть мешочек, внутри которого 12 красных и 8 синих шаров. Теперь, если вы залезете в мешок и вытащите из него 6 шаров, какова вероятность получить максимум 3 Голубые шары?
Пожалуйста, скопируйте приведенную ниже формулу в ячейку H5, затем нажмите кнопку Enter ключ для получения результата.
=ГИПГЕОМ.РАСП(B5,C5,D5,E5,F5)
Примечание: мы также можем непосредственный ввод значений в формуле. Формулу в ячейке H5 можно изменить на:
=ГИПГЕОМ.РАСП(3,6,8,20,ИСТИНА)
Пример второй: функция плотности вероятности
Как и в ситуации выше, у вас также есть мешок, внутри которого 12 красных и 8 синих шаров. Теперь, если вы залезете в мешок и вытащите из него 6 шаров, какова вероятность получить точно 3 Голубые шары?
Пожалуйста, скопируйте приведенную ниже формулу в ячейку H6, затем нажмите кнопку Enter ключ для получения результата.
=ГИПГЕОМ.РАСП(B6,C6,D6,E6,F6)
Примечание: мы также можем непосредственный ввод значений в формуле. Формулу в ячейке H6 можно изменить на:
=ГИПГЕОМ.РАСП(3,6,8,20,НЕПРАВДА)
Относительные функции:
-
Excel EVEN Функция
Функция EVEN округляет числа от нуля до ближайшего четного целого числа.
-
Excel EXP Функция
Функция EXP возвращает результат возведения константы e в энную степень.
Лучшие инструменты для работы в офисе
Kutools for Excel — Помогает вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.
- Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.
Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.
Комментарии (0)
Оценок пока нет. Оцените первым!
Функция ГИПЕРГЕОМ.РАСП возвращает гипергеометрическое распределение.
Описание функции ГИПЕРГЕОМ.РАСП
Возвращает гипергеометрическое распределение. Значение, возвращаемое функцией ГИПЕРГЕОМ.РАСП, — это вероятность заданного количества успехов в выборке, если заданы размер выборки, количество успехов в генеральной совокупности и размер генеральной совокупности.
Функция ГИПЕРГЕОМ.РАСП используется в задачах с конечной генеральной совокупностью, где каждое наблюдение — успех или неудача, а каждое из подмножеств заданного размера выбирается с равной вероятностью.
Синтаксис
=ГИПЕРГЕОМ.РАСП(число_успехов_в_выборке; размер_выборки; число_успехов_в_совокупности; размер_совокупности; интегральная)Аргументы
число_успехов_в_выборкеразмер_выборкичисло_успехов_в_совокупностиразмер_совокупностиинтегральная
Обязательный аргумент. Количество успешных испытаний в выборке.
Обязательный аргумент. Размер выборки.
Обязательный аргумент. Количество успешных испытаний в генеральной совокупности.
Обязательный аргумент. Размер генеральной совокупности.
Обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция ГИПЕРГЕОМ.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.
Замечания
- Все аргументы усекаются до целых.
- Если какой-либо из аргументов не является числом, функция ГИПЕРГЕОМ.РАСП возвращает значение ошибки #ЗНАЧ!.
- Если значение аргумента «число_успехов_в_выборке» < 0 или «число_успехов_в_выборке» больше, чем меньшее из значений аргументов «размер_выборки» и «число_успехов_в_совокупности», функция ГИПЕРГЕОМ.РАСП возвращает значение ошибки #ЧИСЛО!.
- Если значение аргумента «число_успехов_в_выборке» меньше, чем большее из значений 0 и («размер_выборки» — «размер_совокупности» + «число_успехов_в_совокупности»), функция HYPGEOM.DIST возвращает значение ошибки #ЧИСЛО!.
- Если значение аргумента «размер_выборки» ≤ 0 или «размер_выборки» > «размер_совокупности», функция ГИПЕРГЕОМ.РАСП возвращает значение ошибки #ЧИСЛО!.
- Если значение аргумента «число_успехов_в_совокупности» ≤ 0 или «число_успехов_в_совокупности» > «размер_совокупности», то функция ГИПЕРГЕОМ.РАСП возвращает значение ошибки #ЧИСЛО!.
- Если значение аргумента «размер_совокупности» ≤ 0, функция ГИПЕРГЕОМ.РАСП возвращает значение ошибки #ЧИСЛО!.
- Уравнение для гипергеометрического распределения имеет следующий вид:
где:- x — число_успехов_в_выборке
- n — размер_выборки
- M — число_успехов_в_совокупности
- N — размер_совокупности
Функция ГИПЕРГЕОМ.РАСП используется для выборок без замещения из конечной генеральной совокупности.