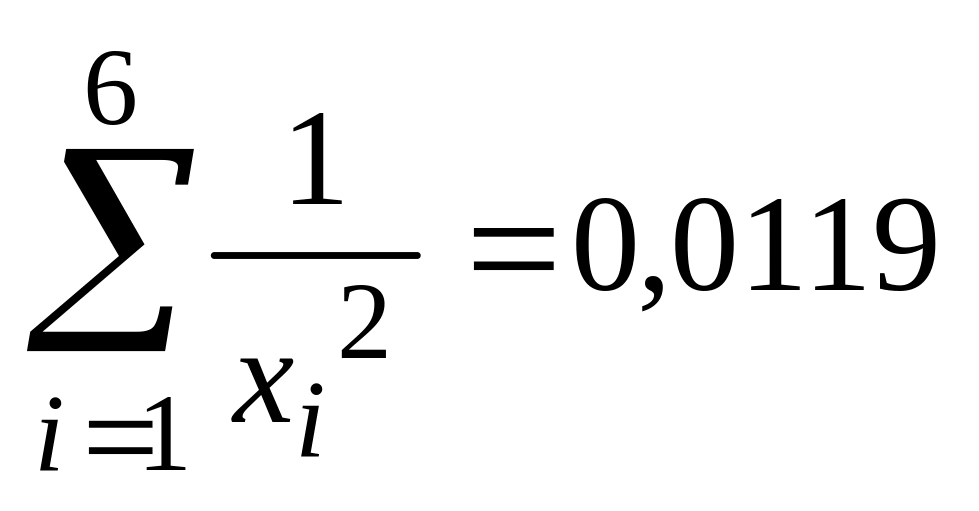Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
лаб стат 4.doc
Скачиваний:
1
Добавлен:
05.05.2019
Размер:
399.87 Кб
Скачать
Самостоятельно
приведите график к следующему виду:
Наблюдения на
экспериментальной животноводческой
ферме показали, что имеется следующая
зависимость между скоростью роста
животных и содержанием белков в
материнском молоке:
|
Животные |
Время удвоения |
Содержание белков |
|
Лошадь |
75 |
2,4 |
|
Корова |
60 |
2,6 |
|
Коза |
43 |
3,3 |
|
Овца |
27 |
4,8 |
|
Мул |
15 |
5,6 |
|
Свинья |
14 |
7,5 |
Найти уравнение
гиперболической зависимости между
скоростью роста животных и содержанием
белков в материнском молоке и построить
график этой зависимости и эмпирических
точек.
Для выполнения
этого задания проделайте следующие
пункты.
-
Перейдите
на следующий рабочий лист. -
Поскольку
в Excel
нет возможности быстрого построения
с помощью стандартных процедур линии
гиперболической регрессии, то для
нахождения ее коэффициентов придется
использовать формулы (4.16-4.17). Содержащиеся
в этих формулах суммы удобнее всего
вычислить с помощью вспомогательной
расчетной таблицы. -
Наберите
в заголовки столбцов расчетной таблицы:
в ячейку А1 –;
в ячейку В1 –;
в ячейку С1 – 1/
;
в ячейку D1
–/
;
в ячейку Е1 –
. -
В
интервал ячеек А2:А7 наберите данные о
времени удвоения массы новорожденных;
а в интервал ячеек В2:В7 наберите данные
о содержании белков в молоке матерей. -
В
ячейку С2 наберите формулу: =1/А2 и
распространите ее с помощью Маркера
заполнения на интервал
ячеек С2:С7. -
В
ячейку D2
наберите формулу: =В2*С2 (или =В2/А2, что
тоже самое) и распространите ее на
интервал ячеек D2:D7
с помощью Маркера
заполнения. -
В
ячейку Е2 наберите формулу: =С2^2 (или
1/A2^2,
что тоже самое) и распространите ее с
помощью Маркера
заполнения на интервал
ячеек Е2:Е7. -
Выделите
ячейку А8 и нажмите на кнопку Автосумма
на панели инструментов. Тогда в этой
ячейке появится сумма чисел диапазона
А2:А7, т.е.
. -
Распространите
полученную формулу Маркером
заполнения на ячейки
диапазона А8:Е8. Тогда:
-
в
ячейке В8 будет сумма
; -
в
ячейке С8 —
; -
в
ячейке D8
—
; -
в
ячейке Е8 —
.
Поскольку
именно эти суммы входят в формулы
(4.17), то по ним легко найти величины Dа
и Db.
Для этого в ячейку А9 наберите: D
=; в ячейку А10 наберите:
«Dа=»;
в ячейку А11: «Db=».
(Греческую заглавную букву D
— «дельта» можно
набрать, если выбрать шрифт Symbol
и нажать одновременно клавиши Shift
и D.)
Теперь
в ячейку В9 наберите формулу: =С8^2-6*Е8; в
ячейку В10 наберите формулу: =С8*В8-6*D8;
в ячейку В11 наберите формулу: =С8*D8-В8*Е8.
Теперь
по формулам (4.16) осталось найти
коэффициенты гиперболической регрессии.
Для этого в ячейку С9 наберите: «а=»;
в ячейку С10: «b=».
Оформите содержание этих ячеек курсивом
и выровняйте их по правому краю.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
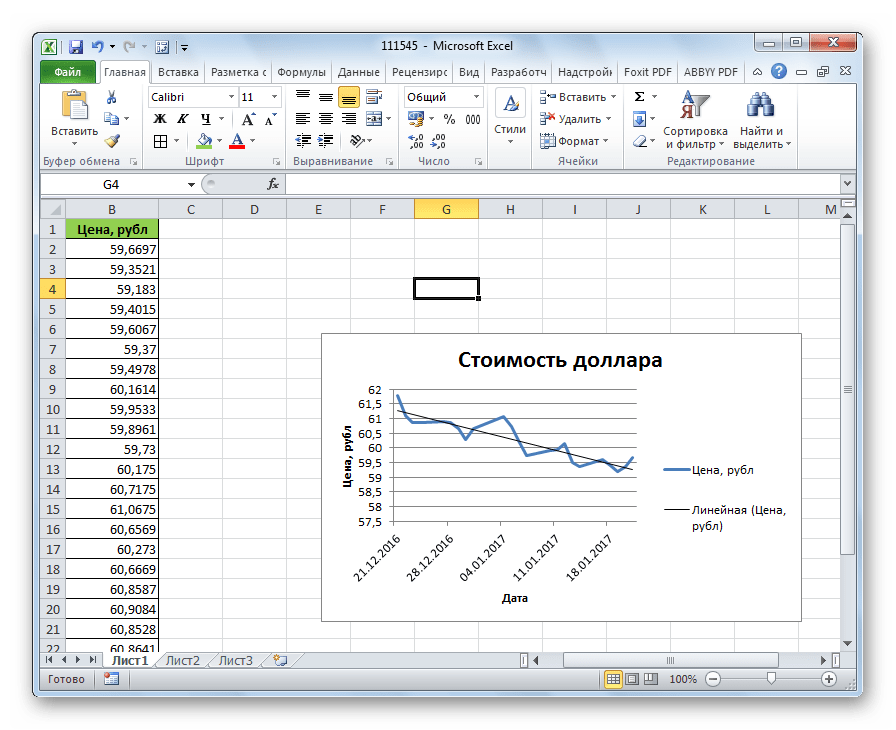
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
A line that bounds a particular chart and shows the behavior as it propagates is known as a trend line. It is generally used for analytics purposes to get a close approximate idea from the chart. The chart can be of any type like Bar Chart, Scattered Chart, Line Chart, etc.
In this article, we are going to see different types of Trendlines in Excel using some practical real-life examples :
Types of Trendlines
1. Linear Trendline : Linear trendlines are mostly used when the data sets are linear in nature. It can be linearly increasing which describes a rise in the data or linearly decreasing which describes a fall in the data. It is of the type :
m : Slope of the line y c : Intercept of the line
Example: The below linear trendline shows the performance of a batsman in a T20 match. The linear trendline is rising with the number of matches played. This shows the player performed well gradually in all the matches and the runs scored kept on increasing.
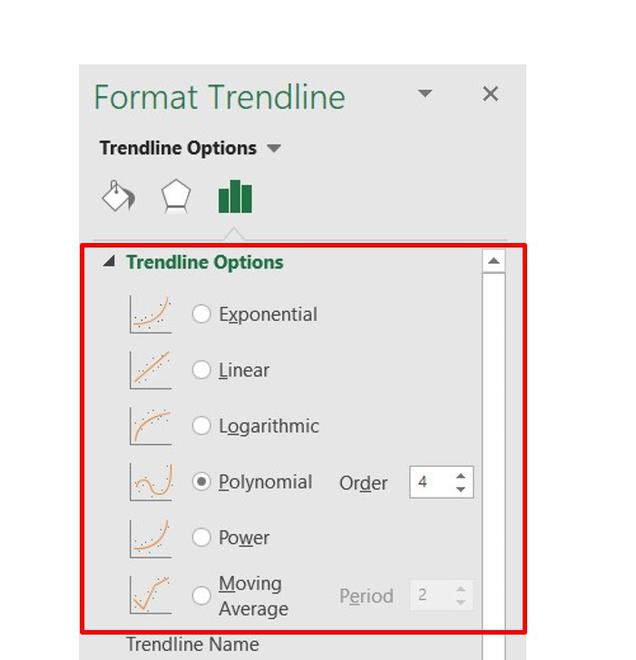
2. Polynomial Trendline: Polynomial trendline is used when the dataset is changing values rapidly i.e. sometimes increasing or decreasing more than once. It is of the type :
The degree of a polynomial is the largest power of x. In the trendline the number of bends is dependent on the degree number. By default, the order will be 2 as we can see in “Order”. The number of bends or hills will increase as you increase the Order value.
Example : The below polynomial trendline shows the performance of a batsman in eight contiguous matches. We can see a rise in the number of runs scored and then reached a peak value and again fallen. So for such types of data sets the polynomial trendline is mostly used.
3. Exponential Trendline: It is mostly used when there is a rise or fall in the dataset exponentially. It is of the type :
Example : Consider a survey which consists of the number of people suffering from a deadly disease. The number of positive cases per month from January to July is the data set here. We can infer from the below chart that the number of cases are exponentially declining till July.
4. Logarithmic Trendline: The best-fit line is mostly used for datasets that either increase or decrease and then maintain a constant level. It is basically the inverse of the exponential trendline. It is of the type :
Example: Consider a survey about the number of people taking vaccines per month. We can see that it is growing and then level off in June and July. We can infer from the below chart that by June maximum people have started to take vaccines.
5. Power Trendline: It is mostly used for datasets that increase at a particular rate, It is more symmetrical and is somewhat similar to the exponential type of curve. It is of the type :
Example: Consider the runs scored by a batsman in ten consecutive test matches. We can infer from the below chart that the performance of the player has increased gradually as he played more matches.
6. Moving Average Trendline : When there are a lot of oscillations i.e. rapid up and down in the values of the datasets, the moving average trendline can be used to make a smooth and effective line around the chart to see the growth and fall of the data. In Excel by default, the Period of the trendline is set to 2. As we increase the value of the Period the line becomes more effective and surrounds the chart. It gets a smooth bend and curves on increasing the Period value.
For example: Consider the performance of a batsman in ten consecutive IPL matches. We can see the performance of the player is not constant and there is rise or fall in the runs scored and also in one of the matches he was out for a duck.
Содержание
- Линия тренда в Excel
- Построение графика
- Создание линии тренда
- Настройка линии тренда
- Прогнозирование
- Вопросы и ответы
Одной из важных составляющих любого анализа является определение основной тенденции событий. Имея эти данные можно составить прогноз дальнейшего развития ситуации. Особенно наглядно это видно на примере линии тренда на графике. Давайте выясним, как в программе Microsoft Excel её можно построить.
Приложение Эксель предоставляет возможность построение линии тренда при помощи графика. При этом, исходные данные для его формирования берутся из заранее подготовленной таблицы.
Построение графика
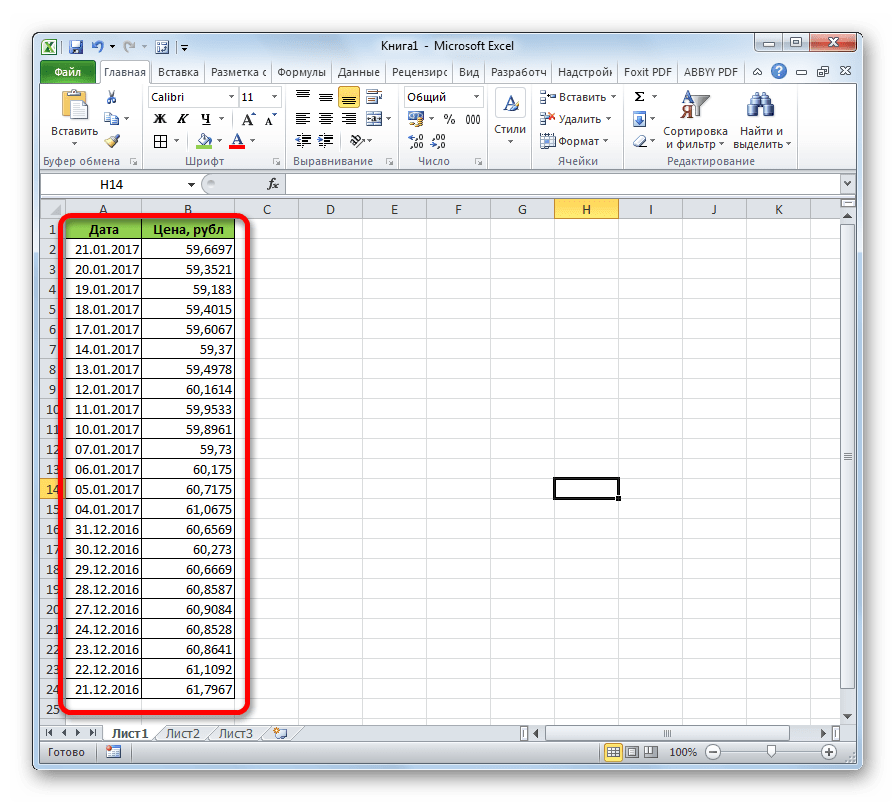
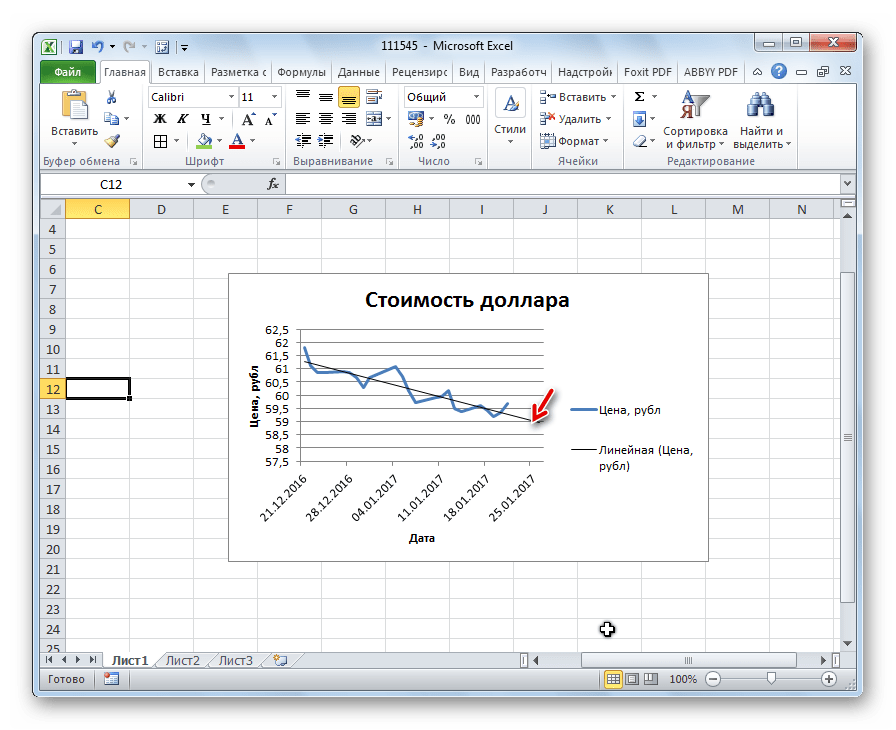
Для того, чтобы построить график, нужно иметь готовую таблицу, на основании которой он будет формироваться. В качестве примера возьмем данные о стоимости доллара в рублях за определенный период времени.
- Строим таблицу, где в одном столбике будут располагаться временные отрезки (в нашем случае даты), а в другом – величина, динамика которой будет отображаться в графике.
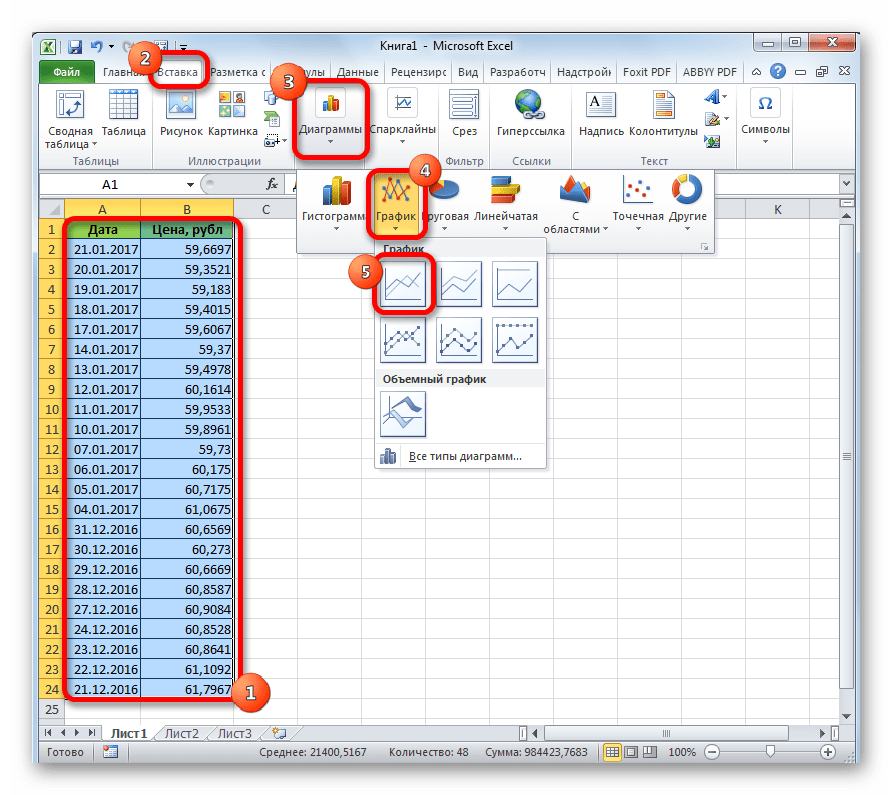
- Выделяем данную таблицу. Переходим во вкладку «Вставка». Там на ленте в блоке инструментов «Диаграммы» кликаем по кнопке «График». Из представленного списка выбираем самый первый вариант.
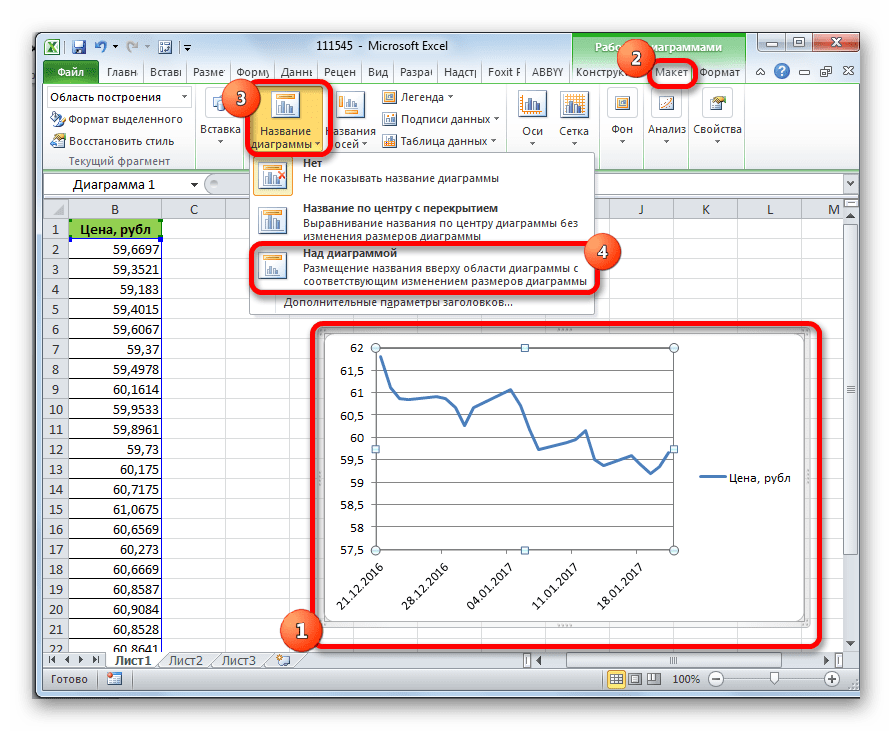
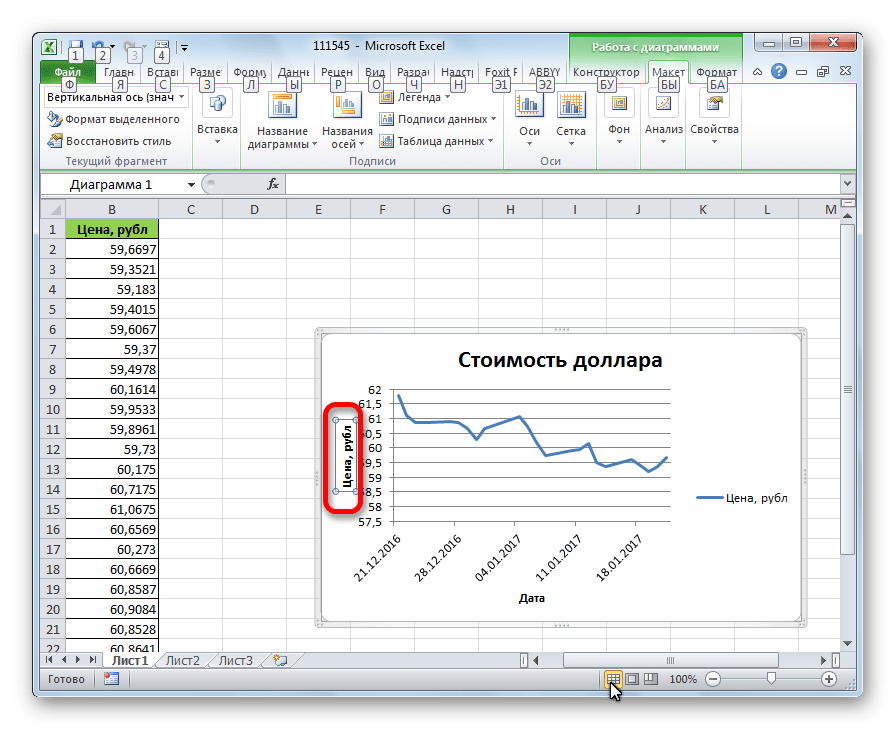
- После этого график будет построен, но его нужно ещё доработать. Делаем заголовок графика. Для этого кликаем по нему. В появившейся группе вкладок «Работа с диаграммами» переходим во вкладку «Макет». В ней кликаем по кнопке «Название диаграммы». В открывшемся списке выбираем пункт «Над диаграммой».
- В появившееся поле над графиком вписываем то название, которое считаем подходящим.
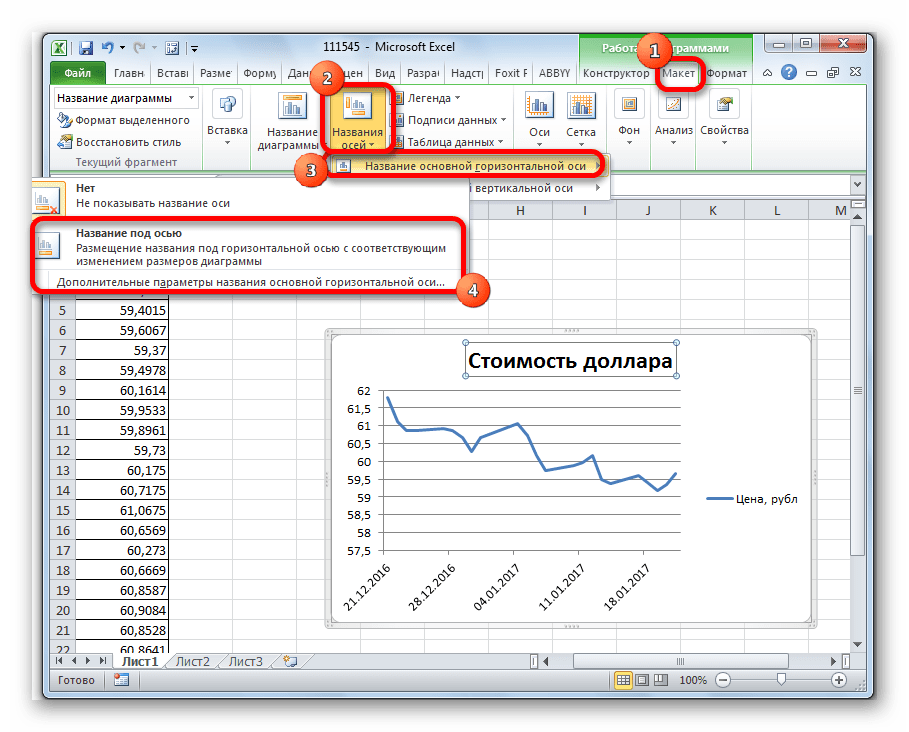
- Затем подписываем оси. В той же вкладке «Макет» кликаем по кнопке на ленте «Названия осей». Последовательно переходим по пунктам «Название основной горизонтальной оси» и «Название под осью».
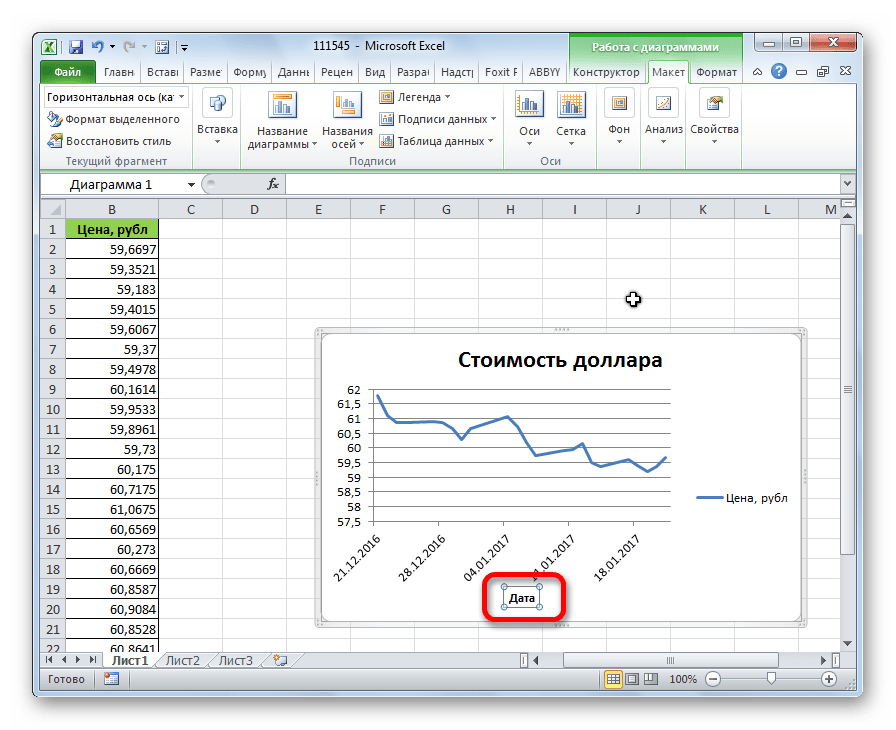
- В появившемся поле вписываем название горизонтальной оси, согласно контексту расположенных на ней данных.
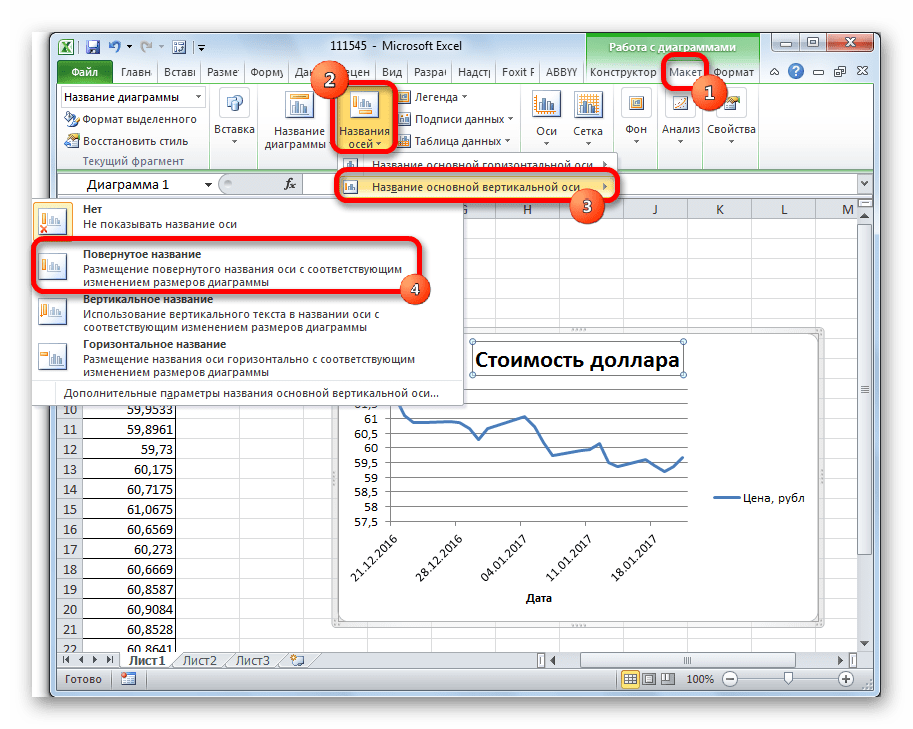
- Для того, чтобы присвоить наименование вертикальной оси также используем вкладку «Макет». Кликаем по кнопке «Название осей». Последовательно перемещаемся по пунктам всплывающего меню «Название основной вертикальной оси» и «Повернутое название». Именно такой тип расположения наименования оси будет наиболее удобен для нашего вида диаграмм.
- В появившемся поле наименования вертикальной оси вписываем нужное название.
Урок: Как сделать график в Excel
Создание линии тренда
Теперь нужно непосредственно добавить линию тренда.
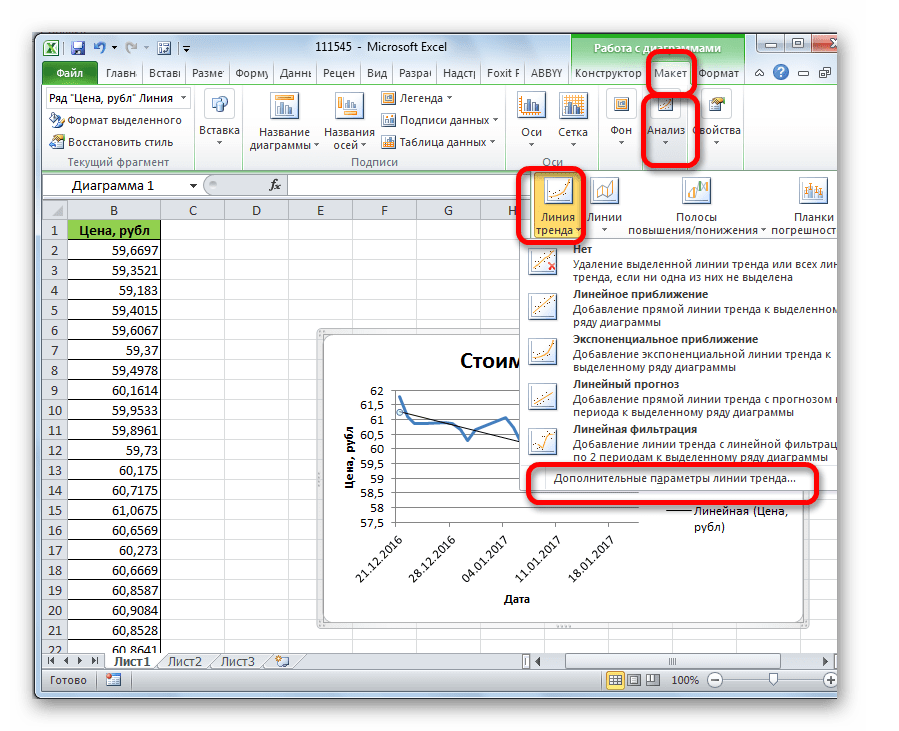
- Находясь во вкладке «Макет» кликаем по кнопке «Линия тренда», которая расположена в блоке инструментов «Анализ». Из открывшегося списка выбираем пункт «Экспоненциальное приближение» или «Линейное приближение».
- После этого, линия тренда добавляется на график. По умолчанию она имеет черный цвет.
Настройка линии тренда
Имеется возможность дополнительной настройки линии.
- Последовательно переходим во вкладке «Макет» по пунктам меню «Анализ», «Линия тренда» и «Дополнительные параметры линии тренда…».
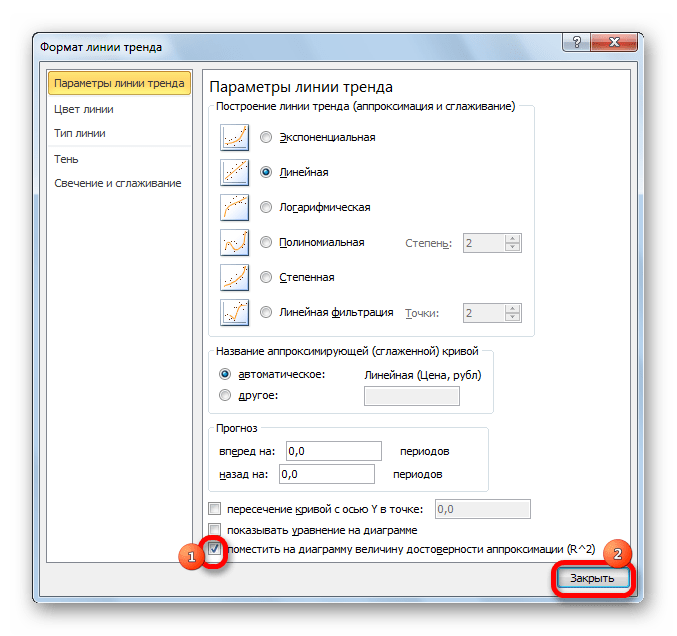
- Открывается окно параметров, можно произвести различные настройки. Например, можно выполнить изменение типа сглаживания и аппроксимации, выбрав один из шести пунктов:
- Полиномиальная;
- Линейная;
- Степенная;
- Логарифмическая;
- Экспоненциальная;
- Линейная фильтрация.
Для того, чтобы определить достоверность нашей модели, устанавливаем галочку около пункта «Поместить на диаграмму величину достоверности аппроксимации». Чтобы посмотреть результат, жмем на кнопку «Закрыть».
Если данный показатель равен 1, то модель максимально достоверна. Чем дальше уровень от единицы, тем меньше достоверность.
Если вас не удовлетворяет уровень достоверности, то можете вернуться опять в параметры и сменить тип сглаживания и аппроксимации. Затем, сформировать коэффициент заново.
Прогнозирование
Главной задачей линии тренда является возможность составить по ней прогноз дальнейшего развития событий.
- Опять переходим в параметры. В блоке настроек «Прогноз» в соответствующих полях указываем насколько периодов вперед или назад нужно продолжить линию тренда для прогнозирования. Жмем на кнопку «Закрыть».
- Опять переходим к графику. В нем видно, что линия удлинена. Теперь по ней можно определить, какой приблизительный показатель прогнозируется на определенную дату при сохранении текущей тенденции.
Как видим, в Эксель не составляет труда построить линию тренда. Программа предоставляет инструменты, чтобы её можно было настроить для максимально корректного отображения показателей. На основании графика можно сделать прогноз на конкретный временной период.
Еще статьи по данной теме:
Помогла ли Вам статья?
Excel для Microsoft 365 Word для Microsoft 365 Outlook для Microsoft 365 PowerPoint для Microsoft 365 Excel для Microsoft 365 для Mac Word для Microsoft 365 для Mac PowerPoint для Microsoft 365 для Mac Excel 2021 Word 2021 Outlook 2021 PowerPoint 2021 Excel 2021 для Mac Word 2021 для Mac PowerPoint 2021 для Mac Excel 2019 Word 2019 Outlook 2019 PowerPoint 2019 Excel 2019 для Mac Word 2019 для Mac PowerPoint 2019 для Mac Excel 2016 Word 2016 Outlook 2016 PowerPoint 2016 Excel 2016 для Mac Word 2016 для Mac PowerPoint 2016 для Mac Excel 2013 Word 2013 Outlook 2013 PowerPoint 2013 Excel 2010 Word 2010 Outlook 2010 PowerPoint 2010 Excel 2007 Excel для Mac 2011 Word для Mac 2011 PowerPoint для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой теме описывается, какие параметры линии тренда доступны в Office.
Используйте линию тренда этого типа для создания прямой линии, которая наилучшим образом описывает простой линейный набор данных. Она применяется в случаях, когда точки данных расположены близко к прямой. Иначе говоря, прямая линия тренда хорошо подходит для величины, которая возрастает или убывает с постоянной скоростью.
Для расчета точек методом наименьших квадратов прямая линия тренда использует следующее уравнение:
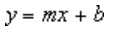
где m — это наклон, а b — смещение.
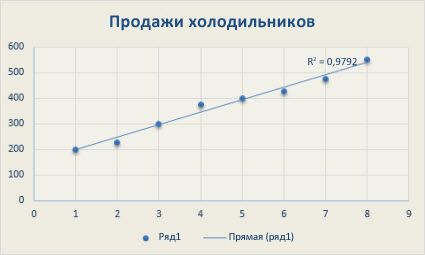
Следующая прямая линия тренда отображает стабильный рост продаж холодильников на протяжении 8 лет. Обратите внимание, что величина достоверности аппроксимации (число от 0 до 1, отображающее степень соответствия ожидаемых значений для линии тренда фактическим данным) равна 0,9792, что свидетельствует о хорошем совпадении расчетной линии с данными.
Отображая оптимизированную кривую, эта линия тренда полезна для описания величины, которая вначале быстро растет или убывает, а затем постепенно стабилизируется. Логарифмическая линия тренда может использовать отрицательные и положительные значения данных.
Для расчета точек методом наименьших квадратов логарифмическая линия тренда использует следующее уравнение:
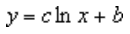
где c и b — константы и ln — функция натурального логарифма.
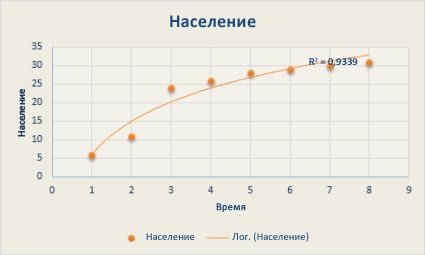
Следующая логарифмическая линия тренда отображает прогнозируемый рост численности населения животных в области с фиксированным пространством, где численность населения была выровнена в результате уменьшения пространства для животных. Обратите внимание, что величина квадрата составляет 0,933, что относительно хорошо подходит для данных.
Эта линия тренда полезна для описания величин, попеременно возрастающих и убывающих. Например, при анализе большого набора данных о нестабильной величине. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Обычно полином второй степени имеет только один экстремум, полином третьей степени — один или два экстремума, а полином четвертой степени — до трех экстремумов.
Для расчета точек методом наименьших квадратов полиномиальная (или криволинейная) линия тренда использует следующее уравнение:
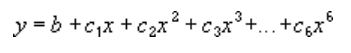
где b и 
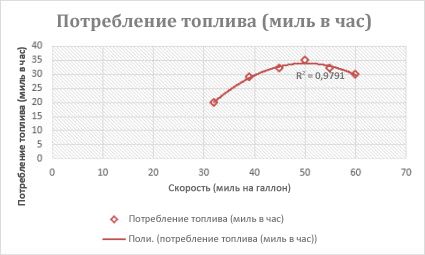
Приведенная ниже полиномиальная линия тренда второй степени (один максимум) отображает зависимость расхода топлива от скорости движения. Близкая к единице величина достоверности аппроксимации (0,979) свидетельствует о хорошем совпадении кривой с данными.
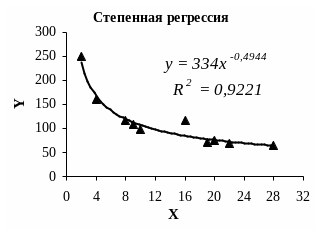
Отображая кривую, эта линия тренда полезна для отображения зависимости, которая содержится в данных, и характеризуется постоянной скоростью роста. Примером такой зависимости может служить ускорение гоночного автомобиля за каждый интервал времени, равный одной секунде. Если в данных имеются нулевые или отрицательные значения, использование степенной линии тренда невозможно.
Для расчета точек методом наименьших квадратов степенная линия тренда использует следующее уравнение:
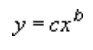
где c и b — константы.
Примечание: При наличии нулевых или отрицательных значений данных этот параметр недоступен.
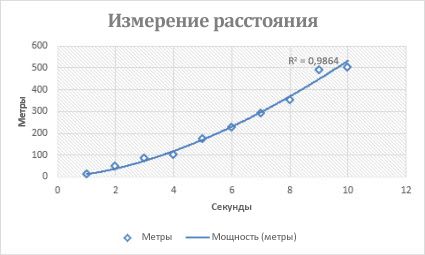
Приведенная ниже диаграмма измерения расстояний отображает зависимость пройденного расстояния от времени. Расстояние выражено в метрах, время — в секундах. Эти данные точно описываются степенной линией тренда, о чем свидетельствует величина достоверности аппроксимации, равная 0,986.
Отображая кривую, эта линия тренда полезна, если скорость изменения данных непрерывно возрастает. Однако для данных, которые содержат нулевые или отрицательные значения, экспоненциальная линия тренда неприменима.
Для расчета точек методом наименьших квадратов экспоненциальная линия тренда использует следующее уравнение:
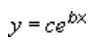
где c и b — константы и e — основание натурального логарифма.
Приведенная ниже экспоненциальная линия тренда отображает содержание радиоактивного углерода-14 в зависимости от возраста органического объекта. Величина достоверности аппроксимации равна 0,990, что означает очень хорошее соответствие кривой данным.
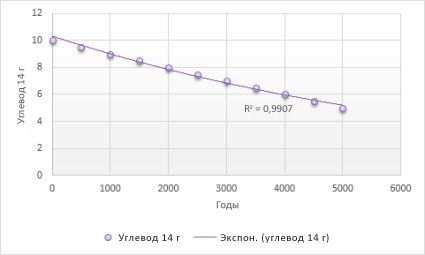
Эта линия тренда позволяет сгладить колебания данных и таким образом более наглядно отображает характер зависимости. Линейный фильтр строится по определенному числу точек данных (задается параметром Точки). Элементы данных усредняются, и полученный результат используется в качестве точки линии тренда. Так, если параметр Точки равен 2, первая точка линии тренда с линейной фильтрацией определяется как среднее значение первых двух элементов данных, вторая точка — как среднее второго и третьего элементов, и так далее.
Линия тренда с линейной фильтрацией использует такое уравнение:
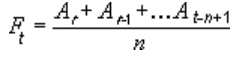
Число точек в линии тренда с скользящее среднее равно общему числу точек ряда за вычетом числа, указанного для параметра «Точки».
В точечной диаграмме линия тренда базируется на порядке расположения значений X в диаграмме. Для получения оптимального результата перед добавлением линейной фильтрации отсортируйте значения X.
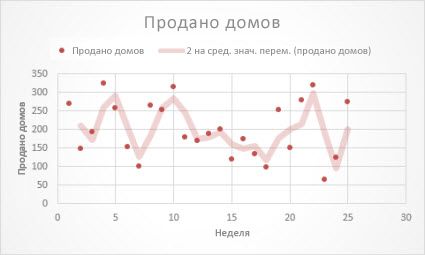
Приведенная ниже линия тренда с линейной фильтрацией отображает тенденцию числа продаж домов на протяжении 26 недель.
Важно: Начиная с Excel 2005 г., Excel скорректировал способ вычисления значенияR2 для линейных линий тренда на диаграммах, где для перехватить линию тренда установлено значение 0 (0). Эта корректировка исправлять вычисления, которые дают неправильные значения R2, и выравнивает вычисление R2 с функцией LINEST. В результате на диаграммах, созданных в предыдущих версиях Excel, могут отображаться разные значения R2. Дополнительные сведения см. в таблице Изменения внутренних вычислений линейных линий тренда на диаграмме.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Добавление линии тренда или скользящего среднего на диаграмму