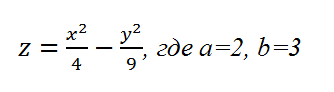Гиперболическая функция в excel - Word и Excel - помощь в работе с программами

17 февраля, 2014 Andrey K

В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.

Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).

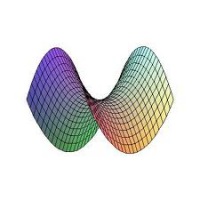
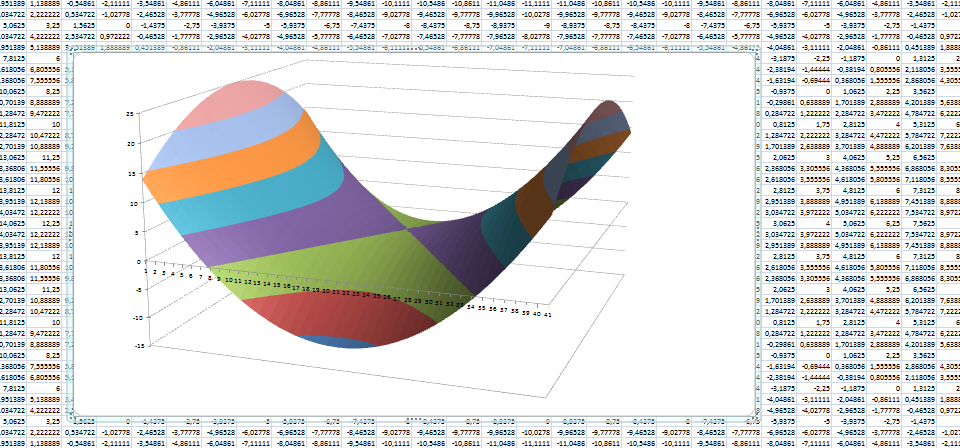
Построим график функции, называемый гиперболический параболоид, в Excel.

Уравнение гиперболического параболоида (общий вид):

где x, y, z — переменные; a, b — константы.

Рассмотрим конкретный случай:

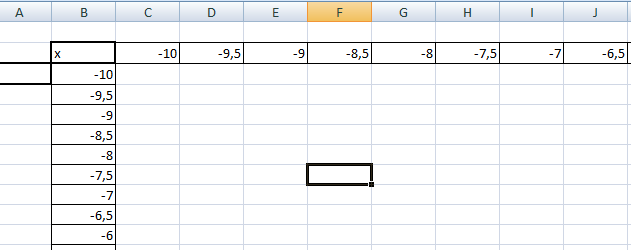
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.

по горизонтали — значения х, по вертикали — значения у.

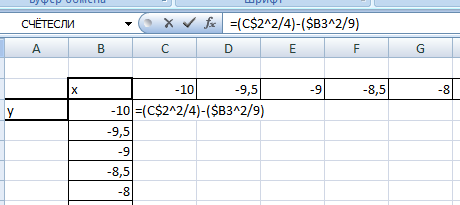
Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.

Для того, чтобы эта формула правильно копировалась с помощью маркера автозаполнения необходимо верно поставить знаки $ в формулу.

=(C$2^2/4)-($B3^2/9) , для ячейки со значением x фиксируем номер строки, для ячейки со значением y фиксируем букву столбца.

Используя маркер автозаполнения, копируем формулу для всех значений x и y.

Получим таблицу, в которой каждой паре (x, y) соответствует координата z.

Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ

Скачать Гиперболический параболоид в Excel

Аналогично строятся другие поверхности:

1) Эллиптический параболоид

2) Однополостный гиперболоид

3) Двухполостный гиперболоид

См. также «Построение графиков функций на плоскости в Excel»

Вы можете оставить комментарий, или ссылку на Ваш сайт.

Оставить комментарий

Источник

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

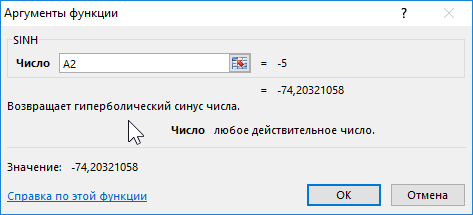
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

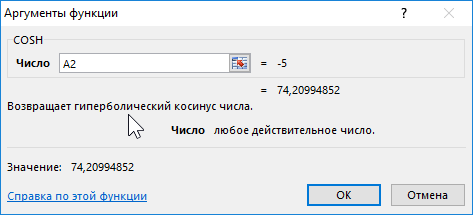
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Примеры использования функций SIN, SINH, COS и COSH в Excel

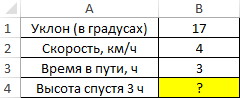
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

Таблица данных:

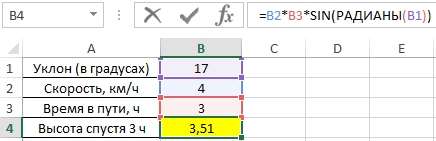
Для решения используем формулу:

=B2*B3*SIN(РАДИАНЫ(B1))

Описание аргументов:

B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

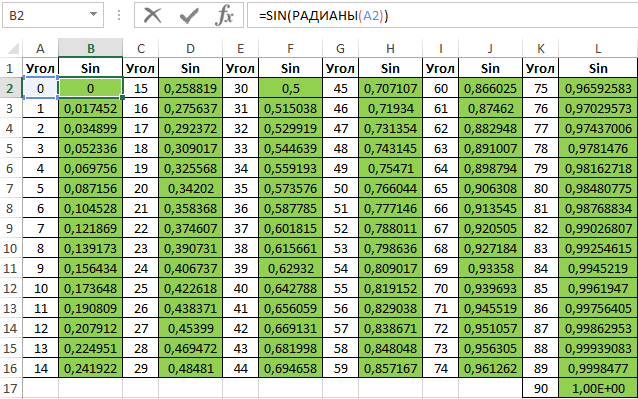
Таблица синусов и косинусов в Excel

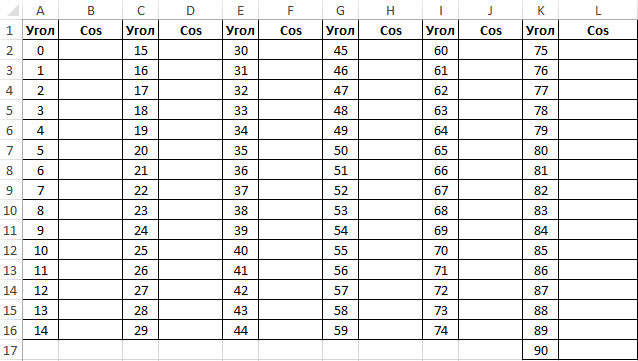
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Заполним столбцы значениями углов в градусах:

Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

=COS(РАДИАНЫ(A2:A16))

Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

Построение графика функций SINH и COSH в Excel

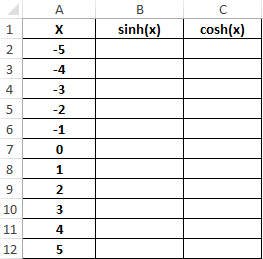
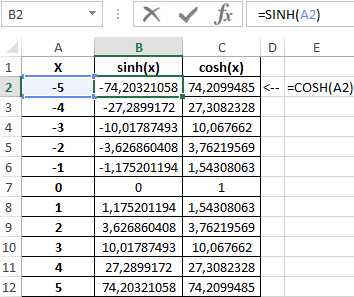
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Исходные данные:

Формула для нахождения синусов гиперболических:

=SINH(A2:A12)

Формула для нахождения косинусов гиперболических:

=COSH(A2:A12)

Таблица полученных значений:

COSH.

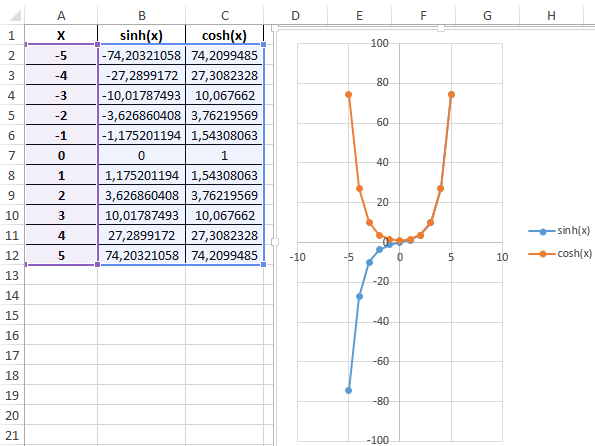
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:

Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

=SIN(число)

Синтаксис функции SINH:

=SINH(число)

Синтаксис функции COS:

=COS(число)

Синтаксис функции COSH:

>=COSH(число)

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

Примечания 1:

Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
Все рассматриваемые функции могут быть использованы в качестве формул массива.

Примечения 2:

Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

Скачать примеры тригонометрических функций SIN и COS

Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
Выражение ПИ()*угол_в_градусах/180.

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции SINH в Microsoft Excel.

Описание

Возвращает гиперболический синус числа.

Синтаксис

SINH(число)

Аргументы функции SINH описаны ниже.

Число — обязательный аргумент. Любое вещественное число.

Замечание

Формула для гиперболического синуса числа имеет следующий вид:

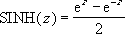
Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=2,868SINH(0,03421,03)	Вероятность получения результата, меньшего, чем 1,03 секунды.	0,1010491

Нужна дополнительная помощь?

Источник

Функция SINH вычисляет гиперболический синус числа.

Синтаксис

=SINH(number)

аргументы

номер (обязательно): Угол в радианах, для которого вы хотите вычислить гиперболический синус.

Возвращаемое значение

Функция SINH возвращает числовое значение.

Примечания к функциям

SINH возвращает #СТОИМОСТЬ! ошибка если номер не числовой.
Формула гиперболического синуса:

Пример

Чтобы вычислить гиперболический синус чисел, перечисленных в таблице, как показано ниже, скопируйте или введите приведенную ниже формулу в верхнюю ячейку (D6) списка результатов и нажмите Enter чтобы получить результат. Затем выберите ячейку результата и перетащите маркер заполнения (маленький квадрат в правом нижнем углу выбранной ячейки) вниз, чтобы применить формулу к ячейкам ниже.

=СИНХ(B6)

Вместо ссылки на ячейку вы можете ввести фактическую номер значение в формуле, как показано ниже.

=СИНХ(-1)

Связанные функции

Функция Excel COTH

Функция COTH возвращает гиперболический котангенс гиперболического угла.

Функция Excel CSCH

Функция CSCH возвращает гиперболический косеканс угла, указанного в радианах.

Функция Excel

Функция TANH вычисляет гиперболический тангенс числа.

Лучшие инструменты для работы в офисе

Kutools for Excel — Помогает вам выделиться из толпы

Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.

Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.

Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)

Одна секунда для переключения между десятками открытых документов!
Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.

Комментарии (0)

Оценок пока нет. Оцените первым!

Источник

Технологическая карта интегрированного урока

Математики и Информатики в 8 классе

Тема урока

Построения графика гиперболической функции в табличном
процессоре Excel.

Цели для ученика

Научиться применять полученные знания и умения работы в электронной таблице
Excel для построения и анализа графиков различных
математических функций

Цели для учителя

Образовательные (математика)

·
обучить учащихся
алгоритму построения графика функции у =f(х+t)+m по известному графику
функции y=f(х).

· обучить учащихся алгоритму построения
графика функции у =kf(х) по известному графику функции y=f(х).

· выбирать аналитическую запись для функции по
виду графика этой функции.

·
Образовательные (информатика).

· отработка умения использования абсолютной и
относительной адресации при решении задач практического характера (нахождение
значения функции)

· формирование навыков работы с электронной
таблицей (построение графиков элементарных математических функций с помощью
электронной таблицы Excel используя мастер диаграмм).

Развивающие

· развитие умений учащихся обобщать полученные
знания, проводить анализ и сравнения, делать необходимые выводы;

· развитие умений грамотно, четко и точно
выражать свои мысли (формулировать ответ или вывод).

· развивать у учащихся познавательный интерес
и информационную компетентность.

Воспитательные

· воспитание аккуратности и внимательности при
выполнении заданий;

·
способствовать овладению
необходимыми навыками самостоятельной учебной деятельности.

Тип урока

Интегрированный урок

Форма урока

Фронтальная с элементами индивидуальной работы на компьютере

Приёмы обучения

·объяснительно-побуждающий,

·инструктивно-практический,

· частично-поисковый,

·фронтальная работа,

·групповая работа.

Методы обучения

·словесные,

·наглядные,

·
практические.

Формы работы

· индивидуальная,

·групповая,

·коллективная.

Формы контроля

·Индивидуальная – учитель проверяет выполнение
заданий на компьютере у каждого ученика

·Фронтальная – ученики отвечают учителю на
поставленные вопросы в процессе фронтального опроса

Математика

Опорные понятия: функция, аргумент, область определения функции, способы
задания функции, координатная плоскость, график функции.

Опорные умения: нахождение значения функции по данным значениям
аргумента, построение графика функции по точкам.

Математика

Новые понятия: сжатие и растяжение графика вдоль осей, «параллельный
перенос» графика.

Новые умения: строить график с помощью алгоритма построения
графика функции у =f(х+t)+m. Определять аналитическую запись для функции по
виду графика этой функции.

Информатика

Опорные понятия: адрес ячейки, относительные и абсолютные ссылки,
формула в ЭТ

Опорные умения: писать формулы в ЭТ с использованием относительных
и абсолютных ссылок, умение копировать формулы методом растяжения

Информатика

Новые понятия: мастер диаграмм, типы диаграмма (точечная
диаграмма), подписи данных

Новые умения: на основе имеющихся данных с помощью мастера
диаграмм строить графики различных функций

Вид используемых на уроке средств ИКТ

·класс, оборудованный ПК,

·мультимедийный проектор,

·экран

Учителя

Темникова Галина Евгеньевна, учитель математики МАОУ лицей № 110

Черноуцан Екатерина Анатольевна, учитель информатики МАОУ лицей №
110

ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА

1
ЭТАП
Организационный момент (1
мин)

УУД :

Регулятивные:

1.Прогнозирование
своей деятельности

Познавательные:

1.Включение в деловой
ритм урока, настрой на учебную деятельность.

Личностные:

1.Осознание
доброжелательных взаимоотношений

2.Умение слушать

Коммуникативные:

1.Планирование
учебного сотрудничества с учителем и со сверстниками.

Деятельность
учителей математики и информатики

1. Учителя приветствуют
и настраивают учащихся на учебно-познавательную деятельность.

3. Учителя проводят
инструктаж по ТБ.

Деятельность обучающихся

1.Приветствуют
учителей.

2.Организуют свое рабочее
место.

2
ЭТАП. Мотивация
учебной деятельности учащихся.

Актуализация и проверка усвоения изученного материала (9 мин)

УУД:

Регулятивные:

1.Принятие учебных
задач, сформулированных вместе с учителем.

2.Применение
полученных знаний на практике

Познавательные:

1.Извлечение необходимой информации из прослушанной

2.Умение анализировать
информацию; делать выводы, структурировать знания, устанавливать логические
связи.

Коммуникативные:

1. Умение слушать,
вступать в диалог

Личностные

1. Повышение
компетентности

Деятельность
учителей математики и информатики

1.Учителя нацеливают
обучающихся на предстоящую работу

2. Учитель математики
разбирает основные теоретические вопросы:

·
Понятие функции,
области определения функции, множества значений функции

·
Способы задания
функции

·
Зависимые и
независимые переменные

·
График гиперболической
функции

·
Свойства гиперболической
функций

3. Учителя предлагают учащимся поставить цели и
задачи урока.

3. Учителя подводят
обучающихся к выводу о применении информационных технологий (программы Excel)
при изучении темы Графики различных функций и формулировке темы урока.

Деятельность обучающихся

1.Настраиваются на
работу

2.Слушают учителя, отвечают
на вопросы

3.Обсуждают и
выдвигают цели и задачи урока

Цели урока

1.Информатика.
Научиться строить графики различных гиперболических функций в ТП Excel. Для
достижение поставленной цели требуется выполнить следующие задачи:

·
задавать данные аргумента
в заданном интервале с заданным шагом

·
писать формулы с
использованием разных типов адресации для нахождения значения функции

·
строить графики с
помощью Мастера диаграмм

2.Математика.
Научиться определять расположение графика гиперболической функции в
зависимости от коэффициентов. Для достижение поставленной цели требуется
выполнить следующие задачи:

·
построить графики
нескольких функций в одной системе координат

·
проанализировать
расположение графиков в зависимости от знаков и значений коэффициентов

3. Делают вывод о
упрощение вычисления значений функций и их визуализация( построение графиков
) с помощью компьютер в программе Excel. Формулируют тему урока. Делают записи в тетради

Тема урока
«Построение графиков различных гиперболической функций с помощью табличного
процессора Excel».

3. ЭТАП. Актуализация знаний. Компьютерный практикум.
(10 мин)

УУД:

Регулятивные:

1.Применение полученных
знаний на практике

2.Работа по плану,
сверяясь с целью

Познавательные:

1.Поиск и выделение
необходимой информации

2.Структурирование
знаний

Коммуникативные:

1.Высказывание своего
мнения

2.Аргументация своего
мнения; учёт разных мнений

Личностные

1.Ориентация в
межличностных отношениях

Деятельность
учителя информатики

1.Предлагает
ученикам сесть за компьютеры и вместе построить график функции на промежутке [-10;10]:

·
Задает
диапазон для аргумента х с шагом 0,5

·
Спрашивает правила
написания формул с помощью относительной и абсолютной адресации

·
Вычисляет значения у(х)

2. Предлагает
ученикам ученика самостоятельно вычислить значения у(х) для остальных функций

Деятельность обучающихся

1.Рассаживаются за
компьютеры и выполнят работу вместе с учителем

2.Самостоятельно вычислить значения у(х)
для остальных функций

4. ЭТАП «Открытие» нового знания. (15 мин)

УУД:

Регулятивные:

1.Принимать участие в решении
учебной задачи

2. Планирование своей деятельности
для решения поставленной задачи, контроль полученного результата, коррекция
полученного результата

Познавательные:

1.Сравнивать объекты по заданным
или самостоятельно определенным критериям

2.Представлять информацию в разных
формах

3.Анализировать информацию; делать
выводы, структурировать знания, устанавливать логические связи.

Коммуникативные:

1. Обмениваться
мнениями; задавать вопросы с целью получения нужной информации, строить
монологические высказывания.

Личностные

1. Повышение
компетентности

Деятельность
учителя информатики

1.Показывает путь
построения графиков с помощью мастера диаграмм:

·
Выбор данных для
построения графика

·
Выбор типа
диаграмм — в нашем случае точечная

·
Задание
подписей данных и рядов

2.Предлагает ученикам
построить графики первых 3-х функций в одной системе координат, следующих 4-х
в другой системе координат

Деятельность
учителя математики

3.Предлагает
проанализировать и сделают выводы о расположении графиков в зависимости от
коэффициентов

4. Предлагает
сформулировать правила движения графиков в зависимости от коэффициентов.

Деятельность обучающихся

1.Слушают учителя,
знакомятся со способом построения графика функции, делают записи в тетради

2.Строят графики по
предложенному плану

3. Анализируют и делают выводы о расположении графиков в зависимости от
коэффициентов для каждого случая

В зависимости от
коэффициентов функции меняется расположение графика и его форма

5 ЭТАП Рефлексия. Подведение
итогов урока. (4 мин)

УУД:

Регулятивные:

1.Проявление открытости
в осмыслении своих действий и самооценки;

2.Прогнозирование
способов саморегуляции и сотрудничества

Познавательные:

1.Оценка промежуточных результатов и саморегуляция для
повышения мотивации учебной деятельности

Коммуникативные:

1. Подведение итогов
совместной и индивидуальной деятельности

Личностные:

1.Личнозначимое
отражение данной темы

2.Смыслообразование
(Какой смысл видит для себя ученик при изучении этой темы)

Деятельность
учителей математики и информатики

1.Просят обучающихся
ответить на следующие вопросы:

·
какие цели, задачи
стояли перед нами в начале урока?

·
смогли ли вы их достичь?

·
какой материал был
трудным, непонятным?

·
что воспринималось легко,
что понравилось?

·
попробуйте дать оценку интеграции
информатики и математики при изучении материала?

·
нужны ли подобные
интегрированные уроки и при изучении каких тем по математики их можно
провести?

Деятельность обучающихся

1.Отвечают на вопросы
учителей, проводят самооценку своей деятельности на уроке, выражают свое
мнение

Цели урока
ставились следующие — научиться строить графики различных гиперболических функций
в ТП Excel и определять расположение графика в зависимости от коэффициентов.

В процессе урока
цели были достигнуты, обучающиеся научились строить графики функций и
определять расположение графиков

Наиболее трудно
было правильно написать формулу для вычисления графика фикции и по
простроенным графикам сделать общий вывод о расположении графика в
зависимости от коэффициентов

Понравилось и было
легко строить график функции с помощью мастера диаграмм

Строить графики в ТП
Excel гораздо быстрее, легче и точнее, чем на бумаге. Можно построить много
графиков для сравнения и анализа

Подобные
интегрированные уроки интересны. Можно их проводить изучая графики и свойства
всех математических функций.

6 ЭТАП Домашнее
задание (1 мин)

УУД:

Регулятивные:

1.Работать по плану,
сверяясь с целью, находить и исправлять ошибки, в т.ч. самостоятельно, используя
ИКТ.

Познавательные:

1.Поиск и выделение
необходимой информации, структурирование знаний, анализ объектов

Коммуникативные:

1. Понимание использования
ИКТ как инструмента для достижения своих целей.

Личностные:

1. Формирование
положительной учебной мотивации

Деятельность
учителей математики и информатики

1. Предлагают построить дома график
функции у=a*x²

Примечания к заданию.

Математика: проанализировать выполненную работу;

Информатика: написать формулу вычисления значения функции в
общем виде

Деятельность обучающихся

1.Записывают домашнее
задание, уточняют особенности его выполнения

Источник