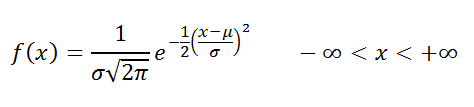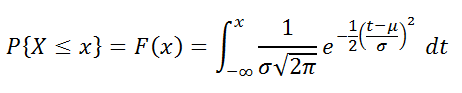Рассмотрим Нормальное распределение. С помощью функции
MS EXCEL
НОРМ.РАСП()
построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по нормальному закону, произведем оценку параметров распределения, среднего значения и стандартного отклонения
.
Нормальное распределение
(также называется распределением Гаусса) является самым важным как в теории, так в приложениях системы контроля качества. Важность значения
Нормального распределения
(англ.
Normal
distribution
)
во многих областях науки вытекает из
Центральной предельной теоремы
теории вероятностей.
Определение
: Случайная величина
x
распределена по
нормальному закону
, если она имеет
плотность распределения
:
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Нормальное распределение
зависит от двух параметров: μ
(мю)
— является
математическим ожиданием (средним значением случайной величины)
, и σ (
сигма)
— является
стандартным отклонением
(среднеквадратичным отклонением). Параметр μ определяет положение центра
плотности вероятности
нормального распределения
, а σ — разброс относительно центра (среднего).
Примечание
: О влиянии параметров μ и σ на форму распределения изложено в статье про
Гауссову кривую
, а в
файле примера на листе Влияние параметров
можно с помощью
элементов управления Счетчик
понаблюдать за изменением формы кривой.
Нормальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
Нормального распределения
имеется функция
НОРМ.РАСП()
, английское название — NORM.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина X, распределенная по
нормальному закону
, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Вышеуказанное распределение имеет обозначение
N
(μ; σ).
Так же часто используют обозначение через
дисперсию
N
(μ; σ
2
).
Примечание
: До MS EXCEL 2010 в EXCEL была только функция
НОРМРАСП()
, которая также позволяет вычислить функцию распределения и плотность вероятности.
НОРМРАСП()
оставлена в MS EXCEL 2010 для совместимости.
Стандартное нормальное распределение
Стандартным нормальным распределением
называется
нормальное распределение
с
математическим ожиданием
μ=0 и
дисперсией
σ=1. Вышеуказанное распределение имеет обозначение
N
(0;1).
Примечание
: В литературе для случайной величины, распределенной по
стандартному
нормальному закону,
закреплено специальное обозначение z.
Любое
нормальное распределение
можно преобразовать в стандартное через замену переменной
z
=(
x
-μ)/σ
. Этот процесс преобразования называется
стандартизацией
.
Примечание
: В MS EXCEL имеется функция
НОРМАЛИЗАЦИЯ()
, которая выполняет вышеуказанное преобразование. Хотя в MS EXCEL это преобразование называется почему-то
нормализацией
. Формулы
=(x-μ)/σ
и
=НОРМАЛИЗАЦИЯ(х;μ;σ)
вернут одинаковый результат.
В MS EXCEL 2010 для
стандартного нормального распределения
имеется специальная функция
НОРМ.СТ.РАСП()
и ее устаревший вариант
НОРМСТРАСП()
, выполняющий аналогичные вычисления.
Продемонстрируем, как в MS EXCEL осуществляется процесс стандартизации
нормального распределения
N
(1,5; 2).
Для этого вычислим вероятность, что случайная величина, распределенная по
нормальному закону
N(1,5; 2)
, меньше или равна 2,5. Формула выглядит так:
=НОРМ.РАСП(2,5; 1,5; 2; ИСТИНА)
=0,691462. Сделав замену переменной
z
=(2,5-1,5)/2=0,5
, запишем формулу для вычисления
Стандартного нормального распределения:
=НОРМ.СТ.РАСП(0,5; ИСТИНА)
=0,691462.
Естественно, обе формулы дают одинаковые результаты (см.
файл примера лист Пример
).
Обратите внимание, что
стандартизация
относится только к
интегральной функции распределения
(аргумент
интегральная
равен ИСТИНА), а не к
плотности вероятности
.
Примечание
: В литературе для функции, вычисляющей вероятности случайной величины, распределенной по
стандартному
нормальному закону,
закреплено специальное обозначение Ф(z). В MS EXCEL эта функция вычисляется по формуле
=НОРМ.СТ.РАСП(z;ИСТИНА)
. Вычисления производятся по формуле
В силу четности функции
плотности стандартного нормального
распределения f(x), а именно f(x)=f(-х), функция
стандартного нормального распределения
обладает свойством Ф(-x)=1-Ф(x).
Обратные функции
Функция
НОРМ.СТ.РАСП(x;ИСТИНА)
вычисляет вероятность P, что случайная величина Х примет значение меньше или равное х. Но часто требуется провести обратное вычисление: зная вероятность P, требуется вычислить значение х. Вычисленное значение х называется
квантилем
стандартного
нормального распределения
.
В MS EXCEL для вычисления
квантилей
используют функцию
НОРМ.СТ.ОБР()
и
НОРМ.ОБР()
.
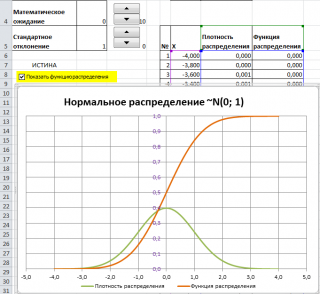
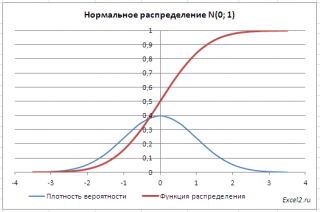
Графики функций
В
файле примера
приведены
графики плотности распределения
вероятности и
интегральной функции распределения
.
Как известно, около 68% значений, выбранных из совокупности, имеющей
нормальное распределение
, находятся в пределах 1 стандартного отклонения (σ) от μ(среднего или математического ожидания); около 95% — в пределах 2-х σ, а в пределах 3-х σ находятся уже 99% значений. Убедиться в этом для
стандартного нормального распределения
можно записав формулу:
=
НОРМ.СТ.РАСП(1;ИСТИНА)-НОРМ.СТ.РАСП(-1;ИСТИНА)
которая вернет значение 68,2689% — именно такой процент значений находятся в пределах +/-1 стандартного отклонения от
среднего
(см.
лист График в файле примера
).
В силу четности функции
плотности стандартного нормального
распределения:
f
(
x
)=
f
(-х)
, функция
стандартного нормального распределения
обладает свойством F(-x)=1-F(x). Поэтому, вышеуказанную формулу можно упростить:
=
2*НОРМ.СТ.РАСП(1;ИСТИНА)-1
Для произвольной
функции нормального распределения
N(μ; σ) аналогичные вычисления нужно производить по формуле:
=2* НОРМ.РАСП(μ+1*σ;μ;σ;ИСТИНА)-1
Вышеуказанные расчеты вероятности требуются для
построения доверительных интервалов
.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении
диаграмм
читайте статью
Основные типы диаграмм
.
Примечание
: Для удобства написания формул в
файле примера
созданы
Имена
для параметров распределения: μ и σ.
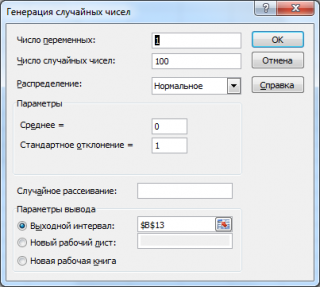
Генерация случайных чисел
С помощью надстройки
Пакет анализа
можно сгенерировать случайные числа, распределенные по
нормальному закону
.
СОВЕТ
: О надстройке
Пакет анализа
можно прочитать в статье
Надстройка Пакет анализа MS EXCEL
.
Сгенерируем 3 массива по 100 чисел с различными μ и σ. Для этого в окне
Генерация
случайных чисел
установим следующие значения для каждой пары параметров:
Примечание
: Если установить опцию
Случайное рассеивание
(
Random Seed
), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию равной 25, можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции
Случайное рассеивание
может запутать. Лучше было бы ее перевести как
Номер набора со случайными числами
.
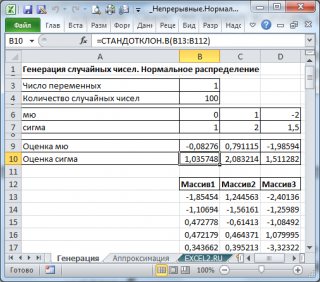
В итоге будем иметь 3 столбца чисел, на основании которых можно, оценить параметры распределения, из которого была произведена выборка: μ и σ
.
Оценку для μ можно сделать с использованием функции
СРЗНАЧ()
, а для σ – с использованием функции
СТАНДОТКЛОН.В()
, см.
файл примера лист Генерация
.
Примечание
: Для генерирования массива чисел, распределенных по
нормальному закону
, можно использовать формулу
=НОРМ.ОБР(СЛЧИС();μ;σ)
. Функция
СЛЧИС()
генерирует
непрерывное равномерное распределение
от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.
файл примера лист Генерация
).
Задачи
Задача1
. Компания изготавливает нейлоновые нити со средней прочностью 41 МПа и стандартным отклонением 2 МПа. Потребитель хочет приобрести нити с прочностью не менее 36 МПа. Рассчитайте вероятность, что партии нити, изготовленные компанией для потребителя, будут соответствовать требованиям или превышать их.
Решение1
: =
1-НОРМ.РАСП(36;41;2;ИСТИНА)
Задача2
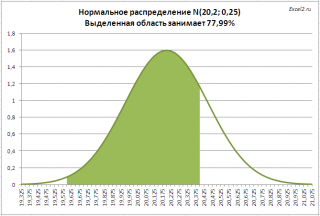
. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Согласно техническим условиям, трубы признаются годными, если диаметр находится в пределах 20,00+/- 0,40 мм. Какая доля изготовленных труб соответствует ТУ?
Решение2
: =
НОРМ.РАСП(20,00+0,40;20,20;0,25;ИСТИНА)- НОРМ.РАСП(20,00-0,40;20,20;0,25)
На рисунке ниже, выделена область значений диаметров, которая удовлетворяет требованиям спецификации.
Решение приведено в
файле примера лист Задачи
.
Задача3
. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Внешний диаметр не должен превышать определенное значение (предполагается, что нижняя граница не важна). Какую верхнюю границу в технических условиях необходимо установить, чтобы ей соответствовало 97,5% всех изготавливаемых изделий?
Решение3
: =
НОРМ.ОБР(0,975; 20,20; 0,25)
=20,6899 или =
НОРМ.СТ.ОБР(0,975)*0,25+20,2
(произведена «дестандартизация», см. выше)
Задача 4
. Нахождение параметров
нормального распределения
по значениям 2-х
квантилей
(или
процентилей
). Предположим, известно, что случайная величина имеет нормальное распределение, но не известны его параметры, а только 2-я
процентиля
(например, 0,5-
процентиль
, т.е. медиана и 0,95-я
процентиль
). Т.к. известна
медиана
, то мы знаем
среднее
, т.е. μ. Чтобы найти
стандартное отклонение
нужно использовать
Поиск решения
. Решение приведено в
файле примера лист Задачи
.
Примечание
: До MS EXCEL 2010 в EXCEL были функции
НОРМОБР()
и
НОРМСТОБР()
, которые эквивалентны
НОРМ.ОБР()
и
НОРМ.СТ.ОБР()
.
НОРМОБР()
и
НОРМСТОБР()
оставлены в MS EXCEL 2010 и выше только для совместимости.
Линейные комбинации нормально распределенных случайных величин
Известно, что линейная комбинация нормально распределённых случайных величин
x
(
i
)
с параметрами μ
(
i
)
и σ
(
i
)
также распределена нормально. Например, если случайная величина Y=x(1)+x(2), то Y будет иметь распределение с параметрами μ
(1)+ μ(2)
и
КОРЕНЬ(σ(1)^2+ σ(2)^2).
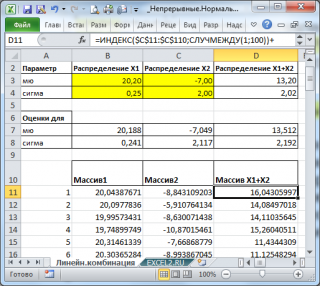
Убедимся в этом с помощью MS EXCEL.
С помощью надстройки
Пакет анализа
сгенерируем 2 массива по 100 чисел с различными μ и σ.
Теперь сформируем массив, каждый элемент которого является суммой 2-х значений, взятых из каждого массива.
С помощью функций
СРЗНАЧ()
и
СТАНДОТКЛОН.В()
вычислим
среднее
и
дисперсию
получившейся
выборки
и сравним их с расчетными.
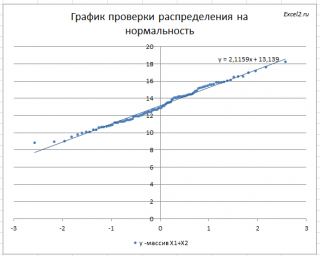
Кроме того, построим
График проверки распределения на нормальность
(
Normal
Probability
Plot
), чтобы убедиться, что наш массив соответствует выборке из
нормального распределения
.
Прямая линия, аппроксимирующая полученный график, имеет уравнение y=ax+b. Наклон кривой (параметр а) может служить оценкой
стандартного отклонения
, а пересечение с осью y (параметр b) –
среднего
значения.
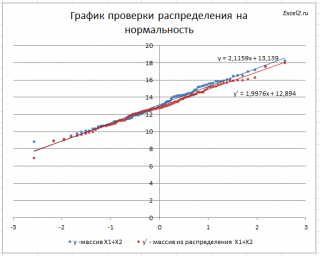
Для сравнения сгенерируем массив напрямую из распределения
N
(μ(1)+ μ(2); КОРЕНЬ(σ(1)^2+ σ(2)^2)
).
Как видно на рисунке ниже, обе аппроксимирующие кривые достаточно близки.
В качестве примера можно провести следующую задачу.
Задача
. Завод изготавливает болты и гайки, которые упаковываются в ящики парами. Пусть известно, что вес каждого из изделий является нормальной случайной величиной. Для болтов средний вес составляет 50г, стандартное отклонение 1,5г, а для гаек 20г и 1,2г. В ящик фасуется 100 пар болтов и гаек. Вычислить какой процент ящиков будет тяжелее 7,2 кг.
Решение
. Сначала переформулируем вопрос задачи: Вычислить какой процент пар болт-гайка будет тяжелее 7,2кг/100=72г. Учитывая, что вес пары представляет собой случайную величину = Вес(болта) + Вес(гайки) со средним весом (50+20)г, и
стандартным отклонением
=КОРЕНЬ(СУММКВ(1,5;1,2))
, запишем решение =
1-НОРМ.РАСП(72; 50+20; КОРЕНЬ(СУММКВ(1,5;1,2));ИСТИНА)
Ответ
: 15% (см.
файл примера лист Линейн.комбинация
)
Аппроксимация Биномиального распределения Нормальным распределением
Если параметры
Биномиального распределения
B(n;p) находятся в пределах 0,1<=p<=0,9 и n*p>10, то
Биномиальное распределение
можно аппроксимировать
Нормальным распределением
.
При значениях
λ
>15
,
Распределение Пуассона
хорошо аппроксимируется
Нормальным распределением
с параметрами: μ
=λ
, σ
2
=
λ
.
Подробнее о связи этих распределений, можно прочитать в статье
Взаимосвязь некоторых распределений друг с другом в MS EXCEL
. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
У нас есть последовательность чисел, состоящая из практически независимых элементов, которые подчиняются заданному распределению. Как правило, равномерному распределению.
Сгенерировать случайные числа в Excel можно разными путями и способами. Рассмотрим только лучше из них.
Функция случайного числа в Excel
- Функция СЛЧИС возвращает случайное равномерно распределенное вещественное число. Оно будет меньше 1, больше или равно 0.
- Функция СЛУЧМЕЖДУ возвращает случайное целое число.
Рассмотрим их использование на примерах.
Выборка случайных чисел с помощью СЛЧИС
Данная функция аргументов не требует (СЛЧИС()).
Чтобы сгенерировать случайное вещественное число в диапазоне от 1 до 5, например, применяем следующую формулу: =СЛЧИС()*(5-1)+1.
Возвращаемое случайное число распределено равномерно на интервале [1,10].
При каждом вычислении листа или при изменении значения в любой ячейке листа возвращается новое случайное число. Если нужно сохранить сгенерированную совокупность, можно заменить формулу на ее значение.
- Щелкаем по ячейке со случайным числом.
- В строке формул выделяем формулу.
- Нажимаем F9. И ВВОД.
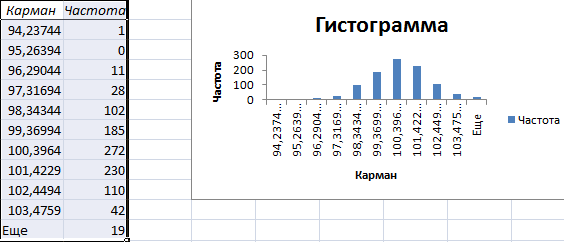
Проверим равномерность распределения случайных чисел из первой выборки с помощью гистограммы распределения.
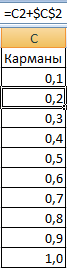
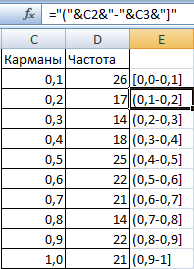
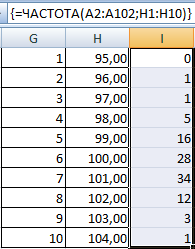
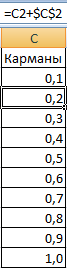
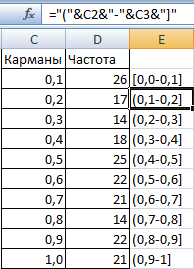
- Сформируем «карманы». Диапазоны, в пределах которых будут находиться значения. Первый такой диапазон – 0-0,1. Для следующих – формула =C2+$C$2.
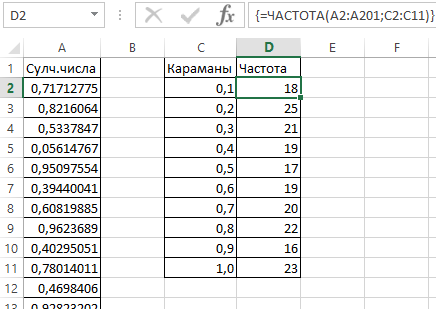
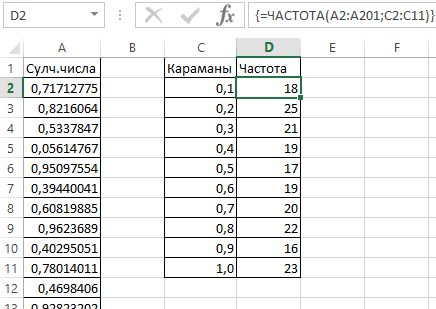
- Определим частоту для случайных чисел в каждом диапазоне. Используем формулу массива {=ЧАСТОТА(A2:A201;C2:C11)}.
- Сформируем диапазоны с помощью знака «сцепления» (=»[0,0-«&C2&»]»).
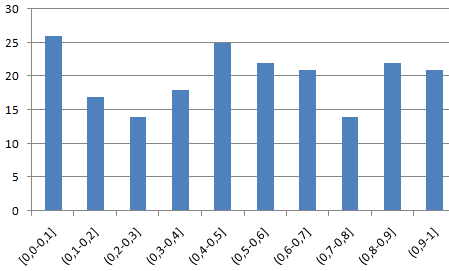
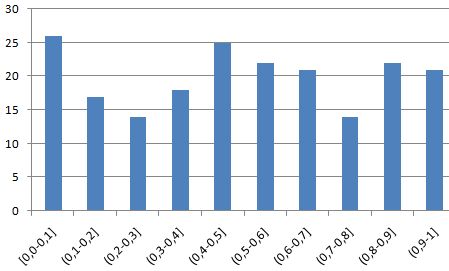
- Строим гистограмму распределения 200 значений, полученных с помощью функции СЛЧИС ().
Диапазон вертикальных значений – частота. Горизонтальных – «карманы».
Функция СЛУЧМЕЖДУ
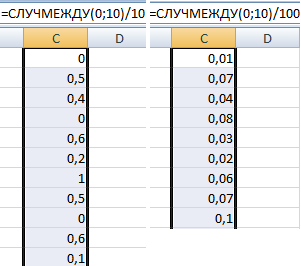
Синтаксис функции СЛУЧМЕЖДУ – (нижняя граница; верхняя граница). Первый аргумент должен быть меньше второго. В противном случае функция выдаст ошибку. Предполагается, что границы – целые числа. Дробную часть формула отбрасывает.
Пример использования функции:
Случайные числа с точностью 0,1 и 0,01:
Как сделать генератор случайных чисел в Excel
Сделаем генератор случайных чисел с генерацией значения из определенного диапазона. Используем формулу вида: =ИНДЕКС(A1:A10;ЦЕЛОЕ(СЛЧИС()*10)+1).
Сделаем генератор случайных чисел в диапазоне от 0 до 100 с шагом 10.
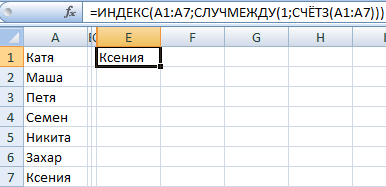
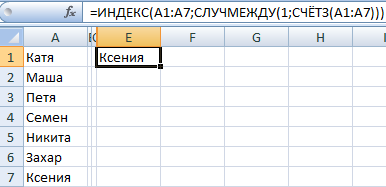
Из списка текстовых значений нужно выбрать 2 случайных. С помощью функции СЛЧИС сопоставим текстовые значения в диапазоне А1:А7 со случайными числами.
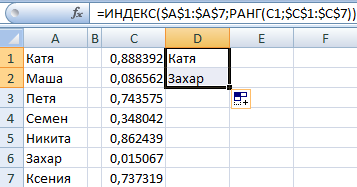
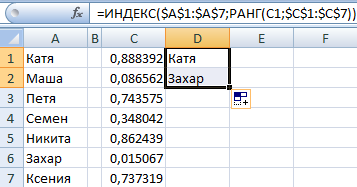
Воспользуемся функцией ИНДЕКС для выбора двух случайных текстовых значений из исходного списка.
Чтобы выбрать одно случайное значение из списка, применим такую формулу: =ИНДЕКС(A1:A7;СЛУЧМЕЖДУ(1;СЧЁТЗ(A1:A7))).
Генератор случайных чисел нормального распределения
Функции СЛЧИС и СЛУЧМЕЖДУ выдают случайные числа с единым распределением. Любое значение с одинаковой долей вероятности может попасть в нижнюю границу запрашиваемого диапазона и в верхнюю. Получается огромный разброс от целевого значения.
Нормальное распределение подразумевает близкое положение большей части сгенерированных чисел к целевому. Подкорректируем формулу СЛУЧМЕЖДУ и создадим массив данных с нормальным распределением.
Себестоимость товара Х – 100 рублей. Вся произведенная партия подчиняется нормальному распределению. Случайная переменная тоже подчиняется нормальному распределению вероятностей.
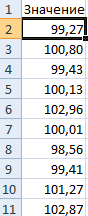
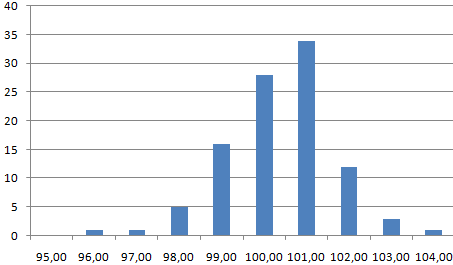
При таких условиях среднее значение диапазона – 100 рублей. Сгенерируем массив и построим график с нормальным распределением при стандартном отклонении 1,5 рубля.
Используем функцию: =НОРМОБР(СЛЧИС();100;1,5).
Программа Excel посчитала, какие значения находятся в диапазоне вероятностей. Так как вероятность производства товара с себестоимостью 100 рублей максимальная, формула показывает значения близкие к 100 чаще, чем остальные.
Перейдем к построению графика. Сначала нужно составить таблицу с категориями. Для этого разобьем массив на периоды:
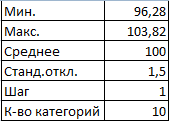
- Определим минимальное и максимальное значение в диапазоне с помощью функций МИН и МАКС.
- Укажем величину каждого периода либо шаг. В нашем примере – 1.
- Количество категорий – 10.
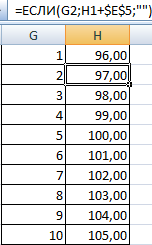
- Нижняя граница таблицы с категориями – округленное вниз ближайшее кратное число. В ячейку Н1 вводим формулу =ОКРВНИЗ(E1;E5).
- В ячейке Н2 и последующих формула будет выглядеть следующим образом: =ЕСЛИ(G2;H1+$E$5;»»). То есть каждое последующее значение будет увеличено на величину шага.
- Посчитаем количество переменных в заданном промежутке. Используем функцию ЧАСТОТА. Формула будет выглядеть так:
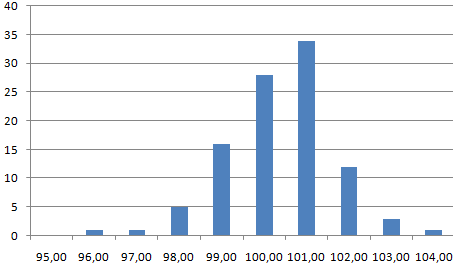
На основе полученных данных сможем сформировать диаграмму с нормальным распределением. Ось значений – число переменных в промежутке, ось категорий – периоды.
График с нормальным распределением готов. Как и должно быть, по форме он напоминает колокол.
Сделать то же самое можно гораздо проще. С помощью пакета «Анализ данных». Выбираем «Генерацию случайных чисел».
О том как подключить стандартную настройку «Анализ данных» читайте здесь.
Заполняем параметры для генерации. Распределение – «нормальное».
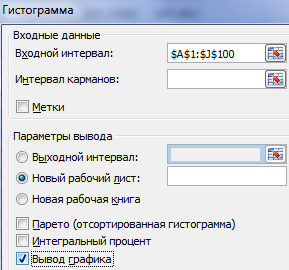
Жмем ОК. Получаем набор случайных чисел. Снова вызываем инструмент «Анализ данных». Выбираем «Гистограмма». Настраиваем параметры. Обязательно ставим галочку «Вывод графика».
Получаем результат:
Скачать генератор случайных чисел в Excel
График с нормальным распределением в Excel построен.
В данной статье мы рассмотрим особенности алгоритма генератора случайных чисел в Excel, и на примерах рассмотрим, как использовать функции СЛЧИС и СЛУЧМЕЖДУ в Excel для генерации случайных чисел, случайных чисел с заданным количеством знаков после запятой, дат и времени.
- Генератор случайных чисел с использованием функции СЛЧИС
- Генератор случайных чисел от нуля до заданной верхней границы диапазона
- Генератор случайных чисел в диапазоне
- Генератор случайных целых чисел в Excel
- Генератор случайных целых чисел в диапазоне с помощью функции СЛУЧМЕЖДУ
- Создание случайных чисел с заданным количеством знаков после запятой
- Генератор случайных дат в Excel
- Генератор случайного времени в Excel
- Генератор случайных букв в Excel
- Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ
- Генератор случайных чисел с помощью Анализа данных
- Пример генерации случайных чисел с нормальным распределением
Генератор случайных чисел с использованием функции СЛЧИС
Функция СЛЧИС является одной из двух функций, специально предназначенных для генерации случайных чисел в Excel. Данная функция возвращает случайное десятичное число (действительное число) между 0 и 1.
СЛЧИС() является энергозависимой функцией, что означает, что при каждом вычислении рабочего листа создается новое случайное число. И это происходит каждый раз, когда вы выполняете какое-либо действие на листе, например, обновляете формулу (не обязательно формулу СЛЧИС, любую другую формулу на листе), редактируете ячейку или вводите новые данные.
Функция СЛЧИС доступна во всех версиях: Excel 2016, Excel 2013, Excel 2010, Excel 2007, Excel 2003.
Поскольку функция Excel СЛЧИС не имеет аргументов, вы просто вводите =СЛЧИС() в ячейке и затем копируете формулу на столько ячеек, сколько хотите:
Генератор случайных чисел в Excel – Генерация случайных чисел
А теперь давайте сделаем еще один шаг и напишем несколько формул СЛЧИС для генерации случайных чисел в соответствии с определенными условиями.
Генератор случайных чисел от нуля до заданной верхней границы диапазона
Чтобы сделать генератор случайных чисел от нуля до любого значения N, вы несколько раз выполняете функцию СЛЧИС с помощью N:
=СЛЧИС()*N
Например, для создания последовательности случайных чисел, больших или равных 0, но менее 50, используйте следующую формулу:
=СЛЧИС()*50
Примечание. Значение верхней границы никогда не включается в возвращаемую случайную последовательность. Например, если вы хотите получить случайные числа от 0 до 10, включая 10, правильная формула =СЛЧИС()*11.
Генератор случайных чисел в диапазоне
Чтобы создать случайное число в диапазоне, т.е. случайное число между любыми двумя указанными вами числами, используйте следующую формулу СЛЧИС:
= СЛЧИС() * (B — A) + A
Где A – это нижнее значение границы (наименьшее число), а B – верхнее значение границы (наибольшее число).
Например, чтобы сделать генератор случайных чисел от 10 до 50, вы можете использовать следующую формулу:
= СЛЧИС()*(50-10)+10
Примечание. Эта формула генерации случайных чисел никогда не вернет число, равное наибольшему числу указанного диапазона (значение B).
Генератор случайных целых чисел в Excel
Чтобы функция Excel СЛЧИС создавала случайные целые числа, возьмите одну из вышеупомянутых формул и заверните ее в функцию ЦЕЛОЕ.
Чтобы сделать генератор случайных целых чисел от 0 до 50:
= ЦЕЛОЕ(СЛЧИС()*50)
Чтобы генерировать случайные целые числа от 10 до 50:
= ЦЕЛОЕ (СЛЧИС()*(50-10)+10)
Генератор случайных чисел в Excel – Генерация случайных целых чисел
Генератор случайных чисел в Excel в диапазоне с помощью функции СЛУЧМЕЖДУ
СЛУЧМЕЖДУ – это еще одна функция в Excel для создания генератора случайных чисел.. Она возвращает случайные целые числа в указанном диапазоне:
СЛУЧМЕЖДУ (нижняя граница; верхняя граница)
Очевидно, что нижняя граница – это наименьшее число, а верхняя граница – наибольшее число в диапазоне случайных чисел, которые вы хотите получить.
Подобно СЛЧИС, СЛУЧМЕЖДУ в Excel является изменчивой функцией, и она также возвращает новое случайное целое число каждый раз, когда ваша таблица пересчитывается или изменяется.
Например, того чтобы сделать генератор случайных целых чисел от 10 до 50 (включая 10 и 50) используйте следующую формулу СЛУЧМЕЖДУ:
= СЛУЧМЕЖДУ(10; 50)
Генератор случайных чисел в Excel – Генерация случайных чисел в заданном диапазоне
Функция СЛУЧМЕЖДУ в Excel может создавать как положительные, так и отрицательные числа случайные числа. Например, чтобы получить список случайных чисел от -10 до 10, введите следующую формулу на листе:
=СЛУЧМЕЖДУ(-10;10)
Функция СЛУЧМЕЖДУ доступна в следующих версиях: Excel 2016, Excel 2013, Excel 2010 и Excel 2007.
В более ранней версии Excel 2003, вы можете использовать формулу СЛЧИС, рассмотренную выше.
Далее в этой статье вы найдете еще несколько примеров формул, демонстрирующих, как использовать функцию СЛУЧМЕЖДУ для создания генератора случайных чисел, отличных от целых.
Создание случайных чисел с заданным количеством знаков после запятой
Хотя функция СЛУЧМЕЖДУ в Excel была предназначена для генерации случайных целых чисел, вы можете использовать ее для генерации случайных десятичных чисел с таким количеством десятичных знаков, сколько хотите.
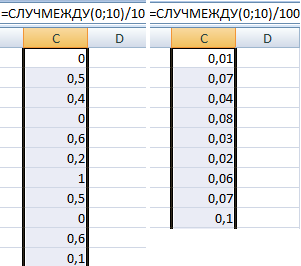
Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:
= СЛУЧМЕЖДУ(нижняя граница*10; верхняя граница*10)/10
Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:
Следующая формула СЛУЧМЕЖДУ возвращает случайные десятичные числа от 1 до 50:
= СЛУЧМЕЖДУ(1*10;50*10)/10
Генератор случайных чисел в Excel – Генерация случайных чисел с одним знаком после запятой
Аналогичным образом, чтобы сделать генератор случайных чисел от 1 до 50 с двумя знаками после запятой, вы умножаете аргументы функции СЛУЧМЕЖДУ на 100, а затем делите результат на 100:
=СЛУЧМЕЖДУ(1*100; 50*100)/100
Генератор случайных чисел в Excel – Генерация случайных чисел с двумя знаками после запятой
Генератор случайных дат в Excel
Чтобы вернуть список случайных дат между данными двумя датами, используйте функцию СЛУЧМЕЖДУ в сочетании с ДАТА:
=СЛУЧМЕЖДУ (ДАТА (дата начала); ДАТА (дата окончания))
Например, чтобы получить список дат между 1 сентября 2017 и 20 ноября 2017 включительно, введите следующую формулу на листе:
=СЛУЧМЕЖДУ(ДАТА(2017;9;1);ДАТА(2017;11;21))
Не забудьте применить формат даты к ячейке (ячейкам), и вы получите список случайных дат, подобных этому:
Генератор случайных чисел в Excel – Генерация случайных дат
Генератор случайного времени в Excel
Во внутренней системе Excel времена хранятся как десятичные числа, и вы можете использовать стандартную функцию Excel СЛЧИС для вставки случайных действительных чисел, а затем просто применить формат времени к ячейкам:
Генератор случайных чисел в Excel – Генерация случайного времени функцией СЛЧИС и применение к ней формата Время
Чтобы сделать генератор случайного времени в указанном диапазоне, требуется более конкретная формула. Рассмотрим подробнее.
Генератор случайного времени в указанном диапазоне
Чтобы вставить произвольное время между любыми двумя указанными вами временными интервалами, используйте функцию ВРЕМЯ в сочетании с Excel СЛЧИС:
= ВРЕМЯ (время начала) + СЛЧИС () * (ВРЕМЯ (время начала) — ВРЕМЯ (время окончания))
Например, чтобы вставить случайное время между 5:30 и 18:00, вы можете использовать одну из следующих формул:
=ВРЕМЯ(5;30;0)+СЛЧИС()*(ВРЕМЯ(18;0;0)-ВРЕМЯ(5;0;0))
Генератор случайных чисел в Excel – Генерация случайного времени в заданном интервале
Генератор случайных букв в Excel
Чтобы вставить случайную букву, необходимо использовать комбинацию трех различных функций:
=СИМВОЛ(СЛУЧМЕЖДУ(КОДСИМВ(«A»);КОДСИМВ(«Z»)))
Где A — первый символ, а Z — последний символ в диапазоне букв, которые вы хотите включить (в алфавитном порядке).
Разберем функции, в приведенной выше формуле:
- КОДСИМВ возвращает числовые коды ANSI для указанных букв.
- СЛУЧМЕЖДУ принимает числа, возвращаемые функциями КОДСИМВ , как нижнее и верхнее значения диапазона.
- СИМВОЛ преобразует случайные коды ANSI, возвращаемые СЛУЧМЕЖДУ, в соответствующие буквы.
Генератор случайных чисел в Excel – Генерация случайных букв
Так как коды ANSI отличаются для прописных и строчных букв, эта формула учитывает регистр.
Если кто-то наизусть знает Коды символов ANSI, ничто не мешает вам передавать коды непосредственно в функцию СЛУЧМЕЖДУ.
Например, чтобы получить произвольные прописные буквы между A (код ANSI 65) и Z (код ANSI 90), вы пишете:
=СИМВОЛ(СЛУЧМЕЖДУ (65;90))
Чтобы генерировать строчные буквы между а (код ANSI 97) в z (код ANSI 122), вы используете следующую формулу:
=СИМВОЛ(СЛУЧМЕЖДУ(97;122))
Чтобы вставить случайный специальный символ, например! «# $% & ‘() * +, -. /, используйте функцию СЛУЧМЕЖДУ с нижним параметром, установленным на 33 (код ANSI для«! »), а верхний параметр — 47 (код ANSI для« / »).
=СИМВОЛ(СЛУЧМЕЖДУ(33;47))
Генератор случайных чисел в Excel – Генерация случайных символов
Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ
Если вы хотите получить постоянный набор случайных чисел, дат или текстовых строк, которые не будут меняться каждый раз, то есть зафиксировать случайные числа, когда лист пересчитывается, используйте один из следующих способов:
- Чтобы остановить функции СЛЧИС или СЛУЧМЕЖДУ от пересчета в одной ячейке, выберите эту ячейку, переключитесь на панель формул и нажмите F9, чтобы заменить формулу на ее значение.
- Чтобы предотвратить функцию случайных чисел в Excel от автоматического обновления значений в нескольких ячейках, используйте функцию Вставить. Выберите все ячейки с формулой генерации случайных значений, нажмите Ctrl+C, чтобы скопировать их, затем щелкните правой кнопкой мыши выбранный диапазон и нажмите «Вставить специальные»—> «Значения».
Генератор случайных чисел в Excel – Вставка значений
Генератор случайных чисел с помощью Анализа данных
С помощью пакета анализа данных вы, например, можете сгенерировать случайные числа нормального распределения или другого распределения. По умолчанию данный пакет не подключен, поэтому необходимо его загрузить. Как это сделать, описано в этой статье.
Пример генерации случайных чисел нормального распределения
Для того чтобы сгенерировать случайные числа нормального распределения, переходим во вкладку «ДАННЫЕ», в группе «Анализ» выбираем «Анализ данных».
Генератор случайных чисел в Excel – Анализ данных
В открывшемся списке выбираем «Генерация случайных чисел» и нажимаем кнопку «ОК».
Генератор случайных чисел в Excel – Генерация случайных чисел
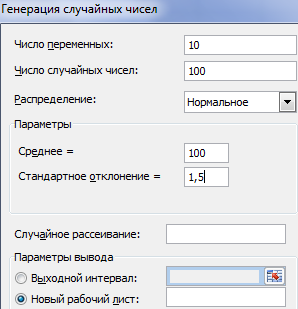
В открывшемся окне в списке «Распределение» выбираем «Нормальное», вводим число переменных, число случайных чисел, среднее и отклонение, а также место, где вы хотите разместить сгенерированные случайные числа.
Генератор случайных чисел в Excel – Генерация случайных чисел нормального распределения
После того, как все данные введены нажимаем кнопку «ОК», и в результате получаем сгенерированные случайные числа нормального распределения.
Ну вот на этом все. Теперь вы научились, как сделать генератор случайных чисел, чисел в диапазоне, чисел с заданным количеством знаков после запятой, случайных дат, случайного времени, а также случайных букв, а также, как сгенерировать случайные числа нормального распределения. Таким образом, владея данными знаниями, вы можете создать не только генератор случайных чисел в Excel, но и генератор паролей.
[ Генератор случайных чисел в Excel скачать ]
To generate a normal distribution in Excel, you can use the following formula:
=NORMINV(RAND(), MEAN, STANDARD_DEVIATION)
You can then copy this formula down to as many cells in Excel as you’d like, depending on how large you’d like the dataset to be.
The following step-by-step example shows how to use this formula to generate a normal distribution in Excel.
Step 1: Choose a Mean & Standard Deviation
First, let’s choose a mean and a standard deviation that we’d like for our normal distribution.
For simplicity, we’ll choose 0 for the mean and 1 for the standard deviation:
Step 2: Generate a Normally Distributed Random Variable
Next, we’ll use the following formula to generate a single normally distributed random variable:
=NORMINV(RAND(), $B$1, $B$2)
The following screenshot shows how to do so:
Step 3: Choose a Sample Size for the Normal Distribution
Next, we can simply copy and paste this formula down to as many cells as we’d like.
For example, we may copy and paste this formula to a total of 20 cells:
The end result is a normally distributed dataset with a mean of 0, standard deviation of 1, and sample size of 20.
Note: You can quickly generate a brand new dataset that follows a normal distribution by simply double clicking on any cell and pressing Enter.
Additional Resources
Online Normal Distribution Dataset Generator
How to Perform a Normality Test in Excel
How to Make a Bell Curve in Excel
Время от времени у пользователей Excel появляется необходимость генерировать случайные числа для того, чтобы использовать их в формулах или же для других целей. Для этого в программе предусмотрен целый арсенал возможностей. Есть возможность сгенерировать случайные числа самыми различными способами. Мы же приведем только те, которые показали себя на практике самым лучшим образом.
Содержание
- Функция случайного числа в Excel
- Выборка случайных чисел с помощью СЛЧИС
- Функция СЛУЧМЕЖДУ
- Как сделать генератор случайных чисел в Excel
- Генератор случайных чисел нормального распределения
Функция случайного числа в Excel
Предположим, у нас есть набор данных, который должен содержать элементы, которые абсолютно не связаны друг с другом между собой. В идеале, чтобы они были сформированы по закону нормального распределения. Для этого нужно использовать функцию случайного числа. Есть две функции, с помощью которых можно достичь поставленной задачи: СЛЧИСЛ и СЛУЧМЕЖДУ. Давайте детально рассмотрим, как их можно использовать на практике.
Выборка случайных чисел с помощью СЛЧИС
Эта функция не предусматривает наличия каких-либо аргументов. Но несмотря на это она дает возможность настраивать диапазон значений, в рамках которых она должна генерировать случайное число. Например, чтобы получить его в рамках от единицы до пяти, нам необходимо использовать такую формулу: =СЛЧИС()*(5-1)+1.
Если эту функцию распределить на другие ячейки с помощью маркера автозаполнения, то мы увидим, что распределение осуществляется равномерно.
В ходе каждого расчета случайного значения, если в любом месте листа изменить какую-угодно ячейку, числа будут автоматически сгенерированы заново. Поэтому сохраняться эта информация не будет. Чтобы сделать так, чтобы они остались, необходимо вручную написать это значение в числовом формате или же воспользовавшись этой инструкцией.
- Делаем клик по ячейке, содержащей случайное число.
- Делаем клик по строке формул, после чего выделяем ее.
- Нажимаем на кнопку F9 на клавиатуре.
- Заканчиваем эту последовательность действий нажатием клавиши Enter.
Проверим то, насколько равномерно распределены случайные числа. Для этого нам нужно воспользоваться гистограммой распределения. Чтобы ее сделать, выполняем следующие шаги:
- Создадим колонку с карманами, то есть, теми ячейками, в которых мы будем держать наши диапазоны. Первый такой – 0-0,1. Формируем следующие с помощью такой формулы: =C2+$C$2.
- После этого нам надо определить, насколько часто встречаются случайные числа, относящиеся к каждому конкретному диапазону. Для этого мы можем использовать формулу массива {=ЧАСТОТА(A2:A201;C2:C11)}.
- Далее, с использованием знака «сцепления» делаем наши следующие диапазоны. Формула простая =»[0,0-«&C2&»]».
- Теперь мы делаем диаграмму, описывающую то, как распределяются эти 200 значений.
В описанном нами примере частота соответствует оси Y, а «карманы» – оси X.
Функция СЛУЧМЕЖДУ
Если говорить про функцию СЛУЧМЕЖДУ, то согласно ее синтаксису, у нее есть два аргумента: нижняя граница и верхняя граница. Важно, чтобы величина первого параметра была меньше, чем второго. Допускается, что границами могут быть целые числа, а дробные формулой не учитываются. Давайте посмотрим, как эта функция работает, на этом скриншоте.
Видим, что точность можно регулировать с помощью деления. Можно получать случайные числа с любой разрядностью после запятой.
Видим, что эта функция гораздо более органична и понятна для обычного человека, чем предыдущая. Поэтому в большинстве случаев можно использовать только ее.
Как сделать генератор случайных чисел в Excel
А теперь давайте сделаем небольшой генератор чисел, который будет получать значения, основываясь на определенном диапазоне данных. Для этого применяется формула =ИНДЕКС(A1:A10;ЦЕЛОЕ(СЛЧИС()*10)+1).
Создадим генератор случайных чисел, которые будут создаваться от нуля до 10. С помощью этой формулы мы можем регулировать шаг, с которым они будут создаваться. Например, можно создать генератор, который будет создавать только значения, заканчивающиеся на ноль.
Или же такой вариант. Давайте предположим, что нам надо выделить два случайных значения из перечня текстовых ячеек.
А чтобы выбрать два случайных числа, необходимо применить функцию ИНДЕКС.
Формула, с помощью которой мы это сделали, приведена на скриншоте выше. =ИНДЕКС(A1:A7;СЛУЧМЕЖДУ(1;СЧЁТЗ(A1:A7))) – с помощью этой формулы мы можем создать генератор для одного текстового значения. Видим, что мы спрятали вспомогательную колонку. Так можете сделать и вы.
Генератор случайных чисел нормального распределения
Проблема функций СЛЧИС и СЛУЧМЕЖДУ в том, что они формируют набор чисел, которые находятся очень далеко от целевого показателя. Вероятность того, что появится число, близкое к нижней границе, середине или верхней границе, одинаковая.
Нормальное распределение в статистике – это такой набор данных, в которых по мере большей отдаленности от центра на графике частота, с которой встречается значение в определенном коридоре, уменьшается. То есть, большая часть значений скапливается вокруг центрального. Давайте с помощью функции СЛУЧМЕЖДУ попробуем создать набор чисел, распределение которых относится к разряду нормального.
Итак, у нас есть товар, производство которого стоит 100 рублей. Следовательно, числа должны генерироваться приблизительно такие же. В этом случае средним значением должно быть 100 рублей. Создадим массив данных, и создадим график, в котором стандартное отклонение составит 1,5 рубля, а распределение значений – нормальное.
Для этого нужно использовать функцию =НОРМОБР(СЛЧИС();100;1,5). Далее программа автоматически меняет вероятности, исходя из того, что самый высокий шанс имеют числа, приближенные к сотне.
Теперь нам осталось лишь построить график стандартным способом, выбрав в качестве диапазона набор сгенерированных значений. В результате, мы видим, что распределение действительно является нормальным.
Вот так все просто. Успехов.
Оцените качество статьи. Нам важно ваше мнение: