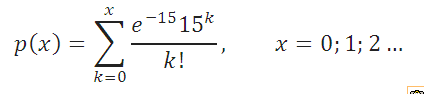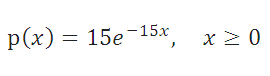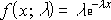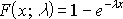Генерация экспоненциального распределения в excel - Word и Excel

Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL

ЭКСП.РАСП()

построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.

Экспоненциальное распределение

(англ.

Exponential

distribution

)

часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение

Экспоненциального распределения

:

Промежутки времени между появлением посетителей в кафе;
Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см.

Распределение Вейбулла

);
Затраты времени на обслуживание одного покупателя.

Плотность вероятности

Экспоненциального распределения

задается следующей формулой:

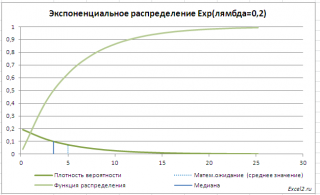
График

плотности распределения вероятности

и

интегральной функции

Экспоненциального

распределения выглядит следующим образом

(см. ниже).

СОВЕТ

: Подробнее о

Функции распределения

и

Плотности вероятности

см. статью

Функция распределения и плотность вероятности в MS EXCEL

Среднее значение

(среднее время между 2-мя случайными событиями) равно

1/λ

. А

дисперсия (квадрат стандартного отклонения)

равна

1/

λ

^2

.

Экспоненциальное распределение

тесно связано с дискретным

распределением Пуассона

. Если

Распределение Пуассона

описывает число случайных событий, произошедших за определенный интервал времени, то

Экспоненциальное распределение

должноописывать длину интервала времени между двумя последовательными событиями.

Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается

распределением Пуассона

со средним значением равным 15 машин в час (параметр распределения

λ

=15). Вероятность того, что на стоянку в течение часа приедет k машин равно:

Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра

экспоненциального распределения

, то параметр

λ

=15

, а плотность соответствующего

экспоненциального распределения

равна:

Экспоненциальное распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для

Экспоненциального распределения

имеется функция

ЭКСП.РАСП()

, английское название — EXPON.DIST(), которая позволяет вычислить

плотность вероятности

(см. формулу в начале статьи) и

интегральную функцию распределения

(вероятность, что случайная величина X, распределенная по

экспоненциальному закону

, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:

Экспоненциальное распределение

имеет обозначение

Exp

(

λ

).

Примечание

: До MS EXCEL 2010 в EXCEL была функция

ЭКСПРАСП()

, которая позволяет вычислить

кумулятивную (интегральную) функцию распределения

и

плотность вероятности

.

ЭКСПРАСП()

оставлена в MS EXCEL 2010 для совместимости.

В

файле примера на листе Пример

приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции

экспоненциального распределения

:

=1-EXP(-

λ

*x)

;
=ГАММА.РАСП(x;1;1/

λ

;ИСТИНА)

, т.к.

экспоненциальное распределение

является частным случаем

Гамма распределения

;
=ВЕЙБУЛЛ.РАСП(x;1;1/

λ

;ИСТИНА)

, т.к.

экспоненциальное распределение

является частным случаем

распределения Вейбулла

;

Примечание

: Для удобства написания формул в

файле примера

создано

Имя

для параметра распределения —

λ

.

Графики функций

В

файле примера

приведены графики

плотности распределения вероятности

и

интегральной функции распределения

.

Примечание

: Для построения

функции распределения

и

плотности вероятности

можно использовать диаграмму типа

График

или

Точечная

(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью

Основные типы диаграмм

Генерация случайных чисел

Для генерирования массива чисел, распределенных по

экспоненциальному закону

, можно использовать формулу

=-LN(СЛЧИС())/

λ

Функция

СЛЧИС()

генерирует

непрерывное равномерное распределение

от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.

файл примера лист Генерация

).

Если случайные числа содержатся в диапазоне

B14:B213

, то оценку параметра

экспоненциального распределения

λ

можно сделать с использованием формулы

=1/СРЗНАЧ(B14:B213)

.

Задачи

Экспоненциальное распределение

широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр

λ

называется

интенсивность отказов

, а

1/

λ

–

среднее время до отказа

.

Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый

Экспоненциальным распределением

с

интенсивностью отказа

равной 10^(-3) в час, таким образом,

λ

=

10^(-3).

Среднее время до отказа

равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за

Среднее время до отказа,

то нужно записать формулу:

Т.е. результат не зависит от параметра

λ

.

В MS EXCEL решение выглядит так:

=ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)

Задача

.

Среднее время до отказа

некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы.

=ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

Источник

17 авг. 2022 г.
читать 2 мин

Экспоненциальное распределение — это распределение вероятностей, которое используется для моделирования времени, в течение которого мы должны ждать, пока не произойдет определенное событие.

Это распределение может быть использовано для ответа на такие вопросы, как:

Как долго владельцу магазина нужно ждать, пока покупатель войдет в его магазин?
Как долго батарея будет продолжать работать, прежде чем она умрет?
Как долго компьютер будет продолжать работать, прежде чем он сломается?

В каждом сценарии нас интересует вычисление того, как долго нам придется ждать, пока не произойдет определенное событие. Таким образом, каждый сценарий может быть смоделирован с использованием экспоненциального распределения.

Если случайная величина X следует экспоненциальному распределению, то кумулятивная функция плотности X может быть записана как:

F (х; λ) = 1 – e -λx

куда:

λ: параметр скорости (рассчитывается как λ = 1/μ)
e: константа, примерно равная 2,718.

Чтобы рассчитать вероятности, связанные с кумулятивной функцией плотности экспоненциального распределения в Excel, мы можем использовать следующую формулу:

=EXPON.DIST(x, lambda, cumulative)

куда:

x : значение экспоненциально распределенной случайной величины
lambda : параметр скорости
cumulative : использовать функцию кумулятивной плотности или нет (ИСТИНА или ЛОЖЬ)

Следующие примеры показывают, как использовать эту формулу на практике.

Пример 1: время до прихода следующего клиента

В среднем новый покупатель заходит в магазин каждые две минуты. После прихода клиента найти вероятность того, что новый клиент прибудет менее чем за одну минуту.

Решение: Среднее время между клиентами составляет две минуты. Таким образом, ставка может быть рассчитана как:

λ = 1/мк
λ = 1/2
λ = 0,5

Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что новый клиент прибудет менее чем за одну минуту:

Вероятность того, что следующего клиента придется ждать менее одной минуты, равна 0,393469 .

Пример 2: Время до следующего землетрясения

Предположим, землетрясение происходит в среднем каждые 400 дней в определенном регионе. После землетрясения найти вероятность того, что следующее землетрясение произойдет не ранее, чем через 500 дней.

Решение: Среднее время между землетрясениями составляет 400 дней. Таким образом, ставка может быть рассчитана как:

λ = 1/мк
λ = 1/400
λ = 0,0025

Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующее землетрясение произойдет менее чем через 500 дней:

Вероятность того, что следующее землетрясение произойдет менее чем через 500 дней, равна 0,7135.

Таким образом, вероятность того, что следующего землетрясения придется ждать более 500 дней, равна 1 – 0,7135 = 0,2865 .

Пример 3: время до следующего телефонного звонка

Предположим, колл-центр получает новый звонок в среднем каждые 10 минут. После звонка клиента найти вероятность того, что новый клиент позвонит в течение 10–15 минут.

Решение: Среднее время между вызовами составляет 10 минут. Таким образом, ставка может быть рассчитана как:

λ = 1/мк
λ = 1/10
λ = 0,1

Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующий клиент позвонит в течение 10-15 минут:

Вероятность того, что новый клиент позвонит в течение 10-15 минут. составляет 0,1447 .

Дополнительные ресурсы

Введение в экспоненциальное распределение
Свойство экспоненциального распределения без памяти
Как построить экспоненциальное распределение в R

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции ЭКСП.РАСП в Microsoft Excel.

Возвращает экспоненциальное распределение. Функция ЭКСП.РАСП используется для моделирования временных задержек между событиями, например времени, которое потребуется на доставку денежного перевода через автоматизированную банковскую систему. В частности, при помощи функции ЭКСП.РАСП можно определить вероятность того, что этот процесс займет не более 1 минуты.

Синтаксис

ЭКСП.РАСП(x;лямбда;интегральная)

Аргументы функции ЭКСП.РАСП описаны ниже.

x — обязательный аргумент. Значение функции.
Лямбда — обязательный аргумент. Значение параметра.
Интегральная — обязательный аргумент. Логическое значение, определяющее форму экспоненциальной функции, которую следует использовать. Если аргумент «интегральная» имеет значение ИСТИНА, функция ЭКСП.РАСП возвращает интегральную функцию распределения; если имеет значение ЛОЖЬ, возвращается функция плотности распределения.

Замечания

Если значение «x» или «лямбда» не является числом, функция ЭКСП.РАСП возвращает значение ошибки #ЗНАЧ!.
Если x < 0, функция ЭКСП.РАСП возвращает значение ошибки #ЧИСЛО!.
Если значение «лямбда» ≤ 0, функция ЭКСП.РАСП возвращает значение ошибки #ЧИСЛО!.
Уравнение для функции плотности вероятности имеет следующий вид:
Уравнение для интегральной функции распределения имеет следующий вид:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,2	Значение функции
10	Значение параметра
Формула	Описание	Результат
=ЭКСП.РАСП(A2;A3;ИСТИНА)	Интегральная экспоненциальная функция распределения	0,86466472
=ЭКСП.РАСП(0,2;10;ЛОЖЬ)	Экспоненциальная функция плотности распределения	1,35335283

Нужна дополнительная помощь?

Источник

The exponential distribution is a probability distribution that is used to model the time we must wait until a certain event occurs.

This distribution can be used to answer questions like:

How long does a shop owner need to wait until a customer enters his shop?
How long will a battery continue to work before it dies?
How long will a computer continue to work before it breaks down?

In each scenario, we’re interested in calculating how long we’ll have to wait until a certain event occurs. Thus, each scenario could be modeled using an exponential distribution.

If a random variable X follows an exponential distribution, then the cumulative density function of X can be written as:

F(x; λ) = 1 – e^-λx

where:

λ: the rate parameter (calculated as λ = 1/μ)
e: A constant roughly equal to 2.718

To calculate probabilities related to the cumulative density function of the exponential distribution in Excel, we can use the following formula:

=EXPON.DIST(x, lambda, cumulative)

where:

x: the value of the exponentially distributed random variable
lambda: the rate parameter
cumulative: whether to use the cumulative density function or not (TRUE or FALSE)

The following examples show how to use this formula in practice.

Example 1: Time Until Next Customer Arrives

A new customer enters a shop every two minutes, on average. After a customer arrives, find the probability that a new customer arrives in less than one minute.

Solution: The average time between customers is two minutes. Thus, the rate can be calculated as:

λ = 1/μ
λ = 1/2
λ = 0.5

Thus, we can use the following formula in Excel to calculate the probability that a new customer arrives in less than one minute:

The probability that we’ll have to wait less than one minute for the next customer to arrive is 0.393469.

Example 2: Time Until Next Earthquake

Suppose an earthquake occurs every 400 days in a certain region, on average. After an earthquake occurs, find the probability that it will take more than 500 days for the next earthquake to occur.

Solution: The average time between earthquakes is 400 days. Thus, the rate can be calculated as:

λ = 1/μ
λ = 1/400
λ = 0.0025

Thus, we can use the following formula in Excel to calculate the probability that the next earthquake takes less than 500 days to occur:

The probability that it will take less than 500 days for the next earthquake is 0.7135.

Thus, the probability that we’ll have to wait more than 500 days for the next earthquake is 1 – 0.7135 = 0.2865.

Example 3: Time Until Next Phone Call

Suppose a call center receives a new call every 10 minutes, on average. After a customer calls, find the probability that a new customer calls within 10 to 15 minutes.

Solution: The average time between calls is 10 minutes. Thus, the rate can be calculated as:

λ = 1/μ
λ = 1/10
λ = 0.1

Thus, we can use the following formula in Excel to calculate the probability that the next customer calls within 10 to 15 minutes:

The probability that a new customer calls within 10 to 15 minutes. is 0.1447.

Additional Resources

An Introduction to the Exponential Distribution
The Memoryless Property of the Exponential Distribution
How to Plot an Exponential Distribution in R

Источник

Функция ЭКСП.РАСП используется для моделирования временных задержек между событиями, например времени, которое потребуется на доставку денежного перевода через автоматизированную банковскую систему.

Описание функции ЭКСП.РАСП

Синтаксис

=ЭКСП.РАСП(x; лямбда; интегральная)

Аргументы

xлямбдаинтегральная

Обязательный аргумент. Значение функции.

Обязательный аргумент. Значение параметра.

Обязательный аргумент. Логическое значение, определяющее форму экспоненциальной функции, которую следует использовать. Если аргумент «интегральная» имеет значение ИСТИНА, функция ЭКСП.РАСП возвращает интегральную функцию распределения; если имеет значение ЛОЖЬ, возвращается функция плотности распределения.

Замечания

Пример

Источник