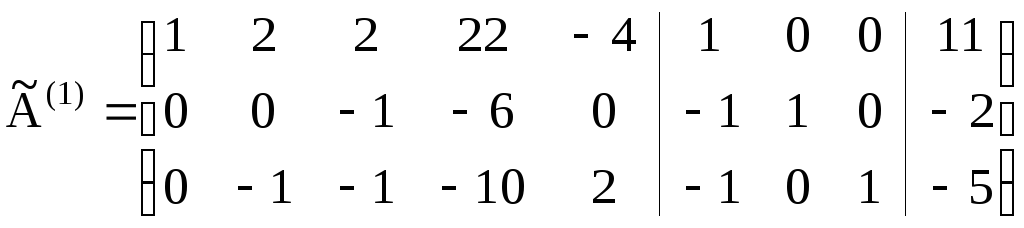Гаусс жордан в excel - Word и Excel - помощь в работе с программами

Преобразование Жордана-Гаусса и симплекс-метод в Excel

Как известно, метод Жордана-Гаусса, он же метод последовательного исключения неизвестных, является модификацией метода Гаусса решения систем линейных алгебраических уравнений (СЛАУ).

Метод базируется на элементарных преобразованиях (переводящих систему в эквивалентную), к которым относятся:

прибавление к обеим частям уравнения системы другого уравнения той же системы, умноженного на число, отличное от нуля;
перестановка местами уравнений в системе;
удаление из системы уравнений вида 0 = 0.

В отличие от метода Гаусса, на каждом шаге одна переменная исключается из всех уравнений, кроме одного.

Шаг метода состоит в следующем:

выбрать в очередном уравнении неизвестное с коэффициентом, отличным от нуля (разрешающим элементом);
разделить выбранное уравнение на разрешающий элемент;
с помощью выбранного уравнения исключить неизвестное при разрешающем элементе из всех остальных уравнений;
на следующем шаге аналогично исключается другое неизвестное из всех уравнений, кроме одного;
процесс продолжается, пока не будут использованы все уравнения.

Алгоритмизировать это можно так:

Для СЛАУ в матричном виде A*x=b (матрица A размерности m*n, совсем необязательно квадратная) составляется следующая таблица:

Таблица с системой уравнений для преобразования Жордана-Гаусса

В таблице выбран разрешающий элемент a_r,s≠0, тогда r — разрешающая строка, s — разрешающий столбец.

Переход к следующей таблице выполняется по правилам:

1. вычисляются элементы разрешающей строки:
a'_r,j=a_r,j/a_r,s — то есть, r-строка таблицы делится на разрешающий элемент;

2. все элементы разрешающего столбца, кроме a_r,s, равного единице, становятся равны нулю;

3. элементы вне разрешающих строки и столбца вычисляются по формуле, изображённой ниже:

Формула преобразования Жордана-Гаусса для элементов вне разрешающих строки и столбца

Легко не запутаться, если увидеть, что числитель этой формулы похож на вычисление определителя матрицы 2 на 2.

4. При ручном расчёте значение в последнем контрольном столбце сравнивается с суммой предыдущих элементов строки. Если значения не совпадают, ошибки надо искать в данной строке. При автоматизированном расчёте контрольный столбец можно опустить.

Возможны следующие случаи:

1. В процессе исключений левая часть уравнения системы обращается в 0, а правая b≠0, тогда система не имеет решения.

2. Получается тождество 0 = 0 — уравнение является линейной комбинацией остальных и строка нулей может быть вычеркнута из системы.

3. После использования всех уравнений для исключения неизвестных, таблица либо содержит искомое решение, либо показывает несовместность системы ограничений.

Запрограммируем метод в Excel одной формулой, изменять которую должно быть не слишком трудоёмко. Например, для решения СЛАУ

Тестовая СЛАУ

заполним коэффициентами системы ячейки листа от A1 до D4 включительно, выберем разрешающий элемент a_1,1=1, а первый шаг метода сделаем в ячейке A6, куда загоним «универсальную» формулу для преобразования Жордана-Гаусса:

=ЕСЛИ(СТРОКА($A$1)=СТРОКА(A1);A1/$A$1; ЕСЛИ(СТОЛБЕЦ($A$1)=СТОЛБЕЦ(A1);0;(A1*$A$1- ДВССЫЛ(АДРЕС(СТРОКА(A1);СТОЛБЕЦ($A$1)))* ДВССЫЛ(АДРЕС(СТРОКА($A$1);СТОЛБЕЦ(A1))))/$A$1))

Здесь ссылка $A$1 показывает разрешающий элемент, а ссылка на текущий элемент не закреплена. Остаётся только растянуть формулу на ячейки A6:D9:

Вид листа для расчёта преобразования Жордана-Гаусса

На следующем шаге разрешающим элементом может быть, например, a_2,2=1 (ячейка B7). Нам останется скопировать формулу из A6 в A11 (по пустой строке оставляем, чтоб визуально разделить шаги метода), войти в режим редактирования формулы (двойной щелчок по ячейке или выбрать её и нажать клавишу F2) и поправить (аккуратно перетащить мышкой за границу) все закреплённые ссылки с ячейки A1 на B7.

Конечно, можно заменить везде в формуле закреплённую ссылку $A$1 на конструкцию вида ДВССЫЛ(ЯЧЕЙКА), образующую динамический адрес ссылки. Скажем, ДВССЫЛ(F8), а в ячейке F8 будет автоматически формироваться адрес ячейки разрешающего элемента по заданным пользователем номеру строки и столбца. Тогда для этих номеров строки и столбца придётся предусмотреть отдельные ячейки, например, так:

Попытка обойтись без перетаскивания ссылки…

Увы, всё это ничего не даст — вместо $A$1 мы просто вынуждены будем закрепить в формуле ДВССЫЛ($F$8) и всё равно потом перетаскивать столько же ссылок при копировании формулы. Кроме того, «вручную» введённые номера строки и столбца придётся ещё и проверять на допустимость (хотя бы как на рисунке), так что, не будем умножать сущностей.

Посмотреть метод в работе можно на двух первых листах приложенного файла Excel (2 разных примера).

На преобразовании Жордана-Гаусса основан и такой универсальный метод решения линейных задач оптимизации, как симплекс-метод. Описания его обычно страшны, длинны и перегружены теоремами. Попробуем сделать простое описание и разработать пригодный для расчёта в Excel алгоритм. На самом деле, симплекс-метод уже встроен в стандартную надстройку Пакет анализа, и программировать его «вручную» не нужно, так что наш код имеет, скорее, учебную ценность.

Сначала минимум теории.

Если вектор-столбцы СЛАУ линейно независимы, соответствующие им переменные являются базисными, а остальные – свободными. Например, в СЛАУ

Базисные и свободные переменные в СЛАУ

переменные x₂ и x₄ — базисные, а x₁ и x₃ — свободные. Базисные переменные между собой независимы, а свободные можно сделать, например, нулями и получить

{ x₂=2, x₄=1 } – базисное решение системы.

Выбирая различные разрешающие элементы, можно получить решения СЛАУ с различными базисами. Любое неотрицательное базисное решение СЛАУ называется опорным.

Симплекс-метод обеспечивает переход от одного опорного решения к другому, пока не будет достигнуто оптимальное решение, дающее минимум целевой функции.

Алгоритм симплекс-метода состоит в следующем:

1. Задача ЛП преобразуется к каноническому виду:

Канонический вид задачи линейного программирования

Это всегда можно сделать следующим образом: к задаче, записанной в стандартной постановке

Стандартная постановка задачи линейного программирования

добавляются дополнительные балансовые переменные, число которых соответствует числу ограничений-неравенств m (ограничения на неотрицательность значений неизвестных не учитываются). После этого неравенства со знаком «≤» превращаются в равенства, например, система ограничений вида

2*x₁+3*x₂≤20

3*x₁+x₂≤15

4*x₁≤16

3*x₂≤12

x1,x2≥0

примет вид

2*x₁+3*x₂+x₃=20

3*x₁+x₂+x₄=15

4*x₁+x₅=16

3*x₂+x₆=12

x1,x2,…,x₆≥0

То есть, «экономический» смысл балансовых переменных очень прост – это «остатки» неиспользованных ресурсов каждого вида.

Если в исходной задаче искался не минимум, а максимум, целевая функция Z заменятся на Z₁ = -Z. Решения задач совпадают, при этом min Z = - max Z₁. Например, цель

Z(x₁,x₂)=2*x₁+5*x₂ (max)

переписывается в виде

Z₁(x₁,x₂)=-2*x₁-5*x₂ (min)

Если в исходной задаче были уравнения-неравенства со знаками «≥» вместо «≤«, обе части каждого такого неравенства умножаются на -1, а знак неравенства меняется на противоположный, например,

3*x₁+x₂+x₄≥15

превращается в

-3*x₁-x₂-x₄≤15

Канонический вид модели получен, для него выписывается симплекс-таблица:

Симплекс-таблица

В левом столбце записываются базисные переменные (БП), если они ещё не выделены – пусто.

2. С помощью шагов Жордана–Гаусса ищется первоначальный опорный план, т.е. СЛАУ приводится к базисному виду с неотрицательными свободными членами b_i>0. При этом целевая функция Z должна быть выражена только через свободные неизвестные (нулевые коэффициенты в Z-строке стоят только под переменными x_i, которые есть в базисе). При выборе разрешающего элемента a_r,s в строку r столбца БП выписываем переменную x_s, если там уже была переменная – вычеркиваем её (выводим из базиса).

3. Выписываем под столбцами x_i опорный план X^*: под свободными переменными — нули, под базисными – соответствующие базисной переменной коэффициенты из столбца b.

Ниже выписываем вектор R по правилу: под базисными переменными – нули, под свободными R_i=Z_i.

Если все R_i≥0, найдено оптимальное решение X^* и значение цели Z_min = -q, иначе нужен новый план~~, а у вас он есть, товарищ Жюков?~~ (п. 4).

4. Для выбора разрешающего столбца s выбираем максимальную по модулю отрицательную компоненту вектора R, разрешающий столбец s выбран. Затем анализируем коэффициенты s-го столбца матрицы системы ограничений. Если все a_i,s≤0, решения нет и Z_min стремится к минус бесконечности, иначе переходим к п.5.

5. Для выбора разрешающей строки r составляем неотрицательные отношения b_i/A_i,s≥0 , i=1,2,...,m, и выбираем среди них наименьшее. Если минимум достигается для нескольких строк, за разрешающую можно принять любую из них, при этом, в новом опорном плане значения некоторых базисных переменных станут равными 0, т.е., получаем вырожденный опорный план.

6. Выполняем преобразование Жордана-Гаусса с разрешающим элементом a_r,s и переходим к п.3

Геометрически симплекс-методу соответствует кратчайший обход вершин n-мерного выпуклого многогранника, образующего область допустимых решений задачи:

Геометрический смысл симплекс-метода

Здесь мы перешли от опорного плана C, представляющего собой одну из вершин многомерного многоугольника, к оптимальному плану E=X^*.

Запрограммировать это всё в Excel нелегко, но можно. В прилагаемом документе приведены 3 примера, реализующие решение задач симплекс-методом. Правда, при выполнени шага менять уже придётся 3 формулы, на листе первого примера на симплекс-метод они выделены жёлтым цветом: расчёт отношений для выбора разрешающей строки в ячейке I2, заполнение столбца БП в ячейке A12, шаг преобразования Жордана-Гаусса в ячейке B12. Как и в примере на преобразование Жордана-Гаусса, изменение формул связано только с необходимостью сослаться на новую строку, содержащую адрес ячейки с разрешающим элементом (для первого шага — ячейка C9).

Скачать примеры на преобразование Жордана-Гаусса и симплекс-метод в архиве .ZIP с документом Excel (73 Кб)

23.03.2014, 08:18 [36161 просмотр]

К этой статье пока нет комментариев, Ваш будет первым

Источник

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х² + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.

Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.

После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

Значения элементов введем в ячейки Excel в виде таблицы.

Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.

Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.

Умножим обратную матрицу Ах^-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.

Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.

Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.

Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.

Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.

В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х³ + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

Х_n+1 = X_n– F (X_n) / M, n = 0, 1, 2, … .

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х³ – 1. М = 11.

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Скачать решения уравнений в Excel

Корень на заданном промежутке один.

Источник

Метод Гаусса-Жордана предназначен для решения систем линейных алгебраических уравнений (СЛАУ). Он является модификацией метода Гаусса . Если метод Гаусса осуществляется в два этапа (прямой ход и обратный) то метод Гаусса-Жордана позволяет решить систему в один этап. Подробности и непосредственная схема применения метода Гаусса-Жордана описаны в примерах.

Во всех примерах $A$ обозначает матрицу системы, $widetilde{A}$ — расширенную матрицу системы. О матричной форме записи СЛАУ можно прочесть .

Пример №1

Решить СЛАУ $ left{ begin{aligned}
& 4x_1-7x_2+8x_3=-23;\
& 2x_1-4x_2+5x_3=-13;\
& -3x_1+11x_2+x_3=16.
end{aligned} right.$ методом Гаусса-Жордана.

Давайте перейдём от последней полученной нами матрице к системе:

$$
left{ begin{aligned}
& 0cdot x_1+1cdot x_2+0cdot x_3=1;\
& 1cdot x_1+0cdot x_2+0cdot x_3=-2;\
& 0cdot x_1+0cdot x_2+1cdot x_3=-1.
end{aligned} right.
$$

Упрощая полученную систему, имеем:

$$
left{ begin{aligned}
& x_2=1;\
& x_1=-2;\
& x_3=-1.
end{aligned} right.
$$

Полное решение без пояснений выглядит так:

Хоть этот способ выбора разрешающих элементов вполне допустим, но предпочтительнее выбирать в качестве разрешающих элементов диагональные элементы матрицы системы. Мы рассмотрим этот способ ниже.

Выбор разрешающих элементов на главной диагонали матрицы системы.

Так как этот способ решения полностью аналогичен предыдущему (за исключением выбора разрешающих элементов), то подробные пояснения пропустим. Принцип выбора разрешающих элементов прост: в первом столбце выбираем элемент первой строки, во втором столбце берём элемент второй строки, в третьем столбце — элемент третьей строки и так далее.

Первый шаг

В первом столбце выбираем элемент первой строки, т.е. в качестве разрешающего имеем элемент 4. Понимаю, что выбор числа 2 кажется более предпочтительным, так как это число всё-таки меньше, нежели 4. Для того, чтобы число 2 в первом столбце переместилось на первое место, поменяем местами первую и вторую строки:

$$
left(begin{array} {ccc|c} 4 & -7 & 8 & -23\ 2 & -4& 5 & -13 \ -3 & 11 & 1 & 16 end{array} right)rightarrow
left(begin{array} {ccc|c} 2 & -4& 5 & -13\ 4 & -7 & 8 & -23 \ -3 & 11 & 1 & 16 end{array} right)
$$

Итак, разрешающий элемент представлен числом 2. Точно так же, как и ранее, разделим первую строку на 2, а затем обнулим элементы первого столбца:

$$
left(begin{array} {ccc|c} 2 & -4& 5 & -13\ 4 & -7 & 8 & -23 \ -3 & 11 & 1 & 16 end{array} right)
begin{array} {l} I:2 \phantom{0} \ phantom{0} end{array} rightarrow
left(begin{array} {ccc|c} 1 & -2& 5/2 & -13/2 \4 & -7 & 8 & -23\ -3 & 11 & 1 & 16 end{array} right)
begin{array} {l} phantom{0} \ II-4cdot I\ III+3cdot I end{array} rightarrow
left(begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\0 & 1 & -2 & 3\ 0 & 5 & 17/2 & -7/2 end{array} right).
$$

Второй шаг

На втором шаге требуется обнулить элементы второго столбца. В качестве разрешающего элемента выбираем элемент второй строки, т.е. 1. Разрешающий элемент уже равен единице, поэтому никаких строк менять местами не будем. Кстати сказать, если бы мы захотели поменять местами строки, то первую строку трогать не стали бы, так как она уже была использована на первом шаге. А вот вторую и третью строки запросто можно менять местами. Однако, повторюсь, в данной ситуации менять местами строки не нужно, ибо разрешающий элемент уже оптимален — он равен единице.

$$
left(begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\0 & 1 & -2 & 3\ 0 & 5 & 17/2 & -7/2 end{array} right)
begin{array} {l} I+2cdot II \ phantom{0}\ III-5cdot II end{array} rightarrow
left(begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \ 0 & 1 & -2 & 3\ 0 & 0 & 37/2 & -37/2 end{array} right).
$$

Второй шаг окончен. Переходим к третьему шагу.

Третий шаг

На третьем шаге требуется обнулить элементы третьего столбца. В качестве разрешающего элемента выбираем элемент третьей строки, т.е. 37/2. Разделим элементы третьей строки на 37/2 (чтобы разрешающий элемент стал равен 1), а затем обнулим соответствующие элементы третьего столбца:

$$
left(begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \ 0 & 1 & -2 & 3\ 0 & 0 & 37/2 & -37/2 end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\ III:frac{37}{2} end{array} rightarrow
left(begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \ 0 & 1 & -2 & 3\ 0 & 0 & 1 & -1 end{array} right)
begin{array} {l} I+2cdot III\II+3/2cdot III\ phantom{0} end{array} rightarrow
left(begin{array} {ccc|c} 1 & 0 & 0 & -2 \ 0 & 1 & 0 & 1\ 0 & 0 & 1 & -1 end{array} right).
$$

Ответ получен: $x_1=-2$, $x_2=1$, $x_3=-1$. Полное решение без пояснений выглядит так:

Все остальные примеры на этой странице будут решены именно вторым способом: в качестве разрешающих будем выбирать диагональные элементы матрицы системы.

Ответ
: $x_1=-2$, $x_2=1$, $x_3=-1$.

Пример №2

Решить СЛАУ $ left{ begin{aligned}
& 3x_1+x_2+2x_3+5x_4=-6;\
& 3x_1+x_2+2x_4=-10;\
& 6x_1+4x_2+11x_3+11x_4=-27;\
& -3x_1-2x_2-2x_3-10x_4=1.
end{aligned} right.$ методом Гаусса-Жордана.

Запишем расширенную матрицу данной системы : $widetilde{A}=left(begin{array} {cccc|c} 3 & 1 & 2 & 5 & -6\ 3 & 1& 0 & 2 & -10 \ 6 & 4 & 11 & 11 & -27 \ -3 & -2 & -2 & -10 & 1 end{array} right)$.

В качестве разрешающих элементов станем выбирать диагональные элементы матрицы системы: на первом шаге возьмём элемент первой строки, на втором шаге элемент второй строки и так далее.

Первый шаг

Нам нужно обнулить соответствующие элементы первого столбца. В качестве разрешающего элемента возьмём элемент первой строки, т.е. 3. Соответственно первую строку придётся разделить на 3, чтобы разрешающий элемент стал равен единице. А затем обнулить все элементы первого столбца, кроме разрешающего:

$$
left(begin{array}{cccc|c}
3 & 1 & 2 & 5 & -6\
3 & 1 & 0 & 2 & -10\
6 & 4 & 11 & 11 & -27\
-3 & -2 & -2 & -10 & 1end{array}right)
begin{array} {l} I:3\ phantom{0}\phantom{0}\phantom{0}end{array} rightarrow
left(begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\
3 & 1 & 0 & 2 & -10\
6 & 4 & 11 & 11 & -27\
-3 & -2 & -2 & -10 & 1end{array}right)
begin{array} {l} phantom{0}\ II-3cdot I\III-6cdot I\IV+3cdot Iend{array} rightarrow\
rightarrowleft(begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\
0 & 0 & -2 & -3 & -4\
0 & 2 & 7 & 1 & -15\
0 & -1 & 0 & -5 & -5end{array}right).
$$

Второй шаг

Переходим к обнулению соответствующих элементов второго столбца. В качестве разрешающего элемента мы уславливались взять элемент второй строки, но сделать этого мы не в силах, так как нужный элемент равен нулю. Вывод: будем менять местами строки. Первую строку трогать нельзя, так как она уже использовалась на первом шаге. Выбор небогат: или меняем местами вторую и третью строки, или же меняем местами четвёртую и вторую. Так как в четвёртой строке наличествует (-1), то пусть в «обмене» поучавствует именно четвёртая строка. Итак, меняем местами вторую и четвёртую строки:

$$
left(begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\
0 & 0 & -2 & -3 & -4\
0 & 2 & 7 & 1 & -15\
0 & -1 & 0 & -5 & -5end{array}right)rightarrow
left(begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\
0 & -1 & 0 & -5 & -5\
0 & 2 & 7 & 1 & -15\
0 & 0 & -2 & -3 & -4end{array}right)
$$

Вот теперь всё в норме: разрешающий элемент равен (-1). Бывает, кстати, что смена мест строк невозможна, но это обговорим в следующем примере №3. А пока что делим вторую строку на (-1), а затем обнуляем элементы второго столбца. Обратите внимание, что во втором столбце элемент, расположенный в четвёртой строке, уже равен нулю, поэтому четвёртую строку трогать не будем.

$$
left(begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\
0 & -1 & 0 & -5 & -5\
0 & 2 & 7 & 1 & -15\
0 & 0 & -2 & -3 & -4end{array}right)
begin{array} {l} phantom{0}\II:(-1) \phantom{0}\phantom{0}end{array} rightarrow
left(begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\
0 & 1 & 0 & 5 & 5\
0 & 2 & 7 & 1 & -15\
0 & 0 & -2 & -3 & -4end{array}right)
begin{array} {l} I-1/3cdot II\ phantom{0} \III-2cdot II\phantom{0}end{array} rightarrow\
rightarrowleft(begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\
0 & 1 & 0 & 5 & 5\
0 & 0 & 7 & -9 & -25\
0 & 0 & -2 & -3 & -4end{array}right).
$$

Третий шаг

Приступаем к обработке третьего столбца. В качестве разрешающего элемента мы условились брать диагональные элементы матрицы системы. Для третьего шага это означает выбор элемента, расположенного в третьей строке. Однако если мы просто возьмём элемент 7 в качестве разрешающего, то всю третью строку придётся делить на 7. Мне кажется, что разделить на (-2) попроще. Поэтому поменяем местами третью и четвёртую строки, и тогда разрешающим элементом станет (-2):

$$
left(begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\
0 & 1 & 0 & 5 & 5\
0 & 0 & 7 & -9 & -25\
0 & 0 & -2 & -3 & -4end{array}right) rightarrow
left(begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\
0 & 1 & 0 & 5 & 5\
0 & 0 & -2 & -3 & -4\
0 & 0 & 7 & -9 & -25end{array}right)
$$

Разрешающий элемент — (-2). Делим третью строку на (-2) и обнуляем соответствующие элементы третьего столбца:

$$
left(begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\
0 & 1 & 0 & 5 & 5\
0 & 0 & -2 & -3 & -4\
0 & 0 & 7 & -9 & -25end{array}right)
begin{array} {l} phantom{0}\ phantom{0} \III:(-2)\phantom{0}end{array}rightarrow
left(begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\
0 & 1 & 0 & 5 & 5\
0 & 0 & 1 & 3/2 & 2\
0 & 0 & 7 & -9 & -25end{array}right)
begin{array} {l} I-2/3cdot III\ phantom{0} \ phantom{0}\IV-7cdot IIIend{array}rightarrow\
rightarrowleft(begin{array}{cccc|c}
1 & 0 & 0 & -1 & -5\
0 & 1 & 0 & 5 & 5\
0 & 0 & 1 & 3/2 & 2\
0 & 0 & 0 & -39/2 & -39end{array}right).
$$

Четвёртый шаг

Переходим к обнулению четвёртого столбца. Разрешающий элемент расположен в четвёртой строке и равен числу $-frac{39}{2}$.

$$
left(begin{array}{cccc|c}
1 & 0 & 0 & -1 & -5\
0 & 1 & 0 & 5 & 5\
0 & 0 & 1 & 3/2 & 2\
0 & 0 & 0 & -39/2 & -39end{array}right)
begin{array} {l} phantom{0}\ phantom{0} \ phantom{0}\IV:left(-frac{39}{2}right) end{array}rightarrow
left(begin{array}{cccc|c}
1 & 0 & 0 & -1 & -5\
0 & 1 & 0 & 5 & 5\
0 & 0 & 1 & 3/2 & 2\
0 & 0 & 0 & 1 & 2end{array}right)
begin{array} {l} I+IV\ II-5cdot IV \ III-3/2cdot IV \ phantom{0} end{array}rightarrow\
rightarrowleft(begin{array}{cccc|c}
1 & 0 & 0 & 0 & -3\
0 & 1 & 0 & 0 & -5\
0 & 0 & 1 & 0 & -1\
0 & 0 & 0 & 1 & 2end{array}right).
$$

Решение окончено. Ответ таков: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$. Полное решение без пояснений:

Ответ
: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.

Пример №3

Решить СЛАУ $left{begin{aligned}
& x_1-2x_2+3x_3+4x_5=-5;\
& 2x_1+x_2+5x_3+2x_4+9x_5=-3;\
& 3x_1+4x_2+7x_3+4x_4+14x_5=-1;\
& 2x_1-4x_2+6x_3+11x_5=2;\
& -2x_1+14x_2-8x_3+4x_4-7x_5=20;\
& -4x_1-7x_2-9x_3-6x_4-21x_5=-9.
end{aligned}right.$ методом Гаусса-Жордана. Если система является неопределённой, указать базисное решение.

Подобные примеры разбираются в теме «Общее и базисное решения СЛАУ» . Во второй части упомянутой темы данный пример решён с помощью метод Гаусса . Мы же решим его с помощью метода Гаусса-Жордана. Пошагово разбивать решение не станем, так как это уже было сделано в предыдущих примерах.

$$
left(begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\
2 & 1 & 5 & 2 & 9 & -3\
3 & 4 & 7 & 4 & 14 & -1\
2 & -4 & 6 & 0 & 11 & 2\
-2 & 14 & -8 & 4 & -7 & 20\
-4 & -7 & -9 & -6 & -21 & -9 end{array}right)
begin{array} {l} phantom{0} \ II-2cdot I\ III-3cdot I\ IV-2cdot I\ V+2cdot I\VI+4cdot I end{array} rightarrow
left(begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\
0 & 5 & -1 & 2 & 1 & 7\
0 & 10 & -2 & 4 & 2 & 14\
0 & 0 & 0 & 0 & 3 & 12\
0 & 10 & -2 & 4 & 1 & 10\
0 & -15 & 3 & -6 & -5 & -29 end{array}right)
begin{array} {l} phantom{0} \ II:5 \ phantom{0}\ phantom{0}\ phantom{0} \ phantom{0}end{array} rightarrow \
left(begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\
0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\
0 & 10 & -2 & 4 & 2 & 14\
0 & 0 & 0 & 0 & 3 & 12\
0 & 10 & -2 & 4 & 1 & 10\
0 & -15 & 3 & -6 & -5 & -29 end{array}right)
begin{array} {l} I+2cdot II \ phantom{0}\ III-10cdot II\ IV:3\ V-10cdot II\VI+15cdot II end{array} rightarrow
left(begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\
0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\
0 & 0 & 0 & 0 & 0 & 0\
0 & 0 & 0 & 0 & 1 & 4\
0 & 0 & 0 & 0 & -1 & -4\
0 & 0 & 0 & 0 & -2 & -8 end{array}right).
$$

Полагаю, что одно из сделанных преобразований всё-таки требует пояснения: $IV:3$. Все элементы четвёртой строки нацело делились на три, поэтому сугубо из соображений упрощения мы разделили все элементы этой строки на три. Третья строка в преобразованной матрице стала нулевой. Вычеркнем нулевую строку:

$$
left(begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\
0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\
0 & 0 & 0 & 0 & 1 & 4\
0 & 0 & 0 & 0 & -1 & -4\
0 & 0 & 0 & 0 & -2 & -8 end{array}right)
$$

Нам пора переходить к третьему шагу, на котором должны быть обнулены элементы третьего столбца. Однако диагональный элемент (третья строка) равен нулю. И смена мест строк ничего не даст. Первую и вторую строки мы уже использовали, поэтому их трогать мы не можем. А четвёртую и пятую строки трогать нет смысла, ибо проблема равенства нулю разрешающего элемента никуда не денется.

В этой ситуации проблема решается крайне незамысловато. Мы не можем обработать третий столбец? Хорошо, перейдём к четвёртому. Может, в четвёртом столбце элемент третьей строки будет не равен нулю. Однако четвёртый столбец «болеет» той же проблемой, что и третий. Элемент третьей строки в четвёртом столбце равен нулю. И смена мест строк опять-таки ничего не даст. Четвёртый столбец тоже не можем обработать? Ладно, перейдём к пятому. А вот в пятом столбце элемент третьей строки очень даже не равен нулю. Он равен единице, что довольно-таки хорошо. Итак, разрешающий элемент в пятом столбце равен 1. Разрешающий элемент выбран, поэтому осуществим дальшейшие преобразования метода Гаусса-Жордана:

$$
left(begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\
0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\
0 & 0 & 0 & 0 & 1 & 4\
0 & 0 & 0 & 0 & -1 & -4\
0 & 0 & 0 & 0 & -2 & -8 end{array}right)
begin{array} {l} I-22/5cdot III \ II-1/5cdot III \ phantom{0}\ IV+III\ V+2cdot III end{array} rightarrow
left(begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 0 & -99/5\
0 & 1 & -1/5 & 2/5 & 0 & 3/5\
0 & 0 & 0 & 0 & 1 & 4\
0 & 0 & 0 & 0 & 0 & 0\
0 & 0 & 0 & 0 & 0 & 0 end{array}right)
rightarrow \
rightarrowleft|text{Удаляем нулевые строки}right|rightarrow
left(begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 0 & -99/5\
0 & 1 & -1/5 & 2/5 & 0 & 3/5\
0 & 0 & 0 & 0 & 1 & 4 end{array}right)$$

Мы привели матрицу системы и расширенную матрицу системы к ступенчатому виду. Ранги обеих матриц равны $r=3$, т.е. надо выбрать 3 базисных переменных. Количество неизвестных $n=5$, поэтому нужно выбрать $n-r=2$ свободных переменных. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли данная система является неопределённой (т.е. имеет бесконечное количество решений). Для нахождения решений системы составим «ступеньки»:

На «ступеньках» стоят элементы из столбцов №1, №2, №5. Следовательно, базисными будут переменные $x_1$, $x_2$, $x_5$. Свободными переменными, соответственно, будут $x_3$, $x_4$. Столбцы №3 и №4, соответствующие свободным переменным, перенесём за черту, при этом, конечно, не забыв сменить им знаки.

$$
left(begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 0 & -99/5\
0 & 1 & -1/5 & 2/5 & 0 & 3/5\
0 & 0 & 0 & 0 & 1 & 4 end{array}right)rightarrow
left(begin{array}{ccc|ccc}
1 & 0 & 0 & -99/5 & -13/5 & -4/5\
0 & 1 & 0 & 3/5 & 1/5 & -2/5\
0 & 0 & 1 & 4 & 0 & 0end{array}right).
$$

Из последней матрицы получим общее решение: $left{begin{aligned}
& x_1=-frac{99}{5}-frac{13}{5}x_3-frac{4}{5}x_4;\
& x_2=frac{3}{5}+frac{1}{5}x_3-frac{2}{5}x_4;\
& x_3 in R;\
& x_4in R;\
& x_5=4.
end{aligned}right.$. Базисное решение найдём, приняв свободные переменные равными нулю, т.е. $x_3=0$, $x_4=0$:

$$
left{begin{aligned}
& x_1=-frac{99}{5};\
& x_2=frac{3}{5};\
& x_3=0;\
& x_4=0;\
& x_5=4.
end{aligned}right.
$$

Задача решена, осталось лишь записать ответ.

Ответ
: Общее решение: $left{begin{aligned}
& x_1=-frac{99}{5}-frac{13}{5}x_3-frac{4}{5}x_4;\
& x_2=frac{3}{5}+frac{1}{5}x_3-frac{2}{5}x_4;\
& x_3 in R;\
& x_4in R;\
& x_5=4.
end{aligned}right.$, базисное решение: $left{begin{aligned}
& x_1=-frac{99}{5};\
& x_2=frac{3}{5};\
& x_3=0;\
& x_4=0;\
& x_5=4.
end{aligned}right.$.

Рассмотрим подробно, как производится пересчет симплекс-таблиц (на примере одной итерации).
Пусть имеется симплекс-таблица представленная на Рис.1
. Решается задача максимизации целевой функции.
Разрешающий столбец соответствует переменной x 2
,
а разрешающая строка переменной x 3
(красные числа), на их пересечении находится разрешающий элемент (клетка с серым фоном).
Первое, что нам необходимо сделать — это заменить. Разрешающая строка показывает,
какая переменная должна быть выведена из базиса (в нашем случае x 3
), а разрешающий столбец показывает какая переменная должна
войти в базис (в нашем случае x 2
). На Рис.2
факт замены акцентирован синей линией.

Теперь пересчитаем элементы стоящие в разрешающей строке. Для этого просто разделим каждый из них на разрешающий элемент (в нашем примере 4
).
А все элементы разрешающего столбца обнулим, кроме элемента стоящего в разрешающей строке. (Смотри Рис.2
)

Рисунок 1

Остальные ячейки таблицы (кроме столбца «Отношение») пересчитываются по так называемому правилу прямоугольника
, смысл которого
проще всего понять на примере. Пусть нужно пересчитать элемент обведенный на Рис.1
красным контуром. Мысленно проводим от него
вертикальную и горизонтальную линии до пересечения, с разрешающей строкой и разрешающим столбцом. Элементы стоящие в местах пересечения
обведены синими контурами (Смотри Рис.1
). Новое значение «красного» элемента будет равно нынешнему значению элемента минус
произведение «синих» деленное на разрешающий («серый») элемент (Смотри Рис.1
). То есть:
18 — (64 * -1) / 4 = 34
, здесь знаком «*
» показана операция умножения.
Записываем новое значение на прежнее место (Смотри Рис.2
красный контур).

Рисунок 2

Пользуясь данным правилом, заполняем все пустые элементы таблицы (кроме столбца «Отношение») Смотри Рис.3
.
После этого определим новый разрешающий столбец. Для этого проанализируем строку «Q»
и так как наша задача на максимум,
то найдем в ней максимальный положительный элемент
, он и определит разрешающий столбец. В нашем случае это 3/2
.
Все элементы разрешающего столбца показаны красным шрифтом (Смотри Рис.3
). Если после очередной итерации в строке «Q»

не окажется положительных элементов — это значит что оптимальное решение достигнуто, итерации прекращаются.
Если бы наша задача была на минимум, то разрешающий столбец определялся бы по минимальному отрицательному элементу, и
если после очередной итерации в строке «Q»
не окажется отрицательных элементов, значит достигнуто оптимальное решение.

Рисунок 3

Теперь заполним столбец «Отношение». Для этого нужно соответствующий (стоящий в той же строке)
элемент столбца «Решение» разделить на соответствующий элемент разрешающего столбца (Смотри Рис.3
).
Обратите внимание
, что данная операция проводится только для положительных
элементов разрешающего столбца и
строка «Q»
в данной операции не участвует. Если после некоторой итерации в разрешающем столбце
не окажется положительных элементов, то данная задача неразрешима ввиду неограниченности целевой функции, итерации прекращаются.

После заполнения столбца «Отношение» определим новую разрешающую строку. Она определяется минимальным элементом из столбца «Отношение».
В нашем случае это 32
, все элементы разрешающей строки показаны красным шрифтом (Смотри Рис.3
).
На этом очередная итерация заканчивается, на следующей итерации переменная x 2
будет выведена из базиса
(об этом нам говорит новая разрешающая строка), ее место займет переменная x 1
(об этом нам говорит новый
разрешающий столбец) и все вычисления повторятся снова.

В общем случае линейное уравнение имеет вид:

Уравнение имеет решение: если хотя бы один из коэффициентов при неизвестных отличен от нуля. В этом случае любой -мерный вектор называется решением уравнения, если при подстановке его координат уравнение обращается в тождество.

Общая характеристика разрешенной системы уравнений

Пример 20.1

Дать характеристику системе уравнений
.

Решение
:

1. Входит ли в состав противоречивое уравнение?
(Если коэффициенты, в этом случае уравнение имеет вид: и называется противоречивым
.)

Если система содержит противоречивое, то такая система несовместна и не имеет решения

2. Найти все разрешенные переменные
. (Неизвестная называется
разрешенной
для системы уравнений, если она входит в одно из уравнений системы с коэффициентом +1, а в остальные уравнения не входит (т.е. входит с коэффициентом, равным нулю).

3. Является ли система уравнений разрешенной?
(Система уравнений называется разрешенной
, если каждое уравнение системы содержит разрешенную неизвестную, среди которых нет совпадающих)

Разрешенные неизвестные, взятые по одному из каждого уравнения системы, образуют полный набор разрешенных неизвестных
системы. (в нашем примере это )

Разрешенные неизвестные, входящие в полный набор, называют также базисными
(), а не входящие в набор — свободными
().

В общем случае разрешенная система уравнений имеет вид:

На данном этапе главное понять что такое разрешенная неизвестная
(входящая в базис и свободная).

Общее Частное Базисное решения

Общим решением
разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные:

Частным решением
называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных.

Базисным решением
называется частное решение, получающееся из общего при нулевых значениях свободных переменных.

Базисное решение (вектор) называется вырожденным
, если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.
Базисное решение называется невырожденным
, если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.

Теорема (1)

Разрешенная система уравнений всегда совместна
(потому что она имеет хотя бы одно решение); причем если система не имеет свободных неизвестных,
(то есть в системе уравнений все разрешенные входят в базис) то она определена
(имеет единственное решение); если же имеется хотя бы одна свободная переменная, то система не определена
(имеет бесконечное множество решений).

Пример 1. Найти общее, базисное и какое-либо частное решение системы уравнений:

Решение
:

1. Проверяем является ли система разрешенной?

Система является разрешенной (т.к. каждое из уравнений содержит в себе разрешенную неизвестную)

2. Включаем в набор разрешенные неизвестные — по одному из каждого уравнения
.

3. Записываем общее решение в зависимости от того какие разрешенные неизвестные мы включили в набор
.

4. Находим частное решение
. Для этого приравниваем свободные переменные, которые мы не включили в набор приравнять к произвольным числам.

Ответ: частное решение
(один из вариантов)

5. Находим базисное решение
. Для этого приравниваем свободные переменные, которые мы не включили в набор к нулю.

Элементарные преобразования линейных уравнений

Системы линейных уравнений приводятся к равносильным разрешенным системам с помощью элементарных преобразований.

Теорема (2)

Если какое-либо уравнение системы умножить на некоторое отличное от нуля число
, а остальные уравнения оставить без изменения, то . (то есть если умножить левую и правую часть уравнения на одно и то же число то получится уравнение, равносильное данному)

Теорема (3)

Если к какому-либо уравнению системы прибавить другое
, а все остальные уравнения оставить без изменения, то получится система, равносильная данной
. (то есть если сложить два уравнения (сложив их левые и правые части) то получится уравнение равносильное данным)

Следствие из Теорем (2 и 3)

Если к какому-либо уравнению прибавить другое, умноженное на некоторое число
, а все остальные уравнения оставить без изменения, то получится система, равносильная данной
.

Формулы пересчета коэффициентов системы

Если у нас есть система уравнений и мы хотим преобразовать ее в разрешенную систему уравнений в этом нам поможет метод Жордана-Гаусса.

Преобразование Жордана
с разрешающим элементом позволяет получить для системы уравнений разрешенную неизвестную в уравнении с номером . (пример 2).

Преобразование Жордана состоит из элементарных преобразований двух типов:

Допустим мы хотим сделать неизвестную в нижнем уравнении разрешенной неизвестной. Для этого мы должны разделить на , так чтобы сумма .

Пример 2 Пересчитаем коэффициенты системы

При делении уравнения с номером на , его коэффициенты пересчитываются по формулам:

Чтобы исключить из уравнения с номером , нужно уравнение с номером умножить на и прибавить к этому уравнению.

Теорема (4) О сокращении числа уравнений системы.

Если система уравнений содержит тривиальное уравнение, то его можно исключить из системы, при этом получится система равносильная исходной.

Теорема (5) О несовместимости системы уравнений.

Если система уравнений содержит противоречивое уравнение, то она несовместна.

Алгоритм метода Жордана-Гаусса

Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:

Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.
Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.
Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.
Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.
Далее заново переходят к пункту 1

Пример 3 Решить систему уравнений методом Жордана-Гаусса.

Найти
: два общих и два соответствующих базисных решения

Решение
:

Вычисления приведены в нижеследующей таблице:

Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель.

В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать.

При графическом методе решения задач ЛП мы фактически из множества вершин, принадлежащих границе множества решений системы неравенств, выбрали такую вершину, в которой значение целевой функции достигало максимума (минимума). В случае двух переменных этот метод совершенно нагляден и позволяет быстро находить решение задачи.

Если в задаче три и более переменных, а в реальных экономических задачах как раз такая ситуация, трудно представить наглядно область решений системы ограничений. Такие задачи решаются с помощью симплекс-метода

или методом последовательных улучшений. Идея метода проста и заключается в следующем.

По определенному правилу находится первоначальный опорный план (некоторая вершина области ограничений). Проверяется, является ли план оптимальным. Если да, то задача решена. Если нет, то переходим к другому улучшенному плану — к другой вершине. значение целевой функции на этом плане (в этой вершине) заведомо лучше, чем в предыдущей. Алгоритм перехода осуществляется с помощью некоторого вычислительного шага, который удобно записывать в виде таблиц, называемых симплекс-таблицами

. Так как вершин конечное число, то за конечное число шагов мы приходим к оптимальному решению.

Рассмотрим симплексный метод на конкретном примере задачи о составлении плана.

Еще раз заметим, что симплекс-метод применим для решения канонических задач ЛП, приведенных к специальному виду, т. е. имеющих базис, положительные правые части и целевую функцию, выраженную через небазисные переменные. Если задача не приведена к специальному виду, то нужны дополнительные шаги, о которых мы поговорим позже.

Рассмотрим задачу о плане производства, предварительно построив модель и приведя ее к специальному виду.

Задача.

Для изготовления изделий А
и В
склад может отпустить сырья не более 80 единиц. Причем на изготовление изделия А
расходуется две единицы, а изделия В
— одна единица сырья. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если изделий А
требуется изготовить не более 50 шт., а изделий В
— не более 40 шт. Причем, прибыль от реализации одного изделия А
— 5 руб., а от В
— 3 руб.

Построим математическую модель, обозначив за х
1 количество изделий А в плане, за х
2 — количество изделий В
. тогда система ограничений будет выглядеть следующим образом:

Приведем задачу к каноническому виду, введя дополнительные переменные:

(3.10)

F = -5x 1 — 3x 2 → min.

Эта задача имеет специальный вид (с базисом, правые части неотрицательны). Ее можно решить симплекс-методом.

I
этап.
Запись задачи в симплекс-таблицу. Между системой ограничений задачи (3.10) и симплекс-таблицей взаимно-однозначное соответствие. Строчек в таблице столько, сколько равенств в системе ограничений, а столбцов — столько, сколько свободных переменных. Базисные переменные заполняют первый столбец, свободные — верхнюю строку таблицы. Нижняя строка называется индексной, в ней записываются коэффициенты при переменных в целевой функции. В правом нижнем углу первоначально записывается 0, если в функции нет свободного члена; если есть, то записываем его с противоположным знаком. На этом месте (в правом нижнем углу) будет значение целевой функции, которое при переходе от одной таблицы к другой должно увеличиваться по модулю. Итак, нашей системе ограничений соответствует таблица 3.4, и можно переходить ко II этапу решения.

Таблица 3.4

базисные			свободные

II
этап
. Проверка опорного плана на оптимальность.

Данной таблице 3.4 соответствует следующий опорный план:

(х
1 , х
2 , х
3 , х
4 , х
5) = (0, 0, 50, 40, 80).

Свободные переменные х
1 , х
2 равны 0; х
1 = 0, х
2 = 0. А базисные переменные х
3 , х
4 , х
5 принимают значения х
3 = 50, х
4 = 40, х
5 = 80 — из столбца свободных членов. Значение целевой функции:

—F

= — 5х
1 — 3х
2 = -5 · 0 — 3 · 0 = 0.

Наша задача — проверить, является ли данный опорный план оптимальным. для этого необходимо просмотреть индексную строку — строку целевой функции F
.

Возможны различные ситуации.

1. В индексной F
-строке нет отрицательных элементов. Значит, план оптимален, можно выписать решение задачи. Целевая функция достигла своего оптимального значения, равного числу, стоящему в правом нижнем углу, взятому с противоположным знаком. Переходим к IV этапу.

2. В индексной строке есть хотя бы один отрицательный элемент, в столбце которого нет положительных. Тогда делаем вывод о том, что целевая функция F
→∞ неограниченно убывает.

3. В индексной строке есть отрицательный элемент, в столбце которого есть хотя бы один положительный. Тогда переходим к следующему III
этапу. пересчитываем таблицу, улучшая опорный план.

III
этап
. Улучшение опорного плана.

Из отрицательных элементов индексной F
-строки выберем наибольший по модулю, назовем соответствующий ему столбец разрешающим и пометим «».

Чтобы выбрать разрешающую строку, необходимо вычислить отношения элементов столбца свободных членов только
к положительным
элементам разрешающего столбца. Выбрать из полученных отношений минимальное. Соответствующий элемент, на котором достигается минимум, называется разрешающим. Будем выделять его квадратом.

В нашем примере, , элемент 2 — разрешающий. Строка, соответствующая этому элементу, тоже называется разрешающей (табл. 3.5).

Таблица 3.5

Выбрав разрешающий элемент, делаем перечет таблицы по правилам:

1. В новой таблице таких же размеров, что и ранее, переменные разрешающей строки и столбца меняются местами, что соответствует переходу к новому базису. В нашем примере: х
1 входит в базис, вместо х
5 , которая выходит из базиса и теперь свободная (табл. 3.6).

Таблица 3.6

базисные			свободные

2. На месте разрешающего элемента 2 записываем обратное ему число .

3. Элементы разрешающей строки делим на разрешающий элемент.

4. Элементы разрешающего столбца делим на разрешающий элемент и записываем с противоположным знаком.

5. Чтобы заполнить оставшиеся элементы таблицы 3.6, осуществляем пересчет по правилу прямоугольника. Пусть мы хотим посчитать элемент, стоящий на месте 50.

Соединяем этот элемент мысленно с разрешающим, находим произведение, вычитаем произведение элементов, находящихся на другой диагонали получившегося прямоугольника. Разность делим на разрешающий элемент.

Итак, . Записываем 10 на место, где было 50. Аналогично:

, , , .

Таблица 3.7

Имеем новую таблицу 3.7, базисными переменными теперь являются переменные {x 3 ,x 4 ,x 1 }. Значение целевой функции стало равно -200, т. е. уменьшилось. Чтобы проверить данное базисное решение на оптимальность надо перейти опять ко II этапу. Процесс, очевидно, конечен, критерием остановки являются пункт 1 и 2 II этапа.

Доведем решение задачи до конца. Для этого проверим индексную строку и, увидев в ней отрицательный элемент , назовем соответствующий ему столбец разрешающим и, согласно III этапу, пересчитаем таблицу. Составив отношения и выбрав среди них минимальное = 40, определили разрешающий элемент 1. теперь пересчет осуществляем согласно правилам 2-5.

Таблица 3.8

базисные

свободные

х
3 = 30, х
2 = 40, х
1 = 20. Свободные переменные равны 0, х
5 = 0, х
4 = 0. Целевая функция принимает значение последнего элемента столбца свободных членов с противоположным знаком: —F
= -220 F

= 220, в нашем примере функция исследовалась на min, и первоначально F

max, поэтому фактически знак поменялся дважды. Итак, х
* = (20, 40, 30, 0, 0), F
* = 220. Ответ к задаче:

Необходимо в план выпуска включить 20 изделий типа А
, 40 изделий типа В, при этом прибыль будет максимальной и будет равна 220 руб.

В конце этого параграфа приведем блок-схему алгоритма симплекс-метода, которая в точности повторяет этапы, но, возможно, для некоторых читателей будет более удобна в пользовании, т. к. стрелочки указывают четкую направленность действий.

Ссылки над прямоугольниками в блок-схеме показывают, к какому этапу или подпункту относится соответствующая группа преобразований. правило нахождения первоначального опорного плана будет сформулировано в пункте 3.7.

Вопросы для самоконтроля

1. Как строится симплекс-таблица?

2. Как отражается смена базиса в таблице?

3. Сформулируйте критерий остановки симплекс-метода.

4. Как организовать пересчет таблицы?

5. С какой строки удобно начинать пересчет таблицы?

При
условии отсутствия “0-строк”
(ограничений-равенств) и “свободных”
переменных (т.е. переменных, на которые
не наложено требование неотрицательности).

2. В случае присутствия
ограничений-равенств и “свободных”
переменных поступают следующим образом.

Выбирают
разрешающий элемент в “0-строке”
и делают шаг модифицированного жорданова
исключения, после чего вычеркивают
этот разрешающий столбец. Данную
последовательность действий продолжают
до тех пор, пока в симплексной таблице
остается хотя бы одна “0-строка”
(при этом таблица сокращается).

Если
же присутствуют и свободные переменные,
то необходимо данные переменные сделать
базисными. И после того, как свободная
переменная станет базисной, в процессе
определения разрешающего элемента при
поиске опорного и оптимального планов
данная строка не учитывается (но
преобразуется).

Вырожденность в задачах линейного программирования

Рассматривая
симплекс-метод, мы предполагали, что
задача линейного программирования
является невырожденной, т.е. каждый
опорный план содержит ровно

положительных компонент, где
– число ограничений в задаче. В вырожденном
опорном плане число положительных
компонент оказывается меньше числа
ограничений: некоторые базисные
переменные, соответствующие данному
опорному плану, принимают нулевые
значения. Используя геометрическую
интерпретацию для простейшего случая,
когда
(число небазисных переменных равно 2),
легко отличить вырожденную задачу от
невырожденной. В вырожденной задаче в
одной вершине многогранника условий
пересекается более двух прямых,
описываемых уравнениями вида
.
Это значит, что одна или несколько сторон
многоугольника условий стягиваются в
точку.

Аналогично
при
в вырожденной задаче в одной
вершине пересекается более 3-х плоскостей
.

В
предположении о невырожденности
задачи находилось только одно значение

,
по которому определялся индекс
выводимого из базиса вектора условий
(выводимой из числа базисных переменной).
В вырожденной задаче
может достигаться на нескольких индексах
сразу (для нескольких строк). В этом
случае в находимом опорном плане
несколько базисных переменных будут
нулевыми.

Если задача
линейного программирования
оказывается вырожденной, то при плохом
выборе вектора условий, выводимого из
базиса, может возникнуть бесконечное
движение по базисам одного и того же
опорного плана. Так называемое, явление
зацикливания. Хотя в практических
задачах линейного программирования
зацикливание явление крайне редкое,
возможность его не исключена.

Один
из приемов борьбы с вырожденностью
состоит в преобразовании задачи путем
“незначительного” изменения вектора
правых частей системы ограничений на
величины
,
таким образом, чтобы задача стала
невырожденной, и, в то же время, чтобы
это изменение не повлияло реально на
оптимальный план задачи.

Чаще реализуемые
алгоритмы включают в себя некоторые
простые правила, снижающие вероятность
возникновения зацикливания или его
преодоления.

Пусть
переменную
необходимо сделать базисной. Рассмотрим
множество индексов,
состоящее из тех,
для которых достигается
.
Множество индексов,
для которых выполняется данное условие
обозначим через.
Еслисостоит из одного элемента, то из базиса
исключается вектор условий(переменнаяделается небазисной).

Если
состоит более чем из одного элемента,
то составляется множество,
которое состоит из
,
на которых достигается
.
Еслисостоит из одного индекса,
то из базиса выводится переменная.
В противном случае составляется множествои т.д.

Практически
правилом надо пользоваться, если
зацикливание уже обнаружено.

Источник

Кафедра экономико-математических методов и моделей

Орлова
И. В., Орлов П.В.

Решение
оптимизационных задач средствами EXCEL.

Краткий
конспект лекций и лабораторная работа
№ 1 по курсу «Экономико-математические
методы и прикладные модели»

Москва

2001 г.

Оглавление

решение
систем линейных уравнений методом
жордана — гаусса 3

Общая
задача оптимизации 5

Графический
метод решения задач линейного
программирования. 6

Симплексный
метод решения задачи линейного
программирования 14

Технология
решения задач линейного программирования
с помощью Поиска решений в среде
EXCEL. 17

Двойственность
в задачах линейного программирования.
Анализ полученных оптимальных решений. 31

Задания
к контрольной работе 40

ЗАДАЧА
1. 40

ЗАДАЧА
2. 40

Список
литературы, имеющейся в библиотеке
ВЗФЭИ. 44

Решение систем линейных уравнений методом жордана — гаусса

Пример
1. Решить
методом Жордана-Гаусса систему линейных
уравнений:

а)
Х₁
+ Х₂
+ 2Х₃
= -1

2Х₁
— Х₂
+ 2Х₃
= -4

4Х₁
+ Х₂
+ 4Х₃
= -2

Решение:

Составим
расширенную матрицу

1
Итерация.

В
качестве направляющего элемента выбираем
элемент
.
Преобразуем первый столбец в единичный.
Для этого к второй и третьей строкам
прибавляем первую строку, соответственно
умноженную на -2 и -4. Получим
матрицу:

На
этом первая итерация закончена.

2
Итерация.

Выбираем
направляющий элемент
.
Так как
,
то делим вторую строку на -3. Затем
умножаем вторую строку на 1 и 3 и складываем
соответственно с первой и третьей
строками. Получим
матрицу:

3
Итерация.

Выбираем
направляющий элемент
.
Так как
,
то делим третью строку на -2. Преобразуем
третий столбец в единичный. Для этого
умножаем третью строку на -4/3 и -2/3 и
складываем соответственно с первой и
второй строками. Получим
матрицу:

откуда
Х₁
= 1, Х₂
= 2, Х₃
= -2.

Пример
2.
Решить методом Жордана — Гаусса систему
линейных уравнений:

Х₁
+ 2Х₂
+ 2Х₃
+22Х₄–4Х₅=
11

Х₁
+2Х₂
+ Х₃
+16Х₄–4Х₅=
9

Х₁
+ Х₂
+ Х₃
+12Х₄-2Х₅=
6

Решение:

Составим
расширенную матрицу

1
Итерация.

В качестве
направляющего элемента выбираем элемент
.
Преобразуем первый столбец в единичный.
Для этого ко второй и третьей строкам
прибавляем первую строку, соответственно
умноженную на -1. Получим матрицу:

На
этом первая итерация закончена.

2
Итерация.

Выбираем направляющий
элемент
.
Умножаем третью строку на -1. Преобразуем
второй столбец в единичный. Для этого
к первой строке прибавляем третью
строку, соответственно умноженную на
-2.

Получим
матрицу:

3
Итерация.

Выбираем направляющий
элемент
.
Так как,
то умножаем вторую строку на –1.
Преобразуем третий столбец в единичный.
Для этого вторую строку складываем с
третьей строкой. Получим матрицу:

	Х1	Х2	Х3	Х4	Х5
	1	2	2	22	-4	1	0	0	11
	1	2	1	16	-4	0	1	0	9
	1	1	1	12	-2	0	0	1	6
	1	2	2	22	-4	1	0	0	11
1	0	0	-1	-6	0	-1	1	0	-2
	0	-1	-1	-10	2	-1	0	1	-5
	1	0	0	2	0	-1	0	2	1
2	0	0	-1	-6	0	-1	1	0	-2
	0	1	1	10	-2	1	0	-1	5
	1	0	0	2	0	-1	0	2	1
3	0	0	1	6	0	1	-1	0	2
	0	1	0	4	-2	0	1	-1	3
	1	0	0	2	0	-1	0	2	1
	0	1	0	4	-2	0	1	-1	3
	0	0	1	6	0	1	-1	0	2

Исходная
система эквивалентна следующей системе
уравнений:

Х₁
+ 2Х₄=
1

Х₂
+4Х₄-2Х₅=
3

Х₃
+6Х₄=
2

Система
уравнений имеет бесконечное множество
решений.

Общее
решение
имеет вид:

Х₁
= 1-2Х₄

Х₂
= 3-4Х₄+2Х₅

Х₃
= 2-6Х_4.

переменные
Х₁,
Х_2,Х₃
являются основными
(или
базисными).
Любое
частное
решение
получается из общего путем придания
конкретных значений свободным переменным.
Если свободные переменные Х₄и Х₅
положить равными нулю, то получим первое
базисное
решение
Х₁
= 1,Х₂
= 3, Х₃
= 2, Х₄
= 0, Х₅=0.

Первое
базисное решение имеет вид: (1,3,2,0,0).

Общее
число групп основных переменных, т.е.
базисных решений не более, чем
==.

Если
все компоненты базисного решения
неотрицательны, то такое решение
называется опорным.

Соседние файлы в папке ЭММиПМ_задачи_(сайт-Москва)

#
14.03.201527.14 Кб15AnomNabl.xls
#
14.03.201561.95 Кб15Invest.xls
#
#
14.03.201574.75 Кб17Tema_3.xls
#
14.03.2015186.88 Кб14Tema_4_5.xls
#
14.03.201521.5 Кб10TZ_milk.xls
#
14.03.201591.65 Кб12ZLP.xls

Источник

В общем случае линейное уравнение имеет вид:

Общая характеристика разрешенной системы уравнений

Пример 20.1

Дать характеристику системе уравнений
.

Решение
:

1. Входит ли в состав противоречивое уравнение?
(Если коэффициенты, в этом случае уравнение имеет вид: и называется противоречивым
.)

Если система содержит противоречивое, то такая система несовместна и не имеет решения

2. Найти все разрешенные переменные
. (Неизвестная называется
разрешенной
для системы уравнений, если она входит в одно из уравнений системы с коэффициентом +1, а в остальные уравнения не входит (т.е. входит с коэффициентом, равным нулю).

3. Является ли система уравнений разрешенной?
(Система уравнений называется разрешенной
, если каждое уравнение системы содержит разрешенную неизвестную, среди которых нет совпадающих)

Разрешенные неизвестные, взятые по одному из каждого уравнения системы, образуют полный набор разрешенных неизвестных
системы. (в нашем примере это )

Разрешенные неизвестные, входящие в полный набор, называют также базисными
(), а не входящие в набор — свободными
().

В общем случае разрешенная система уравнений имеет вид:

На данном этапе главное понять что такое разрешенная неизвестная
(входящая в базис и свободная).

Общее Частное Базисное решения

Общим решением
разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные:

Частным решением
называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных.

Базисным решением
называется частное решение, получающееся из общего при нулевых значениях свободных переменных.

Базисное решение (вектор) называется вырожденным
, если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.
Базисное решение называется невырожденным
, если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.

Теорема (1)

Разрешенная система уравнений всегда совместна
(потому что она имеет хотя бы одно решение); причем если система не имеет свободных неизвестных,
(то есть в системе уравнений все разрешенные входят в базис) то она определена
(имеет единственное решение); если же имеется хотя бы одна свободная переменная, то система не определена
(имеет бесконечное множество решений).

Пример 1. Найти общее, базисное и какое-либо частное решение системы уравнений:

Решение
:

1. Проверяем является ли система разрешенной?

Система является разрешенной (т.к. каждое из уравнений содержит в себе разрешенную неизвестную)

2. Включаем в набор разрешенные неизвестные — по одному из каждого уравнения
.

3. Записываем общее решение в зависимости от того какие разрешенные неизвестные мы включили в набор
.

Ответ: частное решение
(один из вариантов)

Элементарные преобразования линейных уравнений

Теорема (2)

Если какое-либо уравнение системы умножить на некоторое отличное от нуля число
, а остальные уравнения оставить без изменения, то . (то есть если умножить левую и правую часть уравнения на одно и то же число то получится уравнение, равносильное данному)

Теорема (3)

Если к какому-либо уравнению системы прибавить другое
, а все остальные уравнения оставить без изменения, то получится система, равносильная данной
. (то есть если сложить два уравнения (сложив их левые и правые части) то получится уравнение равносильное данным)

Следствие из Теорем (2 и 3)

Если к какому-либо уравнению прибавить другое, умноженное на некоторое число
, а все остальные уравнения оставить без изменения, то получится система, равносильная данной
.

Формулы пересчета коэффициентов системы

Преобразование Жордана состоит из элементарных преобразований двух типов:

Пример 2 Пересчитаем коэффициенты системы

При делении уравнения с номером на , его коэффициенты пересчитываются по формулам:

Чтобы исключить из уравнения с номером , нужно уравнение с номером умножить на и прибавить к этому уравнению.

Теорема (4) О сокращении числа уравнений системы.

Если система уравнений содержит тривиальное уравнение, то его можно исключить из системы, при этом получится система равносильная исходной.

Теорема (5) О несовместимости системы уравнений.

Если система уравнений содержит противоречивое уравнение, то она несовместна.

Алгоритм метода Жордана-Гаусса

Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.
Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.
Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.
Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.
Далее заново переходят к пункту 1

Пример 3 Решить систему уравнений методом Жордана-Гаусса.

Найти
: два общих и два соответствующих базисных решения

Решение
:

Вычисления приведены в нижеследующей таблице:

Метод Гаусса-Жордана. Как найти обратную матрицу
с помощью элементарных преобразований?

Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого
Jordan как Жордан)
сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса
в том числе…

Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.

На некоторое время развевает тоску другой способ
приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Жо
рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?

…да, такое бывает только по любви =)

Для освоения данного урока «чайникам» придётся пойти путём Жо
рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:

Ну, и совсем замечательно, если отработано понижение порядка определителя
.

Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса
и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований
.

Не мудрствуя лукаво:

Пример 1

Решить систему методом Гаусса-Жордана

Решение
: это первое задание урока Метод Гаусса для чайников
, где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:

Теперь вместо обратного хода
в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .

Идеальный с точки зрения простоты случай:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) К первой строке прибавили вторую строку, умноженную на –2.

Не могу удержаться от иллюстрации итоговой системы:

Ответ
:

Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.

Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:

Пример 2

Решить систему линейных уравнений методом Гаусса-Жордана.

Решение
: первая часть задания хорошо знакома:

(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.

(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.

(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7

(4) Третью строку разделили на 2.

Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .

Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:

Находим наименьшее общее кратное
чисел третьего столбца (1, –1 и 3), т.е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа
, и этими соображениями обусловлено 5-е преобразование матрицы:

(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа
. В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.

(8) К первой строке прибавили вторую.

(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!

В результате элементарных преобразований получена эквивалентная исходной система:

Элементарно выражаем базисные переменные через свободную:

и записываем:

Ответ
: общее решение:

В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса
обычно требует трудоёмких и неприятных вычислений с дробями.

И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением
.

Для самостоятельного решения:

Пример 3

Найти базисное решение с помощью элементарных преобразований

Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные
. Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.

Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.

Примечание

: термин «базис» имеет алгебраический смысл и понятие геометрического базиса
здесь не при чём!

Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых
строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений
, причём там выбран другой базис
.

Продолжаем совершенствовать свои навыки на следующей прикладной задаче:

Как найти обратную матрицу методом Гаусса?

Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы
для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.

Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности)
справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:

(Понятно, что обратная матрица должна существовать)

Демо-пример 4

Найдём обратную матрицу для матрицы с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:

(1) Ко второй строке прибавили первую строку, умноженную на –3.

(2) К первой строке прибавили вторую строку.

(3) Вторую строку разделили на –2.

Ответ
:

Сверьтесь с ответом первого примера урока Как найти обратную матрицу?

Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:

Пример 5

Решение
: присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса
:

(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет)
. Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1)
. Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».

(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.

(3) К 3-й строке прибавили 2-ю строку, умноженную на –1

Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.

К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.

(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:

(5) К 1-й и 2-й строкам прибавили третью строку.

(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.

(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.

(8) К первой строке прибавили вторую строку.

(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.

(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали

(44, 44 и 4). Совершенно понятно, что это число 44. Третью строку умножаем на 11.

(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!

Таким образом, обратная матрица:

Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.

Ответ
:

Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице
.

Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.

Аналогичное задание для самостоятельного решения:

Пример 6

Найти обратную матрицу методом Гаусса-Жордана.

Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных
.

Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .

На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».

И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .

Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:

Пример 7

Найти обратную матрицу с помощью элементарных преобразований

Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел)
, я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.

И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)

Желаю успехов!

Решения и ответы:

Пример 3: Решение
: запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:

(1) Первую и вторую строки поменяли местами.

(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.

(3) Третью строку разделили на 3.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 7.

(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.

(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.

(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.

(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2

(10) К первой строке прибавили вторую строку.

(11) Вторую строку разделили на 2.

Выразим базисные переменные через свободные переменные :

Ответ

: общее решение:

Пример 6: Решение
: обратную матрицу найдём с помощью элементарных преобразований:

(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.

(2) Ко 2-й и 3-й строкам прибавили первую строку.

(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.

(4) Вторую строку умножили на 7, третью строку умножили на –9.

(5) К третьей строке прибавили вторую строку.

(6) Вторую строку разделили на 7.

(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.

(8) К первой и второй строкам прибавили третью строку.

(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.

(10) Вторую строку разделили на 2.

(11) Каждую строку разделили на 27.

В результате:
Ответ

:

Пример 7: Решение
: найдём обратную матрицу методом Гаусса-Жордана:

(1) К 1-й и 4-й строкам прибавили 3-ю строку.

(2) Первую и четвёртую строки поменяли местами.

(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:

(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.

(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.

(6) Вторую строку умножили на –1, третью строку разделили на –2.

Ответ

:

Записывается в виде расширенной матрицы, т.е. в столбец свободных членов помещается в одну матрицу с коэффициентами неизвестных. Аалгоритм заключается в приведении исходной матрицы, характеризующей систему линейных уравнений, к единичной путем эквивалентных преобразований (домножения строки матрицы на константу и сложения с другой строкой матрицы). В качестве константы используется 1/a[i][i] , т.е. число, обратное по отношению к элементу диагонали. Естественно, в ряде случаев возникают проблемы, связанные с делением на ноль, которые решаются перестановкой строк и столбцов:

Весь алгоритм можно представить 10 пунктами:

В качестве опорной выбираем первую строку матрицы.

Если элемент опорной строки, индекс которого равен номеру опорной строки, равен нулю, то меняем всю опорную строку на первую попавшуюся строку снизу, в столбце которого нет нуля.

Все элементы опорной строки делим на первый слева ненулевой элемент этой строки.

Из оставшихся снизу строк вычитают опорную строку, умноженную на элемент, индекс которого равен номеру опорной строки.

В качестве опорной строки выбираем следующую строку.

Повторяем действия 2 – 5 пока номер опорной строки не превысит число строк.

В качестве опорной выбираем последнюю строку.

Вычитаем из каждой строки выше опорную строку, умноженную на элемент этой строки с индексом равным номеру опорной строки.

В качестве опорной строки выбираем строку выше.

Повторяем 8 – 9 пока номер опорной строки не станет меньше номера первой строки.

Пример расчета 1

Пусть имеется система уравнений:

Запишем расширенную матрицу системы:

и выполним элементарные преобразования ее строк.

Для этого умножим первую строку на 1 и вычитаем из второй строки; затем умножим первую строку на 2 и вычтем из третьей строки.

В результате мы исключим переменную
x

1
из всех уравнений, кроме первого. Получим:

Теперь вычтем из строки 3 строку 2, умноженную на 3:

Теперь вычитаем из 1 строки сначала 3 строку, а затем 2 строку:

После преобразований получаем систему уравнений:

Из этого следует, что система уравнений имеет следующее решение:

x1 = 1, x2 = 3 , x3 = -1

Пример расчета 2

В качестве примера решим систему уравнений, представленную в виде матрицы (Таблица 1), методом Гаусса – Жордана.

Делим первую строку на 3 (элемент первой строки, расположенный на главной диагонали), получим:

	4/3		1/3

Умножаем первую строку на 1 и вычитаем из второй строки. Умножаем первую строку на 6 и вычитаем из третьей строки. Получим:

	4/3		1/3
	17/3		17/3

В первом столбце все элементы кроме диагонального равны нулю, займемся вторым столбцом, для этого выберем вторую строку в качестве опорной. Вторая Делим ее на 17/3:

4/3

1/3

/17

Умножаем строку 2 на -6 и вычитаем из третьей строки:

4/3

1/3

/17

Теперь третья строка – опорная, делим ее на
-33/17:

4/3

1/3

/17

17/3

Умножаем опорную строку на 3/17 и вычитаем ее из второй. Умножаем третью строку на 1 и вычитаем ее из первой

	4/3

			17/3

Получена треугольная матрица, начинается обратный ход алгоритма
(во время которого получим единичную матрицу). Вторая строка становится опорной. Умножаем третью строку на 4/3 и вычитаем ее из первой:

			10/3

			17/3

Последний столбец матрицы – решение системы уравнений.

В данной статье мы рассмотрим метод Жордана-Гаусса для решения систем линейных уравнений, отличие метода Гаусса от метода Жордана-Гаусса, алгоритм действий, а также приведем примеры решений СЛАУ.

Yandex.RTB R-A-339285-1

Основные понятия

Определение 1

Метод Жордана-Гаусса

— один из методов, предназначенный для решения систем линейных алгебраических уравнений.

Этот метод является модификацией метода Гаусса

— в отличие от исходного (метода Гаусса) метод Жордана-Гаусса позволяет решить СЛАУ в один этап

(без использования прямого и обратного ходов).

Примечание

Матричная запись СЛАУ: вместо обозначения А в методе Жордана-Гаусса для записи используют обозначение Ã — обозначение расширенной матрицы системы.

Пример 1

4 x 1 — 7 x 2 + 8 x 3 = — 23 2 x 1 — 4 x 2 + 5 x 3 = — 13 — 3 x 1 + 11 x 2 + x 3 = 16

Как решить?

Записываем расширенную матрицу системы:

Ã = 4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16

Напоминаем, что слева от черты записывается матрица системы А:

A = 4 — 7 8 2 — 4 5 — 3 11 1

Замечание 1

На каждом шаге решения необходимо выбирать разрешающие элементы матрицы. Процесс выбора может быть различным — в зависимости от того, как выбираются элементы, решения будут отличаться. Можно выбирать в качестве разрешающих элементов диагональные элементы матрицы, а можно выбирать произвольно.

В этой статье мы покажем оба способа решения.

Произвольный способ выбора разрешающих элементов

Первый этап:

Следует обратиться к 1-му столбцу матрицы Ã — необходимо выбрать ненулевой (разрешающий) элемент.

В 1-ом столбце есть 3 ненулевых элемента: 4, 2, -3. Можно выбрать любой, но, по правилам, выбирается тот, чей модуль ближе всего к единице. В нашем примере таким числом является 2.

Цель:

обнулить все элементы, кроме разрешающего, т.е. необходимо обнулить 4 и -3:

4 — 7 8 2 — 4 5 — 3 11 1

Произведем преобразование: необходимо сделать разрешающий элемент равным единице. Для этого делим все элементы 2-ой строки на 2. Такое преобразование имеет обозначение: I I: 2:

4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I I ÷ 2 → 4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16

Теперь обнуляем остальные элементы: 4 и -3:

4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16 I — 4 × I I I I I — (- 3) × I I

Необходимо выполнить преобразования:

I — 4 × I I и I I I — (- 3) × I I = I I I + 3 × I I

Запись I — 4 × I I означает, что от элементов 1-ой строки вычитаются соответствующие элементы 2-ой строки, умноженные на 4.

Запись I I I + 3 × I I означает, что к элементам 3-ей строки прибавляются соответствующие элементы 2-ой строки, умноженные на 3.

I — 4 × I I = 4 — 7 8 — 23 — 4 1 — 2 5 / 2 — 13 / 2 = = 4 — 7 8 — 23 — 4 — 8 10 — 26 = 0 1 — 2 3

Записываются такие изменения следующим образом:

4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16 I — 4 × I I I I I — (- 3) × I I → 0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2

Второй этап

Необходимо обнулить 2-ой столбец, следовательно, нужно выбрать разрешающий элемент: 1, -2, 5. Однако 2-ую строку матрицы мы использовали в первом этапе, так что элемент -2 не может быть использован.

Поскольку необходимо выбирать число, чей модуль ближе всего к единице, то выбор очевиден — это 1. Обнуляем остальные элементы 2-го столбца:

0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I I — (- 2) × I I I I — 5 × I

0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I I + 2 × I I I I — 5 × I → 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2

Третий этап

Теперь требуется обнулить элементы 3-го столбца. Поскольку первая и вторая строки уже использованы, поэтому остается только один вариант: 37 / 2 . Обнуляем с его помощью элементы третьего столбца:

0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2

Выполнив преобразования

I — (- 2) × I I I = I + 2 × I I I и I I — (- 3 2) × I I I = I I + 3 2 × I I

получим следующий результат:

0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | — 2 0 0 1 | — 1

Ответ

: x 1 = — 2 ; x 2 = 1 ; x 3 = — 1 .

Полное решение:

4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I I ÷ 2 → 4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16 I — 4 × I I I I I — (- 3) × I I →

→ 0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I I — (- 2) × I I I I — 5 × I → 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2 I I I ÷ 37 2 →

→ 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | — 2 0 0 1 | — 1 .

Выбор разрешающих элементов на главной диагонали матрицы системы

Определение 2

Принцип выбора разрешающих элементов строится на простом отборе соответствующих элементов: в 1-ом столбце выбирается элемент 1-го столбца, во 2-ом — второй, в 3-ем — третий и т.д.

Первый этап

В первом столбце необходимо выбрать элемент первой строки, т.е. 4. Но поскольку в первом столбце есть число 2, чей модуль ближе к единице, чем 4, то можно поменять местами первую и вторую строку:

4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 → 2 — 4 5 | — 13 4 — 7 8 | — 23 — 3 11 1 | 16

Теперь разрешающий элемент — 2. Как показано в первом способе, делим первую строку на 2, а затем обнуляем все элементы:

4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I ÷ 2 → 2 — 4 5 / 2 | — 13 / 2 4 — 7 8 | — 23 — 3 11 1 | 16 I I — 4 × I I I I + 3 × I → 1 — 2 5 / 2 | — 13 / 2 0 1 — 2 | 3 0 5 17 / 2 | — 7 / 2

Второй этап

На втором этапе требуется обнулить элементы второго столбца. Разрешающий элемент — 1, поэтому никаких изменений производить не требуется:

0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I + 2 × I I I I I — 5 × I I → 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2

Третий этап

На третьем этапе необходимо обнулить элементы третьего столбца. Разрешающий элемент — 37/2. Делим все элементы на 37/2 (чтобы сделать равными 1), а затем обнуляем:

0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2 I I I ÷ 37 2 → 1 0 — 3 / 2 | — 1 / 2 0 1 — 2 | 3 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | — 2 0 1 0 | 1 0 0 1 | — 1

Ответ:

x 1 = — 2 ; x 2 = 1 ; x 3 = — 1 .

4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I ÷ 2 → 2 — 4 5 / 2 | — 13 / 2 4 — 7 8 | — 23 — 3 11 1 | 16 I I — 4 × I I I I + 3 × I → 0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I + 2 × I I I I I — 5 × I I →

→ 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2 I I I ÷ 37 2 → 1 0 — 3 / 2 | — 1 / 2 0 1 — 2 | 3 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | — 2 0 1 0 | 1 0 0 1 | — 1

Пример 2

Решить СЛАУ методом Жордана-Гаусса:

3 x 1 + x 2 + 2 x 3 + 5 x 4 = — 6 3 x 1 + x 2 + 2 x 4 = — 10 6 x 1 + 4 x 2 + 11 x 3 + 11 x 4 = — 27 — 3 x 1 — 2 x 2 — 2 x 3 — 10 x 4 = 1

Как решить?

Записать расширенную матрицу данной системы Ã :

3 1 2 5 | — 6 3 1 0 2 | 10 6 4 11 11 | — 27 — 3 — 2 — 2 — 10 | 1

Для решения используем второй способ: выбор разрешающих элементов на главной диагонали системы. На первом этапе выбираем элемент первой строки, на втором — второй строки, на третьем — третьей и т.д.

Первый этап

Необходимо выбрать разрешающий элемент первой строки, т.е. 3. Затем обнуляем все элементы столбца, разделяя на 3 все элементы:

3 1 2 5 | — 6 3 1 0 2 | — 10 6 4 11 11 | — 27 — 3 — 2 — 2 — 10 | 1 I ÷ 3 → 1 1 / 3 2 / 3 5 / 3 | — 2 3 1 0 2 | — 10 6 4 11 11 | — 27 — 3 — 2 — 2 — 10 | 1 I I — 3 × I I I I — 6 × I I V + 3 × I →

→ 1 1 / 3 2 / 3 5 / 3 | — 2 0 0 — 2 — 3 | — 4 0 2 7 1 | — 15 0 — 1 0 — 5 | — 5

Второй этап

Необходимо обнулить элементы второго столбца. Для этого выделяем разрешающий элемент, но элемент первой строки второго столбца равен нулю, поэтому необходимо менять строки местами.

Поскольку в четвертой строке есть число -1, то меняем местами вторую и четвертую строки:

1 1 / 3 2 / 3 5 / 3 | — 2 0 0 — 2 — 3 | — 4 0 2 7 1 | — 15 0 — 1 0 — 5 | — 5 → 1 1 / 3 2 / 3 5 / 3 | — 2 0 — 1 0 — 5 | — 5 0 2 7 1 | — 15 0 0 — 2 — 3 | — 4

Теперь разрешающий элемент равен -1. Делим элементы второго столбца на -1, а затем обнуляем:

1 1 / 3 2 / 3 5 / 3 | — 2 0 — 1 0 — 5 | — 5 0 2 7 1 | — 15 0 0 — 2 — 3 | — 4 I I ÷ (- 1) → 1 1 / 3 2 / 3 5 / 3 | — 2 0 1 0 5 | 5 0 2 7 1 | — 15 0 0 — 2 — 3 | — 4 I — 1 / 3 × I I I I I — 2 × I →

→ 1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 7 — 9 | — 25 0 0 — 2 — 3 | — 4

Третий этап

На третьем этапе необходимо также обнулить элементы третьего столбца. Для этого находим разрешающий элемент в третьей строке — это 7. Но на 7 делить неудобно, поэтому необходимо менять строки местами, чтобы разрешающий элемент стал -2:

1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 7 — 9 | — 25 0 0 — 2 — 3 | — 4 → 1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 — 2 — 3 | — 4 0 0 7 — 9 | — 25

Теперь делим все элементы третьего столбца на -2 и обнуляем все элементы:

1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 — 2 — 3 | — 4 0 0 7 — 9 | — 25 I I I ÷ (- 2) → 1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 — 9 | — 25 I — 2 / 3 × I I I I V — 7 × I I I →

1 0 0 — 1 | — 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 — 39 / 2 | — 39

Четвертый этап

Обнуляем четвертый столбец. Разрешающий элемент — — 39 2:

1 0 0 — 1 | — 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 — 39 / 2 | — 39 I V ÷ (- 39 2) → 1 0 0 — 1 | — 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 1 | 2 I + I V I I — 5 × I V I I I — 3 / 2 × I V →

→ 1 0 0 0 | — 3 0 1 0 0 | — 5 0 0 1 0 | — 1 0 0 0 1 | 2 .

Ответ

: x 1 = — 3 ; x 2 = — 5 ; x 3 = — 1 ; x 4 = 2

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Каждой системе линейных уравнений поставим в соответствие расширенную матрицу
, полученную присоединением к матрице А
столбца свободных членов:

Метод Жордана–Гаусса
применяется для решения системы m
линейных уравнений с n
неизвестными вида:

Данный метод заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе уравнений с матрицей определенного вида.

Над строками расширенной матрицы осуществляем следующие элементарные преобразования:

1. перестановка двух строк
;

2. умножение строки на любое число, отличное от нуля
;

3. прибавление к одной строке другой строки, умноженной на некоторое число
;

4. отбрасывание нулевой строки (столбца)
.

Пример 2.11.
Решить методом Жордана–Гаусса системы линейных уравнений:

а
) Х 1 + Х 2 + 2Х 3 = -1

2Х 1 — Х 2 + 2Х 3 = -4

4Х 1 + Х 2 + 4Х 3 = -2

Решение: Составим расширенную матрицу:

Итерация 1

В качестве направляющего элемента выбираем элемент . Преобразуем первый столбец в единичный. Для этого ко второй и третьей строкам прибавляем первую строку, соответственно умноженную на (-2) и (-4). Получим матрицу:

На этом первая итерация закончена.

Итерация 2

Выбираем направляющий элемент . Так как , то делим вторую строку на -3. Затем умножаем вторую строку соответственно на (-1) и на 3 и складываем соответственно с первой и третьей строками. Получим матрицу

Итерация 3

Выбираем направляющий элемент . Так как , то делим третью строку на (-2). Преобразуем третий столбец в единичный. Для этого умножаем третью строку соответственно на (-4/3) и на (-2/3) и складываем соответственно с первой и второй строками. Получим матрицу

откуда Х
1 = 1, Х
2 = 2, Х
3 = -2.

Закончив решение, на этапе обучения необходимо выполнять проверку, подставив найденные значения в исходную систему, которая при этом должна обратиться в верные равенства.

б
) Х 1 – Х 2 + Х 3 – Х 4 = 4

Х 1 + Х 2 + 2Х 3 +3Х 4 = 8

2Х 1 +4Х 2 + 5Х 3 +10Х 4 = 20

2Х 1 – 4Х 2 + Х 3 – 6Х 4 = 4

Решение: Расширенная матрица имеет вид:

Применяя элементарные преобразования, получим:

Исходная система эквивалентна следующей системе уравнений:

Х 1 – 3Х 2 – 5Х 4 = 0

2Х 2 + Х 3 + 4Х 4 = 4

Последние две строки матрицы A
(2) являются линейно зависимыми.

Определение.
Строки матрицы e
1 , e
2 ,…, e m
называются линейно зависимыми
, если существуют такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

где 0
=(0, 0…0). Строки матрицы являются линейно независимыми
, когда комбинация этих строк равна нулю тогда и только тогда, когда все коэффициенты равны нулю.

В линейной алгебре очень важно понятие ранга матрицы
, т.к. оно играет очень большое значение при решении систем линейных уравнений.

Теорема 2.3 (о ранге матрицы).
Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы).

Ранг матрицы A
(2) равен 2, т.к. в ней максимальное число линейно независимых строк равно 2 (это первые две строки матрицы).

Теорема 2.4 (Кронекера–Капели).
Система линейных уравнений совместна и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

1. Если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система имеет единственное решение.

2. Если ранг матрицы системы меньше числа переменных, т.е. r < n, то система неопределённая и имеет бесконечное множество решений.

В данном случае система имеет 4 переменных, а её ранг равен 2, следовательно, она имеет бесконечное множество решений.

Определение.
Пусть r
< n
, r
переменных x
1 , x
2 ,…, x r
называются базисными
, если определитель матрицы из коэффициентов при них (базисный минор
) отличен от нуля. Остальные n – r
переменных называются свободными
.

Определение.
Решение
системы, в котором все n – r
свободных переменных равны нулю, называется базисным
.

Совместная система m
линейных уравнений с n
переменными (m < n
) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее , где .

В нашем случае , т.е. система имеет не более 6 базисных решений.

Общее решение имеет вид:

Х 1 = 3Х 2 +5Х 4

Х 3 = 4 – 2Х 2 – 4Х 4

Найдем базисные решения. Для этого полагаем Х 2 = 0, Х 4 = 0, тогда Х 1 =0, Х 3 = 4. Базисное решение имеет вид: (0, 0, 4, 0).

Получим другое базисное решение. Для этого в качестве свободных неизвестных примем Х 3 и Х 4 . Выразим неизвестные Х 1 и Х 2 через неизвестные Х 3 и Х 4:

Х 1 = 6 – 3/2Х 2 – Х 4

Х 2 = 2 – 1/2Х 3 – 2Х 4 .

Тогда базисное решение имеет вид: (6, 2, 0, 0).

Пример 2.12.
Решить систему:

X 1 + 2X 2 – X 3 = 7

2X 1 – 3X 2 + X 3 = 3

4X 1 + X 2 – X 3 = 16

Решение.Преобразуем расширенную матрицу системы

Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0 = –1, следовательно, данная система несовместна. Данный вывод можно также получить, если заметить, что ранг матрицы системы равен 2, тогда как ранг расширенной матрицы системы равен 3.

Источник

	Х1	Х2	Х3	Х4	Х5
	1	2	2	22	-4	1	0	0	11
	1	2	1	16	-4	0	1	0	9
	1	1	1	12	-2	0	0	1	6
	1	2	2	22	-4	1	0	0	11
1	0	0	-1	-6	0	-1	1	0	-2
	0	-1	-1	-10	2	-1	0	1	-5
	1	0	0	2	0	-1	0	2	1
2	0	0	-1	-6	0	-1	1	0	-2
	0	1	1	10	-2	1	0	-1	5
	1	0	0	2	0	-1	0	2	1
3	0	0	1	6	0	1	-1	0	2
	0	1	0	4	-2	0	1	-1	3
	1	0	0	2	0	-1	0	2	1
	0	1	0	4	-2	0	1	-1	3
	0	0	1	6	0	1	-1	0	2

	Х1	Х2	Х3	Х4	Х5
	1	2	2	22	-4	1	0	0	11
	1	2	1	16	-4	0	1	0	9
	1	1	1	12	-2	0	0	1	6
	1	2	2	22	-4	1	0	0	11
1	0	0	-1	-6	0	-1	1	0	-2
	0	-1	-1	-10	2	-1	0	1	-5
	1	0	0	2	0	-1	0	2	1
2	0	0	-1	-6	0	-1	1	0	-2
	0	1	1	10	-2	1	0	-1	5
	1	0	0	2	0	-1	0	2	1
3	0	0	1	6	0	1	-1	0	2
	0	1	0	4	-2	0	1	-1	3
	1	0	0	2	0	-1	0	2	1
	0	1	0	4	-2	0	1	-1	3
	0	0	1	6	0	1	-1	0	2

Преобразование Жордана-Гаусса и симплекс-метод в Excel

Решение уравнений методом подбора параметров Excel

Как решить систему уравнений матричным методом в Excel

Решение системы уравнений методом Крамера в Excel

Решение систем уравнений методом Гаусса в Excel

Примеры решения уравнений методом итераций в Excel

Выбор разрешающих элементов на главной диагонали матрицы системы.

Общая характеристика разрешенной системы уравнений

Общее Частное Базисное решения

Теорема (1)

Элементарные преобразования линейных уравнений

Теорема (2)

Теорема (3)

Следствие из Теорем (2 и 3)

Формулы пересчета коэффициентов системы

Теорема (4) О сокращении числа уравнений системы.

Теорема (5) О несовместимости системы уравнений.

Алгоритм метода Жордана-Гаусса

Вырожденность в задачах линейного программирования

Кафедра экономико-математических методов и моделей

Решение систем линейных уравнений методом жордана — гаусса

Общая характеристика разрешенной системы уравнений

Общее Частное Базисное решения

Теорема (1)

Элементарные преобразования линейных уравнений

Теорема (2)

Теорема (3)

Следствие из Теорем (2 и 3)

Формулы пересчета коэффициентов системы

Теорема (4) О сокращении числа уравнений системы.

Теорема (5) О несовместимости системы уравнений.

Алгоритм метода Жордана-Гаусса

Метод Гаусса-Жордана. Как найти обратную матрицу с помощью элементарных преобразований?

Как найти обратную матрицу методом Гаусса?

Пример расчета 1

Пример расчета 2

Основные понятия

Произвольный способ выбора разрешающих элементов

Выбор разрешающих элементов на главной диагонали матрицы системы

Метод Гаусса-Жордана. Как найти обратную матрицу
с помощью элементарных преобразований?

	Х1	Х2	Х3	Х4	Х5
	1	2	2	22	-4	1	0	0	11
	1	2	1	16	-4	0	1	0	9
	1	1	1	12	-2	0	0	1	6
	1	2	2	22	-4	1	0	0	11
1	0	0	-1	-6	0	-1	1	0	-2
	0	-1	-1	-10	2	-1	0	1	-5
	1	0	0	2	0	-1	0	2	1
2	0	0	-1	-6	0	-1	1	0	-2
	0	1	1	10	-2	1	0	-1	5
	1	0	0	2	0	-1	0	2	1
3	0	0	1	6	0	1	-1	0	2
	0	1	0	4	-2	0	1	-1	3
	1	0	0	2	0	-1	0	2	1
	0	1	0	4	-2	0	1	-1	3
	0	0	1	6	0	1	-1	0	2