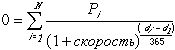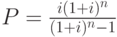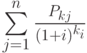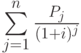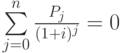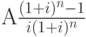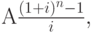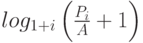Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЧИСТВНДОХ в Microsoft Excel.
Описание
Возвращает внутреннюю ставку доходности для графика денежных потоков, которые не обязательно носят периодический характер. Чтобы рассчитать внутреннюю ставку доходности для ряда периодических денежных потоков, следует использовать функцию ВСД.
Синтаксис
ЧИСТВНДОХ(значения;даты[;предположение])
Аргументы функции ЧИСТВНДОХ описаны ниже.
-
Значения Обязательный. Ряд денежных потоков, соответствующий графику платежей, приведенному в аргументе «даты». Первый платеж является необязательным и соответствует затратам или выплате в начале инвестиции. Если первое значение является затратами или выплатой, оно должно быть отрицательным. Все последующие выплаты дисконтируются на основе 365-дневного года. Ряд значений должен содержать по крайней мере одно положительное и одно отрицательное значение.
-
Даты Обязательный. График дат платежей, который соответствует платежам для денежных потоков. Даты могут быть в любом порядке. Дата должна быть введена с использованием функции ДАТА либо как результат других формул или функций. Например, для указания даты 23 мая 2008 г. воспользуйтесь выражением ДАТА(2008,5,23). Если ввести даты как текст, это может привести к возникновению проблем. .
-
Предп Необязательный. Величина, предположительно близкая к результату ЧИСТВНДОХ.
Замечания
-
В приложении Microsoft Excel даты хранятся в виде последовательных чисел, что позволяет использовать их в вычислениях. По умолчанию дате 1 января 1900 года соответствует номер 1, а 1 января 2008 года — 39448, так как интервал между этими датами составляет 39 448 дней.
-
Числа в аргументе «даты» усекаются до целых.
-
В xiRR ожидается по крайней мере один положительный и один отрицательный денежный поток; в противном случае XIRR возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если любое число в датах не является допустимой датой, то xiRR возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если любое число в датах предшествует начальной дате, то xiRR возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если значения и даты содержат различное количество значений, то #NUM! значение ошибки #ЗНАЧ!.
-
В большинстве случаев задавать аргумент «предп» для функции ЧИСТВНДОХ не требуется. Если этот аргумент опущен, то он полагается равным 0,1 (10 процентов).
-
Функция ЧИСТВНДОХ тесно связана с функцией ЧИСТНЗ. Ставка доходности, вычисляемая функцией ЧИСТВНДОХ — это процентная ставка, соответствующая ЧИСТНЗ = 0.
-
Excel для вычисления XIRR используется метод итеративный метод. Используя изменяемую ставку (начиная с прогноза), XIRR цикличен по вычислениям, пока результат не будет точным в пределах 0,0000001 процента. Если после 100 попыток xiRR не получается найти результат, #NUM! возвращается значение ошибки. Ставка будет изменена до:
где:
-
di = дата i-й (последней) выплаты;
-
d1 = дата 0-й выплаты (начальная дата);
-
Pi = сумма i-й (последней) выплаты.
-
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
Значения |
Даты |
|
|
-10 000 |
1-янв-08 |
|
|
2,750 |
1-мар-08 |
|
|
4,250 |
30-окт-08 |
|
|
3,250 |
15-фев-09 |
|
|
2,750 |
1-апр-09 |
|
|
Формула |
Описание (результат) |
Результат |
|
=ЧИСТВНДОХ(A3:A7; B3:B7; 0,1) |
Внутренняя ставка доходности (0,373362535 или 37,34%) |
37,34 % |
Нужна дополнительная помощь?
Функция ЧИСТВНДОХ предназначена для расчета внутренней ставки доходности по денежным потокам, носящим непериодический характер, и возвращает соответствующее значение в процентах. Для расчета аналогичной ставки по периодическим платежам в Excel предусмотрена функция ВСД.
Расчет рентабельности инвестиций по денежным потокам в Excel
Примеры использования функции ЧИСТВНДОХ в Excel.
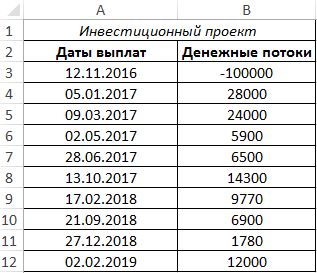
Пример 1. Инвестор получил кредит в размере 100000 руб. под 13% годовых и вложил средства в проект, финансовые потоки которого занесены в таблицу Excel. Определить, является ли его вложение прибыльным.
Вид таблицы данных:
Рассчитаем внутреннюю ставку доходности по формуле:
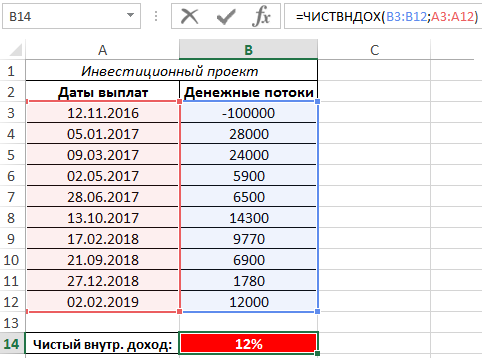
=ЧИСТВНДОХ(B3:B12;A3:A12)
Описание параметров:
- B3:B12 – диапазон ячеек со значениями финансовых выплат. Первое значение соответствует затратам (вложение 100000 рублей в инвестиционный проект), поэтому указано в виде отрицательного числа.
- A3:A12 – диапазон ячеек с датами, соответствующие моментам совершения выплат (введены с использованием функции ДАТА).
Результат вычислений:
Данный инвестиционный проект является убыточным, поскольку кредит был получен по ставке 13%.
Расчет внутренней ставки доходности облигаций в Excel
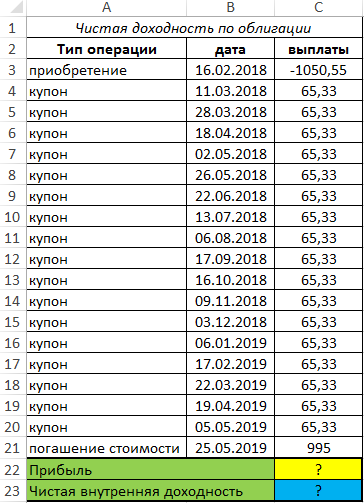
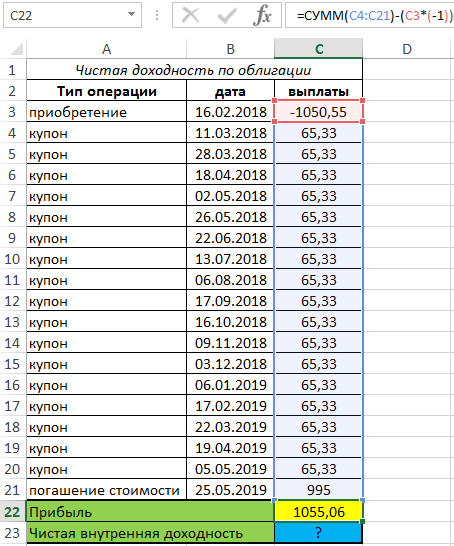
Пример 2. В таблице Excel внесены данные об операциях с облигацией (покупка, выплата купонов, погашение). Выплаты производились несистематично. Определить прибыль и внутреннюю ставку доходности облигации за указанный период.
Вид таблицы данных:
Для определения прибыли используем формулу:
=СУММ(C4:C21)-(C3*(-1))
То есть, определяем разницу между суммарными выплатами по купонам + погашением и расходами на приобретение облигации:
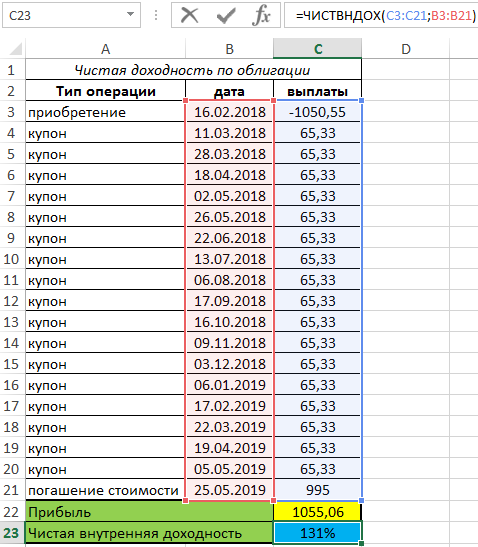
Для определения ставки доходности используем формулу:
=ЧИСТВНДОХ(C3:C21;B3:B21)
Результаты вычислений:
На практике подобные расчеты имеют смысл для достаточно больших периодов времени, поскольку на рынке зачастую возникают кризисные явления. Оптимальный период расчета доходности инвестиционного портфеля с использованием функции ЧИСТВНДОХ – от 5 лет и более.
Особенности расчета внутренней ставки доходности по функции ЧИСТВНДОХ в Excel
Функция ЧИСТВНДОХ имеет следующую синтаксическую запись:
=ЧИСТВНДОХ(значения;даты;[предположение])
Описание аргументов:
- значения – обязательный для заполнения, принимает ссылку на диапазон ячеек, содержащих записи о ряде денежных потоков, соответствующих графику, который задан аргументов даты. Для получения корректного результата ряд значений должен содержать хотя бы одно отрицательное и положительные числа соответственно. Первый платеж может быть равен нулю. Он соответствует начальной выплате или понесенным затратам;
- даты — обязательный для заполнения, принимает ссылку на диапазон ячеек с датами проведения платежей (график денежных потоков). В отличие от функции ВСД, даты можно указывать в произвольном порядке. Для указания дат следует использовать функцию ДАТА. В противном случае результатом работы функции ЧИСТВНДОХ может быть код ошибки;
- [предположение] – необязательный для заполнения, принимает числовое значение, близкое к результату вычисления функции.
Примечания:
- Даты в Excel при проведении вычислений преобразуются в числовые значения. Нецелые числа, переданные в качестве параметра даты, усекаются до целых значений.
- Функция ЧИСТВНДОХ генерирует код ошибки #ЧИСЛО!, если хотя бы одна дата из диапазона даты является недопустимым значением (например, текст или данные логического типа).
- Если один из последующих платежей был произведен ранее, чем первый платеж (ошибка в последовательности указания дат), рассматриваемая функция вернет код ошибки #ЧИСЛО!
- Если в качестве параметров значения и даты были переданы ссылки на диапазоны с различным числом элементов, результатом вычислений будет код ошибки #ЧИСЛО!
- Последний необязательный аргумент в большинстве расчетов не используют. Если он явно не указан, считается, что его значение равно 0,1 (10%).
- Функции ЧИСТВНДОХ и ЧИСТНЗ являются взаимозависимыми. Вычисляемая первой функцией ставка соответствует нулевому чистому дисконтируемому доходу (то есть, при данной ставке результат вычислений ЧИСТНЗ равен нулю).
В
пакете Excel
существует группа функций, предназначенных
для расчета финансовых операций по
кредитам, ссудам, займам. Эти расчеты
основаны на концепции временной стоимости
денег и предполагают неравноценность
денег, относящихся к разным моментам
времени. Эта группа функций охватывает
следующие расчеты:
-
определение
наращенной суммы (будущей стоимости), -
определение
начального значения (текущей стоимости), -
определение
срока платежа и процентной ставки, -
расчет
периодических платежей, связанных с
погашением займов.
Общая
формула расчета, которуюExcel
использует при вычислении финансовых
аргументов, связанных с денежными
потоками, имеет вид:
где
pmt
– фиксированная
(неизменная) периодическая сумма платежа;
n
– общее
число периодов выплат,
r
– процентная
ставка за один период,
type
– число 0
или 1, обозначающее, когда производится
выплата (1 – в начале периода, 0 – в конце
периода),
—
текущая стоимость вклада (займа), по
которому начисляются проценты по ставке
r%
n—ное
число периодов или текущая стоимость
серии фиксированных платежей,
—будущая стоимость вклада (займа) или
будущая стоимость серии фиксированных
периодических платежей.
Если
процентная ставка за период начисления
r=0, то используется следующая формула:
Эти
формулы используют встроенные функцииБC,
КПЕР, ПC,
ПЛТ, ЭФФЕКТ и
другие.
ПС
— текущий объём вклада
Позволяет
рассчитать текущий объем вклада.
Синтаксис
ПС
(норма;кпер;выплата;бс;тип)
норма
— процентная
ставка за период. Так, если Вы получили
ссуду под станок под 15% годовых и делаете
ежемесячные выплаты, то ставка
процента за месяц составит 15%/12, или
1,25%. Аргумент норма
в данном
случае может принимать значения 15%/12
или 1,25% или 0,0125.
кпер
— общее число
периодов выплат годовых процентов. Так,
если Вы получили ссуду на 3 года под
станок и делаете ежемесячные платежи,
то Ваша ссуда имеет 3*12 (или 36) периодов.
Аргумент кпер
в данном случае принимает значение 36.
выплата
—
размер выплаты, производимой в каждом
периоде и не меняющейся в течение всего
времени выплаты процентов. Обычно,
выплата включает основные платежи и
платежи по процентам без учета других
сборов или налогов. Например,
ежемесячная выплата по четырехгодичному
займу в 10 000 руб. под 12% годовых составит
308,3 руб. Аргумент выплата
в данном случае принимает значение
-308,3.
бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
Если бс
опущено, оно полагается равным 0 (будущая
стоимость займа, например, равна 0).
Например, если Вы хотите накопить 50000
руб. в течение18 лет, то 50 000 руб. это и
есть будущая стоимость. Вы можете сделать
предположение о сохранении заданной
процентной ставки и определить, сколько
нужно откладывать каждый месяц.
тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 означает — выплата в конце периода,
1 — выплата в начале периода.
-
Выбранные
единицы измерения для аргументов норма
и кпер
должны соответствовать друг другу.
Если Вы делаете ежемесячные выплаты
по четырехгодичному займу под 12% годовых,
то используйте 12%/12 для задания аргумента
норма,
4*12 для задания аргумента кпер.
Если Вы делаете ежегодные платежи по
тому же займу, то используйте 12% для
задания аргумента норма
и 4 для задания аргумента кпер. -
В
функциях, связанных с интервалами
выплат, выплачиваемые деньги
представляются отрицательным числом,
а получаемые деньги представляются
положительным числом. Например, депозит
в банк на сумму 1 000 руб. представляется
для вкладчика аргументом -1000, а для
банка аргументом 1000.
Пример
Фирме
потребуется 5000 руб. через 12 лет. В
настоящее время фирма располагает
деньгами и готова положить их на депозит
единым вкладом, чтобы через 12 лет он
достиг 5000 руб. Определим необходимую
сумму текущего вклада, если ставка
процента по нему составляет 12% годовых.
Необходимая
сумма текущего вклада составит:
ПС
(12%;12;;5000)=-1283.38 руб.
БС
— стоимость постоянных платежей в
определенные периоды на основе постоянной
процентной ставки
Позволяет
рассчитать объем вклада через определенный
промежуток времени на основе периодических
постоянных платежей и постоянной
процентной ставки.
Синтаксис
БС(норма;кпер;выплата;пс;тип)
ставка
— процентная
ставка за период.
кпер
— количество
периодов, в которые производится выплата
годовых процентов.
выплата—
размер выплаты, производимой в каждом
периоде; это значение постоянно в течение
всего времени выплат. Обычно плата
состоит из основного платежа и платежа
по процентам без учета других налогов
и сборов.
пс
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент пс
опущен,
то он полагается равным 0.
тип
— число,
определяющее когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплата в конце периода, 1 — выплата
в начале периода.
Более
подробная информация об аргументах
функции БЗ и о других функциях выплат
по процентным вкладам приведена в
описании функции ПЗ.
-
Единицы
измерения для аргументов норма
и кпер
должны быть согласованы. Если производятся
ежемесячные платежи по четырехгодичному
займу из расчета 12% годовых, то норма
должна быть 12%/12 , а кпер
должно быть 4*12. Если производятся
ежегодные платежи по тому же займу, то
норма
должна быть
12%, а кпер
должно быть 4. -
Ваш
вклад представляется отрицательным
числом, а деньги, которые вы получите,
представляются положительным числом.
Пример
Определим,
сколько денег будет на счету через год,
если вы собираетесь вложить 1000 рублей
под 6% годовых (что составит в месяц
6%/12 или 0,5%). Причем вы собираетесь
вкладывать по 100 рублей в начале каждого
следующего месяца в течение года.
Через
год на счете будет:
БС
(0,5%;12;-100;-1000;1)=2301,40 р.
ПРПЛТ
— платежи по процентам за период на
основе постоянных периодических выплат
и постоянной процентной ставки
С
помощью данной функции можно рассчитать
процентные платежи за текущий период
при периодических постоянных выплатах
и постоянной процентной ставке. Полное
описание аргументов функции ПРПЛТ
и более подробная информация о функциях,
связанных с ежегодными выплатами,
приведены в описании функции ПС.
Синтаксис
ПРПЛТ(норма;период;кпер;тс;бс;тип)
норма
—
процентная ставка за период.
период
— текущий
период, в котором требуется определить
прибыль (может принимать значения от 1
до кпер).
кпер
— общее число
периодов выплат.
тс
— сумма,
которую составят будущие платежи с
настоящего момента.
бс
— баланс
платежей, который нужно достичь после
последней выплаты.
тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплаты в конце периода, 1 — выплаты
в начале периода.
-
Единицы
измерения для аргументов норма
и кпер
должны быть согласованы. Если производятся
ежемесячные платежи по трехгодичному
займу из расчета 10% годовых, то норма
должна быть 10%/12 , а кпер
должно быть 3*12. Если производятся
ежегодные платежи по тому же займу, то
норма
должна быть 10%, а кпер
должно быть 3. -
Выплачиваемые
денежные средства представляются
отрицательным числом, а получаемые
денежные средства представляются
положительным числом.
Пример
Требуется
определить доход за первый месяц от
четырехгодичного займа в 1000000 рублей
из расчета 15% годовых:
ПРПЛТ(0,15/12;1;48;1000000)
равняется -12500 рублей.
ПЛТ
— расчет постоянных периодических
выплат
Функция
вычисляет величину выплаты за один
период на основе фиксированных
периодических выплат и постоянной
процентной ставки. Выплаты, рассчитанные
функцией ПЛТ, включают основные платежи
и платежи по процентам.
Синтаксис
ПЛТ(норма;кпер;нз;бс;тип)
норма
– норма
прибыли за период займа.
кпер
– общее
число периодов выплат годовой ренты
нз
– текущая стоимость: общая сумма всех
будущих платежей с настоящего момента.
бс
– будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты.
тип
— число,
определяющее, когда должна производиться
выплата.
Пример
Предположим,
что необходимо накопить 4000 руб. за 3
года, откладывая постоянную сумму в
конце каждого месяца. Какой должна быть
эта сумма, если норма процента по вкладу
составляет 12% годовых?
Величина
ежемесячных выплат составит:
ПЛТ(12%/12;12*3;;4000)=-92.86
руб.
ОСПЛТ
— расчет основных платежей по займу
Функция
вычисляет величину основного платежа
(выплаты задолженности) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
на указанный период.
Синтаксис
ОСПЛТ(норма;период;кпер;тс;бс;тип)
норма
– норма
прибыли за период.
период
– период,
который должен быть в интервале от 1 до
кпер.
кпер
– общее
число периодов выплат годовой ренты.
тс
– текущая
стоимость: общая сумма всех будущих
платежей с настоящего периода.
бс
– будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
тип
—
число,
определяющее, когда должна производиться
выплата.
Пример
Банком
выдан кредит в 7000 руб. на 3 года под 17%
годовых, начисляемых один раз в конце
каждого периода.
Определите
размер ежегодных основных выплат по
займу.
Основная
часть платежа на каждый из трех периодов
составит соответственно:
ОСПЛТ(17%;1;3;-70000)=19780.16
руб.
ОСПЛТ(17%;2;3;-70000)=23142.78
руб.
ОСПЛТ(17%;3;3;-70000)=27077.06
руб.
ОБЩПЛТ
— расчет суммы платежей по процентам
по займу между двумя периодами выплат
Функция
вычисляет накопленный доход (сумму
платежей по процентам) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
между двумя периодами выплат.
Синтаксис
ОБЩПЛТ(ставка;кол_пер;нз;нач_период;кон_период;тип)
ставка
– процентная ставка.
кол_пер
– общее
количество периодов выплат.
нз
– текущее
значение.
нач_период
– первый
период.
кон_период
— последний период.
Пример
Пусть
заем под недвижимость сделан на следующих
условиях: процентная ставка –9% годовых;
срок-30 лет, размер ссуды – 125000 руб.,
проценты начисляются ежемесячно.
Найти
сумму выплат по процентам за 2-й год и
за 1-й месяц займа.
Общая
выплата по процентам за второй год
составит:
ОБЩПЛТ(9%/12;30*12;125000;13;24)=-11135.23
руб.
Одна
выплата за первый месяц составит:
ОБЩПЛТ(9%/12;30*12;125000;1;1)=-937.50
руб.
ОБЩДОХОД
— расчет суммы основных выплат по займу
между двумя периодами
Функция
вычисляет сумму основных выплат по
займу, который погашается равными
платежами в конце или начале каждого
расчетного периода, между двумя периодами.
Синтаксис
ОБЩДОХОД
(ставка;кол_пер;нз;нач_период; нач_период;)
ставка
– процентная ставка.
кол_пер
– общее
количество периодов выплат.
нз
– текущее
значение.
нач_период
– первый
период.
кон_период
— последний период.
Пример
Выдана
ссуда размером 1000$ сроком на 6 лет под
15% годовых; проценты начисляются
ежеквартально.
Определите
величину основных выплат за 5 год.
Если
ссуда погашается равными платежами в
конце каждого расчетного периода, то
размер выплаты задолженности за пятый
год составит:
ОБЩДОХОД(15%/4;6*4;1000;17;20)=-201.43$.
Комплексный
пример
Банком
выдан кредит в 10000$ на 5 лет под 12% годовых,
начисляемых один раз в конце каждого
периода. По условиям договора кредит
должен быть погашен равными долями в
течение указанного срока, выплачиваемыми
в конце каждого периода.
Разработать
план погашения кредита.
Периодический
платеж по данной операции составит:
ПЛТ(12%;5;-10000)=2774.10$.
Процентная
часть платежа на первый период составит:
ПРПЛТ(12%;1;5;-10000)=1200,00$.
Основная
часть платежа, направленная на погашение
долга за первый период, составит:
ОСПЛТ(12%;1;5;-10000)=1574.10$.
Как
видно выполняется тождество:
ПРПЛТ()+ОСПЛТ()=ПЛТ()=2774.10$.
Будущее
значение суммы, которую банк получит в
результате проведения операции:
ПЛТ(12%;5;-10000)*5=13870.50$.
Накопленная
сумма процентов за весь период составит:
ОБЩПЛТ(12%;5;10000;1;5;0)=-3870,49$.
Накопленная
сумма в счет погашения по займу за 5 лет
составит:
ОБЩДОХОД(12%;5;10;1;5;0)=-10000.00$.
Как
видно, сумма полученных величин равна
общей сумме, выплаченной по данному
займу:
ОБЩДОХОД()+ОБЩПЛАТ()=13870.49$.
(В
силу заложенного алгоритма расчета
функции ОБЩДОХОД() и ОБЩПЛАТ возвращают
отрицательные значения. Для получения
положительных значений можно задать
их со знаком минус).
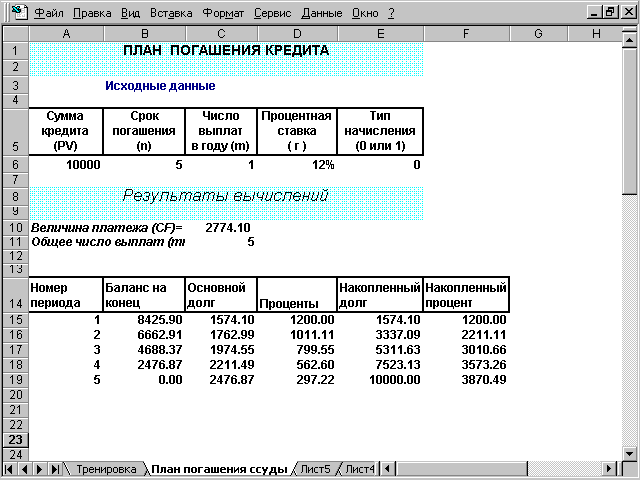
На
рис. 1 приведена таблица с планом погашения
кредита.
ЭФФЕКТ
— эффективная годовая процентная ставка
Позволяет
рассчитать фактическую годовую процентную
ставку, если известны годовая процентная
ставка и количество периодов в году.
Синтаксис
ЭФФЕКТ(нoмuнaльнaя_cmaвкa;кол_пep)
номинальная_ставка
—
номинальная годовая процентная ставка.
кол_пер
— количество
периодов в году.
Рис.
1. План погашения кредита
-
Число
периодов в году округляется до целого. -
Функция
ЭФФЕКТ
выдает значение ошибки #ЗНАЧ! в случае,
если один из аргументов — не число либо,
если номинальная_ставка
меньше 0 или
кол_пер
меньше 1.
Пример
Рассчитаем
эффективную годовую процентную ставку
при ставке 5,25% и четырех периодах в
году.
ЭФФЕКТ(5,25%;4)
равняется 0,053543 или 5,35%.
КПЕР
— определение срока платежа
Эта
функция вычисляет общее число периодов
выплат как для единой суммы вклада
(займа), так и для периодических постоянных
выплат на основе постоянной процентной
ставки. Если платежи производятся
несколько раз в год, найденное значение
необходимо разделить на число расчетных
периодов в году, чтобы найти число лет
выплат.
Синтаксис
КПЕР(норма;выплата;нз;бс;тип)
норма
– норма
прибыли за период.
выплата—
размер выплаты, производимой в каждом
периоде.
нз
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент нз опущен, то он
полагается равным 0.
бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
тип
— число,
определяющее, когда должна производиться
выплата.
Пример
Ожидается,
что ежегодные доходы от реализации
проекта составят 33 млн. руб. Необходимо
рассчитать срок окупаемости проекта,
если инвестиции к началу поступления
доходов составят 100 млн. руб., норма
дисконтирования 12.11%.
Срок
окупаемости проекта составит:
КПЕР(12.11%;33;-100)=4года.
Определение
скорости оборота инвестиций
ВНДОХ
— процентная ставка дохода для ряда
последовательных периодических
выплат или поступлений
Позволяет
рассчитать процентную ставку дохода
от инвестиций для ряда последовательных
операций с денежными средствами,
представленными числовыми значениями.
Объемы операций могут быть различны.
Однако они должны происходить через
равные промежутки времени, например,
ежемесячно или ежегодно. Процентная
ставка дохода, полученного от инвестиции,
состоит из выплат (отрицательные
значения) и поступлений (положительные
значения), которые происходят в регулярные
периоды времени.
Синтаксис
ВНДОХ
(значения;предположение)
значения
— массив или
ссылка на ячейки, содержащие числа, для
которых вычисляется процентная ставка
инвестиций.
предположение
—
прогнозируемая величина.
-
Аргумент
значения
должен включать в себя по крайней мере
одно положительное значение и одно
отрицательное значение, для того, чтобы
можно было вычислить процентную ставку. -
Начиная
со значения прогноз, функция ВНДОХ
выполняет
циклические вычисления, пока не получит
результат с точностью 0,00001 процента
(такой метод вычисления называется
методом итераций). -
Функция
ВНДОХ выдает значение ошибки #ЧИСЛО! в
том случае, если не может получить
результат после 20 попыток. -
Обычно
нет необходимости задавать аргумент
прогноз
для вычислений с помощью функции ВНДОХ.
Если прогноз
опущен, то
он полагается равным 0,1 (10 процентов).
Если ВНДОХ
выдает значение ошибки
#ЧИСЛО!,
можно попытаться выполнить вычисления
еще раз с другим значением аргумента
прогноз.
Пример
Предположим,
что затраты по проекту составят 500 тыс.
руб. Ожидаемые доходы составят 50 , 100 ,
300 и 200 тыс. руб. в течение последующих
4 лет. Оценим
экономическую целесообразность проекта
по скорости оборота инвестиций, если
рыночная норма дохода 12%.
Ячейки
А1:А5 содержат следующие значения: -500,
50, 100, 300 и 200 соответственно.
Внутренняя
скорость оборота инвестиций составит:
ВНДОХ(А1:А5)=9.25%.
Это
меньше, чем рыночная норма, поэтому
проект должен быть отвергнут.
В
том случае, если эта какая-либо из
финансовых функций недоступна из Excel,
следует установить надстройку Пакет
Анализа (Analysis
ToolPak),
а затем подключить его с помощью команды
Сервис
— Надстройки…
ЗАДАЧИ
Аннотация:
Цель работы: научиться работать с финансовыми функциями Excel и создавать отчеты.
Содержание работы:
Использование финансовых функций при экономических расчётах.
Составление финансовых отчетов в Excel.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания.
Оформить отчет и ответить на контрольные вопросы.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
MS Excel предоставляет большой спектр функций финансового анализа от нахождения платы по процентам, амортизации оборудования, регулярных выплат по займу до оценки эффективности капиталовложений.
Рассмотрим функции финансового анализа MS Excel, а также варианты составления финансовых отчетов от расчета затрат на производство до составления отчетной ведомости определения просроченных платежей.
Финансовая функция ПЛТ
Пример 1. Рассмотрим пример расчета с помощью функции рабочего листа ПЛТ 30-летней ипотечной ссуды со ставкой 8% годовых при начальном взносе 20% суммы и ежемесячной (ежегодной) выплате.
Для приведенного на рис. 10.1
рис.
10.1 ипотечного расчета в ячейки введите формулы, показанные на рис. 10.2
рис.
10.2.
Функция ПЛТ(PMT) вычисляет величину выплаты за один период годовой ренты (например, регулярных платежей по займу) при постоянной процентной ставке.
Синтаксис:
ПЛТ (ставка; кпер; пс; бс; тип) (PMT).
- cтавка – процентная ставка за период;
- кпер – общее число периодов выплат;
- пс – текущее значение, т. е. общая сумма, которую составят будущие платежи;
- бс – будущая стоимость или баланс наличности, который нужно достичь после последней выплаты.
Если параметр бс опущен, то его значение полагается равным 0 (например, это означает, что будущая стоимость займа равна 0);
- тип – число, равное 0 или 1, обозначающее, когда должна производиться выплата. Если значение параметра типравно 0 или он опущен, то оплата производится в конце периода, если его значение равно 1, то в начале периода.
Если БС = 0 и тип – 0, то функция ПЛТ возвращает значение:
где: Р – пс; i – ставка; n – кпер.
Примечание
Важно быть последовательным в выборе единиц измерения для задания значений аргументов ставка и кпер. Например, если производятся ежемесячные выплаты по четырехгодичному займу из расчета 12% годовых, то установите значение аргумента ставка равным 12%/12, а значение аргумента кпер равным 4×12. Если же производятся ежегодные платежи по тому же займу, то установите значение аргумента ставка равным 12%, а значение аргумента кпер равным 4.
Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на кпер.
Интервал выплат – это последовательность постоянных денежных платежей, осуществляемых в непрерывный период.
Например, заем под автомобиль или заклад являются интервалами выплат.
В функциях, связанных с интервалами выплат, отдаваемые вами деньги, такие как депозит на накопление, представляются отрицательным числом. Деньги же, которые вы получаете, такие как чеки на дивиденды, представляются положительным числом. Например, депозит в банк на сумму 1000 руб. представляется значением параметра пс равным -1000, если вы вкладчик, и значением 1000, если вы – банк.
Расчет эффективности неравномерных капиталовложений с помощью функций ЧПС, ВНДОХ и Подбора параметра
Рассмотрим следующую задачу. Вас просят дать в долг 10 000 руб. и обещают вернуть через год 2000 руб., через два года – 4000 руб., через три года – 7000 руб. При какой годовой процентной ставке эта сделка имеет смысл?
На рис. 10.3
рис.
10.3 в ячейку В8 введена формула, зависящая от функции ЧПС (NPV):
Кроме того, для автоматизации составления таблицы в ячейку С6 введена формула:
=ЕСЛИ(В6=1;"год"; ЕСЛИ(В6<=4;"года";"лет"))
Для решения задачи выполните следующие действия:
1. Первоначально в ячейку B7 введите произвольный процент, например, 8%.
2. В меню Данные > Анализ «что-если» выбрать команду Подбор параметра. Заполните поля ввода отобразившегося на экране диалогового окна Подбор параметра, как показано на рис. 10.3
рис.
10.3.
В поле Установить в ячейке дается ссылка на ячейку В8, в которой вычисляется чистый текущий объем вклада по формуле:
В поле Значение введите размер ссуды, равный 10000. В поле Изменяя значения ячейки задайте ссылку на ячейку B7, в которой вычисляется годовая процентная ставка.
3. Нажмите кнопку ОК. Средство Подбор параметра рассчитает, при какой годовой процентной ставке чистый текущий объем вклада равен 10000 р.
Искомая процентная ставка выводится в ячейку В7. В нашем случае годовая учетная ставка равна 11,79% (рис. 10.4
рис.
10.4). Можно сделать вывод: если банки предлагают большую годовую процентную ставку, то предлагаемая сделка не выгодна.
увеличить изображение
Рис.
10.3.
Исходные данные по расчету годовой процентной ставки и диалоговое окно Подбор параметра
Функция ЧПС возвращает чистый текущий объем вклада, вычисляемый на основе ряда последовательных поступлений наличных и нормы амортизации.
Чистый текущий объем вклада – это сегодняшний объем будущих платежей (отрицательные значения) и поступлений (положительные значения). Например, вам предлагают следующую сделку. У вас берут в долг некоторую сумму денег и предлагают через k1 год вернуть Рk1 денег, через k2 года вернуть Рk2 денег и т. д. через kn лет вернуть Рkn денег.
Кроме данной сделки у вас есть альтернативный способ использования ваших средств, например, положить их в банк под i% годовых. Тогда чистым текущим объемом вклада считается та сумма денег, которой вы должны располагать в начальный год, чтобы, положив их в банк под i% годовых, получить предлагаемую вам прибыль. В нашем случае чистый текущий объем вклада равен
Синтаксис:
НПЗ (ставка; 1-е значение; 2-е значение;…).
- ставка – процентная ставка за период;
- 1-е значение, 2-е значение, …– от 1 до 29 аргументов, представляющих расходы и доходы. 1-е значение, 2-е значение,…должны быть равномерно распределены по времени и осуществляться в конце каждого периода. НПЗ использует порядок аргументов 1-езначение, 2-е значение, … для определения порядка поступлений и платежей.
Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса 1-го значения и заканчивается с последним денежным взносом в списке.
Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов.
Рис.
10.4.
Результат расчета годовой процентной ставки и окно Результат подбора параметра
Если n – это количество денежных взносов в списке значений, Pj – j значение и i – ставка, то возвращаемое значение функцией ЧПС вычисляется по формуле:
Функция ЧПС тесно связана с функцией ВСД (внутренней скоростью оборота). Функция ВСД возвращает скорость оборота, для которой значение функции ЧПС равняется нулю, т. е.
Функция ВСД (IRR) возвращает внутреннюю скорость оборота для ряда последовательных операций с наличными, представленными числовыми значениями. Объемы операций не обязаны быть регулярными, как в случае ренты.
Внутренняя скорость оборота – это процентная ставка дохода, полученного от инвестиций, состоящих из выплат (отрицательные значения) и поступлений (положительные значения), которые происходят в регулярные периоды времени.
Синтаксис:
- Значение – массив или ссылка на ячейки, содержащие числовые величины, для которых вычисляется внутренняя скорость оборота средств.
Значения должны включать, по крайней мере, одно положительное значение и одно отрицательное значение для того, чтобы можно было вычислить внутреннюю скорость оборота. Данная функция использует порядок значений для интерпретации порядка денежных выплат или поступлений поэтому необходимо вводить значения выплат и поступлений в правильном порядке;
- прогноз – величина, о которой предполагается, что она близка к результату ВСД.
Если п+1 – это количество значений в списке, Pj – j-e значение, то ВНДОХ является корнем относительно i (ставки) следующего уравнения:
Примечание
MS Excel использует метод итераций для вычисления ВСД. Начиная со значения прогноз, функция вндох выполняет циклические вычисления, пока не получит результат с точностью 0,00001. Если функция ВСД не может получить результат после двадцати попыток, то возвращается значение ошибки #ЧИСЛО! В большинстве случаев нет необходимости задавать прогноз для вычислений с помощью функции ВСД. Если прогноз опущен, то он полагается равным 0,1 (10%).
Если ВСД выдает значение ошибки #число!, или если результат далек от ожидаемого, можно попытаться выполнить вычисления еще раз с другим значением аргумента прогноз.
Таким образом, задачу, сформулированную в начале данного раздела, можно решить также при помощи функции вндох. Для этого в ячейку B2 вместо 10000р. надо ввести -10000р., а в ячейку В7 – функцию ВСД(В2:В5), которая и найдет минимальную годовую учетную ставку.
Расчет эффективности капиталовложений с помощью функции ПС
Рассмотрим следующую задачу. Вас просят дать в долг 10 000 руб. и обещают возвращать по 2000 руб. в течение 6 лет. Будет ли выгодна эта сделка при годовой ставке 7%?
В расчете, приведенном на рис. 10.5
рис.
10.5, в ячейку В5 введена формула с функцией ПС о которой речь пойдет ниже в данном разделе:
Кроме того, для автоматизации составления таблицы и получения ответа на вопрос выгодна ли сделка, в ячейки, введите следующие формулы:
| Ячейка | Формула |
|---|---|
| C2 | =ЕСЛИ(В2=1;»год»; ЕСЛИ(В2<=4;»года»;»лет»)) |
| B6 | =ЕСЛИ(В1<В5; «Выгодно дать деньги в долг»; ЕСЛИ (В5=В1; «Варианты равносильны»; «Выгоднее деньги положить под проценты») ) |
Рис.
10.5.
Расчет эффективности капиталовложений
Как видно из рис. 10.5
рис.
10.5, в рассмотренном случае деньги выгоднее положить под проценты.
Функция ПС(PV) возвращает текущий объем вклада на основе постоянных периодических платежей. Функция ПС аналогична функции НПЗ. Основное различие между ними заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. Кроме того, в отличие от денежных взносов переменной величины в функции НПЗ, денежные взносы в функции ПС должны быть постоянны в течение всего периода инвестиции.
Синтаксис:
ПС (ставка; кпер; плт; бс; тип) (PV).
- Ставка – процентная ставка за период;
- Кпер – общее число периодов выплат;
- Плт – величина постоянных периодических платежей;
- Бс – будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если параметр бс опущен, то его значение полагается равным 0 (будущая стоимость займа, например, равна 0);
- Тип – число, равное 0 или 1, обозначающее, когда должна производиться выплата. Если значение параметра тип равно 0 или он опущен, то оплата производится в конце периода, если же его значение равно 1, то в начале периода.
Если тип = 0 и бс = 0, то значение функции ПС вычисляется по следующей формуле:
где: А – выплата; i – ставка; n – кпер.
Именование диапазонов и ячеек
Для того чтобы избавить себя от трудностей по расшифровке ссылок в формулах, следует воспользоваться именами ячеек или диапазонов ячеек. Например, можно присвоить итоговой области, состоящей из диапазона ячеек С2:C10 имя Итого. Теперь для того, чтобы найти суммарные итоги, достаточно воспользоваться формулой =СУММ(Итого) вместо сухой и безликой формулы =СУММ(С2:С10).
Использование имен ячеек или диапазонов ячеек позволяет:
- уменьшить вероятность появления ошибок в формулах. При вводе неизвестного имени MS Excel выводит сообщение #имя?;
- легко читать формулы. Например, формула = Доход-Издержки значительно легче для понимания, чем =В20-С20;
- легко ссылаться на один и тот же набор имен во всей рабочей книге;
- облегчить ввод ссылок на рабочие листы, находящиеся в других рабочих книгах.
Для того чтобы присвоить имя ячейке или диапазону необходимо:
- Выделить ячейку или диапазон.
- Выбрать команду Присвоить имя на вкладке Формулы в группе Определенные имена.
- Ввести подходящее имя в диалоговом окне Присвоение имени (рис. 10.6
рис.
10.6)
Рис.
10.6.
Присвоение имени ячейке и диалоговое окно
Чтобы использовать в формуле определенное имя, его также можно ввести одним из указанных ниже способов.
- c помощью ввода. Введите имя, например, в качестве аргумента формулы.
- c помощью автозавершения формулы. Используйте раскрывающийся список автозавершения формулы, в котором действительные имена перечислены автоматически.
- выбором из команды Использовать в формуле. Выберите определенное имя на вкладке Формулы в группе Определенные имена из списка Использовать в формуле.
Для изменения или удаления имени:
- Выбрать команду Присвоить имя на вкладке Формулы в группе Определенные имена.
- Перейти в поле Имя и отредактировать его.
- Для удаления имени нажмите кнопку Удалить.
- Нажмите кнопку ОК.
Создание имени путем выделения ячеек на листе
В имена можно преобразовать существующие заголовки строк и столбцов.
- Выберите диапазон, которому нужно присвоить имя, включая заголовки строк и столбцов.
- На вкладке Формулы в группе Присвоенные имена выберите команду Создать из выделенного.
- В диалоговом окне Создание имен из выделенного диапазона укажите место, содержащее заголовки, установив флажок в строке выше, в столбце слева, в строке ниже или в столбце справа.
Имя, созданное таким образом, относится только к ячейкам, содержащим значения, а не к существующим надписям строк и столбцов.
Применение имени
Если на рабочем листе формулы были сконструированы раньше чем имена, то при создании имен они автоматически не заменяют соответствующие ссылки в формулах. Для того чтобы это произошло, имена надо применить.
Для этого:
- Выберите ячейку или диапазон ячеек, для которых вы хотите применить имя
- Выполните команду Использовать в формуле в меню Определенные имена (Данные). На экране отобразится диалоговое окно со списком всех имен.
- Выберите требуемое имя.
- Переместите курсор в любую свободную ячейку.
Теперь все ссылки на ячейку или диапазон в формулах рабочего листа заменяться соответствующим именем.
Финансовые функции ПРПЛТ и ОСПЛТ
Пример. Рассмотрим пример вычисления основных платежей, платы по процентам, общей ежегодной платы и остатка долга на примере ссуды 100 000 руб. на срок 5 лет при годовой ставке 2% (рис. 10.7
рис.
10.7).
Итак, присвойте ячейкам следующие имена:
| Ячейка | Имя |
|---|---|
| Bl | Процент |
| В2 | Срок |
| ВЗ | Ежегодная_плата |
| В4 | Размер_ссуды |
Кроме того, в ячейки введите формулы:
| Ячейка | Формула | Описание |
|---|---|---|
| ВЗ | =ПЛТ (Процент; Срок; -Размер_ссуды) | Ежегодная плата |
| D6 | =Размер_ссуды | Начальный остаток долга |
| А7 | =А6+1 | Номер года |
| В7 | =D6*Процент | Плата по процентам за первый год |
| С7 | =Ежегодная_плата-В7 | Основная плата за первый год |
| D7 | =ЕСЛИ (D6-C7<>0;D6-C7) | Остаток долга за первый год |
Примечание
Если в ячейку D7 ввести формулу =D6-C7, то из-за денежного формата при условии что в ячейках D6 и С7 введены нули, в ячейку D7 будет выведен -р, а не 0р. Для избежания этой ситуации в ячейку D7 вводится формула с функцией ЕСЛИ.
В остальные годы эти платы определяются перемещением маркера заполнения диапазона А7:D7 вниз по столбцам до тех пор, пока в столбце остатка долга не появится ноль.
Рис.
10.7.
Вычисление основных платежей и платы по процентам
Отметим, что основную плату и плату по процентам можно было непосредственно найти при помощи функций ОСПЛТ (РРМТ) и ПРПЛТ (IRMT), соответственно.
Функция ПРПЛТ возвращает платежи по процентам за данный период на основе периодических постоянных выплат и постоянной процентной ставки.
Функция ОСПЛТ возвращает величину выплаты на данный период на основе периодических постоянных платежей и постоянной процентной ставки.
Синтаксис:
ПРПЛТ (ставка; период; кпер; пс; бс; тип).
- ОСПЛТ (ставка; период; кпер; пс; бс; тип)
- Ставка – процентная ставка за период;
- период – период, для которого требуется найти прибыль; должен находиться в интервале от 1 до кпер;
- кпер – общее число периодов выплат;
- Пс – текущее значение, т. е. общая сумма, которую составят будущие;
- Бс – будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если Бс опущено, оно полагается равным 0 (будущая стоимость займа, например, равна 0);
- тип – число, равное 0 или 1, обозначающее, когда должна производиться выплата. Если значение параметра тип равно 0 или этот параметр опущен, то оплата производится в конце периода, если же он равен 1, то в начале периода.
Функции ПРПЛТ и ОСПЛТ тесно между собой связаны, а именно:
ПЛПj=ibj-1 ,
ОСНПj = А- ПЛПj,
ВJ= Вj-1 – OCHПj при ![$j in [0; >n]$](https://intuit.ru/sites/default/files/tex_cache/9005e755f4ee553a4691e18da9965852.png)
- j – номер периода; п – кпер;
- ПЛПj, ОСНПj и ВJ – это ПРПЛТ, ОСПЛТ И остаток долга, соответственно, за j-й период,
- ПЛПо=0, ОСНПО = 0, В0 =ПС;
- А – величина выплаты за один период годовой ренты на основе постоянных выплат и постоянной процентной ставки, вычисляемая с помощью функции ПЛТ.
Финансовые функции БС, КПЕР и СТАВКА
Функция БС(FV) вычисляет будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки.
Функция БС подходит для расчета итогов накоплений при ежемесячных банковских взносах.
БС(ставка; кпер; плт; пс; тип) (FV)
- Ставка – процентная ставка за период;
- Кпер – общее число периодов выплат;
- Плт –величина постоянных периодических платежей;
- пс – текущее значение, т. е. общая сумма, которую составят будущие платежи;
- Тип – число, равное 0 или 1, обозначающее, когда должна производиться выплата. Если значение параметра тип равно 0 или он опущен, то оплата производится в конце периода, если же он равен 1, то в начале периода.
Если тип = 0 и пс = 0, то функция БС вычисляет по следующей формуле:
где: А – выплата, i – ставка, n – кпер.
Приведем пример использования функции БС. Предположим, вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Допустим, вы собираетесь вложить 1000 руб. при годовой ставке 6%, а затем хотите вкладывать по 100 руб. в начале каждого следующего месяца в течение следующих 12 месяцев. Сколько денег будет на счету в конце12 месяцев? Результат вычисляется формулой
=БС(6/12%; 12; -100; -1000; 1),
которая возвращает 2301.40р.
Функция КПЕР (NPER) вычисляет общее количество периодов выплаты для данного вклада на основе периодических постоянных выплат и постоянной процентной ставки.
Синтаксис:
КПЕР (ставка; плт; пс; бс; тип)
- Ставка – процентная ставка за период;
- Плт – величина постоянных периодических платежей;
- Пс – текущее значение, т. е. общая сумма, которую составят будущие платежи;
- Бс – будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если параметр Бс опущен, то его значение полагается равным 0 (будущая стоимость займа, например, равна 0);
- тип – число, равное 0 или 1, обозначающее, когда должна производиться выплата. Если значение параметра тип равно 0 или он опущен, то оплата производится в конце периода, если его значение равно 1, то в начале периода.
При тип = 0 и бс = 0 функция КПЕР вычисляет по следующей формуле
где: Р–пс, i – ставка, А– выплата.
Например, если вы берете в долг 1000 руб. при годовой ставке 1% и собираетесь выплачивать по 100 руб. в год, число выплат определяется формулой
которая возвращает значение 11.
ФУНКЦИЯ СТАВКА (RATE) вычисляет процентную ставку за один период, необходимую для получения определенной суммы за заданный срок путем постоянных взносов. Функция СТАВКА вычисляет процентную ставку методом итераций и может не найти решение. Если после 20 итераций погрешность определения ставки превышает 0.0000001, то функция СТАВКА возвращает значение ошибки #ЧИСЛО!.
Синтаксис:
СТАВКА (кпер; плт; пс; бс; тип; нач_прибл).
- Кпер – общее число периодов выплат;
- Плт – величина постоянных периодических платежей; текущее значение, т. е. общая сумма, которую составят будущие платежи;
- Пс – текущее значение, т.е. общая сумма, которую составят будущие платежи;
- Бс – будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если параметр бс опущен, то его значение полагается равным 0 (будущая стоимость займа, например, равна 0);
- тип – число, равное 0 или 1, обозначающее, когда должна производиться выплата. Если значение параметра тип равно 0 или он опущен, то оплата водится в конце периода, если же его значение равно 1, то в начале периода;
- нач_прибл – предполагаемая величина нормы. Если параметр нач_прибл опущен, то его значение полагается равным 10%.
Примечание
Если функция СТАВКА не сходится, следует попытаться использовать различные значения параметра нач_прибл. Обычно функция СТАВКА сходится, если значения параметра нач_прибл берутся из интервала от 0 до 1.
При бс = 0 и тип= 0 функция СТАВКА является корнем следующего уравнения:
где: A – выплата, i – СТАВКА, n – кпер, P – ПС.
Рассмотрим пример использования функции СТАВКА. Чтобы определить процентную ставку для четырехлетнего займа в 8000 руб. с ежемесячной выплатой в 200 руб., можно использовать формулу:
= СТАВКА(48; -200; 8000),
которая вычисляет значение 0.77%. Отметим, что это месячная процентная ставка т. к. период равен месяцу.
Создание простейшей отчетной ведомости
Предположим, что вы – менеджер торговой сети магазинов «Магнит» и вам необходимо составить отчетную ведомость по результатам ее деятельности за летний период с простейшей обработкой данных (рис. 10.8
рис.
10.8).
В этой отчетной ведомости надо определить:
- суммарную и среднюю выручку каждого из магазинов за отчетный период;
- суммарную выручку всех магазинов за каждый месяц отчетного периода;
- место, которое занимает каждый из магазинов в суммарном объеме выручки;
- долю каждого из магазинов в суммарном объеме выручки;
- количество магазинов, имеющих суммарную выручку до 1000 млн. руб., от 1000 млн. руб. до 1500 млн. руб., от 1500 млн. руб. до 2000 млн. руб. и свыше 2000 млн. руб.
При составлении данного отчета необходимо выполнить следующие действия:
- Для нахождения суммарной выручки первого магазина введите в ячейку Е3 формулу =СУММ (В3:D3)
- Выберите ячейку Е3, расположите указатель мыши на маркере заполнения и переместите его вниз на диапазон Е4:Е8.
Это позволит найти суммарную выручку каждого из магазинов.
- Для нахождения суммарного объема выручки всех магазинов за июнь введите в ячейку В9 формулу =СУММ (В3:В8)
- Выберите ячейку В9, расположите указатель мыши на маркере заполнения и переместите его вправо на диапазон С9:Е9. Это позволит найти суммарную выручку сети магазинов как за каждый месяц в отдельности, так и за весь период в целом.
- Для нахождения средней выручки первого магазина введите в ячейку G3 формулу =СРЗНАЧ (В3:D3)
- Выберите ячейку G3, расположите указатель мыши на маркере заполнения и переместите его вниз на диапазон G4:G8. Это позволит найти среднюю выручку каждого из магазинов.
- Для определения доли объема выручки первого магазина по отношению к суммарной выручке всей сети магазинов введите в ячейку Н3 формулу =ЕЗ/$Е$9
- Выберите ячейку Н3, расположите указатель мыши на маркере заполнения и переместите его вниз на диапазон Н4:Н8. Это позволит найти долю объема выручки каждого из магазинов по отношению к суммарной выручке всей сети магазинов.
- Выберите диапазон Н3:Н8 и нажмите кнопку Процентный формат панели инструментов Форматирование. Это позволит установить процентный формат в ячейках выбранного диапазона.
- Для определения места первого магазина в суммарной выручке всей сети магазинов введите в ячейку F3 формулу =РАНГ (Е3; $E$3:$E$8)
- Выберите ячейку F3, расположите указатель мыши на маркере заполнения и переместите его вниз на диапазон F4:F8. Это позволит найти место каждого магазина в суммарной выручке всей сети магазинов.
- Для определения количества магазинов, имеющих суммарную выручку до 1000 млн руб., от 1000 млн руб. до 1500 млн руб., от 1500 млн руб. до 2000 млн руб. и свыше 2000 млн руб., сначала заполните ячейки согласно рис. 10.8
рис.
10.8, а затем выберите диапазон J3:J6 и введите в него формулу массива (не забудьте завершить ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>)
{=ЧАСТОТА(Е3:Е8; I3:I5)},
При составлении отчетной ведомости использовались функции СРЗНАЧ, РАНГ и ЧАСТОТА.
Функция СРЗНАЧ (AVERAGE) находит среднее арифметическое значение из указанного диапазона ячеек.
Синтаксис:
СРЗНАЧ (число1; число2; …).
ФУНКЦИЯ РАНГ (RANK) возвращает ранг числа в списке чисел. Ранг числа – это его величина относительно других значений в списке. (Если список отсортировать, то ранг числа будет его позицией.).
Синтаксис:
РАНГ (число; ссылка; порядок).
- число – число, для которого определяется ранг;
- ссылка – массив или ссылка на список чисел. Нечисловые значения в ссылке игнорируются;
- порядок – число, определяющее способ упорядочения. Если значение параметра порядок равно 0 или он опущен, то MS Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в порядке убывания. Если значение параметра порядок является любым ненулевым числом, то MS Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в порядке возрастания.
Примечание
Функция РАНГ присваивает одинаковым числам одинаковый ранг.
Функция ЧАСТОТА (FREQUENCY)возвращает распределение частот в виде вертикального массива. Для данного множества значений и данного множества карманов (т.е. интервалов в математическом смысле) частотное распределение подсчитывает, сколько исходных значений попадает в каждый интервал.
Синтаксис:
ЧАСТОТА (массив_данных; двоичный_массив).
- массив_данных – массив или ссылка на множество данных, для которых вычисляются частоты; если массив_данных не содержит значений, то функция ЧАСТОТА возвращает массив нулей;
- двоичный_массив – массив или ссылка на множество интервалов, в которые группируются значения аргумента массив_данных. Если двоичный_массив не содержит значений, то функция ЧАСТОТА возвращает количество элементов в аргументе двоичный_массив.
Примечание
Функция СУММ позволяет не только складывать значения ее аргументов, но также и вычитать их. Например, пусть в ячейки А2 и В2 введен размер прибыли за июнь и июль в размере 10 000 руб. и 20 000 руб. соответственно, а в ячейку С2 – убытки за оба месяца в размере 5000руб. Тогда формула =СУММ (А2:В2;-С2) возвращает общую прибыль минус потери за отчетный период. Тот же самый результат дает формула =СУММ (А2: В2)-С2.
Расчет итоговой выручки по объему реализации
Рассмотрим еще один пример составления отчетной ведомости. Предположим, что вы — бухгалтер фирмы «Владос», продающей компьютеры. Вам необходимо найти суммарную стоимость проданных компьютеров за каждый месяц летнего периода. Создаваемый вами отчет представляет собой рабочий лист, состоящую из двух таблиц (рис. 10.9
рис.
10.9):
- таблица расценок товаров;
- таблица объемов реализации товаров.
Для того чтобы найти итоговую выручку в рублях реализации всех товаров за каждый месяц, надо в ячейку Е3 таблицы Отчет ввести формулу массива (не забудьте завершить ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>):
{=СУММ(ВЗ:D3*Цена!$А$3:$С$3)},
а затем заполнить этой формулой диапазон Е4:Е5, потянув маркер заполнения вниз.
Отметим, что, конечно, данную таблицу можно было заполнить без привлечения формулы массива, введя в ячейку Е3 формулу
=СУММПРОИЗВ(ВЗ:D3; Цена!$А$3:$С$3)
с ее последующим копированием и настройкой на диапазон Е4:Е5.
Расчет просроченных платежей
Предположим, что вы менеджер фирмы «ВЛАДОС» по продаже компьютеров. Компьютеры фирма продает в рассрочку, поэтому необходимо вести учет просроченных платежей. Просрочка платежей разбивается на «временные карманы» (рис. 10.10
рис.
10.10):
- от 1 до 14 дней;
- от 15 до 29 дней;
- от 30 до 10000 дней.
На самом деле под последним интервалом подразумевается неограниченный интервал – не менее 30 дней. Для удобства обработки данных вместо неограниченного интервала рассматриваем интервал, ограниченный сверху очень большим числом. С практической точки зрения это одно и то же, что и неограниченный сверху интервал.
Итак, для проведения расчетов введите в ячейки рабочего листа следующие формулы:
| Ячейка | Формула | Описание |
|---|---|---|
| F2 | =ДАТА(2000; 7;15) | Дата переучета |
| E2 | =ЕСЛИ(D2=0;$F$2-C2;» ») | Возвращает период просрочки. Выберите ячейку Е2 и, потянув за маркер заполнения, заполните диапазон Е3:Е22 |
| G3 | {=СУММ(($E$2:$E$22>=I3)*($E$2:$E$22<=J3))} | Эта формула массива возвращает число заказов со сроком просрочки до 14 дней. Не забудьте завершить ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Выберите ячейку G3 и протяните маркер заполнения вниз на диапазон G4:G5 для определения числа просроченных заказов для других временных интервалов |
| H3 | {=СУММ(($E$2:$E$22>=I3)*($E$2:$E$22<=J3)*($B$2:$B$22))} | Эта формула массива возвращает суммарную стоимость заказов периодом просрочки до 14 дней. Не забудьте завершить ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Выберите ячейку НЗ и протяните маркер заполнения на диапазон Н4: Н5 для определения суммарной стоимости просроченных заказов для других временных интервалов |
Функция ДАТА (DATE) возвращает дату в числовом формате для заданной даты.
Синтаксис:
- год – число от 1900 до 9999;
- месяц – число, представляющее номер месяца в году. Если месяц больше 12, то это число прибавляется к первому месяцу указанного года. Например, ДАТА(2000; 14; 2) возвращает числовой формат даты 14 февраля2000 года;
- день – число, представляющее номер дня в месяце. Если день больше числа дней в указанном месяце, то это число прибавляется к первому дню указанного месяца.
Приведем пояснения к формуле {=СУММ ( ($Е$2 : $Е$22>=I3) * ($Е$2 : $Е$22<=J3))}. Напомним, что в данном случае в ячейку I3 введено 1, а в ячейку J3 – 14.В формуле массива условие Е2:Е20>=1 возвращает массив, состоящий из 0 и 1, где 0 стоит на месте ячейки со значением меньше 1 и 1 – со значением не меньше 1.
Следовательно, данная формула вычисляет сумму произведений:
- элементов массива Е2:Е20>=1 (с единицами в случае просрочки заказа по крайней мере на один день и нулями в противном случае);
- элементов массива Е2:Е20<=14 (с единицами в случае просрочки до 14 дней и нулями в противном случае).
Таким образом, эта формула возвращает общее количество просроченных заказов сроком от 1 до 14 дней.
Приведем пояснения к формуле {=СУММ(($Е$2:$Е$22>=I3)*($E$2:$E$22<=J3)*($B$2:$B$22))}.
Напомним, что в ячейку I3 введено 1, а в ячейку J3 – 14. В этой формуле по отношению к предыдущей появился дополнительный сомножитель $В$2:$В$22. Поэтому данная формула вычисляет сумму произведений:
- элементов массива Е2:Е20>=1 (с единицами в случае просрочки заказа по крайней мере на один день и нулями в противном случае);
- элементов массива Е2:Е20<=14 (с единицами в случае просрочки заказа до 14 дней и нулями в противном случае);
- массива $В$2:$В$22 (с ценами процессоров).
Таким образом, эта формула возвращает суммарную стоимость просроченных заказов сроком от 1 до 14 дней.
Вычисление значения с использованием условия
Функция СЧЁТЕСЛИ (COUNTIF) возвращает количество непустых ячеек внутри интервала, удовлетворяющих заданному критерию.
Синтаксис:
СЧЁТЕСЛИ (диапазон; условие).
- диапазон – интервал, в котором нужно подсчитать ячейки;
- условие – в форме числа, выражения или текста, который определяет какие ячейки надо подсчитывать; например, критерий может быть выражен следующим образом: 17, «17», «>17», «Компьютер».
Рассмотрим пример. Пусть ячейки диапазона А1:А4 содержат следующие значения: яблоки, апельсины, персики, яблоки. Тогда =СЧЁТЕСЛИ(А1:А4;»яблоки») возвращает 2.
Пусть ячейки В1:В4 содержат 32, 54, 75 и 86 соответственно. Тогда =СЧЁТЕСЛИ(В1:В4;»>50″) возвращает 3.
Функция СУММЕСЛИ (SUMIF) суммирует ячейки, заданные критерием.
Синтаксис:
СУММЕСЛИ (диапазон; условие; диапазон_суммирования).
- диапазон – это интервал вычисляемых ячеек;
- условие – это критерий в форме числа, выражения или текста, который определяет, какая ячейка добавляется. Например, критерий может быть выражен как 32, «32», «>32», «яблоки»;
- диапазон_суммирования – это фактические ячейки для суммирования. Ячейки в аргументе диапазон_суммирования складываются, если соответствующие им ячейки в аргументе диапазон удовлетворяют условию. Если интервал_суммирования опущен, то в расчетах участвуют ячейки в аргументе диапазон.
Пусть, имеются данные фирмы по работе с недвижимостью «Аякс» о стоимостях квартир и о комиссионных при их продаже (табл. 10.1
таблица
10.1).
| Ячейка | Значение (стоимость квартиры) | Ячейка | Значение (комиссионные от продажи) |
|---|---|---|---|
| А1 | 1000000 | В1 | 7000 |
| А2 | 2000000 | В2 | 14000 |
| А3 | 3000000 | В3 | 21000 |
| А4 | 4000000 | В4 | 28000 |
Тогда следующая формула возвращает сумму комиссионных от продажи квартир, стоимость которых больше чем 150 000.
=СУММЕСЛИ(А1:А4;»>150000″;В1:В4) возвращает 63000.
Продемонстрируем использование функций СЧЁТЕСЛИ и СУММЕСЛИ на примере создания отчетной ведомости, в которой необходимо проследить все заказы, размещенные коммивояжерами фирмы «Самовар», торгующей самоварами, и подсчитать объемы продаж по каждому из них.
Итак, в вашем распоряжении имеется рабочая книга, состоящая из двух рабочих листов (рис. 10.11
рис.
10.11):
- лист Заказы, где приведен список осуществленных продаж за текущий
день каждым из коммивояжеров вашей фирмы;
- лист Коммивояжер со списком всех коммивояжеров вашей фирмы.
Для проведения расчетов введите на рабочем листе Коммивояжер представленные ниже формулы:
| Ячейка | Формула | Описание |
|---|---|---|
| Е2 | =СЧЁТЕСЛИ(Заказы!$A$2:$A$10;A2) | Возвращает число заказов, выполненных Ивановым. Выберите ячейку Е2 и протяните маркер заполнения вниз на диапазон Е3:Е4, для определения числа заказов, выполненных каждым из коммивояжеров |
| F2 | =СУММЕСЛИ(Заказы!$A$2:$A$10;A2;Заказы!$B$2:$B$10) | Возвращает стоимость заказов, выполненных Ивановым. Выберите ячейку F2 и протяните заполнения на диапазон F3:F4 для определения стоимости заказов, выполненных каждым из коммивояжеров |
Расчет комиссионных
В данном примере разработаем функцию, необходимую менеджеру по продажам, которому нужно рассчитать свои комиссионные. Процент комиссионных зависит от объема проданного товара. Тот, кто продает больше и получает более высокий процент комиссионных. Вычисления, выполняемые в данном примере, основаны на правиле начисления комиссионных, предложенном в таблице 10.2.
| Объем продаж за неделю, руб. | Комиссионные, % |
|---|---|
| От 0 до 9999 | 8 |
| От 10000 до 19999 | 10 |
| От 20000 до 39999 | 12 |
| Более 40000 | 14 |
Рис.
10.12.
Расчет комиссионных
Для расчета комиссионных для объемов продаж, приведенных на рабочем листе (рис. 10.12
рис.
10.12), достаточно в ячейку С2 ввести следующую формулу, затем выбрать эту ячейку и, потянув за маркер заполнения, разместить формулы в диапазоне С3:С9 для определения комиссионных за каждую из указанных недель:
=ЕСЛИ(В2<=9999;В2*8%;0)+ЕСЛИ(И(10000<=В2;В2<=19999); В2*10%;0)+ЕСЛИ(И(20000<=В2;В2<=39999);В2*12%;0)+ ЕСЛИ(40000<=В2;В2*14%;0)
Расчет затрат на производство
Составим отчетную ведомость по расчету затрат на производство компакт-дисков (рис. 10.13
рис.
10.13). Упаковка диска фирме обходится в 1 руб./шт., стоимость материалов – 4 руб./шт. Фирма продает готовые диски по цене 10 руб./шт. Технические возможности позволяют выпускать до 5000 дисков в день. Оплата труда рабочих является сдельной и зависит от количества выпущенных дисков по правилу, представленному в таблице 10.3.
| Выпущено дисков, шт. | Оплата труда, руб./шт. |
|---|---|
| За первую тысячу | 0,3 |
| За вторую тысячу | 0,4 |
| За третью тысячу | 0,5 |
| За четвертую тысячу | 0,6 |
| За превышение над четвертой тысячей | 0,7 |
Предположим, что поступил заказ на изготовление 4500 компакт-дисков. Необходимо посчитать суммарные издержки и прибыль после выполнения данного заказа.
Для упрощения чтения формул при помощи команды Вставка > Имя > Присвоить установите имена ячейкам и диапазонам ячеек, перечисленные ниже.
| Диапазон | Имя |
|---|---|
| В1 | ЗаказШт |
| В2 | ПродажнаяЦена |
| В3 | СтоимостьУп |
| В4 | СтоимостьМат |
| В9 | ОбщиеИздержки |
| D2:D6 | ДискиШт |
| E2:E6 | ОплатаРубШт |
| F2:F6 | ОплатаРуб |
Зарплата рабочих в зависимости от объема выпущенных дисков находится в диапазоне F2:F7 по формуле массива (не забудьте завершить ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>).
=ЕСЛИ (ЗаказШт-1000>ДискиШт;1000*ОплатаРубШт; ЕСЛИ (ЗаказШт>ДискиШт;(ЗаказШт-ДискиШт)*ОплатаРубШт; 0))
Кроме того, для завершения расчетов введите в ячейки следующие формулы:
| Ячейка | Формула | Описание |
|---|---|---|
| В6 | =ЗаказШт*СтоимостьМат | Стоимость упаковки |
| В7 | =ЗаказШт*СтоимостьМат | Стоимость материалов |
| В8 | =СУММ(ОплатаРуб) | Суммарная зарплата |
| В9 | =СУММ(В6:В8) | Суммарные издержки |
| В10 | =ЗаказШт*ПродажнаяЦена-ОбщиеИздержки | Суммарная прибыль |
ЗАДАНИЯ
1. Вычислить n-годичную ипотечную ссуду покупки квартиры за Р руб. с годовой ставкой i % и начальным взносом А %. Сделать расчет для ежемесячных и ежегодных выплат для исходных данных, представленных в следующей таблице:
| Вариант | N | P | i | A |
|---|---|---|---|---|
| 1 | 7 | 170000 | 5 | 10 |
| 2 | 8 | 200000 | 6 | 10 |
| 3 | 9 | 220000 | 7 | 20 |
| 4 | 10 | 300000 | 8 | 20 |
| 5 | 11 | 350000 | 9 | 15 |
| 6 | 7 | 210000 | 10 | 15 |
| 7 | 8 | 250000 | 11 | 30 |
| 8 | 9 | 310000 | 12 | 30 |
| 9 | 10 | 320000 | 13 | 25 |
| 10 | 11 | 360000 | 14 | 25 |
2. Вас просят дать в долг P руб. и обещают вернуть P1руб. через год, Р2руб. – через два года и т. д. Pn руб. – через nлет. При какой годовой процентной ставке эта сделка имеет смысл?
| Вариант | n | P | P1 | P2 | P3 | P4 | P5 |
|---|---|---|---|---|---|---|---|
| 1 | 3 | 17000 | 5000 | 7000 | 8000 | ||
| 2 | 4 | 20000 | 6000 | 6000 | 9000 | 7000 | |
| 3 | 5 | 22000 | 5000 | 8000 | 8000 | 7000 | 5000 |
| 4 | 3 | 30000 | 5000 | 10000 | 18000 | ||
| 5 | 4 | 35000 | 5000 | 9000 | 10000 | 18000 | |
| 6 | 5 | 21000 | 4000 | 5000 | 8000 | 10000 | 11000 |
| 7 | 3 | 25000 | 8000 | 9000 | 10000 | ||
| 8 | 4 | 31000 | 9000 | 10000 | 10000 | 15000 | |
| 9 | 5 | 32000 | 8000 | 10000 | 10000 | 10000 | 11000 |
| 10 | 3 | 36000 | 10000 | 15000 | 21000 |
3. Вас просят дать в долг Р руб.. и обещают возвращать по А руб. в течение n лет. При какой годовой процентной ставке эта сделка имеет смысл?
| Вариант | n | P | A |
|---|---|---|---|
| 1 | 7 | 170000 | 30000 |
| 2 | 8 | 200000 | 31000 |
| 3 | 9 | 220 000 | 33 000 |
| 4 | 10 | 300 000 | 34 000 |
| 5 | 11 | 350 000 | 41 000 |
| 6 | 7 | 210000 | 32 000 |
| 7 | 8 | 250 000 | 37000 |
| 8 | 9 | 310000 | 40 000 |
| 9 | 10 | 320 000 | 35 000 |
| 10 | 11 | 360 000 | 41 000 |
4. Вычислить основные платежи, плату по процентам, общую ежегодную выплату и остаток долга на примере ссуды Р руб. под годовую ставку i% на срок п лет.
| Вариант | n | P | i |
|---|---|---|---|
| 1 | 7 | 170000 | 5 |
| 2 | 8 | 200000 | 6 |
| 3 | 9 | 220000 | 7 |
| 4 | 10 | 300000 | 8 |
| 5 | 11 | 350000 | 9 |
| 6 | 7 | 210000 | 10 |
| 7 | 8 | 250000 | 11 |
| 8 | 9 | 310000 | 12 |
| 9 | 10 | 320000 | 13 |
| 10 | 11 | 360000 | 14 |
5. Вы берете в долг Р руб. под годовую ставку i% и собираетесь выплачивать по А руб. в год. Сколько лет займут эти выплаты?
выплачивать по А руб. в год. Сколько лет займут эти выплаты?
| Вариант | P | A | i |
| 1 | 170000 | 31000 | 3 |
| 2 | 200000 | 32000 | 4 |
| 3 | 220 000 | 33 000 | 5 |
| 4 | 300 000 | 34 000 | 6 |
| 5 | 350 000 | 41 000 | 7 |
| 6 | 210000 | 32 000 | 8 |
| 7 | 250 000 | 37000 | 9 |
| 8 | 310000 | 40 000 | 10 |
| 9 | 320 000 | 35 000 | 4 |
| 10 | 360 000 | 41 000 | 5 |
6. Вас просят дать в долг Р руб. в день D и обещают вернуть Р1 руб. в день D1,P1, руб. – в день D2 и т.д.Pn руб. – в день Dn. Имеет ли смысл эта сделка при годовой ставке i % (i, Р, п, Р1,…, Рn из задания 2)?
7. Составить отчетную ведомость реализации товаров п магазинами с месяца А по месяц В, приведенную ранее в примере «Создание простейшей отчетной ведомости»
8. Вы берете в долг Р руб. под годовую ставку i% и собираетесь отдавать по А руб. в год. Сколько лет займут выплаты?
9. Вы собираетесь вкладывать по А руб. в течение п лет при годовой ставке i%. Сколько денег будет на счету через п лет?
10. Определить процентную ставку для n летнего займа в Р руб. с ежегодной выплатой в А руб.
11. Составить таблицу начисления премии по итогам работы сети п магазинов с месяца А по месяц В по следующему правилу:
- если продукции продано не меньше чем на С руб., то комиссионные составляют /%;
- за первое м есто дополнительно начисляется j1 %, за второе место – j2% и т. д., за k-место дополнительно начисляется jk %.