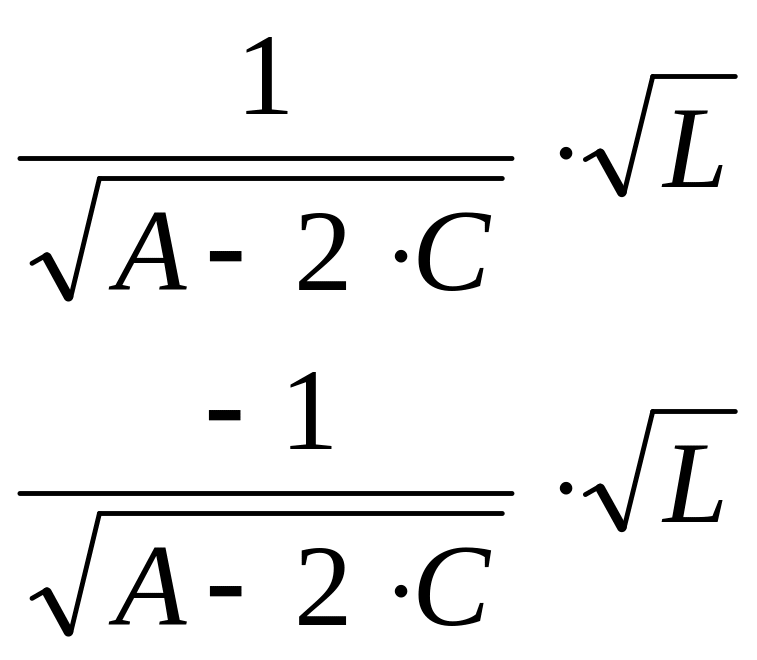Функция в excel это совокупность - Word и Excel - помощь в работе с программами

Содержание

Статистические функции
- МАКС
- МИН
- СРЗНАЧ
- СРЗНАЧЕСЛИ
- МОДА.ОДН
- МЕДИАНА
- СТАНДОТКЛОН
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- РАНГ.СР
Вопросы и ответы

Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.

Статистические функции

Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.

Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных. Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте.

Запустить Мастер функций можно тремя способами:

Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.

Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».

Набрать на клавиатуре сочетание клавиш Shift+F3.

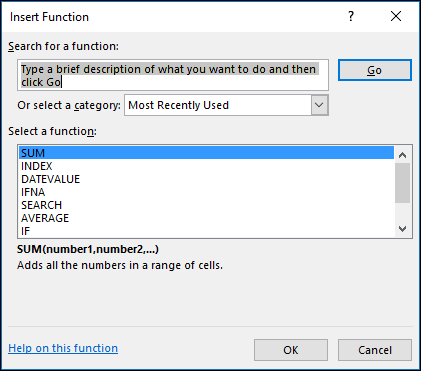
При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».

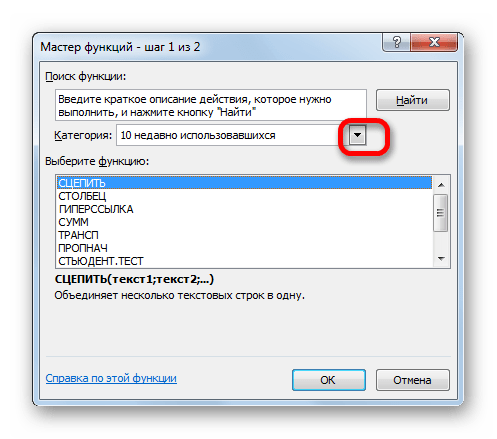
Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».

После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».

Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.

Урок: Мастер функций в Excel

МАКС

Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:

=МАКС(число1;число2;…)

В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.

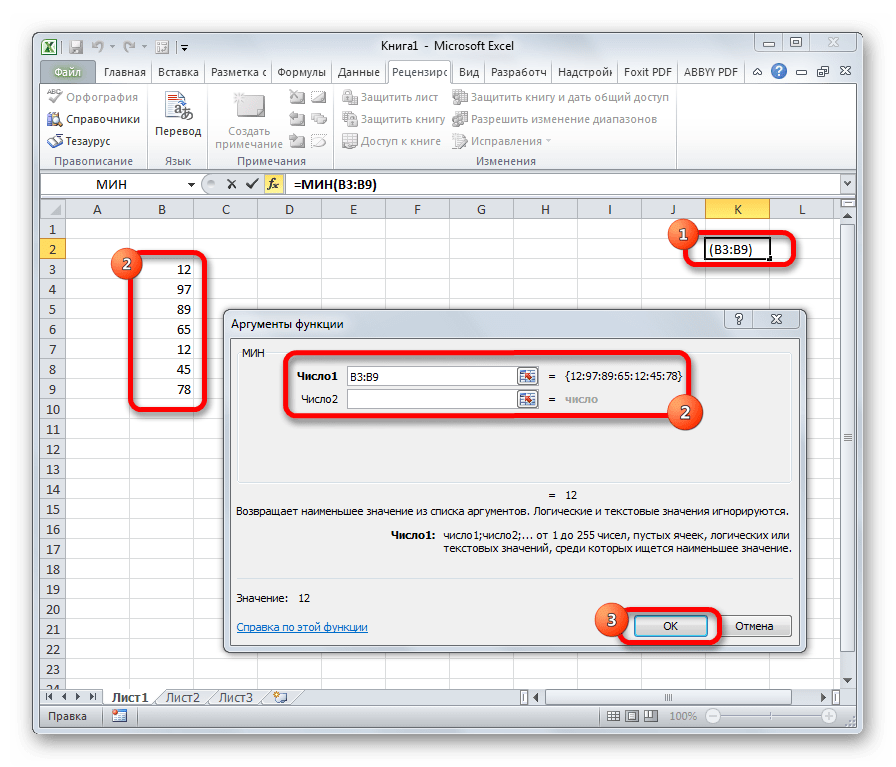
МИН

По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:

=МИН(число1;число2;…)

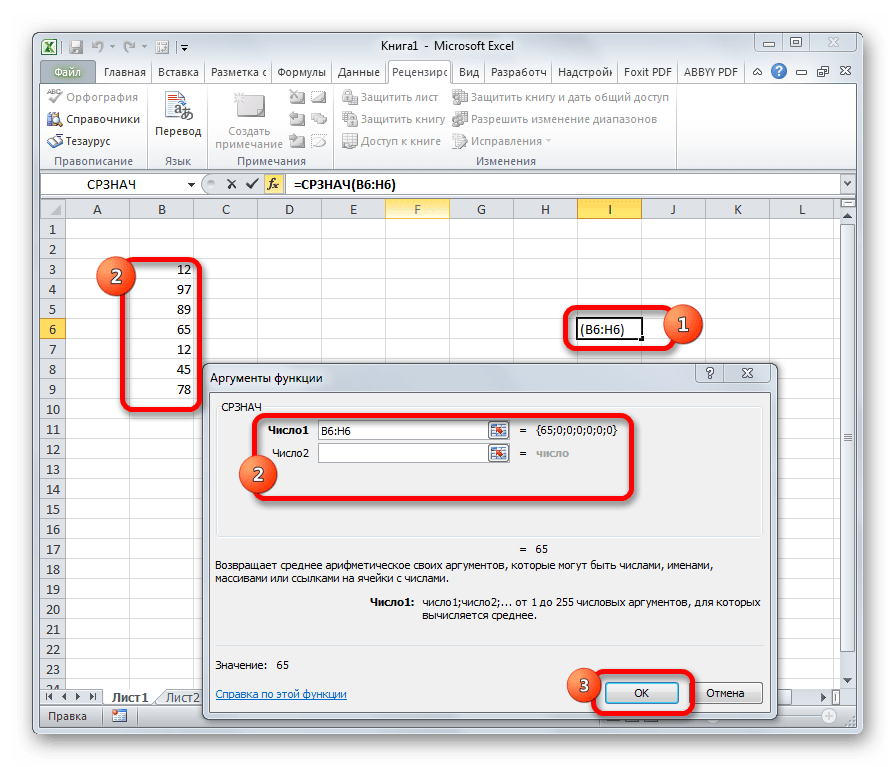
СРЗНАЧ

Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:

=СРЗНАЧ(число1;число2;…)

СРЗНАЧЕСЛИ

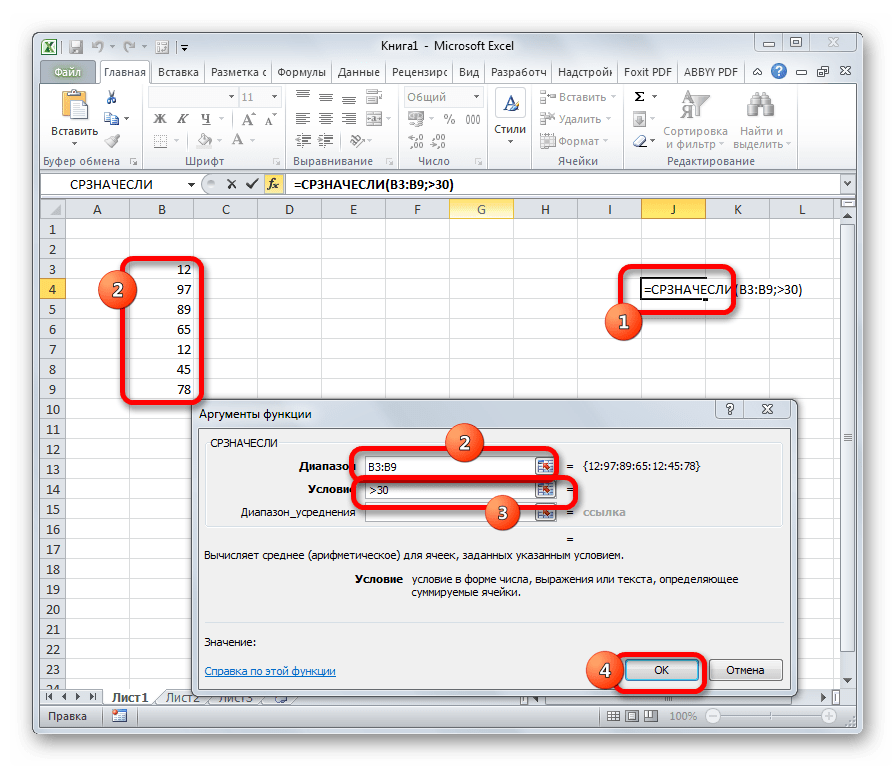
Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:

=СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения])

МОДА.ОДН

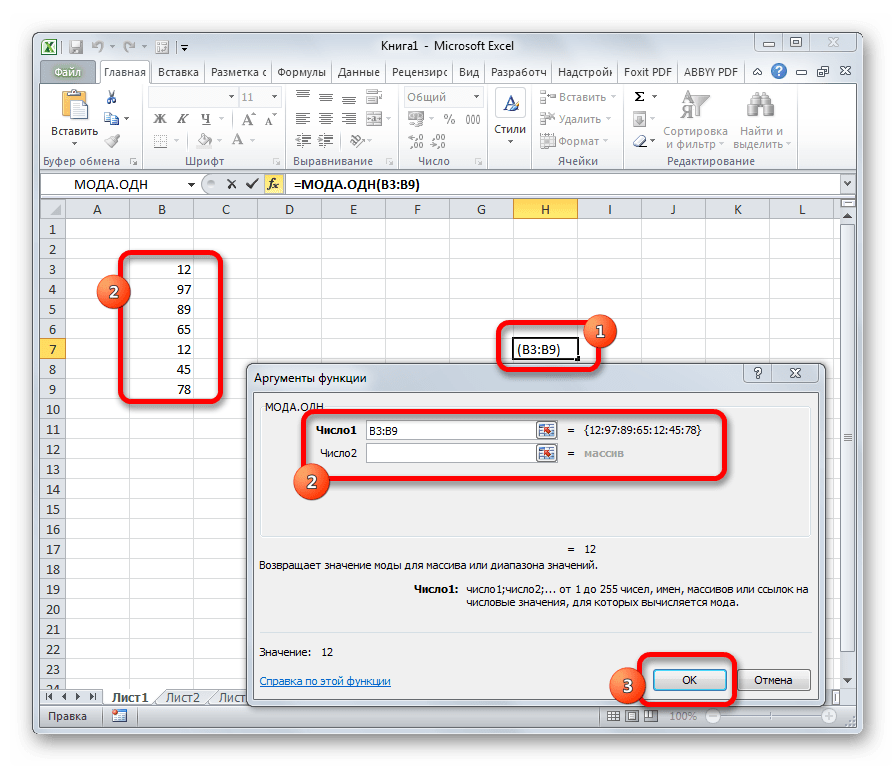
Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.

=МОДА.ОДН(число1;число2;…)

=МОДА.НСК(число1;число2;…)

МЕДИАНА

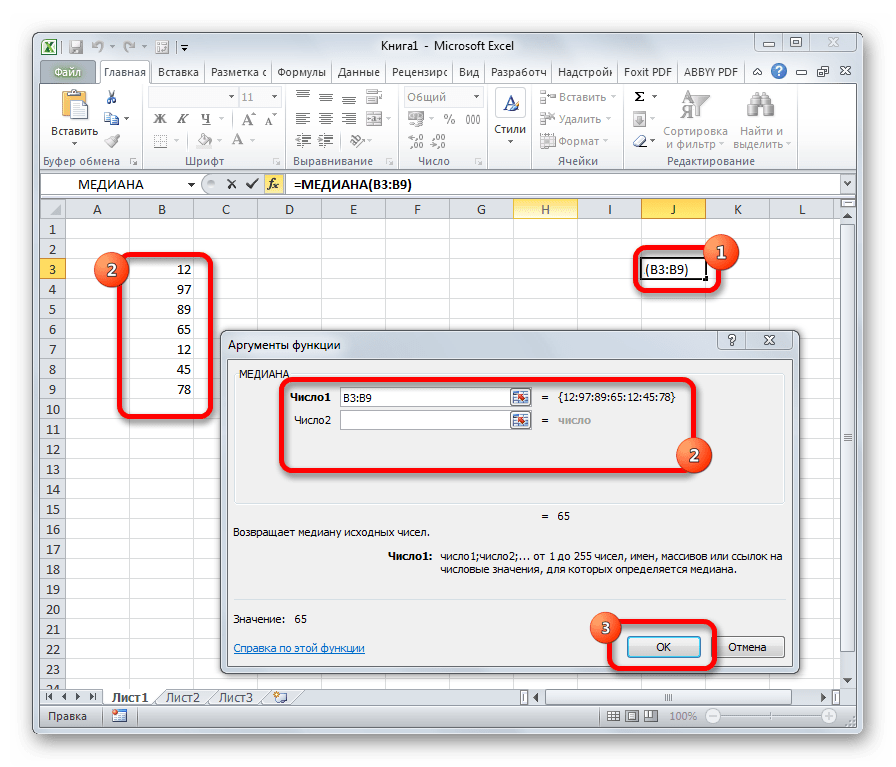
Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:

=МЕДИАНА(число1;число2;…)

СТАНДОТКЛОН

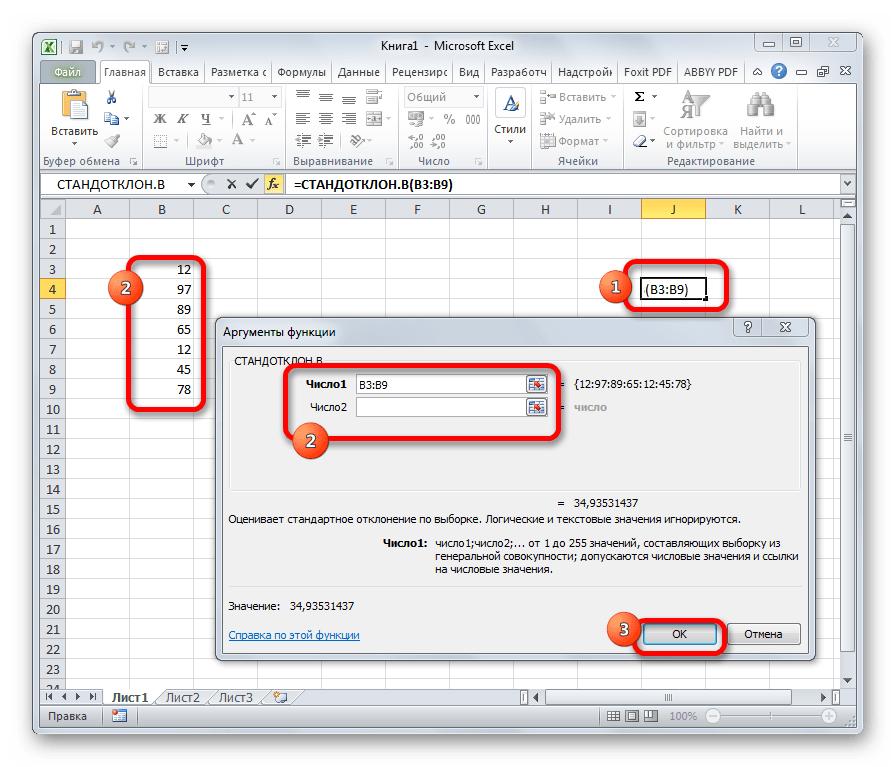
Формула СТАНДОТКЛОН так же, как и МОДА является пережитком старых версий программы. Сейчас используются современные её подвиды – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Первая из них предназначена для вычисления стандартного отклонения выборки, а вторая – генеральной совокупности. Данные функции используются также для расчета среднего квадратичного отклонения. Синтаксис их следующий:

=СТАНДОТКЛОН.В(число1;число2;…)

=СТАНДОТКЛОН.Г(число1;число2;…)

Урок: Формула среднего квадратичного отклонения в Excel

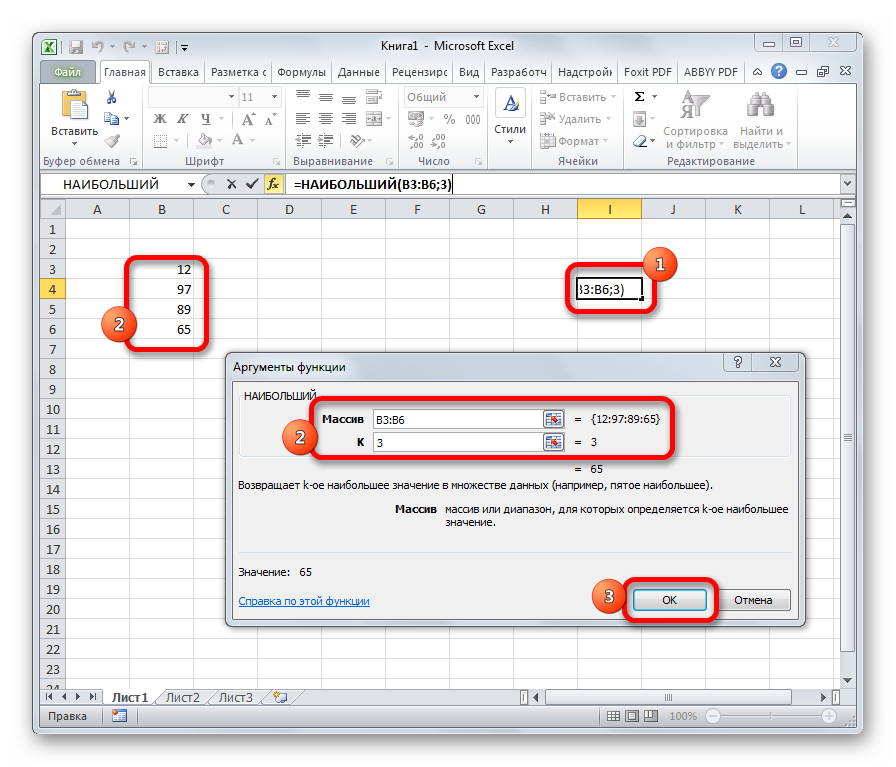
НАИБОЛЬШИЙ

Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:

=НАИБОЛЬШИЙ(массив;k)

В данном случае, k — это порядковый номер величины.

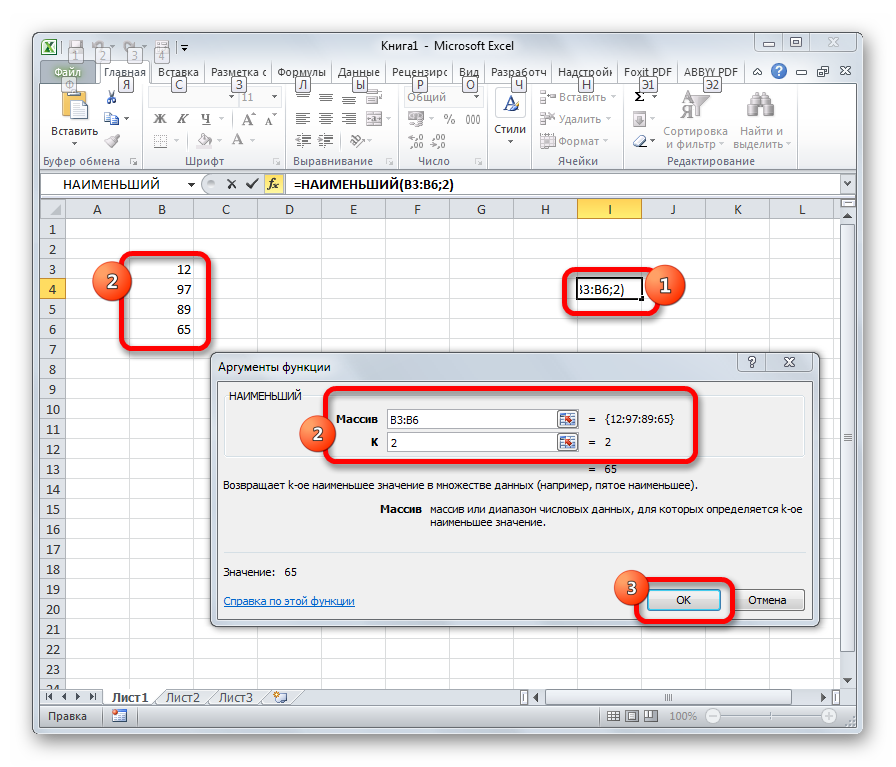
НАИМЕНЬШИЙ

Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:

=НАИМЕНЬШИЙ(массив;k)

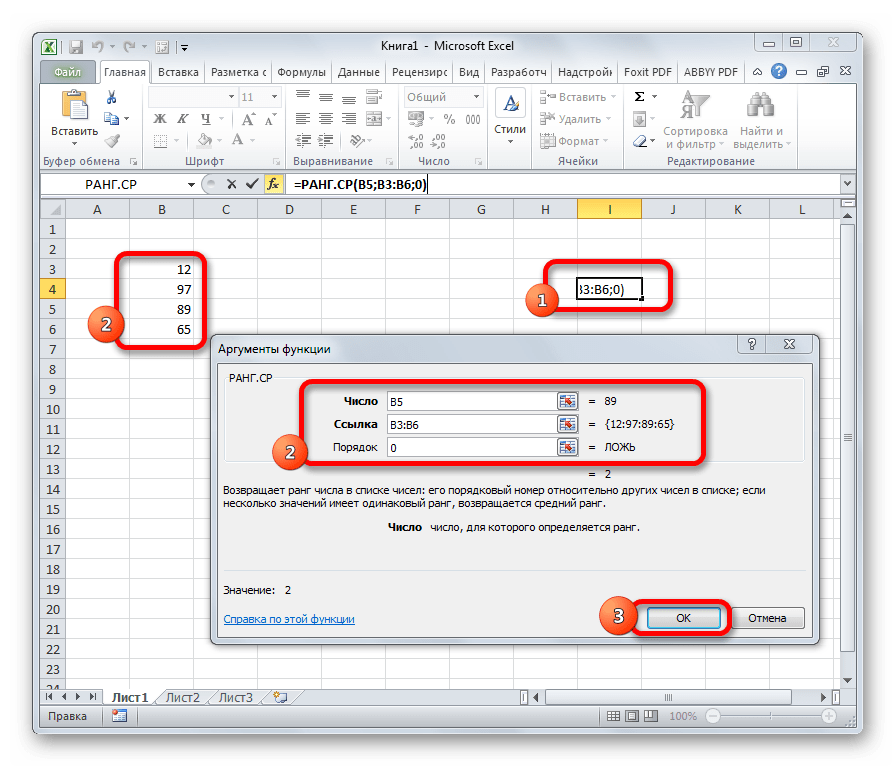
РАНГ.СР

Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:

=РАНГ.СР(число;массив;порядок)

Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.

Источник

Содержание

Использование описательной статистики
Подключение «Пакета анализа»
Размах вариации
Вычисление коэффициента вариации
Шаг 1: расчет стандартного отклонения
Шаг 2: расчет среднего арифметического
Шаг 3: нахождение коэффициента вариации
Простая формула для расчета объема выборки
Пример расчета объема выборки
Задачи о генеральной доле
По части судить о целом
Как рассчитать объем выборки
Как определить статистические выбросы и сделать выборку для их удаления в Excel
Способ 1: применение расширенного автофильтра
Способ 2: применение формулы массива
СРЗНАЧ()
СРЗНАЧЕСЛИ()
МАКС()
МИН()

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».

В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».

Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Размах вариации

Размах вариации – разница между максимальным и минимальным значением:

Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.

С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.

Вычисление коэффициента вариации

Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.

В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.

Шаг 1: расчет стандартного отклонения

Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.

Синтаксис данных функций выглядит соответствующим образом:

= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)

Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.

Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».

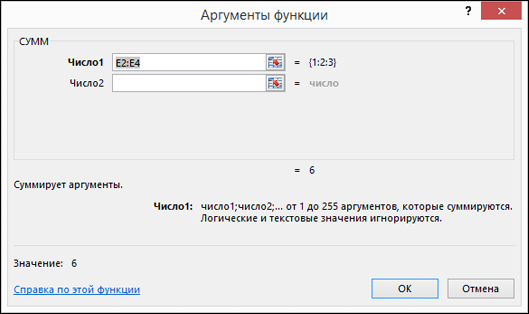
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»

В предварительно выделенной ячейке отображается итог расчета выбранного вида стандартного отклонения.

Шаг 2: расчет среднего арифметического

Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.

«Вставить функцию»

В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».

Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».

Результат вычисления среднего арифметического выводится в ту ячейку, которая была выделена перед открытием Мастера функций.

Шаг 3: нахождение коэффициента вариации

Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.

«Главная»

«Число»

«Процентный»

Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.

Как видим, результат расчета выведен на экран.

Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.

Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:

Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.

После этого, чтобы рассчитать значение и показать результат на экране монитора, щелкаем по кнопке Enter.

Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.

Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.

Разделы: Математика

Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

23 25 24 25 30 24 30 26 28 26
32 33 31 31 25 33 25 29 30 28
23 30 29 24 33 30 30 28 26 25
26 29 27 29 26 28 27 26 29 28
29 30 27 30 28 32 28 26 30 26
31 27 30 27 33 28 26 30 31 29
27 30 30 29 27 26 28 31 29 28
33 27 30 33 26 31 34 28 32 22
29 30 27 29 34 29 32 29 29 30
29 29 36 29 29 34 23 28 24 28

рассчитать числовые характеристики:

моду
медиану
размах ряда
построить полигон частот
построить столбчатую и круговую диаграммы
раскрыть смысловую сторону каждой характеристики

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_i случайной величины меняются от 22 до 36 включительно шагом 1.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Простая формула для расчета объема выборки

где: n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;

p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;

q = (1 – p);

e – допустимая ошибка, в долях.

Пример расчета объема выборки

Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».

Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.

Подставляем эти данные в формулу и считаем:

Получаем объем выборки n = 96 человек.

Задачи о генеральной доле

На вопрос «Накрывает ли доверительный интервал заданное значение p₀?» — можно ответить, проверив статистическую гипотезу H₀:p=p₀. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p^* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H₀ используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле

Гипотеза	H₀:p=p₀	H₀:p₁=p₂
Предположения	Схема испытаний Бернулли	Схема испытаний Бернулли
Оценки по выборке
Статистика K
Распределение статистики K	Стандартное нормальное N(0,1)	Стандартное нормальное N(0,1)

Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле

Значение u_кр находим по таблице функции Лапласа из соотношения 2Ф(u_кр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.

Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
Ф(2.23) = 0.49, u_кр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.

Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.

Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01

Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H₀:p=p₀=0,97 — неизвестная генеральная доля p равна заданному значению p₀=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H₁:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p₀=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства

По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-K_kp)= (-∞;-2,05). Наблюдаемое значение К_набл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.

Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H₀:p₁=p₂ — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H₀:p₁≠p₂ — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.

Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение K_набл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.

По части судить о целом

О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при

достаточном числе наблюдений

. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:

С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.

Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.

Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.

Как рассчитать объем выборки

Достаточный размер выборки зависит от следующих составляющих:

изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)

ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента

Формулы для расчета объема выборки:

Формулы расчета объема выборки

Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.

График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.

Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.

Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.

Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.

Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.

В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.

В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:

Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.

Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.

Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.

Способ 1: применение расширенного автофильтра

Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.

Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».

Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».

После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».

Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».

Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.

Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».

Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.

Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».

Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».

Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.

Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».

Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).

В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».

Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».

Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.

Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».

Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».

При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.

Способ 2: применение формулы массива

Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.

На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.

Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.

Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.

Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Жмем сочетание клавиш Ctrl+Shift+Enter.

Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Опять набираем сочетание клавиш Ctrl+Shift+Enter.

Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.

Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».

В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».

Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».

В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».

В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».

На кнопку с точно таким же названием жмем после возвращения в окно создания условий.

Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.

СРЗНАЧ()

Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.

Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:

Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13

Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).

Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:

СРЗНАЧЕСЛИ()

Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:

В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.

Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:

Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.

МАКС()

Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:

МИН()

Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:

Источники

https://lumpics.ru/descriptive-statistics-in-excel/
https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
http://galyautdinov.ru/post/formula-vyborki-prostaya
https://math.semestr.ru/group/interval-estimation-share.php
https://tidydata.ru/sample-size
https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
https://lumpics.ru/how-to-make-a-sample-in-excel/
https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html

Источник

Нажмите
клавишу ВВОД.

Создание
формулы с функциями

Щелкните
ячейку, в которую требуется ввести
формулу.
Чтобы
начать формулу с функции, на панели
формул

нажмите
кнопку Вставить
функцию

.
Выберите
необходимую функцию.

В
поле Поиск
функции
можно ввести запрос с описанием операции,
которую требуется выполнить, (например,
по словам «сложение чисел» будет
найдена функция СУММ).
Кроме того, можно выбрать категорию в
поле Категория.

Совет.
Список доступных функций см. в разделе
Список
функций для листа (по категориям).

Введите
аргументы.

Совет.
Для ввода в качестве аргументов ссылок
на ячейки нажмите кнопку свертывания
диалогового окна

(которая
временно скрывает диалоговое окно),
выделите ячейки на листе и нажмите
кнопку развертывания
диалогового окна

.

Пример формулы	Описание
=СУММ(A:A)	Суммирует все числа в столбце A
=СРЕДНЕЕ(A1:B4)	Вычисляет среднее значение всех чисел в диапазоне

По
завершении ввода формулы нажмите
клавишу ВВОД.

Совет.
Чтобы выполнить быстрое сложение
значений, также можно воспользоваться
функцией Автосумма.
На вкладке Главная
в группе элементов Правка
нажмите кнопку Автосумма,
а затем выберите необходимую функцию.

К
началу страницы

Создание
формулы с вложенными функциями

Вложенные
функции — это функции, а качестве одного
из аргументов которых заданы другие
функции. В формулу можно вложить до 64
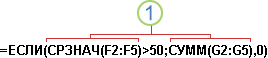
функций. Указанная ниже формула суммирует
набор чисел (G2:G5),
только если среднее значение другого
набора чисел (F2:F5)
больше 50. В
противном случае она возвращает значение
0.

Функции
СРЗНАЧ
и СУММ
вложены в функцию ЕСЛИ.

Щелкните
ячейку, в которую требуется ввести
формулу.
Чтобы
начать формулу с функции, на панели
формул

нажмите
кнопку мастера
функций

.
Выберите
необходимую функцию.

Совет.
Список доступных функций см. в разделе
Список
функций для листа (по категориям).

Чтобы
ввести аргументы, выполните одно или
несколько из указанных ниже действий.
- Для
  ввода в качестве аргументов ссылок на
  ячейки нажмите кнопку
  свертывания диалогового окна
  
  рядом
  с нужным аргументом (которая на время
  скрывает диалоговое окно), выделите
  ячейки на листе и нажмите кнопку
  развертывания
  диалогового окна
  
  .
- Чтобы
  в качестве аргумента задать другую
  функцию, введите ее в соответствующее
  поле аргумента. Например, можно добавить
  СУММ(G2:G5)
  в текстовое поле Значение_если_истина
  функции ЕСЛИ.
- Части
  формулы, отображенные в диалоговом
  окне Аргументы
  функции,
  указывают функцию, выбранную в предыдущем
  действии. Например, при выборе функции
  ЕСЛИ
  в диалоговом окне Аргументы
  функции
  отобразятся аргументы для функции
  ЕСЛИ.

К
началу страницы

Создание
формулы массива, вычисляющей единственный
результат

Формулу
массива
(Формула массива. Формула, выполняющая
несколько вычислений над одним или
несколькими наборами значений, а затем
возвращающая один или несколько
результатов. Формулы массива заключены
в фигурные скобки { } и вводятся нажатием
клавиш CTRL+SHIFT+ВВОД.)
можно использовать для выполнения
некоторых вычислений с единственным
результатом. Данный тип формулы массива
позволяет упростить модель листа путем
замены нескольких отдельных формул
одной формулой массива.

Щелкните
ячейку, в которую требуется ввести
формулу массива.
Введите
необходимую формулу.

Совет.
Формулы массива используют обычный
синтаксис. Они все начинаются со знака
равенства и могут содержать встроенные
функции Excel.

Например,
указанная ниже формула вычисляет
итоговое значение массива цен на акции
без использования строки ячеек для
вычисления и отображения итоговых
значений по каждой акции.

Формула
массива, вычисляющая единственный
результат

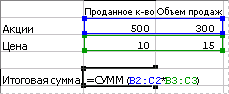
При
вводе формулы ={СУММ(B2:С2*B3:С3)}
в качестве формулы массива она перемножает
количество акций на цену каждой акции
(500*10 и 300*15), после чего складывает
результаты этих вычислений, что дает
общую сумму 9500.

Нажмите
сочетание клавиш CTRL+SHIFT+ВВОД.

Приложение
Excel
автоматически вставляет формулу между
фигурными скобками ({
}).

Примечание.
При
заключении функции в фигурные скобки
вручную она не преобразуется в функцию
массива. Чтобы создать функцию массива,
нажмите сочетание клавиш CTRL+SHIFT+ВВОД.

Важно.
При изменении формулы массива фигурные
скобки ({
})
не будут отображаться в формуле. В таком
случае необходимо еще раз нажать
сочетание клавиш CTRL+SHIFT+ВВОД.

К
началу страницы

Создание
формулы массива, вычисляющей несколько
результатов

Некоторые
функции листа возвращают массивы
значений либо требуют массив значений
в качестве аргумента. Для вычисления
нескольких результатов с помощью формулы
массива в диапазон ячеек, состоящий из
того же числа строк и столбцов, что и
аргументы массива, необходимо ввести
массив.

Выделите
диапазон ячеек, в который требуется
ввести формулу массива.
Введите
необходимую формулу.

Например,
по заданному ряду из трех значений
объема продаж (столбец B)
для ряда из трех месяцев (столбец A)
функция ТЕНДЕНЦИЯ
определяет линейный прогноз объемов
продаж. Для отображения всех вычисляемых
значений формула введена в три ячейки
столбца C
(C1:C3).

Формула
массива, вычисляющая несколько результатов

При
вводе в качестве формулы массива формулы
=ТЕНДЕНЦИЯ(B1:B3;A1:A3)
формируются три отдельных результата
(22196, 17079 и 11962), вычисленные по трем объемам
продаж за три месяца.

Нажмите
сочетание клавиш CTRL+SHIFT+ВВОД.

Приложение
Excel
автоматически вставляет формулу между
фигурными скобками ({
}).

К
началу страницы

Удаление
формулы

При
удалении формулы также удаляются
результаты ее вычислений. Однако можно
удалить только формулу, а результаты
вычислений оставить в ячейке.

Чтобы
удалить формулы вместе с результатами
вычислений, выполните указанные ниже
действия.
1. Выделите
  ячейку или диапазон ячеек, содержащий
  формулу.
2. Нажмите
  клавишу DEL.
Чтобы
удалить только формулу, а результаты
вычислений оставить без изменений,
выполните указанные ниже действия.
1. Выделите
  ячейку или диапазон ячеек, содержащий
  формулу.

Если
формула является формулой массива,
выделите диапазон ячеек, содержащий
ее.

Выделение
диапазона ячеек, содержащего формулу
массива

Щелкните
любую ячейку в формуле массива.
На
вкладке Начальная
страница
в группе Редактирование
выберите команду Найти
и заменить,
а затем выберите в списке пункт Переход.
Нажмите
кнопку Выделить.
Установите
флажок Текущий
массив.

На
вкладке Главная
в группе Буфер
обмена
нажмите кнопку Копировать

.

Клавиши
быстрого доступа
Можно также нажать клавиши CTRL+C.

На
вкладке Главная
в группе Буфер
обмена
нажмите стрелку под кнопкой Вставить

и
выберите пункт Вставить
значения.

К
началу страницы

Советы
и рекомендации по созданию формул

Быстрое
копирование формул
Одну и ту же формулу можно быстро ввести
в диапазон ячеек. Выделите нужный
диапазон, введите формулу, а затем
нажмите сочетание клавиш CTRL+ВВОД.
Например, если в диапазон ячеек C1:C5
ввести формулу =СУММ(A1:B1),
а затем нажать сочетание клавиш CTRL+ВВОД,
приложение Excel
вставит формулу в каждую ячейку диапазона,
используя ячейку A1
в качестве относительной ссылки.

Использование
автозавершения формул
Для упрощения создания и изменения
формул, а также для снижения необходимости
ввода формул вручную и возникновения
синтаксических ошибок рекомендуется
использовать возможность автозавершения
формул. После ввода знака равенства (=)
и начальных букв (начальные буквы играют
роль триггеров
отображения)
приложение Excel
снизу ячейки выводит динамический
список допустимых функций и имен. После
ввода в формулу функции или имени с
помощью триггера
вставки
(нажатия клавиши TAB
или двойного щелчка элемента в списке)
Excel
выводит соответствующие аргументы.
Если по мере ввода формулы вставить
запятую, которая также может выполнять
роль триггера отображения, приложение
Excel
может отобразить дополнительные
аргументы. При вводе в формулу начальных
букв дополнительных функций или имен
снова выводится динамический список
вариантов.

Использование
всплывающих подсказок для функций
При хорошем знании аргументов функции
можно использовать всплывающие подсказки,
которые появляются после ввода имени
функции и открывающей скобки. Чтобы
просмотреть справку по функции, щелкните
ее имя. Чтобы выбрать соответствующий
аргумент в формуле, щелкните имя
аргумента,

К
началу страницы

Распространенные
ошибки при создании формул

В таблице ниже представлены наиболее
часто встречающиеся ошибки, допускаемые
при вводе формул, и способы их устранения.

Рекомендации	Дополнительные сведения
Проверьте согласованность открывающих и закрывающих скобок	Убедитесь, что каждая скобка имеет соответствующую открывающую и закрывающую скобку. При создании формулы Excel отображает вводимые скобки цветом.
Используйте двоеточие для указания диапазона	При указании ссылки на диапазон ячеек в качестве разделителя между первой и последней ячейками диапазона используйте двоеточие (:). Например: A1:A5.
Введите все необходимые аргументы	Некоторые функции имеют обязательные аргументы. Кроме того, убедитесь, что отсутствуют лишние аргументы.
Допускается вложение не более 64 функций	Число уровней вложения функций в пределах одной функции не должно превышать 64.
Имена других листов следует заключать в апострофы	Если формула содержит ссылки на значения ячеек на других листах или в других книгах, а имя другой книги или листа содержит небуквенные символы, его необходимо заключить в одиночные кавычки ( ‘).
Включите путь к внешним книгам	Убедитесь, что каждая внешняя ссылка (Внешняя ссылка. Ссылка на ячейку или диапазон ячеек в другой книге Microsoft Excel или ссылка на имя, определенное в другой книге.) содержит имя книги и путь к этой книге.
Вводите числа без форматирования	Не задавайте формат для чисел, вводимых в формулы. Например, даже если требуется ввести значение 1 000 р., введите в формулу 1000

Стандартные
функции.

Сумм,
средн. Значение,
если (Возвращает
одно значение, если заданное условие
при вычислении дает значение ИСТИНА, и
другое значение, если ЛОЖЬ.

Функция
ЕСЛИ используется при проверке условий
для значений и формул.), гиперссылка
(Создает ярлык или переход, который
открывает документ, расположенный на
сетевом сервере, во внутренней
сети
(Интрасеть. Компьютерная сеть внутри
организации, использующая технологии
Интернета (например, протоколы HTTP
и FTP).
Переходы между документами, веб-страницами
и другими объектами выполняются в
интрасети с помощью гиперссылок.)
или в Интернете. Если щелкнуть ячейку,
содержащую функцию ГИПЕРССЫЛКА, в
Microsoft
Excel
откроется файл, расположение которого
определено с помощью аргумента «адрес».)
, макс
(Возвращает
наибольшее значение из набора значений),sin
(Возвращает синус заданного угла.),
суммесли
(Функция СУММЕСЛИ
используется, если необходимо
просуммировать значения диапазона
(Диапазон. Две или более ячеек листа.
Ячейки диапазона могут быть как смежными,
так и несмежными.),
соответствующие указанным условиям.
Предположим, например, что в столбце с
числами необходимо просуммировать
только значения, большие 5. Для этого
можно использовать указанную ниже
формулу.

=СУММЕСЛИ(B2:B25;»>5″)

В
данном примере на соответствие условиям
проверяются суммируемые значения. При
необходимости можно применить критерии
к одному диапазону, просуммировав
соответствующие значения из другого
диапазона. Например, формула =СУММЕСЛИ(B2:B5;
«Иван»; C2:C5)
суммирует только те значения из диапазона
C2:C5,
для которых соответствующие значения
из диапазона B2:B5
равны «Иван».

)

Использование
формул, функций и диаграмм в Excel

Функции
Excel — это специальные, заранее созданные
формулы для сложных вычислений, в которые
пользователь должен ввести только
аргументы.

Функции
состоят из двух частей: имени функции
и одного или нескольких аргументов. Имя
функции описывает операцию, которую
эта функция выполняет, например, СУММ.

Аргументы
функции Excel — задают значения или ячейки,
используемые функцией, они всегда
заключены в круглые скобки. Открывающая
скобка ставится без пробела сразу после
имени функции. Например, в формуле
«=СУММ(A2;A9)», СУММ — это имя функции, а A2
и A9 — ее аргументы.

Создание
диаграмм сначалп надо чтобы данные были
набраны на листе

Шаг
1. Выбор типа диаграммы.

Первое
окно диалога Мастера диаграмм, предлагает
выбрать тип диаграммы.

Шаг
2. Задание исходных данных диаграммы.

Во
втором окне диалога мастера диаграмм
можно задать данные, используемые Excel
при построении диаграммы.

Второе
окно диалога Мастера диаграмм позволяет
задать исходный диапазон и расположение
в нем рядов данных. Если перед запуском
Мастера был выделен диапазон с исходными
данными, то это поле будет содержать
ссылку на выделенный диапазон.

Excel
выводит подвижную рамку вокруг исходного
диапазона. Если по каким-то причинам
исходный диапазон указан неправильно,
выделите нужный диапазон и введите его
прямо в окне диалога Мастера диаграмм.

Excel
обычно выбирает ориентацию рядов,
предполагая, что диаграмма должна
содержать меньше рядов, чем точек.
Просматривая образец при разной
ориентации рядов, можно выбрать наиболее
эффективный способ отображения данных
в создаваемой диаграмме.

Второе
окно диалога Мастера диаграмм, как и
первое, содержит две вкладки. Чтобы
убедиться, что Excel использует правильные
имена и диапазоны ячеек, для каждого
ряда данных, можно перейти на вкладку
Ряд. Ннажмите кнопку. Далее, чтобы перейти
к следующему шагу.

Шаг
3. Задание параметров диаграммы.

Третье
окно диалога Мастера диаграмм содержит
шесть вкладок. Они позволяют задать
характеристики осей, название диаграммы
и заголовки для ее осей, легенду, подписи
значений в рядах данных и т.д. Все это
можно выполнить при создании диаграммы
или после ее построения.

Шаг
4. Размещение диаграммы.

Excel
может внедрить диаграмму в рабочий лист
или помесить ее на отдельном листе, так
называемом листе диаграммы.

После
построения диаграммы ее можно
отредактировать в режиме редактирования
диаграммы. Для этого нужно дважды
щелкнуть кнопку мыши на диаграмме или
воспользоваться контекстным меню.

2. Выражения. Операнды и операции. Унарные и бинарные операции. Операция присваивания. Арифметические операции.

Переменные
и константы всех типов могут использоваться
в выражениях. Выражение задает
порядок выполнения действий над данными
и состоит из операндов, круглых скобок
и знаков операций. Операнды представляют
собой константы, переменные и вызовы
функций. Операции—
это действия, выполняемые над операндами.

Операндом называется объект (переменная,
константа), над которым совершаются
операции.

Унарные операции

Это
операции с 1 операндом, они имеют вид:

<operation>
a (префиксная форма),
например –a, или

a
<operation> (постфиксная
форма), например a++.

Форма
записи зависит от конкретной операции.

К ним относят (Операции преобразования знака, Побитовые и логические операции.

~ Операция
инвертирования или побитового отрицания.

Операндом может быть любое выражение
целочисленного типа. Операция обеспечивает
побитовое инвертирование двоичного
кода (т.е. побитово заменяет все единицы
на 0 и наоборот).

! Операция
логического отрицания.

Операндом
может быть любое выражение со значением
арифметического типа. Для непосредственного
обозначения логических значений в C++
используются целочисленные значения
0 — ложь и 1 — истина. Кроме того, в логических
операциях любое ненулевое значение
операнда ассоциируется с единицей.
Поэтому отрицанием нулевого значения
является 1, т.е. истина, а отрицанием
любого ненулевого значения оказывается
0, т.е. ложь.

Операция определения
размера

sizeof Операция
определения размера объекта или типа.

Операции увеличения
и уменьшения значения

++
Инкремент, или операция увеличения на
единицу.

— Операция
уменьшения значения операнда на величину,
кратную единице (декремент).

Операция доступа

:: Операция
доступа.

Обеспечивает
обращение к именованной глобальной
области памяти, находящейся вне области
видимости. Эта операция применяется
при работе с одноимёнными объектами,
расположенными во вложенных областях
действия имён. Например, когда во
внутренней области действия скрывается
локальный объект с именем, идентичным
глобальному объекту.

Адресные операции

& Операция
получения адреса операнда.

Бинарные операции

Это
операции с 2 операндами, имеют вид: a
operation b,
например a+b.
Тип и значение результата выражения
любой бинарной операции определяется
в зависимости от принятых в C++
соглашений о преобразовании типов, о
которых будет сказано ниже.

Арифметические
операции

+ Операция
сложения.

– Операция
вычитания.

Операция
используется с операндами арифметического
типа. Один из операндов может иметь тип
указателя. В любом случае значением
выражения является либо сумма значений,
либо сумма адреса и целочисленного
значения, кратного размерам данного
типа.

Результатом
сложения/вычитания двух операндов
арифметического типа является
сумма/разность операндов.

Результат
сложения/вычитания указателя с целым
числом зависит от типа, на который
указывает указатель (будет рассмотрено
позднее в соответствующей главе).

* Операция
умножения.

/ Операция
деления.

Операндами
могут быть выражения арифметического
типа. Значением выражения является
произведение значений операндов (*) или
частное от деления значения первого
операнда на второй операнд (/).

% Операция
получения остатка от деления целочисленных
операндов (деление по модулю).

Операндами
могут быть выражения арифметического
типа. В процессе выполнения операции
операнды приводятся к целому типу. При
ненулевом делителе для целочисленных
операндов выполняется соотношение

(a/b)*b+a%b=a,
где a и b –
уже приведённые к целочисленному типу
значения.

При
неотрицательных операндах результат
операции % положительный. В противном
случае знак остатка может зависеть от
конкретной реализации компилятора.

Операции побитового
сдвига

Эти
операции определены только для
целочисленных операндов.

<<
Операция левого сдвига.

>> Операция
правого сдвига.

Например,
пусть в переменную типа unsigned
char i и
записано число 181, чьё двоичное
представление равно 10110101. Результатом
операции i>>3 будет
являться 00010110, т.е. число 22, а результат
операции i<<4 будет
равен 01100000 96.

Побитовые операции

Поразрядные
операции определены только для
целочисленных операндов.

& Поразрядная
конъюнкция (побитовое И) битовых
представлений значений целочисленных
операндов.

| Поразрядная
дизъюнкция (побитовое ИЛИ) битовых
представлений значений

целочисленных операндов.

^ Поразрядная
исключающая дизъюнкция (побитовое
исключающее ИЛИ) битовых представлений
значений целочисленных операндов.

Операции
сравнения

< Меньше

<= Меньше равно

> Больше

>= Больше равно

= = Равно

!= Не равно

Логические бинарные
операции

&& логическое
И

|| логическое
ИЛИ.

Логические
бинарные операции объединяют выражения
сравнения со значениями истина (!=0) и
ложь (==0). Результат операций приведён
в следующей таблице, где X
– любое число, не равное 0.

A	B	a && b	a \|\| b
0	0	0	0
0	X	0	1
X	0	0	1
X	X	1	1

Операция присваивания

= Простая
форма операции присваивания.

Левый
операнд операции присваивания должен
быть модифицируемым выражением.

В
качестве правого операнда операции
присваивания может выступать любое
выражение. Значение правого операнда
присваивается левому операнду. Значение
выражения оказывается равным значению
правого операнда, в соответствии с
правилами автоматического приведения
типов. Результат операции равен значению
сохраняемого выражения. Это позволяет
записывать несколько операций присваивания
в цепочку.

An=…=A3=A2=A1;

где A1, A2, A3, …,
An являются выражениями. Для
определения значений выражений подобной
структуры в C++ существуют
правила группирования операндов
выражений сложной структуры (эти правила
подробно будут описаны ниже). В соответствии
с одним из этих правил операнды операции
присвоения группируются справа налево:

An=(An-1=…=(A3=(A2=A1))…);

Очевидно,
что в таком выражении все операнды,
кроме самого правого, должны быть
модифицируемыми. В результате выполнения
этого выражения операндам An,
An-1, … A3, A2
будет присвоено значение операнда A1.

Специальные формы операций присваивания

Записи
вида:

A =
A <operation>
B

для бинарных операторов могут быть
записаны с помощью специальной формы
оператора присваивания вида

A
<operation>= B

При
этом эффективность работы такой формы
записи будет даже быстрее ввиду более
рационального использования компилятором
ресурсов компьютера (при включённой
оптимизации кода в современных
компиляторах разницы не будет).

Например,

запись
a=a+2;
эквивалентна записи a+=2;

а
запись i=i&j;
эквивалентна записи i&=j;

Операции обращения к компонентам объекта сложного типа.

К
операциям выбора компонентов объекта
составного типа относятся:

. Операция
прямого выбора — точка.

-> Операция
косвенного выбора.

.* Операция
обращения к компоненте структуры/объединения
по имени объекта (левый операнд операции)
и указателю на компоненту (правый операнд
операции).

->* Операция
обращения к компоненте структуры/объединения
по указателю на объект (левый операнд
операции) и указателю на компоненту
(правый операнд операции).

Операция управления
процессом вычисления значений

, Операция
запятая.

Группирует
выражения слева направо. Разделённые
запятыми выражения вычисляются
последовательно слева направо, в качестве
результата сохраняются тип и значение
самого правого выражения.

A &=
B, A * B,
-A

Эта
операция формально также является
бинарной операцией, хотя операнды этой
операции абсолютно не связаны между
собой

Операция вызова
функции

() Операция
вызова.

Операция явного
преобразования типа

() Операция
преобразования (или приведения) типа.

Операция индексации

[] Операция
индексации.

1. Mathcad: основные принципы работы. Запись формул. Переменные, функции и их использование. Лекция маткад!!!!

MathCAD
— это специфический язык программирования,
который позволяет облегчить решение
математических уравнений. Mathcad
— программное средство, среда для
выполнения на компьютере разнообразных
математических и технических расчетов,
снабженная простым в освоении и в работе
графическим интерфейсом, которая
предоставляет пользователю инструменты
для работы с формулами, числами, графиками
и текстами. В среде Mathcad
доступны более сотни операторов и
логических функций, предназначенных
для численного и символьного решения
математических задач различной сложности.

Функции

Функции
в Mathcad делятся на две группы:

функции
пользователя;

встроенные
функции.

Техника
использования функций обоих типов
абсолютно идентична, а вот задание
отличается принципиально.

Задание
функций пользователя

Особенности
определения функций пользователя (проще
говоря, функций произвольного вида) в
Mathcad полностью совпадают с принятыми в
математике правилами. Для этого необходимо
выполнить следующую последовательность
действий.

1. Введите имя функции.
В общем случае оно может быть совершенно
произвольным, хотя определенные
ограничения все-таки имеются. О них мы
поговорим немного позже.

2. После
имени функции следует ввести пару
круглых скобок, в которых через запятую
нужно прописать все переменные, от
которых зависит функция. Задать функцию
с параметром можно только в том случае,
если ему выше присвоено конкретное
числовое значение. Иначе система выдаст
уже знакомое нам сообщение об ошибке:
This variable is undefined.

3. Введите оператор
присваивания «:=».

4. На месте
черного маркера справа от введенного
оператора присваивания задайте вид
вашей функции. В выражение определяемой
функции могут входить как непосредственно
переменные, так и другие встроенные и
пользовательские функции.

Пример
15. Задание функции пользователя

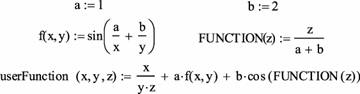
Встроенные
функции

Встроенные
функции — это функции, заданные в
Mathcad изначально. Поэтому, чтобы их
использовать, достаточно просто корректно
набрать имена функций с клавиатуры.
Впрочем, существуют и другие способы
вставки нужной встроенной функции.
Наиболее распространенные из них можно
ввести с панели Calculator (Калькулятор). К
таким функциям относятся синус, косинус,
тангенс, натуральный и десятичный
логарифмы, экспонента. Для того же, чтобы
задать все остальные встроенные функции
Mathcad, нужно открыть специальное окно
Insert Function (Вставить функцию). Проще всего
это можно сделать нажатием одноименной
кнопки панели Standard (Стандартные) с
изображением стилизованного знака
функции (рис. 24).

Рис.
24. Кнопка Insert Function (Вставить функцию)
меню Standard (Стандартные)

Также,
для того чтобы вызвать данное окно
(рис. 25), можно использовать сочетание
клавиш Ctrl+Shift+F или Ctrl+E. И, наконец, ссылка
на него имеется в меню Insert (Вставка).

Рис.
25. Окно Insert Function (Вставить функцию)

Так
как число встроенных функций Mathcad весьма
значительно (несколько сотен), для
удобства они распределены по тематическим
группам. Их список, организованный в
алфавитном порядке, расположен в окне
Function Category (Категория функций). Всего в
Mathcad 32 тематические группы функций.

При
выборе определенной категории функций
ее содержание отобразится в окне Function
Name (Имя Функции). Чтобы ввести нужную
функцию, выделите ее в списке с помощью
мыши или клавиш управления курсором и
нажмите OK (или лучше дважды щелкните на
ней мышью).

По умолчанию в окне Function
Name (Имя функции) отображается полный
список всех встроенных функций, что
соответствует категории All (Все).
Производить поиск в полном списке
несколько быстрее и удобнее, если вы
приблизительно знаете написание имени
нужной вам функции.

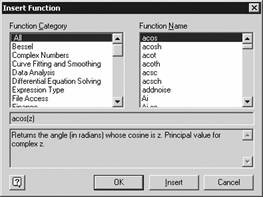
На окне Insert
Function (Вставить функцию) имеется специальная
зона, в которой отображается текст
описания выбранной функции. Так, для
первой функции списка All acos (арккосинус)
читаем: Returns the angle (in radians) whose cosine is z.
Principal value for complex z (Возвращает угол (в
радианах), косинус которого равен z.
Действительная часть для комплексного
z).

В том случае, если вам нужна более
полная информация о некоторой функции,
нежели дает сжатое сообщение окна Insert
Function (Вставить функцию), вы можете
обратиться к справочной системе Mathcad.
Для этого вам нужно, выделив функцию,
информацию о которой необходимо найти,
нажать специальную кнопку Help (Помощь)
в левом нижнем углу окна. При этом будет
открыта статья справочной системы, в
которой имеется упоминание о данной
функции.

При вводе встроенных функций
с клавиатуры следует помнить, что Mathcad
различает регистр символов. Поэтому,
если обычную функцию, образованную
только строчными символами, вы введете
с большой буквы, она распознана не будет.
И, наоборот, функция, которая вводится
с помощью окна Insert Function (Вставить Функцию)
как последовательность прописных букв,
аналогично должна быть набрана и вами.

2. Поразрядные (битовые) операции. Логические операции. Условная операция. Операция sizeof.

(логические
операции)~ Операция
инвертирования или побитового отрицания.

! Операция
логического отрицания.

Операция определения размера

sizeof Операция
определения размера объекта или типа.

В
C
различают два варианта этой операции.
В первом случае операндом может быть
любое l-выражение.
Это выражение записывается справа от
символа операции. Значением выражения
является размер конкретного объекта в
байтах. Во втором случае операндом
является имя типа. Это выражение
записывается в скобках непосредственно
за символом операции. Значением выражения
является размер конкретного типа данных
в байтах. Результатом этой операции
является константа типа size_t.
Этот производный целочисленный
беззнаковый тип определяется конкретной
реализацией. В Visual
C
этот тип эквивалентен типу unsigned
int.

Например,
для переменной i
типа int
операция sizeof
i
вернёт значение 4. Аналогично, для второй
формы операции, sizeof(int)
вернёт 4. Обычно имена переменных также
записываются в скобках для унификации
стиля.

Побитовые операции

Поразрядные
операции определены только для
целочисленных операндов.

& Поразрядная
конъюнкция (побитовое И) битовых
представлений значений целочисленных
операндов.

| Поразрядная
дизъюнкция (побитовое ИЛИ) битовых
представлений значений целочисленных
операндов.

Значение
выражения вычисляется путём побитовых
преобразований, т.е. каждый бит результата
является результатом применения операции
к соответствующим битам операндов.

Например,
если операнды i
и j
имеют тип char,
то результат k=i&j
будет формироваться по следующему
правилу:

Берём
0-й бит операнда i
и 0-й бит операнда j.
Вычисляем
конъюнкцию этих битов.
Записываем
результат в 0-й бит результата k.
Повторяем для
остальных битов, с 1-го по 7-й.

Ниже
приведена таблица истинности для
побитовых операций.

a	b	a & b	a \| b	a ^ b
0	0	0	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	1	0

Логические бинарные операции

&& логическое
И

|| логическое
ИЛИ.

A	B	a && b	a \|\| b
0	0	0	0
0	X	0	1
X	0	0	1
X	X	1	1

Особенности использования логических выражений.

При
составлении и использовании сложных
логических выражений следует помнить
некоторые особенности их вычисления в
языке C. При применении
операций логического И
(&&) и логического ИЛИ (||) выражение
может не вычисляться до конца. Любое
выражение, использующее эти операторы
вычисляется слева направо, но:

Если
значение левого операнда операции &&
равно false (нулю), то значение
правого операнда не вычисляется, т.к.
результат всей операции от него не
зависит.
Если
значение левого операнда операции ||
равен true (не равен нулю),
то значение правого операнда также не
вычисляется.

Поэтому, если в программе встречается
следующий фрагмент:

if(a<3
&& func(x)==3)

{

…

}

то
в некоторых случаях, когда левый операнд
&& равна false, правый
операнд даже не будет вычисляться. Т.е.
если a<3, функция func(x)
будет вызываться, а в противном случае
– нет.

В
длинных цепочках вроде func1(x)!=0
&& func2(x)==0
&& func3(x)<3
&& func4(x)>2
операнды будут вычисляться (и функции
будут вызываться) до тех пор, пока один
из операндов очередной операции &&
не примет очередное значение false.

Поскольку
в C любое ненулевое значение
означает логическое true,
а нулевое значение – false,
то в операторе if (и во
многих других операторах) можно вообще
не применять операции сравнения.

Например:

void
func(double a)

{

if(a)

printf(“a
имеет ненулевое значение”);

if(!func2(a))

printf(“Результат
выполнения func2(a)
равен нулю”);

}

Такой
стиль в своё время считался (да и сейчас
считается) шиком среди «продвинутых
программистов», хотя в тоже время для
многих он наоборот затруднял чтение
программы.

логические
операторы.

Оператор	Значение
&	AND (И)
\|	OR (ИЛИ)
^	XOR (исключающее ИЛИ)
&&	Short-circuit AND (быстрый оператор И)
\|\|	Short-circuit OR (быстрый оператор ИЛИ)
!	NOT (НЕ)

Быстрые
логические операторы

В
С# предусмотрены специальные быстрые
версии логических операторов AND и OR, при
использовании которых программа будет
выполняться быстрее. Рассмотрим, как
они работают. Если при выполнении
оператора AND первый операнд имеет
значение false, результатом будет false,
независимо от значения второго операнда.
Если при выполнении оператора OR первый
операнд имеет значение true, результатом
будет значение true, независимо от значения
второго операнда. Следовательно, в этих
случаях нет необходимости оценивать
второй операнд, и соответственно
программа будет выполняться быстрее.

Быстрый
оператор AND обозначается символом &&,
а быстрый оператор OR — символом ||.
Единственная разница между обычной и
быстрой версиями операторов состоит в
том, что обычные операторы всегда
оценивают и первый, и второй операнды,
а быстрые операторы оценивают второй
операнд только при необходимости.

1. Mathcad: Дискретные аргументы. Векторы, матрицы и операции с ними. Построение графиков функций.

Дискретные
аргументы — особый класс переменных,
который в

пакете
MathCAD зачастую заменяет управляющие
структуры, называе-

мые
циклами (однако полноценной такая замена
не является). Эти пере-

менные
имеют ряд фиксированных значений, либо
целочисленных (1

способ),
либо в виде чисел с определенным шагом,
меняющихся от на-

чального
значения до конечного (2 способ).

Определение дискретного аргумента

MathCad
может выполнять повторяющиеся или
итерационные вычисления отдельных
выражений. С этой целью используется
специальный тип переменных –
дискретные аргументы.

Переменная
типа дискретный аргумент принимает
диапазон значений, например, все целые
числа от 0 до 10. Если в выражении
присутствует дискретный аргумент, то
MathCad вычисляет выражение
столько раз, сколько значений содержит
дискретный аргумент.

Например,
надо вычислить результаты для диапазона
значений t от 10 до 20 с
шагом 1. Это делается следующим образом:

Сначала указывается первое значение
диапазона, затем – второе, в данном
случае 11, а затем нажать на клавишу (;),
чтобы получить изображение многоточия
и ввести последнее значение диапазон

Пример: t:=10,11..20

Пример

t:=10,11..20
Уравнение движения тела,
падающего в поле силы

асс=-9.8 тяжести

Если нажать после
выражения знак = , то получим следующую

таблицу вычисленных
значений:

-490

-502.9

-706.6

…….

……

…..

-1.96^.10³

Итак,
для определения дискретного аргумента
сначала указывается
первое значение диапазона , затем –
второе, затем нажимается клавиша (;)
, чтобы получить изображение многоточия
и вводится последнее
значение диапазона.

Создание вектора или матрицы

Одиночное
число в MathCad
называется скаляром.
Столбец чисел
называется вектором,
а прямоугольная таблица
чисел – матрицей. Общий
термин для вектора или матрицы – массив.
Имеются два способа создать массив:

Заполняя
массив пустых полей из меню Математика
Матрица
Используя дискретный аргумент, чтобы
определить элементы с его помощью.
Считывая элементы массива из файлов
данных.

Можно
различать имена матриц, векторов и
скаляров, используя различный шрифт
для их написания. Например, имена
векторов записывать
жирным,
а имена скалярных
переменных курсивом.

Создание вектора

Математика
 Матрицы
(CTRL/M)
Появляется диалоговое окно.(Insert
– matrix)
Укажите число строк, равное числу
элементов вектора, в поле «Строк»,
например, 3
Напечатайте
1 в поле «Столбец» и нажмите «Создать».
MathCad создаст вектор с
пустыми полями для заполнения.
Заполните
поля и щелкнув мышью (Tab)
– переход на другое поле.

Добавить другой вектор

выделите
вектор в рамочку
Напечатайте
знак +. MathCad показывает
поле для второго вектора
Математика
 Матрицы
Создайте другой вектор с тремя элементами
Введите значения в поля и нажмите =,
чтобы увидеть результат

Сложение
– только одна из операций MathCad,
определенных для векторов и матриц.(также
есть -, *, скалярное произведение,
целочисленные степени, детерминанты и
другие операции).

Матрица
создается так же как вектор.

Вектор
– столбец идентичен матрице с одним
столбцом. Можно также создать вектор-строку,
создав матрицу с одной строкой и многими
столбцами.

При
работе с векторными аргументами, всегда
подразумевают вектор-столбец.
Чтобы превратить вектор-строку в
вектор-столбец используйте оператор
транспонирования (CTRL+1)

2. Приоритеты операций и порядок вычислений. Правила вычисления выражений с логическими операциями. (предыдущий билет). Операция преобразования типов. Автоматическое преобразование типов.

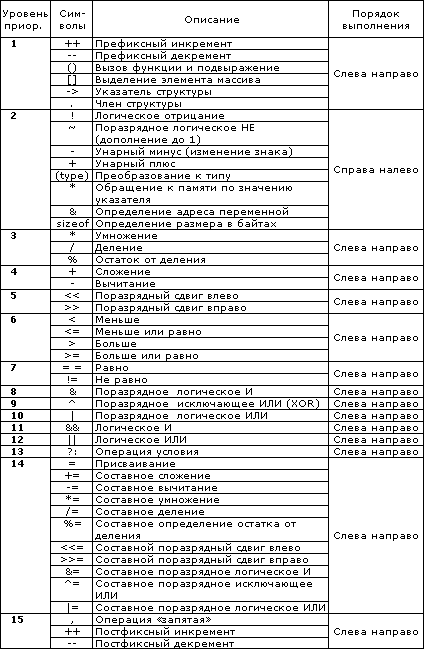
Операция явного преобразования типа

() Операция
преобразования (или приведения) типа.

Эта
бинарная операция в контексте так
называемого постфиксного выражения и
в контексте выражения приведения
обеспечивает изменение типа значения
выражения, представляемого вторым
операндом. Информация о типе, к которому
преобразуется значение второго операнда,
кодируется первым выражением, которое
является спецификатором типа. Например,
(int)d;

Приведение типов.

Идентификаторы
типов данных также часто встречаются
в явном виде в операторе
явного приведения (указания) типов.
Этот оператор выглядит как идентификатор
типа, записанный в скобках непосредственно
перед выражением. Например:

int
i;

double
a;

a=3.65;

i=(int)a;

В
результате выполнения 4-й строчки этой
программы произойдёт приведение значения
переменной типа double к
типу int, которое потом
запишется в переменную i,
в результате чего там окажется значение
3. Здесь (int) – оператор
приведения типов.

Справедливости
ради следует сказать, что даже если бы
записали просто i=a;
то в i всё равно бы записалось
3, значение было бы преобразовано за
счёт автоматического
приведения типов (это
будет рассмотрено ниже).

Автоматическое преобразование типов

Преобразование
типов в арифметических выражениях
осуществляются автоматически к наивысшему
типу. Например, в ходе операции с
операндами типов double и
int операнд типа int
будет преобразован к double.

Преобразование типов при присваивании

В
операциях присваивания тип присваиваемого
значения преобразуется к типу переменной,
получающей это значение. Преобразования
при присваивании допускаются даже в
тех случаях, когда они влекут за собой
потерю информации.

Преобразование
целых типов данных происходит по
следующим правилам:

Если значение попадает в новый диапазон,
то новое значение = старому с точностью
до типа;
Если значение не попадает в новый
диапазон, то результат преобразований
не определён (обрабатывается в зависимости
от компилятора).

Преобразование
вещественных типов:

Значения
типа float преобразуются
к типу double без потери
точности. Значения типа double
при преобразовании к
типу float представляются
с некоторой потерей точности. Е
Если
порядок значения типа double
слишком велик для представления
значением типа float ,
то происходит потеря значимости.

Преобразование
к целым типам значений с плавающей
точкой (в 2 приёма):

Сначала
производится преобразование к типу
long. Дробная
часть плавающего значения отбрасывается
при преобразовании к типу long.
Затем
это значение типа long
преобразуется к требуемому типу. Если
полученное значение слишком велико
для типа long, то
результат преобразований не определён.

Mathcad: Символьные и численные вычисления. Задание точности численных операций. Примеры символьных и численных вычислений. (Лекция маткад, конец)

Операторы. Блок операторов. Условный оператор. Операторы циклов. Оператор возврата из функции. Операторы

Программа
на языке C состоит из
модулей, модуль – из функций, функции
– из операторов. Согласно принципам
структурного программирования нам
известно, что любую программу можно
составить из трех структур: линейной
(следования), разветвляющейся (развилки)
и циклической (повторения).

Для
реализации этих структур в каждом языке
программирования существуют специальные
команды, называемые операторами.

оператора
— выражение, являющееся
законченной инструкци для компьютера,
чьим отличительным признаком является
символ <;> , стоящий в конце.

Блок операторов

Блок
операторов заключается в фигурные
скобки {оператор}.

Общий
вид:

{

Внутренние объявления
и определения данных

Операторы

}

Оператор if-else.

Синтаксис:

If (выражение) оператор1;

[else
оператор2;]

Вначале
вычисляется заключенное в скобки
выражение, которое должно принимать
целое значение или будет преобразовано
к целому значению. В условных операторах
используются арифметические операции,
операции отношения и логические операции.

Далее
выполнение осуществляется по следующей
схеме:

если выражение истинно (т.е. отлично от
0), то выполняется оператор1.
если выражение ложно (т.е. равно 0),то
выполняется оператор2.
если
выражение ложно и отсутствует оператор2
(в квадратные скобки заключена
необязательная конструкция), то
выполняется следующий за if
оператор.

Примечания:

Вторая
часть оператора (еlse
оператор2) является необязательной.
Если значение выражения не равно 0, а
служебное слово else
отсутствует, то
управление передается следующему
оператору программы.
Иногда
в блоке оператора if бывает
нужно выполнить не одно действие, а
несколько. Для этого используется
составной оператор или блок операторов:

if
(i < j)

i++;

else

{

j = i-3;

i++;

}

Этот
пример иллюстрирует тот факт, что на
месте оператор1, так же как и на месте
оператор2 могут находиться блоки
операторов.

Допускается
использование вложенных операторов
if. Оператор if
может быть включен в конструкцию if
или в конструкцию else
другого оператора if. Чтобы
сделать программу более читабельной,
рекомендуется группировать операторы
и конструкции во вложенных операторах
if, используя фигурные
скобки. Если же фигурные скобки опущены,
то компилятор связывает каждое ключевое
слово else с наиболее близким
if, для которого нет else.

Операции
сравнения младше (ниже по приоритету),
чем арифметические операции. Поэтому
значения арифметических выражений,
включённых в выражение сравнения, будут
вычисляться раньше выполнения операции
сравнения. Поэтому вполне уместно
использование выражений типа: i+k>j
или a*5<j+4.

Например:

void
func(int a)

{

if(a%10==0)

printf (“a кратно
десяти”);

else

printf
(“a
не кратно десяти”);

}

Оператор return

Этот
оператор имеет две основные формы
записи:

return;
return
(выражение); Например, return(5+i);

Первая
форма обеспечивает простую передачу
управления из текущей функции обратно
в вызывающую функцию. Применяется для
выхода из функции типа void.

Вторая
форма обеспечивает не только передачу
управления, но еще и возвращение значения
выражения в вызывающую функцию.
Применяется в функциях типа, отличного
от void. Тип возвращаемого
значения идентичен типу функции.

Циклы.

Циклы
необходимы, когда надо повторить
некоторые действия несколько раз, как
правило, пока выполняется некоторое
условие. В языке имеются 3 вида операторов
цикла: for, while
и do…while.

Оба
цикла while и for
являются циклами с
предусловием. При этом проверка истинности
условия осуществляется перед началом
каждой итерации цикла.

Оператор
do…while
– это конструкция цикла с постусловием
(условием на выходе), где истинность
условия проверяется после выполнения
каждой итерации цикла.

Цикл for.

Цикл
(для) имеется практически во всех языках
программирования. Однако, версия этого
цикла, используемая в языке C,
отличается большей гибкостью и
предоставляет больше возможностей.

При
организации цикла, когда его тело должно
быть выполнено фиксированное число
раз, осуществляется 3 операции:
инициализация счётчика,
сравнение его величины с некоторым
граничным значением и изменение значения
счётчика при каждом прохождении тела
цикла.

Синтаксис
оператора for:

for(выражение1;выражение2;выражение
3 ) оператор; где

выражение 1 – выполняется в начале цикла
(инициализация переменной-счётчика);

выражение
2 – проверяет условие продолжения цикла;

выражение 3 – выполняется в конце
итерации (модифицирует переменную-счётчик).

В качестве тела цикла может
выступать один оператор или блок
операторов.

Например:

for(i=1; i<5; i ++)

printf(“i=%dn”, i);

for(i=5; i>3; i—)

{

printf(“Another value…”);

printf(“i=%dn”, i);

}

В
отличие от других языков, в C
оператор for является очень
гибкой конструкцией, т.к. не накладывает
практически никаких ограничений на
содержимое трёх выражений, входящих в
состав оператора. Чтобы понять любую
конструкцию, записанную на основе
оператора for, достаточно
помнить следующие правила:

Первое выражение вызывается один раз
в самом начале цикла, перед первой
итерацией. Может содержать инициализацию
переменной-счётчика, может содержать
более сложное выражение, может быть
пустым.
Второе
выражение – условие продолжения цикла.
В начале каждой итерации происходит
вычисление этого выражения и если оно
равно true, то итерация
выполняется, иначе цикл заканчивается.
Если это выражение равно false
в самом начале цикла, то тело цикла не
будет выполнено ни разу. Выражение
может быть пустым, в этом случае
компилятор считает, что выражение равно
true.
Третье
выражение – операция, выполняемая
каждый раз по окончании очередной
итерации. Обычно используется для
изменения переменной-счётчика. Может
быть пустым.
В
С переменная-счётчик может быть изменена
в теле цикла (в отличие от Pascal).
Поэтому надо учитывать, что операторы
в теле цикла могут оказывать влияние
на длительность цикла.
С помощью оператора <,> в качестве
каждого из 3 выражений можно записывать
выражения, содержащие несколько
операций.

Поясним
всё вышесказанное на примерах:

//—
Вечный цикл ————————————

for(;1;) //
Также можно записать for(;;)

{

…

}

//—
Изменение переменной-счётчика в теле
цикла ——

//—
Цикл пройдёт в 3 итерации для i=0,
2, 4 ———

for(i=0;i<5;i++)

{

…

i+=1;

}

//—
Одновременное изменение нескольких
переменных —

for(i=0,j=3;
i<5 && k>-6; i++,j—)

{

k=func(i,j);

…

}

Но
чаще всего стараются все дополнительные
вычисления проводить в теле цикла
сохраняя тем самым запись самого
оператора for относительно
простой.

Цикл while

Следующий
оператор цикла в языке СИ – это цикл
while (пока). Основная
его форма имеет вид:

while
(условие) оператор;

где условие может принимать нулевое
или ненулевое значение, а оператор может
быть простым или составным.

Выражение,
стоящее в круглых скобках, вычисляется
в цикле while.
Если оно равно true, то
выполняется идущий за ним оператор
(тело цикла) и выражение вычисляется
снова. Если выражение ложно, цикл while
заканчивается и программа
продолжает свою работу.

При
построении цикла while
вы должны включить в
него какие-то конструкции, изменяющие
величину проверяемого выражения так,
чтобы в конце концов, оно стало ложным.
В противном случае выполнение цикла
никогда не завершится.

Эта
последовательность действий, состоящая
из проверки и выполнения оператора,
периодически повторяющегося до тех
пор, пока выражение не станет ложным (в
общем случае, равным 0).

Например,
следующий фрагмент программы:

index=2;

while
(index<5)

printf
(“Neverending story! n”);

печатает
это радостное сообщение бесконечное
число раз, поскольку в цикле отсутствуют
конструкции, изменяющие величину
переменной index, которой
было присвоено значение 2.

Исправим
программу следующим образом:

index=2;

while
(index<5)

{

printf (“It will be over someday…n”);

index++;

}

И
получим печать сообщения только 3 раза.
Разумеется, что то же самое с большим
изяшеством можно реализовать с помощью
цикла for. Цикл while
же используется в реальных программах
в более сложных случаях.

Интересно,
что согласно синтаксису языка C
оператор while может быть
полностью заменён оператором for
в виде for(;условие;).

Решение,
выполнить ли в очередной раз тело цикла,
принимается перед началом его прохождения.
Поэтому, вполне возможно, что тело цикла
не будет выполнено ни разу. Оператор,
образующий тело цикла, может либо
простым, либо составным.

Цикл do…while:

В
общем виде цикл do…while
записывается следующим образом:

оператор;

while
(выражение);

Это
единственная в C конструкция
цикла с постусловием.

Эта
конструкция полностью идентична циклу
while за исключением того,
что проверка условия осуществляется в
конце цикла. Поэтому тло цикла do…while
всегда выполняется, по крайней мере,
один раз.

Использовать
цикл do…while
лучше всего в тех случаях, когда должна
быть выполнена, по крайней мере, одна
итерация, например:

int
item;

item=ReadItem(); //
Последовательно считываем элементы

while(item!=0); //
пока не получим нулевой элемент

1. Mathcad: решение уравнений (различные способы). Символьное решение уравнений

Для
введения знака равенства
в уравнениях используется комбинация
клавиш CTRL+=. Это
очень важно, т.к. с точки зрения Mathcad
такой знак равенства – совершенно
другая операция, чем просто = (показать
результат).

Решать
уравнение символьно гораздо труднее,
чем численно. Может оказаться, что в
символьном виде решение не существует.

Чтобы
символьно решить уравнение существует
команда Решить относительно
переменной из меню
Символика.(Solve)

Для этого:

напечатать
уравнение.
Убедитесь,
что для введения знака равенства была
использована комбинация клавиш CTRL+=
Выделите переменную, относительно
которой нужно решить уравнение, щелкнув
на ней мышью.
Выберите
Решить относительно переменной из меню
Символика.

MathCad решит уравнение
относительно выделенной переменной и
вставит результат в рабочий документ.

Пример:

Чтобы
из приведенной формулы выразить r
через А, выделите r и
выберите команду Решить относительно
переменной

Имеет решения

Для ввода знака
равенства нажмите CTRL/=

Численное решение уравнений.

Решать уравнения
численным методом можно следующими
способами:

С
помощью функции root,
polyroot, lsolve
С
помощью блока Given и функций
Find и Minerr.

Решим уравнение
x²=9.

Функция root
ищет один из корней выражения. Поэтому,
для первого способа решения уравнение
надо представить в виде f(x)=0,
т.е. в нашем случае x²-9=0.

Кроме того, в случае
функции root надо задать
начальное значение x для
поиска. Чем ближе это значение к корню
уравнения, тем меньше времени займет
поиск. root находит только
один из корней, обычно ближайший к
начальному значению x для
поиска.

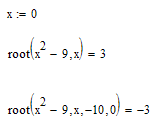
Обратите внимание,
что функция root находит
только один из корней. Если вы хотите
найти корень в определенном диапазоне,
можно задать этот диапазон двумя
последними параметрами, причем значения
заданной функции в этих точках должны
иметь разные знаки.

Корни полинома
также можно найти функцией polyroots,
в ней перечисляем коэффициенты полинома
в виде вектора:

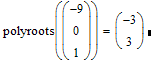
Второй вариант
решения уравнений – использование
блока Given:

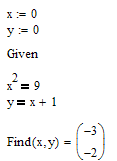
Точно так же как и
в случае с root надо задавать
начальные значения. В блоке Given
можно задать систему уравнений. Функция
Find найдет только одно их
возможных решений. Если решение не может
быть найдено (численный метод не дает
решения с точностью до TOL),
то можно найти минимальное по ошибке
решение, заменив Find() на
MinErr().

Поскольку во всех
этих способах используются численные
методы, то на точность решения будут
влиять значения переменных TOL
и CTOL.

2. Операторы управления: оператор безусловного перехода, операторы продолжения и прерывания итерации цикла (с примерами), оператор switch. Операторы ветвления. Оператор безусловного перехода goto.

Оператор
goto обеспечивает
безусловный переход на указанную метку
в переделах функции.

Синтаксис:
goto
m1;

Метка
с программе записывается в начале строки
и отделяется от операторов двоеточием.
Например:

{

func1();

goto
m1;

func2();
// Никогда не выполняется

m1:
func3();

}

В
сочетании с оператором if
(рассмотренным ниже) оператор goto
может осуществлять условный переход
на определённую метку:

if(a==5)

goto
m2;

В
соответствии с принципами структурного
программирования, применение оператора
goto считается дурным тоном.
Тем не менее в исключительных случаях
(в программах со множественным вложением
условных операторов) его применение
может значительно сократить размер
кода и улучшить его читаемость.

Множественный выбор. Операторы switch-case.

Операция
условия и конструкция if—else
облегчают написание программ, в которых
осуществляется выбор между двумя
вариантами.

Однако
иногда в программе необходимо произвести
выбор одного из нескольких вариантов.
Мы можем это сделать, используя конструкцию
if—else
if—else,
и т.д., но во многих случаях оказывается
более удобным применять оператор switch.

Синтаксис:

switch
(целое выражение)

{

case
метка1:

[Операторы;] (необязат.)

case
метка2:

[Операторы;] (необязат.)

… .
. . .

[default:
операторы;]

}

Оператор
switch вычисляет целое
выражение в круглых
скобках и сравнивает это значение со
всеми значениями (метками), перечисленными
с помощью ключевых слов case.
Каждая метка должна быть либо целой
константой, либо символьной константой,
либо константным выражением. Как только
значение вычисляемого выражения
совпадает с какой-либо меткой, управление
передаётся на оператор, следующий за
меткой.

Если
ни одна из меток не подходит, то управление
передается оператору с меткой default
(если такой имеется). В противном случае
управление передается оператору,
следующему за оператором switch.

Как
выражения, так и метки должны иметь
значения целого типа (включая тип char).

Пример:

switch
(letter)

{

case
‘a’:

case
‘A’: printf
(“Это буква a
(большая или маленькая)”, letter);

break;

case
66: // 66 – код буквы B

printf
(“Это буква B
(большая)”, letter);

break;

case 0x30+2: //0x30+2 – код
цифры 2

printf (“Это цифра 2”,
letter);

break;

default: printf
(“А вот не знаю я что это за символ”);

}

В
отличие от других языков (например
Pascal) в С в операторе
switch-case после
выполнения оператора или группы
операторов, следующих за соответствующим
условию case выполнение
оператора не прекращается, а продолжается
до конца оператора switch,
выполняя все инструкции, написанные
для других case. Это позволяет
записывать несколько последовательных
меток для одной и той же группы операторов.
В этом случае она будет выполняться
если значение выражения равно хотя бы
одной из меток (см. пример выше).

Если
же в программе не требуется выполнение
последующих операторов, то прервать
выполнение можно с помощью оператора
break. Оператор break
прерывает выполнение программы внутри
тела оператора switch (а
также for, while
и do) и передаёт управление
следующему после switch
оператору:

switch
(l)

{

case
‘a’: func1();
// Эта функция вызывается только в случае
l=’a’

case
‘b’:
func2();
// А эта — в случае l=’a’
или l=’b’

break;

case
‘c’:
func3();
// Эта функция вызывается только в случае
l=’c’

}

Поскольку
в большинстве случаев требуется
выполнение только одной группы операторов
для каждого case, то тело
оператора switch обычно
состоит из набора блоков начинающихся
с выражения “case XX:”
и заканчивающегося оператором break.

Как и в других блоках операторов,
внутри switch можно определять
переменные:

switch (letter)

{

int l;

case ‘a’: l=

printf(“%d”,l);

break;

case ‘A’: l=2;

printf(“%d”,l);

break;

}

Обычно
этого не делают, т.к. это ухудшает
удобочитаемость программы.

Каковы
ограничения использования оператора
switch. Его нельзя использовать
для работы со стрингами, значениями с
плавающей точкой. В метках case
нельзя использовать переменные, а также
в них нельзя применять интервалы (как
это можно сделать, например в Basic).
В этих случаях нужно применять конструкции
if-else:

if
(f==3.5)

printf(“f=3.5”);

else

if(f>4
&& f<6)

printf(“4<f<6”)
;

Ole и dde. Связывание и внедрение данных в документы.

Лекция оле

Функции. Определение (описание) функции. Прототип (декларирование) функции. Параметры функции. Передача аргументов в функцию.

Кроме
вызова функций из стандартных заголовочных
файлов, в языке программирования С++
предусмотрена возможность создания
собственных функций. В
языке программирования С++ есть два типа
функций:

Функции,
которые не возвращают значений
Функции,
возвращающие значение

.5.1. Определение и вызов функций

В
отличие от других языков программирования
высокого уровня в языке СИ нет деления
на процедуры, подпрограммы и функции,
здесь вся программа строится только из
функций.

Функция
— это совокупность объявлений и операторов,
обычно предназначенная для решения
определенной задачи. Каждая функция
должна иметь имя, которое используется
для ее объявления, определения и вызова.
В любой программе на СИ должна быть
функция с именем main (главная функция),
именно с этой функции, в каком бы месте
программы она не находилась, начинается
выполнение программы.

При
вызове функции ей при помощи аргументов
(формальных параметров) могут быть
переданы некоторые значения (фактические
параметры), используемые во время
выполнения функции. Функция может
возвращать некоторое (одно !) значение.
Это возвращаемое значение и есть
результат выполнения функции, который
при выполнении программы подставляется
в точку вызова функции, где бы этот вызов
ни встретился. Допускается также
использовать функции не имеющие
аргументов и функции не возвращающие
никаких значений. Действие таких функций
может состоять, например, в изменении
значений некоторых переменных, выводе
на печать некоторых текстов и т.п..

С
использованием функций в языке СИ
связаны три понятия — определение функции
(описание действий, выполняемых функцией),
объявление функции (задание формы
обращения к функции) и вызов функции.

Определение
функции задает тип возвращаемого
значения, имя функции, типы и число
формальных параметров, а также объявления
переменных и операторы, называемые
телом функции, и определяющие действие
функции. В определении функции также
может быть задан класс памяти.

Пример:

int
rus (unsigned char r)

{
if (r>=’А’ && c

В
данном примере определена функция с
именем rus, имеющая один параметр с

именем
r и типом unsigned char. Функция возвращает
целое значение, равное 1,

если
параметр функции является буквой
русского алфавита, или 0 в противном

случае.

В
языке СИ нет требования, чтобы определение
функции обязательно

предшествовало
ее вызову. Определения используемых
функций могут следовать за

определением
функции main, перед ним, или находится в
другом файле.

Однако
для того, чтобы компилятор мог осуществить
проверку соответствия

типов
передаваемых фактических параметров
типам формальных параметров до вызова

функции
нужно поместить объявление
(прототип) функции.

Объявление
функции имеет такой же вид, что и
определение функции, с той лишь

разницей,
что тело функции отсутствует, и имена
формальных параметров тоже

могут
быть опущены. Для функции, определенной
в последнем примере, прототип

может
иметь
вид

int
rus (unsigned char r); или
rus (unsigned char);

В
программах на языке СИ широко используются,
так называемые, библиотечные

функции,
т.е. функции предварительно разработанные
и записанные в библиотеки.

Прототипы
библиотечных функций находятся в
специальных заголовочных файлах,

поставляемых
вместе с библиотеками в составе систем
программирования, и

включаются
в программу с помощью директивы #include.

Если
объявление функции не задано, то по
умолчанию строится прототип функции

на
основе анализа первой ссылки на функцию,
будь то вызов функции или

определение.
Однако такой прототип не всегда
согласуется с последующим

определением
или вызовом функции. Рекомендуется
всегда задавать прототип

функции.
Это позволит компилятору либо выдавать
диагностические сообщения, при

неправильном
использовании функции, либо корректным
образом регулировать

несоответствие
аргументов устанавливаемое при выполнении
программы.

Объявление
параметров функции при ее определении
может быть выполнено в так

называемом
«старом стиле», при котором в скобках
после имени функции следуют

только
имена параметров, а после скобок
объявления типов параметров. Например,

функция
rus из предыдущего примера может быть
определена следующим образом:

int
rus (r)

unsigned
char r;

{
… /* тело функции */ … }

В
соответствии с синтаксисом языка СИ
определение функции имеет следующую

форму:

[спецификатор-класса-памяти]
[спецификатор-типа] имя-функции

([список-формальных-параметров])

{
тело-функции }

Необязательный
спецификатор-класса-памяти задает класс
памяти функции,

который
может быть static или extern. Подробно классы
памяти будут рассмотрены

в
следующем разделе.

Спецификатор-типа
функции задает тип возвращаемого
значения и может задавать

любой
тип. Если спецификатор-типа не задан,
то предполагается, что функция

возвращает
значение типа int.

Функция
не может возвращать массив или функцию,
но может возвращать

указатель
на любой тип, в том числе и на массив и
на функцию. Тип возвращаемого

значения,
задаваемый в определении функции, должен
соответствовать типу в

объявлении
этой функции.

Функция
возвращает значение если ее выполнение
заканчивается оператором

return,
содержащим некоторое выражение. Указанное
выражение вычисляется,

преобразуется,
если необходимо, к типу возвращаемого
значения и возвращается в

точку
вызова функции в качестве результата.
Если оператор return не содержит

выражения
или выполнение функции завершается
после выполнения последнего ее

оператора
(без выполнения оператора return), то
возвращаемое значение не

определено.
Для функций, не использующих возвращаемое
значение, должен быть

использован
тип void, указывающий на отсутствие
возвращаемого значения. Если

функция
определена как функция, возвращающая
некоторое значение, а в операторе

return
при выходе из нее отсутствует выражение,
то поведение вызывающей функции

после
передачи ей управления может быть
непредсказуемым.

Список-формальных-параметров
— это последовательность объявлений
формальных

параметров,
разделенная запятыми. Формальные
параметры — это переменные,

используемые
внутри тела функции и получающие значение
при вызове функции путем

копирования
в них значений соответствующих фактических
параметров.

Список-формальных-параметров
может заканчиваться запятой (,) или
запятой с

многоточием
(,…), это означает, что число аргументов
функции переменно.

Однако
предполагается, что функция имеет, по
крайней мере, столько обязательных

аргументов,
сколько формальных параметров задано
перед последней запятой в

списке
параметров. Такой функции может быть
передано большее число аргументов,

но
над дополнительными аргументами не
проводится контроль типов.

Если
функция не использует параметров, то
наличие круглых скобок

обязательно,
а вместо списка параметров рекомендуется
указать слово void.

Порядок
и типы формальных параметров должны
быть одинаковыми в определении

функции
и во всех ее объявлениях. Типы фактических
параметров при вызове

функции
должны быть совместимы с типами
соответствующих формальных параметров.

Тип
формального параметра может быть любым
основным типом, структурой,

объединением,
перечислением, указателем или массивом.
Если тип формального

параметра
не указан, то этому параметру присваивается
тип int.

Для
формального параметра можно задавать
класс памяти register, при этом для

величин
типа int спецификатор типа можно опустить.

Идентификаторы
формальных параметров используются в
теле функции в качестве

ссылок
на переданные значения. Эти идентификаторы
не могут быть переопределены

в
блоке, образующем тело функции, но могут
быть переопределены во внутреннем

блоке
внутри тела функции.

При
передаче параметров в функцию, если
необходимо, выполняются обычные

арифметические
преобразования для каждого формального
параметра и каждого

фактического
параметра независимо. После преобразования
формальный параметр не

может
быть короче чем int, т.е. объявление
формального параметра с типом char

равносильно
его объявлению с типом int. А параметры,
представляющие собой

действительные
числа, имеют тип double.

Преобразованный
тип каждого формального параметра
определяет, как

интерпретируются
аргументы, помещаемые при вызове функции
в стек.

Несоответствие
типов фактических аргументов и формальных
параметров может быть

причиной
неверной интерпретации.

Тело
функции — это составной оператор,
содержащий операторы, определяющие

действие
функции.

Все
переменные, объявленные в теле функции
без указания класса памяти,

имеют
класс памяти auto, т.е. они являются
локальными. При вызове функции

локальным
переменным отводится память в стеке и
производится их инициализация.

Управление
передается первому оператору тела
функции и начинается выполнение

функции,
которое продолжается до тех пор, пока
не встретится оператор return

или
последний оператор тела функции.
Управление при этом возвращается в
точку,

следующую
за точкой вызова, а локальные переменные
становятся недоступными.

При
новом вызове функции для локальных
переменных память распределяется вновь,

и
поэтому старые значения локальных
переменных теряются.

Параметры
функции передаются по значению и могут
рассматриваться как

локальные
переменные, для которых выделяется
память при вызове функции и

производится
инициализация значениями фактических
параметров. При выходе из

функции
значения этих переменных теряются.
Поскольку передача параметров

происходит
по значению, в теле функции нельзя
изменить значения переменных в

вызывающей
функции, являющихся фактическими
параметрами. Однако, если в

качестве
параметра передать указатель на некоторую
переменную, то используя

операцию
разадресации можно изменить значение
этой переменной.

Пример:

/*
Неправильное использование параметров
*/

void
change (int x, int y)

{
int k=x;

x=y;

y=k;

}

В
данной функции значения переменных x и
y, являющихся формальными

параметрами,
меняются местами, но поскольку эти
переменные существуют только

внутри
функции change, значения фактических
параметров, используемых при вызове

функции,
останутся неизменными. Для того чтобы
менялись местами значения

фактических
аргументов можно использовать функцию
приведенную в следующем

примере.

Пример:

/*
Правильное использование параметров
*/

void
change (int *x, int *y)

{
int k=*x;

*x=*y;

*y=k;

}

При
вызове такой функции в качестве
фактических параметров должны быть

использованы
не значения переменных, а их адреса

change
(&a,&b);

Если
требуется вызвать функцию до ее
определения в рассматриваемом файле,

или
определение функции находится в другом
исходном файле, то вызов функции

следует
предварять объявлением этой функции.
Объявление
(прототип) функции

имеет
следующий формат:

[спецификатор-класса-памяти]
[спецификатор-типа] имя-функции

([список-формальных-параметров])
[,список-имен-функций];

В
отличие от определения функции, в
прототипе за заголовком сразу же следует

точка
с запятой, а тело функции отсутствует.
Если несколько разных функций

возвращают
значения одинакового типа и имеют
одинаковые списки формальных

параметров,
то эти функции можно объявить в одном
прототипе, указав имя одной

из
функций в качестве имени-функции, а все
другие поместить в

список-имен-функций,
причем каждая функция должна сопровождаться
списком

формальных
параметров. Правила использования
остальных элементов формата такие

же,
как при определении функции. Имена
формальных параметров при объявлении

функции
можно не указывать, а если они указаны,
то их область действия

распространяется
только до конца объявления.

Прототип
— это явное объявление функции, которое
предшествует определению

функции.
Тип возвращаемого значения при объявлении
функции должен

соответствовать
типу возвращаемого значения в определении
функции.

Если
прототип функции не задан, а встретился
вызов функции, то строится

неявный
прототип из анализа формы вызова функции.
Тип возвращаемого значения

создаваемого
прототипа int, а список типов и числа
параметров функции

формируется
на основании типов и числа фактических
параметров используемых при

данном
вызове.

Таким
образом, прототип функции необходимо
задавать в следующих случаях:

1.
Функция возвращает значение типа,
отличного от int.

2.
Требуется проинициализировать некоторый
указатель на функцию до того,

как
эта функция будет определена.

Наличие
в прототипе полного списка типов
аргументов параметров позволяет

выполнить
проверку соответствия типов фактических
параметров при вызове функции

типам
формальных параметров, и, если необходимо,
выполнить соответствующие

преобразования.

В
прототипе можно указать, что число
параметров функции переменно, или что

функция
не имеет параметров.

Если
прототип задан с классом памяти static, то
и определение функции должно

иметь
класс памяти static. Если спецификатор
класса памяти не указан, то

подразумевается
класс памяти extern.

Вызов
функции имеет следующий формат:

адресное-выражение
([список-выражений])

Поскольку
синтаксически имя функции является
адресом начала тела функции,

в
качестве обращения к функции может быть
использовано адресное-выражение (в

том
числе и имя функции или разадресация
указателя на функцию), имеющее

значение
адреса функции.

Список-выражений
представляет собой список фактических
параметров,

передаваемых
в функцию. Этот список может быть и
пустым, но наличие круглых

скобок
обязательно.

Фактический
параметр может быть величиной любого
основного типа, структурой,

объединением,
перечислением или указателем на объект
любого типа. Массив и

функция
не могут быть использованы в качестве
фактических параметров, но можно

использовать
указатели на эти объекты.

Выполнение
вызова функции происходит следующим
образом:

1.
Вычисляются выражения в списке выражений
и подвергаются обычным

арифметическим
преобразованиям. Затем, если известен
прототип функции, тип

полученного
фактического аргумента сравнивается
с типом соответствующего

формального
параметра. Если они не совпадают, то
либо производится

преобразование
типов, либо формируется сообщение об
ошибке. Число выражений в

списке
выражений должно совпадать с числом
формальных параметров, если только

функция
не имеет переменного числа параметров.
В последнем случае проверке

подлежат
только обязательные параметры. Если в
прототипе функции указано, что

ей
не требуются параметры, а при вызове
они указаны, формируется сообщение об

ошибке.

2.
Происходит присваивание значений
фактических параметров соответствующим

формальным
параметрам.

3.
Управление передается на первый оператор
функции.

4.
Выполнение оператора return в теле функции
возвращает управление и

возможно,
значение в вызывающую функцию. При
отсутствии оператора return

управление
возвращается после выполнения последнего
оператора тела функции, а

возвращаемое
значение не определено.

Адресное
выражение, стоящее перед скобками
определяет адрес вызываемой

функции.
Это значит что функция может быть вызвана
через указатель на функцию.

Пример:

int
(*fun)(int x, int *y);

Здесь
объявлена переменная fun как указатель
на функцию с двумя параметрами:

типа
int и указателем на int. Сама функция должна
возвращать значение типа int.

Круглые
скобки, содержащие имя указателя fun и
признак указателя *,

обязательны,
иначе запись

int
*fun (intx,int *y);

будет
интерпретироваться как объявление
функции fun возвращающей указатель

на
int.

Вызов
функции возможен только после инициализации
значения указателя fun и

имеет
вид:

(*fun)(i,&j);

В
этом выражении для получения адреса
функции, на которую ссылается

указатель
fun используется операция разадресации
* .

Указатель
на функцию может быть передан в качестве
параметра функции. При

этом
разадресация происходит во время вызова
функции, на которую ссылается

указатель
на функцию. Присвоить значение указателю
на функцию можно в операторе

присваивания,
употребив имя функции без списка
параметров.

Пример:

double
(*fun1)(int x, int y);

double
fun2(int k, int l);

fun1=fun2;
/* инициализация указателя на функцию
*/

(*fun1)(2,7);
/* обращение к функции */

В
рассмотренном примере указатель на
функцию fun1 описан как указатель на

функцию
с двумя параметрами, возвращающую
значение типа double, и также

описана
функция fun2. В противном случае, т.е. когда
указателю на функцию

присваивается
функция описанная иначе чем указатель,
произойдет ошибка.

Рассмотрим
пример использования указателя на
функцию в качестве параметра

функции
вычисляющей производную от функции
cos(x).

Пример:

double
proiz(double x, double dx, double (*f)(double x) );

double
fun(double z);

int
main()

{

double
x; /* точка вычисления производной
*/

double
dx; /* приращение */

double
z; /* значение производной
*/

scanf(«%f,%f»,&x,&dx);
/* ввод значений x и dx */

z=proiz(x,dx,fun);
/* вызов функции */

printf(«%f»,z);
/* печать значения производной */

return
0;

}

double
proiz(double x,double dx, double (*f)(double z) )

{
/* функция вычисляющая производную
*/

double
xk,xk1,pr;

xk=fun(x);

xk1=fun(x+dx);

pr=(xk1/xk-1e0)*xk/dx;

return
pr;

}

double
fun( double z)

{
/* функция от которой вычисляется
производная */

return
(cos(z));

}

Для
вычисления производной от какой-либо
другой функции можно изменить тело

функции
fun или использовать при вызове функции
proiz имя другой функции. В

частности,
для вычисления производной от функции
cos(x) можно вызвать функцию

proiz
в форме

z=proiz(x,dx,cos);

а
для вычисления производной от функции
sin(x) в форме

z=proiz(x,dx,sin);

Любая
функция в программе на языке СИ может
быть вызвана рекурсивно, т.е.

она
может вызывать саму себя. Компилятор
допускает любое число рекурсивных

вызовов.
При каждом вызове для формальных
параметров и переменных с классом

памяти
auto и register выделяется новая область
памяти, так что их значения из

предыдущих
вызовов не теряются, но в каждый момент
времени доступны только

значения
текущего вызова.

Переменные,
объявленные с классом памяти static, не
требуют выделения новой

области
памяти при каждом рекурсивном вызове
функции и их значения доступны в

течение
всего времени выполнения программы.

Классический
пример рекурсии — это математическое
определение факториала n! :

n!
= 1 при n=0;

n*(n-1)!
при n>1 .

Функция,
вычисляющая факториал, будет иметь
следующий вид:

long
fakt(int n)

{

return
( (n==1) ? 1
: n*fakt(n-1) );

}

Хотя
компилятор языка СИ не ограничивает
число рекурсивных вызовов функций,

это
число ограничивается ресурсом памяти
компьютера и при слишком большом числе

рекурсивных
вызовов может произойти переполнение
стека.

1.5.2. Вызов функции с переменным числом параметров

При
вызове функции с переменным числом
параметров в вызове этой функции

задается
любое требуемое число аргументов. В
объявлении и определении такой

функции
переменное число аргументов задается
многоточием в конце списка

формальных
параметров или списка типов аргументов.

Все
аргументы, заданные в вызове функции,
размещаются в стеке. Количество

формальных
параметров, объявленных для функции,
определяется числом аргументов,

которые
берутся из стека и присваиваются
формальным параметрам. Программист

отвечает
за правильность выбора дополнительных
аргументов из стека и

определение
числа аргументов, находящихся в стеке.

Примерами
функций с переменным числом параметров
являются функции из

библиотеки
функций языка СИ, осуществляющие операции
ввода-вывода информации

(printf,scanf
и
т.п.).
Подробно
эти функции рассмотрены во третьей
части книги.

Программист
может разрабатывать свои функции с
переменным числом параметров.

Для
обеспечения удобного способа доступа
к аргументам функции с переменным

числом
параметров имеются три макроопределения
(макросы) va_start, va_arg,

va_end,
находящиеся в заголовочном файле
stdarg.h. Эти макросы указывают на то,

что
функция, разработанная пользователем,
имеет некоторое число обязательных

аргументов,
за которыми следует переменное число
необязательных аргументов.

Обязательные
аргументы доступны через свои имена
как при вызове обычной

функции.
Для извлечения необязательных аргументов
используются макросы

va_start,
va_arg, va_end в следующем порядке.

Макрос
va_start предназначен для установки аргумента
arg_ptr на начало

списка
необязательных параметров и имеет вид
функции с двумя параметрами:

void
va_start(arg_ptr,prav_param);

Параметр
prav_param должен быть последним обязательным
параметром вызываемой

функции,
а указатель arg_prt должен быть объявлен
с предопределением в списке

переменных
типа va_list в виде:

va_list
arg_ptr;

Макрос
va_start должен быть использован до первого
использования макроса

va_arg.

Макрокоманда
va_arg обеспечивает доступ к текущему
параметру вызываемой

функции
и тоже имеет вид функции с двумя
параметрами

type_arg
va_arg(arg_ptr,type);

Эта
макрокоманда извлекает значение типа
type по адресу, заданному указателем

arg_ptr,
увеличивает значение указателя arg_ptr на
длину использованного

параметра
(длина type) и таким образом параметр
arg_ptr будет указывать на

следующий
параметр вызываемой функции. Макрокоманда
va_arg используется столько

раз,
сколько необходимо для извлечения всех
параметров вызываемой функции.

Макрос
va_end используется по окончании обработки
всех параметров функции

и
устанавливает указатель списка
необязательных параметров на ноль
(NULL).

Рассмотрим
применение этих макросов для обработки
параметров функции

вычисляющей
среднее значение произвольной
последовательности целых чисел.

Поскольку
функция имеет переменное число параметров
будем считать концом списка

значение
равное -1. Поскольку в списке должен быть
хотя бы один элемент, у

функции
будет один обязательный параметр.

Пример:

#include

int
main()

{
int n;

int
sred_znach(int,…);

n=sred_znach(2,3,4,-1);

/*
вызов с четырьмя параметрами */

printf(«n=%d»,n);

n=sred_znach(5,6,7,8,9,-1);

/*
вызов с шестью параметрами */

printf(«n=%d»,n);

return
(0);

}

int
sred_znach(int x,…);

{

int
i=0, j=0, sum=0;

va_list
uk_arg;

va_start(uk_arg,x);
/* установка
указателя
uk_arg на
*/

/*
первый необязятельный параметр */

if
(x!=-1) sum=x; /* проверка на пустоту списка
*/

else
return (0);

j++;

while
( (i=va_arg(uk_arg,int))!=-1)

/*
выборка очередного */

{
/* параметра и проверка
*/

sum+=i;
/* на конец списка */

j++;

}

va_end(uk_arg);
/* закрытие списка параметров */

return
(sum/j);

}

1.5.3. Передача параметров функции main

Функция
main, с которой начинается выполнение
СИ-программы, может быть

определена
с параметрами, которые передаются из
внешнего окружения, например,

из
командной строки. Во внешнем окружении
действуют свои правила представления

данных,
а точнее, все данные представляются в
виде строк символов. Для

передачи
этих строк в функцию main используются
два параметра, первый параметр

служит
для передачи числа передаваемых строк,
второй для передачи самих строк.

Общепринятые
(но не обязательные) имена этих параметров
argc и argv. Параметр

argc
имеет тип int, его значение формируется
из анализа командной строки и

равно
количеству слов в командной строке,
включая и имя вызываемой программы

(под
словом понимается любой текст не
содержащий символа пробел). Параметр
argv

это
массив указателей на строки, каждая из
которых содержит одно слово из

командной
строки. Если слово должно содержать
символ пробел, то при записи

его
в командную строку оно должно быть
заключено в кавычки.

Функция
main может иметь и третий параметр, который
принято называть argp,

и
который служит для передачи в функцию
main параметров операционной системы

(среды)
в которой выполняется СИ-программа.

Заголовок
функции main имеет вид:

int
main (int argc, char *argv[], char *argp[])

Если,
например, командная строка СИ-программы
имеет вид:

A:>cprog
working ‘C program’ 1

то
аргументы argc, argv, argp представляются в
памяти как показано в схеме

на
рис.1.

argc
[ 4 ]

argv
[ ]—> [ ]—> [A:cprog.exe]

[
]—> [working]

[
]—> [C program]

[
]—> [1]

[NULL]

argp
[ ]—> [ ]—> [path=A:;C:\0]

[
]—> [lib=D:LIB]

[
]—> [include=D:INCLUDE]

[
]—> [conspec=C:COMMAND.COM]

[NULL]

Рис.1.
Схема размещения параметров командной
строки

Операционная
система поддерживает передачу значений
для параметров argc,

argv,
argp, а на пользователе лежит ответственность
за передачу и использование

фактических
аргументов функции main.

Следующий
пример представляет программу печати
фактических аргументов,

передаваемых
в функцию main из операционной системы и
параметров операционной

системы.

Пример:

int
main ( int argc, char *argv[], char *argp[])

{
int i=0;

printf
(«n Имя программы %s», argv[0]);

for
(i=1; i>=argc; i++)

printf
(«n аргумент
%d равен
%s», argv[i]);

printf
(«n Параметры операционной системы:»);

while
(*argp)

{
printf («n %s»,*argp);

argp++;

}

return
(0);

}

Доступ
к параметрам операционной системы можно
также получить при помощи

библиотечной
функции geteuv, ее прототип имеет следующий
вид:

char
*geteuv (const char *varname);

Аргумент
этой функции задает имя параметра среды,
указатель на значение

которой
выдаст функция geteuv. Если указанный
параметр не определен в среде

в
данный момент, то возвращаемое значение
NULL.

Используя
указатель, полученный функцией geteuv,
можно только прочитать

значение
параметра операционной системы, но
нельзя его изменить. Для изменения

значения
параметра системы предназначена функция
puteuv.

Компилятор
языка СИ строит СИ-программу таким
образом, что вначале работы

программы
выполняется некоторая инициализация,
включающая, кроме всего прочего,

обработку
аргументов, передаваемых функции main, и
передачу ей значений

параметров
среды. Эти действия выполняются
библиотечными функциями _setargv и

_seteuv,
которые всегда помещаются компилятором
перед функцией main.

Если
СИ-программа не использует передачу
аргументов и значений параметров

операционной
системы, то целесообразно запретить
использование библиотечных

функций
_setargv и _seteuv поместив в СИ-программу перед
функцией main функции

с
такими же именами, но не выполняющие
никаких действий (заглушки). Начало

программы
в этом случае будет иметь вид:

_setargv()

{
return ; /* пустая функция */

}

-seteuv()

{
return ; /* пустая функция */

}

int
main()

{
/* главная функция без аргументов */

…

renurn
(0);

}

В
приведенной программе при вызове
библиотечных функций _setargv и _seteuv

будут
использованы функции помещенные в
программу пользователем и не

выполняющие
никаких действий. Это заметно снизит
размер получаемого exe-файла.

Программа
на Си состоит из нескольких функций.
Они могут хранится как в одном файле
так и отдельно. Функции в Си гло-бальные.
Запрещается объявлять одну функ-цию
внутри другой.

Связь
между функциями осуществляется через
аргументы, возвращаемые значения и
внешние переменные.

?Аргументы
функций передаются по значе-нию, т.е.
вызванная функция получает свою временную
копию каждого аргумента, а не его адрес,
это означает, что функция не может
воздействовать на исходный аргумент.

Если
в качестве аргумента выступает имя
массива, то передается адрес начала
этого массива, сами эл не копируются,
таким образом массив передается по
ссылке.

?Внешние
переменные определены вне какой-либо
функции. 1) Когда связь между функциями
осуществляется с помощью большого числа
переменных. Внешние переменные оказываются
более удобными и эффективными, чем
использование длинных списков аргументов.
2) Внешние массивы могут быть
инициализированы, а автомати-ческие
нет. 3) Область действия и время
существования.

Функция
обязательно должна быть объявле-на до
её использования. Заголовок обычно
наз-ют прототипом функции:

тип
имя_функц. (тип [имя_парам1, имя парам2,
…] тип возвращаемого результата

Пример:
int f(int x,y);

Описание
прототипов обычно выполняется в
заголовочных файлах, а для коротких
про-грамм пишутся вначале программы.
Int тип по умолчанию. В Си можно создавать
функ-ции с переменным числом параметров.
Тогда в прототипе в конце ставят точки.
Определе-ние функции может находится
до главной программы и после.

Определение
функции: тип имя_функ (тип [имя_парам..]
{ тело функ return выраж}

Пример:
int f(int a, int b)

{
if (a > b) { printf(«max = %dn», a); return a; }

printf(«max
= %dn», b); return b;}

Вызов
функции: c = f(15, 5); c = f(d, g);f(d, g);

Указатели
на функции В языке Си сама функция не
может быть значением перемен-ной, но
можно определить указатель на функцию.
С ним уже можно обращаться как с
переменной: передавать его другим
функ-циям, помещать в массивы и т.п.

Код
функции в персональном компьютере
занимает физическую память. В этой
памяти есть точка входа, которая
используется для того, чтобы войти в
функцию и запустить ее на выполнение.
Указатель на функцию как раз и адресует
эту точку входа. Это уже будет обычная
переменная и с ней можно делать все, что
можно делать с переменной.

Через
указатель можно войти в функцию, т.е.
запустить ее на выполнение. Объявление
вида: int (*f)( );

говорит
о том, что f — это указатель на функ-цию,
возвращающую целое значение. Первая
пара скобок необходима, без них int *f( );
означало бы, что f — функция, возвращающая
указатель на целое значение. После
объявле-ния указателя на функцию в
программе можно использовать объекты:
*f — сама функция; f — указатель на функцию.
Для любой функции ее имя (без скобок и
аргу-ментов) является указателем на эту
функцию.

Примеры:
int (*comp) () /*comp является указателем на
функцию к-ая возвращает значение типа
int*/ int *comp () /*comp является функцией,
возвращающей указатель на целые*/

Аргументы
функции main( )В программы на языке Си
можно передавать некоторые аргументы.
Когда вначале вычислений производится
обращение к main( ), ей пере-даются три
параметра. Первый из них опре-деляет
число командных аргументов при обращении
к программе. Второй представля-ет собой
массив указателей на символьные строки,
содержащие эти аргументы (в одной строке
— один аргумент). Третий тоже являет-ся
массивом указателей на символьные
строки, он используется для доступа к
параметрам операционной системы (к
пере-менным окружения).

Любая
такая строка представляется в виде:

переменная
= значение

Последнюю
строку можно найти по двум заключительным
нулям.

Назовем
аргументы функции main( ) соответ-ственно:
argc, argv и env (возможны и любые другие
имена). Тогда допустимы следующие
описания: main( ); main(int argc);

main(int
argc, char *argv[ ] );

main(int
argc,char *argv[],char *env[])

Предположим,
что на диске A: есть некото-рая программа
prog.exe. Обратимся к ней следующим образом:

A:>prog.exe
file1 file2 file3 <Enter>

Тогда
argv[0] — это указатель на строку A:prog.exe,
argv[1] — на строку file1 и т.д. На первый
фактический аргумент указывает argv[1], а
на последний — argv[3]. Если argc=1, то после
имени программы в командной строке
параметров нет. В нашем примере argc=4.

Рекурсией
называется такой способ вызова, при
котором функция обращается к самой
себе.

Важным
моментом при составлении рекур-сивной
программы является организация выхода.
Здесь легко допустить ошибку, заключающуюся
в том, что функция будет последовательно
вызывать саму себя беско-нечно долго.
Поэтому рекурсивный процесс должен шаг
за шагом так упрощать задачу, чтобы в
конце концов для нее появилось не
рекурсивное решение. Использование
рекур-сии не всегда желательно, так как
это может привести к переполнению стека.

2.
Язык программирования С++. Стандарт-ная
библиотека С++. Заголовки. Структура
STL. Примеры.

Стандартная
библиотека С++

Стандартная
библиотека C++ включает стандартную
библиотеку Си с небольшими изменениями,
которые делают её более подходящей для
языка C++. В заголовочных файлах убераем
.h и добавляем С в начале:

в
Си time.h, а в C++ ctime.

Все
компоненты стандартной библиотеки С++
находятся в пространстве имен std. Каждая
функция, объект и шаблон класса,
объявленные в стандартном заголовочном
файле, таком, как <vector> или <iostream>,
принадлежат к этому пространству. Каждый
вызов функции std :: using namespace std;

Компилятор
С++ включает стандартную библиотеку
шаблонов STL (Standart Tamplate Library). Возможности
STL:

—
STL Строки (Не существует серьезной
библиотеки, которая бы не включала в
себя свой класс для представления строк
или даже несколько подобных классов.
STL — строки поддерживают как формат
ASCII, так и формат Unicode).

• string
— представляет из себя коллекцию, хранящую
символы char в формате ASCII. Для того, чтобы
использовать данную кол-лекцию, вам
необходимо включить #include <string>.

• wstring
— это коллекция для хранения двухбайтных
символов wchar_t, которые используются для
представления всего набора символов в
формате Unicode. Для того, чтобы использовать
данную коллек-цию, вам необходимо
включить #include <xstring>.

—
Комплексные числа Complex #include <complex>

—
Pair (пара) – одним объектом определяет
пару значений, если между ними
семантиче-ская связь

#include
<utility> pair <string, string> author (“James”,
“Jage”)

—
Умный указатель (auto-ptr) – для уничто-жения
ранее выделенной памяти.

В
С++ нет автоматической сборки мусора.

—
Потоки ввода-вывода для файлов, консоли
и строк; — Обработка исключений класса;

—
Классы по локализации приложений.

Заголовки
Механизм включения с помощью #include — это
чрезвычайно простое средство обработки
текста для сборки кусков исход-ной
программы в одну единицу (файл) для ее
компиляции. Директива #include «to_be_included»
замещает строку, в которой встретилось
#include, содержимым файла «to_be_included».
Его содержимым должен быть исходный
текст на C++, поскольку дальше его будет
читать компилятор.

В
заголовочном файле могут содержаться:

Определения
типов (struct point { int x, y; }); Описания функций
(extern int strlen(const char*);); Определения
inline-функций (inline char get() { return *p++; }); Описания
данных (extern int a;); Определения констант(const
float pi = 3.1415); Перечисления (enum bool { false, true
};); Дирек-тивы include (#include); Определения
макросов (#define Case break;case ); Комментарии
(/* проверка на конец файла */);

но
никогда: Определения обычных функций
(char get() { return *p++; }); Определения данных
(int a; ); Определения сложных константных
объектов(const tbl[] = { /* … */ }).

Структура
STL В библиотеке выделяют пять основных
компонентов: 1. Контейнер (container) — хранение
набора объектов в памяти. 2. Итератор
(iterator) — обеспечение средств доступа к
содержимому контейнера. 3. Алгоритм
(algorithm) — определение вы-числительной
процедуры. 4. Адаптер (adaptor) — адаптация
компонентов для обес-печения различного
интерфейса. 5. Функ-циональный объект
(functor) — сокрытие функции в объекте для
использования дру-гими компонентами.

Разделение
позволяет уменьшить количество
компонентов. Например, вместо написания
отдельной функции поиска элемента для
каждого типа контейнера обеспечивается
единственная версия, которая работает
с каждым из них, пока соблюдаются основные
требования.

Контейнеры
– это классы которые содержат множество
объектов одного типа. Управляют
размещением в памяти и освобождению
этих объектов через конструкторы,
деструкторы, операторы вставки и
удаления.

Контейнеры:

—
последовательности – это конечно число
типов в строго линейном порядке:

• vector
(вектор)- коллекция элементов Т, сохраненных
в массиве, увеличиваемом по мере
необходимости. Для того, чтобы начать
использование данной коллекции, включите
#include <vector>. (vector <int> ivec;)

• list
— коллекция элементов Т, сохраненных,
как двунаправленный связанный список.
Для того, чтобы начать использование
данной коллекции, включите #include <list>.

• deque
(Очередь) Контейнер похож на vector, но с
возможностью быстрой вставки и удаления
элементов на обоих концах . Реали-зован
в виде двусвязанного списка линейных
массивов.

—
адаптеры последовательностей:

• stack
(Стек) — контейнер, в котором добавление
и удаление элементов осуществ-ляется
с одного конца.

• queue
(Очередь) — контейнер, с одного конца
которого можно добавлять элементы, а с
другого — вынимать.

• priority
queue (Очередь с приоритетом) организованная
так, что самый большой элемент всегда
стоит на первом месте.

—
ассоциативные контейнеры – обеспечивают
быстрый поиск данных, основный на ключах:

• set
— Упорядоченное множество уникаль-ных
элементов. При вставке/удалении эле-ментов
множества итераторы, указывающие на
элементы этого множества, не становятся
недействительными. Обеспечивает
стандарт-ные операции над множествами
типа объе-динения, пересечения, вычитания.
Тип элементов множества должен
реализовывать оператор сравнения
operator< или требуется предоставить
функцию-компаратор. Реализо-ван на
основе самобалансирующего дерева
двоичного поиска, #include <set>.

• multiset
— То же что и set, но позволяет хранить
повторяющиеся элементы.

• map
(отображение , словарь)- Упорядо-ченный
ассоциативный массив пар элемен-тов,
состоящих из ключей и соответствую-щих
им значений, pair<const Key, T>. Ключи должны
быть уникальны. Порядок следова-ния
элементов определяется ключами. При
этом тип ключа должен реализовывать
оператор сравнения operator<, либо требуется
предоставить функцию-компаратор,
#include <map>.

• multimap
— То же что и map, но позволяет хранить
несколько одинаковых ключей.

Итераторы
– обобщение указателе, обеспе-чивают
доступ к содержимому контейнера и
навигацию по его элементам. Обычно
ис-пользуются парами (begin() end(), обратные
rbegin(), rend())

—
Входные (input) (++, operator*, operator->, конструктор
копии, =, ==, !=) Обеспечивают доступ для
чтения в одном направлении. Позволяют
выполнить присваивание или копирование
с помощью оператора присваи-ваивания
и конструктора копии;

—
Выходные (output) (++, operator*, конструк-тор
копии) Обеспечивают доступ для записи
в одном направлении. Их нельзя сравнивать
на равенство;

—
Однонаправленные (forward) (++, operator*,
operator->, конструктор копии, конструктор
по умолчанию, =, ==, !=) Обеспечивают доступ
для чтения и записи в одном направ-лении.
Позволяют выполнить присваивание или
копирование с помощью оператора
присваиваивания и конструктора копии.
Их можно сравнивать на равенство;

—
Двунаправленные (bidirectional) (++, —, operator*,
operator->, конструктор копии, конструктор
по умолчанию, r=, ==, !=) Поддерживают все
функции, описанные для однонаправленных
итераторов. Кроме того, они позволяют
переходит к предыдущему элементу;

—
Произвольного доступа (random arcess) (++, —,
operator*, operator->, конструктор копии,
конструктор по умолчанию, =, ==,!=, +, -, +=,
-=, <, >, <=, >=, operator[])Эквивалентны
обычным указателям: поддерживают
ариф-метику указателей, синтаксис
индексации массивов и все формы сравнения.

Алгоритмы
– шаблоны функций для обра-ботки массивов
и контейнеров классов. Решают типовые
задания связанные с обра-боткой
последовательностей одного типа (поиск,
сортировка, мак, мин, объединение).

Обобщенные
алгоритмы не зависят от типов. Доступ
к типам осуществляется с помощью
итераторов (#include <algorithm>).

Адаптеры
– шаблоны класса которые обес-печивают
интерфейсы: Адаптеры контейне-ров,
итераторов, функций.

Функциональные
объекты – классы для которых перегружены
операция вызова функций. основное их
назначение – измене-ние поведения
обобщенных алгоритмов (#include <functional>).

Пример:
ввод чисел, вывести в обратном порядке,
вектор представляет собой массив и
знает сколько элементов хранится.

#include
<iostream> #include <vector>

using
namespace stel;

int
main()

{
vector <int> v; int x;

cout
<<”Введите
числа,
конец-0:”<<endl;

while
(cin>>x, x!=0)

V.push_back(x);
//помещение элемента в вектор

copy
(v.rbegin(), v.rend(), os-tream_iterator<int>(count, “_”));

cout
<< endl;

system(“pause”);
//не
вводится

return
0;}

Архитектура Фон Неймана. Современные способы улучшения производительности вычислительной техники. Архитектура фон Неймана.

Улучшение производительности эвм

Конвейерная
обработка. Что необходимо
для сложения двух вещественных чисел,

представленных
в форме с плавающей запятой? Целое
множество мелких операций таких,как
сравнение порядков, выравнивание
порядков, сложение мантисс, нормализация
и т.п.

Процессоры
первых компьютеров выполняли все эти
«микрооперации» для каждой пары

аргументов
последовательно одна за одной до тех
пор, пока не доходили до

окончательного
результата, и лишь после этого переходили
к обработке следующей пары

слагаемых.
Идея конвейерной обработки заключается
в выделении отдельных этапов

выполнения
общей операции, причем каждый этап,
выполнив свою работу, передавал бы

результат
следующему, одновременно принимая новую
порцию входных данных.

Получаем
очевидный выигрыш в скорости обработки
за счет совмещения прежде

разнесенных
во времени операций.

Кэширование
данных – загрузка
данных из памяти или результатов
вычислений из процессора с дублированием
их в специальную быструю память – кэш.
При повторном обращении к этим же данным,
они будут браться не из медленной
основной памяти, а непосредственно из
быстрой кэш-памяти. Современные процессоры
включают в себя несколько уровней
кэширования, отличающихся объемом и
быстродействием.

Суперскалярность.
Как и в предыдущем примере, только при
построении

конвейера
используют несколько программно-аппаратных
реализаций функциональных

устройств,
например два или три АЛУ, три или четыре
устройства выборки.

Предвыборка
данных (prefetching)
позволяет осуществлять
предварительную выборку данных из
памяти в кэш или ядро процессора заранее,
если ниже по программе встречается
доступ в определенному участку памяти.

Предсказание
переходов позволяет
предсказывать исполнение команды
ветвления (условных команд) на основании
накопленной статистики и выполнять
инструкции, находящиеся после условного
перехода, до того, как будет определено
его направление. Предсказатель переходов
является неотъемлемой частью всех
современных суперскалярных микропроцессоров,
так как в большинстве случаев (точность
предсказания переходов в современных
процессорах превышает 90%) позволяет
оптимально использовать вычислительные
ресурсы процессора.

Hyper
Threading. Перспективное
направление развитие современных

микропроцессоров,
основанное на многонитевой архитектуре.
Основное препятствие на

пути
повышения производительности за счет
увеличения функциональных устройств
–

это
организация эффективной загрузки этих
устройств. Если сегодняшние программные

коды
не в состоянии загрузить работой все
функциональные устройства, то можно

разрешить
процессору выполнять более чем одну
задачу (нить), чтобы дополнительные

нити
загрузили – таки все ФУ (очень похоже
на многозадачность).

Многоядерность.
Можно, конечно, реализовать
мультипроцессирование на уровне

микросхем,
т.е. разместить на одном кристалле
несколько процессоров (Power 4). Но если

взять
микропроцессор вместе с памятью как
ядра системы, то несколько таких ядер
на

одном
кристалле создадут многоядерную
структуру. При этом в кристалле также
могут интегрироваться функции (например,
интерфейсы сетевых и телекоммуникационных
систем), для выполнения которых обычно
используются отдельные наборы микросхем

Структура программы. Source-файлы (исходный код). Header-файлы (заголовки). Объявление переменных. Объявления функций. Объявления функций

Функции всегда
определяются глобально. Они могут быть
объявлены с классом памяти static или
extern. Объявления функций на локальном и
глобальном уровнях имеют одинаковый
смысл.

Правила определения
области видимости для функций отличаются
от правил видимости для переменных и
состоят в следующем.

1. Функция, объявленная
как static, видима в пределах того файла,
в котором она определена. Каждая функция
может вызвать другую функцию с классом
памяти static из своего исходного файла,
но не может вызвать функцию определенную
с классом static в другом исходном файле.
Разные функции с классом памяти static
имеющие одинаковые имена могут быть
определены в разных исходных файлах, и
это не ведет к конфликту.

2. Функция, объявленная
с классом памяти extern, видима в пределах
всех исходных файлов программы. Любая
функция может вызывать функции с классом
памяти extern.

3. Если в объявлении
функции отсутствует спецификатор класса
памяти, то по умолчанию принимается
класс extern.

Все объекты с
классом памяти extern компилятор помещает
в объектном файле в специальную таблицу
внешних ссылок, которая используется
редактором связей для разрешения внешних
ссылок. Часть внешних ссылок порождается
компилятором при обращениях к библиотечным
функциям СИ, поэтому для разрешения
этих ссылок редактору связей должны
быть доступны соответствующие библиотеки
функций.

Прототип
функции —
показывает образец того как применять
функцию в программе, какие значения в
нее передаются и если она возвращает
какое-то значение то прототип указывает
тип возвращаемых данных. Прототип не
имеет скобок { } а после
скобок ( ) ставится ;

Функция —
имеет { «тело» } в фигурных
скобках. Тело это код на Си определяющий
то что делает функция.

; после
вызова функции не ставится !

Программа
на языке Си это текстовый файл, обычно
с расширением .c

Текст
программы называют исходным или
«исходником» или «сурцом»

от
анг. source
code —
это вам ключевые
слова для поиска

Весь
исполняемый код программы на Си находится
в функциях —

т.е.
в фигурных скобках { исполняемый код
программы }

Программа
на Си имеет определенную структуру :

1)
заголовок

2)
включение необходимых внешних
файлов — #include

3)
ваши определения для удобства
работы — #define

4)
объявление глобальных переменных и
констант

Глобальные
переменные и константы

—
объявляются вне какой либо функции.

т.е. не после фигурной скобки {

— доступны
в любом месте программы — значит
можно читать их значения и присваивать
переменным значения там где вам требуется
— в любом месте программы после их
объявления.

5)
описание функций — обработчиков прерываний

6)
описание других функций используемых
в программе

7)
функция main <- это
единственный обязательный пункт !

Шины и интерфейсы: fsb, шины расширения, внешние компьютерные шины. Шины

Компьютерная
шина (computer bus)— в архитектуре компьютера
подсистема, которая передает данные
между функциональными блоками компьютера.
В отличие от связи точка—точка, к шине
можно подключить несколько устройств
по одному набору проводников. Каждая
шина определяет свой набор коннекторов
для физического подключения устройств,
карт и кабелей.

Ранние
компьютерные шины представляли собой
параллельные электрические шины с
несколькими подключениями, но сейчас
данный термин используется для любых
физических механизмов, предоставляющих
такую же логическую функциональность,
как параллельные компьютерные шины.

Ранние
компьютерные шины были группой
проводников, подключающей компьютерную
память и периферию к процессору. Почти
всегда для памяти и для периферии
использовались разные шины, с разным
способом доступа, задержками, протоколами.

В
современных же компьютерах для связи
его основных блоков используются
несколько различных стандартизированных
видов шин, оптимизированных для доставки
данных между определёнными блоками.

Классифицировать шины можно следующим
образом:

Высокоскоростная
шина процессора(Front
Side Bus,FSB)
– служит для обмена
данными между процессором, памятью, а
также контроллерами остальных шин
Шины
расширения – служат
для подключения дополнительных модулей
компьютера
Внешние
шины – служат для
подключения внешних устройств.

Следует
заметить, что деление на шины расширения
и внешние шины весьма условно, т.к. в
настоящее время многие внутренние
устройства компьютера также подключаются
по «внешним шинам».

По
физической организации компьютерные
шины можно разделить на параллельные
и последовательные.

Параллельные
шины организованы в
виде нескольких проводников, по которым
одновременно передается информация.
Например, 8 проводников, по каждому за
1 такт передаётся 1 бит информации. Таким
образом, за 1 такт по такой шине будет
передаваться 1 байт информации.

Последовательные
шины передают всю
информацию по одному проводнику (или
по двум, один — в одну сторону, второй –
в обратную). Например, шина USB
состоит из 4 проводников: 2 для передачи
данных (передающий и принимающий), еще
один – питание +5 вольт и еще один — общий
провод (корпус).

Высокоскоростная шина процессора (fsb)

FSB
– компьютерная шина, выступающая в
качестве магистрального канала между
процессором и чипсетом. В разных чипсетах
используются различные типы FSB
(GTL+, QPB,EV6,
HyperTransport).

HyperTransport
является высокоскоростной шиной,
используемой не только в качестве FSB,
но и в других областях, но в качестве
FSB она получила очень
широкое распространение.

Частота,
на которой работает центральный
процессор, определяется исходя из
частоты FSB и коэффициента умножения,
проставляемого либо системной платой,
либо жестко заблокированным внутри
процессора.

До
определённого момента в развитии
компьютеров частота работы памяти
совпадала с частотой FSB,
на современных персональных компьютерах
частоты FSB и шины памяти
могут различаться. Обычно, частота
памяти выше и задается делителями по
отношению к FSB.

General
Information :

Performance
Rating : PR-6600
(estimated)

Real
Frequency : 3214.74
MHz

Multiplier
: 16x

Startup/Max
Multiplier : 5x / 16x

Front
Side Bus Information :

Bus
Speed : 200.9
MHz

Initial
Frequencies :

Frequency
: 3200 MHz

FSB
Frequency : 200 MHz

Multiplier
: 16x

Frequency
Control :

Core
#1 : 3214.89
MHz

Core
#2 : 3214.86
MHz

Memory
Information :

Type
: DDR2-SDRAM PC2-6400

Frequency
: 401.8
MHz

DRAM/FSB
Ratio : CPU/8

Supported
Channels : Dual (128-bit)

Activated
Channels : Dual

Шины расширения Зачем придумали шины расширения

В
70-х годах, после изобретения первого
микропроцессора и создания первого
персонального компьютера, встал вопрос
о возможностях расширения компьютера
без замены материнской платы. Было
решено использовать гнезда расширения,
расположенные непосредственно на
материнской плате, в которые подключались
платы расширения. Первым компьютером,
обладавшим гнездами расширения, был
Apple II. Он
получил большую популярность именно
благодаря наличию в нем этих гнезд.

Такое
устройство ПК, с возможностью вставлять
в системный блок дополнительные платы,
получило название «открытая
архитектура». IBM PC
– совместимые компьютеры также используют
открытую архитектуру (хотя были попытки
«закрыть» архитектуру на компьютерах
PS/2).

Благодаря
открытой архитектуре сейчас мы можем
выбрать, видеокарту какого производителя
нам покупать, через какой модем выходить
в Интернет и каким звуком наслаждаться.
А благодаря тому, что спецификация шины
расширений подробно документирована
и доступ к документации открыт,
заинтересованные фирмы получили
возможность создавать собственные
платы расширения, увеличивая популярность
и возможности персонального компьютера.

Первая шина

В
1981 году компания IBM вместе
с выпуском персонального компьютера
серии PC/XT
представила шину ISA
(Industrial Standard
Architecture — промышленная
стандартная архитектура). Она стала
одной из первых «шин расширения
ввода-вывода» (expansion
bus) для персональных
компьютеров.

Шина
ISA представляла интерфейс
для подключения различных адаптеров и
контроллеров периферийных устройств.
По своему устройству она была очень
простая и к тому же дешевая в производстве.
ISA имела разрядность 8
bit, тактовая частота шины
была 4.7 МГц и разъем для подключения
устройств имел 62 контакта.

Каждое
устройство, подключенное к шине, получало
свое прерывание (IRQ —
Interrupt ReQuest
— условный сигнал, по
которому устройству разрешалось
передавать или получать данные). А также
шина имела так называемые каналы прямого
доступа в память (DMA
— direct memory
access). Технология
DMA позволяет устройствам
обмениваться данными с памятью через
шину, без участия CPU, что
достаточно сильно снижает нагрузку на
процессор. Пропускная способность
первой системной шины достигала 1.2
Мб/сек.

16-бит

Спустя
три года, в 1984 году, свет увидел
микропроцессор i80286, и IBM
представила миру новый компьютер на
базе этого микропроцессора — IBM
PC/AT (Advanced
Technology). Новый процессор
и новая шина были 16-битными. Так появилась
ISA-16. Шина сохранила
совместимость с предыдущими платами
расширения, но при этом получила
значительные доработки. В первую очередь
это 8 новых линий данных (т.е. появилось
8 новых проводочков для передачи
дополнительных 8-ми бит информации), что
позволило стать шине 16-битной. Частота
шины увеличилась вместе с частотой
процессора до 8.33 МГц, и пропускная
способность выросла до 5.3 Мб/сек, хотя
теоретически она могла бы достигать 16
Мб/сек.

Слот
расширения новой шины состоял из двух
частей — длинной и короткой. Более длинная
часть полностью копировала 8 разрядный
слот предыдущей версии платы, а короткая
часть содержала новые 36 дополнительных
контактов.

Поскольку
частота процессора скоро стала значительно
выше частоты системной шины, появилось
понятие «деление частоты», когда
частота, задаваемая тактовым генератором
для всей системы, делится на некое число
для установки частоты работы шины
расширений.

Стандарт
ISA так понравился различным
производителям компьютеров (не IBM
совместимых), что они начали использовать
его в своих разработках. Например,
некоторые компьютеры Amiga
и Commodore использовали эту
шину.

«Шутка» от ibm

1
апреля 1987 года IBM,
обеспокоенная появлением слишком
большого количества клонов персональных
компьютеров и выходом нового процессора
i80386, представляет миру
новую архитектуру персонального
компьютера IBM PS/2.
В ней использовалась новая системная
шина MCA (Micro
Channel Architecture
— микроканальная архитектура). Новая
шина была разработана практически с
нуля и не обладала обратной совместимостью
с ISA, однако стоит заметить,
что она была гораздо удачнее и
функциональнее. MCA имела
три разных разрядности 8, 16 и 32. Частота
новой шины была 10 МГц, а пропускная
способность 20 Мб/сек (а теоретически
можно получить и все 160 Мб/сек). Кроме
того, в новой шине несколько устройств
могли иметь одинаковое прерывание, и
делить его между собой самостоятельно.
Это еще не все революционные нововведения.
Если раньше установку прерываний на
платах расширения перед установкой в
компьютер приходилось самостоятельно
настраивать путем замыкания перемычек
на плате (как на винчестере ты ставишь
master/slave), то
теперь платы могли самостоятельно
разделять прерывания между собой. Было
и множество других технических
нововведений, которые опережали свое
время.

Желание
заработать денег погубило шину MCA,
не дав ей сколько-нибудь широко
распространиться. За лицензию на
производство новой шины IBM
просило слишком большие деньги, и
независимые производители компьютеров
и плат расширения просто не могли себе
этого позволить. Недовольные таким
поведением IBM,, несколько
крупнейших производителей компьютеров
создали альянс для разработки
альтернативной, более дешевой и простой
шины расширения. И в сентябре 1988 года
Compaq, NEC,
Epson, Hewlett-Packard,
Olivetti и еще несколько
производителей представили 32-разрядное
расширение шины ISA с полной
обратной совместимостью. Новая шина
получила название EISA
(Enhanced ISA
— усовершенствованная
ISA). Это был тяжелый удар
по IBM, поскольку новая
шина обеспечивала все преимущества
шины MCA, плюс обратную
совместимость со старыми системными
платами. EISA имела пропускную
способность 33 Мб/сек, 32-битную шину
адреса, то есть за такт позволяла
адресовать до 4 Гб оперативной памяти,
и, конечно, автонастройку плат расширения
(некий аналог технологии Plug
and Play).
Частота новой шины по прежнему осталась
8.33 МГц.

Интересной
особенностью шины EISA стал
разъем. Внешне он выглядит точно также
как у ISA-16, однако в глубине
разъема находится дополнительный ряд
контактов.

Локальная шина

Итак,
пока IBM бодалась с другими
производителями, мимо проходил Intel
(в то время крупный игрок на рынке
системных плат), которому больше
понравилась EISA, что еще
сильнее уменьшило шансы MCA
завоевать рынок. Но с появлением
процессора i80486 ни у MCA,
ни у EISA не было шансов на
выживание. Четверка от Intel
имела высокие частоты, а пропускная
способность всех существующих на тот
момент шин не позволяла реализовать
все возможности нового процессора. Так
началась разработка нового типа системной
шины — VESA Local
bus (локальная шина).

Была
создана целая ассоциация Video
Equipment Standard
Association (VESA
— ассоциация стандартов видео оборудования),
представившая миру шину VLB
(VESA Local Bus).
Эта шина представляла собой отдельную
относительно высокоскоростную шину
расширений, которая была связана
непосредственно с шиной процессора, и
таким образом позволяла избежать
задержек, связанных с работой более
медленных устройств, подключаемых к
стандартной шине расширений, и увеличить
скорость передачи данных. Но при этом
VL-Bus имела
ряд существенных недостатков: электрическая
нагрузка не позволяла подключать более
трех плат расширения, и шина была
рассчитана только на 486 процессоры.
Производители стали использовать новую
шину как 32 разрядное дополнение к шине
ISA. Таким образом, на
материнской плате появился дополнительный
116-контактный разъем. Этот разъем стал
использоваться в основном для подключения
видео адаптеров и скоростных контроллеров
жестких дисков. VLB работала
с частотой 25-50 МГц, и имела максимальную
скорость обмена 130 Мб/сек.

Оценив
перспективы развития шины (и не увидев
ничего хорошего), в середине 1993 года,
Intel выходит из ассоциации
VESA и принимается за
разработку альтернативной шины.

PCI

Первую
версию шины PCI
(Peripheral Component
Interconnect — взаимосвязь
периферийных компонентов) Intel
закончила еще весной 1991 года. Перед
инженерами компании была поставлена
задача разработать недорогое и
производительное решение, которое
позволит реализовать все возможности
новых процессоров 486/Pentium/PPro.
В 1992 году появилась первая версия шины
PCI, Intel
объявила, что стандарт шины будет
открытым и создала PCI
Special Interest
Group. Благодаря этому любой
заинтересованный разработчик получил
возможность создавать устройства для
шины PCI не тратя деньги
на лицензию. Первая версия шины имела
тактовую частоту 33 МГц, она могла быть
32 или 64 разрядной, и устройства могли
работать с сигналами в 5 В или 3,3 В.
Теоретически, пропускная способность
шины 132 Мбайт/сек, однако в реальности
пропускная способность около 80 Мбайт/сек.

Год
спустя, в 1993 году, появилась вторая
версия шины, а в 1995 появилась версия PCI
2.1 (еще одно название — «параллельная
шина PCI»), которая
существует и по сей день. Она обеспечивает
передачу данных по шине с частотой 66
МГц и максимальная скорость передачи
528 Мб/сек. Кроме этого, шина полностью
поддерживает все возможности технологии
Plug and
Play (PnP).

Как
и ISA, шина PCI
так полюбилась различным разработчикам,
что была перенесена на платформы с
процессорами Alpha, MIPS,
PowerPC, SPARC и
т.д.

Стандарт	Макс. Скорость, Мб/с	Тип слота	Тип карты
PCI 1.x-2.0	133	32 бит, 5 В	32 бит, 5 В
PCI 2.1-2.3 33 MГц	133	32 бит, 5 В	32 бит, 5 В / универсальный
PCI 2.2-2.3 66 MГц	266	32 бит, 3,3 В	32 бит, 3,3 В / универсальный
PCI64 33 МГц (v 2.1)	266	64 бит, 5 В	64 бит, 5 В / универсальный
PCI64 33 МГц (v 2.2)	266	64 бит, 3,3 В	64 бит, 3,3 В / универсальный
PCI64 66 МГц	533	64 бит, 3,3 В	64 бит, 3,3 В / универсальный
PCI-X 1.0	1024	64 бит, 3,3 В	64 бит, 3,3 В / универсальный
PCI-X 1.0	4096	64 бит, 3,3 В	64 бит, 3,3 В

AGP

PCI
всем была хороша, но со временем и она
перестала справляться с объемом данных,
которые передавал видеоадаптер.
Программисты делали игрушки все более
и более красочными, а для передачи
красивой картинки нужна высокая
пропускная способность. Так в 1996 году
Intel объявила о разработке
порта AGP (Accelerated
Graphic Port),
специально предназначенного для
подключения мощных графических адаптеров.
AGP нельзя назвать шиной,
поскольку он предназначен для подключения
только одного устройства. AGP
непосредственно связан с шиной процессора
через северный мост, таким образом, он
не зависит от работы PCI
устройств и не загружает стандартную
шину расширений графической информацией.
Впервые порт AGP увидел
свет вместе с материнским платами для
Pentium II. На
данный момент существует три версии
протокола AGP, плюс
дополнительная спецификация на питание
(AGP Pro) и 4
скорости передачи данных — от 1х (266
Мб/сек) до 8х (2 Гб/сек).

Смерть eisa

С
появлением AGP в персональных
компьютерах стало аж 3 различных слота
расширения: ISA, PCI
и AGP. Со временем, по мере
снижения стоимости PCI-плат,
многие ISA девайсы стали
выпускаться в формате PCI.
В это время Microsoft и Intel
принимают решение убрать ISA
из персональных компьютеров. Вытеснение
происходило в несколько этапов: сначала
в машине было много ISA-слотов
и два-три PCI. Потом количество
слотов сравнялось, а затем ISA
слоты и вовсе исчезли.

Но
с вытеснением ISA возникла
маленькая проблема. Некоторые устройства,
которые не следовало убирать (например,
COM и LPT
порты), работали с использованием ISA
шины. Выход был найден быстро и просто:
шина LPC (Low—Pin
Count). Эта шина
специально предназначена для подключения
разных «незначительных» устройств:
контроллера клавиатуры, LPT
и COM-портов, дисководов.
Пропускная способность у такой шины
всего 6,7 Mб/cек.

PCI Express (PCIE)

Разработка
PCIE нового межкомпонентного интерфейса
была начата фирмой Intel еще тогда, когда
только ожидался выход в свет AGP 3.0 (он же
AGP 8х). Так, программную модель PCI планировали
унаследовать и в новом интерфейсе,
чтобы системы и контроллеры могли быть
доработаны для использования новой
шины путём замены только физического
уровня, без доработки программного
обеспечения. Сам же интерфейс должен
был быть последовательным. Это означало,
во-первых, однозначное подключение
«точка-точка». Во-вторых, упрощалась
схемотехника, разводка и монтаж.
В-третьих, экономилось место.

Анонс
первой базовой спецификации PCI-Express
состоялся в июле 2002 года, когда уже стало
ясно, что PCI-Express – это последовательный
интерфейс, нацеленный на использование
в качестве локальной шины и имеющий
много общего с сетевой организацией
обмена данными, в частности, топологию
типа «звезда» и стек протоколов.

Для
взаимодействия с остальными узлами ПК,
которые так или иначе обходятся
собственными шинами, основной связующий
компонент системной платы – Root
Complex Hub (узел, являющийся перекрёстком
процессорной шины, шины памяти и
PCI-Express) – предусматривает систему мостов
и свитчей. Логика всей структуры такова,
что любые межкомпонентные соединения
непременно оказываются построенными
по принципу «точка-точка», свитчи-коммутаторы
выполняют однозначную маршрутизацию
пакета от отправителя к получателю.

Разъёмы
шины PCI Express (сверху вниз: x4, x16, x1 и x16), по
сравнению с обычным 32-битным разъемом
шины PCI (внизу)

Внешние компьютерные шины

Аналогично
шинам расширения, внешние шины также
развивались, исходя из потребностей
пользователей передавать информацию
с как можно большей скокростью. Также
немаловажными факторами были:

Возможность
«горячего» подключения и отключения
устройств
Упрощение
физического уровня шины (уменьшение
количества проводников, упрощение и
удешевление контроллеров, и т.п.
Упрощение
соединительных кабелей, разъемов,
удешевление комплектующих.
Возможность
увеличения количества подключаемых
устройств.

Наиболее
широко известны следующие внешние шины:

Advanced Technology
Attachment или ATA (также известна, как PATA,
IDE, EIDE, ATAPI) — шина для подключения
дисковой и ленточной переферии.
SATA, Serial
ATA — современный вариант ATA (в отличие
от ATA является последовательной
шиной с возможностью горяцего
подключения).
PC card, ранее
известная как PCMCIA, часто используется
в ноутбуках и других портативных
компьютерах, но теряет своё значение
с появлением USB и встраиванием сетевых
карт и модемов
USB, Universal Serial
Bus, используется для множества внешних
устройств
SCSI, Small Computer
System Interface, шина для подключения дисковых
и ленточных накопителей
Serial Attached SCSI,
SAS — современный вариант SCSI

Классы памяти, время жизни и область видимости программных объектов. Инициализация локальных и глобальных переменных. Время жизни и область видимости программных объектов

Время жизни
переменной (глобальной или локальной)
определяется по следующим правилам.

1. Переменная,
объявленная глобально (т.е. вне всех
блоков), существует на протяжении всего
времени выполнения программы.

2. Локальные
переменные (т.е. объявленные внутри
блока) с классом памяти register или auto,
имеют время жизни только на период
выполнения того блока, в котором они
объявлены. Если локальная переменная
объявлена с классом памяти static или
extern, то она имеет время жизни на период
выполнения всей программы.

Видимость переменных
и функций в программе определяется
следующими правилами.

1. Переменная,
объявленная или определенная глобально,
видима от точки объявления или определения
до конца исходного файла. Можно сделать
переменную видимой и в других исходных
файлах, для чего в этих файлах следует
ее объявить с классом памяти extern.

2. Переменная,
объявленная или определенная локально,
видима от точки объявления или определения
до конца текущего блока. Такая переменная
называется локальной.

3. Переменные из
объемлющих блоков, включая переменные
объявленные на глобальном уровне, видимы
во внутренних блоках. Эту видимость
называют вложенной. Если переменная,
объявленная внутри блока, имеет то же
имя, что и переменная, объявленная в
объемлющем блоке, то это разные переменные,
и переменная из объемлющего блока во
внутреннем блоке будет невидимой.

4. Функции с классом
памяти static видимы только в исходном
файле, в котором они определены. Всякие
другие функции видимы во всей программе.

Метки в функциях
видимы на протяжении всей функции.

Имена формальных
параметров, объявленные в списке
параметров прототипа функции, видимы
только от точки объявления параметра
до конца объявления функции.

1.6.4. Инициализация глобальных и локальных переменных

При инициализации
необходимо придерживаться следующих
правил:

1. Объявления
содержащие спецификатор класса памяти
extern не могут содержать инициаторов.

2. Глобальные
переменные всегда инициализируются, и
если это не сделано явно, то они
инициализируются нулевым значением.

3. Переменная с
классом памяти static может быть
инициализирована константным выражением.
Инициализация для них выполняется один
раз перед началом программы. Если явная
инициализация отсутствует, то переменная
инициализируется нулевым значением.

4. Инициализация
переменных с классом памяти auto или
register выполняется всякий раз при входе
в блок, в котором они объявлены. Если
инициализация переменных в объявлении
отсутствует, то их начальное значение
не определено.

5. Начальными
значениями для глобальных переменных
и для переменных с классом памяти static
должны быть константные выражения.
Адреса таких переменных являются
константами и эти константы можно
использовать для инициализации
объявленных глобально указателей.
Адреса переменных с классом памяти auto
или register не являются константами и их
нельзя использовать в инициаторах.

Пример:

int
global_var;

int
func(void)

{
int local_var; /* по умолчанию auto
*/

static
int *local_ptr=&local_var; /* так
неправильно
*/

static
int *global_ptr=&global_var; /* а
так
правильно
*/

}

В приведенном
примере глобальная переменная global_var
имеет глобальное время жизни и постоянный
адрес в памяти, и этот адрес можно
использовать для инициализации
статического указателя global_ptr. Локальная
переменная local_var, имеющая класс памяти
auto размещается в памяти только на время
работы функции func, адрес этой переменной
не является константой и не может быть
использован для инициализации статической
переменной local_ptr. Для инициализации
локальной регистровой переменной
reg_ptr можно использовать неконстантные
выражения, и, в частности, адрес переменной
local_ptr.

Класс памяти

Класс
памяти определяет
порядок размещения объекта в памяти.

Различают
автоматический и статический классы
памяти. C располагает четырьмя
спецификаторами класса памяти:

auto

static

extern

Спецификаторы
позволяют определить класс памяти
определяемого объекта:

Auto.

Этот
спецификатор автоматического класса
памяти указывает на то, что объект
располагается в локальной (или
автоматически распределяемой) памяти.
Он используется в операторах объявления
в теле функций, а также внутри блоков
операторов, ограниченных фигурными
скобками.

Объекты,
имена которых объявляются со спецификатором
auto, размещаются в локальной
памяти непосредственно перед началом
выполнения функции или блока операторов,
ограниченного фигурными скобками {}.
При этом размер выделяемой памяти
известен ещё на этапе компиляции
программы, поэтому при компиляции могут
быть применены специальные процедуры,
оптимизирующие выделение памяти. Такая
процедура выделения памяти называется
статическим распределением
памяти (не путать со
статическим классом памяти).

При
выходе из блока или при возвращении из
функции, соответствующая область
локальной памяти освобождается и все
ранее размещённые в ней объекты
уничтожаются. Таким образом спецификатор
влияет на время жизни объекта (это время
локально). Спецификатор auto
используется редко, поскольку все
объекты, определяемые непосредственно
в теле функции или в блоке операторов
и так по умолчанию имеют автоматический
класс хранения и располагаются в
локальной памяти. Класс хранения таких
объектов, как аргументы
функций,
также называется автоматическим.
Такое название означает, что область
памяти для хранения этих элементов
данных выделяется автоматически при
вызове функции и также автоматически
освобождается, когда исполнение этой
функции завершается, т. е. временем жизни
аргументов является продолжительность
исполнения функции. Как только функция
завершает работу, их значения будут
утеряны.

Пример
использования: auto int
i;

Ещё
один спецификатор автоматического
класса памяти. Применяется к объектам,
по умолчанию располагаемым в локальной
памяти. Представляет из себя «ненавязчивую
просьбу» к транслятору (если это
возможно) о размещении значений объектов,
объявленных со спецификатором register
в одном из доступных регистров, а не в
локальной памяти. В этом случае доступ
к таким еременным осуществляется гораздо
быстрее. Если по какой-либо причине в
момент начала выполнения кода в данном
блоке операторов регистры оказываются
занятыми, транслятор обеспечивает с
этими объектами обращение, как с объектами
класса auto. Очевидно, что
в этом случае объект располагается в
локальной области памяти. Область
действия и время жизни полностью
идентичны классу auto.

Пример
использования: register int
i;

Static.

Спецификатор
внутреннего статического класса памяти.
Применяется только(!) к именам объектов
и функций (не применяется к аргументам
функций). В C++ этот
спецификатор имеет два значения.

Первое
означает, что определяемый объект
располагается по фиксированному адресу.
Тем самым обеспечивается существование
объекта с момента его определения до
конца выполнения программы (время жизни
– всё время работы программы, хотя
переменная и может быть определена
локально). В отличие от объекта класса
памяти auto, объект не будет
уничтожаться при выходе из функции, где
он был объявлен.

Например,
при каждом вызове функции IncS(),
объявленной следующим образом:

void IncS()

{

int
f=1;

static
int s=1;

f++;

s++;

}

значение
переменной f в начале выполнения функции
будет равно 1, в ходе выполнения функции
оно увеличится на 1, а в конце выполнения
f уничтожится. Значение же переменной
s будет увеличиваться на 1 при каждом
вызове функции, т.к. переменная s является
статической и не уничтожается на
протяжении всей программы. Отметим
также, что при такой записи значение 1
присваивается переменной s только один
раз – при инициализации в момент
создания переменной. При последующих
вызовах функции эта строчка игнорируется.

Второе
значение спецификатора static
означает локальность. Объявленая со
спецификатором static
переменная или функция локальна в одном
программном модуле (то есть, недоступна
из других модулей многомодульной
программы). Может использоваться в
объявлениях как внутри блоков и функций,
так и вне их (в этом случае мы получаем
внешнюю статическую
переменную).

Extern

Спецификатор
внешнего статического класса памяти.
Спецификатор extern
позволяет функции
использовать внешнюю переменную, даже,
если она определяется позже в этом или
другом модуле.

Внешними
называются переменные,
объявленные вне функции. Поскольку при
таком описании к ним автоматически
получают доступ все функции этого
модуля, то таки переменные также называют
глобальными.
С помощью спецификатора extern
можно получить доступ к внешней переменно
и из другого модуля, для чего они чаще
всего и применяются.

Extern
является своего рода модификатором-ссылкой,
указывающим на то, что где-то такая
переменная уже описана. И поэтому в
процессе компиляции не следует выделять
под неё память именно здесь, а следует
найти такую внешнюю переменную в других
модулях на стадии компоновки. Если такая
переменная найдена не будет, то компоновщик
выдаст ошибку «Объект не найден».

Пример:

module
MAIN.CPP

/*
определить внешние данные*/

extern int
iValue1;

extern int
iValue2;

main()

{

save()

printf («значения
равны: %d %d n», iValue1, iValue2);

}

module
SAVE.CPP

/*определить
внешние данные */

int iValue1;

int iValue2;

save()

{

iValue1=10;

iValue1=15;

return;

}

Глобальные
переменные iValue1 и iValue2
объявлены в обоих модулях, но память
под них выделяется только в модуле
Save.cpp. В
модуле Main.cpp
они объявлены с модификатором extern,
это сделано только для того, чтобы
получить доступ к этим глобальным
переменным.

Спецификатор
extern можно использовать
и внутри функций, например:

main()

{

extern
int iValue1;

extern
int iValue2;

save()

printf
(«значения равны: %d %d n», iValue1,
iValue2);

}

В
этом случае доступ к переменным iValue1,
iValue2 другого модуля будет
иметь только эта функция, в остальных
их придётся декларировать заново. Такая
форма записи встречается доволно редко.

Таким
образом, класс памяти extern
расширяет область действия глобальной
переменной, описанной в другом модуле,
при этом память под неё вторично не
выделяется.

1. Компьютерные сети и их виды, топологии компьютерных сетей. Каналы связи их классификация. Примеры сетеобразующего оборудования (компоненты компьютера и отдельные устройства).

2. Директивы препроцессора. Использование директивы #include для подключения header-файлов. Директивы препроцессора (прекомпилера).

Директивы
препроцессора исполняются компилятором
на стадии предварительной обработки,
предшествующей собственно компиляции.
Обычно они сводятся к подстановке,
замене или удалении участков текста из
программы, подаваемой на вход компилятора.
Директивы препроцессора, записанные в
модуле, действуют только в его пределах.

#include

Директива
#include производит прямую
текстовую подстановку содержимого
какого-либо файла непосредственно в то
место модуля, где она была применена.
Существует 2 формы этой директивы:

#include
<my.h>
— в этом случае
подставляемый файл берётся из каталога
для хранения хэдер-файлов стандартных
библиотек (путь к нему прописывается в
параметрах транслятора). Если файл
отсутствует в этом каталоге, то
препроцессор выдаёт ошибку.

#include
«my.h»
— в этом случае подставляемый файл
берётся из текущего каталога. Если файл
отсутствует в этом каталоге, то он
берётся из каталога для хранения
хэдер-файлов стандартных библиотек.
Если же файл отсутствует и в этом
каталоге, то препроцессор выдаёт ошибку.

Допускается
применение относительных и абсолютных
путей к файлу (последнее нежелательно,
т.к. в этом случае проект становится
труднопереносимым на другую машину):

#include
«..UDPSENDTPASocket.h»

Заметим,
что в данном случае, в написании пути
используется одинарный обратный слэш,
хотя в большинстве случаев в C
используется двойной слэш, т.к. комбинация
одинарного слэша и последующего символа
означают спецсимвол.

Вопреки
распространённому ошибочному мнению,
директива #include
не подсоединяет библиотеки к программе.
Эта директива подключает хэдер-файлы
используемых библиотек, т.е. файлы с
описаниями (декларациями) их функций.
В хэдер-файлах описаны имена функций,
списки их параметров, а также дополнительная
информация, например наборы констант
и т.п. На этапе предварительной обработки,
содержимое этих файлов с помощью
директивы #include подставляется
в текст модуля программы, что эквивалентно
обычному объявлению функций, используемых
в модуле, в самом его начале. Это делает
возможным компиляцию
модуля. Подключение же самих библиотек,
содержащих реализации используемых
функций (а точнее, уже откомпилированный
их бинарный код), происходит на этапе
компоновки (линковки). При этом стандартные
библиотеки подключаются автоматически
(компоновщик автоматически детектирует
какую библиотеку надо подключить), а
пользовательские библиотеки должны
быть включены в проект вручную, и пути
к файлам, их содержащим, должны быть
прописаны в файле проекта.

#define и
#undef

Директива
#define позволяет связать
идентификатор
(мы будем называть этот идентификатор
замещаемой частью)
с лексемой (возможно, что пустой), которую
называют строкой
замещения или замещающей частью
директивы #define.

Например,

#define
PI
3.14159

При
выполнении этой директивы препроцессор
заменит в оставшейся части программы
все отдельно стоящие вхождения
идентификатора PI на
соответствующую лексему, в нашем примере
– на плавающий литерал 3.14159.

Директиву
#define часто используют для
объявления констант, используемых в
дальнейшей программе, так называемых
объявленных или символических констант.
Согласно общепринятым правилам, их
идентификаторы обычно записывают
большими буквами.

Например,
результатом выполнения программы:

#include
«stdio.h»

#define
MY_FORMAT «Result = %d»

#define
MY_CONST 5

main()

{

printf(MY_FORMAT,
MYCONST);

}

будет являться
строка «Result = 5». Как
видно из этого примера, препроцессор
допускает вложения констант, объявленных
с помощью директивы #define.

Более сложной
формой директивы #define
является её форма с применением аргумента,
записываемого в скобках непосредственно
после замещаемой части:

#define
DEF(x) (x*2+5)

С её помощью можно
записывать простейшие функции, которые
будут не будут компилироваться в виде
отдельной функции, а будут подставлены
непосредственно в текст программы на
месте её вызова. В ряде случаев это
позволяет сократить размер программы,
объём используемой памяти и повысить
быстродействие программы. Например:

#define
DEF(x) (x*2+5)

main()

{

int
i,j;

j=4;

i=DEF(j);

}

В результате
выполнения программы в переменную i
запишется значение 13. Заметим, что в
настоящее время такой подход используется
очень редко, т.к. достигаемая этим приёмом
экономия памяти ничтожно мала по
сравнению с типичным объёмом памяти
компьютеров.

В директиве #define
замещающая часть может отсутствовать:

#define
MY_FLAG

Такая форма обычно
используется в связке с другими
директивами препроцессора.

Отменить
действие директивы #define
можно с помощью директивы #undef.
После выполнения этой директивы,
дальнейшие замены констант в программе
проводиться не будут.

#define
PI 3.14 + 0.00159

float
pi1 = PI;

#undef
PI

#define
PI 3.14159

float
pi2 = PI;

#ifdef и
#ifndef

Директивы
#ifdef, #else,
#ifndef, #endif
являются директивами условной компиляции.
Их работа очень похожа на работу оператора
if за исключением того,
что эти директивы выполняются на стадии
предварительной обработки программы
перед компиляцией, а не в ходе выполнения
программы.

Директива
#ifdef сохраняет участок
кода, заключённый между ней и директивами
#endif или #else,
если идентификатор, стоящий после #ifdef
был предварительно определён с помощью
директивы #define. В противном
случае, этот участок кода будет удалён.
Например:

#define
INTEGERS

…

#ifdef
INTEGERS

int
i,j;

#endif

…

В
этой программе фрагмент кода между
#ifdef и #endif
будет сохранён, т.к. идентификатор
INTEGERS был объявлен. Если
же его объявление удалить, или отменить
с помощью директивы #undef,
то фрагмент кода int i,j
будет удалён препроцессором по причине
отсутствия объявления идентификатора
INTEGERS.

Более расширенная конструкция выглядит
так:

#define INTEGERS

…

#ifdef INTEGERS

int i,j;

#else

double i,j;

#endif

…

В
этом случае, если идентификатор объявлен,
то сохраняется код на участке от #ifdef
до #else, иначе сохраняется
код от #else до #endif.
Таким образом, если идентификатор
INTEGERS объявлен, то i
и j будут объявлены с типом
int, иначе – double.

Директива
#ifndef полностью противоположна
директиве #ifdef по
функциональности, т.е. она сохраняет
последующий код, если идентификатор,
следующий за ней не был объявлен.
Синтаксис и применение этой директивы
полностью аналогичны директиве #ifdef.

С
помощью применения вышеописанных
директив можно создавать универсальные
программы, которые в зависимости от
описанного набора идентификаторов,
будут транслироваться из одного и того
же исходного кода в совершенно разные
бинарные файлы. Зачастую такую методику
применяют для мультиплатформенных
выражений, учитывая особенности целевых
платформ с помощью комбинаций #ifdef
#else #endif,
например:

#ifdef DOS

#define MyInt short

#else

#define MyInt long

#endif

MyInt i;

Все
вышеописанные действия можно в большинстве
случаев проделать и с помощью обычных
операторов if и глобальных
переменных, но в этом случае размер
получаемой программы будет гораздо
больше.

1.Сеть интернет. Адресация узлов (ip-адреса, доменные адреса, url). Сервисы и используемые протоколы передачи данных.

Internet –
это совокупность сетей, использующая
для объединения сетей единый протокол
обмена информацией TCP/IP.
Само название Internet
означает «между сетей».

Протоколы Internet
унаследовал от старейшей сети США
ARPANET (сеть 60-х годов).

Во времена становления
интернета локальные сети имели свои
специфические протоколы обмена данными.
Для того, чтобы объединить эти сети в
сеть Internet стали использовать
специальные средства, называемые шлюзами
(gateway). Изначально шлюзы
– это совокупность аппаратно-программных
средств, служащих для преобразования
протоколов. Например, это может быть
специальный компьютер или дополнительная
компьютерная программа.

На данный момент в ряде случаев
очень сложно сказать, где заканчивается
Интернет и начинается локальная сеть,
т.к. совокупность локальных и глобальных
сетей по сути дела и образуют интернет.
Сейчас в Интернете и большинстве
локальных сетей используются одни и те
же протоколы сетевого/транспортного
уровня (семейство TCP/IP),
поэтому в явном виде преобразование
протоколов отсутствует (хотя в некоторых
случаях оно происходит, особенно в виде
«обертывания» в другой протокол). Тем
не менее, понятие шлюза осталось. Шлюз,
как и раньше, — оборудование, обеспечивающее
передачу данных между отдельно взятой
локальной сетью и остальными частями
глобальной сети (Интернета). Отметим,
что понятие шлюз весьма широкое, и имеет
ряд других значений.

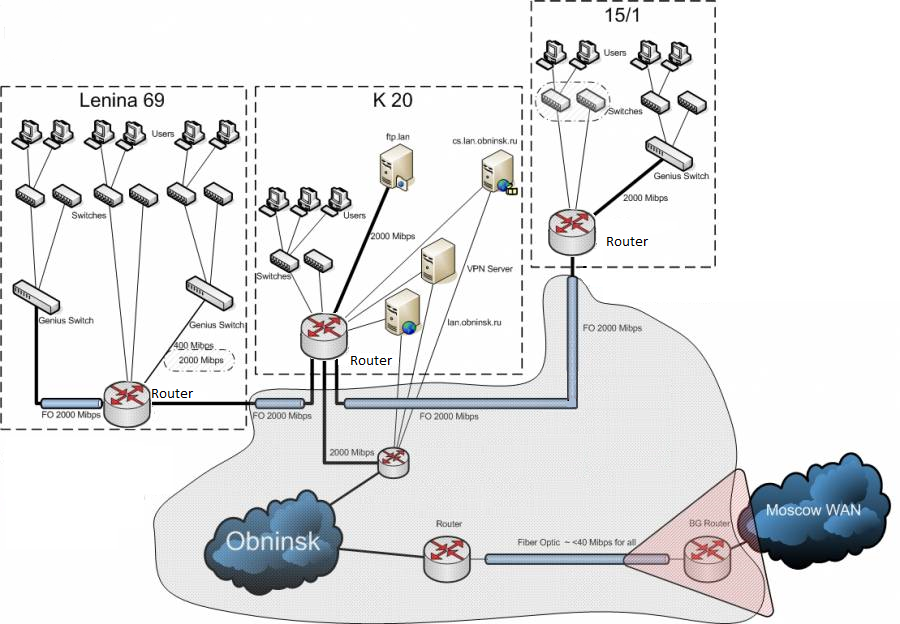
Пакет, являющийся частью передаваемых
данных, на пути в пункт своего назначения
проходит по определенному маршруту.
Маршрут определяет начальную точку
процесса передачи пакета и показывает,
в какой компьютер ваша система должна
передать пакет, чтобы он достиг пункта
назначения.

Когда необходимо передать пакет между
машинами, подключенными к разным
подсетям, то машина-отправитель посылает
пакет в соответствующий шлюз (шлюз
подключен к подсети также как обычный
узел). Оттуда пакет направляется по
определенному маршруту через систему
шлюзов и подсетей, пока не достигнет
шлюза, подключенного к той же подсети,
что и машина-получатель; там пакет
направляется к получателю.

Различные участки сети связаны между
собой посредством маршрутизаторов
(роутеров), коммутаторов (свитчей) и
другого сетевого оборудования. Они
принимают решение, куда направить
пакет(ы). и каким образом их передавать.
Маршрутизатор может выбрать наилучший
путь для передачи сообщения абоненту
сети, фильтрует информацию, проходящую
через него, направляя в одну из сетей
только ту информацию, которая ей
адресована. Кроме того, маршрутизатор
обеспечивает балансировку нагрузки в
сети, перенаправляя потоки сообщений
по свободным каналам связи.

Система адресации в Internet

Для каждого компьютера
устанавливаются два адреса: цифровой
IP-адрес (IP
– Internetwork Protocol
– межсетевой протокол) и доменный адрес.

Оба эти адреса могут применяться
равноправно.

IP-адрес
стандарта IP v.4
имеет общую длину 4 байта. IP
– адрес состоит из четырех сегментов
–чисел, разделенных точками. Каждое
число не превышает 255. Например,
192.168.14.5

Протокол IP
v.6
оперирует адресами длиной в 16 байт.
Компоненты адреса записываются в
шестнадцатеричной форме в следующем
виде: fe80:0000:0000:0000:0202:b3ff:fe1e:8329

Числовая адресация удобна для машинной
обработки таблиц маршрутов, но трудна
для использования ее человеком. Запомнить
наборы цифр гораздо сложнее, чем
мнемонические осмысленные имена.

Для того чтобы решить эту
проблему, были придуманы DNS
(Domain Name
System).
Доменная система имен
– это распределенная база данных,
которая содержит информацию о компьютерах,
включенных в сеть Internet.
По запросу от какого-либо компьютера
DNS по заданному доменному
имени возвращает IP-адрес,
и наоборот.

Доменный адрес
– символьное имя, представляющее собой
набор строк, разделенных точкой. Вначале
идет имя компьютера, затем многоуровневое
имя сети, в которой он находится (c
u67.nntu.sci—nnov.ru
– пример с доменом
технического университета).

Каждое слово уровень в этой системе
называется доменом. Полное доменное
имя должно быть уникальным.

Система
доменных адресов строится по иерархическому
принципу. Однако иерархия эта не строгая.
Пространство имен DNS
имеет вид дерева доменов, с полномочиями,
возрастающими по мере приближения к
корню дерева (т.е. самое последнее слово
– домен первого уровня, жестко выбираемый
из определенного списка, предпоследнее
– домен второго уровня, выбор слов
ограничен менее жестко…).

Список
доменов первого уровня жестко закреплен
по географическому принципу (eu,
ru, fr, cn,
us, и т.д.) либо по смысловому
содержанию:

.gov
— государственные учереждения,

.mil
— военные учереждения,

.com
— коммерческие организации,

.net
— поставщики сетевых услуг,

.org
— безприбыльные организации,

.edu
— учебные заведения;

Регистрациею
доменов регулируют специальные
организации, например, ICANN(Internet
Corporation for
Assigned Names
and Numbers).
Официальным регистратором доменов в
нашей стране является РосНИИРОС, или
RU-CENTER.

При
работе с доменными именами компьютер
в первую очередь обращается к известному
ему доменному серверу,
и выясняет IP адрес,
соответствующий данному доменному
имени. Дальнейшие операции по передаче
данных идут с использованием полученного
IP-адреса.

URL(
Uniform Resource
Locator).

Дальнейшим развитием идеи
доменных имен стали URL.
URL – это универсальная
форма записи местоположения в сети (или
локально) какого-либо ресурса (например,
файла), а также определяющий протокол
доступа к ресурсу.

Простой синтаксис URL:

protocol://host/path,
где

protocol – тип протокола доступа
(http, https,
ftp, file, и
т.п.)

host — имя
машины, с которой необходимо установить
соединение. Может быть в виде доменного
имени сервера, его ip-адреса
или другого идентификатора

path – локальный
относительный путь к ресурсу непосредственно
на сервере.

Например: http://www.microsoft.com/msdn

Зметим, что URL
не является каким либо новым способом
адресации компьютеров в сети, это просто
удобная форма записи, обхединяющая с
себе и адрес компьютера, и адрес ресурса
на нем, и имя протокола доступа. URL
получили широкое распространение с
образованием Internet и World
Wide Web.

Протоколы передачи данных.

При передаче данных будет задействовано
несколько протоколов разного уровня.
Например, при передаче HTTP-запроса,
будет использоваться следующая схема.

Это означает, что HTTP-пакет
будет передаваться внутри TCP
–пакета, или нескольких TCP-пакетов,
если HTTP-пакет не уберется
в один пакет TCP. TCP
пакеты, в свою очередь будет передавать
их внутри IP-пакетов, а IP
– внутри пакетов Ethernet.

Не надо думать, что все эти вложения
будут упакованы в один гигантский
Ethernet-пакет. Например,
максимальный размер Ethernet-пакета
равен 1522 байта (вместе со служебной
информацией), а максимальный размер
IP-пакета – 65535 байт. Поэтому
один IP-пакет будет
передаваться с помощью нескольких
Ehternet-пакетов, которые на
приемной стороне склеются и из результата
склейки можно будет извлечь IP-пакет.

Протокол Ethernet имеет свою
собственную систему адресации, эффективно
работающую внутри небольшого сегмента
сети. Ethernet не иммет
алгоритмов маршрутизации, способных
эффективно работать в глобальных сетях,
поэтому при передаче данных через
крупные и глобальные сети используется
маршрутизация на IP-уровне.
Ehternet же играет роль
канального и физического протокола,
доставляющего данные в пределах сегмента
сети.

TCP/IP

Набор протоколов TCP/IP
состоит из нескольких различных
протоколов, каждый из которых выполняет
в сети определенную задачу. Выделяют
несколько основных протоколов два: TCP,
UDP, IP, но
кроме них также существует набор из
множества дополнительных протоколов,
поддерживающих работоспособность
TCP/IP сетей.

Межсетевой протокол ip (Internet Protocol)

Информация, посылаемая по IP
– сетям, разбивается на порции, называемые
IP – пакетами, максимальной
длиной в 65535 байт. В каждом пакете прописан
IP-адрес – уникальный
идентифиатор точки назначения.

IP не устанавливает логического
соединения, т.е. не контролирует доставку
сообщений конечному пользователю.
Основной задачей IP является
адресация пакетов и их передача между
компьютерами.

Сетевое оборудование,
работающее на уровне IP
(маршрутизаторы),
отправляют пакеты машине-получателю,
при этом используются специальные
алгоритмы маршрутизации, позволяющие
пакету достичь машины с заданным адресом
за несколько «прыжков» между несколькими
маршрутизаторами.

Алгоритм передачи можно представить
следующим образом: каждый маршрутизатор
пересылает пакет либо на точку назначения
(компьютер с заданным адресом), либо на
другой маршрутизатор, который находится
ближе к точке назначения. Тот пересылает
на следующий маршрутизатор – и так
далее.

Протокол управления передачей tcp (Transmission Control Protocol)

Разбивает информацию на пакеты, собирает
их воедино в конечном пункте, производит
контроль над ошибками. Т.е. программа,
реализующая протокол ТСР на машине
получателя, собирает фрагменты в
правильном порядке и проверяет, все ли
они дошли и не испортились ли при
пересылке. Если какой-то пакет потерян
или испорчен, программа посылает запрос
машине-отправителю с просьбой выслать
недостающие пакеты повторно.

TCP устанавливает непосредственное
логическое соединение между компьютерами,
т.е. каждый из них знает о состоянии
другого. Кроме того, программа, реализующая
протокол ТСР на машине получателя,
собирает эти фрагменты в правильном
порядке и проверяет, все ли они дошли и
не испортились ли при пересылке. Если
какой-то пакет потерян или испорчен,
программа посылает запрос машине-отправителю
с просьбой выслать недостающие пакеты
повторно.

Протоколы прикладного (пользовательского) уровня.

Протоколы выполняют различные
сетевые функции. Служба доменных имен
(DNS) обеспечивает
преобразование адресов, протокол
пересылки файлов (FTP)
управляет передачей файлов, а набор
протоколов NFS обеспечивает
доступ к удаленным файловым системам

Принцип работы сетей.

FТР
— протокол передачи файлов

Протокол FТР
предусматривает, что на одной машине
запускается программа, именуемая
«FТР-сервер», а на другой
– «FТР-клиент». Клиент
посылает серверу запросы, напоминающие
команды работы с файловой структурой
ОС (каталогами и файлами DOS,
папками и документами Маc).
Сервер выполняет эти команды. Кроме
команд перехода из каталога в каталог
и просмотра содержимого каталогов можно
выполнять копирование файлов из каталога
на машине сервера в текущий каталог на
машине клиента и обратно, а также
некоторые другие файловые операции.

Набор этих операций настолько
похож на функции команд DOS
(dir, сору delete,
сd) или диспетчера файлов
Windows (а также различных
оболочек вроде Norton
Commander), что зачастую
интерфейс программ-клиентов FТР
неотличим от них (а некоторые программы
– диспетчеры файлов, такие как FAR
Евгения Рошала, позволяют одинаково
работать с каталогами и папками на своей
и удаленной машинах, не различая их).
FTP позволяет пересылать
по сети файлы любого типа : тексты,
изображения, исполняемые программы,
файлы с записями звуковых фрагментов
и т.д.

Электронная почта (e-mail)

Протокол SMTP (Simple Mail Transfer Protocol)

Электронная почта была одним
из первых видов сетевого сервиса,
разработанных в INTERNET.
Электронная почта предусматривает
передачу сообщений от одного пользователя,
имеющего определенный компьютерный
адрес, к другому. Она позволяет людям,
находящимся на больших расстояниях,
быстро связываться друг с другом.

Ее обеспечением в Internet
занимаются специальные почтовые
серверы. Почтовые
серверы получают сообщения от клиентов
и пересылают их по цепочке почтовым
серверам адресатов, где эти сообщения
накапливаются. При установлении
соединения между адресатом и его почтовым
сервером происходит передача поступивших
сообщений на компьютер адресата.

Почтовая служба основана на
прикладных протоколах: SMTP,
IMAP, POP3 и др.
Электронное письмо устроено так же, как
обычное: текст «вложен» в «конверт», в
специальных местах которого указаны
адрес получателя и адрес отправителя
(в качестве адресов используются
lniernet-адреса машин и
системные имена пользователей).

Как и при использовании
обычной почты, в «почтовый конверт»
могут быть вложены не только письма в
строгом смысле слова, но и другие объекты
– файлы, при этом используется
дополнительный формат MIME,
кодирующий содержимое файла, что зачастую
приводит к увеличению его размера.
Кодирование нужно для того. Чтобы
избежать повреждения данных во время
передачи письма по сети, т.к. некоторые
почтовые серверы могут искажать отдельные
коды символов.

Http — протокол пересылки гипертекста

Hypertext Transfer
Protocol (HTTP,
протокол пересылки гипертекста) – это
правила, которыми клиенты и серверы
WWW пользуются для общения
между собой.

Документы, расположенные на
web-серверах, представляют
собой текстовые документы, содержащие
команды специального языка, названного
HTML (Hyper
Text Markup
Lanquaqe, язык разметки
гипертекста). Команды HTML
позволяют структурировать документ,
выделяя в нем логически различающиеся
части текста.

Протокол HTTP
обеспечивает передачу требуемого
HTML-документа на основании
запроса от клиентского компьютера, или
посылку некоторых данных от клиента
серверу в составе запроса. Также HTTP
осуществляет ряд других вспомогательных
действий.

Протокол передачи сетевых новостей

NNTP(Network
News Transfer Protocol)

Служба телеконференций —
прообраз современных WWW-конференций,
работающая по распределенному принципу.
Она состоит из набора News-серверов,
принимающих сообщения (в формате,
напоминающем электронные письма) и
распространяющих сообщения к другим
серверам, а через них – клиентам.
Телеконференциями, или группами новостей,
называются тематические группы, на
которые делятся статьи на сервере
новостей.

В настоящее время система телекоференций
практически вытеснена тематическими
форумами и социальными сетями.

Протокол Telnet.

Tеlnet – представляет
собой средство (протокол), позволяющее
двум компьютерам соединяться по сети
и обмениваться информацией. Посылая
команды со своего компьютера, можно
выполнять их на удаленном компьютере
и видеть на своем дисплее результаты
их выполнения.

Протокол Telnet
определяет такой способ передачи
информации, при котором машина-клиент
делается терминалом машины-сервера
(иными словами, программа, запущенная
на сервере, получает на вход команды,
введенные с удаленного терминала и
переданные по сети, а выходные данные
с программы, работающей на сервере
передаются по сети и выводятся на
удаленном терминале).

Терминал –
это устройство ввода-вывода информации.
Например, монитор и клавиатура ПК вместе
образуют его терминал. В настоящее время
под терминалом в основном подразумевается
некоторая клиентская программа,
запущенная на удаленном компьютере и
перенаправляющая потоки ввода/вывода
удаленному серверу.

2. Виды трансляторов программ. Стадии трансляции программы на языке “c”.

Программа

– алгоритм,
записанный на языке программирования
+ структура данных, с которыми работает
программа. Этапы существования ПО (не
жизненный цикл программы): подвергается
трансляции
– процедура
перевода с языка высокого уровня на
машинный язык. В ходе трансляции может
использоваться переход на промежуточный
язык – кросстрансляции, в качестве
промежуточного языка может использоваться
язык ассемблера. Ассемблер
– программа, осуществляющая перевод с
языка ассемблера на машинный язык.
Машинный
язык
– язык, использующий машинные команды,
записанные в формате воспринимаемом
конкретным вычислительным устройством.
Транслятор
– программа, выполняющая процедуру
трансляции. Существует 2 вида: компилятор
и интерпретатор.

Компилятор

– осуществляет перевод текста программы
на машинный язык целиком. Результат
работы – объектный файл, содержащий
программу на машинном языке и информацию
о данных, используемых программой.
Объектный файл обрабатывается
компоновщиком (линкером) или редактором
связи. Компоновщик обрабатывает
объектные файлы, разрешает внешние
ссылки (делает доступным вызовы объектов
функций или данных из других объектных
файлов или стандартных библиотек),
осуществляет необходимую подготовительную
работу для последующей загрузки программы
на исполнение. Загрузчик программ,
осуществляющих размещение исполняемого
кода и данных в памяти ЭВМ и передающий
управление первой исполняемой команде
программы. В случае персональных ЭВМ
функции загрузчика распределены между
ОС и кодом, включаемым в исполняемый
файл. Исполнение программы начинается
с загрузки в регистр счетчика исполняемых
команд ЦП, адреса первой исполняемой
команды программы. Устройство управления
считывает по этому адресу код команды,
в соответствии с ним считывает значения
операндов, передает код и операнды АЛУ,
которое выполняет необходимые операции.
По завершению выполнения команды
значение регистра счетчика команд
увеличивается на значение длины команды,
которая известна по коду операции.
Процедура повторяется до тех пор, пока
не будет встречена команда stop. Исполняемая
программа обычно завершается возвратом
управления программе, вызвавшей данную
программу (ОС).

Интерпретатор
– покомандно или построчно считывает
программу на исходном языке, переводит
на машинный язык и отправляет на
выполнение. Входом является программа
на языке программирования. Результат
– построчно выполняемая команда.

Компилятор
языка С воспринимает исходный файл,
содержащий программу на языке С, как
последовательность текстовых строк.
Каждая строка завершена символом новой
строки.
Этот символ вставляется текстовым
редактором при нажатии клавиши ENTER

(ВВОД).

Общая
архитектура локальной сети (с подключением
в глобальную сеть). Понятие шлюза.
Система DNS.
«Проблема последней
мили» и варианты
ее решения.

Решение
проблемы «последней мили» для Интернет
Провайдеров

Уровень
развития Интернета в каждой стране
тесно связан с общим уровнем развития
инфраструктуры телекоммуникаций и
компьютеризации. Неудивительно, что
на сегодняшний день наиболее развитой
страной в этом смысле являются США.
Более 65% американцев старше 12 лет имеют
доступ к Интернету, а половина из них
проводит в Сети не менее часа каждый
день.

В
Европе количество пользователей
составляет 34%, однако к 2004 г. эта цифра
составит уже 79%. По числу пользователей
лидирует Англия, имеющая 6,4 млн. семей,
подключенных к Интернету, что составляет
около 27% населения страны. На втором
месте находится Германия с 7,1 млн. семей
(20,7% населения), а на третьем – Франция,
где подключены около 3 млн. семей (12,1%
населения).

Активно
развивается также азиатский рынок
Интернета. В частности, число пользователей
Сети в Японии уже в 2000 г. насчитывало
более 27 млн. По мнению аналитиков, в 2005
г. их количество достигнет 76 млн. человек.
К Сети подключено около 78% японских
предприятий. Широкое распространение
получил Интернет в Гонконге, где им
пользуются более 1,8 млн. человек, что
составляет 37% населения от 12 до 60 лет.
Около 6-10 млн. пользователей Сети живут
в Китае, а к 2003 г. их количество составит
около 21 млн. человек. К 2003 году существенно
увеличится и армия индийских пользователей,
достигнув численности в 9 млн. человек.
Годовые темпы роста числа пользователей
в Китае и Индии превышают 100% в год. Что
касается Молдовы, по некоторым оценкам,
аудитория Интернета в нашей стране
составляет 50.000 человек. К 2004 г. ожидается
увеличение числа постоянных пользователей
до 60.000 человек. Одна из причин сравнительно
медленного развития частного сектора
в молдавской Сети состоит в низком
уровне жизни и, соответственно,
телефонизации. Тем не менее, Интернет
в наши дни – это целая индустрия, быстро
проникающая во все области человеческой
деятельности. Именно сейчас эта индустрия
находится в стадии стремительного
роста, который сохранится в ближайшие
несколько лет. Огромное количество
компаний во всем мире видят в Интернете
большой коммерческий потенциал и
планируют с его помощью перевести свой
бизнес на качественно новый уровень.
Данный факт не может обойти и нашу
страну. Как уже отмечалось выше, рынок
телекоммуникаций в Молдове развивается
достаточно быстрыми темпами. Растет
как количество пользователей Интернета,
так и количество Провайдеров, которые
в принципе предлагают пользователям
достаточно широкий спектр услуг, с точки
зрения соотношения цена-качество.
Наибольший процент пользователей
выходят в сеть через dial-up. Но с развитием
экономики, увеличением уровня жизни в
Молдове, dial-up доступ не может более
удовлетворять возрастающим запросам
потребителей. Данный фактор способствует
развитию спектра услуг постоянного
доступа в Интернет, через выделенные
линии. Таким образом, главная задача
операторов Интернета состоит в соединении
своего узла с сервером конечного
пользователя и обеспечения высокоскоростного
доступа в Интернет, с перспективой
увеличения канала доступа. Для удобства,
данную проблему назвали «проблемой
последней мили». С целью ее решения,
разработано множество технологий и,
соответственно, оборудования, каждая
из которых имеет свои преимущества и
недостатки. Размер вложений в развитие
сети Интернет оператора ограничен
минимальными суммами (порядка нескольких
тысяч долларов), а потребитель не готов
оплачивать высокоскоростной доступ в
Интернет. Наряду с этими проблемами,
позволю себе отметить критичную позицию
правительства и отсутствие соответствующей
законодательной базы, а также сложные
отношения единственного оператора
телефонной связи с операторами Интернет,
то, что не может не отражаться на качестве
и цене для конечного пользователя.
Исходя из вышесказанного, проблема
«последней мили» особенно актуальна в
нашей стране.

В данной работе представлены различные
варианты решения проблемы «последней
мили», их экономическая целесообразность,
а также рассмотрены примеры решения
данной проблемы Интернет операторами
Молдовы.

Проблема
«последней мили» и FMC Александр
Гургенидзе

С появлением NGN-решений
операторского класса для современной
информационно-телекоммуникационной
инфраструктуры завершается переход
на новую парадигму формирования среды
доставки информационных потоков – к
универсальной среде пакетной коммутации,
способной обеспечить однородное
информационное пространство. При этом
прослеживается тенденция повышения
спроса на универсальные услуги,
доступные через любые терминалы
абонента. Непрерывно растет спрос на
информационную мобильность, так как
это несет новое качество жизни,
удовлетворяет потребность абонента
своевременно отреагировать на любое
важное для него событие, независимо
от того, в какой точке земного шара он
находится в данный момент.

Готовы
ли современные технологии удовлетворить
этот спрос? Чтобы ответить на данный
вопрос, необходимо провести сравнительный
анализ существующих решений
широкополосного абонентского доступа.

С
овременная
среда пакетной коммутации обладает
достаточным для предоставления любого
типа услуг набором инструментов для
структурирования и окраски трафика,
управления качеством обслуживания и
балансировкой нагрузки, а также для
создания различных комплексов
персонифицированных услуг практически
для каждого абонента. Таким образом,
с точки зрения абонента, на логическом
уровне вся телекоммуникационная
инфраструктура в ближайшем будущем
станет однородной средой пакетной
коммутации. Различия могут сохраниться
лишь на физическом уровне.

Наиболее
кардинальные изменения претерпевает
инфраструктура фиксированного
абонентского доступа. Требования
широкополосности применительно к
услугам Triple Play заставляют операторов
отказаться от промежуточных решений
на основе xDSL, имеющих существенные
ограничения, и сосредоточиться на
технологиях FTTx и EoF, которые требуют
иной топологии в иерархии абонентского
доступа, то есть выноса узлов абонентского
доступа или даже агрегирования трафика
непосредственно в жилые и промышленные
здания.

Оптика
до квартиры – пока неоправданная
роскошь, поэтому зоны покрытия как
проводных, так и беспроводных технологий
абонентского доступа соизмеримы.
Различия лежат лишь в масштабируемости
узлов и физических средах доставки
сигнала и разграничения доступа. Что
же касается мобильности, то абонент
фиксированной связи, имеющий несколько
точек подключения в фиксированную
сеть, уже сегодня может сконфигурировать
их как единый логический адрес доступа.
Эта логическая точка доступа будет
контекстуально связана с активируемым
в каждый конкретный момент портом,
что обеспечит такому абоненту
ограниченную мобильность, то есть
независимость от конкретного места
подключения.

Комбинация
проводных и беспроводных технологий
позволяет сформировать конвергентное
решение, в котором беспроводной узел
абонентского доступа может выступать
в роли агрегирующего терминала
фиксированной связи. В качестве такого
терминала беспроводного абонентского
доступа могут использоваться хот-споты
Wi-Fi. Однако ограничения стандарта IEEE
802.11 дистанцией 300 м требуют для
однородности покрытия зоны обслуживания
слишком много точек доступа. Они
накладывают дополнительные требования,
связанные с мягким режимом передачи
управления от базы к базе при перемещении
абонентского терминала в пределах
зоны покрытия сети (soft-handover), а также
с авторизацией и роумингом при попадании
абонента в сети других операторов.

Подобные
решения эффективны в зонах с высокой
абонентской концентрацией: бизнес-центры,
вокзалы, аэропорты и т. п. Но если
прокладка оптических кабелей невозможна
или слишком дорога (например, в условиях
гор), а абонентская плотность слишком
мала, в такой ситуации необходима
система радиодоступа масштаба города
типа MAN, то есть технология, называемая
сегодня WiMAX и регламентируемая группой
стандартов IEEE 802.16. Последняя редакция
данного стандарта предусматривает
мобильность абонента. В частности,
система WiMAX PrimeWave 3000 компании L3
Communications уже сегодня может обеспечивать
работу терминала, движущегося со
скоростью около 50 км/ч. В условиях
отсутствия прямой видимости базовая
станция системы имеет зону покрытия
12 км, а прямой видимости – 30 км. Эту
систему можно смело отнести к решению
операторского класса, так как она
имеет развитые средства повышения
эффективности сети доступа.

Физика
передачи данных:

— модуляция
OFDM;

— технология MIMO;

— более
эффективное (в 10 раз по сравнению с
системами 3G) использование спектрального
ресурса.

Глобальные
компьютерные сети объединяют
компьютеры и отдельные локальные сети
различных государств, в том числе и
использующие различные протоколы
обмена. Взаимодействие между абонентами
такой сети может осуществляться
посредством любых традиционных каналов
связи (кабельных, радиорелейных,
спутниковых).

Объединение глобальных, региональных,
корпоративных и других локальных

вычислительных сетей позволяет создавать
многосетевые иерархии.

Локальные сети могут входить как
компоненты в состав региональной сети,
региональные сети – объединяться в
составе глобальной сети и, наконец,
глобальные сети могут также объединяться
между собой, образовывая сложные
структуры.

Топология локальных сетей

Топология
— это конфигурация сети, способ соединения
элементов сети (то есть компьютеров)
друг с другом. Топология крупных сетей
может быть довольно сложной. В случае
небольших локальных сетей чаще всего
встречаются три способа объединения
компьютеров в локальную сеть: «звезда»,
«общая шина» и «кольцо».

Соединение типа «звезда».

Каждый компьютер через специальный
сетевой адаптер подключается отдельным
кабелем к объединяющему устройству.
При необходимости можно объединить
вместе несколько сетей с топологией
«звезда», при этом конфигурация
сети получается разветвленной.

Достоинства:
При соединении типа «звезда» легко
искать неисправность в сети.

Недостатки:
Соединение не всегда надежно, поскольку
выход из строя центрального узла может
привести к остановке сети.

Соединение «общая шина».

Все компьютеры сети подключаются к
одному кабелю; этот кабель используется
совместно всеми рабочими станциями по
очереди. При таком типе соединения все
сообщения, посылаемые каждым отдельным
компьютером, принимаются всеми остальными
компьютерами в сети.

Достоинства: в топологии «общая шина»
выход из строя отдельных компьютеров
не приводит всю сеть к остановке.

Недостатки: несколько труднее найти
неисправность в кабеле и при обрыве
кабеля (единого для всей сети) нарушается
работа всей сети.

Соединение типа «кольцо».

Данные передаются от одного компьютера
к другому; при этом если один компьютер
получает данные, предназначенные для
другого компьютера, то он передает их
дальше (по кольцу).

Достоинства: балансировка нагрузки,
возможность и удобство прокладки кабеля.

Недостатки: физические ограничения на
общую протяженность сети.

Если сеть достаточно крупная,
то в нем может быть применена схема
«снежинка» (иерархическая схема),
которая по сути представляет объединение
нескольких LAN в более
крупную сеть на основе иерархического
принципа.

Для того, чтобы объединить
эти сети в сеть Internet стали
использовать специальные средства,
называемые шлюзами (gateway).
Изначально шлюзы
– это совокупность аппаратно-программных
средств, служащих для преобразования
протоколов. Например, это может быть
специальный компьютер или дополнительная
компьютерная программа.

Каждое слово уровень в этой системе
называется доменом. Полное доменное
имя должно быть уникальным.

.gov
— государственные учереждения,

.mil
— военные учереждения,

.com
— коммерческие организации,

.net
— поставщики сетевых услуг,

.org
— безприбыльные организации,

.edu
— учебные заведения;

2. Локальные и глобальные переменные. Объявление и использование глобальных переменных в программах с несколькими модулями. Инициализация глобальных переменных.

В
зависимости от места объявления
переменной, они делятся на:

Глобальные
(внешние) – переменные,
объявленные вне функций в начале модуля.
Такие переменные существуют на протяжении
всей работы программы (т.е. создаются
в самом её начале, а уничтожатся в момент
окончания работы программы). Областью
действия таких переменных является
весь модуль (т.е. с ними можно работать
из любой функции этого модуля). Она
может быть расширена и на другие модули
с помощью спецификатора extern.
Локальные
– переменные, объявленные
внутри функции, в самом её начале. Время
жизни таких переменных зависит от
использованного спецификатора класса
памяти, но в подавляющем большинстве
случаев локальные переменные используют
класс памяти auto, при
котором они уничтожаются по окончании
функции. Область действия локальных
переменных всегда ограничивается
функцией, где она создана (хотя здесь
есть небольшой ньюанс, связанный со
спецификатором extern).

Источник

Excel для Microsoft 365 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше

Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления. Все функции Excel можно найти на вкладке «формулы» на ленте.

Синтаксис функции Excel

В приведенном ниже примере функции ОКРУГЛ , округленной на число в ячейке A10, показан синтаксис функции.

1. Structure. Структура функции начинается со знака равенства (=), за которым следует имя функции, открывающую круглую скобку, аргументы функции, разделенные запятыми, и закрывающая круглая скобка.

2. имя функции. Чтобы просмотреть список доступных функций, щелкните ячейку и нажмите клавиши SHIFT + F3, чтобы открыть диалоговое окно Вставка функции .

3. аргументы. Аргументы могут быть числами, текстом, логическими значениями, такими как Истина или ложь, массивами, значениями ошибок, например #N/a или ссылками на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.

4. всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.

Примечание: Вам не нужно вводить функции во все прописные буквы, например = «ОКРУГЛИТЬ», так как Excel автоматически заполнит ввод имени функции после нажатия кнопки «Добавить». Если вы неправильно наводите имя функции, например = СУМА (a1: A10), а не = сумм (a1: A10), Excel вернет #NAME? Если позиция, которую вы указали, находится перед первым или после последнего элемента в поле, формула возвращает ошибку #ССЫЛКА!.
Ввод функций Excel

Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. После выбора функции в диалоговом окне Вставка функции Excel запустит мастер функций, который выведет на экран имя функции, каждый из ее аргументов, описание функции и каждый аргумент, текущий результат функции и текущий результат всей формулы.

Для упрощения создания и редактирования формул, а также для минимизации ошибок ввода и синтаксиса используйте Автозаполнение формул. После ввода знака = (знак равенства) и начальных букв функции Excel отобразит динамический раскрывающийся список допустимых функций, аргументов и имен, соответствующих этим буквам. Затем вы можете выбрать один из раскрывающегося списка, и приложение Excel введет его автоматически.
Вложение функций Excel

В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в следующей формуле используется вложенная функция СРЗНАЧ , а результат сравнивается со значением 50.

1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.

Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. иметь значение ИСТИНА либо ЛОЖЬ, вложенная функция также должна возвращать логическое значение (ИСТИНА или ЛОЖЬ). В противном случае Excel выдаст ошибку «#ЗНАЧ!».

<c0>Предельное количество уровней вложенности функций</c0>. В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, функция СРЗНАЧ и функция сумм являются функциями второго уровня, если они используются в качестве аргументов функции если. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.

Нужна дополнительная помощь?

Источник

Содержание

10 популярных статистических функций в Microsoft Excel
Статистические функции
СРЗНАЧ
СРЗНАЧЕСЛИ
МОДА.ОДН
МЕДИАНА
СТАНДОТКЛОН
НАИБОЛЬШИЙ
НАИМЕНЬШИЙ
РАНГ.СР
Статистические функции в Microsoft Excel
Использование статистических функций
СРЗНАЧ
СРЗНАЧЕСЛИ
МЕДИАНА
НАИБОЛЬШИЙ
НАИМЕНЬШИЙ
МОДА.ОДН
СТАНДОТКЛОН
СРГЕОМ
Заключение

10 популярных статистических функций в Microsoft Excel

Статистические функции

Запустить Мастер функций можно тремя способами:

Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.
Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».

При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».

Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».

Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:

СРЗНАЧ

СРЗНАЧЕСЛИ

МОДА.ОДН

МЕДИАНА

СТАНДОТКЛОН

НАИБОЛЬШИЙ

В данном случае, k — это порядковый номер величины.

НАИМЕНЬШИЙ

РАНГ.СР

Источник

Статистические функции в Microsoft Excel

Зная статистические формулы и приемы можно обработать, проанализировать и упорядочить большое количество информации. В Эксель инструменты статистики выведены в отдельную категорию функций. Давайте посмотрим, как их найти, а также, какие из них являются наиболее популярными среди пользователей.

Использование статистических функций

Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.

Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:

Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.
Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.
Используем сочетание клавиш Shift+F3.

Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.

Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.

На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.

Примечание: существует еще один способ выбора требуемой функции. Находясь во вкладке “Формулы” в блоке инструментов “Библиотека функций” щелкаем по значку “Другие функции”, затем выбираем пункт “Статистические” и, наконец, в открывшемся перечне (который можно листать вниз) – нужный оператор.

Давайте теперь рассмотрим наиболее популярные функции.

СРЗНАЧ

Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:

=СРЗНАЧ(число1;число2;…)

В качестве аргументов функции можно указать:

конкретные числа;
ссылки на ячейки, которые можно указать как вручную (напечатать с помощью клавиатуры), так и находясь в соответствующем поле щелкнуть по нужному элементу в самой таблице;
диапазон ячеек – указывается вручную или путем выделения в таблице.
переход к следующему аргументу происходит путем щелчка по соответствующему полю напротив него или просто нажатием клавиши Tab.

Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:

=МАКС(число1;число2;…)

В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.

Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:

=МИН(число1;число2;…)

Аргументы функции заполняются так же, как и для оператора МАКС.

СРЗНАЧЕСЛИ

Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:

=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)

В аргументах указываются:

Диапазон ячеек – вручную или с помощью выделения в таблице;
Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;
Диапазон_усреднения – не является обязательным аргументом для заполнения.

МЕДИАНА

Оператор находит медиану заданного диапазона значений. Синтаксис функции:

=МЕДИАНА(число1;число2;…)

В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.

НАИБОЛЬШИЙ

Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:

=НАИБОЛЬШИЙ(массив;k)

Аргумента функции два: массив и номер позиции – K.

Допустим, имеется ряд чисел 4, 6, 12, 24, 15, 9. Если мы укажем в качестве аргумента “K” число 2, результатом будет значение, равное 15, т.к. оно второе по величине в выбранном диапазоне.

НАИМЕНЬШИЙ

Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:

=НАИМЕНЬШИЙ(массив;k)

МОДА.ОДН

Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:

=МОДА.ОДН(число1;число2;…)

В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.

Для вертикальных массивов, также, используется функция МОДА.НСК.

СТАНДОТКЛОН

Функция СТАНДОТКЛОН также устарела (но ее все еще можно найти, выбрав алфавитный перечень) и теперь представлена двумя новыми:

СТАДНОТКЛОН.В – находит стандартное отклонение выборки
СТАДНОТКЛОН.Г – определяет стандартное отклонение по генеральной совопкупности

Формулы функций выглядят следующим образом:

=СТАДНОТКЛОН.В(число1;число2;…)
=СТАДНОТКЛОН.Г(число1;число2;…)

СРГЕОМ

Оператор находит среднее геометрическое значение для заданного массива или диапазона. Формула функции:

=СРГЕОМ(число1;число2;…)

Заключение

В программе Excel более 100 статистических функций. Мы лишь рассмотрели те, которые используются пользователями чаще других, а также, где их можно найти и как заполнить аргументы для получения корректного результата.

Источник

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

Статистические функции

МАКС

МИН

СРЗНАЧ

СРЗНАЧЕСЛИ

МОДА.ОДН

МЕДИАНА

СТАНДОТКЛОН

НАИБОЛЬШИЙ

НАИМЕНЬШИЙ

РАНГ.СР

Использование описательной статистики

Подключение «Пакета анализа»

Размах вариации

Вычисление коэффициента вариации

Шаг 1: расчет стандартного отклонения

Шаг 2: расчет среднего арифметического

Шаг 3: нахождение коэффициента вариации

Простая формула для расчета объема выборки

Пример расчета объема выборки

Задачи о генеральной доле

По части судить о целом

Как рассчитать объем выборки

Способ 1: применение расширенного автофильтра

Способ 2: применение формулы массива

СРЗНАЧ()

СРЗНАЧЕСЛИ()

МАКС()

МИН()

2. Выражения. Операнды и операции. Унарные и бинарные операции. Операция присваивания. Арифметические операции.

Унарные операции

К ним относят (Операции преобразования знака, Побитовые и логические операции.

Операция присваивания

Специальные формы операций присваивания

Операции обращения к компонентам объекта сложного типа.

1. Mathcad: основные принципы работы. Запись формул. Переменные, функции и их использование. Лекция маткад!!!!

2. Поразрядные (битовые) операции. Логические операции. Условная операция. Операция sizeof.

Операция определения размера

Побитовые операции

Логические бинарные операции

Особенности использования логических выражений.

1. Mathcad: Дискретные аргументы. Векторы, матрицы и операции с ними. Построение графиков функций.

Определение дискретного аргумента

Создание вектора или матрицы

Создание вектора

Операция явного преобразования типа

Приведение типов.

Автоматическое преобразование типов

Преобразование типов при присваивании

Mathcad: Символьные и численные вычисления. Задание точности численных операций. Примеры символьных и численных вычислений. (Лекция маткад, конец)

Операторы. Блок операторов. Условный оператор. Операторы циклов. Оператор возврата из функции. Операторы

Блок операторов

Оператор if-else.

If (выражение) оператор1;

Оператор return

Цикл for.

Цикл while

Цикл do…while:

1. Mathcad: решение уравнений (различные способы). Символьное решение уравнений

Пример:

Численное решение уравнений.

Множественный выбор. Операторы switch-case.

Ole и dde. Связывание и внедрение данных в документы.

Функции. Определение (описание) функции. Прототип (декларирование) функции. Параметры функции. Передача аргументов в функцию.

.5.1. Определение и вызов функций

1.5.2. Вызов функции с переменным числом параметров

1.5.3. Передача параметров функции main

Архитектура Фон Неймана. Современные способы улучшения производительности вычислительной техники. Архитектура фон Неймана.

Улучшение производительности эвм

Структура программы. Source-файлы (исходный код). Header-файлы (заголовки). Объявление переменных. Объявления функций. Объявления функций

Шины и интерфейсы: fsb, шины расширения, внешние компьютерные шины. Шины

Высокоскоростная шина процессора (fsb)

Шины расширения Зачем придумали шины расширения

Первая шина

«Шутка» от ibm

Локальная шина

Смерть eisa

Внешние компьютерные шины

1.6.4. Инициализация глобальных и локальных переменных

Класс памяти

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28