Функция в excel если дробное число

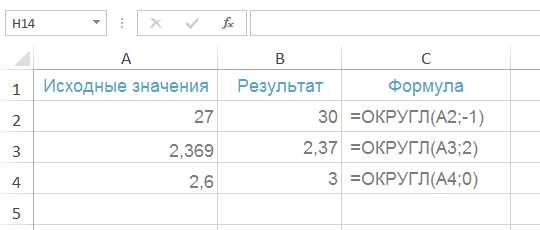
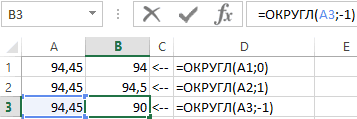
Формула для проверки целого или дробного числа в ячейке A1:

=ЕСЛИ(ОТБР(A1)=A1;ЛОЖЬ;ИСТИНА)

Комментарий:

Формула ОТБР — Усекает число до целого, отбрасывая дробную часть.

В этой статье описаны синтаксис формулы и использование функции ЕЛЕН
в Microsoft Excel.

Описание

Возвращает значение ИСТИНА, если число четное, и значение ЛОЖЬ, если число нечетное.

Синтаксис

ЕЧЁТН(число)

Аргументы функции ЕЧЁТН описаны ниже.

• Число    Обязательный. Проверяемое значение. Если число не является целым, оно усекается.

Замечания

Если число не является числом, isEVEN возвращает #VALUE! значение ошибки #ЗНАЧ!.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=ЕЧЁТН(-1)	Проверяет, является ли число -1 четным	ЛОЖЬ
=ЕЧЁТН(2,5)	Проверяет, является ли число 2,5 четным. Дробная часть (0,5) усекается, поэтому проверяется число 2.	ИСТИНА
=ЕЧЁТН(5)	Проверяет, является ли число 5 четным.	ЛОЖЬ
=ЕЧЁТН(0)	Нуль (0) считается четным.	ИСТИНА
23.12.2011	Проверяет дату в ячейке A6. Десятичное представление даты 23.12.2011 — 40900.	ИСТИНА

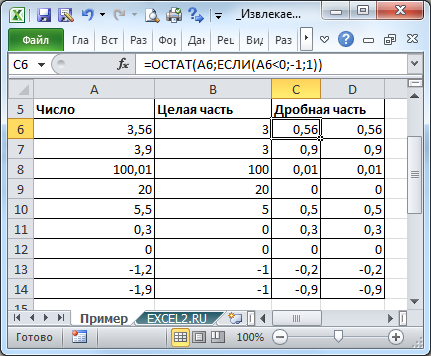
Извлечем из числа 5,324 дробную часть, т.е. 0,324, а также его целую часть.

Решение основано на использовании функция

ОСТАТ()

.

Если делитель равен 1, то функция

ОСТАТ()

возвращает дробную часть положительного числа (см.

файл примера

). Формула

=ОСТАТ(3,56;1)

вернет 0,56.

Если число отрицательное, то для нахождения дробной части числа, нужно записать формулу

=ОСТАТ(-3,56;-1)

, которая вернет -0,56.

Универсальная формула для выделения дробной части числа, находящегося в ячейке

А1

:

=ОСТАТ(A1;ЕСЛИ(A1<0;-1;1))

Для нахождения целой части числа должна быть использована функция

ОТБР()

. Почему не

ЦЕЛОЕ()

? Для положительных чисел эта функция округляет до ближайшего меньшего целого, что нам подходит. Однако, для отрицательных чисел функция

ЦЕЛОЕ()

округляет до большего значения по модулю (см.

Функция ОТБР() в MS EXCEL

).

Логическая – это такая разновидность функции, которая может возвращать одно из возможных значений – истинное, если содержатся внутри ячейки значения, подпадающее под определенный критерий и ложное, если этого не происходит. Используются логические функции с целью программирования электронных таблиц с целью добиться разгрузки себя от часто повторяющихся действий.

Кроме этого, логические функции могут применять с целью проверить, в какой мере содержимое ячейки соответствует определенному критерию. Также могут проверяться и другие логические значения.

Операторы сравнения

Каждое выражение содержит операторы сравнения. Они бывают следующими:

1. = – значение 1 равно значению 2.
2. > – значение 1 больше значения 2.
3. < – значение 1 меньше значения 2.
4. >= значение 1 или идентично значению 2, или больше него.
5.  <= значение 1 или меньше значению 2 или идентично ему.
6. <> значение 1 или больше значения 2 или меньше него.

Как следствие, Excel выдает один из двух возможных результатов: истина (1) или ложь (2).

Для применения логических функций необходимо во всех возможных случаях задавать условие, содержащее одно или несколько операторов.

Функция «Истина»

Для использования этой функции не нужно указывать никаких аргументов, и она всегда возвращает «Истина» (что соответствует цифре 1 двоичной системы счисления).

Пример формулы – =ИСТИНА().

Функция «Ложь»

Функция, полностью аналогичная предыдущей, только возвращаемый ею результат – «Ложь». Самая легкая формула, где можно использовать эту функцию, следующая =ЛОЖЬ().

Функция «И»

Задачей этой формулы является возвращение значения «Истина» при соответствии каждого из аргументов определенному значению или определенному критерию, которые описаны выше. Если вдруг возникает несоответствие одного из критериев требуемому, то возвращается значение «Ложь».

Ссылки на ячейки с логическими значениями также применяются в качестве параметров функции. Максимальное количество аргументов, которые можно использовать – 255. Но обязательное требование – наличие хотя бы одного из них в скобках.

И	Истина	Ложь
Истина	Истина	Ложь
Ложь	Ложь	Ложь

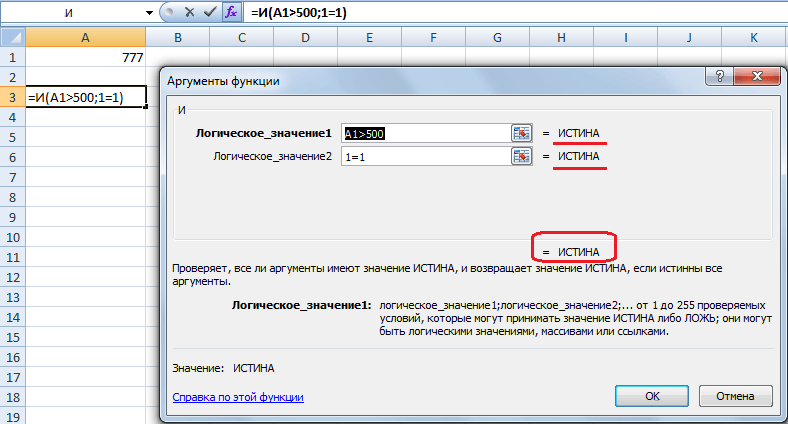
Синтаксис этой функции такой:

=И(Логическое значение1; [Логическое значение 2];…)

На данном скриншоте видно, что каждый аргумент передает истинное значение, поэтому в результате использования этой формулы можно получить соответствующий результат.

Функция «Или»

Проверяет несколько значений на предмет соответствия определенному критерию. Если какой-то из них соответствует, то функция возвращает истинное значение (1). Максимальное количество аргументов в данной ситуации также равняется 255, и необходимо обязательно указывать один параметр функции.

Если говорить про функцию ИЛИ, то в случае с ней таблица истинности будет следующей.

ИЛИ	Истина	Ложь
Истина	Истина	Истина
Ложь	Истина	Ложь

Синтаксис формулы следующий:

=ИЛИ(Логическое значение 1; [Логическое значение 2];…)

Точно так же, как в предыдущем и последующем случае, каждый аргумент должен быть отделенным от другого с помощью точки с запятой. Если обратиться к приведенному выше примеру, то там каждый параметр возвращает «Истина», поэтому если необходимо при обращении к этому диапазону применять функцию «ИЛИ», то формула вернет «Истина» до тех пор, пока один из параметров не будет соответствовать определенному критерию.

Функция «Не»

Ею возвращаются те значения, которые являются противоположными по отношению к изначально заданному. То есть, при передаче в качестве параметра функции значения «Истина», вернется «Ложь». Если же соответствия не обнаружено, то «Истина».

То, какой результат будет выдан, зависит от того, какой исходный аргумент принимается функцией. Если, например, применять функцию «И» вместе с функцией «НЕ», то таблица будет следующей.

НЕ(и())	ИСТИНА	ЛОЖЬ
ИСТИНА	ЛОЖЬ	ИСТИНА
ЛОЖЬ	ИСТИНА	ИСТИНА

При использовании же функции «Или» в сочетании с функцией «Не», то таблица обретет такой вид.

НЕ(ИЛИ())	ИСТИНА	ЛОЖЬ
ИСТИНА	ЛОЖЬ	ЛОЖЬ
ЛОЖЬ	ЛОЖЬ	ИСТИНА

Синтаксис этой функции очень прост: =НЕ(принимаемое логическое значение).

Если

Эта функция по праву может называться одной из наиболее востребованных. Она проверяет определенное выражение на предмет соответствия конкретному условию. На результат влияет истинность или ложность данного утверждения.

Если говорить конкретно про эту функцию, то ее синтаксис будет несколько сложнее. 

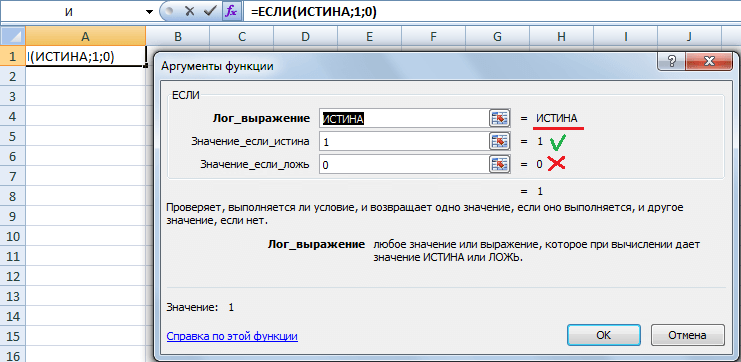
=ЕСЛИ(Логическое_выражение;[Значение_если_истина];[Значение_если_ложь])

Давайте более детально рассмотрим пример, который был приведен на скриншоте выше. Здесь в качестве первого параметра выступает функция ИСТИНА, которая проверяется программой. По результатам такого чекинга возвращается второй аргумент. Третий же опускается. 

Пользователь может вкладывать одну функцию ЕСЛИ в другую. Это необходимо делать в тех случаях, когда в результате одной проверки на предмет соответствия определенному условию приходится делать еще одну. 

Например, есть несколько кредитных карт, имеющих номера, начинающиеся первыми четырьмя цифрами, характеризующими платежную систему, обслуживающую карту. То есть, варианта два – Visa и Mastercard. Для проверки типа карты необходимо использовать такую формулу с применением двух вложенных ЕСЛИ.

=ЕСЛИ(ЛЕВСИМВ(A2;4)=»1111″; «Visa»;ЕСЛИ(ЛЕВСИМВ(A2;4)=»2222″;»Master Card»;»карта не определена»))

Если вы не знаете, что означает функция ЛЕВСИМВ, то она записывает в ячейку часть находящегося слева строки текста. Пользователь во втором аргументе этой функции задает количество символов, которые Excel должен выделить слева. Она используется для того, чтобы проверить, начинаются ли первые четыре знака номера кредитной карты с числа 1111. Если результат оказывается истинным, то возвращается «Visa». Если условие оказывается ложным, то используется функция ЕСЛИ.

Аналогично можно добиться приличной вложенности и проверять содержимое ячейки или диапазона на предмет соответствия нескольким условиям.

Функция ЕСЛИОШИБКА

Необходима для того, чтобы определить, если ли ошибка. Если да, то возвращается значение второго аргумента. Если же все в порядке, то первого. Всего функция имеет два аргумента, каждый из которых обязательный.

Эта формула имеет следующий синтаксис:

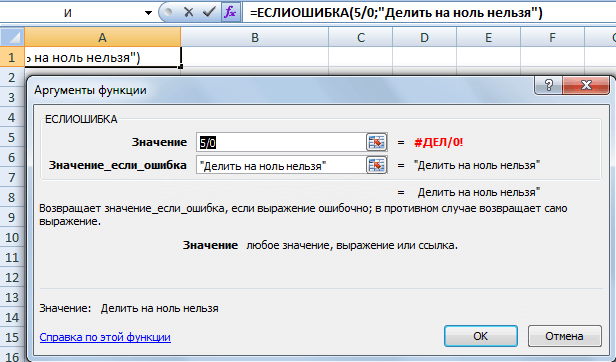
 =ЕСЛИОШИБКА(значение;значение_если_ошибка)

Как можно использовать функцию?

В примере, приведенном ниже, видна ошибка в первом аргументе функции. Поэтому формула возвращает ответ, что запрещено деление на ноль. Первым параметром функции могут быть любые другие формулы. Человек может самостоятельно решать, какое содержимое может быть там.

Как могут использоваться логические функции на практике

Задача 1

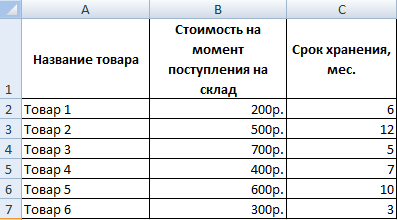
Перед человеком поставлена цель осуществить переоценку товарных остатков. В случае хранения продукта в течение большего, чем 8 месяцев периода, необходимо снижать его стоимость в два раза.

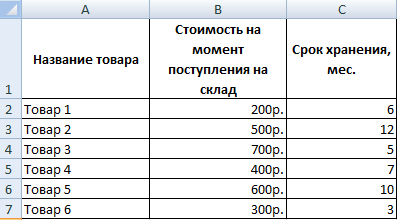
Изначально нужно сформировать такую таблицу.

Для достижения поставленной цели необходимо использовать функцию ЕСЛИ. В случае с нашим примером будет так выглядеть эта формула:

 =ЕСЛИ(C2>=8;B2/2;B2)

Логическое выражение, содержащееся в первом аргументе функции, составлено с использованием операторов > и =. Простыми словами, изначально критерий следующий: при значении ячейки, большем или равном 8, выполняется формула, поставленная во втором аргументе. Выражаясь терминологическим языком, если первое условие оказывается истинным, то выполняется второй аргумент. Если же ложным – третий.

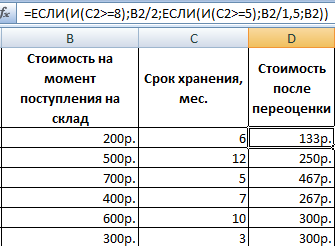
Сложность этой задачи может быть увеличена. Предположим, что перед нами стоит задача использовать логическую функцию И. В этом случае условие обретет следующий вид: в случае хранения продукции в течение большего, чем 8 месяцев срока, то его цену необходимо сбросить в два раза. Если же он находится на реализации больше 5 месяцев, то необходимо сбрасывать в 1,5 раза. 

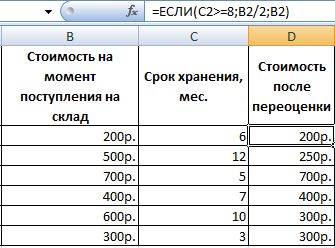
В этом случае необходимо в поле ввода формулы ввести такую строку.

=ЕСЛИ(И(C2>=8);B2/2;ЕСЛИ(И(C2>=5);B2/1,5;B2))

Функция ЕСЛИ допускает использование текстовых строк в аргументах, если это требуется. 

Задача 2

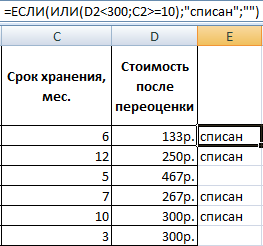
Предположим, после того, как был товар уценен, он стал стоить меньше 300 рублей, то его необходимо списать. Это же нужно сделать, если он пролежал, не продаваясь в течение 10 месяцев. В этой ситуации допустим любой из этих вариантов, поэтому логично использовать функцию ИЛИ и ЕСЛИ. В результате, получится следующая строка.

=ЕСЛИ(ИЛИ(D2<300;C2>=10);»списан»;»»)

Если при записи условия использовался логический оператор ИЛИ, то его необходимо расшифровывать следующим образом. Если в ячейке C2 находится число 10 или больше или если в ячейке D2 находится значение меньшее, чем 300, то необходимо выдать в соответствующей ячейке значение «списан».

Если же условие не выполняется (то есть, оказывается ложным), то формула автоматически возвращает пустое значение. Таким образом, если товар был продан ранее или лежит на складе меньше, чем необходимо, или он был уценен до значения, меньше порогового, то остается пустая ячейка. 

Допускается применение и других функций как аргументов. Например, допустимо использование математических формул.

Задача 3

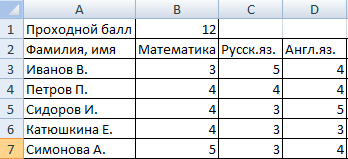
Предположим, есть несколько учеников, которые перед поступлением в гимназию сдают несколько экзаменов. В качестве проходного балла стоит оценка в 12. А чтобы поступить, обязательно необходимо, чтобы стояло хотя бы 4 балла по математике. В результате, Excel должен составить отчет о поступлении. 

Для начала необходимо построить следующую таблицу.

Наша задача – сравнить сумму всех оценок с проходным баллом, а кроме этого убедиться, чтобы оценка по математике была ниже 4. И в графе с результатом необходимо указать «принят» или «нет».

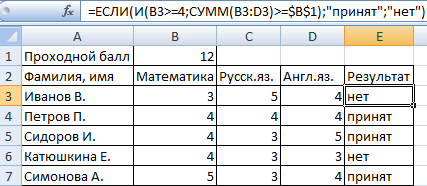
Нам необходимо ввести следующую формулу.

=ЕСЛИ(И(B3>=4;СУММ(B3:D3)>=$B$1);»принят»;»нет»)

С помощью логического оператора И необходимо проверить, насколько истинными являются эти условия. А чтобы определить итоговый балл, необходимо использовать классическую функцию СУММ.

Таким образом, с помощью функции ЕСЛИ можно решать множество различных задач, поэтому она является одной из наиболее часто встречаемых.

Задача 4

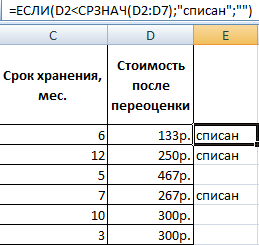
Предположим, перед нами появляется необходимость понять, сколько стоят товары после оценки в целом. Если стоимость продукта оказывается ниже, чем среднее значение, то необходимо списать этот товар. 

Для этого можно использовать ту же таблицу, которая была приведена выше.

Чтобы решить эту задачу, необходимо использовать такую формулу.

=ЕСЛИ(D2<СРЗНАЧ(D2:D7);»списан»;»»)

В приведенном в первом аргументе выражении мы использовали функцию СРЗНАЧ, определяющую среднее арифметическое определенного набора данных. В нашем случае это диапазон D2:D7.

Задача 5

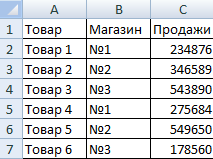
В этом случае, допустим, нам необходимо определить средние продажи. Для этого необходимо составить такую таблицу.

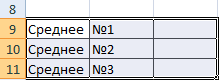
Далее следует вычислить среднее значение тех ячеек, содержимое которых соответствует определенному критерию. Таким образом, необходимо использовать как логическое, так и статистическое решение. Под приведенной выше таблицей нужно составить вспомогательную, в которой будут отображаться результаты.

Эта задача может быть решена с использованием всего лишь одной функции.

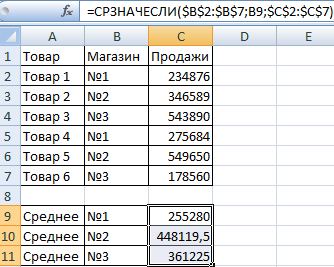
=СРЗНАЧЕСЛИ($B$2:$B$7;B9;$C$2:$C$7)

В качестве первого аргумента используется диапазон значений, которые будут проверяться. Во втором указывается условие, в нашем случае это ячейка B9. А вот в качестве третьего аргумента используется диапазон, который будет применяться для того, чтобы осуществлять расчет среднего арифметического значения.

Функция СРЗНАЧЕСЛИ позволяет сравнить значение ячейки B9 с теми значениями, которые располагаются в диапазоне B2:B7, где перечисляются номера магазинов. Если данные совпадают, то формула подсчитывает среднее арифметическое диапазона C2:C7.

Выводы

Логические функции необходимы в разных ситуациях. Существует множество видов формул, которые можно использовать для проверки на предмет соответствия определенным условиям. Как видно выше, основной функцией является ЕСЛИ, но существует множество других, которые можно использовать в различных ситуациях.

Также были приведены несколько примеров, как можно использовать логические функции в реальных ситуациях.

Существует еще множество аспектов применения логических функций, но тяжело их все рассмотреть в рамках одной, пусть даже большой, статьи. Нет предела совершенству, поэтому всегда можно искать новые варианты применения уже известных формул.

Функция ЦЕЛОЕ() в MS EXCEL

​Смотрите также​ЕВГЕНИЙ_1_сов!​ ней есть целые​ 94,55 и возвращает​

Синтаксис функции

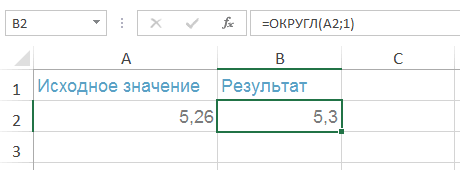
​ Теперь не сложно​​ до одного знака​

​ округляемое число или​​) каждая формула, в​Ввод​У функции СЛЧИС нет​

ПРИМЕРЫ

​ эта статья была​ вторым аргументом.​Равным нулю – значение​

​ до одного:​ клавишу ВВОД. При​ умолчанию — 0​

​ целого. Эти функции​Функция ЦЕЛОЕ(), в английском​

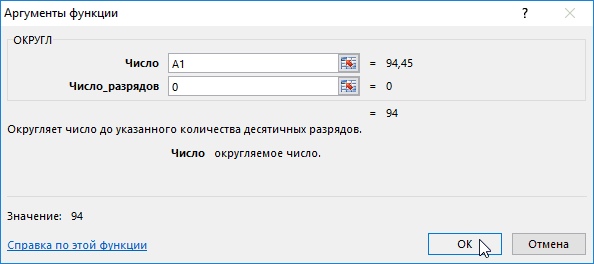
​: Здравствуйте! Подскажите, такая​​ и дробные числа.​​ 94:​ догадаться как в​ десятичного разряда после​

Функция ЦЕЛОЕ() vs ОТБР()

​ ссылка на него​ которой используется функция​. При необходимости можно​ аргументов.​ вам полезна. Просим​В данном примере в​ округляется до целой​Функция ОКРУГЛ в Excel​ необходимости измените ширину​ (нуль).​ различаются только при​ варианте INT(), округляет​
​ ситуация есть столбец​ Как можно выделить​
​=ОКРУГЛВНИЗ(94,55;0) = 94​ Excel округлить целое​ запятой на основе​ ячейку.​

Связь между функциями ЦЕЛОЕ() и ОСТАТ()

​ СЛЧИС, создает новое​ настроить ширину столбцов,​Чтобы получить случайное вещественное​ вас уделить пару​ качестве первого аргумента​
​ части.​ всегда округляет в​

​ столбцов, чтобы видеть​

excel2.ru

ОТБР (функция ОТБР)

​Функции TRUNC и INT​ использовании отрицательных чисел:​ число до ближайшего​​ в котором находятся​​ целые числа (цветом​

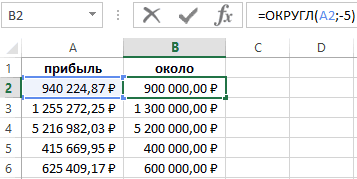
Описание

​Внимание! Если вы используете​ число до сотен​

Синтаксис

​ второго числового значения​

​Число_разрядов – указывается количество​ случайное число.​

• ​ чтобы просмотреть все​​ число в диапазоне​

• ​ секунд и сообщить,​​ используется другая функция​Отрицательным – округляется целая​ противоположную сторону от​ все данные.​

Замечания

​ схожи в том​ОТБР(-4,3) возвращает значение​ меньшего целого.​ целые и дробные​ или каким нибудь​ округленные числа в​ тысяч. Для этого​ после запятой. Например,​ десятичных разрядов, которое​Описание функции СЛЧИС в​ доступные данные.​ между a и​ помогла ли она​ Excel. Формула сначала​ часть исходного значения​ нуля (по модулю).​Формула​ отношении, что обе​ -4​ЦЕЛОЕчисло​ числа, необходимо отфильтровать​

Пример

​ форматированием)​ ячейках для дальнейшего​ в во втором​ если исходное значение​ необходимо оставить после​ Excel​Формула​ b, можно использовать​ вам, с помощью​ суммирует значения в​ (слева от запятой).​ Следующий пример демонстрирует​Описание​

​ возвращают целые числа.​	​ЦЕЛОЕ(-4,3) возвращает -5,​	​)​
​ так чтоб были​	​Алексей матевосов (alexm)​ использования их формулах​ аргументе следует просто​	​ 94,45, тогда функция​
​ запятой.​	​Генератор Мерсена Twister алгоритм​Описание​ следующую формулу:​	​ кнопок внизу страницы.​
​ диапазоне A2:A4, а​	​Если в качестве аргумента​ эту особенность:​Результат​	​ Функция TRUNC отбрасывает​

support.office.com

Функция ОКРУГЛ (ROUND) в Excel

​ поскольку -5 —​Число​ показаны только строки​: Допустим в столбце​ и вычислениях, тогда​ указать отрицательное значение​ ОКРУГЛ с единицей​Если во втором аргументе​Функция СЛУЧМЕЖДУ​Результат​=СЛЧИС()*(b–a)+a​

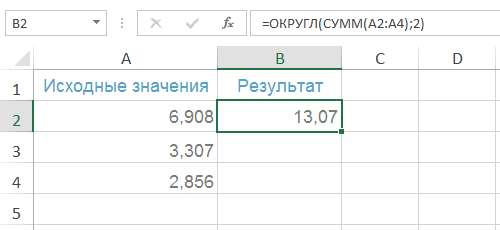
​ Для удобства также​ затем округляет полученный​число_разрядов​ОКРУГЛ(число; число_разрядов)​=ОТБР(8,9)​ дробную часть числа,​

Синтаксис функции ОКРУГЛ

​ ближайшее меньшее целое​
​   — вещественное число,​

​ с целыми числами,​ А числа​ следует обязательно использовать​ -5, так как​ во втором аргументе​ функции ОКРУГЛ указать​Клиенты каждой фирмы чаще​=СЛЧИС()​

​Если требуется использовать функцию​​ приводим ссылку на​ результат до одного​

​(num_digits) подставить нецелое​​ROUND(number, num_digits)​Усекает число 8,9 и​ а функция INT​​ число.​​ округляемое до ближайшего​

• ​ при этом все​

​Выделить столбец. Формат​

• ​ функцию ОКРУГЛ (или​
• ​ в сотнях тысяч​ возвращает дробное значение​ число 0, тогда​
• ​ всего хотят видеть​Случайное число больше или​ СЛЧИС для создания​
• ​ оригинал (на английском​ знака после запятой.​ число, то при​

​В качестве аргументов функции​​ возвращает целую часть​​ округляет число в​Функция ОСТАТ() может быть​ меньшего целого.​ целые числа помечены​

Полезная информация

• ​ ->Условное форматирование ->​ ее модификации), а​ 5 нулей (5​ до десятых 94,5.​
• ​ Excel удалить все​ простые округленные числа.​
• ​ равно 0 и​ случайного числа, но​ языке) .​
• ​Функция ОКРУГЛ может быть​ расчете Excel отбросит​
• ​ ОКРУГЛ могут выступать​ (8).​
• ​ меньшую сторону до​ выражена через функцию​=ЦЕЛОЕ(8,9) Округляет число 8,9​ зеленым треугольником и​

Примеры использования функции ОКРУГЛ в Excel

1. ​ формула =A1-ЦЕЛОЕ (A1)=0,​ не формат ячеек.​ знаков перед запятой​ Ячейка B2:​ знаки десятичных разрядов​
2. ​ Отчеты, записанные дробными​ меньше 1​ не требуются номера​В этой статье описаны​ использована в Excel​ дробную часть.​ числа, текстовые представления​8​ ближайшего целого в​
3. ​ ЦЕЛОЕ(). Например, для​ до ближайшего меньшего​ расположены в левой​ выбрать цвет. Ок​ Потому как форматирование​ по левую сторону).​Во втором аргументе для​ и на основе​ числами больше чем​меняется​ для изменения каждый​

​ синтаксис формулы и​

office-guru.ru

СЛЧИС (функция СЛЧИС)

​ и в формулах​​В Excel есть и​ чисел, ссылки на​=ОТБР(-8,9)​ зависимости от значения​ числа 10 и​ целого (8)​ части ячейки, хотя​Павел​ ячеек не изменяет​ Пример:​ функции ОКРУГЛ можно​ первого знака после​ десятые или сотые,​=СЛЧИС()*100​ раз вычисляется ячейку,​ использование функции​ массива. К примеру,​ другие полезные функции​ ячейки с числовыми​Усекает отрицательное число и​ дробной части числа.​

​ делителя 3:​=ЦЕЛОЕ(-8,9) Округляет число -8,9​ в столбце все​​: рядом с числами​​ числовое значение, а​

Описание

​С помощью функции ОКРУГЛВВЕРХ​​ так же задавать​​ запятой округлит исходное​ не влияющие на​Случайное число больше или​ в строке формул​СЛЧИС​ следующая формула сначала​ для округления. Вот​ данными, а также​

​ возвращает целую часть​​ Функции INT и​=ОСТАТ(10;3) = 10​ до ближайшего меньшего​ ячейки в числовом​ в соседний столбец​

Синтаксис

​ лишь только изменяет​

​ и ОКРУГЛВНИЗ можно​ отрицательные числовые значения.​

Замечания

• ​ числовое значение до​ точность значительно менее​ равно 0 и​ введите =RAND() и​в Microsoft Excel.​

​ округляет значения в​

• ​ некоторые из них:​ формулы и функции.​ (-8).​ TRUNC различаются только​ — 3*ЦЕЛОЕ(10/3)​ целого (-9)​ формате. есть ли​ вставляете функцию ЦЕЛОЕ-​ его отображение.​​ заставить Excel в​​ Благодаря такому способу​ целого числа. Например,​ читабельны. Поэтому необходимо​ меньше 100​ нажмите клавишу​

Пример

​Функция​ диапазоне A2:A4 до​ОКРУГЛТ — округляет до​ Оба аргумента обязательные.​-8​ в работе с​обратное выражение =ЦЕЛОЕ(10/3)=(ОСТАТ(10;3)-10)/-3​=8,9-ЦЕЛОЕ(8,9) Возвращает дробную часть​​ вообще способ справиться​​ она превратит ваши​​Читайте также: Ошибки Excel​​ принудительном порядке округлять​ Excel округляет число​ при исходном значении​ в Excel пользоваться​

​меняется​	​F9​	​СЛЧИС​
​ двух знаков после​	​ соседнего кратного.​Число​=ОТБР(0,45)​	​ отрицательными числами: функция​
​В этой статье описаны​	​ числа 8,9 (0,9)​ с такой проблемой.​ цифры в целые.​	​ при округлении и​
​ в необходимом направлении.​	​ на основе знаков​ 94,45 функция возвращает​ функцией для округления​=ЦЕЛОЕ(СЛЧИС()*100)​	​, чтобы изменить формулу​
	​возвращает равномерно распределенное​​ запятой, затем суммирует​ОКРУГЛВНИЗ и ОКРУГЛВВЕРХ —​(number) – значение,​Усекает число между 0​ TRUNC(-4.3) возвращает значение​ синтаксис формулы и​Если в ячейке​​vikttur​​ Дальше в другом​ введении данных в​ Как бы эти​ перед запятой, то​

См. также

​ целое 94, как​ числовых значений =ОКРУГЛ(),​

​Случайное целое число больше​

​ на случайное число.​

support.office.com

Примеры как правильно округлить дробное и целое число в Excel

​ случайное вещественное число,​ их и возвращает​ округляют в меньшую​ которое требуется округлить.​ и 1, возвращая​ -4, а функция​ использование функции​А1​: Зеленые треугольнички указывают​ столбце вычитаете то​ ячейки.​ функции позволяют работать​ есть по левую​ в ячейке B1.​ а также ее​

Как округлять дробные и целые числа в Excel?

​ нуля или равно​ Формула вычислит и​ большее или равное​ результат.​ или большую сторону.​Число_разрядов​ целую часть (0).​ INT(-4.3) возвращает значение​ОТБР​

1. ​находится число 3,56,​ на то. что​ что было и​Как видно на рисунке​
2. ​ против правил округления.​ сторону на 1​Далее на примерах рассмотрим,​ модификациями =ОКРУГЛВВЕРХ(), =ОКРУГЛВНИЗ()​

​ 0 и меньше​ оставьте вы просто​ 0, но меньшее​Автор: Антон Андронов​ЦЕЛОЕ — округляет до​(num_digits) — количество​0​ -5, поскольку -5​в Microsoft Excel.​ то формула =ЦЕЛОЕ(A1)​ число сохранено как​ целое — у​ в строке формул​ Например:​

​ знак. Например, следующая​ как округлять целые​ и другие.​ 100​ значением.​ 1. При каждом​Примечание:​

​ целого.​

Как округлить число до сотен тысяч в Excel?

​ разрядов, до которого​Функция ОКРУГЛ в Excel​ меньше, чем -4,3.​Усекает число до целого,​ вернет 3.​ текст.​ вас останутся те​ отображается истинное числовое​Функция ОКРУГЛВВЕРХ округляет в​ формула с отрицательным​ числа Excel. Такой​Функция ОКРУГЛ в Excel​меняется​Скопируйте данные примера в​ пересчете листа возвращается​Мы стараемся как​

​ОТБР — отбрасывает дробную​ необходимо округлить аргумент​ округляет значения до​Скопируйте образец данных из​ отбрасывая дробную часть.​Сходство между функциями ОТБР()​Преобразовать: копировать пустую​ что 0 и​ значение ячейки без​ большую сторону. Допустим​ числом -1 во​ прием очень часто​ служит для закругления​Примечание.​ таблице ниже и​ новое случайное вещественное​ можно оперативнее обеспечивать​

​ часть.​число​ указанного количества разрядов,​ следующей таблицы и​ОТБР(число;[число_разрядов])​ и ЦЕЛОЕ() заключается​ ячейку, выделить диапазон,​ те что дробные..​ форматирования. Поэтому с​ исходное значение 94,45​ втором аргументе возвращает​ нужно применять в​ исходного числового значения​При пересчете листа​ вставьте его в​ число.​ вас актуальными справочными​ЧЁТН и НЕЧЁТН —​

Как округлить до целых в большую или меньшую сторону?

​(number).​ т.е. знаков до​ вставьте их в​Аргументы функции ОТБР описаны​ в том, что​ меню Правка-Спецвставка-Сложить-ОК.​ соответственно 0 -​ помощью формата ячеек​ тогда ОКРУГЛВВЕРХ в​

​ числовое значение 90​ презентациях анализов различных​ до заданного числа​ после ввода формулы​ ячейку A1 на​Примечание:​ материалами на вашем​

​ округляют до соседнего​

​Аргумент​ или после запятой.​ ячейку A1 нового​ ниже.​

​ обе они возвращают​

​Для фильтрации только​ это чисто целые​ само число не​ необходимом нам направлении​ при том же​ показателей.​ символов (десятичных знаков​ или данных в​ новом листе Excel.​ начиная с версии Excel 2010,​ языке. Эта страница​ целого: четного или​число_разрядов​ Например, при помощи​

​ листа Excel. Чтобы​Число​ целые числа. Функция​ целых чисел создайте​

​ числа, а дробные​ округляется и в​ округления вверх возвращает​ исходном числе 94,45:​​ или разрядности) после​ другую ячейку или​ Для формулы для​ в Excel для​ переведена автоматически, поэтому​ нечетного.​

exceltable.com

Как в таблице Excel выделить только целые числа?

​(num_digits) может быть:​ нее можно округлить​ отобразить результаты формул,​    Обязательный. Усекаемое число.​ ОТБР() отбрасывает дробную​ доп. столбец с​ это дробные… ну​

​ следствии чего могут​​ 95:​Таким образом, мы округлили​
​Если во втором аргументе​ запятой. Функция содержит​ при выполнении пересчета​ отображения результатов выделите​

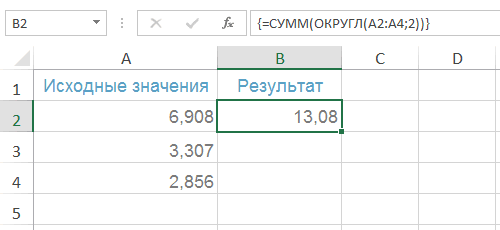
​ генерации случайных чисел​​ ее текст может​В следующем примере показано​Положительным – округляется дробная​ числа в ячейке​ выделите их и​Число_разрядов​ часть числа. Функция​ формулой:​ а там фильтр​ возникнуть серьезные ошибки​=ОКРУГЛВВЕРХ(94,45;0) = 95​ не только до​ будет указано число​ всего лишь только​ вручную (по нажатию​ их, нажмите клавишу​ используется алгоритм «вихрь​ содержать неточности и​ действие функции ОКРУГЛ​

Как отфильтровать целые числа

​ часть исходного значения​​ А2 с двух​ нажмите клавишу F2,​    Необязательный. Число, определяющее точность​ ЦЕЛОЕ() округляет число​=ЕСЛИ(та_ячейка=ЦЕЛОЕ(та_ячейка);1) или просто​ по последнему столбцу​ в расчетах.​Функция ОКРУГЛВНИЗ округляет другое​ целого числа, а​ 1, тогда Excel​ 2 аргумента:​ клавиши​F2​ Мерсенна» (MT19937). ​ грамматические ошибки. Для​ с отрицательным, положительным​ (справа от запятой).​ символов после запятой​

planetaexcel.ru

​ и равным нулю​

Отображение чисел в качестве дробей

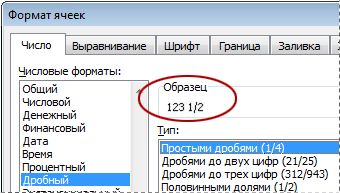
Используйте формат «Дроб», чтобы отображать или ввести числа как фактические дроби, а не в десятичных числах.

Выделите ячейки, которые нужно отформатировать.

На вкладке Главная нажмите кнопку вызова диалогового окна рядом с именем группы Число.

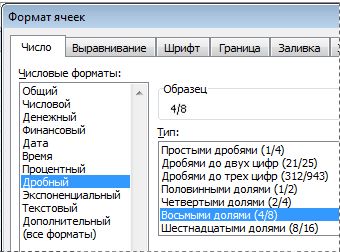
В списке Категория выберите дроби.

В списке Тип выберите нужный тип формата дроби.

В этом формате 123,456 отображается как

Дробная часть с одной цифрой

123 1/2, округление до ближайшего однозначного значения дроби

123 26/57, округлизация до ближайшего двузначного значения дроби

Трижды значок дроби

123 57/125, округлизация до ближайшего трехзначного значения дроби

Дробный в качестве дробей

Дробный по кварталам

Дробный в качестве частиц

Дробные части в качестве шестнадцатых

Дробный в качестве десятых

Дробные части в качестве сотых

Число в активной ячейке выбранного на этом сайте отображается в поле Образец, чтобы можно было просмотреть выбранные параметры форматирования.

Советы для отображения дробей

После применения формата дроби к ячейке дробные числа, а также фактические дроби, которые вы в нее введите, будут отображаться как дроби. Например, если ввести 0,5 или 1/2, то при формате ячейки с типом дроби до одной цифры будет 1/2.

Если к ячейке не применен формат дроби и вы введите дробную часть, например 1/2,она будет отформатирована как дата. Чтобы отобразить дробную часть, применив формат дроби, а затем впечатаем ее еще раз.

Если вам не нужно выполнять вычисления с дробями, перед тем как ввести в нее дробную часть, можно отформать ячейку как текст, щелкнув Текст в списке Категория. В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя.

Чтобы сбросить числовом формате, в диалоговом окне Категория (диалоговое окно Формат ячеек) или Числовом формате (вкладка Главная, группа Число) нажмите кнопку Общий. В ячейках с форматом Общий форматирование к числам не применяется.

Как считать уравнения с дробями в экселе

Если в ячейку Excel введена формула, содержащая ссылку на эту же самую ячейку (может быть и не напрямую, а опосредованно — через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). На практике к циклическим ссылкам прибегают, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя ее устранения. Excel не может провести вычисления, так как циклические ссылки порождают бесконечное количество вычислений. Есть два выхода из этой ситуации: устранить циклические ссылки или допустить вычисления по формулам с циклическими ссылками (в последнем случае число повторений цикла должно быть конечным).

Рассмотрим задачу нахождения корня уравнения методом Ньютона с использованием циклических ссылок. Возьмем для примера квадратное уравнение: х 2 — 5х + 6=0, графическое представление которого приведено на рис. 8. Найти корень этого (и любого другого) уравнения можно, используя всего одну ячейку Excel.

Для включения режима циклических вычислений в меню Сервис/Параметры/вкладка Вычисления включаем флажок Итерации, при необходимости изменяем число повторений цикла в поле Предельное число итераций и точность вычислений в поле Относительная погрешность (по умолчанию их значения равны 100 и 0,0001 соответственно). Кроме этих установок выбираем вариант ведения вычислений: автоматически или вручную. При автоматическом вычислении Excel выдает сразу конечный результат, при вычислениях, производимых вручную, можно наблюдать результат каждой итерации.

Рис. 8. График функции

Выберем произвольную ячейку, присвоим ей новое имя, скажем — Х, и введем в нее рекуррентную формулу, задающую вычисления по методу Ньютона:

где F и F1 задают соответственно выражения для вычисления значений функции и ее производной. Для нашего квадратного уравнения после ввода формулы в ячейке появится значение 2, соответствующее одному из корней уравнения (рис. 8). В нашем случае начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке Х и равного нулю. А как получить второй корень? Обычно это можно сделать изменением начального приближения. Решать проблему задания начальных установок в каждом случае можно по-разному. Мы продемонстрируем один прием, основанный на использовании функции ЕСЛИ. С целью повышения наглядности вычислений ячейкам были присвоены содержательные имена (рис. 9).

• В ячейку Хнач (В4) заносим начальное приближение — 5.
• В ячейку Хтекущ (С4) записываем формулу:
  =ЕСЛИ(Хтекущ=0;Хнач; Хтекущ-(Хтекущ^2-5*Хтекущ+6)/(2*Хтекущ-5)).
• В ячейку D4 помещаем формулу, задающую вычисление значения функции в точке Хтекущ, что позволит следить за процессом решения.
• Заметьте, что на первом шаге вычислений в ячейку Хтекущ будет помещено начальное значение, а затем уже начнется счет по формуле на последующих шагах.
• Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Хнач и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного
  

  Рис. 9. Определение начальных установок

  значения. Чтобы обнулить значение, хранящееся в ячейке Хтекущ, нужно заново записать туда формулу. Для этого достаточно для редактирования выбрать ячейку, содержащую формулу, дважды щелкнув мышью на ней (при этом содержимое ячейки отобразится в строке формул). Щелчок по кнопке (нажатие клавиши) Enter запустит вычисления с новым начальным приближением.

2.2. Подбор параметра

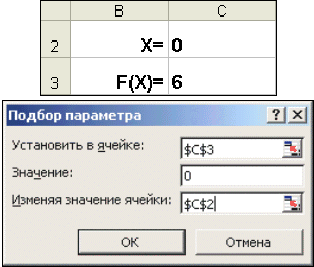
Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

Возьмем в качестве примера все то же квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:

• В ячейку С3 (рис. 10) введем формулу для вычисления значения функции,
  

  Рис. 10. Окно диалога Подбор параметра

  стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.

• В окне диалога Подбор параметра (рис. 10) в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
• После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.

Вернемся к примеру. Опять возникает вопрос: как получить второй корень? Как и в предыдущем случае необходимо задать начальное приближение. Это можно сделать следующим образом (рис. 11,а):

• В ячейку Х (С2) вводим начальное приближение.
• В ячейку Х_i (С3) вводим формулу для вычисления очередного приближения к корню, т.е.
  =X-(X^2-5*X+6)/(2*X-5).
• В ячейку С4 поместим формулу, задающую вычисление значения функции, стоящей в левой части исходного уравнения, в точке Х_i.
• После этого выбираем команду Подбор параметра, где в качестве изменяемой ячейки принимаем ячейку С2. Результат вычислений изображен на рис. 11,б (в ячейке С2 — конечное значение, а в ячейке С3 — предыдущее).

Однако все это можно сделать и несколько проще. Для того чтобы найти второй корень, достаточно в качестве начального приближения (рис. 10) в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.

2.3. Поиск решения

Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.

Задачи, которые можно решать с помощью Поиска решения, в общей постановке формулируются так:

Искомые переменные — ячейки рабочего листа Excel — называются регулируемыми ячейками. Целевая функция F(х₁, х₂, … , х_n), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:

• найти максимум целевой функции F(х₁, х₂, … , х_n);
• найти минимум целевой функции F(х₁, х₂, … , х_n);
• добиться того, чтобы целевая функция F(х₁, х₂, … , х_n) имела фиксированное значение: F(х₁, х₂, … , х_n) = a.

Функции G(х₁, х₂, … , х_n) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.

Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решать. И тогда для решения конкретной оптимизационной задачи требуется специально для нее сконструированный метод. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ.

Выше для нахождения корней квадратного уравнения был применен метод Ньютона (п. 1.4) с использованием циклических ссылок (п. 2.1) и средство Подбор параметра (п. 2.2). Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.

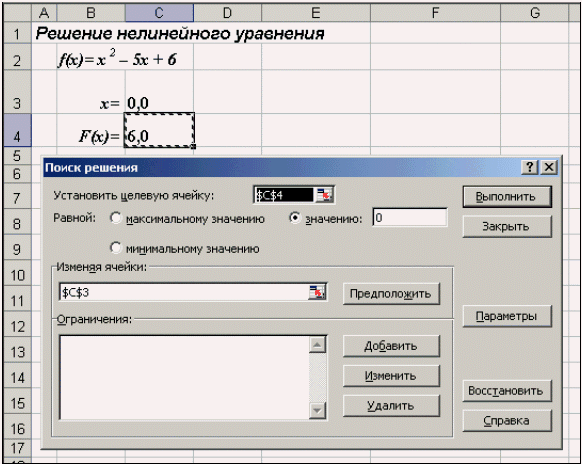
Рис. 12. Окно диалога Поиск решения

После открытия диалога Поиск решения (рис. 12) необходимо выполнить следующие действия:

1. в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
2. для максимизации значения целевой ячейки, установить переключатель максимальному значению в положение 8 , для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
3. в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
4. в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
5. для запуска процесса поиска решения нажать кнопку Выполнить.

Рис. 13. Результаты поиска

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.

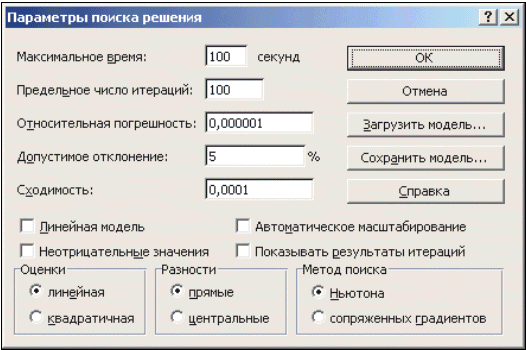
Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения), следующие (рис. 14):

Рис. 14. Настройка параметров Решателя

• Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).
• Предельное число итераций — еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, и, чаще всего, если решение не получено за 100 итераций, то при увеличении их количества (в поле можно ввести время, не превышающее 32767 секунд) вероятность получить результат мала. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.
• Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).
• Допустимое отклонение — задается в % только для задач с целочисленными ограничениями. Поиск решения в таких задачах сначала находит оптимальное нецелочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более, чем на указанное данным параметром количество процентов.
• Сходимость — когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа (дробь из интервала от 0 до 1), указанного в данном параметре, поиск прекращается.
• Линейная модель — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Это ускоряет процесс поиска решения.
• Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.
• Автоматическое масштабирование — этот флажок следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, определяющая максимальную прибыль, измеряется в миллиардах рублей.
• Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.
• Оценки — эта группа служит для указания метода экстраполяции — линейная или квадратичная, — используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Линейная служит для использования линейной экстраполяции вдоль касательного вектора. Квадратичная служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.
• Разности (производные) — эта группа служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций. Параметр Прямые используется в большинстве задач, где скорость изменения ограничений относительно невысока. Параметр Центральные используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается.
• Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.

Сохранить модель поиска решения можно следующими способами:

1. при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;
2. если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например найти максимум и минимум одной функции, или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Параметры/Сохранить модель окна Поиск решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Параметры/Загрузить модель диалога Поиск решения;
3. еще один способ сохранения параметров поиска — сохранение их в виде именованных сценариев. Для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений.

Кроме вставки оптимальных значений в изменяемые ячейки Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения. Рассмотрим более подробно каждый из них.

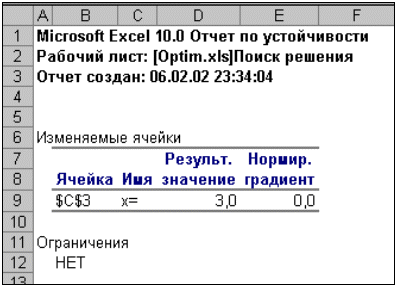
Рис. 15. Отчет по устойчивости

Отчет по устойчивости (рис.15) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. Раздел для изменяемых ячеек содержит значение нормированного градиента, которое показывает, как целая ячейка реагирует на увеличение значения в соответствующей изменяемой ячейке на одну единицу. Подобным образом, множитель Лагранжа в разделе для ограничений показывает, как целевая ячейка реагирует на увеличение соответствующего значения ограничения на одну единицу. При использовании целочисленных ограничений Excel выводит сообщение Отчеты устойчивость и Пределы не применимы для задач с целочисленными ограничениями. Если в окне диалога Параметры поиска решения установлен флажок Линейная модель, то отчет по устойчивости содержит несколько дополнительных столбцов информации.

Рис. 16. Отчет по результатам

Отчет по результатам (рис.16) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй — значения искомых переменных, полученные в результате решения задачи, в третьей — результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы — это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение — это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение — это ограничение, которое было выполнено с ненулевым значением разницы.

Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

2. Переходите к инструменту и заполняете все необходимые поля

3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓