Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
ПЛТ — одна из финансовых функций, возвращающая сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянной процентной ставки.

Воспользуйтесь средством Excel Formula Coach для расчета ежемесячных выплат по ссуде. При этом вы узнаете, как использовать функцию ПЛТ в формуле.
Синтаксис
ПЛТ(ставка; кпер; пс; [бс]; [тип])
Примечание: Более подробное описание аргументов функции ПЛТ см. в описании функции ПС.
Аргументы функции ПЛТ описаны ниже.
-
Ставка Обязательный аргумент. Процентная ставка по ссуде.
-
Кпер Обязательный аргумент. Общее число выплат по ссуде.
-
Пс Обязательный аргумент. Приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.
-
Бс Необязательный. Значение будущей стоимости, то есть желаемого остатка средств после последней выплаты. Если аргумент «бс» опущен, предполагается значение 0 (например, значение будущей стоимости для займа равно 0).
-
Тип Необязательный аргумент. Число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.
|
Тип |
Когда нужно платить |
|---|---|
|
0 или опущен |
В конце периода |
|
1 |
В начале периода |
Замечания
-
Выплаты, возвращаемые функцией ПЛТ, включают основные платежи и платежи по процентам, но не включают налогов, резервных платежей или комиссий, иногда связываемых со ссудой.
-
Убедитесь, что вы последовательны в выборе единиц измерения для задания аргументов «ставка» и «кпер». Если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12 процентов годовых, то используйте значения 12%/12 для задания аргумента «ставка» и 4*12 для задания аргумента «кпер». Если вы делаете ежегодные платежи по тому же займу, то используйте 12 процентов для задания аргумента «ставка» и 4 для задания аргумента «кпер».
Совет Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на «кпер».
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|---|---|---|
|
8 % |
Годовая процентная ставка |
|
|
10 |
Количество месяцев платежей |
|
|
10 000р. |
Сумма займа |
|
|
Формула |
Описание |
Результат |
|
=ПЛТ(A2/12;A3;A4) |
Ежемесячный платеж по займу в соответствии с условиями, указанными в качестве аргументов в диапазоне A2:A4. |
(1 037,03р.) |
|
=ПЛТ(A2/12;A3;A4;;1) |
Ежемесячный платеж по займу в соответствии с условиями, указанными в качестве аргументов в диапазоне A2:A4, за исключением платежей, подлежащих оплате в начале периода. |
(1 030,16р.) |
|
Данные |
Описание |
|
|
6 % |
Годовая процентная ставка |
|
|
18 |
Количество месяцев платежей |
|
|
50 000р. |
Сумма займа |
|
|
Формула |
Описание |
Оперативный результат |
|
ПЛТ(A9/12;A10*12; 0;A11) |
Необходимая сумма ежемесячных платежей для выплаты 50 000р. за 18 лет. |
(129,08 ₽) |
Нужна дополнительная помощь?
Функция ПЛТ в Excel используется для расчета фиксированного значения суммы периодических взносов для выплат задолженностей при условии, что процентная ставка является постоянной величиной, и возвращает соответствующее значение.
Примеры использования функции ПЛТ в Excel
С помощью функции ПЛТ можно рассчитать фиксированную сумму ежемесячного платежа по кредиту в банке, если известны тело кредита, значение годовой процентной ставки и число периодов выплат (либо срок действия договора кредитования). Также функция удобна для расчета суммы ежемесячных выплат по депозитам с дополнительными взносами.
Расчет ежемесячного платежа по кредиту в Excel
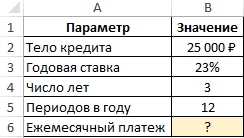
Пример 1. Определить размер ежемесячного платежа по кредиту с процентной ставкой 23% на сумму 25000 рублей, который должен быть выплачен на протяжении 3 лет.
Вид таблицы данных:
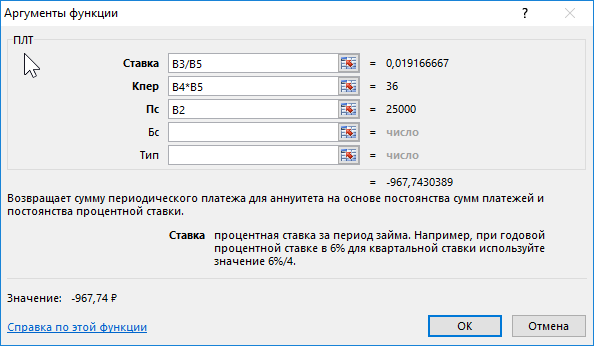
Для получения искомого значения введем следующую формулу:
Описание аргументов:
- B3/B5 – процентная ставка, приведенная к числу периодов выплат в году;
- B4*B5 – число периодов выплат на протяжении действия кредитного договора;
- B2 – начальная стоимость кредита (тело кредита).
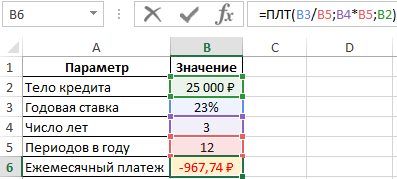
Результат выполнения формулы:
Полученное значение является отрицательным числом, поскольку ежемесячные платежи по кредиту являются расходными операциями для заемщика.
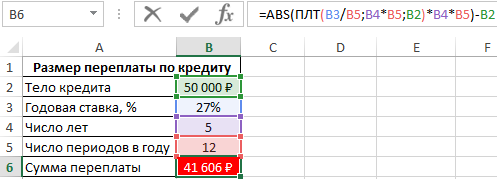
Пример расчета суммы переплаты по кредиту в Excel
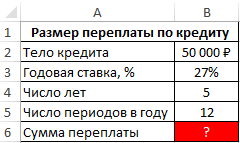
Пример 2. Определить сумму, которую переплатит заемщик, взявший кредит на сумму 50000 с годовой процентной ставкой 27% и 12 периодами выплат в год. Срок кредитования составляет 5 лет.
Вид таблицы данных:
Для расчета суммы переплат необходимо из общей суммы выплат по кредиту за период действия договора вычесть тело кредита. Для этого используем следующую формулу:
=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2
Произведение результата, возвращаемого функцией ПЛТ и количества периодов выплат (B4*B5) соответствует общей сумме выплат за 5 лет. Поскольку функция ПЛТ возвращает отрицательное значение, используем функцию ABS для получения абсолютного значения. В результате вычислений получим:
Клиент банка выплатит 50000 рублей тела кредита и еще около 42000 рублей процентов.
Формула вычисления оптимального ежемесячного платежа по кредиту в Excel
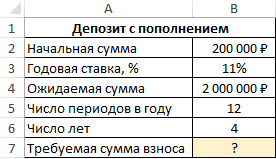
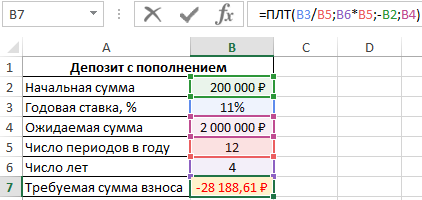
Пример 3. В банке был открыт депозитный счет с начальной суммой 200 000 рублей. Условия договора позволяют выполнять ежемесячное пополнение данного счета. Определить, какую сумму необходимо вносить ежемесячно, чтобы спустя 4 года получить 2000000 рублей. Процентная ставка составляет 11% годовых.
Вид таблицы данных:
Искомое значение может быть определено с помощью следующей формулы:
=ПЛТ(B3/B5;B6*B5;-B2;B4)
Примечание: для получения корректного результата аргумент пс должен принимать отрицательное значение суммы первоначального взноса.
В результате расчетов получим следующее значение:
Для накопления 2 млн. рублей клиенту банка потребуется ежемесячно вносить на депозитный счет примерно 28000 рублей.
Особенности использования функции ПЛТ в Excel
Функция имеет следующую синтаксическую запись:
=ПЛТ(ставка; кпер; пс; [бс]; [тип])
Описание аргументов:
- ставка – обязательный аргумент, характеризующий числовое значение годовой ставки по задолженности. Может быть указан числовым значением в виде десятичной дроби (например, 0,2 – соответствует 20% годовой ставки) или числом в процентном формате;
- кпер – обязательный аргумент, принимающий числовое значение, характеризующее число периодов выплат по задолженности. Может принимать дробные числа, не усекая дробную часть и равномерно распределяя фиксированную сумму платежей между указанным числом периодов;
- пс – обязательный аргумент, принимающий числовое значение, которое характеризует начальную стоимость финансового продукта. В случае с выдачей кредита, это значение эквивалентно телу кредита, то есть сумме средств, которую получает заемщик в кредитной организации;
- [бс] – необязательный для заполнения аргумент, принимающий числовое значение, которое характеризует оставшуюся сумму задолженности. Например, если этот аргумент явно указан, можно определить, какой должна быть сумма ежемесячного взноса, чтобы при текущей процентной ставке остаток задолженности составил указанную сумму спустя определенное число периодов выплат. Если аргумент явно не указан, он принимается равным 0 (нулю), то есть задолженность будет полностью списана.
- [тип] – необязательный для заполнения аргумент, принимающий одно из двух возможных числовых значений:
- 0 – выплаты производятся в конце периода (если явно не указан, используется по умолчанию).
- 1 – выплаты в начале периода.
Примечания:
- При расчете суммы ежемесячных выплат учитывается только значение годовой процентной ставки. В договорах некоторых финансовых организациях могут быть указаны дополнительные сборы и комиссии, влияющие на итоговый результат.
- При указании процентной ставки необходимо выполнять перерасчет в зависимости от количества периодов выплат в году. Платежи могут быть, например, ежемесячными или ежеквартальными. В первом случае аргумент ставка должен быть указан как n%/12, а во втором – n%/4, где n% — годовая процентная ставка.
- Аргумент кпер должен быть указан числом, которое получено в результате произведения количества лет, на которые выдан кредит, и количества периодов выплат в году. Например, если ипотечный кредит был выдан на 20 лет, а платежи необходимо делать ежемесячно, аргумент кпер должен быть указан как 20*12 или 240.
- Для расчета общей суммы платежей по кредиту можно умножить возвращаемый рассматриваемой функцией результат на количество периодов выплат.
Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса — другое дело, а для обычных людей мышеловка»деньги за 15 минут, нужен только паспорт» срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это «потом» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?
Так что очень надеюсь, что изложенный ниже материал вам не пригодится.
Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю 
Вариант 1. Простой кредитный калькулятор в Excel
Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial). Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:
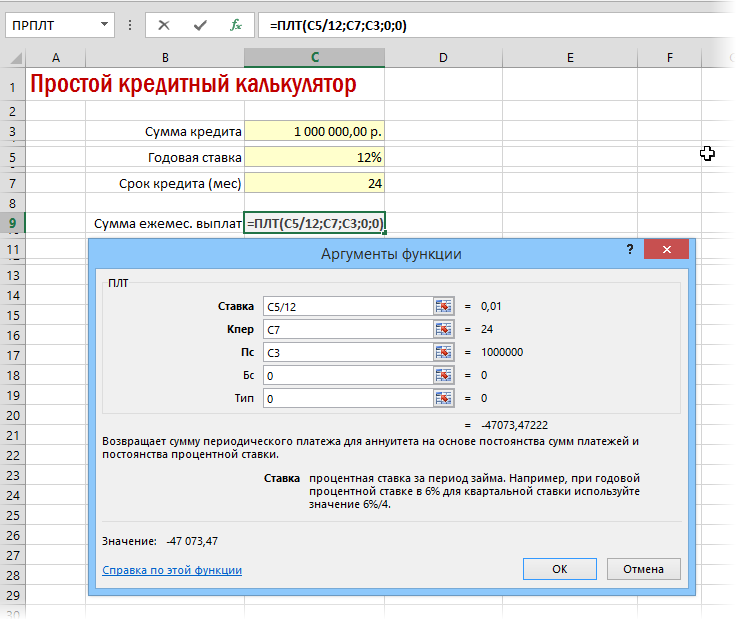
- Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
- Кпер — количество периодов, т.е. срок кредита в месяцах.
- Пс — начальный баланс, т.е. сумма кредита.
- Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
- Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0.
Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:
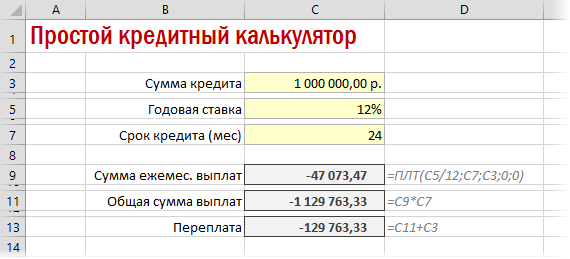
Вариант 2. Добавляем детализацию
Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT). Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):
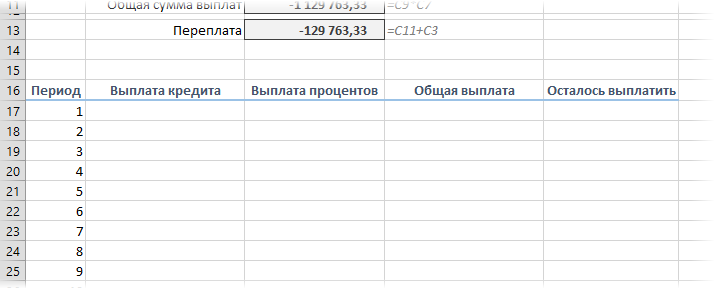
Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:
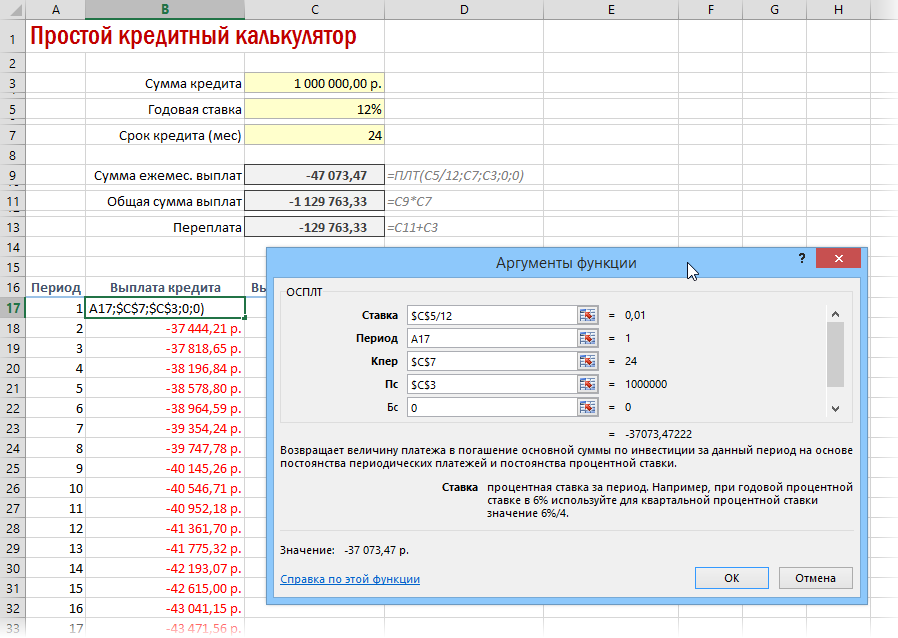
Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:
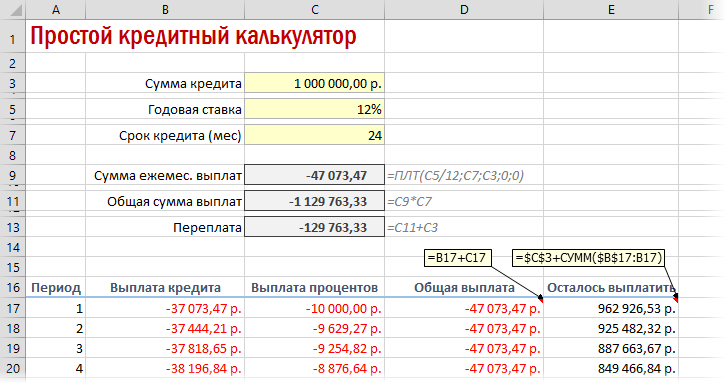
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:
=ЕСЛИ(A17>=$C$7;»»;A17+1)
Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:
=ЕСЛИ(A18<>»»; текущая формула; «»)
Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:
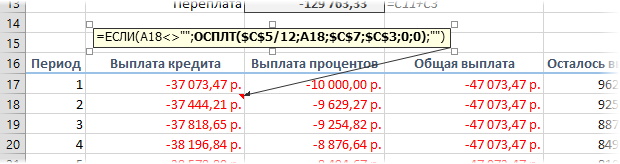
Вариант 3. Досрочное погашение с уменьшением срока или выплаты
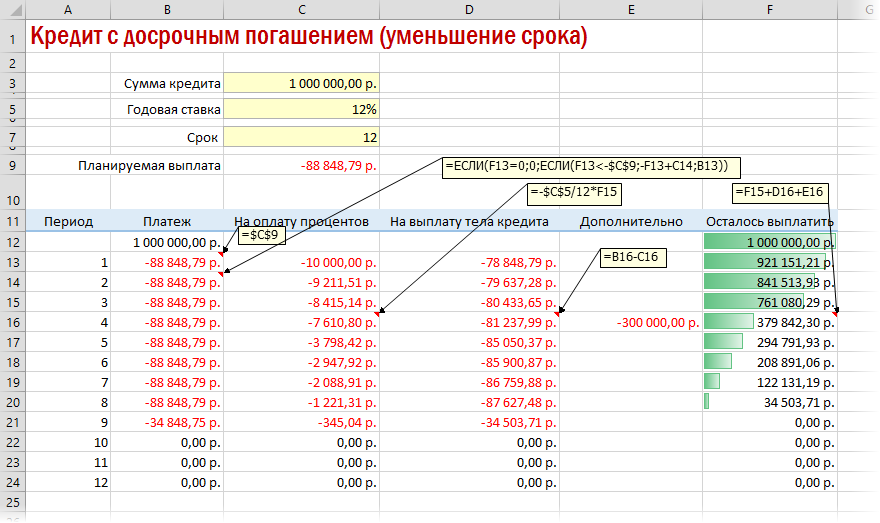
Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.
В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять — не достигли мы нулевого баланса раньше срока:
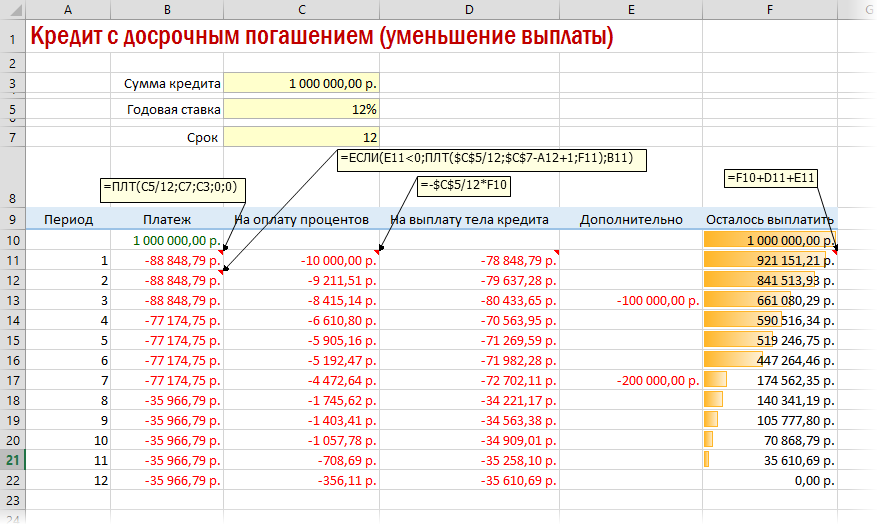
А в случае уменьшения выплаты — заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:
Вариант 4. Кредитный калькулятор с нерегулярными выплатами
Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:
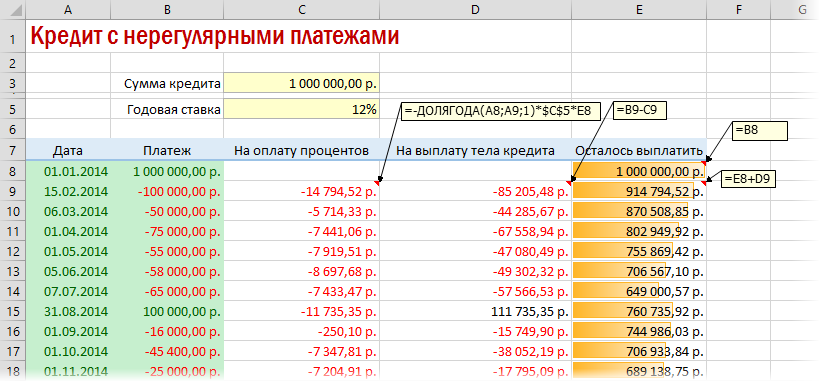
Предполагается что:
- в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
- отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
- подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)
Файлы к уроку:
- Для спонсоров Boosty
- Для спонсоров VK
- YouTube
- VK
Ссылки:
- Страница курса
- Плейлист YouTube
- Плейлист ВК
Описание
В этом уроке мы вспомним как вычислить ежемесячный платеж в Excel. Разберем 4 способа: подбор параметра, поиск решений, функция ПЛТ, формула вычисления ежемесячного платежа.
Решение
Подбор параметра
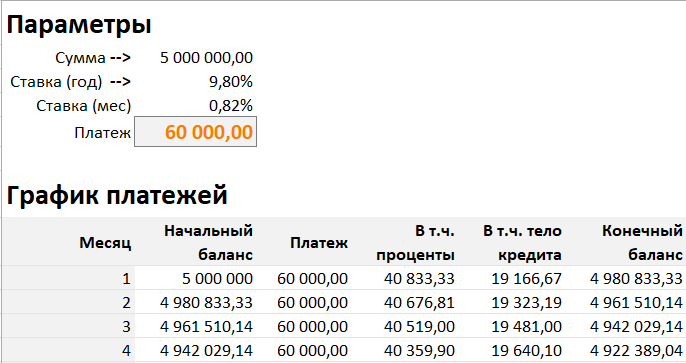
Подготовим таблицу с параметрами и таблицу с графиком платежей. В таблице с параметрами введем временно абсолютно любое число.
Запустим подбор параметра:
- Установить в ячейке — Сослаться на самый последний конечный баланс
- Значение — 0
- Изменяя значение ячейки — Платеж из таблицы с параметрами
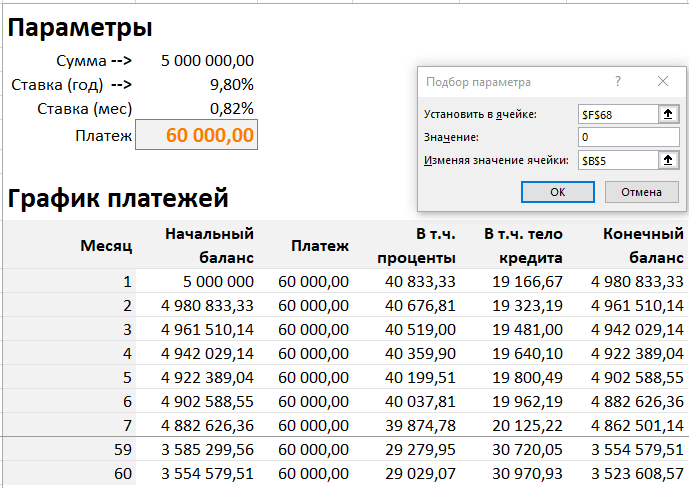
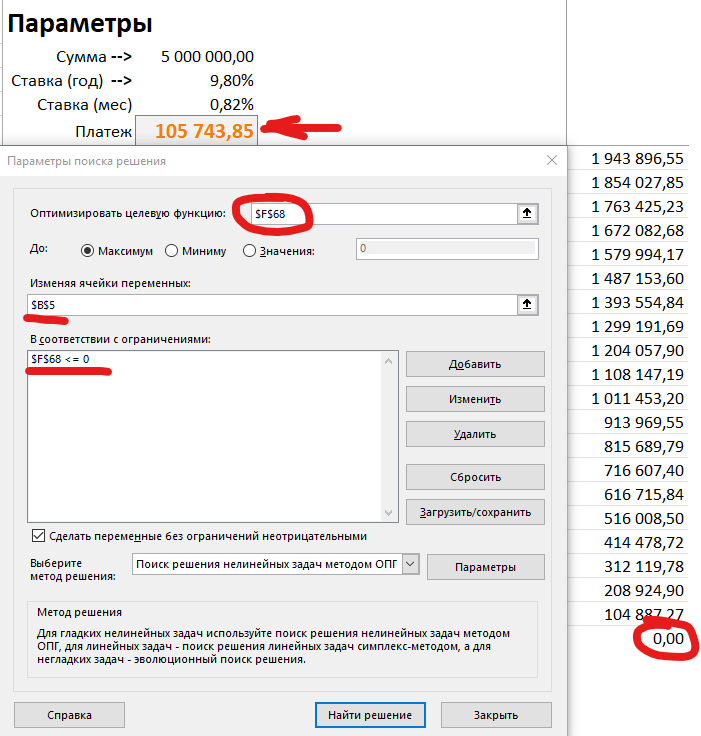
Поиск решений
Сделаем аналогичную заготовку первому способу. Запускаем поиск решений и заполняем форму следующим образом:
- Оптимизировать целевую функцию — Самый последний конечный баланс
- Изменяя ячейки переменных — Ячейка с платежом в таблице с параметрами
- Ограничения — Последний конечный баланс меньше или равен 0
Функция ПЛТ
Для удобства заготовим маленьку таблицу с параметрами.

У функции ПЛТ 3 главных параметра:
- Ежемесячная ставка
- Количество платежей (количество месяцев)
- Сумма кредита
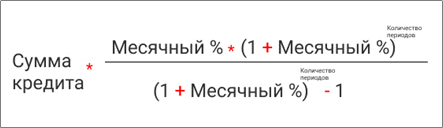
Формула вычисления ежемесячного платежа
Совсем необязательно пользоваться любыми из приведенных способов. Можно просто воспользоваться формулой для вычисления аннуитетного платежа без использования функций и другого функционала Excel.

Примененные функции
- ПЛТ
- Поиск решений
- Подбор параметра
Excel Разное
| Номер урока | Урок | Описание |
|---|---|---|
| 1 | Excel Разное. 4 способа вычислить ежемесячный платеж по кредиту (Подбор параметра, Поиск решений, ПЛТ, формула) | В этом уроке мы разберем 4 способа вычислить ежемесячный платеж по кредиту: подбор параметра, поиск решений, функция ПЛТ, формула для вычисления ежемесячного платежа. |
| 2 | Excel Разное. Суммировать несколько категорий с СУММЕСЛИМН | Разберем как с помощью одной формулы суммировать несколько категорий, используя СУММЕСЛИМН. |
Для Google Docs эти формулы тоже подходят.
1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.
Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.
Какие данные нужны
Для начала надо правильно написать формулу — в любой свободной ячейке.
=ПЛТ(ставка;кпер;пс)
В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:
- Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
- Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
- Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.
Как всё посчитать
Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.
Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.
2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
Какие данные нужны
Формула расчёта довольно простая:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
В ней всего две переменные:
- Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
- Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).
Как всё посчитать
Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:
Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.
3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.
Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.
Какие данные нужны
Формула состоит из трёх компонентов:
=ЧИСТНЗ(ставка;значения;даты)
Второй и третий достаточно ясны:
2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.
Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.
Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.
Как всё посчитать
Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.
Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.
4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.
Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.
Какие данные нужны
Чтобы определить более выгодное предложение, применим формулу:
=ЧИСТВНДОХ(значения;даты)
Достаточно знать всего две переменные:
- Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
- Даты — график платежей, по которым будут выплачивать прибыль.
Как всё посчитать
Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.
5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.
Какие данные нужны
Полезной будет эта формула:
=СТАВКА(кпер;плт;пс)
Три переменных в ней означают следующее:
- Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
- Плт — размер платежей. Считаются и основной долг, и проценты.
- Пс — общая сумма займа. В нашем примере это 100 000 рублей.
Как всё посчитать
Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.
6. PV (ПС) — подсказывает, сколько денег можно взять в долг
Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.
Какие данные нужны
Пригодится формула расчёта текущей стоимости:
=ПС(ставка; кпер; плт)
Для этого потребуется информация, которая есть на сайте любого банка:
- Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
- Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
- Плт — размер комфортного платежа.
Как всё посчитать
Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.
Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.
7. NPER (КПЕР) — помогает рассчитать время накоплений
Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.
Какие данные нужны
Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:
=КПЕР(ставка/периоды_капитализации;плт;пс;бс)
Она состоит из четырёх основных значений и одного дополнительного:
- Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
- Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
- Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
- Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
- Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.
Как всё посчитать
Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.
Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.
Читайте также 🧐
- Как вести бюджет, если у вас непостоянный доход
- 20 полезных шаблонов «Google Таблиц» на все случаи жизни
- 10 крутых приложений, чтобы взять финансы под контроль