Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СТАВКА в Microsoft Excel.
Описание
Возвращает процентную ставку за период аннуитета. Ставка вычисляется с помощью итерации и может иметь ноль или больше решений. Если последовательные результаты rate не сходятся в пределах 0,00000001 после 20 итерации, то ставка возвращает результат #NUM! значение ошибки #ЗНАЧ!.
Синтаксис
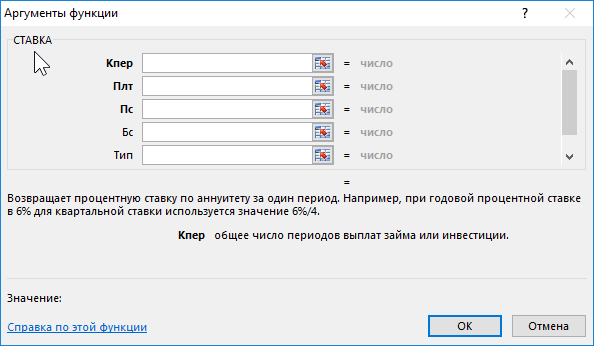
СТАВКА(кпер; плт; пс; [бс]; [тип]; [прогноз])
Примечание: Полное описание аргументов «кпер», «плт», «пс», «бс» и «тип» см. в разделе, посвященном функции ПС.
Аргументы функции СТАВКА описаны ниже.
-
Кпер — обязательный аргумент. Общее количество периодов платежей по аннуитету.
-
Плт Обязательный. Выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ежегодного платежа. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.
-
Пс — обязательный аргумент. К настоящему моменту — общая сумма, на которую сейчас стоит ряд будущих платежей.
-
Fv Необязательный. Будущая стоимость или баланс, который вы хотите достичь после последнего платежа. Если значение «ок» опущено, предполагается значение 0 (например, будущая стоимость займа — 0). Если аргумент «пс» опущен, необходимо включить аргумент «pmt».
-
Тип Необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата.
|
Тип |
Когда нужно платить |
|
0 или опущен |
В конце периода |
|
1 |
В начале периода |
-
Прогноз Необязательный. Предполагаемая величина ставки.
-
Если аргумент «прогноз» опущен, предполагается, что его значение равно 10 %.
-
Если функция СТАВКА не сходится, попробуйте изменить значение аргумента «прогноз». Функция СТАВКА обычно сходится, если значение этого аргумента находится между 0 и 1.
-
Замечания
Убедитесь, что единицы измерения, выбранные для аргументов «прогноз» и «кол_пер» соответствуют друг другу. При ежемесячных выплатах по четырехгодичному займу под 12 процентов годовых используйте значение 12%/12 для аргумента «прогноз» и 4*12 — для аргумента «кол_пер». При ежегодных платежах по тому же займу используйте значение 12% для аргумента «прогноз» и 4 —для аргумента «кол_пер».
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
4 |
Срок займа в годах |
|
|
-200 |
Ежемесячная сумма платежа |
|
|
8000 |
Сумма займа |
|
|
Формула |
Описание |
Результат |
|
=СТАВКА(A2*12; A3; A4) |
Месячная процентная ставка по займу в соответствии с условиями, указанными в диапазоне A2:A4 в качестве аргументов. |
1 % |
|
=СТАВКА(A2*12; A3; A4)*12 |
Годовая процентная ставка по займу в соответствии с теми же условиями. |
9,24 % |
Нужна дополнительная помощь?
Пусть известна сумма и срок кредита, а также величина регулярного аннуитетного платежа.
Рассчитаем в MS EXCEL под какую процентную ставку нужно взять этот кредит, чтобы полностью его погасить за заданный срок. Также в статье разберем случай накопления вклада.
Для расчета процентной ставки в аннуитетной схеме используется функция
СТАВКА()
.
Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение])
возвращает процентную ставку по аннуитету.
Примечание
.
Английский вариант функции: RATE(nper, pmt, pv, [fv], [type], [guess]), т.е. Number of Periods – число периодов.
Вот что написано на сайте MS
: Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1 (подробнее см.
обзорную статью о функциях аннуитета
).
Если постараться решить это уравнение относительно параметра Ставка, то мы получим степенное уравнение (степень уравнения и, соответственно, число его корней будет зависеть от значения Кпер). В отличие от других параметров ПЛТ, БС, ПС и Кпер, найти универсальное решение этого уравнения для всевозможных степеней невозможно, поэтому приходится использовать метод итераций (по сути,
метод подбора
). Чтобы облегчить поиск Ставки методом итераций, используется аргумент
Предположение. Предположение
— это приблизительное значение Ставки, т.е. прогноз на основании нашего знания о задаче. Если значение предположения опущено, то оно полагается равным 10 процентам. Значение
Предположение
также полезно в случае
,
если имеется несколько решений уравнения – в этом случае находится значение Ставки ближайшее к
Предположению
.
Задача1 – Выплата кредита
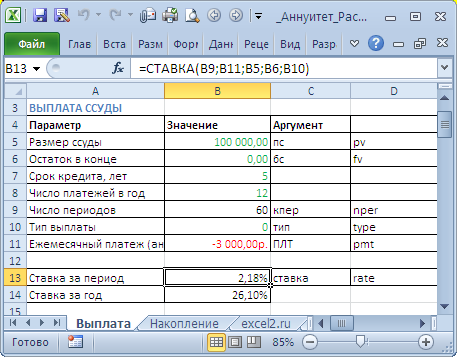
Определим под какую годовую ставку мы можем взять 100 000 руб., выплачивая ежемесячно 3000 руб. в течение 5 лет.
Примечание
. Аннуитетная схема погашения кредита подробно рассмотрена в статье
Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)
.
В условии задачи содержится следующая информация:
- Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
-
Проценты начисляются
в конце
каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0; - В конце срока задолженность должна быть равна 0 (БС=0).
В результате формула для вычисления годовой ставки будет выглядеть так
=12*СТАВКА(12*5;-3000;100000;0;0)
или
=12*СТАВКА(12*5;-3000;100000)
Знак минус у регулярного платежа показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые
банк
дал
нам, -3000 – это деньги, которые мы
возвращаем банку
. Результат вычисления = 26,10%
Формула может вернуть отрицательные значения ставки. Это происходит, когда сумма всех регулярных платежей недостаточна для погашения кредита даже при 0 ставке. Но, в нашем случае все в порядке: 60*(3000)=180000>100000. Отрицательная ставка означает, что банк выплачивает нам проценты за пользование кредитом, что является абсурдом. Это, конечно, ошибка (попробуйте например, в
файле примера на Листе Выплата
установить платеж =-1000).
Если задать платеж = 0 или того же знака, что и сумма кредита, то функция
СТАВКА()
вернет ошибку #ЧИСЛО! Это и понятно, при нулевых платежах погасить кредит невозможно.
Примечание
. С помощью
Подбора параметра
можно найти величину регулярного платежа, который бы обеспечил выплату кредита при заданной процентной ставке (обратная задача). Но, по большому счету, в этом нет необходимости – для этого существует функция
ПЛТ()
.
Задача2 – Накопление суммы вклада
Определим, с какой годовой ставкой мы можем накопить 1 000 000 руб., внося ежемесячно по 10 000 руб. в течение 5 лет. (см.
файл примера на Лист Накопление
)
Примечание
. Аннуитетная схема накопления целевой суммы подробно рассмотрена в статье
Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад
.
Формула для вычисления годовой ставки будет выглядеть так
=12*СТАВКА(12*5;-10000;0;1000000)
=19,38%
Здесь ПС=0, т.е. начальная сумма вклада =0 (
Приведенная Стоимость
). Целевой вклад = 1000000 (БС –
Будущая Стоимость
).
Если суммарное количество взносов будет > целевой стоимости (1000000), то ставка станет отрицательной, чтобы соблюсти наше требование БС=1000000.
Если задать величину пополнения = 0 или того же знака, что и целевая сумма, то функция
СТАВКА()
вернет ошибку #ЧИСЛО! Это и понятно, при нулевых взносах накопить ничего не получится. Взнос того же знака, что и целевая сумма, вероятно, означает, что банк платит нам. Но, это не возможно, т.к. начальная сумма вклада =0, поэтому выдается ошибка.
Функция СТАВКА используется для определения процентной ставки по инвестиции либо денежному займу с аннуитетной структурой графика погашения для одного периода выплат (при условии, что будущая стоимость ценных бумаг, обеспечивающих инвестицию либо кредит является известной величиной) и возвращает полученное значение.
Если при заключении сделки процентная ставка не была установлена жестко, функция СТАВКА позволяет определить размер неявной ставки (то есть такой ставки, которая обеспечила бы получение эквивалентного дохода).
Примеры финансовых расчетов по функции СТАВКА в Excel
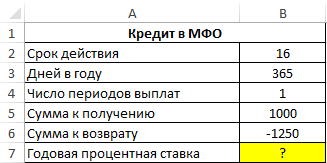
Пример 1. В МФО был взят кредит сроком на 16 дней, сумма которого составляет 1000 долларов. Сумма возврата составляет 1250 долларов. Определить годовую процентную ставку по указанным условиям займа.
Таблица данных:
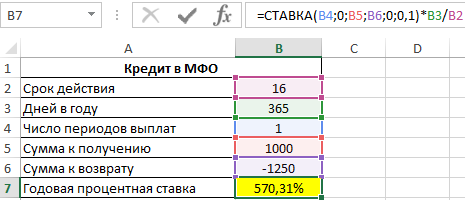
Для расчета в ячейку B7 введем следующую формулу:
=СТАВКА(B4;0;B5;B6;0;0,1)*B3/B2
Описание аргументов:
- B4 – число периодов выплат (в данном случае – 1);
- 0 – размер фиксированной выплаты (поскольку в данном примере только один период выплат, указано значение 0);
- B5 – тело кредита;
- B6 – сумма на момент погашения долга;
- 0 – характеризует тип выплат, при котором выплата производится в конце периода;
- 0,1 – предполагаемое значение процентной ставки (любое число из диапазона от 0 до 1);
- B3/2 – коэффициент для пересчета полученного значения ставки к годовой процентной ставке.
Результат вычислений:
Пи данных условиях микрокредитования сроком займа на 16 дней процентная ставка составляет 570,31% годовых! Несмотря на это, услуги по микрокредитованию сегодня продолжают набирать популярность.
Анализ пенсионных отчислений с использованием функции СТАВКА в Excel
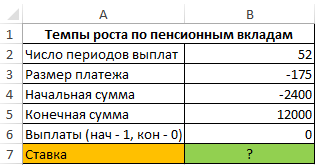
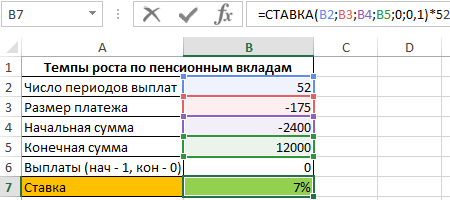
Пример 2. Определить темпы роста пенсионных отчислений (процентную ставку), если баланс средств на конец года составляет 12000 долларов, а в начале года – 2400 долларов. Еженедельные платежи на протяжении года составляли 150 долларов (то есть, количество периодов – 52).
Исходные данные:
Формула для расчета:
=СТАВКА(B2;B3;B4;B5;0;0,1)*52
Описание аргументов:
- B2 – количество периодов выплат;
- B3 – сумма платежа (расходная операция, поэтому отрицательное значение);
- B4 – сумма средств до наступления первого периода выплат;
- B5 – сумма по окончанию последнего периода выплат;
- 0 – выплаты в конце периода;
- 0,1 – произвольное значение из интервала от 0 до 1;
- 52 – количество периода выплат для пересчета размера ставки в годовых.
Результат вычислений:
То есть, пенсионные отчисления выполняются под 7% годовых.
Определение реальной процентной ставки по кредиту
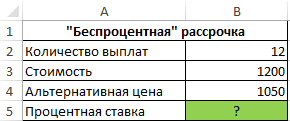
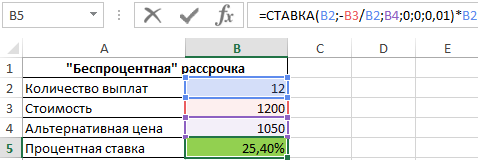
Пример 3. Ноутбук одной и той же модели можно приобрести за 1200 долларов в рассрочку (беспроцентную, судя по рекламе в первом магазине) или за 1050 долларов в другом магазине. Рассрочка выдается на 1 год с 12 периодами выплат. Определить реальный процент «беспроцентной» рассрочки платежей по кредиту.
Исходные данные:
Формула для расчета:
=СТАВКА(B2;-B3/B2;B4;0;0;0,01)*B2
Описание аргументов:
- B2 – число периодов выплат;
- -B3/B2 – выражение для расчета размера ежемесячного платежа;
- B4 – реальная стоимость ноутбука (используется как начальная стоимость финансового инструмента, цена которого повысится до 1200 к окончанию последнего периода выплат);
- 0 – остаток по окончанию последнего периода выплат;
- 0 — выплаты в конце периода;
- 0,01 — произвольное значение предполагаемой ставки.
Результат расчетов:
То есть, фактически в первом магазине клиенту предложили кредит на ноутбук под 25,4% годовых.
Функция СТАВКА в Excel и особенности ее использования
Функция СТАВКА имеет следующий синтаксис:
= СТАВКА(кпер; плт; пс; [бс]; [тип]; [прогноз])
Описание аргументов:
- кпер – обязательный аргумент, характеризующий число периодов выплат по аннуитетной схеме.
- плт – обязательный аргумент, характеризующий фиксированное значение выплаты, производимой в каждый из периодов выплат. Сумма выплаты за каждый период включает две составляющие: тело и проценты без учета прочих комиссий и сборов. Если данный аргумент опущен, следующий аргумент должен быть указан явно.
- пс – обязательный аргумент, характеризующий текущую стоимость задолженности (либо вознаграждения), эквивалентную общей сумме последующих платежей на данный момент. Если значение неизвестно, необходимо явно указать значение 0 (нуль).
- [бс] – необязательный аргумент, характеризующий размер желаемого остатка средств после выполнения последней выплаты согласно графика платежей. Если явно не указан, по умолчанию используется значение 0 (нуль), а аргумент пс становится обязательным для заполнения.
- [прогноз] – необязательный аргумент, характеризующий предполагаемый размер процентной ставки. Если аргумент явно не указан, по умолчанию принимается значение 10%. Если полученное в результате вычислений значение не сходится с указанной прогнозной величиной, величину данного аргумента следует изменить. Рекомендуется выбирать значение для аргумента [прогноз] из диапазона от 0 до 1.
- [тип] – необязательный аргумент, принимающий значения 0 или 1:
- Если введен 0, считается, что выплата производится в конце периода;
- Если введен 1, считается, что выплата производится в начале периода.
Примечания:
- Единицы измерения величин, указанных в качестве аргументов кпер и [прогноз], должны соответствовать друг другу. Например, при расчете ставки по займу, выданному на два года под 16% с ежемесячными выплатами необходимо, в качестве аргумента [прогноз] необходимо использовать значение 16%/12, а кпер – 2*12.
- Если хотя бы в качестве одного из аргументов функции было передано текстовое значение, результатом выполнения функции будет являться код ошибки #ЗНАЧ!.
- Аннуитетная схема выплаты вознаграждения либо погашения задолженности предполагает выплаты фиксированной суммы, включающей вознаграждение или тело кредита и дополнительных процентов (в зависимости от установленной процентной ставки) на протяжении установленного количества периодов выплат. В отличие от классической схемы, при которой проценты начисляются на остаток вознаграждения или задолженности, в аннуитетной схеме соотношение тело кредита/проценты является изменяющейся величиной.
- При выполнении расчетов функция СТАВКА использует итерационный метод. Если после 20 итераций последующие результаты вычислений отличаются друг от друга более, чем на 10-7, результатом вычислений будет являться код ошибки #ЗНАЧ!.
Skip to content
В этом руководстве вы познакомитесь с быстрым способом расчета процентов в Excel, найдете базовую формулу процента и еще несколько формул для расчета процентного изменения, процента от общей суммы и т.д.
Расчет процента нужен во многих ситуациях, будь то комиссия продавца, ваш подоходный налог или процентная ставка по кредиту. Допустим, вам посчастливилось получить скидку 25% на новый телевизор. Это хорошая сделка? И сколько в итоге придется заплатить?
Сейчас мы рассмотрим несколько методов, которые помогут вам эффективно вычислять процент в Excel, а также освоим основные формулы процента, которые избавят вас от догадок при расчетах.
- Базовая формула подсчета процента от числа.
- Как посчитать процент между числами по колонкам.
- Как рассчитать процент по строкам.
- Доля в процентах.
- Считаем процент скидки
- Отклонение в процентах для отрицательных чисел
- Вычитание процентов
- Как избежать ошибки деления на ноль
Что такое процент?
Как вы, наверное, помните из школьного урока математики, процент — это доля от 100, которая вычисляется путем деления двух чисел и умножения результата на 100.
Основная процентная формула выглядит следующим образом:
(Часть / Целое) * 100% = Процент
Например, если у вас было 20 яблок и вы подарили 5 своим друзьям, сколько вы дали в процентном отношении? Проведя несложный подсчет =5/20*100% , вы получите ответ — 25%.
Так обычно рассчитывают проценты в школе и в повседневной жизни. Вычислить процентное соотношение в Microsoft Excel еще проще, поскольку он выполняет некоторые операции за вас автоматически.
К сожалению, универсальной формулы расчета процентов в Excel, которая охватывала бы все возможные случаи, не существует. Если вы спросите кого-нибудь: «Какую формулу процентов вы используете, чтобы получить желаемый результат?», Скорее всего, вы получите ответ типа: «Это зависит от того, какой именно результат вы хотите получить».
Итак, позвольте мне показать вам несколько простых формул для расчета процентов в Excel.
Расчет процентов в Excel.
Основная формула для расчета процента от числа в Excel такая же, как и во всех сферах жизни:
Часть / Целое = Процент
Если вы сравните ее с основной математической формулой для процента, которую мы указали чуть выше, то заметите, что в формуле процента в Excel отсутствует часть * 100. При вычислении процента в Excel вам совершенно не обязательно умножать полученную дробь на 100, поскольку программа делает это автоматически, когда процентный формат применяется к ячейке.
И если в Экселе вы будете вводить формулу с процентами, то можно не переводить в уме проценты в десятичные дроби и не делить величину процента на 100. Просто укажите число со знаком %.
То есть, чтобы, к примеру, посчитать 10% в Экселе, то вместо =A1*0,1 или =A1*10/100, просто запишите формулу процентов =A1*10%.
Хотя с точки зрения математики все 3 варианта возможны и все они дадут верный результат.
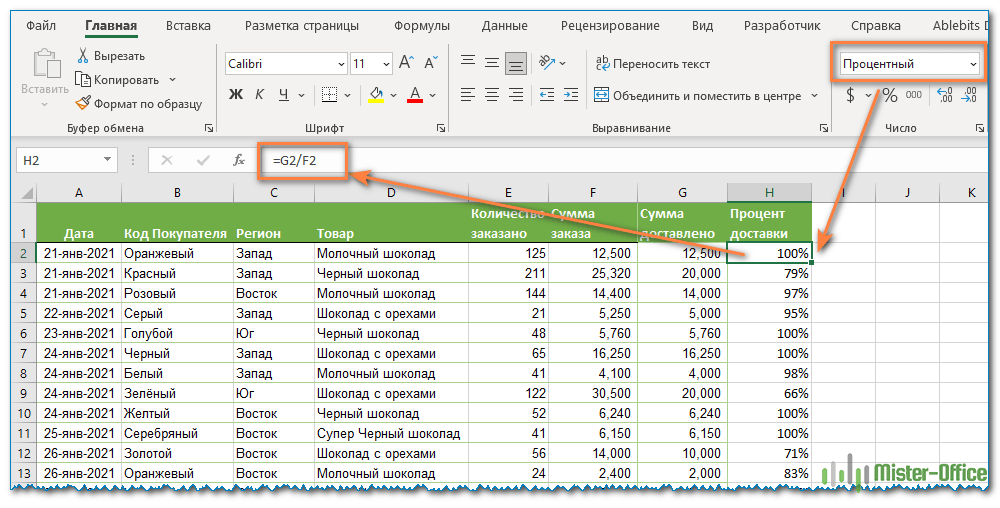
А теперь давайте посмотрим, как можно использовать формулу процента в Excel для реальных данных. Предположим, в вашей таблице Эксель записана сумма заказанных товаров в столбце F и оставленных товаров в столбце G. Чтобы высчитать процент доставленных товаров, выполните следующие действия:
- Введите формулу =G2/F2 в ячейку H2 и скопируйте ее на столько строк вниз, сколько вам нужно.
- Нажмите кнопку «Процентный стиль» ( меню «Главная» > группа «Число»), чтобы отобразить полученные десятичные дроби в виде процентов.
- Не забудьте при необходимости увеличить количество десятичных знаков в полученном результате.
- Готово!
Такая же последовательность шагов должна быть выполнена при использовании любой другой формулы процентов в Excel.
На скриншоте ниже вы видите округленный процент доставленных товаров без десятичных знаков.
Чтобы определить процент доставки, мы сумму доставленных товаров делим на сумму заказов. И используем в ячейке процентный формат, при необходимости показываем десятичные знаки.
Запишите формулу в самую верхнюю ячейку столбца с расчетами, а затем протащите маркер автозаполнения вниз по столбцу. Таким образом, мы посчитали процент во всём столбце.
Как найти процент между числами из двух колонок?
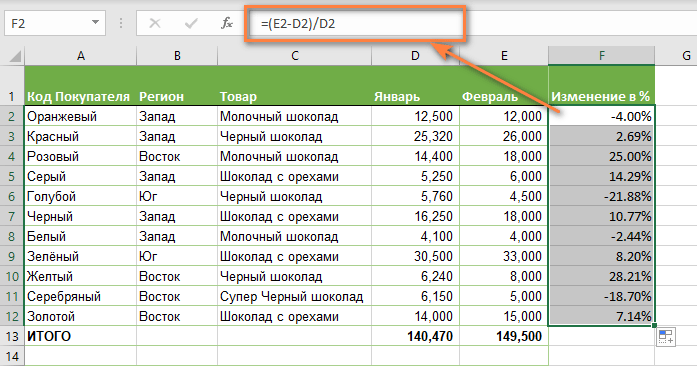
Предположим, у нас имеются данные о продажах шоколада за 2 месяца. Необходимо определить, какие произошли изменения в реализации. Проще и нагляднее всего отклонения в продажах выразить в процентах.
Чтобы вычислить разницу в процентах между значениями A и B, используйте следующую формулу:
Процентное изменение = (B — A) / A
При применении этой формулы к реальным данным важно правильно определить, какое значение равно A, а какое — B. Например, вчера у вас было 80 яблок, а сейчас — 100. Это означает, что теперь у вас на 20 яблок больше, чем раньше, что произошло увеличение на 25%. Если у вас было 100 яблок, а теперь – 90, то количество яблок у вас уменьшилось на 10, то есть на 10%.
Учитывая вышеизложенное, наша формула Excel для процентного изменения принимает следующую форму:
=(новое_значение – старое_значение)/старое_значение
А теперь давайте посмотрим, как вы можете использовать эту формулу процентного изменения в своих таблицах.
В нашем случае —
=(E2-D2)/D2
Эта формула процентного изменения вычисляет процентное увеличение (либо уменьшение) в феврале (столбец E) по сравнению с январём (столбец В).
И затем при помощи маркера заполнения копируем ее вниз по столбцу. Не забудьте применить процентный формат.
Отрицательные проценты, естественно, означают снижение продаж, а положительные — их рост.
Аналогичным образом можно подсчитать и процент изменения цен за какой-то период времени.
Как найти процент между числами из двух строк?
Такой расчет применяется? Если у нас есть много данных об изменении какого-то показателя. И мы хотим проследить, как с течением времени изменялась его величина. Поясним на примере.
Предположим, у нас есть данные о продажах шоколада за 12 месяцев. Нужно проследить, как изменялась реализация от месяца к месяцу. Цифры в столбце С показывают, на сколько процентов в большую или меньшую сторону изменялись продажи в текущем месяце по сравнению с предшествующим.
Обратите внимание, что первую ячейку С2 оставляем пустой, поскольку январь просто не с чем сравнивать.
В С3 записываем формулу:
=(B3-B2)/B2
Можно также использовать и другой вариант:
=B3/B2 — 1
Копируем содержимое этой ячейки вниз по столбцу до конца таблицы.
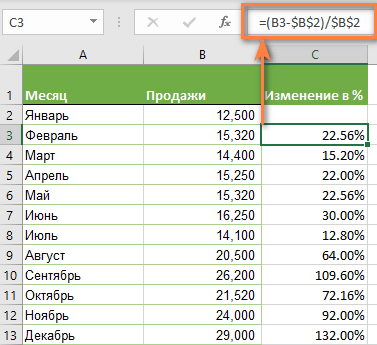
Если нам нужно сравнивать продажи каждого месяца не с предшествующим, а с каким-то базисным периодом (например, с январём текущего года), то немного изменим нашу формулу, использовав абсолютную ссылку на цифру продаж января:
Абсолютная ссылка на $B$2 останется неизменной при копировании формулы в C4 и ниже:
=(B3-$B$2)/$B$2
А ссылка на B3 будет изменяться на B4, B5 и т.д.
Напомню, что по умолчанию результаты отображаются в виде десятичных чисел. Чтобы отобразить проценты , примените к столбцу процентный формат. Для этого нажмите соответствующую кнопку на ленте меню или используйте комбинацию клавиш Ctrl + Shift + %.
Десятичное число автоматически отображается в процентах, поэтому вам не нужно умножать его на 100.
Расчет доли в процентах (удельного веса).
Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.
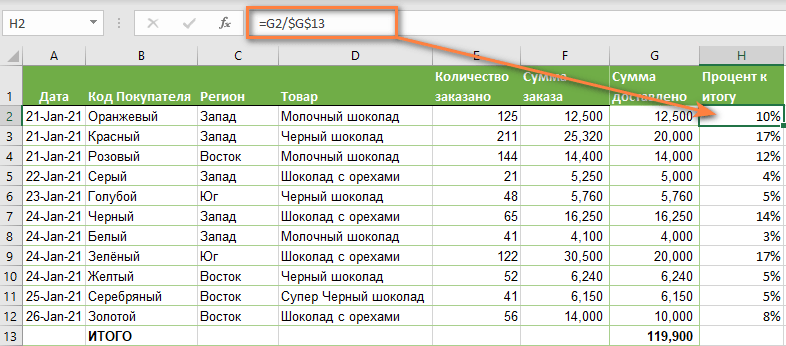
Пример 1. Сумма находится в конце таблицы в определенной ячейке.
Очень распространенный сценарий — это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.
Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы:
=G2/$G$13
Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.
Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.
На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.
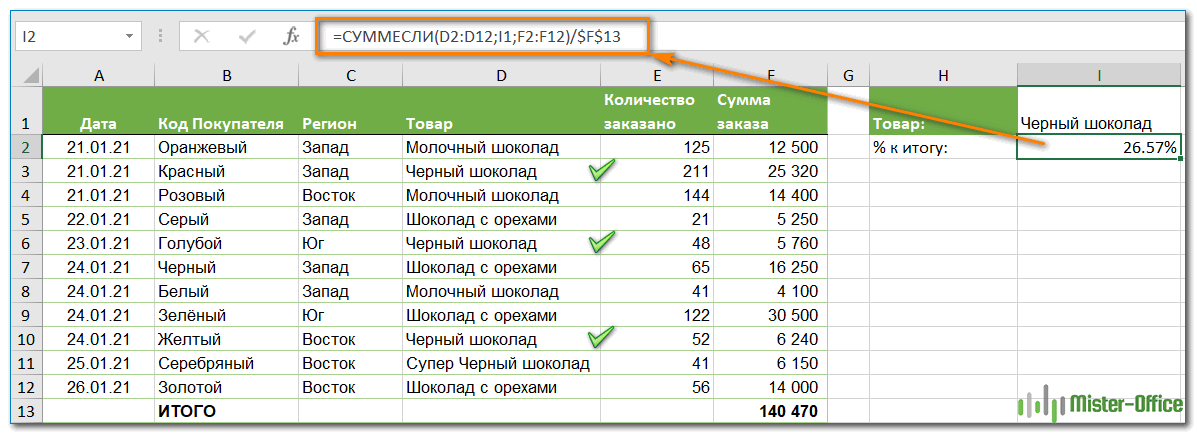
Пример 2. Часть итоговой суммы находится в нескольких строках.
В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.
В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:
=СУММЕСЛИ( диапазон; критерий; диапазон_суммирования ) / Итог
Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:
=СУММЕСЛИ(D2:D12;I1;F2:F12)/$F$13
Естественно, вы можете указать название товара прямо в формуле, например:
=СУММЕСЛИ(D2:D12;”Черный шоколад”;F2:F12)/$F$13
Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.
Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:
=(СУММЕСЛИ(D2:D12;”Черный шоколад”;F2:F12)/$F$13 + =СУММЕСЛИ(D2:D12;”Супер черный шоколад”;F2:F12)) / $F$13
Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.
Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:
- Как использовать функцию СУММЕСЛИ в Excel
- СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями
Процент скидки
Формулы процентов пригодятся для расчета уровня скидки. Итак, отправляясь за покупками, помните следующее:
Скидка в % = (цена со скидкой – обычная цена) / обычная цена
Скидка в % = цена со скидкой / обычная цена — 1
В результатах вычисления процент скидки отображается как отрицательное значение, поскольку новая цена со скидкой меньше старой обычной цены. Чтобы вывести результат в виде положительного числа , оберните формулы в функцию ABS. Например:
=ABS((C2-B2)/B2)
или
=ABS((C2/B2 — 1)
Так будет гораздо привычнее.
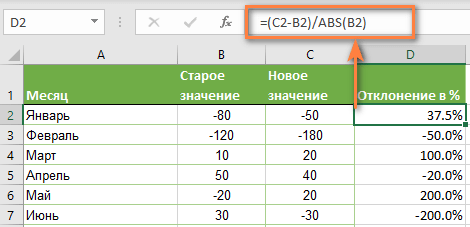
Как рассчитать отклонение в процентах для отрицательных чисел
Если некоторые из исходных значений представлены отрицательными числами, приведенные выше формулы не будут работать.
Обычный обходной путь — сделать знаменатель в формуле положительным числом. Для этого воспользуйтесь функцией ABS:
( Новое_значение – старое_значение ) / ABS( старое_значение )
Со старым значением в B2 и новым значением в C2 формула выглядит следующим образом:
=(C2-B2)/ABS(B2)
Как видите, достаточно корректно работает с самыми разными комбинациями положительных и отрицательных чисел.
Положительный процент означает рост, отрицательный — снижение величины показателя.
Вычитание процентов.
Часто случается, что вам известен процент скидки на товар. И вам нужно высчитать, какой процент от первоначальной стоимости придётся заплатить. Как мы уже говорили, процент в Экселе — это обычное число. Поэтому и правила вычисления здесь – как с обычными числами.
Формула расчета в Excel будет выглядеть так:
=1 – процент_скидки
Как обычно, не забываем про процентный формат ячеек.
Предотвратить ошибки деления на ноль #ДЕЛ/0
Если вы хотите посчитать процент от числа в таблице, и ваш набор данных содержит несколько нулевых значений, заключите формулы в функцию ЕСЛИОШИБКА, чтобы предотвратить появление ошибок деления на ноль (#ДЕЛ/0! или #DIV/0!).
=IFERROR(=ЕСЛИОШИБКА((C2-B2)/B2;0)
=IFERROR(=ЕСЛИОШИБКА(C2/B2-1;0)
Вот как можно вычислить процент от числа в Excel. И даже если работа с процентами никогда не была вашим любимым видом математики, с помощью этих основных процентных формул вы можете заставить Excel делать работу за вас.
На сегодня все, спасибо, что прочитали!
Для Google Docs эти формулы тоже подходят.
1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.
Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.
Какие данные нужны
Для начала надо правильно написать формулу — в любой свободной ячейке.
=ПЛТ(ставка;кпер;пс)
В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:
- Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
- Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
- Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.
Как всё посчитать
Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.
Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.
2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
Какие данные нужны
Формула расчёта довольно простая:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
В ней всего две переменные:
- Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
- Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).
Как всё посчитать
Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:
Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.
3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.
Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.
Какие данные нужны
Формула состоит из трёх компонентов:
=ЧИСТНЗ(ставка;значения;даты)
Второй и третий достаточно ясны:
2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.
Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.
Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.
Как всё посчитать
Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.
Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.
4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.
Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.
Какие данные нужны
Чтобы определить более выгодное предложение, применим формулу:
=ЧИСТВНДОХ(значения;даты)
Достаточно знать всего две переменные:
- Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
- Даты — график платежей, по которым будут выплачивать прибыль.
Как всё посчитать
Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.
5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.
Какие данные нужны
Полезной будет эта формула:
=СТАВКА(кпер;плт;пс)
Три переменных в ней означают следующее:
- Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
- Плт — размер платежей. Считаются и основной долг, и проценты.
- Пс — общая сумма займа. В нашем примере это 100 000 рублей.
Как всё посчитать
Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.
6. PV (ПС) — подсказывает, сколько денег можно взять в долг
Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.
Какие данные нужны
Пригодится формула расчёта текущей стоимости:
=ПС(ставка; кпер; плт)
Для этого потребуется информация, которая есть на сайте любого банка:
- Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
- Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
- Плт — размер комфортного платежа.
Как всё посчитать
Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.
Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.
7. NPER (КПЕР) — помогает рассчитать время накоплений
Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.
Какие данные нужны
Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:
=КПЕР(ставка/периоды_капитализации;плт;пс;бс)
Она состоит из четырёх основных значений и одного дополнительного:
- Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
- Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
- Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
- Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
- Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.
Как всё посчитать
Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.
Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.
Читайте также 🧐
- Как вести бюджет, если у вас непостоянный доход
- 20 полезных шаблонов «Google Таблиц» на все случаи жизни
- 10 крутых приложений, чтобы взять финансы под контроль