Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ТТЕСТ в Microsoft Excel.
Возвращает вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ позволяет определить, вероятность того, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция СТЬЮДЕНТ.ТЕСТ.
Синтаксис
ТТЕСТ(массив1;массив2;хвосты;тип)
Аргументы функции ТТЕСТ описаны ниже.
-
Массив1 Обязательный. Первый набор данных.
-
Массив2 Обязательный. Второй набор данных.
-
Хвосты Обязательный. Число хвостов распределения. Если значение «хвосты» = 1, функция ТТЕСТ возвращает одностороннее распределение. Если значение «хвосты» = 2, функция ТТЕСТ возвращает двустороннее распределение.
-
Тип Обязательный. Вид выполняемого t-теста.
|
Тип |
Выполняемый тест |
|
1 |
Парный |
|
2 |
Двухвыборочный с равными дисперсиями (гомоскедастический) |
|
3 |
Двухвыборочный с неравными дисперсиями (гетероскедастический) |
Замечания
-
Если аргументы «массив1» и «массив2» имеют различное число точек данных, а тип = 1 (парный), то функция ТТЕСТ возвращает значение ошибки #Н/Д.
-
Аргументы «хвосты» и «тип» усекаются до целых значений.
-
Если аргумент «хвосты» или «тип» не является числом, функция ТТЕСТ возвращает значение ошибки #ЗНАЧ!.
-
Если аргумент «хвосты» имеет значение, отличное от 1 и 2, функция ТТЕСТ возвращает значение ошибки #ЧИСЛО!.
-
Функция ТТЕСТ использует данные аргументов «массив1» и «массив2» для вычисления неотрицательной t-статистики. Если хвосты = 1, ТТЕСТ возвращает вероятность более высокого значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими генеральной совокупности с одним и тем же средним. Значение, возвращаемое функцией ТТЕСТ в случае, когда хвосты = 2, вдвое больше значения, возвращаемого, когда хвосты = 1, и соответствует вероятности более высокого абсолютного значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими генеральной совокупности с одним и тем же средним.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные 1 |
Данные 2 |
|
|
3 |
6 |
|
|
4 |
19 |
|
|
5 |
3 |
|
|
8 |
2 |
|
|
9 |
14 |
|
|
1 |
4 |
|
|
2 |
5 |
|
|
4 |
17 |
|
|
5 |
1 |
|
|
Формула |
Описание (результат) |
Результат |
|
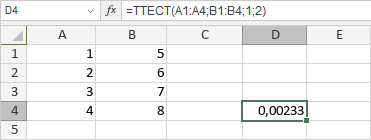
=ТТЕСТ(A2:A10;B2:B10;2;1) |
Вероятность, соответствующая парному критерию Стьюдента, с двусторонним распределением. Используются значения в диапазонах А2:А10 и В2:В10 |
0,19602 |
Нужна дополнительная помощь?

T Test is one of the standard functions that will get you a lot of mileage in working with the stats, and this guide will help you understand the function and how to use it. If you would like to explore the many other features, both as part of the standard program and available through add-ins, you might consider a course in using Excel’s statistical functions.
Understanding T Test
The T Test function in Excel is designed to work on two independent sample sets. It allows you to compare the two sample sets, determining the two means’ difference in relation to the data variation. In simple terms, the result of the test indicates whether the difference is significant or due to random chance.
This supports hypothesis testing that you likely have become familiar with in basic statistics courses or in your job responsibilities, if you work in a field that deals with statistical analysis. If, however, you are not familiar with the processes involved in hypothesis testing, you can enhance your understanding in a basic statistics course online.
Setting up the T Test
A great thing about using Excel to run a T Test is that it simplifies the routine by bundling the calculations in to one function. Of course, instead of running the test in this simplified fashion, you can use a step-by-step approach if you want to see the results of the independent calculations involved in a T Test.
This could be an approach you want to take if you are using the test to lear about statistics, and you can use a number of basic Excel functions to support you in doing this. You can get familiar with the types of functions available in an online course covering Excel essentials.
However, all you really need to perform the T Test in Excel is the sample data you want to perform the test on. For the purpose of this tutorial, we can use these non-specific sample sets
| Sample One | Sample Two | |
| Replicate 1 | 500 | 280 |
| Replicate 2 | 480 | 230 |
| Replicate 3 | 520 | 290 |
| Replicate 4 | 470 | 250 |
| Replicate 5 | 510 | 240 |
You can copy and paste this table in to an Excel spreadsheet if you would like to run a sample test for yourself.
Running the T.Test function
With your data prepared in your Excel spreadsheet, you are ready to set up and run the function. You can do this using the pop-up interface for the function, or you can simply write the function out in the formula bar. Either way, you can generally begin by calling up the function in the formula bar. Select the cell where you want your result to go. Then enter this text:
=T.Test(
If you would like to use the interface for completing this function you can access it by clicking the button to the left of the formula bar, labeled with the fx symbol. Here, we will first walk through the equation as you would type it in. This will help you understand it and easily modify it as needed.
Your first step is to define the ranges containing your sample data, separated by a comma. These will be in the format [Beginning cell in range]:[Ending cell in range]. So, if the sample referenced above begins in cell A1, the first range you will define is B2:B6. Your second range is C2:C6. Make sure you are only using the range for one of the samples, and don’t include any labels. So far, your function should look like this:
=T.Test(B2:B6, C2:C6
The next step, then, is to define the number of distribution tails. For a one-tailed distribution, you will enter 1 and for a two tailed distribution. As you will know from studying statistics, this indicates whether we will test the possibility of a relationship in one direction or two. Here we will indicate a two-tailed test by entering 2. So our function looks like this:
=T.Test(B2:B6, C2:C6, 2
As the final step in building your function is to tell Excel which type of T Test to perform. There are three options indicated by integers 1-3. Here are the types corresponding to each option
1 performs a paired test. If your samples are dependent, you will want to use this option. For example, the paired test is appropriate if your samples were taken from the same group. If your samples are independent, you will choose one of the other two options, based on variance.
2 Performs a two-sample test with equal variance.
3 performs a two-sample test with unequal variance
Let’s assume in this test that our samples are taken from the same group and enter option one. This complete the T.Test formula, and it should look like this.
=T.Test(B2:B6, C2:C6, 2, 1)
To run the test, you simply press the Enter or Return key, and in our example, you will get the result 1.63422E-05. Using a p-value of .05, you will see that this would be low enough to reject the null hypothesis for your study.
In Summary
Hopefully, this walkthrough of the T.Test function in Excel helped you understand this useful statistical tool well enough to use it in your own work. This is just one of many functions that you can use to make your life easier when undertaking statistical analysis, and if you would like to get a handle on others, you might try a course that surveys the Excel Functions.
Add T.Test to your bag of statistics tricks and enjoy crunching the numbers!
Функция ТТЕСТ устаревшая с 2010-й версии Excel, оставлена для обратной совместимости с 2007 и более ранними версиями, рекомендуется воспользоваться функцией СТЬЮДЕНТ.ТЕСТ.
Описание функции ТТЕСТ
Возвращает вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ позволяет определить, вероятность того, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.
Синтаксис
=ТТЕСТ(массив1; массив2; хвосты; тип)Аргументы
массив1массив2хвостытип
Обязательный. Первый набор данных.
Обязательный. Второй набор данных.
Обязательный. Число хвостов распределения. Если значение «хвосты» = 1, функция ТТЕСТ возвращает одностороннее распределение. Если значение «хвосты» = 2, функция ТТЕСТ возвращает двустороннее распределение.
Обязательный. Вид выполняемого t-теста.
- Парный
- Двухвыборочный с равными дисперсиями (гомоскедастический)
- Двухвыборочный с неравными дисперсиями (гетероскедастический)
Замечания
- Если аргументы «массив1» и «массив2» имеют различное число точек данных, а тип = 1 (парный), то функция ТТЕСТ возвращает значение ошибки #Н/Д.
- Аргументы «хвосты» и «тип» усекаются до целых значений.
- Если аргумент «хвосты» или «тип» не является числом, то функция ТТЕСТ возвращает значение ошибки #ЗНАЧ!.
- Если аргумент «хвосты» имеет значение, отличное от 1 и 2, то функция ТТЕСТ возвращает значение ошибки #ЧИСЛО!.
- Функция TTEСT использует данные аргументов «массив1» и «массив2» для вычисления неотрицательной t-статистики. Если хвосты = 1, TTEСT возвращает вероятность более высокого значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими генеральной совокупности с одним и тем же средним. Значение, возвращаемое функцией TTEСT в случае, когда хвосты = 2, вдвое больше значения, возвращаемого, когда хвосты = 1, и соответствует вероятности более высокого абсолютного значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими генеральной совокупности с одним и тем же средним.
Пример
Функция ТТЕСТ
-
статистические функции
- Функция СРОТКЛ
- Функция СРЗНАЧ
- Функция СРЗНАЧА
- Функция СРЗНАЧЕСЛИ
- Функция СРЗНАЧЕСЛИМН
- Функция БЕТАРАСП
- Функция БЕТА.РАСП
- Функция БЕТА.ОБР
- Функция БЕТАОБР
- Функция БИНОМРАСП
- Функция БИНОМ.РАСП
- Функция БИНОМ.РАСП.ДИАП
- Функция БИНОМ.ОБР
- Функция ХИ2РАСП
- Функция ХИ2ОБР
- Функция ХИ2.РАСП
- Функция ХИ2.РАСП.ПХ
- Функция ХИ2.ОБР
- Функция ХИ2.ОБР.ПХ
- Функция ХИ2ТЕСТ
- Функция ХИ2.ТЕСТ
- Функция ДОВЕРИТ
- Функция ДОВЕРИТ.НОРМ
- Функция ДОВЕРИТ.СТЬЮДЕНТ
- Функция КОРРЕЛ
- Функция СЧЁТ
- Функция СЧЁТЗ
- Функция СЧИТАТЬПУСТОТЫ
- Функция СЧЁТЕСЛИ
- Функция СЧЁТЕСЛИМН
- Функция КОВАР
- Функция КОВАРИАЦИЯ.Г
- Функция КОВАРИАЦИЯ.В
- Функция КРИТБИНОМ
- Функция КВАДРОТКЛ
- Функция ЭКСП.РАСП
- Функция ЭКСПРАСП
- Функция F.РАСП
- Функция FРАСП
- Функция F.РАСП.ПХ
- Функция F.ОБР
- Функция FРАСПОБР
- Функция F.ОБР.ПХ
- Функция ФИШЕР
- Функция ФИШЕРОБР
- Функция ПРЕДСКАЗ
- Функция ПРЕДСКАЗ.ETS
- Функция ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ
- Функция ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ
- Функция ПРЕДСКАЗ.ETS.СТАТ
- Функция ПРЕДСКАЗ.ЛИНЕЙН
- Функция ЧАСТОТА
- Функция ФТЕСТ
- Функция F.ТЕСТ
- Функция ГАММА
- Функция ГАММА.РАСП
- Функция ГАММАРАСП
- Функция ГАММА.ОБР
- Функция ГАММАОБР
- Функция ГАММАНЛОГ
- Функция ГАММАНЛОГ.ТОЧН
- Функция ГАУСС
- Функция СРГЕОМ
- Функция РОСТ
- Функция СРГАРМ
- Функция ГИПЕРГЕОМЕТ
- Функция ГИПЕРГЕОМ.РАСП
- Функция ОТРЕЗОК
- Функция ЭКСЦЕСС
- Функция НАИБОЛЬШИЙ
- Функция LINEST
- Функция ЛГРФПРИБЛ
- Функция ЛОГНОРМОБР
- Функция ЛОГНОРМ.РАСП
- Функция ЛОГНОРМ.ОБР
- Функция ЛОГНОРМРАСП
- Функция МАКС
- Функция МАКСА
- Функция МАКСЕСЛИ
- Функция МЕДИАНА
- Функция МИН
- Функция МИНА
- Функция МИНЕСЛИ
- Функция МОДА
- Функция МОДА.НСК
- Функция МОДА.ОДН
- Функция ОТРБИНОМРАСП
- Функция ОТРБИНОМ.РАСП
- Функция НОРМРАСП
- Функция НОРМ.РАСП
- Функция НОРМОБР
- Функция НОРМ.ОБР
- Функция НОРМСТРАСП
- Функция НОРМ.СТ.РАСП
- Функция НОРМСТОБР
- Функция НОРМ.СТ.ОБР
- Функция ПИРСОН
- Функция ПЕРСЕНТИЛЬ
- Функция ПРОЦЕНТИЛЬ.ИСКЛ
- Функция ПРОЦЕНТИЛЬ.ВКЛ
- Функция ПРОЦЕНТРАНГ
- Функция ПРОЦЕНТРАНГ.ИСКЛ
- Функция ПРОЦЕНТРАНГ.ВКЛ
- Функция ПЕРЕСТ
- Функция ПЕРЕСТА
- Функция ФИ
- Функция ПУАССОН
- Функция ПУАССОН.РАСП
- Функция ВЕРОЯТНОСТЬ
- Функция КВАРТИЛЬ
- Функция КВАРТИЛЬ.ИСКЛ
- Функция КВАРТИЛЬ.ВКЛ
- Функция РАНГ
- Функция РАНГ.СР
- Функция РАНГ.РВ
- Функция КВПИРСОН
- Функция СКОС
- Функция СКОС.Г
- Функция НАКЛОН
- Функция НАИМЕНЬШИЙ
- Функция НОРМАЛИЗАЦИЯ
- Функция СТАНДОТКЛОН
- Функция СТАНДОТКЛОН.В
- Функция СТАНДОТКЛОНА
- Функция СТАНДОТКЛОНП
- Функция СТАНДОТКЛОН.Г
- Функция СТАНДОТКЛОНПА
- Функция СТОШYX
- Функция СТЬЮДРАСП
- Функция СТЬЮДЕНТ.РАСП
- Функция СТЬЮДЕНТ.РАСП.2Х
- Функция СТЬЮДЕНТ.РАСП.ПХ
- Функция СТЬЮДЕНТ.ОБР
- Функция СТЬЮДЕНТ.ОБР.2Х
- Функция СТЬЮДРАСПОБР
- Функция УРЕЗСРЕДНЕЕ
- Функция ТЕНДЕНЦИЯ
- Функция ТТЕСТ
- Функция СТЬЮДЕНТ.ТЕСТ
- Функция УНИК
- Функция ДИСП
- Функция ДИСПА
- Функция ДИСПР
- Функция ДИСП.Г
- Функция ДИСП.В
- Функция ДИСПРА
- Функция ВЕЙБУЛЛ
- Функция ВЕЙБУЛЛ.РАСП
- Функция ZТЕСТ
- Функция Z.ТЕСТ
- Using the AVERAGE function
Функция ТТЕСТ — это одна из статистических функций. Возвращает вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ позволяет определить вероятность того, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.
Синтаксис функции ТТЕСТ:
ТТЕСТ(массив1;массив2;хвосты;тип)
где
массив1 — первый диапазон числовых значений.
массив2 — второй диапазон числовых значений.
хвосты — число хвостов распределения. Если значение этого аргумента равно 1, используется одностороннее распределение. Если значение этого аргумента равно 2, используется двустороннее распределение.
тип — числовое значение, определяющее вид выполняемого t-теста. Может использоваться одно из следующих значений:
| Числовое значение | Вид t-теста |
| 1 | Парный |
| 2 | Двухвыборочный с равными дисперсиями (гомоскедастический) |
| 3 | Двухвыборочный с неравными дисперсиями (гетероскедастический) |
Эти значения можно ввести вручную или использовать в качестве аргументов ссылки на ячейки.
Чтобы применить функцию ТТЕСТ,
- выделите ячейку, в которой требуется отобразить результат,
-
щелкните по значку Вставить функцию , расположенному на верхней панели инструментов,
или щелкните правой кнопкой мыши по выделенной ячейке и выберите в меню команду Вставить функцию,
или щелкните по значку перед строкой формул, - выберите из списка группу функций Статистические,
- щелкните по функции ТТЕСТ,
- введите требуемые аргументы через точку с запятой или выделите мышью диапазон ячеек,
- нажмите клавишу Enter.
Результат будет отображен в выбранной ячейке.
Вернуться на предыдущую страницу
Попробуйте бесплатно
Попробуйте и примите решение
Не нужно ничего устанавливать,
чтобы увидеть все функции в действии
Содержание
- Определение термина
- Расчет показателя в Excel
- Способ 1: Мастер функций
- Способ 2: работа со вкладкой «Формулы»
- Способ 3: ручной ввод
- Вопросы и ответы
Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Определение термина
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
- Строим таблицу с двумя рядами переменных.
- Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.
- После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».
- Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».
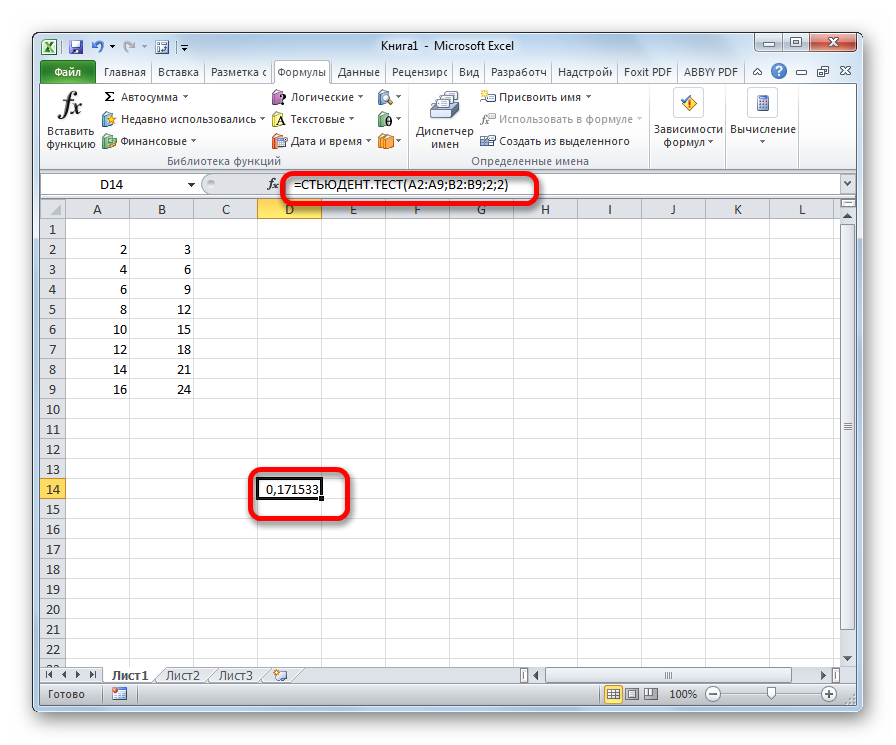
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».
- Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».
- Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
Способ 3: ручной ввод
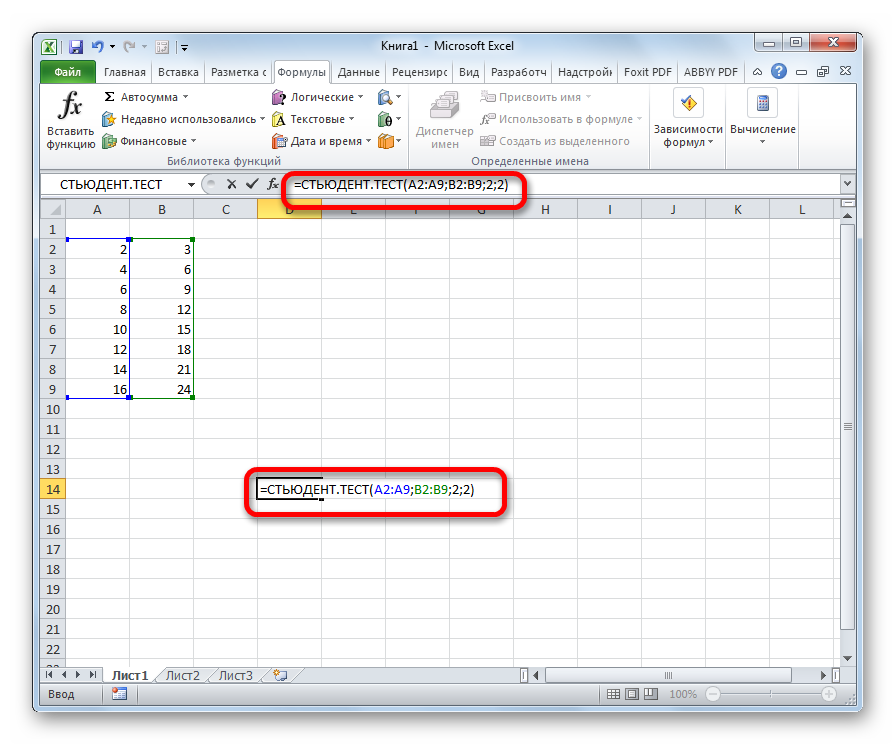
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.
После того, как данные введены, жмем кнопку Enter для вывода результата на экран.
Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Еще статьи по данной теме: