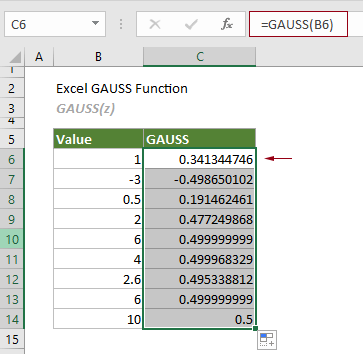
Функция распределения гаусса в excel - Word и Excel - помощь в работе с программами

Функция ГАУСС, подлежащая применению в версиях Excel начиная от 2013 года или новее. Она позволяет вычислить такую вероятность, с которой элемент стандартной нормальной совокупности будет находиться в интервале между средними и стандартными отклонениями от среднего.

Примеры использования функции ГАУСС в Excel

Синтаксис рассматриваемой функции не представляет из себя ничего сложного, ведь функции ГАУСС присущ всего один обязательный аргумент – Z – возвращающий число.

Важно отметить, что существует определенная связь между функцией ГАУСС и такой статистической функцией, как стандартное нормальное распределение, иначе говоря – НОРМ.СТ.РАСП.

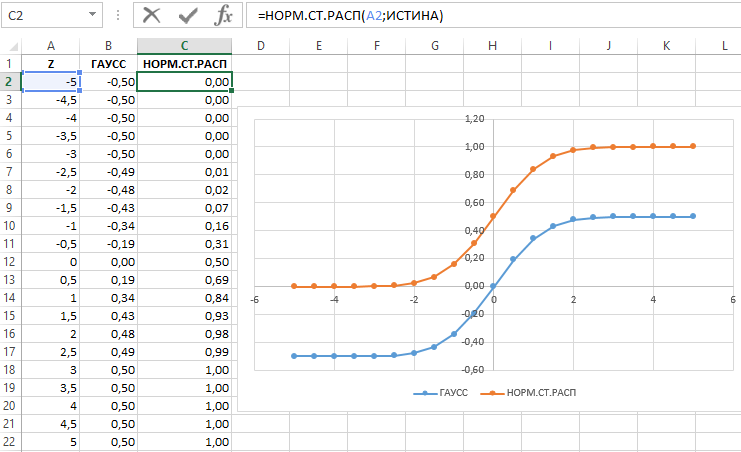
Итак, всегда функция НОРМ.СТ.РАСП (0; Истина) делает возврат 0,5, тогда как ГАУСС (z) имеет в результате значение меньше на 0,5, чем результат функции НОРМ.СТ.РАСП. На рисунке, расположенном ниже, приведен пример использования данных статистических функций для возвращения числа 1,5.

Для наглядности продемонстрируем зависимость между значениями функций графическим способом. Для этого – сформируем таблицу с выборкой чисел, например на интервале от -5 до 5 с шагом 0,5, а затем по имеющимся данным построим график:

На графике четко прослеживается пропорциональная корреляция результатов вычислений функций ГАУСС и НОРМ.СТ.РАСП.

Решение системы вероятности методом ГАУССА в Excel

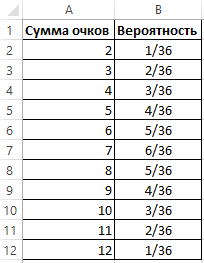
Задача представляет собой вычисление вероятности возможных значений при бросании двух костей.

Пример с игрой в кости является наиболее наглядным, так как мы имеем ограниченный набор данных, которые соответствуют вероятностям. Так, вероятность имеет значение от нуля до единицы, к которому стремится наблюдаемая частота при бесконечно большой выборке или повторении эксперимента.

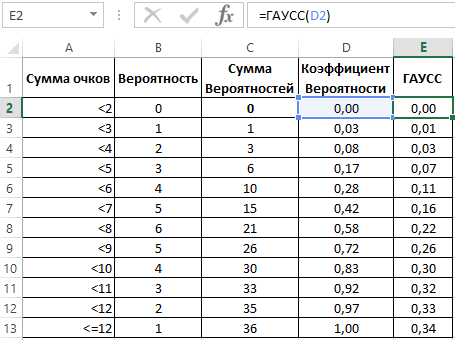
Существует 36 возможных комбинаций. При этом, вероятность того, что при бросании двух костей выпадет 2 очка равна 1/36, а 7 очков – 1/6. Отобразим перечень возможных значений бросания двух игральных костей в таблице, приведя при этом все вероятности к общему знаменателю.

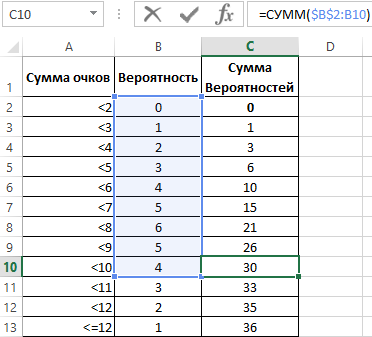
Однако, такой ряд данных не дает возможности для выявления полного распределения, поэтому следует отобразить данные об отдельных вероятностях в рассчитанную по функции распределения. Так необходимо, все вероятности просуммировать последовательно (1+2+3+4+5+6+5+4+3+2+1).

Теперь определяем коэффициент вероятности разделив по отдельности последовательную сумму вероятностей на максимально возможное количество комбинаций 36.

В первом случае нами были рассмотрены отдельные вероятности, во втором – сумма вероятностей от первого возможного значения до заданного.

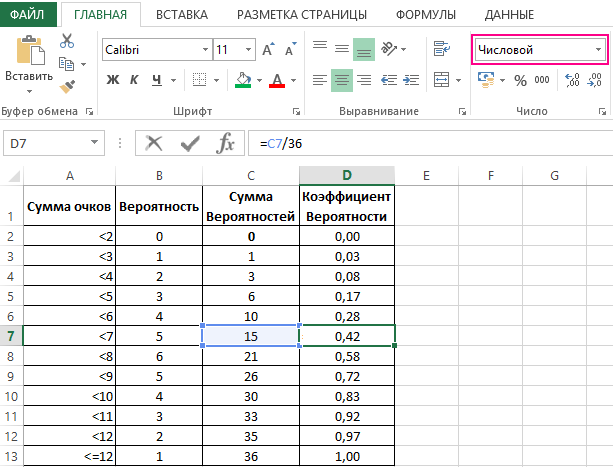
Необходимо преобразовать диапазон ячеек D2:D13 в числовой формат данных, иначе при обращении на них функции ГАУСС будет иметь место ошибка.

В созданный рядом с первоначальной таблицей столбец E введем формулу, которая в качестве аргумента делает обращение к ячейке D2.

Далее, протянем формулу вниз по столбцу, и получим ряд вероятностей с использованием функции ГАУСС.

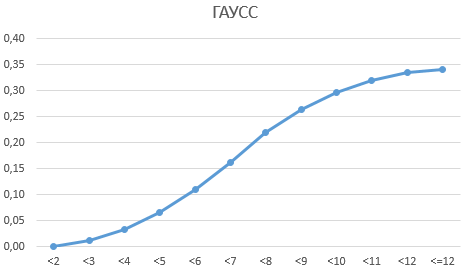
Для более наглядной визуализации, построим график вероятности:

Решение вероятности методом распределения кривой Гаусса в Excel

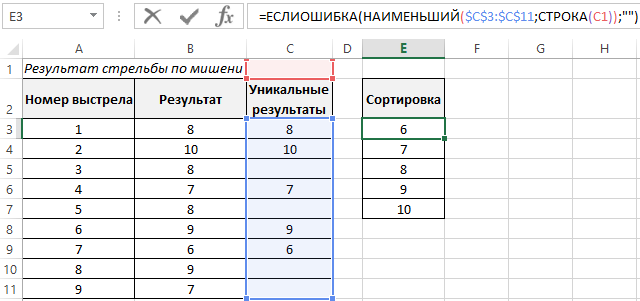
Теперь в качестве примера нормального распределения с помощью функции ГАУСС решим задачу о вероятностном соотношении результатов стрельбы по мишени.

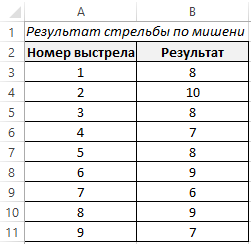
Для этого построим базовую таблицу, которая отражает результаты стрельбы по мишени в девяти подходах.

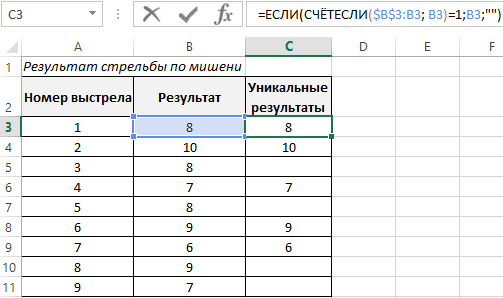
Затем, выберем только уникальные результаты, для этого используем хитрую формулу:

Делаем сортировку формулой для результатов по возрастанию и выводим в отдельную табличку:

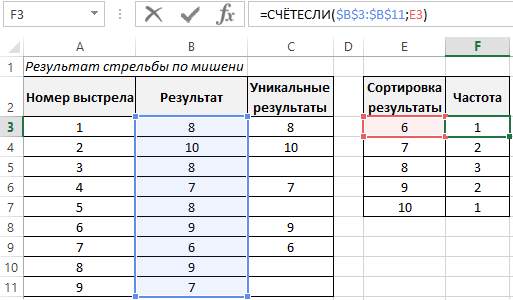
После чего определим частоту встречающихся только для уникальных результатов:

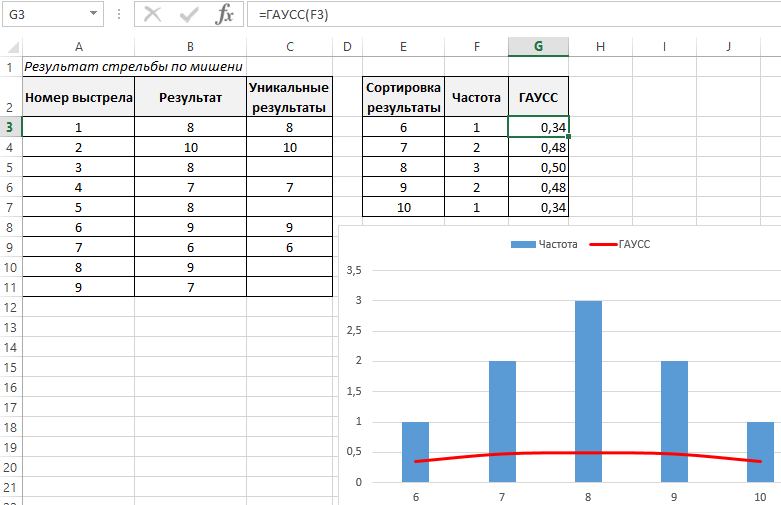
Далее применим функцию ГАУСС к значениям ячеек с частотой встречаемости. Отразим результаты вычислений на графике:

На графике красной линией определено нормальное распределение кривой Гаусса.

Источник

В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

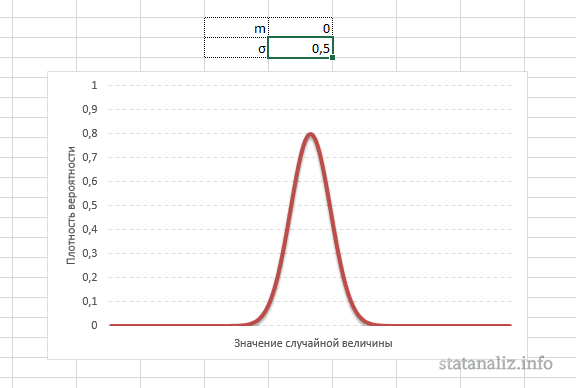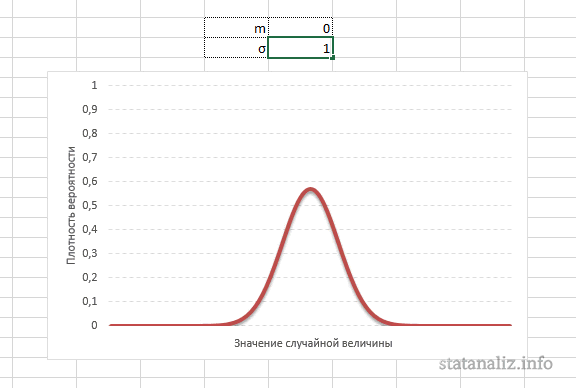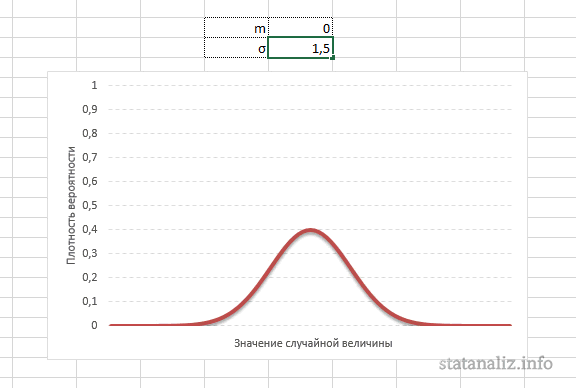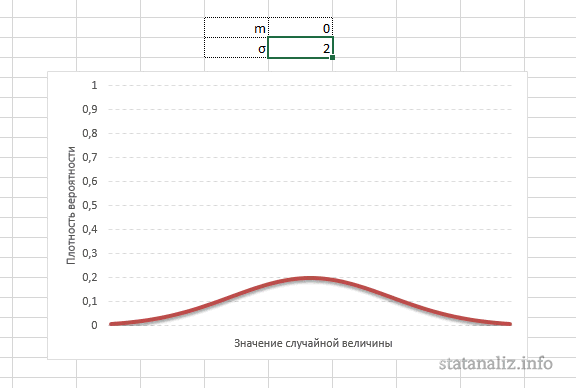
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

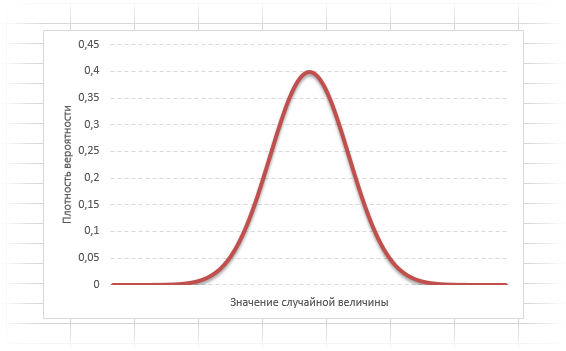
Кривая нормального распределения Гаусса имеет следующий вид.

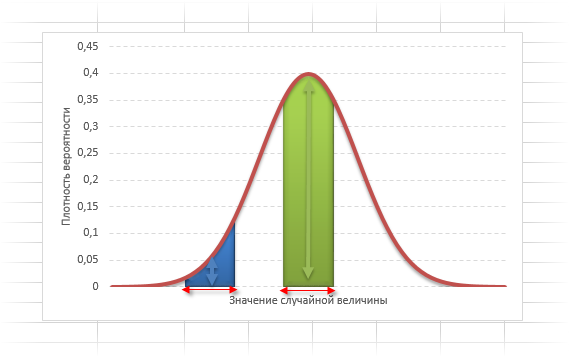
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

π – число пи 3,142;

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

σ² – дисперсия;

ну и сама переменная x, для которой высчитывается плотность вероятности.

Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ²). Кратко обозначается N(m, σ²) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ² характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

P(a ≤ X < b) = Ф(b) – Ф(a)

Стандартное нормальное распределение

Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).

Любое нормальное распределение легко превращается в стандартное путем нормирования:

где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.

Для выборочных данных берутся оценки:

Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.

В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.

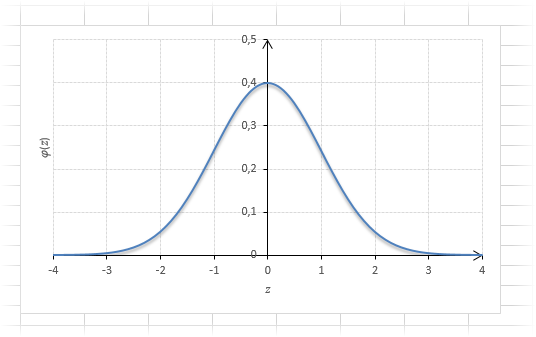
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:

Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:

График плотности:

Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e⁰=1 и остается рассчитать только соотношение 1 на корень из 2 пи.

Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.

Функция стандартного нормального распределения позволяет рассчитывать вероятности.

Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

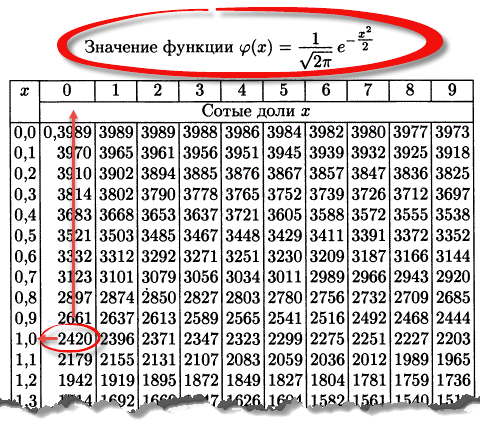
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.

В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).

Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

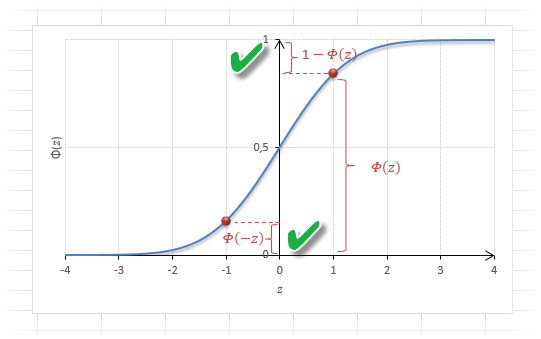
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

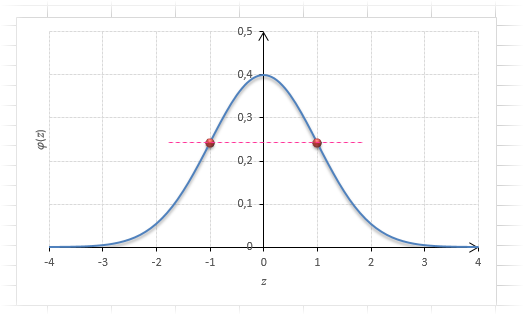
Это факт показан на картинке:

Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

Для наглядности можно взглянуть на рисунок.

На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

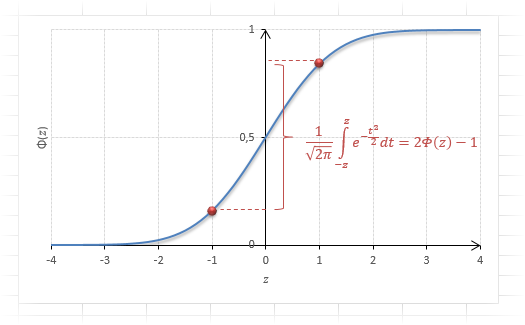
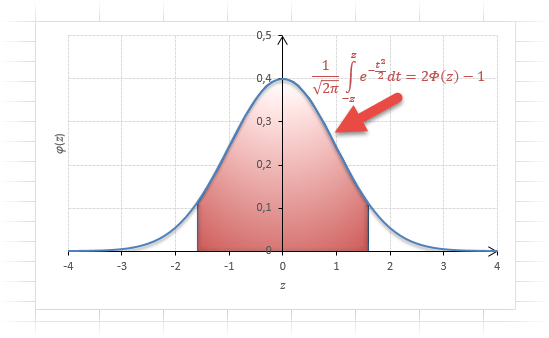
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Рисунок ниже.

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.

Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

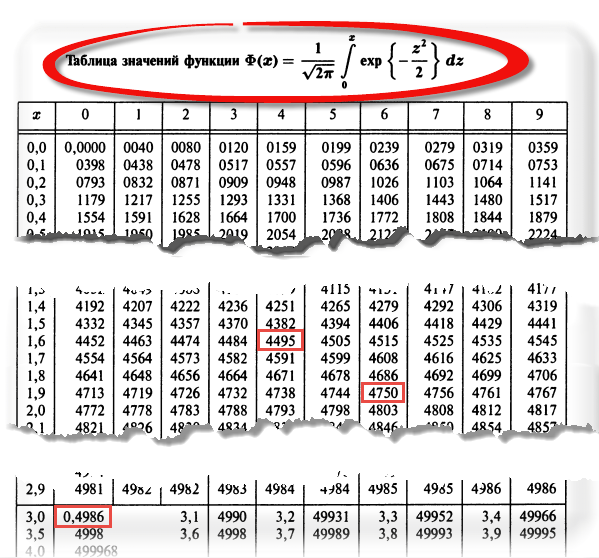
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

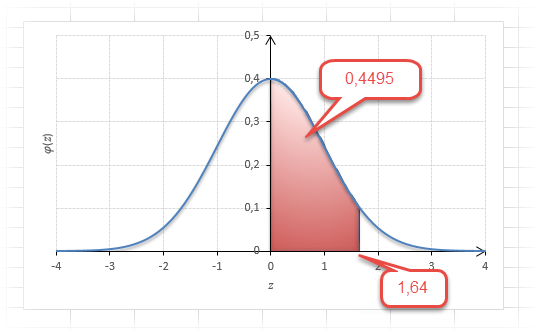
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

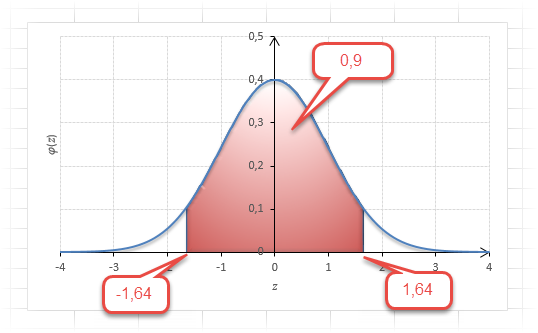
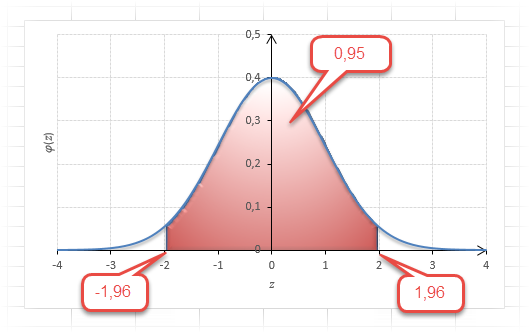
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

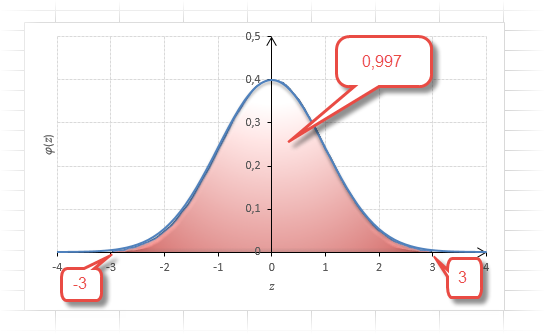
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.

Функция НОРМ.СТ.РАСП

Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).

=НОРМ.СТ.РАСП(z;интегральная)

z – значение стандартизованной переменной

интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).

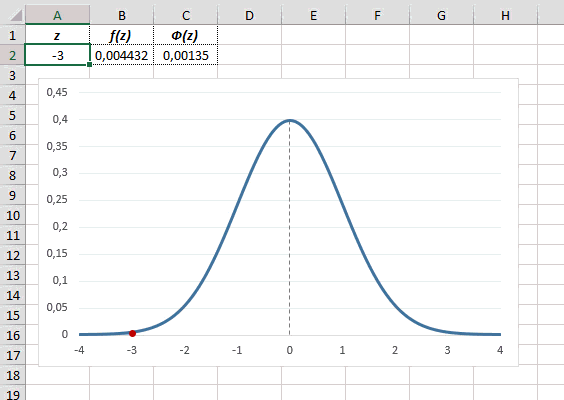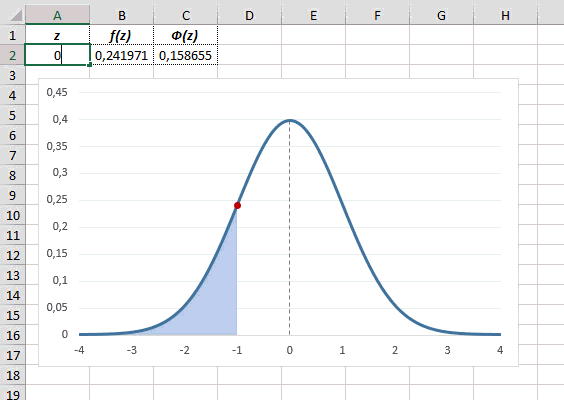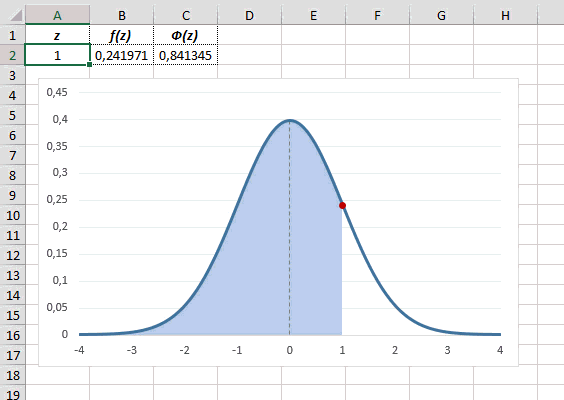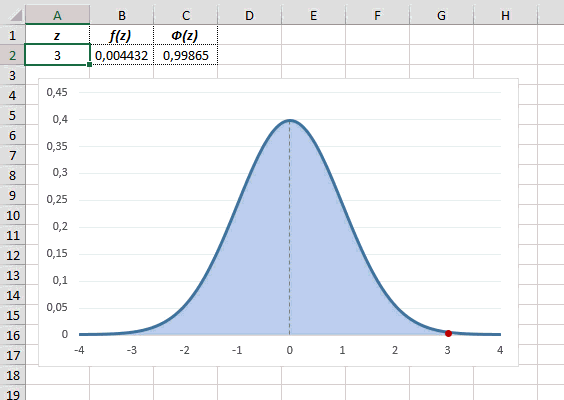
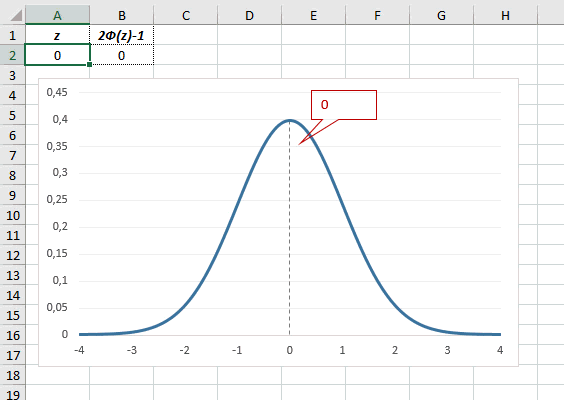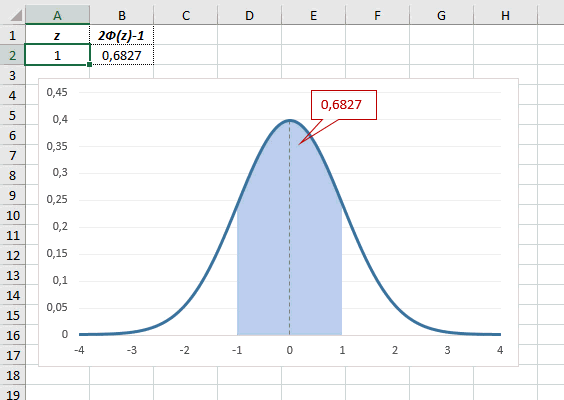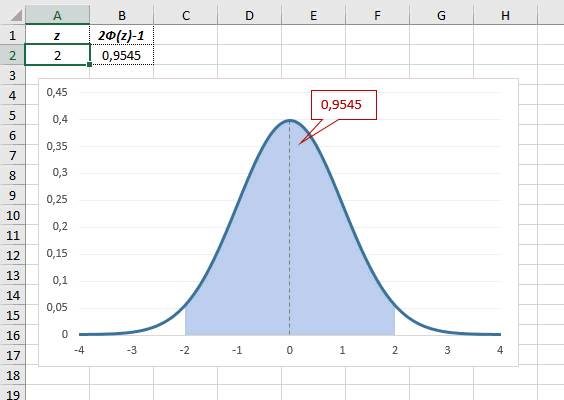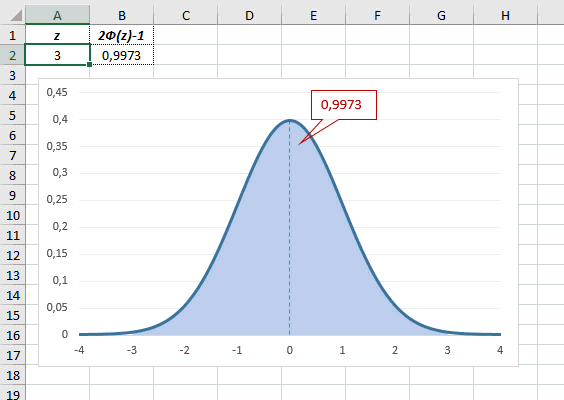
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).

Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.

Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.

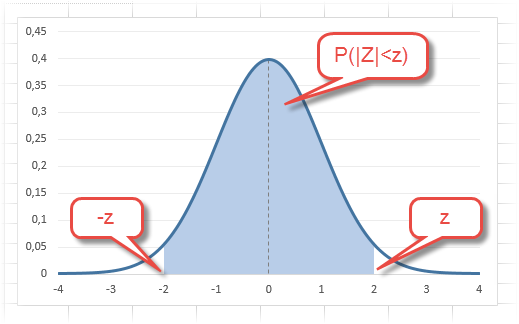
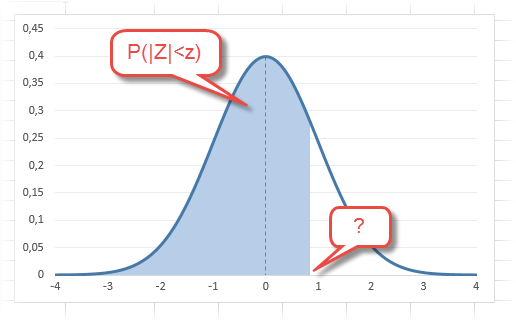
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).

Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.

На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.

Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.

Функция НОРМ.СТ.ОБР

НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:

=НОРМ.СТ.ОБР(вероятность)

вероятность – это вероятность.

Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.

Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.

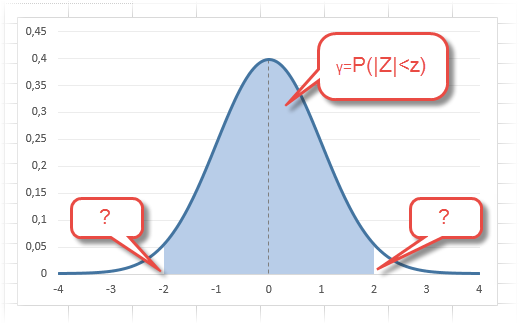
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.

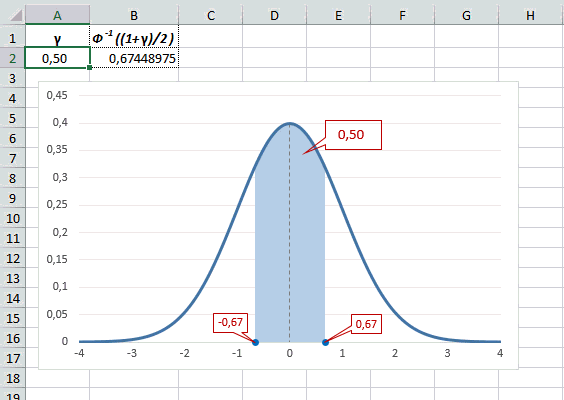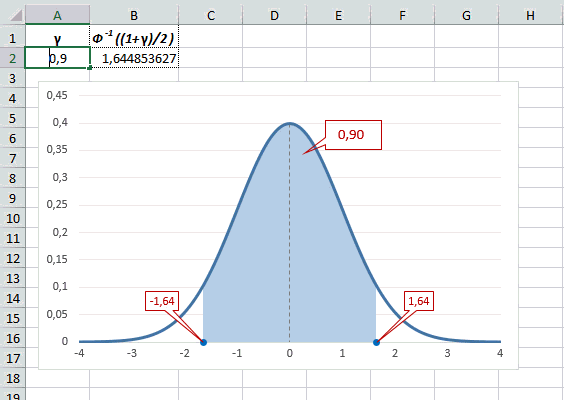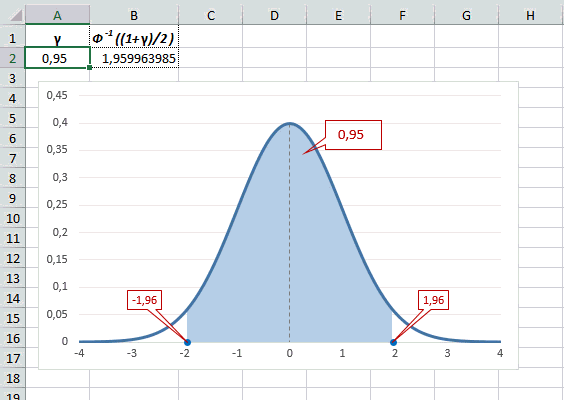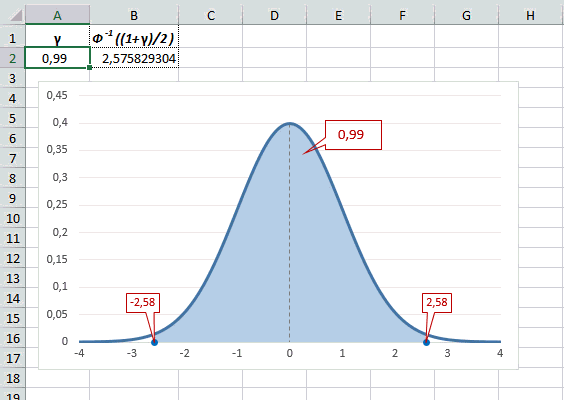
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.

Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.

В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.

Рассмотрим еще пару полезных формул с примерами.

Функция НОРМ.РАСП

Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.

=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)

x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения

среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения

стандартное_откл – среднеквадратичное отклонение – второй параметр модели

интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).

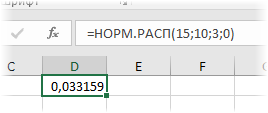
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:

Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.

Функция НОРМ.ОБР

Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.

=НОРМ.ОБР(вероятность;среднее;стандартное_откл)

вероятность – вероятность

среднее – матожидание

стандартное_откл – среднеквадратичное отклонение

Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.

Пример показан в ролике в конце статьи.

Моделирование нормального распределения

Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.

Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.

=НОРМ.ОБР(СЛЧИС();10;3)

Протянем ее на необходимое количество ячеек и нормальная выборка готова.

Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.

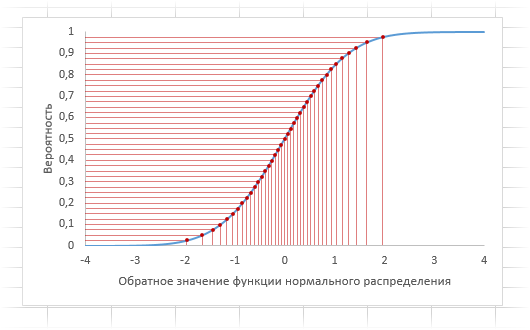
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.

На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.

Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.

Скачать файл с примером.

Поделиться в социальных сетях:

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для Mac 2011 Еще…Меньше

В этой статье описаны синтаксис формулы и использование ГАУСС
в Microsoft Excel.

Описание

Рассчитывает вероятность, с которой элемент стандартной нормальной совокупности находится в интервале между средним и стандартным отклонением z от среднего.

Синтаксис

ГАУСС(z)

Аргументы функции ГАУСС указаны ниже.

Z Обязательный. Возвращает число.

Замечания

Если z не является допустимым числом, гаусс возвращает #NUM! (значение ошибки).
Если z не является допустимым типом данных, гаусс возвращает #VALUE! (значение ошибки).
Поскольку НОРМ.СТ.РАСП(0,Истина) всегда возвращает 0,5, ГАУСС (z) всегда будет на 0,5 меньше, чем НОРМ.СТ.РАСП(z,Истина).

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
‘=ГАУСС(2)	Вероятность, с которой элемент стандартной нормальной совокупности населения находится в интервале между средним и двумя стандартными отклонениями от среднего (результат — 0,47725).	=ГАУСС(2)

К началу страницы

Нужна дополнительная помощь?

Источник

Построим график функции Гаусса имеющий форму Колокообразной кривой (Gaussian function, Bell Curve Shape).

Функция Гаусса широко применяется в статистике для описания нормального распределения, для решения некоторых уравнений физики (уравнения диффузии и теплопроводности) и в ряде других прикладных задач (фильтр Гаусса).

Форма графика функция Гаусса зависит от величины 3-х коэффициентов:

a

(высота пика),

b

(положение центра),

c

(отвечает за ширину кривой).

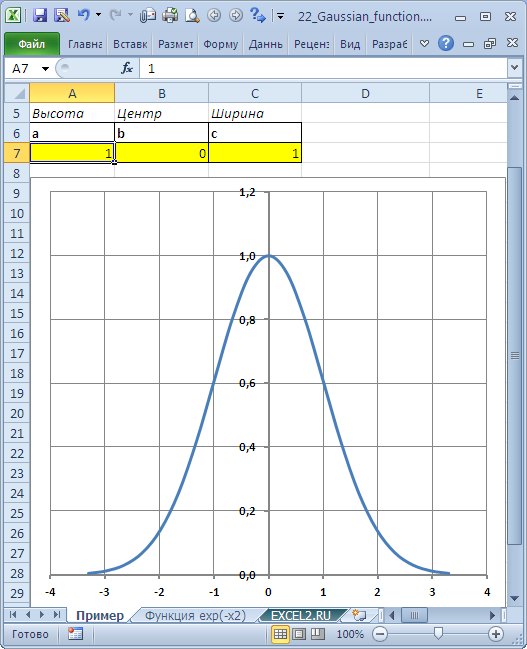
В

файле примера

построен график функции (использована диаграмма

Точечная с гладкими кривыми

). Коэффициенты находятся в отдельных ячейках, что позволяет быстро построить график нужной функции.

Если коэффициент

а

=1/КОРЕНЬ(2*ПИ())

, то функция Гаусса является функцией распределения плотности верояности нормально распределенной случайной выличины с математическим ожиданием =

b

и со стандарным отклонением =

с

.

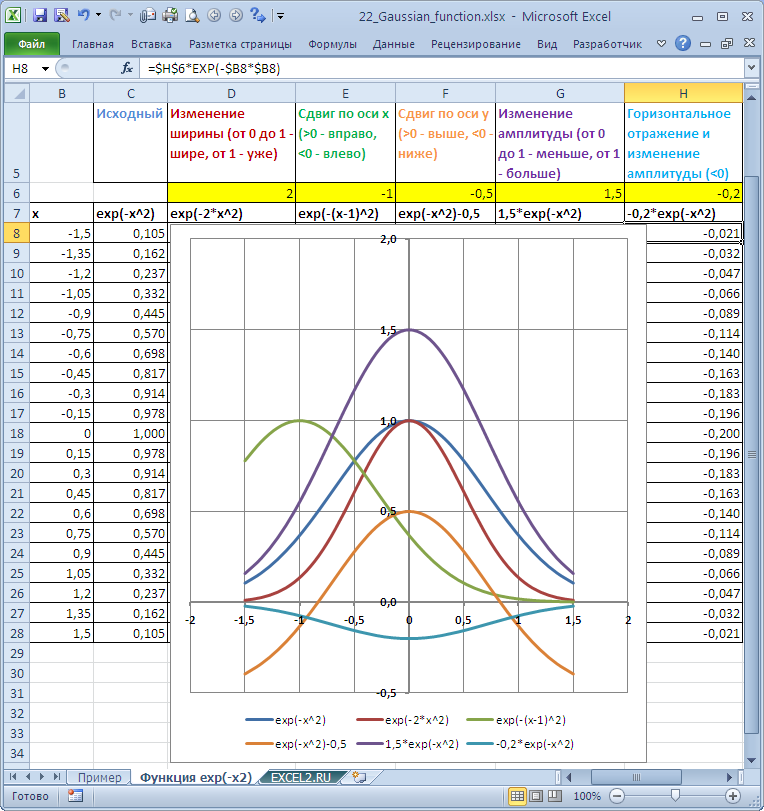
В

файле примера

также построен график для функции y(x)=exp(-x^2) с различными коэффициентами.

СОВЕТ

: Для начинающих пользователей EXCEL советуем прочитать статью

Основы построения диаграмм в MS EXCEL

, в которой рассказывается о базовых настройках диаграмм, а также

статью об основных типах диаграмм

Источник

Содержание

Начиная
Шаг № 1: Найдите среднее значение.
Шаг № 2: Найдите стандартное отклонение.
Шаг № 3: Установите значения оси X для кривой.
Шаг №4: Вычислите значения нормального распределения для каждого значения оси x.
Шаг № 5: Создайте диаграмму рассеяния с плавными линиями.
Шаг № 6: Настройте таблицу меток.
Шаг № 7: Вставьте данные метки в диаграмму.
Шаг № 8: Измените тип диаграммы для серии этикеток.
Шаг № 9: Измените масштаб горизонтальной оси.
Шаг № 10: Вставьте и разместите метки пользовательских данных.
Шаг № 11: Перекрасить маркеры данных (необязательно).
Шаг № 12: Добавьте вертикальные линии (необязательно).

В этом руководстве будет показано, как создать кривую нормального распределения во всех версиях Excel: 2007, 2010, 2013, 2016 и 2022.

В статистике колоколообразная кривая (также известная как стандартное нормальное распределение или кривая Гаусса) представляет собой симметричный график, который иллюстрирует тенденцию данных к кластеризации вокруг центрального значения или среднего значения в данном наборе данных.

Ось Y представляет относительную вероятность появления данного значения в наборе данных, в то время как ось X отображает сами значения на диаграмме, чтобы создать колоколообразную кривую, отсюда и название.

График помогает нам проанализировать, является ли конкретное значение частью ожидаемой вариации или статистически значимым и, следовательно, требует более внимательного изучения.

Поскольку в Excel нет встроенных решений, вам придется построить график самостоятельно. Вот почему мы разработали надстройку Chart Creator — инструмент, который позволяет создавать расширенные диаграммы Excel всего за несколько щелчков мышью.

В этом пошаговом руководстве вы узнаете, как с нуля создать кривую нормального распределения в Excel:

Чтобы построить кривую Гаусса, вам нужно знать две вещи:

Значение (также известное как стандартное измерение). Это определяет центр кривой, который, в свою очередь, характеризует положение кривой.
Стандартное отклонение (SD) измерений. Это определяет разброс ваших данных в нормальном распределении — или, говоря простым языком, насколько широкой должна быть кривая. Например, на приведенной выше колоколообразной кривой одно стандартное отклонение среднего представляет собой диапазон между оценками экзамена от 53 до 85.

Чем ниже SD, тем выше кривая и меньше будут разбросаны ваши данные, и наоборот.

Стоит упомянуть правило 68-95-99,7, которое можно применить к любой кривой нормального распределения, что означает, что примерно 68% ваших данных будет размещено в пределах одного стандартного отклонения от среднего, 95% — в пределах двух стандартных отклонений и 99,7% — в пределах. три SD.

Теперь, когда вы знаете основы, давайте перейдем от теории к практике.

Начиная

В целях иллюстрации предположим, что у вас есть результаты теста 200 учеников и вы хотите выставить им оценки «по кривой», то есть оценки учеников будут основаны на их относительной успеваемости по отношению к остальной части класса:

Шаг № 1: Найдите среднее значение.

Как правило, вам с самого начала задаются среднее значение и стандартное отклонение, но если это не так, вы можете легко вычислить эти значения всего за несколько простых шагов. Давайте сначала разберемся со средним.

Поскольку среднее значение указывает среднее значение выборки или совокупности данных, вы можете найти стандартное измерение, используя функцию СРЕДНЕЕ.

Введите следующую формулу в любую пустую ячейку (F1 в этом примере) рядом с вашими фактическими данными (столбцы A а также B), чтобы вычислить среднее значение экзаменационных баллов в наборе данных:

Небольшое примечание: чаще всего вам может потребоваться округлить вывод формулы в большую сторону. Для этого просто оберните его функцией ROUND следующим образом:

1	= ОКРУГЛ (СРЕДНИЙ (B2: B201); 0)

Шаг № 2: Найдите стандартное отклонение.

Один упал, один остался. К счастью, в Excel есть специальная функция, которая сделает за вас всю грязную работу по поиску стандартного отклонения:

1	= СТАНДОТКЛОН.P (B2: B201)

Опять же, формула выбирает все значения из указанного диапазона ячеек (B2: B201) и вычисляет его стандартное отклонение — не забудьте также округлить результат.

1	= ОКРУГЛ (СТАНДОТКЛОН.P (B2: B201); 0)

Шаг № 3: Установите значения оси X для кривой.

По сути, диаграмма представляет собой огромное количество интервалов (представьте их как шаги), соединенных линией, чтобы создать плавную кривую.

В нашем случае значения оси X будут использоваться для иллюстрации конкретной оценки экзамена, а значения оси Y будут указывать нам вероятность того, что студент получит этот результат на экзамене.

Технически вы можете включить столько интервалов, сколько захотите — вы можете легко стереть избыточные данные позже, изменив масштаб горизонтальной оси. Просто убедитесь, что вы выбрали диапазон, включающий три стандартных отклонения.

Давайте начнем подсчет с одного (так как студент не может получить отрицательный результат на экзамене) и дойдем до 150 — неважно, 150 это или 1500 — чтобы создать еще одну вспомогательную таблицу.

Выберите любую пустую ячейку под данными диаграммы (например, E4) и введите “1,” значение, определяющее первый интервал.
Перейдите к Дом таб.
в Редактирование группа, выберите «Наполнять.”
Под «Серия в,» Выбрать «Столбец.”
Для «Значение шага,» тип “1.” Это значение определяет приращения, которые будут автоматически добавляться, пока Excel не достигнет последнего интервала.
Для «Стоп-значение,» тип «150,” значение, которое соответствует последнему интервалу, и нажмите «OK.”

Чудом 149 ячеек в столбце E (E5: E153) были заполнены значениями от 2 до 150.

ПРИМЕЧАНИЕ. Не скрывайте исходные ячейки данных, как показано на снимках экрана.. В противном случае методика не сработает.

Шаг №4: Вычислите значения нормального распределения для каждого значения оси x.

Теперь найдите значения нормального распределения — вероятность того, что студент получит определенный балл за экзамен, представленный определенным значением оси X — для каждого из интервалов. К счастью для вас, в Excel есть рабочая лошадка для выполнения всех этих вычислений: функция НОРМ.РАСП.

Введите следующую формулу в ячейку справа (F4) вашего первого интервала (E4):

1	= НОРМ.РАСП (E4; $ F $ 1; $ F $ 2; ЛОЖЬ)

Вот декодированная версия, которая поможет вам соответствующим образом настроить:

1	= НОРМ.РАСП ([первый интервал], [среднее (абсолютное значение)], [стандартное отклонение (абсолютное значение), ЛОЖЬ)

Вы блокируете среднее значение и стандартное отклонение, чтобы можно было легко выполнить формулу для оставшихся интервалов (E5: E153).

Теперь дважды щелкните маркер заполнения, чтобы скопировать формулу в остальные ячейки (F5: F153).

Шаг № 5: Создайте диаграмму рассеяния с плавными линиями.

Наконец, пришло время строить колоколообразную кривую:

Выберите любое значение в вспомогательной таблице, содержащей значения осей x и y (E4: F153).
Перейти к Вставлять таб.
Щелкните значок «Вставить точечную (X, Y) или пузырьковую диаграмму» кнопка.
Выбирать «Разброс с плавными линиями ».

Шаг № 6: Настройте таблицу меток.

Технически у вас есть кривая колокола. Но его будет трудно прочитать, поскольку в нем отсутствуют какие-либо данные, описывающие это.

Давайте сделаем нормальное распределение более информативным, добавив метки, иллюстрирующие все значения стандартного отклонения ниже и выше среднего (вы также можете использовать их для отображения z-значений).

Для этого создайте еще одну вспомогательную таблицу следующим образом:

Сначала скопируйте среднее значение (F1) рядом с соответствующей ячейкой в столбце X-Value (I5).

Затем вычислите значения стандартного отклонения ниже среднего, введя эту простую формулу в ячейка I4:

Проще говоря, формула вычитает сумму предыдущих значений стандартного отклонения из среднего. Теперь перетащите маркер заполнения вверх, чтобы скопировать формулу в оставшиеся две ячейки (I2: I3).

Повторите тот же процесс для стандартных отклонений выше среднего, используя зеркальную формулу:

Таким же образом выполните формулу для двух других ячеек (I7: I8).

Наконец, заполните значения метки оси Y (J2: J8) с нулями, так как вы хотите, чтобы маркеры данных располагались на горизонтальной оси.

Шаг № 7: Вставьте данные метки в диаграмму.

Теперь добавьте все данные, которые вы подготовили. Щелкните правой кнопкой мыши график и выберите «Выберите данные.”

В появившемся диалоговом окне выберите «Добавлять.”

Выделите соответствующие диапазоны ячеек из вспомогательной таблицы —I2: I8 для «Значения серии X» а также J2: J8 для «Значения серии Y »-и нажмите «OK.”

Шаг № 8: Измените тип диаграммы для серии этикеток.

Наш следующий шаг — изменить тип диаграммы недавно добавленной серии, чтобы маркеры данных отображались в виде точек. Для этого щелкните правой кнопкой мыши график диаграммы и выберите «Изменить тип диаграммы.”

Затем создайте комбинированную диаграмму:

Перейдите к Комбо таб.
Для Серия «Series2», изменение «Тип диаграммы» к «Разброс.”
- Примечание. Убедитесь, что «Серия1»Остается как«Скаттер с плавными линиями. » Иногда Excel изменяет его, когда вы делаете Комбо Также убедитесь, что «Серия1”Не перемещается на вторичную ось — флажок рядом с типом диаграммы не должен быть отмечен.
Нажмите «Ok.”

Шаг № 9: Измените масштаб горизонтальной оси.

Отцентрируйте диаграмму на колоколообразной кривой, отрегулировав масштаб горизонтальной оси. Щелкните правой кнопкой мыши горизонтальную ось и выберите «Ось формата»Из меню.

Когда появится панель задач, сделайте следующее:

Перейти к Параметры оси таб.
Установить Минимальные границы значение «15.”
Установить Максимальные границы значение «125.”

Вы можете настроить диапазон шкалы оси по своему усмотрению, но, поскольку вы знаете диапазоны стандартного отклонения, установите значения границ немного дальше от каждого из ваших третьих стандартных отклонений, чтобы показать «хвост» кривой.

Шаг № 10: Вставьте и разместите метки пользовательских данных.

По мере того, как вы совершенствуете свою диаграмму, не забудьте добавить пользовательские метки данных. Сначала щелкните правой кнопкой мыши любую точку, представляющую Серия «Series2» и выберите «Добавьте метки данных.”

Затем замените метки по умолчанию на те, которые вы установили ранее, и поместите их над маркерами данных.

Щелкните правой кнопкой мыши на любом Серия «Series2» метка данных.
Выбирать «Отформатируйте метки данных.”
На панели задач переключитесь на Параметры метки таб.
Проверить «Значение X» коробка.
Снимите флажок «Значение Y» коробка.
Под «Положение ярлыка,» выбирать «Выше.”

Кроме того, теперь вы можете удалить линии сетки (щелкните их правой кнопкой мыши> Удалить).

Шаг № 11: Перекрасить маркеры данных (необязательно).

Наконец, перекрасьте точки, чтобы они соответствовали вашему стилю диаграммы.

Щелкните правой кнопкой мыши любой Серия «Series2» метка данных.
Щелкните значок «Наполнять» кнопка.
Выберите свой цвет из появившейся палитры.

Также удалите границы вокруг точек:

Снова щелкните правой кнопкой мыши тот же маркер данных и выберите «Контур.”
Выбирать «Без контура.”

Шаг № 12: Добавьте вертикальные линии (необязательно).

В качестве окончательной настройки вы можете добавить на диаграмму вертикальные линии, чтобы подчеркнуть значения SD.

Выберите график диаграммы (таким образом линии будут вставлены прямо в диаграмму).
Перейти к Вставлять таб.
Щелкните значок «Формы» кнопка.
Выбирать «Линия.”

Удерживайте «СДВИГ» при перетаскивании мыши, чтобы нарисовать идеально вертикальные линии от каждой точки до того места, где каждая линия пересекается с колоколообразной кривой.

Измените заголовок диаграммы, и ваша улучшенная кривая колокола будет готова отображать ваши ценные данные о распределении.

И вот как вы это делаете. Теперь вы можете выбрать любой набор данных и создать колоколообразную кривую нормального распределения, выполнив эти простые шаги!

Источник

Наблюдения и советы этой статьи мы подготовили на основании опыта команды Функция ГАУССА вычисляет вероятность того, что член стандартной нормальной совокупности находится между средним значением и стандартным отклонением z от среднего.

Внимание: эта функция ГАУССА доступна только в Excel 2013 и более поздних версиях.

Синтаксис

=GAUSS(z)

аргументы

z (обязательно): Число, которое вы хотите оценить функцией ГАУССА.

Замечания

1. #NUM! ошибка возникает, если z не является допустимым числом;

2. #СТОИМОСТЬ! ошибка возникает, если z не является допустимым типом данных;

3. Если вы используете Excel 2010 и более ранние версии, вы можете применить следующую формулу, чтобы получить тот же результат, что и функция ГАУСС.

=NORM.S.DIST(z,TRUE)-0.5

4. Поскольку НОРМ.СТ.РАСП(0, ИСТИНА) всегда возвращает 0.5, ГАУСС(z) всегда будет на 0.5 меньше результата, возвращаемого функцией НОРМ.СТ.РАСП(z, ИСТИНА).

Возвращаемое значение

Возвращает числовое значение.

Пример

В следующих примерах показано, как использовать функцию ГАУСС в Excel.

Выберите ячейку (например, C6) рядом с числом, по которому вы хотите оценить функцию ГАУССА, введите приведенную ниже формулу и нажмите кнопку Enter ключ, чтобы получить первый результат. Выберите эту ячейку результата, а затем перетащите ее Ручка автозаполнения вниз, чтобы получить остальные результаты.

=GAUSS(B6)

Ноты:

1) Аргумент в приведенной выше формуле предоставляется как ссылка на ячейку. Вы можете напрямую ввести число в качестве аргумента в формуле. Здесь формулу в C6 можно изменить на:

=ГАУСС(1)

2) Если вы используете Excel 2010 и более ранние версии, вы можете применить следующую формулу, чтобы получить тот же результат, что и функция ГАУСС.

=НОРМ.СТ.РАСП(B6,ИСТИНА)-0.5

Лучшие инструменты для работы в офисе

Kutools for Excel — Помогает вам выделиться из толпы

Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.

Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.

Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)

Одна секунда для переключения между десятками открытых документов!
Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.

Комментарии (0)

Оценок пока нет. Оцените первым!

Источник

Содержание

Общие сведения
Моделирование нормальных случайных величин
Вероятность
Плотность вероятности нормального распределения
Распределение Гаусса
Таблица нормального распределения
Нормальное распределение. Построение графика в Excel. Концепция шести сигм
Как построить график с нормальным распределением в Excel
Нормальное распределение в Excel
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.ОБР
Функция НОРМ.РАСП
Функция НОРМРАСПР в EXCEL

Общие сведения

Если величина является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то центрированное и нормированное распределение такой величины при достаточно большом числе слагаемых стремится к нормальному распределению.

Это следует из центральной предельной теоремы теории вероятностей. В окружающем нас мире часто встречаются величины, значение которых определяется совокупностью многих независимых факторов. Этот факт, а также то, что распределение считалось типичным, обычным, привели к тому, что в конце XIX века стал использоваться термин «нормальное распределение». Нормальное распределение играет заметную роль во многих областях науки, например в математической статистике и статистической физике.

Случайная величина, имеющая нормальное распределение, называется нормальной, или гауссовской, случайной величиной.

Моделирование нормальных случайных величин

Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.

Использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.

Вероятность

Вероятность, что подброшенная монета упадёт орлом вверх 50%, что при броске шестигранного кубика выпадет 4 – 16,7%, что завтра на кого-нибудь упадёт метеорит – 0.00000000294%. Это простые примеры, достаточно разделить количество желаемых событий на общее количество случаев и мы получаем вероятность события, но когда результаты эксперимента могут быть не только орлом или решкой (что эквивалентно да/нет), а большим набором данных. Например, вес батона хлеба, если мы возьмём в магазине 1000 буханок хлеба и взвесим каждую, то мы узнаем, что на самом деле батон не весит 400 грамм, результаты будут варьироваться в диапазоне 384-416 грамм (допуск разброса веса предусмотрен ГОСТом).

Плотность вероятности нормального распределения

Такую форму график получит потому, что большинство значений близко к 400. Это – пример нормального распределения, множество событий имеют закон нормального распределения, например, вес или рост для определённого возраста, или среднее время Вашего похода до магазина и многие другие события также подчиняются закону нормального распределения.

Вот так работают маркетологи: проводят опрос 1000 человек и получают представление о всём населении

В случае таблицы Вы имеете дело с дискретными данными, т.е. для каждого веса есть определённая вероятность, но в случае графика дело немного меняется, теперь мы говорим не о 1000 буханок, которые мы взвесили, а обо всех буханках в мире сразу! Зачем? Что бы не взвешивать все буханки. Имея закон распределения, который мы получили взвесив 1000 буханок (мы могли взвесить 100, 200, 500, сколько угодно), мы можем предположить, что сколько бы мы буханок не взяли, замерив их, мы получим ту же форму колокола. Используя термины статистики, все буханки хлеба – это генеральная совокупность, 1000 замеренных буханок – выборка.

Теперь, возьмём одну буханку хлеба, какова вероятность, что её вес будет между 390г и 400г?

Вероятность события между a и b:

P(a ≤ X ≤ b) = P(X ≤ b) – P(X ≤ a)

Распределение вероятности – это функция, в которой для каждого события Х присваивается вероятность p, что событие произойдёт

Распределение Гаусса

Нормальное распределение получило своё название абсолютно справедливо: по статистике, большинство событий происходят именно с вероятностью нормального распределения, но что это значит? Это означает, например, что когда Вы видите на упаковке хлеба обозначение “Вес: 400±16г” – вес батона имеет нормальное распределение со средним значением 400г и стандартным отклонением 16г.

Таблица нормального распределения

Таблица нормального распределения – это затабулированные значения функции нормального распределения.

Для нахождения вероятности события Z₀ можно воспользоваться таблицей нормального распределения ниже. На пересечении строк (n) и столбцов (m) находится значение вероятности n+m.

Z₀	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0	0.500	0.504	0.508	0.512	0.516	0.520	0.524	0.528	0.532	0.536
0.1	0.540	0.544	0.548	0.552	0.556	0.560	0.564	0.568	0.571	0.575
0.2	0.579	0.583	0.587	0.591	0.595	0.599	0.603	0.606	0.610	0.614
0.3	0.618	0.622	0.625	0.629	0.633	0.637	0.641	0.644	0.648	0.652
0.4	0.655	0.659	0.663	0.666	0.670	0.674	0.677	0.681	0.684	0.688
0.5	0.692	0.695	0.699	0.702	0.705	0.709	0.712	0.716	0.719	0.722
0.6	0.726	0.729	0.732	0.736	0.739	0.742	0.745	0.749	0.752	0.755
0.7	0.758	0.761	0.764	0.767	0.770	0.773	0.776	0.779	0.782	0.785
0.8	0.788	0.791	0.794	0.797	0.799	0.802	0.805	0.808	0.811	0.813
0.9	0.816	0.819	0.821	0.824	0.826	0.829	0.832	0.834	0.837	0.839
1	0.841	0.844	0.846	0.849	0.851	0.853	0.855	0.858	0.860	0.862
1.1	0.864	0.867	0.869	0.871	0.873	0.875	0.877	0.879	0.881	0.883
1.2	0.885	0.887	0.889	0.891	0.892	0.894	0.896	0.898	0.900	0.901
1.3	0.903	0.905	0.907	0.908	0.910	0.911	0.913	0.915	0.916	0.918
1.4	0.919	0.921	0.922	0.924	0.925	0.926	0.928	0.929	0.931	0.932
1.5	0.933	0.934	0.936	0.937	0.938	0.939	0.941	0.942	0.943	0.944
1.6	0.945	0.946	0.947	0.948	0.950	0.951	0.952	0.953	0.954	0.955
1.7	0.955	0.956	0.957	0.958	0.959	0.960	0.961	0.962	0.963	0.963
1.8	0.964	0.965	0.966	0.966	0.967	0.968	0.969	0.969	0.970	0.971
1.9	0.971	0.972	0.973	0.973	0.974	0.974	0.975	0.976	0.976	0.977
2	0.977	0.978	0.978	0.979	0.979	0.980	0.980	0.981	0.981	0.982
2.1	0.982	0.983	0.983	0.983	0.984	0.984	0.985	0.985	0.985	0.986
2.2	0.986	0.986	0.987	0.987	0.988	0.988	0.988	0.988	0.989	0.989
2.3	0.989	0.990	0.990	0.990	0.990	0.991	0.991	0.991	0.991	0.992
2.4	0.992	0.992	0.992	0.993	0.993	0.993	0.993	0.993	0.993	0.994
2.5	0.994	0.994	0.994	0.994	0.995	0.995	0.995	0.995	0.995	0.995
2.6	0.995	0.996	0.996	0.996	0.996	0.996	0.996	0.996	0.996	0.996
2.7	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997
2.8	0.997	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998
2.9	0.998	0.998	0.998	0.998	0.998	0.998	0.999	0.999	0.999	0.999
3	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999
3.1	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999
3.2	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	1.000
Таблица нормального распределения. Красным выделены часто используемые значения при выборе критической области

Нормальное распределение. Построение графика в Excel. Концепция шести сигм

Наверное, не все знают, что в Excel есть встроенная функция для построения нормального распределения. Графики нормального распределения часто используются для демонстрации идей статистической обработки данных.

Функция НОРМРАСП имеет следующий синтаксис:

НОРМРАСП (Х; среднее; стандартное_откл; интегральная)

Х — аргумент функции; фактически НОРМРАСП можно трактовать как y=f(x); при этом функция возвращает вероятность реализации события Х

Среднее (µ) — среднее арифметическое распределения; чем дальше Х от среднего, тем ниже вероятность реализации такого события

Стандартное_откл (σ) — стандартное отклонение распределения; мера кучности; чем меньше σ, тем выше вероятность у тех Х, которые расположены ближе к среднему

Интегральная — логическое значение, определяющее форму функции. Если «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения, тот есть суммарную вероятность всех событий для аргументов от -∞ до ХХ, точнее говоря, вероятность событий находящихся в некотором диапазоне вокруг Х

Например, для µ=0 имеем:

Здесь по оси абсцисс единица измерения – σ, или (что то же самое), можно сказать, что график построен для σ = 1. То есть, «-2» на графике означает -2σ. По оси ординат шкала убрана умышленно, так как она лишена смысла. Точнее говоря, высота кривой зависит от плотности точек на оси абсцисс, по которым мы строим график. Например, если на интервал от 0 до 1σ приходится 10 точек, то высота в максимуме составит 4%, а если 20 точек – 2%. Здесь проценты означают вероятность попадания случайной величины в узкий диапазон окрестности точки на оси абсцисс. Зато имеет смысл площадь под кривой на определенном интервале. И эта площадь не зависит от плотности точек. Так, например, площадь под кривой на интервале от 0 до 1σ составляет 34,13%. Это значение можно интерпретировать следующим образом: с вероятностью 68,26% случайная величина Х попадет в диапазон µ ± σ.

Теперь, наверное, вам будет лучше понятен смысл выражения «качество шести сигм». Оно означает, что производство налажено таким образом, что случайная величина Х (например, диаметр вала) находясь в диапазон µ ± 6σ, всё еще удовлетворяет техническим условиям (допускам). Это достигается за счет значительного уменьшения сигмы, то есть случайная величина Х очень близка к нормативному значению µ. На графике ниже представлено три ситуации, когда границы допуска остаются неизменными, а благодаря повышению качества (уменьшению вариабельности, сужению сигма) доля брака сокращается:

На первом рисунке только 1,5σ попадают в границы допуска, то есть только 86,6% деталей являются годными. На втором рисунке уже 3σ попадают в границы допуска, то есть 99,75% являются годными. Но всё еще 25 деталей из каждых 10 000 произведенных являются браком. На третьем рисунке целых 6σ попадают в границы допуска, то есть в брак попадут только две детали на миллиард изготовленных!

Вообще-то говоря, измерение качества в терминах сигм использует не совсем нормальное распределение. Вот что пишет на эту тему Википедия:

Опыт показывает, что показатели процессов имеют тенденцию изменяться с течением времени. В результате со временем в промежуток между границами поля допуска будет входить меньше, чем было установлено первоначально. Опытным путём было установлено, что изменение параметров во времени можно учесть с помощью смещения в 1,5 сигма. Другими словами, с течением времени длина промежутка между границами поля допуска под кривой нормального распределения уменьшается до 4,5 сигма вследствие того, что среднее процесса с течением времени смещается и/или среднеквадратическое отклонение увеличивается.

Широко распространённое представление о «процессе шесть сигма» заключается в том, что такой процесс позволяет получить уровень качества 3,4 дефектных единиц на миллион готовых изделий при условии, что длина под кривой слева или справа от среднего будет соответствовать 4,5 сигма (без учёта левого или правого конца кривой за границей поля допуска). Таким образом, уровень качества 3,4 дефектных единиц на миллион готовых изделий соответствует длине промежутка 4,5 сигма, получаемых разницей между 6 сигма и сдвигом в 1,5 сигма, которое было введено, чтобы учесть изменение показателей с течением времени. Такая поправка создана для того, чтобы предупредить неправильною оценку уровня дефектности, встречающееся в реальных условиях.

С моей точки зрения, не вполне внятное объяснение. Тем не менее, во всем мире принята следующая таблица соответствия числа дефектов и уровня качества в сигмах:

Как построить график с нормальным распределением в Excel

Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.

Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.

Нормальное распределение в Excel

В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.

Функция НОРМ.СТ.РАСП

=НОРМ.СТ.РАСП(z;интегральная)

z – значение стандартизованной переменной

интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).

Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).

Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.

Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.

Функция НОРМ.СТ.ОБР

=НОРМ.СТ.ОБР(вероятность)

вероятность – это вероятность.

Функция НОРМ.РАСП

=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)

стандартное_откл – среднеквадратичное отклонение – второй параметр модели

интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).

Функция НОРМРАСПР в EXCEL

Щелкнем на кнопке ОК. В диапазоне А4:А16 будет сформирована последовательность значений х.

Установим курсор в ячейку В4 и выполним команду меню Вставка/Функция. В открывшемся окне Мастер функций выберем категорию Статистические, а в списке функций – НОРМРАСП.

Установим значения параметров функции НОРМРАСП: для параметра х установим ссылку на ячейку А4, для параметра Среднее – введем число 0, для параметра Стандартное_откл – число 1, для параметра Интегральное – число 0 (весовая).

Источники

https://ru.wikipedia.org/wiki/%D0%9D%D0%BE%D1%80%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5
https://dic.academic.ru/dic.nsf/ruwiki/1116983
https://k-tree.ru/tools/statistics/normal.php
https://excelka.ru/voprosy/kak-v-excel-postroit-krivuyu-normalnogo-raspredeleniya.html
https://statanaliz.info/statistica/teoriya-veroyatnostej/normalnoe-raspredelenie-v-excel/
http://bourabai.ru/einf/excel_diagram.htm

Источник

Глава 2

Глава 2.

Нормальный закон
распределения. Функция Гаусса.

Откройте программу
Excel.
Если Вы выполняли задания по информатике
раньше и сохранили свой файл, откройте
его. Задание выполняйте на новом листе.
Введите его название: нормальный
закон распределения.
В ячейку G1
введите дату выполнения работы, в ячейку
G2
– факультет
и номер группы, в ячейку G3
– фамилии
студентов, выполняющих работу.

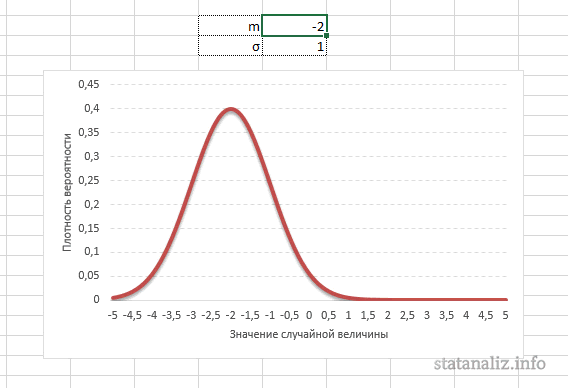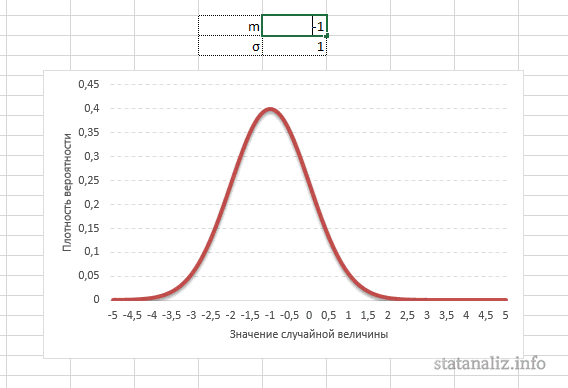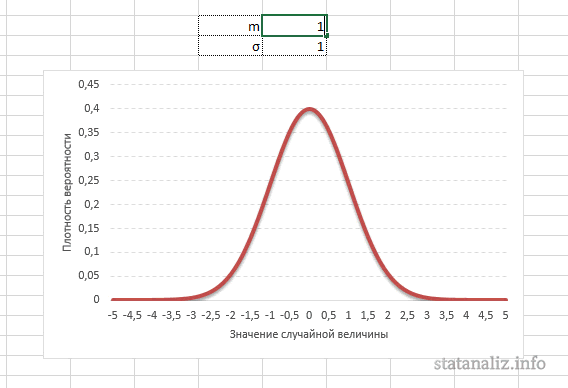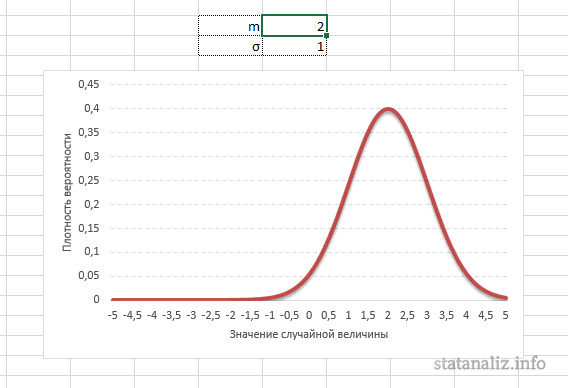
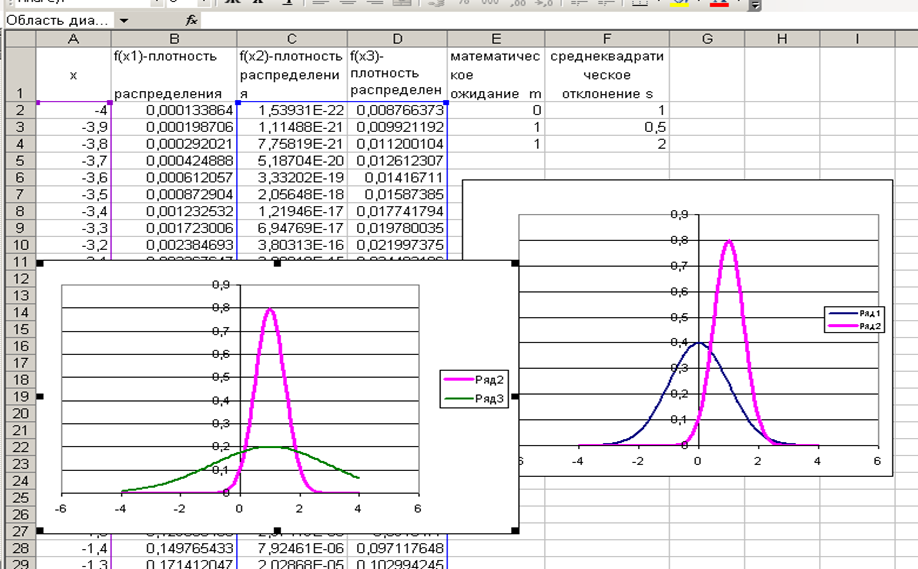
Задание 1. а)
Построить
на одной диаграмме на интервале х
є
[-4;
4] с шагом
0,1 три графика при разных значениях
параметров µ и :

1) µ = 0 и 
= 1,

2) µ = 1 и 
= 0.5,

3) µ = 1 и 
= 2.

б) определить,
как меняется вид графика при изменении
параметров µ и .

в) определить
x
и y
координаты максимума и точек перегиба
функции f(x).

Нормальный закон
распределения плотности вероятности
f(x)
непрерывной случайной величины x
описывается выражением (функцией
Гаусса):
.

Рис. 2.1

Выполнение
задания. Для
вычисления f(x)
используйте
математические функции КОРЕНЬ(Х) и
EXP(X)
= e^x.
Значения параметров µ и 
задайте в
отдельных ячейках.

Столбец для х
заполните заданными значениями (начиная
с –4, используя набор команд Правка
— Заполнить — Прогрессия).
Для заполнения столбца значений f(x)
введите
формулу в одну ячейку и используйте
Копировать
и
Вставить.

Внимание.
При построении
графиков в программе Мастер
диаграмм
следует пользоваться типом диаграммы:
точечная.
Именно этот тип диаграммы позволяет
построить изображение в масштабе по
обеим осям (см. рис. 2.2).

Рис. 2.2.

Задание 2.
Выполнить построение графиков задания
1, вычисляя функцию плотности распределения
с помощью статистической функции
НОРМРАСП. Сравнить полученные результаты.

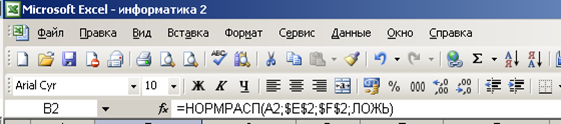
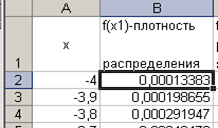
Выполнение
задания.
Задание выполняйте на новом листе.
Введите его название: нормальный
закон распределения(2).

В
Excel
существует
специальная статистическая функция с
четырьмя параметрами НОРМРАСП(
x,
среднее, стандартное откл, интегральная)
для расчета
нормального закона распределения.
Первые три параметра используются в
функции Гаусса. Для четвертого параметра
справка Excel
дает следующую информацию: интегральная
– это логическое значение, определяющее
форму функции. Если интегральная
имеет значение
ИСТИНА, то функция НОРМРАСП возвращает
интегральную функцию распределения;
если этот аргумент имеет значение ЛОЖЬ,
то возвращается функция плотности
распределения. Функция плотности
распределения – это и есть функция
Гаусса (см. рис. 2.3).

Рис. 2.3

Для задания
статистической функции НОРМРАСП
используйте Мастер
функций. В
окне Аргументы
функции в
строке интегральная
наберите слово ложь.
Выглядеть это должно примерно так, как
на рис. 2.4. При выделении ячейки, содержащей
формулу, Excel
показывает
связи ячеек:

Рис. 2.4.

Задание 3.
Даны три случайные величины Х₁,
Х₂
, Х₃,
распределенные по нормальному закону
с разными значениях параметров μ
и 

для Х₁μ
= 0, 
= 1;

для
Х₂ μ
= 1, 
= 0,5;

для Х₃ μ
= 1, 
= 2.

Для всех трех
величин рассчитать вероятности того,
что они лежат в интервалах от μ-
до μ+,
от μ-2
до μ+2
и от μ-3
до μ+3.

Внимание.
Для нахождения
вероятности P(a
< x
< b)
того, что случайная величина x,
распределенная по нормальному закону
со средним значением μ
и среднеквадратическим отклонением 
лежит в интервале от а
до b,
необходимо вычислить интеграл:
.
Этот интеграл можно представить в виде
разности интегралов
,
а интеграл

задается в Excel
с помощью функции НОРМРАСП с четвертым
параметром интегральная
ИСТИНА. Таким
образом, вероятность вычисляется как
разность

P(a
< x
< b)
= НОРМРАСП( b,
μ,
,
истина) —

— НОРМРАСП( а,
μ,
,
истина)

Задание 4а.
Предположим, что длительность цикла
работы сердца распределена по нормальному
закону. Построить кривую распределения
плотности вероятности для длительности
цикла работы сердца (в секундах).
Необходимые параметры задать
самостоятельно. Рассчитать вероятность
того, что длительность цикла лежит в
интервале от 0,7 до 0,9 с.

Задание 4б.
Предположим, что длительность дыхательного
цикла распределена по нормальному
закону. Построить кривую распределения
плотности вероятности для длительности
дыхательного цикла (в секундах).
Необходимые параметры задать
самостоятельно. Рассчитать вероятность
того, что длительность цикла лежит в
интервале от 3 до 5 с.

Задание 5а.
Предположим, что рост мужчин и рост
женщин распределены по нормальному
закону. Построить на одной диаграмме
две кривые распределения плотности
вероятности для роста мужчин и женщин.
Необходимые параметры задать
самостоятельно.

Задание 5б.
Предположим, что систолическое давление
у здоровых людей и у людей с диагнозом
гипертония распределены по нормальному
закону. Построить на одной диаграмме
две кривые распределения плотности
вероятности для систолического давления.
Необходимые параметры задать
самостоятельно.

Задание 5в.
Предположим, что размеры (в см) грудной
клетки, грудной клетки на вдохе и на
выдохе у взрослых мужчин распределены
по нормальному закону. Построить на
одной диаграмме три кривые распределения
плотности вероятности для размера
грудной клетки, грудной клетки на вдохе
и на выдохе у взрослых мужчин. Необходимые
параметры задать самостоятельно.

Задание 5г.
Предположим, что рост школьников,
студентов и баскетболистов распределены
по нормальному закону. Построить на
одной диаграмме три кривые распределения
плотности вероятности для роста
школьников, студентов и баскетболистов.
Необходимые параметры задать
самостоятельно.

Окончание
работы.

После выполнения
заданий сохраните файл в папке ИНФОРМАТИКА
под именем, содержащем номер группы и
фамилии тех, кто выполнял работу.
Например, 92гр.Иванов,Петров

Контрольные
вопросы к занятию по информатике:

Нормальный
закон распределения. Функция Гаусса.

Нормальный закон
распределения плотности вероятности
непрерывной случайной величины.
График функции
Гаусса
.
Координаты
максимума и точек перегиба функции.
Параметры
нормального закона распределения:
математическое ожидание µ (среднее
значение) и среднеквадратическое
отклонение .
Как меняется
график функции плотности вероятности
при изменении параметров µ и ?
Чему равна
вероятность того, что случайная величина,
распределенная по нормальному закону,
лежит в интервалах а) [ µ — 3 ;
µ + 3 ],
б) [ µ -2 ;
µ +2],
в) [ µ — ;
µ + ]?
Правило трех сигм
().

Литература

Морозов Ю.В. Основы
высшей математики и статистики. М.
Медицина, 1998

Стр.124 — 128

Соседние файлы в папке методичка_1

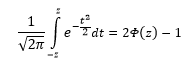
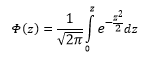
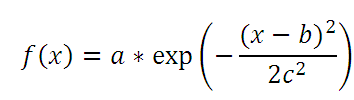
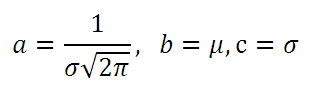
Источник