Access для Microsoft 365 Access 2021 Access 2019 Access 2016 Access 2013 Access 2010 Access 2007 Еще…Меньше
Возвращает double, указывающий платеж для аннуитета на основе периодических фиксированных платежей и фиксированной процентной ставки.
Синтаксис
Pmt(
ставка,
кпер
,
пс
[ ,пс ] [ ,тип ] )
Синтаксис функции PMT имеет указанные здесь аргументы.
|
Аргумент |
Описание |
|
|
Обязательный аргумент. Значение double, обозначающее процентную ставку за период. Например, если вы берете кредит на автомобиль с годовой процентной ставкой, равной 10 %, и ежемесячными выплатами, ставка за период будет равна 0,1/12 (0,0083). |
|
|
Обязательный аргумент. Целое число, указывающее общее количество периодов оплаты. Например, при ежемесячных выплатах по четырехгодичному кредиту на машину число периодов выплат равно 4*12 (или 48). |
|
|
Обязательный аргумент. Двойной номер, определяющий стоимость (или общую сумму), которая на данный момент оценивается в ряд платежей, которые будут выплачиваться в будущем. Например, при получении кредита на покупку автомобиля сумма кредита для кредитора равноценна будущим ежемесячным платежам по кредиту. |
|
|
Необязательный аргумент. Вариант, обозначающий будущую стоимость или баланс, которые вы хотите достичь после последней выплаты. Например, будущая стоимость для займа равна 0 р., поскольку это значение останется после последней выплаты. Но если вы хотите накопить за 18 лет 50 000 $ на образование ребенка, будущая стоимость равна 50 000 $. Если этот аргумент не задан, используется значение 0. |
|
|
Необязательный аргумент. Вариант, определяющий, когда должна производиться выплата. Укажите значение 0, если платежи выплачиваются в конце периода оплаты, или 1, если они выплачиваются в начале периода. Если этот аргумент не задан, используется значение 0. |
Замечания
Выплатами называется ряд фиксированных платежей наличными, которые выполняются в определенный период времени. Это может быть заём (например, ипотека) или инвестиция (например, сберегательный вклад с ежемесячным пополнением).
При вычислении значений ставка и кпер нужно использовать периоды оплаты, выраженные в одних и тех же единицах. Например, если ставка вычисляется с использованием месяцев, значение кпер также должно рассчитываться с использованием месяцев.
Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.
Пример запроса
|
|
|
|
SELECT PMTSample.*, Pmt([AnnualRate]/12,[TermInYears]*12,-[LoanAmount],0,0) AS MonthlyRepayments FROM PMTSample; |
Возвращает все поля из таблицы «PMTSample», вычисляет фиксированные ежемесячные платежи, необходимые для выплаты «LoanAmount» на основе «AnnualRate», и отображает результаты в столбце MonthlyRepayments. |
Пример VBA
Примечание: В примерах ниже показано, как использовать эту функцию в модуле Visual Basic для приложений (VBA). Чтобы получить дополнительные сведения о работе с VBA, выберите Справочник разработчика в раскрывающемся списке рядом с полем Поиск и введите одно или несколько слов в поле поиска.
В этом примере функция Pmt используется для возврата ежемесячного платежа по кредиту за фиксированный период. Дано процентная ставка за период (APR / 12), общее количество платежей (TotPmts), стоимость (к настоящему моменту) или основной суммы займа (PVal), будущая стоимость займа (FVal) и число, которое указывает, должна ли выплата быть выплатой в начале или в конце периода (PayType).
Dim Fmt, FVal, PVal, APR, TotPmts, PayType, Payment
' When payments are made.
Const ENDPERIOD = 0, BEGINPERIOD = 1
Fmt = "###,###,##0.00" ' Define money format.
FVal = 0 ' Usually 0 for a loan.
PVal = InputBox("How much do you want to borrow?")
APR = InputBox("What is the annual " & _
"percentage rate of your loan?")
If APR > 1 Then APR = APR / 100 ' Ensure proper form.
TotPmts = InputBox("How many monthly " & _
"payments will you make?")
PayType = MsgBox("Do you make payments " & _
"at the end of month?", vbYesNo)
If PayType = vbNo Then
PayType = BEGINPERIOD
Else PayType = ENDPERIOD
End If
Payment = Pmt(APR / 12, TotPmts, -PVal, FVal, PayType)
MsgBox "Your payment will be " & _
Format(Payment, Fmt) & " per month."
Нужна дополнительная помощь?
Функция
ПЛТ(
)
, английский вариант PMT(),
позволяет рассчитать месячную сумму платежа по кредиту в случае аннуитетных платежей (когда за кредит платится равными частями).
Блок статей, посвященных теории и расчетам параметров аннуитета
размещен здесь
. В этой статье рассмотрены только синтаксис и примеры использования функции
ПЛТ()
.
Синтаксис функции
ПЛТ()
ПЛТ(ставка; кпер; пс; [бс]; [тип])
Ставка.
Процентная ставка по кредиту (ссуде).
Кпер.
Общее число выплат по кредиту.
пс.
Сумма кредита.
Бс.
Необязательный аргумент. Требуемое значение остатка по кредиту после последнего платежа. Если этот аргумент опущен, предполагается, что он равен 0 (кредит будет полностью возвращен).
Тип.
Необязательный аргумент. Принимает значение 0 (нуль) или 1. Если =0 (или опущен), то принимается, что регулярный платеж осуществляется в конце периода, если 1, то в начале периода (сумма регулярного платежа будет несколько меньше).
Выплаты, возвращаемые функцией
ПЛТ()
, включают основные платежи и платежи по процентам, но не включают налогов, резервных платежей или комиссий, иногда связываемых со ссудой.
Пример 1
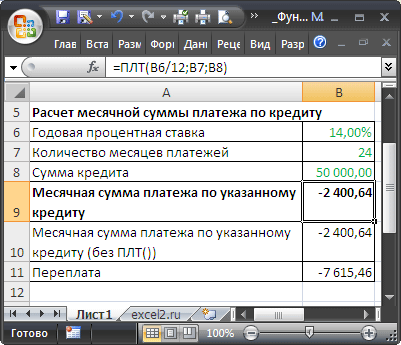
Предположим, человек планирует взять кредит в размере 50 000 руб. (ячейка
В8
) в банке под 14% годовых (
B6
) на 24 месяца (
В7
) (см.
файле примера
).
Расчет Месячной суммы платежа по такому кредиту с помощью функции
ПЛТ()
=ПЛТ(B6/12;B7;B8)
СОВЕТ
: Убедитесь, что Вы последовательны в выборе временных единиц измерения для задания аргументов «ставка» и «кпер». В нашем случае рассчитываются
ежемесячные
выплаты по двухгодичному займу (24
месяца
) из расчета 14 процентов годовых (
14% / 12 месяцев
).
Расчет Месячной суммы платежа по такому кредиту с помощью БЕЗ функции
ПЛТ()
=-B8*(B6/12*(1+B6/12)^B7)/((1+B6/12)^B7-1)
Для нахождения суммы переплаты, умножьте возвращаемое функцией
ПЛТ()
значение на «кпер» (получите число со знаком минус) и прибавьте сумму кредита. В нашем случае переплата составит 7 615,46 руб. (за 2 года).
Пример 2
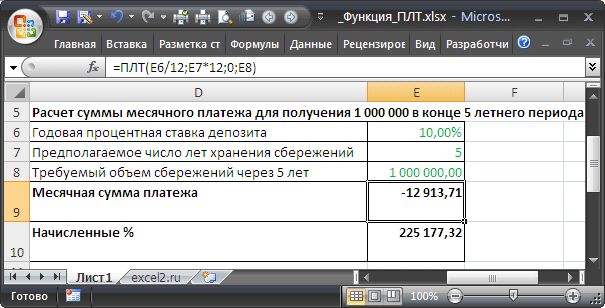
Предположим, человек планирует ежемесячно откладывать деньги, чтобы скопить через 5 лет (ячейка
E7
) 1 млн. рублей (
E8
). Деньги ежемесячно он планирует относить в банк и пополнять свой вклад. В банке действует процентная ставка 10% (
E6
) и человек полагает, что она будет действовать без изменений в течение 5 лет. Какую сумму человек должен ежемесячно относить в банк, чтобы таким образом через 5 лет скопить 1 млн. руб.? (см.
файле примера
).
Расчет ежемесячной суммы платежа в таком случае можно также с помощью функции
ПЛТ()
=ПЛТ(E6/12;E7*12;0;E8)
К концу 5 летнего периода сумма начисленных процентов составит более 225 тыс. руб., т.е. если бы человек просто складывал бы деньги себе в сейф, то он скопил бы только порядка 775 тыс. руб.
Функция ПЛТ возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки.
Описание функции ПЛТ
Возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки.
Синтаксис
=ПЛТ(ставка; кпер; пс; [бс]; [тип])Аргументы
ставкакперпсбстип
Обязательный. Процентная ставка по ссуде.
Обязательный. Общее число выплат по ссуде.
Обязательный. Приведенная (текущая) стоимость, т. е. общая сумма, которая на данный момент равноценна ряду будущих платежей, называется также «основной суммой».
Необязательный. Значение будущей стоимости, т. е. желаемого остатка средств после последнего платежа. Если аргумент «бс» опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0).
Необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата.
| Тип | Когда нужно платить |
|---|---|
| 0 или опущен | В конце периода |
| 1 | В начале периода |
Замечания
- Выплаты, возвращаемые функцией ПЛТ, включают основные платежи и платежи по процентам, но не включают налогов, резервных платежей или комиссий, иногда связываемых со ссудой.
- Убедитесь, что вы последовательны в выборе единиц измерения для задания аргументов «ставка» и «кпер». Если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12 процентов годовых, то используйте значения 12%/12 для задания аргумента «ставка» и 4*12 для задания аргумента «кпер». Если вы делаете ежегодные платежи по тому же займу, то используйте 12 процентов для задания аргумента «ставка» и 4 для задания аргумента «кпер».
Примеры
Пример1Пример задачи1
Задача
Клиент банка осуществляет заем в размере 5000 руб. под 6% годовых на 6 месяцев. Определить ежемесячные платежи клиента. Платежи осуществляются в конце месяца.
Решение
Введем первоначальные данные:

Заполним поля функции:
Ответ: ежемесячные платежи составят 847,98 руб.
Отметим, что для банка выданный кредит – это отрицательная величина, а рассчитанные ежемесячные поступления от клиента – положительная величина.
Файл с решением
В Функция PMT в Excel — это финансовая функция, используемая для расчета выплаты ссуды на основе платежей и процентных ставок. Формула функции PMT: PMT (ставка; кпер; пв;[fv], [type]).
Синтаксис функции PMT
- Ставка: Процентная ставка по кредиту (обязательно).
- Nper: Общее количество платежей по кредиту (обязательно).
- Pv: Приведенная стоимость или общая сумма, которой сейчас стоит серия будущих платежей (обязательно).
- FV: Баланс, которого вы хотите достичь после последнего оплаченного платежа или будущих платежей (необязательно).
- Тип: Цифра ноль или единица указывает срок выплаты.
В этом уроке мы хотим найти ежемесячный платеж.
Открыть Майкрософт Эксель.
Используйте существующую таблицу или создайте таблицу.
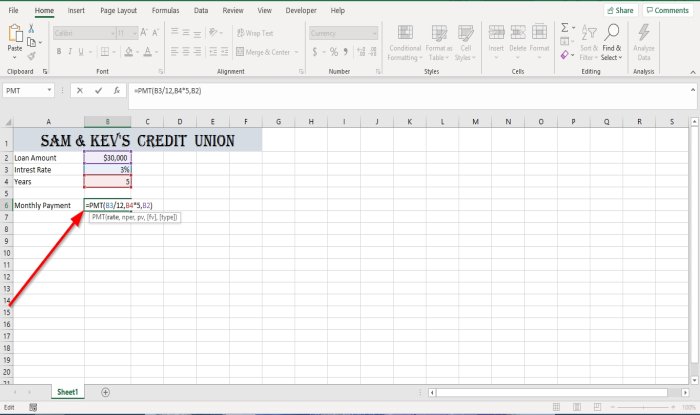
В ячейке напротив ежемесячного платежа введите = PMT затем скобка.
Внутри скобки введите B3 потому что это ячейка, содержащая процентную ставку. Затем разделите B3 к двенадцатый (B3 / 12) для преобразования годовой процентной ставки в ежемесячную. Затем поместите запятая.
Тип B4, потому что это ячейка, которая содержит год, который будет способствовать общим платежам по ссуде, но поскольку мы платим ежемесячные платежи, мы должны умножить количество лет на двенадцатую на количество платежей (b4 * 12). потом Запятая.
Теперь мы введем приведенную стоимость ссуды (Pv) — сумма кредита в ячейке Би 2.
Затем закройте скобку и нажмите Enter; вы увидите результаты.
Есть два других варианта использования функции PMT.
Первый вариант — щелкнуть Вставить функцию (FX) в верхней части таблицы.
An Вставить функцию диалоговое окно откроется.
В диалоговом окне «Вставить функцию» выберите Финансовые категория.
Выбирать ГУП в группе Выбор функции и щелкните Ok.
А Аргументы функции появится диалоговое окно.
Внутри диалогового окна, где вы видите Ставка, тип B3 / 12 в поле ввода.
Где ты видишь Nper тип B4 * 12 в поле ввода.
Где ты видишь Pv, тип Би 2и щелкните Ok, вы увидите результаты.
Fv и Тип необязательны; они не нужны.
Вариант два — нажать кнопку Формулы таб.
На Формула вкладку, щелкните значок Финансированиеl кнопка в Библиотека функций группа и выберите ГУП.
An Аргументы Функция появится диалоговое окно.
в Аргументы Функция диалоговое окно сделайте то же самое, что упомянуто выше в первом варианте, чтобы увидеть результаты.
Читать: Как использовать функцию DSUM в Microsoft Excel.
Если у вас есть вопросы, оставьте комментарий ниже.
Формула для расчета аннуитетного платежа выглядит следующим образом:
Обозначение аргументов:
A – сумма кредита;
R – процентная ставка;
N – срок кредита;
Пример
Предположим мы хотим взять кредит на 50000 рублей, под 25% годовых на 30 месяцев, подставим известные значения в формулу, чтобы получить сумму месячного аннуитетного платежа, получается:
A = 50000 (сумма кредита)
R = 0.25/12 (месячная процентная ставка)
N = 30 (срок кредита в месяцах)
В результате расчета этой формулы мы получим значение 2258.158, это означает, что тридцать месяцев нам придется выплачивать эту сумму.
Расчет аннуитетного платежа с помощью Excel
Для расчета месячного платежа в Excel есть функция PMT (ПЛТ на русском).
Функция PMT имеет синтаксис: =PMT(rate, nper, pv, [fv],[type])
Аргументы функции PMT(ПЛТ):
rate — процентная ставка;
nper – срок кредита;
pv – сумма кредита;
аргументы [fv] и [type] являются необязательными, [fv] – значение будущей стоимости, аргумент [type] определяет, когда нужно платить он может быть равен 0 – в конце периода (по умолчанию) и 1 – в начале периода.
Возьмем за основу пример выше, подставим значения в эту функцию и сравним результат (перед сумой кредита нужно поставить знак минус, чтобы получить положительное число).
Как видим, значения совпадают, мы можем изменить формат ячейки на числовой и увидеть неокругленную сумму 2258,158162640140
Расчет аннуитетного платежа с помощью SAS
В SAS есть очень гибкая функция mort, с помощью которой можно вычислять не только сумму месячного аннуитетного платежа, но и сумму кредита, ставку и срок.
Функция mort имеет следующий синтаксис: MORT(a,p,r,n).
Аргументы функции mort
a – сумма кредита;
p – платеж;
r – процентная ставка;
n – срок кредита;
Наша цель определить сумму месячного аннуитетного платежа, подставим в правильном порядке значения из предыдущего примера в функцию mort, для второго аргумента поставим символ точку «.» получим следующий код:
data mort_example;
payment = mort(50000, . , 0.25/12, 30);
run;
proc print data=mort_example;
run;
После выполнения данного кода увидим результат:
Как было написано выше, с помощью функции mort можно вычислять любые другие неизвестные аргументы, предположим мы знаем сумму месячного платежа, сумму кредита и ставку, требуется вычислить срок, тогда функция вызываться должна так:
term = mort( 50000, 2258.16 , 0.25/12, .);
Расчет аннуитетного платежа с помощью Oracle PL SQL
В БД Oracle нет встроенной функции для расчета месячного аннуитетного платежа, но её довольно просто написать самому, например вот так:
create or replace function getMortPayment(pAmount in number,
pRate in number,
pTerm in number ) return number
is
/*Формула расчета месячного аннуитетного платежа
p := a * r * ((1+r)^n) / ((1+r)^n) -1; */
vPayment number;
begin
vPayment := pAmount * pRate* power((1+pRate),pTerm)/
(power((1+pRate),pTerm)-1) ;
return vPayment;
end;
Вызовем функцию
select getMortPayment(pAmount => 50000, pRate => 0.25/12, pTerm => 30) as p from dual
Получим результат 2258,15816264014
Как видим, рассчитать месячный аннуитетный платеж совсем не сложно