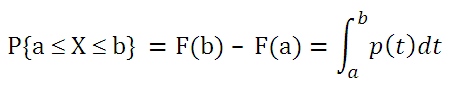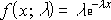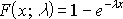Функция плотности вероятности в excel

Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта

www.excel2.ru

. Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL

.

Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.

Генеральная совокупность и случайная величина

Пусть у нас имеется

генеральная совокупность

(population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.

Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.

Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения

генеральная совокупность

представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.

В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.

Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является

случайной величиной

. По определению, любая

случайная величина

имеет

функцию распределения

, которая обычно обозначается F(x).

Функция распределения

Функцией распределения

вероятностей

случайной величины

Х называют функцию F(x), значение которой в точке х равно вероятности события X

F(x) = P(X

Поясним на примере нашего станка. Хотя предполагается, что наш станок производит только один тип деталей, но, очевидно, что вес изготовленных деталей будет слегка отличаться друг от друга. Это возможно из-за того, что при изготовлении мог быть использован разный материал, а условия обработки также могли слегка различаться и пр. Пусть самая тяжелая деталь, произведенная станком, весит 200 г, а самая легкая — 190 г. Вероятность того, что случайно выбранная деталь Х будет весить меньше 200 г равна 1. Вероятность того, что будет весить меньше 190 г равна 0. Промежуточные значения определяются формой Функции распределения. Например, если процесс настроен на изготовление деталей весом 195 г, то разумно предположить, что вероятность выбрать деталь легче 195 г равна 0,5.

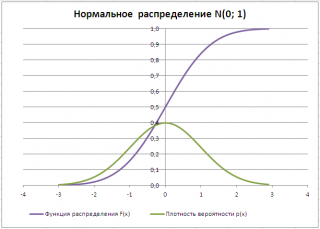
Типичный график

Функции распределения

для непрерывной случайной величины приведен на картинке ниже (фиолетовая кривая, см.

файл примера

):

В справке MS EXCEL

Функцию распределения

называют

Интегральной

функцией распределения

(

Cumulative

Distribution

Function

,

CDF

).

Приведем некоторые свойства

Функции распределения:

• 
  Функция распределения
  
  F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
• 
  Функция распределения
  
  – неубывающая функция;
• Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x
  
  ₁
  <=X
  2

  )=F(x
  
  ₂
  
  )-F(x
  
  ₁
  
  ).

Существует 2 типа распределений:

непрерывные распределения

и

дискретные распределения

.

Дискретные распределения

Если случайная величина может принимать только определенные значения и количество таких значений конечно, то соответствующее распределение называется

дискретным

. Например, при бросании монеты, имеется только 2 элементарных исхода, и, соответственно, случайная величина может принимать только 2 значения. Например, 0 (выпала решка) и 1 (не выпала решка) (см.

схему Бернулли

). Если монета симметричная, то вероятность каждого исхода равна 1/2. При бросании кубика случайная величина принимает значения от 1 до 6. Вероятность каждого исхода равна 1/6. Сумма вероятностей всех возможных значений случайной величины равна 1.

Примечание

: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье

Распределения случайной величины в MS EXCEL

.

Непрерывные распределения и плотность вероятности

В случае

непрерывного распределения

случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для

непрерывной случайной величины

равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой

функции плотности распределения p(x)

. Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение

функции распределения

на этом интервале:

Как видно из формулы выше

плотность распределения

р(х) представляет собой производную

функции распределения

F(x), т.е. р(х) = F’(x).

Типичный график

функции плотности распределения

для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):

Примечание

: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье

Распределения случайной величины в MS EXCEL

.

В литературе

Функция плотности распределения

непрерывной случайной величины может называться:

Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF)

.

Чтобы все усложнить, термин

Распределение

(в литературе на английском языке —

Probability

Distribution

Function

или просто

Distribution

)

в зависимости от контекста может относиться как

Интегральной

функции распределения,

так и кее

Плотности распределения.

Из определения

функции плотности распределения

следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от

Функции распределения,

больше 1. Например, для

непрерывной равномерной величины

, распределенной на интервале [0; 0,5]

плотность вероятности

равна 1/(0,5-0)=2. А для

экспоненциального распределения

с параметром

лямбда

=5, значение

плотности вероятности

в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.

Напомним, что

плотность распределения

является производной от

функции распределения

, т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что

плотность распределения

>1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере

экспоненциального распределения

).

Примечание

: Площадь, целиком заключенная под всей кривой, изображающей

плотность распределения

, равна 1.

Примечание

: Напомним, что функцию распределения F(x) называют в функциях MS EXCEL

интегральной функцией распределения

. Этот термин присутствует в параметрах функций, например в

НОРМ.РАСП

(x; среднее; стандартное_откл;

интегральная

). Если функция MS EXCEL должна вернуть

Функцию распределения,

то параметр

интегральная

, д.б. установлен ИСТИНА. Если требуется вычислить

плотность вероятности

, то параметр

интегральная

, д.б. ЛОЖЬ.

Примечание

: Для

дискретного распределения

вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL

плотность вероятности

может называть даже «функция вероятностной меры» (см. функцию

БИНОМ.РАСП()

).

Вычисление плотности вероятности с использованием функций MS EXCEL

Понятно, что чтобы вычислить

плотность вероятности

для определенного значения случайной величины, нужно знать ее распределение.

Найдем

плотность вероятности

для

стандартного нормального распределения

N(0;1) при x=2. Для этого необходимо записать формулу

=НОРМ.СТ.РАСП(2;ЛОЖЬ)

=0,054 или

=НОРМ.РАСП(2;0;1;ЛОЖЬ)

.

Напомним, что

вероятность

того, что

непрерывная случайная величина

примет конкретное значение x равна 0. Для

непрерывной случайной величины

Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).

Вычисление вероятностей с использованием функций MS EXCEL

1) Найдем вероятность, что случайная величина, распределенная по

стандартному нормальному распределению

(см. картинку выше), приняла положительное значение. Согласно свойству

Функции распределения

вероятность равна F(+∞)-F(0)=1-0,5=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу

=НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА)

=1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).

2) Найдем вероятность, что случайная величина, распределенная по

стандартному нормальному распределению

, приняла отрицательное значение. Согласно определения

Функции распределения,

вероятность равна F(0)=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу

=НОРМ.СТ.РАСП(0;ИСТИНА)

=0,5.

3) Найдем вероятность того, что случайная величина, распределенная по

стандартному нормальному распределению

, примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу

=НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА)

.

Все расчеты, приведенные выше, относятся к случайной величине, распределенной по

стандартному нормальному закону

N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье

Распределения случайной величины в MS EXCEL

приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.

Обратная функция распределения (Inverse Distribution Function)

Вспомним задачу из предыдущего раздела:

Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.

Вероятность этого события равна 0,5.

Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение
медиану

или 50-ю

процентиль

).

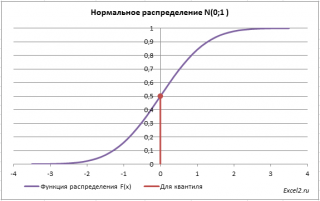
Для этого необходимо на графике

функции распределения

найти точку, для которой F(х)=0,5, а затем найти абсциссу этой точки. Абсцисса точки =0, т.е. вероятность, того что случайная величина Х примет значение <0, равна 0,5.

В MS EXCEL используйте формулу

=НОРМ.СТ.ОБР(0,5)

=0.

Однозначно вычислить значение

случайной величины

позволяет свойство монотонности

функции распределения.

Обратите внимание, что для вычисления обратной функции мы использовали именно

функцию распределения

, а не

плотность распределения

. Поэтому, в аргументах функции

НОРМ.СТ.ОБР()

отсутствует параметр

интегральная

, который подразумевается. Подробнее про функцию

НОРМ.СТ.ОБР()

см. статью про

нормальное распределение

.

Обратная функция распределения

вычисляет

квантили распределения

, которые используются, например, при

построении доверительных интервалов

. Т.е. в нашем случае число 0 является 0,5-квантилем

нормального распределения

. В

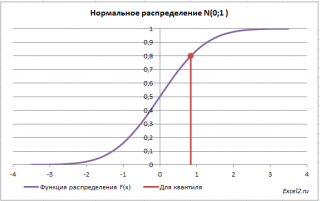
файле примера

можно вычислить и другой

квантиль

этого распределения. Например, 0,8-квантиль равен 0,84.

В англоязычной литературе

обратная функция распределения

часто называется как Percent Point Function (PPF).

Примечание

: При вычислении

квантилей

в MS EXCEL используются функции:

НОРМ.СТ.ОБР()

,

ЛОГНОРМ.ОБР()

,

ХИ2.ОБР(),

ГАММА.ОБР()

и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

Функция ФИ в Excel предназначена для определения значения плотности вероятности величины, описанной законом стандартного нормального распределения, и возвращает соответствующее число.

Значения функции плотности стандартного нормального распределения в Excel

Если случайная величина распределена непрерывно, она может иметь любое значение, взятое из интервала, в котором она определена. Такое число значений стремится к бесконечности, следовательно, вероятность попадания в какую-либо определенную точку из данного интервала стремится к нулю (сумма вероятностей должна соответствовать числу 1). Поэтому, является возможным только определение вероятности нахождения некоторой величины в заданном интервале значений. С этой целью было введено понятие плотности вероятности – производная функции распределения. Для вычисления вероятности определяют площадь, образованную кривой графика, осью абсцисс и двумя вертикальными линиями, проведенными от точек, соответствующих граничным значениям исследуемого интервала.

Рассматриваемая функции вычисляет то же значение, которое возвращает функция НОРМ.СТ.РАСП, у которой второй аргумент принимает значение ЛОЖЬ.

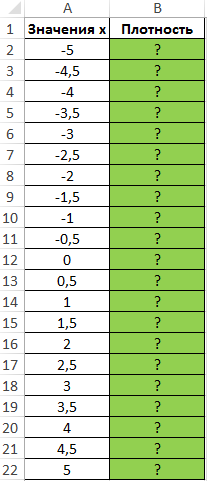
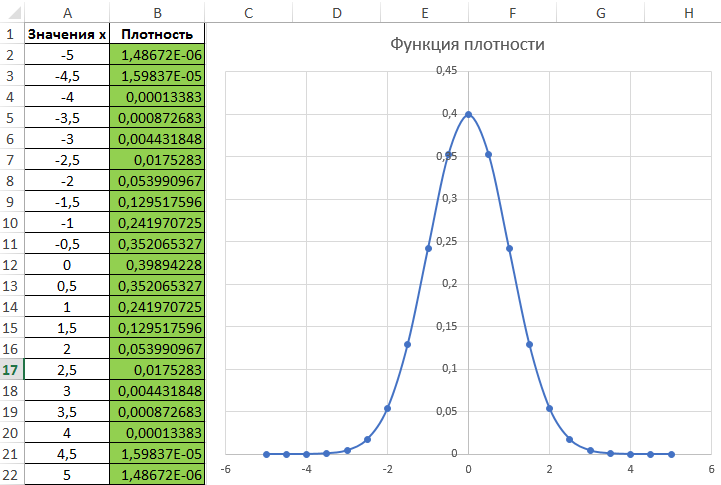
Пример 1. Построить график плотности вероятности для известных значений x, которые внесены в таблицу Excel.

Вид таблицы данных:

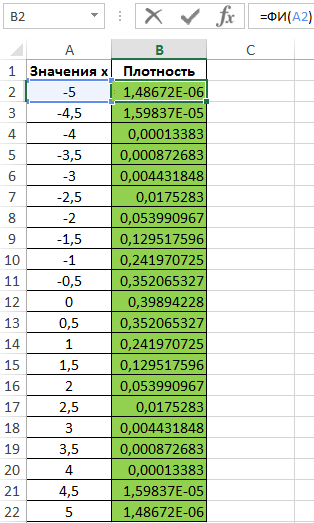
Для построения графика определим значения плотности для известных значений x. Используем формулу, предварительно выделив ячейки в диапазоне B2:B22:

=ФИ(A2)

Полученные значения:

Используем полученные данные для построения графика:

Значение плотности вероятности имеет смысл при определении вероятности нахождения величины в некотором диапазоне. Ее используют для вычисления интеграла с указанными граничными значениями некоторой величины, в результате чего получают вероятность нахождения некоторого значения в диапазоне, заданного этими граничными значениями.

В Excel функция плотности используется преимущественно для построения графиков. Вероятность определяется функцией НОРМ.СТ.РАСП (для стандартного нормального распределение) с последним аргументом, принимающим значение ИСТИНА.



Пример расчета плотности стандартного нормального распределения в Excel

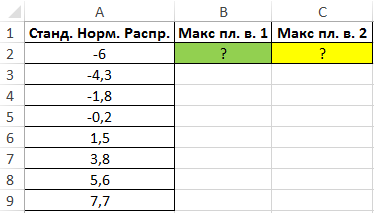
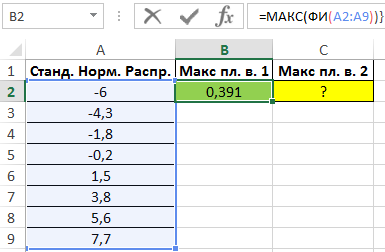
Пример 2. Определить максимальное значение плотности вероятности для ряда значений двумя различными способами.

Вид таблицы данных:

Максимальное значение плотности вероятности для некоторой величины, распределенной по стандартному нормальному закону, можно определить с помощью функции МАКС, исследуя массив значений, возвращаемых функцией ФИ в формуле массива CTRL+SHIFT+Enter:

=МАКС(ФИ(A2:A9))

Полученный результат:

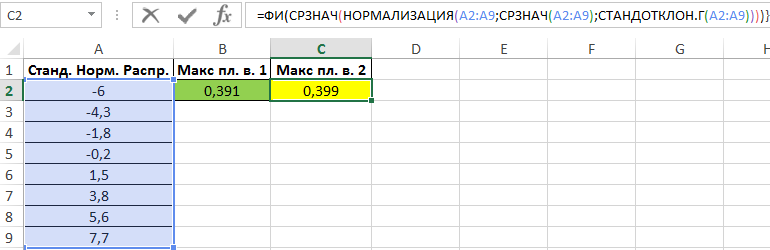
Другой способ – нахождение значения плотности для среднего значения известных величин. Однако, для начала необходимо стандартизировать имеющийся ряд значений с помощью функции НОРМАЛИЗАЦИЯ. Для нахождения используем формулу (вводить как формулу массива CTRL+SHIFT+Enter):

Полученное значение:

Небольшая разница в полученных значениях свидетельствует о том, что исследуемый ряд значений можно рассматривать как нормальное стандартное распределение некоторой величины.

Правила использования функции ФИ в Excel

Функция ФИ имеет следующую синтаксическую запись:

=ФИ(x)

• x – обязательный, принимает число для некоторой величины, распределенной по стандартному нормальному закону, для которой необходимо определить значение плотности распределения.

Примечания:

1. В качестве аргумента функции можно передавать ссылку на ячейку с числовыми данными или само число. Функция ФИ автоматические преобразует логические значения и текстовые строки, содержащие числа, к числовым значениям.
2. Если аргумент функции принимает данные, не преобразуемые к числовым значениям, результатом выполнения ФИ будет код ошибки #ЗНАЧ!
3. Для больших значений, значение плотности вероятности которых стремится к нулю, функция возвращает число 0. Например, =ФИ(100) вернет число 0.

В этой статье описаны синтаксис формулы и использование функции ЭКСП.РАСП в Microsoft Excel.

Возвращает экспоненциальное распределение. Функция ЭКСП.РАСП используется для моделирования временных задержек между событиями, например времени, которое потребуется на доставку денежного перевода через автоматизированную банковскую систему. В частности, при помощи функции ЭКСП.РАСП можно определить вероятность того, что этот процесс займет не более 1 минуты.

Синтаксис

ЭКСП.РАСП(x;лямбда;интегральная)

Аргументы функции ЭКСП.РАСП описаны ниже.

• x     — обязательный аргумент. Значение функции.

• Лямбда     — обязательный аргумент. Значение параметра.

• Интегральная     — обязательный аргумент. Логическое значение, определяющее форму экспоненциальной функции, которую следует использовать. Если аргумент «интегральная» имеет значение ИСТИНА, функция ЭКСП.РАСП возвращает интегральную функцию распределения; если имеет значение ЛОЖЬ, возвращается функция плотности распределения.

Замечания

• Если значение «x» или «лямбда» не является числом, функция ЭКСП.РАСП возвращает значение ошибки #ЗНАЧ!.

• Если x < 0, функция ЭКСП.РАСП возвращает значение ошибки #ЧИСЛО!.

• Если значение «лямбда» ≤ 0, функция ЭКСП.РАСП возвращает значение ошибки #ЧИСЛО!.

• Уравнение для функции плотности вероятности имеет следующий вид:

  

• Уравнение для интегральной функции распределения имеет следующий вид:

  

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,2	Значение функции
10	Значение параметра
Формула	Описание	Результат
=ЭКСП.РАСП(A2;A3;ИСТИНА)	Интегральная экспоненциальная функция распределения	0,86466472
=ЭКСП.РАСП(0,2;10;ЛОЖЬ)	Экспоненциальная функция плотности распределения	1,35335283

Распределение вероятностей – одно из центральных понятий теории
вероятности и математической статистики. Определение распределения вероятности
равносильно заданию вероятностей всех СВ, описывающих некоторое случайное
событие. Распределение вероятностей некоторой СВ, возможные значения которой x₁, x₂, … x_n образуют
выборку, задается указанием этих значений и соответствующих им вероятностей p₁, p₂,… p_n. (p_n должны быть
положительны и в сумме давать единицу).

В данной лабораторной работе будут рассмотрены и построены с помощью MS Excel наиболее
распространенные распределения вероятности: биномиальное и нормальное.

1 Биномиальное распределение

Представляет собой распределение вероятностей числа наступлений
некоторого события («удачи») в n повторных
независимых испытаниях, если при каждом испытании вероятность наступления этого
события равна p. При этом
распределении разброс вариант (есть или нет события) является следствием
влияния ряда независимых и случайных факторов.

 Примером практического использования биномиального распределения
может являться контроль качества партии фармакологического препарата. Здесь
требу­ется подсчитать число изделий (упаковок), не соответствующих требованиям.
Все причины, влияющие на качество препарата, принимаются одинаково вероятными и
не зависящими друг от друга. Сплошная проверка качества в этой ситуации не
возможна, поскольку изделие, прошедшее испытание, не подлежит дальнейшему
использованию. Поэтому для контроля из партии наудачу выбирают определенное
количество образцов изделий (n). Эти образцы всестороннее
проверяют и регистрируют число бракованных изделий (k). Теоретически число
бракованных изделий может быть любым, от 0 до n.

В Excel функция БИНОМРАСП
применяется для вычисления вероятности в задачах с фиксированным числом тестов
или испытаний, когда результатом любого испытания может быть только успех или
неудача.

Функция использует следующие
параметры:

БИНОМРАСП (число_успехов;
число_испытаний; вероятностъ_успеха; интегральная), где

число_успехов — это количество успешных
испытаний;

число_испытаний — это число независимых
испытаний (число успехов и число испытаний должны быть целыми числами);

вероятность_ успеха — это вероятность успеха
каждого испытания;

интегральный — это логическое значение,
определяющее форму функции.

Если данный параметр имеет
значение ИСТИНА (=1), то считается интегральная функция распределения
(вероятность того, что число успешных испытаний не менее значения число_
успехов);

если этот параметр имеет
значение ЛОЖЬ (=0), то вычисляется значение функ­ции плотности
распределения (вероятность того, что число успешных испытаний в точности равно
значению аргумента число_ успехов).

Пример 1. Какова вероятность того,
что трое из четырех новорож­денных будут мальчиками?    

Решение:

1.   Устанавливаем табличный курсор в свободную
ячейку, например в А1. Здесь должно оказаться значение искомой
вероятности.

2.   Для получения значения вероятности
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка
функции (fx).

3.   В появившемся диалоговом окне Мастер
функций — шаг 1 из 2 слева в поле Катего­рия указаны виды функций.
Выбираем Статистическая. Справа в поле Функция выбираем функцию БИНОМРАСП
и нажимаем на кнопку ОК.

Появляется диалоговое окно
функции. В поле Число_s вводим с клавиатуры
количество успешных испытаний (3). В поле Испытания вво­дим с клавиатуры
общее количество испытаний (4). В рабочее поле Вероятность_s
вводим с клавиатуры вероятность успеха в отдельном испытании (0,5). В поле Интегральный
вводим с клавиатуры вид функции распределения — интегральная или весовая (0).
Нажимаем на кнопку ОК.

В ячейке А1 появляется
искомое значение вероятности р = 0,25. Ровно 3 мальчика из 4
новорожденных могут появиться с вероят­ностью 0,25.

Если изменить формулировку
условия задачи и выяснить вероятность того, что появится не более трех
мальчиков, то в этом случае в рабочее поле Интегральный вводим 1 (вид
функции распределения интегральный). Вероятность этого события будет равна
0,9375.

Задания для самостоятельной работы

1. Какова вероятность того, что восемь из десяти студентов,
сдающих зачет, получат «незачет». (0,04)

2.
Нормальное распределение

Нормальное распределение — это совокупность объектов, в кото­рой крайние значения
некоторого признака — наименьшее и наибольшее — появ­ляются редко; чем ближе значение признака к математическому ожиданию,
тем чаще оно встречается. Например, распределение студентов по их весу приближа­ется
к нормальному распределению. Это распределение имеет очень широкий круг приложений в
статистике, включая проверку гипотез.

Диаграмма нормального
распределения симметрична относительно точки а (математического
ожидания). Ме­диана нормального распределения равна тоже а. При этом в
точке а функция f(x) достигает своего максимума, который равен

.

В Excel для вычисления значений
нормального распределения используются фун­кция НОРМРАСП, которая
вычисляет значения вероятности нормальной функции распределения для указанного
среднего и стандартного отклонения.

Функция имеет параметры:

НОРМРАСП (х; среднее;
стандартное_откл; интегральная), где:

х — значения выборки, для
которых строится распределение;

среднее — среднее арифметическое
выборки;

стандартное_откл — стандартное отклонение
распределения;

интегральный — логическое значение,
определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то
функция НОРМРАСП возвращает интег­ральную функцию распределения; если это
аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности
распределения.

Если среднее = 0 и
стандартное_откл = 1, то функция НОРМРАСП возвращает стан­дартное
нормальное распределение.

Пример 2. Построить график
нормальной функции распределения f(x) при x, меняющемся от 19,8 до 28,8
с шагом 0,5, a=24,3 и

=1,5.

Решение

1. В ячейку А1 вводим символ
случайной величины х, а в ячейку B1 — символ фун­кции
плотности вероятности — f(x).

2. Вводим в диапазон А2:А21
значе­ния х от 19,8 до 28,8 с шагом 0,5. Для этого воспользуемся
маркером автозаполнения: в ячейку А2 вводим левую границу диапазона (19,8), в
ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:А3. Затем за правый
нижний угол протягиваем мышью до ячейки А21 (при нажатой левой кнопке мыши).

3.   Устанавливаем табличный курсор в ячейку В2 и
для получения значения веро­ятности воспользуемся специальной функцией —
нажимаем на панели инстру­ментов кнопку Вставка функции (fx). В появившемся диалоговом
окне Мастер функций — шаг 1 из 2 слева в поле Категория указаны виды
функций. Выбираем Статистическая. Справа в поле Функция выбираем
функцию НОРМРАСП. Нажимаем на кнопку ОК.

4. Появляется диалоговое
окно НОРМРАСП. В рабочее поле X вводим адрес ячейки А2
щелчком мыши на этой ячейке. В рабочее поле Среднее вводим с клавиатуры
значение математиче­ского ожидания (24,3). В рабочее поле Стандартное_откл
вводим с клавиатуры значение среднеквадратического отклонения (1,5). В ра­бочее
поле Интегральная вводим с клавиатуры вид функции распределения (0).
Нажимаем на кнопку ОК.

5. В ячейке В2 появляется
вероятность р = 0,002955. Указателем мыши за правый нижний угол табличного
курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В21
копируем функцию НОРМРАСП в диапазон В3:В21.

6. По полученным данным строим искомую диаграмму
нормальной функции рас­пределения. Щелчком указателя мыши на кнопке на панели
инструментов вызы­ваем Мастер диаграмм. В появившемся диалоговом окне
выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки
Далее указываем диапазон данных — В1:В21 (с помощью мыши). Проверяем,
положение переключателя Ряды в: столбцах. Выбираем закладку Ряд и с
помощью мыши вводим диапазон подписей оси X: А2:А21. Нажав на кнопку Далее,
вводим названия осей Х и У и нажимаем на кнопку Готово. 

 Рис. 1 График нормальной функции распределения

Получен приближенный график
нормальной функции плотности распределения (см. рис.1).

Задания для самостоятельной работы

1. Построить график нормальной
функции плотности распределения f(x) при x, меняющемся от 20 до 40 с
шагом 1 при

=   3.

 

3. Генерация случайных величин

Еще одним аспектом
использования законов распределения вероятностей являет­ся генерация случайных величин. Бывают ситуации, когда необходимо
получить пос­ледовательность случайных чисел. Это, в частности, требуется для
моделирования объектов, имеющих случайную природу, по известному распределению
вероятно­стей.

Процедура генерации
случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из
одного или не­скольких распределений.

В MS Excel для генерации СВ используются функции из категории Математические:

СЛЧИС () – выводит на экран  равномерно
распределенные случайные числа больше или равные 0 и меньшие 1;

СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экран
случайное число, лежащее между про­извольными заданными
значениями.

В случае использования
процедуры Генерация случайных чисел из пакета Анализа необходимо
запол­нить следующие поля:

— число переменных
вводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то все
столбцы в выходном диапазоне будут заполнены;

— число случайных чисел
вводится число случайных значений, которое необ­ходимо вывести для
каждой переменной, если число случайных чисел не будет введе­но, то все строки выходного диапазона будут заполнены;

— в поле распределение необходимо выбрать тип распределения,
которое следует использовать для генерации случайных переменных:

1.  равномерное — характеризуется
верxней и нижней границами. Переменные из­влекаются с одной и
той же вероятностью для всех значений интервала.

2. нормальное
— характеризуется средним значением и стандартным отклонени­ем. Обычно для
этого распределения используют среднее значе­ние
0 и стандартное отклонение 1.

3. биномиальное
— характеризуется вероятностью успеха (величина р) для неко­торого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биномиальной случайной
переменной;

4. дискретное
— характеризуется значением СВ и соответствующим ему интервалом вероятности, диапазон должен состоять из двух столбцов: левого,
содержаще­го значения, и правого, содержащего
вероятности, связанные со значением в дан­ной строке. Сумма вероятностей должна быть
равна 1;

5. распределения Бернулли, Пуассона
и Модельное.

— в поле случайное рассеивание
вводится произвольное значение, для которого необ­ходимо
генерировать случайные числа. Впоследствии можно снова использовать это
значение для получения тех же самых случайных чисел.

— выходной диапазон
вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и
на эк­ран будет выведено сообщение в случае
возможного наложения выходного диапа­зона на исходные
данные.

Рассмотрим пример.                                                                                  

Пример 3. Повар столовой может готовить 4 различных первых блюда (уха, щи, борщ, грибной суп). Необходимо составить меню на месяц, так чтобы
первые блюда чередовались в случайном порядке.

Решение

1.        
Пронумеруем первые
блюда по порядку: 1 — уха, 2 — щи, 3 — борщ, 4 — грибной суп. Введем числа 1-4 в диапазон А2:А5 рабочей таблицы.

2.        
Укажем желаемую вероятность появления
каждого первого блюда. Пусть все блюда будут
равновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.

3.        
В меню Сервис
выбираем пункт Анализ данных и далее указываем строку Генерация
случайных чисел. В появившемся диалоговом окне указываем Число
переменных — 1, Число случайных чисел — 30 (количество
дней в месяце). В поле Распределение указываем Дискретное (только натуральные числа). В поле Входной
интервал значений и вероятностей
вводим (мышью) диапазон, содержащий номера супов и их
вероятности. – А2:В5.

4.        
Указываем выходной
диапазон и нажимаем ОК. В столбце С появляются случайные числа: 1, 2, 3,
4.

 

Задание для
самостоятельной работы

1.      Сформировать
выборку из 10 случайных чисел, лежащих в диапазоне от 0 до 1.

2.      Сформировать
выборку из 20 случайных чисел, лежащих в диапазоне от 5 до 20.

3.      Пусть
спортсмену необходимо составить график тренировок на 10 дней, так чтобы
дистанция, пробегаемая каждый день, случайным образом менялась от 5 до 10 км.

4.      Составить
расписание внеклассных мероприятий на неделю для случайного проведения:
семинаров, интеллектуальных игр, КВН и спец. курса.

5.      Составить
расписание на месяц для случайной демонстрации на телевидении одного из четырех
рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1
должна быть в два раза выше, чем остальных рекламных роликов.

• 

=EXPON.DIST(x, lambda, cumulative)