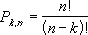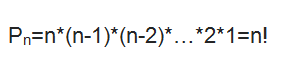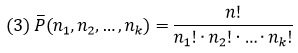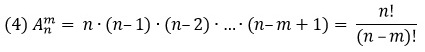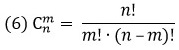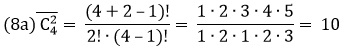Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ПЕРЕСТ в Microsoft Excel.
Описание
Возвращает количество перестановок для заданного числа объектов, которые выбираются из общего числа объектов. Перестановка — это любое множество или подмножество объектов или событий, в котором важен внутренний порядок. Перестановки отличаются от сочетаний, для которых внутренний порядок не имеет значения. Эта функция используется, например, для вычисления вероятностей в лотереях.
Синтаксис
ПЕРЕСТ(число;число_выбранных)
Аргументы функции ПЕРЕСТ описаны ниже.
-
Число Обязательный. Целое число, задающее количество объектов.
-
Число_выбранных Обязательный. Целое число, задающее количество объектов в каждой перестановке.
Замечания
-
Оба аргумента усекаются до целых.
-
Если число или number_chosen не является числом, то #VALUE! значение ошибки #ЗНАЧ!.
-
Если число ≤ 0 или number_chosen < 0, то #NUM! значение ошибки #ЗНАЧ!.
-
Если число < number_chosen, то переНУТ возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Уравнение для числа перестановок имеет следующий вид:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
100 |
Количество объектов |
|
|
3 |
Количество объектов в каждой перестановке |
|
|
Формула |
Описание |
Результат |
|
=ПЕРЕСТ(A2;A3) |
Количество возможных перестановок для аргументов, указанных в диапазоне A2:A3. |
970200 |
|
=ПЕРЕСТ(3;2) |
Количество возможных перестановок для группы из 3 объектов, 2 из которых выбраны. |
6 |
Нужна дополнительная помощь?
Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.
Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!
Лучшее спасибо — порекомендовать эту страницу
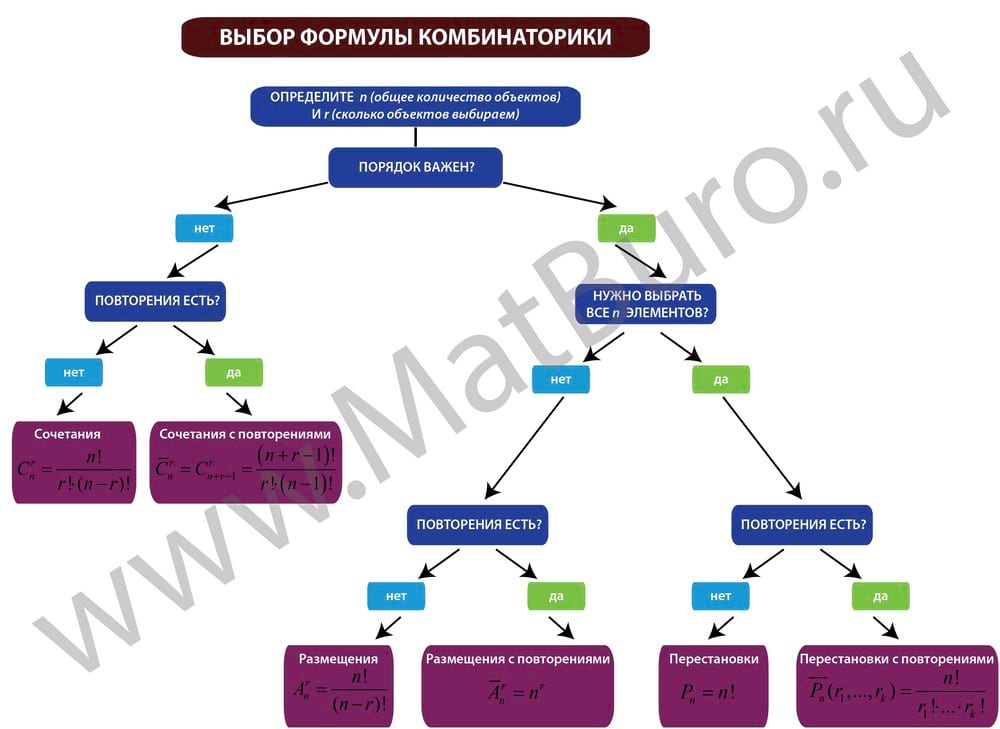
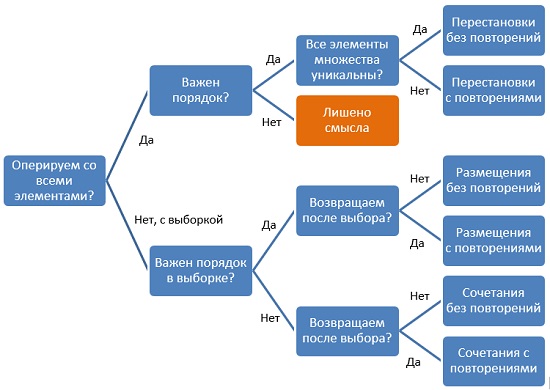
Как выбрать формулу комбинаторики?
Нужно последовательно (см. схему выше) ответить на несколько вопросов:
- Сколько у нас есть объектов (число $n$)?
- Важен ли их порядок в комбинации?
- Могут ли встречаться повторяющиеся элементы?
- Нужно выбрать все элементы или только $klt n$?
Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:
Схема выбора формул с примерами задач
Консультируем по решению задач комбинаторики
Перестановки в Excel
Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно
$$P_n=n!=1cdot 2cdot 3 cdot … cdot (n-1) cdot n$$
Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.
Подробнее: факториал в эксель.
Для нахождения числа перестановок в Excel можно использовать одну из двух функций:
=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$), где $n$ — число переставляемых объектов.
Задача. Сколькими способами можно расставить 10 различных книг на одной полке?
Вводим число объектов 10 и получаем ответ: 3628800 способов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор перестановок.
Перестановки с повторениями в Excel
Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,… $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?
Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть
$$ P_n (n_1,n_2,…,n_k)=frac{n!}{n_1! cdot n_2!cdot … cdot n_k!}. $$
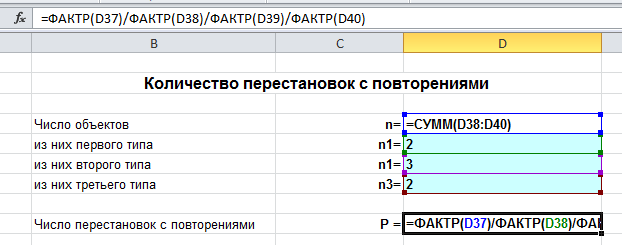
Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР(), которая находит факториал чисел и обычные действия (умножение, деление).
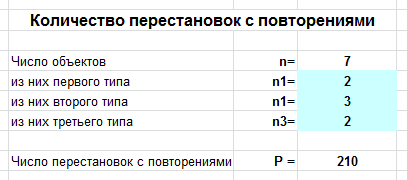
Задача. Сколько различных слов можно составить из букв слова «колокол»?
Вводим число букв $n=7$, а также $n_1=2$ (2 буквы «к»), $n_2=3$ (3 буквы «о»), $n_3=2$ (2 буквы «л»), и получаем ответ: 210 слов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор перестановок c повторениями.
Размещения в Excel
Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно
$$A_n^k=frac{n!}{(n-k)!}=ncdot (n-1)cdot … cdot (n-k+1) $$
Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$).
Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?
Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор размещений.
Размещения с повторениями в Excel
Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле
$$overline{A}_n^k=ncdot ncdot … cdot n = n^k. $$
Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$).
Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?
Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.
В режиме формул это выглядит так:
Еще: онлайн калькулятор размещений с повторениями.
Сочетания в Excel
Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно
$$C_n^k=frac{n!}{(n-k)!cdot k!} $$
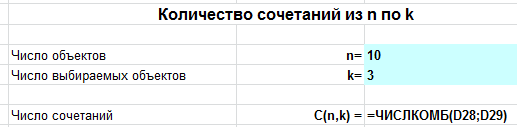
Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$).
Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?
Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор сочетаний.
Сочетания с повторениями в Excel
Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле
$$overline{C}_n^k=C_{k+n-1}^k=frac{(k+n-1)!}{(n-1)!cdot k!}$$
Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$).
Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?
Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор сочетаний с повторениями.
Полезные ссылки
Для собственных расчетов скачайте файл: Комбинаторика в Excel.
|
|
Решебник задач по комбинаторике
Подсчитаем в MS EXCEL количество перестановок из n элементов. С помощью формул выведем на лист все варианты перестановок (английский перевод термина: permutation).
Перестановкой множества из n элементов называется расположение элементов в определенном порядке.
Элементами множества могут быть числа, буквы и вообще любые объекты. Главное, чтобы эти элементы были различными. Т.к. любому объекту можно сопоставить число, то для Перестановок обычно используют конечное множество целых чисел, например, {1; 2; 3; 4; 5}. Хотя множества из букв также можно часто встретить в литературе. Например, все различные Перестановки множества из трех элементов {a, b, c} – это
abc
,
acb
,
bac
,
bca
,
cab
,
cba
.
Число Перестановок n элементов равно n! (факториал).
Для вычисления факториала в MS EXCEL есть функция
=ФАКТР()
, английский вариант FACT(). Понятно, что число перестановок растет очень быстро с ростом n: для n=7 число перестановок равно 5040. Справедливости ради, нужно отметить, что зачастую сами варианты перестановок находить не требуется, главное – найти их количество.
Примечание
:
Перестановки можно считать частным случаем размещений при n=k (см. статью
Размещения без повторений: Комбинаторика в MS EXCEL
). Поэтому для вычисления количества перестановок можно использовать функцию
ПЕРЕСТ()
. Для n=7 число Перестановок вычисляется по формуле
=ПЕРЕСТ(7;7)
Примечание
: О Перестановках с повторениями (с возвращением элементов обратно во множество, из которого они берутся, после выборки каждого элемента) можно прочитать в статье
Перестановки с повторениями: Комбинаторика в MS EXCEL
.
В
файле примера
создана универсальная формула для вывода всех Перестановок для заданного n. Например, для n=3.
Задача
6 машин
разных
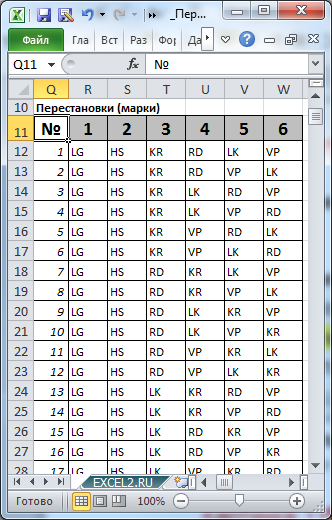
марок участвуют в гонках на выживание: LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo. Определить число возможных вариантов распределения мест между всеми участниками.
Нам нужно определить число перестановок 6 машин на 6-и местах. Т.е. n=6. Оказывается, что таких перестановок 720:
=ПЕРЕСТ(6;6)
или 6!
=ФАКТР(6)
Воспользуемся
файлом примера
, чтобы найти все варианты перестановок.
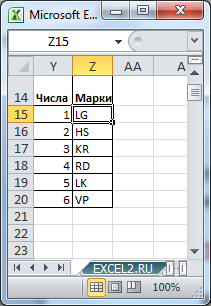
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …
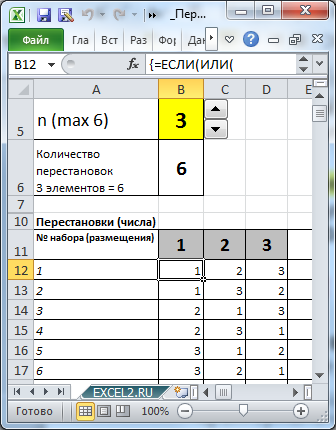
Введя в ячейке
В5
значение 6, определим все варианты расстановок машин на занятых ими в гонке местах.
Примечание
: О Размещениях можно прочитать в статье
Размещения без повторений: Комбинаторика в MS EXCEL
, а о Сочетаниях в статье
Сочетания без повторений: Комбинаторика в MS EXCEL
.
Перебор всех возможных перестановок может потребоваться для решения различных задач (см. статью
Поиск решения MS EXCEL (6.2). Задача коммивояжера (полный граф, нелинейная модель)
и
Вычисление определителя матрицы в MS EXCEL
).
Инверсии перестановок
Для каждой перестановки
a
1,
a
2,
a
3,…,
a
n из
n
целых чисел 1, 2, 3, …,
n
, инверсией называется пара (
a
i,
a
j) если для i < j выполняется
a
i >
a
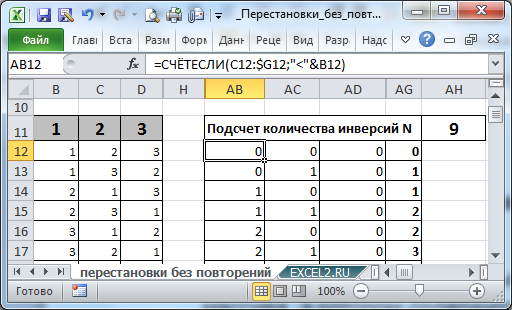
j. Число инверсией в перестановке показывает насколько перестановка является «несортированной» по возрастанию.
Например, число инверсий в перестановке 1, 2, 3, 4 равно 0 (перестановка из 4-х целых чисел отсортирована по возрастанию от 1 до 4), а число инверсий в перестановке 4, 3, 1, 2 равно 5, т.к.:
-
первый элемент (i=1) равен 4 и он больше
3-х
чисел (с j=2, 3, 4), которые расположены правее (4>3, 4>1, 4>2), т.е. мы имеем 3 инверсии; -
второй элемент (i=2) равен 3 и он больше
2-х
чисел (с j=3, 4), которые расположены правее (3>1, 3>2), т.е. мы имеем еще 2 инверсии; - так третий элемент (i=3) равен 1 и он меньше числа с j=4, которое расположено правее (1<2), то эта пара не является инверсией. Т.е. у перестановки 4, 3, 1, 2 число инверсий равно 3+2+0=5.
В
файле примера
для каждой Перестановки подсчитывается число инверсией.
Инверсии перестановок, например, используются при вычислении определителя матрицы (см. статью
Вычисление определителя матрицы в MS EXCEL
).
Комбинаторика в Excel
Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:
- Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
- Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
- Важен ли порядок элементов в выборке?
- После выбора элемента мы его возвращаем назад?
Рис. 1. Дерево решений, какую формулу комбинаторики использовать
Скачать заметку в формате Word или pdf, примеры в формате Excel
Перестановки без повторений
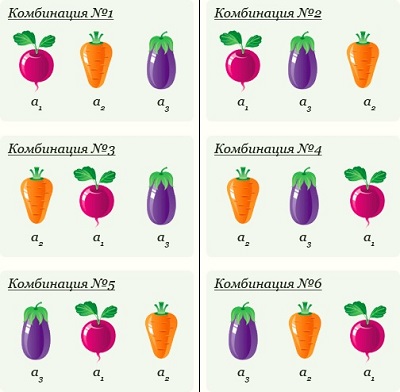
Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.
Рис. 2. Перестановки (картинка взята здесь)
Если все n элементы разные, то число перестановок обозначается Pn от perturbation.
С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!
Например
По определению: 1! = 1; 0! = 1.
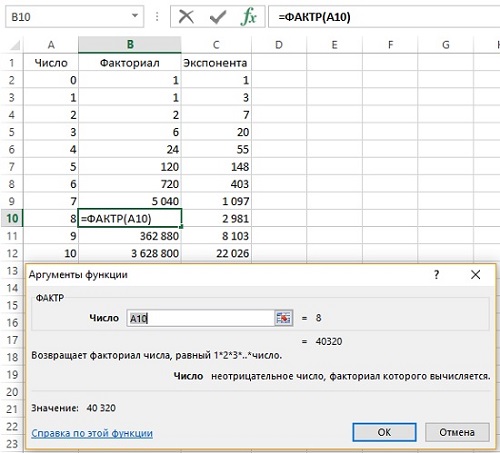
Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).
Рис. 3. Расчет числа перестановок без повторений с помощью факториала
Перестановки с повторениями
Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).
Рис. 4. Перестановки с повторениями (картинка найдена здесь)
В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 раз, второй – n2 раз, третий – n3 раз, …, k-й – nk раз (где n1 + n2 + … + nk = n) называется перестановкой с повторениями из n элементов.
Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?
Решение. Буквы а и н повторяются 2 раза, а буква м один раз.
Размещение без повторений
Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается от arrangement.
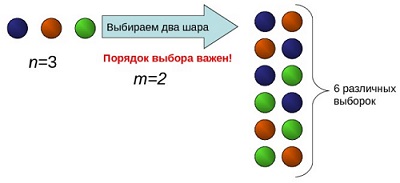
Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):
Рис. 5. Размещение без повторений (картинка из презентации)
Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).
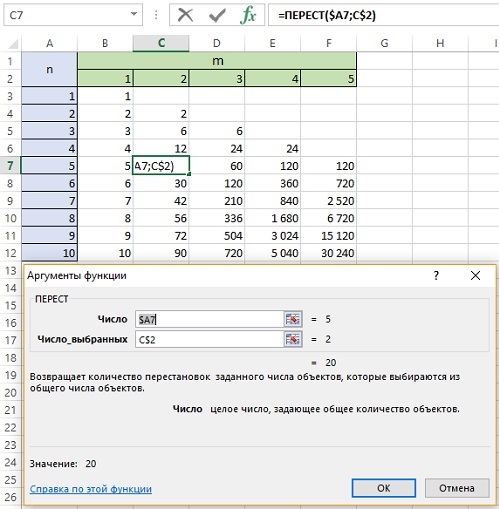
Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)
Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу
Размещение с повторениями
Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.
Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).
Рис. 7. Размещение с повторениями
В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:
В Excel используется функция ПЕРЕСТА(n;k).
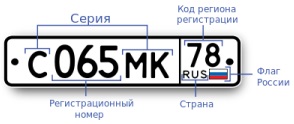
Задача. Сколько различных номеров можно составить в одном коде региона?
Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).
Рис. 8. Номер автомобиля
Решение. Можно воспользоваться формулой для размещения с повторениями:
Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.
Сочетания без повторений
Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).
Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):
Рис. 9. Сочетания без повторений из 4 по 2
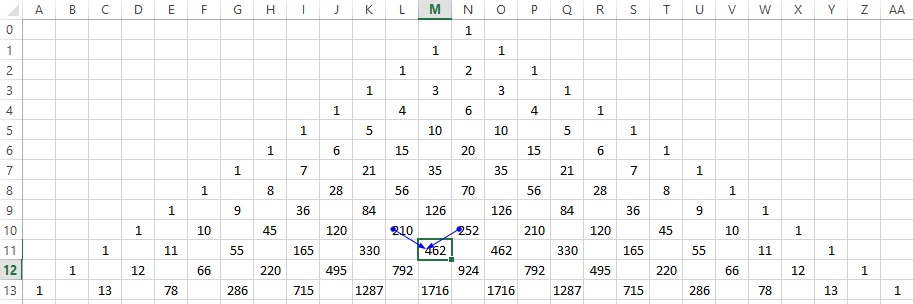
Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями
где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:
Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
В Excel используется функция =ЧИСЛКОМБ(n;m).
Сочетания с повторениями
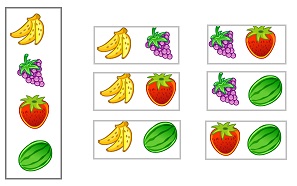
Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.
Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).
Рис. 11. Сочетания с повторениями
В общем случае, число сочетаний с повторениями:
Для нашего примера с фруктами
В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.
В этом учебном материале вы узнаете, как использовать Excel функцию ПЕРЕСТ с синтаксисом и примерами.
Описание
Microsoft Excel функция ПЕРЕСТ возвращает количество перестановок для указанного количества элементов.
Функция ПЕРЕСТ — это встроенная в Excel функция, которая относится к категории статистических функций.
Её можно использовать как функцию рабочего листа (WS) в Excel.
Как функцию рабочего листа, функцию РАЗРЕШИТЬ можно ввести как часть формулы в ячейку рабочего листа.
Синтаксис
Синтаксис функции ПЕРЕСТ в Microsoft Excel:
ПЕРЕСТ(число;число_выбранных)
Аргументы или параметры
- число
- Количество элементов.
- число_выбранных
- Количество элементов в каждой перестановке.
Возвращаемое значение
Функция ПЕРЕСТ возвращает числовое значение.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000
Тип функции
- Функция рабочего листа (WS)
Пример (как функция рабочего листа)
Рассмотрим несколько примеров функции ПЕРЕСТ, чтобы понять, как использовать Excel функцию ПЕРЕСТ в качестве функции рабочего листа в Microsoft Excel:
На основании, приведенной выше электронной таблицы Excel, будут возвращены следующие примеры функции ПЕРЕСТ:
|
=ПЕРЕСТ(A1; A2) Результат: 30240 =ПЕРЕСТ(10; 5) Результат: 30240 =ПЕРЕСТ(A1; A3) Результат: 720 =ПЕРЕСТ(21; 5) Результат: 2441880 =ПЕРЕСТ(4; 3) Результат: 24 |