Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает обратное нормальное распределение для указанного среднего и стандартного отклонения.
Примечание: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция НОРМ.ОБР.
Синтаксис
НОРМОБР(вероятность;среднее;стандартное_откл)
Аргументы функции НОРМОБР описаны ниже.
-
Вероятность Обязательный. Вероятность, соответствующая нормальному распределению.
-
Среднее Обязательный. Среднее арифметическое распределения.
-
Стандартное_откл Обязательный. Стандартное отклонение распределения.
Замечания
-
Если какой-либо из аргументов не является числом, то #VALUE! значение ошибки #ЗНАЧ!.
-
Если вероятность <= 0 или вероятность >= 1, то НОРМИНВ возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если standard_dev ≤ 0, norMINV возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если среднее = 0 и стандартное_откл = 1, функция НОРМОБР использует стандартное нормальное распределение (см. НОРМСТОБР).
Если задано значение вероятности, функция НОРМОБР ищет значение x, для которого функция НОРМРАСП(x, среднее, стандартное_откл, ИСТИНА) = вероятность. Однако точность функции НОРМОБР зависит от точности НОРМРАСП. В функции НОРМОБР для поиска применяется метод итераций. Если поиск не закончился после 100 итераций, функция возвращает значение ошибки #Н/Д.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
0,908789 |
Вероятность, соответствующая нормальному распределению |
|
|
40 |
Среднее арифметическое распределения |
|
|
1,5 |
Стандартное отклонение распределения |
|
|
Формула |
Описание |
Результат |
|
=НОРМОБР(A2;A3;A4) |
Обратное значение нормального интегрального распределения для приведенных выше условий |
42,000002 |
Нужна дополнительная помощь?
The term normalization in itself is a buzzword that is popular amongst people who come from different fields such as Machine Learning, Data Science, Statistics, etc. Normalization is a general term that means to scale down values inside a certain range. The origin of the word normalization being a buzzword comes from the fact that it is often misunderstood by people and is interchangeably used with another statistical term standardization. In this article, we are going to demystify both of these terms and later we will read how we can implement these techniques on a sample dataset in Excel.
Normalization (Or Min-Max scaling) data in excel
It is the process of scaling data in such a way that all data points lie in a range of 0 to 1. Thus, this technique, makes it possible to bring all data points to a common scale. The mathematical formula for normalization is given as:
, where X is the data point, Xmax and Xmin are the maximum and minimum value in the group of records respectively. The process of normalization is generally used when the distribution of data does not follow the Gaussian distribution.
Let’s have a look at one example to see how can we perform normalization on a sample dataset. Suppose, we have a record of the height of 10 students inside a class as shown below:
| Height (in cm) |
| 152 |
| 155 |
| 168 |
| 175 |
| 153 |
| 162 |
| 173 |
| 166 |
| 158 |
| 156 |
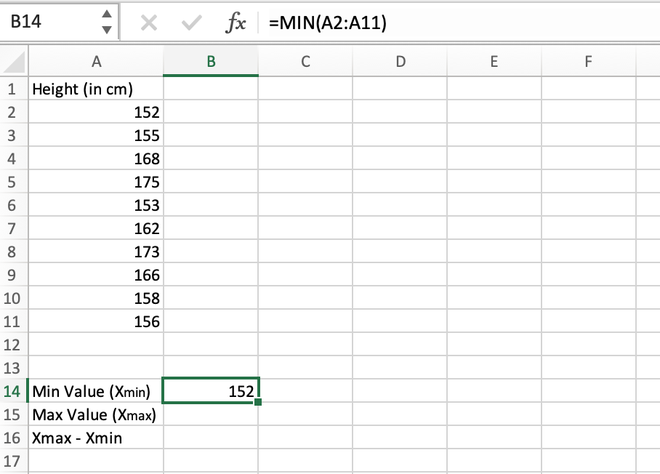
Step 1: Calculate the minimum value in the distribution. It can be calculated using the MIN() function. The minimum value comes out to be 152 which is stored in the B14 cell.
Calculating the minimum value using the MIN() function
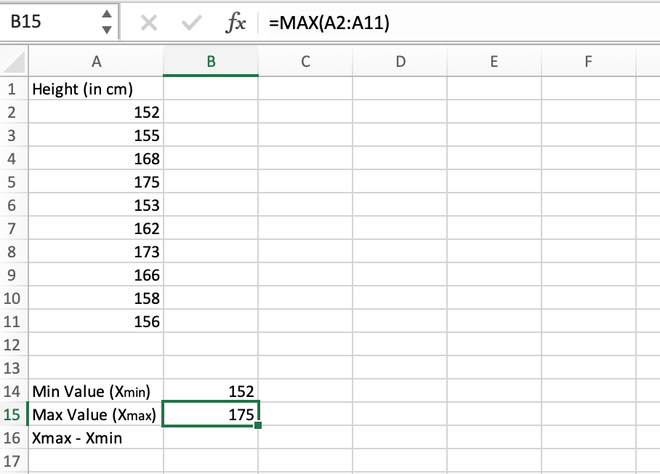
Step 2: Calculate the maximum value in the distribution. It can be calculated using the MAX() function. The maximum value comes out to be 175 which is stored in the B15 cell.
Calculating the maximum value using the MAX() function
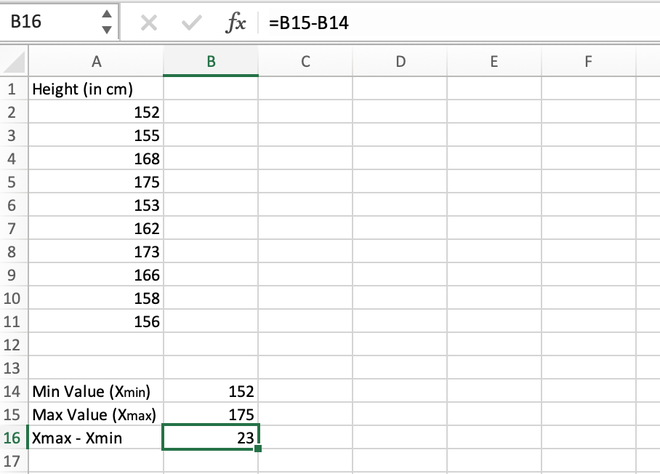
Step 3: Find the difference between the maximum and minimum values. Their difference comes out to be 175 – 152 = 23 which is stored in the B16 cell.
Calculating the difference (Max-Min)
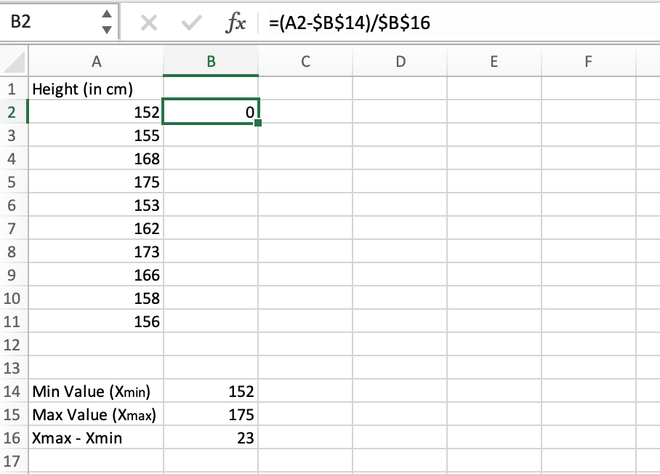
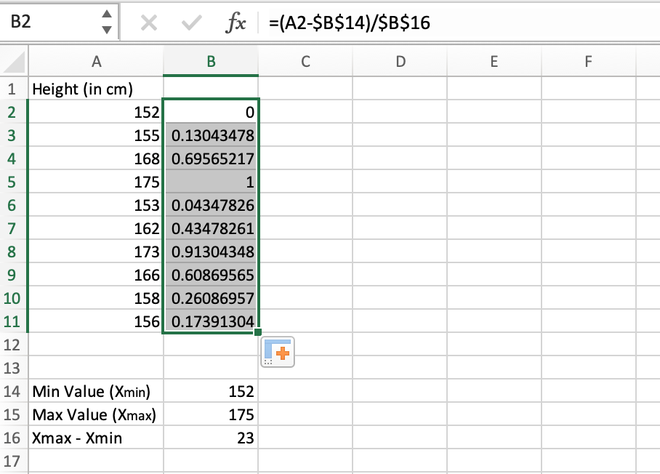
Step 4: For the first data stored in the A2 cell, we will calculate the normalized value as shown in the below video.
Calculating the normalized value for the first element
Step 5: We can manually calculate all values one by one for each data record or we can directly get values for all the other cells using the auto-fill feature of Excel. For this, go to the right corner of the B2 cell until a (+) symbol appears, and then drag the cursor to the bottom to auto-populate values inside all the cells.
Calculating the normalized value for the entire range
Note: While calculating the first normalized value in the B2 cell, it should be made sure that the reference address for the B14 and B16 cells should be locked using Fn + F4 button otherwise an error will be thrown.
If we have a close look at the results, we can notice all the values lies in the range 0 to 1.
Standardization (Or Z-score normalization)
Standardization is a process in which we want to scale our data in such a way that the distribution of our data has its mean as 0 and standard deviation as 1. The mathematical formula for standardization is given as:
, where where X is the data point, Xmean is the mean of the distribution and σx is the standard deviation of the distribution.
The process of standardization is generally used when we know the distribution of data follows the gaussian distribution.
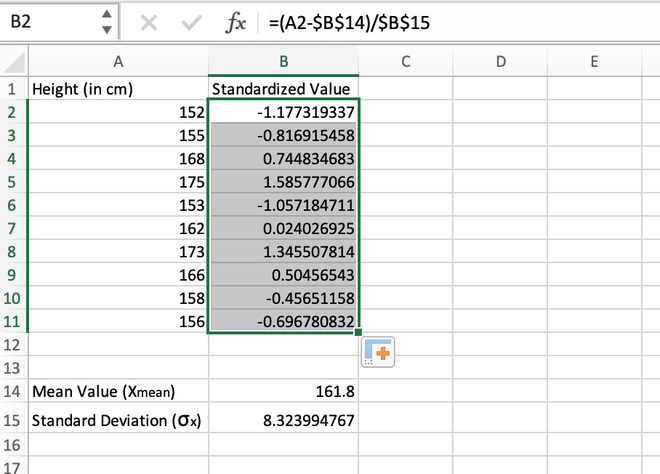
Method 1: Calculating z-score normalization manually
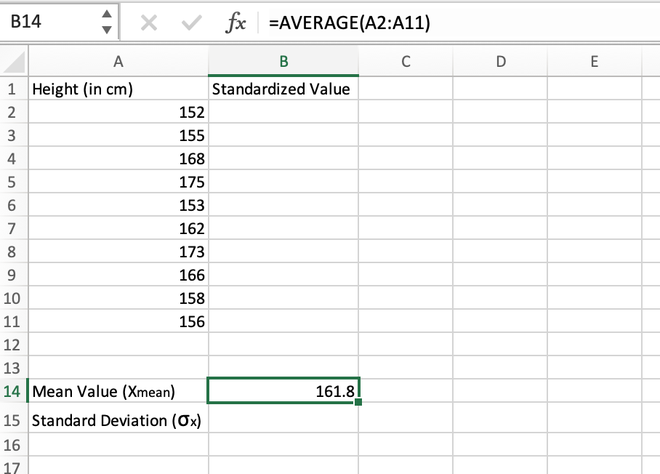
Step 1: Calculate the mean/average of the distribution. It can be done using the AVERAGE() function. The mean value comes out to be 161.8 and is stored in the B14 cell.
Calculating the mean value using the AVERAGE() function
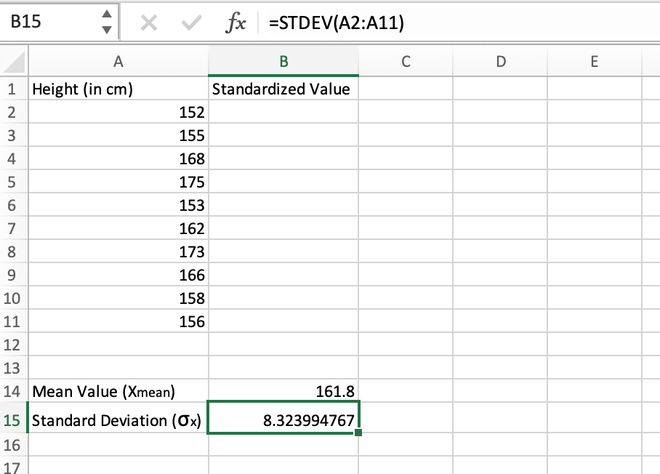
Step 2: Calculate the standard deviation of the distribution which can be done using the STDEV() function. The standard deviation comes out to be 8.323994767 which is stored in the B15 cell.
Calculating the standard deviation using the STDEV() function
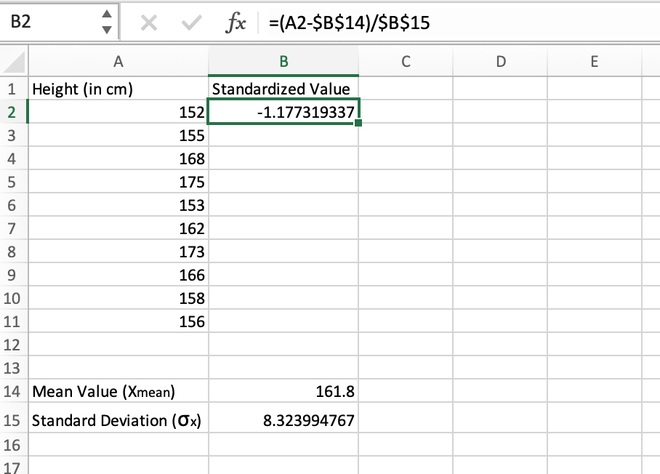
Step 3: For the first data stored in the A2 cell, we will calculate the standardized value as shown in the image given below.
Calculating the standardized value for the first element
Step 4: After manually calculating the first value, we can simply use the auto-fill feature of Excel to populate the standardized values for all other records.
Calculating the standardized value for the entire range using auto-fill
Note: While calculating the first standardized value in the B2 cell, it should be made sure that the reference address for the B14 and B15 cells should be locked using Fn+F4 button otherwise an error will be thrown.
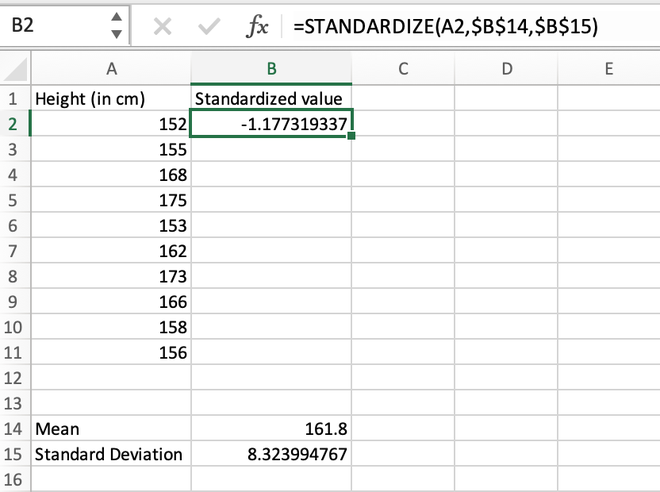
Method 2: Calculating Z-score normalization using the STANDARDIZE() function
We can even use the built-in STANDARDIZE() function to find the standardized value of an element. The syntax for STANDARDIZE() function is given as:
=STANDARDIZE(x,mean,std_dev)
Where x is the specific element/range of cells, mean is the average/arithmetic mean of all the elements in the record, and std_dev is the standard deviation of all the elements in the record
Step 1: Calculate the mean/average of the distribution. It can be done using the AVERAGE() function. The mean value comes out to be 161.8 and is stored in the B14 cell.
Calculating the mean value using the AVERAGE() function
Step 2: Calculate the standard deviation of the distribution which can be done using the STDEV() function. The standard deviation comes out to be 8.323994767 which is stored in the B15 cell.
Calculating the standard deviation using the STDEV() function
Step 3: For the first data stored in the A2 cell, we will calculate the standardized value as shown in the below image.
Calculating the standardized value for the first element using the STANDARDIZE() function
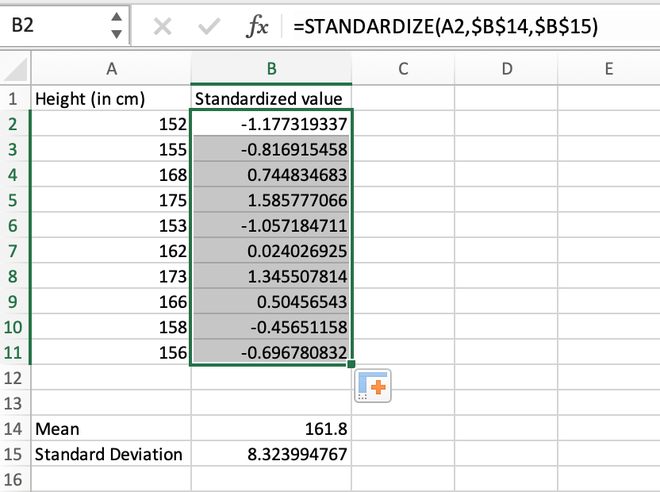
Step 4: After manually calculating the first value, we can simply use the auto-fill feature of Excel to populate the standardized values for all other records.
Calculating the standardized value for the entire range using auto-fill
Функция НОРМАЛИЗАЦИЯ в Excel предназначена для нахождения нормализованного значения некоторой величины из распределения, характеризующегося известными показателями стандартного отклонения и среднего.
Примеры использования функции НОРМАЛИЗАЦИЯ в Excel
Значение, определяемое функцией НОРМАЛИЗАЦИЯ, используется для вычисления вероятности нахождения некоторой величины в диапазоне значений. Эту вероятность можно рассчитать в Excel с помощью функции НОРМ.СТ.РАСП. Таким образом, эти функции имеют следующую взаимосвязь: =НОРМ.СТ.РАСП(НОРМАЛИЗАЦИЯ(аргументы)).
Таким образом, функция НОРМАЛИЗАЦИЯ может быть использована для преобразования нормального распределения к стандартному нормальному. У такого распределения дисперсия равна 1, а математическое ожидание – 0. Таким образом, рассматриваемая функция использует следующий алгоритм вычислений:
Z=(x-M)/D
где:
- Z – вычисляемая величина, распределенная по стандартному нормальному закону;
- x — исходное значение;
- M – математическое ожидание;
- D – дисперсия.
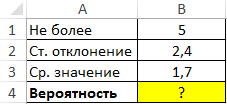
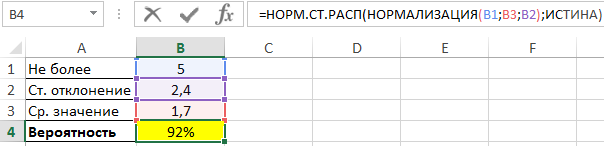
Пример 1. Определить вероятность того, что некоторая величина, которая распределена по нормальному закону, меньше или равна значению 5. Для ряда значений этой величины известны следующие показатели: среднее – 1,7, стандартное отклонение – 2,4.
Вид таблицы данных:
Для нахождения вероятности используем следующую формулу:
Для вычисления вероятности вхождения в диапазон (<=5) используем функцию НОРМ.СТ.РАСП со вторым аргументом, принимающим значение ИСТИНА (интегральная). Значение z (нормализованное) определено с помощью рассматриваемой функции.
Искомое число вероятности:
В итоговом результате вычисления функции получаем относительное – 92%.
Расчет процента вероятности с помощью нормализации в Excel
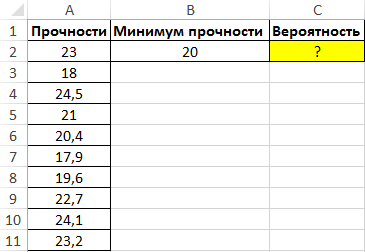
Пример 2. Данные о прочности изделий из исследуемой партии приведены в таблице Excel. Определить вероятность того, что потребитель купит партию изделий, прочность которых будет равна 20 Мпа или превысит это значение.
Вид таблицы данных:
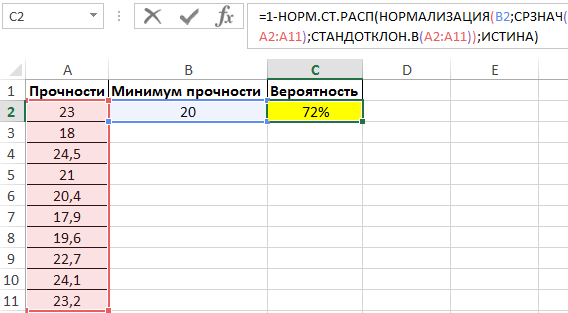
Для нахождения вероятности используем следующую формулу:
С помощью функции НОРМ.СТ.РАСП определяем вероятность того, что прочность изделий из партии не будет соответствовать условию (больше 20Мпа). Поэтому искомое значение получаем в виде разности 1 и найденной вероятности. Для определения среднего значения и стандартного отклонений для исследуемого ряда используем функции СРЗНАЧ и СТАНДОТКЛОН.В соответственно.
Полученный результат:
Правила использования функции НОРМАЛИЗАЦИЯ в Excel
Функция имеет следующую синтаксическую запись:
=НОРМАЛИЗАЦИЯ(x;среднее;стандартное_откл)
Описание аргументов (все обязательны для заполнения):
- x – принимает числовое значение, соответствующее величине, для которой требуется определить нормализованное значение;
- среднее – принимает числовое значение, характеризующее величину среднего арифметического исследуемого числового ряда;
- стандартное_откл – принимает число, которое соответствует величине стандартного отклонения, определенной для исследуемой последовательности.
Примечания:
- Каждый аргумент рассматриваемой функции необходимо указывать как число либо передавать ссылку на ячейку, содержащую числовые данные. НОМАЛИЗАЦИЯ будет возвращать код ошибки #ЗНАЧ!, если любой из аргументов указан в виде данных, которые не могут быть преобразованы к числовым значениям.
- Если рассматриваемая функция принимает в качестве любого аргумента данные логического типа (ИСТИНА, ЛОЖЬ), выполняется автоматическое преобразование к соответствующим числовым значениям (1, 0 соответственно).
- Если аргумент стандартное_откл задан в виде числа из диапазона отрицательных значений или 0 (нулем), функция вернет код ошибки #ЧИСЛО!
17 авг. 2022 г.
читать 2 мин
«Нормализация» набора значений данных означает масштабирование значений таким образом, чтобы среднее значение всех значений равнялось 0, а стандартное отклонение равнялось 1.
В этом руководстве объясняется, как нормализовать данные в Excel.
Пример: как нормализовать данные в Excel
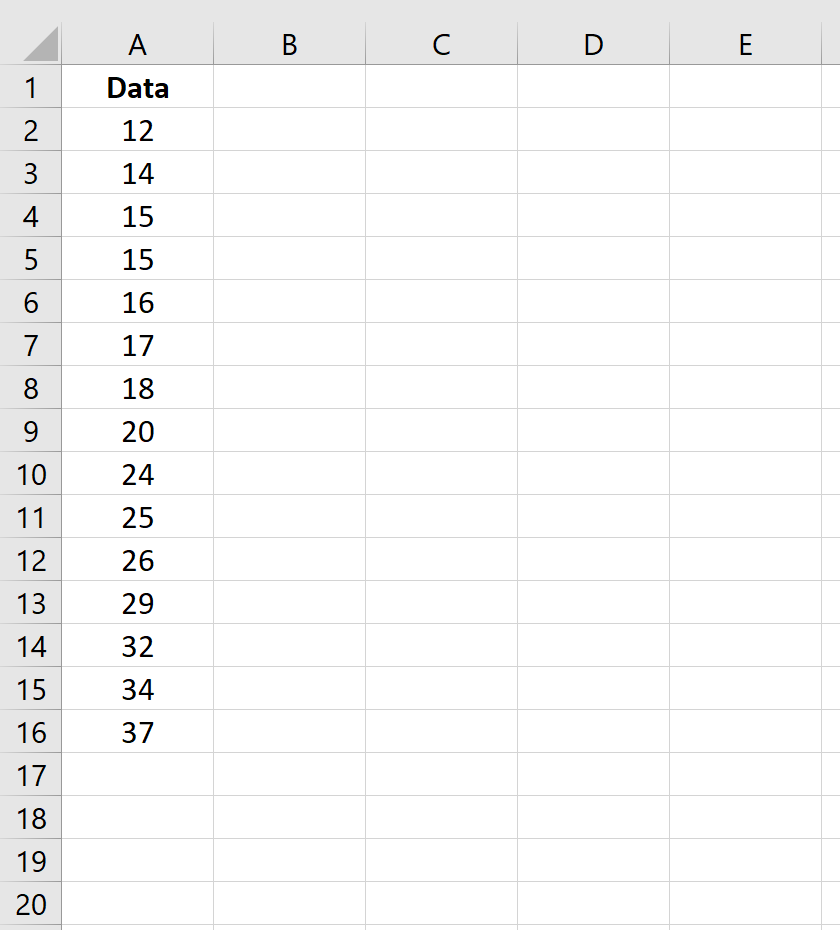
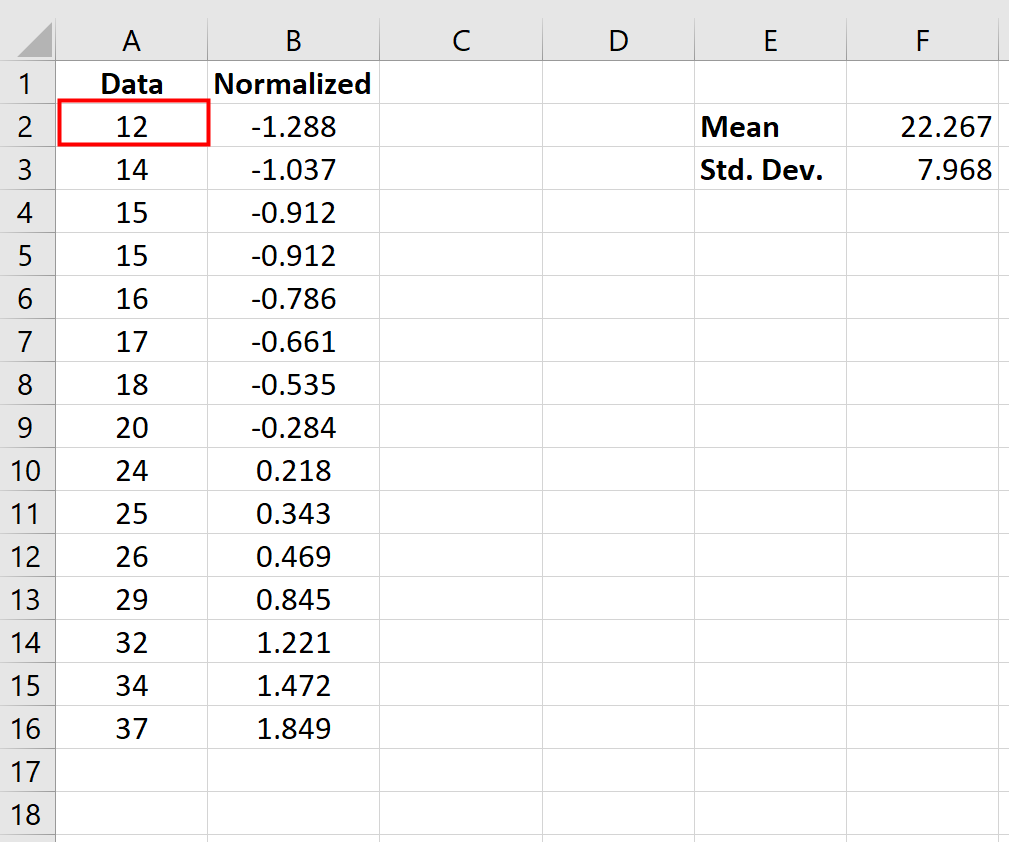
Предположим, у нас есть следующий набор данных в Excel:
Выполните следующие шаги, чтобы нормализовать этот набор значений данных.
Шаг 1: Найдите среднее значение.
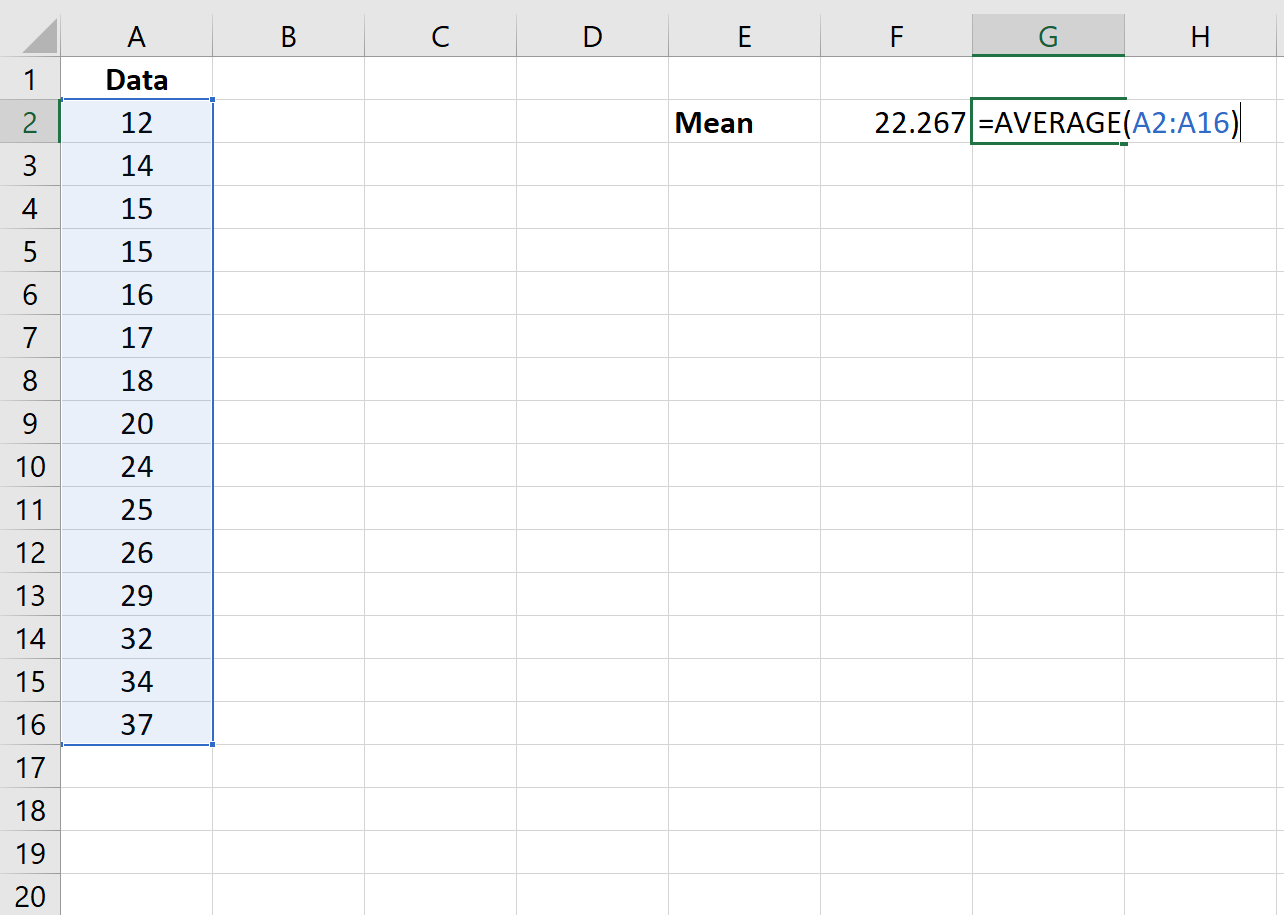
Во-первых, мы будем использовать функцию =AVERAGE(диапазон значений) , чтобы найти среднее значение набора данных.
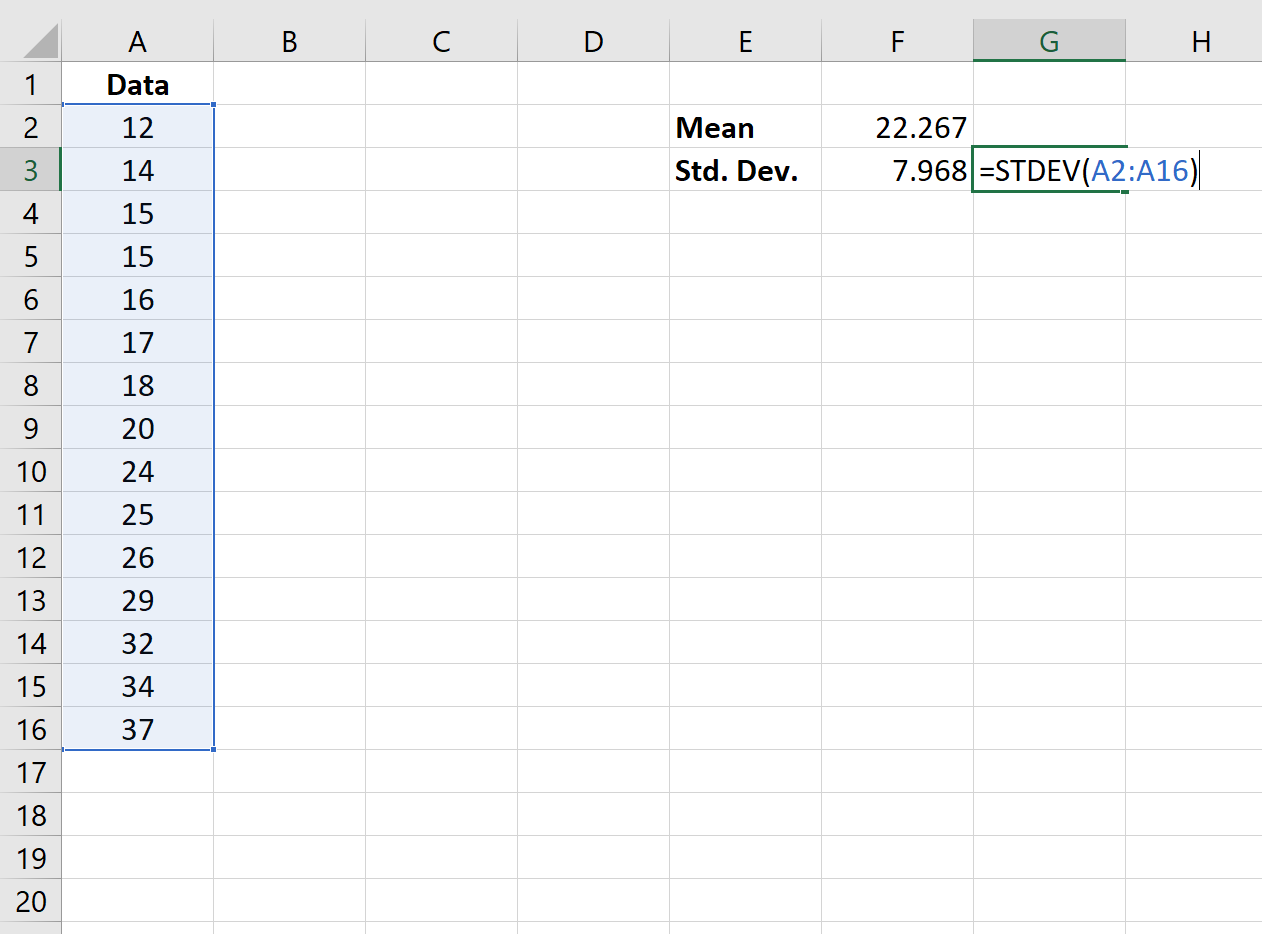
Шаг 2: Найдите стандартное отклонение.
Далее мы будем использовать функцию = СТАНДОТКЛОН (диапазон значений) , чтобы найти стандартное отклонение набора данных.
Шаг 3: нормализуйте значения.
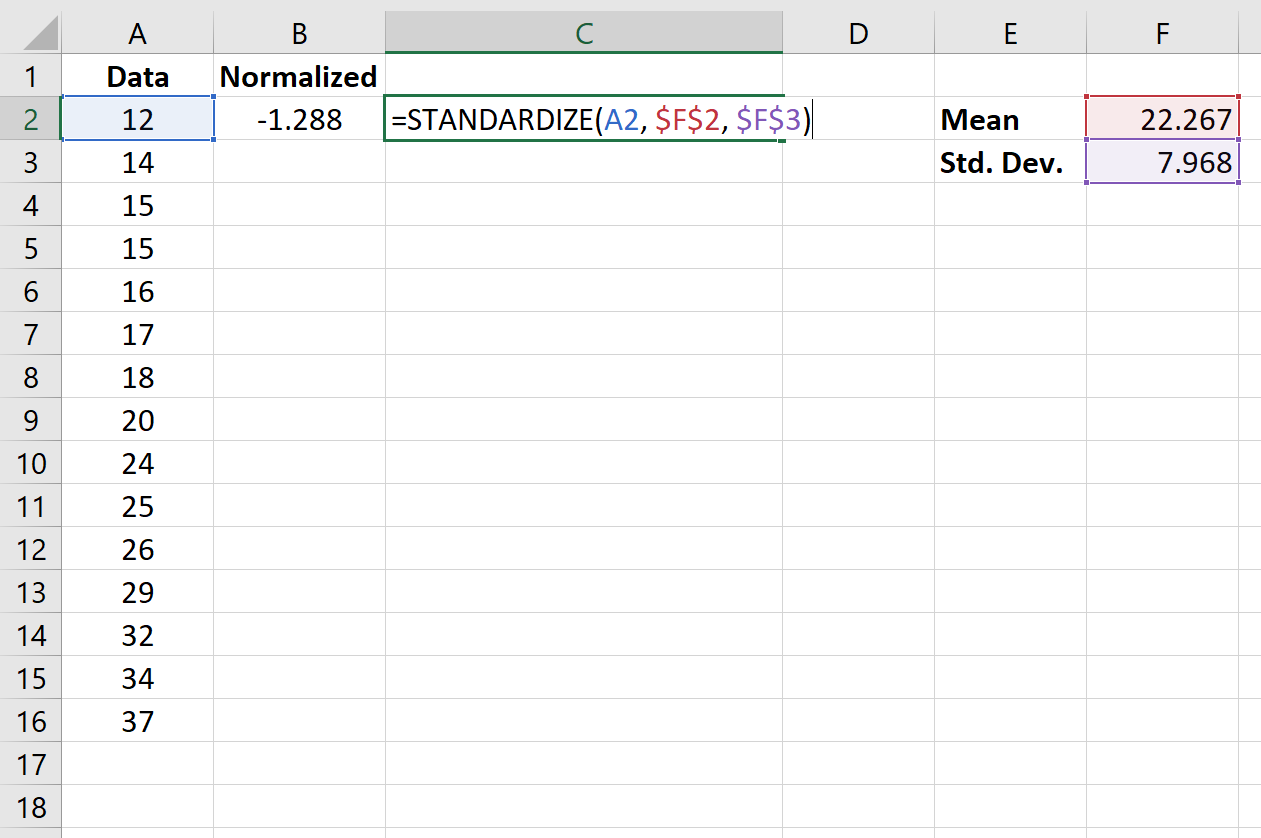
Наконец, мы будем использовать функцию STANDARDIZE(x, mean, standard_dev) для нормализации каждого из значений в наборе данных.
ПРИМЕЧАНИЕ:
Функция СТАНДАРТИЗАЦИЯ использует следующую формулу для нормализации заданного значения данных:
Нормализованное значение = (x – x ) / с
куда:
- х = значение данных
- x = среднее значение набора данных
- s = стандартное отклонение набора данных
На следующем изображении показана формула, используемая для нормализации первого значения в наборе данных:
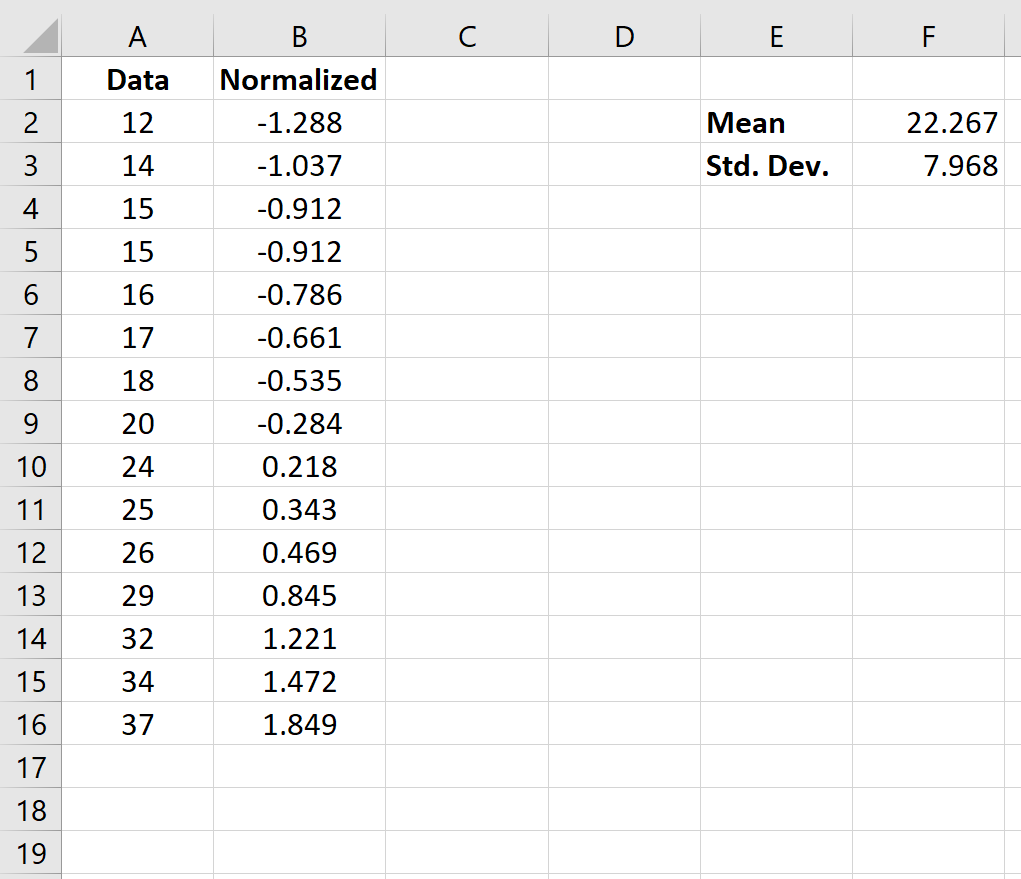
Как только мы нормализуем первое значение в ячейке B2, мы можем навести указатель мыши на правый нижний угол ячейки B2, пока не появится маленький +.Дважды щелкните + , чтобы скопировать формулу в оставшиеся ячейки:
Теперь каждое значение в наборе данных нормализовано.
Как интерпретировать нормализованные данные
Формула, которую мы использовали для нормализации заданного значения данных x, была следующей:
Нормализованное значение = (x – x ) / с
куда:
- х = значение данных
- x = среднее значение набора данных
- s = стандартное отклонение набора данных
Если конкретная точка данных имеет нормализованное значение больше 0, это указывает на то, что точка данных больше среднего. И наоборот, нормализованное значение меньше 0 указывает на то, что точка данных меньше среднего значения.
В частности, нормализованное значение говорит нам, сколько стандартных отклонений исходной точки данных от среднего. Например, рассмотрим точку данных «12» в нашем исходном наборе данных:
Нормализованное значение для «12» оказалось равным -1,288, которое было рассчитано как:
Нормализованное значение = (х – х ) / с = (12 – 22,267) / 7,968 = -1,288
Это говорит нам о том, что значение «12» на 1,288 стандартных отклонения ниже среднего значения в исходном наборе данных.
Каждое из нормализованных значений в наборе данных может помочь нам понять, насколько близко или далеко конкретное значение данных от среднего. Небольшое нормализованное значение указывает, что значение близко к среднему, в то время как большое нормализованное значение указывает, что значение далеко от среднего.
На чтение 3 мин. Просмотров 74 Опубликовано 15.07.2021
Статистические вычисления значительно ускоряются с использованием программного обеспечения. Один из способов сделать эти вычисления – использовать Microsoft Excel. Из всего разнообразия статистических данных и вероятностей, которые могут быть получены с помощью этой программы для работы с электронными таблицами, мы рассмотрим функцию НОРМ.ОБР.
Содержание
- Причина использования
- Аргументы для NORM.INV
- Примеры расчетов
- NORM.S.INV
Причина использования
Предположим, что у нас есть нормально распределенная случайная величина, обозначенная x . Можно задать один вопрос: «При каком значении x у нас есть нижние 10% распределения?» Шаги, которые мы должны выполнить для этого типа проблемы:
- Используя стандартную таблицу нормального распределения, найдите z , который соответствует 10% наименьшего распределения.
- Воспользуйтесь формулой z -score и решите ее для x . Это дает нам x = μ + z σ, где μ – среднее значение распределения, а σ – стандартное отклонение.
- Вставьте все наши значения в приведенную выше формулу. Это дает нам ответ.
В Excel все это делает за нас функция НОРМ.ОБР.
Аргументы для NORM.INV
Чтобы использовать функцию, просто введите в пустую ячейку следующее:
= NORM.INV (
data-type = “code”>
Аргументы этой функции по порядку:
- Вероятность – это совокупная доля распределения, соответствующая площади в левой части распределения.
- Среднее – это было обозначено выше как μ и является центром нашего распределения.
- Стандартное отклонение – оно было обозначено выше как σ и учитывает разброс нашего распределения.
Просто введите каждый из этих аргументов через запятую, разделяя их. После ввода стандартного отклонения закройте круглые скобки с помощью) и нажмите клавишу ввода. ключ. Результатом в ячейке является значение x , которое соответствует нашей пропорции.
Примеры расчетов
Мы увидим, как использовать эту функцию, на нескольких примерах вычислений. Для всего этого мы будем предполагать, что IQ обычно распределяется со средним значением 100 и стандартным отклонением 15. Мы ответим на следующие вопросы:
- Каков диапазон значений самых низких 10% всех оценок IQ?
- Каков диапазон значений самых высоких 1% всех оценок IQ?
- Каков диапазон значений средних 50% всех оценок IQ?
Для вопроса 1 мы вводим = NORM .INV (.1,100,15). Выходной сигнал Excel составляет примерно 80,78. Это означает, что оценки ниже или равные 80,78 составляют самые низкие 10% всех оценок IQ.
Для вопроса 2 нам нужно немного подумать, прежде чем использовать функция. Функция НОРМ.ОБР предназначена для работы с левой частью нашего распределения. Когда мы спрашиваем о верхней пропорции, мы смотрим на правую часть.
Верхний 1% эквивалентен вопросу о нижних 99%. Вводим = НОРМ.ОБР (0,99,100,15). Выходной сигнал Excel составляет приблизительно 134,90. Это означает, что баллы, превышающие или равные 134,9, составляют 1% лучших оценок IQ.
Для вопроса 3 мы должны быть еще более умными. Мы понимаем, что средние 50% находятся, когда мы исключаем нижние 25% и верхние 25%.
- Для нижних 25% вводим = НОРМ.ОБР (0,25,100,15) и получаем 89,88.
- Для верхних 25% вводим = НОРМ.ОБР (0,75, 100, 15) и получаем 110,12
NORM.S.INV
Если мы работаем только со стандартными нормальными распределениями, то NORM.S.INV функция работает немного быстрее. Для этой функции среднее значение всегда равно 0, а стандартное отклонение всегда равно 1. Единственный аргумент – это вероятность.
Связь между двумя функциями:
NORM.INV (Probability, 0, 1) = NORM.S.INV (Probability)
data-type = “code”>
Для любых других нормальных распределений мы должны использовать функцию НОРМ.ОБР.