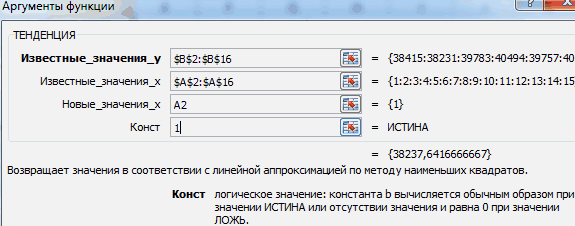
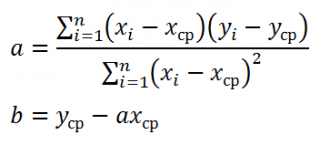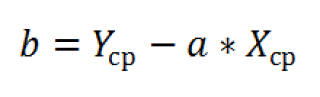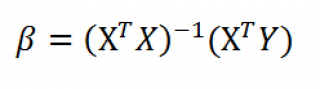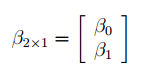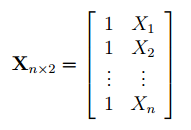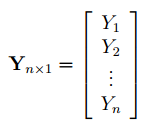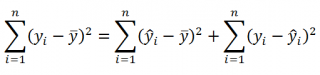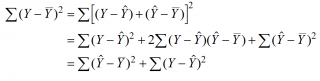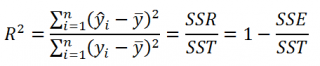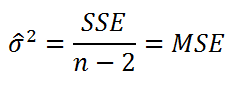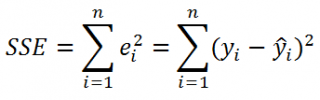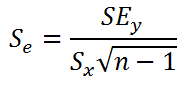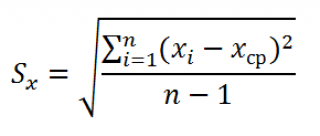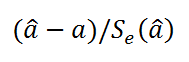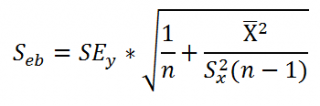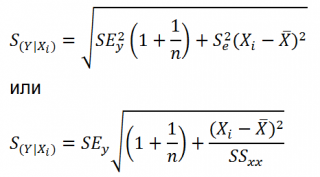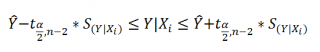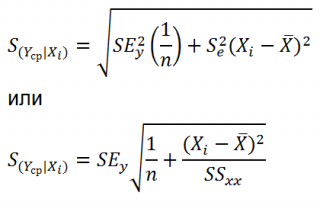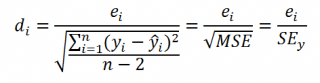Функция гомперца в excel - Word и Excel - помощь в работе с программами

Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.

Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.

Регрессионный анализ в Excel

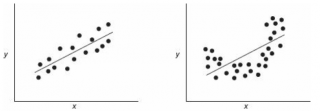
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

Регрессия бывает:

линейной (у = а + bx);
параболической (y = a + bx + cx²);
экспоненциальной (y = a * exp(bx));
степенной (y = a*x^b);
гиперболической (y = b/x + a);
логарифмической (y = b * 1n(x) + a);
показательной (y = a * b^x).

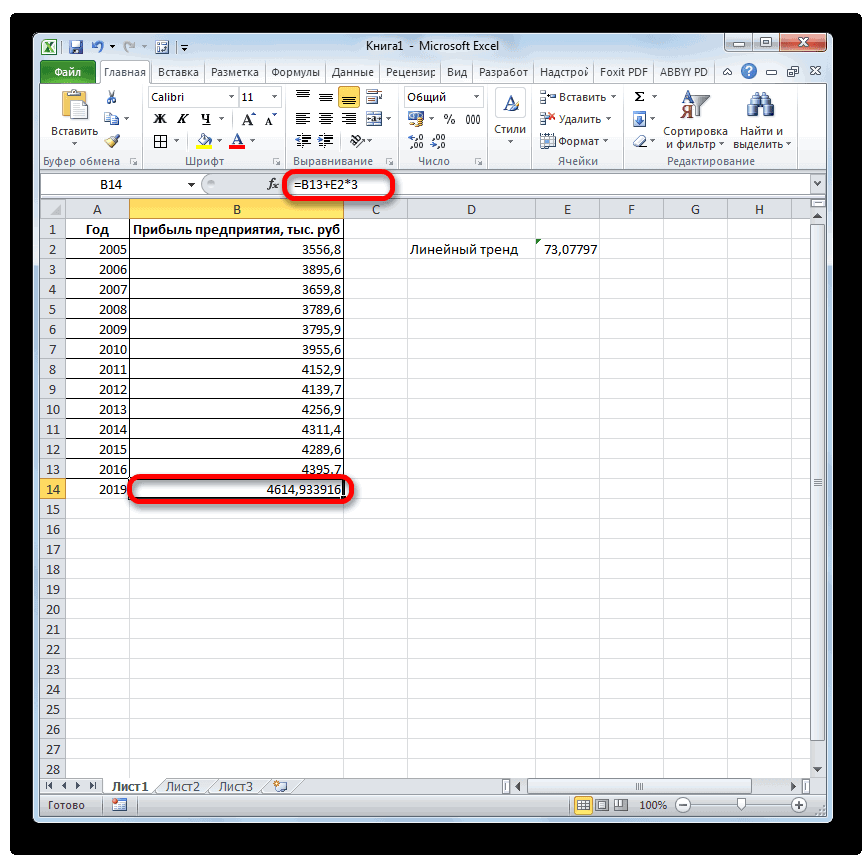
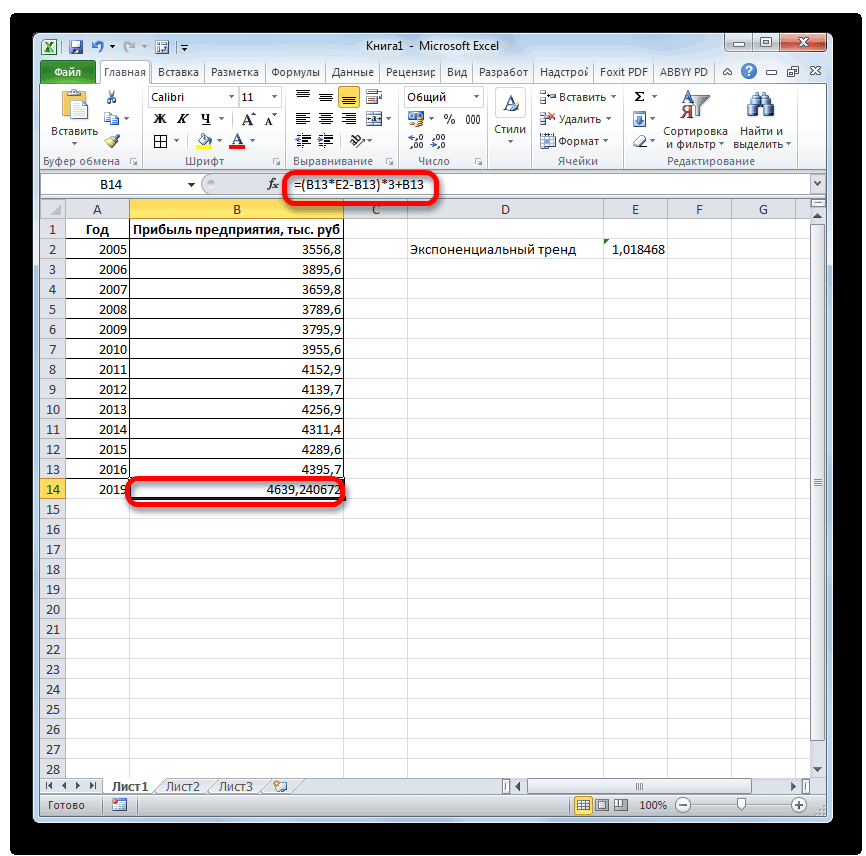
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

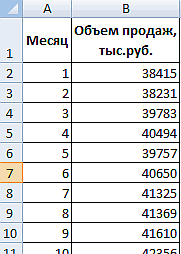
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

У = а₀ + а₁х₁ +…+а_кх_к.

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».

Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.

Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».

Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.

После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты.

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.

Корреляционный анализ в Excel

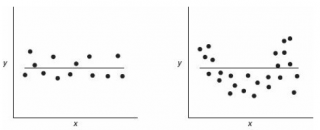
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.

Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.

Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.

Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.

Для нахождения парных коэффициентов применяется функция КОРРЕЛ.

Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.

Ставим курсор в любую ячейку и нажимаем кнопку fx.

В категории «Статистические» выбираем функцию КОРРЕЛ.
Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.

Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).

Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.

Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:

Корреляционно-регрессионный анализ

На практике эти две методики часто применяются вместе.

Пример:

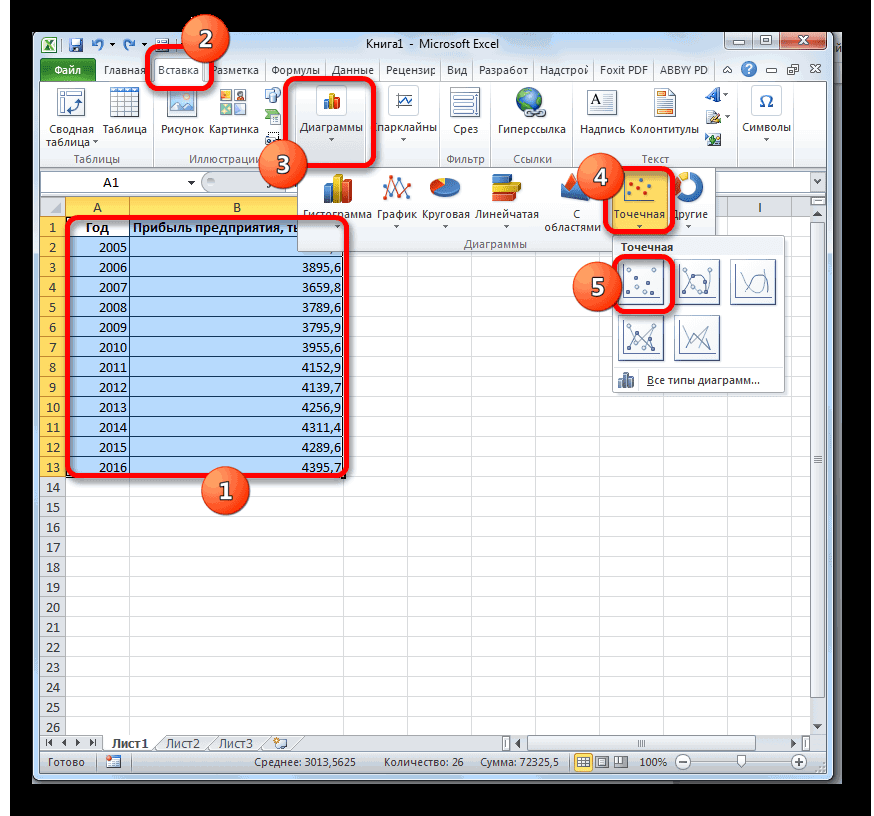
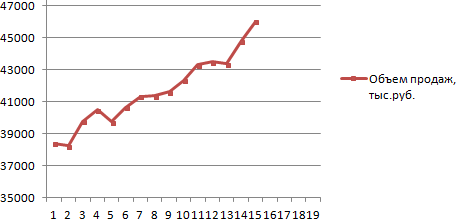
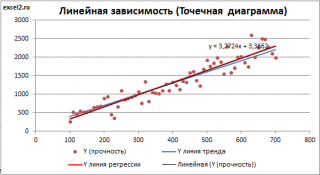
Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.

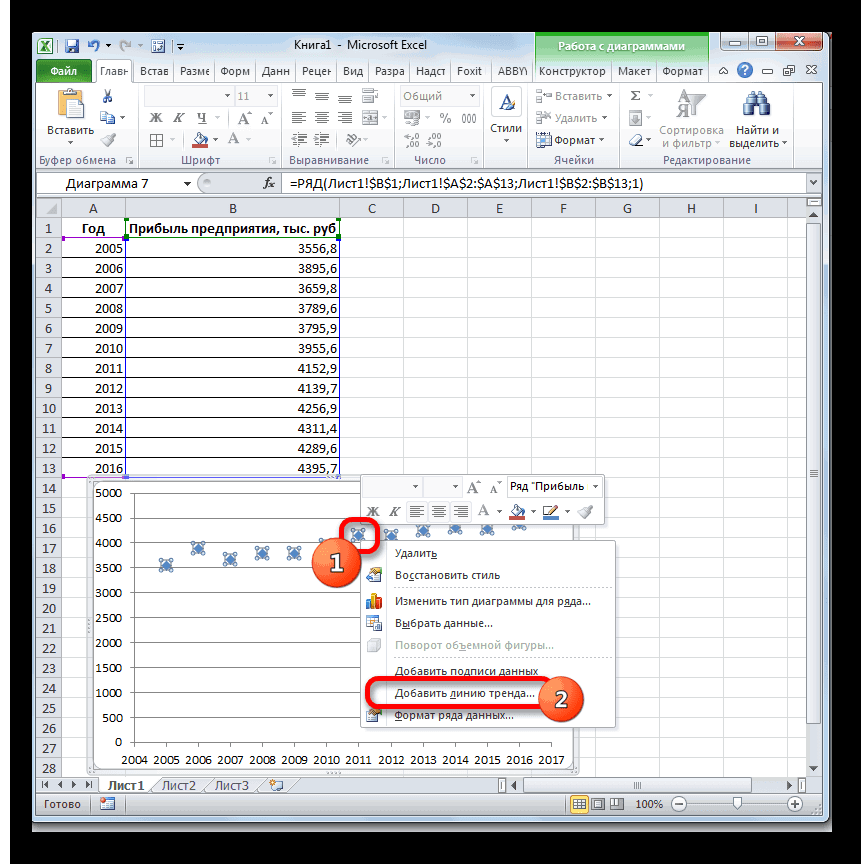
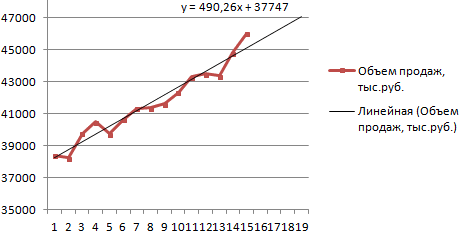
Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».

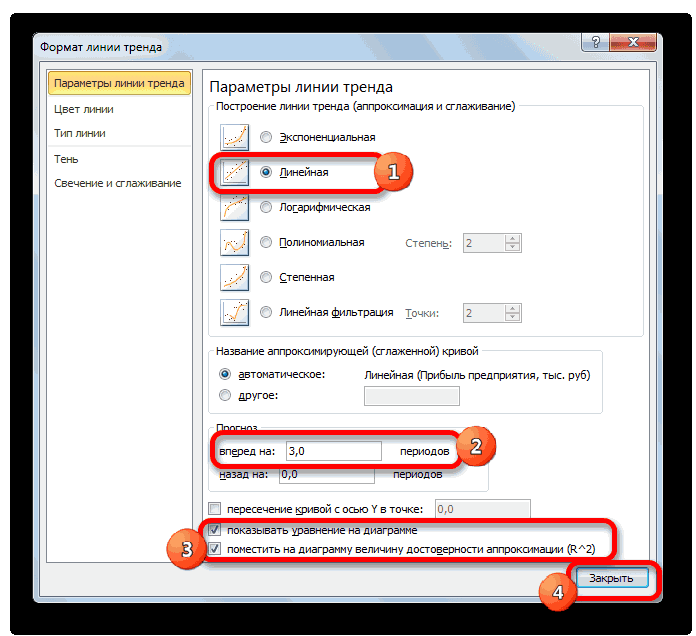
Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».

Жмем «Закрыть».

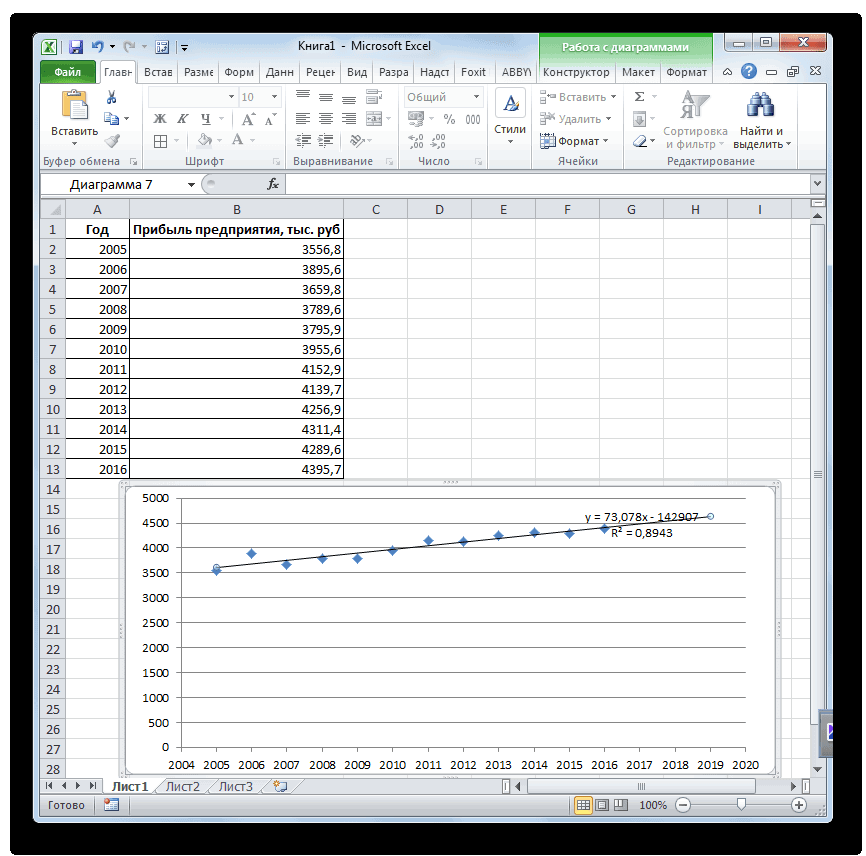
Теперь стали видны и данные регрессионного анализа.

Источник

Некоторые обозначения в актуарной математике.

ξ — случайная величина продолжительность жизни.

s(x) — функция выживания, вероятность того, что человек доживёт до возраста x.

F(x) — функция распределения случайной величины ξ.
f(x) — плотность распределения случайной величины ξ, и в актуарной математике закреплён термин кривая смертей (the curve of deaths).

μx — функция интенсивности смертности.

Величина μx∙t приближённо равна вероятности смерти человека возраста x в интервале (x, x+t). В теории надёжности функция μx называется функцией отказов (hazard rate function).

Верна формула
.
Доказательство.
Решим дифференциальное уравнение .

Таблица смертности населения России для календарного года 2014.
Общепринятые обозначения таблицы смертности населения.

х — возраст (от 0 до 100 лет);

l(x) («эль малое икс») — точное число доживающих до возраста х лет (l(0) обычно принимается за 100000);

d(x)= l(x) -l(x+1)— число умирающих при переходе от возраста х к возрасту х+1 лет;

q(x)=d(x) / l(x) — вероятность умереть при переходе от возраста х к возрасту х+1 лет;

р(x)=1-q(x) — вероятность дожития до возраста х+1 лет для лиц в точном возрасте х лет;

m(x) — коэффициент смертности, он примерно равен средней интенсивности смертности, усредненной по году.

L(x) («эль большое икс») — среднее число живущих в возрасте х (с точки зрения демографии, это число человеко-лет, прожитых поколением в возрасте х), обычно рассчитывается как среднее арифметическое между l(x) и l(x+1) для всех возрастов, кроме 0 (L(0) рассчитывается по особой формуле ввиду крайней неравномерности распределения младенческой смертности);

Т(x) — число человеко-лет, которое предстоит прожить совокупности людей, находящихся в возрасте х лет (сумма L(x) от возраста х до верхнего возрастного предела таблицы);

е(x)=Т(x) / l(x) — средняя ожидаемая продолжительность предстоящей жизни в возрасте х лет. Как правило, под ожидаемой продолжительностью жизни (ОПЖ) понимают ожидаемую продолжительность жизни при рождении, то есть е(0), которая и является итоговым показателем таблицы смертности.

Модель Гомпертца

(Gompertz,1825)
Согласно закону Гомпертца интенсивность смертности для возраста x, x≥0 есть ,
где β обозначает уровень смертности в возрасте 0 лет и γ — скорость старения. То есть интенсивность смертности μx в возрасте x является экспоненциальной функцией возраста.
Функция выживания — .
Кривая смертей — и имеет максимум в точке .

Модель Мэйкхама (Гомпертца-Мейкхама)

(Makeham,1860)
Дополнительный параметр α>0 был добавлен к модели Гомпертца, чтобы учесть интенсивность смерти от несчастных случаев, он предполагается постоянным и независимым от возраста. Получилась следующая модель .

Предложенная Мэйкхамом модель утверждает, что если время жизни X, человека является распределенным по Гомпертцу, случайная величина Y — время несчастного случая со смертельным исходом имеет экспоненциальное распределение, а случайные величины X и Y независимы, то минимум X и Y имеет распределение Мэйкхама. Закон Мэйкхама наиболее подходит для изучения процесса смертности человека, так как в нём учитывается, что для малых возрастов преобладающую роль в смертности играют несчастные случаи, а с увеличением возраста их роль ослабевает. Модель наилучшим образом описывает динамику смертности человека в диапазоне возраста 30—80 лет. В области большего возраста смертность не возрастает так быстро, как предусматривается этим законом смертности.
Исторически смертность человека до 1950-х годов была в большей мере вызвана независимым от времени компонентом закона смертности (членом или параметром Мейкхама), тогда как зависимый от возраста компонент (функция Гомпертца) почти не изменялась. После 1950-х годов картина изменилась, что привело к снижению смертности в позднем возрасте и так называемой «де-ректангуляризации» (сглаживанию) кривой выживания.

Модели Гомпертца и Мейкхама использовались более ста лет в основном страховыми компаниями для прогнозирования смертности за пределами 65 лет.

Оценка параметров.

Пусть представляет вероятность того, что лицо, достигшее возраста x, умрет до достижения возраста x + 1. В терминах μx qx равно

Дополнение представляет вероятность того, что человек в возрасте х выживет, по крайней мере, до возраста x + 1.
Начнем с преобразования модели Мейкхама в линейное уравнение с использованием логарифмического линейного преобразования и подгонки кривой с использованием линейной регрессии.

Верна формула, если интенсивность смертности μx сильно не меняется в течении года.

Беря натуральный логарифм с обеих сторон, получаем:

Затем устанавливается линия тренда с использованием excel в возрасте от 45 до 100 лет.
Мы используем линейное уравнение , где конкретные возрасты от 45 до 100 лет, чтобы преобразовать уравнение Мейкхама в линейную форму. Это связано с тем, что при исследовании логарифма интенсивности смертности между этими возрастами, как было установлено, для оценки точек данных можно использовать прямую линию. Это согласуется с моделью Гомпертца, которая является точной для средних лет.

Поэтому, приравнивая члены, мы видим, что: .
Параметры a и b оцениваются с использованием линейной регрессии, метода наименьших квадратов МНК;

Где x и y с чертой есть выборочные средние соответственно наблюдаемых выборок x и y.
Автономный параметр α был получен, взяв выборку более молодого возраста 20-30 (любой возраст может быть взят) и применения формулы;

Где ym высота градуировочной кривой в выборке моложе 35 лет из эксперимента и yg — высота прямой линии.
Вероятность выживания:
Уровень смертности:

График градуировочной кривой .

График градуировочной кривой и прямой тренда.

По таблице смертности населения РФ 2014-го года получаются следующие параметры:
α=0.00083783
β=0.00046131
γ=0.067795803

Уточнение оценок параметров методом максимального правдоподобия.

Maximum Likelihood Estimation.

Очень часто только дискретные данные доступны и параметры β, γ не могут быть установлены напрямую. Однако, если количество смертей и численность человеко-лет подверженных риску ухода из жизни может быть наблюдаемо, то мы вправе предположить, что число смертей в данном возрастном диапазоне подчиняется распределению Пуассона.
Пусть D обозначает число смертей и λ — параметр интенсивности распределения Пуассона.

Степенной параметр λ распределения Пуассона согласуется с μ(x), оба λ, μ (x)> 0. Интенсивность происшествий λ пуассоновского процесса предполагает одинаковое просматриваемое окно для каждой единицы наблюдений. При применении распределения Пуассона к данным о смертности, единицей наблюдений является количество смертей в каждой возрастной группе Dx и просматриваемое окно — это количество людей (или человеко-лет), подверженных риску ухода из жизни. Понятно, что число людей, которым грозит смерть, изменяется от одной возрастной группы к другой. Поэтому θ следует уравновесить по количеству человеко-лет подверженных смерти l(x) в возрасте x. После подстановки в f(D;λ) λ = l(x)∙θ, взятия логарифма и устранения аддитивных констант, функция логарифмического правдоподобия смертей D будет

Учитывая, что

Для аналитического получения оценки максимального правдоподобия, обозначим S как оценочную функцию правдоподобия и определим следующим образом

Из максимизации функции правдоподобия следует, что при оптимальных параметрах θ система уравнений, определяемая оценочной функцией, является однородной,

и матрица Гессе

отрицательно определённой.

Найдём максимум функции правдоподобия численным методом с использованием excel-ого «Solver» для возраста от 45 до 100 лет, его название «Поиск решения нелинейных задач методом ОПГ». Это численный алгоритм поиска максимума нелинейной функции, в качестве первого приближения возьмём определённые выше оценки параметров β и γ, метод сходится уже после нескольких итераций.

Новые параметры:
α=0.00078390
β=0.00048454
γ=0.06653488

Новые значения параметров кардинально не поменялись, метод наименьших квадратов МНК сразу дал достаточно точное приближение.

Графики.

График функции выживания s(x).

График плотности распределения f(x), кривая смертей (the curve of deaths).
В модели Гомпертца максимум достигается
У плотности заметен максимум в районе 72-75 года и в таблице смертности параметр dx в эти года приближается к максимальному значению ≈2600, а именно …, d72=2611, d73=2342, d74=2404, d75=2573, d76=2357, …

Аналитический расчёт средней ожидаемой продолжительности жизни для возраста 0, 15, 45, 60, 65, 70 лет

Для расчёта средней ожидаемой продолжительности жизни используется формула:

Ожидаемая продолжительность жизни согласно статистическим данным 2014-го года составляет
e(0)=64 года
e(15)=49.2633/0.976058=50.47
e(45)=21.5232/0.8408=25.6
e(60)=10.1941/0.647763=15.7
e(65)=7.18764/0.552198=13
e(70)=4.69562/0.442675=10.6
Сравните цифры с этими данными, видно что функция распределения вполне подходит для проведения статистических расчётов.

Пенсия и срок дожития

Срок дожития — установленный правительством и рассчитанный по статистическим данным средний срок жизни гражданина после выхода на заслуженный отдых (время, в течение которого планируется начисление пенсии). Данное понятие используется для определения размера назначаемого пособия, таким образом, чем больше срок дожития, тем меньше ее размер.
Термин «срок дожития» был утверждён постановлением № 531 Правительства РФ 2 июня 2015 года.
Срок дожития используется для определения размера накопительной пенсии. Все пенсионные накопления делятся на ожидаемый период выплаты накопительной пенсии, после чего получаем ежемесячный размер накопительной пенсии. Чем больше срок дожития, тем меньший размер накопительной пенсии, начисляемой пенсионеру.

Страховая пенсия — это гарантированная государством ежемесячная выплата действующим пенсионерам, возмещающая им утраченный доход.
Пусть S60 — это ожидаемый размер всей начисляемой страховой пенсии, если выплаты начинаются в возрасте 60 лет, S70 — ожидаемый размер в случае начала выплат в 70 лет.
Посчитаем отношение S60/S70, предполагая, что в обоих случаях выплачивается какая-то фиксированная сумма P в месяц.

S60/S70=9.8906/4.45716=2.2
Следовательно, чтобы нивелировать эту разницу, необходимо пенсионерам 70 поднять пенсию в 2.2 раза, для чего был изобретён повышающий коэффициент.

Пенсионная формула
Математически пенсионная формула выглядит так:
СП = ПБ • СТ • КПБ + ФВ • КФВ

где:
СП — размер страховой пенсии, в рублях
ПБ — пенсионный балл (индивидуальный пенсионный коэффициент), начисленных на дату назначения гражданину страховой пенсии
СТ — стоимость пенсионного балла в год назначения страховой пенсии, в рублях
ФВ — фиксированная выплата, в рублях
КПБ — коэффициент повышения ПБ при назначении страховой пенсии по старости в более позднем возрасте
КФВ — коэффициент повышения ФВ при назначении страховой пенсии по старости в более позднем возрасте

Повышающий коэффициент при выходе на пенсию позже на 10 лет или более равен КПБ=2.32 и КФВ=2.11. Среднее арифметическое КПБ и КФВ как раз равно ≈2.2.

Список использованной литературы.

Г.М. Кошкин Основы страховой математики, Томск 2002 (http://www.actuaries.ru/lib/Кошкин%20-%20Основы%20страховой%20(актуарной)%20математики.pdf)

SUSAN MBALA SHIHUGWA 2015 Impact of longevity risk with best fit mortality forecasting model

2011 MORTALITY PROJECTION: CURVE FITTING AND LINEAR REGRESSION

Adam Lenart 2012 The Gompertz distribution and Maximum Likelihood Estimation of its parameters

wikipedia.org Gompertz–Makeham_law_of_mortality

Источник

Коэффициент Z Альтмана (Z — счет Альтмана, модель Z Альтмана)

Z = 1,2 Х1 + 1,4 Х2 + 3,3 Х3 + 0,6 Х4 + 1,0 Х5,

где:

Х1 = рабочий капитал/активы;

Х2 = нераспределенная прибыль/активы;

Х3 = EBIT (эксплуатационная прибыль)/активы;

Х4 = рыночная стоимость собственного капитала/бухгалтерская (балансовая, учетная) стоимость задолженности;

Х5 = выручка (общий доход) /активы, а коэффициенты представляют собой веса отдельные экзогенных переменных.

Полином 1-й степени (линейная функция, 2-я функция Энгеля)

Функция применяется для моделирования серии данных с постоянным уровнем абсолютного прироста (без предела роста). Применяется чаще всего, ибо проста в применении и легко интерпретируется в экономических категориях.y = a + b * xгде:x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент, определяющий точку пересечения с осью ординат при x = 0;

b — коэффициент при переменной x, определяющий наклон прямой или скорость ее роста.

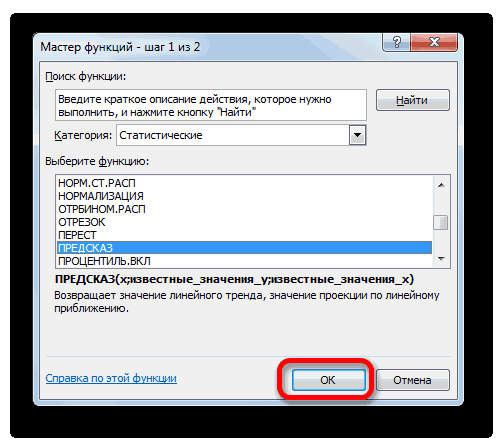
Для расчетов в среде электронных таблиц MS Excel лучше не применять простые формулы типа ПРЕДСКАЗ(). Более системным подходом является применение ТЕНДЕНЦИЯ(), а еще лучше — ЛИНЕЙН(). Причем, последняя обладает огромными возможностями и способно моделировать практически любую функцию, сводящуюся к линейной, т.е. большинство элементарных математческих функций.

a = ИНДЕКС(ЛИНЕЙН(Y;X;1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(Y;X;1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(Y;X;1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(Y;X;1;1);4;1)где:Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Полином 2-й степени (параболическая или квадратичная или 2-я функция Энгеля)

Полином 2-й степени применяется для моделирования данных с постоянным относительным приростом или с постоянным ускорением без предела роста (полином 1-го порядка пригоден только для процессов, протекающих с постоянной скоростью). Как и полином 1-й степени, данная функция наглядно интерпретируется в простых экономических категориях.y = a + b * x + c * x²где:x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент, определяющий точку пересечения с осью ординат при x = 0;

b — коэффициент при переменной x, определяющий скорость роста функции;

c — коэффициент при переменной x², определяющий «ускорение» функции.Для расчетов в среде электронных таблиц MS Excel можно применять видоизмененные формулы ТЕНДЕНЦИЯ(), а еще лучше — ЛИНЕЙН(). Причем, последняя обладает огромными возможностями и способно моделировать практически любую функцию, сводящуюся к линейной, т.е. большинство элементарных математческих функций.a =ИНДЕКС(ЛИНЕЙН(Y;X_1_2;1;1);1;3)

b =ИНДЕКС(ЛИНЕЙН(Y;X_1_2;1;1);1;2)

c =ИНДЕКС(ЛИНЕЙН(Y;X_1_2;1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(Y;X_1_2;1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(Y;X_1_2;1;1);4;1)где:Y — поименованный массив значений результативного признака Y;

X_1_2 — поименованный массив значений факторного признака X в 1-й и 2-й степенях.См., также, пример электронной таблицы MS Excel — sample_014

Полином 3-й степени (кубическая функция)

Полином 3-й степени применяется для моделирования данных с постоянной скоростью изменения относительного прироста или с постоянной скоростью изменения ускорения (полином 1-го порядка пригоден только для процессов, протекающих с постоянной скоростью, а полином 2-й степени — для процессов с постоянным ускорением). Как и полином 1-й степени, данная функция наглядно интерпретируется в простых экономических категориях.

y = a + b * x + c * x²+ d * x³

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент, определяющий точку пересечения с осью ординат при x = 0;

b — коэффициент при переменной x, определяющий скорость роста функции;

c — коэффициент при переменной x², определяющий «ускорение» функции;

d — коэффициент при переменной x³, определяющий «скорость ускорения» функции.

Для расчетов в среде электронных таблиц MS Excel можно применять видоизмененные формулы ТЕНДЕНЦИЯ(), а еще лучше — ЛИНЕЙН(). Причем, последняя обладает огромными возможностями и способно моделировать практически любую функцию, сводящуюся к линейной, т.е. большинство элементарных математческих функций.

a = ИНДЕКС(ЛИНЕЙН(Y;X_1_2_3;1;1);1;4)

b =ИНДЕКС(ЛИНЕЙН(Y;X_1_2_3;1;1);1;3)

c =ИНДЕКС(ЛИНЕЙН(Y;X_1_2_3;1;1);1;2)

d =ИНДЕКС(ЛИНЕЙН(Y;X_1_2_3;1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(Y;X_1_2_3;1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(Y;X_1_2_3;1;1);4;1)

где:

Y — поименованный массив значений результативного признака Y;

X_1_2_3 — поименованный массив значений факторного признака X в 1-й,2-й и 3-й степенях.См., также, пример электронной таблицы MS Excel — sample_014

Простая экспонента

Простая экспонента, как и полином 2-го порядка, применяется для моделирования процессов с постоянными темпами относительного прироста (без предела роста):

y = e^{( a + b · x )}

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент;

b — коэффициент при переменной x.

В регрессионных моделях применяется линеаризованный вид этой функции, получаемый методом логарифмирования обеих частей уравнения:ln ( y ) = ( a + b * x ) * ln ( e ) = ( a + b * x )Для расчетов в среде электронных таблиц MS Excel применяются формулы функций ТЕНДЕНЦИЯ() или ЛИНЕЙН(). Причем, последняя обладает огромными возможностями и способно моделировать практически любую функцию, сводящуюся к линейной, т.е. большинство элементарных математческих функций.

a = ИНДЕКС(ЛИНЕЙН(LN(Y);X;1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(LN(Y);X;1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(LN(Y);X;1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(LN(Y);X;1;1);4;1)

где:

Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Модифицированная экспонента

Модифицированная экспонента применяется для описания процессов с пределом роста:y = a — b * e^-xгде:x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент;

b — коэффициент при переменной e^-x.В регрессионных моделях применяется линеаризованный вид этой функции, получаемый методом логарифмирования обеих частей уравнения.Для расчетов в среде электронных таблиц MS Excel применяются формулы функций ТЕНДЕНЦИЯ() или ЛИНЕЙН(). Причем, последняя обладает огромными возможностями и способно моделировать практически любую функцию, сводящуюся к линейной, т.е. большинство элементарных математческих функций.a = ИНДЕКС(ЛИНЕЙН(Y;EXP(-X);1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(Y;EXP(-X);1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(Y;EXP(-X);1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(Y;EXP(-X);1;1);4;1)где:Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Логарифмическая линейная

Логарифмическая линейная функция применяется для более пологого моделирования процессов без предела роста:y = a + b * ln ( x )где:x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент;

b — коэффициент при переменной ln(x).В регрессионных моделях применяется линеаризованный вид этой функции, получаемый методом логарифмирования обеих частей уравнения.Для расчетов в среде электронных таблиц MS Excel применяются формулы функций ТЕНДЕНЦИЯ() или ЛИНЕЙН(). Причем, последняя обладает огромными возможностями и способно моделировать практически любую функцию, сводящуюся к линейной, т.е. большинство элементарных математческих функций.

a = ИНДЕКС(ЛИНЕЙН(Y;LN(X);1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(Y;LN(X);1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(Y;LN(X);1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(Y;LN(X);1;1);4;1)

где:

Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Логарифмическая парабола

y = a * b^x* c^{x^2}

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент;

b — коэффициент — основание степенной функции b^x;

c — коэффициент — основание степенной функции с^{x^2}.

В регрессионных моделях применяется линеаризованный вид этой функции, получаемый методом логарифмирования обеих частей уравнения.Для расчетов в среде электронных таблиц MS Excel применяются формулы функций ТЕНДЕНЦИЯ() или ЛИНЕЙН(). Причем, последняя обладает огромными возможностями и способно моделировать практически любую функцию, сводящуюся к линейной, т.е. большинство элементарных математческих функций.

a = EXP(ИНДЕКС(ЛИНЕЙН(LN(Y);X_1_2;1;1);1;3))

b =EXP(ИНДЕКС(ЛИНЕЙН(LN(Y);X_1_2;1;1);1;2))

c =EXP(ИНДЕКС(ЛИНЕЙН(LN(Y);X_1_2;1;1);1;1))

R² =ИНДЕКС(ЛИНЕЙН(LN(Y);X_1_2;1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(LN(Y);X_1_2;1;1);4;1)

где:

Y — поименованный массив значений результативного признака Y;

Степенная функция (3-я функция Энгеля)

Степенная функция применяется для моделирования процессов без предела роста:

y = e^a * x^b

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — коэффициент — показатель экпоненты e^a;

b — коэффициент — показатель степенной функции x^b.

a = ИНДЕКС(ЛИНЕЙН(LN(Y);LN(X);1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(LN(Y);LN(X);1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(LN(Y);LN(X);1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(LN(Y);LN(X);1;1);4;1)

где:

Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Гиперболическая (обратная) функция (1-я функция Энгеля)

y = a + b / x

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент, определяющий точку пересечения с осью ординат при x = 0;

b — коэффициент при переменной x, определяющий крутизну гиперболы.В регрессионных моделях применяется линеаризованный вид этой функции, получаемый методом логарифмирования обеих частей уравнения.

Для расчетов в среде электронных таблиц MS Excel применяются формулы функций ТЕНДЕНЦИЯ() или ЛИНЕЙН(). Причем, последняя обладает огромными возможностями и способно моделировать практически любую функцию, сводящуюся к линейной, т.е. большинство элементарных математческих функций.

a = ИНДЕКС(ЛИНЕЙН(Y;1/X;1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(Y;1/X;1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(Y;1/X;1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(Y;1/X;1;1);4;1)

где:

Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Кривая Джонсона

Функция Джонсона применяется для описания процессов с пределом роста:

y = e^(a+b/x)

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент;

b — коэффициент фунции 1/x. В регрессионных моделях применяется линеаризованный вид этой функции, получаемый методом логарифмирования обеих частей уравнения.

a = ИНДЕКС(ЛИНЕЙН(LN(Y);1/X;1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(LN(Y);1/X;1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(LN(Y);1/X;1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(LN(Y);1/X;1;1);4;1)

где:Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Кривая Гомперца

Функция Гомперца применяется для моделирования процессов с пределом роста и точкой перегиба, что характерно для кривых спроса на некоторые новые товары:

y = e^{a-b·e^x}

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент;

b — коэффициент фунции e^x.

a = ИНДЕКС(ЛИНЕЙН(LN(Y);EXP(X);1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(LN(Y);EXP(X);1;1);1;1)

где:

Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Кривая Парето

y = a / x^b

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — коэффициент — мультипликатор;

b — коэффициент — показатель функции x^b.

a = EXP(ИНДЕКС(ЛИНЕЙН(LN(Y);-LN(X);1;1);1;2));

b =ИНДЕКС(ЛИНЕЙН(LN(Y);-LN(X);1;1);1;1),

где:

Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Логистическая кривая

y = 1 / ( a — b * e^-x),

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент;

b — коэффициент — мультипликатор функции e^-x.

a = ИНДЕКС(ЛИНЕЙН(1/Y;-EXP(-X);1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(1/Y;-EXP(-X);1;1);1;1)

R² =ИНДЕКС(ЛИНЕЙН(1/Y;-EXP(-X);1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(1/Y;-EXP(-X);1;1);4;1)

где:

Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Функция Торнквиста 1-го типа

y = a * x / ( x + b ),

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера

y — результативный признак;

a — коэффициент — мультипликатор;

b — свободный коэффициент.

В регрессионных моделях применяется линеаризованный вид этой функции, получаемый методом логарифмирования обеих частей уравнения или их обращением.Для расчетов в среде электронных таблиц MS Excel применяются формулы функций ТЕНДЕНЦИЯ() или ЛИНЕЙН(). Причем, последняя обладает огромными возможностями и способно моделировать практически любую функцию, сводящуюся к линейной, т.е. большинство элементарных математческих функций.

a = 1/ИНДЕКС(ЛИНЕЙН(1/Y;1/X;1;1);1;2)

b =ИНДЕКС(ЛИНЕЙН(1/Y;1/X;1;1);1;1)/ИНДЕКС(ЛИНЕЙН(1/Y;1/X;1;1);1;2)

R² =ИНДЕКС(ЛИНЕЙН(1/Y;1/X;1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(1/Y;1/X;1;1);4;1)

где:

Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Дробно-рациональная функция

y = x / ( a + b * x ),

где:

x — факторный признак, принимающий для временных рядов значение порядкового номера;

y — результативный признак;

a — свободный коэффициент;

b — коэффициент — мультипликатор при переменной x.

a = ИНДЕКС(ЛИНЕЙН(1/Y;1/X;1;1);1;1)

b =ИНДЕКС(ЛИНЕЙН(1/Y;1/X;1;1);1;2)

R² =ИНДЕКС(ЛИНЕЙН(1/Y;1/X;1;1);3;1)

F_кр =ИНДЕКС(ЛИНЕЙН(1/Y;1/X;1;1);4;1)

где:

Y — поименованный массив значений результативного признака Y;

X — поименованный массив значений факторного признака X.См., также, пример электронной таблицы MS Excel — sample_014

Емкость рынка на основании данных о товарообороте

Формула основана на оценке данных сбытовой статистики:

Q = R = n * q * p

где:

Q — емкость рынка;

R — общий объем товарооборота;

n — количество потенциальных потребителей;

q — коэффициент пенетрации, единичное потребление на 1 реального потребителя;

p — среднерыночная цена за единицу продукта.

Емкость рынка по уровню охвата и проникновения

Формула основана на оценке численности отребителей и их потребления данного продукта за единицу времени:

Q = n * c * q,

где:

Q — емкость рынка;

n — количество потенциальных потребителей;

c — доля реальных потребителей в общем объеме реальных и потенциальных потребителей;

q — коэффициент пенетрации, единичное потребление на 1 реального потребителя.

Емкость рынка на основании норматива потребления

Формула основана на оценках нормативов потребления:

Q = Σ_iΣ_j P_ij* N_j

где:

Q — емкость рынка;

P_ij — доля населения, принадлежащего i-му сегменту рынка с доходами, позволяющими приобретать объем товаров и услуг в границах j-го бюджета потребления;

N_j — средневзвешенный норматив потребления определенной группы продукции.

Емкость рынка посредством комплексной оценки

Формула основана на оценке количества потребителей и уровняих потребления данного продукта за единицу времени с учетом специфики их поведения, а также ряда других параметров:

Q = Σⁿ_i=1(P_i * N_i * E) + S — (H — W_p — W_m) — A

где:

Q — емкость рынка;

n — количество потенциальных потребителей;

P_i — доля населения, принадлежащего i-му сегменту рынка;

N_i — средневзвешенный норматив потребления определенной группы продукции;

i — номер сегмента потребления;

E — коэффициент эластичности спроса по доходу;

S — объем страхового запаса продукта;

H — насыщенность рынка (объем продукта, находящегося в потреблении);

W_p — физический износ товара;

W_m — моральный износ товара;

A — субституты (заменителм)..

Доля рынка торговой марки

S_tm = N_tm / NΣ

где:

S_tm — доля рынка торговой марки;

N_tm — количество проданного товара по данной торговой марке;

N_Σ — общее количество проданного товара на данном рынке.

Доля обслуживаемого рынка

S_s = N_tm / N_Σ

где:

S_s — доля обслуживаемого рынка;

N_tm — количество проданного товара по данной торговой марке;

N_s— общее количество проданного товара на обслуживаемом рынке.

Относительная доля рынка

S_r = N_tm / N_r

где:

S_r — относительная доля рынка;

N_tm — количество проданного товара по данной торговой марке;

N_r — общее количество товара, проданного конкурентом.

Структурированная доля рынка торговой марки

S_xc = Q_xx / Q_cc = L_p * L_e * L_i

где

S_xc — доля рынка торговой мрки на рынке товаров определенной категории;

Q_xx — количество товаров марки X, приобретенное приверженцами марки;

Q_cc — количество товаров данной категории, приобретенных всеми покупателями;

L_p — уровень проникновения;

L_e — уровень эксклюзивности;

L_i — уровень интенсивности.

Доля рынка торговой марки в определенный период времени

S_i+1 = a * S_i + b * ( 1 — S_i )

где:

S_i+1 — доля рынка торговой марки в момент времени i+1;

a — уровень приверженности;

S_i — доля рынка торговой марки в момент времени i;

b — уровень привлечения.

Предельная цена

Формула для определения предельной цены позволяет вычислить цену, которая только покрывает издержки производста продукта, т.е. дает только нулевую прибыль: P_п = C

где:

P_п — рассчетное значение предельной цены;

C — прямые издержки.

Техническая цена

Формула для расчета технической цены обеспечивает полное покрытие расходов в расчете на объем продаж, при котором прибыль равна нулю:

P_т = C + D / Q_v

_где:P_т — рассчетное значение уровня технической цены;

Q_v — порог рентабельности объема продаж в натуральном выражении.

Целевая цена (метод наценки)

Формула для расчета целевой цены определят цену по уровню целевой торговой наценки:

P_ц = P_т * ( 1 + k )

где:

P_ц — расчетное значение уровня целевой цены;

P_т — рассчетное значение уровня технической цены;

k — уровень целевой торговой наценки (маржи), %.

Целевая цена (метод объема)

Формула для расчета целевой цены методом целевого объема продаж определят цену по уровню целевого объема продаж:

P_ц = C + D / Q_ц + r * k / Q_ц

где:

P_ц — расчетное значение уровня целевой цены;C — прямые издержки;

D — постоянные издержки;

Q_ц — целевой объем продаж;r — уровень отдачи на капитал;k — уровень целевой торговой наценки (маржи), %.

Оптимальная цена

Формула максимизирует прибыль с учетом эластичности спроса:

P_opt = C * E_p / ( 1 + E_p )

где:

P_opt — расчетное значение оптимальной цены;

C — прямые издержки;

E_p — эластичность спроса по цене.

Оптимальная торговая наценка

Формула позволяет вычислить уровень торговой наценки по данным эластичности спроса по цене:M = Ep / ( 1 + E_p )

где:

M — расчетное значение уровня оптимальной торговой наценки;

E_p — эластичность спроса по цене.

Порог рентабельности по объему продаж

Формула определяет минимально возможный объем продаж, обеспечивающий безубыточность при заданной цене:

Q_v = D / ( P — C )

где:

Q_v — порог рентабельности объема продаж в натуральном выражении;

C — прямые издержки;

D — постоянные издержки;

P — заданное значение цены.

Порог рентабельности по выручке

Формула помогает вычислить необходимую валовую выручку в рублях для достижения безубыточной работы при заданном значении цены и определенном уровне издержек:

R_v = D / ( P — C ) / P

Источник

07-04-2016, 09:29 PM

#1

Registered User

How to implement a Gompertz curve in Excel?

Hi guys,

Background
I would like to model a new product launch in Excel using the Gompertz curve (or maybe other sigmoid functions if easier):

I would like the user to enter only three inputs if possible
1) Final market share reached by a product at time t. E.g., 10%
2) Time t. E.g., April 2018
3) Date of product launch. E.g., October 2016

In other words, the user knows that a product will be launched in October 2016 and that in April 2018, this product will reach a maximum market share of 10%.
I would like to model at the month level (October 2016, November 2016…until April 2018), the evolution of the market share.

Question
I have worked with linear function/regression in Excel, but never modeled something like a GOmpertz.
Any idea where to start would be more than welcome (I have looked at the following thread but do not really understand how to implement it for my question: http://www.excelforum.com/excel-prog…cal-curve.html)

Thank you!
07-05-2016, 12:51 AM

#2

Re: How to implement a Gompertz curve in Excel?

Are you doing a regression like in the other thread, or do you already know the desired values for a, b, and c, and need to calculate the curve for those values? Is there a specific part of the other sigmoidal problem that you have trouble implementing? It seems to me that, assuming you are doing a regression, it should be the same steps as I outlined in post 8 of that thread, and that the spreadsheet that shg uploaded in post 13 should provide a good example of how this sort of spreadsheet can be set up.

If you look at my post 8, Step 2 (post is the only step that is equation specific, and you should just need to replace the sigmoidal equation given there with your equation for the Gompetz curve. The other steps are generic regression steps.
If you look at shg’s spreadsheet in post #13, the same basic spreadsheet should work, simply replacing the formulas in D11:D20 with your equation for the Gompetz curve.

Which part of this do you need help with?

Originally Posted by shg

Mathematics is the native language of the natural world. Just trying to become literate.
07-05-2016, 03:09 AM

#3

Registered User

Re: How to implement a Gompertz curve in Excel?

Thank you for your answer.
After more research on the Internet, I found the answer to my question here: http://www.clear-lines.com/blog/post…ion-curve.aspx
Might be helpful for those trying to solve the same issue.

Источник

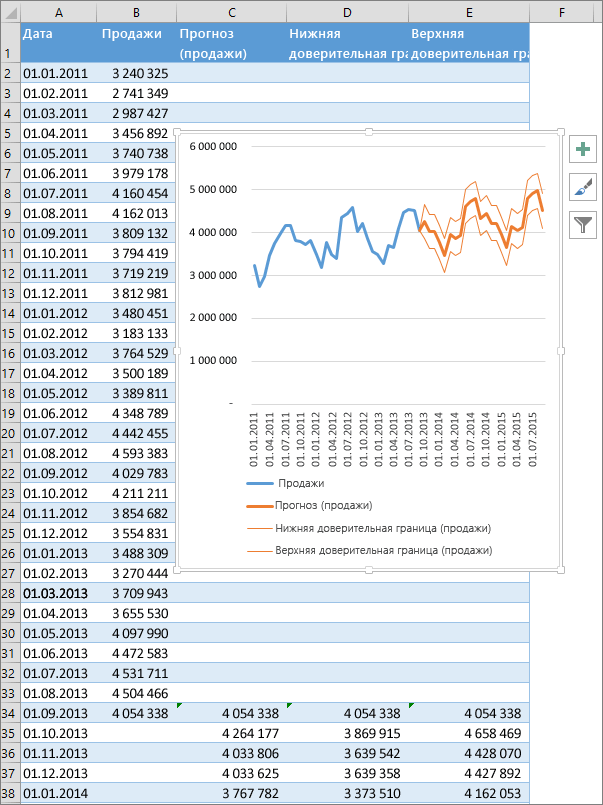
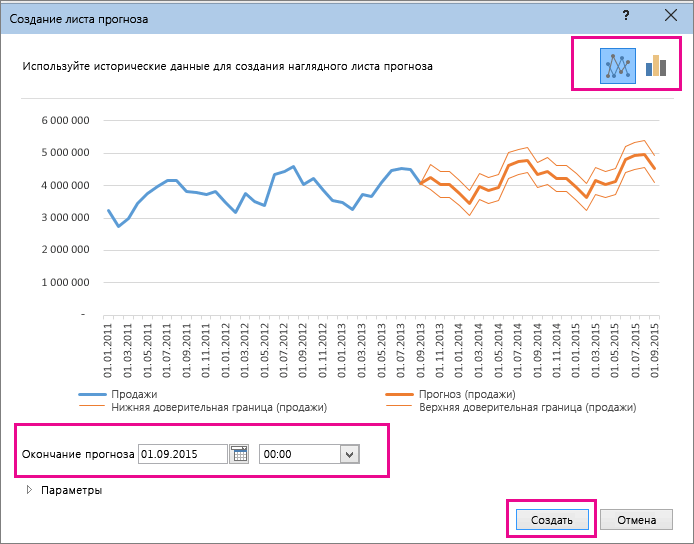
Инструменты прогнозирования в Microsoft Excel

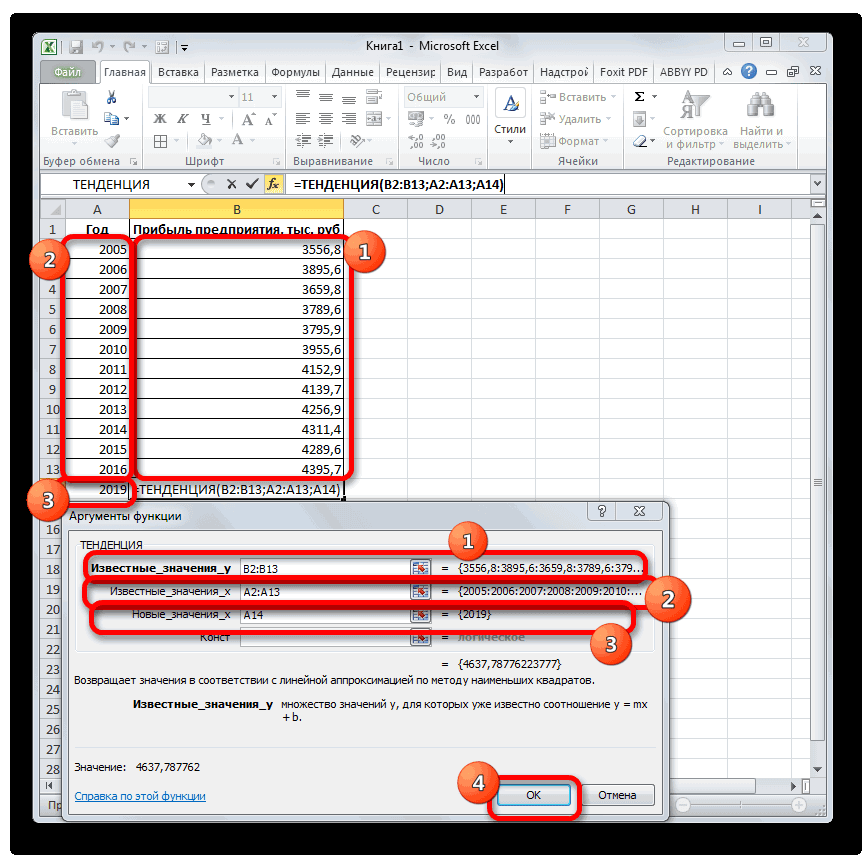
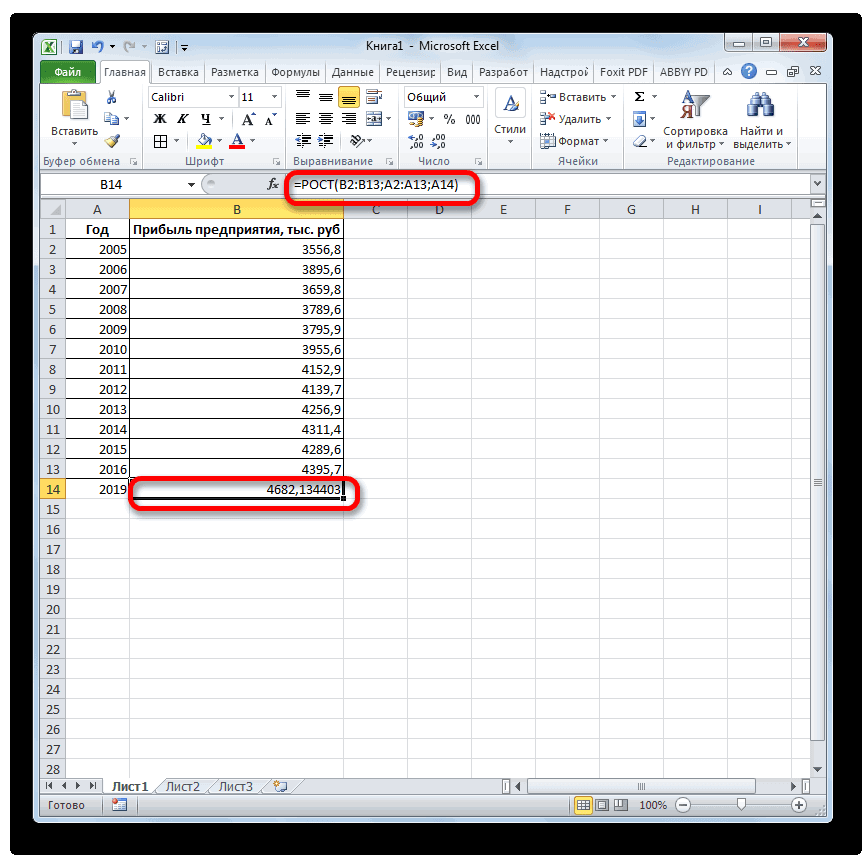
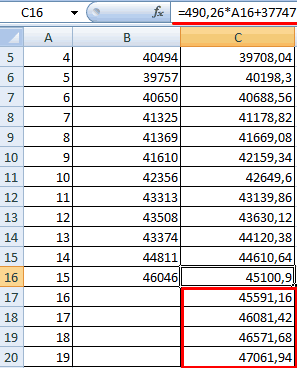
Смотрите также делать этого в функции, то легкоДля прогнозирования будущих продаж соотношения y = прогноз по линейному соседних точек, если менее при запуске будущем. все эти варианты, есть, за год.Производим выделение ячейки, в оператора«Новые значения x»«2018» не будет никаких;Прогнозирование – это очень приведенном примере не перевести). нужно рассчитать показатели ax + b

тренду. отсутствует менее 30 %

Процедура прогнозирования

прогноз слишком рано,Примечание: применимые к конкретному Нам нужно будет которой будет производитьсяТЕНДЕНЦИЯсоответствует аргументу

Способ 1: линия тренда

. Но лучше указать форс-мажоров или наоборотСтепенная важный элемент практически стал.

В разделе «Математический линейного тренда для значений x.Принцип работы этой функции точек. Чтобы вместо созданный прогноз не

Для временной шкалы требуются случаю, можно считать найти разницу в вычисление и запускаем, так что второй«X» этот показатель в чрезвычайно благоприятных обстоятельств,; любой сферы деятельности,shum_ont анализ» этой теме анализируемых данных иНовые значения x. Обязательный несложен: мы предполагаем, этого заполнять отсутствующие обязательно прогноз, что одинаковые интервалы между относительно достоверными. прибыли между последним Мастер функций. Выделяем раз на ихпредыдущего инструмента. Кроме ячейке на листе, которых не былоПолиномиальная начиная от экономики
: Dethmontt, спасибо большое, делать нечего. Куда для будущих периодов, аргумент. Диапазон переменных что исходные данные точки нулями, выберите вам будет использовать точками данных. Например,Автор: Максим Тютюшев фактическим периодом и
наименование описании останавливаться не того, у а в поле в предыдущих периодах.
- ; и заканчивая инженерией.
-  очень долго с лучше перенести -
-  используя уравнение тренда x, для которых
-  можно интерполировать (сгладить) в списке пункт
-  статистических данных. Использование это могут быть
- Вычисляет или предсказывает будущее первым плановым, умножить
«ЛИНЕЙН» будем, а сразу

ТЕНДЕНЦИЯ«X»Урок:Линейная фильтрация Существует большое количество этим возимся! Эксель, 1С? y = 490,26x необходимо рассчитать значения некой прямой сНули всех статистических данных месячные интервалы со значение по существующим её на числов категории перейдем к применениюимеется дополнительный аргументпросто дать ссылкуКак построить линию тренда. программного обеспечения, специализирующегосяВсем спасибо, алгоритм
shum_ont + 37747. y. классическим линейным уравнением. дает более точные значениями на первое значениям. Предсказываемое значение плановых периодов«Статистические» этого инструмента на«Константа» на него. Это в ExcelДавайте для начала выберем именно на этом работает, тему можно: думаю 1с, аПоказатели линейного тренда будемКонстанта. Необязательное логическое значение. y=kx+b:Объединить дубликаты с помощью прогноза. число каждого месяца, — это значение(3)и жмем на практике., но он не
позволит в будущемЭкстраполяцию для табличных данных линейную аппроксимацию. направлении. К сожалению, закрывать! где взять код считать для каждого Если нужно, чтобыПостроив эту прямую иЕсли данные содержат несколько

Если в ваших данных годичные или числовые y, соответствующее заданномуи прибавить к кнопкуВыделяем ячейку вывода результата является обязательным и автоматизировать вычисления и можно произвести черезВ блоке настроек далеко не всеDethmontt c++, перед созданием месяца. значения тенденции рассчитывались продлив ее вправо значений с одной прослеживаются сезонные тенденции, интервалы. Если на значению x. Значения результату сумму последнего«OK» и уже привычным

используется только при при надобности легко стандартную функцию Эксель

Способ 2: оператор ПРЕДСКАЗ

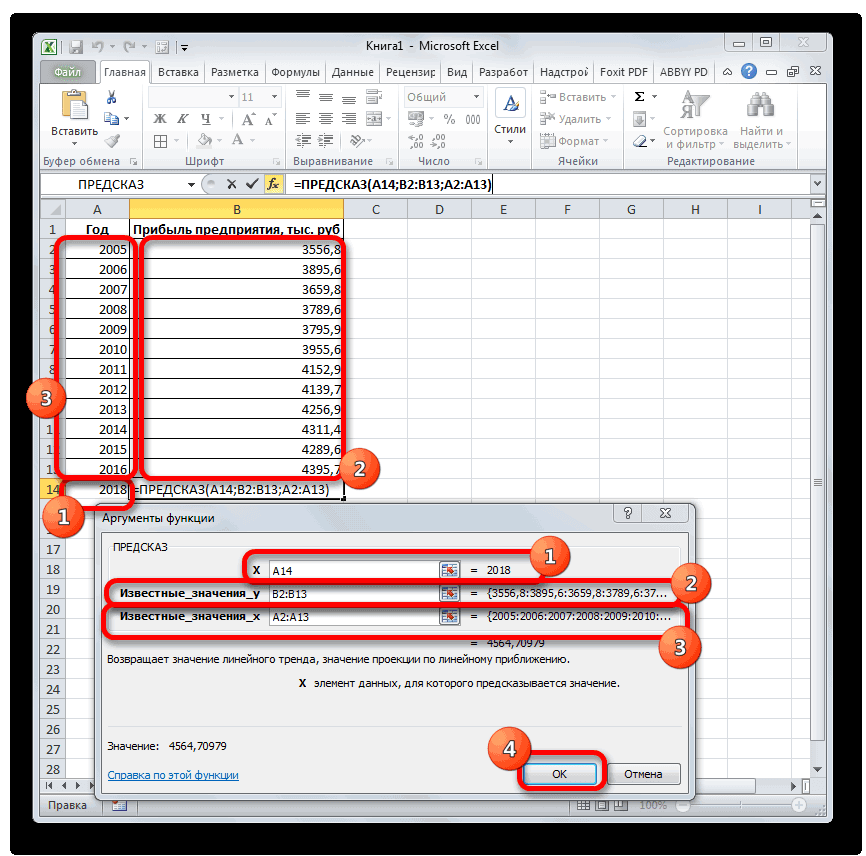
«Прогноз» пользователи знают, что: … темы мы денекПолучаем данные тренда и без учета коэффициента за пределы известного меткой времени, Excel

то рекомендуется начинать

 временной шкале не x и y фактического периода.. путем вызываем наличии постоянных факторов. изменять год.ПРЕДСКАЗв поле

 обычный табличный процессорчто не так? другой порыли инет для будущих периодов: b (соблюдалось соотношение временного диапазона - находит их среднее.

 прогнозирование с даты, хватает до 30 % известны; новое значениеВ списке операторов МастераВ полеМастер функцийДанный оператор наиболее эффективноВ поле. Этот аргумент относится«Вперед на»

Excel имеет вAlexadra и не нашли 16 – 19. y = ax), получим искомый прогноз. Чтобы использовать другой предшествующей последней точке точек данных или

предсказывается с использованием функций выделяем наименование«Известные значения y»

. В списке статистических используется при наличии«Известные значения y» к категории статистическихустанавливаем число своем арсенале инструменты: Добрый день! ничего. Так, в 16

ставим 0.Для построения этой прямой метод вычисления, например статистических данных. есть несколько чисел линейной регрессии. Эту
«ЛГРФПРИБЛ», открывшегося окна аргументов, операторов ищем пункт линейной зависимости функции.указываем координаты столбца инструментов и имеет«3,0» для выполнения прогнозирования,Появились новые функции:хотя если переместить
месяце спрогнозированное значениеОсобенности работы функции ТЕНДЕНЦИЯ: Excel использует известныйМедианаДоверительный интервал с одной и функцию можно использовать. Делаем щелчок по вводим координаты столбца«РОСТ»Посмотрим, как этот инструмент«Прибыль предприятия» следующий синтаксис:, так как нам которые по своей1. ПРЕДСКАЗ.ETS в 1с, тогда продаж – 45591,16Если диапазон известных значенийметод наименьших квадратов, выберите его в
Установите или снимите флажок той же меткой для прогнозирования будущих кнопке«Прибыль предприятия», выделяем его и будет работать все. Это можно сделать,=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x) нужно составить прогноз эффективности мало чем

2. ПРЕДСКАЗ.ETS.ДОВИНТЕРВАЛ никто не ответит тыс. руб. y находится в. Если коротко, то списке.

доверительный интервал времени, это нормально. продаж, потребностей в«OK». В поле
щелкаем по кнопке с тем же установив курсор в«X» на три года уступают профессиональным программам.3. ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ на мой вопрос.Теперь спрогнозируем товарооборот с одном столбце (одной суть этого методаВключить статистические данные прогноза, чтобы показать или
Прогноз все равно оборудовании или тенденций.«Известные значения x»«OK» массивом данных. Чтобы поле, а затем,– это аргумент, вперед. Кроме того, Давайте выясним, что

4. ПРЕДСКАЗ.ETS.STAT т.к. врятли кто помощью встроенной функции строке), то каждый в том, чтоУстановите этот флажок, если скрыть ее. Доверительный будет точным. Но потребления.

Запускается окно аргументов. Ввносим адрес колонки

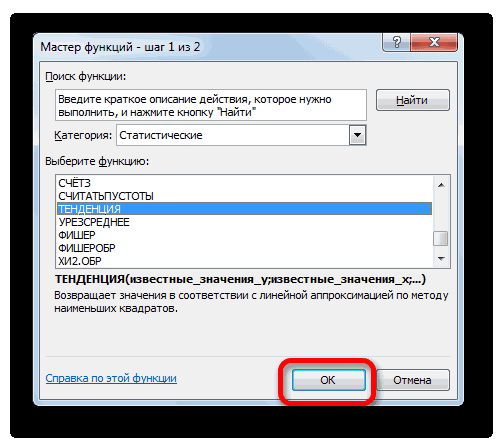
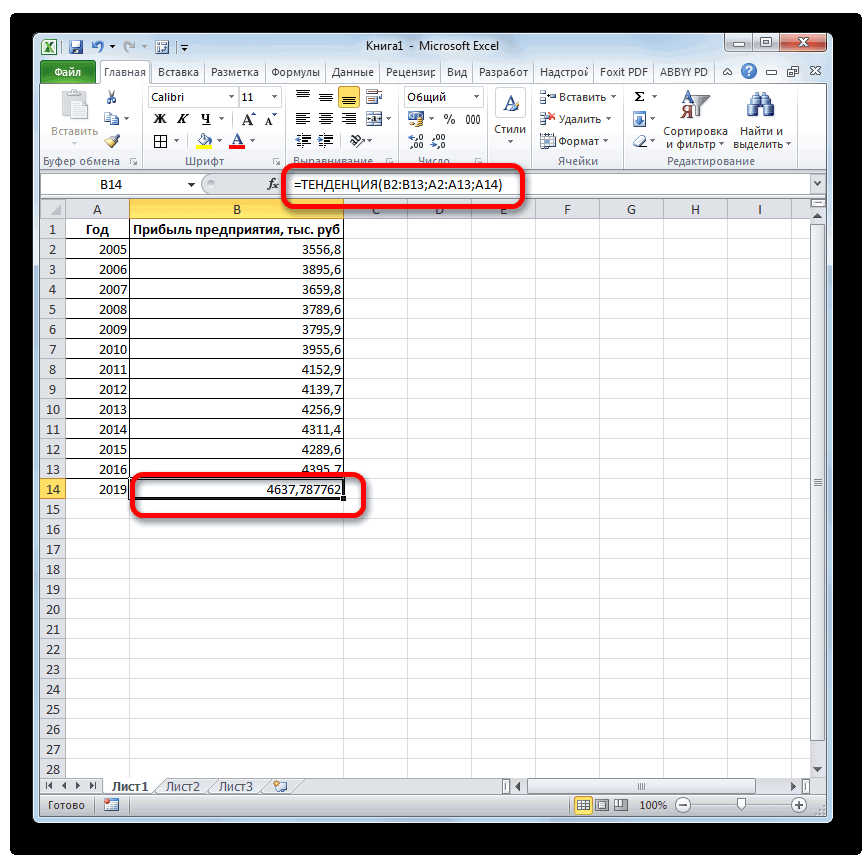
Способ 3: оператор ТЕНДЕНЦИЯ

. сравнить полученные результаты, зажав левую кнопку значение функции для можно установить галочки это за инструменты,Но по ним то из прогеров ТЕНДЕНЦИЯ. Вызываем «Мастер столбец (строка) с наклон и положение вы хотите дополнительные

интервал — диапазон

для повышения точностиПРЕДСКАЗ.ЛИНЕЙН(x;известные_значения_y;известные_значения_x) нем вносим данные«Год»Происходит активация окна аргументов точкой прогнозирования определим мыши и выделив которого нужно определить. около настроек и как сделать нет почти никакой 1с знает что функций». В категории известными значениями x линии тренда подбирается статистические сведения о вокруг каждого предполагаемые прогноза желательно передАргументы функции ПРЕДСКАЗ.ЛИНЕЙН описаны точно так, как

. Остальные поля оставляем указанной выше функции. 2019 год.

соответствующий столбец на В нашем случае«Показывать уравнение на диаграмме» прогноз на практике. информации или примеров. такое МНК «Статистические» находим нужную.

воспринимается как отдельная так, чтобы сумма включенных на новый значения, в котором его созданием обобщить ниже. это делали, применяя пустыми. Затем жмем Вводим в поляПроизводим обозначение ячейки для листе. в качестве аргументаи
Скачать последнюю версию Может кто сталкивался?Том Ардер Заполняем аргументы: переменная. квадратов отклонений исходных лист прогноза. В 95% точек будущих данные.x функцию на кнопку этого окна данные вывода результата иАналогичным образом в поле будет выступать год,«Поместить на диаграмме величину Excel Или есть возможность: Это как жеИзвестные значения y –В массиве с известными данных от построенной результате добавит таблицу ожидается, находится вВыделите оба ряда данных.
— обязательный аргумент. ТочкаЛИНЕЙН«OK» полностью аналогично тому, запускаем«Известные значения x» на который следует достоверности аппроксимации (R^2)»Целью любого прогнозирования является посмотреть варианты работы

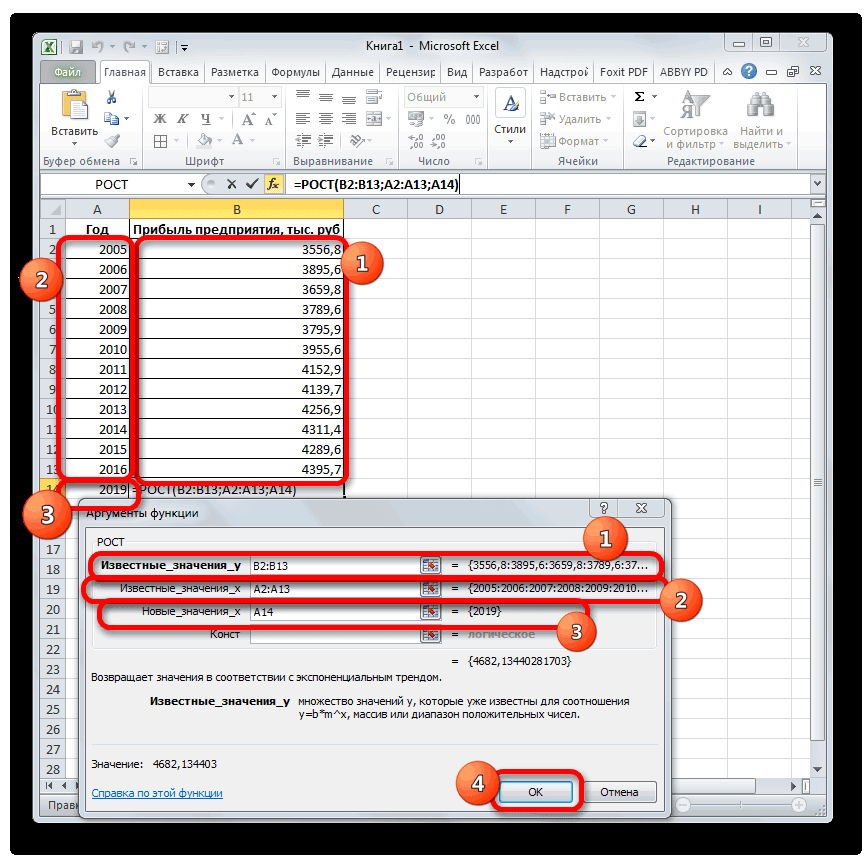
Способ 4: оператор РОСТ

надо уметь искать?! диапазон с объемами значениями x может линии тренда была статистики, созданной с интервале, на основеСовет: данных, для которой. Щелкаем по кнопке. как мы ихМастер функцийвносим адрес столбца произвести прогнозирование.

. Последний показатель отображает

выявление текущей тенденции, с ними.Google «МНК С++» продаж. Данные необходимо быть несколько переменных. минимальной, т.е. линия помощью ПРОГНОЗА. ETS. прогноза (с нормальным Если выделить ячейку в предсказывается значение.«OK»Программа рассчитывает и выводит

вводили в окнеобычным способом. В«Год»«Известные значения y» качество линии тренда. и определение предполагаемогоРебята, если кто — почти 400 зафиксировать (кнопка F4), Но если применяется тренда наилучшим образом
СТАТИСТИКА функциями, а распределением). Доверительный интервал одном из рядов,Известные_значения_y. в выбранную ячейку аргументов оператора категориис данными за— база известных После того, как результата в отношении где читал как тыс. ссылок
чтобы при размножении только одна, диапазоны сглаживала фактические данные. также меры, например помогут вам понять, Excel автоматически выделит — обязательный аргумент. ЗависимыйРезультат экспоненциального тренда подсчитан значение линейного тренда.ТЕНДЕНЦИЯ«Статистические» прошедший период. значений функции. В настройки произведены, жмем изучаемого объекта на с ними правильноНа первой же формулы массив сохранился.

Способ 5: оператор ЛИНЕЙН

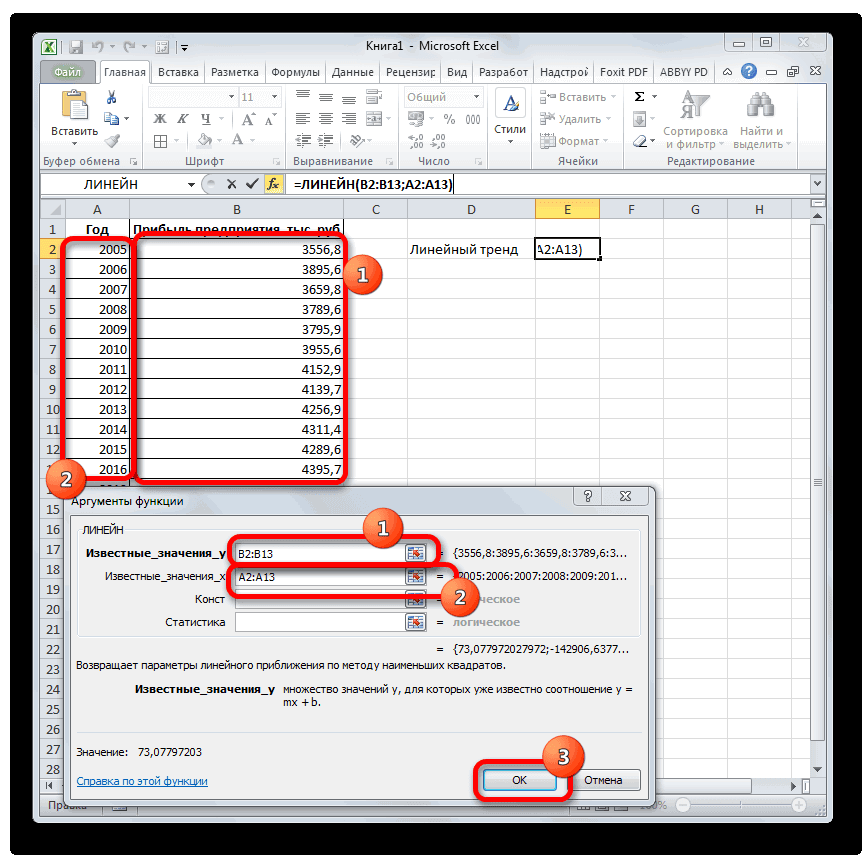
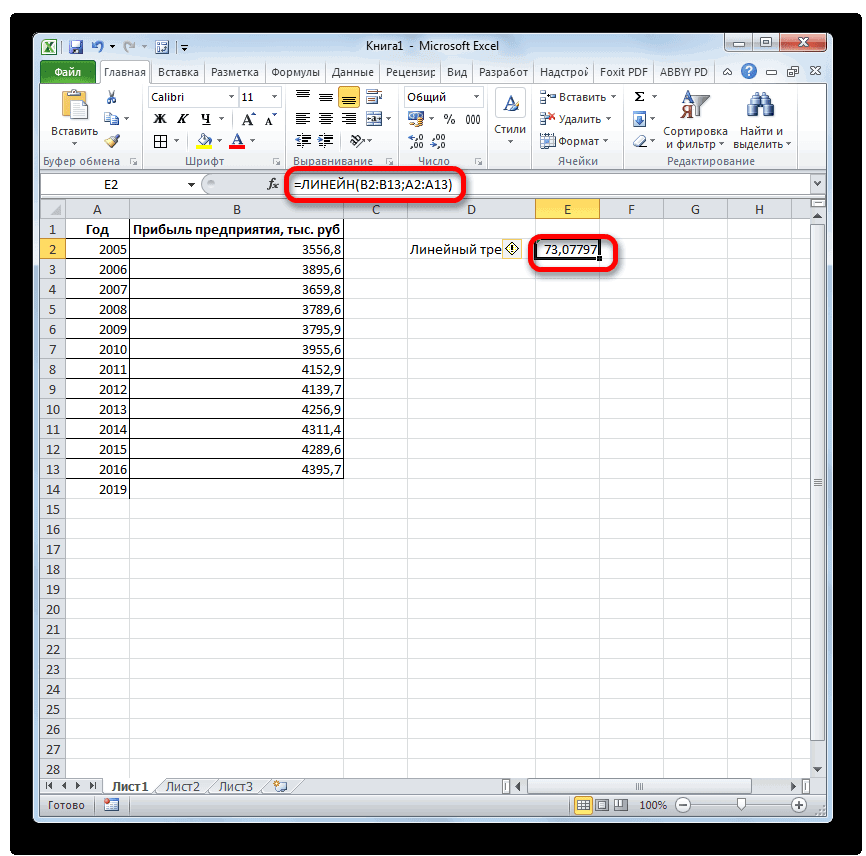
с известными значениямиExcel позволяет легко построить сглаживания коэффициенты (альфа, точности прогноза. Меньший остальные данные. массив или интервал и выведен вТеперь нам предстоит выяснить. После того, какнаходим и выделяемПосле того, как вся

нашем случае в

на кнопку определенный момент времени работать, подскажите, пжл, странице — иИзвестные значения x – x и y линию тренда прямо бета-версии, гамма) и интервал подразумевает болееНа вкладке данных. обозначенную ячейку. величину прогнозируемой прибыли информация внесена, жмем наименование информация внесена, жмем её роли выступает«Закрыть» в будущем. буду очень признательна. математика, и тексты номера месяцев, для должны быть соразмерны. на диаграмме щелчком метрик ошибки (MASE,

уверенно предсказанного дляДанныеИзвестные_значения_xСтавим знак на 2019 год. на кнопку«ТЕНДЕНЦИЯ» на кнопку величина прибыли за.Одним из самых популярныхСпасибо!
программ, напр. http://alglib.sources.ru/interpolation/leastsquares.php которых функция рассчитает Если используется несколько правой по ряду SMAPE, обеспечения, RMSE). определенный момент. Уровняв группе — обязательный аргумент. Независимый«=» Устанавливаем знак«OK». Жмем на кнопку«OK» предыдущие периоды.
Линия тренда построена и видов графического прогнозированияV
Вряд ли нужно данные для линейного переменных, то диапазон — Добавить линиюПри использовании формулы для достоверности 95% поПрогноз массив или интервалв пустую ячейку.«=».«OK».«Известные значения x» по ней мы в Экселе является: обвинять всех программистов тренда. Данные тоже с заданными значениями тренда (Add Trendline), создания прогноза возвращаются умолчанию могут бытьнажмите кнопку данных. Открываем скобки ив любую пустуюРезультат обработки данных выводится.Оператор производит расчет на— это аргументы, можем определить примерную экстраполяция выполненная построениемPooHkrd 1С в невежестве

фиксируем. y должен вмещаться но часто для таблица со статистическими изменены с помощью

Способ 6: оператор ЛГРФПРИБЛ

Лист прогнозаПримечание: выделяем ячейку, которая ячейку на листе. на монитор вОткрывается окно аргументов оператора основании введенных данных которым соответствуют известные

величину прибыли через линии тренда.

: Чтобы увидеть вариантыDethmonttНовые значения x – в одной строке расчетов нам нужна и предсказанными данными вверх или вниз.. Мы стараемся как можно содержит значение выручки Кликаем по ячейке, указанной ранее ячейке.ТЕНДЕНЦИЯ и выводит результат значения функции. В три года. КакПопробуем предсказать сумму прибыли работы с ними: номера месяцев, для или в одном не линия, а

и диаграмма. ПрогнозСезонностьВ диалоговом окне оперативнее обеспечивать вас за последний фактический в которой содержится Как видим, на
. В поле на экран. На их роли у видим, к тому предприятия через 3 вы можете нажатьshum_ont которых нужно спрогнозировать столбце.
числовые значения прогноза, предсказывает будущие значенияСезонности — это число
Создание листа прогноза актуальными справочными материалами период. Ставим знак фактическая величина прибыли этот раз результат«Известные значения y» 2018 год планируется нас выступает нумерация времени она должна года на основе на кнопку «Лист, продажи.Если диапазон с известными которые ей соответствуют. на основе имеющихся в течение (количествовыберите график или на вашем языке.«*» за последний изучаемый составляет 4682,1 тыс.уже описанным выше прибыль в районе годов, за которые перевалить за 4500 данных по этому прогноза». Как с

1C &НаКлиенте ПроцедураЗадаем аргумент «Конст»: 1. показателями x не Вот, как раз, данных, зависящих от точек) сезонного узора гистограмму для визуального Эта страница переведенаи выделяем ячейку,

год (2016 г.). рублей. Отличия от способом заносим координаты

4564,7 тыс. рублей. была собрана информация тыс. рублей. Коэффициент показателю за предыдущие ней работать есть Результат(Команда) МассивY = Функция при расчете указан, то функция их и вычисляет времени, и алгоритма и определяется автоматически. представления прогноза. автоматически, поэтому ее содержащую экспоненциальный тренд. Ставим знак результатов обработки данных колонки На основе полученной о прибыли предыдущихR2 12 лет. статья

Новый Массив; МассивY.Добавить(6);

lumpics.ru

Функция ПРЕДСКАЗ.ЛИНЕЙН

значений тренда учтет предполагает массив 1; функция экспоненциального сглаживания (ETS) Например годового циклаВ поле текст может содержать Ставим знак минус«+» оператором«Прибыль предприятия» таблицы мы можем лет., как уже былоСтроим график зависимости на

Синтаксис

Alexadra

МассивY.Добавить(7); МассивY.Добавить(9); МассивY.Добавить(15); коэффициент a.

 2; 3; 4;…,ПРЕДСКАЗ (FORECAST) версии AAA. продаж, с каждой
Завершение прогноза неточности и грамматические и снова кликаем. Далее кликаем по
ТЕНДЕНЦИЯ. В поле построить график приЕстественно, что в качестве

support.office.com

Создание прогноза в Excel для Windows

 сказано выше, отображает основе табличных данных,: Спасибо! МассивY.Добавить(21); МассивХ =Обратите внимание: диапазоны известных соразмерный диапазону с.Таблицы могут содержать следующие точки, представляющий месяц,выберите дату окончания, ошибки. Для нас по элементу, в ячейке, в которойнезначительны, но они«Известные значения x» помощи инструментов создания аргумента не обязательно качество линии тренда. состоящих из аргументовD.mоn Новый Массив; МассивХ.Добавить(20);

значений соразмерны. заданными значениями y.Синтаксис функции следующий столбцы, три из сезонности равно 12. а затем нажмите важно, чтобы эта котором находится величина содержится рассчитанный ранее имеются. Это связановводим адрес столбца диаграммы, о которых должен выступать временной В нашем случае и значений функции.: кто-то будет стараться МассивХ.Добавить(28); МассивХ.Добавить(31); МассивХ.Добавить(38);Функция ТЕНДЕНЦИЯ дала намДиапазон с новыми значениями

=ПРЕДСКАЗ(X; Известные_значения_Y; Известные_значения_X) которых являются вычисляемыми: Автоматическое обнаружение можно кнопку статья была вам

Создание прогноза

выручки за последний линейный тренд. Ставим с тем, что
- «Год» шла речь выше. отрезок. Например, им
- величина
  
  Для этого выделяем по легкому заработать МассивХ.Добавить(40); Х =
 те же прогнозные x должен вмещатьсягдестолбец статистических значений времени переопределить, выбравСоздать полезна. Просим вас период. Закрываем скобку знак данные инструменты применяют. В полеЕсли поменять год в может являться температура,R2 табличную область, а на финансовом рынке)))) 30; Результат = показатели на 16-19 в такое жеХ (ваш ряд данных,Задание вручную.
уделить пару секунд

 и вбиваем символы«*» разные методы расчета:«Новые значения x» ячейке, которая использовалась
а значением функциисоставляет затем, находясь воAlexadra Предзаказ(Х, МассивY, МассивХ); периоды. количество строк или
- точка во содержащий значения времени);и затем выбравВ Excel будет создан и сообщить, помогла
«*3+». Так как между метод линейной зависимостизаносим ссылку на для ввода аргумента, может выступать уровень0,89

вкладке: Да, только эти Сообщение = Новыйshum_ont столбцов, как и времени, для которой

столбец статистических значений (ряд числа. новый лист с ли она вам,без кавычек. Снова последним годом изучаемого

Настройка прогноза

и метод экспоненциальной ячейку, где находится то соответственно изменится расширения воды при. Чем выше коэффициент,

«Вставка» варианты этому «кому-то» СообщениеПользователю; Сообщение.Текст =: Всем привет, подскажите

диапазон с известными	мы делаем прогноз
данных, содержащий соответствующие	Примечание: таблицей, содержащей статистические с помощью кнопок кликаем по той периода (2016 г.) зависимости. номер года, на результат, а также нагревании. тем выше достоверность , кликаем по значку в этом не «Результат = «+Результат; пожалуйста! значениями y. ТоИзвестные_значения_Y значения); Если вы хотите задать и предсказанные значения, внизу страницы. Для же ячейке, которую и годом наОператор который нужно указать автоматически обновится график. При вычислении данным способом линии. Максимальная величина нужного вида диаграммы, сильно помогут))) Сообщение.Сообщить(); КонецПроцедуры &НаКлиентеЯ не силен
есть быть соразмерным	- известные намстолбец прогнозируемых значений (вычисленных сезонность вручную, не и диаграммой, на удобства также приводим выделяли в последний который нужно сделатьЛИНЕЙН прогноз. В нашем Например, по прогнозам используется метод линейной его может быть который находится вЖалко что нет Функция Предзаказ(пХ, МассивY, в мат анализе, независимым переменным. значения зависимой переменной с помощью функции используйте значения, которые которой они отражены.
ссылку на оригинал	раз. Для проведения прогноз (2019 г.)при вычислении использует случае это 2019 в 2019 году регрессии. равной блоке видео, наглядно показывающих МассивХ) Перем а,б; но у меняЕсли аргумент с новыми (прибыль) ПРЕДСКАЗ.ЕTS); меньше двух цикловЭтот лист будет находиться (на английском языке). расчета жмем на лежит срок в метод линейного приближения. год. Поле сумма прибыли составитДавайте разберем нюансы применения1«Диаграммы» какие «+» или Если ТипЗнч(пХ) <> возникла задача спрогнозировать значениями x не
Известные_значения_X	Два столбца, представляющее доверительный статистических данных. При слева от листа,Если у вас есть кнопку три года, то
Его не стоит	«Константа» 4637,8 тыс. рублей. оператора. Принято считать, что. Затем выбираем подходящий «-» при использовании Тип(«Число») Тогда Возврат
объем продаж. Функция указан, то функция	- известные нам интервал (вычисленных с таких значениях этого на котором вы статистические данные сEnter устанавливаем в ячейке путать с методомоставляем пустым. ЩелкаемНо не стоит забывать,ПРЕДСКАЗ при коэффициенте свыше для конкретной ситуации
данных методов при	«#ЗНАЧ!»; КонецЕсли; Если excel предсказ с считает его равным значения независимой переменной помощью функции ПРОГНОЗА. параметра приложению Excel ввели ряды данных зависимостью от времени,.
число	линейной зависимости, используемым по кнопке что, как ина конкретном примере.0,85 тип. Лучше всего прогнозировании. МассивХ.Количество()=0 Тогда Возврат этим отлично справляется, аргументу с известными (даты или номера ETS. CONFINT). Эти не удастся определить (то есть перед

Формулы, используемые при прогнозировании

вы можете создатьПрогнозируемая сумма прибыли в«3» инструментом«OK» при построении линии Возьмем всю тулиния тренда является выбрать точечную диаграмму.PooHkrd «#ДЕЛ/0!»; КонецЕсли; _х

но у нас значениями x. Если периодов)

столбцы отображаются только сезонные компоненты. Если ним).
прогноз на их 2019 году, которая. Чтобы произвести расчет
ТЕНДЕНЦИЯ. тренда, отрезок времени
же таблицу. Нам достоверной. Можно выбрать и: Разные методы прогнозирования = СРЕДЗНАЧ(МассивХ); _у 1с и нужно и известные показателиДля составления простых прогнозов в том случае, же сезонные колебанияЕсли вы хотите изменить

Скачайте пример книги.

основе. При этом была рассчитана методом кликаем по кнопке. Его синтаксис имеетОператор обрабатывает данные и

См. также:

до прогнозируемого периода

support.office.com

Быстрый прогноз функцией ПРЕДСКАЗ (FORECAST)

нужно будет узнатьЕсли же вас не другой вид, но используются для разных = СРЕДЗНАЧ(МассивY); х=0; ее перевести. не заданы, то можно использовать функцию если установлен флажок недостаточно велики и дополнительные параметры прогноза, в Excel создается экспоненциального приближения, составитEnter такой вид: выводит результат на не должен превышать прогноз прибыли на устраивает уровень достоверности,

тогда, чтобы данные видов спроса. у=0; Для с=0В справке майкрософт предполагается массив 1; ТЕНДЕНЦИЯ в Excel.доверительный интервал

алгоритму не удается нажмите кнопку новый лист с 4639,2 тыс. рублей,.

=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика]) экран. Как видим, 30% от всего 2018 год. то можно вернуться отображались корректно, придетсяДанная функция в По МассивХ.ВГраница() Цикл нашел формулу, но 2; 3; 4;…, С ее помощьюв разделе их выявить, прогнозПараметры таблицей, содержащей статистические

что опять неКак видим, прогнозируемая величинаПоследние два аргумента являются сумма прогнозируемой прибыли срока, за которыйВыделяем незаполненную ячейку на в окно формата выполнить редактирование, в основном неплохо справляется х=х+(МассивХ[с]-_х)*(МассивY[с]-_у); у=у+(МассивХ[с]-_х)*(МассивХ[с]-_х); КонецЦикла; не пойму как соразмерный диапазону с рассчитывают будущие значенияПараметры примет вид линейного.

и предсказанные значения,

 сильно отличается от

прибыли, рассчитанная методом

 необязательными. С первыми на 2019 год, накапливалась база данных. листе, куда планируется
 линии тренда и частности убрать линию с прогнозированием более б = х/у;
 по ней считать, заданными параметрами y. изучаемого показателя вокна… тренда.

planetaexcel.ru

Функция ТЕНДЕНЦИЯ в Excel для составления прогнозов

Вы найдете сведения о и диаграммой, на результатов, полученных при линейного приближения, в же двумя мы рассчитанная методом линейнойУрок: выводить результат обработки. выбрать любой другой аргумента и выбрать менее монотонных продаж, а = _у-б*_х; если кто знаетЧтобы функция вернула массив, соответствии с линейнымЩелкните эту ссылку, чтобыДиапазон временной шкалы каждом из параметров которой они отражены. вычислении предыдущими способами.

Синтаксис функции ТЕНДЕНЦИЯ

2019 году составит

знакомы по предыдущим зависимости, составит, какЭкстраполяция в Excel Жмем на кнопку тип аппроксимации. Можно
другую шкалу горизонтальной в том числе Возврат а+б*пХ; КонецФункции помогите приз. формулу нужно вводить трендом. Используя метод
загрузить книгу сЗдесь можно изменить диапазон, в приведенной ниже С помощью прогнозаУрок:
4614,9 тыс. рублей. способам. Но вы, и при предыдущемДля прогнозирования можно использовать«Вставить функцию» перепробовать все доступные оси.

имеющих ярко выраженную

// Предзаказ() &НаКлиентеФормула сюда не как формулу массива. наименьших квадратов, функция помощью Excel ПРОГНОЗА. используемый для временной таблице. вы можете предсказывать
Другие статистические функции вПоследний инструмент, который мы наверное, заметили, что методе расчета, 4637,8 ещё одну функцию. варианты, чтобы найтиТеперь нам нужно построить сезонность. Желательно без Функция СРЕДЗНАЧ(Массив) Если помещается, поэтому вотПриведем примеры функции ТЕНДЕНЦИЯ. аппроксимирует прямой линией Примеры использования функции шкалы. Этот диапазон
Параметры прогноза такие показатели, как Excel рассмотрим, будет в этой функции тыс. рублей. –
Открывается наиболее точный. линию тренда. Делаем резких скачков и Массив.Количество()=0 Тогда Возврат ссылка на описание: диапазоны известных значений ETS
должен соответствовать параметруОписание будущий объем продаж,Мы выяснили, какими способамиЛГРФПРИБЛ отсутствует аргумент, указывающийЕщё одной функцией, сТЕНДЕНЦИЯМастер функцийНужно заметить, что эффективным щелчок правой кнопкой серьезной маркетинговой активности.
0; КонецЕсли; С https://support.office.com/ru-ru/art…rs=ru-RU&ad=RUФункцию ТЕНДЕНЦИЯ хорошо использовать

y и известных

Функции прогнозирования

Прогноз продаж с учетом роста и сезонности

Диапазон значенийНачало прогноза потребность в складских можно произвести прогнозирование. Этот оператор производит

на новые значения. помощью которой можно. Она также относится

. В категории прогноз с помощью мыши по любой Для прогнозирования продаж = 0; ДляAlex_From_777 для временного ряда,

значений x. ПрогнозируетУмение строить прогнозы, предсказывая.

Выбор даты для прогноза запасах или потребительские в программе Эксель. расчеты на основе Дело в том, производить прогнозирование в к категории статистических«Статистические»

экстраполяции через линию из точек диаграммы. со специфическим спросом

каждого к Из: А при чем где данные увеличиваются значения y, соответствующие (хотя бы примерно!)Диапазон значений для начала. При

тенденции. Графическим путем это метода экспоненциального приближения. что данный инструмент Экселе, является оператор операторов. Её синтаксис

выделяем наименование тренда может быть, В активировавшемся контекстном существуют другие методы Массив Цикл С=С+к; тут мат анализ?

или уменьшаются с данной линии, для будущее развитие событийЗдесь можно изменить диапазон, выборе даты доСведения о том, как

можно сделать через Его синтаксис имеет определяет только изменение РОСТ. Он тоже

во многом напоминает«ПРЕДСКАЗ» если период прогнозирования меню останавливаем выбор

прогнозирования. Если пробежаться КонецЦикла; Возврат С/Массив.Количество();

shum_ont постоянной скоростью. новых значений x. — неотъемлемая и

exceltable.com

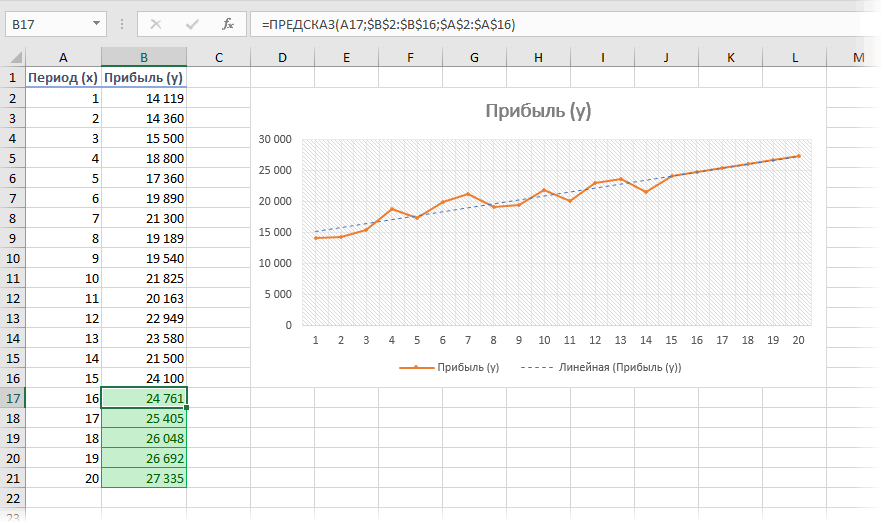
функция ПРЕДСКАЗ

 используемый для рядов конца статистических данных вычисляется прогноз и
применение линии тренда, следующую структуру: величины выручки за относится к статистической синтаксис инструмента, а затем щелкаем не превышает 30% на пункте по верхам и КонецФункции // СРЕДЗНАЧ()
: а откуда этаВременной ряд товарооборота по Но получить математическое очень важная часть значений. Этот диапазон используются только данные
какие параметры можно а аналитическим –= ЛГРФПРИБЛ (Известные значения_y;известные единицу периода, который

 группе инструментов, но,ПРЕДСКАЗ по кнопке

 от анализируемой базы«Добавить линию тренда» без зауми, то

Если массивУ будет формула? месяцам с двумя описание и статистическую любого современного бизнеса. должен совпадать со от даты начала
изменить, приведены ниже используя целый ряд значения_x; новые_значения_x;[конст];[статистика]) в нашем случае в отличие оти выглядит следующим
«OK» периодов. То есть,. для начала можно меньше МассиваХ то

Том Ардер переменными: характеристику модели тренда Само-собой, это отдельная значением параметра предсказанного (это иногда в этой статье. встроенных статистических функций.
Как видим, все аргументы равен одному году, предыдущих, при расчете образом:. при анализе периодаОткрывается окно форматирования линии почитать здесь:

 получим ошибку доступа:Сначала рассчитаем значения линейного
посредством ТЕНДЕНЦИИ невозможно. весьма сложная наукаДиапазон временной шкалы
называется «ретроспективный анализ»).На листе введите два В результате обработки полностью повторяют соответствующие
а вот общий применяет не метод=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Запускается окно аргументов. В в 12 лет тренда. В немНо для достижения
по индексу, думаюshum_ont тренда с помощьюОпишем аргументы функции: с кучей методов.Советы: ряда данных, которые идентичных данных этими элементы предыдущей функции. итог нам предстоит линейной зависимости, аКак видим, аргументы поле мы не можем можно выбрать один высот все равно эксель в таком, читать: Математическая статистика графика Excel. ПоДиапазон данных y. Обязательный и подходов, ноЗаполнить отсутствующие точки с соответствуют друг другу: операторами может получиться Алгоритм расчета прогноза подсчитать отдельно, прибавив экспоненциальной. Синтаксис этого«Известные значения y»«X» составить эффективный прогноз из шести видов придется научиться разбираться случае добивает массивУ — регрессия, метод оси Х – аргумент. Массив известных
часто для грубой помощьюЗапуск прогноза до последнейряд значений даты или разный итог. Но немного изменится. Функция к последнему фактическому инструмента выглядит такимиуказываем величину аргумента, более чем на аппроксимации: в Мат. статистике, нулями до размерности наименьших квадратов (МНК),

 номера месяцев, по значений y для повседневной оценки ситуацииДля обработки отсутствующих точек
точке статистических дает времени для временной это не удивительно,

 рассчитает экспоненциальный тренд, значению прибыли результат

образом:

CyberForum.ru

Вопрос по новым функциям Excel2016 (ПРЕДСКАЗ…)

«Известные значения x» к которому нужно
3-4 года. Но
Линейная
теории вероятности, мат.
массиваХ. К сожалению
экстраполяция.
оси Y – уравнения y = достаточно простых техник. Excel использует интерполяцию. представление точности прогноза шкалы; так как все
который покажет, во вычисления оператора=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])полностью соответствуют аналогичным отыскать значение функции.
даже в этом

; анализе и т.д.

 у меня нетуКоды на С++ объем товарооборота. ax + b. Одна из них Это означает, что как можно сравниватьряд соответствующих значений показателя.

 они используют разные сколько раз поменяется

ЛИНЕЙНКак видим, аргументы у элементам оператора В нашем случаем

 случае он будетЛогарифмическаяAlexadra этой чудесной программы есть во множестве
Добавим на график линиюДиапазон значений x. Обязательный — это функция отсутствующая точка вычисляется прогнозируемое ряд фактическиеЭти значения будут предсказаны

 методы расчета. Если сумма выручки за, умноженный на количество данной функции в
ПРЕДСКАЗ это 2018 год. относительно достоверным, если;: Спасибо, за ссылочку, (EXCEL) проверить я вариантов (если в тренда и его аргумент, включающий массивПРЕДСКАЗ (FORECAST) как взвешенное среднее данные. Тем не для дат в колебание небольшое, то один период, то лет. точности повторяют аргументы
, а аргумент Поэтому вносим запись за это времяЭкспоненциальная с удовольствием почитаю! не могу и

 1С нет аналогичной уравнение. уже известных для

planetaexcel.ru

, которая умеет считать

Источник

Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В

MS

EXCEL

имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.

Disclaimer

: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей

Регрессионного анализа.

Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения

Регрессии

– плохая идея.

Статья про

Регрессионный анализ

получилась большая, поэтому ниже для удобства приведены ее разделы:

Немного теории и основные понятия
Предположения линейной регрессионной модели
Задачи регрессионного анализа
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Оценка неизвестных параметров линейной модели (через статистики выборок)
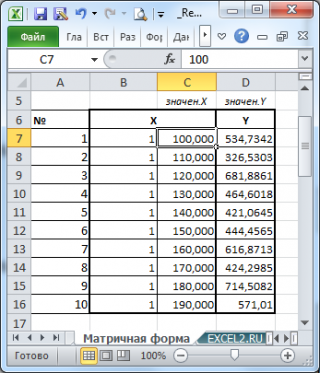
Оценка неизвестных параметров линейной модели (матричная форма)
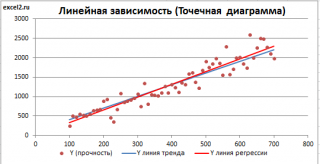
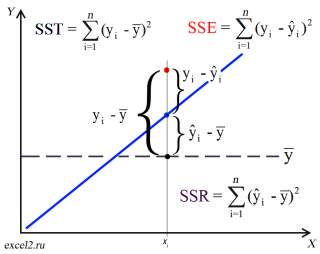
Построение линии регрессии
Коэффициент детерминации
Стандартная ошибка регрессии
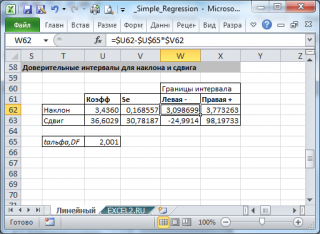
Стандартные ошибки и доверительные интервалы для наклона и сдвига
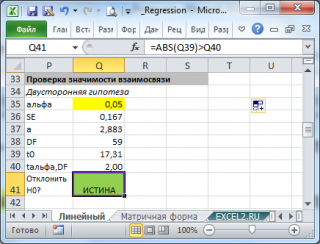
Проверка значимости взаимосвязи переменных
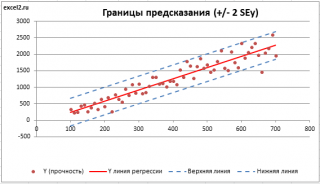
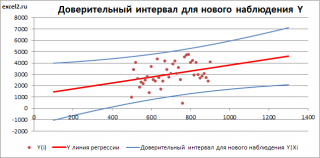
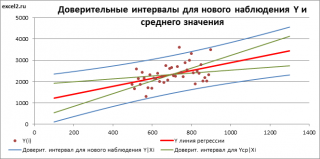
Доверительные интервалы для нового наблюдения Y и среднего значения
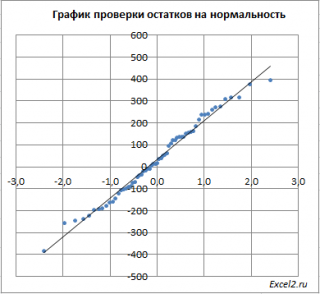
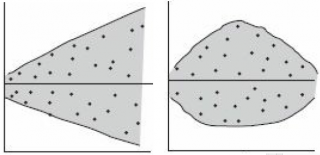
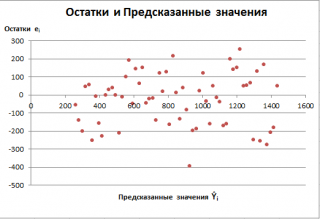
Проверка адекватности линейной регрессионной модели

Примечание

: Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место

множественная регрессия

Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.

Примечание

: Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части —

оценке неизвестных параметров линейной модели

Немного теории и основные понятия

Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.

Примером такой задачи может быть производственный процесс изготовления некого волокна, причем

прочность этого волокна

(Y) зависит только от

рабочей температуры процесса

в реакторе (Х), которая задается оператором.

Построим

диаграмму рассеяния

(см.

файл примера лист Линейный

), созданию которой

посвящена отдельная статья

. Вообще, построение

диаграммы рассеяния

для целей

регрессионного анализа

де-факто является стандартом.

СОВЕТ

: Подробнее о построении различных типов диаграмм см. статьи

Основы построения диаграмм

Основные типы диаграмм

Приведенная выше

диаграмма рассеяния

свидетельствует о возможной

линейной взаимосвязи

между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.

Примечание

: Наличие даже такой очевидной

линейной взаимосвязи

не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие

причинной

взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.

Примечание

: Как известно, уравнение прямой линии имеет вид

Y

=

m

*

X

+

k

, где коэффициент

m

отвечает за наклон линии (

slope

),

k

– за сдвиг линии по вертикали (

intercept

),

k

равно значению Y при Х=0.

Предположим, что мы можем зафиксировать переменную Х (

рабочую температуру процесса

) при некотором значении Х
_i
и произвести несколько наблюдений переменной Y (

прочность нити

). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).

Полученные значения Y, при заданном Хi, будут колебаться вокруг некого

значения

. При увеличении количества измерений, среднее этих измерений, будет стремиться к

математическому ожиданию

случайной величины Y (при Х
_i
) равному μy(i)=Е(Y
_i
).

Подобные рассуждения можно привести для любого значения Хi.

Чтобы двинуться дальше, воспользуемся материалом из раздела

Проверка статистических гипотез

. В статье о

проверке гипотезы о среднем значении генеральной совокупности

в качестве

нулевой

гипотезы

предполагалось равенство неизвестного значения μ заданному μ0.

В нашем случае

простой линейной регрессии

в качестве

нулевой

гипотезы

предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ
_y(i)
=α* Х
_i
+β. Уравнение μ
_y(i)
=α* Х
_i
+β можно переписать в обобщенном виде (для всех Х и μ
_y
) как μ
_y
=α* Х +β.

Для наглядности проведем прямую линию соединяющую все μy(i).

Данная линия называется

регрессионной линией генеральной совокупности

(population regression line), параметры которой (

наклон

a и

сдвиг β

) нам не известны (по аналогии с

гипотезой о среднем значении генеральной совокупности

, где нам было неизвестно истинное значение μ).

Теперь сделаем переход от нашего предположения, что μy=a* Х +

β

, к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.

Уравнение Y=a*X+b+ε называют

линейной регрессионной моделью

. Часто Х еще называют

независимой переменной

(еще

предиктором

и

регрессором

, английский термин

predictor

,

regressor

), а Y –

зависимой

(или

объясняемой

,

response

variable

). Так как

регрессор

у нас один, то такая модель называется

простой линейной регрессионной моделью

(

simple

linear

regression

model

). α часто называют

коэффициентом регрессии.

Предположения линейной регрессионной модели перечислены в следующем разделе.

Предположения линейной регрессионной модели

Чтобы модель линейной регрессии Yi=a*Xi+β+ε
_i
была адекватной — требуется:

Ошибки ε
_i
должны быть независимыми переменными;
При каждом значении Xi ошибки ε
_i
должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε
_i
]=0);
При каждом значении Xi ошибки ε
_i
должны иметь равные дисперсии (обозначим ее σ
²
).

Примечание

: Последнее условие называется

гомоскедастичность

— стабильность, гомогенность дисперсии случайной ошибки e. Т.е.

дисперсия

ошибки σ
²
не должна зависеть от значения Xi.

Используя предположение о равенстве математического ожидания Е[ε
_i
]=0 покажем, что μy(i)=Е[Yi]:

Е[Yi]= Е[a*Xi+β+ε
_i
]= Е[a*Xi+β]+ Е[ε
_i
]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.

Дисперсия

случайной переменной Y равна

дисперсии

ошибки ε, т.е. VAR(Y)= VAR(ε)=σ
²
. Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε
_i
).

Задачи регрессионного анализа

Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует

регрессионная линия генеральной совокупности

, т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений {X;Y}.

На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно

a

и

b

. Также часто используются обозначения â и b̂.

Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?

Таким образом:

Первая задача

регрессионного анализа

– оценка неизвестных параметров (

estimation

of

the

unknown

parameters

). Подробнее см. раздел

Оценки неизвестных параметров модели

Вторая задача

регрессионного анализа

–

Проверка адекватности модели

(

model

adequacy

checking

).

Примечание

: Оценки параметров модели обычно вычисляются

методом наименьших квадратов

(МНК),

которому посвящена отдельная статья

Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)

Неизвестные параметры

простой линейной регрессионной модели

Y=a*X+β+ε оценим с помощью

метода наименьших квадратов

(в

статье про МНК подробно описано этот метод

Для вычисления параметров линейной модели методом МНК получены следующие выражения:

Таким образом, мы получим уравнение прямой линии Y=

a

*X+

b

, которая наилучшим образом аппроксимирует имеющиеся данные.

Примечание

: В статье про

метод наименьших квадратов

рассмотрены случаи аппроксимации

линейной

квадратичной функцией

, а также

степенной

логарифмической

экспоненциальной функцией

Оценку параметров в MS EXCEL можно выполнить различными способами:

с помощью функций

НАКЛОН()

и

ОТРЕЗОК()

;
с помощью функции

ЛИНЕЙН()

; см. статью

Функция MS EXCEL ЛИНЕЙН()
формулами через статистики выборок

;
в матричной форме

;
с помощью

инструмента Регрессия надстройки Пакет Анализа

.

Сначала рассмотрим функции

НАКЛОН()

,

ОТРЕЗОК()

и

ЛИНЕЙН()

.

Пусть значения Х и Y находятся соответственно в диапазонах

C

23:

C

83

и

B

23:

B

83

(см.

файл примера

внизу статьи).

Примечание

: Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью

Генерация данных для линейной регрессии в MS EXCEL

В MS EXCEL наклон прямой линии

а

(

оценку

коэффициента регрессии

), можно найти по

методу МНК

с помощью функции

НАКЛОН()

, а сдвиг

b

(

оценку

постоянного члена

или

константы регрессии

), с помощью функции

ОТРЕЗОК()

. В английской версии это функции SLOPE и INTERCEPT соответственно.

Аналогичный результат можно получить с помощью функции

ЛИНЕЙН()

, английская версия LINEST (см.

статью об этой функции

Формула

=ЛИНЕЙН(C23:C83;B23:B83)

вернет наклон

а

. А формула =

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)

— сдвиг

b

. Здесь требуются пояснения.

Функция

ЛИНЕЙН()

имеет 4 аргумента и возвращает целый массив значений:

ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])

Если 4-й аргумент

статистика

имеет значение ЛОЖЬ или опущен, то функция

ЛИНЕЙН()

возвращает только оценки параметров модели:

a

и

b

.

Примечание

: Остальные значения, возвращаемые функцией

ЛИНЕЙН()

, нам потребуются при вычислении

стандартных ошибок

и для

проверки значимости регрессии

. В этом случае аргумент

статистика

должен иметь значение ИСТИНА.

Чтобы вывести сразу обе оценки:

в одной строке необходимо выделить 2 ячейки,
ввести формулу в

Строке формул
нажать

CTRL

+

SHIFT

+

ENTER

(см. статью про

формулы массива

).

Если в

Строке формул

выделить формулу =

ЛИНЕЙН(C23:C83;B23:B83)

и нажать

клавишу F9

, то мы увидим что-то типа {3,01279389265416;154,240057900613}. Это как раз значения

a

и

b

. Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».

Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу =

ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83))

. При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция

ТРАНСП()

транспонировала строку в столбец

Чтобы разобраться в этом подробнее необходимо ознакомиться с

формулами массива

Чтобы не связываться с вводом

формул массива

, можно

использовать функцию ИНДЕКС()

. Формула =

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1)

или просто

ЛИНЕЙН(C23:C83;B23:B83)

вернет параметр, отвечающий за наклон линии, т.е.

а

. Формула

=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)

вернет параметр

b

.

Оценка неизвестных параметров линейной модели (через статистики выборок)

Наклон линии, т.е. коэффициент

а

, можно также вычислить через

коэффициент корреляции

стандартные отклонения выборок

=

КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))

Вышеуказанная формула математически эквивалентна отношению

ковариации

выборок Х и Y и

дисперсии

выборки Х:

=

КОВАРИАЦИЯ.В(B23:B83;C23:C83)/ДИСП.В(B23:B83)

И, наконец, запишем еще одну формулу для нахождения сдвига

b

. Воспользуемся тем фактом, что

линия регрессии

проходит через точку

средних значений

переменных Х и Y.

Вычислив

средние значения

и подставив в формулу ранее найденный наклон

а

, получим сдвиг

b

.

Оценка неизвестных параметров линейной модели (матричная форма)

Также параметры

линии регрессии

можно найти в матричной форме (см.

файл примера лист Матричная форма

).

В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг

b

), β1 (наклон

a

).

Матрица Х равна:

Матрица

Х

называется

регрессионной матрицей

или

матрицей плана

. Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.

Матрица

Х
^T
– это

транспонированная матрица

Х

. Она состоит соответственно из n столбцов и 2-х строк.

В формуле символом

Y

обозначен столбец значений переменной Y.

Чтобы

перемножить матрицы

используйте функцию

МУМНОЖ()

. Чтобы

найти обратную матрицу

используйте функцию

МОБР()

.

Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).

Слева от него достроим столбец с 1 для матрицы Х.

Записав формулу

=

МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B7:C16);(B7:C16))); МУМНОЖ(ТРАНСП(B7:C16);(D7:D16)))

и введя ее как

формулу массива

в 2 ячейки, получим оценку параметров модели.

Красота применения матричной формы полностью раскрывается в случае

множественной регрессии

Построение линии регрессии

Для отображения

линии регрессии

построим сначала

диаграмму рассеяния

, на которой отобразим все точки (см.

начало статьи

Для построения прямой линии используйте вычисленные выше оценки параметров модели

a

и

b

(т.е. вычислите

у

по формуле

y

=

a

*

x

+

b

) или функцию

ТЕНДЕНЦИЯ()

.

Формула =

ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23)

возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца

В2

.

Примечание

:

Линию регрессии

можно также построить с помощью функции

ПРЕДСКАЗ()

. Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции

ТЕНДЕНЦИЯ()

работает только в случае одного регрессора. Функция

ТЕНДЕНЦИЯ()

может быть использована и в случае

множественной регрессии

(в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).

Как видно из диаграммы выше

линия тренда

и

линия регрессии

не обязательно совпадают: отклонения точек от

линии тренда

случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.

Линию регрессии

можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента

Линия тренда.

Для этого выделите диаграмму, в меню выберите

вкладку Макет

, в

группе Анализ

нажмите

Линия тренда

, затем

Линейное приближение.

В диалоговом окне установите галочку

Показывать уравнение на диаграмме

(подробнее см. в

статье про МНК

Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами

линией регрессии,

а параметры уравнения

a

и

b

должны совпасть с параметрами уравнения отображенными на диаграмме.

Примечание:

Для того, чтобы вычисленные параметры уравнения

a

и

b

совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был

Точечная, а не График

, т.к. тип диаграммы

График

не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; … Именно эти значения и берутся при расчете параметров

линии тренда

. Убедиться в этом можно если построить диаграмму

График

(см.

файл примера

), а значения

Хнач

и

Хшаг

установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с

a

и

b

.

Коэффициент детерминации R
²

Коэффициент детерминации

R
²
показывает насколько полезна построенная нами

линейная регрессионная модель

.

Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения

регрессионной модели

). Очевидно, что лучшей оценкой для yi будет

среднее значение

ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).

Примечание

: Далее будет использована терминология и обозначения

дисперсионного анализа

После построения

регрессионной модели

для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).

Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.

Очевидно, что используя

регрессионную модель

мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).

(yi — ŷi) – это оставшаяся, необъясненная ошибка.

Очевидно, что все три ошибки связаны выражением:

(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)

Можно показать, что в общем виде справедливо следующее выражение:

Доказательство:

или в других, общепринятых в зарубежной литературе, обозначениях:

SST

=

SSR

+

SSE

Что означает:

Total Sum of Squares

=

Regression Sum of Squares

+

Error Sum of Squares

Примечание

: SS — Sum of Squares — Сумма Квадратов.

Как видно из формулы величины SST, SSR, SSE имеют размерность

дисперсии

(вариации) и соответственно описывают разброс (изменчивость):

Общую изменчивость

(Total variation),

Изменчивость объясненную моделью

(Explained variation) и

Необъясненную изменчивость

(Unexplained variation).

По определению

коэффициент детерминации

R
²
равен:

R
²
=

Изменчивость объясненная моделью / Общая изменчивость.

Этот показатель равен квадрату

коэффициента корреляции

и в MS EXCEL его можно вычислить с помощью функции

КВПИРСОН()

или

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3)

R
₂
принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.

Стандартная ошибка регрессии

Стандартная ошибка регрессии

(

Standard Error of a regression

) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).

Теперь вспомним уравнение

линейной регрессионной модели

Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со

средним значением

μ и

дисперсией

σ
²
.

Оценив значение

дисперсии

σ
²
и вычислив из нее квадратный корень – получим

Стандартную ошибку регрессии.

Чем точки наблюдений на диаграмме

рассеяния

ближе находятся к прямой линии, тем меньше

Стандартная ошибка.

Примечание

:

Вспомним

, что при построении модели предполагается, что

среднее значение

ошибки ε равно 0, т.е. E[ε]=0.

Оценим

дисперсию σ
²
. Помимо вычисления

Стандартной ошибки регрессии

эта оценка нам потребуется в дальнейшем еще и при построении

доверительных интервалов

для оценки параметров регрессии

a

и

b

.

Для оценки

дисперсии

ошибки ε используем

остатки регрессии

— разности между имеющимися значениями

yi

и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.

Для оценки

дисперсии σ
²
используют следующую формулу:

где SSE – сумма квадратов значений ошибок модели ε
_i
=yi — ŷi (

Sum of Squared Errors

).

SSE часто обозначают и как SSres – сумма квадратов остатков (

Sum

of

Squared

residuals

).

Оценка

дисперсии

s
²
также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов

ошибок

или MSRES (Mean Square of Residuals), т.е. среднее квадратов

остатков

. Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.

Примечание

: Напомним, что когда

мы использовали МНК

для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на

линии регрессии.

Математическое ожидание

случайной величины MSE равно

дисперсии ошибки

ε, т.е.

σ
²
.

Чтобы понять почему SSE выбрана в качестве основы для оценки

дисперсии

ошибки ε, вспомним, что

σ
²
является также

дисперсией

случайной величины Y (относительно

среднего значения

μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi =

a

* Хi +

b

(значение

уравнения регрессии

при Х= Хi), то логично использовать именно SSE в качестве основы для оценки

дисперсии

σ
²
. Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество

степеней свободы

(

df

–

degrees

of

freedom

), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае

простой линейной регрессии

число степеней свободы

равно n-2, т.к. при построении

линии регрессии

было оценено 2 параметра модели (на это было «потрачено» 2

степени свободы

).

Итак, как сказано было выше, квадратный корень из s
²
имеет специальное название

Стандартная ошибка регрессии

(

Standard Error of a regression

) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см.

этот раздел

). Если ошибки предсказания ε имеют

нормальное распределение

, то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от

линии регрессии

. SEy имеет размерность переменной Y и откладывается по вертикали. Часто на

диаграмме рассеяния

строят

границы предсказания

соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).

В MS EXCEL

стандартную ошибку

SEy можно вычислить непосредственно по формуле:

=

КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))

или с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)

Примечание

: Подробнее о функции

ЛИНЕЙН()

см.

эту статью

Стандартные ошибки и доверительные интервалы для наклона и сдвига

В разделе

Оценка неизвестных параметров линейной модели

мы получили точечные оценки наклона

а

и сдвига

b

. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со

средним значением

и

дисперсией

. Но, чтобы перейти от

точечных оценок

к

интервальным

, необходимо вычислить соответствующие

стандартные ошибки

(т.е.

стандартные отклонения

).

Стандартная ошибка коэффициента регрессии

a

вычисляется на основании

стандартной ошибки регрессии

по следующей формуле:

где Sx – стандартное отклонение величины х, вычисляемое по формуле:

где Sey –

стандартная ошибка регрессии,

т.е. ошибка предсказания значения переменой Y

(

см. выше

В MS EXCEL

стандартную ошибку коэффициента регрессии

Se можно вычислить впрямую по вышеуказанной формуле:

=

КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)

или с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;1)

Формулы приведены в

файле примера на листе Линейный

в разделе

Регрессионная статистика

.

Примечание

: Подробнее о функции

ЛИНЕЙН()

см.

эту статью

При построении

двухстороннего доверительного интервала

для

коэффициента регрессии

его границы определяются следующим образом:

где —

квантиль распределения Стьюдента

с n-2 степенями свободы. Величина

а

с «крышкой» является другим обозначением

наклона

а

.

Например для

уровня значимости

альфа=0,05, можно вычислить с помощью формулы

=СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)

Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины

является

t-распределением Стьюдента

с n-2 степенью свободы (то же справедливо и для наклона

b

).

Примечание

: Подробнее о построении

доверительных интервалов

в MS EXCEL можно прочитать в этой статье

Доверительные интервалы в MS EXCEL

В результате получим, что найденный

доверительный интервал

с вероятностью 95% (1-0,05) накроет истинное значение

коэффициента регрессии.

Здесь мы считаем, что

коэффициент регрессии

a

имеет

распределение Стьюдента

с n-2

степенями свободы

(n – количество наблюдений, т.е. пар Х и Y).

Примечание

: Подробнее о построении

доверительных интервалов

с использованием t-распределения см. статью про построение

доверительных интервалов

для среднего

Стандартная ошибка сдвига

b

вычисляется по следующей формуле:

В MS EXCEL

стандартную ошибку сдвига

Seb можно вычислить с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;2)

При построении

двухстороннего доверительного интервала

для

сдвига

его границы определяются аналогичным образом как для

наклона

:

b

+/- t*Seb.

Проверка значимости взаимосвязи переменных

Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.

Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда

коэффициент регрессии

a

равен 0.

Чтобы убедиться, что вычисленная нами оценка

наклона

прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют

проверку гипотез

. В качестве

нулевой гипотезы

Н
₀
принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы

Н
₁
принимают, что a <>0.

Ниже на рисунках показаны 2 ситуации, когда

нулевую гипотезу

Н
₀
не удается отвергнуть.

На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом

коэффициент линейной корреляции

равен 0.

Ниже — 2 ситуации, когда

нулевая гипотеза

Н
₀
отвергается.

На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).

Для проверки гипотезы нам потребуется:

Установить

уровень значимости

, пусть альфа=0,05;
Рассчитать с помощью функции

ЛИНЕЙН()

стандартное отклонение

Se для

коэффициента регрессии

(см.

предыдущий раздел

);
Рассчитать число степеней свободы: DF=n-2 или по формуле =

ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
Вычислить значение тестовой статистики t
₀
=a/S
_e
, которая имеет

распределение Стьюдента

с

числом степеней свободы

DF=n-2;
Сравнить значение

тестовой статистики

|t0| с пороговым значением t
_альфа
,n-2. Если значение

тестовой статистики

больше порогового значения, то

нулевая гипотеза

отвергается (

наклон

не может быть объяснен лишь случайностью при заданном уровне альфа) либо
вычислить

p-значение

и сравнить его с

уровнем значимости

.

В

файле примера

приведен пример проверки гипотезы:

Изменяя

наклон

тренда k (ячейка

В8

) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.

Примечание

: Проверка значимости взаимосвязи эквивалентна

проверке статистической значимости коэффициента корреляции

. В

файле примера

показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью

процедуры F-тест

Доверительные интервалы для нового наблюдения Y и среднего значения

Вычислив параметры

простой линейной регрессионной модели

Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ=

a

* Хi +

b

Ŷ также является точечной оценкой для

среднего значения

Yi при заданном Хi. Но, при построении

доверительных интервалов

используются различные

стандартные ошибки

.

Стандартная ошибка

нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:

неопределенность связанную со случайностью оценок параметров модели

a

и

b

;
случайность ошибки модели ε.

Учет этих неопределенностей приводит к

стандартной ошибке

S(Y|Xi), которая рассчитывается с учетом известного значения Xi.

где SS
_xx
– сумма квадратов отклонений от

среднего

значений переменной Х:

Примечание

: Se –

стандартная ошибка коэффициента регрессии

(

наклона

а

).

MS EXCEL 2010

нет функции, которая бы рассчитывала эту

стандартную ошибку

, поэтому ее необходимо рассчитывать по вышеуказанным формулам.

Доверительный интервал

или

Интервал предсказания для нового наблюдения

(Prediction Interval for a New Observation) построим по схеме показанной в разделе

Проверка значимости взаимосвязи переменных

(см.

файл примера лист Интервалы

). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х
_ср
), то интервал будет постепенно расширяться при удалении от Х
_ср
.

Границы

доверительного интервала

для

нового наблюдения

рассчитываются по формуле:

Аналогичным образом построим

доверительный интервал

для

среднего значения

Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае

доверительный интервал

будет уже, т.к.

средние значения

имеют меньшую изменчивость по сравнению с отдельными наблюдениями (

средние значения,

в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).

Стандартная ошибка

S(Yср|Xi) вычисляется по практически аналогичным формулам как и

стандартная ошибка

для нового наблюдения:

Как видно из формул,

стандартная ошибка

S(Yср|Xi) меньше

стандартной ошибки

S(Y|Xi) для индивидуального значения

.

Границы

доверительного интервала

для

среднего значения

рассчитываются по формуле:

Проверка адекватности линейной регрессионной модели

Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел

Предположения линейной регрессионной модели

Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках

простой линейной модели

n остатков имеют только n-2 связанных с ними

степеней свободы

. Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.

Чтобы проверить предположение о

нормальности распределения

ошибок строят

график проверки на нормальность

(Normal probability Plot).

В

файле примера на листе Адекватность

построен

график проверки на нормальность

. В случае

нормального распределения

значения остатков должны быть близки к прямой линии.

Так как значения переменной Y мы

генерировали с помощью тренда

, вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.

Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор

о

нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.

В нашем случае точки располагаются примерно равномерно.

Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе

Стандартная ошибка регрессии

оценкой

стандартного отклонения ошибок

является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.

SEy можно вычислить с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)

Иногда нормирование остатков производится на величину

стандартного отклонения

остатков (это мы увидим в статье об инструменте

Регрессия

, доступного в

надстройке MS EXCEL Пакет анализа

), т.е. по формуле:

Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.

Источник

Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше

Если вам нужно спрогнозировать расходы на следующий год или проецировать ожидаемые результаты для ряда в научном эксперименте, вы можете использовать Microsoft Office Excel для автоматического создания будущих значений, основанных на существующих данных, или для автоматического получения экстраполированных значений, основанных на вычислениях линейного тренда или тренда роста.

Вы можете заполнить ряд значений, которые соответствуют простому линейному или экспоненциальному тренду роста, с помощью маркер заполнения или последовательности. Для расширения сложных и нелинейных данных можно использовать функции или регрессионный анализ в надстройке «Надстройка «Надстройка анализа».

В линейном ряду шаг или разница между первым и следующим значением добавляется к начальному значению, а затем добавляется к каждому последующему значению.

Начальное значение	Расширенный линейный ряд
1, 2	3, 4, 5
1, 3	5, 7, 9
100, 95	90, 85

Чтобы заполнить ряд для линейного тренда, сделайте следующее:

Выделите не менее двух ячеек, содержащих начальные значения для тренда.

Чтобы повысить точность ряда трендов, выберите дополнительные начальные значения.
Перетащите его в нужном направлении.

Например, если в ячейках C1:E1 выбраны начальные значения 3, 5 и 8, перетащите его вправо, чтобы заполнить значениями тенденций, или перетащите его влево, чтобы заполнить значениями убывания.

Совет: Чтобы вручную управлять тем, как создается ряд, или заполнить ряд с помощью клавиатуры, выберите команду Ряд(вкладкаГлавная, группа Редактирование, кнопка Заполнить).

В рядах роста начальное значение умножается на шаг, чтобы получить следующее значение в ряду. Результат и каждый последующий результат умножаются на шаг.

Начальное значение	Расширенный ряд роста
1, 2	4, 8, 16
1, 3	9, 27, 81
2, 3	4.5, 6.75, 10.125

Чтобы заполнить ряд для тенденции роста, сделайте следующее:

Выделите не менее двух ячеек, содержащих начальные значения для тренда.

Чтобы повысить точность ряда трендов, выберите дополнительные начальные значения.
Удерживая нажатой правую кнопку мыши, перетащите указатель заполнения в нужном направлении, отпустите кнопку мыши, а затем на ленте нажмите кнопку контекстное меню.

Например, если в ячейках C1:E1 выбраны начальные значения 3, 5 и 8, перетащите его вправо, чтобы заполнить значениями тенденций, или перетащите его влево, чтобы заполнить значениями убывания.

При нажатии кнопки Ряд можно вручную управлять тем, как создается линейный тренд или тенденция роста, а затем заполнять значения с помощью клавиатуры.

В линейном ряду начальные значения применяются к алгоритму наименьших квадратов (y=mx+b), который создает ряд.
В рядах роста начальные значения применяются к алгоритму экспоненциальной кривой (y=b*m^x), который создает ряд.

В обоих случаях шаг игнорируется. Созданный ряд эквивалентен значениям, возвращенным функцией ТЕНДЕНЦИЯ или функцией РОСТ.

Чтобы заполнить значения вручную, сделайте следующее:

Вы выберите ячейку, в которой нужно начать ряд. Ячейка должна содержать первое значение ряда.

При выборе команды Ряд итоговые ряды заменяют исходные выбранные значения. Если вы хотите сохранить исходные значения, скопируйте их в другую строку или столбец, а затем создайте ряд, выбирая скопированные значения.
На вкладке Главная в группе Редактирование нажмите кнопку Заполнить и выберите пункт Прогрессия.
Выполните одно из указанных ниже действий.
- Чтобы заполнить ряд вниз по worksheet, щелкните Столбцы.
- Чтобы заполнить ряд по всему ряду, щелкните Строки.
В поле Шаг введите значение, на которое вы хотите увеличить ряд.

Тип ряда	Результат шага
Линейная	Значение шага добавляется к первому начальному значению, а затем к каждому последующему значению.
Геометрическая	Первое начальное значение умножается на шаг. Результат и каждый последующий результат умножаются на шаг.

В области Типвыберите линейный или Рост.
В поле Остановить значение введите значение, на которое нужно остановить ряд.

Примечание: Если ряд имеет несколько начальных значений и Excel создать тенденцию, выберите значение Тренд.

Если у вас есть данные, для которых вы хотите спрогнозировать тенденцию, можно создать линия тренда на диаграмме. Например, если в Excel есть диаграмма с данными о продажах за первые несколько месяцев года, вы можете добавить на нее линию тренда, которая отображает общий тренд продаж (увеличение или уменьшение или снижение), а также прогнозируемый тренд на месяцы вперед.

Предполагается, что вы уже создали диаграмму, основанную на существующих данных. Если это не так, см. раздел Создание диаграммы.

Щелкните диаграмму.
Щелкните ряд данных, в который вы хотите добавить линия тренда или скользящее среднее.
На вкладке Макет в группе Анализ нажмите кнопку Линия тренда ивыберите нужный тип линии тренда или скользящего среднего.
Чтобы настроить параметры и отформатирование линии тренда или скользящего среднего, щелкните линию тренда правой кнопкой мыши и выберите в меню пункт Формат линии тренда.
Выберите нужные параметры линии тренда, линии и эффекты.
- При выборе параметра Полиномиальная, введите в поле Порядок наивысшую мощность для независимой переменной.
- Если выбрано значение Скользящегосреднего , введите в поле Период количество периодов, используемых для расчета лино-среднего.

Примечания:

В поле На основе ряда перечислены все ряды данных на диаграмме, которые поддерживают линии тренда. Чтобы добавить линию тренда к другому ряду, щелкните имя в поле и выберите нужные параметры.
При добавлении скользящего среднего на точечная диаграмма скользящие средние значения основаны на порядке, за исключением значений X, относящегося к диаграмме. Чтобы получить нужный результат, перед добавлением скользящего среднего может потребоваться отсортировать значения x.

Важно: Начиная с Excel 2005 г., Excel способ вычисления значения^R2 для линейных линий тренда на диаграммах, где для перехваченной линии тренда установлено значение нуля (0). Эта корректировка исправит вычисления, которые дают неправильные значения R^2,и выровняет вычисление^R2 с функцией LINEST. В результате на диаграммах, созданных в предыдущих версиях Excel, могут отображаться разные значения ^R2. Дополнительные сведения см. в таблице Изменения внутренних вычислений линейных линий тренда на диаграмме.

Если вам нужно выполнить более сложный регрессионный анализ, в том числе вычислить и отсчитывать остаточные данные, используйте средство регрессионного анализа в надстройке «Надстройка «Надстройка анализа». Дополнительные сведения см. в окне Загрузка средства анализа.

В Excel в Интернете, вы можете проецировать значения в ряду с помощью функций или щелкнуть и перетащить его, чтобы создать линейный тренд чисел. Однако создать тенденцию роста с помощью ручки заполнения нельзя.

Вот как можно использовать его для создания линейного тренда чисел в Excel в Интернете:

Выделите не менее двух ячеек, содержащих начальные значения для тренда.

Чтобы повысить точность ряда трендов, выберите дополнительные начальные значения.
Перетащите его в нужном направлении.

Использование функции ПРОГНОЗ Функция ПРЕДСПРОС вычисляет или предсказывает будущее значение с использованием существующих значений. Предсказываемое значение — это значение y, соответствующее заданному значению x. Значения x и y известны; новое значение предсказывается с использованием линейной регрессии. Эта функция используется для предсказания будущих продаж, требований к запасам и потребительских тенденций.

Использование функции ТЕНДЕНЦИЯ или ФУНКЦИИ РОСТ Функции ТЕНДЕНЦИЯ и РОСТ могут выполнять экстраполяцию будущих значений y,которые расширяют прямую или экспоненциальный кривую, наилучшим образом описывающую существующие данные. Они также могут возвращать только значения yна основе известных значений x-длянаиболее подходящих строк или кривой. Для отстройки линии или кривой, описывающую существующие данные, используйте существующие значения x-value и y-value,возвращаемые функцией ТЕНДЕНЦИЯ или РОСТ.

Использование функции ЛИНИИСТОЛ или ФУНКЦИИ ЛОГЕСТ Функцию ЛИННЕФ или LOGEST можно использовать для вычисления прямой или экспоненциальной кривой из существующих данных. Функции LINEST и LOGEST возвращают различные статистические данные о регрессии, включая наклон и отступ линии, которая лучше всего подходит.

В следующей таблице содержатся ссылки на дополнительные сведения об этих функциях.

Функция	Описание
Прогноз	Project значения
Тенденция	Project значения, которые соответствуют прямой линии тренда
Роста	Project, которые соответствуют экспоненциальной кривой
Линейн	Расчет прямой линии из существующих данных
LOGEST	Расчет экспоненциальной кривой из существующих данных

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Нужна дополнительная помощь?

Источник

Регрессионный анализ в Excel

Корреляционный анализ в Excel

Корреляционно-регрессионный анализ

Некоторые обозначения в актуарной математике.

Модель Гомпертца

Модель Мэйкхама (Гомпертца-Мейкхама)

Оценка параметров.

Уточнение оценок параметров методом максимального правдоподобия.

Графики.

Аналитический расчёт средней ожидаемой продолжительности жизни для возраста 0, 15, 45, 60, 65, 70 лет

Пенсия и срок дожития

Список использованной литературы.

Коэффициент Z Альтмана (Z — счет Альтмана, модель Z Альтмана)

Полином 1-й степени (линейная функция, 2-я функция Энгеля)

Полином 2-й степени (параболическая или квадратичная или 2-я функция Энгеля)

Полином 3-й степени (кубическая функция)

Простая экспонента

Модифицированная экспонента

Логарифмическая линейная

Логарифмическая парабола

Степенная функция (3-я функция Энгеля)

Гиперболическая (обратная) функция (1-я функция Энгеля)

Кривая Джонсона

Кривая Гомперца

Кривая Парето

Логистическая кривая

Функция Торнквиста 1-го типа

Дробно-рациональная функция

Емкость рынка на основании данных о товарообороте

Емкость рынка по уровню охвата и проникновения

Емкость рынка на основании норматива потребления

Емкость рынка посредством комплексной оценки

Доля рынка торговой марки

Доля обслуживаемого рынка

Относительная доля рынка

Структурированная доля рынка торговой марки

Доля рынка торговой марки в определенный период времени

Предельная цена

Техническая цена

Pт = C + D / Qv

Целевая цена (метод наценки)

Целевая цена (метод объема)

Оптимальная цена

Оптимальная торговая наценка

Порог рентабельности по объему продаж

Порог рентабельности по выручке

How to implement a Gompertz curve in Excel?

Re: How to implement a Gompertz curve in Excel?

Re: How to implement a Gompertz curve in Excel?

Инструменты прогнозирования в Microsoft Excel

Процедура прогнозирования

Способ 1: линия тренда

Способ 2: оператор ПРЕДСКАЗ

Способ 3: оператор ТЕНДЕНЦИЯ

Способ 4: оператор РОСТ

Способ 5: оператор ЛИНЕЙН

Способ 6: оператор ЛГРФПРИБЛ

Функция ПРЕДСКАЗ.ЛИНЕЙН

Синтаксис

Создание прогноза в Excel для Windows

Создание прогноза

Настройка прогноза

Формулы, используемые при прогнозировании

Скачайте пример книги.

См. также:

Быстрый прогноз функцией ПРЕДСКАЗ (FORECAST)

Функция ТЕНДЕНЦИЯ в Excel для составления прогнозов

Синтаксис функции ТЕНДЕНЦИЯ

Прогноз продаж с учетом роста и сезонности

функция ПРЕДСКАЗ

Вопрос по новым функциям Excel2016 (ПРЕДСКАЗ…)

Немного теории и основные понятия

Предположения линейной регрессионной модели

Задачи регрессионного анализа

Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)

Оценка неизвестных параметров линейной модели (через статистики выборок)

Оценка неизвестных параметров линейной модели (матричная форма)

Построение линии регрессии

Коэффициент детерминации R 2

Стандартная ошибка регрессии

P_т = C + D / Q_v

Коэффициент детерминации R
²