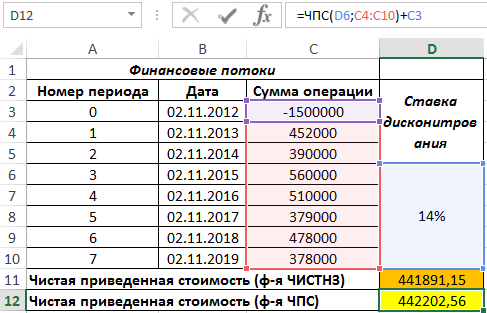
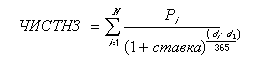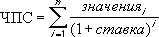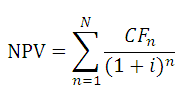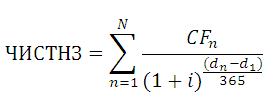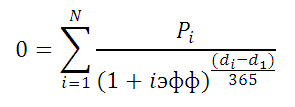Функция ЧИСТНЗ предназначена для расчета приведенной стоимости на основе данных о имеющихся денежных потоках и датах проведения этих платежей (непериодические платежи), и возвращает соответствующее числовое значение.
Функции ЧИСТНЗ и ЧПС рассчитывают один и тот же экономический параметр, однако вторая может быть использована только для определения приведенной стоимости для ряда периодических финансовых потоков (проводимых через определенные промежутки времени, например, через 365 дней).
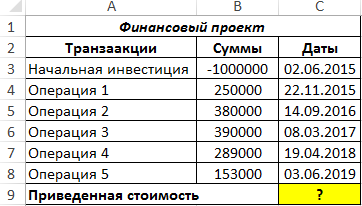
Пример расчета приведенной стоимости проекта в Excel
Пример 1. Определить значение чистой приведенной стоимости для проекта, начальные затраты на реализацию которого составили 1 млн у. е. Длительность проекта составила 5 лет, ставка дисконтирования – 13%.
Вид таблицы данных:
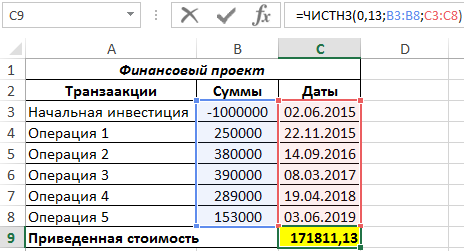
Для определения искомого значения используем функцию:
Описание аргументов:
- 0,13 – числовое значение ставки дисконтирования (13%);
- B3:B8 – диапазон ячеек с числовыми данными о денежных потоках;
- C3:C8 – диапазон ячеек с датами совершения финансовых операций.
Результат:
Это был базовый пример использования функции ЧИСТНЗ в Excel
Расчет приведенной стоимости денежного потока в Excel
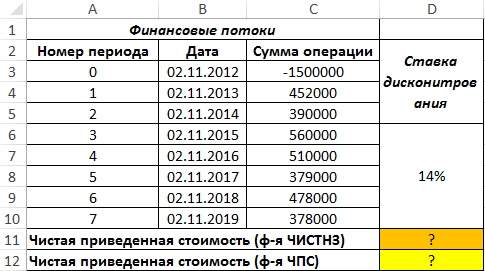
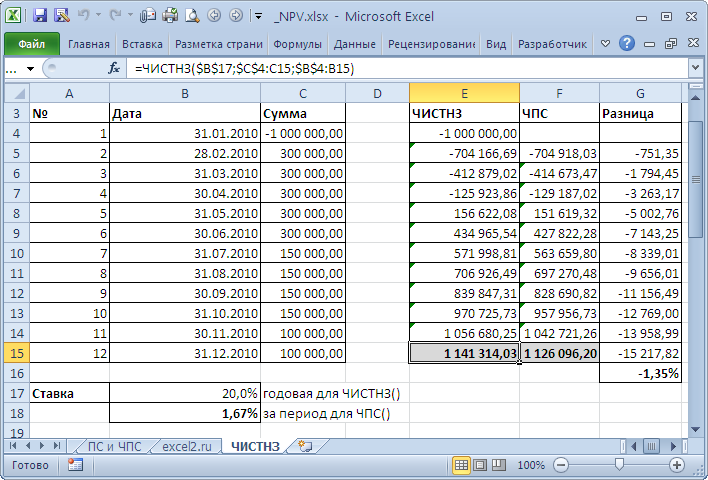
Пример 2. Рассчитать значение чистой приведенной стоимости для финансовых потоков, представленных в таблице, с использованием функции ЧПС, сравнить данные, применив функцию ЧИСТНЗ, объяснить расхождения в полученных результатах.
Вид таблицы данных:
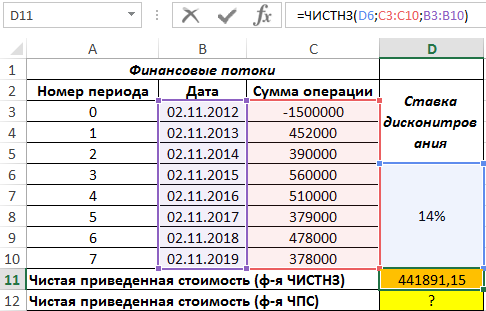
Вначале рассчитаем значение приведенной стоимости с использованием рассматриваемой функции:
В результате получим:
Если бы в табличном редакторе Excel отсутствовала формула ЧИСТНЗ, кроме ручного способа можно было бы рассчитать приведенную стоимость с помощью функции ЧПС следующим образом:
Поскольку функция ЧПС учитывает только платежи, к результатам ее вычислений добавлено значение первоначальных затрат (+C3).
Результат вычислений:
Как видно, результаты немного различны. Это обусловлено тем, что функция ЧИСТНЗ учитывает реальное количество дней в году (в високосном году дней больше на 1). Несмотря на то, что все платежи производились 2-го числа 11 месяца ежегодно, их нельзя считать периодичными, поскольку в списке дат есть високосный год и реальное число дней между 2.11.2016 и 2.11.2017 равен 366 дней. Функция ЧИСТНЗ в подобных расчетах дает более точный результат.
Правила использования функции ЧИСТНЗ в Excel
Функция имеет следующую синтаксическую запись:
=ЧИСТНЗ(ставка;значения;даты)
Описание аргументов:
- ставка – обязательный для заполнения, принимает числовое значение ставки дисконтирования для исследуемого потока финансовых движений.
- значения – обязательный для заполнения, принимает ссылку на диапазон ячеек, содержащих данные о денежных потоках. Фактически, это столбец, в котором приведен график платежей. Указанные значения могут быть как затратами, так и поступлениями. Любая затрата указывается в виде отрицательного числового значения (например, — 10000). Для корректных расчетов хотя бы одно число в графике платежей должно быть отрицательным. Дисконтирование выплат осуществляется на основе года длительностью в 365 дней.
- даты – обязательный для заполнения, принимает ссылку на ячейки с датами, соответствующим моментам совершения финансовых операций (расходы или получение прибыли). Первая дата соответствует началу графика платежей. Последующие должны являться более поздними датами относительно первой. Периодичность дат – необязательное условие. Например, 1-й платеж может быть совершен 1.01.2018, 2-й – 3.07.2018, 3-й – 14.09.2018 и т. д.
Примечания:
- Для корректных расчетов значения в столбце, передаваемые в качестве аргумента даты, должны быть записаны с использованием функции ДАТА. Если они указаны в виде числовых значений (например, записанная в Excel дата 03.06.2019 соответствует числу 43619), дробные части таких чисел будут усечены (например, 43619,3 будет считаться равным 43619).
- Любое значение, переданное в качестве любого из трех аргументов, должно являться числом (или данными типа ДАТА – аргумент даты). Если этой условие не соблюдено, функция ЧИСТНЗ вернет код ошибки #ЧИСЛО!
- Если любая из дат, содержащихся в столбце с датами совершения платежей, является более ранней датой, чем момент осуществления первого платежа, функция ЧИСТНЗ вернет код ошибки #ЧИСЛО!
- Если число ячеек в столбцах с данными о платежах и соответствующими им датами различны, функция ЧИСТНЗ вернет ошибку #ЧИСЛО!
Для проверки значений, вычисленных с использованием функции ЧИСТНЗ, можно использовать формулу:
Эта формула положена в основу алгоритма расчета рассматриваемой функции. Аргументы:
- d0 – дата начальной выплаты (принимается как нулевая выплата, в отличие от функции ЧПС, где начальная выплата является 1-й, чем в первую очередь и обуславливаются различия в результатах вычислений);
- di – дата, соответствующая последней финансовой операции по графику;
- Pi – сумма платежа последней финансовой операции по графику.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЧПС в Microsoft Excel.
Описание
Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).
Синтаксис
ЧПС(ставка; значение1; [значение2],…)
Аргументы функции ЧПС описаны ниже.
-
Ставка Обязательный аргумент. Ставка дисконтирования за один период.
-
Значение1, значение2,… Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 254 аргументов, представляющих выплаты и поступления.
-
Аргументы «значение1, значение2, …» должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.
-
Функция ЧПС использует порядок аргументов «значение1, значение2, …» для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.
-
Аргументы, которые являются пустыми ячейками, логическими значениями или текстовыми представлениями чисел, значениями ошибок или текстом, который невозможно преобразовать в числа, игнорируются.
-
Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Замечания
-
Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса «значение1» и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов. Дополнительные сведения см. в приведенных ниже примерах.
-
Если n — количество денежных потоков в списке значений, формула для функции ЧПС имеет следующий вид:
-
ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции. Сведения о функциях платежей по ссуде и финансовых функциях см. в описании функции ПС.
-
ЧПС связана также с функцией ВСД (внутренняя ставка доходности). ВСД — это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(…); …) = 0.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|---|---|---|
|
0,1 |
Годовая ставка дисконтирования |
|
|
-10 000 |
Начальная стоимость инвестиции через один год |
|
|
3000 |
Доход за первый год |
|
|
4200 |
Доход за второй год |
|
|
6800 |
Доход за третий год |
|
|
Формула |
Описание |
Результат |
|
=ЧПС(A2; A3; A4; A5; A6) |
Чистая приведенная стоимость данной инвестиции |
1 188,44 ₽ |
Пример 2
|
Данные |
Описание |
|
|---|---|---|
|
0,08 |
Годовая ставка дисконтирования. Она может представлять показатель инфляции или процентную ставку по конкурирующим инвестициям. |
|
|
-40 000 |
Начальная стоимость инвестиции |
|
|
8000 |
Доход за первый год |
|
|
9200 |
Доход за второй год |
|
|
10000 |
Доход за третий год |
|
|
12000 |
Доход за четвертый год |
|
|
14500 |
Доход за пятый год |
|
|
Формула |
Описание |
Результат |
|
=ЧПС(A2; A4:A8)+A3 |
Чистая приведенная стоимость данной инвестиции |
1 922,06 ₽ |
|
=ЧПС(A2; A4:A8; -9000)+A3 |
Чистая приведенная стоимость данной инвестиции с учетом убытка (9000) на шестом году |
(3 749,47 ₽) |
К началу страницы
Нужна дополнительная помощь?
Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул
MS
EXCEL.
Начнем с определения, точнее с определений.
Чистой приведённой стоимостью (Net present value, NPV) называют
сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню
(взято из Википедии). Или так:
Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт
cfin.
ru)
Или так:
Текущая
стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика
.
Толковыйсловарь
. —
М
.
:
»
ИНФРА
—
М
«,
Издательство
»
ВесьМир
«.
Дж
.
Блэк
.)
Примечание1
. Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется
ЧПС()
, то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с
Приведенной стоимостью
.
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма
Приведенных стоимостей
денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
Совет
: при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи
Приведенная стоимость
.
Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу
сложных процентов
.
Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция
ЧПС()
(английский вариант — NPV()). В ее основе используется формула:
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
Примечание2
. Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить:
Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год)
. Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).
Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV <0 и проект убыточен.
Выбор периода дисконтирования для функции ЧПС()
При выборе периода дисконтирования нужно задать себе вопрос: «Если мы прогнозируем на 5 лет вперед, то можем ли мы предсказать денежные потоки с точностью до месяца/ до квартала/ до года?». На практике, как правило, первые 1-2 года поступления и выплаты можно спрогнозировать более точно, скажем ежемесячно, а в последующие года сроки денежных потоков могут быть определены, скажем, один раз в квартал.
Примечание3
. Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.
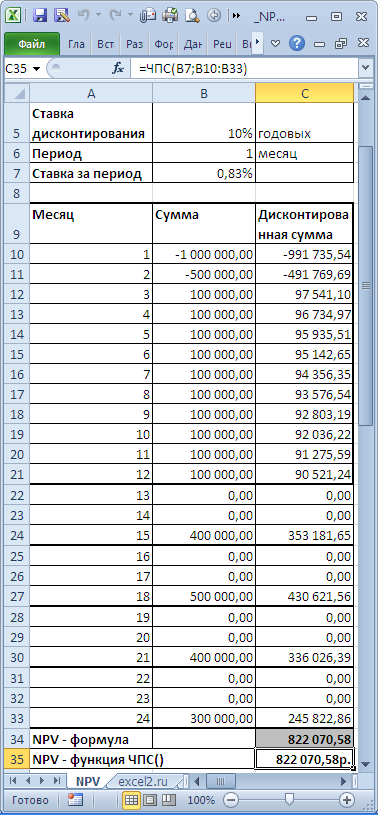
Определившись со сроками денежных потоков, для функции
ЧПС()
нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см.
файл примера, лист NPV
).
В таблице NPV подсчитан двумя способами: через функцию
ЧПС()
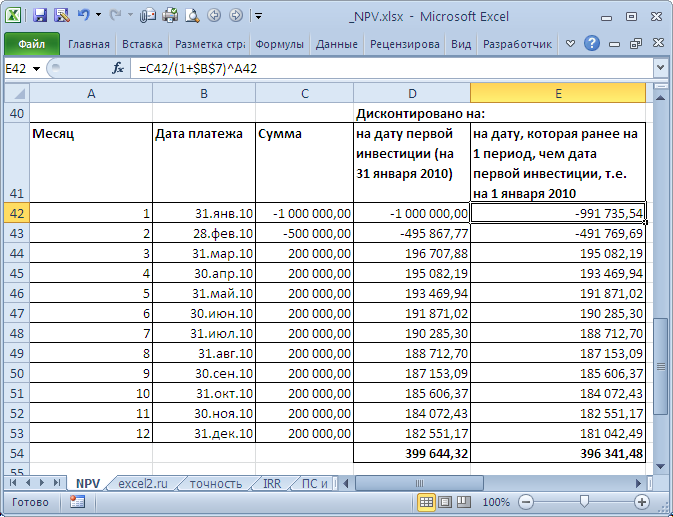
и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции
ЧПС()
, а нужно просто прибавить к получившемуся результату (см.
файл примера
). Сравнение 2-х вариантов дисконтирования приведено в
файле примера
, лист NPV:
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см.
файл примера, лист Точность
).
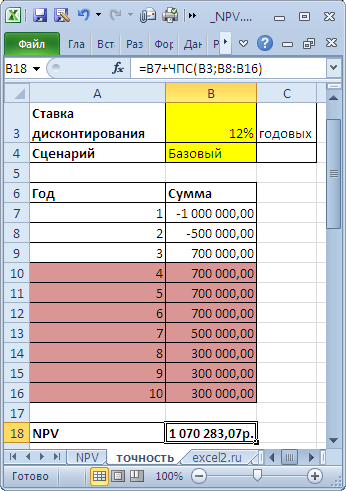
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
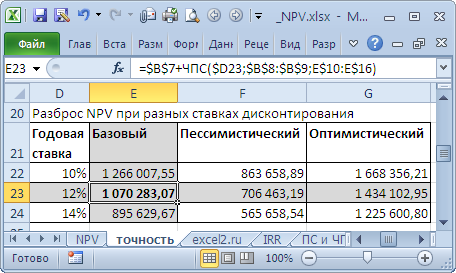
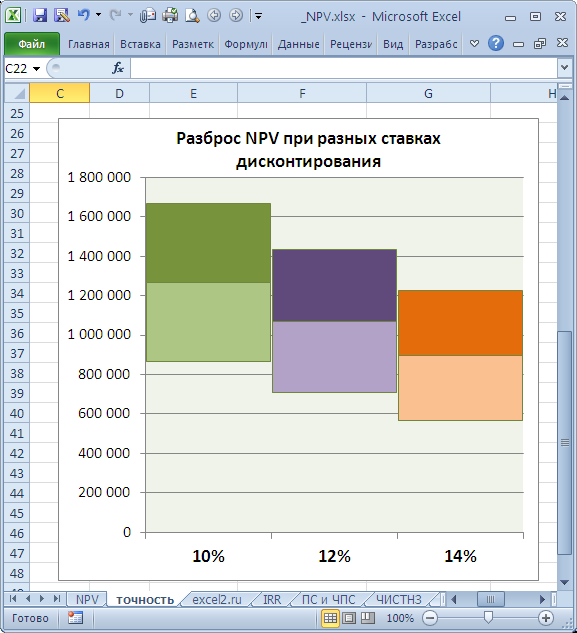
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
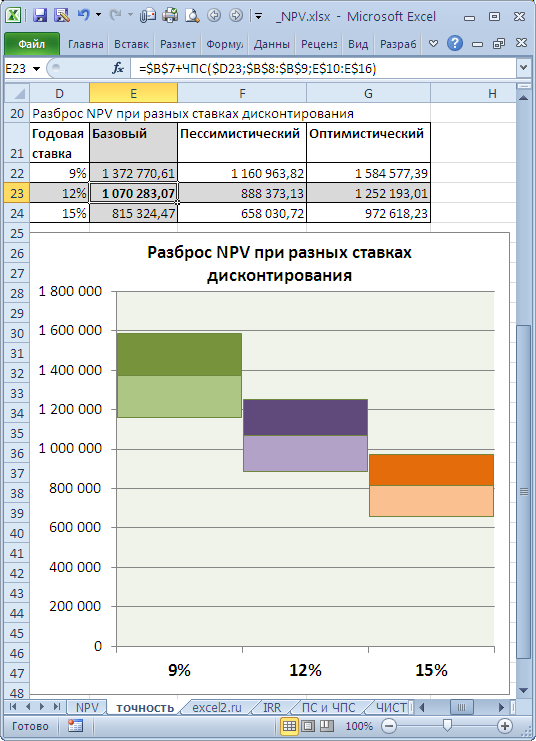
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
Внутренняя ставка доходности
IRR
(ВСД)
Внутренняя ставка доходности (англ.
internal rate of return
, IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см.
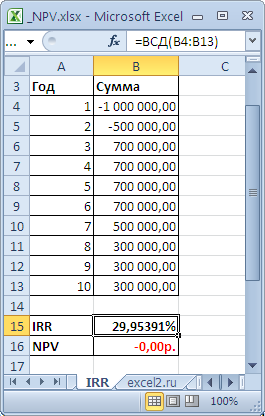
файл примера, лист IRR
).
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
Для расчета IRR используется функция
ВСД()
(английский вариант – IRR()). Эта функция тесно связана с функцией
ЧПС()
. Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией
ВСД()
, всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле:
=ЧПС(ВСД(B5:B14);B5:B14)
Примечание4
. IRR можно рассчитать и без функции
ВСД()
: достаточно иметь функцию
ЧПС()
. Для этого нужно использовать инструмент
Подбор параметра
(поле «Установить в ячейке» должно ссылаться на формулу с
ЧПС()
, в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Напомним, что
аннуитет
представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию
ПС()
(см.
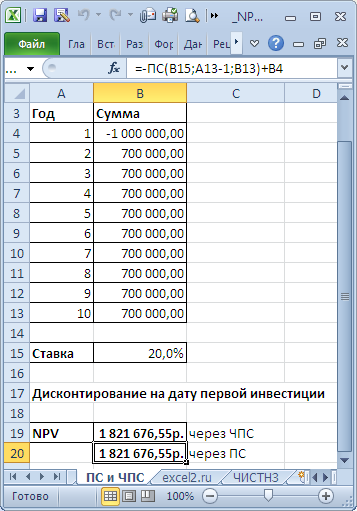
файл примера, лист ПС и ЧПС
).
В этом случае все денежные потоки (диапазон
В5:В13
, 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке
В4
. Ставка дисконтирования расположена в ячейке
В15
со знаком минус. В этом случае формула
=B4+ЧПС(B15;B5:B13)
дает тот же результат, что и
= B4-ПС(B15;9;B13)
Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за
любые
промежутки времени, то используется функция
ЧИСТНЗ()
(английский вариант – XNPV()).
Функция
ЧИСТНЗ()
возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.
Принципиальным отличием от
ЧПС()
является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у
ЧИСТНЗ()
всегда годовая, т.к. указана база 365 дней, а не за период, как у
ЧПС()
. Еще отличие от
ЧПС()
: все денежные потоки всегда дисконтируются на дату первого платежа.
В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций
ЧИСТНЗ()
и
ЧПС()
. Эти функции возвращают несколько отличающиеся результаты. Для задачи из
файла примера, Лист ЧИСТНЗ
разница составила порядка 1% (период = 1 месяцу).
Это связано с тем, что у
ЧИСТНЗ()
длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у
ЧПС()
указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет
високосного
года).
Внутренняя ставка доходности ЧИСТВНДОХ()
По аналогии с
ЧПС()
, у которой имеется родственная ей функция
ВСД()
, у
ЧИСТНЗ()
есть функция
ЧИСТВНДОХ()
, которая вычисляет годовую ставку дисконтирования, при которой
ЧИСТНЗ()
возвращает 0.
Расчеты в функции
ЧИСТВНДОХ()
производятся по формуле:
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).
Примечание5
. Функция
ЧИСТВНДОХ()
используется для
расчета эффективной ставки по потребительским кредитам
.
Функция ПС возвращает приведенную к текущему моменту стоимость инвестиций. Очевидно, что деньги в будущем будут иметь ценность, отличную от настоящей. Функция ПС вычисляет сумму, которая на настоящий момент равноценна ряду будущих выплат. Вот ее синтаксис: ПС(ставка; кпер;плт;бс;тип ).
Аргументы финансовых функций
Пять основных финансовых функций Excel имеют много общих аргументов. Ниже перечислены типовые аргументы и их смысловое значение.
- Ставка. Процентная ставка, выплачиваемая по займу или используемая для дисконтирования будущих денежных потоков. Период, который охватывает процентная ставка, должен быть тем же, что и в параметрах Кпер и Плт.
- Кпер. Количество периодов. Это может быть количество платежей по займу или количество лет депозитного вклада. Количество периодов должно быть выражено в тех же единицах, которые используются в аргументах Ставка и Плт. К примеру, 30-летний заем с помесячными выплатами будет содержать 360 периодов. Именно это значение следует подставлять в параметр Кпер, а не 30.
- Плт. Размер одного платежа. В рассматриваемых финансовых функциях платежи должны иметь одинаковый размер во всех периодах, а периоды должны быть равнозначны. Величина платежа включает в себя как выплату по основному займу, так и выплату процентов.
- БС. Будущая стоимость инвестиции, рассчитанная на основе периодических постоянных (т.е. равных по величине) платежей и постоянной процентной ставки. Это последняя операция транзакции. Во многих случаях (например, при единовременном погашении займа) не существует будущей стоимости.
- ПС. Текущая приведенная стоимость инвестиции. Это первая операция транзакции, например, получение займа или вклад денег на депозит. Если транзакция состоит только из платежей, в ней может не существовать приведенной стоимости.
- Тип. Этот аргумент определяет время внесения платежей.
- Прбл. Приблизительное значение результата. При вычислении процентной ставки программе для получения результата может потребоваться выполнить множество итераций. Можно облегчить программе решение этой задачи, указав значение, близкое к ожидаемому результату.
Вычисление приведенной стоимости
В примере, приведенном ниже в этом разделе, вычисляется приведенное значение серии будущих выплат, иногда называемых ежегодной рентой. Если каждый год в течение десяти лет вносится платеж размером в 1200 долларов, то приведенная стоимость этих платежей составляет 6780,27 долларов: =ПС(,12;10;1200;0;0). Другими словами, если плательщик в настоящий момент предложит вам 6800 долларов, вам будет выгоднее их взять, чем получать в течение 10 лет по 1200 долларов. Если он предложит меньшую сумму, лучше подождать регулярных ежегодных платежей.
В приведенной выше формуле вы, наверное, заметили, что процентная ставка взята как бы ниоткуда. Функция ПС обычно используется для определения, сколько стоят на настоящий момент будущие выплаты. В этих ситуациях конкретная процентная ставка недоступна.
[stextbox id=»info»]Существует множество мнений относительно того, какую процентную ставку лучше использовать при определении приведенной стоимости. Выбор процентной ставки в значительной мере зависит от вас самих. Одни говорят, что нужно использовать текущую процентную ставку по банковским депозитам, другие утверждают, что нужно брать процентную ставку по инвестициям, не связанным с рисками, таким как казначейские облигации. В данном примере была использована процентная ставка по инвестициям в ценные бумаги.[/stextbox]
В приведенном выше примере была использована процентная ставка 12%. В результате получилось, что инвестиция размером в 6800 долларов принесет тот же доход, что и десятилетнее ожидание платежей по 1 200 долларов. Если плательщик предложит вам 7000 долларов немедленно, вы можете вложить их и получить лучший финансовый результат. Теперь давайте вернемся к таблицам и предположим, что у вас есть обязательства, по которым вы должны ежегодно выплачивать кому-то по 1200 долларов в течение 10 лет. Формула выглядит следующим образом: =ПС(,12;10;-1200;0;0).
Вместо входящего, в этой формуле использован исходящий денежный поток. Результат (-$6 780,27) также имеет знак, противоположный предыдущему примеру. В обоих примерах сумма платежей формирует всю транзакцию, поэтому будущей стоимости не существует. Также в примере использовано значение по умолчанию аргумента Тип. Аргументы БС и Тип не являются обязательными; они были включены в пример только для наглядности. На рис. 1 этот расчет показан в рабочей книге.
Рис. 1. Вычисление приведенной стоимости
[stextbox id=»alert»]Из соображений простоты в формулах примеров, приведенных в тексте, используются только константы. На практике чаще всего в аргументы функций подставляются ссылки на ячейки.[/stextbox]
Приведенная стоимость единовременной будущей выплаты
В предыдущих примерах мы имели дело с сериями последовательных регулярных выплат, однако иногда существует всего одна будущая единовременная выплата. В качестве примера представим себе, что некоторый богатый родственник решил дать вам 100 тысяч долларов, но вы не можете получить их до своего сорокалетия. Если сейчас вам 25 лет, приведенная стоимость будущего платежа составит 31524,17 долларов. Эта сумма получена с помощью следующей формулы: =ПС(,08;15;0;100000).
Таким образом, это будет единовременный платеж ровно через 15 лет. Если бы у вас были сейчас какие-либо деньги, вы смогли бы инвестировать их под 8% годовых. Так как периодических платежей не будет, аргумент Тип в формуле опущен. Результат формулы свидетельствует о том, что если бы у вас было сейчас 31524,17 долларов и вы бы инвестировали их под 8%, то через 15 лет получили бы сотню тысяч долларов (рис. 2).
Рис. 2. Приведенное значение будущей единовременной выплаты
Приведенная стоимость периодических платежей с суммой погашения
В некоторых случаях периодические платежи идут в одной связке с большой суммой единовременной выплаты в конце периода займа. В качестве примера предположим, что ваш родственник попросил вас инвестировать в его бизнес. Он предложил следующие условия: если вы внесете инвестицию в 50 тысяч долларов сейчас, то он будет вам выплачивать ежемесячно по 200 долларов в течение пяти лет, после чего заплатит единовременным платежом еще 60 тысяч долларов. Чтобы определить, имеет ли такая инвестиция для вас смысл, найдите приведенную стоимость всех выплат: =ПС(,1/12;60;200;60000/1).
Рис. 3. Вычисление приведенной стоимости будущих платежей с погашением
Давайте внимательно посмотрим на каждый из аргументов (рис. 3).
- Вы определили, что при любых обстоятельствах сможете получить прибыль в 10% годовых, используя свои деньги в течение пяти лет. По этой причине процентную ставку мы установили в 10%.
- Все аргументы должны охватывать один и тот же временной период. Так как выплаты будут осуществляться ежемесячно, все аргументы должны быть преобразованы соответствующим образом:
- аргумент Ставка делим на 12 месяцев;
- аргумент Кпер получаем, умножив 5 лет на 12 месяцев в году;
- аргументы Плт и БС оставляем без изменений;
- аргументу Тип присваиваем значение 1, так как предполагается, что первый платеж будет совершен немедленно.
Из этой формулы выходит, что приведенная стоимость всех будущих выплат составляет 46698,82 доллара. Следовательно, можно сделать вывод: лучше вложить свои пятьдесят тысяч долларов в какое-либо другое предприятие, чем на данных условиях отдать родственнику.
Подставляя в аргументы функции различные значения, можно найти нужное решение. Данный результат вы можете выставить в качестве контрпредложения. При этом вы даже можете воспользоваться функцией подбора параметра программы Excel. Для этого выберите команду Данные → Работа с данными → Анализ «что если’ → Подбор параметра. Эта функция поможет подобрать такие значения аргументов, при которых приведенная стоимость будущих выплат составит нужную вам сумму.
Содержание
- Предварительные данные о чистой приведенной стоимости
- Особенности использования функции ЧПС
- Пример расчета чистой приведенной стоимости
Расчет чистой приведенной стоимости в Excel подводит закономерный итог нашим обстоятельным публикациям, посвященным теме приведенной стоимости вообще и чистой приведенной стоимости (NPV) – в частности.
Помимо специальных калькуляторов и таблиц, наиболее эффективным на текущий момент представляется расчет чистой приведенной стоимости именно средствами Excel, хотя бы потому, что это легко, удобно и отвечает современным представлениям об эффективных расчетах.
В сегодняшней статье мы разберем стандартную функцию ЧПС, используемую для нахождения значений чистой приведенной стоимости в таблицах Microsoft Excel, уделив внимание ее синтаксису и приведя несколько наглядных примеров ее практического применения.
Предварительные данные о чистой приведенной стоимости
Освежить свои представления о приведенной и чистой приведенной стоимости можно соответственно здесь и здесь.
Ради экономии вашего (прежде всего) времени ограничусь лишь напоминанием общеизвестной формулы, которую нам придется впоследствии увязывать со стандартной функцией Excel.
Как мы помним, когда речь идет о расчете чистой приведенной стоимости n-ного количества денежных потоков, мы прибегаем к помощи следующей весьма изящной математической конструкции:
Здесь Pi обозначает численное значение денежного потока (которое, кстати говоря, может иметь и отрицательное значение, когда речь идет об оттоках денежных средств), а r – некоторая процентная ставка (ставка дисконтирования).
Разработчики Excel позаботились о том, чтобы предельно упростить стоящую перед нами задачу расчета данного показателя, разработав функцию ЧПС, имеющую следующий формат:
=ЧПС (r, P1, P2, …).
Обязательными в этой функции являются только два параметра: r – размер процентной ставки и P1 – денежный поток в 1-ом периоде. Остальными параметрами можно пренебречь.
Всего формула позволяет обработать 254 значения Pi.
Значения P1, P2, …, Pnмогут быть положительными (в случае ПОСТУПЛЕНИЯ денежных средств) или отрицательными (когда имеют место будущие ВЫПЛАТЫ).
В свою очередь, результат функции ЧПС будет напрямую зависеть от исследуемых эмпирических данных и, как следствие, может принимать как положительные, так и отрицательные значения.
Особенности использования функции ЧПС
Ввести одномоментно 254 значения в одну ячейку бывает весьма утомительно.
Лучше заранее заполнить численными значениями некоторый диапазон, а затем подставлять в формулу ЧПС ссылки на входящие в диапазон ячейки.
Такой подход позволит легко комбинировать данные и исправлять возможные ошибки.
Следует помнить, что для расчета функции ЧПС важен ПОРЯДОК, в котором следуют значения P1, P2, …, Pn. Изменение этого порядка приведет к разным значениям нашей функции.
Предполагается также, что расчет производится для случая, когда выплаты или поступления отстоят друг от друга на один и тот же период (неделя, месяц, год и т.д.), то есть имеет место равномерное распределение денежных потоков во времени.
Все аргументы должны иметь численный формат. Ошибочно введенные в формулу ЧПС буквенные значения или символы при расчетах будут проигнорированы.
Пример расчета чистой приведенной стоимости
Не смею больше испытывать ваше терпение и предлагаю немедля окунуться в завораживающий мир расчета чистой приведенной стоимости с помощью функции ЧПС.
Итак, обещанный пример. Внимательно смотрим на иллюстрацию ниже:
Организуйте на листе вашей таблицы Excel размещение данных, аналогичных вышеприведенным.
Здесь важно заполнить ячейки A1, A2, A3, A4 и A5 конкретными числовыми данными, а в ячейку A7 поместить (важен каждый символ) выражение =ЧПС(A1; A2; A3; A4; A5).
Значение ячейки A7 как раз и будет содержать результат вычисления чистой приведенной стоимости ряда A2:A5.
Соответствующий диапазон, естественно, вы можете расширить или сузить, как вам заблагорассудится, а результирующее значение поместить в любую другую удобную для вас ячейку.
Здесь главное – понять принцип.
Обратите внимание, что значение в ячейке A3 имеет отрицательное значение (-5350).
Это означает, что имеет место выплата денежных средств (что в данном случае соответствует размеру первоначальных инвестиций).
Значения всех следующих аргументов являются положительными, так как мы имеем дело с поступлениями, символизирующими отдачу от наших инвестиций.
Заметим также, что наша функция в ячейке A7 может иметь и более краткий вид: =ЧПС(A1; A2:A5).
Такая запись соответствует синтаксическим стандартам Excel и позволяет сэкономить в ряде случаев и время, и нервы…
Итоговое значение (4110,00р) в денежном формате отображено во все той же ячейке A7.
Обязательно ВРУЧНУЮ проработайте приведенный выше пример.
Вы получите очень важный навык расчета реального финансового показателя – чистой приведенной стоимости – с помощью таблиц Excel.
Если вы планируете серьезно погрузиться в мир инвестиций, вам придется кое-что уметь и кое в чем разбираться.
Умение считать не на бумажке, а с использованием современного программного обеспечения – один из таких навыков.
Дополнительная информация по теме представлена в статье Расчет NPV в Excel (пример).
Удачных инвестиций!
Present value (PV) is the current value of an expected future stream of cash flow. Present value can be calculated relatively quickly using Microsoft Excel.
The formula for calculating PV in Excel is =PV(rate, nper, pmt, [fv], [type]).
Key Takeaways
- Present value (PV) is the current value of a stream of cash flows.
- PV analysis is used to value a range of assets from stocks and bonds to real estate and annuities.
- PV can be calculated in Excel with the formula =PV(rate, nper, pmt, [fv], [type]).
- If FV is omitted, PMT must be included, or vice versa, but both can also be included.
- NPV is different from PV, as it takes into account the initial investment amount.
Formula for PV in Excel
Again, the formula for calculating PV in Excel is
=PV(rate, nper, pmt, [fv], [type]).
The inputs for the present value (PV) formula in excel includes the following:
- RATE = Interest rate per period
- NPER = Number of payment periods
- PMT = Amount paid each period (if omitted—it’s assumed to be 0 and FV must be included)
- [FV] = Future value of the investment (if omitted—it’s assumed to be 0 and PMT must be included)
- [TYPE] = When payments are made (0, or if omitted—assumed to be at the end of the period, or 1—assumed to be at the beginning of the period)
Some keys to remember for PV formulas is that any money paid out (outflows) should be a negative number. Money in (inflows) are positive numbers.
NPV vs. PV Formula in Excel
While you can calculate PV in Excel, you can also calculate net present value (NPV). Present value is discounted future cash flows. Net present value is the difference between PV of cash flows and PV of cash outflows.
The big difference between PV and NPV is that NPV takes into account the initial investment. The NPV formula for Excel uses the discount rate and series of cash outflows and inflows.
Key differences between NPV and PV:
- The PV formula in Excel can only be used with constant cash flows that don’t change.
- NPV can be used with variable cash flows.
- PV can be used for regular annuities (payments at the end of the period) and annuities due (payments at the beginning of the period).
- NPVs can only be used for payments or cash flows at the end of the period.
Example of PV Formula in Excel
If you expect to have $50,000 in your banking account 10 years from now, with the interest rate at 5%, you can figure out the amount that would be invested today to achieve this.
You can label cell A1 in Excel «Years.» Besides that, in cell B1, enter the number of years (in this case 10). Label cell A2 «Interest Rate» and enter 5% in cell B2 (0.05). Now in cell A3, label it “Future Value” and put $50,000 into cell B3.
The built-in function PV can easily calculate the present value with the given information. Enter «Present Value» into cell A4, and then enter the PV formula in B4, =PV(rate, nper, pmt, [fv], [type], which, in our example, is «=PV(B2,B1,0,B3).»
Since there are no intervening payments, 0 is used for the «PMT» argument. The present value is calculated to be ($30,695.66), since you would need to put this amount into your account; it is considered to be a cash outflow, and so shows as a negative. If the future value was shown as an outflow, then Excel will show the present value as an inflow.
PV in Excel.
Special Considerations
For the PV formula in Excel, if the interest rate and payment amount are based on different periods, adjustments must be made. A popular change that’s needed to make the PV formula in Excel work is changing the annual interest rate to a period rate. That’s done by dividing the annual rate by the number of periods per year.
For example, if your payment for the PV formula is made monthly then you’ll need to convert your annual interest rate to monthly by dividing by 12. As well, for NPER, which is the number of periods, if you’re collecting an annuity payment monthly for four years, the NPER is 12 times 4, or 48.
What Is the Difference Between Present Value (PV) and Future Value (FV)?
Present value uses the time value of money to discount future amounts of money or cash flows to what they are worth today. This is because money today tends to have greater purchasing power than the same amount of money in the future. Taking the same logic in the other direction, future value (FV) takes the value of money today and projects what its buying power would be at some point in the future.
Why Is Present Value Important?
Present value is important in order to price assets or investments today that will be sold in the future, or which have returns or cash flows that will be paid in the future. Because transactions take place in the present, those future cash flows or returns must be considered but using the value of today’s money.
When Might You Need to Calculate Present Value?
Present value calculations are quite common. Any asset that pays interest, such as a bond, annuity, lease, or real estate, will be priced using its net present value. Stocks are also often priced based on the present value of their future profits or dividend streams using discounted cash flow (DCF) analysis.
На чтение 7 мин Просмотров 23.6к.
Приведенную стоимость рассчитывают с целью определения сегодняшней цены инвестиций, доход от которых будет получен в будущем периоде. То есть, показатель отражает текущую стоимость активов с учетом доходности.
Содержание
- Понятие приведенной стоимости
- Зачем рассчитывают приведенную стоимость
- Расчет приведенной стоимости
- Формула для вычисления приведенной стоимости
- Пошаговый алгоритм расчета приведенной стоимости
- Пример вычисления приведенной стоимости
- Альтернативные методы расчета приведенной стоимости
- Расчет приведенной стоимости в Excel
Понятие приведенной стоимости
Приведенная стоимость (далее ПД) представляет собой значение доходности вложений на сегодняшний день. Если говорить простыми словами, приведенная стоимость – это объем денежных средств, которые инвестор получит в будущем периоде, переведенный в стоимость на сегодняшний день.
Кроме понятия «приведенная стоимость», в экономике существует такой термин, как «чистая приведенная стоимость» (далее ЧПД). ЧПД – это совокупность финансовых оборотов от вложений, переведенных в стоимость на момент проведения анализа.
Чистая приведенная стоимость отличается от ПД тем, что при определении первого показателя учитываются первоначальные финансовые вложения. То есть, сумма, которую компания инвестировала для получения дохода, отнимается из будущей стоимости актива, приведенной к значению на сегодняшний день.
Зачем рассчитывают приведенную стоимость
Приведенную стоимость рассчитывают с целью определения объема денежных средств, которые инвестор получит в будущем в стоимостной оценке на дату проведения анализа. Например, сегодня компания вложила 1 млн. рублей в развитие проекта. Неизвестно, сколько предприятие получит от реализации программы. Однако данное значение можно вычислить при помощи формулы расчета приведенной стоимости.
Как правило, в будущем денежные средства имеют совсем иную цену, в сравнении с днем сегодняшним. А особенностью вычисления приведенной стоимости считается тот факт, что анализ отражает сумму дохода в стоимости на сегодняшний день. Для этого будущий доход дисконтируется.
Расчет приведенной стоимости
Расчет приведенной стоимости значительно отличается от вычисления будущей доходности. Для того, чтобы вычислить приведенную стоимость, для начала, необходимо найти будущую доходность. Именно от этой суммы отталкивается аналитик, производящий анализ. Будущая стоимость в дальнейшем приводится к сегодняшнему значению путем дисконтирования.
Важно! Результат расчета приведенной стоимости показывает не сумму средств, которую инвестор получит в будущем, а объем финансов, необходимых для инвестирования.
То есть, вычисляя показатель ПС, сначала нужно понять, сколько инвестор хочет заработать от вложений. Затем можно приступать к расчетам при помощи арифметической формулы. Итог анализа – это и есть сумма, которой компания должна располагать на сегодняшний день, чтобы получить задуманный объем дохода.
Формула для вычисления приведенной стоимости
Анализ приведенной стоимости строится на расчете показателя. Его вычисление реализуется при помощи формул. Вид арифметического выражения напрямую зависит от метода начисления процентов: простого или сложного:
- Метод простых процентов предполагает расчет приведенной стоимости в традиционном порядке. Объем ожидаемых доходов дисконтируют в обычном порядке.
- Прием сложных процентов предполагает присоединение суммы процентов прошлого периода к общему объему финансов. Данную операцию в экономической теории называют капитализацией.
В связи с этим, каждый период денежный поток, поддающийся дисконтированию, должен быть разным:
| Метод определения приведенной стоимости | Формула | Расшифровка формулы |
| Простые проценты | БС / (1 + СД)н | БС – будущая стоимость;
СД – ставка дисконтирования; Н – число периодов инвестирования |
| Сложные проценты | БС / (1 + СДп)н*м | БС – будущая стоимость;
СДп – ставка дисконтирования за период; Н – число периодов инвестирования; М – число капитализаций в год |
Важно! Оценивая результаты расчета приведенной стоимости методом простых и сложных процентов, нужно опираться на наименьший результат. Это означает, что для получения одной и той же суммы дохода компании придется вложить меньше собственных средств.
Кроме ПС, можно определить показатель чистой приведенной стоимости. Вычисления проводятся также при помощи формулы:
(БС / (1 + СД)н) – ПИ,
где БС – будущая стоимость (предполагаемый доход);
СД – ставка дисконтирования (процентная ставка по договору);
Н – число периодов инвестирования;
ПИ – объем первоначальных вложений.
Таким образом, чистая приведенная стоимость — это ПС за исключением суммы инвестирования в проект.
Пошаговый алгоритм расчета приведенной стоимости
Для расчета ПС рекомендуется использовать пошаговую инструкцию, которая поможет избежать ошибок:
- Определяем период инвестирования. То есть, промежуток времени, через который инвестор планирует получить определенный доход.
- Вычисляем объем прибыли от инвестирования при условии соблюдения договора. Обычно показатель берется из документации по планированию.
- Находим ставку дисконтирования. Она определяется путем деления процентной ставки доходности на 100. В случае применения методики сложных процентов, определяем число случаев капитализации за 1 год.
- Рассчитываем приведенную стоимость путем замены буквенных выражений формулы на соответствующие числовые значения.
Сам процесс вычисления не сложен. Труднее исключить допущение ошибок, так как будущую доходность принято считать путем сложения денежных потоков.
Пример вычисления приведенной стоимости
Приведем пример вычисления приведенной стоимости на основании следующих условий. Компания планирует получить доход 1 млн. рублей от помещения денежных средств на депозит сроком на 5 лет. Банк предлагает два варианта начисления процентов: сложный (12% годовых) и простой (10% годовых). Перед заключением договора необходимо выбрать оптимальный метод. Для этого рассчитывается приведенная стоимость приемом сложных и простых процентов.
В первую очередь, определим приведенную стоимость методом простых процентов:
1 млн. руб. / (1 + 0,1)5 = 951465, 68 руб.
Таким образом, чтобы через 5 лет получить доход в размере 1 млн. рублей под 10% годовых, необходимо вложить 951465, 68 рублей. Теперь найдем приведенную стоимость методом сложных процентов. Допустим, проценты начисляются каждый месяц, пополнений не предусмотрено:
1 млн. руб. / (1 + 0,12 / 12)5 * 12 = 550375,73 руб.
Получается, что вложив 550375,73 руб. под сложные проценты 12% годовых, через 5 лет компания сможет иметь доход 1 млн. рублей Таким образом, гораздо выгоднее поместить средства на депозит под сложные проценты, так как при условии получения одинакового дохода за аналогичный промежуток времени необходимо вложить гораздо меньше средств.
Чтобы рассчитать чистую приведенную стоимость, из ожидаемого дохода нужно отнять рассчитанный показатель ПС:
- ЧПС методом простых процентов: 1 млн. руб. – 951465,68 руб. = 48534,32 рубля;
- ЧПС методом сложных процентов: 1 млн. руб. – 550375,73 = 449624,27 рублей.
Таки образом, можно сделать вывод о том, что чистая приведенная стоимость методом сложных процентов гораздо выше, чем при альтернативном варианте.
Альтернативные методы расчета приведенной стоимости
Альтернативным методом расчета приведенной стоимости является автоматизированный прием, основанный на использовании специализированных программ. Существует масса сервисов, которые помогают безошибочно рассчитать показатель. Если подобных инструментов нет, можно использовать стандартный Excel.
Excel – это программа, входящая в стандартный пакет Microsoft Office. Сервис наделен множествами функций, которые позволяют безошибочно проводить расчеты в автоматическом режиме по заданным параметрам. Главная сложность использования Excel заключается в неумении пользователей применять встроенные сервисы.
Основным достоинством расчета приведенной стоимости в Excel является то, что программа имеет функцию вычисления данного показателя. Поэтому нет необходимости вводить формулу. Достаточно выбрать инструмент и выделить участвующие в расчете ячейки.
Расчет приведенной стоимости в Excel
Вычисление приведенной стоимости в Excel производится при помощи встроенного инструмента. Нет необходимости вводить сложные формулы. Достаточно выбрать опцию и отразить ячейки, принимающие участие в анализе. Определение ПС в Excel имеет следующий алгоритм:
- создаем таблицу (начиная с 4 и далее строки), состоящую из трех столбцов – период, сумма периода и приведенная стоимость;
- в ячейках первого столбца отражаем последовательность периодов, в ячейках второго – сумму денежных потоков;
- третий столбец посвящен приведенной стоимости по временным промежуткам;
- чуть выше таблицы, например, в первой строке, прописываем значение ставки дисконтирования, во второй – итоговое значение приведенной стоимости, но ячейка, посвященная результату показателя, будет пустой;
- итоговую приведенную стоимость также необходимо отобразить в заключительной ячейке столбца показателя;
- после того, как все данные введены, можно приступать к указанию формул.
Положительной особенностью Excel является тот факт, что программа имеет встроенный инструмент для расчета приведенной стоимости. Достаточно найти функцию и выделить ячейки, необходимые для расчета. Сама формула для вычисления и результат сформируются автоматически.
Важно! Для расчета чистой приведенной стоимости отражение временных промежутков нужно начинать с нулевого года с отрицательным значением суммы инвестиций.
В дальнейшем, автоматически сформированную формулу нужно видоизменить, добавив сумму ячейки первоначальных вложений. Конечный результат ПС должен быть всегда положительным.
Содержание
- Что такое NPV простыми словами
- Зачем нужен показатель NPV
- Формула расчета NPV
- Экономический смысл показателя NPV
- Значение ставки дисконтирования при расчёте NPV
- Расчет приведенной стоимости денежного потока в Excel
- Применение приведённой NPV на практике
- Плюсы и недостатки
- Тщательный анализ результата
- Вычисление приведенной стоимости
- Приведенная стоимость единовременной будущей выплаты
- Прогнозирование денежного потока в Excel
- Срок окупаемости в Excel: пример расчёта
- Алгоритм и формула расчета ЧДД
- ЧДД проектов: какой выбрать
- Анализ полученных результатов
- Как проводить анализ результатов
- Что такое чистая приведенная стоимость и правило чистой приведенной стоимости?
- Определите все денежные потоки, связанные с инвестициями – все притоки и оттоки.
- Определите соответствующую ставку дисконтирования или ставку альтернативной доходности r для инвестиционного проекта.
- Используя эту ставку дисконтирования, найдите текущую (приведенную) стоимость (PV) каждого денежного потока.
- Суммируйте все приведенные значения стоимости.
- Примените правило чистой приведенной стоимости.
- Простые проценты
- Сложные проценты
- Сложные проценты (несколько сумм)
Что такое NPV простыми словами
NPV называют чистую стоимость денежных потоков, приведенную к моменту расчета проекта. Благодаря формуле расчета NPV удается оценить собственную экономическую эффективность проекта и сравнить между собой несколько объектов инвестирования.
Английская аббревиатура NPV (Net Present Value) имеет в русском языке несколько аналогов:
- Чистая приведенная стоимость (ЧПС). Этот вариант является наиболее распространенным, даже в «Microsoft Excel» формула называется именно таким образом.
- Чистый дисконтированный доход (ЧДД). Название связано с тем, что денежные потоки дисконтируются и лишь после этого суммируются.
- Чистая текущая стоимость (ЧТС). Все доходы и убытки от деятельности за счет дисконтирования приводятся к текущей стоимости денег. Поясним: с точки зрения экономики, если мы заработаем 1000 руб., то получим потом на самом деле меньше, чем если бы мы получили ту же сумму прямо сейчас.
Дисконтирование — это определение стоимости денежного потока путём приведения стоимости всех выплат к определённому моменту времени. Дисконтирование является базой для расчётов стоимости денег с учётом фактора времени.
NPV представляет собой уровень прибыли, который ожидает участников инвестиционного проекта. Математически этот показатель определяют за счет дисконтирования значений чистого денежного потока, при этом неважно, о каком потоке идет речь: отрицательном либо положительном.
Чистый дисконтированный доход можно рассчитать за любой период времени проекта с его начала (за 5, 7 лет, 10 лет, пр.) – все зависит от необходимости.
Если максимально упростить определение, то NPV – это доход, который получит владелец проекта за период планирования, оплатив все текущие затраты и рассчитавшись с налоговыми органами, персоналом, кредитором (инвестором), в том числе выплатив проценты (или с учетом дисконтирования).
Допустим, за 10 лет планирования предприятие получило выручку в 5,57 млрд руб., тогда как общая сумма налогов и всех затрат равна 2,21 млрд руб. Значит, сальдо от основной деятельности окажется 3,36 млрд руб.
Но это пока не искомый результат – из данной суммы нужно вернуть первоначальные инвестиции, допустим, 1,20 млрд руб. Чтобы упростить подсчет, будем считать, что проект финансируется за счет средств инвестора по нулевой ставке дисконтирования. Тогда, если рассчитать показатель NPV, он составит 2,16 млрд руб. за 10 лет планирования.
Если увеличить срок планирования, то увеличится и размер ЧДД. Смысл этого показателя в том, что он позволяет рассчитать еще на этапе разработки бизнес-плана, какой реальный доход может получить инициатор проекта.
Повторим, что NPV – один из ключевых показателей оценки эффективности инвестиционных проектов. Поэтому если рассчитать его даже с малейшей неточностью, можно столкнуться с потенциально неэффективным вложением средств.
Зачем нужен показатель NPV
Если у вас на примете есть перспективный бизнес-проект, в который вы готовы вложить деньги, советуем рассчитать его чистую приведенную стоимость.
Как рассчитать NPV проекта? Используйте такой порядок действий:
- Оцените денежные потоки от проекта, то есть первоначальное вложение (отток) и ожидаемые поступления (притоки) денежных средств.
- Определите стоимость капитала (cost of capital), так как этот показатель станет для вас ставкой дисконтирования.
- Продисконтируйте притоки и оттоки от проекта по ставке, которую вам удалось рассчитать на предыдущем шаге.
- Сложите все дисконтированные потоки – это и будет NPV проекта.
Далее можете принимать решение об инвестициях, но помните: в проект стоит вкладываться при NPV больше нуля, если же этот показатель ниже нуля, лучше отказаться от своей задумки.
На самом деле, все просто – если NPV равен нулю, значит, денежных потоков от проекта хватит, чтобы:
- возместить инвестированный капитал;
- обеспечить доход на этот капитал.
При положительном NPV проект принесет прибыль, и чем выше его уровень, тем выгоднее окажутся вложения в проект.
Кредиторы, то есть люди, дающие деньги в долг, имеют фиксированный доход, поэтому все средства, превышающие этот показатель, остаются акционерам. Если компания решает одобрить проект с нулевым NPV, акционеры сохранят свою позицию – компания станет больше, но акции не поднимутся в цене. При положительном NPV проекта акционеры станут богаче.
NPV позволяет рассчитать, какой из инвестиционных проектов выгоднее, когда их несколько, но компания не имеет средств на реализацию сразу всех. В этом случае приступают к проектам с наибольшей возможностью заработать или с самым высоким NPV.
Сегодня нужно просто рассчитать NPV, чтобы оценить выгодность инвестиционных проектов. Среди достоинств этого показателя аналитики называют:
- четкие критерии принятия решения об инвестировании – первоначальные инвестиции, выручка на каждом этапе, доходность альтернативных вложений;
- учет изменения стоимости денег с течением времени;
- учет рисков за счет использования различных ставок дисконтирования.
Но не стоит заблуждаться и считать этот показатель абсолютно точным коэффициентом. Нередко сложно корректно рассчитать ставку дисконтирования, особенно когда речь идет о многопрофильных проектах. Также отметим, что при расчете не учитывается вероятность исхода каждого проекта.
Формула расчета NPV
Как рассчитать чистый дисконтированный доход NPV? Казалось бы, все просто: нужно вычесть из всех притоков денежных средств все оттоки по каждому временному отрезку, после чего привести полученные значения к моменту расчета.
Но рассчитать этот показатель невозможно без формулы:

Где:
- IC – сумма первоначальных инвестиций;
- N – число периодов (месяцев, кварталов, лет), за которые нужно рассчитать оцениваемый проект;
- t – отрезок времени, для которого необходимо рассчитать чистую приведенную стоимость;
- i – расчетная ставка дисконтирования для оцениваемого варианта вложения инвестиций;
- CFt – ожидаемый денежный поток (чистый) за установленный временной период.
Экономический смысл показателя NPV
Если рассматривать показатель более глубоко, можно констатировать, что это результирующая величина, полученная при учёте всех исходящих и входящих денежных поступлений анализируемого инвестиционного проекта, приведённая ко времени выполнения подобного анализа.
Полученное значение даёт инвестору представление о том, на что он может рассчитывать при вложении (с учётом погашения первоначальных затрат, понесённых на начальном этапе развития проекта и периодических оттоков в процессе его реализации).
Благодаря тому, что все денежные потоки рассчитываются с учётом рисков и временной стоимости, величину NPV инвестиционного проекта можно охарактеризовать, как стоимость, которая добавляется проектом, либо как совокупную прибыль инвестора.
Главной целью любого бизнеса является получение прибыли.
Для того, чтобы не инвестировать в рисковые проекты, инвестор проводит предварительную оценку возможных вариантов инвестирования. Причём все такие предложения на стадии их предварительно изучения оцениваются в сравнении с доходностью безрисковых вложений (банковский депозит).
Для понимания алгоритма расчёта чистой приведённой стоимости следует учитывать, что в его основу положена методология дисконтирования всех имеющихся денежных потоков. Именно поэтому решение о инвестировании в тот или иной проект принимается после его предварительного расчёта NPV проекта, в рамках которого:
- оцениваются все ожидаемые притоки и оттоки капитала за расчётный период;
- определяется его стоимость (для инвестора эта величина рассматривается в качестве ставки дисконтирования);
- с учётом упомянутой ставки дисконтируются все поступающие и истекающие потоки;
- результаты суммируются. Полученный результат и является величиной приведённой стоимости проекта.
Полученное число может иметь такие значения.
NPV = 0. Это информирует инвестора, что у него имеется вероятность вернуть вложенные средства с минимальной прибылью.
NPV < 0. Подобные инвестиционные проекты дальнейшему рассмотрению не подлежат. NPV > 0. Вложение средств должно принести прибыль.
Значение ставки дисконтирования при расчёте NPV
Изучая чистую приведённую стоимость обязательно следует уделять серьёзное внимание показателю — ставка дисконтирования. Часто её именуют иначе — альтернативной стоимостью вложений. Показатель, используемый в формуле расчёта, обозначает минимальную величину доходности, которую инвестор считает для себя приемлемой при рисках, сопоставимых с имеющимися у реализуемого проекта.
Инвестор может оперировать средствами, привлекаемыми из различных источников (собственных либо заёмных).
1. В первом случае устанавливаемая ставка дисконтирования, является личной оценкой допустимых рисков рассматриваемого инвестиционного проекта.
Её оценка может иметь несколько подходов. Самые простые, это:
- Выбор безрисковой ставки, корректируемой с учётом вероятности возникновения специфических рисков.
В качестве таковой обычно рассматриваются доходность по ценным бумагам государства, в котором реализуется проект, ставка доходности по корпоративным облигациям компаний отрасли.
- Необходимая и минимально достаточная (с точки зрения потенциального инвестора) рентабельность (показатель ROE).
При этом, лицо, принимающее решение об инвестировании, определяет ставку дисконтирования по одному из возможных вариантов:
- в проект вкладываются средства, имеющиеся на депозите в конкретном банке. Следовательно, альтернативная стоимость не должна быть меньше имеющейся банковской ставки;
- В проект инвестируются средства, выведенные из бизнеса и являющиеся временно свободными. В случае возникновения потребности в них, оперативное изъятие всей суммы из проекта невозможно. Потребуется кредит. Поэтому в качестве текущей стоимости средств выбирается рыночная кредитная ставка;
- Средняя доходность основного бизнеса составляет Y%. Соответственно от инвестиционного проекта требуется получать не меньше.
2. При работе с заёмными средствами ставка будет рассчитана как величина производная от стоимости привлекаемых из различных источников средств.
Как правило ставка, устанавливаемая инвестором, в подобных случаях превышает аналогичный показатель стоимости заёмных денежных средств.
При этом не просто учитывается изменение стоимости средств во времени, но и закладываются возможные риски, связанные с неопределённостью поступления денежных потоков и их объёмов.
Это является главной причиной, по которой ставкой дисконтирования считают средневзвешенную стоимость привлекаемого для последующего инвестирования капитала (WACC).
Именно этот показатель рассматривается в качестве требуемой нормы доходности на средства, вложенные в конкретный инвестиционный проект.
Чем выше ожидаемые риски, тем выше ставка.
Расчётные методы определения данного параметра менее наглядны, чем графические. Особенно когда требуется сравнить привлекательность двух или более проектов.
Например, сравнивая проекты «А» и «Б» (смотри график) можно сделать следующие выводы:
При ставке, превышающей значение 7%, величина NPV проекта А выше, чем у Б (что предупреждает о возможной ошибке в выборе при арифметическом сопоставлении).
К тому же инвестиционный проект «Б», обозначенный на графике красной кривой, подвержен более значительным изменениям в связи с изменяющейся ставкой дисконтирования (такое может быть объяснено разновеликими величинами поступающих средств в одинаковый период времени).
Следует учитывать факт существенного снижения величины ставок дисконтирования во времени, что накладывает определённые временные ограничение. Рассчитать их можно не более, чем за 10 лет.
Анализ графиков позволяет сделать вывод о том, что меняющаяся ставка дисконтирования приводит к изменениям величины показателя NPV (причём последний меняется нелинейно).
Поэтому для более взвешенной оценки необходимо не просто сравнивать величины для разных инвестиционных проектов, но и учитывать изменения последних при разных величинах ставки.
По умолчанию при расчете в Excel, ставка дисконтирования принимается равной 10%.
Пример. Рассчитать значение чистой приведенной стоимости для финансовых потоков, представленных в таблице, с использованием функции ЧПС, сравнить данные, применив функцию ЧИСТНЗ, объяснить расхождения в полученных результатах.
Вид таблицы данных:

Вначале рассчитаем значение приведенной стоимости с использованием рассматриваемой функции:
В результате получим:

Если бы в табличном редакторе Excel отсутствовала формула ЧИСТНЗ, кроме ручного способа можно было бы рассчитать приведенную стоимость с помощью функции ЧПС следующим образом:
Поскольку функция ЧПС учитывает только платежи, к результатам ее вычислений добавлено значение первоначальных затрат (+C3).
Результат вычислений:

Как видно, результаты немного различны. Это обусловлено тем, что функция ЧИСТНЗ учитывает реальное количество дней в году (в високосном году дней больше на 1). Несмотря на то, что все платежи производились 2-го числа 11 месяца ежегодно, их нельзя считать периодичными, поскольку в списке дат есть високосный год и реальное число дней между 2.11.2016 и 2.11.2017 равен 366 дней. Функция ЧИСТНЗ в подобных расчетах дает более точный результат.
Применение приведённой NPV на практике
Универсальные формулы приведённой стоимости активно используют опытные и начинающие инвесторы. Такой подход помогает оценить целесообразность внесения финсредств. Эксперты рекомендуют использовать три варианта расчёта приведённой NPV:
- Если чистая стоимость в приведённый период =0, это указание, что инвестиции окупаются, но сам вкладчик не получит никакой прибыли. К примеру: если гражданин использовал кредитные деньги, то поступающие финпотоки благоприятствуют расчёту с кредитором полностью. Инвестор сможет выплатить все начисленные %, а сам счёт останется неизменным. Здесь лучше найти иные варианты вклада, с более оптимистичным приведённым результатом чистой итоговой стоимости.
- Когда при изучении приведённого показателя NPV было получено плюсовое значение стоимости, то инвестиция полностью окупается. А сама цифра отображает цифру прибыли вкладчика. Конечно, в этом случае инвестиции более чем оправданы, так как в итоге человек получает хорошую прибыль.
- В редких случаях после многочисленных расчётов стоимости выходит отрицательное значение приведённой цифры. В такой ситуации инвестиции пользователя не окупаются, а сам вкладчик остаётся с убытками. Если исследуемый проект с минусовым значением, от работы с ним правильнее отказаться.
К инвестпроектам могут относиться только те бизнес-идеи, у которых преобладают положительные значения цифр. Когда вкладчик не может определиться, тогда предпочесть лучше вариант с наибольшим показателем чистого приведённого NPV.
Плюсы и недостатки
Универсальный метод расчёта приведённой стоимости был разработан экспертами для того, чтобы каждый человек имел возможность получения итоговой прибыли. Но, как и у любого другого финансового инструмента, у чистого приведённого NPV есть выгодные и негативные стороны.
К основным преимуществам можно отнести:
- Проводить корректировку объёма финпотоков и приведённой стоимости во времени можно за счёт учёта дисконтставки проекта.
- Действуют простые однозначные правила, помогающие со сложными решениями, которые касаются инвестпривлекательности идеи.
- Можно ввести учёт премии за рисковую составляющую в составе дисконтставки. Стоит отметить, что для высокорисковых проектов допустимо использовать повышенный процент.
Несмотря на все вышеперечисленные преимущества, у чистого приведённого NPV есть и негативные стороны. Каждый специалист должен помнить о ряде ограничений:
- Неопытному человеку сложно спрогнозировать будущие денежные потоки. Если пользователь решил разобраться в столь ответственном этапе работы, то все полученные им расчёты должны быть точными, так как от этого зависит итоговый объём приведённого NPV.
- Трудно оценить сложные инвестпроекты. Особые сложности возникают из-за многочисленных рисков, которых очень много в долгосрочном горизонте. Специалист должен скорректировать дисконтставки.
- Приведённый NPV может использоваться только для отображения абсолютного показателя дохода. Чтобы результаты анализа были достоверными, нужно дополнительно рассчитывать относительные показатели (внутренней нормы по доходности, инвестрентабельности).
- Стандартная форма приведённого NPV не корректируется на реинвест финансовых потоков.
Тщательный анализ результата
Специалистами было разработана базовое правило, обязательное для оценки уровня КПД инвестиций — принять план-проект можно только в том случае, если итоговая величина имеет значение «+». Если же этот параметр «-», то рассматриваемый инвестиционный проект будет убыточным. Цифра «0» свидетельствует о том, что доходные потоки от реализуемой программы могут возместить затратную часть, без поступления прибыли.
Приведённый NPV напрямую связан с приведённой стоимостью (PV). Эксперты применяют эту терминологию для оценки интенсивности финпоступлений в будущие периоды, которые соотносятся с настоящим моментом дисконта. Вычисление чистого NPV чаще всего включает расчёт приведённой стоимости. Узнать параметр довольно просто, главное — использовать специальную формулу.
Такой подход позволяет узнать следующие данные: плотность, размещение средств, возвратность и единовременное погашение:
PV = FV / (1+ r), здесь:
- PV — это общая сумма финсредств для размещения на общих условиях срочности, плотности и возвратности.
- FV — сумма, которая может быть использована для погашения долга. Включает в себя размер займа, проценты.
- r — процентная ставка, используемая в качестве платы за те финансы, которые были взяты в кредит.
Вычисление приведенной стоимости
В примере, приведенном ниже в этом разделе, вычисляется приведенное значение серии будущих выплат, иногда называемых ежегодной рентой. Если каждый год в течение десяти лет вносится платеж размером в 1200 долларов, то приведенная стоимость этих платежей составляет 6780,27 долларов: =ПС(,12;10;1200;0;0). Другими словами, если плательщик в настоящий момент предложит вам 6800 долларов, вам будет выгоднее их взять, чем получать в течение 10 лет по 1200 долларов. Если он предложит меньшую сумму, лучше подождать регулярных ежегодных платежей.
В приведенной выше формуле вы, наверное, заметили, что процентная ставка взята как бы ниоткуда. Функция ПС обычно используется для определения, сколько стоят на настоящий момент будущие выплаты. В этих ситуациях конкретная процентная ставка недоступна.
Существует множество мнений относительно того, какую процентную ставку лучше использовать при определении приведенной стоимости. Выбор процентной ставки в значительной мере зависит от вас самих. Одни говорят, что нужно использовать текущую процентную ставку по банковским депозитам, другие утверждают, что нужно брать процентную ставку по инвестициям, не связанным с рисками, таким как казначейские облигации. В данном примере была использована процентная ставка по инвестициям в ценные бумаги.
В приведенном выше примере была использована процентная ставка 12%. В результате получилось, что инвестиция размером в 6800 долларов принесет тот же доход, что и десятилетнее ожидание платежей по 1 200 долларов. Если плательщик предложит вам 7000 долларов немедленно, вы можете вложить их и получить лучший финансовый результат. Теперь давайте вернемся к таблицам и предположим, что у вас есть обязательства, по которым вы должны ежегодно выплачивать кому-то по 1200 долларов в течение 10 лет. Формула выглядит следующим образом: =ПС(,12;10;-1200;0;0).
Вместо входящего, в этой формуле использован исходящий денежный поток. Результат (-$6 780,27) также имеет знак, противоположный предыдущему примеру. В обоих примерах сумма платежей формирует всю транзакцию, поэтому будущей стоимости не существует. Также в примере использовано значение по умолчанию аргумента Тип. Аргументы БС и Тип не являются обязательными; они были включены в пример только для наглядности. На рис. 1 этот расчет показан в рабочей книге.
Рис. 1. Вычисление приведенной стоимости
Из соображений простоты в формулах примеров, приведенных в тексте, используются только константы. На практике чаще всего в аргументы функций подставляются ссылки на ячейки.
Приведенная стоимость единовременной будущей выплаты
В предыдущих примерах мы имели дело с сериями последовательных регулярных выплат, однако иногда существует всего одна будущая единовременная выплата. В качестве примера представим себе, что некоторый богатый родственник решил дать вам 100 тысяч долларов, но вы не можете получить их до своего сорокалетия. Если сейчас вам 25 лет, приведенная стоимость будущего платежа составит 31524,17 долларов. Эта сумма получена с помощью следующей формулы: =ПС(,08;15;0;100000).
Таким образом, это будет единовременный платеж ровно через 15 лет. Если бы у вас были сейчас какие-либо деньги, вы смогли бы инвестировать их под 8% годовых. Так как периодических платежей не будет, аргумент Тип в формуле опущен. Результат формулы свидетельствует о том, что если бы у вас было сейчас 31524,17 долларов и вы бы инвестировали их под 8%, то через 15 лет получили бы сотню тысяч долларов.
Рис. 2. Приведенное значение будущей единовременной выплаты
Прогнозирование денежного потока в Excel
Заполните таблицу «Денежные потоки»:
- в ячейку В9 введите значение первоначальных инвестиций,
- в ячейку В10 — формулу «=B8-B9»
- в ячейку С8 введите сумму поступлений в первый год,
- в D8 – формулу «=C8*1,3»,
- в С9 — «=C8*0,8»,
- протяните формулу из ячейки D8 вправо до 2019 года, рассчитайте итоговое значение;
- протяните вправо формулы из ячеек С9 и В10,
- протяните формулу из ячейки G8 на две ячейки вниз.
- В ячейку В11 формулу «=B10», в ячейку С11 формулу =B11+C10, протяните ячейку С11 вправо до F11, сверьте значение в ячейке F11 cо значением в G10.
Теперь рассчитаны денежные потоки, в том числе нарастающим итогом.
Срок окупаемости в Excel: пример расчёта
Для расчёта срока окупаемости в примере Excel введите в ячейку В17 формулу «=СЧЁТЕСЛ?(B11:G11;»<1″)+1». Смысл этой формулы: подсчёт всех отрицательных значений и прибавление единицы даст номер года, в котором совокупный денежный поток станет неотрицательным.
Алгоритм и формула расчета ЧДД
ЧДД рассчитывается с использованием такой формулы:
NPV = сумма результатов за каждый год капиталовложения CF / ((1 + r) в степени t),
где обозначения имеют следующий смысл:
Расчет денежных потоков
- CF – сальдо потока денежного, рассчитанного как разница между тем, что предприятие получило, и тем, что потратило
- t – количество лет, за который производится расчет
- r – ставка дисконтирования инвестиции
- n – продолжительность внедрения самого инвестиционного проекта
При изучении денежных потоков и их приведенной стоимости очень важно подойти непосредственно к выбору ставки дисконтирования. При осуществлении ее выбора необходимо учитывать не только особенности теории стоимости денег во времени, но и учитывать в обязательном порядке риск неопределенности. Лучше в качестве ставки дисконтирования выбирать именно средневзвешенную стоимость капитала, вложенного в инвестиционный проект. По итогу такого выбора существует закономерность: чем будут больше риски неопределенности, тем больше будет сама ставка, и наоборот.
ЧДД проектов: какой выбрать
Есть два инвестиционных проекта с инвестиционными вложениями в 10 тыс. рублей. Известны денежные потоки по каждому проекту по годам. Проект А: 5, 4, 3, 1. Проект Б имеет такие денежные потоки: 1, 3, 4, 6. Ставка дисконтирования 10%. Какой проект лучше?
Для начала необходимо рассчитать ЧДД для проекта А за каждый год:
- 5 / (1 + 0,1) в 1-й степени = 4545,5
- 4 / (1 + 0,1) во 2-й степени = 3305,8
- 3 / (1 + 0,1) в 3-й степени = 2253,9
- 1 / (1 + 0,1) в 4-й степени = 683,0
По результатам расчета ЧДД потока по проекту инвестирования А за 4-е года составит: 10788,2 (все ЧДД за четыре года суммируются: 4545,5 +…+ 683). Если отнять первоначальные капиталовложения, то ЧДД = 10788,2 – 10000 = 788,2.
По аналогии рассчитывается ЧДД по проекту Б, где она составит 491,5.
Вывод: вкладывать деньги можно в оба проекта, но выгоднее в проект А.
Анализ полученных результатов
Таким образом, NPV – это тот способ изучения инвестиционной доходности проекта, позволяющий уже сегодня понять, сколько денег необходимо вложить, и какая от них будет отдача. Также можно понять, за сколько окупится проект.
Как проводить анализ результатов
Реализация метода NPV базируется на таких основах:
Полученные результаты
- Дисконтирование денежных потоков происходит в целом по стоимости вложенного в капитал. Перед проведением расчета необходимо всегда найти приведенный к текущему временному периоду размер как входящих, так и исходящих потоков, и только после этого осуществить расчет ЧДД.
- Все значения по дисконтированным денежным потокам всегда необходимо складывать, чтобы потом проводить оценку полученного результата.
- Проводится оценка полученного потока. При полученном NPV больше 0 инвестиционный проект можно реализовать в действительность. Если же такая стоимость равна 0, тогда все на усмотрение инвестора: проект может быть принят или отклонен. Связано это с тем, что ЧДД = 0 свидетельствует о том, что потоки покроют инвестированный капитал и может даже дадут получить небольшою норму прибыли, но больше никаких выгод для инвестора не будет. Стоимость акций проекта не изменится в будущем.
Что такое чистая приведенная стоимость и правило чистой приведенной стоимости?
Чистая приведенная стоимость характеризует стоимость инвестиций, а правило чистой приведенной стоимости – это метод выбора среди альтернативных инвестиций.
Чистая приведенная стоимость инвестиций (NPV, от англ. ‘net present value’) – это приведенная (текущая) стоимость притока денежных средств за вычетом приведенной стоимости оттока денежных средств.
Слово «чистая» (англ. ‘net’) в этом термине означает вычитание приведенной стоимости оттоков (затрат) инвестиций из приведенной стоимости притоков (доходов) для получения чистого финансового результата.
Процедура вычисления NPV и применения правила NPV заключаются в следующем:
Определите все денежные потоки, связанные с инвестициями – все притоки и оттоки.
При оценке денежных потоков мы руководствуемся двумя принципами.
- Во-первых, мы включаем в расчет только дополнительные денежные потоки, возникающие в результате осуществления проекта. Мы не учитывает невозвратные затраты (англ. ‘sunk costs’), т.е. расходы, которые были совершены до начала проекта и которые нельзя возместить в течение проекта.
- Во-вторых, мы учитываем налоговые последствия, используя стоимость денежных потоков после уплаты налогов.
Определите соответствующую ставку дисконтирования или ставку альтернативной доходности r для инвестиционного проекта.
Для дисконтирования денежных потоков часто используется средневзвешенная стоимость капитала (WACC).
Этот показатель представляет собой средневзвешенное значение ставок доходности после налогообложения для обыкновенных акций, привилегированных акций и долгосрочных долговых обязательств компании, где весом является доля каждого источника финансирования в целевой структуре капитала компании.
Используя эту ставку дисконтирования, найдите текущую (приведенную) стоимость (PV) каждого денежного потока.
Приток имеет положительный знак (+) и увеличивает NPV. Отток имеет отрицательный знак (-) и уменьшает NPV.
Суммируйте все приведенные значения стоимости.
Сумма приведенной стоимости всех денежных потоков (притоков и оттоков) является чистой приведенной стоимостью инвестиций.
Примените правило чистой приведенной стоимости.
Правило NPV (англ. ‘net present value rule’) заключается в следующем:
- Если NPV инвестиции является положительным значением, инвестор должен ее осуществить.
- Если NPV отрицательна, инвестор не должен осуществлять эту инвестицию.
- Если у инвестора есть две возможные инвестиции, но он может выбрать только одну (т.е. взаимоисключающие проекты), инвестору следует выбрать инвестицию с более высокой положительной NPV.
Простые проценты
Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).
В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).
Примечание . В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция ПС() используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить ПС() рассчитать Приведенную стоимость и по методу простых процентов (см. файл примера ).
Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета Будущей стоимости (FV): FV = PV * (1+i*n) где PV – Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i – процентная ставка за период начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.
Из этой формулы получим, что:
PV = FV / (1+i*n)
Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).
Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.
Сложные проценты
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования простых процентов изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».
Приведенную стоимость PV (или ПС) в этом случае можно рассчитать, используя формулу наращения для сложных процентов .
FV = РV*(1+i)^n где FV (или S) – будущая (или наращенная сумма), i – годовая ставка, n – срок ссуды в годах,
т.е. PV = FV / (1+i)^n
При капитализации m раз в год формула Приведенной стоимости выглядит так: PV = FV / (1+i/m)^(n*m) i/m – это ставка за период.
Например, сумма 100 000р. на расчетном счету через 3 года эквивалентна сегодняшней сумме 69 892,49р. при действующей процентной ставке 12% (начисление % ежемесячное; пополнения нет). Результат получен по формуле =100000 / (1+12%/12)^(3*12) или по формуле =ПС(12%/12;3*12;0;-100000).
Отвечая на вопрос из предыдущего раздела «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? нам нужно сравнить две Приведенные стоимости: 69 892,49р. (сложные проценты) и 68 965,52р. (простые проценты). Т.к. Приведенная стоимость, рассчитанная по предложению банка для вклада с простыми процентами, меньше, то это предложение выгоднее (сегодня нужно вложить денег меньше, чтобы через 3 года получить ту же сумму 100 000,00р.)
Сложные проценты (несколько сумм)
Определим приведенную стоимость нескольких сумм, которые принадлежат разным периодам. Это можно сделать с помощью функции ПС() или альтернативной формулы PV = FV / (1+i)^n
Установив значение ставки дисконтирования равной 0%, получим просто сумму денежных потоков.
Источники
- https://rdv-it.ru/company/press-center/blog/kak-rasschitat-npv/
- https://arakis.su/articles/npv-chistaja-privedennaja-stoimost-raschet/
- https://exceltable.com/funkcii-excel/raschet-privedennoy-stoimosti-chistnz
- https://vse-investicii.ru/razvitie-proektov/chistaya-privedyonnaya-stoimost
- http://Excel2010.ru/kak-v-excel-vychislit-privedennuyu-stoimost.html
- http://finexcel.ru/raschyot-pokazatelej-investicionnogo-proekta-v-excel/
- https://PravoDeneg.net/buhuchet/uchet/privedennaya-stoimost-denezhnogo-potoka.html
- https://fin-accounting.ru/cfa/l1/quantitative/cfa-nvp-and-net-present-value-rule
- https://excel2.ru/articles/raschet-privedennoy-nastoyashchey-tekushchey-stoimosti-v-ms-excel
Функция ПС возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат. Например, в момент займа его сумма является приведенной (нынешней) стоимостью для заимодавца.
Описание функции
Возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат. Например, в момент займа его сумма является приведенной (нынешней) стоимостью для заимодавца.
Синтаксис
=ПС(ставка; кпер; плт; [бс]; [тип])Аргументы
ставкакперплтбстип
Обязательный. Процентная ставка за период.
Например, если получен кредит на автомобиль под 10 процентов годовых и выплаты производятся ежемесячно, процентная ставка за месяц составит 10%/12 (0,83%). В качестве значения аргумента «ставка» нужно ввести в формулу 10%/12, 0,83% или 0,0083.
Обязательный. Общее число периодов платежей для ежегодного платежа.
Например, если получен кредит на 4 года на покупку автомобиля и платежи производятся ежемесячно, то кредит имеет 4*12 (или 48) периодов. В качестве значения аргумента «кпер» в формулу нужно ввести число 48.
Обязательный. Выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ежегодного платежа. Обычно аргумент «плт» состоит из выплат в счет основной суммы и платежей по процентам, но не включает в себя другие сборы или налоги.
Например, ежемесячная выплата по кредиту в размере 10 000 р. под 12 процентов годовых на 4 года составит 263,33р. В качестве значения аргумента «плт» нужно ввести в формулу число -263,33. Если он опущен, аргумент «бс» является обязательным.
Необязательный. Значение будущей стоимости, т. е. желаемого остатка средств после последнего платежа. Если аргумент «бс» опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0).
Предположим, что для определенной цели требуется накопить 50 000 р. за 18 лет: в этом случае будущая стоимость равна 50 000 р. Предположив, что заданная процентная ставка останется без изменений, можно определить, какую сумму необходимо откладывать каждый месяц. Если аргумент «бс» опущен, необходимо использовать аргумент «плт».
Необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата.
| Тип | Когда нужно платить |
|---|---|
| 0 или опущен | В конце периода |
| 1 | В начале периода |
Замечания
- Убедитесь, что единицы измерения, выбранные для аргументов «ставка» и «кпер», соответствуют друг другу. Например, если производятся ежемесячные выплаты по четырехгодичному займу из расчета 12 процентов годовых, используйте значение12%/12 для задания аргумента «ставка» и 4*12 — для аргумента «кпер». Если платежи по тому же займу производятся ежегодно, используйте значение 12% для аргумента «ставка» и 4 — для аргумента «кпер».
- При расчете аннуитетов используются следующие функции:
ОБЩПЛАТ ОСПЛТ ОБЩДОХОД ПС БС СТАВКА БЗРАСПИС ЧИСТВНДОХ ПРПЛТ ЧИСТНЗ ПЛТ - Аннуитет — это ряд выплат одинаковых денежных сумм, осуществляемых в течение длительного периода. Примерами аннуитета могут служить заем на покупку автомобиля или заклад. Дополнительные сведения см. в описаниях функций, связанных с аннуитетами.
- В функциях, связанных с аннуитетами, выплачиваемые денежные средства, например депозит на сбережения, представляются в виде отрицательных чисел, а получаемые, такие как чеки на дивиденды, — положительными. Например, банковский депозит на сумму 1000р. будет представлен аргументом -1000 для вкладчика и аргументом 1000 — для банка.
- В Microsoft Excel каждый из финансовых аргументов выражается через другие аргументы. Если ставка не равна 0, то,
Если ставка равна 0, то,
(плт * клер) + пс + бс = 0
Примеры
Пример1Пример задачи1
Задача
Фирме требуется 500 тыс. рублей через три года. Определить какую сумму необходимо внести фирме сейчас, чтобы к концу третьего года вклад увеличился до 500 тыс. рублей, если процентная ставка составляет 12% годовых.
Решение
Ответ: -355890 руб. Число отрицательно, т.к. характеризует отток денежных средств.
Файл с решением