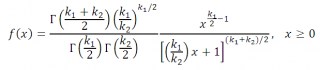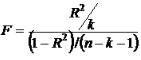Функция excel а обр

В этой статье описаны синтаксис формулы и использование F.ОПС
 в Microsoft Excel.

Описание

Возвращает значение, обратное F-распределению вероятности. Если p = F.РАСП(x;…), то F.ОБР(p;…) = x. F-распределение может использоваться в F-тесте, который сравнивает степени разброса двух наборов данных. Например, можно проанализировать распределение доходов в США и Канаде, чтобы определить наличие их схожести по степени плотности доходов.

Синтаксис

F.ОБР(вероятность;степени_свободы1;степени_свободы2)

Аргументы функции F.ОБР описаны ниже.

• Вероятность     — обязательный аргумент. Вероятность, связанная с интегральным F-распределением.

• Степени_свободы1     — обязательный аргумент. Числитель степеней свободы.

• Степени_свободы2     — обязательный аргумент. Знаменатель степеней свободы.

Замечания

• Если какой-либо из аргументов не является числом, то F.ОV возвращает #VALUE! значение ошибки #ЗНАЧ!.

• Если вероятность < 0 или вероятность > 1, то F.ОПС возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если значение аргумента «степени_свободы1» или «степени_свободы2» не является целым числом, оно усекается.

• Если deg_freedom1 < 1 или deg_freedom2 < 1, то F.ОV возвращает #NUM! значение ошибки #ЗНАЧ!.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,01	Вероятность, связанная с интегральным F-распределением
6	Числитель степеней свободы
4	Знаменатель степеней свободы
Формула	Описание	Результат
=F.ОБР(A2;A3;A4)	Значение, обратное F-распределению вероятностей для приведенных выше данных	0,10930991

К началу страницы

Функция F.ОБР возвращает значение, обратное F-распределению вероятности.

Описание функции F.ОБР

Возвращает значение, обратное F-распределению вероятности. Если p = F.РАСП(x;…), то F.ОБР(p;…) = x. F-распределение может использоваться в F-тесте, который сравнивает степени разброса двух наборов данных. Например, можно проанализировать распределение доходов в США и Канаде, чтобы определить, похожи ли эти две страны по степени плотности доходов.

Синтаксис

=F.ОБР(вероятность; степени_свободы1; степени_свободы2)

Аргументы

Замечания

• Если какой-либо из аргументов не является числом, функция F.ОБР возвращает значение ошибки #ЗНАЧ!.
• Если вероятность < 0 или вероятность > 1, функция F.ОБР возвращает значение ошибки #ЧИСЛО!.
• Если значение аргумента «степени_свободы1» или «степени_свободы2» не является целым числом, оно усекается.
• Если степени_свободы1 < 1 или степени_свободы2 < 1, функция F.ОБР возвращает значение ошибки #ЧИСЛО!.

Пример

Описание

Excel F.INV Функция возвращает обратное F-распределение вероятностей. Если p (вероятность) = F.РАСП(x,…), то F.ОБР(p,…)= x.

Синтаксис и аргументы

Синтаксис формулы

Ф.ОБР(вероятность,степень_свободы1,степень_свободы2)

аргументы

• Probability: Требуемая вероятность кумулятивного распределения F.

• Deg_freedom1: Требуется, числитель степеней свободы. Должно быть > 1.

• Deg_freedom2: Требуется, знаменатель степеней свободы. Должно быть > 1.

Замечания

1. Функция возвращает #ЗНАЧ! значение ошибки, если какие-либо аргументы функции F.ОБР являются нечисловыми значениями.

2. Функция возвращает #ЧИСЛО! значение ошибки, когда:

• Вероятность < 0 или > 1;
• Либо степень_свободы1, либо степень_свободы2 < 1.

3. Если deg_freedom1 или deg_freedom2 не является целым числом, оно будет усечено.

Версия

Excel 2010 и более поздние версии

Использование и примеры

Основное использование

Например, в списке C2:C4 содержатся аргументы вероятности, deg_freedom1 и deg_freedom2, чтобы получить относительную обратную вероятность F, используйте следующую формулу:

=F.INV(C2,C3,C4)

Нажмите Enter .

---

Другие функции:

• Excel COVARIANCE.P Функция
  Функция Excel COVARIANCE.P возвращает дисперсию совокупности двух наборов данных, которая используется для определения взаимосвязи между двумя наборами данных.

• Excel FDIST Функция
  Функция Excel FDIST возвращает (правостороннее) распределение вероятностей F, которое обычно используется для измерения степени разнообразия между двумя наборами данных.

• Excel EXPON.DIST Функция
  Функция EXPON.DIST, используемая в Excel 2010, возвращает экспоненциальное распределение на основе заданного значения x и параметра распределения.

• Excel F.DIST Функция
  Функция Excel F.РАСП возвращает F-распределение вероятностей, которое обычно используется для измерения степени разнообразия между двумя наборами данных.

---

Лучшие инструменты для работы в офисе

Kutools for Excel — Помогает вам выделиться из толпы

Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.

• Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
• Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
• Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
• 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.

---

Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)

• Одна секунда для переключения между десятками открытых документов!
• Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
• Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
• Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.

Комментарии (0)

Оценок пока нет. Оцените первым!

Рассмотрим распределение Фишера (F-распределение). С помощью функции

MS

EXCEL

F

.РАСП()

построим графики функции распределения и плотности вероятности, поясним применение этого распределения для целей математической статистики.

F-распределение

(англ. F-distribution)

применяется для целей дисперсионного анализа (ANOVA), при

проверке гипотезы о равенстве дисперсий двух нормальных распределений (F-тест)

и др.

Определение

: Если U

₁

и U

₂

независимые случайные величины, имеющие

ХИ2-распределение

с k

₁

и k

₂

степенями свободы

соответственно, то распределение случайной величины:

носит название

F

-распределения

с параметрами k

₁

и k

₂

.

Плотность

F

-распределения

выражается формулой:

где Г(…) – гамма-функция:

если

альфа

– положительное целое, то Г(

альфа

)=(

альфа

-1)!

СОВЕТ

: Подробнее о

Функции распределения

и

Плотности вероятности

см. статью

Функция распределения и плотность вероятности в MS EXCEL

.

Приведем пример случайной величины, имеющей

F

-распределение.

Пусть имеется 2

нормальных распределения

N(μ

₁

;σ

₁

) и N(μ

₂

; σ

₂

), из которых сделаны выборки размером n

₁

и n

₂

. Если s

₁

²

и s

₂

²

–

дисперсии этих выборок

, то отношение

имеет

F

-распределение.

Это соотношение нам потребуется при проверке

гипотезы о равенстве дисперсий двух нормальных распределений (F-тест)

.

Графики функций

F

-распределение

при небольших параметрах (<50) имеет несимметричную форму, скошенную вправо (длинный правый хвост).

Среднее значение

равно k

₂

/(k

₂

-2) при k

₂

>2,

дисперсия

равна 2*k

₂

²

*(k

₁

+k

₂

-2)/(k

₁

*(k

₂

-4)*(k

₂

-2)

²

) при k

₂

>4.

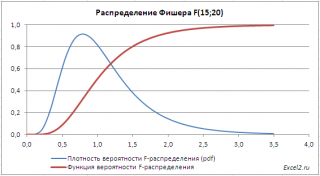
В

файле примера на листе График

приведены

графики плотности распределения

вероятности и

интегральной функции распределения

.

Примечание

: Для построения

функции распределения

и

плотности вероятности

можно использовать диаграмму типа

График

или

Точечная

(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью

Основные типы диаграмм

.

F-распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для

F-распределения

имеется специальная функция

F.РАСП()

, английское название – F.DIST(), которая позволяет вычислить

плотность вероятности

(см. формулу выше) и

интегральную функцию распределения

(вероятность, что случайная величина Х, имеющая

F

—

распределение

, примет значение меньше или равное х, P(X <= x)).

Примечание

:

Плотность вероятности

можно также вычислить впрямую, с помощью формул (см.

файл примера

).

До MS EXCEL 2010 в EXCEL была функция

FРАСП()

, которая позволяет вычислить

функцию распределения

(точнее — правостороннюю вероятность, т.е. P(X>x)). Функция

FРАСП()

оставлена в MS EXCEL 2010 для совместимости. Аналогом

FРАСП()

является функция

F.РАСП.ПХ()

, появившаяся в MS EXCEL 2010.

Примеры расчетов приведены в

файле примера на листе Функции

.

В MS EXCEL имеется еще одна функция, использующая для расчетов

F-распределение

– это

F.ТЕСТ(массив1;массив2)

. Эта функция возвращает результат

F-теста

: двухстороннюю вероятность того, что разница между дисперсиями выборок «массив1» и «массив2» несущественна. Предполагается, что

выборки

делаются из

нормального распределения

.

Подробнее об использовании этой функции см.

статью про проверку гипотез о равенстве двух дисперсий

.

Обратная функция F-распределения

Обратная функция используется для вычисления

альфа

—

квантилей

, т.е. для вычисления значений

x

при заданной вероятности

альфа

, причем

х

должен удовлетворять выражению P{X<=x}=

альфа

.

В MS EXCEL обратная функция реализована с помощью функции

F.ОБР()

.

Функция

F.ОБР.ПХ()

используется для вычисления

верхнего квантиля

. Т.е. если в качестве аргумента функции указан уровень значимости, например 0,05, то функция вернет такое значение случайной величины х, для которого P(X>x)=0,05. В качестве сравнения: функция

F.ОБР()

вернет такое значение случайной величины х, для которого P(X<=x)=0,05.

В MS EXCEL 2007 и ранее вместо

F.ОБР.ПХ()

использовалась функция

FРАСПОБР()

.

Вышеуказанные функции можно взаимозаменять, т.к. следующие формулы возвращают одинаковый результат:

=F.ОБР(0,05;k1;k2) =F.ОБР.ПХ(1-0,05;k1;k2) = FРАСПОБР (1-0,05;k1;k2)

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

Функция FПАСПОБР в Excel используется для проверки значимости модели регрессии с применением F-критерия (критерий Фишера), и возвращает числовое значение, соответствующее обратному значению для F-распределения вероятностей (верхнему квантилю). Например, если в качестве вероятности (первый аргумент функции) было введено значение уровня значимости, к примеру, 0,08, то FПАСПОБР вычислит значение случайной величины x, для которой выполняется следующее условие – P(X>x) = 0,08.

Функция FРАСПОБР для оценки значимости параметров модели регрессии

Критическое значения F может быть определено в случае, если в качестве первого аргумента рассматриваемой функции будет введено значение уровня значимости.

Для расчета F используется следующая формула:

Функция оперирует двумя дополнительными критериями:

1. Числитель степеней свободы: n1 = k.
2. Знаменатель степеней свободы: n2 = (n – k – 1).

Через переменную k обозначают число факторов, которые были включены в исследуемую модель регрессии.

В Excel предусмотрена функция для расчета вероятности для распределения Фишера – FРАСП. Между данной и рассматриваемой функциями существует следующая взаимосвязь: =FРАСПОБР(FРАСП(x;n1;n2);n1;n2)=x.

Примечание:

В MS Office 2007 и более поздних версиях была введена функция F.ОБР.ПХ, которая заменила рассматриваемую функцию. FПАСПОБР была оставлена для обеспечения совместимости с документами, созданными в более старых версиях Excel.



Определение верхнего квартиля F-распределения Фишера в Excel

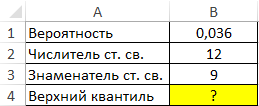
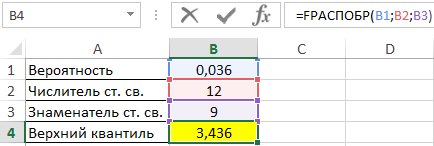
Пример 1. В таблице указаны вероятность, связанная с распределением Фишера, а также числитель и знаменатель степеней свободы соответственно. Определить верхний квантиль данного F-распределения.

Вид таблицы данных:

Вычислим искомое значение с помощью функции:

=FРАСПОБР(B1;B2;B3)

Полученное число:

Оценка в Excel эффективности использования технологий на производстве

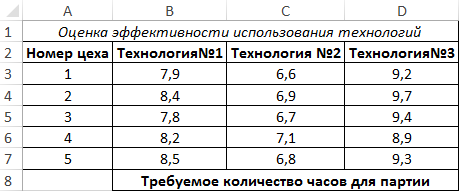
Пример 2. На заводе есть несколько цехов по производству одного типа продукции. Существует 3 различные технологии изготовления данной продукции. Для оценки были записаны данные о количестве часов, необходимых для производства одной партии продукции каждым цехом с использованием каждой из трех технологий. Оценить эффективность использования технологий, проанализировать полученные значения.

Вид таблицы данных:

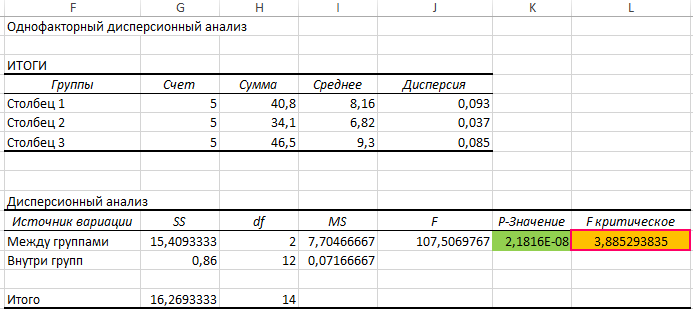
Проведем однофакторный дисперсионный анализ для данных, находящихся в диапазоне ячеек B3:D7, используя соответствующую надстройку Excel. Полученная таблица результатов:

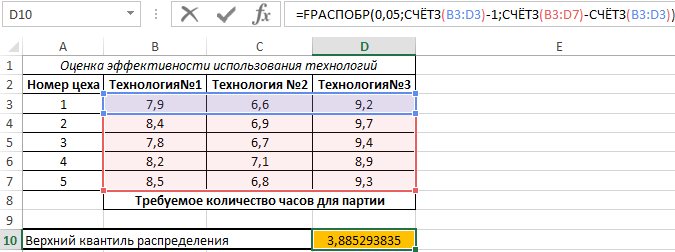
По условия поставленной задачи нас интересует выделенное значение. Поскольку оно <0,05, между данными существует линейная зависимость. В результате анализа уже было определено значение, возвращаемое функцией FРАСПОБР (F критическое). Для расчета можно было использовать функцию:

Здесь СЧЁТЗ(B3:D3) определяет число полей данных, а СЧЁТЗ(B3:D7) – количество исследуемых числовых значений.

Полученное число:

Особенности использования функции FРАСПОБР в Excel

Функция имеет следующую синтаксическую запись:

=FРАСПОБР(вероятность;степени_свободы1;степени_свободы2)

Описание аргументов:

• вероятность – обязательный, принимает числовое значение, характеризующее вероятность, которая связана с распределением Фишера;
• степени_свободы1 – обязательный, принимает числовое значение, соответствующее числителю степеней свободы (равно числу факторов исследуемой регрессии);
• степени_свободы2 – обязательный, принимает числовое значение, соответствующее знаменателю степеней свободы.

Примечания:

1. Рассматриваемая функция принимает в качестве любого из аргументов только числовые значения и данные, которые могут быть преобразованы к числам. Если любой из аргументов принимает данные недопустимого типа, будет сгенерирован код ошибки #ЗНАЧ!
2. Первый аргумент должен быть задан числом из диапазона от 0 до 1. В противном случае функция FПАСПОБР вернет код ошибки #ЧИСЛО!
3. Второй и третий аргумент функции должны быть заданы числами из диапазона от 1 до 10^10. При вводе значений, находящихся вне допустимого диапазона, будет сгенерирован код ошибки #ЧИСЛО!
4. Рассматриваемая функция использует итеративный подход к вычислениям (последовательный подбор приближенного значения в циклах). Если спустя 100 итераций решение не было найдено, результатом выполнения функции FПАСПОБР будет код ошибки #Н/Д.