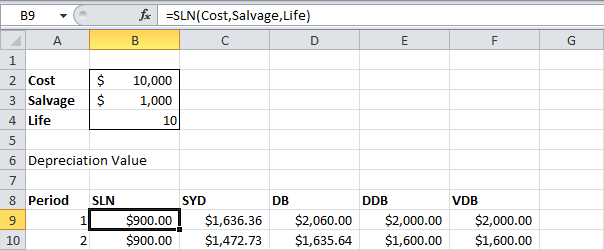Функция ддоб в excel

Функция ДДОБ возвращает значение амортизации актива за указанный период, используя метод двойного уменьшения остатка или иной явно указанный метод.

Описание функции ДДОБ

Возвращает значение амортизации актива за указанный период, используя метод двойного уменьшения остатка или иной явно указанный метод.

Синтаксис

=ДДОБ(нач_стоимость; ост_стоимость; время_эксплуатации; период; [коэффициент])

Важно! Значения всех аргументов должны быть положительными числами.

Аргументы

Замечания

• Метод двойного уменьшения остатка вычисляет амортизацию, используя увеличенный коэффициент. Амортизация является максимальной в первый период и уменьшается в последующие. Для вычисления амортизации за период с помощью функции ДДОБ используется следующая формула:

  Min( (cost - total depreciation from prior periods) * (factor/life); (cost - salvage - total depreciation from prior periods) )

• Если требуется использовать другой метод вычисления амортизации, измените значение аргумента «коэффициент».
• Если необходимо использовать метод прямой амортизации в случае, когда амортизация превышает вычисленную величину амортизации, воспользуйтесь функцией ПУО.

Пример

Ддоб (функция ддоб)

Применимо
к: Microsoft
Excel 2010, Excel
Web App, SharePoint
Online for enterprises, SharePoint
Online for professionals and small businesses

Печать

Показать
все

В
этой статье описаны синтаксис формулы
и использование функции ДДОБ в
Microsoft Excel.

Описание

Возвращает
значение амортизации актива за указанный
период, используя метод двойного
уменьшения остатка или иной явно
указанный метод.

Синтаксис

ДДОБ(нач_стоимость,
ост_стоимость, время_эксплуатации,
период, [коэффициент])

Функция
ДДОБ имеет аргументы,
указанные ниже.

• Нач_стоимость    —
  обязательный аргумент. Затраты на
  приобретение актива.

• Ост_стоимость    —
  обязательный аргумент. Стоимость в
  конце периода амортизации (иногда
  называемая остаточной стоимостью
  имущества); может быть равна нулю.

• Время_эксплуатации    —
  обязательный аргумент. Количество
  периодов, за которые собственность
  амортизируется (иногда называемое
  периодом амортизации).

• Период    —
  обязательный аргумент. Период, для
  которого требуется вычислить амортизацию.
  Для представления периода должна
  использоваться та же единица измерения,
  что и для аргумента «время_эксплуатации».

• Коэффициент    —
  необязательный аргумент. Процентная
  ставка снижающегося остатка. Если
  коэффициент опущен, он полагается
  равным 2 (метод удвоенного процента со
  снижающегося остатка).

 ВАЖНО.   Значения
всех пяти аргументов должны быть
положительными числами.

Замечания

• Метод
  двойного уменьшения остатка вычисляет
  амортизацию, используя увеличенный
  коэффициент. Амортизация является
  максимальной в первый период и уменьшается
  в последующие. Для вычисления амортизации
  за период с помощью функции ДДОБ
  используется следующая формула:

Мин(
(нач_стоимость — суммарная амортизация
за предшествующие периоды) *
(коэффициент/время_эксплуатации),
(нач_стоимость — остаточная_стоимость
— суммарная амортизация за предшествующие
периоды))

• Если
  требуется использовать другой метод
  вычисления амортизации, измените
  значение аргумента «коэффициент».

• Если
  необходимо использовать метод прямой
  амортизации в случае, когда амортизация
  превышает вычисленную величину
  амортизации, воспользуйтесь функцией
  ПУО.

Пример

Чтобы
лучше понять этот пример, скопируйте
его на пустой лист.

Копирование
примера

 ПРИМЕЧАНИЕ.   Результаты
округляются до двух знаков после запятой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Использование финансовых функций при экономических расчётах

Функция ПЛТ

Функция ПЛТ (PMT) – возвращает сумму периодического платежа на основе постоянства сумм платежей и постоянства процентной ставки.

Синтаксис:

ПЛТ(СТАВКА;КПЕР;ПС;[БС];ТИП)

• СТАВКА – Удельная ставка за период займа.
• КПЕР– общее число периодов выплат.
• ПС– текущая стоимость: общая сумма всех будущих платежей с настоящего момента.
• БС – будущая стоимость или баланс наличности, которую нужно достичь после последней выплаты.Если аргумент БС опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение БС равно 0.
• ТИП– логическое значение (0 или 1), обозначающее, должна ли производиться выплата в конце периода (0) или в начале периода (1).

Функция ПЛТ может быть использована для анализа всевозможных ссуд. Необходимым условием является непротиворечивость аргументов функции.

Пример 1. Предположим, что нужно воспользоваться 9-процентной 15-летней ссудой. Объем ссуды составляет 150 000 000 рублей. C помощью Мастера функций можно определить величины ежемесячных выплат. Предварительно следует привести все другие значения к месячной норме.

Ввести таблицу (рис. 9.1
рис.
9.1 ), начиная с ячейки А1:

В ячейки В 3 и В 4 ввести соответствующие формулы.

Процентная ставка (СТАВКА) – годовая, поэтому для получения месячной ставки (Удельная ставка) соответствующее значение делится на 12 (0,09/12).

Срок действия ссуды – 15 лет, поэтому с учетом 12 платежей год общее количество месячных выплат (КПЕР) составит 12х15.

Для ячейки В6 пошаговыми действиями Мастера функций выполните настройку функции ПЛТ. Для вызова Мастера функций необходимо выбрать команду Вставить функцию (значок f_x) в меню Формулы.

После этого в поле Значение диалогового окна Мастера функций вы увидите сумму ежемесячного взноса. А после нажатия на кнопку Готово результат отобразится в ячейке.

Примечание. Необходимо исходные данные заносить в ячейки на рабочий лист Excel, давая им в левом столбце соответствующие названия параметров, а для рассчитываемых параметров использовать формулы. Тогда при изменении исходных данных будет автоматически выполнен перерасчет по формулам.

Функция БС

Функция БС(FV) предназначена для расчета будущей стоимости периодических постоянных платежей и единой суммы вклада или займа на основе постоянной процентной ставки.

БС – будущее значение, возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки.

Синтаксис:

БС (СТАВКА; КПЕР; ПЛТ; ПС; ТИП).

• СТАВКА – это процентная ставка за период.
• КПЕР– это общее число периодов платежей.
• ПЛТ– это выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно ПЛТ состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов.
• ПС – это текущая стоимость, или общая сумма всех будущих платежей с настоящего момента. Если аргумент ПС опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента ПЛТ.
• ТИП– это число 0 или 1, обозначающее, когда должна производиться выплата: 0 – в конце периода, 1 – в начале периода. Если аргумент опущен, то он полагается равным 0.

Для аргументов СТАВКА и КПЕР используются согласованные единицы измерения. Если производятся ежемесячные платежи по четырехгодичному займу из расчета 12% годовых, то СТАВКА должна быть 12%/12, а КПЕР должно быть 4*12. Если производятся ежегодные платежи по тому же займу, то СТАВКА должна быть 12%, а КПЕР должно быть 4.

Все аргументы, означающие деньги, которые вы платите (например, депозитные вклады), представляются отрицательными числами; деньги, которые вы получаете (например, дивиденды), представляются положительными числами.

Например, вы собираетесь вложить под 12% годовых (что составит в месяц 12%/12 или 1%). Вы собираетесь вкладывать по 1000 руб. в конце каждого следующего месяца в течении следующих 12 месяцев. Сколько денег будет на счету в конце12 месяцев?

Результат 12682,50 руб.

Для выполнения расчета вызывается Мастер функций, в поле Категории выбираются финансовые функции и в поле Функция выбирается функция БС. В появившемся окне заполняются соответствующие поля путем подстановки значений аргументов, а если данная функция вычисляется в расчете, то вместо этого указываются адреса исходных данных из таблицы расчета.

Функция ПС

Функция ПС (PV) предназначена для расчета текущей стоимости как единой суммы вклада (займа), так и будущих фиксированных периодических платежей. Этот расчет является обратным по отношению к будущей стоимости (БС).

ПС (PV )– возвращает текущий объем вклада. Текущий объем -это общая сумма, которую составят будущие платежи. Например, когда вы берете взаймы деньги, заимствованная сумма и есть текущий объем для заимодавца.

Синтаксис:

ПС (СТАВКА; КПЕР; ПЛТ; БС; ТИП).

Например, определите необходимую сумму текущего вклада в банк, чтобы через пять лет он достиг 5000 руб. при 20% годовых и ежегодном начислении процентов в конце года. Синтаксис: ПС (20%, 5, 5000). Результат 2009,39.

Функция КПЕР

Для определения срока платежа и процентной ставки используются функции КПЕР (NPER) и СТАВКА (RATE).

Функция КПЕР вычисляет общее число периодов выплат как для единой суммы вклада (займа), так и для периодических постоянных выплат на основе постоянной процентной ставки. Если платежи производятся несколько раз в год, то для того, чтобы найти число лет выплат, общее число периодов надо разделить на число периодов в году.

Синтаксис:

КПЕР (СТАВКА; ПЛТ; ПС; БС; ТИП).

• СТАВКА– это процентная ставка за период.
• ПЛТ– это выплата, производимая в каждый период; он не может меняться в течение всего периода выплат. Обычно платеж состоит из основного платежа и платежа по процентам, никакие другие сборы или налоги не учитываются.
• ПС– это текущая стоимость, или общая сумма всех будущих платежей с настоящего момента.
• БС– это будущая стоимость, или баланс наличности, который должен быть достигнут после последней выплаты. Если аргумент БС опущен, то предполагается, что он равен 0 (будущая стоимость займа, например, равна 0).
• ТИП– это число 0 или 1, обозначающее, когда должна производиться выплата.

Например, рассчитаем срок погашения ссуды размером 5000 руб., выданной под 20% годовых при погашении ежемесячными платежами по 200 руб.

КПЕР (20%/12; -200; 5000).

Результат 32,6 месяца или 2,7 года.

Функция СТАВКА

Функция СТАВКА (RATE) определяет значение процентной ставки за один расчетный период. Для нахождения годовой процентной ставки полученное значение необходимо умножить на число расчетных периодов в году.

СТАВКА вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО!.

Синтаксис:

СТАВКА (кпер; плт; пс; бс; тип; предположение).

• Кпер– общее число периодов платежей по аннуитету.
• Плт– регулярный платеж (один раз в период), величина которого остается постоянной в течение всего срока аннуитета. Обычно плт состоит из платежа основной суммы и платежа процентов, но не включает других сборов или налогов. Если аргумент опущен, должно быть указано значение аргумента БС.
• Пс– приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.
• Бс– требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (например, бс для займа равно 0).
• Тип– число 0 или 1, обозначающее, когда должна производиться выплата.
• Предположение – предполагаемая величина ставки. Если значение предположения опущено, то оно полагается равным 10 процентам.

Если функция СТАВКА не сходится, попробуйте подставить различные значения для предположения. СТАВКА обычно сходится, если величина предположения находится между числами 0 и 1.

Например, надо определить процентную ставку для четырёхлетнего займа в 8000 руб. с ежемесячной выплатой в 200 руб.

Результат 0,008, или 0,8 в месяц или 9,6% годовых.

Функции по расчету амортизации: AПЛ, АСЧ и ДДОБ

Под амортизацией подразумевается уменьшение стоимости имущества в процессе эксплуатации. Обычно оценивают величину этого уменьшения на единицу времени.

Функция АПЛ (SLN) возвращает величину амортизации имущества за один период времени, используя метод равномерной амортизации.

Синтаксис:

АПЛ (нач_стоимость;ост_стоимость;время_эксплуатации).

• нач_стоимость – начальная стоимость имущества;
• ост_стоимость –остаточная стоимость в конце периода амортизации;
• время_эксплуатации – количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации).

Предположим, вы купили за 6000 руб. компьютер, который имеет срок эксплуатации 5 лет, после чего оценивается в 1000 руб. Снижение стоимости для каждого года эксплуатации вычисляется формулой

которая возвращает значение 1000 р.

Функция АСЧ(SYD) возвращает годовую амортизацию имущества для указанного периода.

АСЧ (нач_стоимость; ост_стоимость; время_эксплуатации; период)

• нач_стоимость – начальная стоимость имущества;
• ост_стоимость – остаточная стоимость в конце периода амортизации;
• время_эксплуатации – количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации);
• период – номер периода для вычисления амортизации (должен быть измерен в тех же единицах, что и время полной амортизации).

При расчете предыдущего примера получим:

• за первый год эксплуатации компьютера амортизация вычисляется формулой

которая возвращает значение 1666.67р.

• за последний – формулой

которая возвращает 333. 33 р.

Функция ДДОБ (DDB) возвращает величину амортизации имущества для указанного периода, используя метод двукратного (или k-кратного) учета амортизации.

Синтаксис:

ДДОБ (стоимость; остаточная_стоимость; время_эксплуатации; период; k-коэффициент).

• стоимость–начальная стоимость имущества;
• остаточная_стоимость– остаточная стоимость в конце периода;
• время_эксллуатадии– количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации);
• период – номер периода для вычисления амортизации (должен быть измерен в тех же единицах, что и время полной амортизации);
• коэффициент– норма снижения балансовой стоимости (амортизации). Если коэффициент опущен, то предполагается, что он равен 2 (методдвукратного учета амортизации).

Метод двукратного учета амортизации предполагает ускоренную амортизацию имущества. При этом амортизация максимальна в первый период и снижается в последующие периоды.

В примере с компьютером по методу двукратной амортизации она составит:

• =ДДОБ (6000; 1000; 5; 1) возвращает 2400.00р.
• =ДДОБ (6000; 1000; 5; 2) возвращает 1440.00р.
• =ДДОБ (6000; 1000; 5; 3) возвращает 864.00р.
• =ДДОБ (6000; 1000; 5; 4) возвращает 296.00р.
• =ДДОБ (6000; 1000; 5; 5) возвращает 0.00р.

Примечание

В заключение попытаемся разобраться, как работают функции АПЛ, АСЧ, ДОБ и ДДОБ.

Проще всего дело обстоит с функцией АПЛ. Она возвращает одну и ту же амортизацию за каждый период.

Значения функции АСЧ изменяются по линейному закону. Разность любых двух ее значений за последовательные периоды постоянна. Таким образом значения за последовательные периоды образуют убывающую арифметическую прогрессию, подобранную таким образом, чтобы суммарная амортизация равнялась разности между начальной и остаточной стоимостью.

Значения функции ДДОБ изменяются также по экспоненциальному закону. Но коэффициент этой геометрической прогрессии не вычисляется, а является параметром.

Анализ «Что-если»

Анализ «Что-если» позволяет прогнозировать значение какой-либо функции (математической, финансовой, статистической и др.) при изменении её аргументов.

Существует четыре способа прогнозирования значений с помощью:

• таблиц подстановки данных,
• сценариев
• подбора параметров
• поиска решения.

1 способ. Таблица подстановки данных

Таблица подстановки данных представляет собой блок ячеек, в котором выводятся результаты подстановки различных значений переменных в одну или несколько формул.

Анализ может проводиться для функций с одной переменной или для функций с двумя переменными. Причем в случае одной переменной можно табулировать сразу несколько функций, зависящих от этой переменной.

Анализ формулы начинается с подготовки таблицы подстановки:

1. Левую верхнюю ячейку блока, отведенного под таблицу, оставить пустой.
2. В левый столбец блока, начиная со второй ячейки, последовательно ввести значения варьируемой переменной.
3. В верхнюю строку блока, начиная со второй ячейки, ввести ссылки на ячейки с анализируемыми формулами.

Допускается и другая ориентация таблицы, когда значения варьируемой переменной вводятся в первую строку, а анализируемые форму-лы – в первый столбец блока.

1. Выделить таблицу подстановки (в ячейки, расположенные рядом с таблицей, можно ввести пояснительные надписи, но эти ячейки не входят в таблицу подстановки данных и, следовательно, не выделяются).
2. В меню Данные выбрать Анализ «Что-если» и выбрать команду Таблица данных.
3. Если значения варьируемой переменной расположены в столбце, то надо щелкнуть по полю Подставлять значения по строкам и ввести в это поле адрес изменяемой ячейки (т.е. ячейки, которая играет роль варьируемой переменной в формуле). Если значения варьируемой переменной расположены в строке, то адрес изменяемой ячейки вводится в поле Подставлять значения по столбцам.
4. Щелкнуть по кнопке ОК. Таблица будет заполнена значениями.

В случае анализа зависимости формулы от двух переменных таблица подстановки подготавливается по-другому:

1. В левую верхнюю ячейку блока, отведенного под таблицу, ввести ссылку на ячейку с анализируемой формулой.
2. В левый столбец блока, начиная со второй ячейки, последовательно ввести значения одной из варьируемых переменных.
3. В верхнюю строку блока, начиная со второй ячейки, ввести значения другой варьируемой переменной.
4. Выделить таблицу подстановки.
5. В меню Данные выбрать Анализ «Что-если» и выбрать команду Таблица данных.
6. В поле Подставлять значения по строкам в ввести ссылку на ячейку с переменной, значения для которой расположены в левом столбце таблицы подстановки.
7. В поле Подставлять значения по столбцам ввести ссылку на ячейку с переменной, значения для которой расположены в первой строке таблицы подстановки.
8. Щелкнуть по кнопке ОК. Таблица будет заполнена значениями.

Если в какой-либо ячейке записана формула, содержащая элементы из других ячеек, то при изменении значения в какой-нибудь или нескольких ячейках изменится результат в ячейке, содержащей формулу.

Пример 2.

Определить какими будут выплаты по ссуде при меняющейся процентной ставке (для примера 1)

В ячейки А9:В13 введите следующие значения, оставив пустой строку перед числовыми значениями (рис. 9.2
рис.
9.2 ):

В ячейку В10 скопировать ссылку на ячейку с формулой для расчета ежемесячных выплат.

Для расчета выплат по каждой из ставок воспользуйтесь возможностью автоматической подстановки значений в нужную ячейку (в нашем случае в В1).

Для этого нужно:

1. Выделить диапазон А10:В13, включив в него значения процентных ставок и расчетную формулу (формула должна находиться в ячейке, расположенной правее и выше заданных значений).
2. В меню Данные выбрать Анализ «Что-если» и выбрать команду Таблица данных.
3. В поле «Подставлять значения по строкам в:» указать ячейку В1 (рис.9.3 ).

Рядом с каждой процентной ставкой появится соответствующий результат.

Измените значения процентных ставок или расширьте предлагаемый диапазон и вновь воспользуйтесь таблицей подстановки значений.

2 способ. Диспетчер сценариев

Средства Microsoft Excel позволяют создавать и сохранять в виде сценариев наборы входных значений, приводящих к различным результатам.

Сценарий – это множество входных значений, называемых изменяемыми ячейками, которое можно сохранить под указанным именем, а затем применить к модели рабочего листа, чтобы проследить, как значения изменяемых ячеек влияют на другие значения модели. Для каждого сценария можно определить до 32 изменяемых ячеек.

Чтобы создать сценарий, следует:

1. В меню Данные выбрать команду Анализ «Что-если», указав Диспетчер сценариев (рис. 9.4
рис.
9.4 ).

Появится окно «Диспетчер сценариев» (рис. 9.5
рис.
9.5)

2. Щелкнуть по кнопке Добавить. Откроется окно Добавление сценария (рис. 9.6
рис.
9.6).

3. В поле Название сценария ввести имя сценария.

4. В поле Изменяемые ячейки ввести ссылки на изменяемые ячейки. Несколько ссылок отделяются друг от друга точками с запятыми. Ссылки можно ввести с клавиатуры или выделить их на рабочем листе. Несмежные ячейки добавляются при нажатой клавише <Ctrl>.

5. Щелкнуть по кнопке ОК.

6. В открывшемся диалоговом окне Значения ячеек сценария ввести значения каждой изменяемой ячейки (рис. 9.7
рис.
9.7).

7. Для создания других сценариев щелкнуть по кнопке Добавить (откроется диалоговое окно Добавление сценария) и повторить пункты 3 – 6.

Для завершения работы с Диспетчером сценариев щелкнуть по кнопке ОК, а затем – по кнопке Закрыть.

Рекомендуется сохранить в качестве сценария первоначальные значения изменяемых ячеек, чтобы потом можно было быстро восстановить эти значения.

Для просмотра сценария нужно:

1. В меню Данные выбрать команду Анализ данных и указать Диспетчер сценариев.
2. В поле Сценарии выделить имя сценария, который необходимо просмотреть.
3. Щелкнуть по кнопке Вывести.

Вместо пунктов 2 и 3 можно дважды щелкнуть по имени нужного сценария.

Чтобы отредактировать сценарий, надо:

1. В меню Данные выбрать команду Анализ данных и указать Диспетчер сценариев.
2. В поле Сценарии выделить имя сценария, который необходимо отредактировать.
3. Щелкнуть по кнопке Изменить.
4. Внести необходимые изменения: можно изменить имя сценария, изменяемые ячейки, значения изменяемых ячеек.
5. Для завершения работы с Диспетчером сценариев щелкнуть по кнопке ОК, а затем – по кнопке Закрыть.

Для создания итогового отчета по сценариям следует:

1. В меню Данные выбрать команду Анализ данных и указать Диспетчер сценариев.
2. Щелкнуть по кнопке Отчет.
3. Выбрать тип отчета: Структура или Сводная таблица.

В отчете типа Структура перечислены все сценарии с определенными для них значениями ячеек. Этот тип отчета полезен тогда, когда каждый пользователь определяет сценарий со своими данными.

Отчет типа Сводная таблица предоставляет возможность эмпирического анализа сценариев. Этот тип отчета полезен тогда, когда сценарий имеет несколько наборов значений изменяющихся ячеек, заданных различными пользователями; с помощью сводных таблиц можно выполнить анализ для разных комбинаций сценариев.

1. В поле Ячейки результата ввести ссылки на ячейки, значения которых надо представить в отчете. В качестве разделителя ссылок используется запятая. Ссылки можно ввести с клавиатуры или выделить их на рабочем листе. Несмежные ячейки добавляются при нажатой клавише <Ctrl>. Итоговые отчеты создаются на отдельных листах.

3 способ. Подбор параметра

Пусть имеется формула, которая прямо или косвенно зависит от некоторого параметра. Задача состоит в определении такого значения этого параметра, которое позволяет получить нужный результат формулы. При подборе параметра значение влияющей ячейки (параметра) изменяется до тех пор, пока формула, зависящая от этой ячейки не возвратит заданное значение.

Математическая суть задачи состоит в решении уравнения X = a, где функция х описывается заданной формулой, х – искомый параметр, а – требуемый результат формулы.

Для решения этой задачи необходимо выполнить следующие действия:

1. Выделить ячейку, содержащую формулу, для которой нужно найти определенное решение.
2. В меню Данные > Анализ «что-если» выбрать команду Подбор параметра. В поле Установить в ячейке ввести ссылку на ячейку, содержащую формулу (по умолчанию в это поле вводится адрес текущей ячейки).
3. В поле Значение ввести значение, которое нужно получить по заданной формуле.
4. В поле Изменяя ячейку ввести ссылку на ячейку, содержащую значение изменяемого параметра (эта ячейка называется изменяемой).
5. Щелкнуть по кнопке ОК.

Пример 3.

Дано уравнение: ,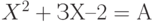

где: А – требуемый результат формулы; Х – искомый параметр.

Определить такое значение параметра X, при котором А будет равно 20.

1. Занести в ячейку A1 любое значение, например, 1.
2. Ввести в ячейку А2 указанную формулу, которая примет следующий вид: =A1^2+3*A1-2. В формуле указана ссылка на ячейку А1, в которой условно находится параметр X.
3. Задать команду Данные > Анализ «что-если» > Подбор параметра (рис. 9.8
   рис.
   9.8 ).
4. В поле Установить в ячейке указать А2 (по умолчанию в это поле вводится адрес текущей ячейки).
5. В поле Значение ввести – 20.
6. В поле Изменяя значение ячейки указать адрес ячейки, в которой должен находиться параметр X, т.е. А1.

После выполнения команды в изменяемой ячейке появится значение параметра X, при котором результат формулы равняется заданной величине. При этом будет пересчитана вся таблица, т.е. изменятся значения, прямо или косвенно зависящие от изменяемого параметра.

Подбор параметра можно выполнять графически, перетаскивая точки данных на диаграмме.

При подборе параметра одна из ячеек обязательно должна содержать формулу.

ЗАДАНИЯ

1. Используя соответствующие финансовые функции, решите следующие задачи, (номер варианта задания – номер компьютера в учебной аудитории).
2. Для созданной задачи изменить величины ее параметров так, чтобы (не меняя формулы) результат вычислений тоже изменился.
3. Выполнить анализ данных «Что – если», используя таблицу подстановок.
4. Изменить результат вычислений задачи с помощью Сценария. Вывести итоговый отчет типа структура.
5. Изменить результат вычисления при помощи Подбора параметров.

Вариант 1.

1. Определить величину ежемесячной амортизации имущества (АПЛ (SLN)) при условии, что начальная стоимость его 10000р., а остаточная (в конце периода амортизации) 2000р.; амортизация имущества занимает период 10 месяцев.
2. Затем вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 1500р..
3. Определить величину ежемесячной амортизации имущества (АПЛ), используя таблицу подстановок:
4. при различных периодах: 5, 7, 8, 9, 10, 12 месяцев;
5. при различных периодах: 5, 7, 8, 9, 10, 12 месяцев, а также при остаточных стоимостях 5000, 4500, 4000, 3000, 2000, 1000 соответственно.
6. Составить сценарий, если начальная стоимость имущества изменится на 15000р.
7. Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 1500р.

Вариант 2.

1. Вычислить, на сколько снизится стоимость основных фондов, рассчитанная по методу двойной амортизации (ДДОБ), если начальная стоимость имущества 30000р., а в конце периода эксплуатации 4000р. Время эксплуатации считать равным 3 года, период, для которого вычисляется амортизация, равным 2,5 года.
2. Вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 5000р..
3. Определить величину ДДОБ используя таблицу подстановок:
4. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года;
5. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года; и начальной стоимости 70000, 60000, 50000, 40000, 30000 руб. соответственно.
6. Составить сценарий, если величина начальной стоимости изменится на 35000р.
7. Подобрать параметр срока эксплуатации, если стоимость основных фондов снизится на 1000р.

Вариант 3.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 50000р. со ставкой 5% годовых сроком на 4 года и будущей стоимостью 5000р.
2. Вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 7%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сроком на 5, 7, 8, 9, 10 лет соответственно.
6. Составить сценарий, если величина кредита изменится на 60000р, а срок на 5 лет.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 7000р.

Вариант 4.

1. Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 45000р., сроком на год, с ежемесячной выплатой 3000р. и годовой ставкой процента, равной 5%.
2. Затем, вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 3%.
3. Определить величину всех выплат (БС) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 50000, 60000, 70000, 80000, 90000, 100000 руб. соответственно.
6. Составить сценарий, если величина кредита изменится на 50000р.
7. Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 85000р.

Вариант 5.

1. Вычислить общее количество периодов выплаты (КПЕР) фирмой, взявшей кредит в размере 73000р. Ставка процента постоянна и равна 6%. Ежемесячные выплаты фирмой также постоянны и равны 5500р.
2. Вычислить эту величину (не меняя формулу) при условии, что величина кредита изменится на 60000р.
3. Определить величину КПЕР используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 50000, 60000, 70000, 80000, 90000, 100000 руб. соответственно.
6. Затем составить сценарий, если величина процентной ставки изменится на 12%.
7. Подобрать параметр величины кредита, если выплата будет производиться 19 месяцев.

Вариант 6.

1. Определить величину ежемесячной амортизации имущества (АПЛ) при условии, что начальная стоимость его 40000р., а остаточная (в конце периода амортизации) 9000р.; амортизация имущества занимает период 2 года.
2. Вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 7000р.
3. Определить величину АПЛ используя таблицу подстановок:
4. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и том же периоде;
5. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и периоде 0,5; 1, 1,5; 2, 3 года соответственно.
6. Составить сценарий, если начальная стоимость имущества изменится на 55000р.
7. Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 3500р.

Вариант 7.

1. Вычислить, на сколько снизится стоимость основных фондов, рассчитанная по методу двойной амортизации (ДДОБ), если начальная стоимость имущества 80000р., а в конце периода эксплуатации 10000р. Время эксплуатации считать равным 17 месяцев, период, для которого вычисляется амортизация, равным10 месяцев.
2. Вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 7000р.
3. Определить величину ДДОБ спользуя таблицу подстановок:
4. при варьировании начальной стоимости: 50000, 60000, 70000, 90000, 110000 и том же периоде амортизации;
5. при варьировании начальной стоимости: 50000, 60000, 70000, 90000, 110000 и периоде 5; 6, 7, 8, 9 месяцев соответственно.
6. Составить сценарий, если величина начальной стоимости изменится на 75000р.
7. Подобрать параметр срока эксплуатации, если стоимость основных фондов снизится на 2500р.

Вариант 8.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 90000р. со ставкой 7% на период, равный 1 году и будущей стоимостью 9000р.
2. После, вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 10%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 70000, 80000, 90000, 100000, 120000 руб. соответственно.
6. Составить сценарий, если величина кредита изменится на 80000р., а срок на 2 года.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 5000р.

Вариант 9.

1. Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 67000р., сроком на 3 года, с ежемесячной выплатой 7000р. и годовой ставкой процента, равной 4,5%.
2. Вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 6%.
3. Определить величину БС используя таблицу подстановок:
4. при процентных ставках 5%, 6%, 7% , 8% и 9% годовых;
5. при процентной ставке 5%, 6%, 7% , 8% и 9% годовых, и суммах кредита 70000, 80000, 90000, 100000, 120000 руб. соответственно.
6. После, составить сценарий, если величина кредита изменится на 59000р.
7. Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 103000р.

Вариант 10.

1. Вычислить общее количество периодов выплаты (КПЕР) фирмой, взявшей кредит в размере 93000р. Ставка процента постоянна и равна 6,5%. Ежемесячные выплаты фирмой также постоянны и равны 6500р.
2. Вычислить эту величину (не меняя формулу) при условии, что величина кредита изменится на 80000р.
3. Определить величину КПЕР используя таблицу подстановок:
4. при процентных ставках 5%, 6%,7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 100000,90000, 80000, 70000, 60000, 50000 руб. соответственно.
6. Затем составить сценарий (условие п.1), если величина процентной ставки изменится на 9%, а ежемесячная выплата 4500р.
7. Подобрать параметр величины кредита, если выплата будет производиться 2 года.

Вариант 11.

1. Определить величину ежемесячной амортизации имущества (АПЛ) при условии, что начальная стоимость его 100000р., а остаточная (в конце периода амортизации) 10000р.; амортизация имущества занимает период 4 года.
2. Затем вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 12000р.
3. Определить величину АПЛ используя таблицу подстановок:
4. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и том же периоде;
5. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 10000 и периоде 1, 2, 3, 3,5 и 4 года соответственно.
6. После, составить сценарий, если начальная стоимость имущества изменится на 97000р.
7. Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 7500р.

Вариант 12.

1. Вычислить, на сколько снизится стоимость основных фондов, рассчитанная по методу двойной амортизации (ДДОБ), если начальная стоимость имущества 123000р., а в конце периода эксплуатации 9000р. Время эксплуатации считать равным 13 месяцев, период, для которого вычисляется амортизация, равным8 месяцев.
2. После, вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 9500р.
3. Определить величину ДДОБ используя таблицу подстановок:
4. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года;
5. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года; и начальной стоимости 70000, 60000, 50000, 40000, 30000 руб. соответственно.
6. Затем составить сценарий, если величина начальной стоимости изменится на 115000р.
7. Подобрать параметр срока эксплуатации, если стоимость основных фондов снизится на 5500р.

Вариант 13.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 74000р. со ставкой 8% годовых на период, равный 5 лет и будущей стоимостью 5000р.
2. После, вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 14%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% ,10%, 12% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10%, 12% годовых, и сроке кредита 3, 4, 5, 6, 7, 8 лет соответственно.
6. Затем составить сценарий, если величина кредита изменится на 87000р.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 7500р.

Вариант 14.

1. Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 77000р., сроком на 2 года, с ежемесячной выплатой 9000р. и годовой ставкой процента, равной 7,5%.
2. Затем, вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 9%.
3. Определить, используя таблицу подстановок:
4. величину всех выплат (БС) при процентных ставках 7%, 8% , 9% и 10% годовых;
5. величину всех выплат (БС) при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, а сроке займа 5, 7, 8, 9, 10 лет соответственно.
6. Составить сценарий, если величина кредита изменится на 86000р.
7. Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 120000р.

Вариант 15.

1. Вычислить общее количество периодов выплаты (КПЕР) фирмой, взявшей кредит в размере 113000р. Ставка процента постоянна и равна 10%. Ежемесячные выплаты фирмой также постоянны и равны 8500р.
2. Вычислить эту величину (не меняя формулу) при условии, что величина кредита изменится на 100000р.
3. Определить общее количество периодов выплаты (КПЕР), используя таблицу подстановок:
4. при процентных ставках 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сумме кредита 50000, 70000, 80000, 90000, и 100000 руб. соответственно.
6. Составить сценарий, если величина процентной ставки изменится на 8,5%, а сумма кредита на 85000 руб. Сохранить отчет типа структура.
7. Подобрать параметр величины кредита, если выплата будет производиться 4 года.

Вариант 16.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 80000р. со ставкой 8% годовых сроком на 6 лет и будущей стоимостью 8000р.
2. Вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 12%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сроком на 5, 7, 8, 9, 10 лет соответственно.
6. Составить сценарий, если величина кредита изменится на 120000р, а срок на 10 лет.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 7000р.

Вариант 17.

1. Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 65000р., сроком на 3 года, с ежемесячной выплатой 4000р. и годовой ставкой процента, равной 6,5%.
2. Затем, вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 5%.
3. Определить величину всех выплат (БС) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 50000, 60000, 70000, 80000, 90000, 100000 руб. соответственно.
6. Составить сценарий, если величина кредита изменится на 70000р., а срок на 5 лет.
7. Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 95000р.

Вариант 18.

1. Определить величину ежемесячной амортизации имущества (АПЛ) при условии, что начальная стоимость его 90000р., а остаточная (в конце периода амортизации) 9000р.; амортизация имущества занимает период 5 лет.
2. Затем вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 10000р.
3. Определить величину АПЛ используя таблицу подстановок:
4. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и том же периоде;
5. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 10000 и периоде 1, 2, 3, 3,5 и 4 года соответственно.
6. После, составить сценарий, если начальная стоимость имущества изменится на 127000р., а период на 7 лет
7. Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 7500р.

Вариант 19.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 60000р. со ставкой 6% годовых сроком на 4 года и будущей стоимостью 6000р.
2. Вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 7%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сроком на 5, 7, 8, 9, 10 лет соответственно.
6. Составить сценарий, если величина кредита изменится на 80000р, а срок на 5 лет.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 2000р.

Вариант 20.

1. Определить, на сколько снизится стоимость имущества (ДДОБ) на заданный период, используя метод двойной амортизации,если начальная стоимость имущества 120000р., а в конце периода эксплуатации 12000р. Время эксплуатации считать равным 26 месяцев, период, для которого вычисляется амортизация, равным 12 месяцев.
2. Вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 9000р.
3. Определить величину ДДОБ используя таблицу подстановок:
4. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года;
5. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года и варьировании начальной стоимости: 70000, 80000, 90000, 100000, 110000 соответственно.
6. Составить сценарий, если величина начальной стоимости изменится на 95000р.
7. Подобрать параметр срока эксплуатации, если стоимость имущества снизится до 7000р.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Для чего предназначены функции: ПЛТ; БС; ПС; КПЕР и СТАВКА? Поясните синтаксис перечисленных функций.
2. Назначение и способы анализа «Что если»?
3. Для чего предназначена «Таблица подстановок», опишите технологию ее применение для функций с одной переменной и для функций с двумя переменными?
4. Что такое сценарий, как его создать, просмотреть, изменить, получить итоговый отчет на отдельном листе?
5. Сущность операции Подбор параметра, как она выполняется?

Программа Excel предлагает сразу несколько функций для расчета амортизации: ФУО, ДДОБ, АПЛ, АСЧ и ПУО. Рассмотрим функцию АПЛ для линейного метода вычисления амортизации и функцию ПУО с регрессивным методом.

Амортизация в первом и последнем году использования основных средств обычно существенно отличается от любого года в промежуточном периоде. Первая конвенция (общее принятое правило) – амортизация в первом году не рассчитывается как за полный год. Обычно это полгода, месяца либо же квартала. В случае полугодовой конвенции принимается как факт, что основные средства были приобретены в первом или втором полугодии, поэтому в текущем году будут амортизационные отчисления только за полгода.

Формула расчета линейной амортизации по функции АПЛ в Excel

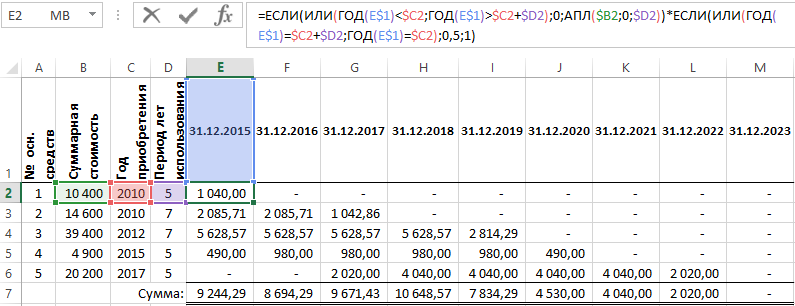
Ниже на рисунке представлен график амортизации пяти основных средств рассчитан линейным методом с принятой полугодовой конвенцией:

Столбцы A:D содержат следующие данные заполненные пользователем графика амортизации:

1. Номер основных средств – уникальный идентификатор для каждого основного средства. Он не является обязательным в этом графике, но будет удобным при отметке средств.
2. Суммарная стоимость – сумма начальной стоимости ввода в эксплуатацию основных средств. Содержит цену приобретения средства, а также налоги, заплаченные при приобретении, расходы на доставку к месту эксплуатации и все другие сопутствующие расходы, связанные с вводом в эксплуатацию каждого основного средства. Данная суммарная стоимость так же еще часто называется «базой» или «базовой стоимостью».
3. Год приобретения – год, в котором основное средство было введено в эксплуатацию. Может отличаться от года, в котором была проведена оплата за средство. Данный год определяет начало всего амортизационного периода эксплуатации.
4. Период лет использования – оцененное число лет, на протяжении которых средство будет использоваться.

Ячейки диапазона E2:M6 содержат следующую формулу:

Самая главная часть выше приведенной формулы – это функция =АПЛ($B2;0;$D2), которая рассчитывает амортизацию линейным методом за один период. Функция имеет 3 аргумента:

1. Начальная стоимость.
2. Остаточная стоимость.
3. Время эксплуатации.

Для упрощения в данном примере было указано значение остаточной стоимости равно нулю. Это значит, что в конце срока эксплуатации основное средство будет вольностью изношено амортизацией.

Сама функция АПЛ является очень простой. Но так как вы имеете дело с графиком амортизации, придется приложить немного усилий для его подготовки. Первая в формуле функция ЕСЛИ проверяет находиться ли дата, узнанная в заголовке текущего столбца в периоде эксплуатации основного средства. Если дата в ячейке E$1 является ранней чем дата приобретения основного средства $C2 – это значит, что средство еще не введено в эксплуатацию и амортизационные отчисления равны 0. Если же вместо этого значение даты в ячейке E$1 является позднейшей от даты приобретения $C2 плюс период лет использования $D2, тогда это значит, что основное средство полностью изношено и выведено из эксплуатации. А его амортизационные отчисления также равны 0. Оба условия помещены внутри функции ИЛИ, благодаря чему если одно из условий будет выполнено, то целое выражение будет возвращать значение ИСТИНА, а значит значение во втором аргументе функции ЕСЛИ, которое =0. Если же ни одно условие не будет выполнено формула возвратит результат вычислении функции АПЛ.

Вторая часть формулы также содержит слияние функций ИЛИ и ЕСЛИ. Использование в них логическое выражение определяет, будет ли год, записанный в ячейке E$1 первым =$C2 или последним =$C2+$D2 годом периода амортизации. Если значение одного с выражений является ИСТИНА, размер амортизационных отчислений вычисленный линейным методом умножается на 0,5 (то есть разделяется по полам), согласно с принятой полугодовой конвенцией амортизации в данном примере.

Все ссылки, использованные в выше приведенной формуле, являются смешанными (частично абсолютными), благодаря чему формулу можно копировать во все нижние и правые ячейки. Ссылки в формулах будут соответственно изменятся автоматически. Ссылка на целую первую строку позволяет выражениям вычислять результаты с учетом дат записанных в заголовках столбцах первой строки листа Excel. Аналогично ссылки на целые столбцы B:D позволяют копированным формулам использовать одни и те же значения со столбцов «Суммарная стоимость», «Год приобретения» и «Период лет использования».



Функция ДДОБ для расчета ускоренной амортизации основных средств в Excel

При линейном методе расчета амортизации на протяжении всего срока эксплуатации основного средства выполняются отчисления в одинаковых размерах. Некоторые фирмы применяют ускоренную амортизацию, в которой отчисление в начале периода больший, чем в конце. Теория гласит, что основное средство расходует в начале срока эксплуатации большую часть своей стоимости чем в конце. В таком случае необходимо применять регрессивный метод амортизации вместо линейного.

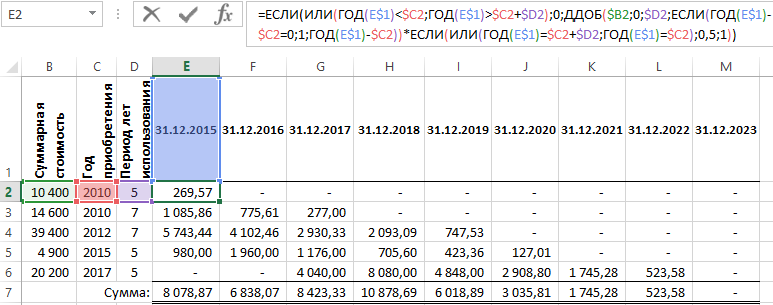
Программа Excel предлагает функцию ДДОБ для расчета ускоренной амортизации. Данная функция вычисляет амортизационные отчисления для остаточной стоимости основного средства по линейному методу двойного уменьшения остатка с увеличенным коэффициентом:

В результате в первый период эксплуатации возвращается максимальная амортизация, которая уменьшается в последующие периоды. Проблема с этой функцией заключается в том, что она не амортизирует целое основное средство в период его эксплуатации:

Поэтому амортизационные отчисления каждый раз уменьшаются, но не достигают нулевой стоимости при окончании срока эксплуатации основного средства.

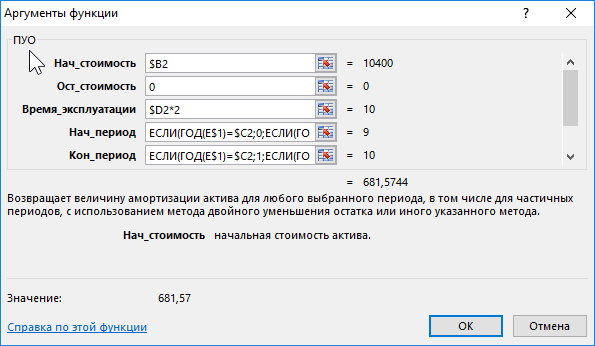
Формула ПУО для расчета амортизации регрессивным методом в Excel

Ускоренная амортизация наиболее часто применяется в начале срока эксплуатации основного средства, но, когда размер отчисления будет ниже размера результата вычисления линейным методом, тогда на остаток срока эксплуатации будет применятся обычный расчет амортизации линейным методом. Хорошо, что Excel располагает функцией ПУО, которая как раз и работает по данному принципу действия.

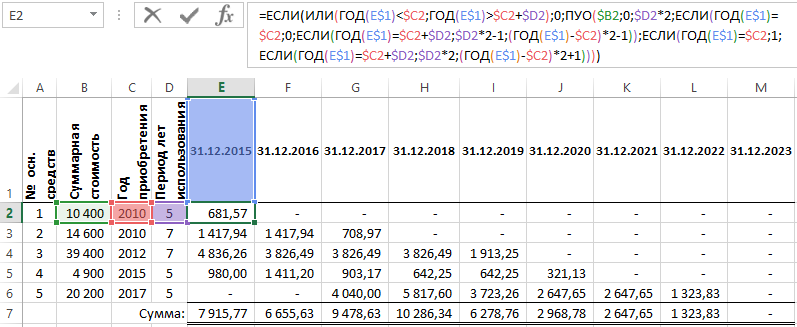
Ниже на рисунке представлен график амортизации с использование следующей формулы:

Как не сложно заметить данная формула более сложная, чем в предыдущем примере, в котором была использована функция АПЛ. Но любое большое и сложное всегда можно разложить на маленькое и простое.

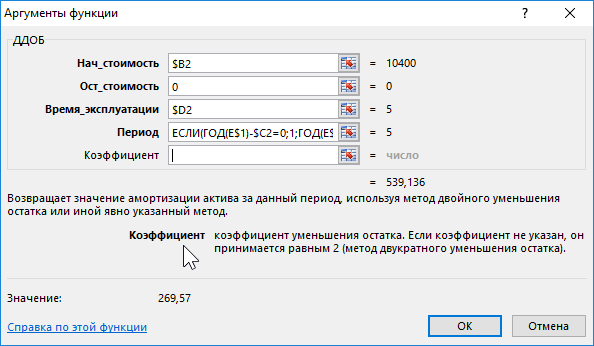
Первая часть формулы является идентичной части формулы с функцией АПЛ, описанной выше в данной статье. Если дата в строке 1 не включена в срок эксплуатации основных средств, тогда амортизационные отчисления =0. В противном случае вычисляется результат, возвращаемый функцией ПУО и используется как содержимое третьего аргумента для функции ЕСЛИ. Функция же ПУО содержит в свой аргумент начало и конец периода амортизации вычисление которых будут описаны ниже:

Первые три аргумента функции ПУО такие же, как и в функции АПЛ: начальная стоимость, остаточная стоимость и время эксплуатации. Функция АПЛ возвращает одно и тоже значение для каждого периода амортизации, поэтому в ней нет необходимости указывать расчетные периоды. Вместо этого функция ПУО возвращает разные значения в зависимости от номера периода расчета амортизации. Последние 2 аргумента функции ПУО (начальный и конечный период) определяют только те номера периодов, которых будет касается вычисление функции. Период эксплуатации, указанный в ячейке $D2 удвоенный, о чем речь пойдет далее.

Ни одна функция Excel не учитывает принятой конвекции амортизации. Это значит, что амортизация рассчитывается так, как бы все основные средства были приобретены первого числа первого года. На практике – это далеко не так. В данном примере принята полугодовая конвенция, согласно которой в первом и последнем полугодии эксплуатации основного средства начисляется только половина вычисленного амортизационного отчисления. Чтобы с помощью функции ПУО рассчитать амортизацию согласно с полугодовой конвенцией, необходимо немного «обмануть» Excel так, чтобы он посчитал срок эксплуатации основного средства в два раза большим.

Если период эксплуатации средства составляет 5 лет, в тоже время начало и конец первого года определены номерами 0 и 1. Во втором году это будут уже номера 1 и 3, в третьем 3 и 5. Данная схема повторяется аж до последнего года, определенного номерами 9 и 10 (число десять значит двойной пятилетний период эксплуатации средства). Начальный период вычисляется выше указанной формулой следующим способом:

1. Если год учитывается в вычислениях, и он является годом приобретения средства, начальный период ему присваивается под номером 0.
2. Если год учитывается в вычислениях, и он является последним годом периода, тогда начальный период равен двойному сроку эксплуатации средства минус 1.
3. В случаи всех остальных лет от года приобретения вычитается текущий год, а результат умножается на число 2 и вычитается от полученного результата число 1.

Часть формулы вычисляющая конечный период подобна на часть формулы вычисляющей начальный период. Для первого года конечный период был определен числом 1, а в последнем году уже конечный период определяется как количество лет полного периода эксплуатации средства, умноженное на число 2, а от результата вычитается число 1. В промежуточных годах вычисления выглядят также за исключением того, что единица добавляется (+1), а не вычитается.

Скачать графики линейной и регрессивной амортизации в Excel

Например, в случае основного средства в семилетнем периоде эксплуатации умножая 7 периодов на 2, вы применяете полугодовую конвенцию амортизации с регрессивным методом вычисления с помощью функции ПУО.

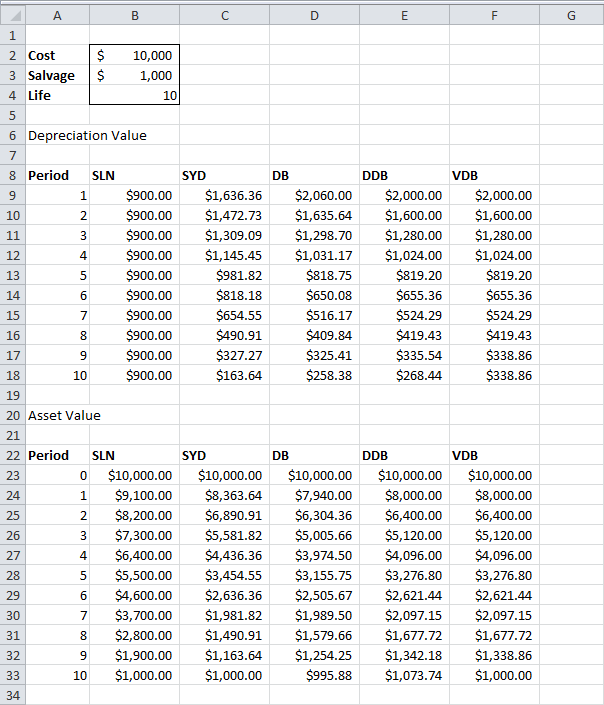
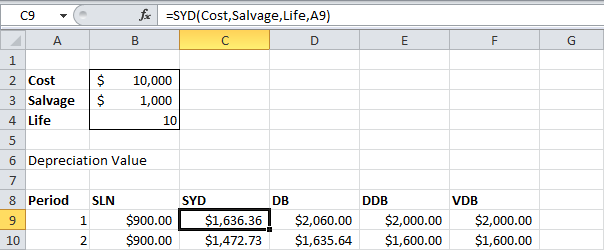
Excel предлагает пять различных функций для расчёта амортизации. Рассмотрим актив с первоначальной стоимостью $10000, ликвидационной (остаточной) стоимостью $1000 и сроком полезной службы 10 периодов (лет). Ниже показаны результаты всех пяти функций. Далее о каждой из этих функций мы расскажем более подробно.

Большинство активов теряют большую часть своей ценности в начале своего срока полезной службы. Функции АСЧ (SYD), ФУО (DB), ДДОБ (DDB) и ПУО (VDB) учитывают этот фактор.

АПЛ

Функция АПЛ (SLN) – проста, как прямая линия. Каждый год амортизационные отчисления считаются равными.

Функция АПЛ выполняет следующие вычисления:

• Амортизационные отчисления = ($10000–$1000)/10 = $900.
• Если мы 10 раз вычтем полученную сумму из первоначальной стоимости актива, то его стоимость в результате амортизации изменится с $10000 до $1000 за 10 лет (это показано в нижней части первого рисунка в начале статьи).

АСЧ

Функция АСЧ (SYD) также проста – она рассчитывает амортизацию методом суммы годовых чисел. Как показано ниже, для данной функции также требуется указать количество периодов.

Функция АСЧ выполняет следующие вычисления:

• Срок полезной службы 10 лет даёт сумму чисел 10+9+8+7+6+5+4+3+2+1 = 55
• Актив за рассматриваемый срок (10 лет) теряет $9000 стоимости.
• Величина амортизации 1 = 10/55*$9000 = $1636.36;
  Величина амортизации 2 = 9/55*$9000 = $1472.73 и так далее.
• Если вычесть все полученные величины амортизации из первоначальной стоимости актива $10000, то мы получим остаточную стоимость $1000 после срока полезной службы 10 лет (смотрите нижнюю часть первого рисунка в начале статьи).

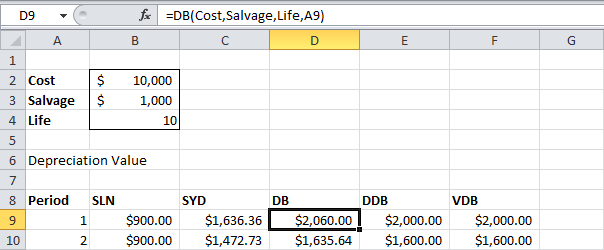
ФУО

Функция ФУО (DB) немного сложнее. Для расчёта величин амортизации используется метод фиксированного уменьшения остатка.

Функция ФУО выполняет следующие вычисления:

• Ставка = 1–((остат_стоимость/нач_стоимость)^(1/срок_эксплуатации)) = 1–($1000/$10000)^(1/10)) = 0.206. Результат округлён до тысячных долей.
• Величина амортизации период 1 = $10000*0.206 = $2060.00;
  Величина амортизации период 2 = ($10000-$2060.00)*0.206 = $1635.64 и так далее.
• Если вычесть все полученные величины амортизации из первоначальной стоимости актива $10000, то мы получим остаточную стоимость $995.88 после срока полезной службы 10 лет (смотрите нижнюю часть первого рисунка в начале статьи).

Замечание: Функция ФУО имеет пятый необязательный аргумент. Этот аргумент можно использовать, если нужно указать количество месяцев эксплуатации в первом расчётном году (если этот аргумент пропущен, то количество месяцев эксплуатации в первом году считается равным 12). Например, если актив был приобретён в начале второго квартала года, т.е. в первом году срок эксплуатации актива составил 9 месяцев, то для пятого аргумента функции нужно указать значение 9. В этом случае в формулах, которые Excel использует для расчёта амортизации для первого и последнего периода есть некоторое различие (последним периодом будет 11-й год, состоящий только из 3-х месяцев эксплуатации).

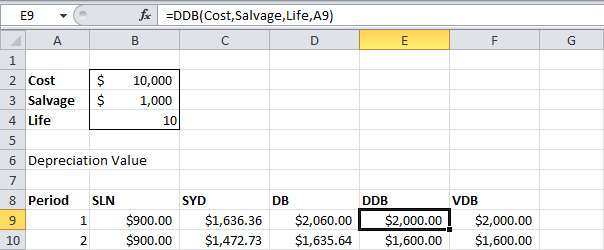
ДДОБ

Функция ДДОБ (DDB) – двойное уменьшение остатка, снова из числа простых. Однако, при использовании этой функции не всегда достигается требуемая остаточная стоимость.

Функция ДДОБ выполняет следующие вычисления:

• При сроке полезной службы 10 лет получаем ставку 1/10 = 0.1. Метод, используемый функцией, называется методом двойного уменьшения остатка, следовательно, мы должны удвоить ставку (коэффициент = 2).
• Величина амортизации период 1 = $10000*0.2 = $2000;
  Величина амортизации период 2 = ($10000-$2000)*0.2 = $1600 и так далее.

Как уже было сказано, при использовании этой функции не всегда достигается требуемая остаточная стоимость. В данном примере, если вычесть все полученные величины амортизации из первоначальной стоимости актива $10000, то в результате через 10 лет получим значение остаточной стоимости $1073.74 (смотрите нижнюю часть первого рисунка в начале статьи). Читайте далее, чтобы узнать, как исправить эту ситуацию.

Замечание: Функция ДДОБ имеет пятый не обязательный аргумент. Значение этого аргумента определяет различный коэффициент для процентной ставки снижающегося остатка.

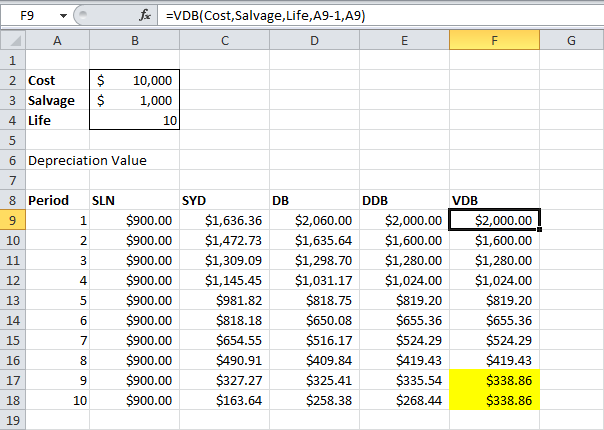
ПУО

Функция ПУО (VDB) по умолчанию использует метод двойного уменьшения остатка. Четвёртый аргумент определяет начальный период, пятый аргумент определяет конечный период.

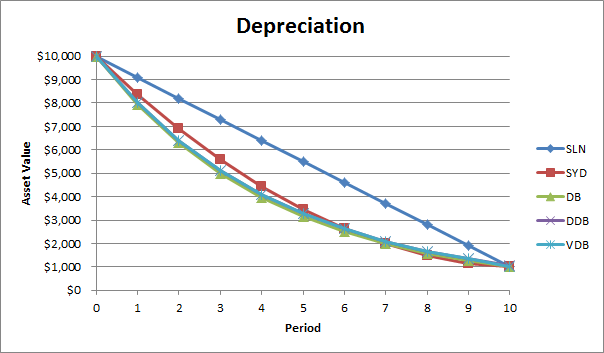
Функция ПУО выполняет те же вычисления, что и функция ДДОБ. Однако, при необходимости она переключается в режим вычислений «прямая линия», когда это необходимо (выделено жёлтым) для того, чтобы достичь значения остаточной стоимости (смотрите нижнюю часть первого рисунка в начале статьи). Переключение в режим вычислений «прямая линия» происходит только в том случае, когда величина амортизации по методу «прямая линия» превышает величину амортизации по методу «двойного уменьшения остатка».

В восьмом периоде величина амортизации по методу двойного уменьшения остатка = $419.43. На данном этапе мы имеем сумму для списания амортизации равную $2097.15-$1000 (смотрите нижнюю часть первого рисунка в начале статьи). Если использовать метод «прямая линия» для дальнейших вычислений, то для оставшихся трёх периодов мы получим величину амортизации $1097/3=$365.72. Это значение не превышает значения, полученного методом двойного уменьшения остатка, поэтому переключения на метод «прямая линия» не происходит.

В девятом периоде величина амортизации по методу двойного уменьшения остатка = $335.54. На данном этапе мы имеем сумму для списания амортизации равную $1677.72-$1000 (смотрите нижнюю часть первого рисунка в начале статьи). Если использовать метод «прямая линия» для дальнейших вычислений, то для оставшихся двух периодов мы получим величину амортизации $677.72/2 = $338.86. Это значение превышает значение, полученное методом двойного уменьшения остатка, поэтому происходит переключение на метод «прямая линия».

Замечание: Функция ПУО значительно более гибкая, чем функция ДДОБ. С её помощью можно вычислять величину амортизации сразу для нескольких периодов.

Функция содержит шестой и седьмой необязательные аргументы. При помощи шестого аргумента можно определить другой коэффициент для процентной ставки снижающегося остатка. Если для седьмого аргумента установить значение ИСТИНА (TRUE), то переключения в режим вычислений «прямая линия» не происходит.