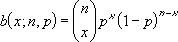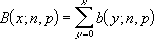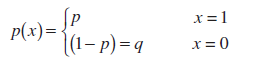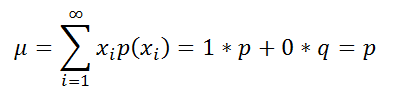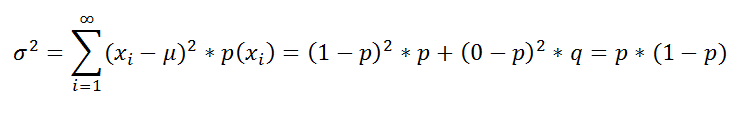Функция биномрасп в excel

Возвращает отдельное значение биномиального распределения. Функция БИНОМРАСП используется в задачах с фиксированным числом тестов или испытаний, когда результатом любого испытания может быть только успех или неудача, испытания независимы, а вероятность успеха одинакова на протяжении всего эксперимента. Например, при помощи БИНОМРАСП можно вычислить, с какой вероятностью двое из трех следующих новорожденных будут мальчиками.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.

Дополнительные сведения о новом варианте этой функции см. в статье Функция БИНОМ.РАСП.

Синтаксис

БИНОМРАСП(число_успехов;число_испытаний;вероятность_успеха;интегральная)

Аргументы функции БИНОМРАСП описаны ниже.

• Число_успехов     — обязательный аргумент. Количество успешных испытаний.

• Число_испытаний     — обязательный аргумент. Количество независимых испытаний.

• Вероятность_успеха     — обязательный аргумент. Вероятность успеха каждого испытания.

• Интегральная     — обязательный аргумент. Логическое значение, определяющее форму функции. Если «накопительный» имеет number_s, функция БИНОМРАСП возвращает накопительную функцию распределения. Если имеется ложь, возвращается функция вероятностной массы, которая является вероятностью number_s успеха.

Замечания

• Число_успехов и число_испытаний усекаются до целых.

• Если number_s, испытаний или probability_s не является числом, бинОМЕТ возвращает #VALUE! значение ошибки #ЗНАЧ!.

• Если number_s < 0 или number_s >, бинОМЕТ возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если probability_s < 0 или probability_s > 1, бинОМЕТ возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если x = число_успехов, n = число_испытаний и p = вероятность_успеха, то весовая функция биномиального распределения выглядит следующим образом:

  

  где

  

  — ЧИСЛКОМБ(n;x).

• Если x = число_успехов, n = число_испытаний и p = вероятность_успеха, то интегральное биномиальное распределение выглядит следующим образом:

  

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
6	Количество успешных испытаний
10	Количество независимых испытаний
0,5	Вероятность успеха в каждом испытании
Формула	Описание	Результат
=БИНОМРАСП(A2;A3;A4;ЛОЖЬ)	Вероятность того, что ровно 6 испытаний из 10 будут успешными	0,2050781

Функция БИНОМРАСП устаревшая с 2010-й версии Excel, оставлена для обратной совместимости с 2007 и более ранними версиями, рекомендуется воспользоваться БИНОМ.РАСП

Описание функции БИНОМРАСП

Синтаксис

=БИНОМРАСП(число_успехов; число_испытаний; вероятность_успеха; интегральная)

Аргументы

Замечания

Пример

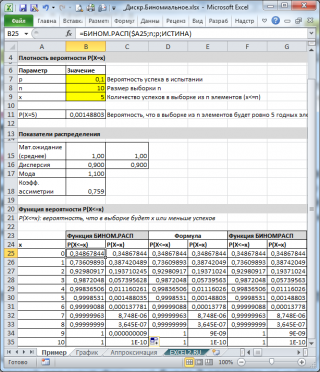
Рассмотрим Биномиальное распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL

БИНОМ.РАСП()

построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения p, математического ожидания распределения и стандартного отклонения. Также рассмотрим распределение Бернулли.

Определение

. Пусть проводятся

n

испытаний, в каждом из которых может произойти только 2 события: событие «успех» с вероятностью

p

или событие «неудача» с вероятностью

q

=1-p (так называемая

Схема Бернулли,

Bernoulli

trials

).

Вероятность получения ровно

x

успехов в этих

n

испытаниях равна:

Примечание

:

Порядок получения успехов значения не имеет. Если важен порядок, то см. статью

Отрицательное Биномиальное распределение

.

Количество успехов в выборке

x

является случайной величиной, которая имеет

Биномиальное распределение

(англ.

Binomial

distribution

)

p

и

n

–

являются параметрами этого распределения.

Примечание

: Запись

означает количество

сочетаний

из

n

элементов по

x

. Для сочетаний также используется запись

. Подробнее о сочетаниях см. статью

Сочетания без повторений: Комбинаторика в MS EXCEL

.

Напомним, что для применения

схемы Бернулли

и соответственно

Биномиального распределения,

должны быть выполнены следующие условия:

• каждое испытание должно иметь ровно два исхода, условно называемых «успехом» и «неудачей».
• результат каждого испытания не должен зависеть от результатов предыдущих испытаний (независимость испытаний).
• вероятность успеха
  
  p
  
  должна быть постоянной для всех испытаний.

Биномиальное распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для

Биномиального распределения

имеется функция

БИНОМ.РАСП()

, английское название — BINOM.DIST(), которая позволяет вычислить вероятность того, что в выборке будет ровно

х

«успехов» (т.е.

функцию плотности вероятности

p(x), см. формулу выше), и

интегральную функцию распределения

(вероятность того, что в выборке будет

x

или меньше «успехов», включая 0).

СОВЕТ

: Подробнее о

Функции распределения

и

Плотности вероятности

см. статью

Функция распределения и плотность вероятности в MS EXCEL

.

До MS EXCEL 2010 в EXCEL была функция

БИНОМРАСП()

, которая также позволяет вычислить

функцию распределения

и

плотность вероятности

p(x).

БИНОМРАСП()

оставлена в MS EXCEL 2010 для совместимости.

В

файле примера

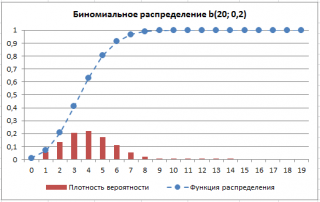
приведены графики

плотности распределения вероятности

и

интегральной функции распределения

.

Биномиальное распределения

имеет обозначение

B

(

n

;

p

)

.

Примечание

: Для построения

интегральной функции распределения

идеально подходит диаграмма типа

График

, для

плотности распределения

–

Гистограмма с группировкой

. Подробнее о построении диаграмм читайте статью Основные типы диаграмм.

Примечание

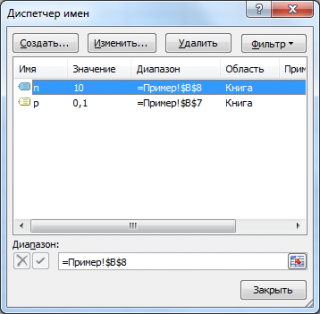
: Для удобства написания формул в

файле примера

созданы Имена для параметров

Биномиального распределения

: n и p.

В

файле примера

приведены различные расчеты вероятности с помощью функций MS EXCEL:

Как видно на картинке выше, предполагается, что:

• В бесконечной совокупности, из которой делается выборка, содержится 10% (или 0,1) годных элементов (параметр
  
  p
  
  , третий аргумент функции =
  
  БИНОМ.РАСП()
  
  )
• Чтобы вычислить вероятность, того что в выборке из 10 элементов (параметр
  
  n
  
  , второй аргумент функции) будет ровно 5 годных элементов (первый аргумент), нужно записать формулу:
  
  =БИНОМ.РАСП(5; 10; 0,1; ЛОЖЬ)
  
• Последний, четвертый элемент, установлен =ЛОЖЬ, т.е. возвращается значение функции
  
  плотности распределения
  
  .

Если значение четвертого аргумента =ИСТИНА, то функция

БИНОМ.РАСП()

возвращает значение

интегральной функции распределения

или просто

Функцию распределения

. В этом случае можно рассчитать вероятность того, что в выборке количество годных элементов будет из определенного диапазона, например, 2 или меньше (включая 0).

Для этого нужно записать формулу: =

БИНОМ.РАСП(2; 10; 0,1; ИСТИНА)

Примечание

: При нецелом значении х,

дробная часть отбрасывается

. Например, следующие формулы вернут одно и тоже значение:

=БИНОМ.РАСП(

2

; 10; 0,1; ИСТИНА)

=БИНОМ.РАСП(

2,9

; 10; 0,1; ИСТИНА)

Примечание

: В

файле примера

плотность вероятности

и

функция распределения

также вычислены с использованием определения и функции

ЧИСЛКОМБ()

.

Показатели распределения

В

файле примера на листе Пример

имеются формулы для расчета некоторых показателей распределения:

• математического ожидания

  =n*p;

• дисперсии

  (квадрата стандартного отклонения) = n*p*(1-p);

• моды

  = (n+1)*p;

• коэффициента асимметрии

  =(1-2*p)*КОРЕНЬ(n*p*(1-p)).

Выведем формулу

математического ожидания

Биномиального распределения

, используя

Схему Бернулли

.

По определению случайная величина Х в

схеме Бернулли

(Bernoulli random variable) имеет

функцию распределения

:

Это распределение называется

распределение Бернулли

.

Примечание

:

распределение Бернулли

– частный случай

Биномиального распределения

с параметром n=1.

Найдем

математическое ожидание

(

среднее,

mean

)

распределения Бернулли

(

x

принимает только 2 значения).

Предположим, что мы провели

n

последовательных

испытаний Бернулли

и у нас сформировалась

выборка

, состоящая из n элементов: x1, x2, …, xn (каждое из которых равно 0 или 1). Сумма этих случайных величин Y=X1+X2+…+Xn, в свою очередь, также является случайной величиной и, как мы помним, будет иметь

Биномиальное распределение

с параметрами

n

и

p

.

Учитывая, что

математическое ожидание

для каждого

x

_i

равно

p

, то для соответствующего

Биномиального распределения μ=p*n.

Аналогичным образом, можно вычислить

дисперсию

Биномиального распределения.

Для этого сначала найдем

дисперсию

(

второй момент, variance

)

распределения Бернулли

:

Соответственно, дисперсия для

Биномиального распределения

равна

σ

²

=n*p*(1-p)= n*p*q.

Генерация случайных чисел. Распределение Бернулли

С помощью надстройки

Пакет анализа

можно

сгенерировать случайные числа

, извлеченные из

распределения Бернулли

.

СОВЕТ

: О надстройке

Пакет анализа

можно прочитать в статье

Надстройка Пакет анализа MS EXCEL

.

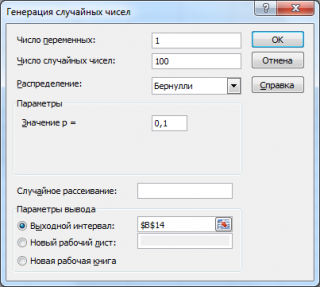
Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5 и 0,9. Для этого в окне

Генерация случайных чисел

установим следующие параметры для каждой вероятности p:

Примечание

: Если установить опцию

Случайное рассеивание

(

Random Seed

), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию =25 можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции

Случайное рассеивание

может запутать. Лучше было бы ее перевести как

Номер набора со случайными числами

.

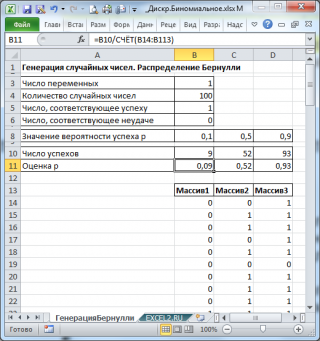
В итоге будем иметь 3 столбца по 100 чисел, на основании которых можно, например, оценить вероятность успеха

p

по формуле:

Число успехов/100

(см.

файл примера лист ГенерацияБернулли

).

Примечание

: Для

распределения Бернулли

с p=0,5 можно использовать формулу

=СЛУЧМЕЖДУ(0;1)

, которая соответствует

дискретному равномерному распределению

.

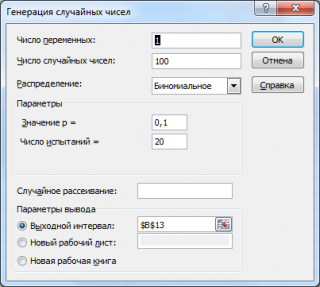
Генерация случайных чисел. Биномиальное распределение

С помощью надстройки

Пакет анализа

можно

сгенерировать случайные числа

, извлеченные из

Биномиального

распределения

.

Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5; 0,9. Количество испытаний n установим 20. Для этого в окне

Генерация случайных чисел

установим следующие параметры для каждой вероятности p:

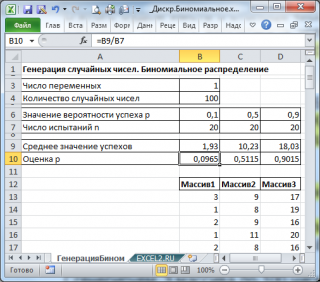
В итоге будем иметь 3 столбца чисел, на основании которых можно, например, оценить вероятность успеха

p

по формуле:

Среднее значение успехов/

n

(см.

файл примера лист ГенерацияБином

).

Примечание

: Для генерирования массива чисел, распределенных по

Биномиальному закону

, можно использовать формулу

=БИНОМ.ОБР(20; p; СЛЧИС())

, где p – вероятность успеха. Функция

СЛЧИС()

генерирует

непрерывное равномерное распределение

от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.

файл примера лист ГенерацияБином

).

Оценка параметра p

В

схеме Бернулли

оценить параметр распределения

p

можно по формуле

=СУММ(B14:B113)/СЧЁТ(B14:B113)

. В формуле предполагается, что массив случайных чисел находится в диапазоне

B14:B113

.

Оценить параметр

Биномиального распределения

p

можно по формуле

= СРЗНАЧ(B13:B112)/n

(предполагается, что случайные числа сгенерированы формулой

=БИНОМ.ОБР(n; p; СЛЧИС()

). Также в формуле предполагается, что массив случайных чисел находится в диапазоне

B13:B112

.

Обратная функция БИНОМ.ОБР()

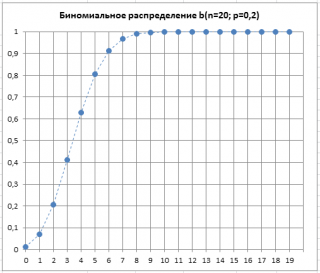
Вспомним график функции

Биномиального распределения

:

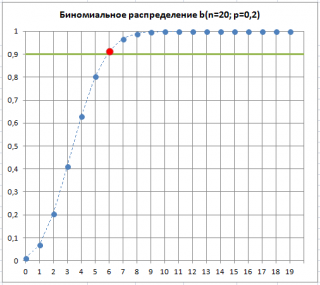
Решим задачу. Предположим, что для целей контроля качества нам требуется определить наибольшее допустимое количество дефектных изделий, которое еще позволяет обойтись без отбраковки всей партии.

Задана величина выборки из партии (

n

=20) и

р=

0,2 — доля дефектных изделий, которая обычно наблюдается в данном производственном процессе. Также пусть задана вероятность допустить

ошибку 1-го рода

(см.

статью про уровень доверия

) равная 90%. Пороговый приемочный критерий можно вычислить по формуле

=БИНОМ.ОБР(20; 0,2; 90%)

. Формула вернет значение 6 — наибольшее количество дефектных изделий, допустимое в

выборке

.

Примечание

: Третий аргумент функции

БИНОМ.ОБР()

называется

Альфа

(

α error, type I error, риск производителя, альфа-риск

) и представляет собой вероятность допустить

ошибку 1-го рода

при

проверке статистической гипотезы

(см. статью

Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)

).

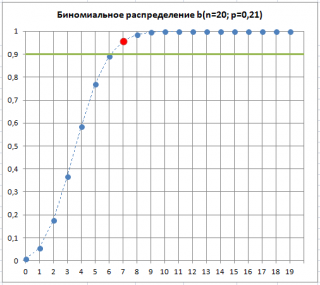
Предположим, что в выборке обнаружилось 7 дефектных изделий. Это означает, что «очень вероятна» ситуация, что изменилась доля дефектных изделий

p

, которая является характеристикой нашего производственного процесса. Хотя такая ситуация «очень вероятна», но существует вероятность (альфа-риск, ошибка 1-го рода, «ложная тревога»), что все же

p

осталась без изменений, а увеличенное количество дефектных изделий обусловлено случайностью выборки.

Как видно на рисунке ниже, 7 – количество дефектных изделий, которое допустимо для процесса с p=0,21 при том же значении

Альфа

. Это служит иллюстрацией, что при превышении порогового значения дефектных изделий в выборке,

p

«скорее всего» увеличилось. Фраза «скорее всего» означает, что существует всего лишь 10% вероятность (100%-90%) того, что отклонение доли дефектных изделий выше порогового вызвано только сучайными причинами.

Таким образом, превышение порогового количества дефектных изделий в выборке, может служить сигналом, что процесс расстроился и стал выпускать б

о

льший процент бракованных изделий.

Примечание

: До MS EXCEL 2010 в EXCEL была функция

КРИТБИНОМ()

, которая эквивалентна

БИНОМ.ОБР()

.

КРИТБИНОМ()

оставлена в MS EXCEL 2010 и выше для совместимости.

Связь Биномиального распределения с другими распределениями

Если параметр

n

Биномиального распределения

стремится к бесконечности, а

p

стремится к 0, то в этом случае

Биномиальное распределение

может быть аппроксимировано

Распределением Пуассона

. Можно сформулировать условия, когда приближение

распределением Пуассона

работает хорошо:

• 
  p
  <0,1
  
  (чем меньше
  
  p
  
  и больше
  
  n
  
  , тем приближение точнее);
• 
  p
  
  >0,9
  
  (учитывая, что
  
  q
  
  =1-
  
  p
  
  , вычисления в этом случае необходимо производить через
  
  q
  
  (а
  
  х
  
  нужно заменить на
  
  n
  
  —
  
  x
  
  ). Следовательно, чем меньше
  
  q
  
  и больше
  
  n
  
  , тем приближение точнее).

При 0,1<=p<=0,9 и n*p>10

Биномиальное распределение

можно аппроксимировать

Нормальным распределением

.

В свою очередь,

Биномиальное распределение

может служить хорошим приближением

Гипергеометрического распределения

, когда размер совокупности N

Гипергеометрического распределения

гораздо больше размера выборки n (т.е., N>>n или n/N<<1).

Подробнее о связи вышеуказанных распределений, можно прочитать в статье

Взаимосвязь некоторых распределений друг с другом в MS EXCEL

. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

Распределение вероятностей – одно из центральных понятий теории
вероятности и математической статистики. Определение распределения вероятности
равносильно заданию вероятностей всех СВ, описывающих некоторое случайное
событие. Распределение вероятностей некоторой СВ, возможные значения которой x₁, x₂, … x_n образуют
выборку, задается указанием этих значений и соответствующих им вероятностей p₁, p₂,… p_n. (p_n должны быть
положительны и в сумме давать единицу).

В данной лабораторной работе будут рассмотрены и построены с помощью MS Excel наиболее
распространенные распределения вероятности: биномиальное и нормальное.

1 Биномиальное распределение

Представляет собой распределение вероятностей числа наступлений
некоторого события («удачи») в n повторных
независимых испытаниях, если при каждом испытании вероятность наступления этого
события равна p. При этом
распределении разброс вариант (есть или нет события) является следствием
влияния ряда независимых и случайных факторов.

 Примером практического использования биномиального распределения
может являться контроль качества партии фармакологического препарата. Здесь
требу­ется подсчитать число изделий (упаковок), не соответствующих требованиям.
Все причины, влияющие на качество препарата, принимаются одинаково вероятными и
не зависящими друг от друга. Сплошная проверка качества в этой ситуации не
возможна, поскольку изделие, прошедшее испытание, не подлежит дальнейшему
использованию. Поэтому для контроля из партии наудачу выбирают определенное
количество образцов изделий (n). Эти образцы всестороннее
проверяют и регистрируют число бракованных изделий (k). Теоретически число
бракованных изделий может быть любым, от 0 до n.

В Excel функция БИНОМРАСП
применяется для вычисления вероятности в задачах с фиксированным числом тестов
или испытаний, когда результатом любого испытания может быть только успех или
неудача.

Функция использует следующие
параметры:

БИНОМРАСП (число_успехов;
число_испытаний; вероятностъ_успеха; интегральная), где

число_успехов — это количество успешных
испытаний;

число_испытаний — это число независимых
испытаний (число успехов и число испытаний должны быть целыми числами);

вероятность_ успеха — это вероятность успеха
каждого испытания;

интегральный — это логическое значение,
определяющее форму функции.

Если данный параметр имеет
значение ИСТИНА (=1), то считается интегральная функция распределения
(вероятность того, что число успешных испытаний не менее значения число_
успехов);

если этот параметр имеет
значение ЛОЖЬ (=0), то вычисляется значение функ­ции плотности
распределения (вероятность того, что число успешных испытаний в точности равно
значению аргумента число_ успехов).

Пример 1. Какова вероятность того,
что трое из четырех новорож­денных будут мальчиками?    

Решение:

1.   Устанавливаем табличный курсор в свободную
ячейку, например в А1. Здесь должно оказаться значение искомой
вероятности.

2.   Для получения значения вероятности
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка
функции (fx).

3.   В появившемся диалоговом окне Мастер
функций — шаг 1 из 2 слева в поле Катего­рия указаны виды функций.
Выбираем Статистическая. Справа в поле Функция выбираем функцию БИНОМРАСП
и нажимаем на кнопку ОК.

Появляется диалоговое окно
функции. В поле Число_s вводим с клавиатуры
количество успешных испытаний (3). В поле Испытания вво­дим с клавиатуры
общее количество испытаний (4). В рабочее поле Вероятность_s
вводим с клавиатуры вероятность успеха в отдельном испытании (0,5). В поле Интегральный
вводим с клавиатуры вид функции распределения — интегральная или весовая (0).
Нажимаем на кнопку ОК.

В ячейке А1 появляется
искомое значение вероятности р = 0,25. Ровно 3 мальчика из 4
новорожденных могут появиться с вероят­ностью 0,25.

Если изменить формулировку
условия задачи и выяснить вероятность того, что появится не более трех
мальчиков, то в этом случае в рабочее поле Интегральный вводим 1 (вид
функции распределения интегральный). Вероятность этого события будет равна
0,9375.

Задания для самостоятельной работы

1. Какова вероятность того, что восемь из десяти студентов,
сдающих зачет, получат «незачет». (0,04)

2.
Нормальное распределение

Нормальное распределение — это совокупность объектов, в кото­рой крайние значения
некоторого признака — наименьшее и наибольшее — появ­ляются редко; чем ближе значение признака к математическому ожиданию,
тем чаще оно встречается. Например, распределение студентов по их весу приближа­ется
к нормальному распределению. Это распределение имеет очень широкий круг приложений в
статистике, включая проверку гипотез.

Диаграмма нормального
распределения симметрична относительно точки а (математического
ожидания). Ме­диана нормального распределения равна тоже а. При этом в
точке а функция f(x) достигает своего максимума, который равен

.

В Excel для вычисления значений
нормального распределения используются фун­кция НОРМРАСП, которая
вычисляет значения вероятности нормальной функции распределения для указанного
среднего и стандартного отклонения.

Функция имеет параметры:

НОРМРАСП (х; среднее;
стандартное_откл; интегральная), где:

х — значения выборки, для
которых строится распределение;

среднее — среднее арифметическое
выборки;

стандартное_откл — стандартное отклонение
распределения;

интегральный — логическое значение,
определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то
функция НОРМРАСП возвращает интег­ральную функцию распределения; если это
аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности
распределения.

Если среднее = 0 и
стандартное_откл = 1, то функция НОРМРАСП возвращает стан­дартное
нормальное распределение.

Пример 2. Построить график
нормальной функции распределения f(x) при x, меняющемся от 19,8 до 28,8
с шагом 0,5, a=24,3 и

=1,5.

Решение

1. В ячейку А1 вводим символ
случайной величины х, а в ячейку B1 — символ фун­кции
плотности вероятности — f(x).

2. Вводим в диапазон А2:А21
значе­ния х от 19,8 до 28,8 с шагом 0,5. Для этого воспользуемся
маркером автозаполнения: в ячейку А2 вводим левую границу диапазона (19,8), в
ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:А3. Затем за правый
нижний угол протягиваем мышью до ячейки А21 (при нажатой левой кнопке мыши).

3.   Устанавливаем табличный курсор в ячейку В2 и
для получения значения веро­ятности воспользуемся специальной функцией —
нажимаем на панели инстру­ментов кнопку Вставка функции (fx). В появившемся диалоговом
окне Мастер функций — шаг 1 из 2 слева в поле Категория указаны виды
функций. Выбираем Статистическая. Справа в поле Функция выбираем
функцию НОРМРАСП. Нажимаем на кнопку ОК.

4. Появляется диалоговое
окно НОРМРАСП. В рабочее поле X вводим адрес ячейки А2
щелчком мыши на этой ячейке. В рабочее поле Среднее вводим с клавиатуры
значение математиче­ского ожидания (24,3). В рабочее поле Стандартное_откл
вводим с клавиатуры значение среднеквадратического отклонения (1,5). В ра­бочее
поле Интегральная вводим с клавиатуры вид функции распределения (0).
Нажимаем на кнопку ОК.

5. В ячейке В2 появляется
вероятность р = 0,002955. Указателем мыши за правый нижний угол табличного
курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В21
копируем функцию НОРМРАСП в диапазон В3:В21.

6. По полученным данным строим искомую диаграмму
нормальной функции рас­пределения. Щелчком указателя мыши на кнопке на панели
инструментов вызы­ваем Мастер диаграмм. В появившемся диалоговом окне
выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки
Далее указываем диапазон данных — В1:В21 (с помощью мыши). Проверяем,
положение переключателя Ряды в: столбцах. Выбираем закладку Ряд и с
помощью мыши вводим диапазон подписей оси X: А2:А21. Нажав на кнопку Далее,
вводим названия осей Х и У и нажимаем на кнопку Готово. 

 Рис. 1 График нормальной функции распределения

Получен приближенный график
нормальной функции плотности распределения (см. рис.1).

Задания для самостоятельной работы

1. Построить график нормальной
функции плотности распределения f(x) при x, меняющемся от 20 до 40 с
шагом 1 при

=   3.

 

3. Генерация случайных величин

Еще одним аспектом
использования законов распределения вероятностей являет­ся генерация случайных величин. Бывают ситуации, когда необходимо
получить пос­ледовательность случайных чисел. Это, в частности, требуется для
моделирования объектов, имеющих случайную природу, по известному распределению
вероятно­стей.

Процедура генерации
случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из
одного или не­скольких распределений.

В MS Excel для генерации СВ используются функции из категории Математические:

СЛЧИС () – выводит на экран  равномерно
распределенные случайные числа больше или равные 0 и меньшие 1;

СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экран
случайное число, лежащее между про­извольными заданными
значениями.

В случае использования
процедуры Генерация случайных чисел из пакета Анализа необходимо
запол­нить следующие поля:

— число переменных
вводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то все
столбцы в выходном диапазоне будут заполнены;

— число случайных чисел
вводится число случайных значений, которое необ­ходимо вывести для
каждой переменной, если число случайных чисел не будет введе­но, то все строки выходного диапазона будут заполнены;

— в поле распределение необходимо выбрать тип распределения,
которое следует использовать для генерации случайных переменных:

1.  равномерное — характеризуется
верxней и нижней границами. Переменные из­влекаются с одной и
той же вероятностью для всех значений интервала.

2. нормальное
— характеризуется средним значением и стандартным отклонени­ем. Обычно для
этого распределения используют среднее значе­ние
0 и стандартное отклонение 1.

3. биномиальное
— характеризуется вероятностью успеха (величина р) для неко­торого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биномиальной случайной
переменной;

4. дискретное
— характеризуется значением СВ и соответствующим ему интервалом вероятности, диапазон должен состоять из двух столбцов: левого,
содержаще­го значения, и правого, содержащего
вероятности, связанные со значением в дан­ной строке. Сумма вероятностей должна быть
равна 1;

5. распределения Бернулли, Пуассона
и Модельное.

— в поле случайное рассеивание
вводится произвольное значение, для которого необ­ходимо
генерировать случайные числа. Впоследствии можно снова использовать это
значение для получения тех же самых случайных чисел.

— выходной диапазон
вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и
на эк­ран будет выведено сообщение в случае
возможного наложения выходного диапа­зона на исходные
данные.

Рассмотрим пример.                                                                                  

Пример 3. Повар столовой может готовить 4 различных первых блюда (уха, щи, борщ, грибной суп). Необходимо составить меню на месяц, так чтобы
первые блюда чередовались в случайном порядке.

Решение

1.        
Пронумеруем первые
блюда по порядку: 1 — уха, 2 — щи, 3 — борщ, 4 — грибной суп. Введем числа 1-4 в диапазон А2:А5 рабочей таблицы.

2.        
Укажем желаемую вероятность появления
каждого первого блюда. Пусть все блюда будут
равновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.

3.        
В меню Сервис
выбираем пункт Анализ данных и далее указываем строку Генерация
случайных чисел. В появившемся диалоговом окне указываем Число
переменных — 1, Число случайных чисел — 30 (количество
дней в месяце). В поле Распределение указываем Дискретное (только натуральные числа). В поле Входной
интервал значений и вероятностей
вводим (мышью) диапазон, содержащий номера супов и их
вероятности. – А2:В5.

4.        
Указываем выходной
диапазон и нажимаем ОК. В столбце С появляются случайные числа: 1, 2, 3,
4.

 

Задание для
самостоятельной работы

1.      Сформировать
выборку из 10 случайных чисел, лежащих в диапазоне от 0 до 1.

2.      Сформировать
выборку из 20 случайных чисел, лежащих в диапазоне от 5 до 20.

3.      Пусть
спортсмену необходимо составить график тренировок на 10 дней, так чтобы
дистанция, пробегаемая каждый день, случайным образом менялась от 5 до 10 км.

4.      Составить
расписание внеклассных мероприятий на неделю для случайного проведения:
семинаров, интеллектуальных игр, КВН и спец. курса.

5.      Составить
расписание на месяц для случайной демонстрации на телевидении одного из четырех
рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1
должна быть в два раза выше, чем остальных рекламных роликов.