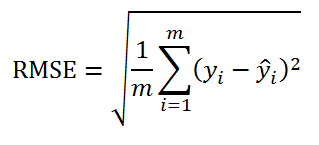17 авг. 2022 г.
читать 2 мин
Автокорреляция измеряет степень сходства между временным рядом и его запаздывающей версией в течение последовательных интервалов времени.
Его также иногда называют «последовательной корреляцией» или «запаздывающей корреляцией», поскольку он измеряет взаимосвязь между текущими значениями переменной и ее историческими значениями.
Когда автокорреляция во временном ряду высока, становится легко предсказать будущие значения, просто ссылаясь на прошлые значения.
Автокорреляция в Excel
В Excel нет встроенной функции для расчета автокорреляции, но мы можем использовать единую формулу для расчета автокорреляции для временного ряда для заданного значения задержки.
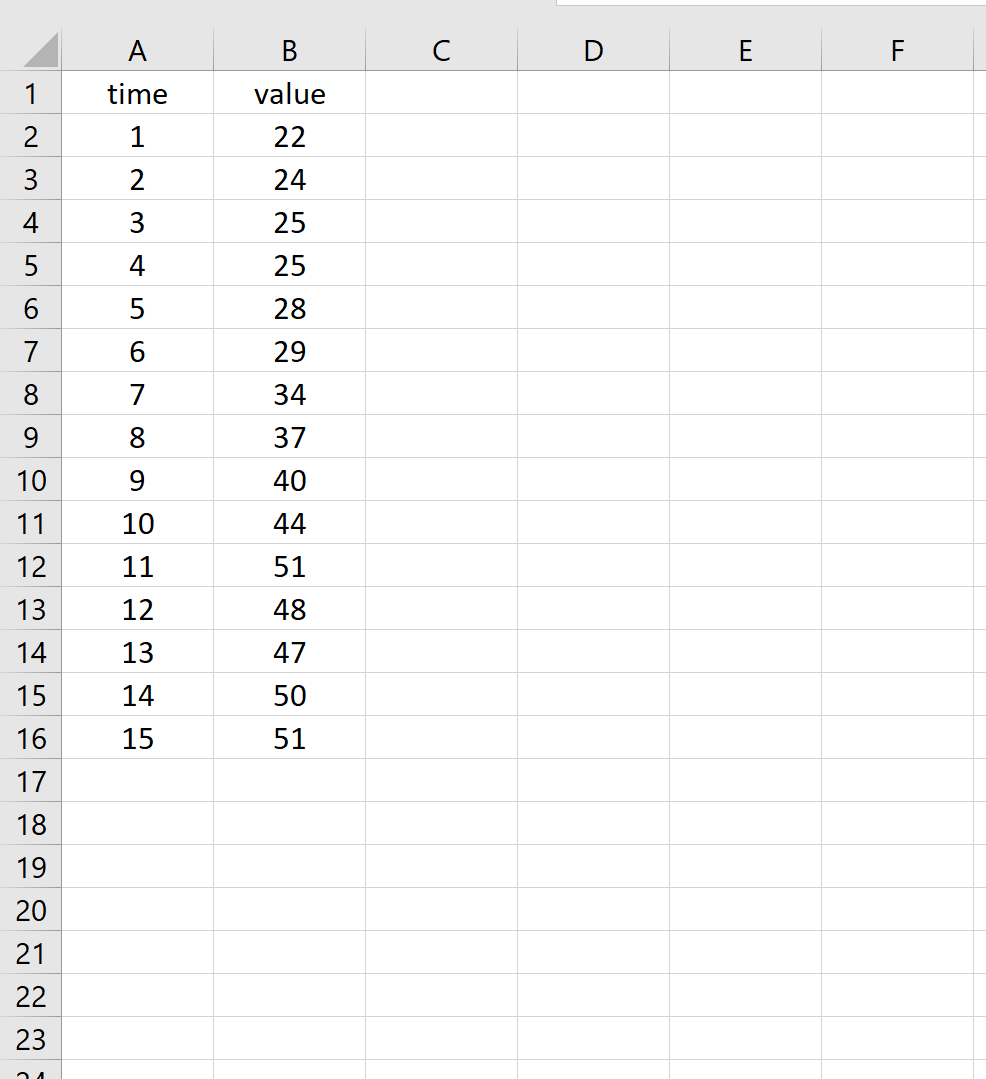
Например, предположим, что у нас есть следующий временной ряд, который показывает значение определенной переменной в течение 15 различных периодов времени:
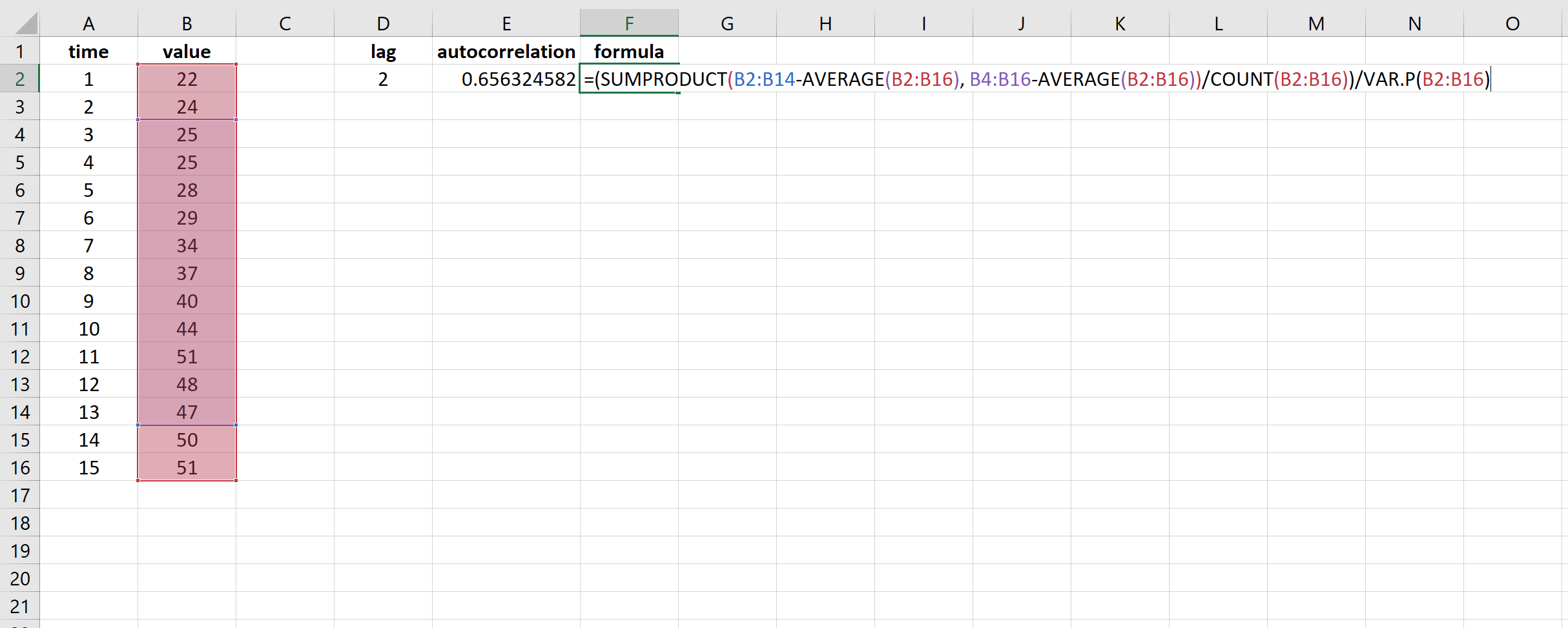
Мы можем использовать следующую формулу для расчета автокорреляции при задержке k = 2.
=(SUMPRODUCT( B2:B14 -AVERAGE( B2:B16 ), B4:B16 -AVERAGE( B2:B16 ))/COUNT( B2:B16 ))/VAR.P( B2:B16 )
В результате получается значение 0,656325.Это автокорреляция при задержке k = 2.
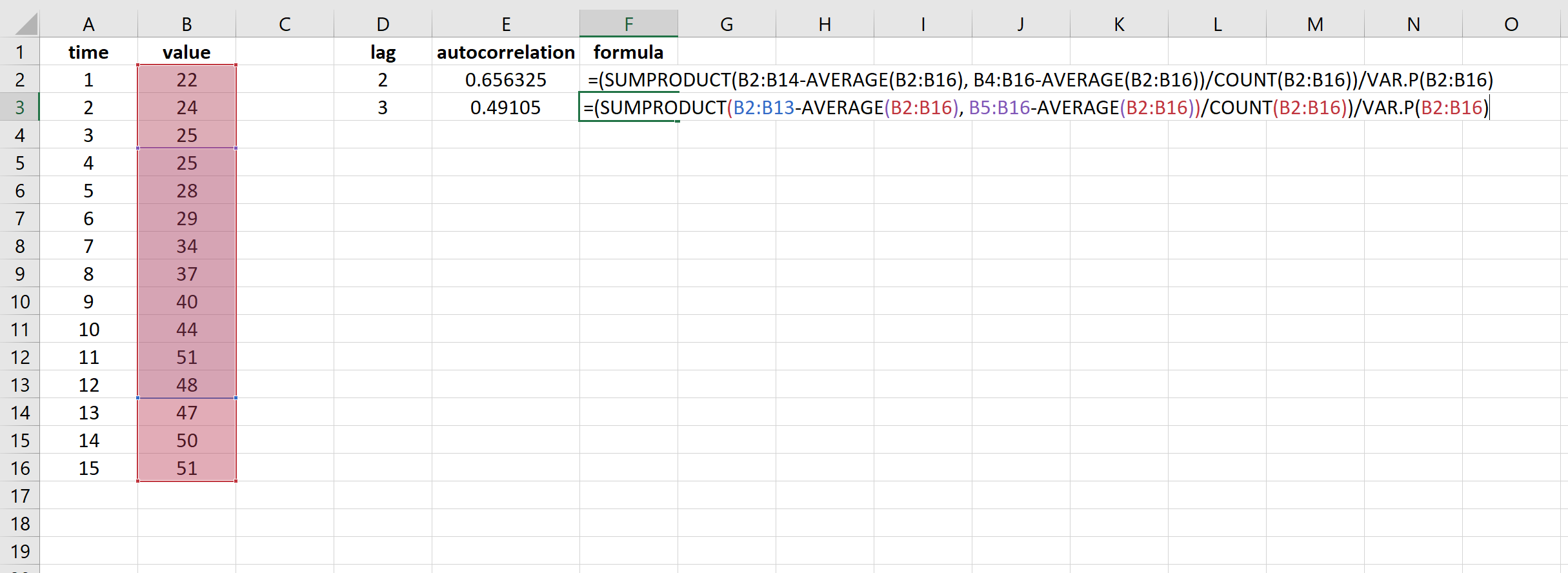
Мы можем вычислить автокорреляцию при лаге k = 3, изменив диапазон значений в формуле:
=(SUMPRODUCT( B2:B13 -AVERAGE( B2:B16 ), B5:B16 -AVERAGE( B2:B16 ))/COUNT( B2:B16 ))/VAR.P( B2:B16 )
В результате получается значение 0,49105.Это автокорреляция при задержке k = 3.
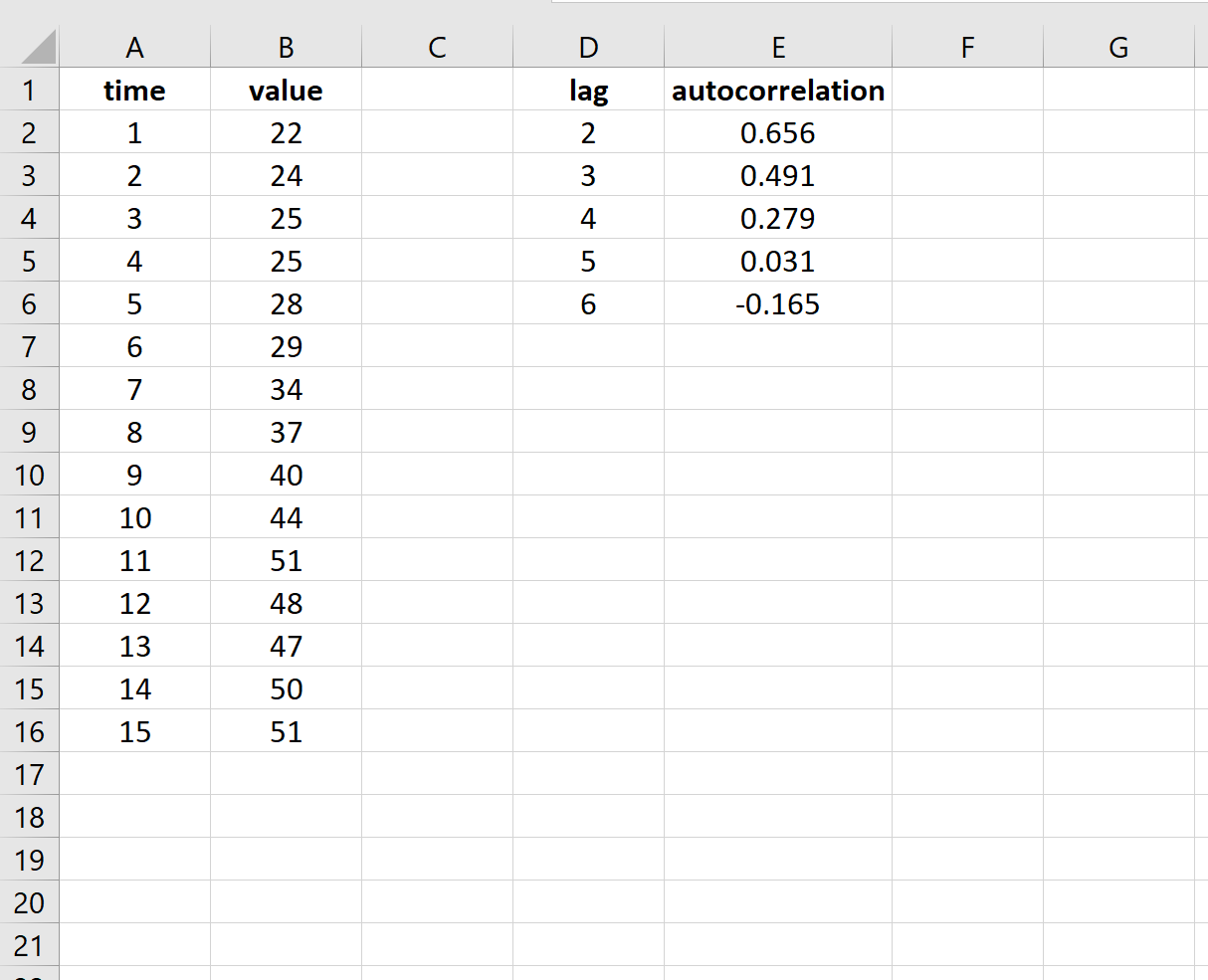
Мы можем найти автокорреляцию для каждого лага, используя аналогичную формулу. Вы заметите, что чем выше задержка, тем ниже автокорреляция. Это типично для процесса авторегрессионного временного ряда.
Вы можете найти больше руководств по временным рядам Excel на этой странице .
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Autocorrelation measures the degree of similarity between a time series and a lagged version of itself over successive time intervals.
It’s also sometimes referred to as “serial correlation” or “lagged correlation” since it measures the relationship between a variable’s current values and its historical values.
When the autocorrelation in a time series is high, it becomes easy to predict future values by simply referring to past values.
Autocorrelation in Excel
There is no built-in function to calculate autocorrelation in Excel, but we can use a single formula to calculate the autocorrelation for a time series for a given lag value.
For example, suppose we have the following time series that shows the value of a certain variable during 15 different time periods:
We can use the following formula to calculate the autocorrelation at lag k =2.
=(SUMPRODUCT(B2:B14-AVERAGE(B2:B16), B4:B16-AVERAGE(B2:B16))/COUNT(B2:B16))/VAR.P(B2:B16)
This results in a value of 0.656325. This is the autocorrelation at lag k = 2.
We can calculate the autocorrelation at lag k = 3 by changing the range of values in the formula:
=(SUMPRODUCT(B2:B13-AVERAGE(B2:B16), B5:B16-AVERAGE(B2:B16))/COUNT(B2:B16))/VAR.P(B2:B16)
This results in a value of 0.49105. This is the autocorrelation at lag k = 3.
We can find the autocorrelation at each lag by using a similar formula. You’ll notice that the higher the lag, the lower the autocorrelation. This is typical of an autoregressive time series process.
You can find more Excel time series tutorials on this page.
history 4 августа 2021 г.
- Группы статей
Сам метод скользящего среднего рассмотрен в статье Скользящее среднее в MS EXCEL, в которой показано как для этого использовать инструмент MS EXCEL Пакет анализа, а также линию тренда и формулы.
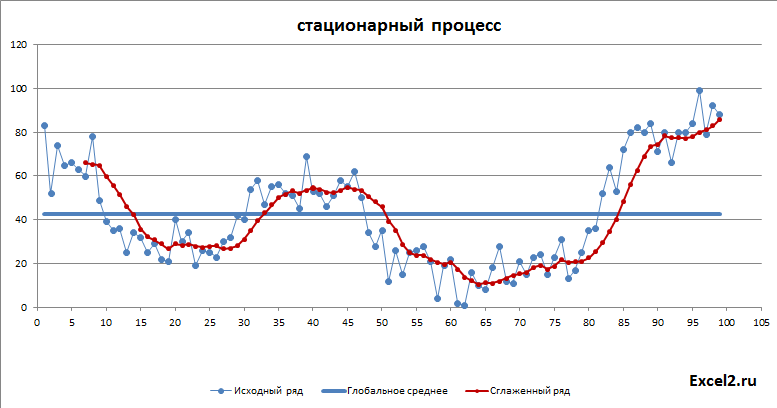
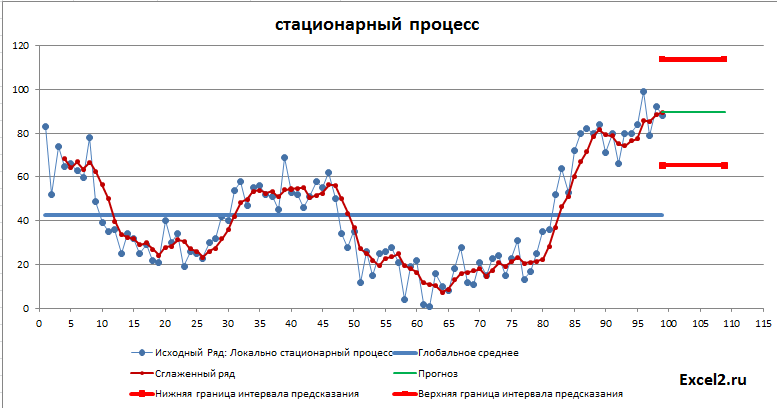
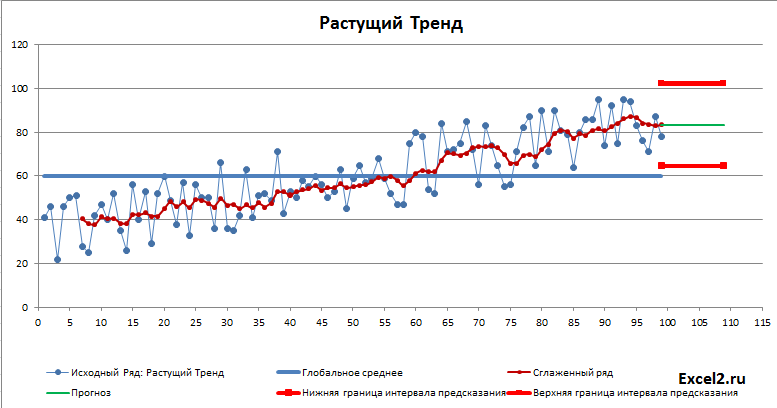
В этой статье рассмотрим не сам метод сглаживания, а его применение для прогнозирования. Как было сказано во вводной статье про прогнозирование, метод прогнозирования подбирается в соответствии с процессом, который генерирует значения временного ряда. Поэтому в файле примера используется как стационарные процессы, будем называть их постоянными, т.к. у них среднее и дисперсия постоянные (хотя фактически это белый шум со смещенным средним), и растущий тренд. Для оценки точности прогнозирования рассчитываются ошибки модели, строится интервал прогнозирования (на самом деле не интервал прогнозирования, а некий доверительный интервал на основе вычисленной ошибки). Так же оценивается адекватность модели.
Примечание: Конечно, прогнозировать процессы типа белого шума, бесперспективное занятие, но, во-первых в файле примера демонстрируются характеристики этого процесса (строится диаграмма рассеяния, функция автокорреляции, диаграмма разброса ошибок и пр.), а во-вторых таблицу с исходными значениями можно заменить и все характеристики будут пересчитаны в файле примера автоматически.
Построение исходного и сглаженного ряда
Для построения рядов можно использовать диаграмму типа График или Точечная. Выберем последний тип – Точечная (ниже будет пояснено почему Точечная в данном случае удобнее).
Для исходных рядов нам понадобится 4 столбца с данными (2 «постоянных» процесса, ряд с цикличностью и тренд). В файле примера на листе Исходный и сглаженный ряд это столбцы T:W.
Один из исходных рядов – динамический (столбец U, назовем его «постоянный» процесс с изменениями), т.е. его значения пересчитываются при любом изменении данных листа или после нажатии клавиши F9. Это сделано с помощью формулы =СЛУЧМЕЖДУ($T$10-2*$T$9;$T$10+2*$T$9)
За среднее значение этого ряда взято среднее значение ряда из столбца T =СРЗНАЧ(T13:T111), а диапазон изменения – 2 стандартных отклонения того же ряда =СТАНДОТКЛОН.В(T13:T112).
Такой автоматически генерирующийся ряд удобен для оценки модели – можно получить целый набор прогнозных значений, ошибок и доверительных интервалов. Фактически, конечно, функция СЛУЧМЕЖДУ() генерирует белый шум (с заданным смещением среднего относительно 0).
Примечание: Про функцию СЛУЧМЕЖДУ() можно почитать здесь. Эта функция генерирует непрерывное равномерное распределение, чтобы сгенерировать выборку из нормального или любого другого распределения см. эту статью.
Выбор нужно типа процесса организован с помощью группы переключателей, которая связана с ячейкой I11.
Значения выбранного исходного ряда подставляются в столбце В с помощью формулы =СМЕЩ(T13;;$I$11-1). Подробнее про функцию СМЕЩ() см. здесь.
Сглаженный ряд разместим рядом в столбце С, этот ряд будет формироваться для заданного периода усреднения (ячейка A7) с помощью формулы =ЕСЛИ(A13<$A$7;НД();СРЗНАЧ(СМЕЩ(B13;-$A$7+1;;$A$7)))
Примечание: Про построение сглаженного ряда см. Скользящее среднее в MS EXCEL.
Период усреднения для удобства задается с помощью элемента управления счетчик.
Осталось сформировать данные для линии среднего значений исходного ряда. Для этого понадобится только 2 точки (см. диапазон F43:G44).
Теперь все готово для построения диаграммы.
Примечание: для тех, кто не имеет большого опыта в построении диаграмм MS EXCEL предлагается прочитать эту статью.
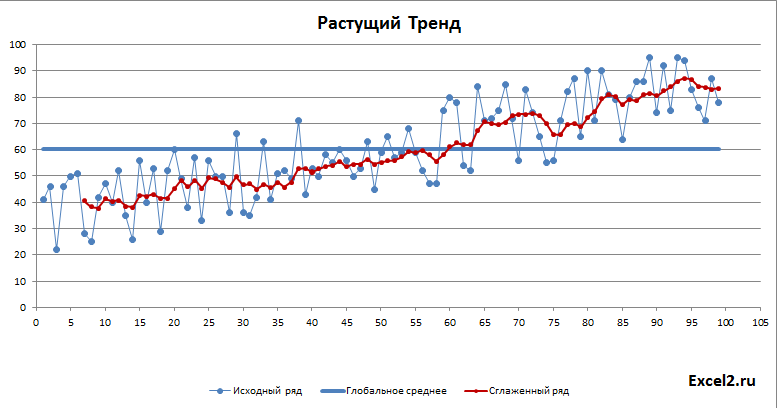
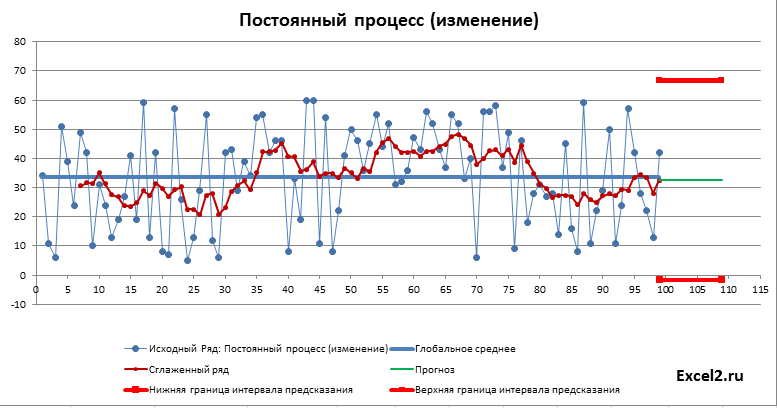
Для тренда сглаженный ряд будет выглядеть так:
Расчет прогнозного значения
Напомним, что метод скользящего среднего состоит в вычислении средних значений на основе предшествующих значений исследуемого числового ряда. Пусть последнее значение ряда произошло в момент i.
В случае усреднения за 3 периода скользящее среднее в момент i равно:
Yскол.i=(Yi+ Yi-1+ Yi-2)/3
Именно так считает инструмент Пакета Анализа «Скользящее среднее». Понятно, что нас интересует прогноз в будущий момент времени i+1. Положим, что прогнозное значение ряда в момент i+1 равно Yпрогнозн.i+1= Yскол.i
В итоге получаем эквивалентную формулу
Yпрогнозн.i+1=(Yi+ Yi-1+ Yi-2)/3
Для наглядности прогнозное значение на диаграмме изобразим в виде горизонтальной линии зеленого цвета (длина линии ничего не значит). Для этого понадобится только 2 точки (см. диапазон F8:G9).
Хотя использование метода скользящего среднего для прогнозирования носит скорее академический, нежели практический интерес, все же покажем как построить что-то типа «интервала предсказания». Для построения интервала воспользуемся ошибкой, которая вычисляется в надстройке Пакет анализа по формуле:
=КОРЕНЬ(СУММКВРАЗН(ИР;СР)/m)
Где m – количество периодов усреднения
ИР — m последних значений Исходного Ряда (ИР)
СР — m последних значений Сглаженного Ряда (СР)
Т.е. данная стандартная ошибка вычисляется по формуле:
RMSE – это Root Mean Squared Error (среднеквадратическая ошибка).
В файле примера на листе «Прогнозное значение» эта ошибка вычислена по формуле
=КОРЕНЬ(СУММКВРАЗН(СМЕЩ($B$112;-A7;;A7);СМЕЩ($C$112;-A7;;A7))/$A$7)
A7 содержит количество периодов усреднения
СМЕЩ($B$112;-A7;;A7) – это ссылка на диапазон исходного ряда (последние m значений)
СМЕЩ($C$112;-A7;;A7) – это ссылка на диапазон сглаженного ряда
СУММКВРАЗН() вычисляет сумму квадратов разностей
Если вычислить ошибки прогнозирования в отдельном столбце D, то формула для RMSE упростится:
=КОРЕНЬ(СУММКВ(СМЕЩ($D$112;-A7;;A7))/$A$7)
Границы интервала (для заданного уровня значимости альфа) вычисляются как:
Верхняя граница = Yпрогнозн.i+1 + RMSE*tm-1,1-альфа/2
Нижняя граница = Yпрогнозн.i+1 — RMSE*tm-1,1-альфа/2
tm-1,1-альфа/2 — верхний α/2-квантиль распределения Стьюдента с m-1 степенью свободы (это просто число, которое показывает сколько ошибок RMSE нужно, чтобы «интервал предсказания» накрыл прогнозное значение с вероятностью 1-альфа).
Примечание: «Интервал предсказания» вычислен лишь по аналогии с построением доверительного интервала для оценки среднего, для которого у нас была статистическая модель. Для случая скользящего среднего корректность такого построения обосновывается отдельно. В данной статье «Интервал предсказания» построен лишь с целью демонстрации самого процесса построения интервалов предсказания.
Верхний α/2-квантиль вычислим по формуле =СТЬЮДЕНТ.ОБР.2Х(C8;A7-1)
в ячейке С8 находится альфа – уровень значимости (обычно 5%).
Как видно из диаграммы выше для нашего стационарного процесса (фактически белый шум) прогнозное значение ожидаемо находится около глобального среднего, а доверительный интервал охватывает весь диапазон изменений исходного ряда, т.е. будущее значение этого ряда может появиться на всем интервале, что фактически говорит нам о невозможности предсказания.
Как и следовало ожидать, для растущего тренда картинка существенно отличается: доверительный интервал уже в 2 раза меньше и прогнозное значение находится вдали от глобального среднего.
Автокорреляция исходного ряда
Исследуем исходный ряд на наличие автокорреляции. Подробно об автокорреляции см. отдельную статью.
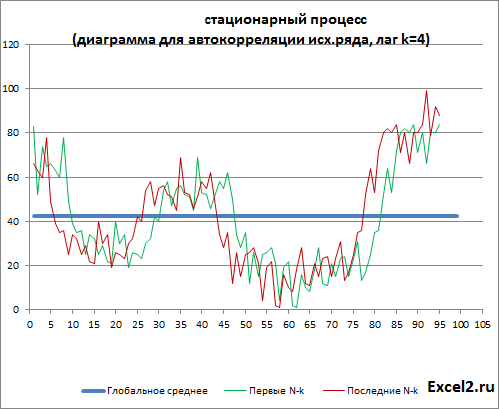
Автокорреляция (Autocorrelation, Lagged correlation, Serial correlation) – корреляция значений временного ряда с собственными значениями, сдвинутыми по времени на один или несколько периодов (лагов). Ниже показана диаграмма содержащая исходный ряд и ряд сдвинутый на лаг k=4 (общее количество значений ряда N уменьшится на k, глобальное среднее на диаграмме оставлено как у исходного ряда).
Примечание: Диаграмма построена на листе «Автокорреляция ИР» в файле примера. ИР – Исходный Ряд.
Для оценки автокорреляции используют 3 основных инструмента: график временного ряда (Time Series Plot), диаграмму рассеивания (Lagged Scatterplot) в зависимости от лага и функцию автокорреляции (Autocorelation Function, ACF).
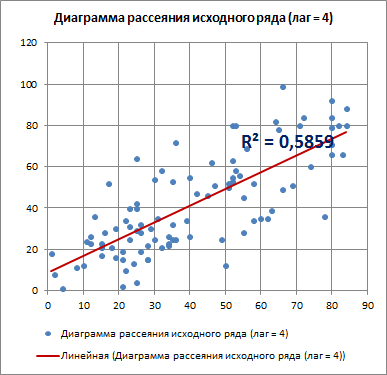
Диаграмма рассеяния используется для отображения возможной взаимосвязи между двумя переменными.
В нашем случае будем исследовать корреляционную зависимость между двумя рядами данных, сдвинутых на лаг k относительно друг друга (см. диаграмму выше).
Для лага k=4 диаграмма рассеяния, очевидно, демонстрирует наличие линейной положительной корреляции.
С помощью инструмента диаграммы «Линия тренда» построена линия регрессии и вычислим коэффициент детерминации R2. Ниже мы вычислим R2 с помощью формул, т.к. это просто квадрат коэффициента автокорреляции.
Примечание: Линия тренда подробно описана в разделе Построение линии регрессии статьи про Простую линейную регрессию.
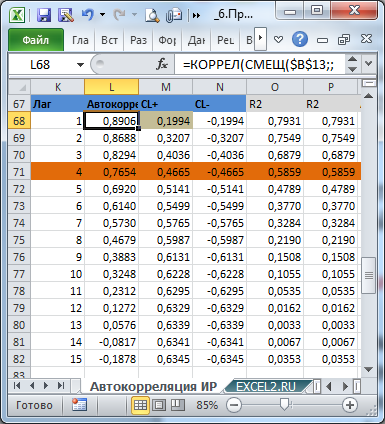
Вычислим коэффициенты автокорреляции для лагов от 1 до 15.
=КОРРЕЛ(СМЕЩ($B$13;;;$B$10-K68);СМЕЩ($B$13;K68;;$B$10-K68))
Два массива в аргументах функции КОРРЕЛ() – это просто 2 ряда, которые сдвинуты на лаг k (ячейка K68) относительно друг друга:
СМЕЩ($B$13;;;$B$10-K68)
СМЕЩ($B$13;K68;;$B$10-K68)
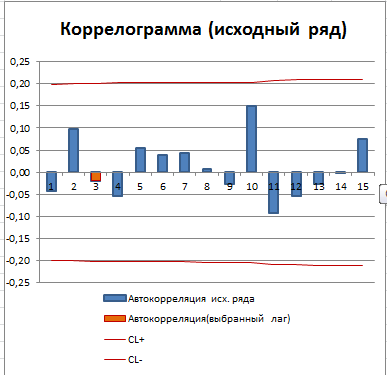
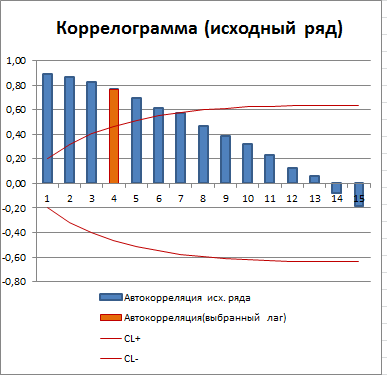
Зависимость коэффициента автокорреляции от лага – это функция автокорреляции (ACF). График ACF – это коррелограмма. Для стационарного процесса (у нас это «постоянный» процесс, фактически белый шум) коррелограмма имеет следующий вид:
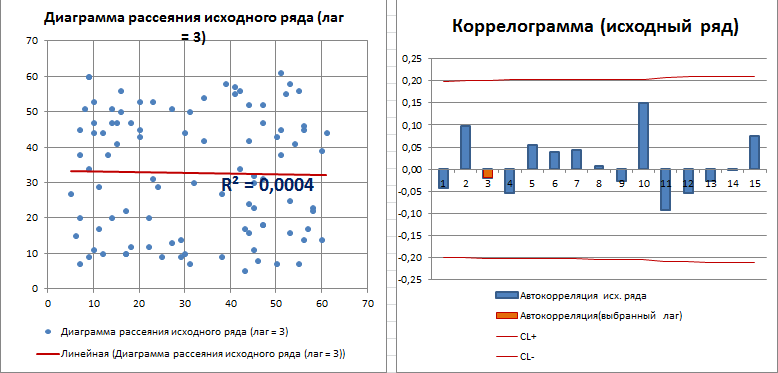
Для другого стационарного процесса (с апериодической цикличностью) коррелограмма имеет совершенно другой вид:
Все коэффициенты автокорреляции, которые выше границ доверительного интервала, являются статистически значимыми (про расчет доверительного интервала для ACF см. статью про Автокорреляцию). Диаграмма рассеяния для выбранного лага (столбец гистограммы, который выделен цветом) также подтверждает отсутствие автокорреляции.
Коэффициент детерминации R2, указанный на диаграмме рассеяния можно рассчитать возведя в квадрат коэффициент корреляции или применив формулу
=КВПИРСОН(СМЕЩ($B$13;;;$B$10-K68);СМЕЩ($B$13;K68;;$B$10-K68))
для тех же массивов, полученных из исходного ряда.
Вычисление ошибок модели
Для прогнозирования значения временного ряда мы использовали модель скользящего среднего с определенным периодом усреднения m. Какое значение является лучшим для прогнозирования?
Критерием оптимальности m является минимизация ошибки модели.
Существует целый ряд формул для вычисления ошибок, но самой лучшей ошибкой для оценки точности модели является среднеквадратичная ошибка (RMSE), вычисленная нами ранее.
Кроме применяются еще несколько других ошибок:
• MAE (Mean Absolute Error, Средняя Абсолютная ошибка). В EXCEL вычисляется по формуле =СРЗНАЧ(ABS(СМЕЩ($D$112;-D10;;D10))). Сначала диапазон ошибок СМЕЩ($D$112;-D10;;D10) в столбце D берется по модулю, затем находится среднее значение. Эта ошибка менее чувствительна к одиночным выбросам, т.к. значения ошибок не возводятся в квадрат.
• MAPE (Mean Absolute Percentage Error, Средняя Абсолютная Процентная Ошибка). В EXCEL вычисляется по формуле =СРЗНАЧ(ABS(СМЕЩ($D$112;-D10;;D10)/СМЕЩ($B$112;-D10;;D10))) Вычисляется практически аналогично MAE, но вместо просто ошибки берется по модулю ее отношение к значению исходного ряда. Получается безразмерная величина. Подходит для исходных рядов с трендом или ярко выраженной сезонностью.
• ME (Mean Error, Средняя ошибка). Эта ошибка показывает имеет ли прогноз смещение. МЕ должна быть около 0. =СРЗНАЧ(СМЕЩ($D$112;-D10;;D10)). ME может быть положительной и отрицательной.
• MPE (Mean Percentage Error, Средняя Процентная ошибка). Вычисляется практически аналогично ME, но вместо просто ошибки берется ее отношение к значению исходного ряда. MPE может быть положительной и отрицательной. =СРЗНАЧ((СМЕЩ($D$112;-D10;;D10)/СМЕЩ($B$112;-D10;;D10)))
Все ошибки вычислены в файле примера на листе Ошибки модели в диапазоне M7:Q11.
Как было сказано выше, для построения «интервала предсказания» прогнозного значения использовалась среднеквадратичная ошибка (RMSE) причем вычисленная не для всего ряда, а лишь на периоде усреднения. Это соответствует формулам MS EXCEL в Пакете анализа. На обоих горизонтах расчета RMSE дает близкие значения, причем в зависимости от лага или значений ряда RMSE вычисленная на периоде усреднения m может давать непредсказуемо либо меньшее либо большее значение по сравнению с RMSE вычисленной для всего ряда (в этом можно убедиться проанализировав RMSE для динамически изменяемого постоянного процесса).
Проверка адекватности модели
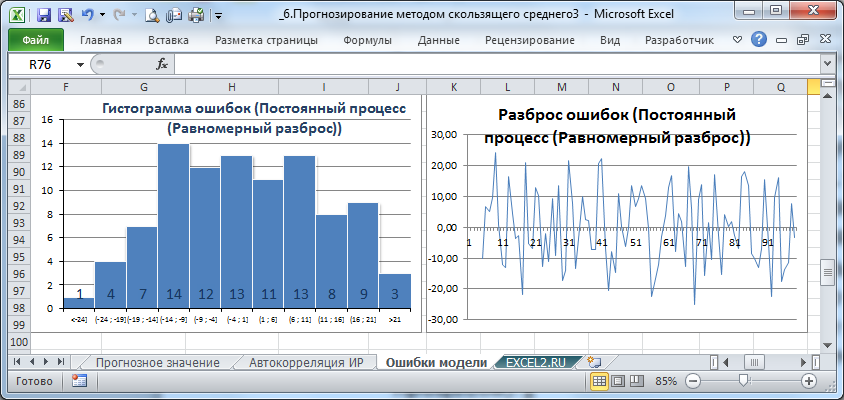
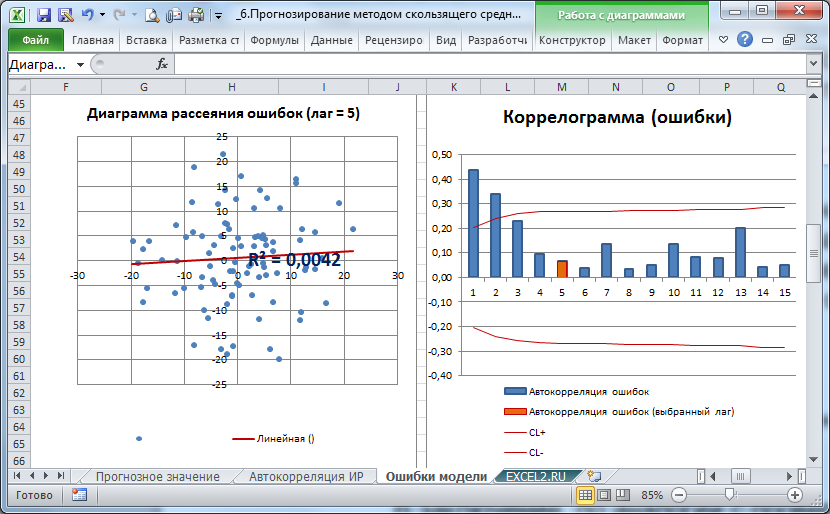
На листе Ошибки модели построена диаграмма разброса ошибок и гистограмма ошибок. Эти диаграммы автоматически перестраиваются в зависимости от выбранного лага или типа исходного ряда.
Диаграмму разброса ошибок можно построить на основе диаграммы MS EXCEL типа График. Специальных знаний построения диаграмм практически не требуется. Впрочем, как и для построения Гистограммы. Несколько сложнее построить таблицу исходных данных для гистограммы. Об этом подробно рассказано в статье Гистограмма распределения
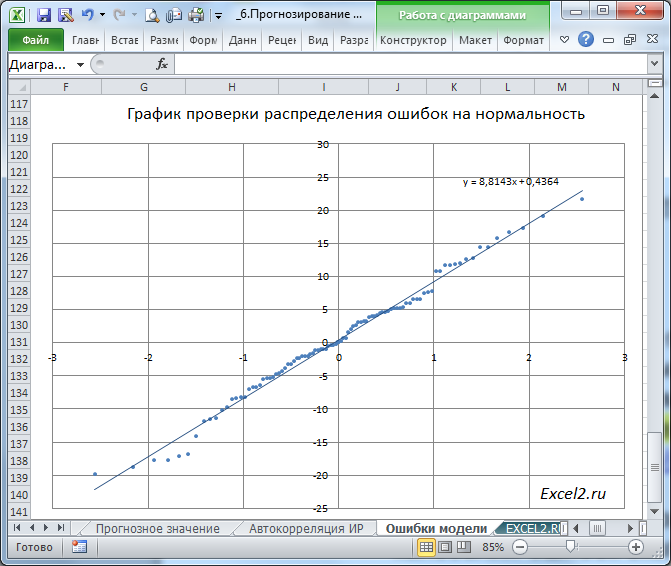
Диаграмма разброса ошибок должна демонстрировать колебания ошибок около 0, а гистограмма — типичную выборку из нормального распределения. Проверить распределение ошибок на нормальность можно построить соответствующий график.
Подробнее о проверке распределения на нормальность см. в этой статье.
В заключение, по аналогии с проверкой исходного ряда на автокорреляцию можно вычислить автокорреляцию ошибок и построить диаграммы рассеяния и коррелограмм.
На картинке выше приведены диаграмма рассеяния и коррелограмм для ошибок «постоянного» процесса.
Примечание: На листе «скользящее среднее» объединены все диаграммы, о которых рассказывалось выше в статье.
Автокорреляция уровней временного ряда
Автокорреляция уровней временного ряда
При наличии тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих значений.
Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда yt и уровнями этого ряда, сдвинутыми на несколько шагов во времени yt—t.
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Максимальный лаг должен быть не больше (n/4).
Коэффициент автокорреляции уровней ряда первого порядка, измеряющий зависимость между соседними уровнями ряда yt и yt-1, т. е. при лаге 1, рассчитывается по формуле:
Аналогично определяются коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями yt и yt-2 и определяется по формуле:
Коэффициент автокорреляции характеризует тесноту только линейной связи текущего и анализируемого уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага называется коррелограммой.
При помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Анализ структуры ряда можно проводить следующим образом:
Ø если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию;
Ø если наиболее высоким оказался коэффициент автокорреляции порядка τ, ряд содержит циклические колебания с периодичностью в τ моментов времени;
Ø если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из предположений относительно структуры ряда:
· ряд не содержит тенденции и циклических колебаний, а включает только случайную компоненту,
· ряд содержит сильную нелинейную тенденцию.
Пример. Динамика урожайности зерновых культур за гг. характеризуется данными (ц/га), представленными в табл. 1.
Таблица 1 — Урожайность зерновых культур за гг.
Пример выполнения задания № 2 в Excel и Calc
2015-05-18
4794
Имеются поквартальные данные о прибыли некоторой компании за четыре года (табл. 16).
| Год | Квартал | Прибыль компании, млн у.е., Yt |
| I | ||
| II | ||
| III | ||
| IV | ||
| I | ||
| II | ||
| III | ||
| IV | ||
| I | ||
| II | ||
| III | ||
| IV | ||
| I | ||
| II | ||
| III | ||
| IV |
Требуется дать прогноз прибыли компании на второй квартал следующего года.
1. Построим график временного ряда с помощью Мастера диаграмм, предварительно выделив два столбца переменных t = 1, 2, …, 16, и отвечающие этим моментам уровни yt:
тип диаграммы – «График» (MS Excel) или «Линия» (OO Calc), вид – «График с маркерами» (MS Excel) или «Линии и точки» (OO Calc);
диапазон данных – в MS Excel выделяем значения переменных yt, переходим на вкладку «Ряд», курсор устанавливаем в строке «Подписи оси Х» и выделяем в таблице значения кварталов, в OO Calc на этом шаге ставим флажок у команды «Первый столбец как надпись», шаг «Ряд данных» пропускаем, нажимая «Далее»;
элементы диаграммы – оформляем заголовки, оси, сетку, нажимаем «Готово» (рис. 16).
Поскольку амплитуда колебаний в уровнях ряда (рис. 16) изменяется (уменьшается в данном случае), для него следует выбрать мультипликативную модель.
2. Автокорреляционную функцию временного ряда можно построить с использованием в Excel встроенной функции КОРРЕЛ, а в Calc – CORREL (рис. 17). Аргументы названных функций – это уровни изучаемого ряда, сдвинутые между собой на заданный промежуток времени L (смотри пример из разд. 2.2).
Рис. 16. График временного ряда
Полученные значения коэффициентов автокорреляции для L = 1, 2, …, 4 следует проверить на существенность. При этом наблюдаемое значение t-статистики находим по формуле:
Полученную для каждого лага t-статистику сравнивают с критическим значением распределения Стьюдента t (a/2,n) для заданного уровня значимости a и числа степеней свободы n = n – L– 2. Если наблюдаемое значение t-статистики превосходит критическое t (a/2, n), то коэффициент автокорреляции r(L) значим.
Критическое значение t (a/2, n) в Excel находят с помощью встроенной функции СТЬДРАСПОБР(a, n), а в Calc – TINV(a, n).
В нашем примере (рис. 17) при заданном уровне значимости a = 0,05 статистически значимыми будут r(1) и r(4).
Рис. 17. Автокорреляционная функция изучаемого ряда
По графику временного ряда (рис. 16) и автокорреляционной функции для данного временного ряда (рис. 17) делаем вывод о наличии в уровнях ряда периодических колебаний (период колебаний равен 4 кварталам) и общей убывающей тенденции.
3. Построение мультипликативной модели.
Шаг первый. Лаг максимального значения коэффициента автокорреляции равен четырем, поэтому сначала моделируем квартальную сезонную компоненту S.
Проведем выравнивание исходных уровней ряда с использованием процедуры скользящей средней. Применяя для нашего примера ту же методику, что и для аддитивной модели (табл. 7, разд. 2.4), получим значения центрированных скользящих средних, которые приведены на рис. 18 (ячейки F7:F18).
Рис. 18. Процедура оценивания сезонной компоненты ряда
Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (ячейки G7:G18 на рис. 18). Используем эти данные для определения индексов сезонности St (разд. 2.5).
Для удобства расчета St составим вспомогательную таблицу (рис. 19). Блок D4:G7 содержит разнесённые по кварталам оценки сезонной компоненты. Соответствующие средние значения приведены в ячейках D9:G9.
Напомним, что в мультипликативной модели сумма индексов сезонности должна быть равна числу периодов в цикле (в нашем примере четырём – четыре квартала в году). Проверим выполнение этого требования (ячейка J9 на рис. 19):
Определим корректирующий коэффициент (ячейка L9): .
Рис. 19. Расчет индексов сезонности
Скорректируем значения индексов сезонности, умножив средние оценки на корректирующий коэффициент k (ячейки D10:G10 на рис.19).
В результате выполнения указанных действий в нашем примере получим следующие значения индексов сезонности: для 1-го квартала ; для 2-го квартала ; для 3-го квартала ; для 4-го квартала .
Экономический смысл этих показателей состоит в следующем. Прибыль компании в 1-м квартале ниже среднегодовой прибыли в 0,914 раза, во 2-м и 3-м кварталах – выше в 1,202 и 1,082 раза, соответственно. В 4-м квартале прибыль компании ниже среднегодового значения в 0,802 раза.
Шаг второй. Определимся с формой тренда в нашем примере. Для этого устраним влияние сезонной компоненты, разделив каждый уровень исходного ряда на соответствующее значение индекса сезонности. Полученные в результате десезонализированные данные (ячейки D4:D19 на рис. 20) помогают визуально определить форму тренда (рис. 21).
Рис. 20. Ряд десезонализированных данных
Рис. 21. График десезонализированного ряда
Шаг третий. По результатам визуального анализа (рис. 21) для описания тренда можно предложить линейную функцию . Выборочные оценки b0и bl для неизвестных коэффициентов β0 и β1 найдём по формулам (25) и (26), при этом вместо значений ytследует брать десезонализированные, т. е. очищенные от влияния сезонной компоненты данные. В результате получим b0 = 90,565и bl = –2,773.
Таким образом, оценочное уравнение тренда:
Тот же результат можно получить, используя стандартные средства в электронных таблицах Excel или Calc. Для этого помечаем одну из точек десезонализированных данных (рис. 21) и из контекстного меню выбираем команду «Добавить линию тренда» (Excel) или «Вставить линию тренда» (Calc).
В диалоговом окне «Линия тренда» в Excel присутствуют две закладки, первая из них содержит образцы форм линии регрессии (тренда). В нашем примере заказываем линейную форму.
Переходим во вторую закладку – «Параметры». Устанавливаем флажки на опциях «Показать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации».
Аналогично в Calc в диалоговом окне «Линия тренда» на закладке «Тип» выбираем тип регрессии – «Линейный», устанавливаем флажки на опциях «Показать уравнение» и «Показать коэффициент корреляции R 2 ».
Результаты выполнения указанных действий в виде оценочного уравнения тренда, его графика и значения коэффициента достоверности аппроксимации представлены на рис. 22.
Рис. 22. Построение линейного тренда в Excel
Таким образом, для изучаемого ряда выполнено моделирование сезонной Stи трендовой Тtсоставляющих, других систематических компонент автокорреляционная функция не показывает (рис. 17). Продемонстрируем смысл полученных результатов.
По уравнению тренда оценим его уровни в каждый момент времени t = 1, 2, …, 16 (ячейки Е4:Е19 на рис. 23).
Соответствующая этим данным прямая на рис. 24 даёт графическое представление трендовой модели изучаемого ряда.
Модель ряда с поправкой на сезонность получается при умножении уровней Tt на значения индексов сезонности St (ячейки F4:F19 на рис. 23). Значения (Т×S) изображены на рис. 24 в виде уровней, помеченных маркерами-кружками.
Визуальный анализ данных рис. 24 показывает, что тренд с поправкой на сезонность обеспечивает хорошее соответствие результатов моделирования реальным данным наблюдений.
Рис. 23. Расчёт компонентного состава изучаемого ряда
Рис. 24. Уровни исходного ряда (ромбики), его трендовая модель (квадратики) и трендовая модель с поправкой на сезонность (кружки)
4. Оценим качество модели временного ряда посредством коэффициента детерминации R 2 по формуле (31).
Предварительно рассчитаем абсолютную ошибку Et, которая в мультипликативной модели определяются по формуле (33), результаты расчётов Et приведены в ячейках D4:D19 на рис. 25.
Тогда сумма квадратов абсолютных ошибок равна 207,7 (ячейка E20 на рис. 25). Общая сумма квадратов отклонений фактических уровней ряда от его среднего уровня равна 5023 (ячейка F20 на рис. 25). Отсюда найдём долю объясненной дисперсии уровней ряда по формуле (31): .
Таким образом, коэффициент детерминации R 2 равен 0,959, то есть построенная модель объясняет 95,9 % общей вариации уровней временного ряда, представляющего прибыль компании за 16 кварталов.
Высокое значение коэффициента детерминации гарантирует качество построенной модели и, следовательно, возможность её применения для прогнозирования.
Рис. 25. Оценка качества построенной модели
5. Прогнозирование по мультипликативной модели.
Трендовый прогноз для второго квартала следующего, то есть пятого, года (t = 18) предсказывает величину прибыли:
Уточним трендовый прогноз, поправив его на сезонность. Индекс сезонности для второго квартала . Тогда скорректированный на сезонность прогноз прибыли компании на второй квартал 5-го года:
Оба прогноза относятся к разряду точечных и, следовательно, определяют наиболее вероятную величину прибыли компании во втором квартале следующего года.
Варианты к заданию № 2
Вариант 1. Имеются данные о перевозках грузов железнодорожным транспортом (млн т) за четыре года.
| Год | Квартал | Перевозка грузов, млн т | Год | Квартал | Перевозка грузов, млн т |
Сделать прогноз ожидаемого объема перевозок на третий квартал 2000-го года.
Вариант 2. Имеются данные об объеме экспорта из Российской Федерации (млрд долл.) за 1995–1998 гг.
| Год | Квартал | Экспорт | Год | Квартал | Экспорт |
| 50,4 | 51,6 | ||||
| 52,4 | |||||
| 53,2 | |||||
| 50,8 | 52,6 | ||||
| 56,8 |
Сделать прогноз объема экспорта из России за второй квартал 1999-го года.
Вариант 3. Имеются данные о перевозках грузов железнодорожным транспортом (млн т) за четыре года.
| Год | Квартал | Объем перевозок, млн т | Год | Квартал | Объем перевозок, млн т |
| 13,7 | 15,7 | ||||
| 12,1 | 13,3 | ||||
| 12,7 | 14,1 | ||||
| 16,7 | 18,7 | ||||
| 14,9 | 16,7 | ||||
| 12,5 | 14,3 | ||||
| 13,7 | 14,7 | ||||
| 17,7 | 18,5 |
Сделать прогноз ожидаемого объема перевозок на второе полугодие 2000-го года.
Вариант 4. Имеются данные об импорте товаров некоторой страны (млн долл.) за 1996–1999 гг.
| Год | Квартал | Импорт товаров, млн долл. | Год | Квартал | Импорт товаров, млн долл. |
| 17,2 | 19,2 | ||||
| 15,6 | 16,8 | ||||
| 16,2 | 17,6 | ||||
| 20,2 | 22,2 | ||||
| 18,4 | 20,2 | ||||
| 17,8 | |||||
| 17,2 | 18,2 | ||||
| 21,2 |
Сделать прогноз ожидаемого объема импорта за первый квартал 2000-го года.
Вариант 5. Имеются поквартальные данные по розничному товарообороту России (% к предыдущему периоду) в 1997–2000 гг.
| Год | Квартал | Товаро- оборот, % | Год | Квартал | Товаро- оборот, % |
| 37,3 | 39,3 | ||||
| 35,7 | 36,9 | ||||
| 36,3 | 37,7 | ||||
| 40,3 | 42,3 | ||||
| 38,5 | 40,3 | ||||
| 36,1 | 37,9 | ||||
| 37,3 | 38,3 | ||||
| 41,3 | 42,1 |
Сделать прогноз ожидаемого товарооборота России на третий квартал 2001-го года.
Вариант 6. Имеются поквартальные данные о прибыли (тыс. долл.) некоторой компании за четыре года.
| Год | Квартал | Прибыль, тыс. долл. | Год | Квартал | Прибыль, тыс. долл. |
Сделать прогноз ожидаемой прибыли компании за первое полугодие 2000-го года.
Вариант 7. Имеются данные об объеме экспорта из Российской Федерации (млрд долл.) за 1995–1998 гг.
| Год | Квартал | Экспорт, млрд долл. | Год | Квартал | Экспорт, млрд долл. |
| 80,6 | 82,6 | ||||
| 80,2 | |||||
| 79,6 | |||||
| 83,6 | 85,6 | ||||
| 81,8 | 83,6 | ||||
| 79,4 | 81,2 | ||||
| 80,6 | 81,6 | ||||
| 84,6 | 85,4 |
Сделать прогноз объема экспорта из России за третий квартал 1999-го года.
Вариант 8. Имеются поквартальные данные об объемах выпуска продукции (тыс. шт.) некоторой фирмой за 1996–1999 гг.:
| Год | Квартал | Объем выпуска, тыс. шт. | Год | Квартал | Объем выпуска, тыс. шт. |
Сделать прогноз ожидаемого объема выпуска продукции за первое полугодие 2000-го года.
Вариант 9. Имеются данные о перевозках грузов транспортом (млн тонн) за четыре года.
| Год | Квартал | Объем перевозок, млн тонн | Год | Квартал | Объем перевозок, млн тонн |
| 40,5 | 42,5 | ||||
| 38,9 | 40,1 | ||||
| 39,5 | 40,9 | ||||
| 43,5 | 45,5 | ||||
| 41,7 | 43,5 | ||||
| 39,3 | 41,1 | ||||
| 40,5 | 41,5 | ||||
| 44,5 | 45,3 |
Сделать прогноз ожидаемого объема перевозок на первое полугодие 2000-го года.
Вариант 10. Имеются данные об импорте товаров некоторой страны (млн долл.) за 1999–2002 годы:
| Год | Квартал | Импорт товаров, млн долл. | Год | Квартал | Импорт товаров, млн долл. |
| 45,8 | 47,8 | ||||
| 44,2 | 45,4 | ||||
| 44,8 | 46,2 | ||||
| 48,8 | 50,8 | ||||
| 48,8 | |||||
| 44,6 | 46,4 | ||||
| 45,8 | 46,8 | ||||
| 49,8 | 50,6 |
Сделать прогноз ожидаемого объема импорта за первый квартал 2003-го года.
При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней 2-х или более рядов динамики различного содержания, но связанных между собой. Эта задача решается методами коррелирования:
- уровней ряда динамики
- отклонений фактических уровней от тренда
- последовательных разностей
Коррелирование уровней динамических рядов с применением парного коэффициента корреляции правильно показывает тесноту связи лишь в том случае, если в каждом из них отсутствует автокорреляция . Наличие зависимости между последующими и предшествующими уровнями динамического ряда в статистической литературе называют автокорреляцией .
Поэтому прежде, чем коррелировать ряды динамики по уровням, необходимо проверить каждый из рядов на наличие или отсутствие в них автокорреляции . Применение методов классической теории корреляции в динамических рядах связано с некоторыми особенностями. Прежде всего, это наличие для большинства динамических рядов зависимости последующих уровней от предыдущих.
Коэффициент автокорреляции вычисляется по непосредственным данным рядов динамики, когда фактические уровни одного ряда рассматриваются как значения факторного признака, а уровни этого же ряда со сдвигом на один период, принимаются в качестве результативного признака (этот сдвиг называется лагом). Коэффициент автокорреляции рассчитывается на основе формулы коэффициента корреляции для парной зависимости:
где:
- yt – фактические уровни ряда,
- yt+1– уровни того же ряда со сдвигом на 1 период (коэффициент автокорреляции первого порядка).
Примечание: во избежание путаницы, следует обратить внимание на порядок, по которому будет производиться сдвиг уровней, а именно, вниз или вверх. Соответственно и в формулах по разным источникам, ряд со сдвигом отображают либо так yt-1 либо yt+1
Формула для расчета коэффициента автокорреляции уровней ряда 1-го порядка:
Формула для расчета коэффициента автокорреляции уровней ряда 2-го порядка:
Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду, фактическое значение коэффициента автокорреляции сопоставляют с табличным для 5% или 1% уровня значимости (т. е. по величине вероятности допустить ошибку при принятии гипотезы о независимости уровней ряда). Если расчетное значение меньше табличного, то гипотеза об отсутствии автокорреляции принимается и, наоборот, в противном случае, отвергается.
Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции ) называют коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т. е. определить присутствие в ряде той или иной компоненты. Так, если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка m, то ряд содержит циклические колебания с периодичностью в m моментов времени. Если же ни один из коэффициентов автокорреляции не является значимым, то можно сделать одно из двух предположений:
- либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;
- либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
Необходимо подчеркнуть, что линейные коэффициенты автокорреляции характеризуют тесноту только линейной связи текущего и предыдущих уровней ряда. Поэтому, по коэффициентам автокорреляции можно судить только о наличии или отсутствии линейной зависимости (или близкой к линейной). Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако, при этом могут иметь убывающую тенденцию.
Для проверки ряда на наличие нелинейной тенденции рекомендуется вычислить линейные коэффициенты автокорреляции для временного ряда, состоящего из логарифмов исходных уровней. Отличные от нуля значения коэффициентов автокорреляции будут свидетельствовать о наличии нелинейной тенденции.
Пример расчета:
Коэффициент автокорреляции 1 порядка
Расчет коэффициента автокорреляции 1-го порядка
Сдвигаем исходный ряд на 1 уровень. Следует учитывать, что с увеличением лага на единицу, число пар значений, по которым рассчитывается коэффициент автокорреляции , уменьшается на 1. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило: максимальный лаг не должен превышать n : 4 (n-число уровней ряда). Исходный ряд состоял из 8 уровней. Расчет производится не по 8, а по 7 парам наблюдений. Получаем следующие данные:
|
yt |
14017 |
14909 |
15333.5 |
15381.1 |
15548.8 |
22214.2 |
32267.6 |
|
yt — 1 |
14909 |
15333.5 |
15381.1 |
15548.8 |
22214.2 |
32267.6 |
42597.5 |
Для расчета коэффициента автокорреляции , необходимо рассчитать параметры уравнения авторегрессии:
Линейный коэффициент автокорреляции (L=1):
|
yt |
yt-1 |
yt 2 |
yt-1 2 |
yt • yt-1 |
|
14017 |
14909 |
196476289 |
222278281 |
208979453 |
|
14909 |
15333.5 |
222278281 |
235116222.25 |
228607151.5 |
|
15333.5 |
15381.1 |
235116222.25 |
236578237.21 |
235846096.85 |
|
15381.1 |
15548.8 |
236578237.21 |
241765181.44 |
239157647.68 |
|
15548.8 |
22214.2 |
241765181.44 |
493470681.64 |
345404152.96 |
|
22214.2 |
32267.6 |
493470681.64 |
1041198009.76 |
716798919.92 |
|
32267.6 |
42597.5 |
1041198009.76 |
1814547006.25 |
1374519091 |
|
129671.2 |
158251.7 |
2666882902.3 |
4284953619.55 |
3349312512 |
Так как коэффициент автокорреляции первого порядка оказался высоким, то исследуемый ряд содержит только тенденцию. Проверка значимости коэффициента автокорреляции дает следующий результат:
По таблице распределения Стьюдента (двусторонняя критическая область) с уровнем значимости α=0.05 и степенями свободы k=5 находим: tкрит (n-m-1; α/2) > (5; 0.025) = 2.571. Поскольку 2,16<2,571 (tнабл < tкрит), то принимаем гипотезу о равенстве коэффициента автокорреляции =0, что, в свою очередь, подтверждает наличие сильной нелинейной тенденции. Другими словами, коэффициент автокорреляции статистически — не значим.
Коэффициент автокорреляции 2 порядка
Расчет коэффициента автокорреляции 2-го порядка
Теперь cдвигаем исходный ряд на 2 уровня. Исходный ряд состоял из 8 уровней. Расчет производится не по 8, а уже по 6 парам наблюдений. Получаем следующую таблицу:
|
yt |
14017 |
14909 |
15333.5 |
15381.1 |
15548.8 |
22214.2 |
|
yt — 2 |
15333.5 |
15381.1 |
15548.8 |
22214.2 |
32267.6 |
42597.5 |
Проведя аналогичные расчеты, как при сдвиге исходного ряда на 1 уровень, получаем:
Линейный коэффициент автокорреляции (L=2):
|
yt |
yt-2 |
yt 2 |
yt-2 2 |
yt • yt-2 |
|
14017 |
15333.5 |
196476289 |
235116222.25 |
214929669.5 |
|
14909 |
15381.1 |
222278281 |
236578237.21 |
229316819.9 |
|
15333.5 |
15548.8 |
235116222.25 |
241765181.44 |
238417524.8 |
|
15381.1 |
22214.2 |
236578237.21 |
493470681.64 |
341678831.62 |
|
15548.8 |
32267.6 |
241765181.44 |
1041198009.76 |
501722458.88 |
|
22214.2 |
42597.5 |
493470681.64 |
1814547006.25 |
946269384.5 |
|
97403.6 |
143342.7 |
1625684892.54 |
4062675338.55 |
2472334689.2 |
Коэффициент автокорреляции второго порядка также оказался высоким — исследуемый ряд содержит только тенденцию. Но проверка значимости коэффициента автокорреляции опять не подтверждает значимость коэффициента автокорреляции :
По таблице распределения Стьюдента (двусторонняя критическая область) с уровнем значимости α=0.05 и степенями свободы k=4 находим: tкрит (n-m-1; α/2) > (4; 0.025) = 2.776. Поскольку 1,73<2,776 (tнабл < tкрит), то принимаем гипотезу о равенстве коэффициента автокорреляции =0, тем самым подтверждая наличие сильной нелинейной тенденции. Другими словами, коэффициент автокорреляции статистически — не значим.
Коэффициенты автокорреляции в MS Excel
Для расчета значений автокорреляционной функции в MS Excel целесообразно использовать функцию КОРРЕЛ (массив1; массив2). Так, если уровни исходного временного ряда располагаются в ячейках А1:А20, то для расчета коэффициентов автокорреляции можно вводить функции:
r1: =КОРРЕЛ (А1:А19; А2:А20)
r2: =КОРРЕЛ (А1:А18; А3:А20)
r3: =КОРРЕЛ (А1:А17; А4:А20)
r4:=КОРРЕЛ (А1:А16; А5:А20)
И т. д., постоянно сдвигая диапазон ячеек массива 1-вверх, массива 2- вниз, в зависимости от количества уровней в ряду динамики.
Остальные коэффициенты автокорреляции рассчитаем в MS Excel:
|
Лаг |
Коэффициент автокорреляции уровней |
Коррелограмма |
|
1 |
0,96538 |
********** |
|
2 |
0,86291 |
******** |
|
3 |
0,74906 |
******* |
|
4 |
0,88313 |
********* |
При анализе наиболее высоким оказался коэффициент автокорреляции уровней первого и четвертого порядков. Следовательно, исследуемый ряд содержит тенденцию и циклические колебания.
Проверка значимости коэффициентов
Существует другая методика проверки значимости коэффициентов автокорреляции , что, в свою очередь, дает основания подтвердить (отклонить) наличие в ряду динамики автокорреляции .
Значимость каждого в отдельности коэффициента автокорреляции принято проверять с помощью критерия стандартной ошибки. С его помощью удается выявить среди запаздывающих переменных те, которые необходимо включить в модель. Коэффициент автокорреляции можно считать значимым, если не выполняется неравенство с принятым уровнем надежности (95%):
где n – число пар наблюдений временного ряда, k – лаг (смещение данных ряда). Если рассчитанное значение автокорреляции попадает в этот интервал, то можно сделать вывод, что данные не показывают наличие автокорреляции k-го порядка с 95% уровнем надежности:
Для r1 объем выборки составляет (n-1)=(8-1)=7 пар наблюдений:
Неравенство не выполняется – наличие автокорреляции .
Для r2 объем выборки составляет (n-2)=(8-2)=6 пар наблюдений:
Неравенство не выполняется – наличие автокорреляции .
Для r3 объем выборки составляет (n-3)=(8-3)=5 пар наблюдений:
Неравенство выполняется – автокорреляция отсутствует.
Для r4 объем выборки составляет (n-4)=(8-4)=4 пары наблюдений:
Неравенство выполняется – автокорреляция отсутствует.
Данный анализ подтвердил наличие автокорреляции в ряду динамики, что дало основание отклонить применение парного линейного коэффициента корреляции при коррелировании уровней. В этом случае необходимо коррелировать отклонения или последовательные разности (см. ниже корреляция взаимосвязанных рядов динамики). Статистическая недостоверность коэффициентов корреляции подтвердила наличие в ряду динамики сильной нелинейной тенденции, для выявления которой необходимо провести дополнительный анализ, а также циклические колебания с периодичностью в k моментов времени. Конечно же, важным моментом анализа является сама содержательная характеристика исследуемого показателя (в данном примере он обезличен, но на практике этот показатель подвержен сильному влиянию конъюнктуры рынка по объему его производства и международных цен, что, в свою очередь, дает основание утверждать о присутствии циклической компоненты).
Аналитическое выравнивание по параболе 2-го порядка и анализ коррелированности отклонений исходного уровня (yi) от выравненного (yt) с использованием статистики Дарбина-Уотсона, дает следующие результаты:
|
yi |
yt= 1048.72t2 -5775.81t+20782.31 |
ei = yi-yt |
e2 |
(ei — ei-1)2 |
|
14017 |
16055.22 |
-2038.22 |
4154344.17 |
0 |
|
14909 |
13425.58 |
1483.42 |
2200547.96 |
12401985.18 |
|
15333.5 |
12893.38 |
2440.12 |
5954201.3 |
915272.61 |
|
15381.1 |
14458.62 |
922.48 |
850961.22 |
2303254.3 |
|
15548.8 |
18121.32 |
-2572.52 |
6617851.19 |
12214983.39 |
|
22214.2 |
23881.46 |
-1667.26 |
2779752.33 |
819494.81 |
|
32267.6 |
31739.05 |
528.55 |
279369.51 |
4821595.15 |
|
42597.5 |
41694.08 |
903.42 |
816169.2 |
140525.02 |
|
23653196.89 |
33617110.46 |
Критические значения d1(dL) и d2 (dU) определяются на основе специальных таблиц для требуемого уровня значимости (α) и числа наблюдений n = 8, где количество объясняющих переменных m=1. Автокорреляция отсутствует, если выполняется следующее условие: d1 < DW и d2 < DW < 4 — d2. По таблице распределений Дарбина-Уотсона для n=8 и k=1 (уровень значимости 5%) находим: d1 = 1.08; d2 = 1.36. Поскольку 1.08 < 1.42 и 1.36 < 1.42 < 4 — 1.36, то автокорреляция остатков отсутствует.
В зависимости от величины и знака расчетного значения статистики Дарбина-Уотсона, возможны следующие ситуации.
Возможные варианты:
1. Если коэффициент автокорреляции является положительной величиной (DW>0), то при проверке гипотез возможно возникновение следующих ситуаций:
- Если наблюдаемое значение критерия Дарбина-Уотсона меньше критического значения его нижней границы DW<d1, то нулевая гипотеза (H0) об отсутствии автокорреляции первого порядка между остатками модели регрессии отклоняется.
- Если наблюдаемое значение критерия Дарбина-Уотсона больше критического значения его верхней границы DW>d2, то нулевая гипотеза (H0) об отсутствии автокорреляции первого порядка между остатками модели регрессии принимается.
- Если наблюдаемое значение критерия Дарбина-Уотсона находится между верхней и нижней критическими границами d1<DW< d2 нет достаточных оснований для принятия единственно правильного решения, необходимы дополнительные исследования.
2. Если коэффициент автокорреляции является отрицательной величиной (DW<0), то при проверке гипотез возможно возникновение следующих ситуаций:
- Если наблюдаемое значение критерия Дарбина-Уотсона больше критической величины (4–d1) DW>4–d1, то нулевая гипотеза (H0) об отсутствии автокорреляции первого порядка между остатками модели регрессии отклоняется
- Если наблюдаемое значение критерия Дарбина-Уотсона меньше критической величины (4–d2) DW<4–d2, то нулевая гипотеза (H0) об отсутствии автокорреляции первого порядка между остатками модели регрессии принимается.
- Если наблюдаемое значение критерия Дарбина-Уотсона находится в критическом интервале между величинами (4–d1) и (4–d2) 4–d1<DW<4–d2, то достаточных оснований для принятия единственно правильного решения нет, необходимы дополнительные исследования.
Данный временной ряд наилучшим образом аппроксимируется параболой 3-го порядка, нежели параболой 2-го порядка, тем самым, подтверждая сильную нелинейную тенденцию ряда (R2=0.9898).
Далее, для анализа второго временного ряда, который будет выбран в качестве взаимосвязанного с рассмотренным выше, так же необходимо провести анализ на наличие (отсутствие) автокорреляции . Затем произвести расчет и анализ коэффициента корреляции 2-х взаимосвязанных рядов динамики по нижеприведенным формулам.
Взаимосвязанные ряды динамики
Применение корреляции в динамических рядах имеет ряд особенностей, недоучет которых не позволяет получить правильной оценки взаимосвязи между рядами динамики, которые, в свою очередь, рассматриваются как результативный и факторный признаки.
В рядах динамики из-за автокорреляции (влияние изменений уровней предыдущих рядов на последующие), необходимо из уровней каждого ряда исключить тренд — основную тенденцию, налагаемую на ряд развитием во времени и найти корреляцию отклонений от тренда по формулам:
где: dy (dx) — остаточные отклонения фактических уровней ряда от выровненных, соответственно, для уровней временного ряда, принятого в качестве результативного (dy) и в качестве факторного (dx) признаков, либо использовать последовательные разности уровней взаимосвязанных рядов динамики (цепные абсолютные приросты) — (Δx, Δy).
Коррелируя отклонения или последовательные разности взаимосвязанных динамических рядов, при переходе от самих уровней к их отклонениям от выровненных значений, исключается влияние общей тенденции на колеблемость (изменчивость) самих уровней.
Смотри также:
- Корреляция и регрессия
- Компоненты и сезонная декомпозиция временного ряда
- Сезонная корректировка временного ряда
- Проверка выполнимости предпосылок МНК
- Метод наименьших квадратов