Изучим как сделать арифметическую и геометрическую прогрессии в Excel, а также в общем случае рассмотрим способы создания числовых последовательностей.
Перед построением последовательностей и различных прогрессий, как обычно, вспомним их детальные определения.
Числовая последовательность — это упорядоченный набор произвольных чисел a1, a2, a3, …, an, … .
Арифметической прогрессией называется такая числовая последовательность, в которой каждый член, начиная со второго, получается из предыдущего добавлением постоянной величины d (также называют шагом или разностью):
Геометрическая прогрессия — это последовательность чисел, в котором каждый член, начиная со второго, получается умножением предыдущего члена на ненулевое число q (также называют знаменателем):
С определениями закончили, теперь самое время перейти от теории к практике.
Рассмотрим 2 способа задания прогрессии в Excel — с помощью стандартного инструмента Прогрессия и через формулы.
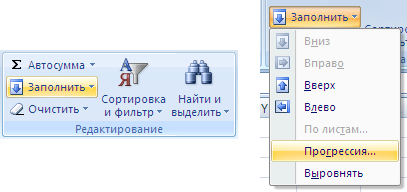
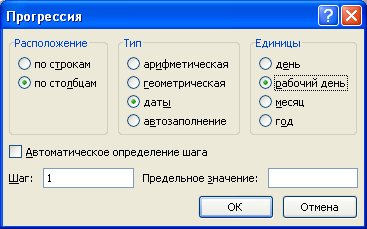
В первом случае на панели вкладок выбираем Главная -> Редактирование -> Заполнить -> Прогрессия:
Далее мы увидим диалоговое окно с настройками параметров:
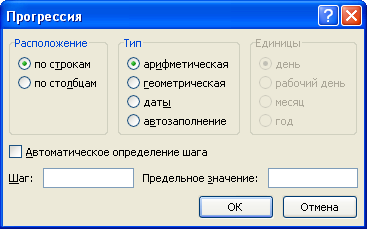
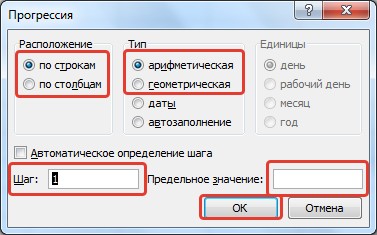
В данных настройках мы можем выбрать дополнительные параметры, которые позволят нам более детально настроить и заполнить прогрессию в Excel:
- Расположение — расположение заполнения (по столбцам или строкам);
- Тип — тип (арифметическая, геометрическая, даты и автозаполнение);
- Единицы — вид данных (при выборе даты в качестве типа);
- Шаг — шаг (для арифметической) или знаменатель (для геометрической);
- Автоматическое определение шага — автоматическое определение шага, если заданы несколько значений последовательности;
- Предельное значение — ограничение по значению последнего элемента последовательности.
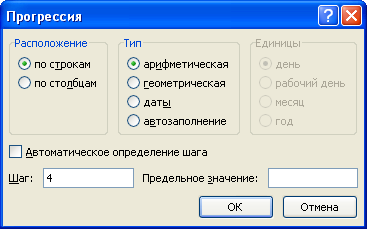
Разберем как сделать арифметическую прогрессию в Excel на конкретном примере.
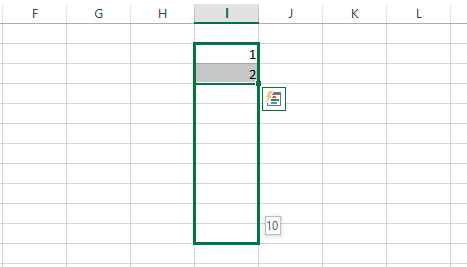
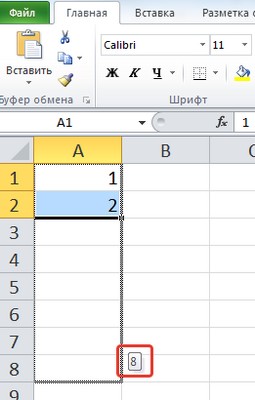
Создадим набор чисел 3, 7, 11, … , то есть первый элемент равняется 3, а шаг равен 4.
Выделяем диапазон (к примеру, A1:J1) в котором мы хотим разместить набор чисел (диапазон можно и не выделять, однако в этом случае в настройках будет необходимо указать предельное значение), где в первой ячейке будет указан первый элемент (в нашем примере это 3 в ячейке A1), и указываем параметры (расположение, тип, шаг и т.д.):
В результате мы получим заполненный диапазон с заданным набором чисел:
Аналогичный результат можно получить и при задании элементов с помощью формул.
Для этого также задаем начальный элемент в первой ячейке, а в последующих ячейках указываем рекуррентную формулу члена арифметической прогрессии (то есть текущий член получается как сумма предыдущего и шага):
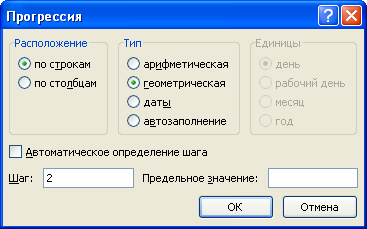
Геометрическая прогрессия в Excel
Принцип построения геометрической прогрессии в Excel аналогичен разобранному выше построению арифметической.
Единственное отличие — в настройках характеристик указываем в качестве типа геометрическую прогрессию.
Например, создадим набор чисел 4, 8, 16, … , то есть первое число равно 4, а каждое последующее в 2 раза больше предыдущего.
Также задаем начальный элемент (4 в ячейке A1), выделяем диапазон данных (например, A1:J1) и указываем параметры:
В итоге получаем:
Идентичного результата также можно добиться и через использование формул:
Числовая последовательность в Excel
Арифметическая и геометрическая прогрессии являются частными случаями числовой последовательности, в общем же случае ее можно создать, как минимум, тремя способами:
- Непосредственное (прямое) перечисление элементов;
- Через общую формулу n-го члена;
- С помощью рекуррентного соотношения, которое выражает произвольный член через предыдущие.
Первый способ подразумевает под собой ручной ввод значений в ячейки. Удобный вариант при вводе небольшого количества значений, в обратном же случае данный способ достаточно трудозатратный.
Второй и третий способы более универсальны, так как позволяют автоматически посчитать значения членов с помощью формул, что удобно при большом количестве элементов.
Поэтому поподробнее остановимся на построении последовательностей данными способами.
Рассмотрим создание числовой последовательности на примере построения обратных чисел к натуральным, то есть набора чисел 1, 1/2, 1/3, … , в котором общая формула n-го члена принимает вид Fn=1/n.
Создадим дополнительный ряд в отдельной строчке, куда для удобства расчета поместим порядковые номера (1, 2, 3 и т.д.), на которые будут ссылаться формулы:
В варианте с рекуррентной формулой рассмотрим пример с набором чисел Фибоначчи, в котором первые два числа равны 1 и 1, а каждый последующее число равно сумме двух предыдущих.
В итоге произвольный член можно представить в виде рекуррентного соотношения Fn = Fn-1 + Fn-2 при n > 2.
Определяем начальные элементы (две единицы) в двух ячейках, а остальные задаем с помощью формулы:
Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!
Поделиться с друзьями:
Поиск по сайту:
Автозаполнение ячеек в Excel однотипными данными — одна из популярнейших «фишек» этого табличного редактора. Этот простейший процесс — когда вы вводите два числа, а затем просто протягиваете выделение насколько нужно, а программа автоматически заполняет столбец или строку следующими цифрами (датами, буквами и т.п.) идущими по порядку, сэкономил нам столько времени на ввод, что и подумать страшно!
Простейшая арифметическая прогрессия в excel — ввести два первых числа прогрессии (чтобы установить шаг), выделить их, и протащить мышью правый нижний угол выделения до нужной строки
Если записать в соседние ячейки числа, например 1 и 2, то в следующих ячейках появятся значения 4, 5, 6, если записать 500 и 1000, следующими числами будут 1500, 2000 и т.д.
Оба этих числовых ряда будут простейшими арифметическими прогрессиями с заданным шагом — в первом случае с шагом 1, во втором — с шагом 500.
Но, что если мы имеем дело не с простейшей арифметической, а с геометрической прогрессией?
Нет никаких проблем. Введите начальное число в одну из ячеек, а затем выделите диапазон ячеек, в котором и хотите увидеть свою прогрессию.
Инструмент для построения сложных прогрессий в MS Excel
На вкладке «Главная» в группе «Редактирование» найдите инструмент «Заполнить» и выберите пункт «Прогрессия».
В открывшемся окне установите нужные параметры (шаг прогрессии, тип прогрессии и предельное значение, если необходимо), а затем жмите «Ок».
Выбранная вами прогрессия будет мгновенно выведена в пределах выделенного вами диапазона на листе табличного редактора.
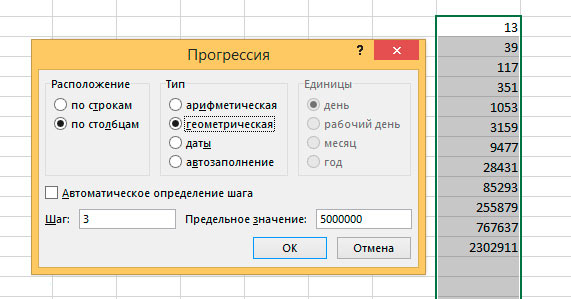
Пример построения геометрической прогрессии с шагом равным 3 и максимальным числом ограниченным 5000000
Также вас может заинтересовать:
Инструмент Прогрессия дарит нам несколько замечательных возможностей. С помощью него можно заполнить диапазон ячеек данными по определенному закону: в арифметической или геометрической прогрессии. Для этого не нужно даже знать формулы. Для значений в формате дат предусмотрено создание специфических последовательностей.
Инструмент Прогрессия доступен через меню
Для начала работы введите начальное значение (первый член) прогрессии. Затем выделите диапазон ячеек, куда будут вводиться данные, и вызовите инструмент.
Числовые последовательности
Арифметическая прогрессия представляет собой
числовую последовательность
, где каждое число больше (или меньше) предыдущего на одно и тоже значение (шаг).
Примеры:
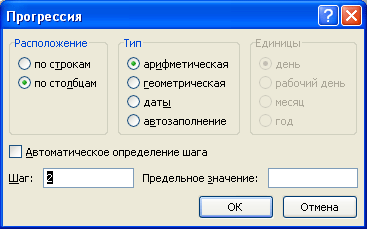
Арифметическая прогрессия с шагом 2 — это последовательность чисел 1, 3, 5, 7, 9, 11, … В окне инструмента
Прогрессия
нужно выбрать
Арифметическая
и установить
Шаг
равным 2.
Геометрическая прогрессия с шагом 2 — это последовательность чисел 2, 4, 8, 16, …. Этот пример позволяет быстро вспомнить степени 2. В окне инструмента
Прогрессия
нужно выбрать
Геометрическая
и установить
Шаг
равным 2.
Конечно, арифметическую прогрессию 1, 3, 5, 7, 9, 11, … можно организовать путем формулы
=А1+2
, а геометрическую 2, 4, 8, 16, … —
=А1*2
. Это уже как кому удобнее.
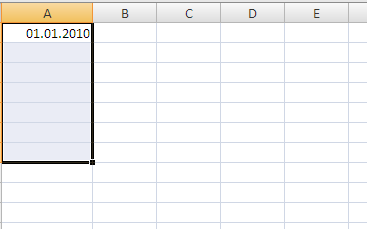
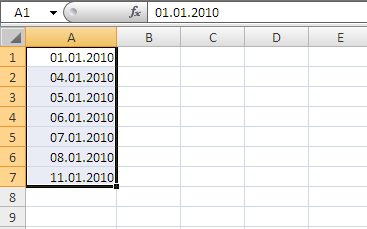
Последовательности дат и рабочих дней
В инструменте
Прогрессия
есть одна замечательная возможность по заполнению значений в формате дат. Вводим дату, выбираем диапазон,
вызываем инструмент
Прогрессия
, выбираем Тип
Даты
, выбираем Единицы
Рабочий день
.
В итоге получаем диапазон, заполненный только одними
рабочими днями
(не суббота и не воскресенье).
Если выберем в качестве единиц месяц, то месяц будет прибавляться к начальной дате и т.д. Эти возможности уже за несколько секунд не реализуешь, нужно вспоминать формулы. А если вспомнить, что еще можно и шаг прогрессии задавать, то можно гарантировать, что формула простой не получится.
Числовые последовательности
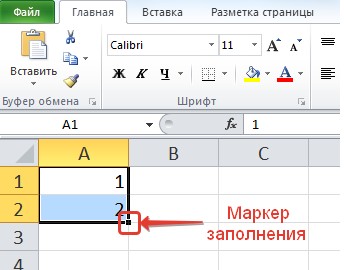
Чтобы, к примеру, сделать нумерацию строк, можно вводить номера 1, 2, 3 и т.д. вручную. А можно использовать автозаполнение.
Для автоматического ввода номеров напишем в ячейке А1 число 1, в ячейке А2 число 2. Выделим обе ячейки. Обратим внимание, что при наведении курсора в правый нижний угол ячейки А2 появился черный квадратик — это маркер заполнения.
Если навести на него курсор мыши, то курсор примет вид черного крестика. Теперь нужно нажать левую кнопку мыши и, удерживая, потянуть вниз. Рядом с курсором появляется значение, которое будет введено в последнюю ячейку, если отпустить кнопку мыши.
- Если в ячейку А1 ввести значение 1, а потом нажать на клавиатуре клавишу Ctrl и потянуть вниз за маркер заполнения этой ячейки, то значения следующих ячеек будут увеличиваться на 1.
- Чтобы ввести последовательность нечетных чисел (шаг увеличения чисел равен 2), введем в ячейку А1 число 1, а в ячейку А2 число 3. Далее выделим обе ячейки и за маркер заполнения потянем вниз. Мы получим последовательность чисел 1, 3, 5, 7 и т.д.
- Аналогично можно получить последовательность четных чисел, для этого нужно ввести числа 2 и 4 (шаг равен 2).
- Ввод арифметической (геометрической) прогрессии. Для создания арифметической прогрессии введем в ячейку А1 значение первого члена прогрессии. На вкладке Главная в группе Редактирование выберем команду Заполнить — Прогрессия.
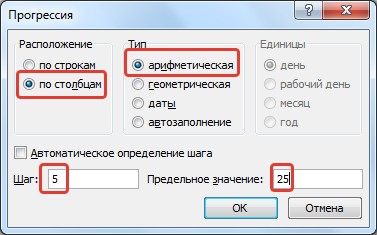
В диалоговом окне Прогрессия можно установить параметры: Расположение, Тип прогрессии, Шаг, Предельное значение.
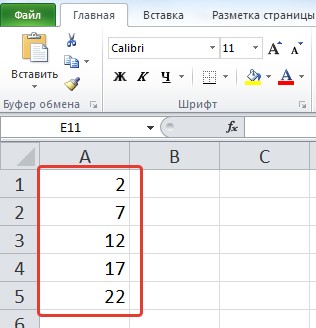
Если выбрать расположение по столбцам арифметической прогрессии с шагом 5 и предельным значением 25 (при этом в ячейке А1 введено значение 2, а сама ячейка выделена), то получим следующее заполнение:
Примечание
- Автозаполнение можно использовать не только по столбцам, но и по строкам. Для этого нужно вводить начальные значения в сроке и перетаскивать маркер заполнения не вниз, а вправо.
- Если нужно заполнять последовательность чисел в порядке возрастания, то маркер нужно перетаскивать вниз или вправо. Если в порядке убывания — вверх или влево.
Последовательность дней недели
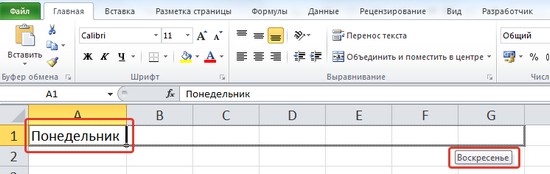
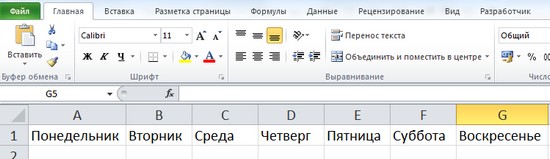
Чтобы ввести последовательность дней недели, достаточно в первую ячейку ввести Понедельник (или другой день) и потянуть за маркер заполнения этой ячейки в нужном направлении.
Последовательность Месяцы
Точно так же, как и в примере последовательности дней недели, в Excel можно получить последовательность месяцев, введя в первую ячейку нужный месяц (например, январь).
Последовательность дат
Введя в ячейку дату (например, 20.06.2015), можно получить последовательность дат.
Повторение последовательности
Если в ячейки А1, А2, А3 введены числа 1, 2, 3 соответственно и мы хотим, чтобы эта последовательность повторялась, выделим эти ячейки и при нажатой клавише Ctrl за маркер заполнения протянем вниз (или вправо), то мы получим последовательность 1, 2, 3, 1, 2, 3, 1, 2, 3…
Примечание
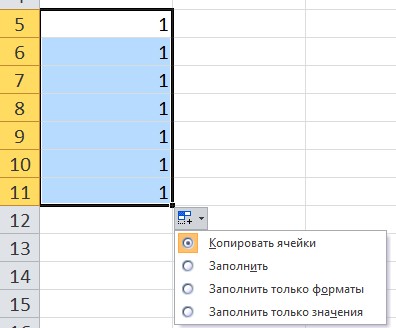
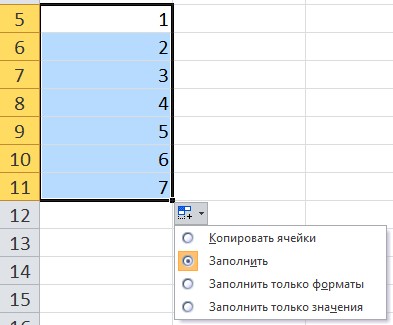
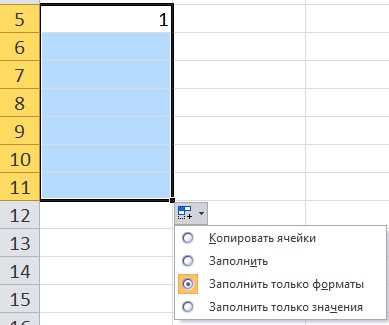
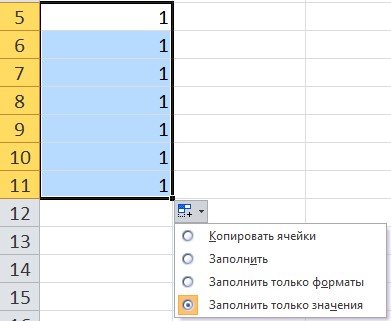
При использовании функции автозаполнения рядом с диапазоном появляется кнопка Параметры автозаполнения. При нажатии на нее можно выбрать нужный вариант.
В качестве примера введем в ячейку значение 1, за маркер заполнения протянем вниз. Обратим внимание, какой результат будет, если выбрать каждый из вариантов автозаполнения:
- Копирование ячейки — все значения равны 1.
- Заполнить — получим прогрессию с шагом 1.
- Заполнить только форматы — не будет значений, копируется форматирование ячеек.
Заполнить только значения — все значения равны 1, при этом форматирование ячейки не копируется.
Кстати, Excel позволяет делать свои списки последовательностей, которые потом можно использовать для автозаполнения таблиц. Читайте инструкцию >>>
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Расчет арифметической прогрессии и построение диаграммы
Формула
для вычисления n-го члена арифметической
прогрессии имеет вид: an
= a1
+ d * (n-1).
Сумма
n первых членов — Sn
арифметической прогрессии равна
Sn
= (a1
+ an)
* n/2, где a1
— первый член прогрессии, an
— n-й член прогрессии, d — разность
арифметической прогрессии.
Следующие задания
нужно выполнять на разных рабочих листах
в одной рабочей книге.
Задание.
Составить таблицу, вычисляющую n-й член
и сумму арифметической прогрессии.
Первый член прогрессии n1
равен – 2, разность d равна 0,725. Построить
точечную диаграмму для 10 членов и 10 сумм
арифметической прогрессии как показано
на рис. 5.
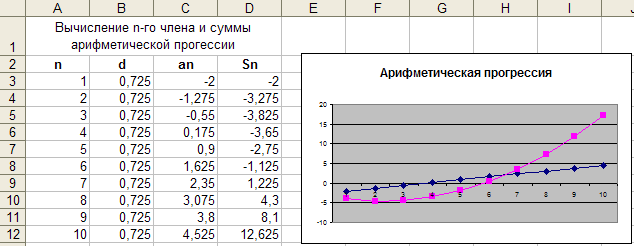
Рис.
5. Таблица с вычислениями n-го члена и
суммы арифметической прогрессии с
точечной диаграммой
Этапы
выполнения задания
Создание
таблицы
В
ячейку А1 ввести заголовок «Вычисление
n-го члена и суммы арифметической
прогрессии». Оформите строку заголовка.
При
оформлении строки заголовка в ячейках
C2 и D2 потребуется использовать нижний
индекс. В строке формул выделите нужный
символ и задайте ему способ отображения,
для этого выберите команду
Формат-Ячейки-Шрифт-Нижний
индекс.
Заголовки должны быть выровнены по
центру, шрифт полужирный (см. рис. 5).
Разместите
последовательность чисел от 1 до 10. Для
этого введите в А3 число 1 и затем в А4
ячейку число 2. Выделите обе
ячейки А3 и
А4. В правом нижнем углу прямоугольника
выделения находится небольшой квадратик
– маркер автозаполнения.
Поместите
указатель мыши на маркер заполнения
(при этом указатель примет вид тонкого
креста), нажмите левую кнопку мыши и
протащите указатель до ячейки А12 (рис.
6).
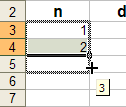
Рис. 6. Автозаполнение
При таком способе
выделения ячеек для последующего
автозаполнения (копирования) Excel
«запоминает» принцип, по которому нужно
заполнять ячейки, а справа появляется
подсказка со значением числа в
соответствующей ячейке.
Введите
в ячейку В4 значение разности арифметической
прогрессии d: 0,725. Зацепите маркер
автозаполнения и заполните нижние
ячейки.
В
ячейку С3 введите значение первого члена
арифметической прогрессии: –2.
В
ячейку С4 запишите формулу: =С3+В3,
т.е (сумма первого члена прогрессии и
разности прогрессии).
Выделите С4 и
скопируйте формулу на оставшиеся ячейки.
Обратите внимание, что имена ячеек
изменяются, т.к. формула содержит
относительную ссылку.
В
ячейку D3 введите формулу, вычисляющую
сумму n первых членов арифметической
прогрессии, которая для записи в Excel
имеет вид:
=(-2+C3)*A3/2
или =($C$3+C3)*A3/2,
что соответствует формуле нахождения
суммы арифметической прогрессии.
Скопируйте
эту формулу на оставшиеся ячейки.
Обратите внимание, что имя одной ячейки
не изменяется, так как была задана
абсолютная
ссылка.
Создание
диаграммы
Выделите
диапазон
ячеек С3:D12
со значениями
членов арифметической прогрессии и
суммы членов арифметической прогрессии.
Вызовите
Мастер
диаграмм
и выберите тип График,
затем График
с накоплением, на котором отдельные
значения помечены маркерами.
После
выполнения задания измените в ячейке
С3 значение первого члена прогрессии
на –3 и после этого придется в ячейках
D3:D12 изменить формулы расчета суммы
прогрессии, если была использована
формула
=(-2+C3)*A3/2, если же использовалась
формула =($C$3+C3)*A3/2 изменения вносить не
потребуется, т.к. она не содержит числового
значения первого члена прогрессии.
Обратите внимание
на изменения точечной диаграммы.
В
завершении переименуйте Лист2 на Арифм.
прогрессия.
Составленная
таблица не очень удобна для анализа
различных арифметических прогрессий,
т.к. при изменении одного параметра
прогрессии изменения приходится вносить
во все соответствующие ячейки.
Задание. На Листе3
составьте универсальную таблицу для
расчета арифметической прогрессии и
анализа ее с помощью диаграмм – рис. 7.
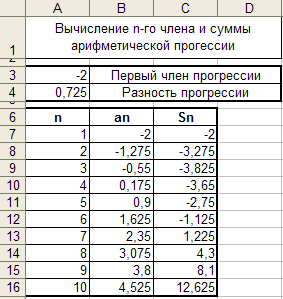
Рис. 7. Универсальная
таблица для анализа арифметической
прогрессии
Указания
Первый
член и разность арифметической прогрессии
находятся в ячейках А3 и А4, соответственно.
Формулы
для вычисления значений членов
арифметической прогрессии: ячейка В7:
=А3;
ячейка В8:
=
В7+$А$4
(используется
формула с абсолютной ссылкой на ячейку
А4). Эта формула копируется на оставшиеся
ячейки столбца В. Обратите внимание на
изменение относительных ссылок при
копировании формулы. Ячейка С7:
=($А$3+В7)*А7/2
(содержит абсолютную ссылку на ячейку
А3).
Переименуйте
Лист3 и дайте ему новое имя –
Универс.таб.арифм.прогрес.
Не забудьте
построить диаграмму!
После
выполнения задания убедитесь в том, что
полученная таблица «работает» при
различных значениях исходных данных
арифметической прогрессии.
11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #