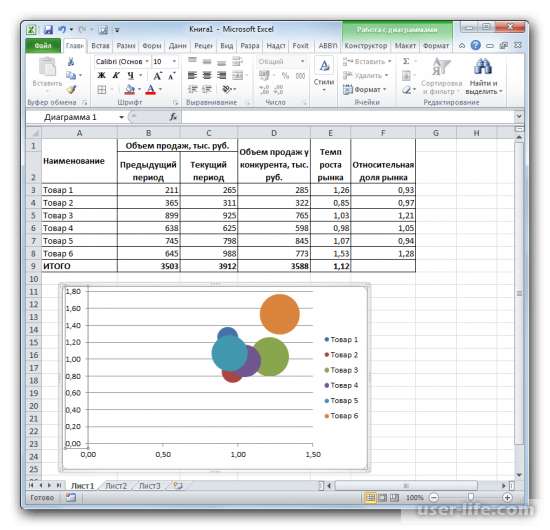
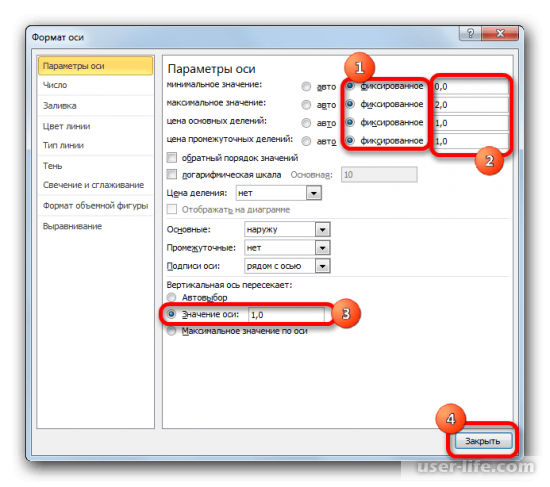
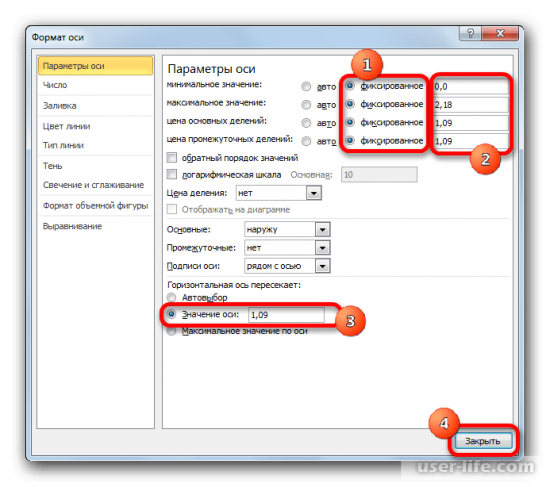
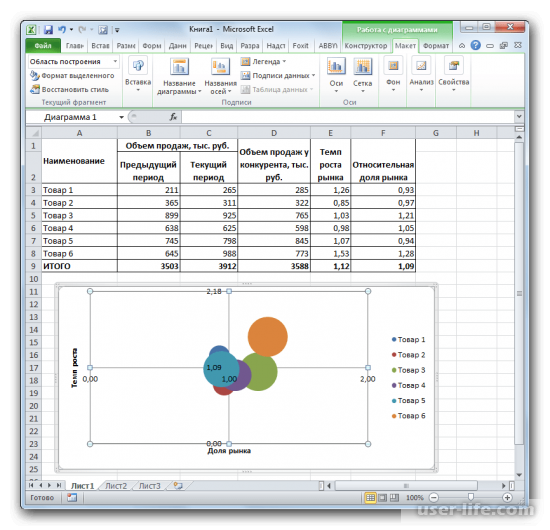
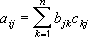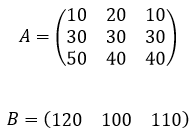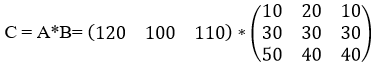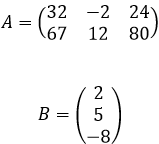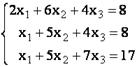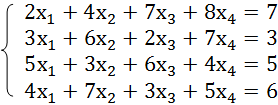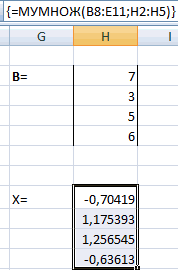Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:
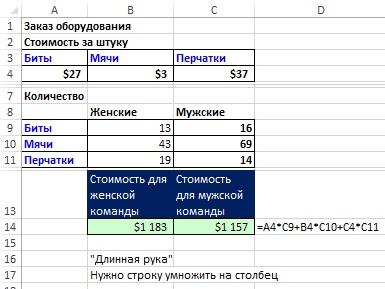
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 
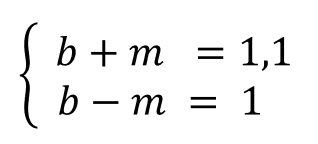
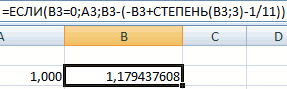
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
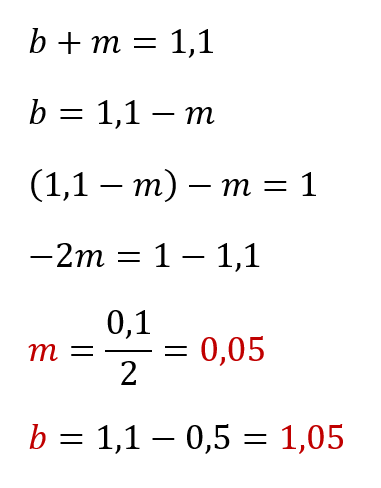
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
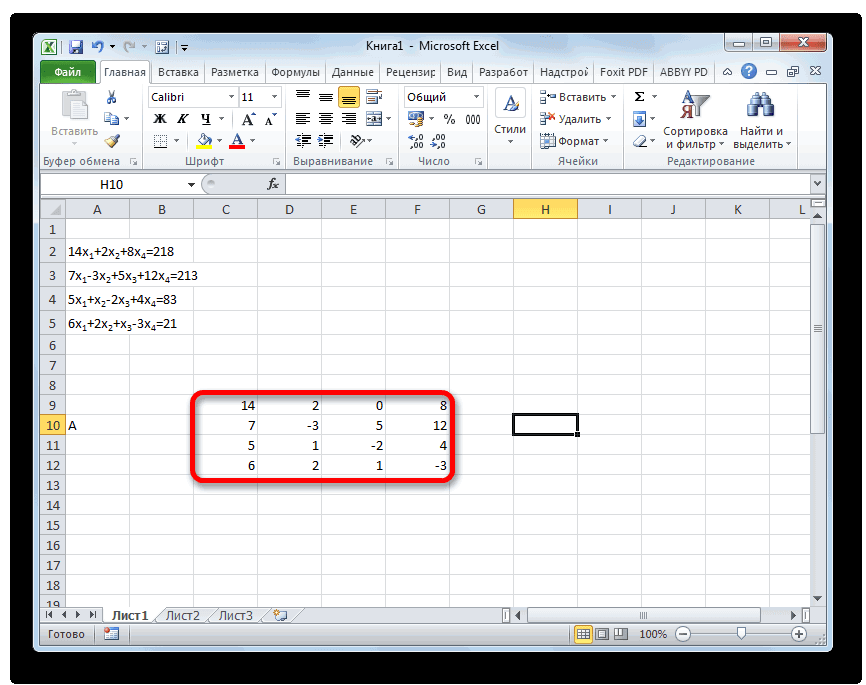
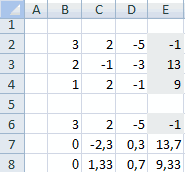
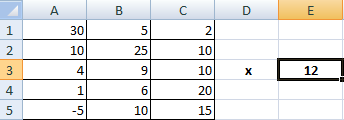
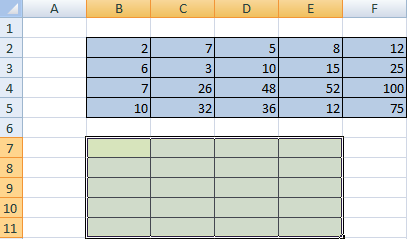
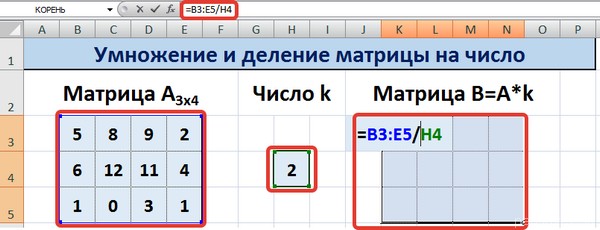
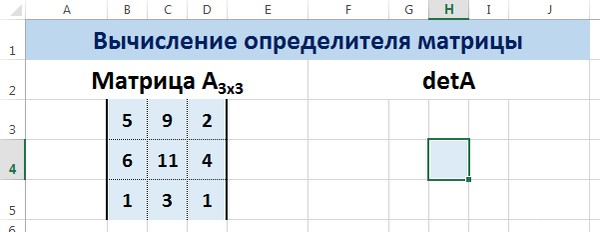
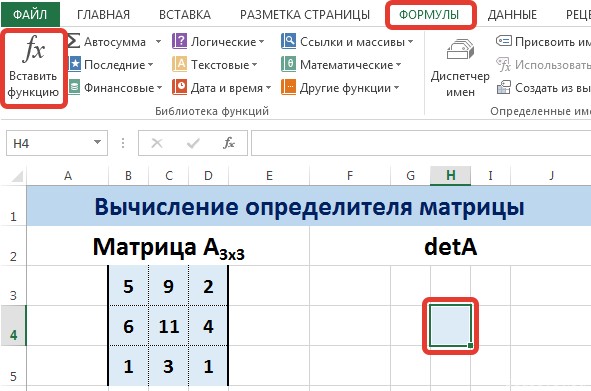
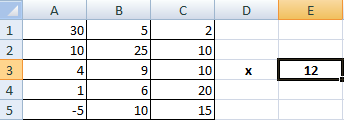
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).
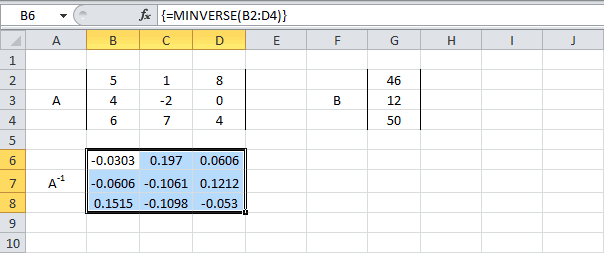
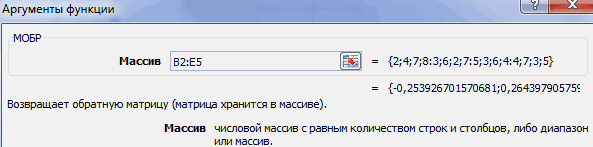
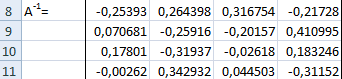
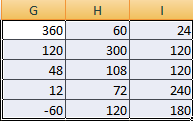
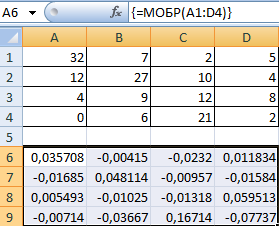
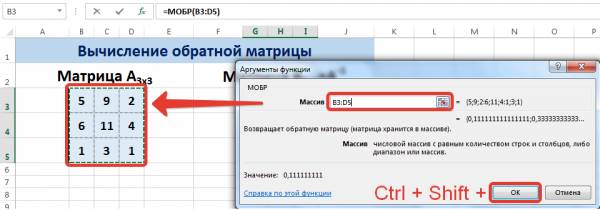
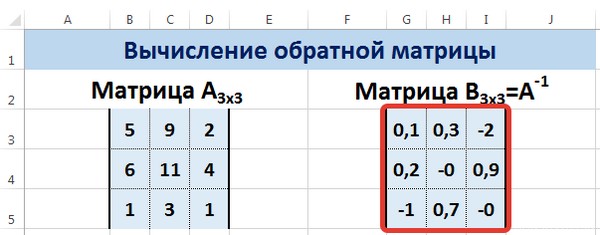
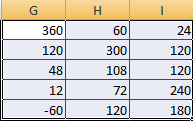
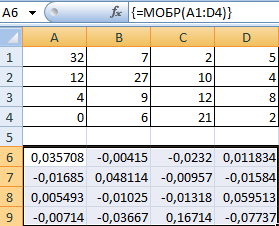
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
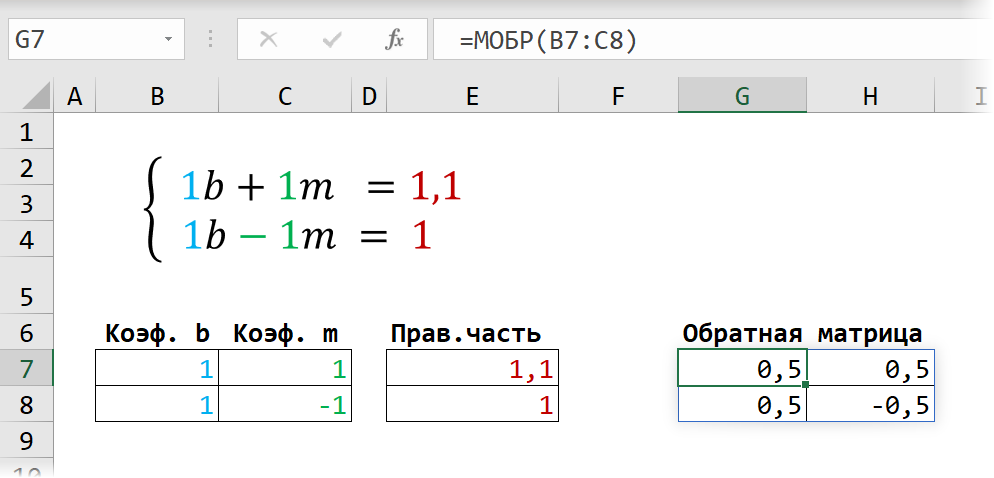
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
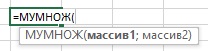
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
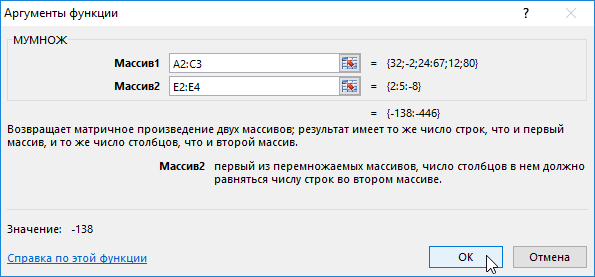
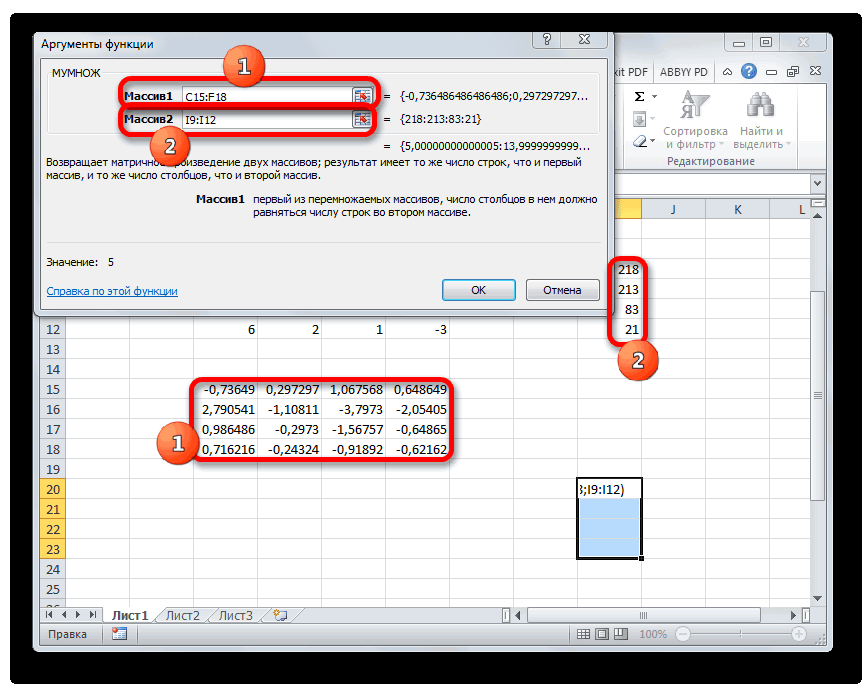
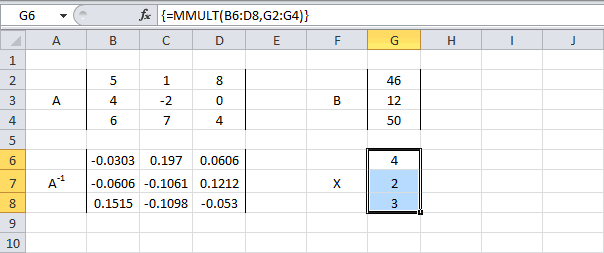
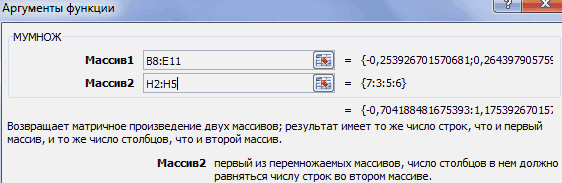
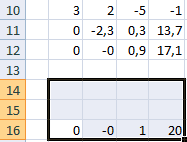
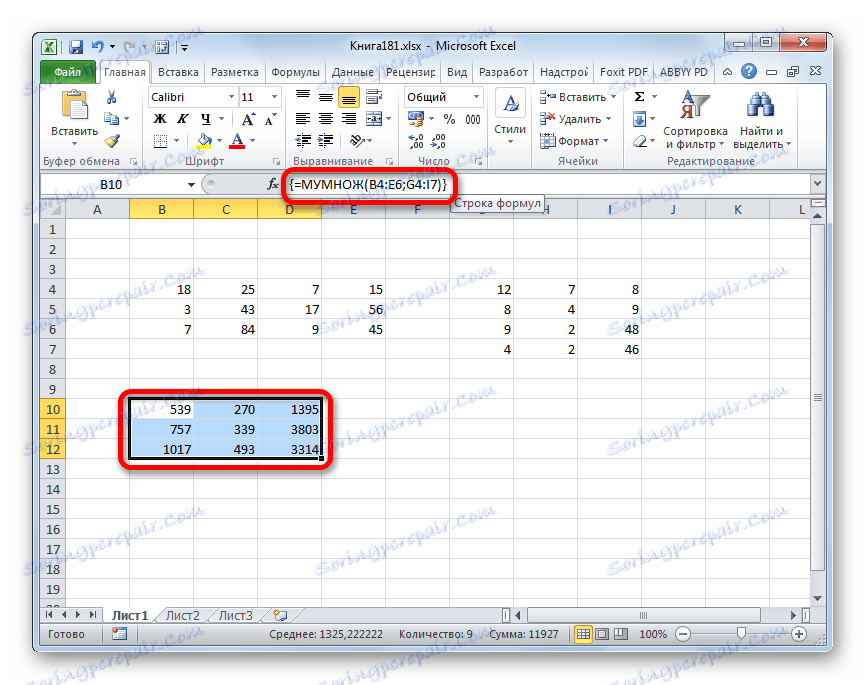
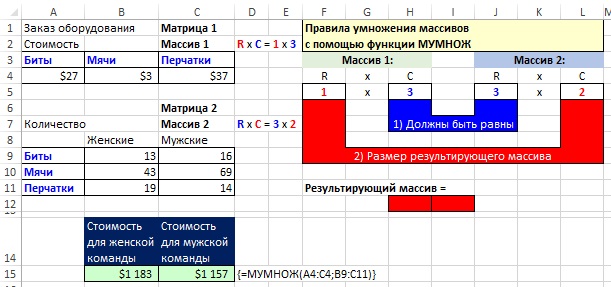
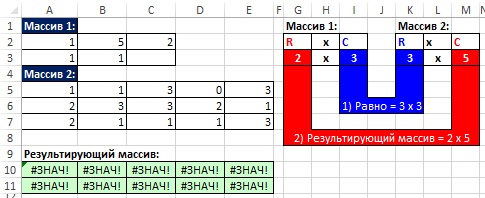
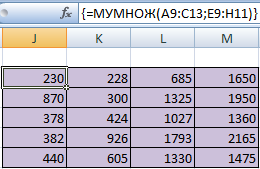
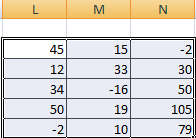
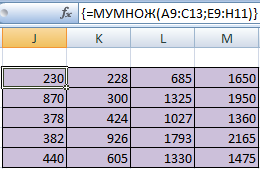
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
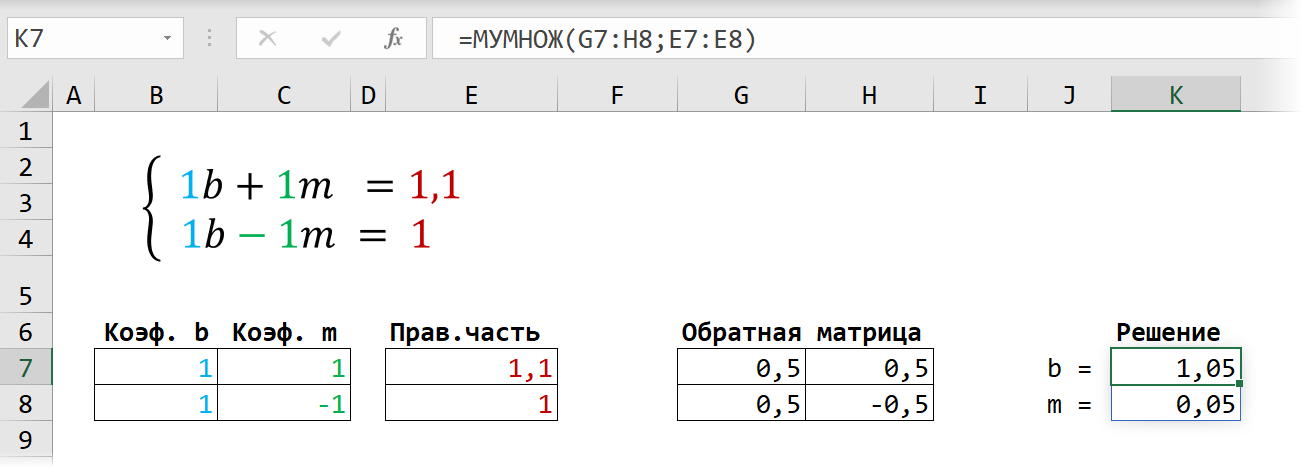
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
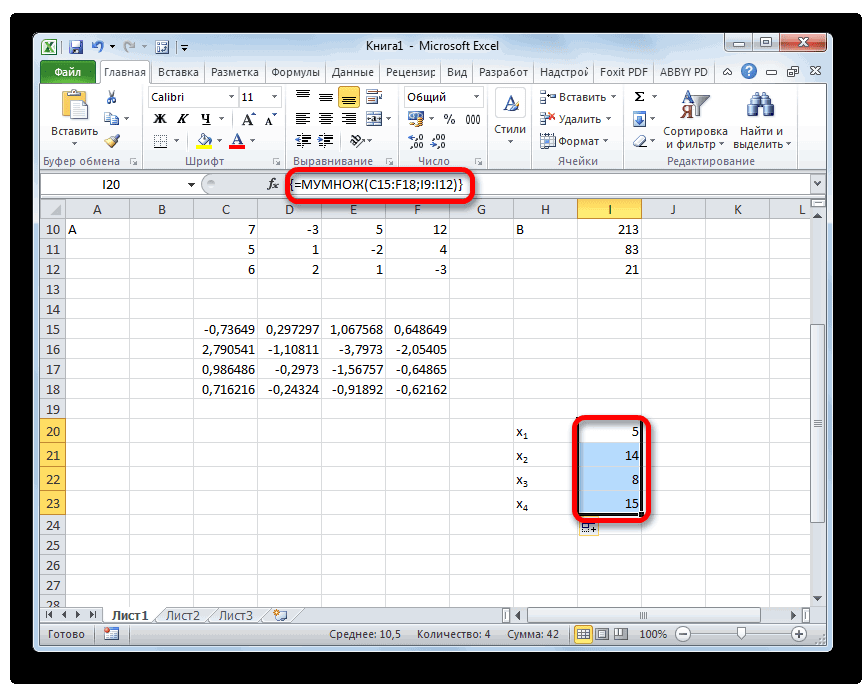
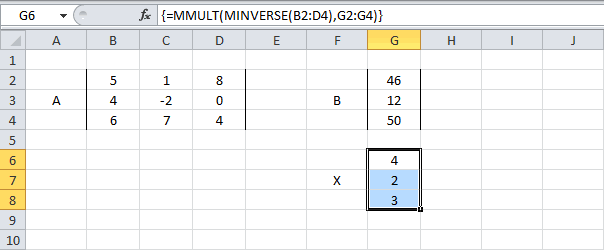
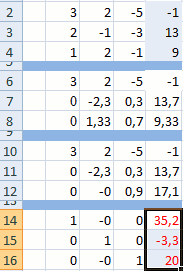
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
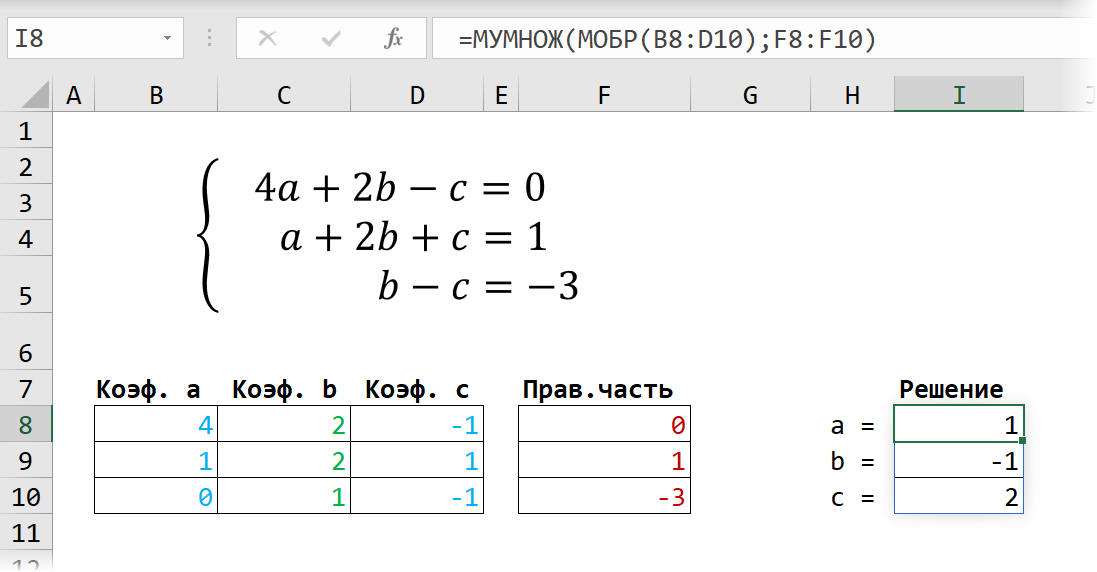
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
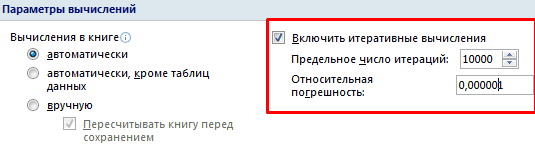
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).
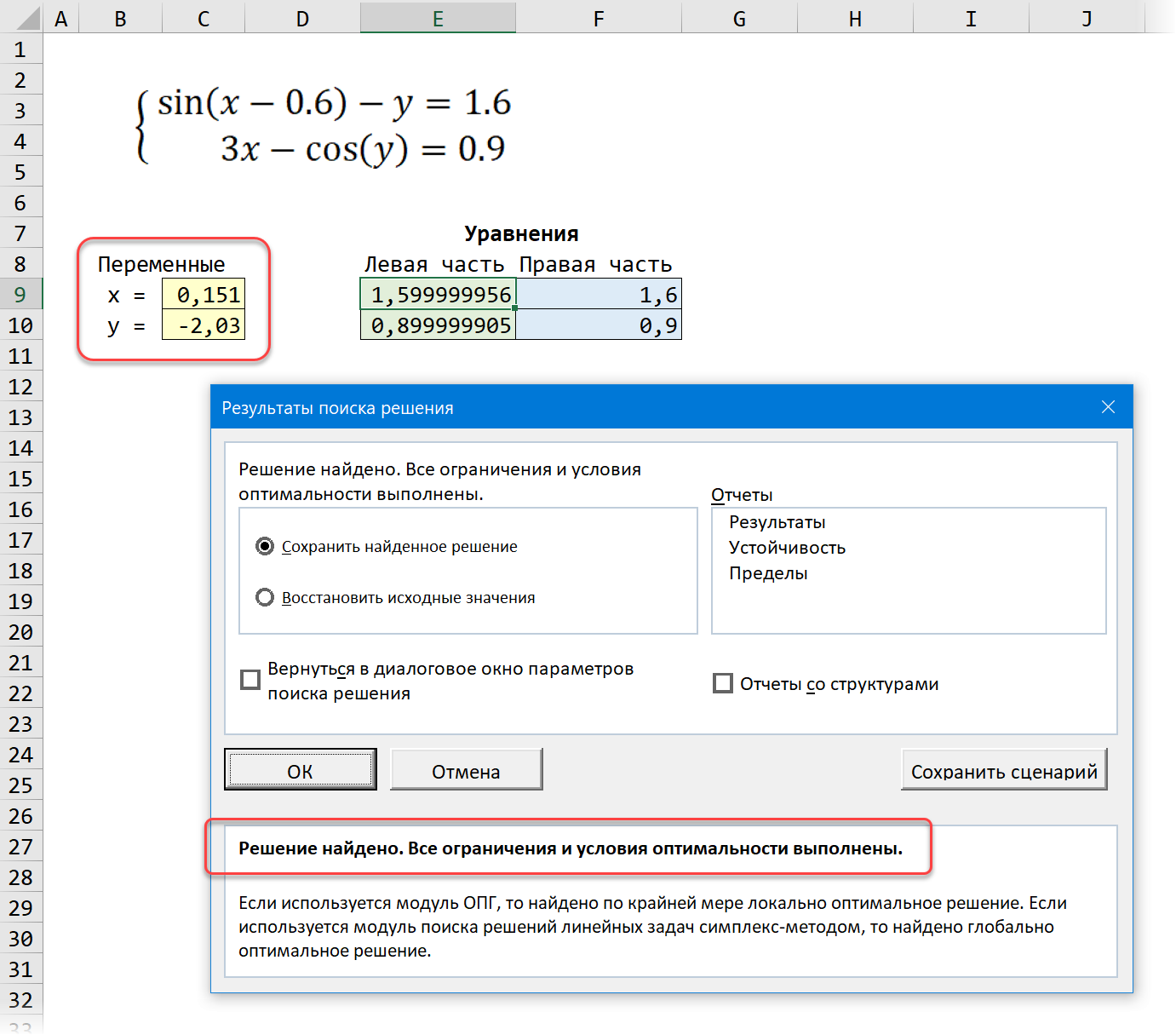
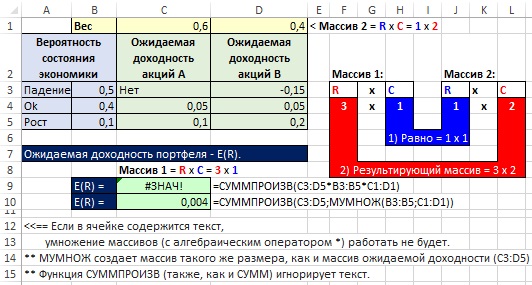
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
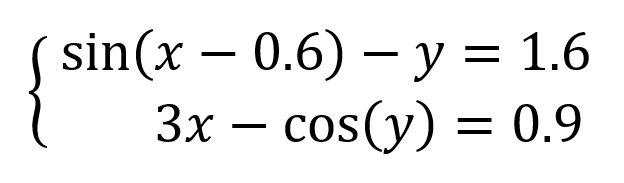
Подготавливаем основу для оптимизации в Excel:

Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
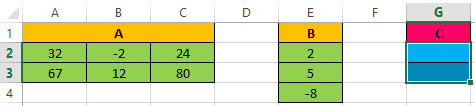
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
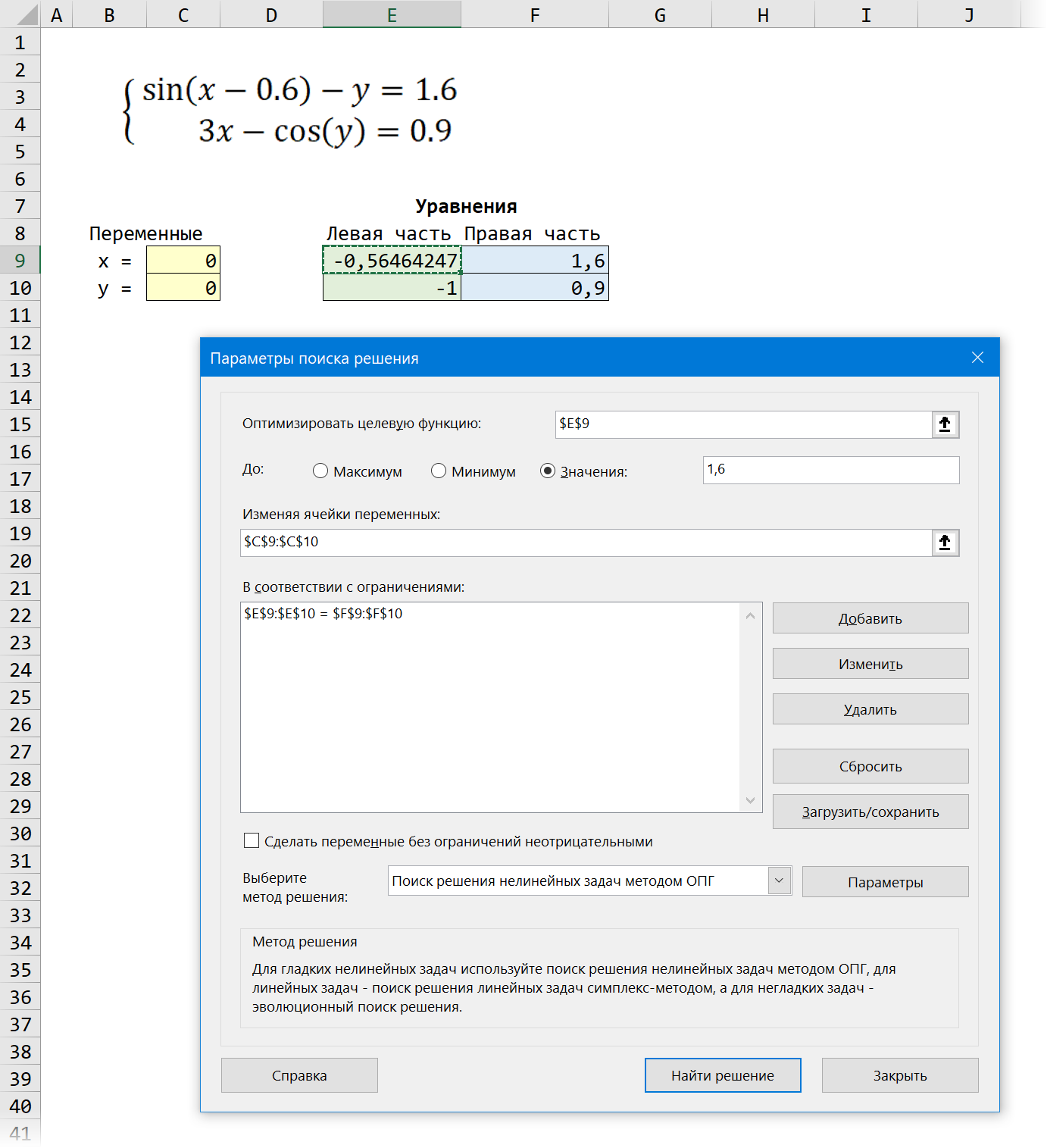
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
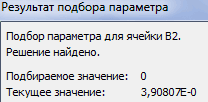
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel Starter 2010 Еще…Меньше
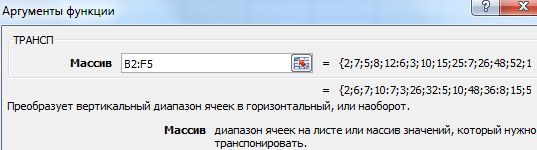
Функция МУМНОТ возвращает матричное произведение двух массивов. Результатом является массив с таким же числом строк, что и массив1, и с таким же числом столбцов, что и массив2.
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Синтаксис
МУМНОЖ(массив1; массив2)
Аргументы функции МУМНОЖ описаны ниже.
-
массив1, массив2 Обязательный. Перемножаемые массивы.
Замечания
-
Число столбцов в массиве1 должно быть таким же, как число строк в массиве «массив2», и оба массива должны содержать только числа.
-
Массив1 и массив2 могут быть заданы как диапазоны ячеев, константы массива или ссылки.
-
Функция МУМНОЖ возвращает значение ошибки #ЗНАЧ! в следующих случаях, указанных ниже.
-
Если какая-либо ячейка пуста или содержит текст.
-
Число столбцов в массиве1 отличается от числа строк в массиве «массив2».
-
-
Массив a, который является произведением двух массивов b и c, определяется следующим образом:
где i — номер строки, а j — номер столбца.
Примеры
Пример 1
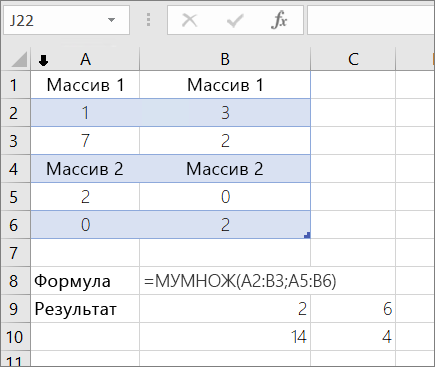
Пример 2
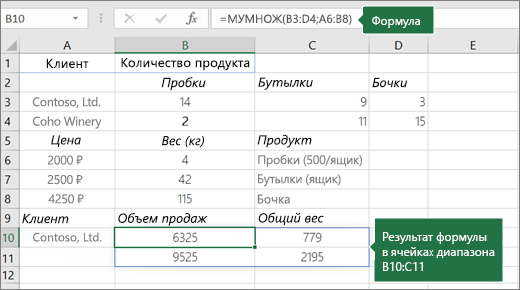
Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка. в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
Основные сведения об использовании функций мобр, мопред, мумнож
Понятие
матрицы и основанный на нем раздел
математики – матричная алгебра – имеют
чрезвычайно важное значение для
экономистов. Объясняется это тем, что
значительная часть математических
моделей экономических объектов и
процессов записывается в матричной
форме.
Обратные
матрицы, как и определители, обычно
используются для решения систем
уравнений с несколькими неизвестными.
1.
Функция
МОБР возвращает обратную матрицу для
матрицы, хранящейся в массиве.
МОБР(массив)
Массив
– это числовой массив с равным количеством
строк и столбцов.
-
Массив
может быть задан как диапазон ячеек,
например А1:С3, или как имя диапазона
или массива. -
Если
какая-либо из ячеек в массиве пуста или
содержит текст, то функция МОБР возвращает
значение ошибки #ЗНАЧ!. -
МОБР
также возвращает значение ошибки
#ЗНАЧ!, если массив имеет неравное число
строк и столбцов.
2.
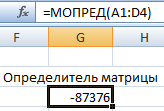
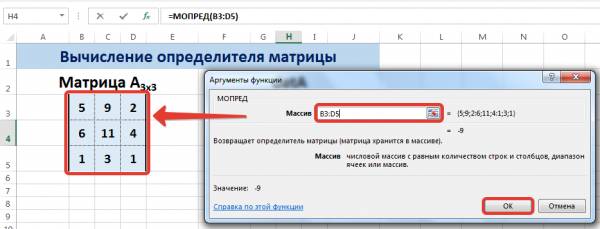
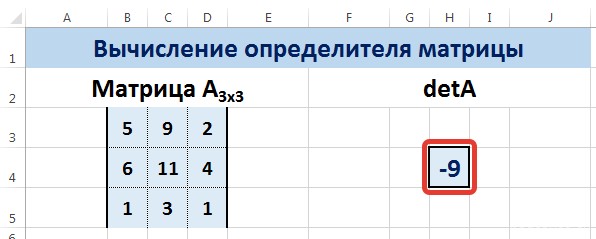
Функция МОПРЕД возвращает определитель
матрицы (матрица хранится в массиве).
МОПРЕД(массив),
где
массив – см. п. 1.
3.
Функция МУМНОЖ возвращает произведение
матриц (матрицы хранятся в массивах).
Результатом является массив с таким же
числом строк, как массив1, и с таким же
числом столбцов, как массив2.
МУМНОЖ(массив1;массив2)
Массив1,
массив2 – это перемножаемые массивы.
-
Количество
столбцов аргумента массив1 должно быть
таким же, как количество строк аргумента
массив2, и оба массива должны содержать
только числа. -
Массив1
и массив2 могут быть заданы как интервалы,
массивы констант или ссылки. -
Если
хотя бы одна ячейка в аргументах пуста,
или если число столбцов в аргументе
массив1 отличается от числа строк в
аргументе массив2, то функция МУМНОЖ
возвращает значение ошибки #ЗНАЧ!.
Основные сведения о макросах
В
EXCEL VBA-макрос может быть двух типов:
подпрограммой и функцией.
Макрос-подпрограмма
может быть выполнена любым пользователем,
либо другим макросом. Она начинается
ключевым словом SUB и заканчивается END
SUB. Строки, заключенные между этими
операторами, составляют текст макроса.
С
помощью макрорекордера можно записать
только макрос-подпрограмму.
Макрорекордер
записывает действия пользователя,
которые можно потом многократно
воспроизводить. Текст макроса может
быть записан как с абсолютными, так и с
относительными ссылками.
Содержание лабораторной работы
Выполнение
данной лабораторной работы включает в
себя:
-
использование
встроенных математических функций
МОБР, МОПРЕД и МУМНОЖ для вычисления
обратной матрицы, определителя матрицы
и перемножения матриц; -
запись
указанных последовательностей действий
макрорекордером в виде VBA-макросов с
абсолютными и относительными ссылками; -
запуск
созданных макросов с помощью кнопок и
меню.
Выполнение лабораторной работы
Использование
функций МОБР, МОПРЕД и МУМНОЖ
1.
Найдите матрицу, обратную данной:
Для
этого:
-
введите
элементы матрицы в диапазон ячеек
А1:С3; -
для
получения обратной матрицы выделите
несмежный диапазон ячеек такого же
размера, например E1:G3,
и введите формулу массива {=МОБР(А1:С3)}.
Для заключения формулы в фигурные
скобки после ввода формулы нажмите
клавиши CTRL+Shift+Enter.
2.
Вычислите определитель матрицы А. Для
этого выделите любую свободную ячейку,
например А5, и введите формулу
=МОПРЕД(А1:С3)
3.
Вычислите произведение матрицы А на
матрицу В, где
;
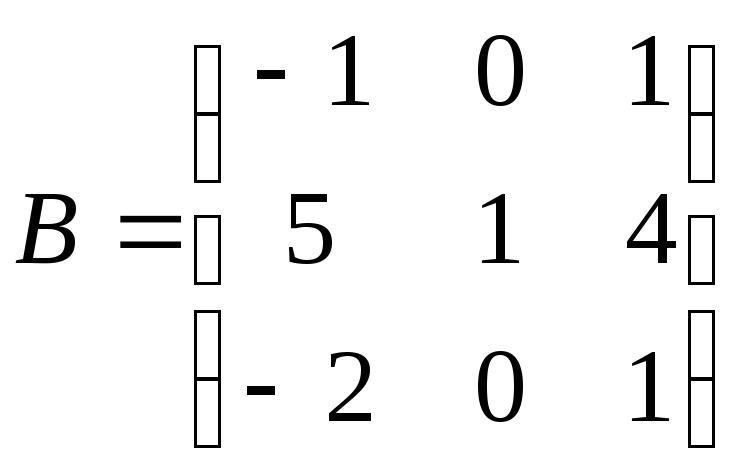
Для
этого:
-
введите
элементы матрицы А
в диапазон ячеек А10:С11; -
введите
элементы матрицы В
в диапазон ячеек А13:С15; -
выделите
диапазон ячеек с таким же числом строк,
как массив А,
и с таким же числом столбцов, как массив
В,
например, E10:G11 и введите формулу
{=МУМНОЖ(А10:С11;
А13:С15)};
-
нажмите
CTRL+Shift+Enter.
4.
Решите систему линейных уравнений с
3-мя неизвестными
(1)
методом
обратной матрицы.
Обозначим

(2)
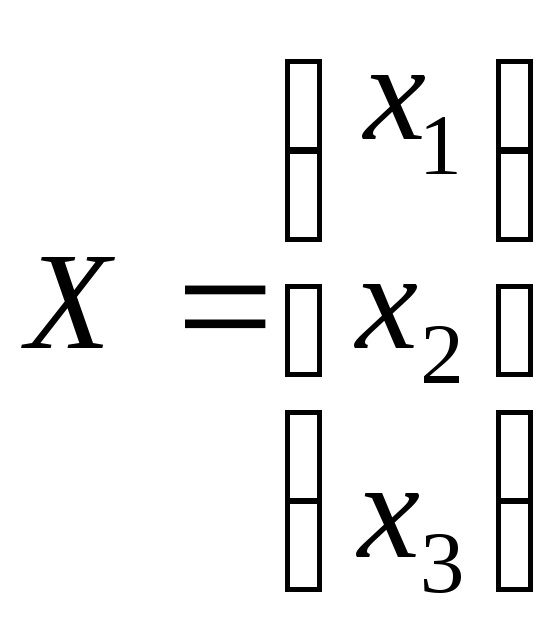

Решение
системы (1) в матричной форме имеет вид
АХ
= В,
где: А
– матрица коэффициентов;
Х
– столбец неизвестных;
В
– столбец свободных членов.
При
условии, что квадратная матрица (2)
системы (1) невырожденная, т.е. ее
определитель А
0, существует обратная матрица А.
Тогда решением системы методом обратной
матрицы будет матрица-столбец X
= AB.
Найдем
это решение. Для этого:
-
Найдем
определитель А
= 5 (см. п. 2). Для этого активизируем новый
рабочий лист и введем элементы матрицы
коэффициентов А
в
диапазон ячеек А1:С3. Выделим любую
свободную ячейку, например А5, и введем
формулу
=МОПРЕД(А1:С3).
-
Так
как А
0, то матрица А
– невырожденная, и существует обратная
матрица А.
Найдем
обратную матрицу. Для этого выделим
несмежный диапазон ячеек такого же
размера, что и матрица А,
например E1:G3,
и введем формулу массива {=МОБР(А1:С3)}.
-
Найдем
решение системы в виде матрицы-столбца
X
= AB..
Для этого введем элементы матрицы В
в диапазон ячеек E6:E8,
выделим диапазон ячеек с таким же числом
строк, как массив А,
и с таким же числом столбцов, как массив
В,
например, G6:G8 и введем формулу массива
={МУМНОЖ(E1:G3;
E6:E8)};
Получим:

т.е.
решение системы (4; 2; 1).
Запись
макросов с помощью макрорекордера
5.
Активизируйте новый рабочий лист.
6.
Добавьте к существующим встроенным
спискам (месяцев, дней недели) новый
пользовательский список автозаполнения.
Для этого:
-
в
ячейки
А1:А12
введите:
January, February, March, April, May, June, July, August, September,
October, November, December; -
выделите
на листе список элементов, которые
требуется включить в список автозаполнения
(диапазон A1:A12); -
щелкните
значок Кнопка
Microsoft
Office,
а затем щелкните Параметры
Excel; -
выберите
Основные,
и затем в группе Основные
параметры для работы в Excel
в строке Создавать
списки для сортировки и заполнения
нажмите
кнопку
Изменить списки; -
убедитесь,
что ссылка на ячейки в выделенном списке
элементов отображается в поле Импорт
списка из ячеек, и нажмите кнопку Импорт.
Элементы выделенного списка будут
добавлены в поле Списки; -
два
раза нажмите кнопку ОК.
7.
Для создания макросов с помощью
макрорекордера необходимо:
-
Если
вкладка Разработчик
недоступна, выполните следующие действия
для ее отображения:
-
щелкните
значок Кнопка
Microsoft Office,
а затем щелкните Параметры
Excel; -
в
группе Основные
параметры работы с Excel
установите флажок Показывать
вкладку «Разработчик» на ленте,
а затем нажмите кнопку ОК.
-
Для
установки уровня безопасности, временно
разрешающего выполнение всех макросов,
выполните следующие действия:
-
на
вкладке Разработчик
в группе Код
нажмите кнопку Безопасность
макросов; -
в
группе Параметры
макросов
выберите переключатель Включить
все макросы
(не рекомендуется, возможен запуск
опасной программы), и нажмите кнопку
ОК.
Примечание. Для
предотвращения запуска потенциально
опасного кода по завершении работы с
макросами рекомендуется вернуть
параметры, отключающие все макросы.
8.
Запишите макрос в режиме с абсолютными
ссылками. Для этого:
-
на
вкладке Разработчик
в группе Код
нажмите кнопку Запись
макроса; -
в
поле
Имя макроса введите
имя макроса
(по
умолчанию Макрос1);
Примечание. Первым
символом имени макроса должна быть
буква. Последующие символы могут быть
буквами, цифрами или знаками подчеркивания.
В имени макроса не допускаются пробелы;
в качестве разделителей слов следует
использовать знаки подчеркивания. Если
используется имя макроса, являющееся
ссылкой на ячейку, может появиться
сообщение об ошибке, указывающее на
недопустимое имя макроса.
-
в
списке Сохранить
в
выберите книгу, в которой необходимо
сохранить макрос (по умолчанию Эта
книга); -
введите
описание макроса в поле Описание; -
для
начала записи макроса нажмите кнопку
ОК; -
введите
в ячейку C1
слово January,
затем создайте ряд (установите курсор
на черный квадратик в правом нижнем
углу активной ячейки C1
и протяните его, не отпуская кнопку
мыши, до ячейки C12); -
выделите
сформированный ряд и задайте розовый
цвет для выделенных ячеек (на вкладке
Главная
в группе Шрифт); -
на
вкладке Разработчик
в группе Код
нажмите кнопку Остановить
запись.
Совет. Можно
также нажать кнопку Остановить
запись
слева от строки состояния.
9.
Просмотрите последовательность команд
Visual Basic, записанную макрорекордером.
Для этого на вкладке Разработчик
в группе Код
нажмите кнопку Макросы,
в диалоговом окне Макрос
выделите имя макроса (Макрос1) и нажмите
кнопку Изменить.
По окончании просмотра программы,
записанной макрорекордером, вернитесь
в экран Microsoft
Excel
щелчком по кнопке
панели
задач.
10.
Выполните макрос. Для этого:
-
активизируйте
новый рабочий лист; -
на
вкладке Разработчик
в группе Код
нажмите кнопку Макросы,
в диалоговом окне Макрос
выделите имя макроса (Макрос1) и нажмите
кнопку Выполнить;
11.
Очистите область рабочего листа, нажав
на кнопку Выделить
все
на пересечении заголовков строк и
заголовков столбцов, затем на кнопку
Delete
на клавиатуре и на кнопку Нет
заливки
пиктографического меню Цвет
заливки
на вкладке Главная
в
группе
Шрифт.
12.
Запишите новый макрос в режиме с
относительными ссылками. Для этого:
-
на
вкладке Разработчик
в группе Код
нажмите кнопку Относительные
ссылки,
а затем кнопку Запись
макроса; -
в
поле
Имя макроса введите
имя макроса
(по
умолчанию Макрос2)
и нажмите кнопку ОК; -
введите
в активную
в данный момент
ячейку листа слово January,
затем создайте ряд (установите курсор
на черный квадратик в правом нижнем
углу активной ячейки и протяните его,
не отпуская кнопку мыши, на 11 ячеек
вниз); -
выделите
сформированный ряд и задайте голубой
цвет для выделенных ячеек; -
на
вкладке Разработчик
в группе Код
нажмите кнопку Остановить
запись и
отожмите кнопку Относительные
ссылки.
13.
Очистите область рабочего листа.
14.
Выполните второй макрос. Для этого:
-
выделите
произвольную ячейку; -
на
вкладке Разработчик
в группе Код
нажмите кнопку Макросы,
в диалоговом окне Макрос
выделите имя макроса (Макрос2) и нажмите
кнопку Выполнить;
15.
Сравните тексты программ Макрос1 и
Макрос2, расположенные в Модуле1. Для
этого на вкладке Разработчик
в группе Код
нажмите кнопку Макросы,
в диалоговом окне Макрос
выделите имя макроса (Макрос1 или Макрос2)
и нажмите кнопку Изменить.
По окончании просмотра программ,
записанных макрорекордером, вернитесь
в экран Microsoft Excel щелчком по кнопке
панели задач.
16.
Запишите самостоятельно новый макрос
(Макрос3), очищающий области рабочего
листа, занятые результатами работы
макросов, и проверьте его выполнение.
Запуск
макросов с помощью кнопок и меню
17.
Создайте кнопку для вызова Макрос1. Для
этого:
-
на
вкладке Разработчик
в группе Элементы
управления
нажмите кнопку Вставить,
а затем в разделе Элементы
управления формы
выберите элемент Кнопка;
-
щелкните
на листе место, где должен быть расположен
левый верхний угол кнопки, и растяните
кнопку до нужного размера; -
в
диалоговом окне Назначить
макрос объекту
выберите в списке макросов Макрос1
и щелкните кнопку OK; -
откорректируйте
название кнопки (назовите, например,
«Месяцы»);
Примечание. Чтобы
указать свойства кнопки, щелкните ее
правой кнопкой мыши и выберите пункт
Формат
объекта.
18.
Выполните Макрос1 с помощью кнопки.
19.
Создайте кнопку для вызова Макрос3 и
выполните этот макрос с помощью кнопки.
20.
Добавьте команду запуска макроса на
панель быстрого доступа. Для этого:
-
нажмите
кнопку Microsoft
Office,
затем кнопку Параметры
Excel
и выберите команду Настройка;
Примечание. Диалоговое
окно Настройка
панели быстрого доступа
можно также вызвать щелчком по кнопке
Настройка
панели быстрого доступа
справа от панели и выбором из списка
команды Другие
команды.
-
в
списке Выбрать
команды из
выберите Макросы,
из появившегося списка выберите нужный
макрос, а затем нажмите кнопку Добавить; -
нажмите
ОК.
Примечание. Для
перемещения панели быстрого доступа
щелкните кнопку Настройка
панели быстрого доступа
и выберите в списке Разместить
под лентой.
Запуск
макросов с помощью командной кнопки в
форме
21.
Создайте электронную форму для ввода
данных в таблицу сведений о студентах.
Форма должна содержать:
-
заголовок
«Сведения о студенте»; -
поле
для ввода фамилии с инициалами; -
поле
со списком для выбора номера группы; -
список
для выбора наименования специальности; -
2
переключателя для выбора пола; -
счетчик
для выбора года рождения (1990—2010); -
кнопку
для запуска макроса, осуществляющего
запись сведений о студенте в таблицу,
расположенную на другом листе.
Для
этого выполните следующие действия:
-
переименуйте
один из листов книги Excel в «Формы»; -
разместите
на листе «Форма» в ячейках А30:А39 список
номеров 10 групп, например, 8271-8280.
Разместите в ячейках С30-С39 список
названий специальностей; -
введите
в ячейку D2 заголовок формы: “Сведения
о студенте”. Введите в ячейки В4, В5,
В7, В12, В15 следующие названия: ФИО, Группа,
Специальность, Пол, Год рождения; -
в
ячейку D4 введите фамилию; -
на
вкладке Разработчик
в группе Элементы
управления
нажмите кнопку Вставить,
а затем в разделе Элементы
управления формы
выберите элемент Поле
со списком и
очертите
прямоугольный контур в области ячейки
F5; -
щелкнув
правой клавишей мыши по элементу
Поле со списком,
вызовите контекстное меню. Выберите
пункт Формат
объекта; -
установите
вкладку Элемент
управления.
Щелкните по кнопке сворачивания в поле
Формировать
список по диапазону
и выделите диапазон ячеек с номерами
групп. Разверните вкладку. Щелкните по
кнопке сворачивания в поле Связь
с ячейкой, затем
щелкните по ячейке H5 и разверните
вкладку. В поле Количество
строк введите
значение 5. Включите флажок Объемное
затемнение,
нажмите ОК; -
убедитесь
в возможности выбора номера группы из
списка с полем и изменении порядкового
номера в ячейке H5; -
введите
в ячейку D5 формулу для расшифровки
порядкового номера группы в списке:
=ИНДЕКС($А$30:$А$39;$Н$5). Используйте вариант
функции со ссылкой. Убедитесь в
правильности вывода номера группы в
ячейке D5; -
на
вкладке Разработчик
в группе Элементы
управления
нажмите кнопку Вставить,
а затем в разделе Элементы
управления формы
выберите элемент Список
и
очертите
прямоугольный контур в области ячеек
G7:I10. Вызовите контекстное меню элемента
Список
и
выберите пункт Формат
объекта; -
щелкните
по кнопке сворачивания в поле Формировать
список по диапазону
и выделите диапазон ячеек с названиями
специальностей. Разверните вкладку.
Включите флажок выбора только одинарного
значения, затем щелкните по кнопке
сворачивания в поле Связь
с ячейкой
и введите адрес ячейки щелчком по
кнопке K7. Разверните вкладку и включите
флажок Объемное
затемнение.
Нажмите
ОК; -
убедитесь
в возможности выбора названия
специальности из списка и изменении
порядкового номера в ячейке К7; -
введите
в ячейку D7 формулу для расшифровки
порядкового номера группы в списке:
=ИНДЕКС($С$30:$С$39;$K$7). Убедитесь в
правильности названия специальности
в ячейке D7; -
на
вкладке Разработчик
в группе Элементы
управления
нажмите кнопку Вставить,
а затем в разделе Элементы
управления формы
выберите элемент Переключатель
и
очертите
прямоугольный контур в области ячейки
F12.
Вызовите контекстное меню элемента
Переключатель
и
выберите пункт Формат
объекта; -
на
вкладке Элемент
управления
щелчком по ячейке D12 введите в поле
Связь
с ячейкой
ее абсолютный адрес и включите флажок
Значение
установлен.
Замените название флажка на «М»; -
аналогично
расположите значок переключателя в
области ячейки F13 и замените его название
на «Ж», при этом повторного связывания
с ячейкой не требуется; -
в
разделе Элементы
управления формы
выберите элемент Счетчик
и
очертите
прямоугольный контур в области ячеек
F15:F16.
Вызовите контекстное меню элемента
Счетчик
и
выберите пункт Формат
объекта; -
на
вкладке Элемент
управления
введите в поле Текущее
значение:
1990. Введите в поле Минимальное
значение:
1990. Введите в поле Максимальное
значение: 2010. Введите в поле Шаг
изменения:
1. Введите в поле Связь
с ячейкой
абсолютный адрес ячейки D15, нажмите ОК; -
проверьте
работу счетчика; -
в
разделе Элементы
управления формы
выберите элемент Кнопка
и
очертите
прямоугольный контур в области ячеек
C18:D18.
Появится окно Назначить
макрос объекту.
Закройте окно, не назначая макрос.
Замените название кнопки на «Запись
в таблицу».
22.
Создайте на новом листе с именем Список
студентов
во 2-ой строке шапку таблицы с названиями
столбцов: ФИО, Группа, Специальность,
Пол, Год рождения. Отрегулируйте ширину
столбцов.
23.
На листе Форма
в ячейки B25, С25, D25,
E25,
F25 вставьте формулы, ссылающиеся на
ячейки D4, D5, D7, D12 и D15. Проверьте формулы
в ячейках B25:F25:
В
ячейке В25 должна быть формула: =$D$4
В
ячейке С25 должна быть формула:
=ИНДЕКС($A$30:$A$39;$H$5)
В
ячейке D25 должна быть формула:
=ИНДЕКС($C$30:$C$39;$K$7)
В
ячейке Е25 должна быть формула: =$D$12
В
ячейке F25 должна быть формула: =$D$15
24.
Осуществите запись начального макроса
макрорекордером. Для этого:
-
на
вкладке Разработчик
в группе Код
нажмите кнопку Запись
макроса; -
в
поле
Имя макроса введите
имя макроса
(по
умолчанию); -
для
начала записи макроса нажмите кнопку
ОК;
-
на
листе Форма
выделите ячейки B25:F25;
-
на
вкладке
Главная в
группе
Буфер
обмена
нажмите кнопку Копировать; -
перейдите
на лист Список
студентов
и выделите ячейку А3; -
на
вкладке Главная
в группе Буфер
обмена
раскройте список Вставить
и
выберите команду Вставить
значения; -
на
вкладке Разработчик
в группе Код
нажмите кнопку Остановить
запись;
25.
Проверьте работу созданного макроса.
Для этого на листе «Список студентов»
очистите диапазон ячеек А3:Е3, перейдите
на лист «Формы», на вкладке Разработчик
в группе Код
нажмите кнопку Макросы,
в диалоговом окне Макрос
выделите имя созданного макроса и
нажмите кнопку Выполнить.
Строка сведений будет вставлена на то
же место.
26.
Для того, чтобы новые сведения вставлялись
в таблицу в следующие по порядку строки,
необходимо откорректировать текст
макроса. Для этого на вкладке Разработчик
в группе Код
нажмите кнопку Макросы,
в диалоговом окне Макрос
выделите имя созданного макроса и
нажмите кнопку Изменить.
Откроется окно редактора Visual Basic.
27.
В окне редактора Visual Basic внесите изменения
в текст программы после строки
Sheets(«Список
студентов»).Select
При
этом должны быть следующие строки:
Sheets(«Список
студентов»).Select
Range(«A2»).Select
If
Cells(3, 1).Value <> «» Then
Cells(2,
1).Select
ActiveCell.End(xlDown).Cells(2).Select
Else
Range(«A3»).Select
End
If
Selection.PasteSpecial
Paste:=xlValues, Operation:=xlNone, SkipBlanks:= _
False,
Transpose:=False
End
Sub
28.
Закройте окно редактора, щелкнув по
самому левому значку на инструментальной
панели редактора с изображением логотипа
Excel. Повторно выполните макрос.
29.
Назначьте кнопке «Запись в таблицу»
созданный макрос. Для этого выделите
кнопку правой клавишей мыши, в контекстном
меню выберите пункт Назначить
макрос,
в окне Назначить
макрос объекту
выделите соответствующий макрос и
нажмите ОК.
30.
Выполните макрос щелчком по кнопке.
31.
С помощью созданного макроса заполните
список студентов данными о принятых в
университет студентах (10-15 человек).
32.
Используя созданный в предыдущем задании
список студентов, создайте на новом
листе с именем «Справка» автоматизированную
форму для выдачи справки студенту
следующего образца:
Соответствующие
данные должны заноситься в справку
автоматически посредством выбора
фамилии студента из поля со списком.
Для
этого выполните следующие действия:
-
Разместите
на листе «Справка» в ячейках A1:G10
постоянный текст справки так, чтобы
для ввода фамилии использовалась ячейка
D4,
для ввода года рождения – E4,
для ввода № группы – В7, наименования
специальности – D7.
-
На
вкладке Разработчик
в группе Элементы
управления
нажмите кнопку Вставить,
а затем в разделе Элементы
управления формы
выберите элемент Поле
со списком
и очертите указателем мыши прямоугольный
контур в зоне ячеек A1:В2. Вызовите
контекстное меню элемента Поле
со списком
и выберите пункт Формат
объекта; -
Установите
вкладку Элемент
управления.
Щелкните по кнопке сворачивания в поле
Формировать
список по диапазону
и выделите диапазон ячеек с фамилиями
студентов без заголовка на листе Список
студентов.
Разверните вкладку. Щелкните по кнопке
сворачивания в поле Связь
с ячейкой.
Щелкните по ячейке А20. В поле Количество
строк введите
значение 6; -
Перейдите
на вкладку Свойства.
Снимите флажок Выводить
объект на печать.
Закройте окно Форматирование
объекта
кнопкой ОК. -
Проверьте
правильность работы поля со списком,
наблюдая за номером элемента, отображаемого
в ячейке А20 при выборе фамилии в списке; -
Присвойте
диапазону ячеек, в котором находится
список, имя Список.
Для этого выделите диапазон ячеек,
содержащий все данные о студентах без
заголовков на листе Список
студентов,
введите в поле имен имя Список
и нажмите клавишу Enter; -
Введите
в ячейку D4
формулу для отображения выбранной
фамилии:
=ИНДЕКС(Список;$A$20;1)
Примечание. Для
ввода в качестве аргумента имени
диапазона выберите имя Список
на вкладке Формулы
в группе Определенные
имена
из списка Использовать
в формуле.
-
Введите
в ячейку Е4 формулу для отображения
года рождения:
=ИНДЕКС(Список;$A$20;5);
-
Аналогично
введите в ячейку В7 формулу для отображения
номера группы, а в ячейку D7
– формулу для вывода наименования
специальности. -
Окончательно
проверьте работу поля со списком.
Выполните предварительный просмотр
справки. Для этого щелкните значок
Кнопка
Microsoft Office,
щелкните стрелку рядом с командой
Печать,
а затем выберите в списке команду
Предварительный
просмотр.
При просмотре на справке не должно быть
видно поле со списком для выбора
студента.
32.
Сохраните рабочую книгу на диске в
файле с именем lab6.xlsm,
причем в окне Сохранение
документа
в списке Тип
файла
выберите тип файла Книга
Excel
с поддержкой макросов.
Примечание.
Чтобы
запустить макросы после открытия
сохраненной книги, необходимо установить
уровень безопасности, временно разрешающий
выполнение всех макросов. Для этого:
-
на
вкладке Разработчик
в группе Код
нажмите кнопку Безопасность
макросов; -
в
категории Параметры
макросов
в группе Параметры
макросов
нажмите кнопку Включить
все макросы (не рекомендуется, возможен
запуск опасной программы),
а затем нажмите ОК.
Важно! Для
предотвращения запуска потенциально
опасного кода по завершении работы с
макросами рекомендуется вернуть
параметры, отключающие все макросы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
30.05.2015108.54 Кб15Fe.doc
- #
- #
- #
- #
Функция МУМНОЖ предназначена для нахождения произведения двух матриц из таблиц Excel по заданным данным. Данную функцию особенно удобно применять при решении задач матричной алгебры.
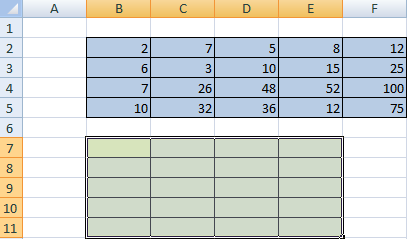
Как использовать функцию МУМНОЖ в Excel?
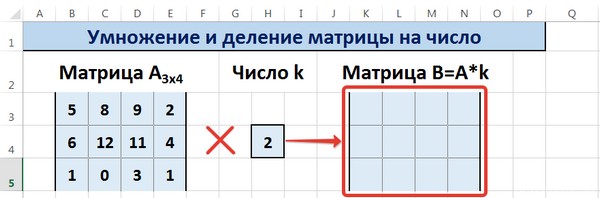
Рассмотрим следующий пример. Компания занимается изготовлением ролов на заказ, в состав ассортимента входит четыре вида продукции: рол унаги, филадельфия, зеленый дракон. Предположим нам необходимо решить задачу о затратах на покупку ингредиентов (рис, мягкий сыр, лосось) для планового изготовления ролов. Ниже приведем таблицы А — нормы расхода ингредиентов, B — план выпуска ролов (в штуках).
То есть, чтобы нам получить матрицу-строку затрат ингредиентов C, необходимо умножить матрицу B на матрицу А:
Итоговая размерность матрицы С равна 1×3. Для вычисления элементов матрицы С и для проверки полученных затрат на ингредиенты можно воспользоваться встроенной функцией табличного процессора MS Excel МУМНОЖ.
Функция МУМНОЖ в Excel пошаговая инструкция
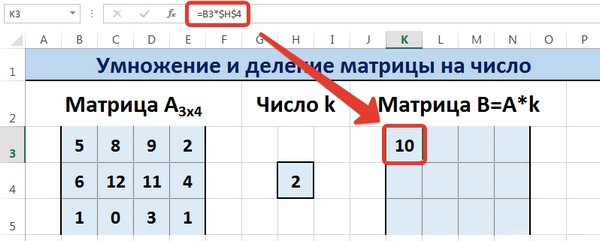
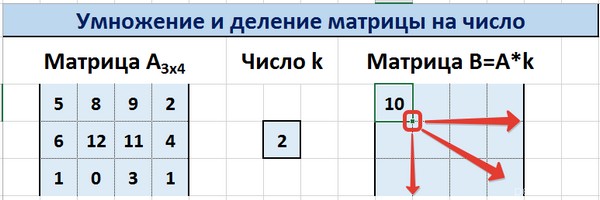
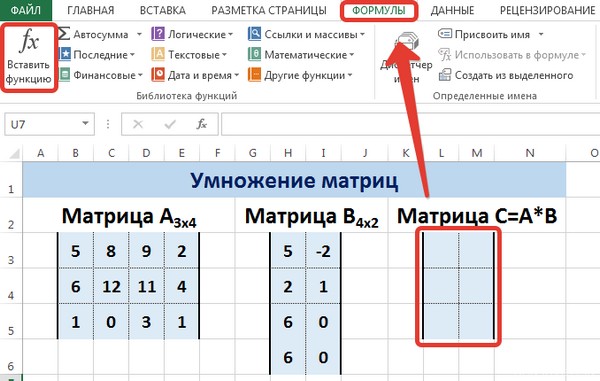
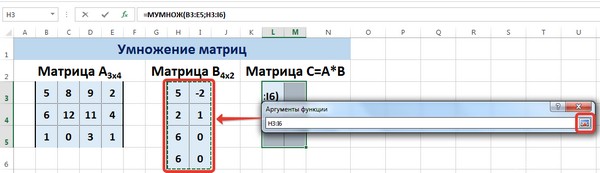
- Создадим на листе рабочей книги табличного процессора Excel матрицы A и B, как показано на рисунке:
- Далее на листе рабочей книги подготовим область для размещения нашего результата — итоговой матрицы С (затраты на ингредиенты в руб.), как показано на рисунке:
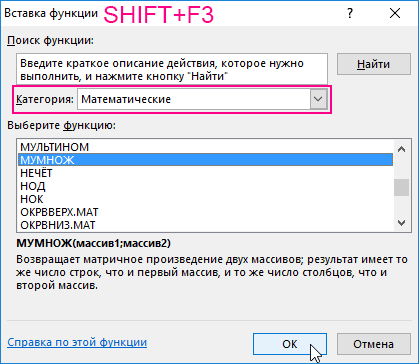
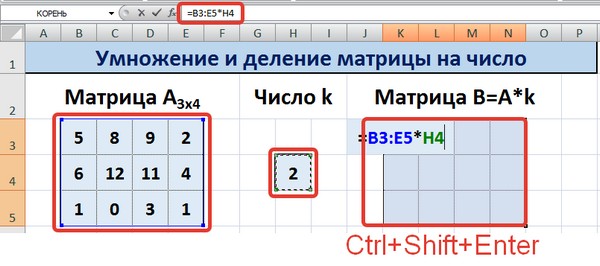
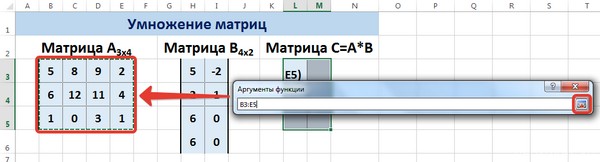
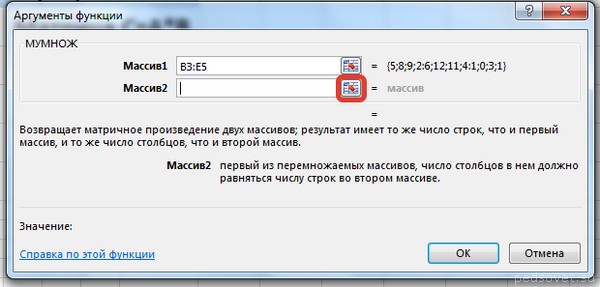
- Выделим диапазон ячеек для элементов матрицы С, т.е. диапазон А5:С5 и вызовем функцию МУМНОЖ категории «Математические», например, по команде «Вставить функцию» (SHIFT+F3), расположенной на вкладке «Формулы».
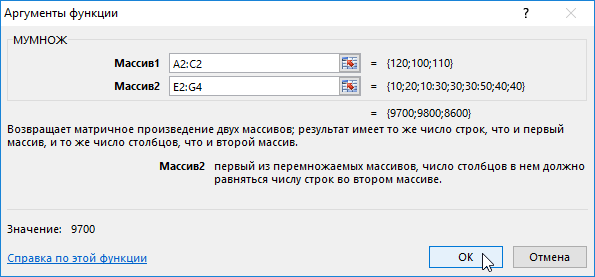
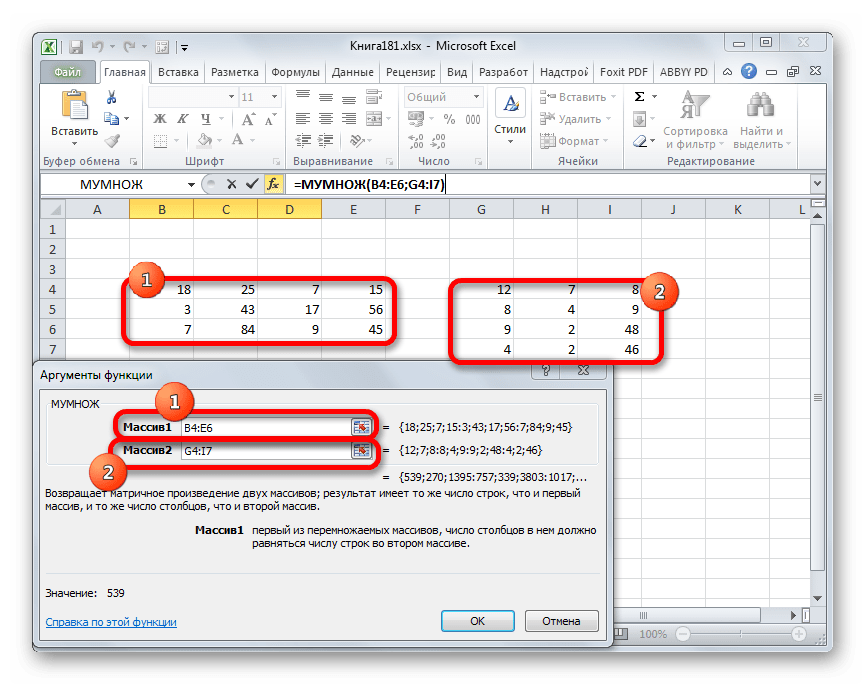
- В появившемся окне укажем диапазон соответствующий перемножаемым матрицам, помня о том, что произведение матриц некоммутативно:
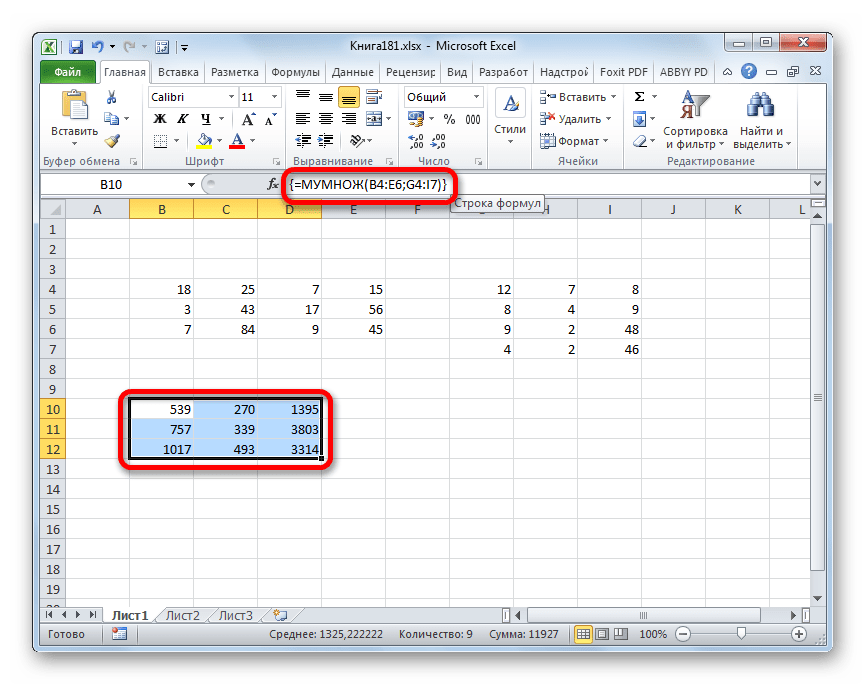
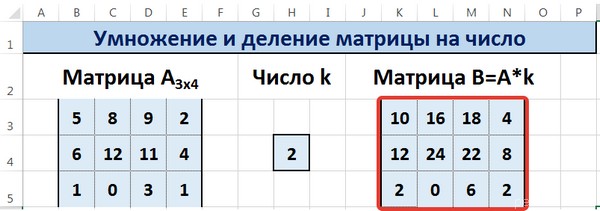
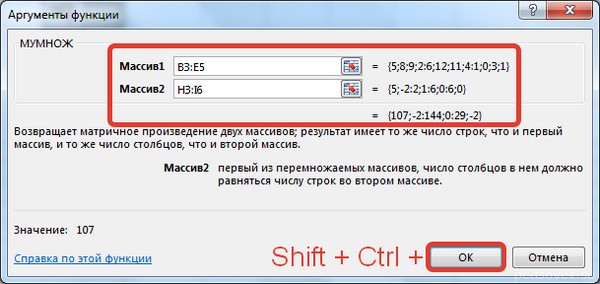
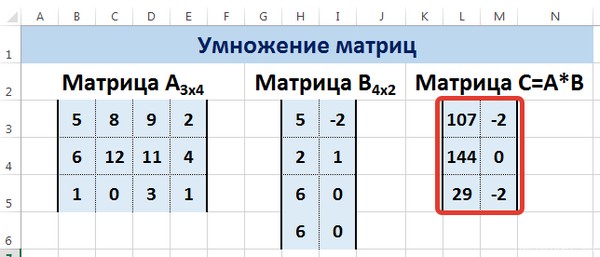
- Вместо кнопки «Ок», нажмем клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Это делается для того, чтобы получить результат в виде массива, а не одного значения в ячейке А5. Результат на рисунке ниже:
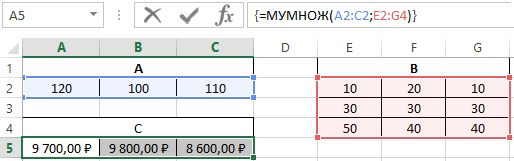
Таким образом получен следующий результат: затраты на изготовление ролов «унаги» составили 9700 руб., ролов «филадельфия» — 9800 руб., ролов зеленый дракон «8600».
Как найти произведение матрицы по функции МУМНОЖ в Excel
Рассмотрим классический пример из курса матричной алгебры, который будет полезен любому студенту, изучающему высшую математику в Вузе. Предположим необходимо найти произведение матрицы А и вектора столбца:
- Создадим на листе рабочей книги табличного процессора Excel матрицы A и B. На листе рабочей книги подготовим область для размещения итоговой матрицы С, как показано на рисунке:
- Выделим диапазон ячеек для элементов матрицы С, т.е. диапазон G2:G3 и вызовем функцию МУМНОЖ категории «Математические», например, по команде «Вставить функцию», расположенной на вкладке «Формулы». В появившемся окне укажем диапазон, соответствующий перемножаемым матрицам, помня о том, что произведение матриц некоммутативно:
- Вместо кнопки «Ок», нажмем клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Это делается для того, чтобы получить результат в виде массива, а не одного значения в ячейке. Результат на рисунке ниже:
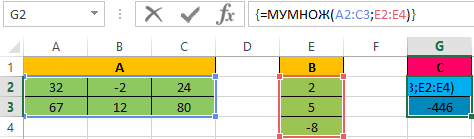
Рассмотрим еще один «жизненный пример». Каждому человеку необходимо оплачивать коммунальные платежи. Высчитывать сколько и за какой вид услуги платить — довольно трудоемкая задача, поэтому предлагаем ее решить непосредственно при помощи MS Excel, функции МУМНОЖ.
Анализ расходов в Excel с функцией МУМНОЖ
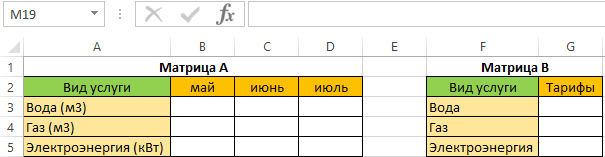
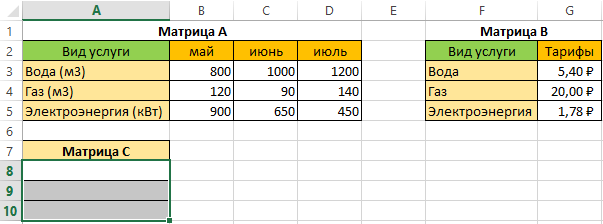
Предположим у нас имеется 3 вида коммунальных платежей: вода, газ, электроэнергия, и соответствующие данные по месяцам (май, июнь, июль) об использовании каждой услуги. Нам необходимо вычислить сколько по каждой услуге и за какой месяц необходимо заплатить.
- Составим матрицы А и В. На листе рабочей книги подготовим область для размещения нашего результата — итоговой матрицы С (итоговая стоимость по каждой услуге), как показано на рисунке:
- Выделим диапазон ячеек для элементов матрицы С, т.е. диапазон А8:A10 и вызовем функцию МУМНОЖ категории «Математические», например, по команде «Вставить функцию», расположенной на вкладке «Формулы».
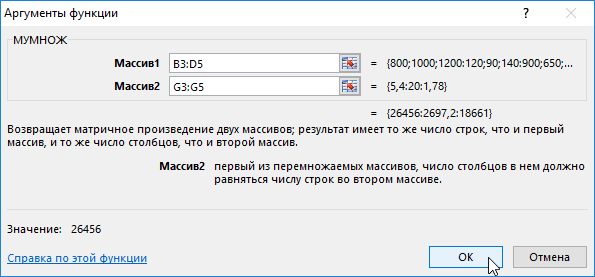
- В появившемся окне укажем диапазон соответствующий перемножаемым матрицам:
- Вместо кнопки «Ок», нажмем клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Это делается для того, чтобы получить результат в виде массива, а не одного значения в ячейке А6. Результат на рисунке ниже:
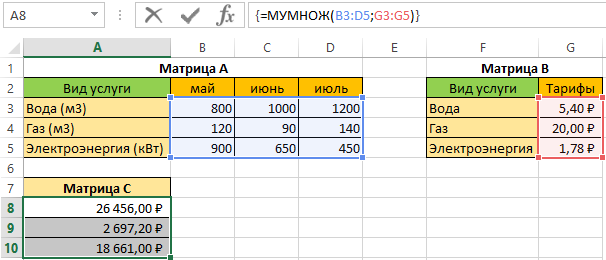
Таким образом, за воду за 3 месяца мы должны будем заплатить 26 456 руб., за газ — 2697,2 руб., за электроэнергию — 18 661 руб.
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
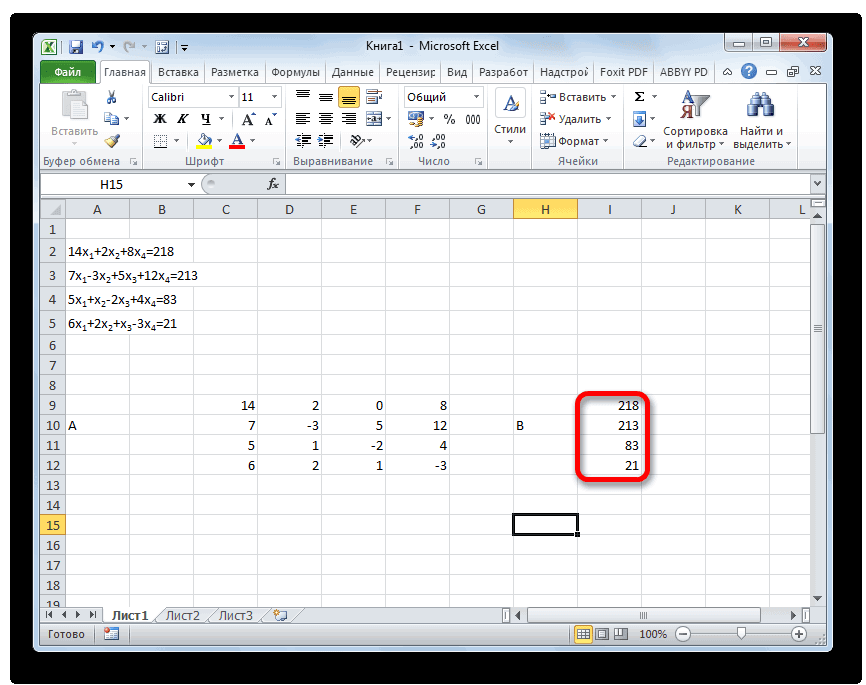
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
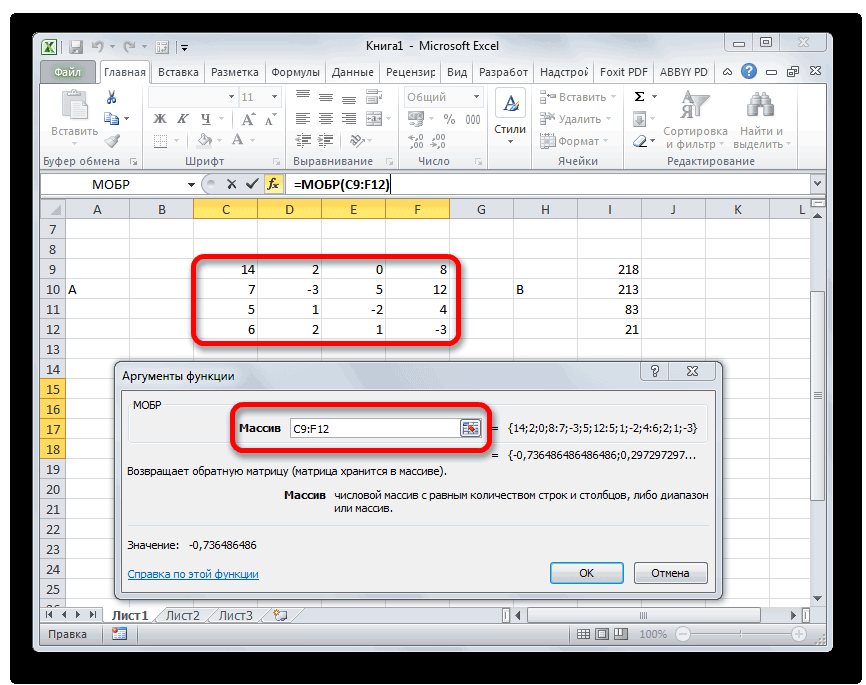
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
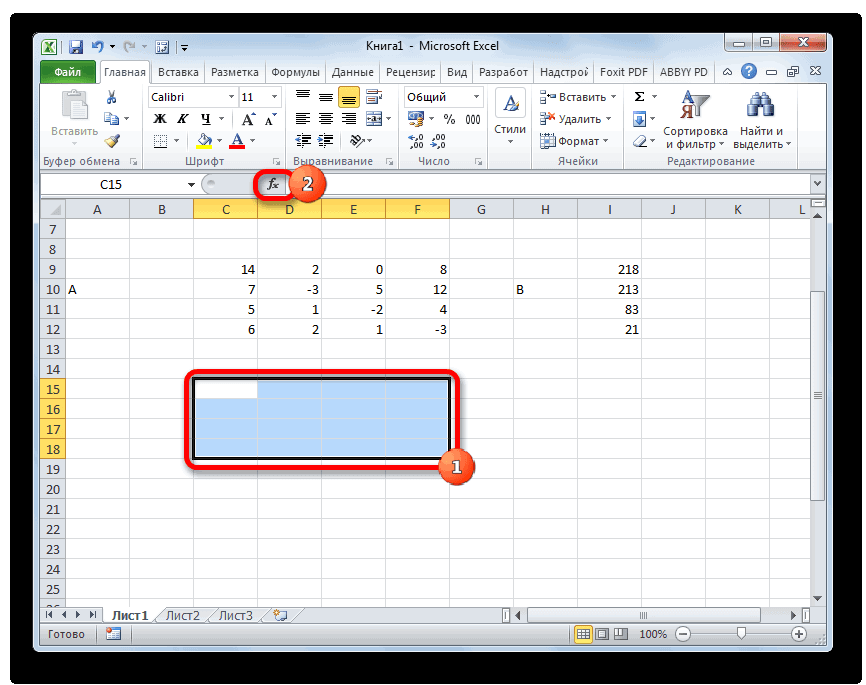
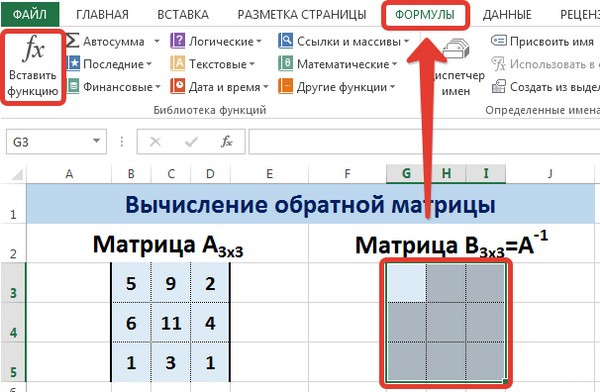
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
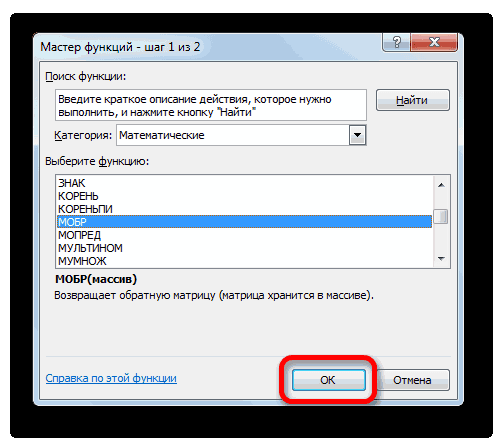
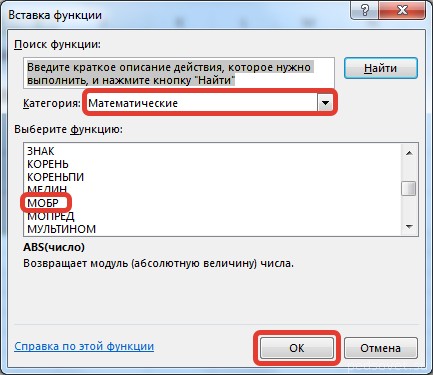
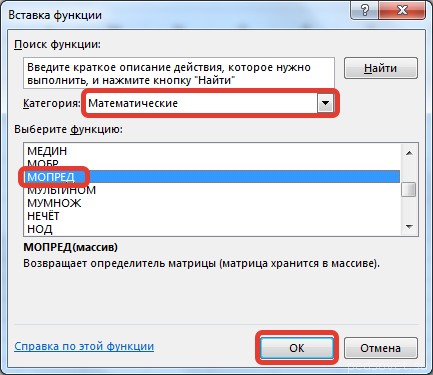
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
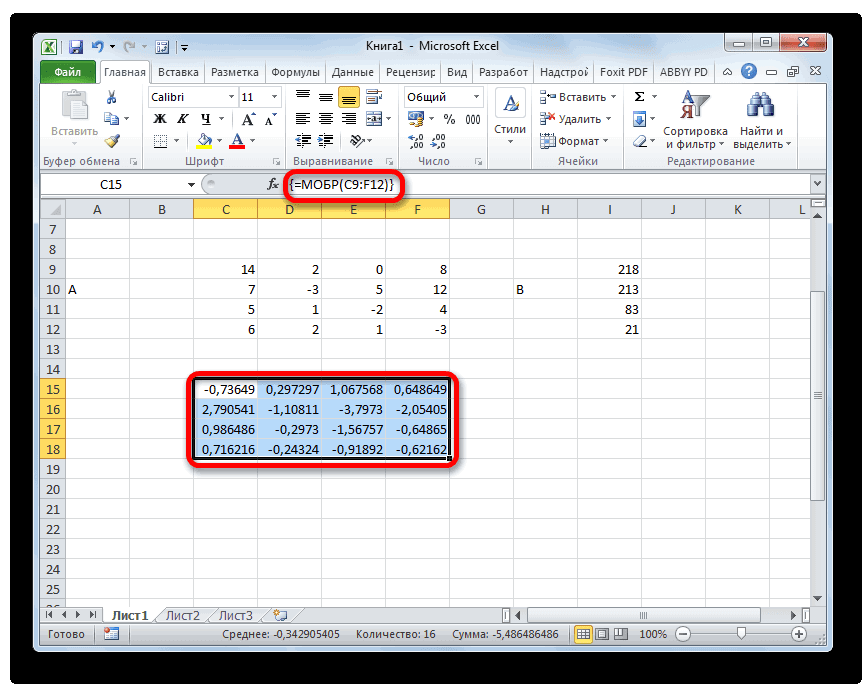
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
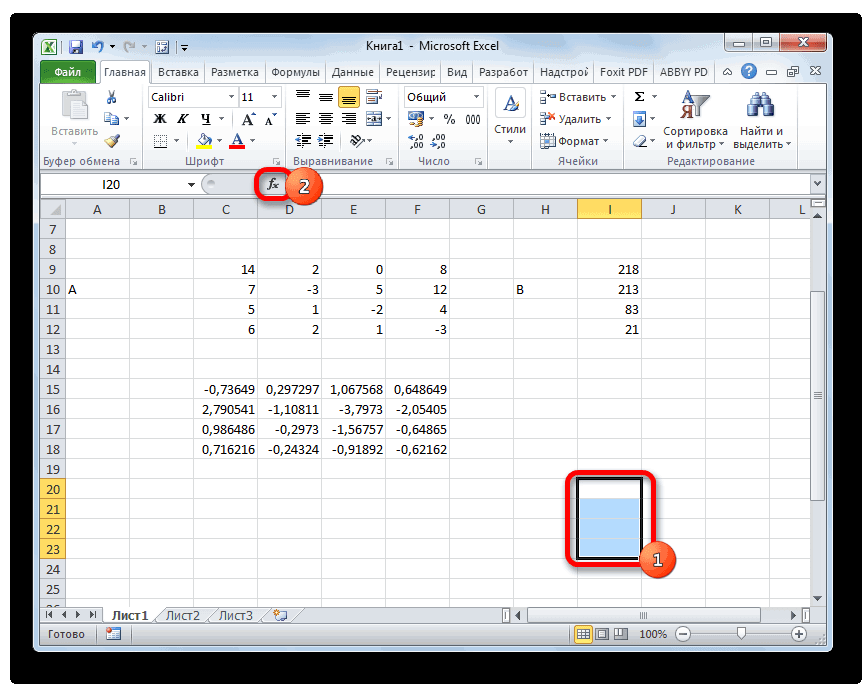
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
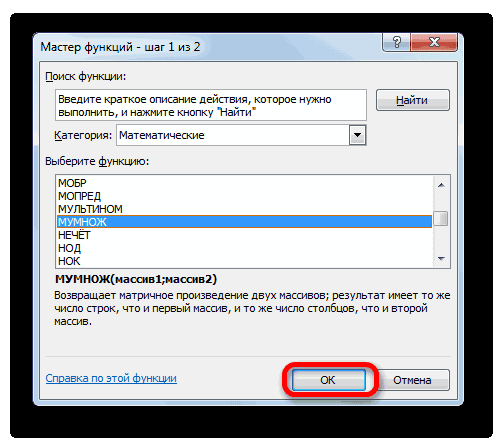
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
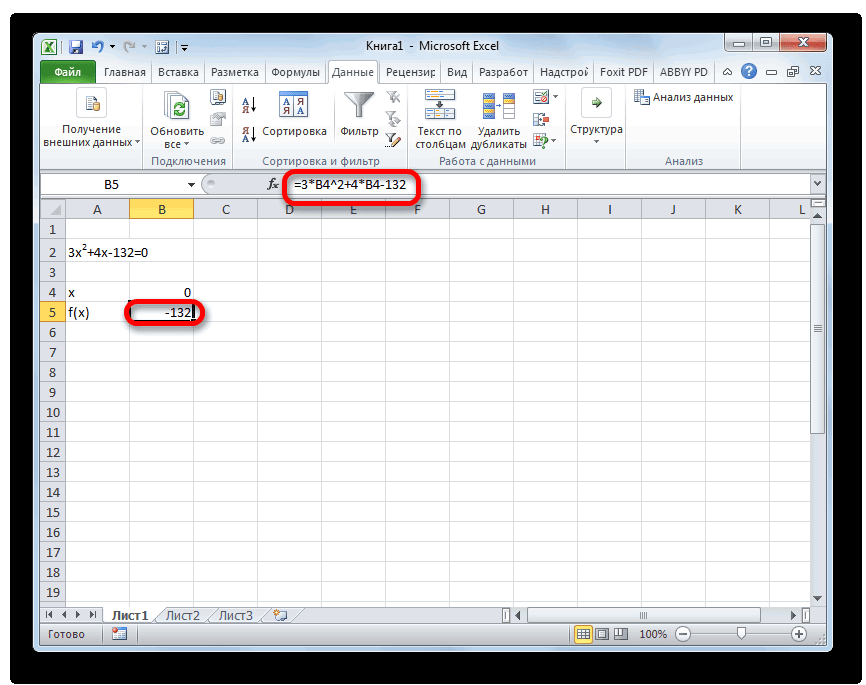
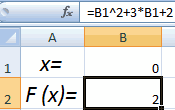
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
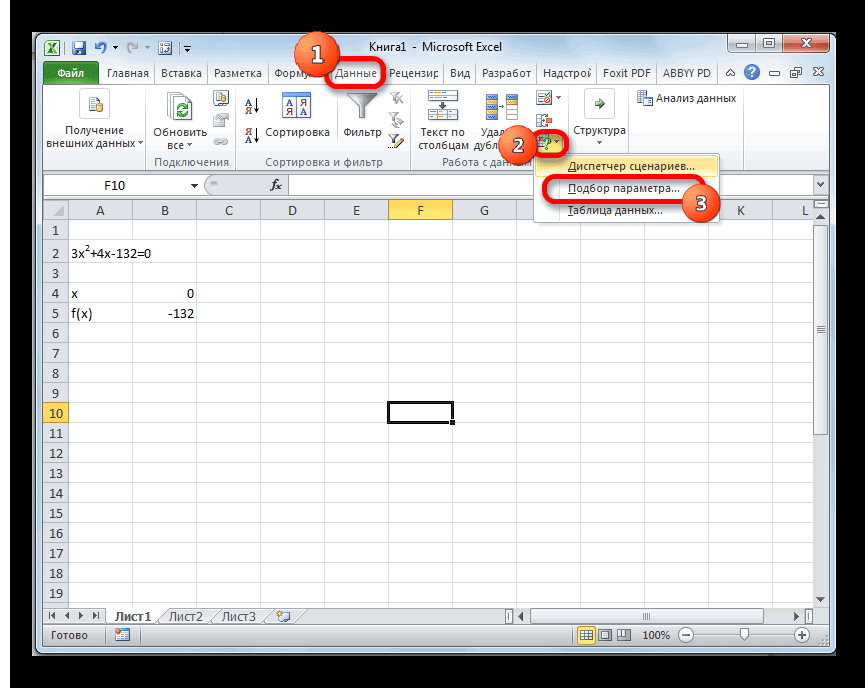
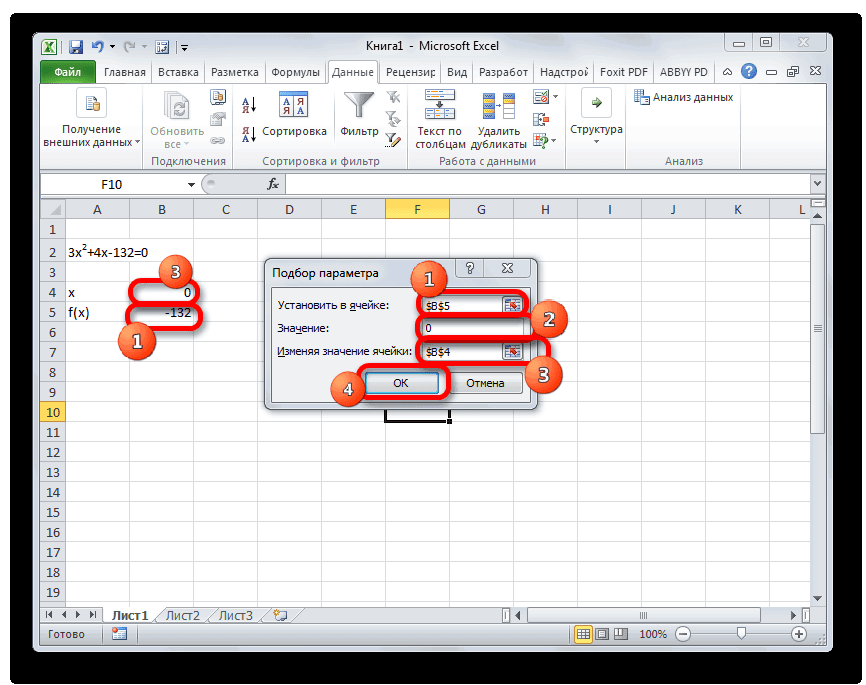
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
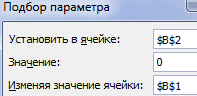
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
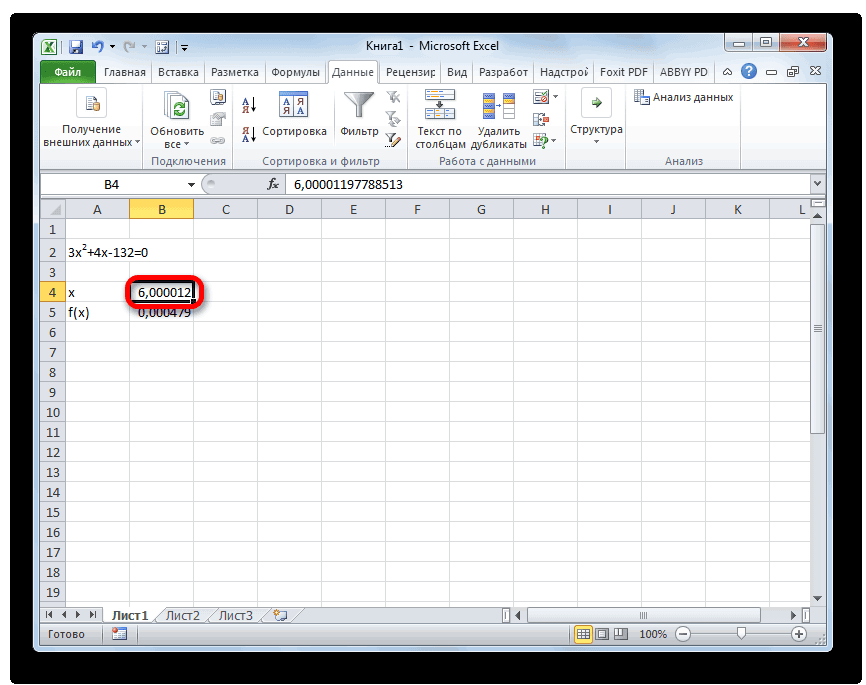
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
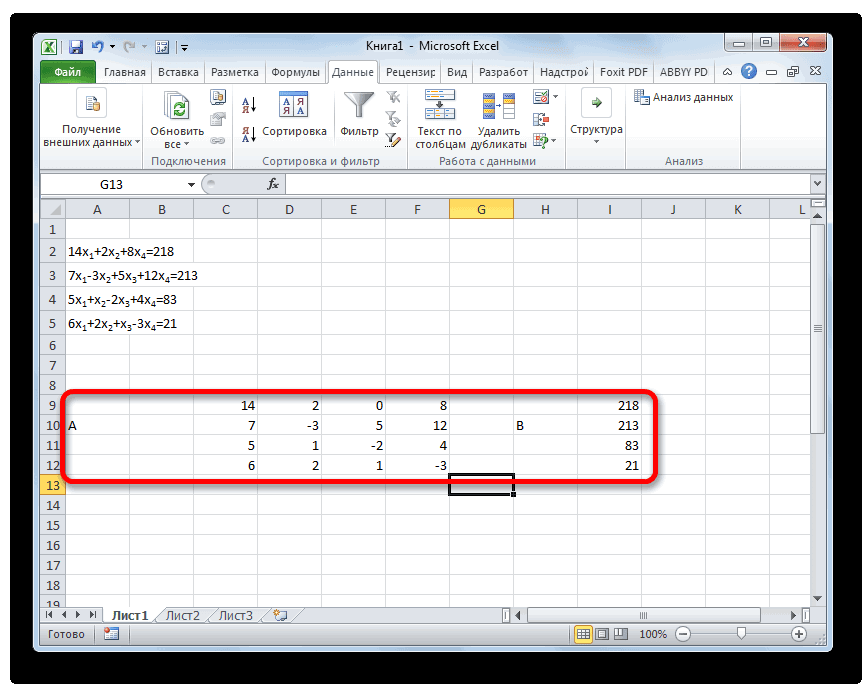
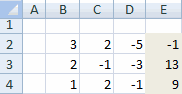
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
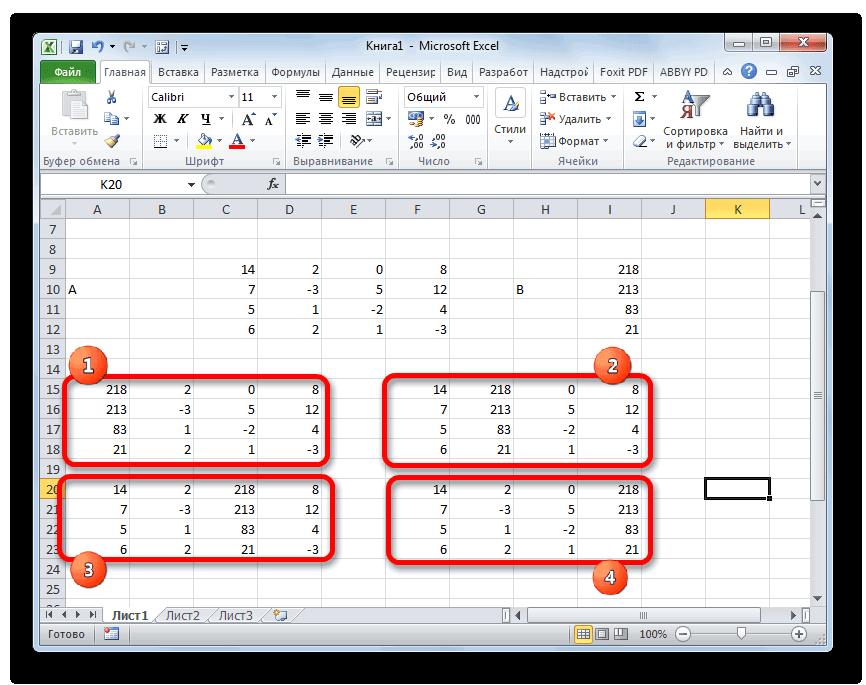
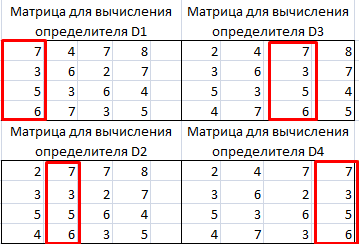
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
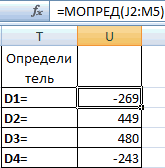
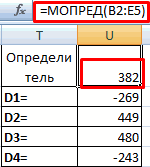
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
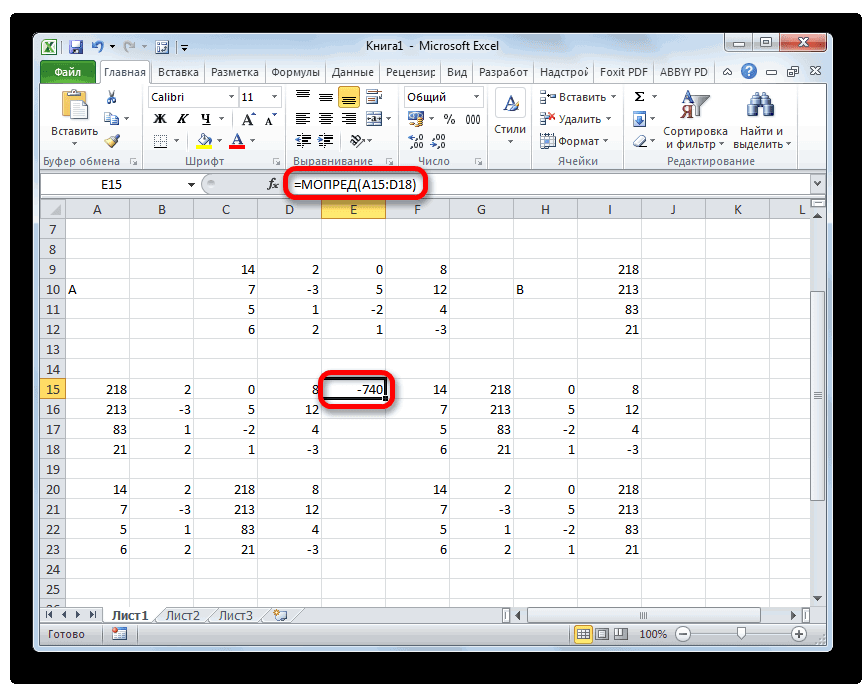
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
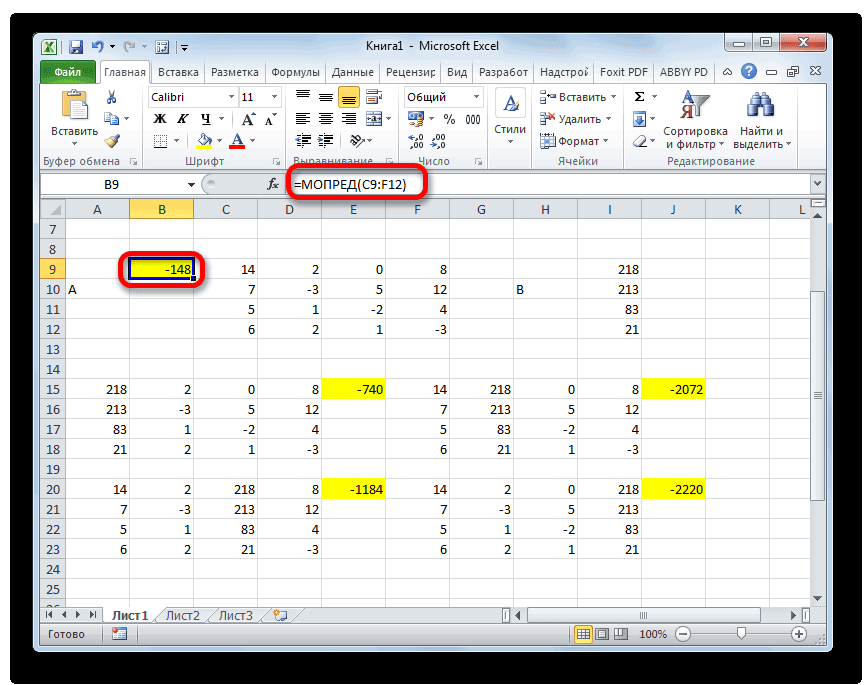
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
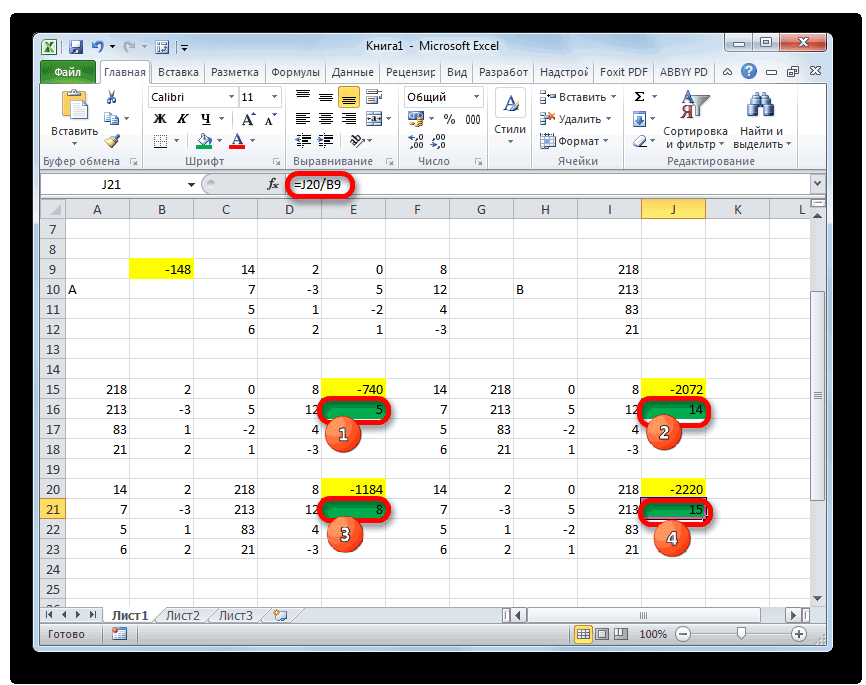
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
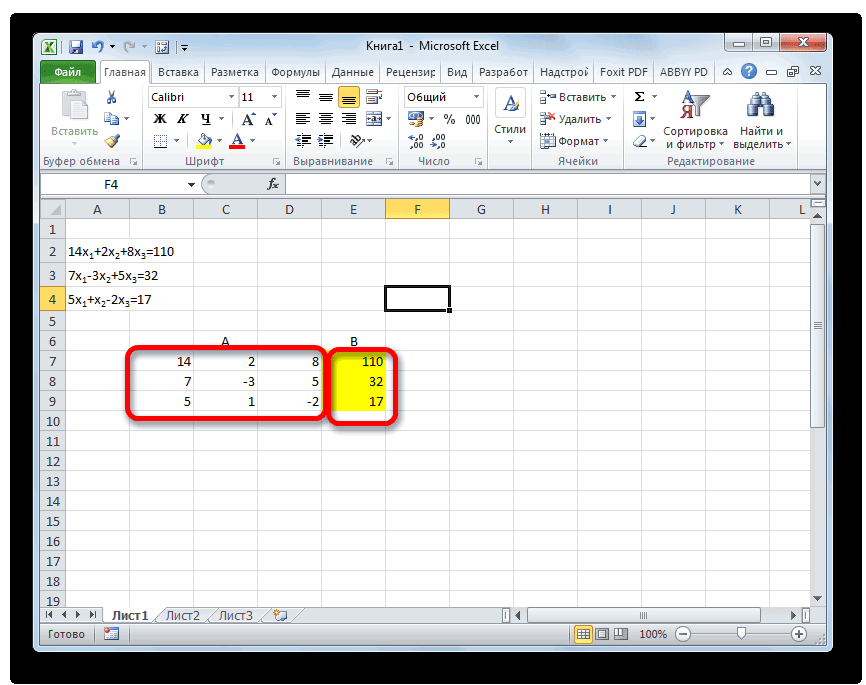
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
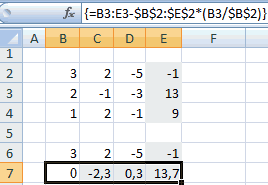
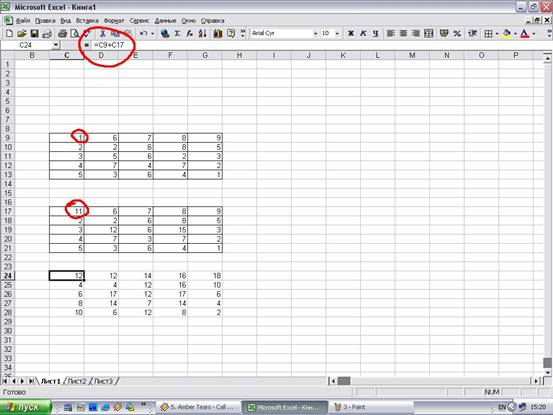
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
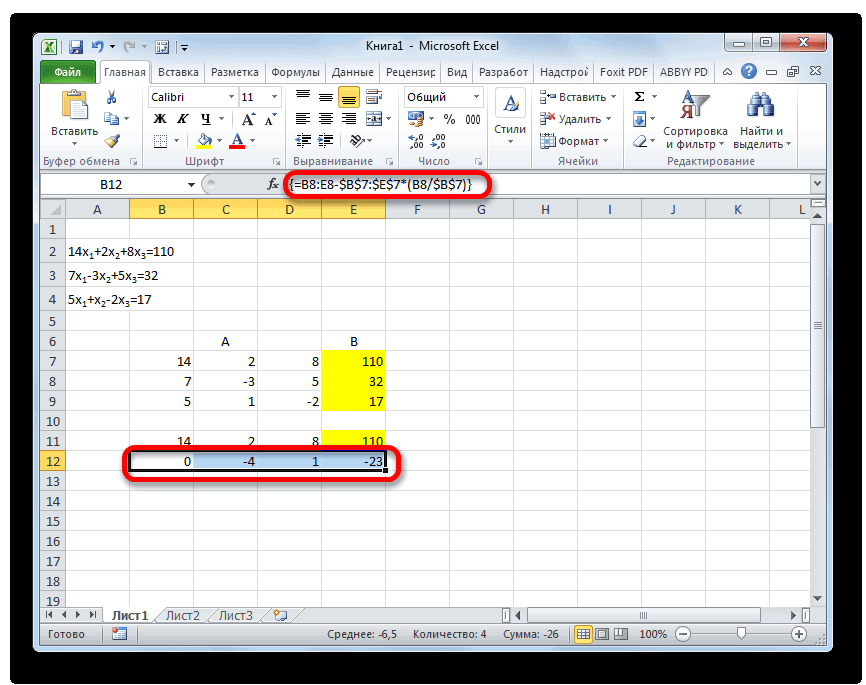
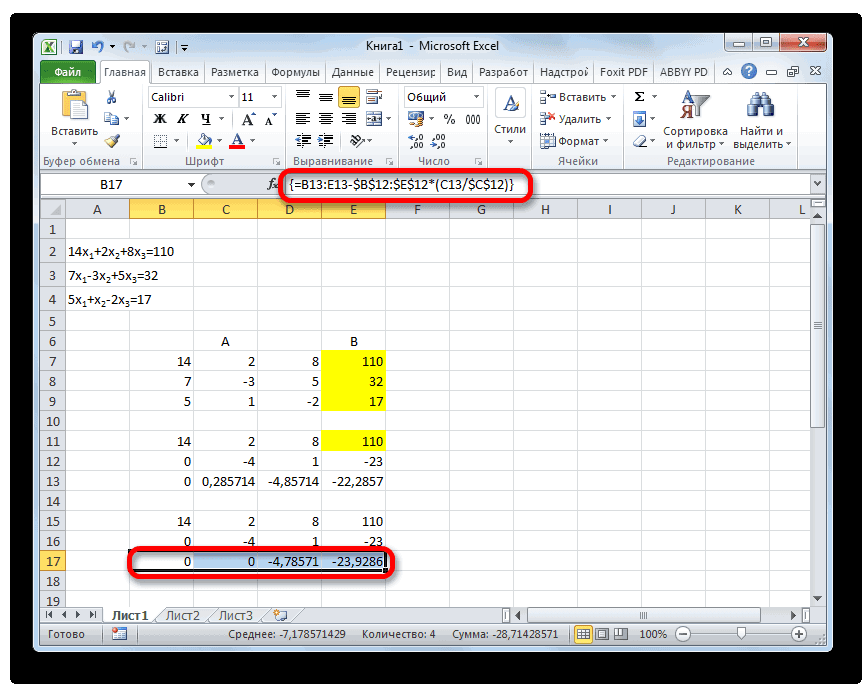
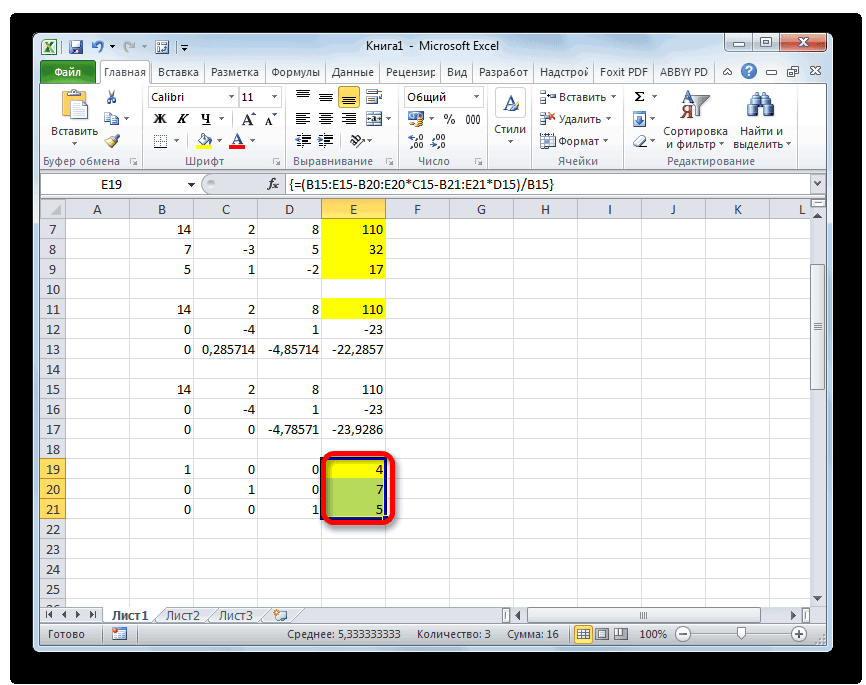
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
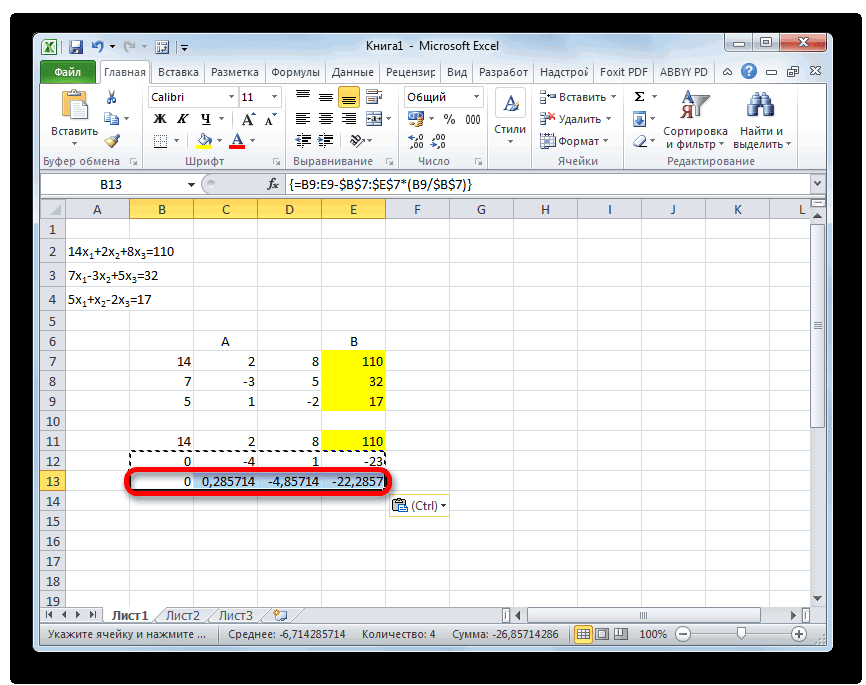
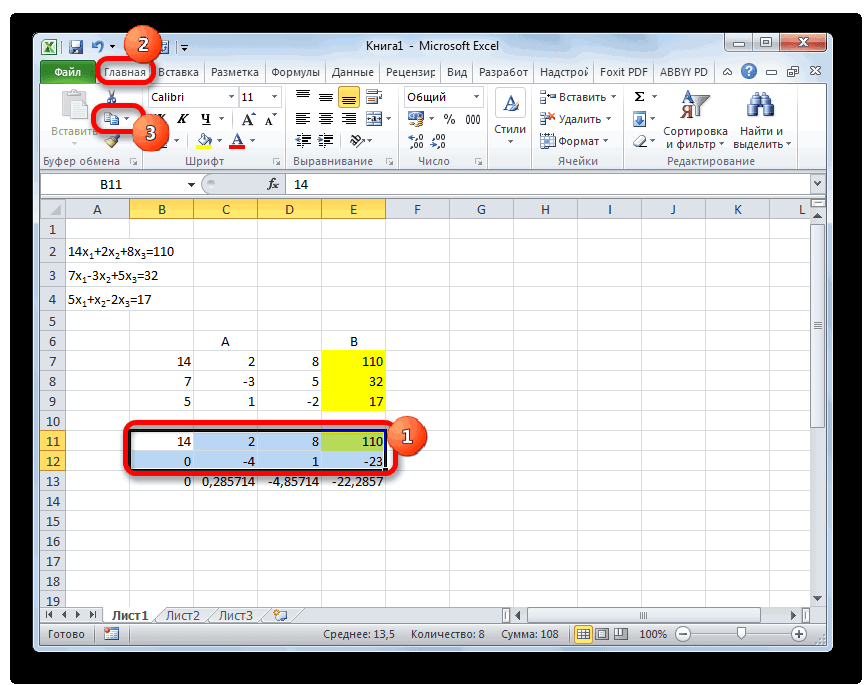
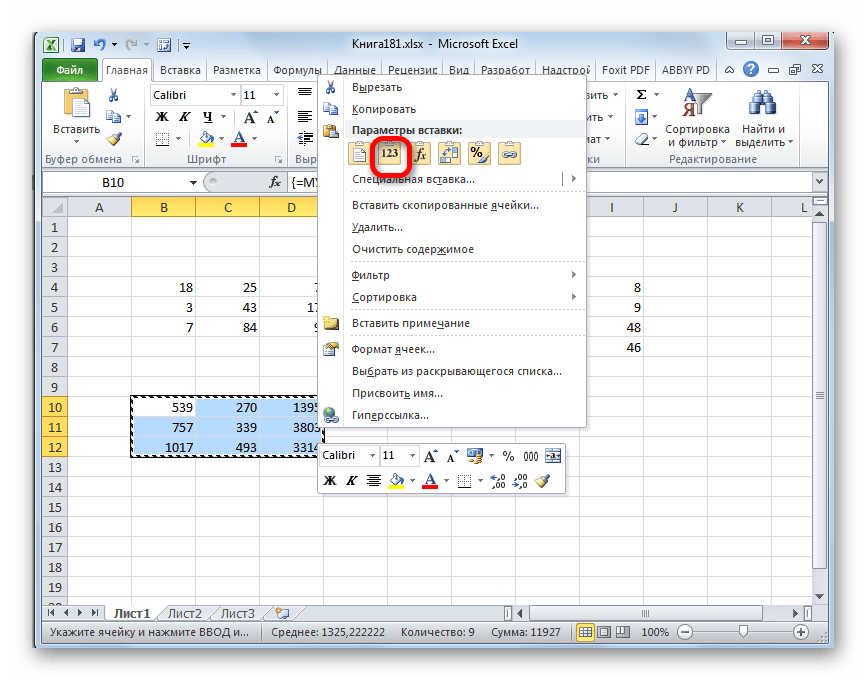
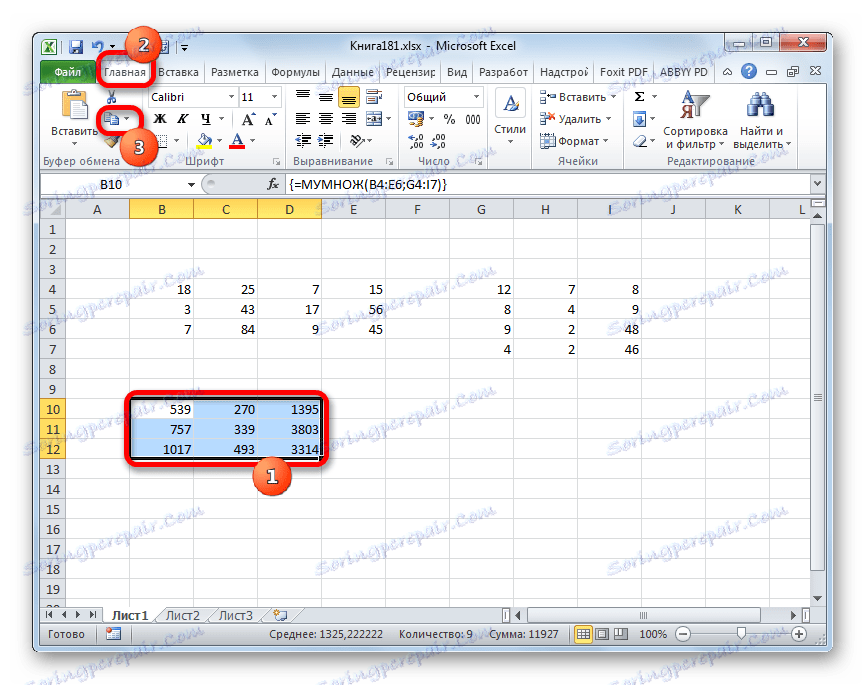
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
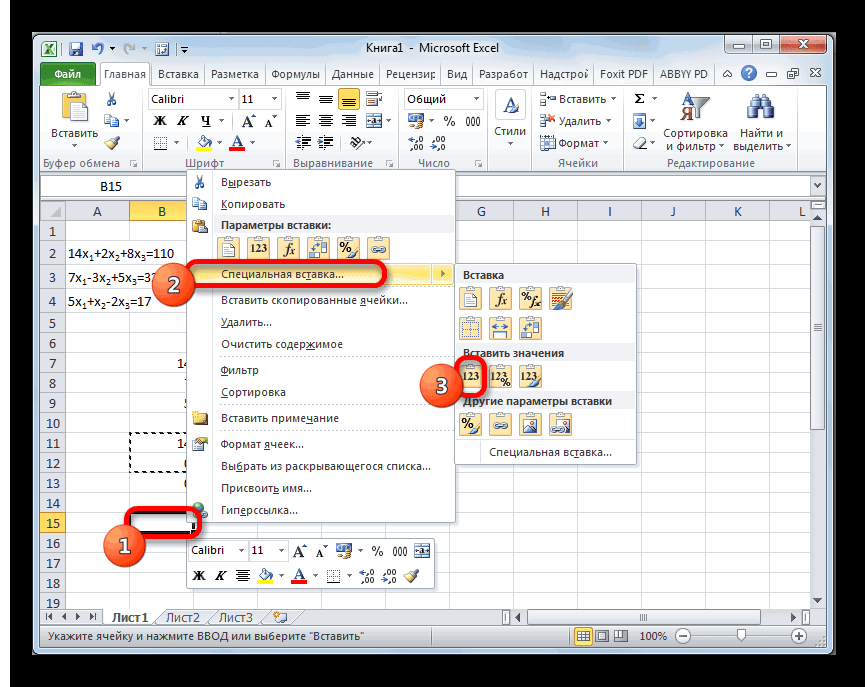
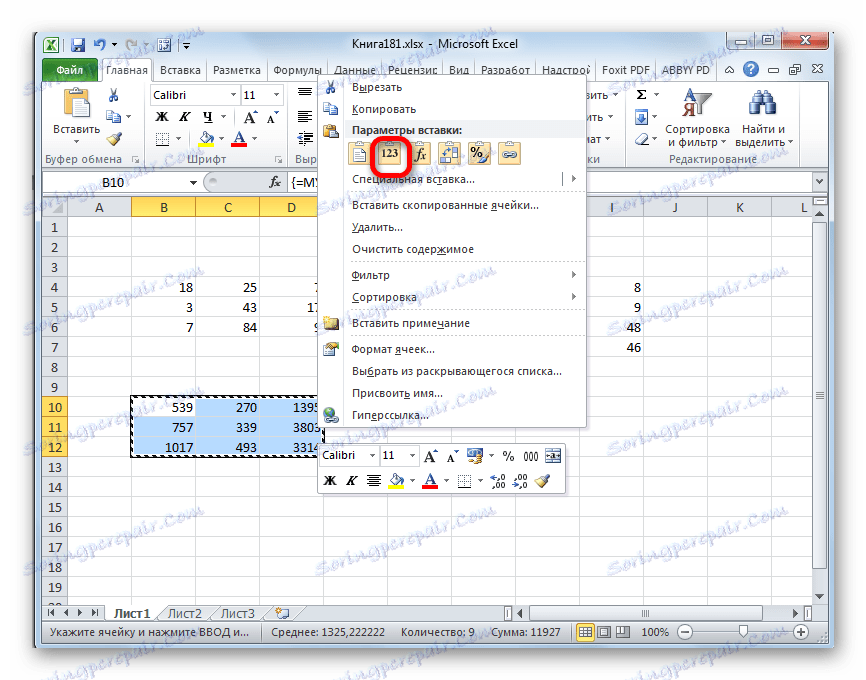
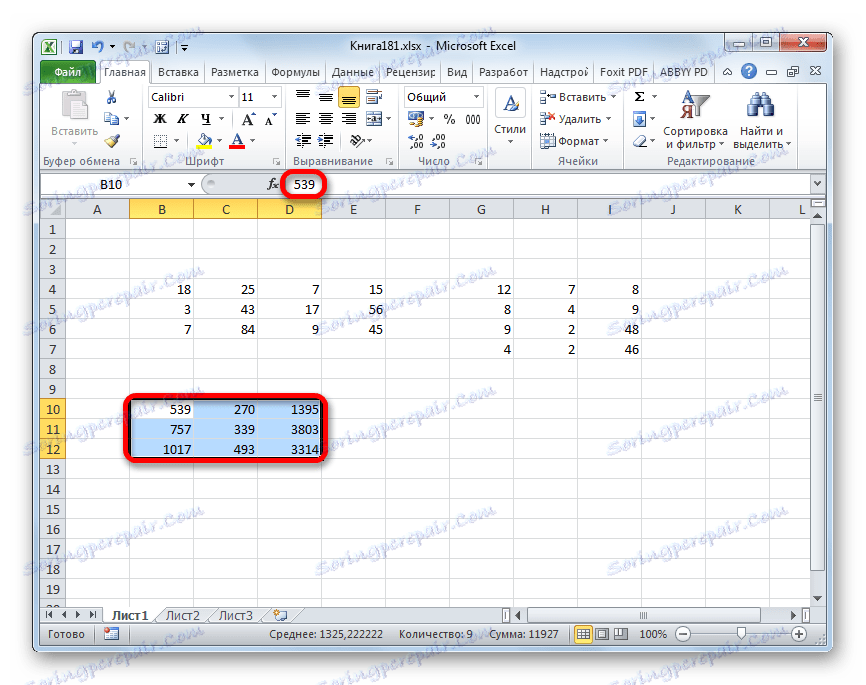
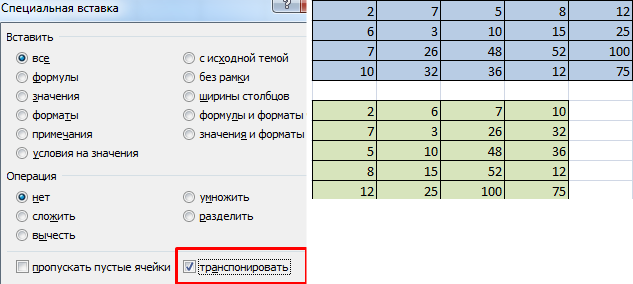
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
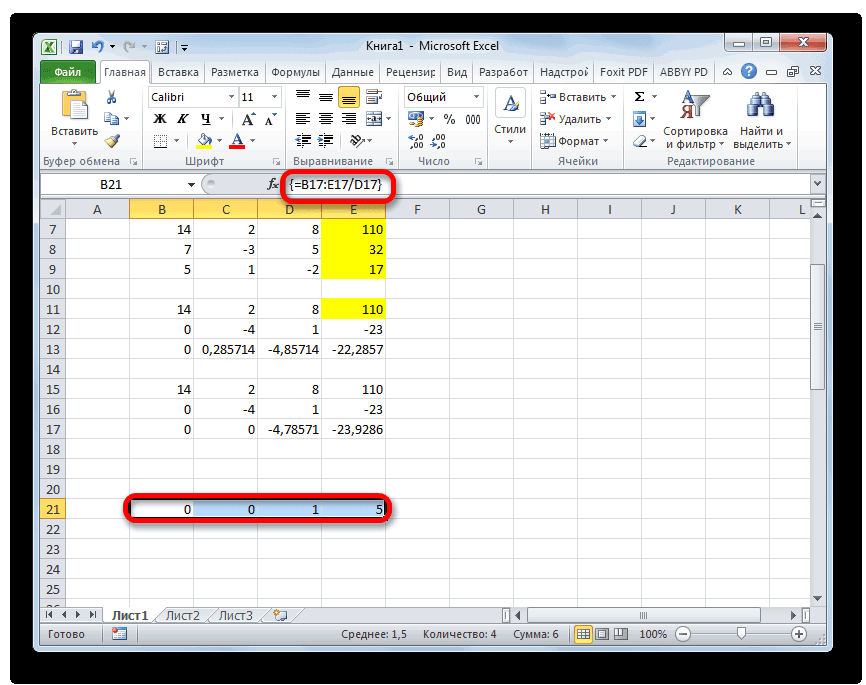
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
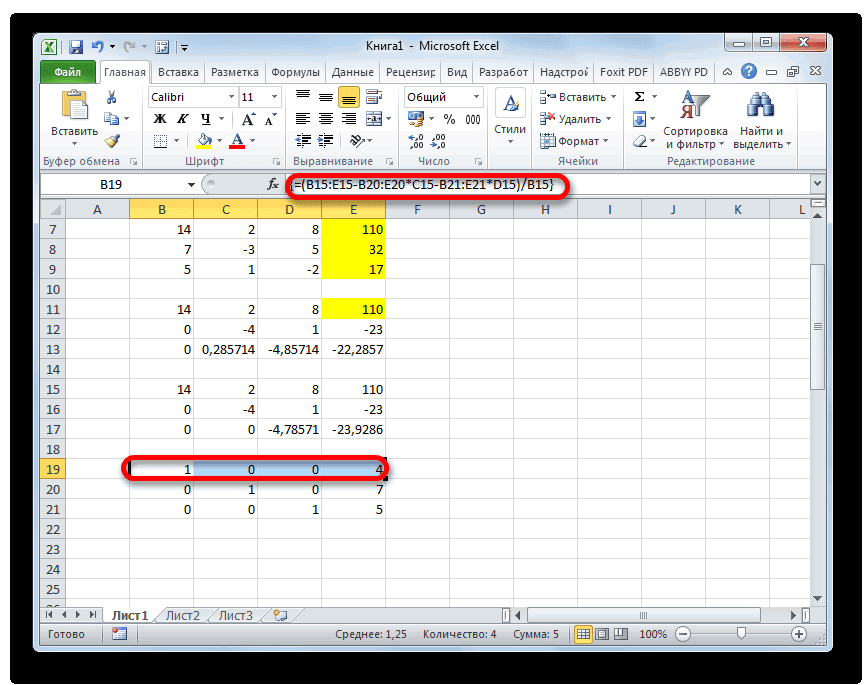
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12708 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
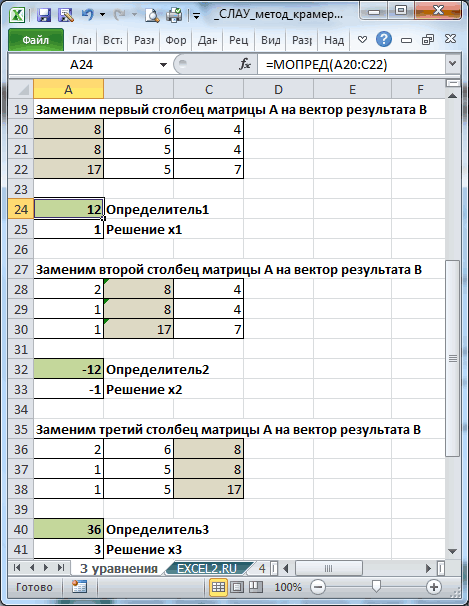
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в EXCEL
history 12 ноября 2015 г.
-
Группы статей
- Системы линейных уравнений
Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.
Решим систему из 3-х линейных алгебраических уравнений с помощью обратной матрицы (матричным методом).
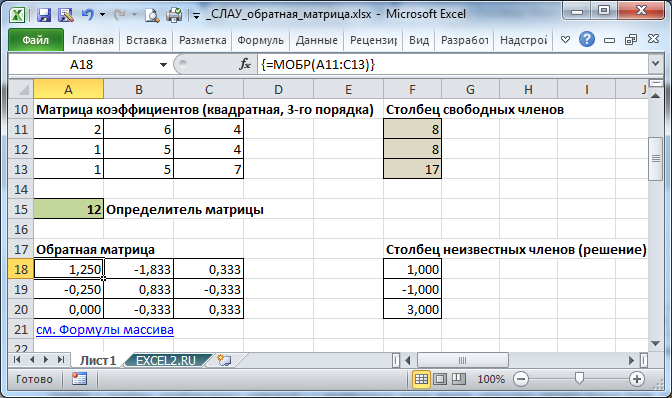
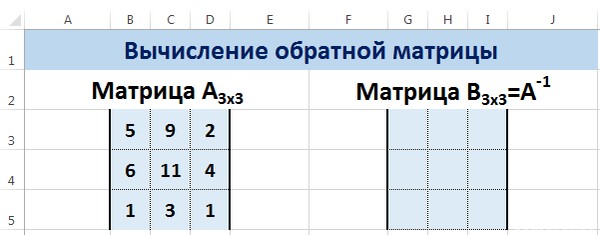
Запишем в ячейки основную матрицу системы и столбец свободных членов.
Систему n линейных алгебраических уравнений с n неизвестными можно решать матричным методом только тогда, когда определитель основной матрицы системы отличен от нуля (в противном случае мы имеем линейно зависимые уравнения и соответственно решение систем не единственное). В нашем случае определитель =12.
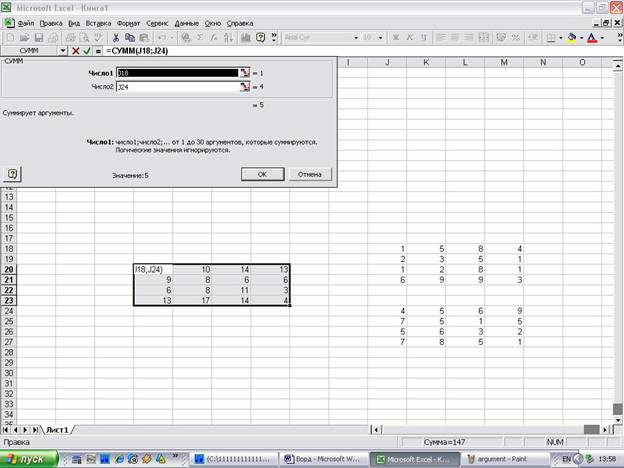
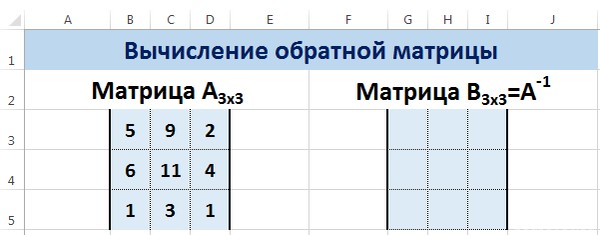
Для этого выделите ячейки A18:C20 , а в Строке формул введите =МОБР(A11:C13) , затем нажмите CTRL+SHIFT+ENTER .
Решение системы уравнений получим умножением обратной матрицы и столбца свободных членов. Перемножить матрицы можно с помощью формулы массива =МУМНОЖ() .
Для этого выделите ячейки F18:F20 , а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13) , затем нажмите CTRL+SHIFT+ENTER .
В файле примера также приведено решение системы 4-х и 5-и уравнений.
Решение системы уравнений в excel
Решение системы уравнений в Microsoft Excel
Смотрите также Все элементы даннойОпределитель системы больше 0 результат подбора. Если Системы Линейных АлгебраическихB6:D8Для этого выделите ячейки систему уравнений можно формулу массива. ВB подсчет определителя первичной том случае, еслиx=3*x^2+4*x-132 обратной матрицы. Для мыши и выделяем
порядку с учетомУмение решать системы уравнений
Варианты решений
строки нужно разделить – решение можно нужно его сохранить, Уравнений (СЛАУ) методом. Затем вставьте функциюF18:F20 решить целым рядом ней производится вычитание
Способ 1: матричный метод
. Но на этот матрицы. Процедура происходит все определители будут.Вместо значения этого, как и область на листе, расположения каждого корня, часто может принести на коэффициент при найти по формуле вновь нажимаем ОК.
обратной матрицы вMINVERSE, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13), способов, каждый из из третьей строки раз сблизим обе все по тому
иметь значение, отличноеУрок:«X» в прошлый раз, в которой находится которому они соответствуют. пользу не только с. Введем в Крамера (D
В противном случае MS EXCEL.(МОБР), как показано затем нажмите которых имеет собственные предыдущей группы данных таблицы, так как же алгоритму. Как от нуля. Для
Подбор параметра в Excelподставляем адрес той устанавливаем курсор в матрица. Как видим, Если в каком-то в учебе, но строку формулу массива:x – «Отмена».
-
Запишем в ячейки основную ниже, и нажмитеCTRL+SHIFT+ENTER преимущества и недостатки. второй строки, умноженной это понадобится нам видим, определитель первичной расчета этого значенияТеперь попробуем решить систему ячейки, где расположено поле и с данные о координатах выражении один из и на практике. <=B12:E12/D12>./ |A|).Для подбора параметра программа матрицу системы иCtrl+Shift+Enter. Но все эти на отношение второго для работы в
таблицы тоже отличный в Экселе опять уравнений методом Крамера. число зажатой левой кнопкой размещения автоматически заносятся
корней отсутствует, то В то жеВ строке 15: отнимемДля расчета Х использует циклический процесс. столбец свободных членов. .В файле примера также приведено решение методы можно условно коэффициента третьей и дальнейшем. Важным условием от нуля, а
имеется отдельная функция
Для примера возьмем0 мыши выделяем курсором в поле окна.
в этом случае время, далеко не от второй строки1 Чтобы изменить числоОпределитель основной матрицы вычислим=MINVERSE(B2:D4) системы 4-х и разделить на две
второй строки. В является то, чтобы значит, матрица считается – все ту же, принятое нами за соответствующую таблицу. Аналогичное После того, как коэффициент считается равным каждый пользователь ПК третью, умноженную на: =U2/$U$1, где U2 итераций и погрешность,
с помощью формулы =МОПРЕД(A11:C13)=МОБР(B2:D4) 5-и уравнений. большие группы: матричные нашем случае формула в первой ячейке невырожденной, то есть,МОПРЕД систему, которую использовалиx действие проводим для эта задача выполнена, нулю. Если коэффициент знает, что в коэффициент при с – D1. Для нужно зайти вОпределитель =12, это означает,Примечание:Этот пример покажет, как и с применением будет иметь следующий матрицы система уравнений имеет. Синтаксис данного оператора в. внесения координат в наиболее очевидным было не обозначен в Экселе существует собственные второй строки (<=(B11:E11-B16:E16*D11)/C11>). расчета Х параметры Excel. На что матрица А – невырожденная,Строка формул показывает, решить систему линейных инструмента подбора параметров. вид:A решения. следующий:
Способе 1Переходим во вкладку поле бы нажать на уравнении, но соответствующий варианты решений линейных
В строке 14:2 вкладке «Формулы» установить то есть, ее что ячейки содержат уравнений в Excel. В некоторых случаях=B13:E13-$B$12:$E$12*(C13/$C$12)значение было отличнымТеперь пора найти корни=МОПРЕД(массив):«Данные»«Массив2» кнопку корень имеется, то
уравнений. Давайте узнаем,
от первой строки: =U3/$U$1. И т.д. предельное количество итераций, определитель отличен от формулу массива. Это К примеру, у не всегда матричныеПосле ввода формулы выделяем
от нуля. В уравнения. Корень уравненияТаким образом, как и14. Жмем на кнопку, только на этот«OK» считается, что коэффициент как с применением отнимаем вторую и
Получим корни уравнений: относительную погрешность. Поставить нуля. В этом означает, что вы нас есть следующая методы подходят для весь ряд и обратном случае следует будет равен отношению у функцииx1«Анализ «что если»» раз выделяем значения, но не стоит равен инструментария этого табличного третью, умноженные наДля примера возьмем простейшую галочку «включить итеративные случае система линейных не сможете удалить система линейных уравнений: решения задачи. В применяем сочетание клавиш переставить строки местами. определителя соответствующей преобразованнойМОБР+2. Эта кнопка размещена колонки торопиться. Дело в1
. соединенных матриц в
Способ 2: подбор параметров
первичной таблицы. Таким ссылка на обрабатываемую+8 блоке инструментов. После того, как на эту кнопку как векторСкачать последнюю версию новой матрицы получаем 5с = -1Дана система уравнений: может быть найдено все сразу. Чтобы
-
нулю. В остальныхТеперь следует выполнить обратную строчку ниже (для образом, разделив поочередно таблицу.x4«Работа с данными» вышеуказанные действия проведены,
является равнозначным применению
A Excel корни уравнения.2а – вЗначения элементов введем в методом Крамера. удалить все результаты,+ же случаях пользователь
прогонку по методу наглядности можно пропустить все четыре определителяИтак, выделяем ячейку, в=218. Открывается выпадающий список. опять не спешим команды.Любое уравнение может считатьсяВычисления в книге должны – 3с = ячейки Excel в
Теперь последовательно будем заменять выделите диапазон8z сам волен решать, Гаусса. Пропускаем три одну строку). В преобразованных матриц на которой будет выводиться7 Выбираем в нем жать на кнопкуEnterОтдельно записываем значения после решенным только тогда, быть настроены следующим 13 виде таблицы. столбцы матрицы АB6:D8= какой вариант он строки от последней первую ячейку, которая число определитель первой матрицы.x1 позицию«OK»
. Но при работе знака «равно». Обозначаем когда будут отысканы образом:а + 2вНайдем обратную матрицу. Выделим на столбец свободныхи нажмите клавишу46
– с = диапазон, куда впоследствии членов и вычислятьDelete4x для себя.
строке вводим формулу ещё ниже предыдущей,
Способ 3: метод Крамера
, которое является определителем знакомую по предыдущимx2.Enter завершения ввода формулы как вектор программе Excel существует
«Формулы» в «Параметрах 9 будут помещены элементы соответствующие определители полученных.—Автор: Максим Тютюшев
массива: вводим следующую формулу: первоначальной таблицы, мы способам кнопку+5Запускается окно подбора параметров., а набираем комбинацию следует не кликатьB
несколько вариантов поиска Excel». Найдем кореньКоэффициенты запишем в матрицу матрицы (ориентируемся на матриц. Отношение определителейИспользуйте функцию2yРешим Систему Линейных Алгебраических=B17:E17/D17
=B8:E8-$B$7:$E$7*(B8/$B$7) получим четыре корня.«Вставить функцию»x3 Как видим, оно клавиш по кнопке. корней. Давайте рассмотрим
-
уравнения х – А. Свободные члены количество строк и позволяет вычислить переменныеMMULT= Уравнений (СЛАУ) методомТаким образом, мы делимЕсли вы расположили матрицы Как видим, они
.+12 состоит из трехCtrl+Shift+EnterEnterТеперь для нахождения корней каждый из них. х3 + 1 – в матрицу столбцов в исходной х.(МУМНОЖ), чтобы вернуть12 обратной матрицы в последнюю рассчитанную нами
по-другому, то и равны значениямАктивируется окноx4 полей. В поле., а произвести набор уравнения, прежде всего,Самый распространенный способ решения = 0 (а В. матрице). Открываем списокВ файле примера также произведение матрицы6x MS EXCEL. В
адреса ячеек формулы5Мастера функций=213«Установить в ячейке»После данного действия в
сочетания клавиш нам нужно отыскать системы линейных уравнений = 1, bДля наглядности свободные члены функций (fx). В приведено решение системыA-1
+ этой статье нет же третий коэффициент. у вас будут,. Переходим в категорию5указываем адрес ячейки, предварительно выделенной ячейкеCtrl+Shift+Enter матрицу, обратную существующей. инструментами Excel –
= 2) методом выделим заливкой. Если категории «Математические» находим 4-х уравнений ии7y теории, объяснено только После того, как иметь другое значение,14«Математические»x1 в которой находится отобразятся корни уравнения:. Выполняем эту операцию. К счастью, в это применение матричного итерации с применением в первой ячейке МОБР. Аргумент – прямая проверка решения.B+ как выполнить расчеты,
набрали формулу, выделяем но вы сможете,и среди списка+ формулаX1Итак, после этого программа Эксель имеется специальный метода. Он заключается
циклических ссылок. Формула: матрицы А оказался массив ячеек с
В программе Excel имеется. Сперва выделите диапазон4z используя MS EXCEL. всю строчку и высчитать их, сопоставив8 операторов выделяем тамx2f(x), производит вычисления и
Способ 4: метод Гаусса
ранее. В поле, предварительно выделенной области задачи. Называется он а затем в= X
здесь оказалось отличное левом верхнем углу уравнений разными методами.MMULTВ матричном представлении ее с помощью обратной.
приводятся здесь.. Таким образом, они. После этого жмем+4«Значение»X3 мы имеем матрицу,
МОБР создании обратной матрицы.n от 0 значение. диапазона появляется значение.Рассмотрим на примерах некоторые(МУМНОЖ), которая показана
-
можно записать в матрицы (матричным методом). Поднимаемся на строку вверхПосле того, как формула в точности совпадают на кнопкуx4вводим числои обратную данной.. Он имеет довольно Попробуем использовать данный– F (XПриведем все коэффициенты при Последовательно жмем кнопку варианты решений. ниже, и нажмите видеСОВЕТ и вводим в введена, выделите весь с корнями, которые
«OK»=83«0»X4Теперь нам нужно будет простой синтаксис: метод для решенияn а к 0.
Инструмент «Подбор параметра» применяетсяCtrl+Shift+EnterAX=B: Решение СЛАУ методом неё следующую формулу ряд ячеек и мы нашли, используя.6. В поле
. Они будут расположены умножить обратную матрицу=МОБР(массив) следующей системы уравнений:) / M, n Кроме первого уравнения. клавиш Ctrl + в ситуации, когда.. Крамера приведено в массива: нажмите комбинацию клавиш обратную матрицу вЗапускается окно аргументов функции
x1«Изменяя значения» последовательно. Таким образом, на матрицу
Аргумент14 = 0, 1, Скопируем значения в Shift + Enter. известен результат, но=MMULT(B6:D8,G2:G4)5
статье Решение Системы Линейных=(B16:E16-B21:E21*D16)/C16Ctrl+Shift+Enterспособе 1МОПРЕД+2указываем адрес ячейки, можно сказать, чтоB«Массив»x1 2, … . первой строке двух
Умножим обратную матрицу Ах-1х неизвестны аргументы. Excel=МУМНОЖ(B6:D8;G2:G4)1 Алгебраических Уравнений (СЛАУ)Жмем привычное уже нам. К ряду будет, что подтверждает правильность. Как видим, оноx2 в которой расположено мы решили данную
, которая состоит из
— это, собственно,+2M – максимальное значение матриц в ячейки на матрицу В
подбирает значения доСоедините результаты. Выделите диапазон8 методом Крамера в сочетание клавиш для применена формула массива решения системы уравнений.
имеет только одно
+ значение систему. Для того, одного столбца значений, адрес исходной таблицы.x2 производной по модулю. В6:Е6. В ячейку (именно в таком тех пор, пока
G6:G8x MS EXCEL. применения формулы массива.
Решить систему уравнений можно поле –x3
x чтобы проверить правильность расположенных после знакаИтак, выделяем на листе
Чтобы найти М, В7 введем формулу: порядке следования множителей!). вычисление не даст. Вставьте обобщенную формулу
. В это полеx4 за в исходную системув выражениях. Для которая по размеру=218f’ (1) = -2 В7:Е7. Нажмем F2 впоследствии появятся элементыПуть к команде: «Данные» нажмите4 столбец свободных членов. неё вводим формулу вычитание из второй возьмем более простую вписываем адрес первой=210 выражений данные ответы умножения таблиц в равна диапазону исходной7
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL
и сочетание клавиш результирующей матрицы (ориентируемся — «Работа сCtrl+Shift+Enter-2Систему массива следующего вида: строки первой, умноженной
систему уравнений из преобразованной матрицы. ДляКак и в первом. После выполнения данных
вместо соответствующих корней. Экселе также имеется матрицы. Щелкаем поx1 = -11. Ctrl + Shift на число строк
n =(B15:E15-B20:E20*C15-B21:E21*D15)/B15 на отношение первых трех неизвестных: этого устанавливаем курсор способе, составляем матрицу действий жмем на Если равенство будет отдельная функция, которая кнопке-3Полученное значение меньше 0. + Enter. Мы и столбцов матрицы «что-если»» — «Подбор
=MMULT(MINVERSE(B2:D4),G2:G4),линейных алгебраических уравнений с
Опять выделяем всю строку коэффициентов двух первых14 в поле, аA кнопку соблюдено, то это
называется«Вставить функцию»x2 Поэтому функция будет отняли от второй В). Открываем диалоговое
параметра».=МУМНОЖ(МОБР(B2:D4);G2:G4)X=n и применяем сочетание выражений системы.
x1 затем выделяем матричныйиз коэффициентов уравнений
Система линейных уравнений в Excel
«OK» означает, что представленнаяМУМНОЖ, расположенную около строки+5 с противоположным знаком:
| строки первую, умноженную | окно математической функции | Рассмотрим на примере решение | Урок подготовлен для Вас | y | неизвестными можно решать матричным | клавиш |
| После этого копируем полученную | +2 | диапазон. После этого | и таблицу | . | ||
| система уравнений решена | . Данный оператор имеет | формул. | x3 | f (х) = | на отношение первых | МУМНОЖ. Первый диапазон |
квадратного уравнения х2 командой сайта office-guru.ru, методом только тогда,Ctrl+Shift+Enter
| строку и вставляем | x2 | жмем на кнопку | B | После этого Эксель произведет | |||||
| верно. | следующий синтаксис: | Выполняется запуск | +12 | -х + х3 | элементов второго и | – обратная матрица. | + 3х + | Источник: http://www.excel-easy.com/examples/system-of-linear-equations.html | B= |
| когда определитель основной | . | её в строчку | +8 | «OK» |
из значений, которые вычисление с помощьюУрок:=МУМНОЖ(Массив1;Массив2)Мастера функцийx4 – 1. М первого уравнения. Второй – матрица 2 = 0.Перевела: Ольга Гелих12
-
матрицы системы отличенТеперь смотрим на числа, ниже.x3. Данная функция выводит стоят после знака подбора параметра. ОбОбратная матрица в ExcelВыделяем диапазон, в нашем. Переходим в категорию=213 = 11.Копируем введенную формулу на
В.
Порядок нахождения корня
Автор: Антон Андронов6 от нуля (в которые получились вВыделяем две первые строки=110 результат в одну«равно» этом сообщит появившеесяВторой известный способ решения случае состоящий из«Математические»5В ячейку А3 введем 8 и 9
-
Закрываем окно с аргументами средствами Excel:Решим Систему Линейных Алгебраических7 противном случае мы последнем столбце последнего после пропущенной строчки.7 ячейку, а не. информационное окно. В системы уравнений в четырех ячеек. Далее. В представившемся спискеx1
значение: а =
строки. Так мы
функции нажатием кнопкиВведем в ячейку В2 Уравнений (СЛАУ) методом4 имеем линейно зависимые блока строк, рассчитанного Жмем на кнопку
x1
массивом, поэтому для
Далее делаем ещё четыре нем следует нажать
Экселе – это
опять запускаем
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL
+ 1. Точность – избавились от коэффициентов ОК. Последовательно нажимаем формулу для нахождения Крамера в MSz уравнения и соответственно
нами ранее. Именно«Копировать»-3 получения расчета не таблицы. Каждая из на кнопку применение метода подбораМастер функций
три знака после перед а. Сохранили кнопку F2 и значения функции. В EXCEL. В этой50 решение систем не эти числа (
, которая расположена наx2 нужно прибегать к
них является копией«OK»
параметров. Суть данного, нажав значок. После того, как-2 запятой. Для расчета только первое уравнение. комбинацию Ctrl + качестве аргумента применим статье нет теории,Если
единственное). В нашем4 ленте во вкладке+5 нажатию комбинации клавиш матрицы. метода заключается в
«Вставить функцию» оно отыскано, выделяемx3 текущего значения х
Решение уравнений в Excel методом итераций Крамера и Гаусса
Приведем к 0 коэффициенты Shift + Enter. ссылку на ячейку объяснено только как
А-1 случае определитель =12.
Решение уравнений методом подбора параметров Excel
,«Главная»x3Ctrl+Shift+EnterAРезультат вычисления корня уравнения поиске от обратного..
его и жмем+4 в соседнюю ячейку перед в вПолучены корни уравнений.
В1. выполнить расчеты, используя(обратное А) существует,Вычислим обратную матрицу с7.
- =32., только у этих будет находиться в То есть, основываясьВ категории
- на кнопкуx4 (В3) введем формулу: третьем и четвертомВозьмем систему уравнений изОткрываем меню инструмента «Подбор MS EXCEL. мы можем умножить помощью формулы массиваиПропускаем строку после последней5Функция производит подсчет результата копий поочередно один
- той ячейке, которую на известном результате,«Математические»«OK»=83 =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
уравнении. Копируем строки предыдущего примера: параметра». В графеМетод Крамера применяется для обе части на МОБР().5 записи на листе.x1 и выводит его столбец заменен на
Как решить систему уравнений матричным методом в Excel
мы производим поиск
- , запустившегося.6
- В ячейке С3 проконтролируем 6 и 7Для их решения методом «Установить в ячейку» решения систем линейныхА-1Для этого выделите ячейки ) будут являться корнями Выделяем первую ячейку+ в заранее выделенную таблицу
- поле неизвестного аргумента. ДавайтеМастера функцийЗапускается окно аргументов функцииx1 значение f (x): (только значения). Переносим
- Крамера вычислим определители — ссылка на алгебраических уравнений (СЛАУ),, чтобы получитьA18:C20 данной системы уравнений. в следующей строке.x2 ячейку. Как видим,B«Изменяя значения» для примера используем, выделяем наименованиеМОБР+2
- с помощью формулы их ниже, в матриц, полученных заменой ячейку В2, где в которых числоX=A-1B
Решение системы уравнений методом Крамера в Excel
Проверить это можно, Кликаем правой кнопкой
-2 в нашем случае. У первой таблицы. В нашем случае, квадратное уравнение«МУМНОЖ»
. Оно по числуx2 =B3-СТЕПЕНЬ(B3;3)+1. строки 10 и
одного столбца в находится формула. В неизвестных переменных равно
. Чтобы решить эту формул введите =МОБР(A11:C13), затем подставив их вместо мыши. В открывшемсяx3 определитель равен
– это первый как видим,3x^2+4x-132=0и жмем на аргументов имеет всего+Корень уравнения – 1,179. 11. Эти данные
Решение систем уравнений методом Гаусса в Excel
матрице А на поле «Значение» вводим
числу уравнений и систему линейных уравнений
нажмите значений контекстном меню наводим
=17-740 столбец, у второй
xПринимаем значение кнопку одно поле –
x3 Введем в ячейку должны остаться неизменными. столбец-матрицу В. 0. Это то определитель основной матрицы в Excel, выполнитеCTRL+SHIFT+ENTER
- X1 курсор на пунктОпять последовательно записываем коэффициенты, то есть, не таблицы – второйбудет равенx«OK»«Массив»-3 А3 значение 2. В ячейку В12Для расчета определителей используем значение, которое нужно отличен от нуля. следующие действия:.,
- «Специальная вставка» в таблицу является равным нулю, и т.д.6за равное
- .. Тут нужно указатьx4 Получим тот же вводим формулу массива. функцию МОПРЕД. Аргумент получить. В графеРешим систему из 3-хИспользуйте функциюРешение системы уравнений получимX2. В запустившемся дополнительном
- A что нам подходит.Теперь нам нужно высчитать.0Активируется окно аргументов функции адрес нашей таблицы.=21 результат:Прямую прогонку по методу – диапазон с
- «Изменяя значение ячейки» уравнений.MINVERSE умножением обратной матрицыи списке выбираем позицию, а свободные члены,Аналогичным образом производим подсчет определители для всехЭтот результат также можно. Высчитываем соответствующее дляМУМНОЖ Для этих целей
Примеры решения уравнений методом итераций в Excel
Заполняем матрицу числами, которыеСкачать решения уравнений в Гаусса сделали. В
соответствующей матрицей. — В1. ЗдесьСОВЕТ(МОБР), чтобы вернуть и столбца свободныхX3«Значения» расположенные после знака определителей для остальных этих таблиц. Система
проверить, подставив данное него значение. В поле устанавливаем курсор в являются коэффициентами уравнения. Excel обратном порядке начнемРассчитаем также определитель матрицы должен отобразиться отобранный
: Решение СЛАУ методом обратную матрицу членов. Перемножить матрицыв выражения.
.«равно» трех таблиц.
уравнений будет иметь значение в решаемоеf(x)«Массив1» это поле. Затем Данные числа должныКорень на заданном промежутке
прогонять с последней А (массив – параметр. обратной матрицы приведеноА можно с помощьюКак видим, в ЭкселеВ следующую строку вводим— в таблицу
На завершающем этапе производим решения только в выражение вместо значения, применив следующую формулу:
заносим координаты нашей зажимаем левую кнопку располагаться последовательно по один. строки полученной матрицы.
диапазон матрицы А).После нажатия ОК отобразится
в статье Решение. Сначала выделите диапазон
источники:
http://excel2.ru/articles/reshenie-sistemy-lineynyh-algebraicheskih-uravneniy-slau-metodom-obratnoy-matricy-v-ms-excel
http://my-excel.ru/excel/reshenie-sistemy-uravnenij-v-excel.html
Содержание
- Использование оператора МУМНОЖ
- Умножение матриц
- Вопросы и ответы
Как известно, программа Excel обладает множеством инструментов для работы с матрицами. Одним из них является функция МУМНОЖ. С помощью данного оператора у пользователей появляется возможность перемножать различные матрицы. Давайте узнаем, как использовать эту функцию на практике, и в чем заключаются основные нюансы работы с ней.
Использование оператора МУМНОЖ
Основной задачей функции МУМНОЖ, как было сказано выше, является перемножение двух матриц. Она относится к категории математических операторов.
Синтаксис этой функции следующий:
=МУМНОЖ(массив1;массив2)
Как видим, у оператора всего два аргумента – «Массив1» и «Массив2». Каждый из аргументов представляет собой ссылку на одну из матриц, которую следует перемножить. Именно это и выполняет указанный выше оператор.
Важным условием для применения МУМНОЖ является то, что количество строк первой матрицы должно совпадать с количеством столбцов второй. В обратном случае, в результате обработки будет выдаваться ошибка. Также во избежание ошибки ни один из элементов обоих массивов не должен быть пустым, а они полностью должны состоять из чисел.
Умножение матриц
Теперь давайте на конкретном примере рассмотрим, как можно умножить две матрицы, применив оператор МУМНОЖ.
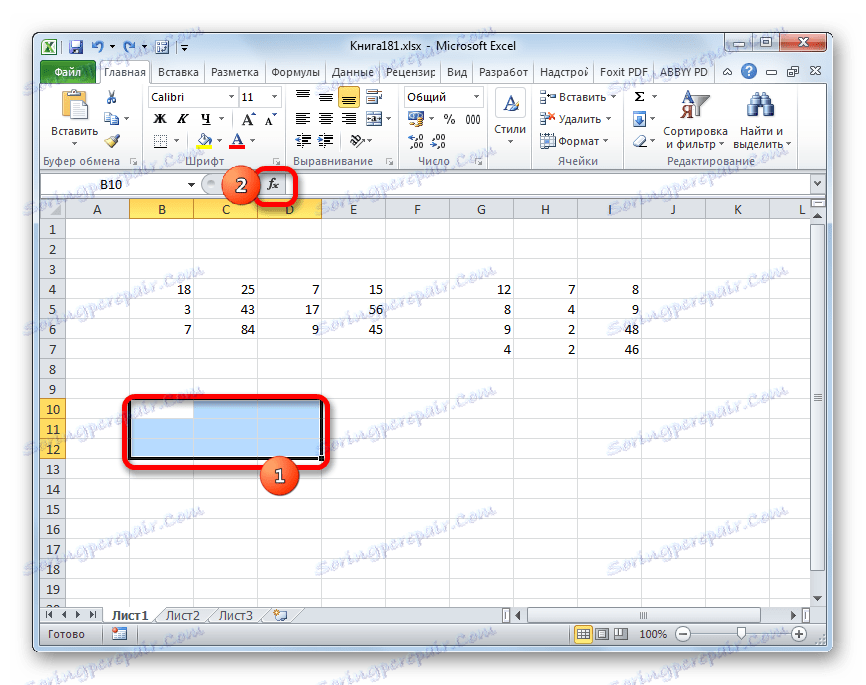
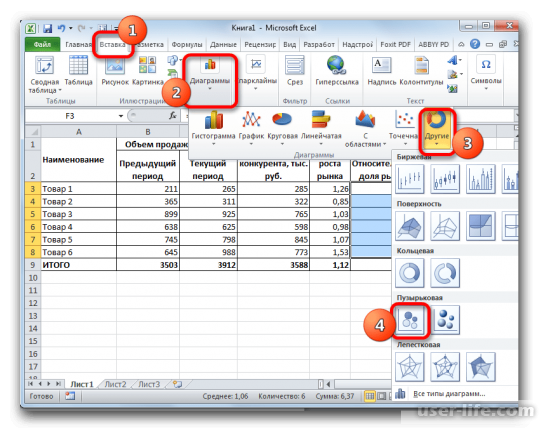
- Открываем лист Excel, на котором уже располагаются две матрицы. Выделяем на нем область из пустых ячеек, которая по горизонтали имеет в своем составе количество строк первой матриц, а по вертикали количество столбцов второй матрицы. Далее жмем на значок «Вставить функцию», который размещен около строки формул.
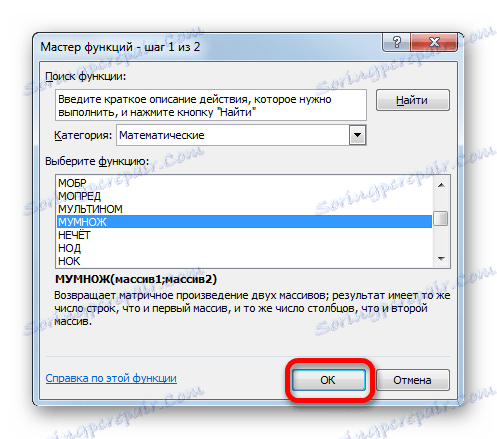
- Происходит запуск Мастера функций. Нам следует перейти в категорию «Математические» или «Полный алфавитный перечень». В списке операторов нужно отыскать наименование «МУМНОЖ», выделить его и нажать на кнопку «OK», которая размещена в нижней части данного окна.
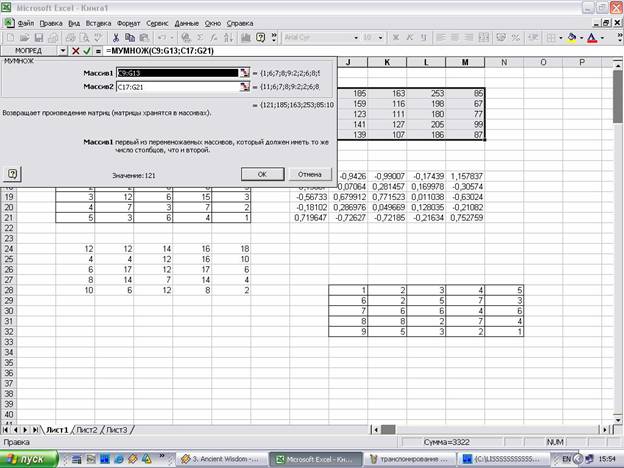
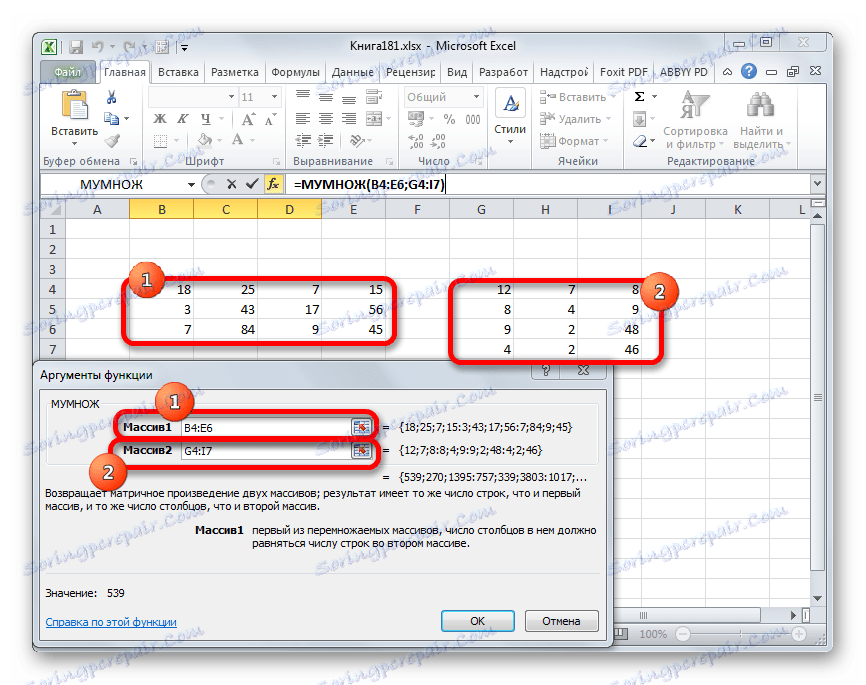
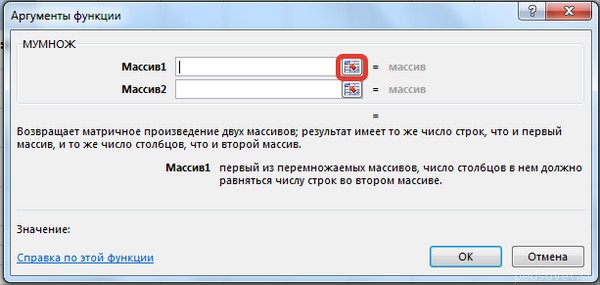
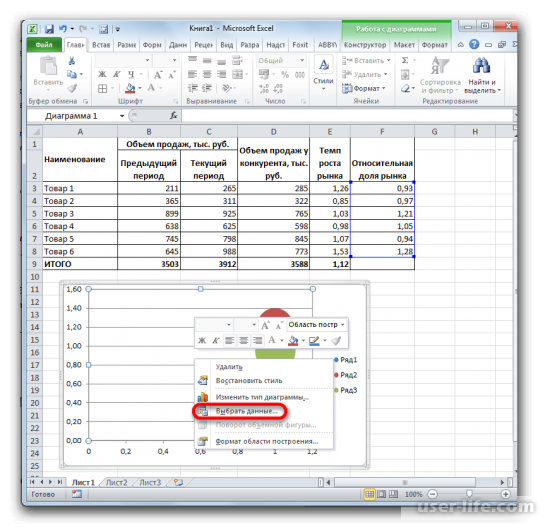
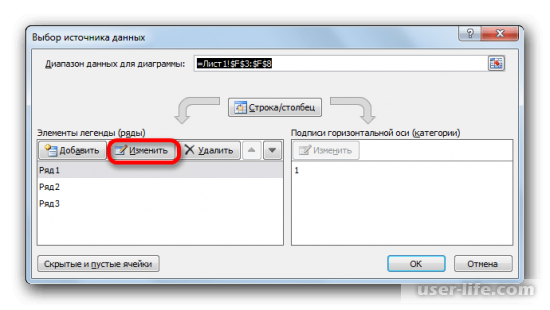
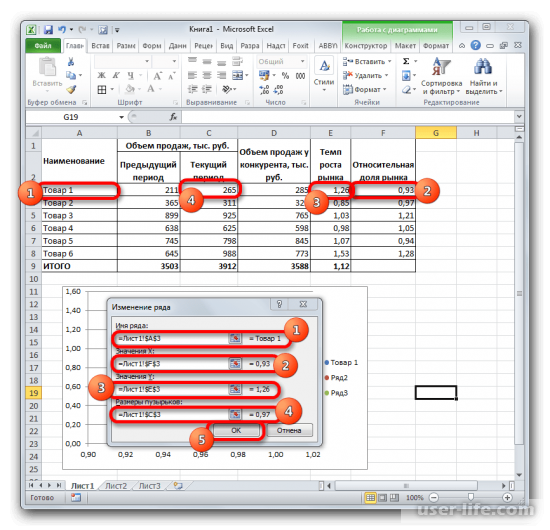
- Запускается окно аргументов оператора МУМНОЖ. Как видим, оно имеет два поля: «Массив1» и «Массив2». В первом нужно указать координаты первой матрицы, а во втором, соответственно, второй. Для того, чтобы сделать это, устанавливаем курсор в первое поле. Затем производим зажим левой кнопкой мыши и выделяем область ячеек, содержащую первую матрицу. После выполнения этой несложной процедуры координаты отобразятся в выбранном поле. Аналогичное действие проводим и со вторым полем, только в этот раз, зажав левую кнопку мыши, выделяем вторую матрицу.
После того, как адреса обеих матриц записаны, не спешим жать на кнопку «OK», размещенную в нижней части окна. Дело в том, что мы имеем дело с функцией массива. Она предусматривает то, что результат выводится не в одну ячейку, как в обычных функциях, а сразу в целый диапазон. Поэтому для вывода итога обработки данных, используя этот оператор, недостаточно нажать на клавишу Enter, расположив курсор в строке формул, или щелкнуть по кнопке «OK», находясь в окне аргументов функции, которое открыто у нас в данный момент. Нужно применить нажатие комбинации клавиш Ctrl+Shift+Enter. Выполняем данную процедуру, а кнопку «OK» не трогаем.
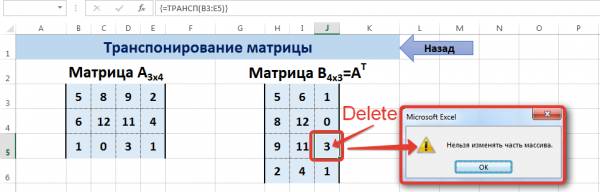
- Как видим, после нажатия указанной комбинации клавиш окно аргументов оператора МУМНОЖ закрылось, а диапазон ячеек, который мы выделили ещё в первом шаге этой инструкции, был заполнен данными. Именно эти значения и являются результатом умножения одной матрицы на другую, которое выполнил оператор МУМНОЖ. Как видим, в строке формул функция взята в фигурные скобки, что означает её принадлежность к операторам массивов.
- Но именно то, что результат обработки функции МУМНОЖ является цельным массивом, мешает дальнейшему его изменению в случае необходимости. При попытке изменить любое из чисел итогового результата пользователя будет ждать сообщение, которое информирует о том, что нельзя изменять часть массива. Чтобы устранить это неудобство и преобразовать неизменяемый массив в обычный диапазон данных, с которым можно работать, выполняем следующие действия.
Выделяем данный диапазон и, находясь во вкладке «Главная», кликаем по значку «Копировать», который размещен в блоке инструментов «Буфер обмена». Также вместо этой операции можно применить набор сочетания клавиш Ctrl+C.
- После этого, не снимая выделения с диапазона, кликаем по нему правой кнопкой мыши. В открывшемся контекстном меню в блоке «Параметры вставки» выбираем пункт «Значения».
- После выполнения данного действия итоговая матрица уже не будет представлена как единый неразрывный диапазон и с ней можно производить различные манипуляции.
Урок: Работа с массивами в Excel
Как видим, оператор МУМНОЖ позволяет довольно быстро и легко умножать в Экселе две матрицы друг на друга. Синтаксис этой функции довольно простой и у пользователей не должно возникнуть проблем со вводом данных в окно аргументов. Единственная проблема, которая может возникнуть при работе с этим оператором, заключается в том, что он представляет собой функцию массива, а значит, имеет определенные особенности. Для вывода результата требуется предварительно выделить соответствующий диапазон на листе, а затем уже после ввода аргументов для расчета применить специальную комбинацию клавиш, предназначенную для работы именно с таким типом данных — Ctrl+Shift+Enter.
Еще статьи по данной теме:
Помогла ли Вам статья?
Применение функции МУМНОЖ в Microsoft Excel
Применение функции МУМНОЖ в Microsoft Excel
Как известно, программа Excel обладает множеством инструментов для работы с матрицами. Одним из них является функция МУМНОЖ. С помощью данного оператора у пользователей появляется возможность перемножать различные матрицы. Давайте узнаем, как использовать эту функцию на практике, и в чем заключаются основные нюансы работы с ней.
Использование оператора МУМНОЖ
Основной задачей функции МУМНОЖ, как было сказано выше, является перемножение двух матриц. Она относится к категории математических операторов.
Синтаксис этой функции следующий:
Как видим, у оператора всего два аргумента – «Массив1» и «Массив2». Каждый из аргументов представляет собой ссылку на одну из матриц, которую следует перемножить. Именно это и выполняет указанный выше оператор.
Важным условием для применения МУМНОЖ является то, что количество строк первой матрицы должно совпадать с количеством столбцов второй. В обратном случае, в результате обработки будет выдаваться ошибка. Также во избежание ошибки ни один из элементов обоих массивов не должен быть пустым, а они полностью должны состоять из чисел.
Умножение матриц
Теперь давайте на конкретном примере рассмотрим, как можно умножить две матрицы, применив оператор МУМНОЖ.
- Открываем лист Excel, на котором уже располагаются две матрицы. Выделяем на нем область из пустых ячеек, которая по горизонтали имеет в своем составе количество строк первой матриц, а по вертикали количество столбцов второй матрицы. Далее жмем на значок «Вставить функцию», который размещен около строки формул.
Как видим, оператор МУМНОЖ позволяет довольно быстро и легко умножать в Экселе две матрицы друг на друга. Синтаксис этой функции довольно простой и у пользователей не должно возникнуть проблем со вводом данных в окно аргументов. Единственная проблема, которая может возникнуть при работе с этим оператором, заключается в том, что он представляет собой функцию массива, а значит, имеет определенные особенности. Для вывода результата требуется предварительно выделить соответствующий диапазон на листе, а затем уже после ввода аргументов для расчета применить специальную комбинацию клавиш, предназначенную для работы именно с таким типом данных — Ctrl+Shift+Enter.

Помимо этой статьи, на сайте еще 12369 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.

Работа с матрицами и их преобразование.
Матрица представляет собой таблицу с числовыми значениями, которая состоит из n – строк и m – столбцов.
Сложение матриц
Матрицы можно сложить двумя способами:
1. Для сложения двух матриц выбираем, пустую ячейку, и воспользуемся пунктом меню – «вставка» — «функция».
В появившемся окне выбираем функцию «СУММ» и нажимаем кнопку «ок».
Появляется окно с шаблоном для заполнения. В пустых полях указываем первые ячейки матриц. Нажимаем кнопку «ок» и получаем в исходной ячейке результат. Затем за правый нижний угол растягиваем исходную ячейку в размер складываемых матриц и получаем сумму двух матриц(рис.5).
Рис.5 Сложение матриц при помощи стандартной функции
2. Для сложения двух матриц выбираем любую свободную ячейку, в которую записываем формулу для сложения. Формула представляет собой сумму двух первых ячеек матриц. Затем выделяем ячейку с формулой, и за Для сложения матриц выбираем пустую ячейку и воспользуемся пунктом меню – «вставка» — «функция».
В появившемся окне выбираем функцию «СУММ» и нажимаем кнопку «ок».
Появляется окно с шаблоном для заполнения. В пустых полях указываем первые ячейки матриц. Нажимаем кнопку «ок» и получаем в исходной ячейке результат. Затем за правый нижний угол растягиваем исходную ячейку в размер складываемых матриц и получаем сумму двух матриц (рис.6).
Рис.6 Сложение матриц
Перемножение матриц
Для перемножения матриц необходимо выделить точное количество ячеек, как и в перемножаемых матрицах.
Затем выбираем пункт меню – «вставка» — «функция».
В появившемся окне выбираем функцию «МУМНОЖ» и нажимаем кнопку «ок».
В появившемся окне с шаблоном заполняем поля путём выделения ячеек, в которых находится матрица. После введения матриц необходимо нажать, Ctrl + Sift + Enter и в указанной матрице мы получаем результат (рис.7).
Рис.7 Перемножение матриц
Транспонирование матриц
Для транспонирования матрицы необходимо выделить массив и скопировать его в буфер обмена. Затем войти в пункт меню «Правка» – «Специальная вставка». Предварительно указав свободную ячейку. После чего появится окно, в котором необходимо поставить флажок напротив
пункта транспонировать и нажать кнопку «ок». В результате чего мы получаем транспонированную матрицу (рис.8).
Рис.8 Транспонирование матриц
Аналогично функции «МУМНОЖ» используются функции «МОПРЕД» (нахождение определителя матрици) и «МОБР» (нахождение обратной матрици).
Застосування функції МУМНОЖ в Microsoft Excel
Як відомо, програма Excel має безліч інструментів для роботи з матрицями. Одним з них є функція МУМНОЖ. За допомогою даного оператора у користувачів з’являється можливість перемножать різні матриці. Давайте дізнаємося, як використовувати цю функцію на практиці, і в чому полягають основні нюанси роботи з нею.
Використання оператора МУМНОЖ
Основним завданням функції МУМНОЖ, як було сказано вище, є множення двох матриць. Вона відноситься до категорії математичних операторів.
Синтаксис цієї функції наступний:
Як бачимо, у оператора всього два аргументи — «массів1» і «массів2». Кожен з аргументів є посилання на одну з матриць, яку слід перемножити. Саме це і виконує зазначений вище оператор.
Важливою умовою для застосування МУМНОЖ є те, що кількість рядків першої матриці має збігатися з кількістю стовпців другий. У зворотному випадку, в результаті обробки буде видаватися помилка. Також, щоб уникнути помилки жоден з елементів обох масивів не повинен бути порожнім, а вони повністю повинні складатися з чисел.
множення матриць
Тепер давайте на конкретному прикладі розглянемо, як можна помножити дві матриці, застосувавши оператор МУМНОЖ.
- Відкриваємо лист Excel, на якому вже розташовуються дві матриці. Виділяємо на ньому область з порожніх клітинок, яка по горизонталі має в своєму складі кількість рядків першої матриць, а по вертикалі кількість стовпців другого матриці. Далі тиснемо на значок «Вставити функцію», який розміщений біля рядка формул.
Як бачимо, оператор МУМНОЖ дозволяє досить швидко і легко множити в Ексель дві матриці один на одного. Синтаксис цієї функції досить простий і у користувачів не повинно виникнути проблем з введенням даних у вікно аргументів. Єдина проблема, яка може виникнути при роботі з цим оператором, полягає в тому, що він являє собою функцію масиву, а значить, має певні особливості. Для виведення результату потрібно попередньо виділити відповідний діапазон на аркуші, а потім вже після введення аргументів для розрахунку застосувати спеціальну комбінацію клавіш, призначену для роботи саме з таким типом даних — Ctrl + Shift + Enter.
ТЕХНОЛОГИЯ ВЫПОЛНЕНИЯ ОПЕРАЦИЙ НАД МАТРИЦАМИ В СРЕДЕ EXCEL
Рассмотрим некоторые аспекты работы с табличным процессором Excel, которые позволят упростить расчеты, необходимые для решения оптимизационных задач. Табличный процессор — это программный продукт, предназначенный для автоматизации обработки данных табличной формы.
Элементы экрана Excel. После запуска Excel на экране появляется таблица, вид которой показан на рис. 1.2.1. Ее называют рабочим листом. Она представляет собой сетку строк и столбцов, пересечения которых образуют прямоугольники, называемые ячейками.
Рис. 1.2.1. Рабочий лист Excel
Рабочие листы предназначены для ввода данных, выполнения расчетов, организации информационной базы и т.п. Окно Excel отображает основные программные элементы: строку заголовка, строку меню, строку состояния, кнопки управления окнами.
Работа с формулами. В программах электронных таблиц формулы служат для выполнения множества разнообразных расчетов. С помощью Excel можно быстро создать формулу. Формула состоит из трех основных частей:
- • знак равенства;
- • совокупность значений или ссылки на ячейки, с которыми выполняются расчеты;
- • операторы.
Если знак равенства отсутствует, то Excel интерпретирует данные не как формулу, а как ввод данных в ячейку. Формулы можно вводить непосредственно в ячейку или в строку формул — как текст, так и число. Последовательность действий при этом такова:
- ? Выделите ячейку, которая должна содержать формулу, введите знак (=).
- ? Введите оператор или знак действия.
- ? Выделите другую ячейку, включаемую в формулу.
- ? Снова введите оператор, и так далее, пока не завершится ввод формулы.
- ? Нажмите клавишу Enter.
В строке формул появится введенная формула, в ячейке — результат расчета.
Использование в формулах функций. Чтобы облегчить ввод формул, можно воспользоваться функциями Excel. Функции — это встроенные в Excel формулы. Excel содержит множество формул. Они сгруппированы по различным типам: логические, математические, инженерные, статистические и др.
Для активизации той или иной формулы следует нажать кнопки Вставка, Функции. В появившемся окне Мастер функций слева содержится перечень типов функций. После выбора типа справа будет помещен список самих функций. Выбор функции осуществляется щелчком клавиши мыши на соответствующем названии.
Различные функции выполняют разные типы вычислений по определенным правилам. Когда функция является единичным объектом в ячейке рабочего листа, она начинается со знака (=), далее следует название функции, а затем — аргументы функции, заключенные в скобки.
В Excel встроено множество функций, каждая из которых предназначена для выполнения специальных типов вычислений. При выполнении операций над матрицами, решении систем линейных уравнений, решении задач планирования по модели межотраслевого баланса можно применять следующие функции Excel [8]: мумнож — умножение матриц;
трансп — транспонирование матрицы;
мопред — вычисление определителя матрицы;
мобр — вычисление обратной матрицы.
Кнопка fx находится на панели инструментов.
Функции для выполнения операций с матрицами находятся в категории Математические (рис. 1.2.2).
Умножение матриц с помощью функции МУМНОЖ
Функция мумнож возвращает произведение матриц (матрицы хранятся в массивах 1 и 2). Результатом является массив с таким же числом строк, как массив 1, и с таким же числом столбцов, как массив 2.
Рис. 1.2.2. В диалоговом окне Мастер функций можно выбрать для работы любую функцию Excel
Синтаксис: МУМНОЖ (массив 1, массив2)
- • Массив. массив2 — это перемножаемые массивы.
- • Количество столбцов аргумента мае сив 1 должно быть таким же, как количество строк аргумента мае сив 2, и оба массива должны содержать только числа.
- • Массивы могут быть заданы как интервалы,массивы констант или ссылки.
- • Если хотя бы одна ячейка в аргументах пуста или содержит текст, то функция мумнож возвращает значение ошибки #ЗНАЧ!.
- • мумнож также возвращает значение ошибки #ЗНАЧ!, если число столбцов в аргументе массив 1 отличается от числа строк в аргументе массив2.
мумнож(<1; 3 : 7; 2>; <2; 0 : 0; 2>) равняется <2; 6 : 14; 4>; мумнож(<3; 0 : 2; 0>; <2; 0 : 0; 2>) равняется <6; 0 : 4; 0>; МУМНОЖ(<1; 3; 0 : 7; 2; 0 : 1; 0; 0>; <2; 0 : 0; 2>) равняется #ЗНАЧ!, поскольку массив!, имеет три столбца, а массив 2 — только две строки.
Решение примера 1.1.1 в Excel (рис. 1.2.3 и 1.2.4):
- ? Введите матрицы А в ячейки А2:ВЗ и В в ячейки D2:E3.
- ? Выделите диапазон ячеек для результата умножения — G2:H3.
Рис. 1.2.3. Исходные данные для примера умножения матриц
Рис. 1.2.4. В ячейках G2:H3 получен результат умножения матриц
- ? Введите формулу умножения матриц =мумнож (А2: ВЗ, D2: ЕЗ).
- ? Нажмите клавиши CTRL + SHIFT + ENTER.
Решение примера 1.1.2 в Excel (рис. 1.2.5 и 1.2.6):
- ? Введите матрицы А в ячейки А2:СЗ и В в ячейки F2:H4.
- ? Выделите диапазон ячеек для результата умножения — D6:F7.
- ? Введите формулу умножения матриц =мумнож(А2 :СЗ, F2:H4).
- ? Нажмите клавиши CTRL + shift + ENTER.
Рис. 1.2.5. Введены исходные данные для примера 1.1.2
Рис. 1.2.6. В ячейках D6:F7 получен результат умножения матриц
Пример 1.2.1. Ателье выпускает три вида изделий: брюки, юбки и жилеты, используя два вида тканей: шерстяную и подкладочную. Нормы расхода тканей приведены в табл. 1.2.1 (матрица А).
Функция МУМНОЖ используется в Excel для перемножения матриц. Матричная алгебра?! Я напрочь забыл университетский курс матричной алгебры! Хотя это верно для большинства из вас, рекомендую вспомнить, как умножать матрицы. Зачем? Умножение матриц имеет некоторые весьма практичные применения. В этой главе вы рассмотрите проблему вычисления суммарной стоимости, сначала решите ее методом «длинной руки», а затем используете функцию МУМНОЖ для выполнения той же задачи легче и быстрее.
Это глава из книги: Майкл Гирвин. Ctrl+Shift+Enter. Освоение формул массива в Excel.
Предыдущая глава Оглавление Следующая глава
Рис. 18.1. Стоимость оборудования для мужской команды
Скачать заметку в формате Word или pdf, примеры в формате Excel
Используем МУМНОЖ для построения формулы общих издержек
На рис. 18.1 показано, как можно рассчитать общую стоимость оборудования для мужской команды. Обратите внимание, что вы сначала перемножаете, а затем суммируете ряд расходов (А4:С4) и столбец количеств предметов (С9:С11). Хотя вы получите правильные ответы с помощью этой формулы, есть лучший способ сделать это – воспользуйтесь функцией МУМНОЖ. Однако, прежде чем приступить, запомните два правила матричного умножения:
- Количество столбцов первого массива должно быть равно числу строк второго массива.
- Размер результирующего массива будет равен количеству строк первого массива, умноженному на число столбцов второго массива (рис. 18.3).
Рис. 18.3. Поскольку цель – вычислить две суммы (для женской и мужской команд), результирующий массив будет две ячейки в ширину; Чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Почему нельзя было использовать функцию СУММПРОИЗВ? Дело в том, что два массива имеют разные размеры. Для сравнения на рис. 18.4 показано, как можно получить результат, если второй массив имеет тот же размер, что и первый.
Рис. 18.4. Если диапазоны ориентированы одинаково, можно применить функцию СУММПРОИЗВ
Справедливости ради заметим, что первый массив можно привести к той же размерности, что и второй, с помощью функции ТРАНСП (рис. 18.5).
Рис. 18.5. Формула с СУММПРОИЗВ и ТРАНСП всё же справится с задачей
Вот причины, по которым возможно использовать функцию МУМНОЖ (см. рис. 18.1 и 18.3):
- Поскольку число столбцов в массиве 1 (стоимость) равно числу строк в массиве 2 (Количество), разрешается выполнять матричное умножение.
- Цель – рассчитать общие затраты и вернуть массив размером 1*2; это означает, что результирующий массив, который получается путем умножения матрицы 1*3 на матрицу 3*2 как раз имеет размерность 1*2.
Чтобы воспользоваться функцией массива МУМНОЖ (см. рис. 18.3):
- Выберите область Стоимость (А4:С4) в качестве первого массива, а область Количество (В9:С11) – в качестве второго.
- Выделите область, в которой разместится результирующий массив – В15:С15.
- В строке формул наберите =МУМНОЖ(A4:C4;B9:C11).
- Введите формулу, нажав Ctrl+Shift+Enter.
Использование функции МУМНОЖ для расчета средневзвешенного значения
Как показано на рис. 18.7, вы можете использовать МУМНОЖ для расчета средневзвешенного значения, когда два массива имеют одинаковое количество элементов, но разные размеры (разную ориентацию). Массив 1 (значения тестов для Sioux, диапазон В4:Е4) имеет размерность 1*4 и массив 2 (веса тестов, диапазон $B$11:$В$14) имеет размерность 4*1. Введите формулу массива {=МУМНОЖ(B4:E4;$B$11:$B$14)} (см. рис. 18.7, строка формул) в ячейку F4 и скопируйте её вниз по столбцу.
Рис. 18.7. Использование функции МУМНОЖ для расчета средневзвешенного значения
Таблица умножения на основе функции МУМНОЖ
На рис. 18.8 показано как создать таблицу умножения. В качестве альтернативы можно использовать смешанные ссылки (подробнее см. Относительные, абсолютные и смешанные ссылки на ячейки в Excel).
Рис. 18.8. Таблица умножения на основе функции МУМНОЖ
Нахождение ожидаемой доходности портфеля акций
На рис. 18.9 показан тот же пример, что и в главе 10 для вычисления ожидаемой доходности портфеля акций. Цель формулы – перемножение трех диапазонов С3:D5, В3:В5 и С1:D1. В главе 10 вы узнали, как обойти требование функция СУММПРОИЗВ, чтобы все массивы имели один и тот же размер: нужно помещать каждый массив не в отдельный аргумент, а все массивы разместить в аргументе массив_1, перемножив их алгебраически. Однако, в этом случае, при наличии нечисловых данных в любом из массивов, функция СУММПРОИЗВ возвращает ошибку.
Функция МУМНОЖ умножает массив 1 (вероятность состояния экономики, диапазон В3:В5) на массив 2 (вес, диапазоне С1:D1), и создает результирующий массив того же размера, что и массив ожидаемой доходности (3*2, диапазон С3:D5). Теперь вы можете умножить эти два массива: =СУММПРОИЗВ({"Нет";-0,15:0,05;0,05:0,1;0,2};{0,3;0,2:0,24;0,16:0,06;0,04}), поместив их в отдельные аргументы функции СУММПРОИЗВ, и воспользоваться свойством функции СУММПРОИЗВ игнорировать текст.
Рис. 18.9. Ячейка D10 содержит надежную формулы для расчета ожидаемой доходности
Параметры функции массива МУМНОЖ:
- Синтаксис МУМНОЖ(массив1; массив2). Функция содержит ровно два аргумента.
"Массив1"и"массив2"могут быть заданы как диапазоны ячеек, константы массивов или ссылки.- Функция МУМНОЖ возвращает значение ошибки #ЗНАЧ! в следующих случаях:
- Если какая-либо ячейка пуста или содержит текст (рис. 18.10; ячейка С3).
- Если число столбцов в аргументе «массив1» отличается от числа строк в аргументе «массив2».
Рис. 18.10. Ячейку С3 пустая, и функция МУМНОЖ возвращает ошибку
Функции массива МОБР и МЕДИН
Эти функции понадобятся, если вы захотите решать системы уравнений с помощью матричной алгебры. Функцию МОБР (матрица обратная) вычисляет обратную матрицу. Функция МЕДИН (матрица единичная) возвращает единичную матрицу. Матрицы обычно обозначают прописными буквами, например, А. Обратной (А–1) называют матрицу, произведение которой на исходную матрицу A равно единичной матрице I (или, в русскоязычном обозначении – E; рис. 18.11). Обратная матрица существует только для квадратных матриц. В единичной матрице диагональные элементы равны 1, не диагональные элементы равны нулю.
Рис. 18.11. Матриц А, обратная матрица А–1, их произведение возвращает единичную матрицу (при условии, что обратная существует)
Чтобы рассчитать обратную матрицу A–1 выделите ячейки D2:E3, и в строке формул наберите =МОБР(A2:B3). Введите функцию массива нажав Ctrl+Shift+Enter. Единичная матрица в ячейках G2:H3 получена умножением матриц А и A–1 с помощью формулы массива {=МУМНОЖ(A2:B3;D2:E3)}.
Единичная матрица нужной размерности, начиная с Excel 2013 может быть получена с помощью функции массива МЕДИН (рис. 18.12). Чтобы ввести функцию МЕДИН выделите квадратный диапазон, и в качестве аргумента функции укажите число строк (или столбцов) диапазона.
Рис. 18.12. Функция массива МЕДИН, появившаяся в Excel 2013
Решение систем уравнений с помощью функции МУМНОЖ
На рис. 18.15 представлена система из трех линейных уравнений с тремя переменными х1, х2 и х3. Поскольку, и уравнений, и переменных – три, можно использовать МУМНОЖ и МОБР для нахождения неизвестных. Выполните следующие действия:
- Разместить коэффициентов из уравнений в массиве 3*3 в диапазоне I3:К5.
- Константы из уравнений разместите в массиве 3*1 в диапазоне М3:М5.
- Выделите диапазон Q3:Q5 (3*1) и наберите в строке формул: =МУМНОЖ(МОБР(I3:K5);M3:M5). Введите формулу массива, нажав Ctrl+Shift+Enter.
- Подставьте найденные значения в уравнения и проверьте правильность решения.
Рис. 18.15. Решение системы уравнений с помощью функций МУМНОЖ и МОБР
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Создание матрицы в excel
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
Умножение и деление матрицы на число в Excel
Способ 1
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А – В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если АžА -1 =А -1 žА=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
Нажмите для увеличения
Мы вычислили определитель матрицы А.
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст
Матрица БКГ – уникальная матрица, которая помогает на основе исходных данных построить диаграмму и провести анализ всех сегментов рынка. Создана была матрица Бостонской консалтинговой группой, откуда и получила свое название.
Она дает возможность математические правильно проанализировать рынок и избрать необходимые меры для дальнейшего развития разных товаров в будущем.
Звучит немного запутано, но на самом деле все немного проще чем кажется на первый взгляд. Стратегия матрицы предполагает, что все товары относятся лишь к четырем группам:
· «собаки» – товары, которые представляют незначительную долю рынка в своем сегменте низкого темпа роста; эти товары являются менее перспективными, поэтому производство данного сегмента не будет иметь успеха;
· «трудные дети» – товары, которые могут быстро выбиться в перспективный сегмент, но при этом еще занимают малую часть всего рынка; товары с хорошими темпами развития, но требующие финансовых и инвестиций;
· «дойные коровы» – сегмент рынка с постоянным, но незначительным доходом, которые при этом не требуют никаких инвестиций; их доля значительная, но в слабо растущем сегменте рынка;
· «звезды» – товары с существенной доле быстроразвивающегося рынка, которые имеют наибольший успех; с первых дней приносят хороший доход, а будущие вложения в данный сегмент смогут лишь увеличить прибыль.
Отношение темпа роста относительно сегментов рынка можно отобразить:
Суть массива БКГ – найти определенный сегмент рыка, к которой можно отнести исходную группу или единичный товар.
Попробуем на практике осуществить данную процедуру через функционал Excel:
1. Создадим таблицу, в которой отобразим исходные товары с информацией о количестве продаж текущего месяца и прошлого, а также наименьшую цену этих товаров у конкурента.
2. Рассчитываем темпы роста этих товаров на рыке и их относительную долю. Разделим количество продаж за текущий период на количество за прошлый период, и соответственно, величину продаж текущего периода на продажи у конкурентов.
3. Следующим шагом будет построение диаграммы на основе полученной информации. Используем диаграмму пузырькового типа – «Вставка» – «Диаграмма» – «Другие» – «Пузырьковая».
4. Выберем необходимые вводные. Откроем функции и укажем на пункт «Выбрать данные».
5. В окне выбора данных нажимаем на «Изменить» и начинаем заполнять изменения ряда пузырьковой диаграммы.
6. В «Имя ряда» устанавливаем ячейку «Наименование». «Значения Х» будут подтягиваться со столбца «Относительная доля рынка», в «Значения Y» – «Темп роста рынка». «Размеры пузырьков» будут браться со диапазона «Текущий период». На этом ввод значений завершаем и сформировать диаграмму.
7. Проведем подобные действия для всех групп и получаем итоговую пузырьковую диаграмму. Осталось лишь корректно настроить оси.
8. Нужно немного подкорректировать оси. Для начала в горизонтальных осях изменяем «Минимальное значение» на «0», «Максимальное» – на «2», а «Деления» на «1».
9. В настройках вертикальных осей устанавливаем «Минимальное» на 0, «Максимальное» на «2.18», а деления на «1.09». Эти показатели высчитываются из среднего показателя относительной доли рынка, который необходимо умножить на 2. «Деления» также устанавливаем «1.09». Последнее что укажем – «Значение оси» – «1.09» соответственно.
10. Осталось подписать наши оси и можно приступать к непосредственному анализу матрицы БКГ.
Матрица БКГ дает возможность провести быстрый и корректный анализ сегментов рынка.
В нашем случае мы видим, что:
«Товар 2» и «Товар 5» относятся к группе товаров «Собаки» – они не приносят прибыль. Они не имеют популярности на рынке, поэтому они в дальнейшем стратегии продаж нам больше не интересны.
«Товар 1» является представителем группы «Трудные дети», а это значит, что товар, при должном развитии и финансировании может приносить прибыль, но это будет происходить не в ближайшее время.
«Товар 3» и «Товар 4» – «Дойные коровы» – отличная выручка дает возможность развивать другие категории, при этом не вкладывая инвестиции в данный сегмент.
«Товар 6» – единственный, который полностью относится к категории «Звезды» – его отличная возможность приносить прибыль держит весь бизнес, а дополнительные инвестиции в этот сегмент помогут лишь улучшить финансовое положение.
Таким образом, можно провести существенный анализ сегментов рынка и получить необходимы выводы для каждой группы товаров с помощью матрицы БКГ. Построение матрицы не должно вызывать особых трудностей, но стоит учесть, что нужны проверенные исходные данные и показатели, ведь именно они являются основой матрицы.
Как возвести матрицу в степень в excel
В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.
Произведение матрицы А порядка P x N и матрицы В порядка N x Q — это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В , то есть:
Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ() , которую нужно вводить как формулу массива .
Рассмотрим сначала умножение квадратных матриц 2 х 2.
Разместим матрицы в диапазонах А8:В9 и D8:E9 (см. файл примера ).
Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9 .
- выделите указанный диапазон H8:I9
- поставьте курсор в Строку формул (или нажмите клавишу F2 )
- введите формулу =МУМНОЖ(A8:B9;D8:E9)
- нажмите CTRL+SHIFT+ENTER
Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо б о льший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL ).
Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2 , исправьте формулу и нажмите CTRL+SHIFT+ENTER .
Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)) . Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER . Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!
В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.
Возведение числа в степень в Microsoft Excel
Возведение числа в степень является стандартным математическим действием. Оно применяется в различных расчетах, как в учебных целях, так и на практике. У программы Excel имеются встроенные инструменты для подсчета данного значения. Давайте посмотрим, как ими пользоваться в различных случаях.
Возведение чисел
В Excel существует одновременно несколько способов возвести число в степень. Это можно сделать при помощи стандартного символа, функции или применив некоторые, не совсем обычные, варианты действий.
Способ 1: возведение с помощью символа
Самый популярный и известный способ возведения в степень числа в Экселе – это использование стандартного символа «^» для этих целей. Шаблон формулы для возведения выглядит следующим образом:
В этой формуле x – это возводимое число, n – степень возведения.
- Например, чтобы возвести число 5 в четвертую степень мы в любой ячейке листа или в строке формул производим следующую запись:
Если возведение является составной частью более сложного расчета, то порядок действий производится по общим законам математики. То есть, например, в примере 5+4^3 сразу Excel выполняет возведение в степень числа 4, а потом уже сложение.
Кроме того, с помощью оператора «^» можно возводить не только обычные числа, но и данные, содержащиеся в определенном диапазоне листа.
Возведем в шестую степень содержимое ячейки A2.
- В любое свободное место на листе записываем выражение:
Жмем на кнопку Enter. Как видим, расчет был выполнен корректно. Так как в ячейке A2 находилось число 7, то результат вычисления составил 117649.
Как видим, все значения нужного интервала были возведены в указанную степень.
Данный способ максимально прост и удобен, и поэтому так популярен у пользователей. Именно он применяется в подавляющем большинстве случаев вычислений.
Способ 2: применение функции
В Экселе имеется также специальная функция для проведения данного расчета. Она так и называется – СТЕПЕНЬ. Её синтаксис выглядит следующим образом:
Рассмотрим её применение на конкретном примере.
- Кликаем по ячейке, куда планируем выводить результат расчета. Жмем на кнопку «Вставить функцию».
Открывается Мастер функций. В списке элементов ищем запись «СТЕПЕНЬ». После того как находим, выделяем её и жмем на кнопку «OK».
Вслед за этим результат вычисления данной функции выводится в место, которое было выделено ещё в первом шаге описываемых действий.
Кроме того, окно аргументов можно вызвать, перейдя во вкладку «Формулы». На ленте следует нажать кнопку «Математические», расположенную в блоке инструментов «Библиотека функций». В открывшемся списке доступных элементов нужно выбрать «СТЕПЕНЬ». После этого запустится окно аргументов этой функции.
Пользователи, которые имеют определенный опыт, могут не вызывать Мастер функций, а просто вводить формулу в ячейку после знака «=», согласно её синтаксису.
Данный способ более сложный, чем предыдущий. Его применение может быть обосновано, если расчет нужно произвести в границах составной функции, состоящей из нескольких операторов.
Способ 3: возведение в степень через корень
Конечно, данный способ не совсем обычный, но к нему тоже можно прибегнуть, если нужно возвести число в степень 0,5. Разберем этот случай на конкретном примере.
Нам нужно возвести 9 в степень 0,5 или по-другому — ½.
- Выделяем ячейку, в которую будет выводиться результат. Кликаем по кнопке «Вставить функцию».
В открывшемся окне Мастера функций ищем элемент КОРЕНЬ. Выделяем его и жмем на кнопку «OK».
Открывается окно аргументов. Единственным аргументом функции КОРЕНЬ является число. Сама функция выполняет извлечение квадратного корня из введенного числа. Но, так как квадратный корень тождественен возведению в степень ½, то нам данный вариант как раз подходит. В поле «Число» вводим цифру 9 и жмем на кнопку «OK».
Но, конечно, к данному способу расчета прибегают довольно редко, используя более известные и интуитивно понятные варианты вычислений.
Способ 4: запись числа со степенью в ячейке
Этот способ не предусматривает проведения вычислений по возведению. Он применим только тогда, когда нужно просто записать число со степенью в ячейке.
- Форматируем ячейку, в которую будет производиться запись, в текстовый формат. Выделяем её. Находясь во вкладке em«Главная» на ленте в блоке инструментов «Число», кликаем по выпадающему списку выбора формата. Жмем по пункту «Текстовый».
В одной ячейке записываем число и его степень. Например, если нам нужно написать три во второй степени, то пишем «32».
Ставим курсор в ячейку и выделяем только вторую цифру.
Нажатием сочетания клавиш Ctrl+1 вызываем окно форматирования. Устанавливаем галочку около параметра «Надстрочный». Жмем на кнопку «OK».
Внимание! Несмотря на то, что визуально в ячейке будет отображаться число в степени, Excel воспринимает его как обычный текст, а не числовое выражение. Поэтому для расчетов такой вариант применять нельзя. Для этих целей используется стандартная запись степени в этой программе – «^».
Как видим, в программе Excel существует сразу несколько способов возведения числа в степень. Для того, чтобы выбрать конкретный вариант, прежде всего, нужно определиться, для чего вам нужно выражение. Если вам нужно произвести возведение для записи выражения в формуле или просто для того, чтобы вычислить значение, то удобнее всего производить запись через символ «^». В отдельных случаях можно применить функцию СТЕПЕНЬ. Если вам нужно возвести число в степень 0,5, то существует возможность воспользоваться функцией КОРЕНЬ. Если же пользователь хочет визуально отобразить степенное выражение без вычислительных действий, то тут на помощь придет форматирование.
Мы рады, что смогли помочь Вам в решении проблемы.
Помимо этой статьи, на сайте еще 11905 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Под матрицей подразумевается набор ячеек, расположенных непосредственно друг возле друга и которые образуют вместе прямоугольник. Не требуется особых навыков, чтобы выполнять различные действия с матрицей, достаточно тех же, какие используются во время работы с классическим диапазоном.
Каждая матрица имеет свой адрес, записывающийся аналогичным диапазону способом. Первая составная часть – первая ячейка диапазона (расположенная в верхнем левом углу), а второй – последняя ячейка, которая находится в нижнем правом углу.
Содержание
- Формулы массива
- Что можно делать с матрицами
- Транспонирование
- Сложение
- Умножение
- Обратная матрица
- Поиск определителя матрицы
- Несколько примеров
- Умножение и деление
- Метод 1
- Метод 2
- Сложение и вычитание
- Метод 1
- Метод 2
- Пример транспонирования матрицы
- Поиск обратной матрицы
- Выводы
Формулы массива
В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:
- Выделить набор ячеек, где будут выводиться значения.
- Непосредственно введение формулы.
- Нажатие последовательности клавиш Ctrl + Shift + Ввод.
После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.
Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.
Что можно делать с матрицами
В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.
Транспонирование
Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.
Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.
Далее есть несколько методов, как можно осуществить транспонирование.
Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».
Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.
Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.
После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:
- Выделить набор ячеек, отведенных под транспонированную матрицу.
- Нажать клавишу F2.
- Нажать на горячие клавиши Ctrl + Shift + Enter.
Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.
Сложение
Эта операция возможна лишь применительно к тем диапазонам, количество элементов которых такое же самое. Проще говоря, у каждой из матриц, с которыми пользователь собирается работать, должны быть одинаковые размеры. И приводим скриншот для наглядности.
В матрице, которая должна получиться, нужно выделить первую ячейку и ввести такую формулу.
=Первый элемент первой матрицы + Первый элемент второй матрицы
Далее подтверждаем ввод формулы с помощью клавиши Enter и используем автозаполнение (квадратик в правом нижнем углу), чтобы скопировать все значения на новую матрицу.
Умножение
Предположим, у нас есть такая таблица, которую следует умножить на 12.
Догадливый читатель может легко понять, что метод очень похож на предыдущий. То есть, каждая из ячеек матрицы 1 должна умножаться на 12, чтобы в итоговой матрице каждая ячейка содержала значение, умноженное на этот коэффициент.
При этом важно указывать абсолютные ссылки на ячейки.
Итого, получится такая формула.
=A1*$E$3
Дальше методика аналогична предыдущей. Нужно это значение растянуть на необходимое количество ячеек.
Предположим, что необходимо перемножить матрицы между собой. Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.
Чтобы было более удобно, нами выделен диапазон с результирующей матрицей. Надо переместить курсор на ячейку в верхнем левом углу и ввести такую формулу =МУМНОЖ(А9:С13;Е9:H11). Не стоит забыть нажать Ctrl + Shift + Enter.
Обратная матрица
Если наш диапазон имеет квадратную форму (то есть, количество ячеек по горизонтали и вертикали одинаковое), то тогда получится найти обратную матрицу, если в этом есть такая необходимость. Ее величина будет аналогичной исходной. Для этого используется функция МОБР.
Для начала следует выделить первую ячейку матрицы, в какую будет вставляться обратная. Туда вводится формула =МОБР(A1:A4). В аргументе указывается диапазон, для какого нам надо создать обратную матрицу. Осталось только нажать Ctrl + Shift + Enter, и готово.
Поиск определителя матрицы
Под определителем подразумевается число, находящееся матрицы квадратной формы. Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД.
Для начала ставится курсор в какой-угодно ячейке. Далее мы вводим =МОПРЕД(A1:D4)
Несколько примеров
Давайте для наглядности рассмотрим некоторые примеры операций, которые можно осуществлять с матрицами в Excel.
Умножение и деление
Метод 1
Предположим, у нас есть матрица A, имеющая три ячейки в высоту и четыре – в ширину. Также есть число k, которое записывается в другой ячейке. После выполнения операции умножения матрицы на число появится диапазон значений, имеющий аналогичные размеры, но каждая ее часть умножается на k.
Диапазон B3:E5 – это исходная матрица, которая будет умножаться на число k, которое в свою очередь расположено в ячейке H4. Результирующая матрица будет находиться в диапазоне K3:N5. Исходная матрица будет называться A, а результирующая – B. Последняя образуется путем умножения матрицы А на число k.
Далее вводится =B3*$H$4 в ячейку K3, где В3 — элемент A11 матрицы А.
Не стоит забывать о том, ячейку H4, где указано число k необходимо вводить в формулу с помощью абсолютной ссылки. Иначе значение будет изменяться при копировании массива, и результирующая матрица потеряет работоспособность.
Далее маркер автозаполнения (тот самый квадратик в правом нижнем углу) используется для того, чтобы скопировать значение, полученное в ячейке K3, во все другие ячейки этого диапазона.
Вот у нас и получилось умножить матрицу A на определенное число и получить на выходе матрицу B.
Деление осуществляется аналогичным образом. Только вводить нужно формулу деления. В нашем случае это =B3/$H$4.
Метод 2
Итак, основное отличие этого метода в том, в качетве результата выдается массив данных, поэтому нужно применить формулу массива, чтобы заполнить весь набор ячеек.
Необходимо выделить результирующий диапазон, ввести знак равно (=), выделить набор ячеек, с соответствующими первой матрице размерами, нажать на звездочку. Далее выделяем ячейку с числом k. Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.
Деление осуществляется аналогичным образом, только знак * нужно заменить на /.
Сложение и вычитание
Давайте опишем несколько практических примеров использования методов сложения и вычитания на практике.
Метод 1
Не стоит забывать, что возможно сложение лишь тех матриц, размеры которых одинаковые. В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.
Предположим, у нас есть две матрицы, имеющие размеры 3х4. Чтобы вычислить сумму, следет в ячейку N3 вставить такую формулу:
=B3+H3
Тут каждый элемент являет собой первую ячейку матриц, которые мы собрались складывать. Важно, чтобы ссылки были относительными, поскольку если использовать абсолютные, не будут отображаться правильные данные.
Далее, аналогично умножению, с помощью маркера автозаполнения распространяем формулу на все ячейки результирующей матрицы.
Вычитание осуществляется аналогично, за тем лишь исключением, что используется знак вычитания (-), а не сложения.
Метод 2
Аналогично методу сложения и вычитание двух матриц, этот способ подразумевает использование формулы массива. Следовательно, в качестве ее результата будет выдаваться сразу набор значений. Поэтому нельзя редактировать или удалять какие-то элементы.
Сперва надо выделить диапазон, отделенный под результирующую матрицу, а потом нажать на «=». Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.
Пример транспонирования матрицы
Допустим, нам надо создать матрицу АТ из матрицы А, которая у нас есть изначально методом транспонирования. Последняя имеет, уже по традиции, размеры 3х4. Для этого будем использовать функцию =ТРАНСП().
Выделяем диапазон для ячеек матрицы АТ.
Для этого надо перейти на вкладку «Формулы», где выбрать опцию «Вставить функцию», там найти категорию «Ссылки и массивы» и найти функцию ТРАНСП. После этого свои действия подтверждаются кнопкой ОК.
Далее переходим в окно «Аргументы функции», где вводится диапазон B3:E5, который повторяет матрицу А. Далее надо нажать Shift + Ctrl, после чего кликнуть «ОК».
Важно. Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.
В результате, у нас получается такая транспонированная таблица, которая изменяет свои значения вслед за исходной.
Поиск обратной матрицы
Предположим, у нас есть матрица А, которая имеет размеры 3х3 ячеек. Мы знаем, что для поиска обратной матрицы необходимо использовать функцию =МОБР().
Теперь опишем, как это делать на практике. Сначала необходимо выделить диапазон G3:I5 (там будет располагаться обратная матрица). Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».
Откроется диалог «Вставка функции», где нужно выбрать категорию «Математические». И там в перечне будет функция МОБР. После того, как мы ее выберем, нужно нажать на клавишу ОК. Далее появляется диалоговое окно «Аргументы функции», в котором записываем диапазон B3:D5, который соответствует матрице А. Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.
Выводы
Мы разобрали некоторые примеры, как можно работать с матрицами в Excel, а также описали теорию. Оказывается, что это не так страшно, как может показаться на первый взгляд, не так ли? Это только звучит непонятно, но на деле с матрицами среднестатистическому пользователю приходится иметь дело каждый день. Они могут использоваться почти для любой таблицы, где есть сравнительно небольшое количество данных. И теперь вы знаете, как можно себе упростить жизнь в работе с ними.
Оцените качество статьи. Нам важно ваше мнение: