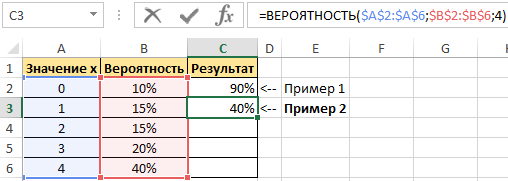
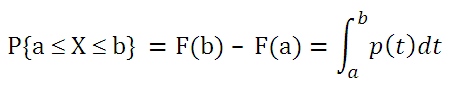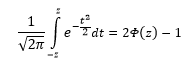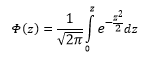Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
- ДИСП;
- ГИПЕРГЕОМ.РАСП;
- СРЗНАЧ и другие.
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
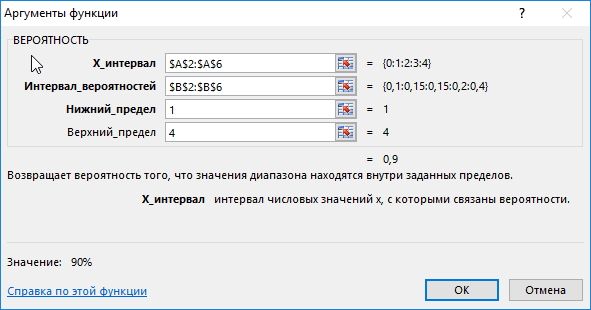
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
Для этого введем функцию со следующими аргументами:
тут:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
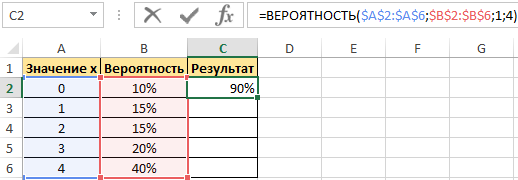
В результате выполненных вычислений получим:
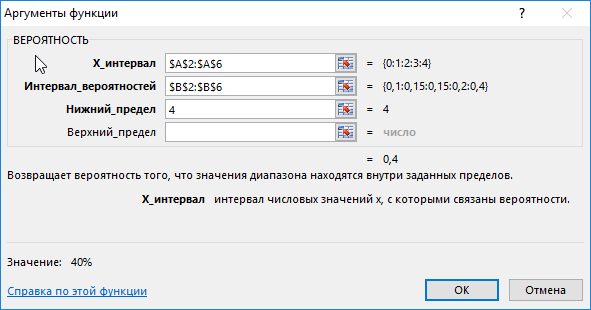
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
Введем в ячейку С3 введем функцию с такими аргументами:
тут:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Получим:
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Введем формулу:
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Скачать примеры функции ВЕРОЯТНОСТЬ в Excel
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Полезная страница? Сохрани или расскажи друзьям
Комбинаторика и вероятность
Ниже вы найдете основные формулы Excel, которые могут применяться при решении вероятностных задач и задач по комбинаторике.
| ЧИСЛКОМБ / COMBIN |
Возвращает количество сочетаний без повторений. |
| ФАКТР / FACT |
Вычисляет факториал числа. |
| СЛЧИС / RAND |
Выдает случайное число в интервале от 0 до 1 (равномерно распределенное). |
| СЛУЧМЕЖДУ / RANDBETVEEN |
Выдает случайное число в заданном интервале. |
| БИНОМРАСП / BINOMDIST |
Вычисляет отдельное значение биномиального распределения. |
| ГИПЕРГЕОМЕТ / HYRGEOMDIST |
Определяет гипергеометрическое распределение. |
| НОРМРАСП / NORMDIST |
Вычисляет значение нормальной функции распределения. |
| НОРМОБР / NORMINV |
Выдает обратное нормальное распределение. |
| НОРМСТРАСП / NORMSDIST |
Выдает стандартное нормальное интегральное распределение. |
| НОРМСТОБР / NORMSINV |
Выдает обратное значение стандартного нормального распределения. |
| ПЕРЕСТ / PERMUT |
Находит количество размещений без повторений |
| ВЕРОЯТНОСТЬ / PROB |
Определяет вероятность того, что значение из диапазона находится внутри заданных пределов. |
Подробнее: Формулы комбинаторики в Excel.
Подробно решим ваши задачи по теории вероятностей
Математическая статистика
При решении задач по математической статистике можно использовать те формулы, что перечислены выше, а также следующие (сгруппированы для удобства: обработка выборки, разные распределения, остальные формулы):
Обработка выборки: формулы Excel
| СРОТКЛ / AVEDEV |
Вычисляет среднее абсолютных значений отклонений точек данных от среднего. |
| СРЗНАЧ / AVERAGE |
Вычисляет среднее арифметическое аргументов. |
| СРГЕОМ / GEOMEAN |
Вычисляет среднее геометрическое. |
| СРГАРМ / HARMEAN |
Вычисляет среднее гармоническое. |
| ЭКСЦЕСС / KURT |
Определяет эксцесс множества данных. |
| МЕДИАНА / MEDIAN |
Находит медиану заданных чисел. |
| МОДА / MODE |
Определяет значение моды множества данных. |
| КВАРТИЛЬ / QUARTILE |
Определяет квартиль множества данных. |
| СКОС / SKEW |
Определяет асимметрию распределения. |
| СТАНДОТКЛОН / STDEV |
Оценивает стандартное отклонение по выборке. |
| ДИСП / VAR |
Оценивает дисперсию по выборке. |
Законы распределений: формулы Excel
| БЕТАРАСП / BETADIST |
Определяет интегральную функцию плотности бета-вероятности. |
| БЕТАОБР / BETAINV |
Определяет обратную функцию к интегральной функции плотности бета-вероятности. |
| ХИ2РАСП / CHIDIST |
Вычисляет одностороннюю вероятность распределения хи-квадрат. |
| ХИ2ОБР / CHIINV |
Вычисляет обратное значение односторонней вероятности распределения хи-квадрат. |
| ЭКСПРАСП / EXPONDIST |
Находит экспоненциальное распределение. |
| FРАСП / FDIST |
Находит F-распределение вероятности. |
| FРАСПОБР / FINV |
Определяет обратное значение для F-распределения вероятности. |
| ФИШЕР / FISHER |
Находит преобразование Фишера. |
| ФИШЕРОБР / FISHERINV |
Находит обратное преобразование Фишера. |
| ГАММАРАСП / GAMMADIST |
Находит гамма-распределение. |
| ГАММАОБР / GAMMAINV |
Находит обратное гамма-распределение. |
| ПУАССОН / POISSON |
Выдает распределение Пуассона. |
| СТЬЮДРАСП / TDIST |
Выдает t-распределение Стьюдента. |
| СТЬЮДРАСПОБР / TINV |
Выдает обратное t-распределение Стьюдента. |
| ВЕЙБУЛЛ / WEIBULL |
Выдает распределение Вейбулла. |
Другое (корреляция, регрессия и т.п.)
| ДОВЕРИТ / CONFIDENCE |
Определяет доверительный интервал для среднего значения по генеральной совокупности. |
| КОРРЕЛ / CORREL |
Находит коэффициент корреляции между двумя множествами данных. |
| СЧЁТ / COUNT |
Подсчитывает количество чисел в списке аргументов. |
| СЧЁТЕСЛИ / COUNTIF |
Подсчитывает количество непустых ячеек, удовлетворяющих заданному условию внутри диапазона. |
| КОВАР / COVAR |
Определяет ковариацию, то есть среднее произведений отклонений для каждой пары точек. |
| ПРЕДСКАЗ / FORECAST |
Вычисляет значение линейного тренда. |
| ЛИНЕЙН / LINEST |
Находит параметры линейного тренда. |
| ПИРСОН / PEARSON |
Определяет коэффициент корреляции Пирсона. |
Справочный файл по формулам Excel
Нужна шпаргалка по функциям Excel под рукой? Скачивайте файл: Математические и статистические формулы Excel
Полезные ссылки
|
|
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике:
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование proB
Функция Microsoft Excel.
Описание
Возвращает вероятность того, что значение из интервала находится внутри заданных пределов. Если верхний_предел не задан, то возвращается вероятность того, что значения в аргументе x_интервал равняются значению аргумента нижний_предел.
Синтаксис
ВЕРОЯТНОСТЬ(x_интервал;интервал_вероятностей;[нижний_предел];[верхний_предел])
Аргументы функции ВЕРОЯТНОСТЬ описаны ниже.
-
x_интервал Обязательный. Диапазон числовых значений x, с которыми связаны вероятности.
-
Интервал_вероятностей Обязательный. Множество вероятностей, соответствующих значениям в аргументе «x_интервал».
-
Нижний_предел Необязательный. Нижняя граница значения, для которого вычисляется вероятность.
-
Верхний_предел Необязательный. Верхняя граница значения, для которого вычисляется вероятность.
Замечания
-
Если значение в prob_range ≤ 0 или любое значение в prob_range > 1, функция PROB возвращает #NUM! (значение ошибки).
-
Если сумма значений в prob_range не равна 1, функция PROB возвращает #NUM! (значение ошибки).
-
Если верхний_предел опущен, то функция ВЕРОЯТНОСТЬ возвращает вероятность равенства значению аргумента нижний_предел.
-
Если x_интервал и интервал_вероятностей содержат различное количество точек данных, то функция ВЕРОЯТНОСТЬ возвращает значение ошибки #Н/Д.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Значение x |
Вероятность |
|
|
0 |
0,2 |
|
|
1 |
0,3 |
|
|
2 |
0,1 |
|
|
3 |
0,4 |
|
|
Формула |
Описание |
Результат |
|
=ВЕРОЯТНОСТЬ(A3:A6;B3:B6;2) |
Вероятность того, что x является числом 2. |
0,1 |
|
=ВЕРОЯТНОСТЬ(A3:A6;B3:B6;1;3) |
Вероятность того, что x находится в интервале от 1 до 3. |
0,8 |
Нужна дополнительная помощь?
17 авг. 2022 г.
читать 2 мин
Вероятность описывает вероятность того, что некоторое событие произойдет.
Мы можем рассчитать вероятности в Excel, используя функцию PROB , которая использует следующий синтаксис:
ПРОБ(x_диапазон, вероятностный_диапазон, нижний_предел, [верхний_предел])
куда:
- x_range: диапазон числовых значений x.
- prob_range: диапазон вероятностей, связанных с каждым значением x.
- нижний_предел: нижний предел значения, для которого вы хотите получить вероятность.
- upper_limit: Верхний предел значения, для которого вы хотите получить вероятность. По желанию.
В этом руководстве представлено несколько примеров использования этой функции на практике.
Пример 1: Вероятность игры в кости
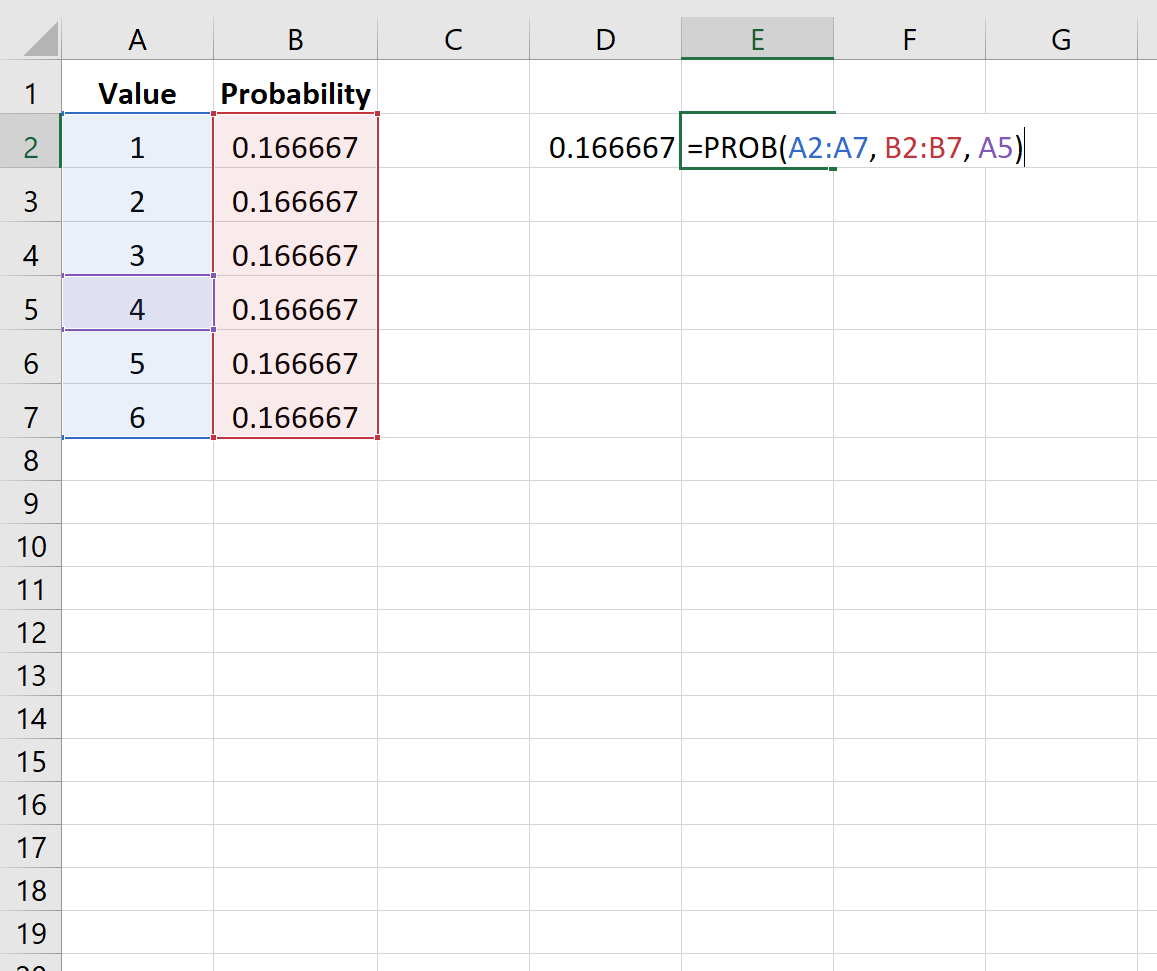
На следующем изображении показана вероятность выпадения кубика с определенным значением при данном броске:
Поскольку кости с одинаковой вероятностью выпадут на каждом значении, вероятность одинакова для каждого значения.
На следующем рисунке показано, как найти вероятность того, что кубик выпадет на число от 3 до 6:
Вероятность оказывается равной 0,5 .
Обратите внимание, что аргумент верхнего предела является необязательным. Таким образом, мы могли бы использовать следующий синтаксис, чтобы найти вероятность того, что кости приземлятся только на 4:
Вероятность оказывается равной 0,166667 .
Пример 2: Вероятность продаж
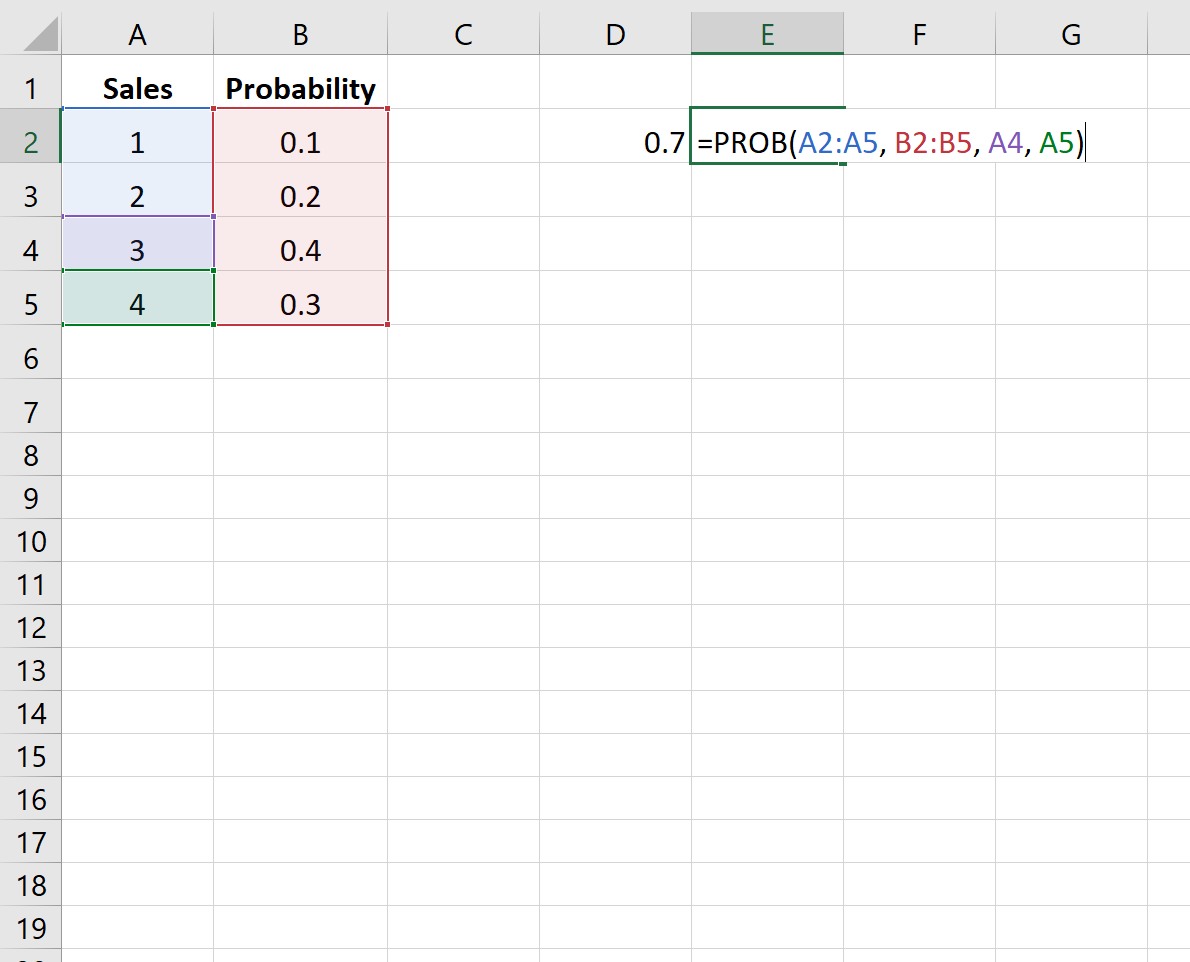
На следующем изображении показана вероятность того, что компания продаст определенное количество товаров в предстоящем квартале:
На следующем рисунке показано, как найти вероятность того, что компания совершит 3 или 4 продажи:
Вероятность оказывается равной 0,7 .
Дополнительные ресурсы
Как рассчитать относительную частоту в Excel
Как рассчитать кумулятивную частоту в Excel
Как создать частотное распределение в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Probability describes the likelihood that some event occurs.
We can calculate probabilities in Excel by using the PROB function, which uses the following syntax:
PROB(x_range, prob_range, lower_limit, [upper_limit])
where:
- x_range: The range of numeric x values.
- prob_range: The range of probabilities associated with each x value.
- lower_limit: The lower limit on the value for which you want a probability.
- upper_limit: The upper limit on the value for which you want a probability. Optional.
This tutorial provides several examples of how to use this function in practice.
Example 1: Dice Probabilities
The following image shows the probability of a dice landing on a certain value on a given roll:
Since the dice is equally likely to land on each value, the probability is the same for each value.
The following image shows how to find the probability that the dice lands on a number between 3 and 6:
The probability turns out to be 0.5.
Note that the upper limit argument is optional. So, we could use the following syntax to find the probability that the dice lands on just 4:
The probability turns out to be 0.166667.
Example 2: Sales Probabilities
The following image shows the probability of a company selling a certain number of products in the upcoming quarter:
The following image shows how to find the probability that the company makes either 3 or 4 sales:
The probability turns out to be 0.7.
Additional Resources
How to Calculate Relative Frequency in Excel
How to Calculate Cumulative Frequency in Excel
How to Create a Frequency Distribution in Excel
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта
www.excel2.ru
. Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL
.
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется
генеральная совокупность
(population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения
генеральная совокупность
представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является
случайной величиной
. По определению, любая
случайная величина
имеет
функцию распределения
, которая обычно обозначается F(x).
Функция распределения
Функцией распределения
вероятностей
случайной величины
Х называют функцию F(x), значение которой в точке х равно вероятности события X
F(x) = P(X
Поясним на примере нашего станка. Хотя предполагается, что наш станок производит только один тип деталей, но, очевидно, что вес изготовленных деталей будет слегка отличаться друг от друга. Это возможно из-за того, что при изготовлении мог быть использован разный материал, а условия обработки также могли слегка различаться и пр. Пусть самая тяжелая деталь, произведенная станком, весит 200 г, а самая легкая — 190 г. Вероятность того, что случайно выбранная деталь Х будет весить меньше 200 г равна 1. Вероятность того, что будет весить меньше 190 г равна 0. Промежуточные значения определяются формой Функции распределения. Например, если процесс настроен на изготовление деталей весом 195 г, то разумно предположить, что вероятность выбрать деталь легче 195 г равна 0,5.
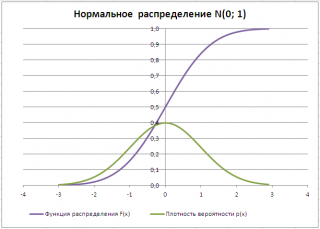
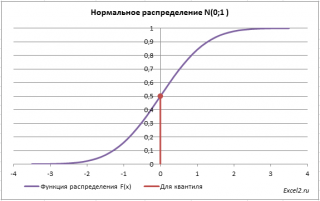
Типичный график
Функции распределения
для непрерывной случайной величины приведен на картинке ниже (фиолетовая кривая, см.
файл примера
):
В справке MS EXCEL
Функцию распределения
называют
Интегральной
функцией распределения
(
Cumulative
Distribution
Function
,
CDF
).
Приведем некоторые свойства
Функции распределения:
Функция распределения
F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
Функция распределения
– неубывающая функция;-
Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x
1
<=X
2)=F(x
2
)-F(x
1
).
Существует 2 типа распределений:
непрерывные распределения
и
дискретные распределения
.
Дискретные распределения
Если случайная величина может принимать только определенные значения и количество таких значений конечно, то соответствующее распределение называется
дискретным
. Например, при бросании монеты, имеется только 2 элементарных исхода, и, соответственно, случайная величина может принимать только 2 значения. Например, 0 (выпала решка) и 1 (не выпала решка) (см.
схему Бернулли
). Если монета симметричная, то вероятность каждого исхода равна 1/2. При бросании кубика случайная величина принимает значения от 1 до 6. Вероятность каждого исхода равна 1/6. Сумма вероятностей всех возможных значений случайной величины равна 1.
Примечание
: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье
Распределения случайной величины в MS EXCEL
.
Непрерывные распределения и плотность вероятности
В случае
непрерывного распределения
случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для
непрерывной случайной величины
равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой
функции плотности распределения p(x)
. Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение
функции распределения
на этом интервале:
Как видно из формулы выше
плотность распределения
р(х) представляет собой производную
функции распределения
F(x), т.е. р(х) = F’(x).
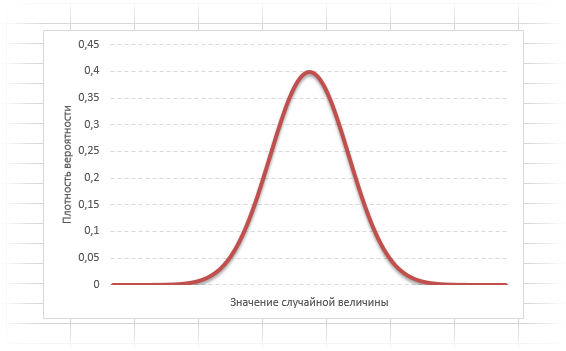
Типичный график
функции плотности распределения
для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):
Примечание
: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье
Распределения случайной величины в MS EXCEL
.
В литературе
Функция плотности распределения
непрерывной случайной величины может называться:
Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF)
.
Чтобы все усложнить, термин
Распределение
(в литературе на английском языке —
Probability
Distribution
Function
или просто
Distribution
)
в зависимости от контекста может относиться как
Интегральной
функции распределения,
так и кее
Плотности распределения.
Из определения
функции плотности распределения
следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от
Функции распределения,
больше 1. Например, для
непрерывной равномерной величины
, распределенной на интервале [0; 0,5]
плотность вероятности
равна 1/(0,5-0)=2. А для
экспоненциального распределения
с параметром
лямбда
=5, значение
плотности вероятности
в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Напомним, что
плотность распределения
является производной от
функции распределения
, т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что
плотность распределения
>1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере
экспоненциального распределения
).
Примечание
: Площадь, целиком заключенная под всей кривой, изображающей
плотность распределения
, равна 1.
Примечание
: Напомним, что функцию распределения F(x) называют в функциях MS EXCEL
интегральной функцией распределения
. Этот термин присутствует в параметрах функций, например в
НОРМ.РАСП
(x; среднее; стандартное_откл;
интегральная
). Если функция MS EXCEL должна вернуть
Функцию распределения,
то параметр
интегральная
, д.б. установлен ИСТИНА. Если требуется вычислить
плотность вероятности
, то параметр
интегральная
, д.б. ЛОЖЬ.
Примечание
: Для
дискретного распределения
вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL
плотность вероятности
может называть даже «функция вероятностной меры» (см. функцию
БИНОМ.РАСП()
).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить
плотность вероятности
для определенного значения случайной величины, нужно знать ее распределение.
Найдем
плотность вероятности
для
стандартного нормального распределения
N(0;1) при x=2. Для этого необходимо записать формулу
=НОРМ.СТ.РАСП(2;ЛОЖЬ)
=0,054 или
=НОРМ.РАСП(2;0;1;ЛОЖЬ)
.
Напомним, что
вероятность
того, что
непрерывная случайная величина
примет конкретное значение x равна 0. Для
непрерывной случайной величины
Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по
стандартному нормальному распределению
(см. картинку выше), приняла положительное значение. Согласно свойству
Функции распределения
вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу
=НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА)
=1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по
стандартному нормальному распределению
, приняла отрицательное значение. Согласно определения
Функции распределения,
вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу
=НОРМ.СТ.РАСП(0;ИСТИНА)
=0,5.
3) Найдем вероятность того, что случайная величина, распределенная по
стандартному нормальному распределению
, примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу
=НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА)
.
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по
стандартному нормальному закону
N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье
Распределения случайной величины в MS EXCEL
приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела:
Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение
медиану
или 50-ю
процентиль
).
Для этого необходимо на графике
функции распределения
найти точку, для которой F(х)=0,5, а затем найти абсциссу этой точки. Абсцисса точки =0, т.е. вероятность, того что случайная величина Х примет значение <0, равна 0,5.
В MS EXCEL используйте формулу
=НОРМ.СТ.ОБР(0,5)
=0.
Однозначно вычислить значение
случайной величины
позволяет свойство монотонности
функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно
функцию распределения
, а не
плотность распределения
. Поэтому, в аргументах функции
НОРМ.СТ.ОБР()
отсутствует параметр
интегральная
, который подразумевается. Подробнее про функцию
НОРМ.СТ.ОБР()
см. статью про
нормальное распределение
.
Обратная функция распределения
вычисляет
квантили распределения
, которые используются, например, при
построении доверительных интервалов
. Т.е. в нашем случае число 0 является 0,5-квантилем
нормального распределения
. В
файле примера
можно вычислить и другой
квантиль
этого распределения. Например, 0,8-квантиль равен 0,84.
В англоязычной литературе
обратная функция распределения
часто называется как Percent Point Function (PPF).
Примечание
: При вычислении
квантилей
в MS EXCEL используются функции:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР(),
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Комбинаторика и вероятность
Ниже вы найдете основные формулы Excel, которые могут применяться при решении вероятностных задач и задач по комбинаторике.
ФАКТР / FACT
СЛЧИС / RAND
Выдает случайное число в интервале от 0 до 1 (равномерно распределенное).
СЛУЧМЕЖДУ / RANDBETVEEN
Выдает случайное число в заданном интервале.
БИНОМРАСП / BINOMDIST
Вычисляет отдельное значение биномиального распределения.
ГИПЕРГЕОМЕТ / HYRGEOMDIST
Определяет гипергеометрическое распределение.
НОРМРАСП / NORMDIST
Вычисляет значение нормальной функции распределения.
НОРМОБР / NORMINV
Выдает обратное нормальное распределение.
НОРМСТРАСП / NORMSDIST
Выдает стандартное нормальное интегральное распределение.
НОРМСТОБР / NORMSINV
Выдает обратное значение стандартного нормального распределения.
ПЕРЕСТ / PERMUT
ВЕРОЯТНОСТЬ / PROB
Определяет вероятность того, что значение из диапазона находится внутри заданных пределов.
Математическая статистика
При решении задач по математической статистике можно использовать те формулы, что перечислены выше, а также следующие (сгруппированы для удобства: обработка выборки, разные распределения, остальные формулы):
Обработка выборки: формулы Excel
СРОТКЛ / AVEDEV
Вычисляет среднее абсолютных значений отклонений точек данных от среднего.
СРЗНАЧ / AVERAGE
Вычисляет среднее арифметическое аргументов.
СРГЕОМ / GEOMEAN
Вычисляет среднее геометрическое.
СРГАРМ / HARMEAN
Вычисляет среднее гармоническое.
ЭКСЦЕСС / KURT
Определяет эксцесс множества данных.
МЕДИАНА / MEDIAN
Находит медиану заданных чисел.
МОДА / MODE
Определяет значение моды множества данных.
КВАРТИЛЬ / QUARTILE
Определяет квартиль множества данных.
СКОС / SKEW
Определяет асимметрию распределения.
СТАНДОТКЛОН / STDEV
Оценивает стандартное отклонение по выборке.
ДИСП / VAR
Оценивает дисперсию по выборке.
Законы распределений: формулы Excel
БЕТАРАСП / BETADIST
Определяет интегральную функцию плотности бета-вероятности.
БЕТАОБР / BETAINV
Определяет обратную функцию к интегральной функции плотности бета-вероятности.
ХИ2РАСП / CHIDIST
Вычисляет одностороннюю вероятность распределения хи-квадрат.
ХИ2ОБР / CHIINV
Вычисляет обратное значение односторонней вероятности распределения хи-квадрат.
ЭКСПРАСП / EXPONDIST
Находит экспоненциальное распределение.
FРАСП / FDIST
Находит F-распределение вероятности.
FРАСПОБР / FINV
Определяет обратное значение для F-распределения вероятности.
ФИШЕР / FISHER
Находит преобразование Фишера.
ФИШЕРОБР / FISHERINV
Находит обратное преобразование Фишера.
ГАММАРАСП / GAMMADIST
ГАММАОБР / GAMMAINV
Находит обратное гамма-распределение.
ПУАССОН / POISSON
Выдает распределение Пуассона.
СТЬЮДРАСП / TDIST
Выдает t-распределение Стьюдента.
СТЬЮДРАСПОБР / TINV
Выдает обратное t-распределение Стьюдента.
ВЕЙБУЛЛ / WEIBULL
Выдает распределение Вейбулла.
Другое (корреляция, регрессия и т.п.)
ДОВЕРИТ / CONFIDENCE
Определяет доверительный интервал для среднего значения по генеральной совокупности.
КОРРЕЛ / CORREL
Находит коэффициент корреляции между двумя множествами данных.
СЧЁТ / COUNT
Подсчитывает количество чисел в списке аргументов.
СЧЁТЕСЛИ / COUNTIF
Подсчитывает количество непустых ячеек, удовлетворяющих заданному условию внутри диапазона.
КОВАР / COVAR
Определяет ковариацию, то есть среднее произведений отклонений для каждой пары точек.
ПРЕДСКАЗ / FORECAST
Вычисляет значение линейного тренда.
ЛИНЕЙН / LINEST
Находит параметры линейного тренда.
ПИРСОН / PEARSON
Определяет коэффициент корреляции Пирсона.
Справочный файл по формулам Excel
Нужна шпаргалка по функциям Excel под рукой? Скачивайте файл: Математические и статистические формулы Excel
Полезные ссылки
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике:
Пример 4.В партии 20 изделий, из них 5 бракованных. Найти вероятность того, что в выборке из 4 изделий ровно одно бракованное.
Решение. В данной задаче, прежде всего, определим значения параметров: число_успехов_ в_ выборке = 1; размер_ выборки = 4; число_ успехов_ в_ совокупности = 5; размер_ совокупности = 20.
Искомую вероятность можно рассчитать с помощью функции =ГИПЕРГЕОМЕТ(1; 4; 5; 20), которая дает значение 0,4696.
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно событияА.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 – р.
Вероятность того, что при n повторных независимых испытаниях событие А осуществится ровно k раз вычисляется по формуле Бернулли: 
Для нахождения наиболее вероятного числа успехов k по заданным n и р можно воспользоваться неравенствами np – q £ k£ np + p или правилом: если число np + p не целое, то k равно целой части этого числа.
В случае, если n велико, р мало, а 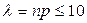

Пример 5. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии на протяжении каждых из 6 суток постоянна и равна p = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1— р = 1 — 0,75 = 0,25. Искомая вероятность по формуле Бернулли равна 
Пример 6. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность, что в течение часа ровно 5 абонентов позвонят на станцию.
Решение.Так как р = 0,01 мало и n = 400 велико, то будем пользоваться приближенной формулой Пуассона при l = 400 × 0,01 = 4. Тогда Р400(5) » 
В случае, когда число повторных испытаний большое и формула Бернулли неприменима, используют формулы Лапласа.
Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 


Имеются таблицы, в которых помещены значения функции 
Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 


При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами для интеграла 

Пример 7. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение. По условию n = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа: 


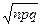

Пример 8. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение.Воспользуемся интегральной формулой Лапласа: n = 400; k1= 70; k2=100; р = 0,2; q = 0,8; 

Для вычисления в Excel используем формулу нормального распределения =НОРМРАСП(100; 80; 8; 1) — НОРМРАСП(70; 80; 8; 1), которая дает значение 0,8882. При этом параметр интегральная = 1, остальные значения параметров определяются аналогично примеру, рассмотренному выше.
В этой статье описаны синтаксис формулы и использование функции ВЕРОЯТНОСТЬ в Microsoft Excel.
Описание
Возвращает вероятность того, что значение из интервала находится внутри заданных пределов. Если верхний_предел не задан, то возвращается вероятность того, что значения в аргументе x_интервал равняются значению аргумента нижний_предел.
Синтаксис
Аргументы функции ВЕРОЯТНОСТЬ описаны ниже.
x_интервал Обязательный. Диапазон числовых значений x, с которыми связаны вероятности.
Интервал_вероятностей Обязательный. Множество вероятностей, соответствующих значениям в аргументе «x_интервал».
Нижний_предел Необязательный. Нижняя граница значения, для которого вычисляется вероятность.
Верхний_предел Необязательный. Верхняя граница значения, для которого вычисляется вероятность.
Замечания
Если любое значение в аргументе интервал_вероятностей меньше 0 или если какое-либо значение в аргументе интервал_вероятностей больше 1, то функция ВЕРОЯТНОСТЬ возвращает значение ошибки #ЧИСЛО!.
Если сумма значений в аргументе интервал_вероятностей не равна 1, функция ВЕРОЯТНОСТЬ возвращает значение ошибки #ЧИСЛО!.
Если верхний_предел опущен, то функция ВЕРОЯТНОСТЬ возвращает вероятность равенства значению аргумента нижний_предел.
Если x_интервал и интервал_вероятностей содержат различное количество точек данных, то функция ВЕРОЯТНОСТЬ возвращает значение ошибки #Н/Д.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
В этой статье объясняется, как можно рассчитать вероятность в Excel с помощью функции ВЕРОЯТНОСТЬ с несколькими примерами.
Вероятность — это математическая мера, которая определяет вероятные шансы на то, что событие (или набор событий) произойдет в ситуации. Другими словами, это просто вероятность того, что что-то произойдет. Вероятность события измеряется путем сравнения количества благоприятных событий с общим количеством возможных исходов.
Например, когда мы подбрасываем монету, шанс получить «голову» составляет половину (50%), как и вероятность получить «хвост». Потому что общее количество возможных исходов равно 2 (голова или хвост). Предположим, в вашем местном сводке погоды говорится, что вероятность дождя составляет 80%, затем, вероятно, пойдет дождь.
Существует множество приложений вероятности в повседневной жизни, таких как спорт, прогноз погоды, опросы, карточные игры, прогнозирование пола ребенка в утробе матери, статика и многое другое.
Вычисление вероятности может показаться сложным процессом, но MS Excel предоставляет встроенную формулу для простого вычисления вероятности с помощью функции ВЕРОЯТНОСТЬ. Давайте посмотрим, как найти вероятность в Excel.
Рассчитайте вероятность с помощью функции ВЕРОЯТНОСТЬ
Обычно вероятность рассчитывается путем деления количества благоприятных событий на общее количество возможных исходов. В Excel вы можете использовать функцию ВЕРОЯТНОСТЬ для измерения вероятности события или диапазона событий.
Функция ВЕРОЯТНОСТЬ — это одна из статистических функций в Excel, которая вычисляет вероятность того, что значения из диапазона находятся в указанных пределах. Синтаксис функции ВЕРОЯТНОСТЬ следующий:
= PROB(x_range, prob_range, [lower_limit], [upper_limit])куда,
- x_range: это диапазон числовых значений, который показывает различные события. Значения x связаны с вероятностями.
- prob_range: это диапазон вероятностей для каждого соответствующего значения в массиве x_range, и значения в этом диапазоне должны составлять до 1 (если они указаны в процентах, должны складываться до 100%).
- lower_limit (необязательно): это нижнее предельное значение события, для которого вы хотите получить вероятность.
- upper_limit (необязательно) : это верхнее предельное значение события, для которого вы хотите получить вероятность. Если этот аргумент игнорируется, функция возвращает вероятность, связанную со значением lower_limit.
Пример вероятности 1
Давайте узнаем, как использовать функцию ВЕРОЯТНОСТЬ на примере.
Прежде чем приступить к расчету вероятности в Excel, следует подготовить данные для расчета. Вы должны ввести дату в таблицу вероятностей с двумя столбцами. Диапазон числовых значений следует ввести в один столбец, а соответствующие вероятности — в другой столбец, как показано ниже. Сумма всех вероятностей в столбце B должна быть равна 1 (или 100%).
После ввода числовых значений (продажи билетов) и их вероятностей их получения вы можете использовать функцию СУММ, чтобы проверить, составляет ли сумма всех вероятностей в сумме «1» или 100%. Если общее значение вероятностей не равно 100%, функция ВЕРОЯТНОСТЬ вернет # ЧИСЛО! ошибка.
Допустим, мы хотим определить вероятность того, что продажи билетов находятся в диапазоне от 40 до 90. Затем введите данные верхнего и нижнего пределов в таблицу, как показано ниже. Нижний предел установлен на 40, а верхний предел установлен на 90.
Чтобы рассчитать вероятность для данного диапазона, введите следующую формулу в ячейку B14:
=PROB(A3:A9,B3:B9,B12,B13)Где A3: A9 — это диапазон событий (продаж билетов) в числовых значениях, B3: B9 содержит вероятность получения соответствующего количества продаж из столбца A, B12 — это нижний предел, а B13 — верхний предел. В результате формула возвращает значение вероятности 0,39 в ячейке B14.
Затем щелкните значок «%» в группе «Число» на вкладке «Главная», как показано ниже. И вы получите «39%», что является вероятностью продажи билетов от 40 до 90.
Расчет вероятности без верхнего предела
Если верхний предел (последний) аргумент не указан, функция ВЕРОЯТНОСТЬ возвращает вероятность, равную значению lower_limit.
В приведенном ниже примере аргумент upper_limit (последний) опущен в формуле, формула возвращает «0,12» в ячейке B14. Результат равен «B5» в таблице.
Когда мы переведем его в процент, мы получим «12%».
Пример 2: Вероятности игры в кости
Давайте посмотрим, как рассчитать вероятность на более сложном примере. Предположим, у вас есть два кубика, и вы хотите найти вероятность выпадения суммы при броске двух кубиков.
В таблице ниже показана вероятность того, что каждый кубик выпадет на определенное значение при конкретном броске:
Когда вы бросаете два кубика, вы получаете сумму чисел от 2 до 12. Цифры в красном — это сумма двух чисел на кубиках. Значение в C3 равно сумме C2 и B3, C4 = C2 + B4 и так далее.
Вероятность выпадения 2 возможна только тогда, когда мы получаем 1 на обоих кубиках (1 + 1), поэтому шанс = 1. Теперь нам нужно рассчитать шансы на выпадение с помощью функции СЧЁТЕСЛИ.
Нам нужно создать другую таблицу с суммой бросков в одном столбце и их шансом получить это число в другом столбце. Нам нужно ввести приведенную ниже формулу шанса броска в ячейку C11:
=COUNTIF($C$3:$H$8,B11)Функция СЧЁТЕСЛИ подсчитывает количество шансов на общее количество бросков. Здесь указан диапазон $ C $ 3: $ H $ 8 и критерий B11. Диапазон делается абсолютной ссылкой, поэтому он не корректируется, когда мы копируем формулу.
Затем скопируйте формулу из C11 в другие ячейки, перетащив ее в ячейку C21.
Теперь нам нужно вычислить индивидуальные вероятности суммы чисел, выпавших на барабанах. Для этого нам нужно разделить значение каждого шанса на общее значение шансов, которое составляет 36 (6 x 6 = 36 возможных бросков). Используйте приведенную ниже формулу, чтобы найти индивидуальные вероятности:
=B11/36Затем скопируйте формулу в остальные ячейки.
Как видите, у 7 наибольшая вероятность выпадения.
Теперь предположим, что вы хотите найти вероятность получения бросков выше 9. Для этого вы можете использовать приведенную ниже функцию ВЕРОЯТНОСТЬ:
=PROB(B11:B21,D11:D21,10,12)Здесь B11: B21 — диапазон событий, D11: D21 — связанные вероятности, 10 — нижний предел, а 12 — верхний предел. Функция возвращает 0,17 в ячейке G14.
Как видите, вероятность выпадения двух кубиков при сумме бросков больше 9 составляет 0,17 или 17%.
Вы также можете рассчитать вероятность без функции ВЕРОЯТНОСТЬ, используя простой арифметический расчет.
Как правило, вы можете найти вероятность наступления события, используя эту формулу:
P(E) = n(E)/n(S)Где,
- n (E) = количество появлений события.
- n (S) = Общее количество возможных результатов.
Например, предположим, что у вас есть два мешка, заполненные шарами: «Мешок А» и «Мешок Б». В сумке A 5 зеленых, 3 белых, 8 красных и 4 желтых шара. В мешке B 3 зеленых шара, 2 белых шара, 6 красных и 4 желтых шара.
Какова вероятность того, что два человека одновременно выберут 1 зеленый шар из мешка A и 1 красный шар из мешка B? Вот как это вычислить:
Чтобы определить вероятность подобрать зеленый шар из мешка A, используйте эту формулу:
=B2/20Где B2 — количество красных шаров (5), деленное на общее количество шаров (20). Затем скопируйте формулу в другие ячейки. Теперь у вас есть индивидуальные вероятности подобрать каждый цветной шар из мешка A.
Используйте приведенную ниже формулу, чтобы найти индивидуальные вероятности попадания шаров в мешок B:
=F2/15Здесь вероятность конвертируется в проценты.
Вероятность собрать зеленый шар из мешка A и красный шар из мешка B вместе:
=(probability of picking a green ball from bag A) x (probability of picking a red ball from bag B)=C2*G3Как видите, вероятность вытащить зеленый шар из мешка A и красный шар из мешка B одновременно составляет 3,3%.
Вот и все.
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
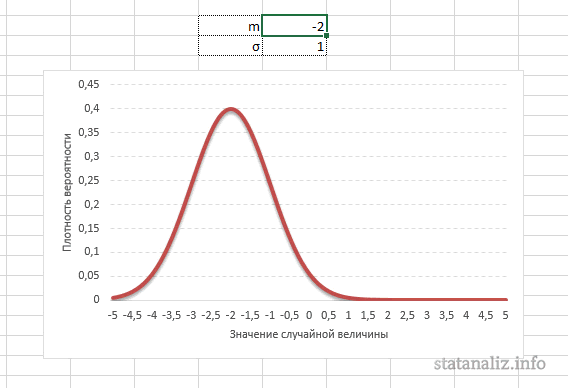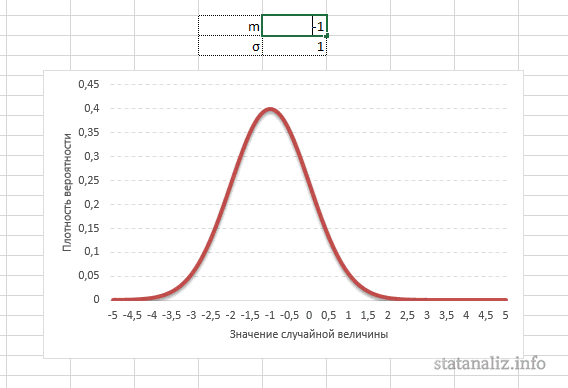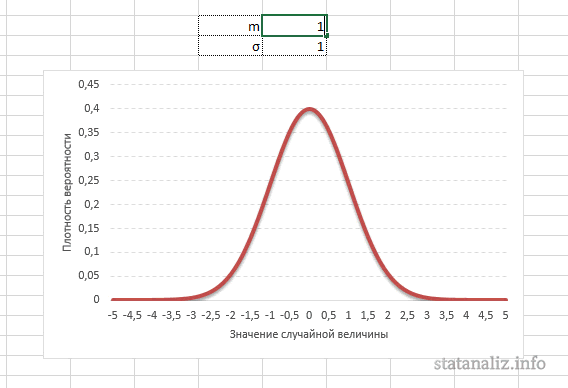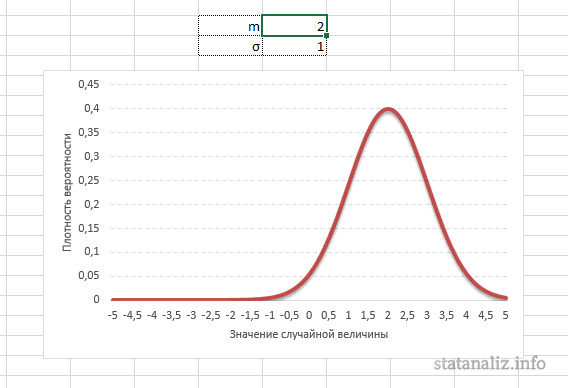
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
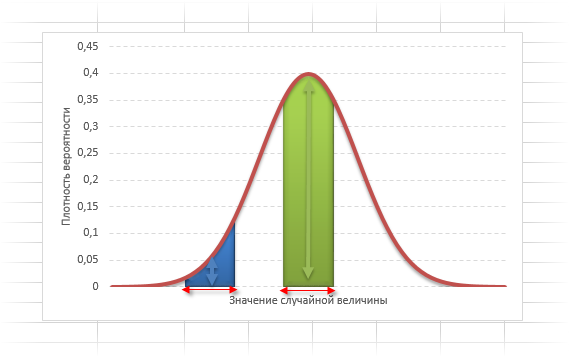
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
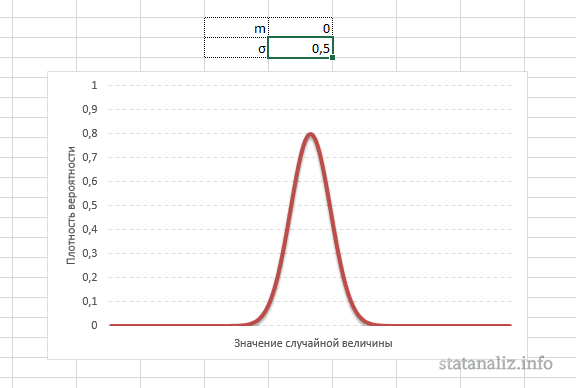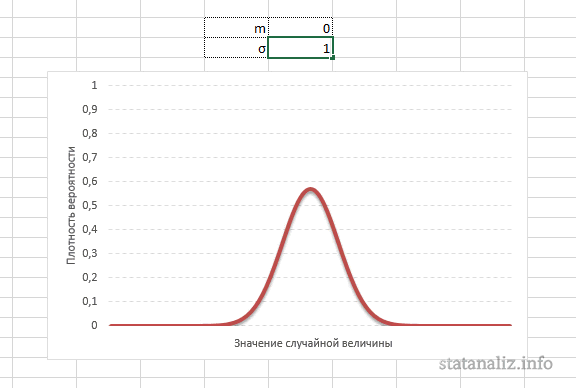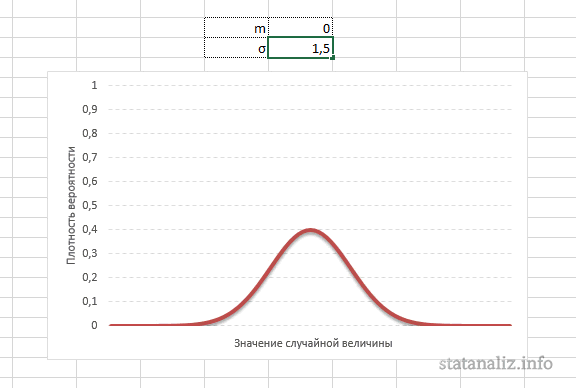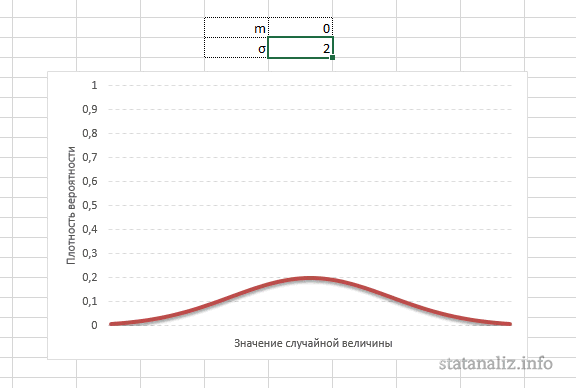
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
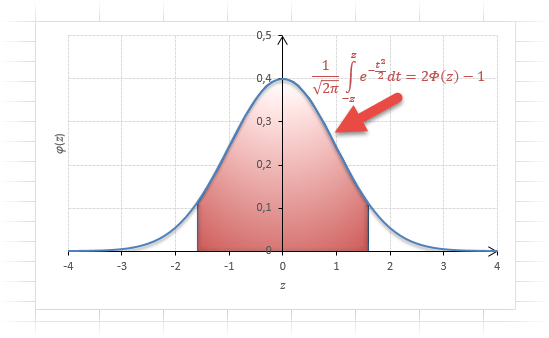
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
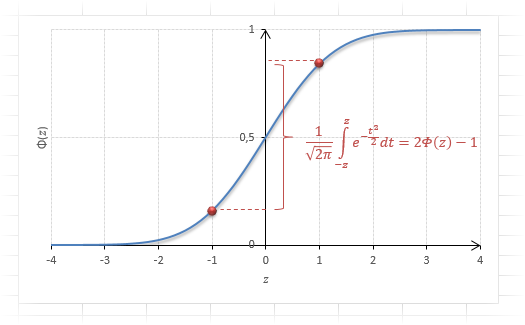
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
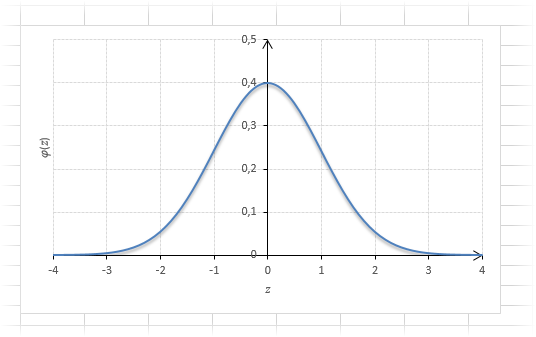
График плотности:
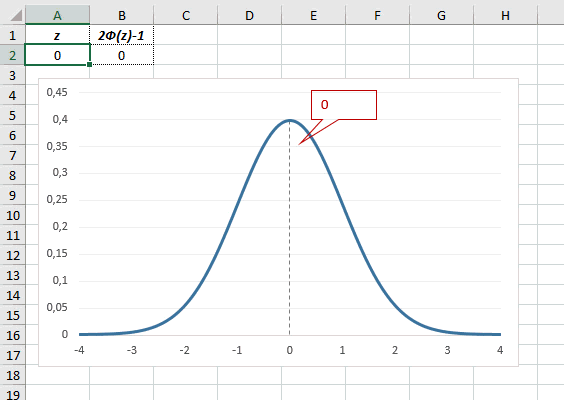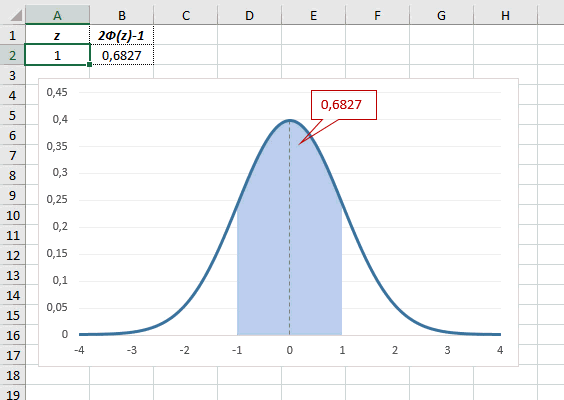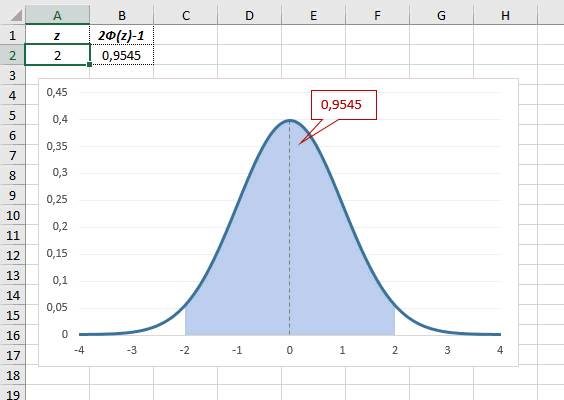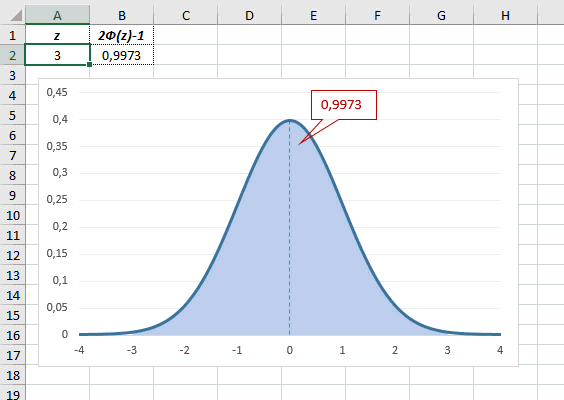
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
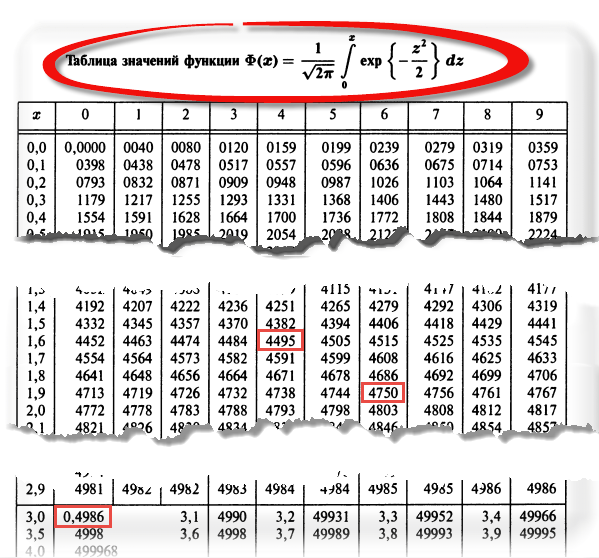
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
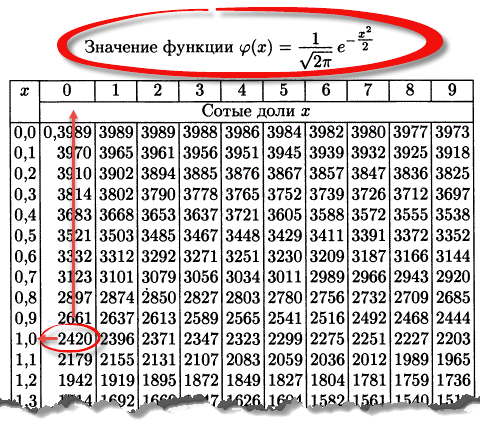
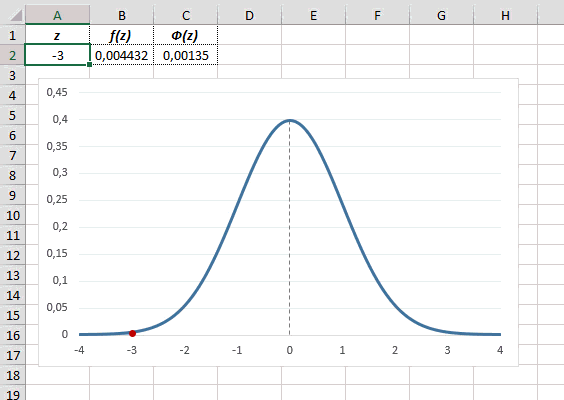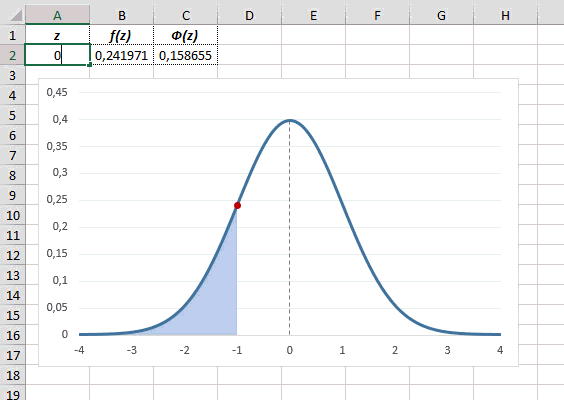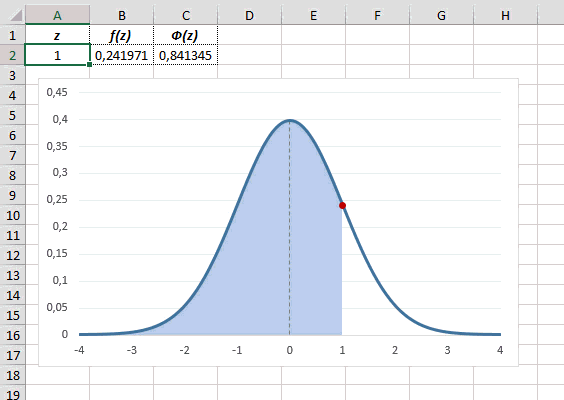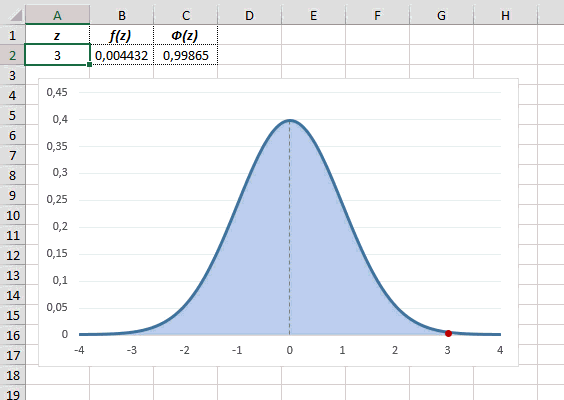
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
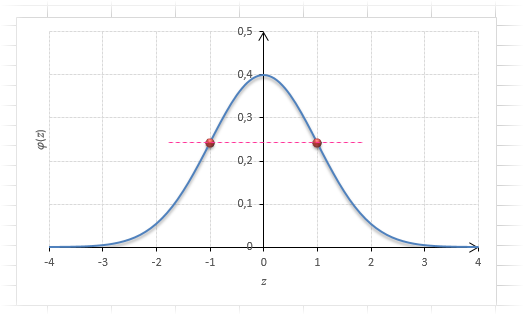
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
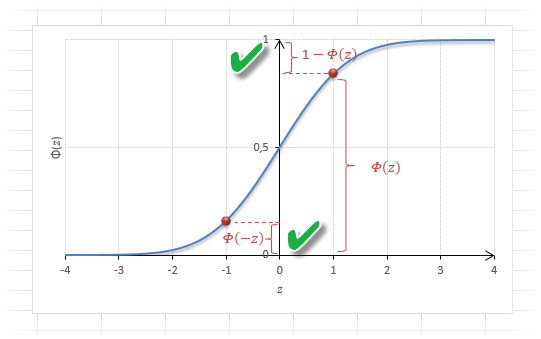
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
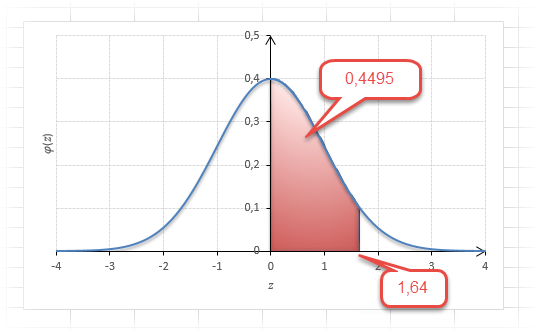
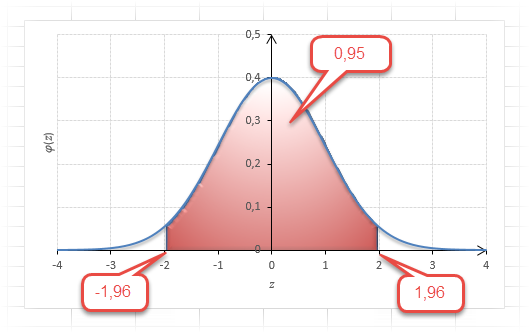
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
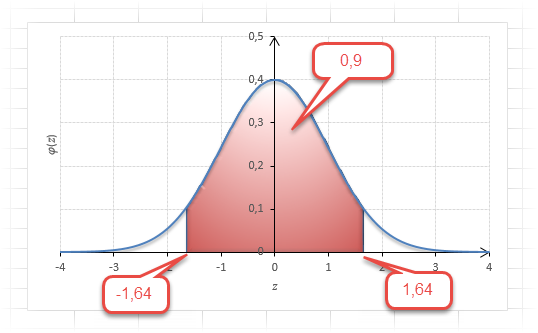
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
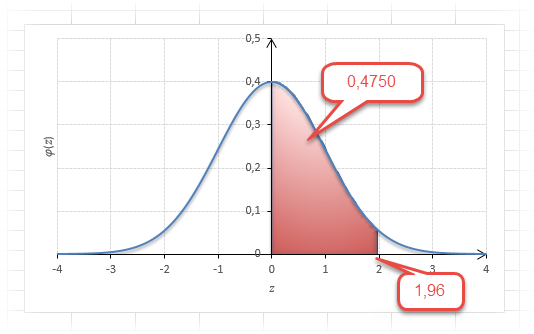
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
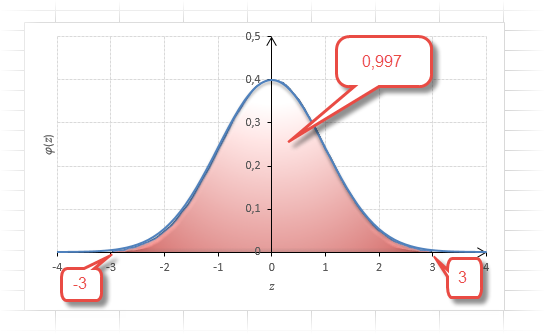
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
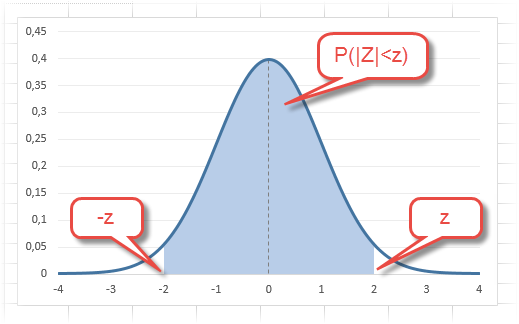
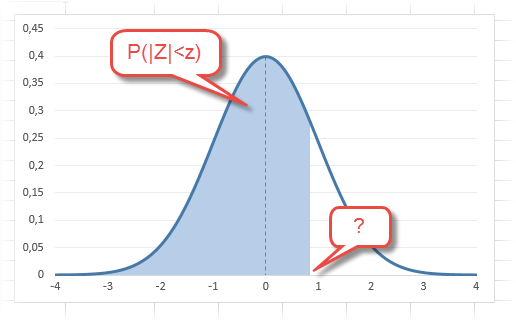
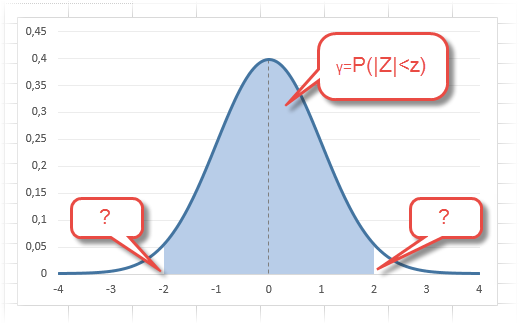
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
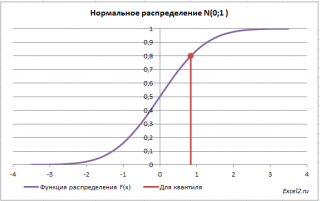
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
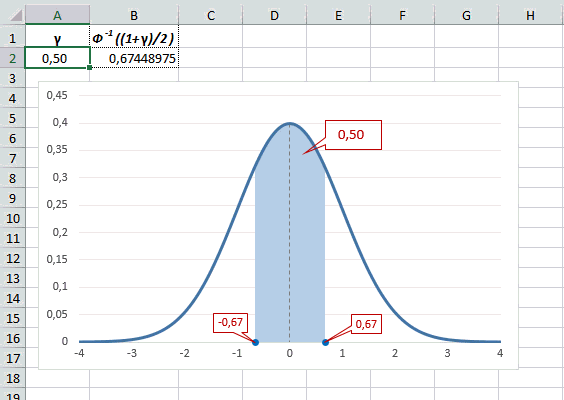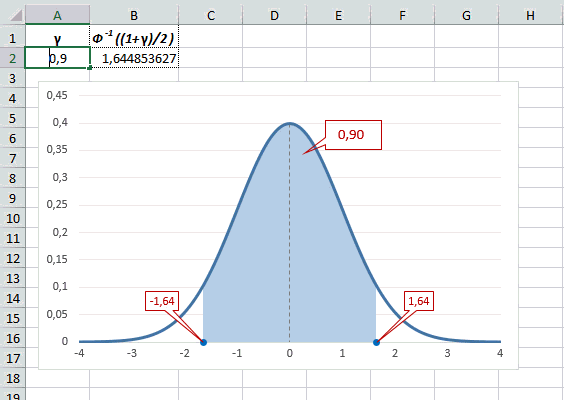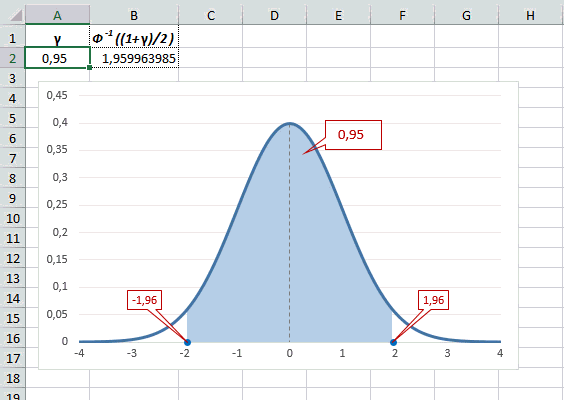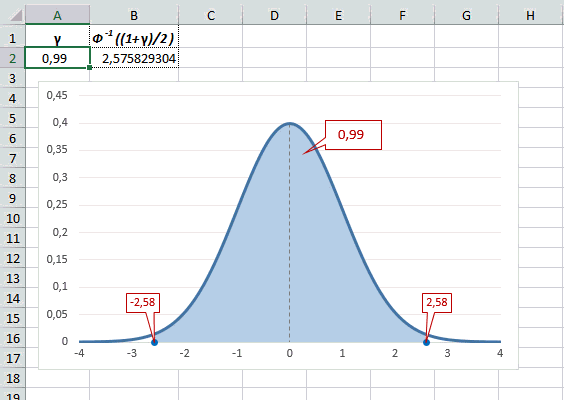
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
Функция НОРМ.РАСП
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
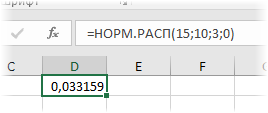
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
Моделирование нормального распределения
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
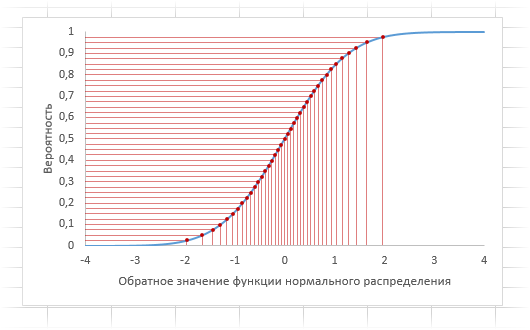
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.
На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.
Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.
Скачать файл с примером.
Поделиться в социальных сетях: