Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
- в виде схемы;
- в виде матрицы.
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
- открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
- закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
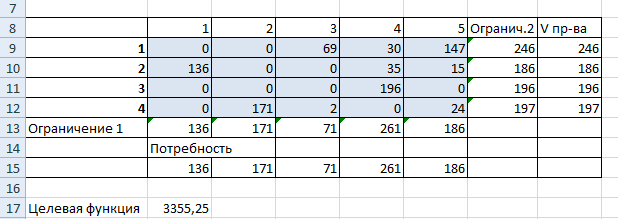
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
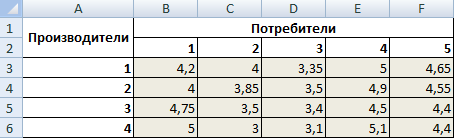
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 |
Задача: минимизировать транспортные расходы по перевозке продукции.
- Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
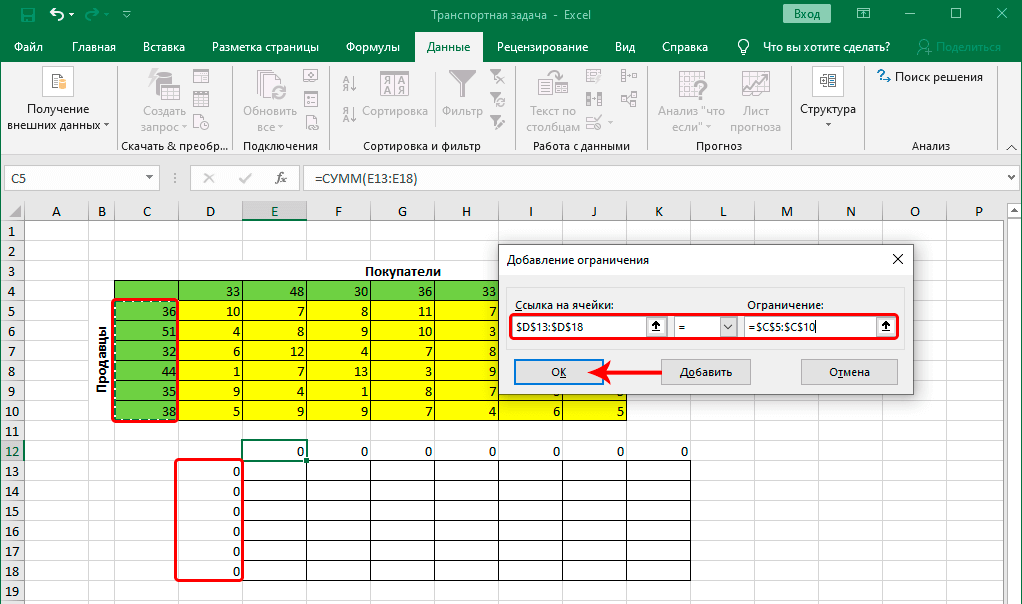
- Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
- Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
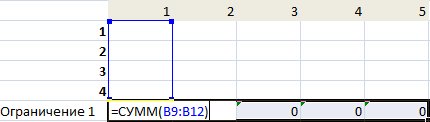
- Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
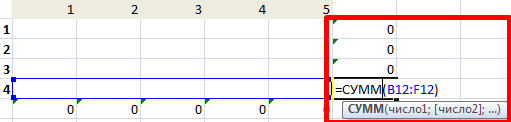
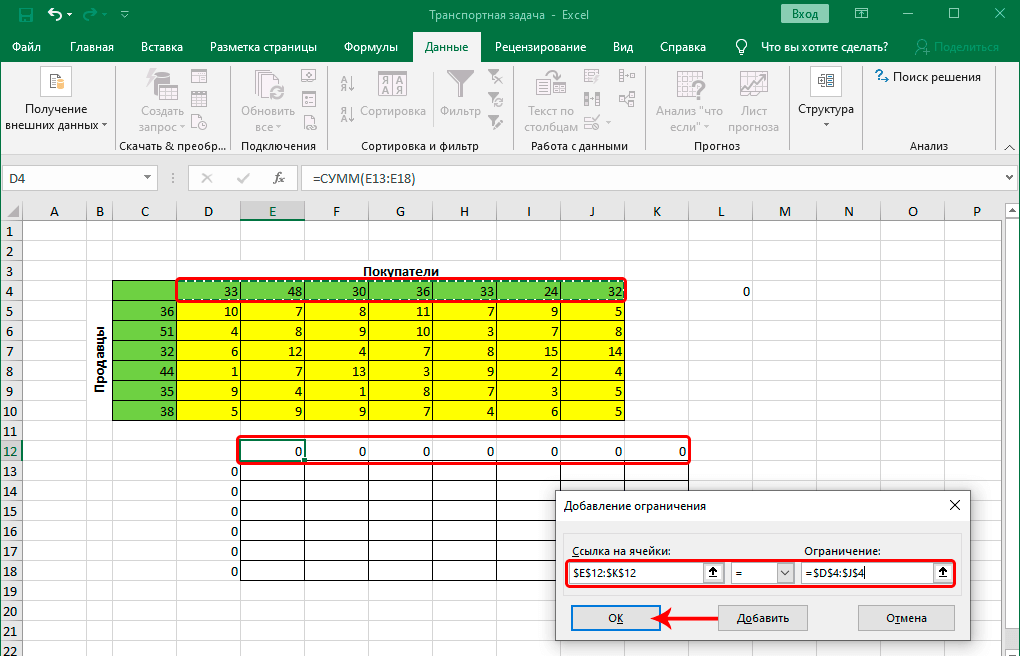
- Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
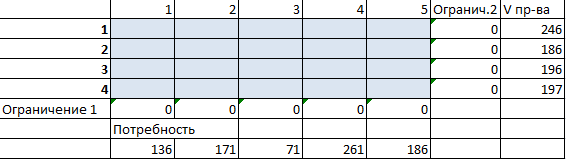
- Вносим известные значения потребности в товаре и объема производства.
- Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
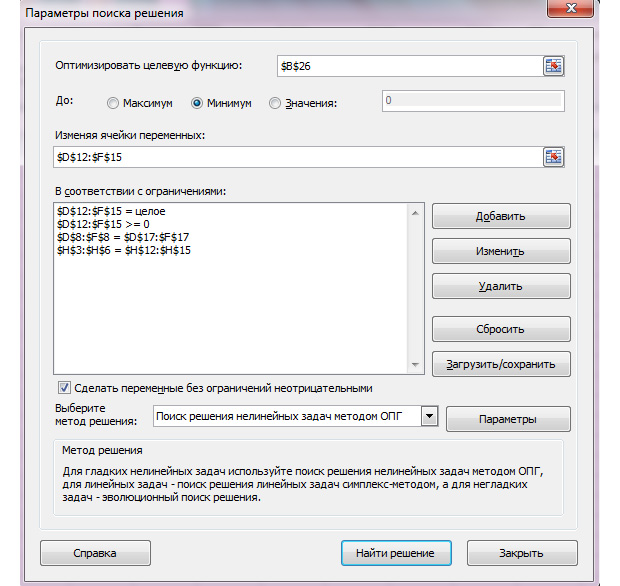
- Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
- Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.
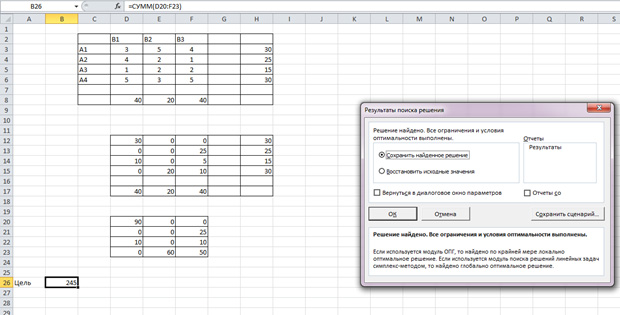
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
- суммарный объем производства превышает суммарную потребность в товаре;
- суммарная потребность больше суммы запасов.
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Читайте также по теме: решение транспортной задачи методом потенциалов в Excel.
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Содержание
- Транспортная задача: описание
- Подготовительный этап: включение функции “Поиск решения”
- Пример задачи и ее решение
- Условия
- Алгоритм решения
- Заключение
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
- Закрытая – совокупное предложение продавца равняется общему спросу.
- Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
- Открываем меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
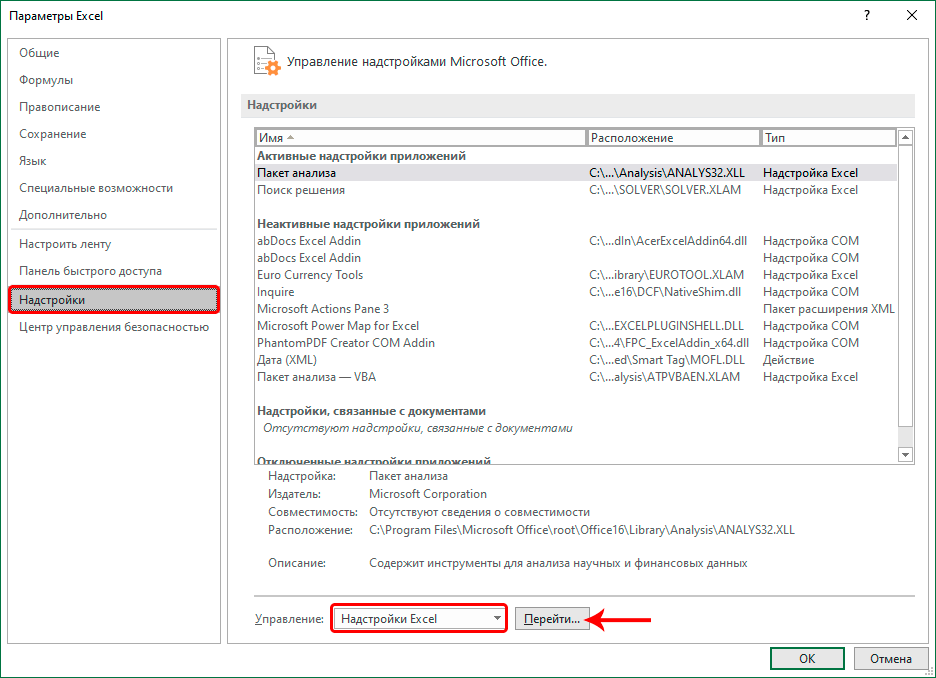
- В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
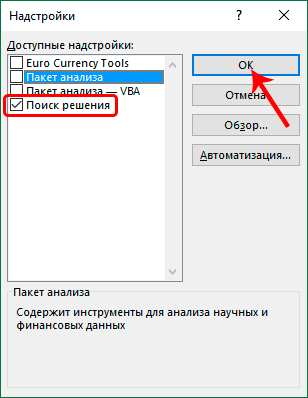
- В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
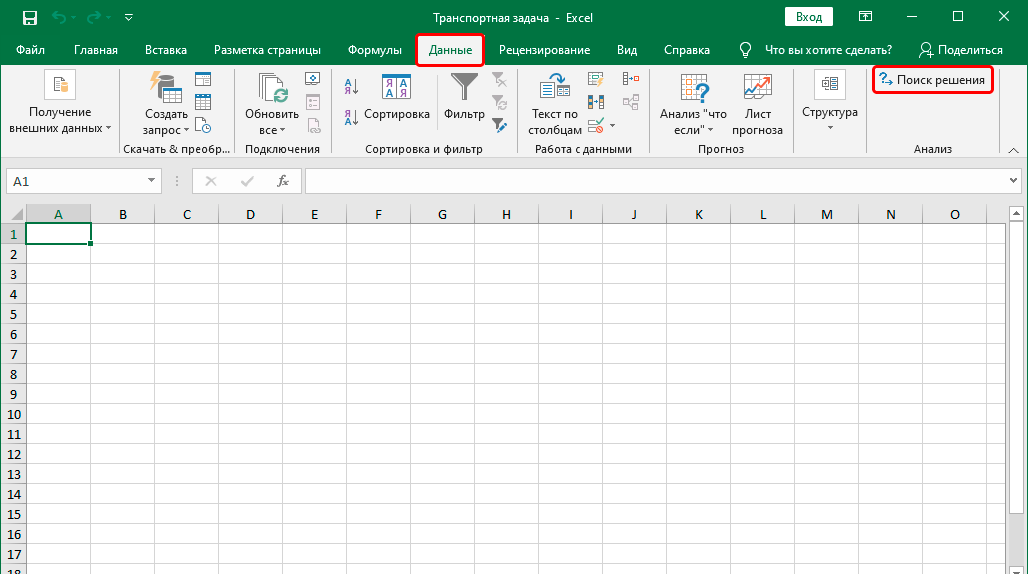
- В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
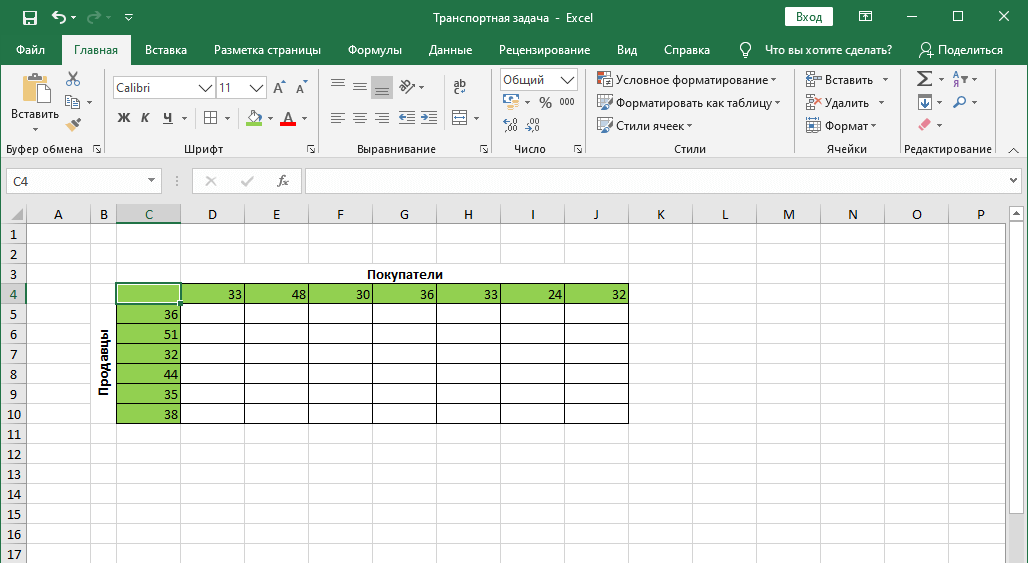
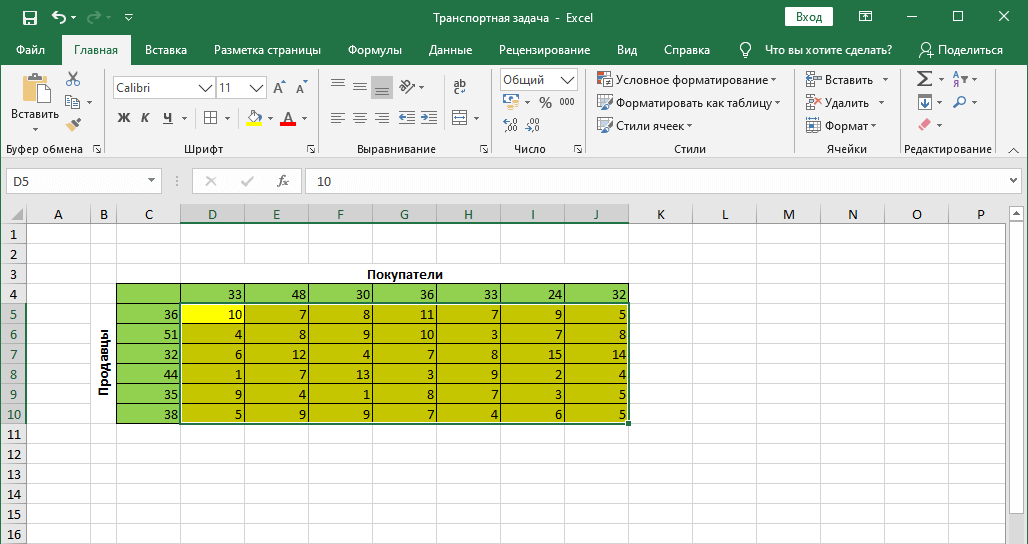
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
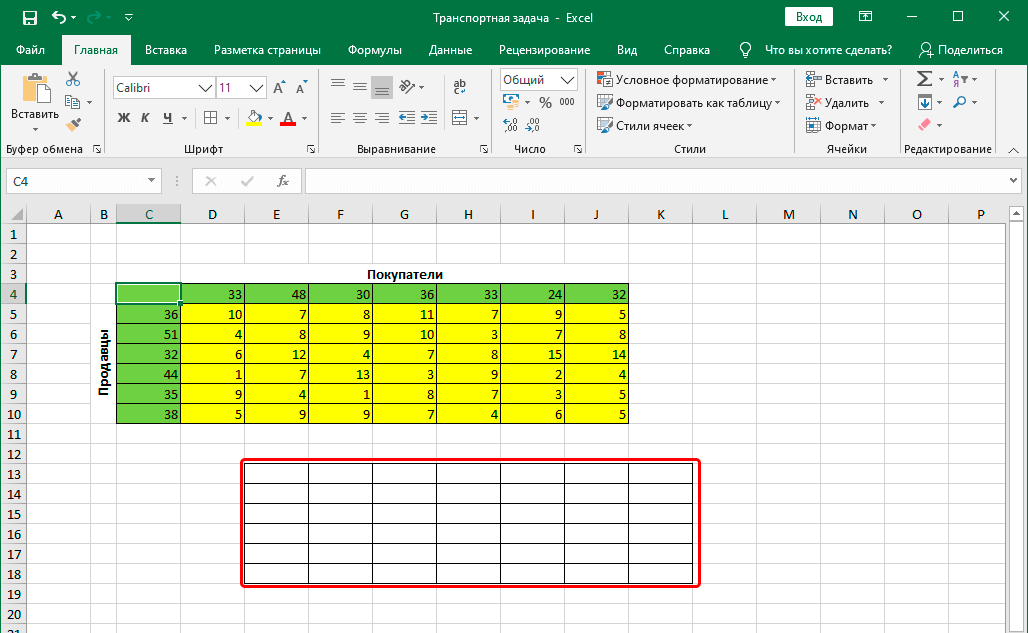
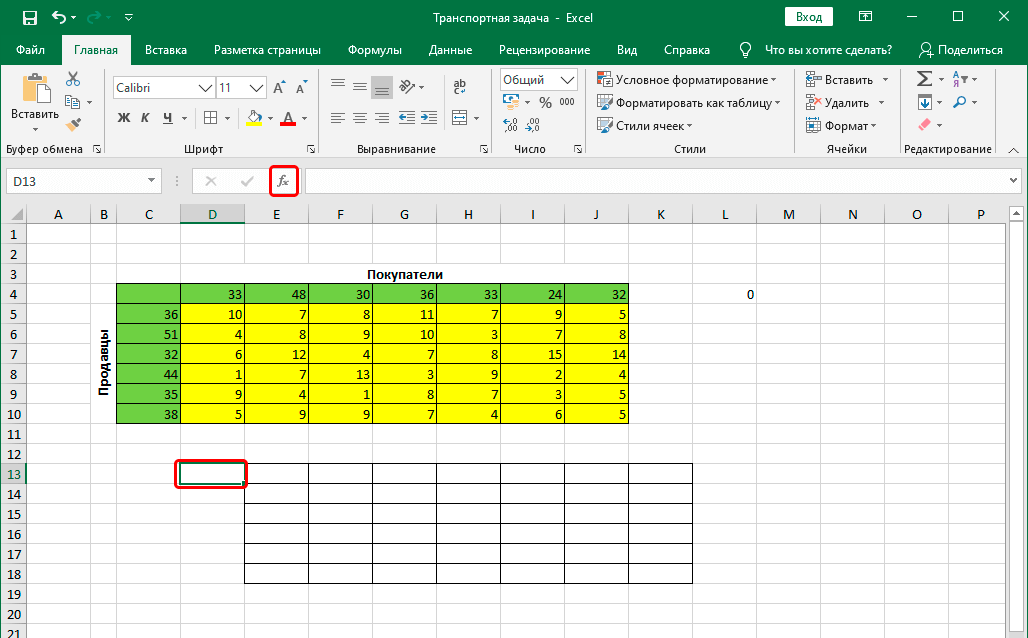
- Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
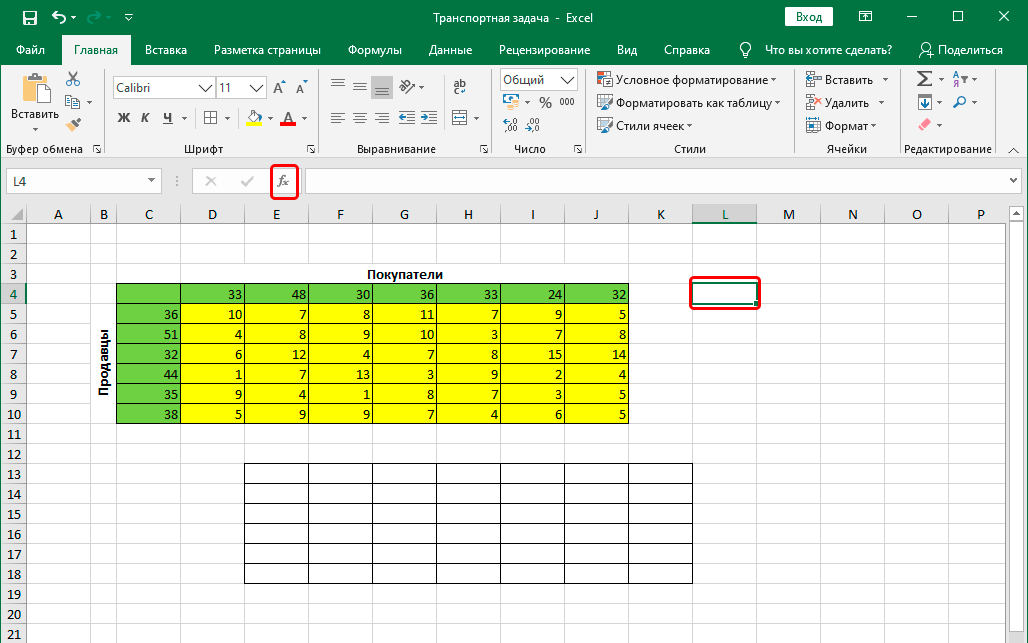
- Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
- В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
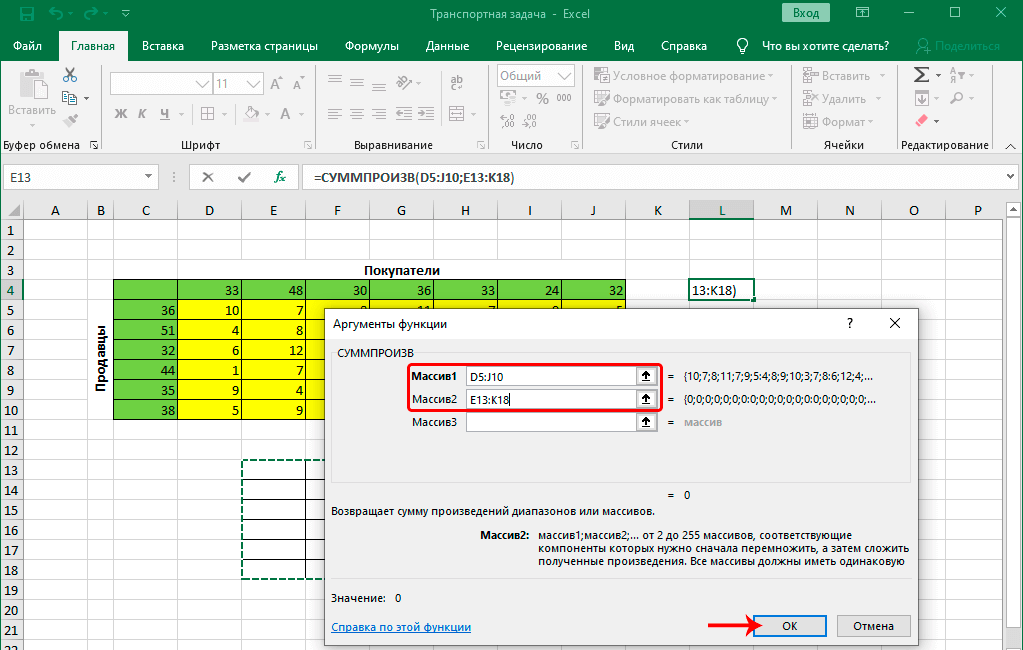
- На экране отобразится окно, в котором нужно заполнить аргументы:
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
- по готовности жмем OK.
- Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
- На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
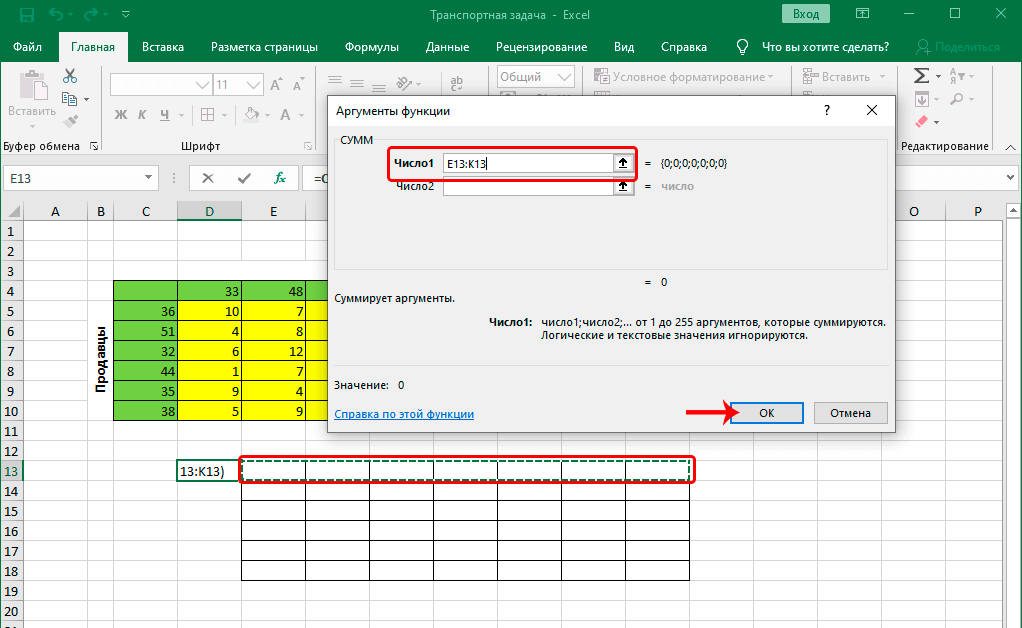
- Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
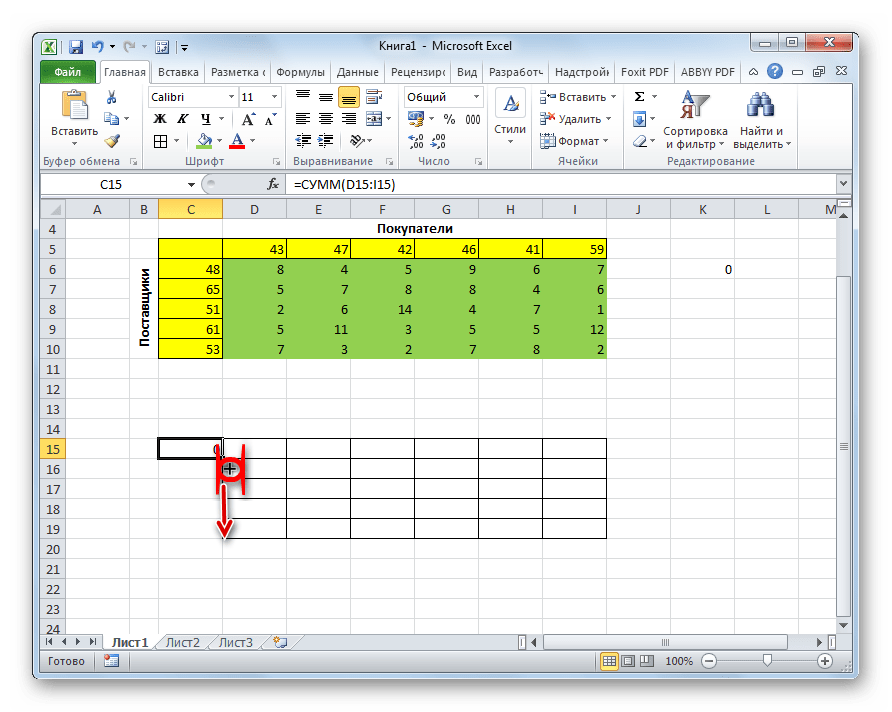
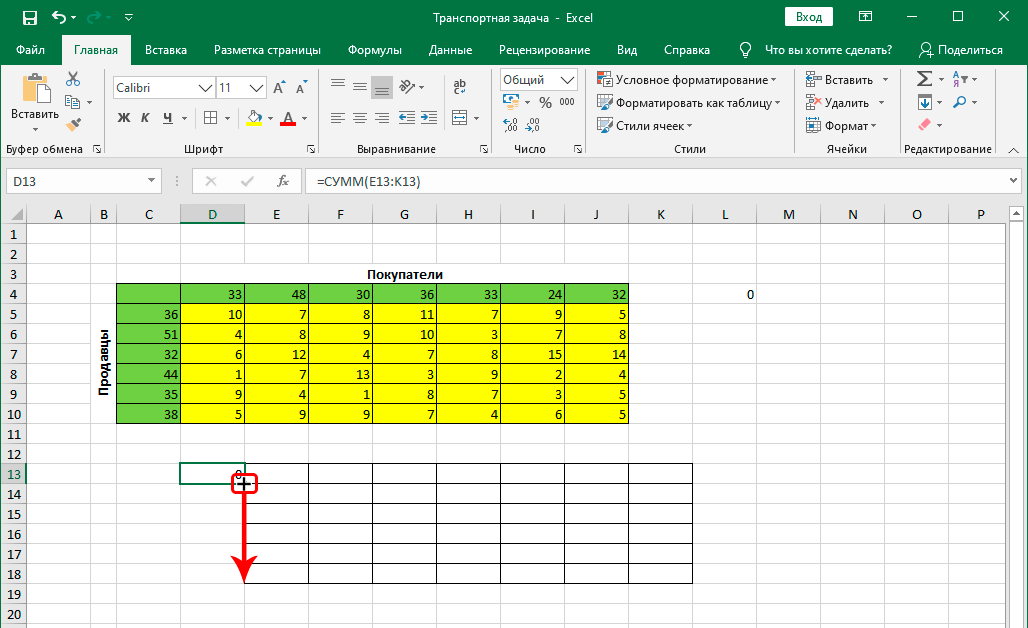
- В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
- Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
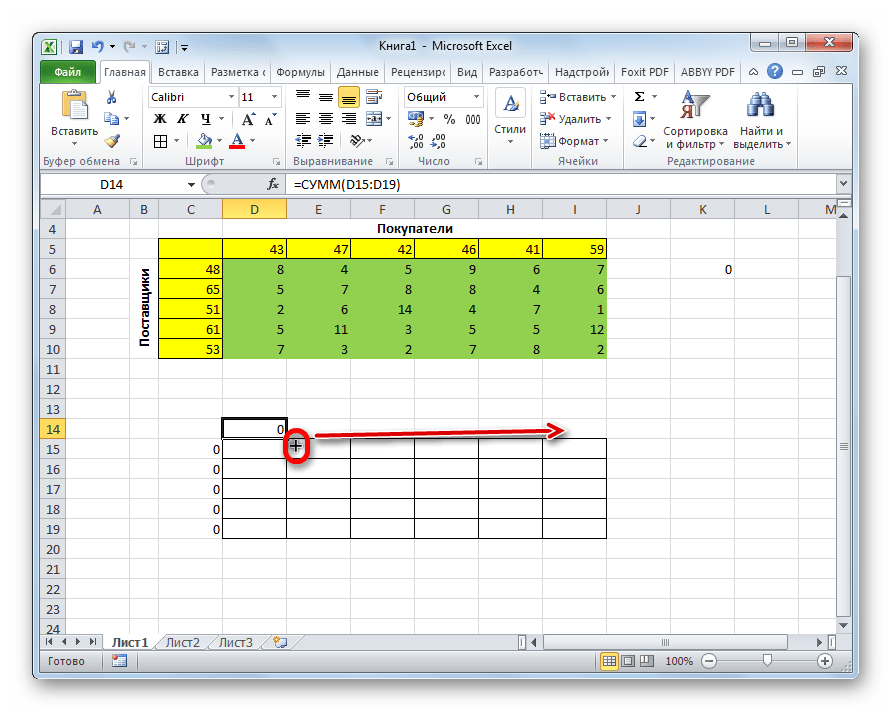
- Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
- В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
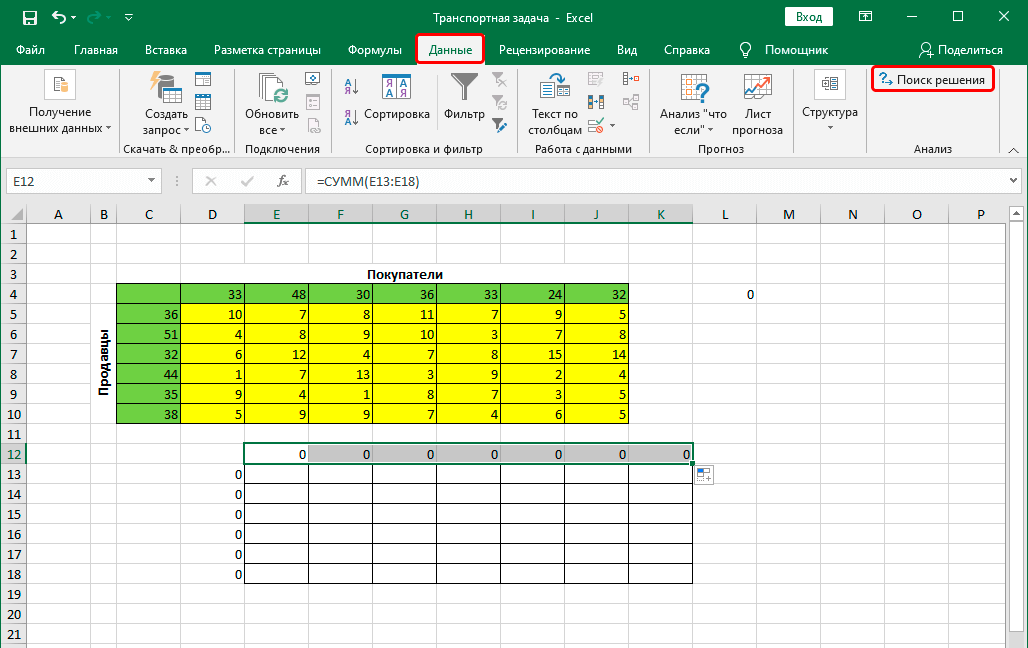
- С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
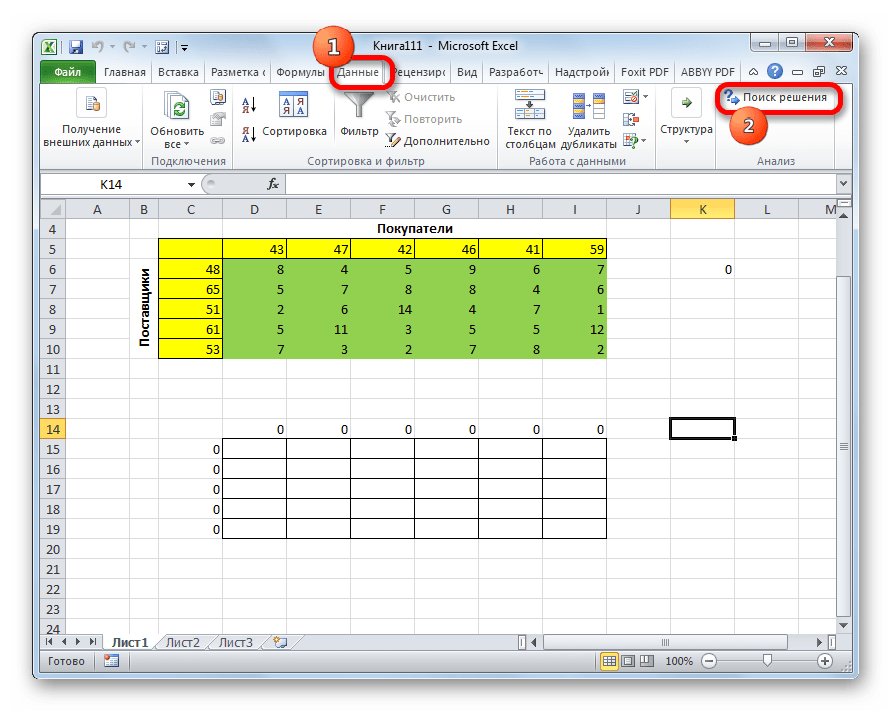
- Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
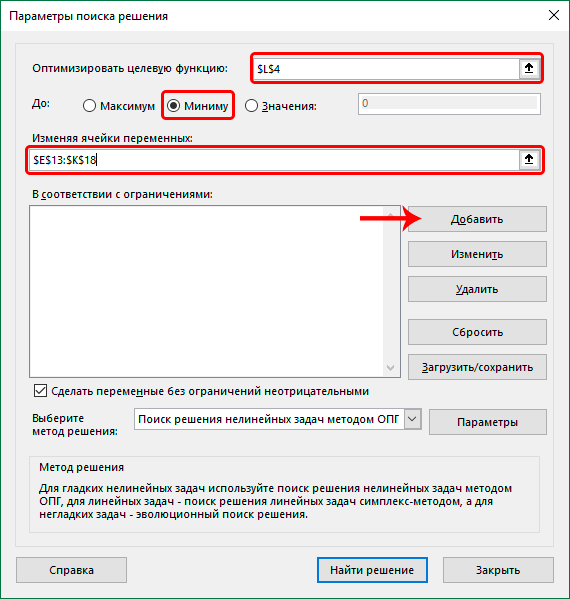
- Перед нами появится окно с параметрами функции:
- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
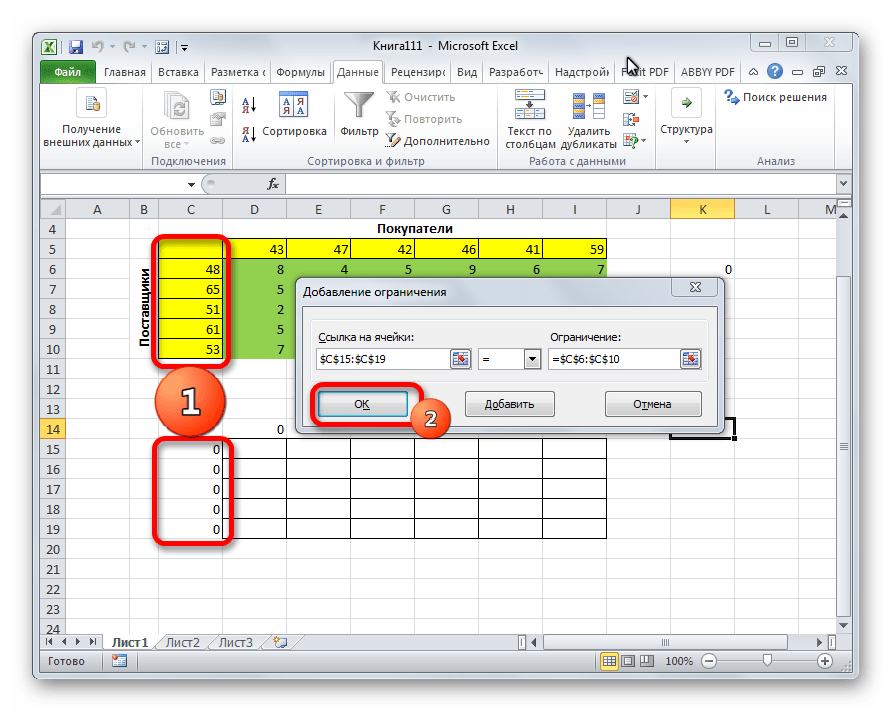
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
- Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.
- Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
- Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
- больше или равно нулю;
- целое число.
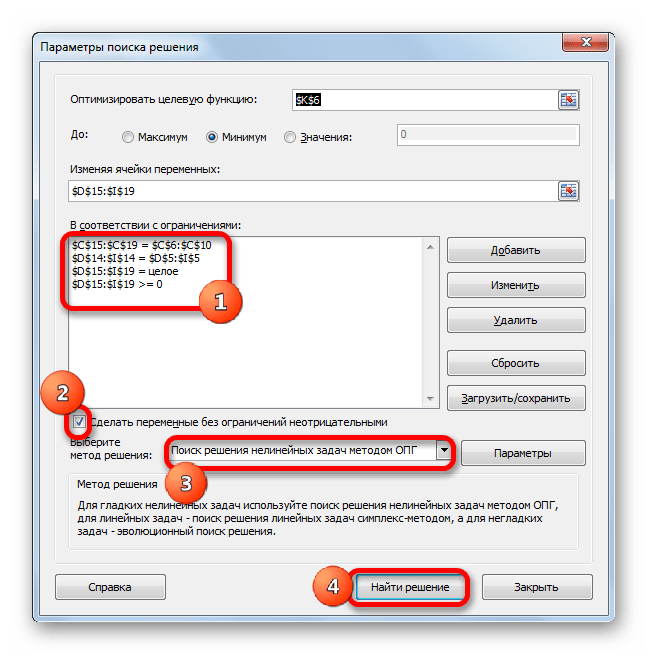
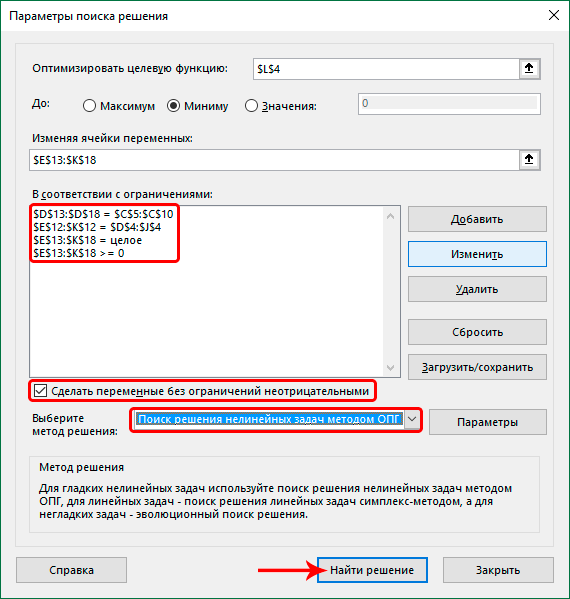
- В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
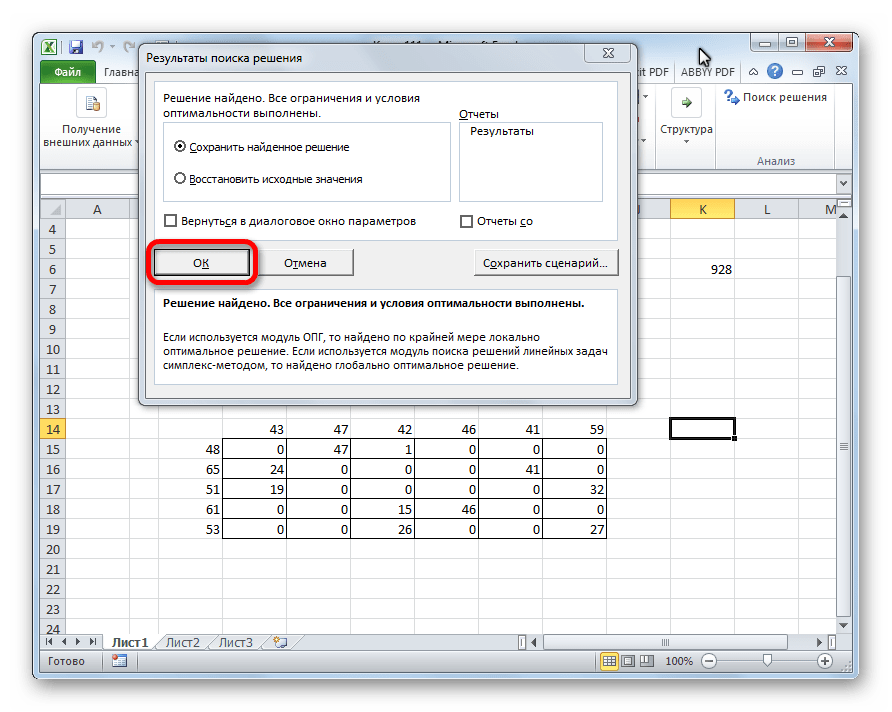
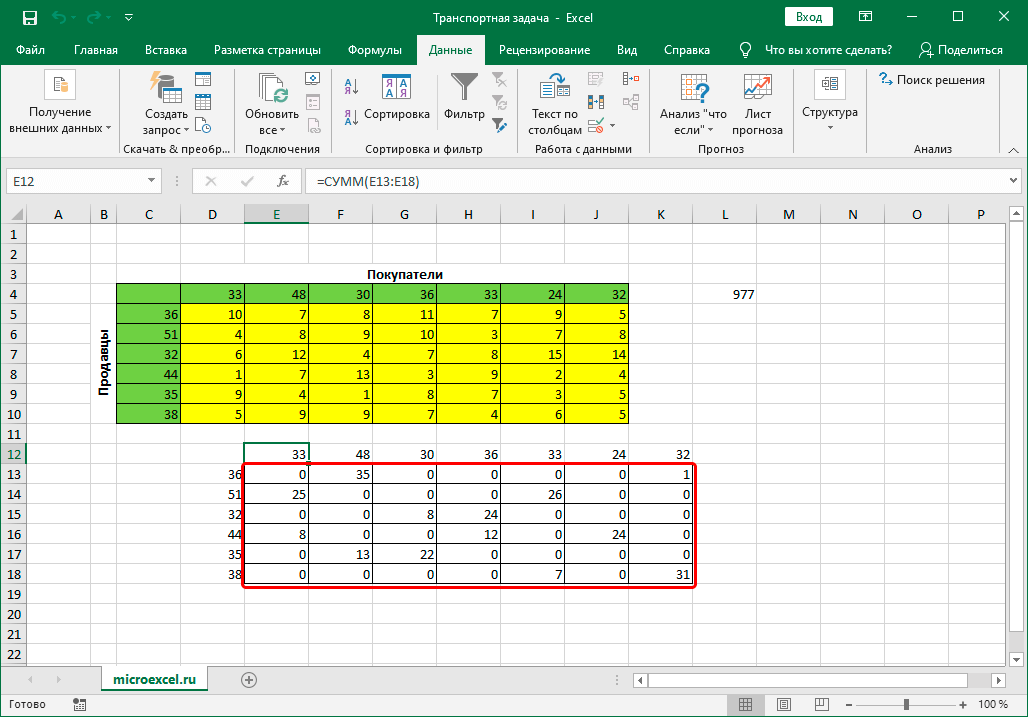
- В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
- Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.
Содержание
- Общее описание транспортной задачи
- Инструменты для решения транспортной задачи в Эксель
- Пример решения транспортной задачи в Excel
- Условия задачи
- Решение задачи
- Вопросы и ответы
Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.
Общее описание транспортной задачи
Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.
Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.
Инструменты для решения транспортной задачи в Эксель
Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.
- Делаем перемещение во вкладку «Файл».
- Кликаем по подразделу «Параметры».
- В новом окне переходим по надписи «Надстройки».
- В блоке «Управление», который находится внизу открывшегося окна, в выпадающем списке останавливаем выбор на пункте «Надстройки Excel». Делаем клик по кнопке «Перейти…».
- Запускается окно активации надстроек. Устанавливаем флажок возле пункта «Поиск решения». Кликаем по кнопке «OK».
- Вследствие этих действий во вкладке «Данные» в блоке настроек «Анализ» на ленте появится кнопка «Поиск решения». Она нам и понадобится при поиске решения транспортной задачи.
Урок: функция «Поиск решения» в Экселе
Теперь давайте разберем конкретный пример решения транспортной задачи.
Условия задачи
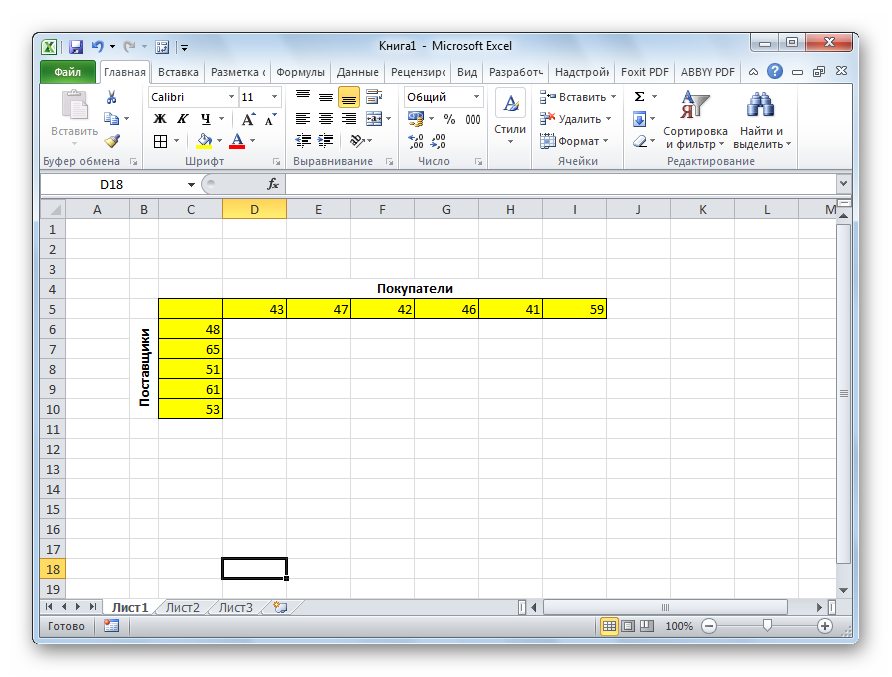
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.
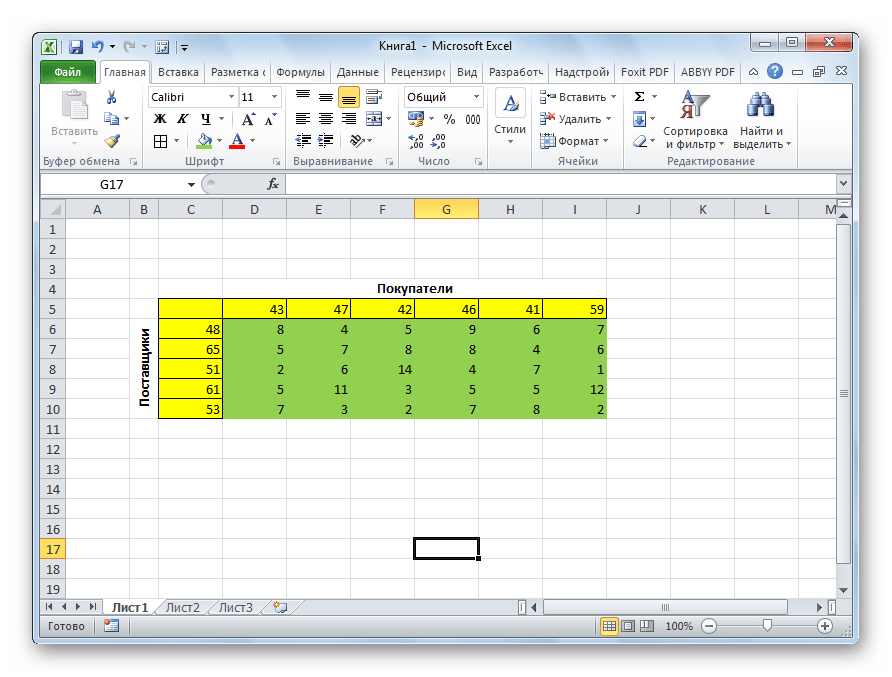
Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.
Решение задачи
Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.
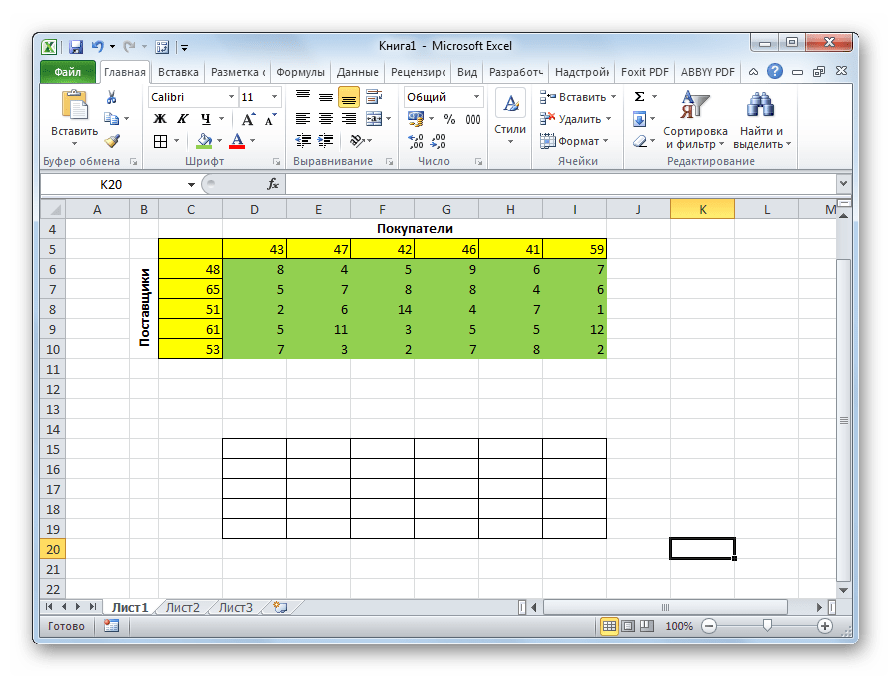
- Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
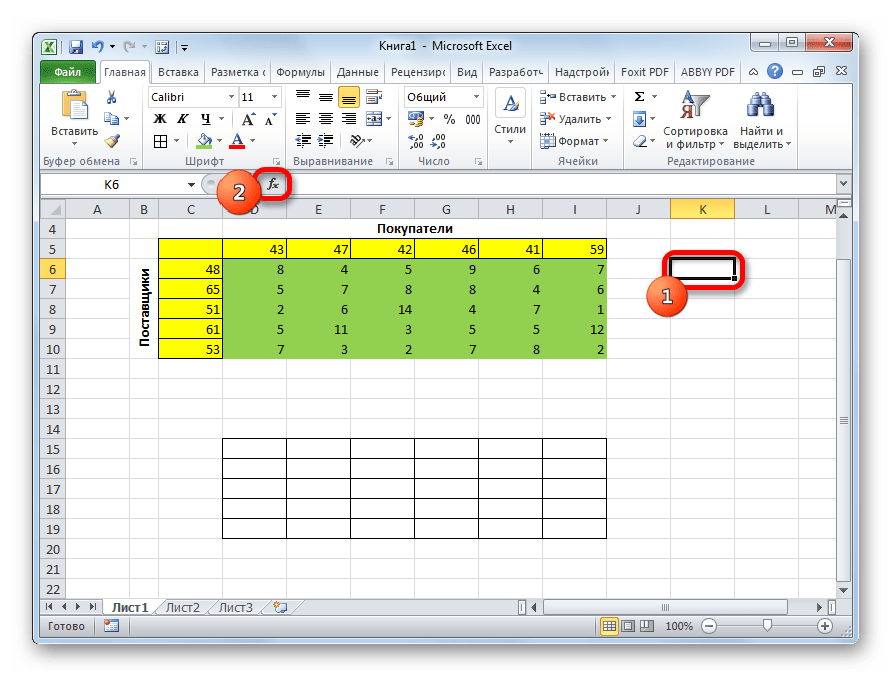
- Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
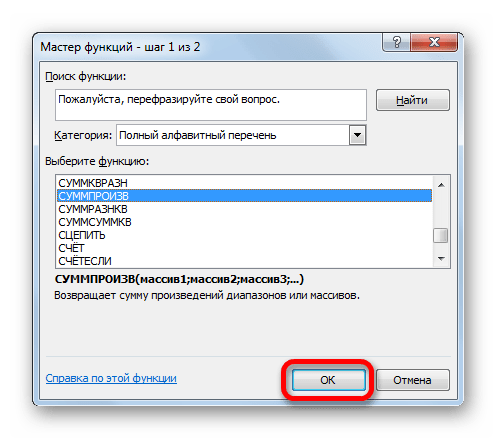
- Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
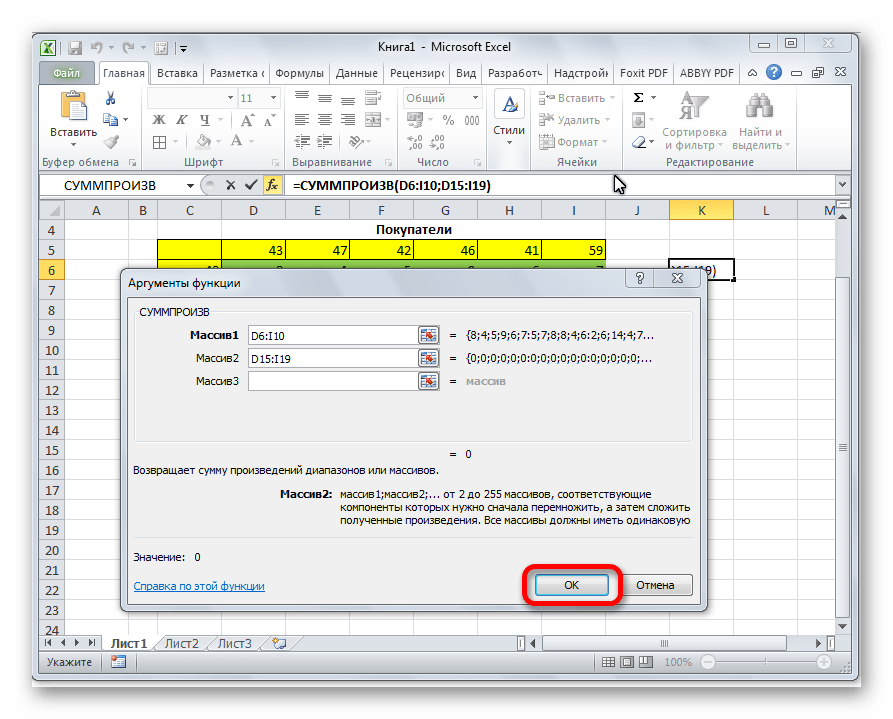
- Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
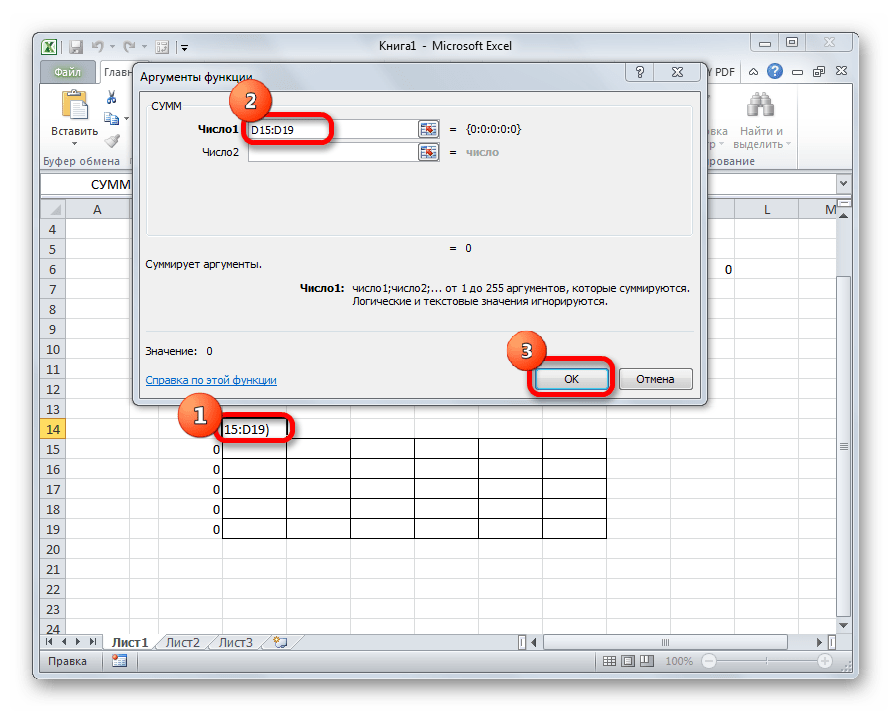
- Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
- Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
- Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
- Копируем маркером заполнения формулу на всю строку.
- Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
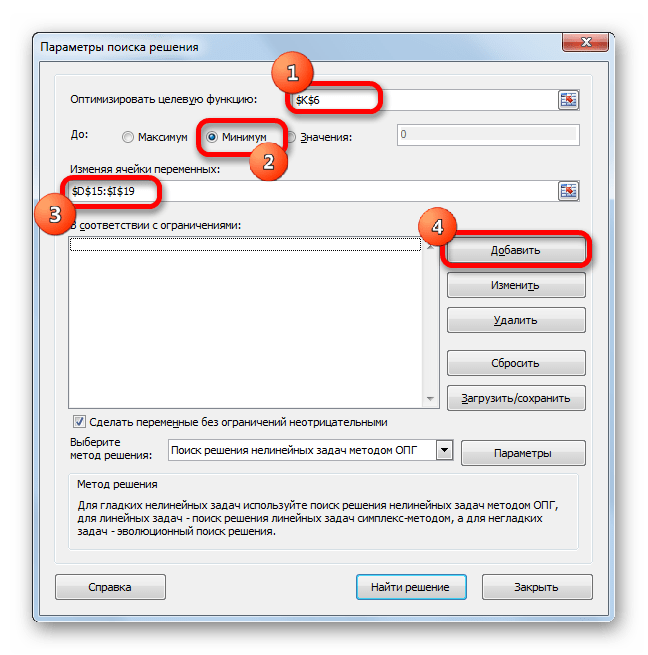
- Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
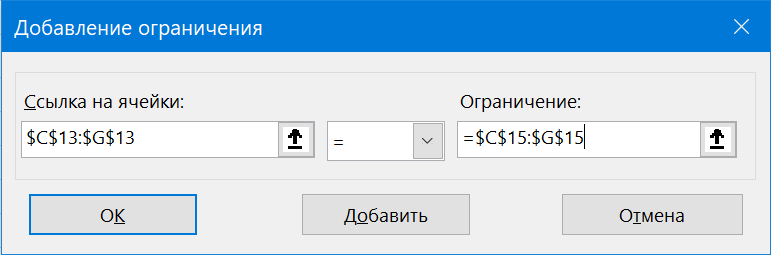
- Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
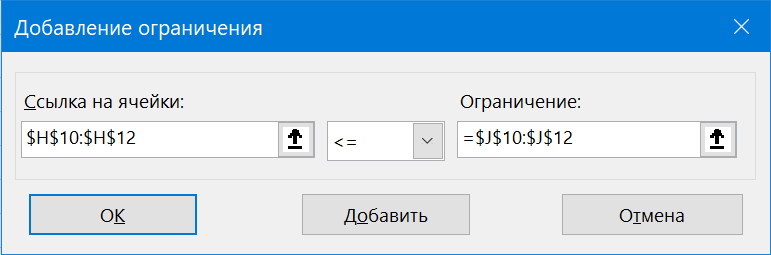
- Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
- После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».
Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.
Еще статьи по данной теме:
Помогла ли Вам статья?
Excel – очень функциональная программа. Она может использоваться для решения огромного пласта задач, с которыми приходится сталкиваться в бизнесе. Одна из самых распространённых – транспортная задача. Представим, что нам нужно понять, какой способ перевозки от производителя к конечному покупателю самый оптимальный по затратам времени, денег и других ресурсов. Эта проблема довольно популярная, независимо от того, в какой сфере работает бизнес. Поэтому давайте более подробно разберемся, как её реализовать с помощью Excel.
Содержание
- Описание транспортной задачи
- Как включить функцию “Поиск решения” в Excel
- Пример решения транспортной задачи в Excel
- Условия задачи
- Решение – пошаговый алгоритм
- Заключение
Описание транспортной задачи
Итак, у нас есть два контрагента, которые постоянно взаимодействуют друг с другом. В нашем случае это покупатель и продавец. Нам нужно посчитать, как перевозить товары таким образом, чтобы издержки были минимальны. Для этого нужно представить все данные в схематической или матричной форме. В Эксель используем последний вариант. В целом, выделяют два типа транспортных задач:
- Закрытые. В этом случае спрос и предложение находятся в балансе.
- Открытые. Здесь нет равенства между спросом и предложением. Чтобы получить решение этой задачи, нужно сперва ее привести к первому типу, уравняв спрос и предложение. Для этого нужно ввести дополнительный показатель – наличие условного покупателя или продавца. Кроме этого, нужно внести определенные изменения в таблицу издержек.
Как включить функцию “Поиск решения” в Excel
Для решения транспортных задач в Excel существует специальная функция, которая называется «Поиск решения». Она не активирована по умолчанию, поэтому нужно сделать следующие шаги:
- Открыть меню «Файл», которое находится в левом верхнем углу окна программы.
- После этого нажимаем на кнопку с параметрами.
- Далее находим подраздел «Настройки» и переходим в меню управления надстройками. Это маленькие программы, которые выполняются в рамках среды Microsoft Excel. Видим, что сначала мы нажали на меню «Надстройки», а потом в правой части внизу выставили пункт «Надстройки Excel» и нажали на кнопку «Перейти». Все нужные действия выделены красными прямоугольниками и стрелочками.
- Далее включаем надстройку «Поиск решения», после чего подтверждаем свои действия нажатием клавиши ОК. Исходя из описания настройки, мы видим, что она предназначена для анализа сложных данных, таких как научные и финансовые.
- После этого переходим во вкладку «Данные», где видим новую кнопку, которая называется так же, как и надстройка. Ее можно найти в группе инструментов «Анализ».
Осталось только кликнуть по этой кнопке, и мы переходим к решению транспортной задачи. Но перед этим следует немного подробнее поговорить про инструмент «Поиск решения» в Excel. Это специальное дополнение Эксель, которое дает возможность находить самое быстрое решение задачи. Характерная особенность – учет ограничений, которые пользователь задает на этапе подготовки. Если говорить простым языком, это подпрограмма, дающая возможность определить самый лучший способ достижения определенной задачи. К таким задачам могут относиться следующие:
- Инвестирование, загрузка склада или любая другая подобная деятельность. В том числе, и доставка товара.
- Лучший способ. Сюда входят такие задачи, как достижение максимальной прибыли при минимальных издержках, способы достижения самого лучшего качества при имеющихся ресурсах и так далее.
Кроме транспортных задач, эта надстройка используется и для таких целей:
- Разработка плана производства. То есть, сколько нужно выработать единиц товара, чтобы достичь максимального дохода.
- Найти распределение рабочих сил по разным видам работ, чтобы суммарные затраты на производство товара или услуг были самыми маленькими.
- Установить, сколько минимально времени понадобится на то, чтобы выполнить все работы.
Как видим, задачи бывают самыми разными. Универсальное правило применения этой надстройки – необходимо перед решением задачи создать модель, которая бы соответствовала ключевым характеристикам поставленной проблемы. Моделью является совокупность функций, которые используют переменные в качестве своих аргументов. То есть, значения, которые могут изменяться.
Важно учесть, что оптимизация набора значений осуществляется исключительно по одному показателю, который называется целевой функцией.
Надстройка «Поиск решения» осуществляет перебор разных значений переменных, которые передаются целевой функции таким образом, чтобы она была максимальной, минимальной или равной определенному значению (именно это и является ограничением). Есть еще одна функция, которая несколько похожая по своему принципу действия, и какую нередко путают с «Поиском решения». Называется она «Подбор параметра». Но если копнуть более глубоко, то разница между ними колоссальная:
- Функция «Подбор параметра» не работает больше, чем с одной переменной.
- Она не предусматривает возможности задавать ограничения для переменных.
- Способна определять только равенство целевой функции определенному значению, но не дает возможности находить максимум и минимум. Поэтому для нашей задачи она не подходит.
- Способна эффективно вычислять лишь если модельно линейного типа. Если модель нелинейная, то она находит значение, которое наиболее близкое к изначальному.
Транспортная задача по своей структуре значительно сложнее, поэтому надстройки «Подбор параметра» для этого недостаточно. Давайте разберемся более детально, как реализовать на практике функцию «Поиск решения» на примере транспортной задачи.
Пример решения транспортной задачи в Excel
Для того, чтобы наглядно продемонстрировать, как на практике решать транспортные задачи в Excel, давайте приведем пример.
Условия задачи
Предположим, у нас есть 6 продавцов и 7 покупателей. Спрос и предложение между ними распространяется соответственно следующим способом: 36, 51, 32, 44, 35 и 38 единиц – продавцы и 33, 48, 30, 36, 33, 24 и 32 единицы – покупатели. Если просуммировать все эти значения, то обнаружится, что спрос и предложение находятся в балансе. Следовательно, эта задача закрытого типа, которая решается очень просто.
Кроме этого, у нас есть информация о том, сколько нужно потратить на перевозку из пункта А в пункт Б (они на примере выделены желтыми ячейками).
Решение – пошаговый алгоритм
Теперь, после того, как мы ознакомились с таблицами с исходными данными, можем воспользоваться следующим алгоритмом, чтобы решить эту задачу:
- Сперва делаем таблицу, состоящую из 6 строк и 7 колонок.
- После этого переходим в какую-угодно ячейку, не содержащую никаких значений и при этом лежащую за пределами новосозданной таблицы и вставляем функцию. Для этого нажимаем на кнопку fx, которая находится слева от строки ввода функции.
- У нас появляется окно, в котором нам нужно выбрать категорию «Математические». А какая функция нас интересует? Та, которая выделена на этом скриншоте. Функция СУММИПРОИЗВ умножает диапазоны или массивы между собой и суммирует их. Как раз то, что нам нужно. После этого нажимаем клавишу ОК.
- Далее на экране появится окно, в котором необходимо указать параметры функции. Они следующие:
- Массив 1. Это первый аргумент, в котором записываем тот диапазон, который выделен жёлтым цветом. Задать параметры функции можно как используя клавиатуру, так и выделив соответствующую область с помощью левой кнопки мыши.
- Массив 2. Это второй аргумент, в качестве которого выступает новосозданная таблица. Действия выполняются аналогичным образом.
Подтверждаем свое действие нажатием клавиши ОК.
- После этого делаем левый клик мыши по той ячейке, которая служит верхней левой в новосозданной таблице. Теперь снова нажимаем кнопку вставки функции.
- Выбираем ту же категорию, что и в предыдущем случае. Но на этот раз нас интересует функция СУММ.
- Теперь наступил этап заполнения аргументов. В качестве первого аргумента записываем верхнюю строку таблицы, которую мы создали в начале. Точно так же, как и раньше, это можно сделать путем выделения этих ячеек на листе, так и вручную. Подтверждаем свои действия нажатием клавиши ОК.
- Увидим результаты в ячейке с функцией. В данном случае это ноль. Далее переносим курсор в правый нижний угол, после чего появится маркер автозаполнения. Выглядит он, как маленький чёрный плюсик. Если он появился, зажимаем левую кнопку мыши и перемещаем курсор до последней ячейки в нашей таблице.
- Это дает нам возможность перенести формулу во все остальные ячейки и получить правильные результаты без необходимости выполнения дополнительных расчетов.
- Следующий шаг – выбор левой верхней ячейки и вставка функции СУММ в нее. После этого заносим аргументы и с помощью маркера автозаполнения заполняем все оставшиеся ячейки.
- После этого приступаем непосредственно к решению задачи. Для этого воспользуемся дополнением, которое мы включили ранее. Переходим на вкладку «Данные», и там находим инструмент «Поиск решения». Нажимаем по этой кнопке.
- Теперь перед нашим взором появилось окошко, через которое можно настроить параметры нашего дополнения. Давайте каждый из этих параметров разберем:
- Оптимизировать целевую функцию. Здесь нам нужно выбрать ячейку, содержащую функцию СУММПРОИЗВ. Видим, что эта опция дает возможность выбрать функцию, для которой будет осуществляться поиск решения.
- До. Здесь выставляем опцию «Минимум».
- Изменяя ячейки переменных. Здесь указываем диапазон, соответствующий той таблице, которую мы создавали в самом начале (за исключением суммирующей строки и столбца).
- В соответствии с ограничениями. Здесь нам нужно добавить ограничения, нажав кнопку «Добавить».
- Мы помним, какое ограничение нам нужно создать – сумма значений спросов покупателей и предложений продавцов должны быть одинаковыми.
- Задача ограничений осуществляется следующим образом:
- Ссылка на ячейки. Здесь заносим диапазон таблицы для расчётов.
- Условия. Это математическая операция на предмет соответствия которой проверяется диапазон, заданный в первом поле ввода.
- Значение условия или ограничение. Сюда заносим подходящую колонку в исходной таблице.
- После того, как все действия будут выполнены, нажимаем кнопку ОК, тем самым подтверждая наши действия.
Точно такие же операции производим для верхних строк, задавая следующее условие: они должны быть равны.
Следующий этап – задание условий. Нам необходимо установить следующие критерии для суммы ячеек в таблице – больше или равно нулю, целое число. В результате у нас появляется такой перечень условий, при которых задача решается. Здесь нужно убедиться, что поставлен флажок возле опции «Сделать переменные без ограничений неотрицательными». Также в нашей ситуации требуется, чтобы был выбран метод решения задачи – «Поиск решения нелинейных задач методов ОПГ». Теперь можно смело говорить, что настройка осуществлена. Поэтому осталось только выполнить расчеты. Для этого нажимаем на кнопку «Найти решение».
После этого все данные будут рассчитаны автоматически, а потом Эксель покажет окно с результатами. Оно необходимо для того, чтобы перепроверить работу компьютера, поскольку возможны ошибки, если условия ранее были заданы неверно. Если все правильно, то нажимаем кнопку «ОК» и видим готовую таблицу.
Если же оказывается, что у нас задача стала открытого типа, то это плохо, поскольку нужно отредактировать исходную таблицу так, чтобы задача превратилась в закрытую. Тем не менее, когда это сделать, оставшийся алгоритм будет такой же.
Заключение
Как видим, Excel может использоваться и для очень сложных вычислений, которые на первый взгляд не доступны простой компьютерной программе, которая установлена почти у каждого. Тем не менее, это так. Сегодня мы уже рассмотрели продвинутый уровень использования. Данная тема не такая простая, но как говорится, дорогу осилит идущий. Главное – следовать плану действий, и точно выполнять все действия, указанные выше. Тогда ошибок не возникнет, а программа самостоятельно выполнит все необходимые расчеты. Не нужно будет думать, какую функцию использовать и так далее.
Оцените качество статьи. Нам важно ваше мнение:
На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).
Как решить транспортную задачу в Excel
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Использовать можно любую версию программы — 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).
Алгоритм решения ТЗ в Эксель
- Составить математическую модель транспортной задачи — то есть получить таблицу со стоимостью перевозок, запасами груза у поставщиков и потребностями потребителей (и, возможно, дополнительными ограничениями).
- Если задача открытая (несбалансированная), то добавить потребителя или поставщика с нулевыми тарифами перевозки.
- Внести на лист таблицы Excel данную модель в виде матрицы тарифов (затрат).
- Создать рядом на листе еще одну таблицу, где будут выводиться искомые перевозки (такой же размерности, что и таблица тарифов). Просуммировать перевозки по строкам и столбцам (чтобы сравнивать с аналогичными ячейками — предельными ограничениями задачи — запасами поставщиков и потребностями потребителей).
- Ввести в ячейку формулу, подсчитывающую суммарную стоимость перевозок (это число мы должны минимизировать по смыслу транспортной задачи)
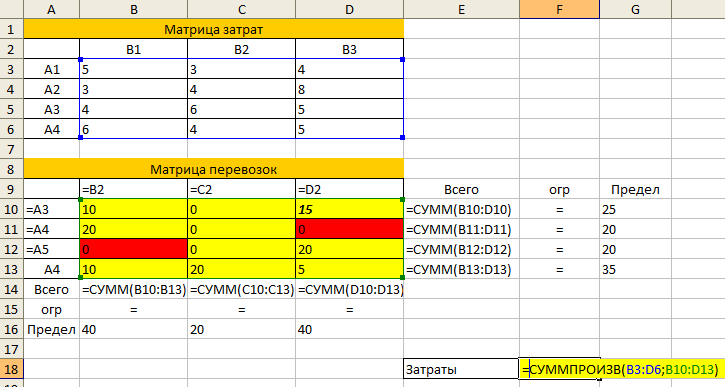
В режиме формул таблица будет выглядеть так:
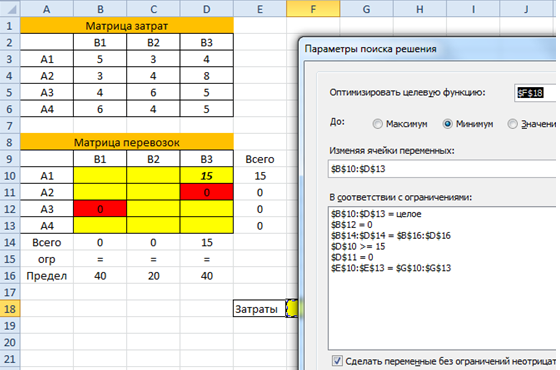
- Запустить надстройку Поиск решения и указать а) ячейку, которую мы минимизируем, б) все ограничения на запасы поставщиков и потребности потребителей, в) дополнительные ограничения (иногда бывают запреты перевозок или требования по минимальному объему груза между определенными пунктами, как в данном случае).
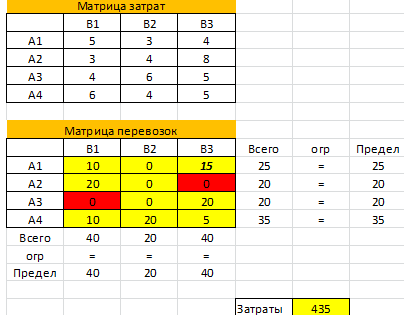
- Получить решение транспортной задачи: в целевой ячейке вы увидите минимальную стоимость перевозок (в примере 435), а в таблице перевозок — искомые значения объема перевозимого груза (см. желтые ячейки).
- Проанализировать решение, если требуется и записать более подробно, например
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.
Лучшее спасибо — порекомендовать эту страницу
Транспортные задачи: примеры в Excel
Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.
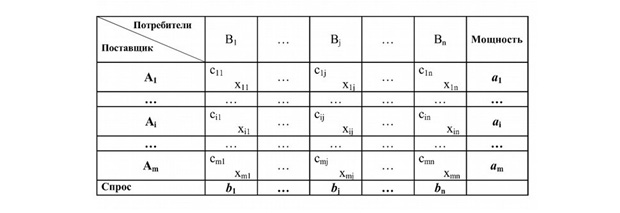
Задача 2. Исходные данные задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху — мощности потребителей.
Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решений.
Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.
Также заданы расстояния между предприятиями.
Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.
Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.
Задача 5. Свести задачу к виду ТЗ и решить с помощью надстройки «Поиск решения»
Четыре ремонтные мастерские могут за год отремонтировать соответственно 400, 500, 450 и 550 машин при себестоимости ремонта одной машины в 500, 700, 650 и 600 рублей. Планируется годовая потребность в ремонте пяти автобаз: 550, 350, 300, 375 и 400 машин.
Ремонт машин с 1 автобазы должен осуществляться в 100% случаев силами ремонтных мастерских.
На 4 АБ возможно самостоятельное проведение ремонтных работ (бесплатное) в объеме, не превышающем 8% от планируемой годовой потребности этой мастерской. Платное (на стороне) — совсем не возможно.
Вторая, третья и пятая АБ могут «ремонтироваться» на стороне, стоимость ремонта +трансп.расходы каждой машины в таком случае составит 695 руб.
Дана матрица, характеризующая транспортные расходы на доставку машины с j-й автобазы в i-ю ремонтную мастерскую. Определить минимальную годовую потребность в кредитах на выполнение указанного объема работ по всем автобазам
Решаем транспортные задачи любой сложности
Полезные ссылки
|
|
- Лыкова Н.П.
Российский государственный гуманитарный университет
NovaInfo 7, скачать PDF
Опубликовано 13 октября 2011
Раздел: Технические науки
Просмотров за месяц: 90
Аннотация
Одним из важнейших на данный момент разделом логистики, является транспортная логистика. Которая представляет собой систему по организации доставки, а именно по перемещению каких-либо материальных предметов, веществ и прочего из одной точки в другую по оптимальному маршруту.
Ключевые слова
MS EXCEL, РЕШЕНИЕ, ЛОГИЧЕСКИЕ ЗАДАЧИ
Текст научной работы
Одним из важнейших на данный момент разделом логистики, является транспортная логистика. Которая представляет собой систему по организации доставки, а именно по перемещению каких-либо материальных предметов, веществ и прочего из одной точки в другую по оптимальному маршруту.
Оптимальным считается маршрут, по которому возможно доставить логистический объект, в кратчайшие сроки (или предусмотренные сроки) с минимальными затратами, а также с минимальным вредом для объекта доставки.
Одним из способов нахождения такого оптимального маршрута может служить решение транспортных задач в MS Excel.
Транспортная задача является частным типом задачи линейного программирования и формулируется следующим образом: имеется m пунктов отправления (или пунктов производства) А_i,dots,А_m, в которых сосредоточены запасы однородных продуктов в количестве a_1,dots,а_m единиц. Имеется n пунктов назначения (или пунктов потребления) В_1,dots,В_m, потребность которых в указанных продуктах составляет b_1,dots,b_n единиц. Известны также транспортные расходы Сij, связанные с перевозкой единицы продукта из пункта Ai в пункт Вj, i=1,dots,m; j=1,dots,n.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления А_1,А_2,dots,А_n в n пунктов назначения В_1,В_2,dots,В_n.
В качестве критерия оптимальности (целевая функция) обычно задается минимальная суммарная стоимость перевозок всего груза или минимальная суммарная транспортная работа по доставке грузов, которая может быть пропорциональна времени доставки грузов потребителям или расстоянию между поставщиками и потребителями. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная суммарная стоимость перевозок всего груза.
Обозначим Cij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через ai — запасы груза в i -ом пункте отправления, через bj — потребности в грузе в j-ом пункте назначения, а через xi — количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая модель транспортной задачи состоит в определении минимального значения функции:
F=sum_{i=1}^msum_{j=1}^nc_{ij}x_{ij}rightarrow min, (1)
при условиях
sum_{i=1}^mx_{ij}=b_j, j = 1,2,…,n, (2)
sum_{j=1}^nx_{ij}=a_i, i = 1,2,…,m (3)
x_{ij}geq0, i=1,2,dots,m, j=1,2,dots,n. (4)
Поскольку переменные x_{ij}geq0, i=1,2,dots,m, j=1,2,dots,n. удовлетворяют системам линейных уравнений (2) и (3) и условию неотрицательности (4), обеспечиваются доставка необходимого количества груза в каждой из пунктов назначения, вывоз всего имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.
Суммарное количество груза у поставщиков равно sum_{i=1}^ma_i суммарная потребность в грузе в пунктах назначения равна sum_{j=1}^nb_j. Если суммарная потребность в грузе в пунктах назначения равна суммарному запасу груза в пунктах отправления, т. е.
sum_{i=1}^ma_i=sum_{j=1}^nb_j, (5)
то такая транспортная задача называется закрытой или сбалансированной. В противном случае — открытой или несбалансированной.
В случае превышения суммарного запаса над суммарной потребностью, т.е. если
sum_{i=1}^ma_i>sum_{j=1}^nb_j,
вводится фиктивный n+1-й потребитель (или пункт назначения) с потребностью, равной:
b_{n+1}=sum_{i=1}^ma_i-sum_{j=1}^nb_j
а соответствующие транспортные тарифы от всех поставщиков до фиктивного потребителя полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (5).
В случае превышения суммарной потребности в грузе над суммарными запасами поставщиков, т. е. если
sum_{i=1}^ma_i<sum_{j=1}^nb_j
вводится фиктивный m+l-й пункт отправления с запасом груза в нем, равным:
a_{m+1}=sum_{i=1}^ma_i-sum_{j=1}^nb_j
а соответствующие транспортные тарифы от фиктивного поставщика до всех потребителей полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (5)
Предположим, что sum_{i=1}^ma_i=sum_{j=1}^nb_j, т. е. общий объем производства равен общему объему потребления. Требуется составить такой план перевозок (откуда, куда и сколько единиц продукта везти), чтобы удовлетворить спрос всех пунктов потребления за счет реализации всего продукта, произведенного всеми пунктами производства, при минимальной общей стоимости всех перевозок.
Рассмотрим алгоритм решения таких задач на конкретном примере:
Продукты, находящиеся на четырех складах — С1, С2, С3, С4 необходимо развезти по пяти магазинам — Ml, М2, МЗ, М4 и М5. Потребности этих магазинов в продуктах равны соответственно 15, 14, 25, 5 и 9 ед. Запасы продуктов на складах С1, С2, СЗ, С4 составляют соответственно 23, 15, 45, 15 ед. Тарифы по доставке продуктов (руб./ед. груза) приведены в таблице:
|
Склады |
Магазины |
||||
|
М1 |
М2 |
М3 |
М4 |
М5 |
|
|
С1 |
10 |
3 |
4 |
5 |
6 |
|
С2 |
2 |
1 |
11 |
14 |
3 |
|
С3 |
4 |
13 |
3 |
2 |
8 |
|
С4 |
5 |
13 |
4 |
12 |
7 |
Составьте план перевозок продуктов, при котором суммарные расходы по их доставке будут минимальными.
Так как данная задача относится к задачам линейного программирования, то решение начинается с построения математической модели:
begin{cases}x_{11}+x_{12}+x_{13}+x_{14}=23 \ x_{21}+x_{22}+x_{23}+x_{24}=15 \ x_{31}+x_{32}+x_{33}+x_{34}=45 \ x_{41}+x_{42}+x_{43}+x_{44}=15 \ x_{11}+x_{12}+x_{13}+x_{14}=15 \ x_{21}+x_{22}+x_{23}+x_{24}=14 \ x_{31}+x_{32}+x_{33}+x_{34}=25 \ x_{41}+x_{42}+x_{43}+x_{44}=5 \ x_{51}+x_{52}+x_{53}+x_{54}=9 \ xijgeq0,i=1,2,3,4,j=1,2,3,4,5end{cases}
При данном плане перевозок суммарная их стоимость составит (целевая функция):
F=10x_{11}+3x_{12}+4x_{13}+5x_{14}+6x_{15}+
+2x_{21}+1x_{22}+11x_{23}+14x_{24}+3x_{25}+
+4x_{31}+13x_{32}+3x_{33}+2x_{34}+8x_{35}+
+5x_{41}+13x_{42}+4x_{43}+12x_{44}+7x_{45}+
+0x_{51}+0x_{52}+0x_{53}+0x_{54}+0x_{55}rightarrow min
Дальнейшее решение задачи ведётся в MS Excel.
Составляется таблица с исходными данными (рис. 1)
Затем заполняем столбец с ограничениями, при помощи функции СУММ (для ячейки Н4 =СУММ (В4:F4)), а формулу СУММПРОИЗВ мы вводим в строке с целевой функцией (=СУММПРОИЗВ (B4:F8;B15:F19)).
После введения всех данных и формул, мы ставим курсор на ячейку с формулой целевой функции и вызываем программу Поиск решения.
В поле изменяя ячейки выбираем ячейки с неизвестными переменными (B4:F8), а поле ограничения вводим наложенные нами ограничения.
Далее во вкладке параметры выбираем значения: линейная модель, неотрицательные значения и автоматическое масштабирование.
После чего получаем ответ к задаче (рис. 2)
Решив математическую модель, пришли к выводу, что
из пункта 1-го необходимо поставлять 8 ед. продукции на 2-й склад, из 2-го необходимо 6 ед. на 2-й и 9 на 5-й, из 3-го 15 ед. на 1-й, 25 на 3-й, 5 на 4-й, из 4-го продукции не требуется, при этом затраты на перевозку составят 202 ден. ед.
Как видно из примера, решение задачи с помощью MS Excel быстрое и удобное, так как:
- создав один раз таблицу, её можно применять для задач такого же типа изменяя только исходные данные;
- практически все необходимые для решения задачи формулы уже представлены в MS Excel;
- решение задачи занимает в несколько раз меньше времени, нежели её же решение вручную;
- точность решения гораздо выше, чем вручную, а погрешности сведены к минимуму.
Читайте также
-
Принятие управленческих решений в образовательном процессе
- Половнева М.В.
-
Табличная имитация алгоритмов искусственного интеллекта в MS Excel
- Любивая Т.Г.
-
К вопросу о практическом применении RFM-анализа клиентской базы (на примере магазина «Подарки»)
- Генералов И.Г.
- Жавронович М.Ю.
- Суслов С.А.
-
Практическое применение информационных технологий в изучении экономики АПК
- Петрова Л.В.
-
Разбор и анализ таблиц Excel с помощью MS XML в TestComplete
- Долганов А.А.
Список литературы
- Акулич И.Л. Математическое программирование в примерах и задачах: учебное пособие для ВУЗов. — М.: Высшая школа, 2004
- Красс М. Математика для экономических специальностей. Учебник. 3-е изд., перераб и доп. М, Экономист, 2004.
Цитировать
Князева, А.А. Применение MS Excel в решение логистических задач / А.А. Князева, Н.П. Лыкова. — Текст : электронный // NovaInfo, 2011. — № 7. — URL: https://novainfo.ru/article/1364 (дата обращения: 17.04.2023).
Поделиться
Как рассчитать стоимость доставки в Эксель
Формула Vlookup — калькулятор стоимости доставки
- Как рассчитать стоимость доставки по определенному весу в Excel.
- Общая формула
- =VLOOKUP(lookup_value, table_array, col_index,[range_lookup])*lookup_value.
- аргументы
- =VLOOKUP(F4, B3:C7,2,1)*F4.
- нажмите Enter ключ, чтобы получить полную стоимость доставки.
- Как использовать формулу Vlookup для рассчета стоимости доставки в Excel.
- Формула Vlookup используется для поиска значения в таблице и возвращает соответствующее значение из указанной строки и столбца.
- Для рассчета стоимости доставки необходимо указать значение веса в ячейке F4.
- Аргументы формулы Vlookup состоят из значения, таблицы, индекса столбца и логического значения.
- После ввода формулы в ячейку и нажатия клавиши Enter, будет выведена полная стоимость доставки.
- Для рассчета стоимости доставки груза на 1 км необходимо использовать формулу: стоимость бензина на 1 км × 4 = цена перевозки за 1 км.
- Для введения простых формул в Excel нужно выделить ячейку и ввести знак равенства, константы и операторы, а затем нажать клавишу Enter.
- Расчет стоимости доставки может осуществляться по весу или объему, а также зависит от выбранного метода доставки и количества посылок.
- Для рассчета стоимости доставки груза необходимо учитывать фактический вес и объем груза, а также выбранный метод доставки.
- Чтобы сделать автоматический расчет в Excel, нужно в параметрах выбрать категорию Формулы и включить итеративные вычисления.
- Для вставки формулы в ячейку таблицы необходимо выделить ячейку, нажать кнопку Формула и создать нужную формулу с помощью диалогового окна.
- Как рассчитать стоимость доставки формула
- Как вести расчеты в Excel
- Как правильно просчитать логистику
- Как рассчитать стоимость за килограмм
- Как формируется стоимость доставки
- Как правильно рассчитать стоимость доставки груза
- Как сделать автоматический расчет в Excel
- Как сделать расчет в таблице
- Как быстро посчитать в Excel
- Сколько стоит доставка груза
- Как рассчитать транспортные расходы на единицу товара
- Какой программой пользуются логисты
- Как вычислить стоимость
- Как рассчитать стоимость одного изделия
- Как определить цену товара формула
- Что входит в стоимость доставки
- Как рассчитать объем доставки
- Как посчитать объем доставки
- Как создать таблицу в Excel для расчета
- Как посчитать сумму в столбце
- Как сделать формулу в Excel сумма
- Что должен уметь хороший логист
- Сколько стоит отправить груз транспортной компанией
- Что нужно знать каждому Логисту
- Как рассчитать стоимость своей работы
- Сколько грамм в 1 кг
- Как рассчитать розничную цену товара
- Сколько стоит километр доставки
- Можно ли стоимость доставки включать в стоимость товара
- Как рассчитать стоимость перевозки тонна километр
- Как работать с формулой Если в Excel
- Как связать формулы в Excel
- Как сделать Автоформатирование в Excel
- Как должен работать логист
- Какой транспортной компанией дешевле отправить груз в 2022
- Как начать работу логистом
- Сколько стоит 1 километр доставки
- Как рассчитать стоимость формула
Как рассчитать стоимость доставки формула
Это цена езды автомобиля без учета расхода масла, износа запчастей и потраченного времени. Чтобы определить цену доставки груза на 1 км, необходимо воспользоваться следующей формулой: Стоимость бензина на 1 км × 4= цена перевозки за 1 км. 5×4=20 рублей.
Как вести расчеты в Excel
Создание простой формулы в Excel:
- Выделите на листе ячейку, в которую необходимо ввести формулу.
- Введите = (знак равенства), а затем константы и операторы (не более 8192 знаков), которые нужно использовать при вычислении. В нашем примере введите =1+1. Примечания:
- Нажмите клавишу ВВОД (Windows) или Return (Mac).
Как правильно просчитать логистику
В общем случае она выглядит так: Расчет по весу (тариф за 1 кг по указанному маршруту умножается на количество). То же самое, но по объему (тариф за 1 м3, умноженный на количество кубов, +10 % на укладку). Полученные цифры сравниваются, и выбирается наибольшее значение.
Как рассчитать стоимость за килограмм
Просто нужно стоимость разделить на массу и умножить результат на тысячу. Или можно проще, сразу делить на массу переведенную в кг. Это на самом деле очень просто. В одном килограмме 1000 грамм, то есть 180 грамм это 0.18 килограмма (запятую просто переносим на три знака влево).
Как формируется стоимость доставки
Стоимость доставки рассчитывается автоматически и складывается из нескольких факторов: региона и города, куда будет осуществляться доставка; выбранного способа доставки; количества посылок, на которое был разделён заказ.
Как правильно рассчитать стоимость доставки груза
Принято считать, что в 1 м3 «должно быть» 250 кг. Если в 1 м3 вашего груза больше 250 кг, то расчет стоимости перевозки идет по фактическому весу. Если груз легкий, но объемный и масса 1 м3 меньше 250 кг, то стоимость перевозки вычисляется по формуле 1 м3 = 250 кг.
Как сделать автоматический расчет в Excel
На вкладке Файл нажмите кнопку Параметры и выберите категорию Формулы. В Excel 2007 нажмите кнопку «Microsoft Office», выберите «Параметры Excel»и щелкните категорию «Формулы». В разделе Параметры вычислений установите флажок Включить итеративные вычисления.
Как сделать расчет в таблице
Вставка формулы в ячейку таблицы:
- Выделите ячейку таблицы, в которой должен находиться результат. Если ячейка не пустая, удалите ее содержимое.
- В разделе Работа с таблицами на вкладке Макет в группе Данные нажмите кнопку Формула.
- С помощью диалогового окна Формула создайте формулу.
Как быстро посчитать в Excel
Вы можете быстро подвести итоги в таблице Excel, включив параметр Переключить строку итогов. Щелкните любое место таблицы. Щелкните вкладку Конструктор таблиц > Параметры стилей > Строка итогов. Строка Итог будет вставлена в нижней части таблицы.
Сколько стоит доставка груза
Грузоперевозки по России цена
|
Марка автомобиля |
Тип |
Мин. стоимость заказа по Межгороду |
|---|---|---|
|
Газель 2 тонны |
Тент — Изотерм |
5000 руб. |
|
Газель 2 тонны |
Рефрижератор |
8000 руб. |
|
Бычок 5 тонник |
Тент — Изотерм |
6000 руб. |
|
Бычок 5 тонник |
Рефрижератор |
10.000 руб. |
Как рассчитать транспортные расходы на единицу товара
Формула расчета транспортных расходов на единицу товара: Стоимость доставки / себестоимость партии товара * себестоимость единицы товара.
Какой программой пользуются логисты
ITOB:FMS — комплекс програм для логистов по управлению транспортом ITOB:FMS объединяет функционал логистических программ для управления собственным и сторонним транспортом: «1С:Управление автотранспортом 8» и «1С:Центр спутникового мониторинга ГЛОНАСС/GPS».
Как вычислить стоимость
Цена каждого товара устанавливается путем простого умножения затрат на (1+M). Например, компания розничной торговли, работающая с большим количеством товаров, может рассчитать все цены, просто добавив нужную наценку к закупочной цене.
Как рассчитать стоимость одного изделия
Для этого все затраты предприятия делятся на количество изготовленных изделий. Получаем полную себестоимость одного изделия. Затем определяем желаемую прибыль, например, 20% от полной себестоимости изделия. Далее нужно сложить полную себестоимость изделия с суммой прибыли, и получим цену изделия.
Как определить цену товара формула
В первом варианте цена устанавливается так: из суммы полных затрат на производство товара и его внедрения на рынок (постоянные и переменные затраты) к ним прибавляется сумма ожидаемой прибыли и все делится на запланированное количество продукции: Цена = (Полные затраты + Прибыль) / Количество товара.
Что входит в стоимость доставки
Как вычисляется тариф по перевозкам
При расчете тарифа, как правило, используется стоимость одного километра пути. Основные издержки приходятся на топливо, материалы и оборудование. Также к этому добавляются расходы на оплату различных взносов (в том числе налогов) и инфраструктуру.
Как рассчитать объем доставки
Необходимо взять и перемножить три основных параметра груза — длину, ширину и высоту. Параметры должны рассчитываться в сантиметрах. Затем нужно поделить получившееся число на 5000.
Как посчитать объем доставки
Классическая формула расчета груза V=A*B*H. 5. Знаком V, обозначается общий объем груза, A — длина груза в метрах, B — ширина груза, Ah — высота груза.
Как создать таблицу в Excel для расчета
Проверьте, как это работает!:
- Выберите ячейку данных.
- На вкладке Главная выберите команду Форматировать как таблицу.
- Выберите стиль таблицы.
- В диалоговом окне Форматирование таблицы укажите диапазон ячеек.
- Если таблица содержит заголовки, установите соответствующий флажок.
- Нажмите кнопку ОК.
Как посчитать сумму в столбце
Один из простых и быстрых способов сложить значения в Excel — использовать авто сумму. Просто выберите пустую ячейку непосредственно под столбцом данных. Затем на вкладке Формула нажмите кнопку Авто сумма > сумму. Excel будет автоматически отсвечен диапазон для суммы.
Как сделать формулу в Excel сумма
Чтобы создать формулу: Введите в ячейку =СУММ и открываю скобки (. Чтобы ввести первый диапазон формул, который называется аргументом (частью данных, которую нужно выполнить), введите A2:A4 (или выберите ячейку A2 и перетащите ее через ячейку A6).
Что должен уметь хороший логист
Квалифицированный логист должен знать:
Основы организации перевозок; менеджмент транспортных услуг; основы экономики, коммерции; Page 2 документооборот; нормы транспортного и таможенного законодательства и т. п.
Сколько стоит отправить груз транспортной компанией
Игорь Бахарев
|
Компания |
Обрешётка |
Отслеживание |
|---|---|---|
|
Деловые Линии |
1300 р./м³, минимальная стоимость — 700 р, есть скидка 50% для определённых категорий |
15 р. |
|
ПЭК |
610 р./м³, минимальная стоимость 300 р. |
Бесплатно |
|
GTD (Кит) |
1000 р./м³, минимальная стоимость 500 р. |
Бесплатно |
|
ЖелДорЭкспедиция |
1000 р./м³, минимальная стоимость 600 р. |
Бесплатно |
Что нужно знать каждому Логисту
Абсолютно всем логистам необходимо:
- Знать основы делопроизводства и документооборота.
- Уметь работать с офисными программами (MS Office, 1C и другие CRM).
- Иметь представление о сфере, в которой они работают.
- Хорошо знать географию родной страны (а если речь идёт о международных перевозках, то и зарубежных стран).
Как рассчитать стоимость своей работы
Себестоимость + прибыль.
Стоимость услуги равна издержкам на ее создание плюс доля прибыли, которую хочется получить. Для начала нужно узнать себестоимость услуги, а после просто добавить долю ожидаемой прибыли.
Сколько грамм в 1 кг
В 1-м килограмме содержится 1000 грамм.
Как рассчитать розничную цену товара
Для этого разделите стоимость товара на стоимость закупки, от результата отнимите 1 и умножьте на 100%.
Сколько стоит километр доставки
Тарифы грузоперевозок
|
Тип автотранспорта |
Объём кузова (м3) |
Стоимость |
|---|---|---|
|
Газель тент |
9 |
от 20 руб /км |
|
Газель фургон |
10 |
от 20 руб /км |
|
Цельнометаллический |
9 |
от 20 руб /км |
|
Спринтер тент |
16 |
от 22 руб /км |
Можно ли стоимость доставки включать в стоимость товара
Организация-поставщик вправе при реализации товаров одним покупателям учитывать транспортные расходы на их доставку в цене товара, а другим — выделять их в качестве отдельной услуги.
Как рассчитать стоимость перевозки тонна километр
Калькулятор ниже и выполняет это довольно простой расчет — сначала рассчитывается общая стоимость перевозки, как произведение расстояния на цену за километр, потом рассчитывается количество тоннокилометров, как произведение расстояния на массу перевезенного груза, и дальше общая стоимость делится на количество
Как работать с формулой Если в Excel
Функция ЕСЛИ, одна из логических функций, служит для возвращения разных значений в зависимости от того, соблюдается ли условие. Например: =ЕСЛИ(A2>B2;«Превышение бюджета»;«ОК») =ЕСЛИ(A2=B2; B4-A4;«»)
Как связать формулы в Excel
В ячейку, куда мы хотим вставить связь, ставим знак равенства (так же как и для обычной формулы), переходим в исходную книгу, выбираем ячейку, которую хотим связать, щелкаем Enter. Вы можете использовать инструменты копирования и автозаполнения для формул связи так же, как и для обычных формул.
Как сделать Автоформатирование в Excel
Выберите Файл > Параметры. В окне Excel параметры выберите параметры > проверки > проверки. На вкладке Автоформат при типе заведите флажки для автоматического форматирования, которые вы хотите использовать.
Как должен работать логист
Логист — это специалист, который организует транспортные потоки. Он координирует доставку товаров от производства до точек реализации. Логист продумывает способы и маршруты перевозки от упаковки, погрузки на складе до передачи заказчику. Он организовывает особую транспортировку для опасных или скоропортящихся грузов.
Какой транспортной компанией дешевле отправить груз в 2022
В 2022 году самой дешёвой транспортной компанией России может быть названа DPD. Компания предлагает лучшие цены на доставку грузов весом 1 и 5 кг по подавляющему числу направлений, а также предлагает хорошие условия по многим направлениям для 10 и 20 кг.
Как начать работу логистом
Оптимальное начало карьеры в логистике — это работа на стартовых операционных позициях, то есть сотрудником склада, водителем или диспетчером. Такой старт позволяет будущему менеджеру или аналитику на практике понять основные логистические процессы и понять, в каком направлении ему интересно развиваться дальше.
Сколько стоит 1 километр доставки
Тарифы пробега по России
|
Марка автомобиля |
Грузовая подъёмность |
Тарифы, за 1 км пробега а/м по России, межгород |
|---|---|---|
|
Газель — фермер |
1,5т. |
19 руб/км |
|
Бычок |
3т. |
18 руб/км |
|
Бычок (гидроборт) |
3т. |
21 руб/км |
|
Бычок — рефрижератор |
3т. |
23 руб/км |
Как рассчитать стоимость формула
В первом варианте цена устанавливается так: из суммы полных затрат на производство товара и его внедрения на рынок (постоянные и переменные затраты) к ним прибавляется сумма ожидаемой прибыли и все делится на запланированное количество продукции: Цена = (Полные затраты + Прибыль) / Количество товара.
Оставить отзыв (1)
В этой статье мы пошагово рассмотрим, как решить транспортную задачу посредством функций MS Excel. Задачи данного типа изучаются студентами на таких дисциплинах, как исследование операций и методы оптимальных решений.
Условие
Есть некие предприятия и склады с грузом. Каждое предприятие, нуждается в определённом объёме нашего груза. Каждый склад доставляет тонну груза по собственному тарифу. Таким образом, нужно составить маршрут, по которому мы развезём объём груза, удовлетворяющий каждое предприятие, и при этом затратим меньше всего средств.
Так транспортная задача выглядит в своём наиболее общем и типовом виде.
С – это цена за тонну. X – это то, сколько мы привезём тонн со склада на предприятие. Например, если мы примем X11 равным 5, это будет значить, что со склада А1 к потребителю B1 мы повезём 5 тонн по цене C11. Вот нам и нужно как-то распределить всё так, чтобы потратить меньше всего денег.
Варианты решения
Транспортную задачу можно решить «вручную». Существует несколько подходов к её решению на бумаге. Среди них:
- Метод опорного плана;
- Метод минимального элемента;
- Метод Фогеля.
Как правило, решая задачу одним из этих способов, вы получаете решение, находите потенциалы для него и понимаете, что в числе потенциалов есть положительные значения. Соответственно, это говорит о том, что вы нашли неверное решение. Далее вам нужно действовать, что называется, наугад. Вы переставляете различные цифры в таблице, пробуете разные варианты, словом, ищите решение методом «научного тыка». Далее снова пересчитываете потенциалы, и снова ничего не срастается.
Однозначного алгоритма, работающего безотказно в любых условиях, к сожалению, пока не придумали.
Однако для решения транспортной задачи или проверки полученного нами на бумаге результата, мы можем воспользоваться функционалом MS Excel.
Транспортная задача в Экселе
Для решения нам потребуется надстройка «Поиск решения». Возможно, она не будет активирована в вашем редакторе по умолчанию, поэтому, проделываем следующую очередность действий:
- Жмём «Файл»;
- В появившемся меню нажимаем по предпоследней кнопке «Параметры»;
- Вновь находим предпоследний пункт «Надстройки» и переходим в «Управление»:
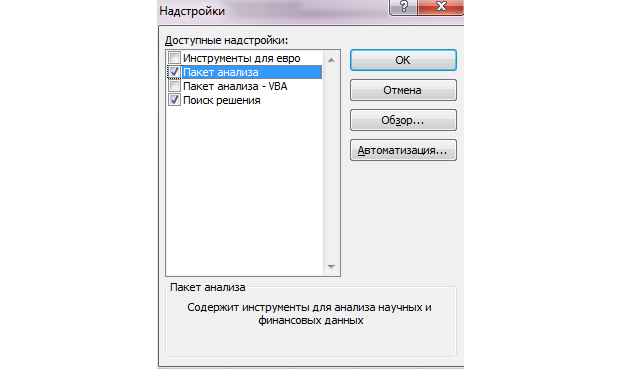
- Ставим галочку в появившемся окне рядом с пунктов «Поиск решения» и жмём «ОК».
Поиск решения активирован. Далее он будет нами использован.
Пример задачи
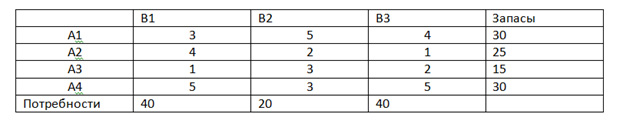
На складах A1 — A4 есть суммарно 100 тонн зерна, и их нужно развести по текущим расценкам в пункты B1 – B3, потратив как можно меньше средств на доставку. Тарифы на доставку указаны в центре таблицы.
Шаг 1
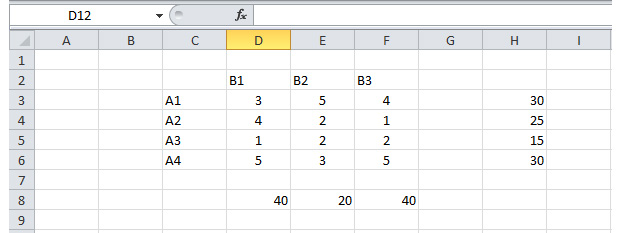
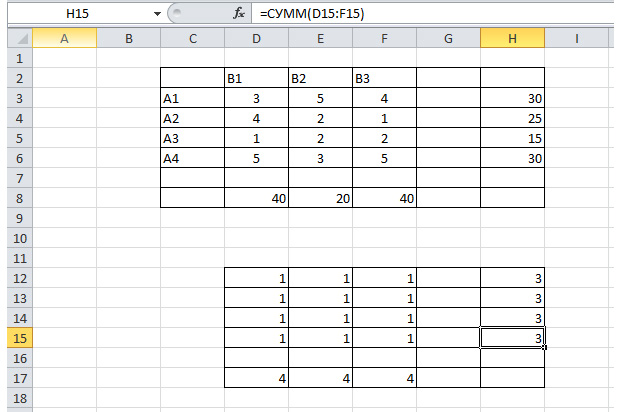
Дублируем нашу таблицу в Excel.
Шаг 2
Рисуем другую таблицу.
Диапазон ячеек D12 – F15 заполняем единицами. Эти значения мы впоследствии будем изменять, чтобы найти самый дешёвый вариант перевозки. В диапазоне H12 – H15 должна быть сумма трёх единиц таблицы в строке D12 – F12, а в D17 – F17 – сумма четырёх единиц в столбце. Так напротив каждой строки и каждого столбца
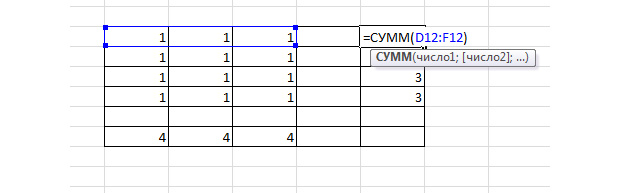
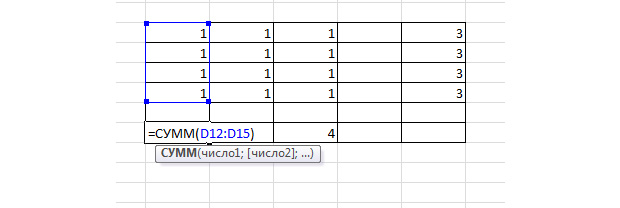
Шаг 3
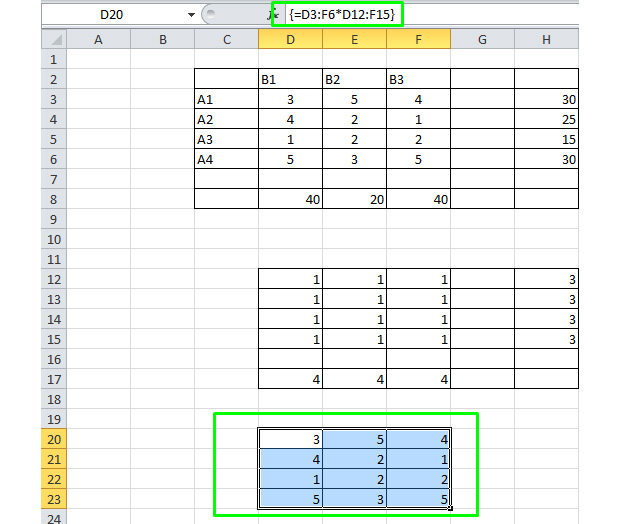
Рисуем третью таблицу, которая перемножит соответствующие ячейки первых двух таблиц.
Для этого выделяем диапазон 3 на 4 клетки, жмём на кнопку « = », выделяем диапазон D3-F6, жмём на клавиатуре « * », выделяем D12 – F15 и зажимаем сочетание клавиш Ctrl + Shift + Enter. Всё, вы перемножили значения.
Шаг 4
Теперь суммируем все значения последней таблицы. Для этого просто выберите произвольную свободную ячейку в MS Excel. Введите в неё « =СУММ( » и выделите третью таблицу. Нажмите Enter.
Шаг 5
Переходим во вкладку «Данные» и находим там «Поиск решения».
Щелкаем по данной кнопке. Далее всё делаем, как представлено на рисунке.
Описываю сверху вниз всё окно. Выберите целевую ячейку ту, которую мы сделали в 4-ом шаге нашего решения. Далее выберите минимум. В поле «Изменяя ячейки переменных» выберите диапазон, где мы проставили единицы. Выставляем ограничения. Значения, которые будут находиться вместо единиц, должны быть больше нуля и целыми, а потребности не должны превысить запасов. Жмём «Найти решение».
Получаем следующий результат.
Если вы всё сделали правильно, то у вас должно быть всё точно так же.
Заключение
По второй таблице сверху вы видите, сколько тонн и куда мы повезём. В третьей таблице вы видите, сколько это будет стоить. Например, мы повезём 30 тонн в B1 со склада A1 и 10 тонн со склада A3, так как спрос у пункта B1 равен 40. Аналогично и с другими пунктами.
Оптимизация доставки
Постановка задачи
Предположим, что компания, где вы работаете, имеет три складских помещения, откуда товар поступает в пять ваших магазинов, разбросанных по всей Москве.
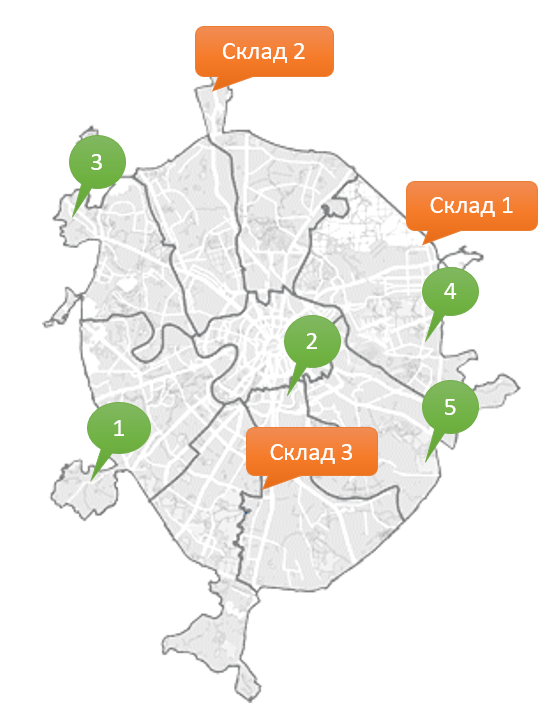
Каждый магазин в состоянии реализовать определенное, известное нам количество товара. Каждый из складов имеет ограниченную вместимость. Задача состоит в том, чтобы рационально выбрать – с какого склада в какие магазины нужно доставлять товар, чтобы минимизировать общие транспортные расходы.
Перед началом оптимизации необходимо будет составить несложную таблицу на листе Excel – нашу математическую модель, описывающую ситуацию:
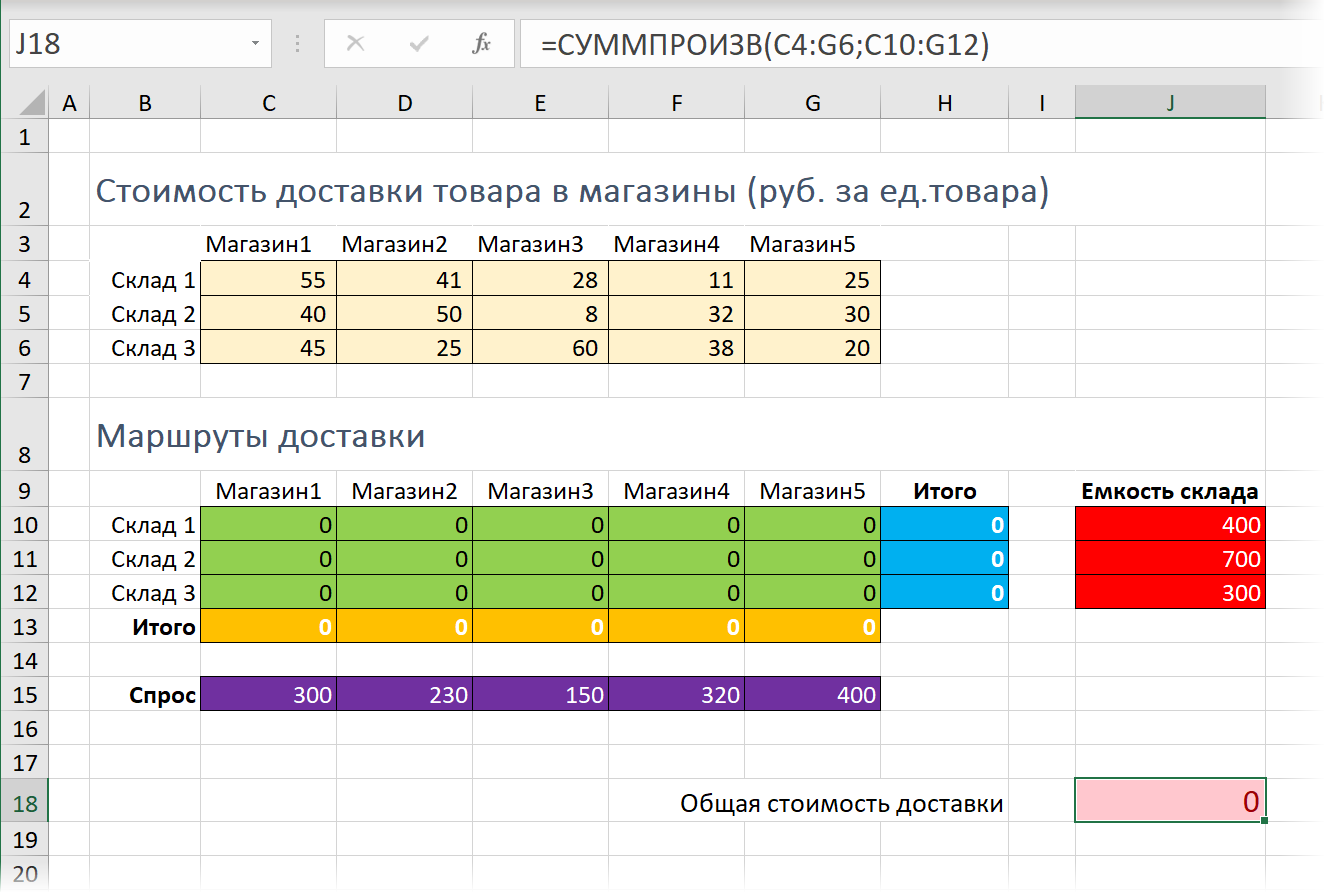
Подразумевается, что:
- Светло-желтая таблица (C4:G6) описывает стоимость доставки одной единицы товара от каждого склада до каждого магазина.
- Лиловые ячейки (C15:G14) описывают необходимое для каждого магазина количество товаров на реализацию.
- Красные ячейки (J10:J13) отображают емкость каждого склада – предельное количество товара, которое склад вмещает.
- Желтые (C13:G13) и синие (H10:H13) ячейки – соответственно, суммы по строке и столбцу для зеленых ячеек.
- Общая стоимость доставки (J18) вычисляется как сумма произведений количества товаров на соответствующие им стоимости доставки — для подсчёта здесь используется функция СУММПРОИЗВ (SUMPRODUCT).
Таким образом, наша задача сводится к подбору оптимальных значений зеленых ячеек. Причем так, чтобы общая сумма по строке (синие ячейки) не превышала вместимости склада (красные ячейки), и при этом каждый магазин получил необходимое ему количество товаров на реализацию (сумма по каждому магазину в желтых ячейках должна быть как можно ближе к требованиям – лиловым ячейкам).
Решение
В математике подобные задачи выбора оптимального распределения ресурсов сформулированы и описаны уже давно. И, конечно же, давно разработаны способы их решения не тупым перебором (что очень долго), а за весьма небольшое количество итераций. Excel предоставляет пользователю такой функционал с помощью надстройки Поиск решения (Solver) с вкладки Данные (Data):

Если на вкладке Данные вашего Excel такой команды нет – ничего страшного — значит надстройка просто еще не подключена. Для ее активации откройте Файл, далее выберите Параметры – Надстройки – Перейти (Options — Add-Ins — Go To). В открывшемся окне поставьте галочку напротив нужной нам строки Поиск решения (Solver).
Запустим надстройку:
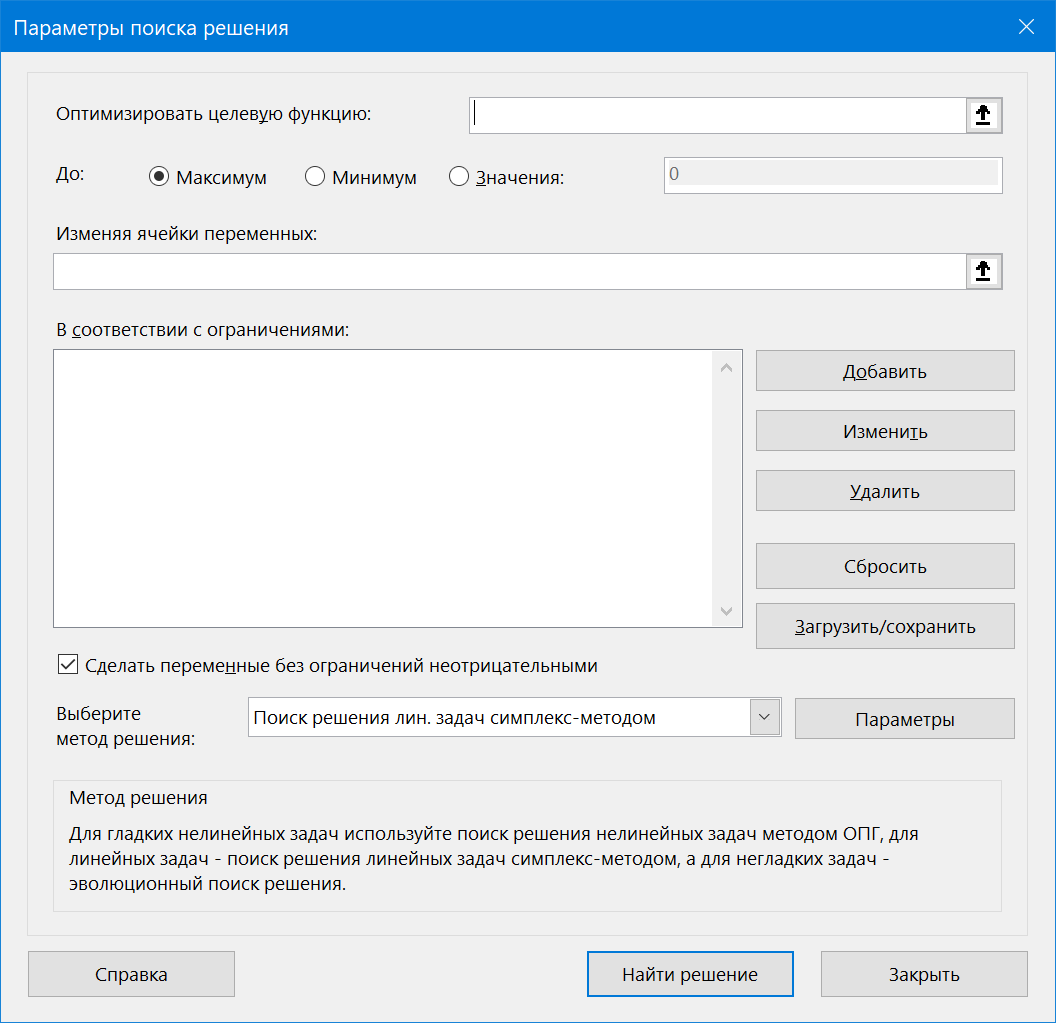
В этом окне нужно задать следующие параметры:
- Оптимизировать целевую функцию (Set target cell) – тут необходимо указать конечную главную цель нашей оптимизации, т.е. розовую ячейку с общей стоимостью доставки (J18). Целевую ячейку можно минимизировать (если это расходы, как в нашем случае), максимизировать (если это, например, прибыль) или попытаться привести к заданному значению (например, вписаться ровно в выделенный бюджет).
- Изменяя ячейки переменных (By changing cells) – здесь укажем зеленые ячейки (C10:G12), варьируя значения которых мы хотим добиться нашего результата – минимальных затрат на доставку.
- В соответствии с ограничениями (Subject to the Constraints) – список ограничений, которые надо учитывать при проведении оптимизации. Для добавления ограничений в список нужно нажать кнопку Добавить (Add) и ввести условие в появившееся окно. В нашем случае, это будет ограничение на спрос:
и ограничение на предельный объем складов:
Кроме очевидных ограничений, связанных с физическими факторами (вместимость складов и средств перевозки, ограничения бюджета и сроков и т.д.) иногда приходится добавлять ограничения «специально для Excel». Так, например, Excel легко может устроить вам «оптимизацию» стоимости доставки, предложив возить товары из магазинов обратно на склад — расходы при этом станут отрицательными, т.е. мы получим прибыль! 
Чтобы этого не случилось лучше оставить включенным флажок Сделать переменные без ограничений неотрицательными или даже иногда явно прописать такие моменты в списке ограничений.
После настройки всех необходимых параметров окно должно выглядеть следующим образом:
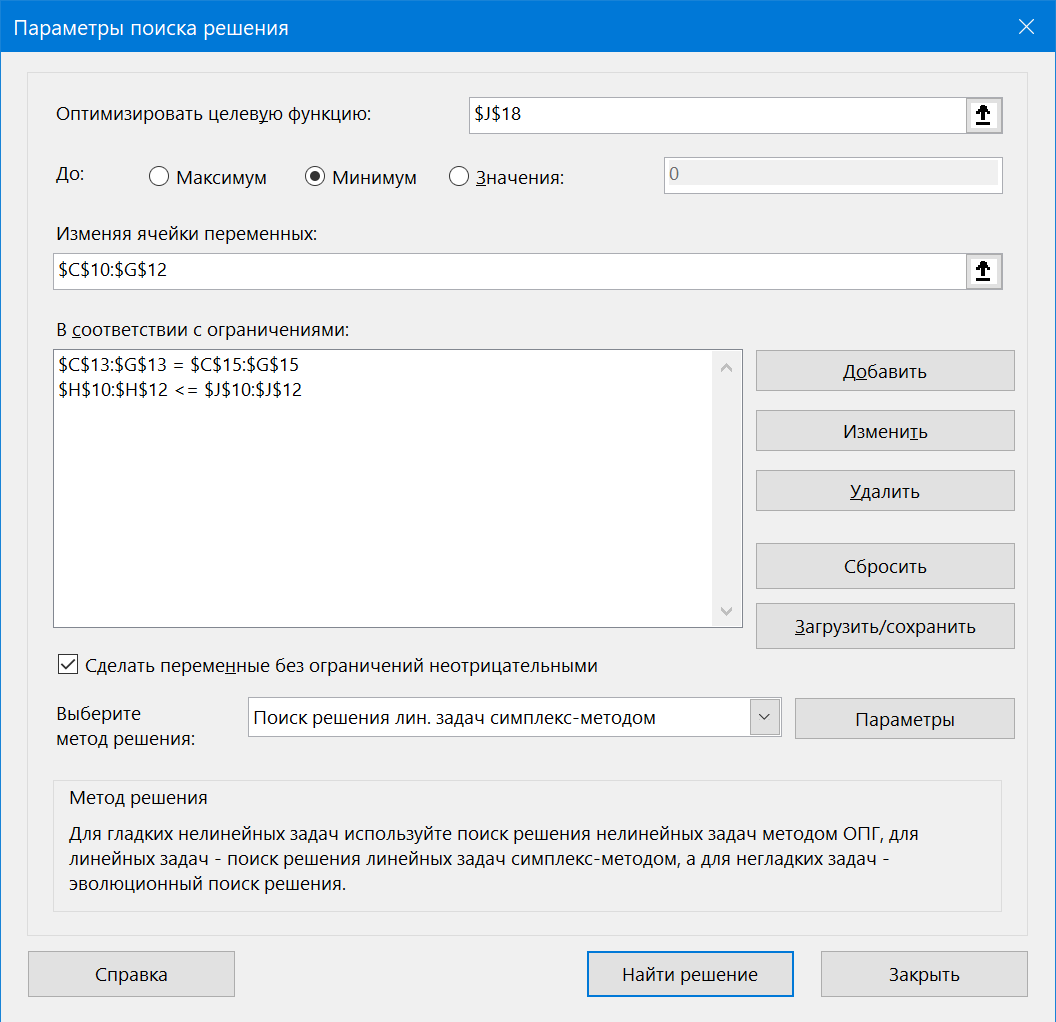
В выпадающем списке Выберите метод решения (Select a solving method) дополнительно требуется подобрать подходящий математический метод для решения на выбор из трех вариантов:
- Симплекс-метод — простой и быстрый метод для решения линейных задач, т.е. задач, где выход линейно зависит от входа.
- Метод общего понижающего градиента (ОПГ) — для нелинейных задач, где между входными и выходными данными есть сложные нелинейные зависимости (например, зависимость продаж от расходов на рекламу).
- Эволюционный поиск решения — относительно новый метод оптимизации, основанный на принципах биологической эволюции (привет Дарвину). Этот метод работает в разы дольше первых двух, но может решать практически любые задачи (нелинейные, дискретные).
Наша задача явно относится к линейным: доставили 1 шт — затратили 40 р., доставили 2 шт — затратили 80 р. и т.д., так что симплекс-метод будет наилучшим выбором.
Теперь, когда данные для расчета введены, нажмем кнопку Найти решение (Solve), чтобы начать оптимизацию. В тяжелых случаях с большим количеством изменяемых ячеек и ограничений нахождение решения может занять продолжительное время (особенно с эволюционным методом), но наша задача для Excel проблемы не составит – через пару мгновений мы получим следующие результаты:
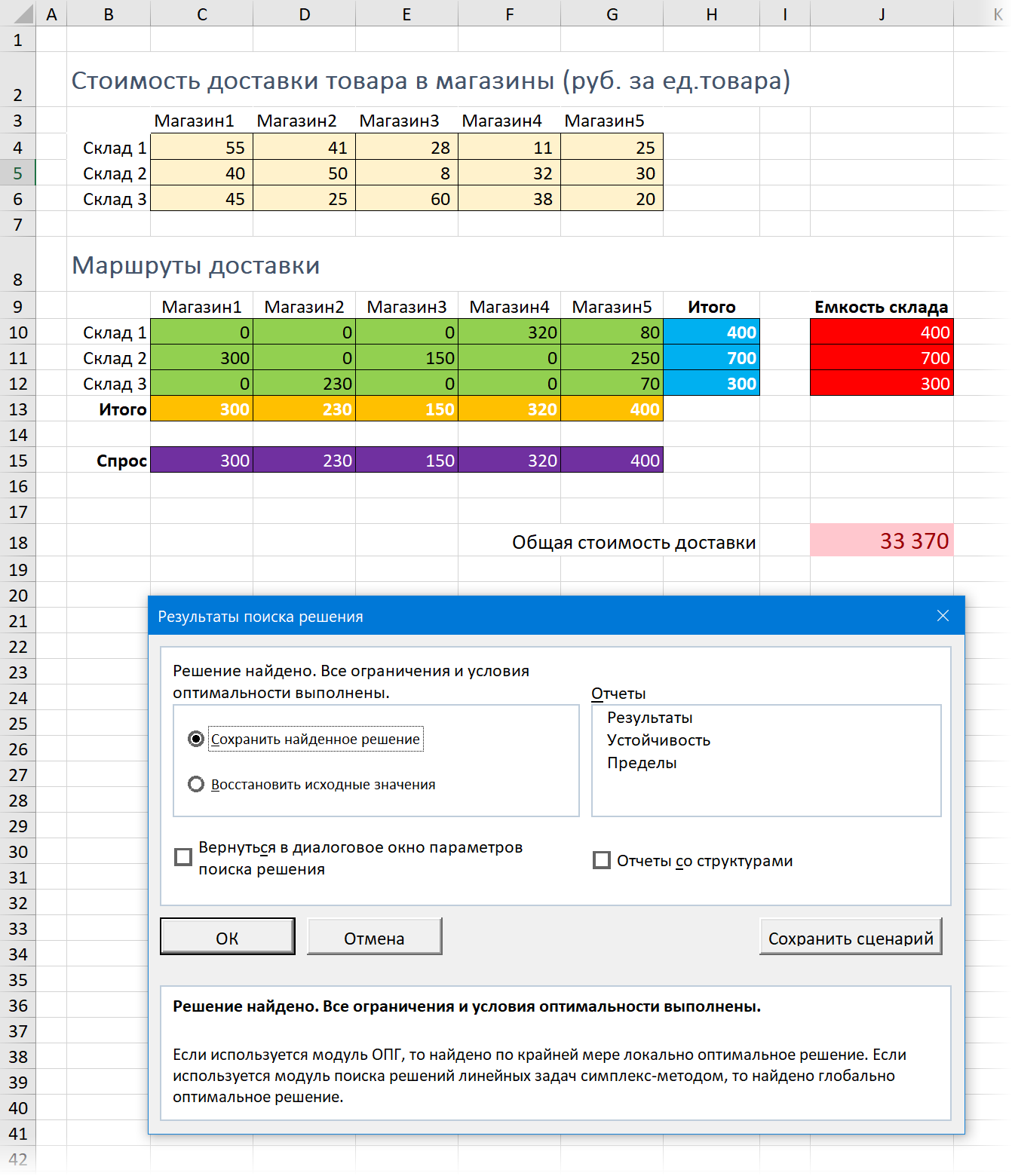
Обратите внимание на то, как интересно распределились объемы поставок по магазинам, не превысив при этом емкости наших складов и удовлетворив все запросы по требуемому количеству товаров для каждого магазина.
Если найденное решение нам подходит, то можно его сохранить, либо откатиться назад к исходным значениям и попробовать еще раз с другими параметрами. Также можно сохранить подобранную комбинацию параметров как Сценарий. По желанию пользователя Excel может построить три типа Отчетов по решаемой задаче на отдельных листах: отчет по результатам, отчет по математической устойчивости решения и отчет по пределам (ограничениям) решения, однако они, в большинстве случаев, интересны только специалистам.
Бывают, однако, ситуации, когда Excel не может найти подходящего решения. Имитировать такой случай можно, если указать в нашем примере требования магазинов в сумме большие, чем общая вместимость складов. Тогда при выполнении оптимизации Excel попытается приблизиться к решению, насколько это возможно, а затем выдаст сообщение о невозможности найти решение. Тем не менее, даже в этом случае мы имеем массу полезной информации – в частности можем видеть «слабые звенья» наших бизнес-процессов и понять направления совершенствования.
Рассмотренный пример, конечно, является относительно простым, но легко масштабируется под решение гораздо более сложных задач. Например:
- Оптимизация распределения финансовых средств по статьям расходов в бизнес-плане или бюджете проекта. Ограничениями, в данном случае, будут являться объемы финансирования и сроки выполнения проекта, а целью оптимизирования – максимизация прибыли и минимизация расходов на проект.
- Оптимизация расписания сотрудников с целью минимизации фонда заработной платы предприятия. Ограничениями, в этом случае, будут пожелания каждого сотрудника по графику занятости и требования штатного расписания.
- Оптимизация инвестиционных вложений – необходимость грамотно распределить средства между несколькими банками, ценными бумагами или акциями предприятий с целью, опять же, максимизации прибыли или (если это более важно) минимизации рисков.
В любом случае, надстройка Поиск решения (Solver) является весьма мощным и красивым инструментом Excel и достойна того, чтобы вы обратили на нее свое внимание, поскольку может выручить во многих сложных ситуациях, с которыми приходится сталкиваться в современном бизнесе.
Это материал служит продолжением серии моих предыдущих статей по эффективному управлению товарными запасами. Сегодня мы разберем тему, как в excel вести учет товара. Как в одну таблицу excel свести товарные остатки, заказы, ранее заказанные товары, АВС анализ и так далее.
Несомненно, эту статью можно рассматривать, как отдельный материал для учета и планирования товара и его запасов в excel. Я постараюсь все наглядно и просто показать, избегая макросов.
Содержание:
- Excel, как отличный инструмент учета товара
- Как в excel вести учет товара, самый простой шаблон
- Как в excel вести учет товара с учетом прогноза будущих продаж
- Расстановка в excel страхового запаса по АВС анализу
- Учет в excel расширенного АВС анализа
Аналитика в Excel
Итак, все начинается даже не с аналитики, а просто с упорядочивания данных по товарам. Excel, это отличный инструмент, для подобных задач. Лучшего пока не придумали. По крайней мере для малого и среднего бизнеса, это самый эффективный и доступный метод ведения товарных остатков, не говоря об аналитике запасов, АВС анализа, прогноза будущих закупок и так далее.
Мы начнем с самого простого. Затем будет углубляться и расширять возможности ведения товарного учета в excel. Каждый выберет, на каком уровне будет достаточно для своей работы.
Как в Excel вести учет товара, простой шаблон
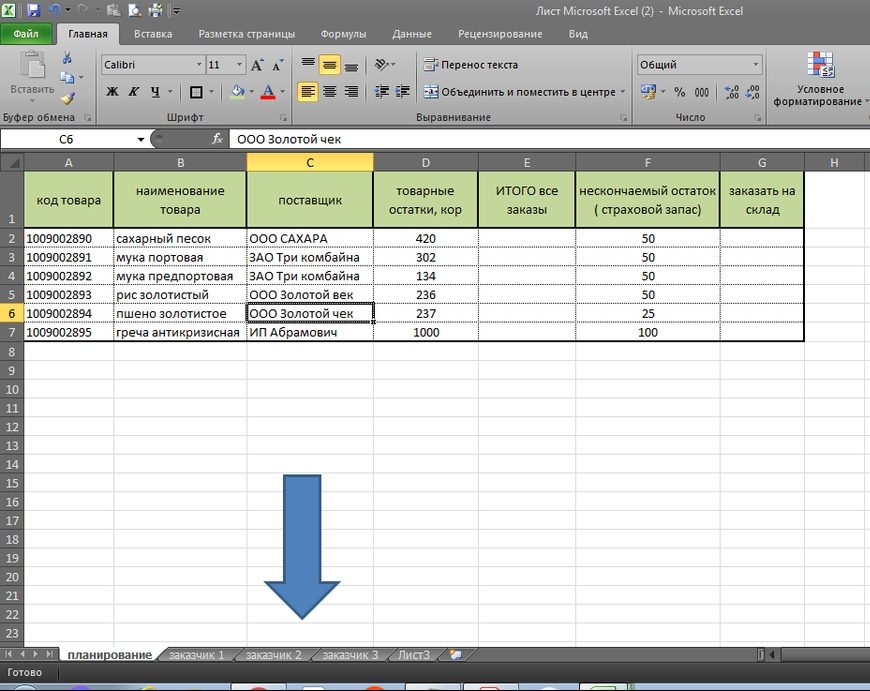
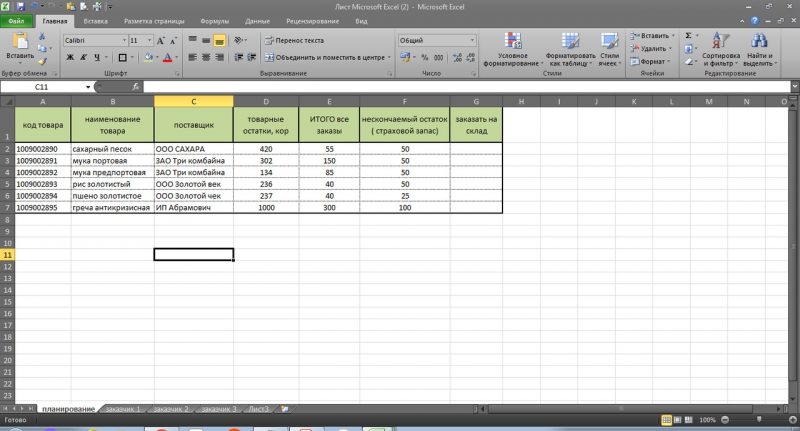
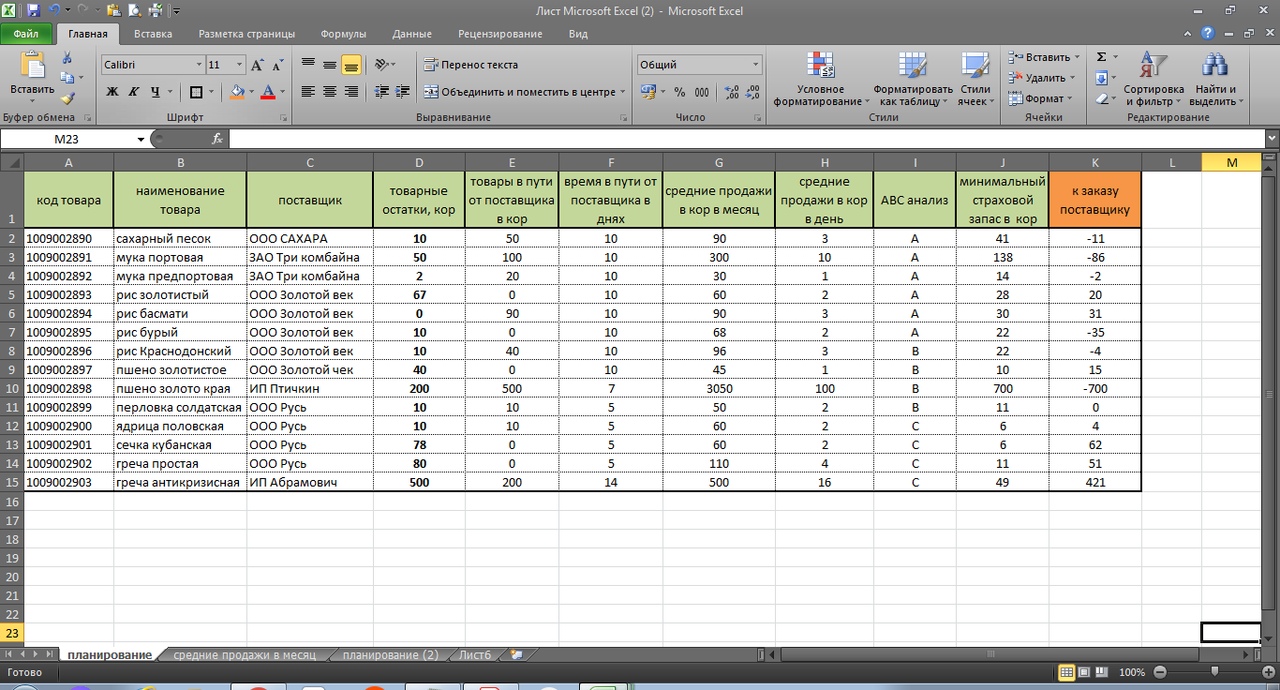
Начинаем с самого простого, а именно с того, когда организация собирает заявки с магазинов и нужно свести заказы воедино, сделать заказ поставщику. (см. рис 1)
В столбце Е, с помощью простой формулы мы сведем заявки с наших разных клиентов. Столбец F, это наш нескончаемый остаток или страховой запас. В столбец G мы получим данные, сколько нам потребуется заказать поставщику исходя из наших остатков, заявок магазинов и страхового запаса.
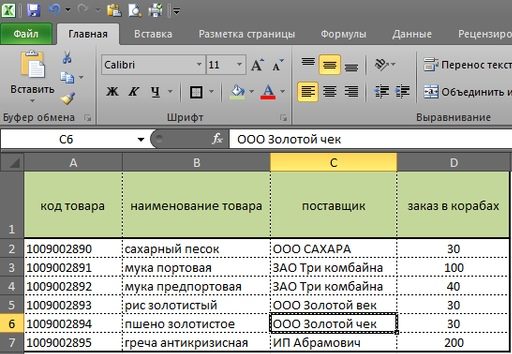
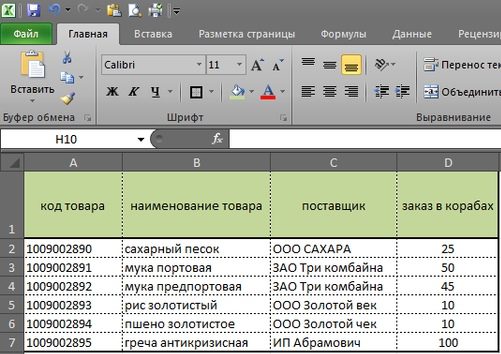
Синяя стрелка указывает на закладки, где «Заказчик 1», «Заказчик 2» и так далее. Это заявки с наших магазинов или клиентов, см рис 2 и рас. 3. У каждого заказчика свое количество, в нашем случае, единица измерения — в коробах.
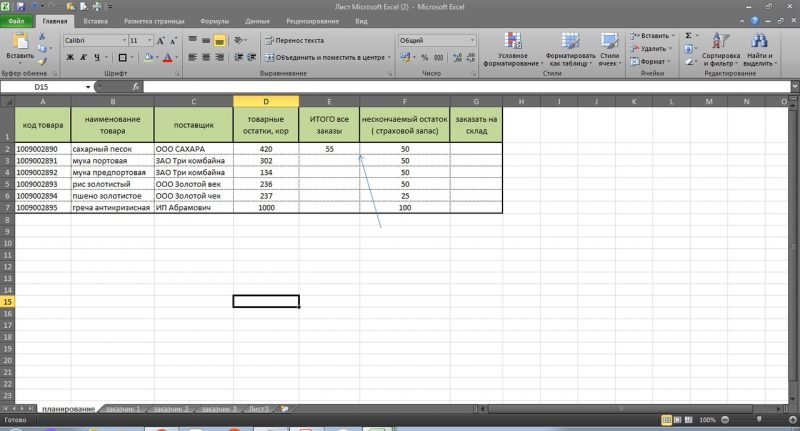
Теперь мы можем рассмотреть, как в excel вести учет товара, когда требуется свести заявки в одну таблицу. С помощью простой формулы, в первую очередь, мы сводим все заявки с магазинов в столбец Е., см рис 4.
=(‘заказчик 1′!D2+’заказчик 2’!D2)
Протягиваем формулу вниз по столбцу Е и получаем данные по всем товарам. см. рис 5. Мы получили сводную информацию со всех магазинов. (здесь учтено только, 2 магазина, но думаю, суть понятна)
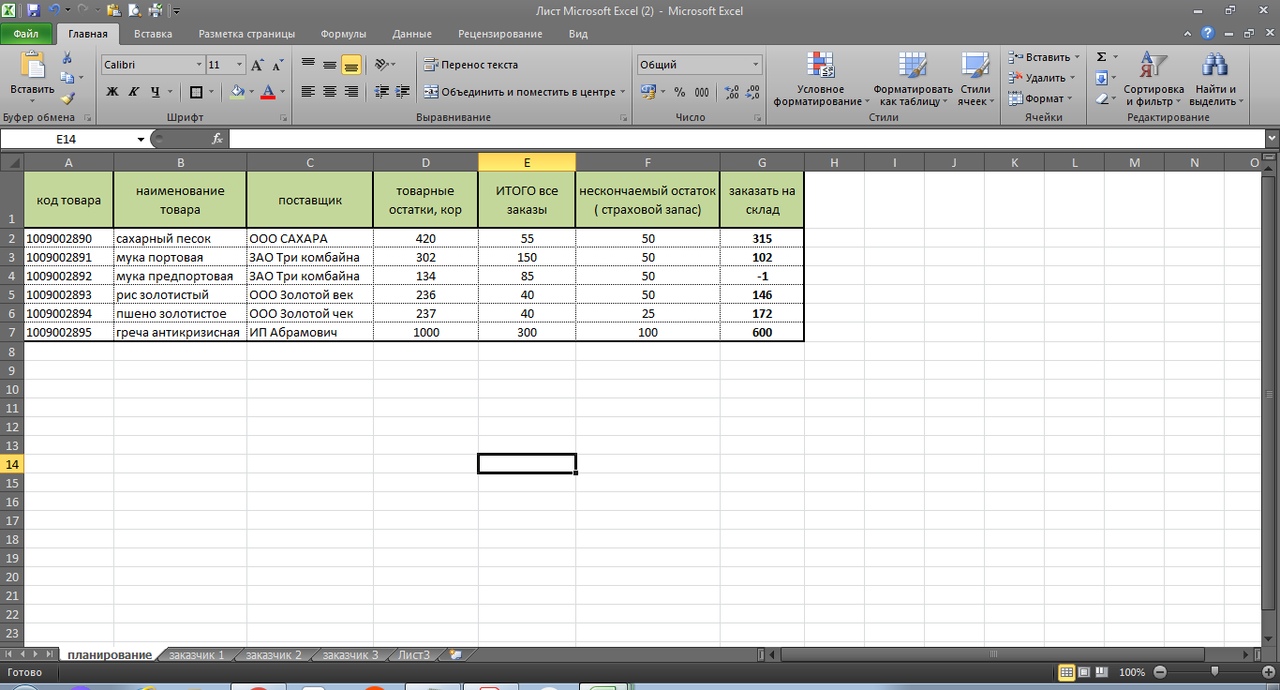
Теперь у нам остается учесть товарные остатки, и заданный минимальный страховой запас для того, что бы сделать заказ поставщику на нужное нам количество. Также прописываем простую формулу:
=(D2-E2)-F2
протягиваем формулу вниз по столбцу и получаем к заказу поставщику 1 короб по муке предпортовой. По остальным товарам есть достаточный товарный запас.
Обратите внимание, что F (страховой запас) мы также вычли из остатка, что бы он не учитывался в полученных цифрах к заказу.
Повторюсь, здесь лишь суть расчета.
Мы понимаем, что заказывать 1 короб, наверное нет смысла. Наш страховой запас, в данном случае не пострадает из-за одной штуки.
Теперь, мы переходим к более сложным расчетам, когда мы будем основываться на анализе продаж прошлых периодов, с учетом расширенного АВС анализа, страхового запаса, товаров в пути и так далее.
Как в Excel вести учет товара на основе продаж прошлых периодов
Как управлять складскими запасами и строить прогноз закупок в Excel основываясь на продажах прошлых периодов, применяя АВС анализ и другие инструменты, это уже более сложная задача, но и гораздо более интересная.
Я здесь также приведу суть, формулы, логику построения управления товарными запасами в Excel.
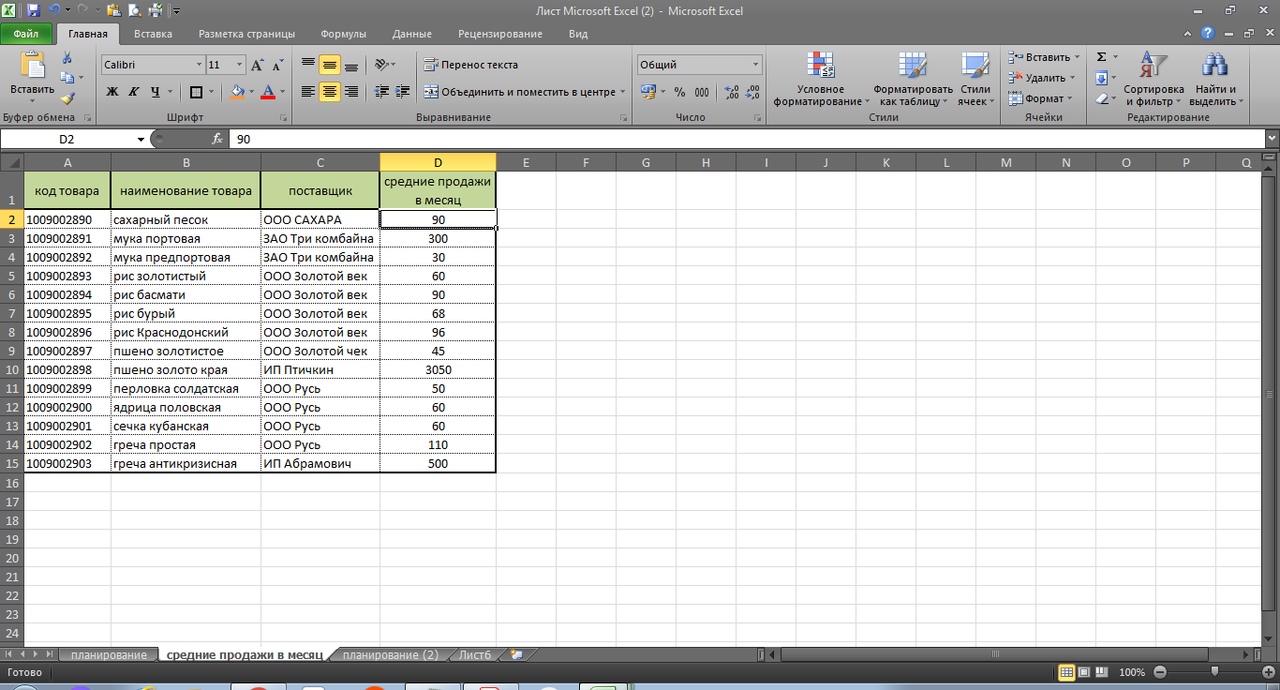
Итак, у мы выгружаем с базы средние продажи в месяц. Пока в данном варианте будем считать, что они стабильны.
Далее их подтягиваем средние продажи в столбец G нашего планировщика, то есть в сводный файл.
Делаем это с помощью формулы ВПР.
=ВПР(A:A;’средние продажи в месяц’!A:D;4;0)
Суть этой формулы заключается в том, что требуемые данные подтягиваются по уникальному коду или другому значению, не зависимо от того, в каком порядке они находятся в источнике денных.
Также мы можем подтянуть и другие требуемые данные, например нужную нам информацию, что уже везется нам поставщиком, как товары в пути. Мы их также обязательно должны учесть.
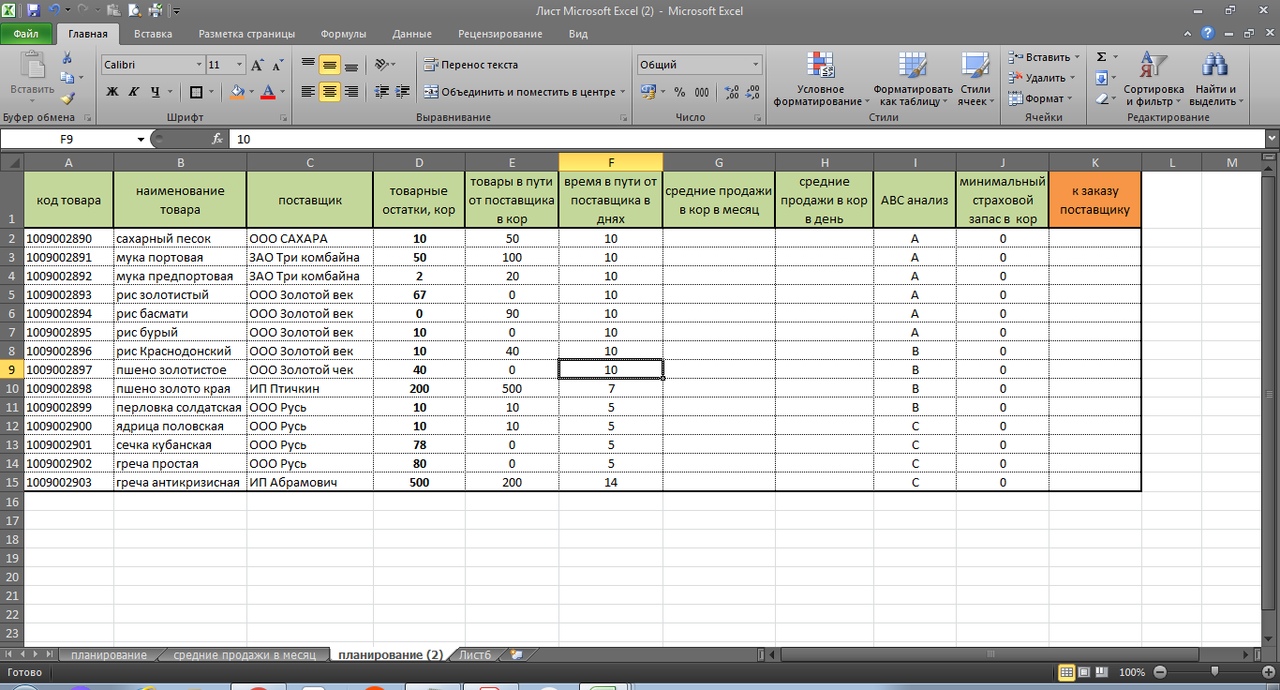
В итоге, у нас получается вот такая картина:
Первое. Средние продажи в месяц, мы превратили, в том числе для удобства в средние продажи в день, простой формулой = G/30,5 (см. рис 9). Средние продажи в день — столбец H
Второе. Мы учли АВС анализ по товарам. И ранжировали страховой запас относительно важности товара по рейтингу АВС анализа. (Эту важную и интересную тему по оптимизации товарных запасов мы разбирали в предыдущей статье)
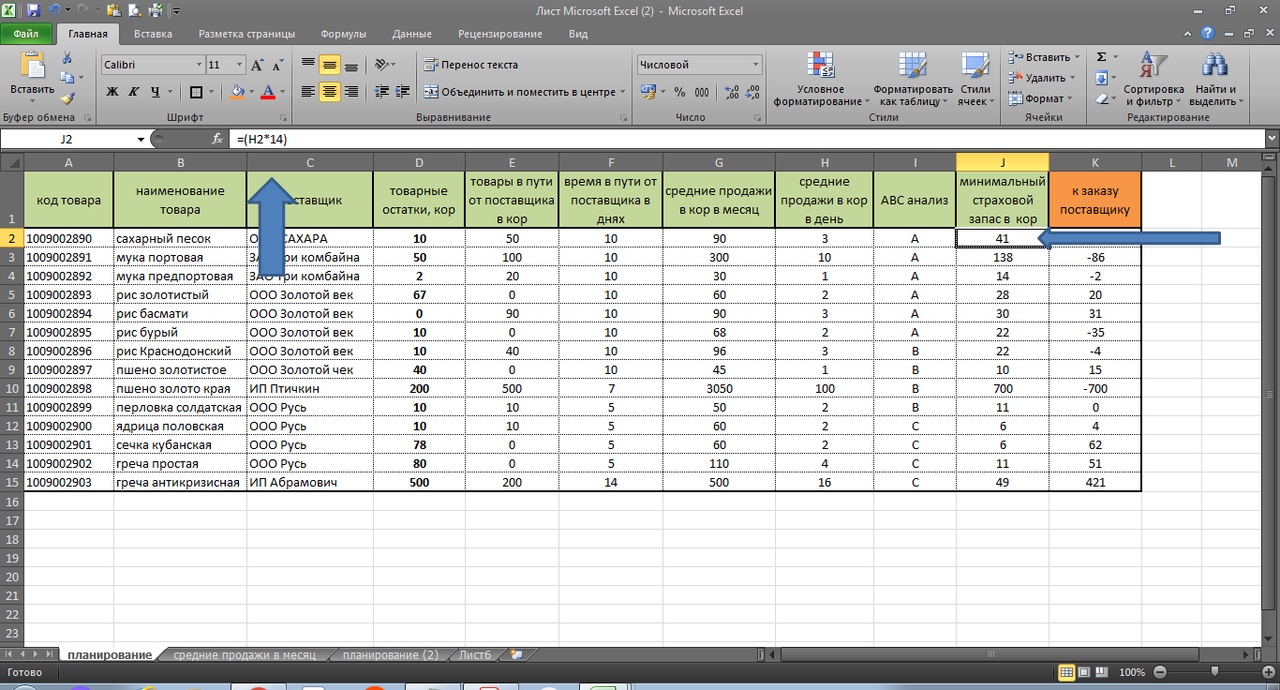
По товарам рейтинга А, (где А — наиболее прибыльный товар) мы заложили страховой запас в днях относительно средних дневных продаж в 14 дней. Смотрим первую строку и у нас получилось:
3 коробки продажи в день *14 дней продаж = 42 дня. (41 день у нас потому, что Excel округлил при расчете 90 коробов в месяц/30,5 дней в месяце). См. формулу
=(H2*14)
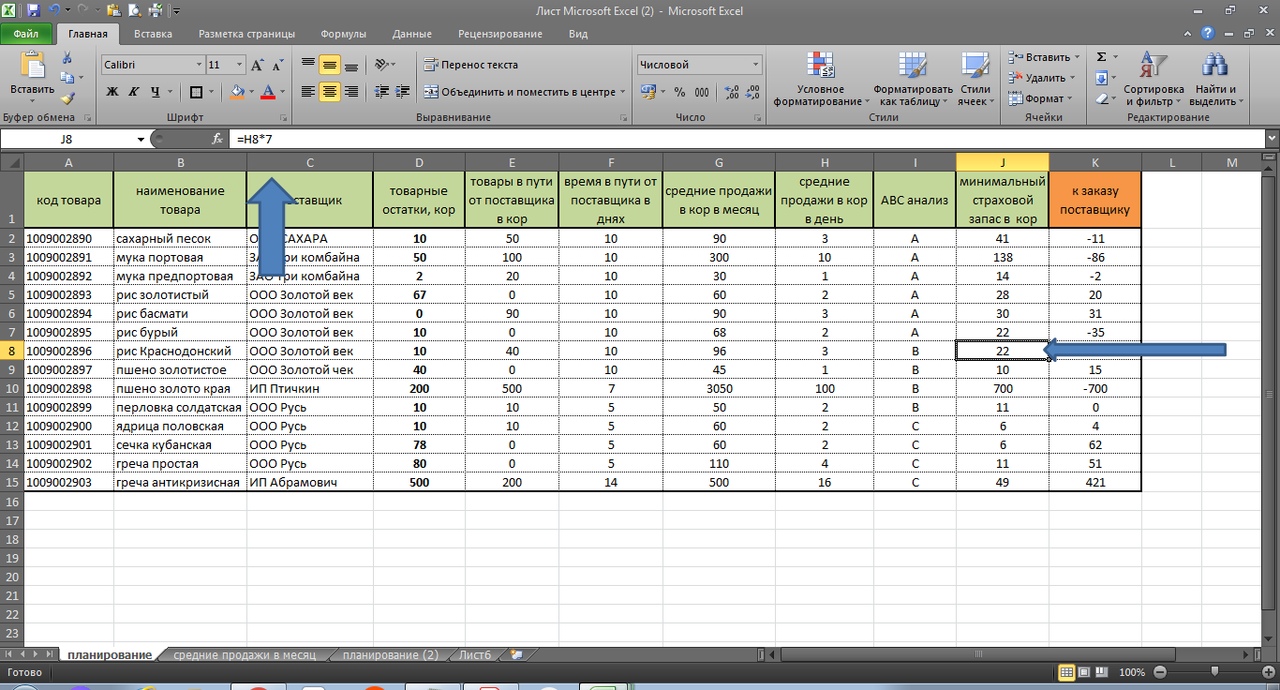
Третье. По рейтингу товара В, мы заложили 7 дней страхового запаса. См рис 11. ( По товарам категории С мы заложили страховой запас всего 3 дня)
Вывод
Таким образом, сахарного песка (см. первую строчку таблицы) мы должны заказать 11 коробов. Здесь учтены 50 коробов в пути, 10 дней поставки при средних продажах 3 короба в день).
Товарный остаток 10 коробов + 50 коробов в пути = 60 коробов запаса. За 10 дней продажи составят 30 коробов (10*3). Страховой запас у нас составил 41 короб. В итоге, 60 — 30 — 42 = минус 11 коробов, которые мы должны заказать у поставщика.
Для удобства можно (-11) умножить в Ecxel на минус 1. Тогда у нас получиться положительное значение.
Конечно, здесь показал только образец и суть как вести учет товара и запасов в Excel. Но уже большой шаг вперед относительно субъективных ощущений и возможностей небольших предприятий. И все можно детализировать и уточнять. В следующей главе мы рассмотрим это.
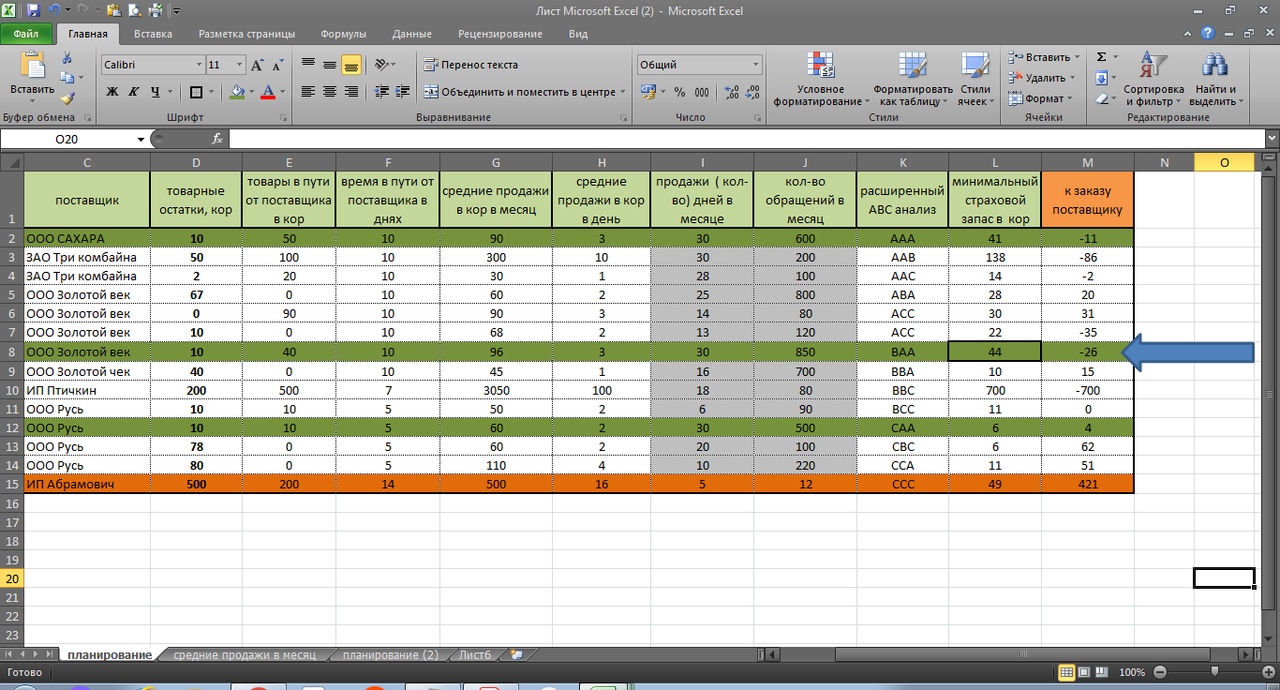
Складской учет товаров в Excel с расширенным АВС анализом.
Складской учет товаров в Excel можно делать аналитически все более углубленным по мере навыков и необходимости.
В предыдущей главе мы использовали для удовлетворения спроса покупателя и оптимизации страхового запаса, АВС анализ, когда по категории А мы сделали бОльший страховой запас, а по категории С, — минимальный страховой запас. Если в первой главе, ( в самом простом варианте) страховой запас мы создали вручную, во второй главе — отталкивались от среднедневных продаж. Страховой запас формировали в днях. Об этом более подробно мы говорили в моей предыдущей статье.
Здесь АВС анализ сделаем более углубленным, что поможет нам быть еще более точным.
Если ранжирование товара по АВС анализу, у нас велось с точки зрения прибыльности каждого товара, где А, это наиболее прибыльный товар, В — товар со средней прибыльностью и С — с наименьшей прибыльностью, то теперь АВС дополнительно ранжируем по следующим критериям:
«А» — товар с каждодневным спросом
«В» — товар со средним спросом ( например 7-15 дней в месяц)
«С» — товар с редким спросом ( менее 7 дней в месяц)
Этот же принцип можно использовать не по количеству дней в месяце, а по количеству месяцев в году.
И еще зададим один критерий. Это количество обращений к нам, к поставщику.
Здесь количество обращений, это сколько отдельных заказов, покупок было сделано по каждому товару не зависимо от количества, стоимости и прибыльности товара. Здесь мы видим картину, насколько наши покупатели часто обращаются к нам по каждому товару. Об этом подробно говорили в моей статье «Прогноз спроса в управлении товарными запасами. Анализ XYZ и другие инструменты эффективного анализа»
“А” – количество обращений от 500 и выше
“В” – 150 – 499 обращений.
“С” – менее 150 обращений в месяц.
В итоге, товары имеющие рейтинг ААА, это самый ТОП товаров, по которым требуется особое внимание.
Расширенный АВС анализ в таблице Excel
См. рис. 12. Мы выделили серым цветом столбцы, где учли товар по АВС в части постоянного спроса в днях и по количеству обращений. Также эти данные можем перенести из выгруженных данных нашей базы с помощью формулы ВПР.
Теперь у нас рейтинг АВС анализа видоизменился и это может привести нас к пересмотру страхового запаса.
Обратите внимание на выделенную зеленым первую строку. Товар имеет рейтинг ААА. Также смотрим на восьмую строку. Здесь рейтинг товара ВАА. Может имеет смысл страховой запас этого товару сделать больше, чем заданных 7 дней?
Для наглядности, так и сделаем, присвоив этому товару страховой запас на 14 дней. Теперь по нему страховой запас выше, чем это было ранее. 44 коробки против 22 коробок. См. рис. 11.
А что на счет рейтинга «ССС»? Нужен ли по этому товару страховой запас? И вообще, при нехватке оборотных средств и площадей склада, нужен ли этот товар в нашей номенклатуре?
Также интересно по товару с рейтингом САА.
Прибыль не высокая, но именно к нам идут за этим товаром. Я бы уделил также особое внимание этому товару. За счет его высокой оборачиваемости, достигаемой, в том числе, за счет его постоянного наличия, мы и повышаем прибыль.
Управление товарными запасами в Excel. Заключение
В аналитику Excel можно и включить товар с признаком сезонности. Можно включить сравнение отклонений заказов с наших филиалов или магазинов, когда мы сразу же увидим несоизмеримо маленький или большой заказ. Это защитит нас от дефицита или излишнего товарного запаса.
Не важно сколько машин или партий товаров у нас в пути, и когда по каждому поставщику свой цикл поставки. Можно учесть многое, что конечном счете, оптимизирует наши запасы и увеличивает чистую прибыль.
Это лишь степень владения Excel. Сегодня мы разбирали достаточно простые таблицы.
Одна из следующих моих публикаций, будет посвящена, как, с помощью нескольких простых формул Excel можно быстро обрабатывать большой массив данных.
Буду рад, если по вопросу, как в Excel вести учет товара, был Вам полезен.
Пишите в комментариях, задавайте вопросы. Могу рассмотреть вариант взаимовыгодного сотрудничества по формированию и налаживанию учета товара и запасов в Excel. Эта работа для меня любима и интересна.