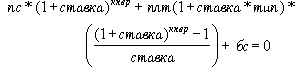Примеры, описанные в этом уроке, доступны в файле Excel: Часто Используемые Формулы.xlsx, только их самостоятельное написание гарантирует, что вы запомните этот урок.
Самые популярные формулы в Excel: расчет процентов и маржи
Зачастую знание самого Excelя оказывается недостаточным и необходимо знание основных математических формул.
Много раз я уже убеждался, что даже человек с базовым экономическим образованием сталкивался с проблемой расчета цены без НДС имея такие данные: цена с НДС составляет 100$ и ставка НДС — 23%, и с удивлением утверждавшего, что он не в состоянии это сделать.
Ниже я представляю решение проблем, с которыми чаще всего сталкивается обычный сотрудник или кандидат на должность, где требуется знание Excel.
Формулы расчета процентов в Excel
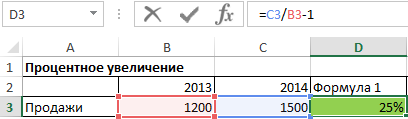
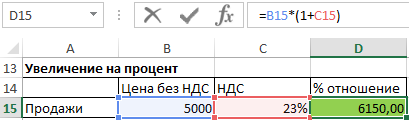
Процентное увеличение вычисляем по следующей формуле:
Увеличение процента = новая стоимость / старая стоимость — 1
Эта формула использовалась в следующем примере для расчета процентного увеличения, которое составило 25%.
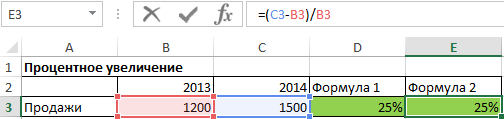
Ту же формулу также можно написать в следующей форме:
Прибавление процента = (новая стоимость – старая стоимость) / старая стоимость
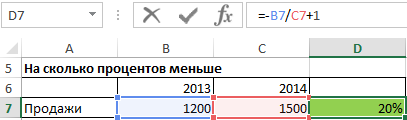
Иногда бывает, что процентное изменение за год рассчитывается «с другой стороны», в приведенном ниже примере мы можем сказать, что продажи в 2013 году были на 20% меньше, чем в 2014 году. Получатели такой информации недолго думая запоминают, что разница составляет 20%, тогда как на самом деле, как мы рассчитали в примере 1 (этот пример и предыдущий имеют одни и те же данные), она составляет 25%.
Это является преднамеренным введением в заблуждение получателя информации, и я не рекомендую использовать такой подход, разве что кто-то занимается политикой и должен придерживаться принятых в этой сфере стандартов.
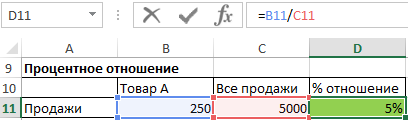
Чтобы найти процентное отношение, например, какого-то товара в общем объеме продаж, мы делим объем продажи этого товара на общий объем продаж.
Процентное отношение = продажи товара A / общий объем продаж
Для увеличения заданного значения на процент, например, для увеличения цены на 23% налога на добавленную стоимость, служит следующая формула:
Стоимость с НДС = стоимость без учета НДС * (1 + процент изменения)
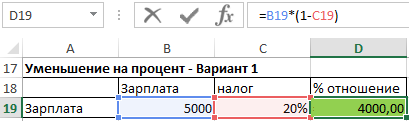
Аналогично выглядит формула уменьшения значения на процент, с той лишь разницей, что вместо знака плюс используется минус:
Новое значение = Старое значение * (1 — процент изменения)
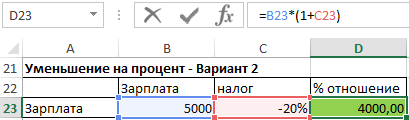
Иногда процент, на который нам нужно что-то уменьшить, дается со знаком минус (уменьшить на -20%), что теоретически является ошибкой (два минуса должны давать плюс), но, к сожалению, такой вариант популярен и должен пониматься как уменьшение на 20%. В таком случае используем ту же формулу, что и при увеличении на процент (минус уже в %).
Новое значение = Старое значение * (1 + проценты изменения)
И конечно же, уменьшить значение на процент — это одно, а «вывести» процент который был добавлен — совсем другое.
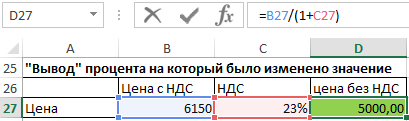
В следующем примере мы бы хотели бы найти цену без НДС от цены с НДС, НДС составляет 23 %.
Используем следующую формулу. Для того чтобы добавить определенный процент к значению, мы умножали значение на (1 + %), чтобы «вывести» процент — разделим значение на (1 + %) (деление является противоположным умножению действием).
Стоимость без НДС = Стоимость с НДС / (1 + % НДС)
Как вы можете видеть, в приведенном примере нам удалось получить первоначальное значение цены без НДС, показанного на двух примерах выше.
Многие люди задают вопрос, почему обратным действием для увеличения значения на какой-то процент не является уменьшение на тот же процент.
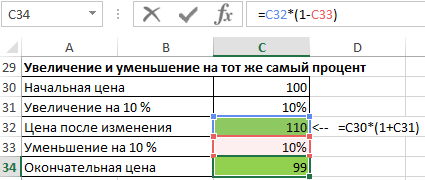
Давайте рассмотрим следующий пример, в котором цена была изменена дважды.
Начальная цена составляла 100$, она была увеличена на 10%, а после этого изменения она составляла 110$ (10% от 100 это 10, 10 + 100 = 110).
После первого изменения цена была снижена на 10% и в итоге составила 99$ (10% от 110 это 11). 110 -11 это 99).
Как видно, цена не вернулась к своему первоначальному значению. Чем больше было бы процентное изменение, тем больше была ба разница между начальной и окончательной ценой.
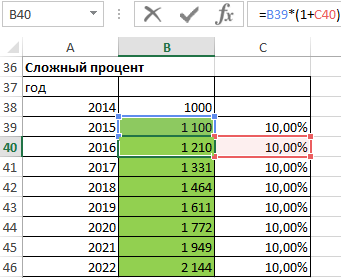
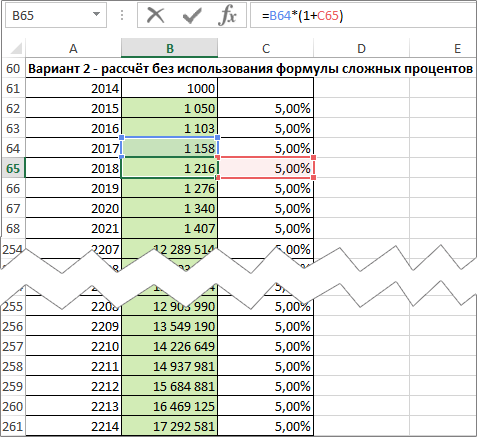
В приведенном ниже примере стоимость какой-то инвестиций увеличивается на 10% каждый год, мы хотели бы рассчитать, за сколько лет эта величина удвоится.
В первой из зеленых ячеек вводим формулу увеличения на процент и перетаскиваем ее в следующие ячейки. Удвоения этой суммы мы не должны ждать аж десять лет. Величина будет в два раза больше первоначальной суммы в седьмом году, а в восьмом значительно превысит свою двукратность. Происходит так, потому что процент во втором и каждом последующем инвестиционном году рассчитывается не из первоначальной суммы, а из уже увеличенной суммы.
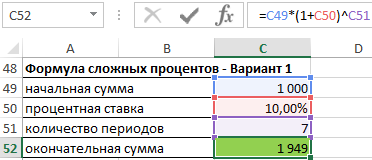
Тот же результат можно получить гораздо быстрее, используя формулу для сложных процентов.
Окончательная сумма = начальная сумма * (1 + процентная ставка) ^ количество периодов
символ ^ означает степень)
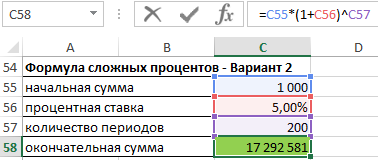
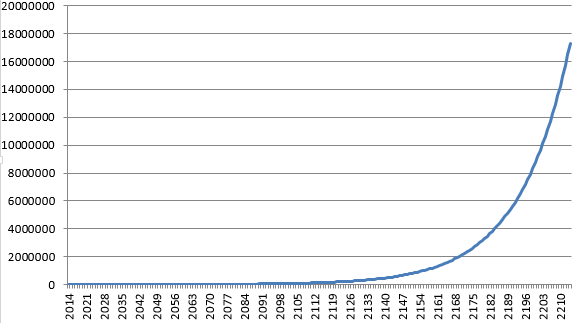
В следующем примере сложных процентов некто задается вопросом, если бы он положил на вклад 1 000 $ под фиксированную процентную ставку в размере 5 % годовых и с ежегодной капитализацией процентов, были бы его пра-пра-праправнуки через 200 лет миллионерами.
После применения вышеприведенной формулы к таким данным, на вышеупомянутый вопрос мы получим утвердительный ответ. Через 200 лет на счету будет сумма более 17 миллионов $.
Если мы решим рассчитать ту же задачу с использованием 200 формул для увеличения на процент, отметим, что прирост суммы депозита на заключительном этапе несравненно больше, чем в начальные периоды. За последние несколько лет величина депозита увеличивалась почти на 1 млн. $ ежегодно.
Такой рост величины депозита в последующие периоды типичен для экспоненциальных функций, то есть тех, в которых переменная, в данном случае количество лет, находится в степени.
Должны ли мы теперь поспешить в банки с целью открытия таких депозитных счетов? Если бы мы хотели рассмотреть эти расчеты не как пример, а серьезно, следовало бы нам также учесть инфляцию, риск банкротства банка, риск девальвации валюты депозита или даже смену системы, национализацию банковских депозитов, дефолт государства или войну. С учетом этих факторов, более разумным способом инвестирования 1 000 $, по-видимому, является использование их для повышения своей профессиональной квалификации, например, обучение Excel и VBA :-).
Читайте также: Прибавить и отнять процент в Excel от числа с примерами.
Формулы расчета маржи в Excel
Вычисление маржи для многих людей является большой проблемой, потому что они думают о добавлении маржи как о добавлении процента к заданной величине.
Фактически, маржа — это не процент от «накладных расходов», а процент, которым является прибыль в конечной цене продукта или услуги.
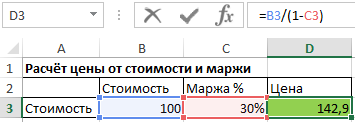
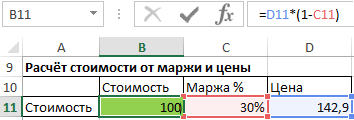
При данной стоимости и проценте маржи, цена рассчитывается по следующей формуле:
Цена = Стоимость / (1- процент маржи)
Маржа должна быть менее 100%, потому что невозможно продать что-то, зарабатывая при этом 100% и более, при этом каждая хозяйственная деятельность связана с некоторыми издержками.
В то же время, маржа может быть отрицательной, тогда компания продает свои товары или услуги ниже себестоимости и теряет на каждой операции.
Вопреки тому как может казаться, это не редкое явление, в некоторых отраслях, например, при продаже принтеров нормальным явлениям является их продажа ниже себестоимости. Производители покрывают эти потери продавая услуги и картриджи (чернила) с высокой маржей. Такая стратегия используется для упрощения привлечения клиентов.
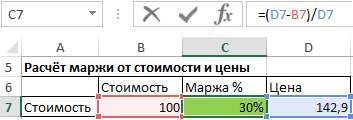
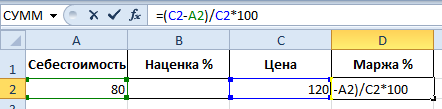
Чтобы рассчитать маржу, зная стоимость и цену, используем следующую формулу:
Процент маржи = (цена – стоимость) / цена
Вышеуказанная формула также может быть записана как: процент маржи = 1 — стоимость / цена.
Однако, если искомым элементом является стоимость, мы используем следующую формулу, такую же, которую мы используем для уменьшения суммы на процент.
Другими словами, мы понижаем цену на размер маржи и получаем стоимость.
Стоимость = цена * (1 — маржа)
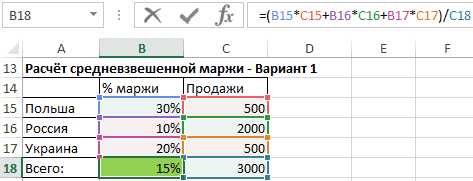
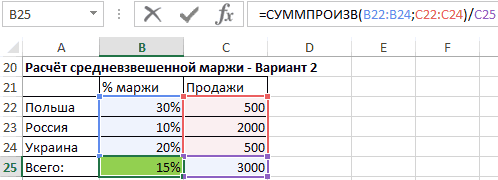
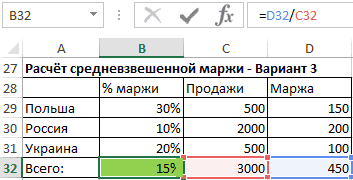
Средневзвешенная маржа от продаж
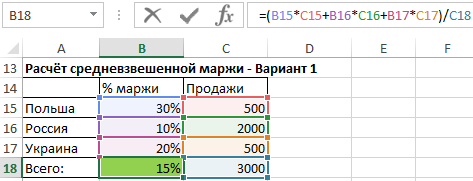
Для вычисления средней маржи мы не можем использовать обычное среднее значение, мы должны вычислить его с использованием средневзвешенного значения, где весом являются объёмы продаж.
Мы можем сделать это тремя способами:
- Используя первый способ, мы перемножаем каждую процентную маржу на соответствующий ей объем продаж, суммируем результаты и эту сумму делим на сумму всего объёма продаж. Эта формула даёт нам полный контроль над методом расчёта и позволяет понять, на чём основывается средневзвешенное значение.
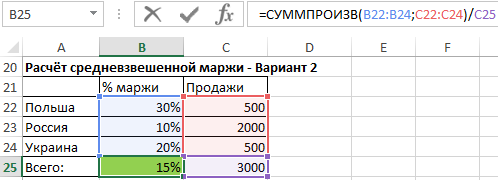
- При использовании второго способа, нам служит функция СУММПРОИЗВ, которая суммирует произведения маржи и соответствующий ей объем продаж. Результат, который возвращает функция мы должны ещё разделить на общий объём продаж. Эта функция подробно описана в статье «Основные функции».
- Третий способ является для многих самым простым, но требуется создание дополнительного столбца с маржей от суммы каждой продажи. Значения в столбце K получаем путём умножения каждой процентной маржи на соответствующий ей объем продаж. Чтобы рассчитать средневзвешенную маржу, просто разделите сумму маржи на сумму всех продаж.
Читайте также: Как посчитать маржу и наценку в Excel.
Я предлагаю вам удалить содержимое всех зелёных полей в файле упражнений к этому уроку и самостоятельно ввести формулы без подглядывания в вышеприведённое описание. Если вам удастся ввести их все правильно, значит вы освоили этот материал, если нет — всегда можно начать снова и снова, и так пока не получите результат.
Для Google Docs эти формулы тоже подходят.
1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.
Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.
Какие данные нужны
Для начала надо правильно написать формулу — в любой свободной ячейке.
=ПЛТ(ставка;кпер;пс)
В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:
- Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
- Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
- Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.
Как всё посчитать
Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.
Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.
2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
Какие данные нужны
Формула расчёта довольно простая:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
В ней всего две переменные:
- Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
- Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).
Как всё посчитать
Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:
Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.
3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.
Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.
Какие данные нужны
Формула состоит из трёх компонентов:
=ЧИСТНЗ(ставка;значения;даты)
Второй и третий достаточно ясны:
2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.
Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.
Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.
Как всё посчитать
Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.
Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.
4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.
Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.
Какие данные нужны
Чтобы определить более выгодное предложение, применим формулу:
=ЧИСТВНДОХ(значения;даты)
Достаточно знать всего две переменные:
- Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
- Даты — график платежей, по которым будут выплачивать прибыль.
Как всё посчитать
Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.
5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.
Какие данные нужны
Полезной будет эта формула:
=СТАВКА(кпер;плт;пс)
Три переменных в ней означают следующее:
- Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
- Плт — размер платежей. Считаются и основной долг, и проценты.
- Пс — общая сумма займа. В нашем примере это 100 000 рублей.
Как всё посчитать
Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.
6. PV (ПС) — подсказывает, сколько денег можно взять в долг
Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.
Какие данные нужны
Пригодится формула расчёта текущей стоимости:
=ПС(ставка; кпер; плт)
Для этого потребуется информация, которая есть на сайте любого банка:
- Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
- Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
- Плт — размер комфортного платежа.
Как всё посчитать
Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.
Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.
7. NPER (КПЕР) — помогает рассчитать время накоплений
Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.
Какие данные нужны
Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:
=КПЕР(ставка/периоды_капитализации;плт;пс;бс)
Она состоит из четырёх основных значений и одного дополнительного:
- Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
- Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
- Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
- Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
- Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.
Как всё посчитать
Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.
Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.
Читайте также 🧐
- Как вести бюджет, если у вас непостоянный доход
- 20 полезных шаблонов «Google Таблиц» на все случаи жизни
- 10 крутых приложений, чтобы взять финансы под контроль
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Mobile Еще…Меньше
Управление личными финансами может быть сложной задачей, особенно если вам нужно планировать свои платежи и сбережения. Excel формулы и шаблоны бюджетов помогут вам вычислить будущую стоимость своих задолженности и инвестиций, что упростит расчет времени, необходимого для достижения целей. Используйте следующие функции:
-
ПЛТ: возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и процентной ставки.
-
КПЕР: возвращает количество периодов выплаты для инвестиции на основе регулярных постоянных выплат и постоянной процентной ставки.
-
ПВ: возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат.
-
БС: возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки.
Расчет ежемесячных платежей для погашения задолженности по кредитной карте
Предположим, остаток к оплате составляет 5400 долларов США под 17% годовых. Пока задолженность не будет погашена полностью, вы не сможете рассчитываться картой за покупки.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
=ПЛТ(17%/12;2*12;5400)
получаем ежемесячный платеж в размере 266,99 долларов США, который позволит погасить задолженность за два года.
-
Аргумент «ставка» — это процентная ставка на период погашения кредита. Например, в данной формуле ставка 17% годовых делится на 12 — количество месяцев в году.
-
Аргумент КПЕР 2*12 — это общее количество периодов выплат по кредиту.
-
Аргумент ПС или приведенной стоимости составляет 5400 долларов США.
Расчет ежемесячных платежей по ипотеке
Представьте дом стоимостью 180 000 долларов США под 5% годовых на 30 лет.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
=ПЛТ(5%/12;30*12;180000)
получена сумма ежемесячного платежа (без учета страховки и налогов) в размере 966,28 долларов США.
-
Аргумент «ставка» составляет 5%, разделенных на 12 месяцев в году.
-
Аргумент КПЕР составляет 30*12 для ипотечного кредита сроком на 30 лет с 12 ежемесячными платежами, оплачиваемыми в течение года.
-
Аргумент ПС составляет 180 000 (нынешняя величина кредита).
Расчет суммы ежемесячных сбережений, необходимой для отпуска
Необходимо собрать деньги на отпуск стоимостью 8500 долларов США за три года. Процентная ставка сбережений составляет 1,5%.
С помощью функции ПЛТ(ставка;КПЕР;ПС;БС)
=ПЛТ(1,5%/12;3*12;0;8500)
получаем, что чтобы собрать 8500 долларов США за три года, необходимо откладывать по 230,99 долларов США ежемесячно.
-
Аргумент «ставка» составляет 1,5%, разделенных на 12 месяцев — количество месяцев в году.
-
Аргумент КПЕР составляет 3*12 для двенадцати ежемесячных платежей за три года.
-
Аргумент ПС (приведенная стоимость) составляет 0, поскольку отсчет начинается с нуля.
-
Аргумент БС (будущая стоимость), которую необходимо достичь, составляет 8500 долларов США.
Теперь допустим, вы хотите собрать 8500 долларов США на отпуск за три года, и вам интересно, какую сумму необходимо положить на счет, чтобы ежемесячный взнос составлял 175,00 долларов США. Функция ПС рассчитает размер начального депозита, который позволит собрать желаемую сумму.
С помощью функции ПС(ставка;КПЕР;ПЛТ;БС)
=ПС(1,5%/12;3*12;-175;8500)
мы узнаем, что необходим начальный депозит в размере 1969,62 долларов США, чтобы можно было откладывать по 175,00 долларов США в месяц и собрать 8500 долларов США за три года.
-
Аргумент «Ставка» составляет 1,5%/12.
-
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
-
Аргумент ПЛТ составляет -175 (необходимо откладывать по 175 долларов США в месяц).
-
Аргумент БС (будущая стоимость) составляет 8500.
Расчет срока погашения потребительского кредита
Представьте, что вы взяли потребительский кредит на сумму 2500 долларов США и согласились выплачивать по 150 долларов США ежемесячно под 3% годовых.
С помощью функции КПЕР(ставка;ПЛТ;ПС)
=КПЕР(3%/12;-150;2500)
выясняем, что для погашения кредита необходимо 17 месяцев и несколько дней.
-
Аргумент «Ставка» составляет 3%/12 ежемесячных платежей за год.
-
Аргумент ПЛТ составляет -150.
-
Аргумент ПС (приведенная стоимость) составляет 2500.
Расчет суммы первого взноса
Скажем, вы хотите приобрести автомобиль стоимостью 19 000 долларов США под 2,9 % годовых за три года. Вы хотите, чтобы ежемесячные платежи были на уровне 3500 долларов США в месяц, поэтому вам нужно выяснить сумму своего взноса. В этой формуле результатом функции ПС является сумма займа, которая затем вычитается из цены покупки, чтобы получить первый взнос.
С помощью функции ПС(ставка;КПЕР;ПЛТ)
= 19000-ПС(2,9%/12; 3*12;-350)
выясняем, что первый взнос должен составлять 6946,48 долларов США.
-
Сначала в формуле указывается цена покупки в размере 19 000 долларов США. Результат функции ПС будет вычтен из цены покупки.
-
Аргумент «Ставка» составляет 2,9%, разделенных на 12.
-
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
-
Аргумент ПЛТ составляет -350 (необходимо будет выплачивать по 350 долларов США в месяц).
Оценка динамики увеличения сбережений
Начиная с 500 долларов США на счету, сколько можно собрать за 10 месяцев, если класть на депозит по 200 долларов США в месяц под 1,5% годовых?
С помощью функции БС(ставка;КПЕР;ПЛТ;ПС)
=БС(1,5%/12;10;-200;-500)
получаем, что за 10 месяцев выйдет сумма 2517,57 долларов США.
-
Аргумент «Ставка» составляет 1,5%/12.
-
Аргумент КПЕР составляет 10 (месяцев).
-
Аргумент ПЛТ составляет -200.
-
Аргумент ПС (приведенная стоимость) составляет -500.
См. также
ПЛТ
КПЕР
ПС
БС
Нужна дополнительная помощь?
Excel – это отличный бизнес-инструмент, который можно использовать для разных целей. В том числе, для ценообразования. Допустим, у нас есть определенная норма, сколько накручивать на одной цене, а также есть себестоимость каждого товара. Если есть один товар, то это можно сделать вручную. Но что делать, когда нужно рассчитать маржу сразу большого количества товаров?
И вообще, есть разница между наценкой и маржой? Давайте разберемся с этими ключевыми понятиями, а также определим, как их рассчитывать.
Содержание
- Расчет маржи и наценки в Excel: формулы
- Формула расчета маржи
- Средневзвешенная маржа от продаж
- Формула расчета наценки
- В чем разница между маржей и наценкой (пример)
- Расчет маржи в процентах, если известна наценка
- Расчет наценки в процентах, если известна маржа
Расчет маржи и наценки в Excel: формулы
Итак, у нас есть два показателя, каждый из которых нам известен. Первый – это цена. Это окончательная стоимость товара, за сколько его нужно продавать или он сейчас продается. Маржа является очень важным параметром, который дает возможность определить множество других характеристик проекта или бизнеса, таких как:
- Прибыльность проекта или бизнеса в целом.
- То, насколько изменчива прибыльность у этой организации.
- Какие клиенты приносят больше всего денег.
- Какие проекты являются наиболее ресурсозатратными и окупаются ли эти вложения.
- Куда направляется валовый доход.
- Как соотносится зарплата сотрудников и маржинальность проектов.
- Какое количество денег приносит каждая из услуг.
В зависимости от этих результатов и принимаются управленческие решения. Например, осознается необходимость уменьшить расходы, увеличить стоимость товаров или услуг или же отказаться от проектов, которые требовательны к ресурсам, но не приносят целевой прибыли.
Что нужно сделать для того, чтобы определить наценку и маржу?
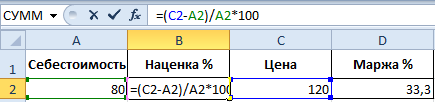
Формула расчета маржи
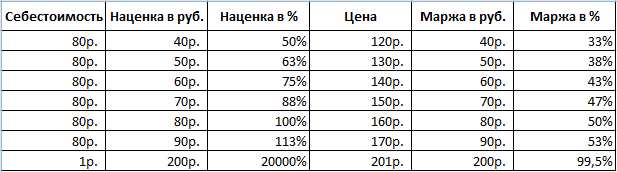
Давайте сделаем такую табличку.
В нашем случае нас интересует ячейка, подписанная, как «Маржа». То есть, D2. В ней следует указать такую формулу (показана на скриншоте).
Таким образом, маржа у нас стала составлять 33,3%. Простыми словами, треть.
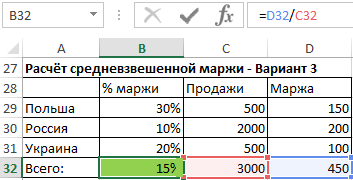
Средневзвешенная маржа от продаж
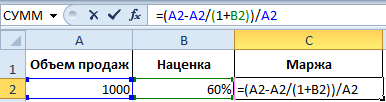
Если же нам нужно определить среднюю маржу, недостаточно использовать предыдущую формулу, поскольку данные будут неточными. Значительно лучше применять средневзвешенное значение, которое учитывает весовой коэффициент. В нашем случае это объемы продаж.
Есть три способа определения средневзвешенной маржи.
- Умножение каждой маржи, полученной по формуле в предыдущем пункте, на соответствующий весовой коэффициент, коим является объем продаж. В этом случае мы можем полностью контролировать вычислительный процесс и понимать, что является основой для расчета средневзвешенного значения.
3 - Воспользоваться функцией СУММПРОИЗВ, которая делает то же самое, только автоматически. Если детально, то она работает следующим образом: умножает маржу на весовой коэффициент, а получившиеся значения суммирует. Но в этом случае возвращенного формулой результата недостаточно, поскольку его нужно еще разделить на общее количество проданного товара или суммарный вес.
4 - Наиболее простой для среднестатистического человека метод, но он занимает место на листе. Необходимо создать еще одну колонку, в которой прописывается формула получения маржи от конкретной сделки. Нам нужно произведение процентной маржи на объем продаж в определенной стране. После этого нужно полученный результат разделить на общую сумму продаж.
5
Настоятельно рекомендуется потренироваться в вычислениях перед тем, как использовать эти формулы в работе. Это поможет существенно сэкономить рабочее время.
Формула расчета наценки
Возвращаемся к той таблице, которая нами была создана изначально. Наценка у нас находится в ячейке B2. Следовательно, там вводим такую формулу.
В качестве результата формула выводит наценку в 50%. Если посчитать этот показатель вручную, мы получим ту же долю от числа.
В чем разница между маржей и наценкой (пример)
Очень часто люди путают понятия маржи и наценки, поскольку и те, и другие основаны на прибыли и расходах. При этом разница между этими терминами колоссальная. Они просто по разному рассчитываются, как видно из формул, которые были приведены выше.
С помощью наценки предприятия могут получить прибыль с произведенного товара. Если бы ее не было, то торговля стала бы убыточной. А маржой является окончательный результат, который получился после того, как была выполнена наценка. Чтобы было более понятно, давайте приведем формулы, которые описывают каждое из понятий, касающихся рассматриваемой нами темы.
- Цена – себестоимость вместе с наценкой.
- Наценка – это мера накрутки цены. Чтобы ее получить, нужно знать окончательную стоимость и себестоимость и отнять второй компонент от первого.
- Маржа – это процент прибыли, которую получает предприятие или частный продавец с одной сделки. Максимальное значение маржи – не равно 100%. Дело в том, что себестоимость всегда включена в цену, которая составляет определенный, пусть даже минимальный, процент.
Маржа может быть равна наценке при условии, что вычисление осуществляется в абсолютных показателях (то бишь, числами). Если же определять процент, то наценка всегда будет больше маржи.
Вот таблица, которая демонстрирует эту разницу на примере.
Наценка может и превышать 100%, поскольку она рассчитывается, как доля от себестоимости. То есть, если человек добавляет к стоимости сумму в 20 раз больше, чем реально его произвел, то наценка составит 20 тысяч процентов. При этом маржа не может быть больше, чем 99,9999(…).
При этом маржа будет равной наценке, если измерять ее в количестве денег, которые остаются после наценки, исключая себестоимость.
При этом маржа изменяется пропорционально наценке. Чем она больше, тем выше маржа. Поэтому если мы знаем наценку, то можно определить маржу и наоборот. Если перед человеком стоит задача получить конкретную чистую прибыль, то следует определить, какая нужна наценка. И это можно сделать. Простыми словами, чтобы получить маржу, необходимо знать сумму продаж и наценку, а чтобы получить наценку, необходимо иметь сумму продаж и маржу.
Отдельно выделяется такое понятие – как маржинальность. Это фактически мера того, насколько рентабельный бизнес. Чем выше маржинальность, тем выгоднее заниматься определенным бизнесом.
Как это понятие рассматривать на практике? Выражаясь простым языком, маржой является доля прибыли на один чек, выписанный клиенту или покупателю. Предположим, мы рекламируем какой-то проект. Чтобы это сделать, нам понадобилось заплатить 10 тысяч на привлечение одного клиента + операционные затраты на предоставление услуги. В этом случае маржа составила 5 тысяч рублей. В процентном отношении в этом примере маржа составит 33 процента.
Между понятиями маржинальности и рентабельности можно смело ставить знак равно, поскольку эти термины абсолютно идентичны по своему смыслу.
Маржинальность – это не только категория бизнеса, но и маркетинга. В этой сфере под этим термином подразумевается прибыльность конкретного продвигаемого проекта.
Какой уровень маржинальности считать хорошим? Если этот показатель выше 10 процентов, то это считается нормой. Если выше 20-25 процентов, то это говорит о бизнесе, как об очень выгодном. Важно понимать, что маржа на старте бизнеса будет ниже, потому что он не сразу приносит доход. Поэтому нужно регулярно сравнивать этот показатель за разные периоды (что, впрочем, важно и для давно работающего бизнеса). Некоторые компании вообще через некоторое время выходят на маржинальность в 51 процент, что является просто потрясающим показателем.
Кстати, согласно опросам, проведенным маркетинговой платформой HubSpot, 15% вообще не знает, какая маржинальность их бизнеса. Если вы принадлежите к этому числу, то теперь вы знаете, как это сделать в Excel.
Есть еще такой параметр, который называется валовой маржой. Это количество средств, которые остаются свободными после вычета издержек, не связанных непосредственно с конкретным проектом. Это также термин из маркетинга. То есть, в валовую маржу не входят такие расходы, как аренда, зарплаты, аренда, покупка материалов, канцелярии, техники и так далее. Оптимальным значением валовой маржи считается 50-60%.
Чтобы рассчитать этот показатель, необходимо вычесть из дохода те средства, которые были потрачены непосредственно на обеспечение конкретной деятельности. Это можно сделать абсолютно без никаких функций Excel, достаточно только иметь необходимые показатели.
Существует еще несколько видов маржи:
- Операционная маржа. Это разновидность маржи, которая определяет количество дохода, который остался после того, как из него были вычтены все издержки, которые касаются основной деятельности. Чтобы его рассчитать, необходимо знать операционную прибыль или убыток, а также общий доход. Формула следующая =A1/B1, где в ячейке A1 может находиться как чистая прибыль, так и убыток. Соответственно, B1 содержит общий доход (или объем продаж). Этот показатель всегда выражается в процентах. Этот показатель может использоваться для оценки рентабельности не только всего предприятия, но и его отдела, а также конкретного проекта. Если операционная маржа отрицательная, это печальный звонок. Кстати, с помощью функции условного форматирования можно настроить отображение отрицательной операционной маржи в ячейке красным цветом. Фактически этот параметр идентичен чистой прибыли за тем лишь исключением, что нам нужно определить ее долю в общем доходе, чтобы вычислить операционную маржу.
- PBIT маржа. Это прибыльность, которая рассчитывается еще до окончательного учета дохода.
- PBT. Это «грязная прибыль», то есть та сумма, которую получилось заработать до вычета налогов.
Чтобы рассчитать маржинальность на практике, необходимо следовать такому простому алгоритму:
- Стоимость человекочаса.
- Накладные расходы – оплата труда, аренда, страхование и другие.
- Накладные расходы на час. Чтобы это сделать, нужно умножить все часы, которые были оплачены, на количество сотрудников.
- Определение валовой и чистой маржи на каждого клиента.
Все это можно сделать в Excel. Но это уже более продвинутый уровень. Главное – понимать принцип, как это делать, а все остальное – дело техники.
Расчет маржи в процентах, если известна наценка
Чтобы было более понятно, давайте приведем реальный кейс. Предположим, у нас есть организация, которая вышла на такие показатели за отчетный период:
- Продажи составили 1000.
- Наценка была 60 процентов.
- Таким образом, себестоимость составила 60%.
На основе этих данных можно определить маржу. Математические операции следующие:
- 1000-625=375.
- 375/1000=37,5%.
По аналогии строится расчет маржи при известной наценке и во всех остальных ситуациях.
Расчет наценки в процентах, если известна маржа
Теперь представим другой кейс. У нас отчетные показатели следующие:
- Объем продаж остался тем же – 1000.
- Маржа составила 37,5 процентов.
- Соответственно, на базе этих цифр получаем себестоимость по формуле (1000-х)/1000=37,5%.
Далее стандартными математическими операциями получаем неизвестное из уравнения. В качестве него выступает 625. Теперь, когда мы знаем себестоимость, мы можем определить наценку. Это делается в два простых шага, которые мы выучили еще в школе:
- От общего объема выполненных организацией продаж вычитается себестоимость товаров. Получаем наценку, которая составляет 375 (поскольку мы от 1000 отняли 625).
- Теперь нам нужно перевести ее в процентный вид. Для этого мы разделяем наценку на себестоимость продукции и получаем результат 60%.
Таким образом, рассчитать маржу и наценку в Excel не составляет никакого труда. Хотя эти значения могут быть идентичными в абсолютном выражении, в относительном они имеют огромную разницу, поскольку наценка рассчитывается от себестоимости, а маржа – от общей суммы товара.
В любом случае, оба эти показателя чрезвычайно важны для ведения любого бизнеса, создания социального проекта и ведения другой деятельности, в которой приходится рассчитывать эти показатели и ориентироваться на них.
Оцените качество статьи. Нам важно ваше мнение:
Содержание
- Как найти стоимость Эксель?
- Как найти стоимость в Excel?
- Как в Экселе посчитать сумму через одну ячейку?
- Как сделать формулу в Excel сумма?
- Как сделать автоматический расчет в Excel?
- Как вычислить стоимость?
- Как найти цену формула?
- Как посчитать сумму в таблице?
- Как работает формула Суммеслимн?
- Как считать ячейки?
- Как найти сумму чисел?
- Как в Excel посчитать сумму по горизонтали?
- Как в Excel посчитать сумму ячеек с текстом?
- Как выглядит формула стоимости?
- Как узнать себе стоимость?
- Как рассчитать цену за единицу товара?
- Как написать математическую формулу в Excel?
- Расчет цены в Excel с учетом заданной маржи и себестоимости
- Что такое маржа
- Расчет цены с учетом маржи и себестоимости
- Примеры функции ПС в Excel для расчета стоимости инвестиции
- Примеры использования функции ПС в Excel
- Расчет платежеспособности заемщика кредита по функции ПС в Excel
- Расчет возможности погашения кредита депозитом с функцией ПС
- Особенности использования финансовой функции ПС в Excel
Как найти стоимость Эксель?
Как посчитать цену, зная маржу и себестоимость? Если М=(Ц-С)/Ц, то Ц=С/(1-М). В принципе, все просто. Нужно забить в Excel значения маржи и себестоимости, а затем вписать формулу цены.
Как найти стоимость в Excel?
- Выделите ячейку, которую нужно вычислить.
- На вкладке Формулы в группе Зависимости формул нажмите кнопку Вычислить формулу.
- Нажмите кнопку Вычислить, чтобы проверить значение подчеркнутой ссылки.
- Продолжайте этот процесс, пока не будут вычислены все части формулы.
Как в Экселе посчитать сумму через одну ячейку?
Например, формула =СУММЕСЛИ(B2:B5; «Иван»; C2:C5) суммирует только те значения из диапазона C2:C5, для которых соответствующие значения из диапазона B2:B5 равны «Иван». Если необходимо выполнить суммирование ячеек в соответствии с несколькими условиями, используйте функцию СУММЕСЛИМН.
Как сделать формулу в Excel сумма?
Использование функции СУММ для суммирования чисел в диапазоне:
- Введите в ячейку =СУММ и открываю скобки (.
- Чтобы ввести первый диапазон формул, который называется аргументом (частью данных, которую нужно выполнить), введите A2:A4 (или выберите ячейку A2 и перетащите ее через ячейку A6).
Как сделать автоматический расчет в Excel?
Откройте вкладку Формулы и в группе Вычисления щелкните элемент Параметры вычислений, а затем — Выполнять автоматически.
Как вычислить стоимость?
Цена каждого товара устанавливается путем простого умножения затрат на (1+M). Например, компания розничной торговли, работающая с большим количеством товаров, может рассчитать все цены, просто добавив нужную наценку к закупочной цене.
Как найти цену формула?
Формула нахождения стоимости: С = Ц × К, где С — стоимость, Ц — цена, К — количество. Пример решения задачи на нахождение стоимости: 1 банка меда стоит 150 руб.
Как посчитать сумму в таблице?
Функция =SUM(BELOW) складывает числа в столбце, расположенные под выбранной ячейкой. Функция =SUM(RIGHT) складывает числа в строке, расположенные справа от выбранной ячейки. Изменив складываемые числа, выберите сумму и нажмите клавишу F9, чтобы отобразить новые результаты.
Как работает формула Суммеслимн?
Функция СУММЕСЛИМН — одна из математических и тригонометрических функций, которая суммирует все аргументы, удовлетворяющие нескольким условиям. Например, с помощью функции СУММЕСЛИМН можно найти число всех розничных продавцов, (1) проживающих в одном регионе, (2) чей доход превышает установленный уровень.
Как считать ячейки?
На вкладке Формулы щелкните Вставить, наведите указатель мыши на пункт Статистические и выберите одну из следующих функции:
- СЧЁТЗ: подсчитывает количество непустых ячеек.
- СЧЁТ: подсчитывает количество ячеек, содержащих числа.
- СЧИТАТЬПУСТОТЫ: подсчитывает количество пустых ячеек.
Как найти сумму чисел?
Как найти сумму и разность любых чисел
Чтобы найти сумму двух чисел, надо к одному числу прибавить другое, то есть выполнить действие сложения. Например, чтобы найти сумму чисел 5 и 9, надо выполнить действие: 5 + 9 = 14.
Как в Excel посчитать сумму по горизонтали?
Просто выберите пустую ячейку непосредственно под столбцом данных. Затем на вкладке Формула нажмите кнопку Авто сумма > сумму. Excel будет автоматически отсвечен диапазон для суммы. (При выборе пустой ячейки справа от сумм выбираемых ячеек авто сумма может работать и по горизонтали.)
Как в Excel посчитать сумму ячеек с текстом?
Суммировать ячейки, содержащие текст и числа на основе определенного текста, с удобной функцией:
- Выберите Статистический из Тип формулы раскрывающийся список;
- В разделе Выберите формулу список, щелкните, чтобы выбрать Сумма на основе того же текста вариант;
Как выглядит формула стоимости?
Как найти стоимость товара, зная его цену и количество? C — стоимость товара, — его цена, n — количество товара. Формула стоимости товара: C = · n. 6.
Как узнать себе стоимость?
Как рассчитать себестоимость товара
Когда бизнес производит один вид товара, рассчитать себестоимость можно так: сложить все расходы за конкретный период, затем разделить их на количество произведенной или проданной продукции за этот же период. Конкретные затраты зависят от целей расчета и особенностей производства.
Как рассчитать цену за единицу товара?
Как автоматически рассчитать стоимость товара за одну единицу? Пример. Изготовлено 20 000 товаров на сумму 17 050 руб. Если взять калькулятор и сумму поделить на количество, то получим стоимость за одну единицу товара, а именно 0.8525 руб.
Как написать математическую формулу в Excel?
Создание простой формулы в Excel:
- Выделите на листе ячейку, в которую необходимо ввести формулу.
- Введите = (знак равенства), а затем константы и операторы (не более 8192 знаков), которые нужно использовать при вычислении. В нашем примере введите =1+1. Примечания:
- Нажмите клавишу ВВОД (Windows) или Return (Mac).
Источник
Расчет цены в Excel с учетом заданной маржи и себестоимости
Зачастую расчеты, которые легко произвести на бумаге и калькуляторе, вызывают затруднения при попытке занести их в Excel. Но если научиться это делать, то в будущем можно сэкономить массу времени. Узнаем, как рассчитать цену продукта с учетом заданной маржи.
Что такое маржа
Фактически, это синоним слова наценка, выраженный в денежном эквиваленте. Если же речь идет о процентах, то маржа и наценка будут иметь разные значения. Все дело в определении. Сравните:
- Маржа – отношение разницы цены и себестоимости к цене.
- Наценка – отношение разницы цены и себестоимости к себестоимости.
Отсюда и разница.
Расчет цены с учетом маржи и себестоимости
Теперь, зная, чем маржа отличается от наценки, можем вывести формулу цены. Как посчитать цену, зная маржу и себестоимость?
Если М=(Ц-С)/Ц, то Ц=С/(1-М).
В принципе, все просто. Нужно забить в Excel значения маржи и себестоимости, а затем вписать формулу цены. Но это формула для одного случая, а в экономике затраты, от которых и зависит маржа, постоянно меняются. Поэтому подготовим полный расчет с учетом остальных переменных.
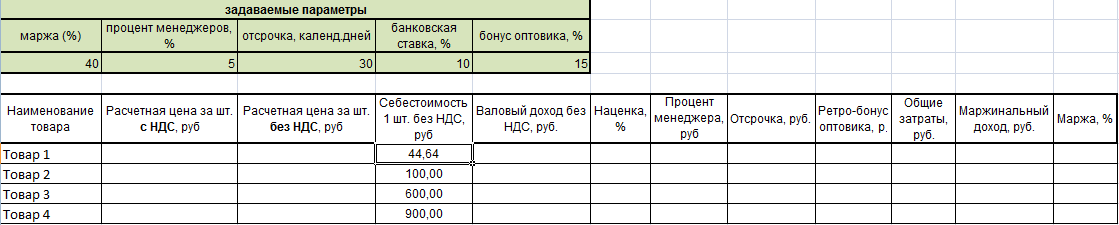
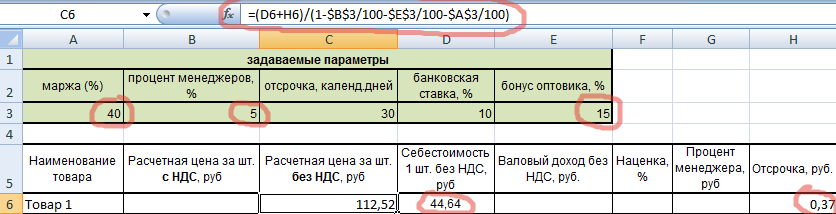
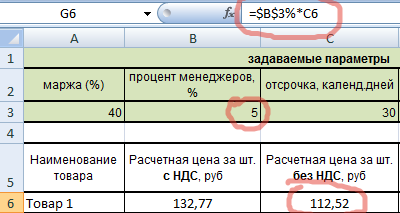
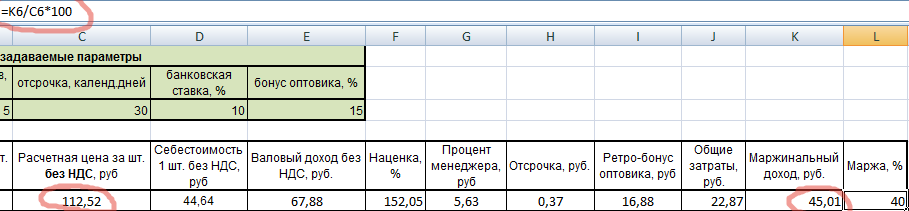
Составим таблицу для расчетов и предварительно укажем задаваемые параметры (если говорить математическими терминами – заполним дано).
В таблицу вписаны только известные нам пока значения – себестоимости товаров. Задаваемые параметры тоже постоянны. Пойдем по порядку.
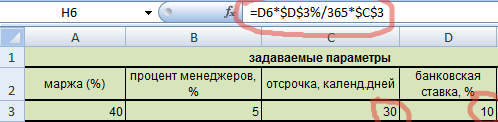
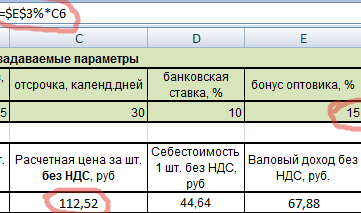
Рассчитаем отсрочку по формуле. Умножим себестоимость на банковскую ставку, поделим на число дней в году и на количество дней отсрочки.
Видим, что ячейки, в которых прописаны ставка и отсрочка, абсолютны, поэтому заключены в значки доллара. Это сделано для того, чтобы при протягивании формулы, эти значения оставались неизменными.
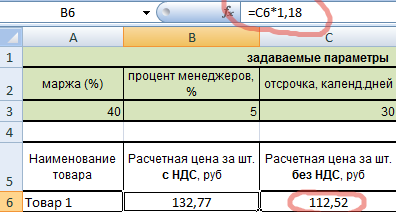
Теперь можем рассчитать расчетную цену без НДС по экономической формуле.
Ну и цену с НДС (1,18 – это коэффициент НДС).
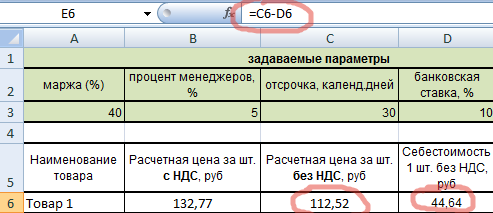
Далее – валовый доход (разница цены и себестоимости).
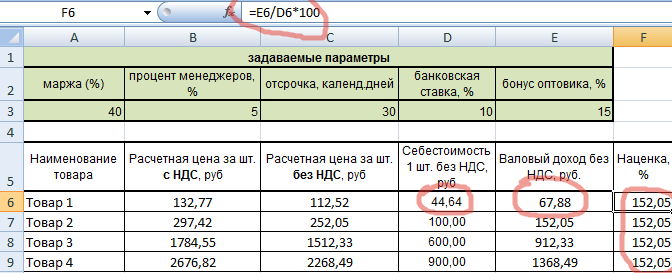
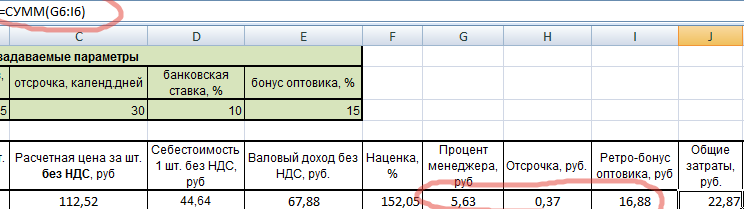
Теперь рассчитываем наценку. Она должна получиться одинаковой. В нашем случае формула наценки упрощена, т.к. валовый доход рассчитан операцией ранее.
Наценка действительно получилась одинаковой. Значит, мы на верном пути.
Процент менеджера: 5% от расчетной цены.
Аналогично: ретро-бонус – это 15% от расчетной цены.
Общие затраты: это сумма трех составляющих (проценты менеджеру и оптовику, а также отсрочка).
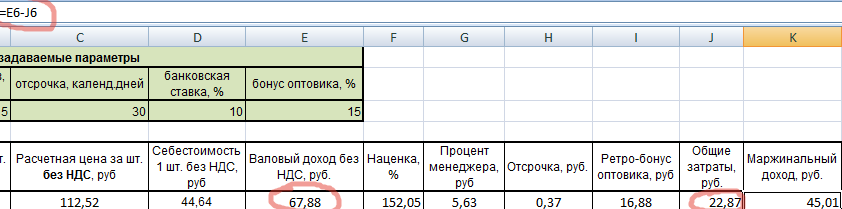
Маржинальный доход считается как разница валового дохода и затрат.
Готово. Осталось проверить, правильно ли были произведены расчеты. Для этого подсчитаем маржу по еще одной формуле: как отношение маржинального дохода к цене.
Маржа действительно получилась 40%. Значит все верно. Теперь, пользуясь таблицей, можем изменять значение маржи или себестоимости и сразу видеть все показатели. При этом будет сохранять равенство всех наценок и проверочное значение маржи.
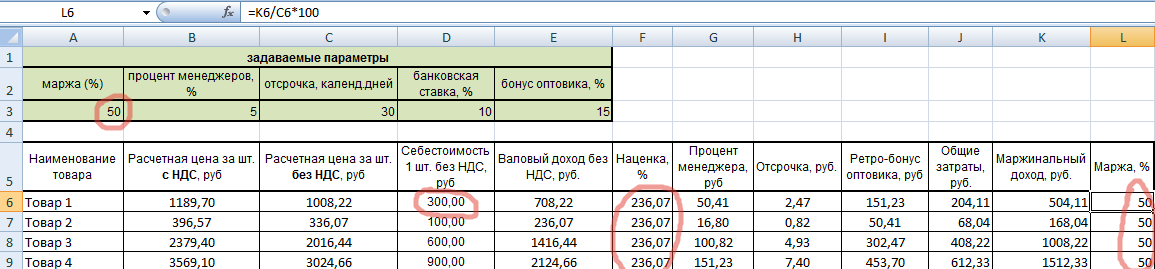
Попробуем изменить маржу на 50% (в задаваемых параметрах). Смотрим, что получается.
Или изменим себестоимость первого товара.
Как видим, все показатели автоматически изменяются, а экономические принципы сохраняются. Аналогично можно изменять и другие задаваемые параметры.
Источник
Примеры функции ПС в Excel для расчета стоимости инвестиции
Функция ПС используется для расчета стоимости инвестиции (покупка ценных бумаг, оформление кредита), приведенной на момент оформления сделки, и возвращает соответствующее значение. Такая стоимость эквивалентна общей сумме последующих выплат на протяжении установленного числа периодов выплат. К примеру, на момент выдачи кредита банком для последнего его сумма является приведенной стоимостью инвестиции.
Примеры использования функции ПС в Excel
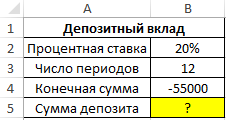
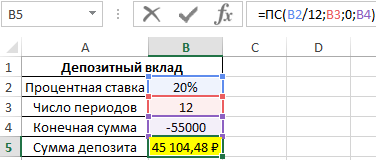
Пример 1. Для покупки ноутбука в будущем, стоимость которого составляет 55000 рублей, было решено сделать депозит в банке и по истечению срока действия договора забрать требуемую сумму. Процентная ставка – 20% годовых, срок действия – 12 месяцев (капитализация – каждый месяц). Определить, какую сумму должен внести вкладчик.
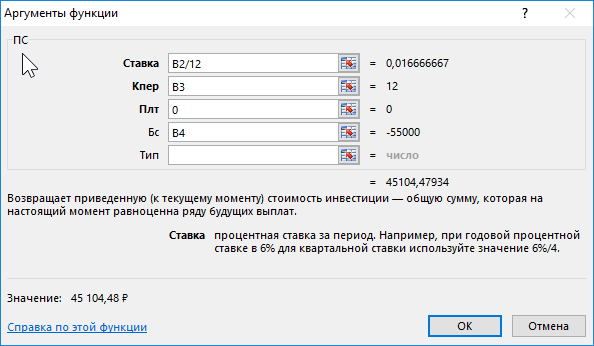
Формула для расчета:
- B2/12 – ставка на период выплат (12 – число месяцев в году);
- B3 – число периодов выплат;
- 0 – фиксированная сумма выплат по депозиту (неизвестна, так как вкладчик может забрать деньги по окончанию действия договора, то есть, спустя 12 месяцев);
- B4 – сумма, получаемая вкладчиком по окончанию действия договора.
То есть, на депозит требуется внести примерно 45105 рублей.
Расчет платежеспособности заемщика кредита по функции ПС в Excel
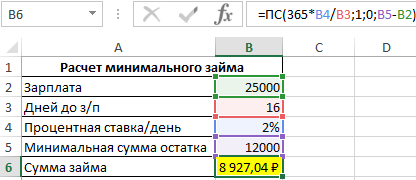
Пример 2. Зарплата клиента МФО составляет 25000 рублей. Причина обращения – полное отсутствие денег. До следующей зарплаты осталось 16 дней. Какую минимальную сумму кредита может взять заемщик, если микрозайм выдается под 2% в день, а минимальная сумма, на которую он может прожить в месяц, составляет 12000 рублей?
Формула для расчета:
- 365*B4/B3 – пересчет процентной ставки на указанный период дней (деньги нужны до зарплаты, значит период кредитования – 16 дней);
- 1 – количество периодов выплат (в МФО, как правило, устанавливают один период выплат – по окончанию срока кредитования);
- 0 – фиксированная сумма выплат в каждом из периодов (явно не указан, поскольку используем аргумент [бс];
- B5-B2 – максимальная сумма, которую сможет выплатить заемщик по кредиту при условии, что у него должно остаться не менее 12000 рублей после оплаты задолженности.
То есть, чтобы заемщик не попал в так называемую «долговую яму» или зависимость от МФО, ему не следует брать в долг более чем 9000 рублей.
Расчет возможности погашения кредита депозитом с функцией ПС
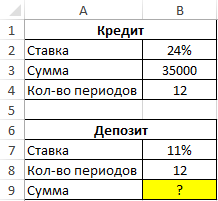
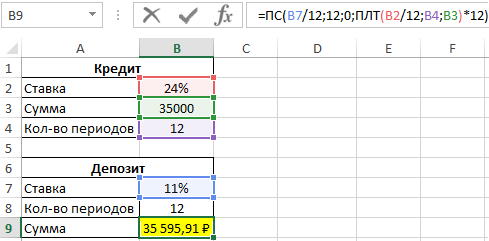
Пример 3. Заемщик взял кредит в банке на сумму 35000 рублей под 24% годовых на 1 год. Депозитный вклад на какую сумму он должен сделать (11% годовых, срок – 1 год), чтобы он смог рассчитаться с задолженностью по кредиту на полученные средства?
Формула для расчета:
- B7/12 – процентная ставка на 1 период выплат;
- 12 – число периодов выплат;
- 0 – фиксированная сумма выплат (явно не указываем);
- ПЛТ(B2/12;B4;B3)*12 – общая сумма выплат по кредиту, рассчитанная как произведение размера ежемесячной выплаты на количество периодов выплат (месяцев).
То есть, для покрытия расходов по кредиту необходимо сделать депозит на сумму примерно 35600 рублей (при указанных выше условиях кредитования и внесения депозита) с учетом того, что вклад был сделан одновременно с получением кредита.
Ситуация на первый взгляд выглядит абсурдной, однако некоторые договора кредитования исключают возможность досрочного погашения задолженности без штрафных санкций. Поэтому в данной стратегии есть свой экономический смысл при определенных финансовых условиях. Если у заемщика спустя некоторое время после оформления договора появилась определенная сумма средств, данный способ позволит сэкономить на оплате процентов по кредиту.
Особенности использования финансовой функции ПС в Excel
Функция ПС используется наряду с прочими функциями (СТАВКА, БС, ПЛТ и др.) для финансовых расчетов и имеет следующий синтаксис:
=ПС( ставка; кпер; плт; [бс]; [тип])
- ставка – обязательный аргумент, который характеризует значение процентной ставки за 1 период выплат. Задается в виде процентного или числового формата данных. Например, если кредит был выдан под 12% годовых на 1 год с 12 периодами выплат (ежемесячный фиксированный платеж), то необходимо произвести пересчет процентной ставки на 1 период следующим способом: R=12%/12, где R – искомая процентная ставка. В качестве аргумента формулы ПС может быть указана как, например, 1% или 0,01;
- кпер – обязательный аргумент, характеризующий целое числовое значение, равное количеству периодов выплат. Например, если был сделан депозит в банк сроком на 3 года с ежемесячной капитализацией (вклад увеличивается каждый месяц), число периодов выплат рассчитывается как 12*3=36, где 12 – месяцы в году, 3 – число лет, на которые был сделан вклад;
- плт – обязательный аргумент, характеризующий числовое значение, соответствующее фиксированный платеж за каждый период. На примере кредита, плт включает в себя часть тела кредита и проценты. Дополнительные проценты и комиссии не учитываются. Должен быть взят из диапазона отрицательных чисел, поскольку выплата – расходная операция. Аргумент может быть опущен (указан 0), но в этом случае аргумент [бс] будет являться обязательным для заполнения;
- [бс] – необязательный аргумент (за исключением указанного выше случая), характеризующий числовое значение, равное остатку средств на конец действия договора. Равен 0 (нулю), если не указан явно;
- [тип] – необязательный аргумент, принимающий числовые значения 0 и 1, характеризующий момент выполнения платежей: в конце и в начале периода соответственно. Равен 0 (нулю) по умолчанию.
- Функция ПС используется для расчетов финансовых операций, выплаты в которых производятся по аннуитетной схеме, то есть фиксированными суммами через определенные промежутки времени определенное количество раз.
- Расходные операции для получателя записываются числами с отрицательным знаком. Например, депозит на сумму 10000 рублей для вкладчика равен -10000 рублей, а для банка – 10000 рублей.
- Между всеми функциями, связанными с аннуитетными схемами погашения стоимости существует следующая взаимосвязь:
- Приведенная выше формула значительно упрощается, если процентная ставка равна нулю, и принимает вид: (плт * кпер) + пс + бс = 0.
- В качестве аргументов функции ПС должны использоваться данные числового формата или текстовые представления чисел. Если в качестве одного из аргументов была передана текстовая строка, которая не может быть преобразована в числовое значение, функция ПС вернет код ошибки #ЗНАЧ!.
Примечание 2: с точки зрения практического применения функции ПС, ее рационально использовать для депозитных операций, поскольку заемщик вряд ли забудет, на какую сумму он оформлял кредит. Функция ПС позволяет узнать, депозит на какую сумму требуется внести, чтобы при известных годовой процентной ставке и числе периодов капитализации получить определенную сумму средств. Эта особенность будет подробно рассмотрена в одном из примеров.
Источник