Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
Описание
Возвращает синус заданного угла.
Синтаксис
SIN(число)
Аргументы функции SIN описаны ниже.
-
Число Обязательный. Угол в радианах, для которого вычисляется синус.
Замечание
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|---|---|---|
|
=SIN(ПИ()) |
Синус пи радиан (0, приблизительно). |
0,0 |
|
=SIN(ПИ()/2) |
Синус пи/2 радиан. |
1,0 |
|
=SIN(30*ПИ()/180) |
Синус угла 30 градусов. |
0,5 |
|
=SIN(РАДИАНЫ(30)) |
Синус 30 градусов. |
0,5 |
Нужна дополнительная помощь?
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
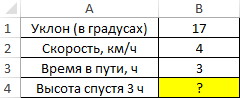
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Таблица данных:
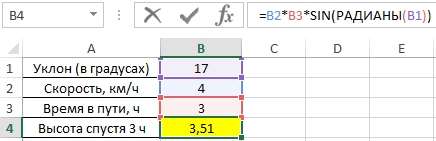
Для решения используем формулу:
=B2*B3*SIN(РАДИАНЫ(B1))
Описание аргументов:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
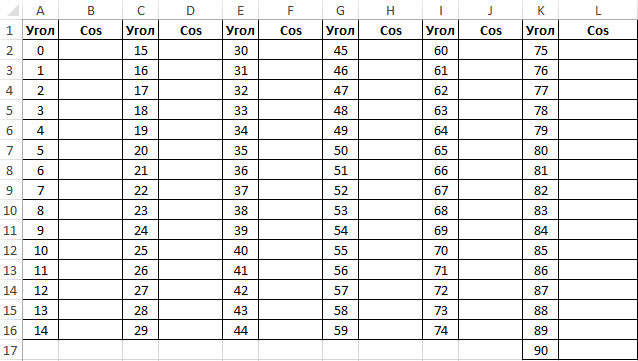
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
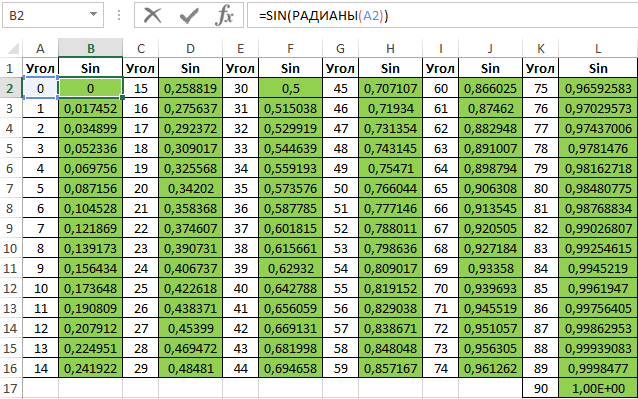
=COS(РАДИАНЫ(A2:A16))
Вычислим значения для всех значений углов. Полученный результат:
Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.
Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
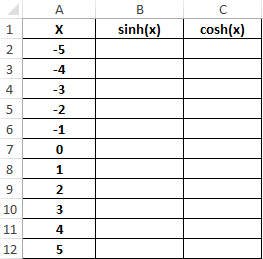
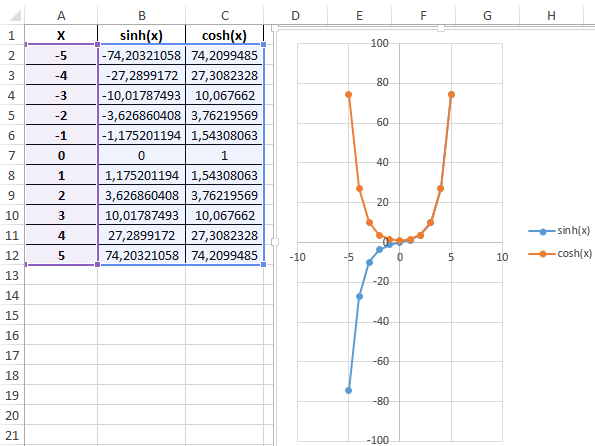
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Исходные данные:
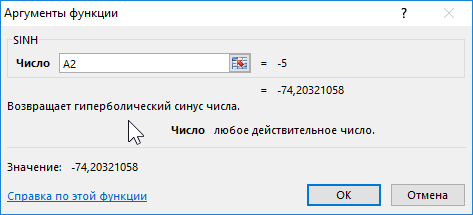
Формула для нахождения синусов гиперболических:
=SINH(A2:A12)
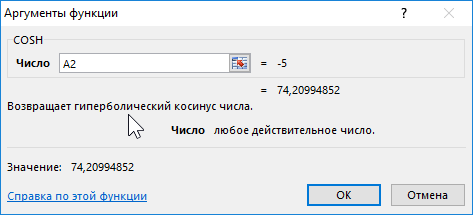
Формула для нахождения косинусов гиперболических:
=COSH(A2:A12)
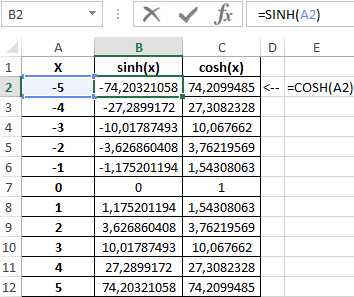
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
=SIN(число)
Синтаксис функции SINH:
=SINH(число)
Синтаксис функции COS:
=COS(число)
Синтаксис функции COSH:
>=COSH(число)
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
Примечания 1:
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
Примечения 2:
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
Скачать примеры тригонометрических функций SIN и COS
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
SIN (функция SIN)
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
Описание
Возвращает синус заданного угла.
Синтаксис
Аргументы функции SIN описаны ниже.
Число Обязательный. Угол в радианах, для которого вычисляется синус.
Замечание
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Тригонометрические функции SIN COS в Excel для синуса и косинуса
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
Как в экселе считать синус в градусах
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
Описание
Возвращает синус заданного угла.
Синтаксис
Аргументы функции SIN описаны ниже.
Число Обязательный. Угол в радианах, для которого вычисляется синус.
Замечание
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
В этой практической задаче я покажу вам как при помощи возможностей Excel 2010 найти значение косинуса угла в 136 градусов. Задачка из школьной программы, так что этот практический урок будет полезен не только родителям, но и школьникам. Заодно вы узнаете какими тригонометрическими функциями обладает Excel 2010.
Обратите внимание на то, что в тригонометрических функциях программы Excel углы измеряются не в градусах, а в радианах. Поэтому, прежде чем вычислить косинус угла 136°, его нужно перевести в радианы. Это можно сделать двумя способами.
Первый: умножить 136 на число пи и разделить произведение на 180.
Второй: воспользоваться специальной функцией, которая переводит градусы в радианы.
SIN (функция SIN)
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
Описание
Возвращает синус заданного угла.
Синтаксис
Аргументы функции SIN описаны ниже.
Число Обязательный. Угол в радианах, для которого вычисляется синус.
Замечание
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Тригонометрические функции SIN COS в Excel для синуса и косинуса
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://exceltable.com/funkcii-excel/primery-funkciy-sin-sinh-cos-cosh
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
Функция SIN Excel — это встроенная тригонометрическая функция в Excel, которая используется для вычисления значения синуса заданного числа или, с точки зрения тригонометрии, значения синуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.
Функция SIN в Excel
Функция SIN в Excel вычисляет синус указанного угла. Функция SIN в Excel относится к категории математических / тригонометрических функций в Excel. SIN в excel всегда возвращает числовое значение.
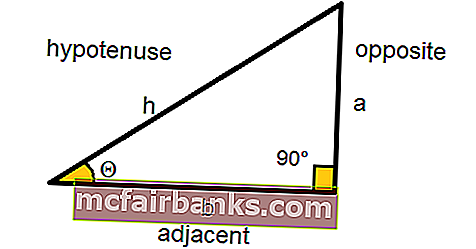
В математике и тригонометрии SINE — это тригонометрическая функция угла, который в прямоугольном треугольнике равен длине противоположной стороны (прямоугольной стороны), деленной на длину гипотенузы и представленной как :
Sin Θ = противоположная сторона / гипотенуза
Sin Θ = а / ч
Формула SIN в Excel
Ниже представлена формула SIN в Excel.
Где число — это аргумент, переданный формуле SIN в радианах.
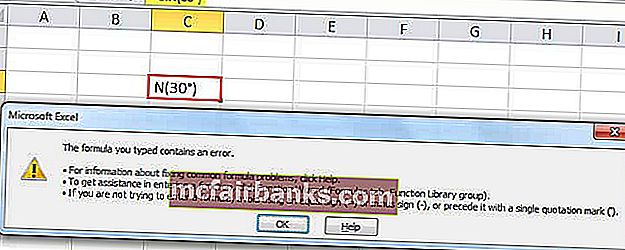
Если мы напрямую передадим угол в SIN в функции excel, он не распознает его как допустимый аргумент. Например, если мы передадим 30 ° в качестве аргумента для этого SIN в функции Excel, она не распознает его как допустимый аргумент. Excel отобразит сообщение об ошибке.
Следовательно, аргумент, который нам нужно передать, должен быть в радианах.
Чтобы преобразовать угол в радианы, есть два метода
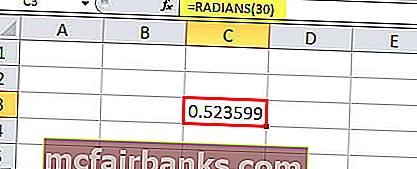
- Используйте встроенную функцию РАДИАНЫ Excel. Функция РАДИАНЫ преобразует градусы в радианы.
Например, чтобы преобразовать 30 ° в радианы, мы будем использовать эту функцию, она принимает градус в виде числа, 30 ° — как 30.
= РАДИАНЫ (30) даст радиан 0,52
- Во втором случае мы можем использовать математическую формулу для перевода градуса в радиан. Формула
Радиан = градусы * (π / 180) (π = 3,14)
В Excel также есть функция, которая возвращает значение Пи с точностью до 15 цифр, а функция — ПИ ()
Поэтому для преобразования градуса в радианы мы будем использовать формулу
Радиан = градусы * (PI () / 180)
Как использовать функцию SIN в Excel?
Функция SIN в Excel очень проста и удобна в использовании. Давайте разберемся, как работает SIN in excel на некоторых примерах.
Вы можете скачать этот SIN в шаблоне Excel здесь — SIN в шаблоне Excel
SIN в Excel, пример №1
Расчет значения синуса с использованием функции SIN в Excel и функции РАДИАНЫ в Excel
Расчет значения синуса с использованием функции SIN в Excel и функции PI
Функция синуса в Excel имеет множество реальных приложений; он широко используется в архитектуре для расчета высоты и длины геометрических фигур. Он также используется в GPS, оптике, вычислении траекторий, для поиска кратчайшего маршрута на основе географической широты и долготы, радиовещания и т. Д. Даже электромагнитная волна строится в виде графика функции синуса и косинуса.
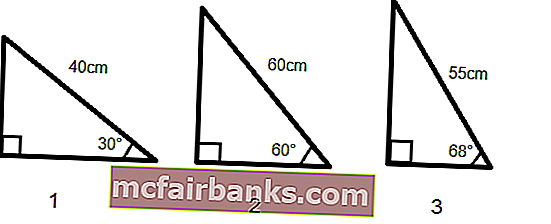
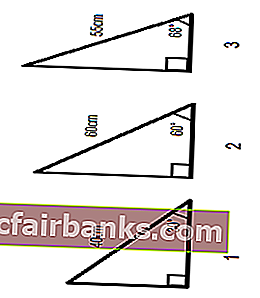
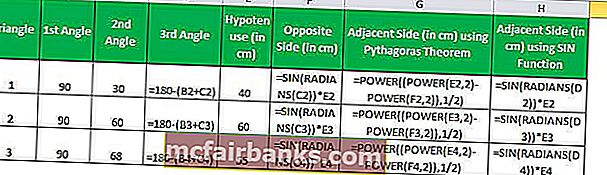
Предположим, у нас есть три прямоугольных треугольника с указанием их углов и длины одной стороны, и нам нужно вычислить длину двух других сторон.
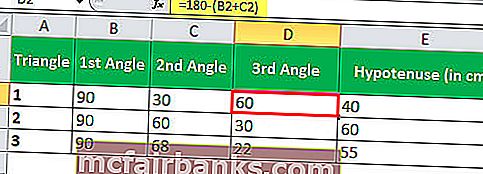
Сумма всех углов на треугольнике равна 180 °, следовательно, мы можем легко вычислить третий угол.
Мы знаем, Sin Θ = противоположное / гипотенуза
Таким образом, длина противоположной стороны будет Sin Θ * гипотенуза
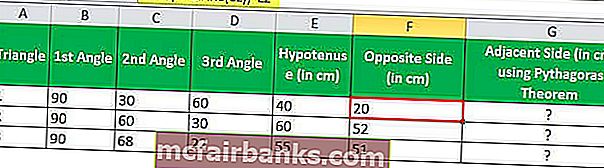
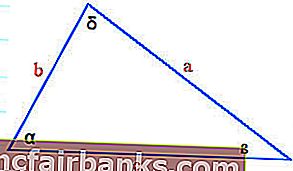
В Excel длина противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле SIN.
= ГРЕХ (РАДИАНЫ (C2)) * E2
Применяя приведенную выше формулу SIN для трех треугольников, мы можем получить длину перпендикуляров треугольников
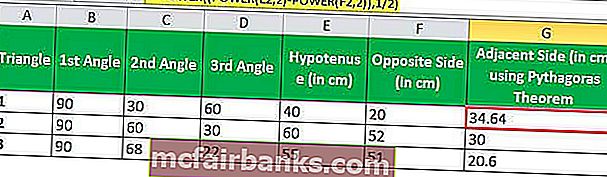
Для третьей стороны (смежной стороны) у нас есть два метода — с помощью теоремы Пифагора или с помощью функции SIN в Excel с других углов.
Согласно теореме Пифагора, сумма квадратов двух сторон прямоугольного треугольника эквивалентна квадрату гипотенузы.
Гипотенуза2 = Противоположная2 + Соседняя2
Соседний = (Гипотенуза2 — Противоположный2) 1/2
В Excel мы запишем это как,
= МОЩНОСТЬ ((МОЩНОСТЬ (Гипотенуза; 2) -МОЩНОСТЬ (напротив; 2)); 1/2)
Применяя эту формулу, вычисляем длину смежной стороны
= МОЩНОСТЬ ((МОЩНОСТЬ (E2,2) -МОЩНОСТЬ (F2,2)); 1/2)
Используя второй метод, мы можем использовать СИНУС 3-го угла для вычисления значения соседней стороны.
Если мы повернем треугольники на 90 ° влево, противоположная сторона поменяется местами со смежной стороной, и SIN угла между гипотенузой и смежной стороной поможет вычислить значение третьей стороны.
= ГРЕХ (РАДИАНЫ (D2)) * E2
SIN в Excel, пример №2
Есть высокое здание неизвестной высоты, и солнечный луч в какой-то момент времени делает угол в точке A 75 °, создавая тень от здания длиной 70 метров. Нам нужно найти высоту башни
Высота здания будет рассчитана с использованием SIN в функции excel.
SIN 75 ° = высота здания / длина тени в точке A
Следовательно, высота здания = SIN 75 ° * Длина тени в точке A
Следовательно, высота здания будет
= SIN (РАДИАНЫ (B3)) * B2
Высота здания 67,61 метра.
SIN в Excel, пример №3
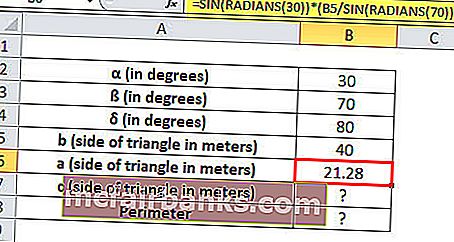
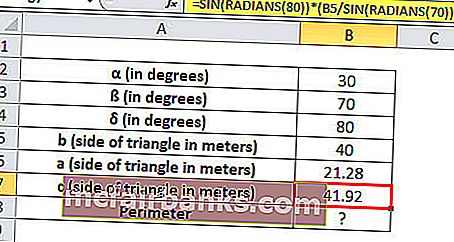
У нас есть земля в форме треугольника, для которого даны два угла: 30 ° и 70 °, и нам известна только длина одной стороны треугольника, которая составляет 40 метров. Нам нужно найти длину трех других сторон и периметр треугольника.
Для треугольника, когда одна сторона и все углы известны, мы можем вычислить другие стороны по правилу SINE
Правило синуса в тригонометрии дает соотношение углов и сторон треугольника по формуле SIN
a / sin α = b / sin ß = c / sin δ
В этом случае,
α = 30 °, ß = 70 ° и δ = 180 ° — (30 ° + 70 °) = 80 ° и одна сторона треугольника b = 40 метров
Чтобы найти другие стороны треугольника, мы будем использовать правило синуса.
а = Sin α * (b / sin ß)
Следовательно,
a = ГРЕХ (РАДИАНЫ (30)) * (B5 / ГРЕХ (РАДИАНЫ (70)))
Длина стороны а = 21,28 метра
Точно так же третья сторона c будет
c = Sin δ * (b / sin ß)
Следовательно,
c = SIN (РАДИАНЫ (80)) * (B5 / SIN (РАДИАНЫ (70)))
Три стороны треугольника имеют длину 21,28, 40, 41,92 метра.
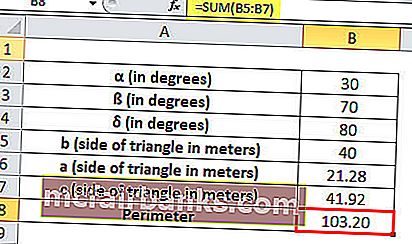
Периметр треугольника равен сумме всех сторон.
Следовательно, периметр будет = СУММ (B5: B7)
Original text
Contribute a better translation