Составим в MS EXCEL график погашения кредита дифференцированными платежами.
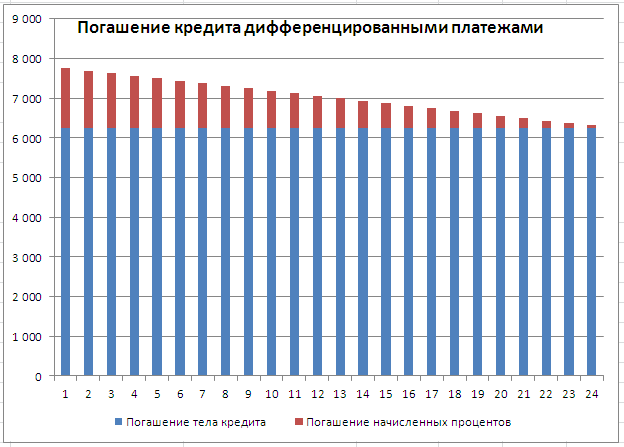
При расчете графика погашения кредита дифференцированными платежами сумма основного долга делится на равные части пропорционально сроку кредитования. Регулярно, в течение всего срока погашения кредита, заемщик выплачивает банку эти части основного долга плюс начисленные на его остаток проценты. Если кредитным договором период погашения установлен равным месяцу, то из месяца в месяц сумма основного долга пропорционально уменьшается. Поэтому при дифференцированных платежах основные расходы заемщик несет в начале кредитования, размеры ежемесячных платежей в этот период самые большие. Но постепенно, с уменьшением остатка ссудной задолженности, уменьшается и сумма начисленных процентов по кредиту. Выплаты по кредиту значительно сокращаются и становятся не такими обременительными для заемщика.
Примечание
. При расчете кредита дифференцированными платежами сумма переплаты по процентам будет ниже, чем при
аннуитетных платежах
. Не удивительно, что сегодня практически все российские банки применяют в расчетах аннуитетную схему погашения кредита. Сравнение двух графиков погашения кредита приведено в статье
Сравнение графиков погашения кредита дифференцированными аннуитетными платежами в MS EXCEL
.
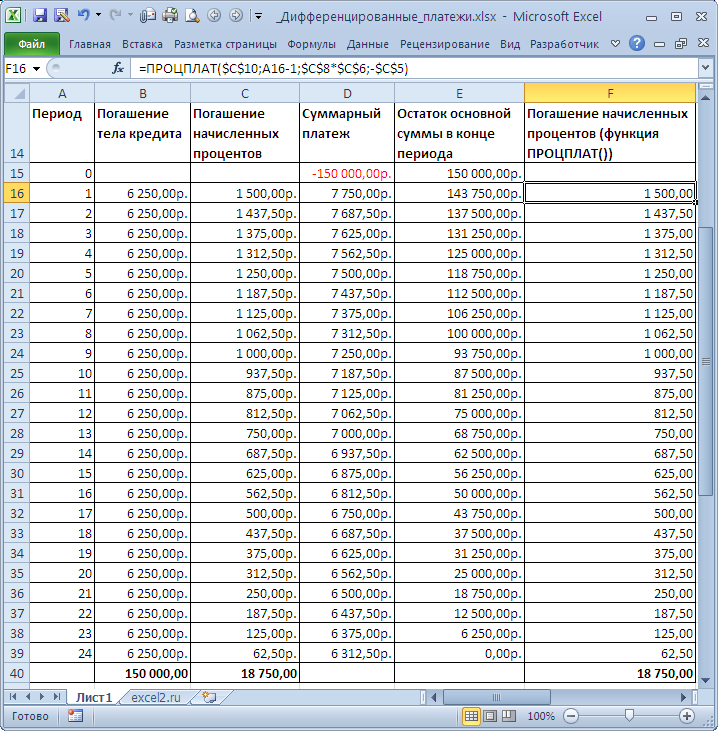
График погашения кредита дифференцированными платежами
Задача
. Сумма кредита =150т.р. Срок кредита =2 года, Ставка по кредиту = 12%. Погашение кредита ежемесячное, в конце каждого периода (месяца).
Решение. Сначала вычислим часть (долю) основной суммы кредита, которую заемщик выплачивает за период: =150т.р./2/12, т.е. 6250р. (сумму кредита мы разделили на общее количество периодов выплат =2года*12 (мес. в году)). Каждый период заемщик выплачивает банку эту часть основного долга плюс начисленные на его остаток проценты. Расчет начисленных процентов на остаток долга приведен в таблице ниже – это и есть график платежей.
Для расчета начисленных процентов может быть использована функция ПРОЦПЛАТ(ставка;период;кпер;пс), где Ставка — процентная ставка
за период
;
Период
– номер периода, для которого требуется найти величину начисленных процентов;
Кпер
— общее число периодов начислений;
ПС
–
приведенная стоимость
на текущий момент (для кредита ПС — это сумма кредита, для вклада ПС – начальная сумма вклада).
Примечание
. Не смотря на то, что названия аргументов совпадают с названиями аргументов
функций аннуитета
–
ПРОЦПЛАТ()
не входит в группу этих функций (не может быть использована для расчета параметров аннуитета).
Примечание
. Английский вариант функции — ISPMT(rate, per, nper, pv)
Функция
ПРОЦПЛАТ()
предполагает начисление процентов
в начале каждого периода
(хотя в справке MS EXCEL это не сказано). Но, функцию можно использовать для расчета процентов, начисляемых и в конце периода для это нужно записать ее в виде ПРОЦПЛАТ(ставка;период-1;кпер;пс), т.е. «сдвинуть» вычисления на 1 период раньше (см.
файл примера
). Функция
ПРОЦПЛАТ()
начисленные проценты за пользование кредитом указывает с противоположным знаком, чтобы отличить денежные потоки (если выдача кредита – положительный денежный поток («в карман» заемщика), то регулярные выплаты – отрицательный поток «из кармана»).
Расчет суммарных процентов, уплаченных с даты выдачи кредита
Выведем формулу для нахождения суммы процентов, начисленных за определенное количество периодов с даты начала действия кредитного договора. Запишем суммы процентов начисленных в первых периодов (начисление и выплата в конце периода): ПС*ставка (ПС-ПС/кпер)*ставка (ПС-2*ПС/кпер)*ставка (ПС-3*ПС/кпер)*ставка … Просуммируем полученные выражения и, используя формулу суммы арифметической прогрессии, получим результат. =ПС*Ставка* период*(1 — (период-1)/2/кпер) Где, Ставка – это процентная ставка за период (=годовая ставка / число выплат в году), период – период, до которого требуется найти сумму процентов. Например, сумма процентов, выплаченных за первые полгода пользования кредитом (см. условия задачи выше) = 150000*(12%/12)*6*(1-(6-1)/2/(2*12))=8062,50р. За весь срок будет выплачено =ПС*Ставка*(кпер+1)/2=18750р. Через функцию
ПРОЦПЛАТ()
формула будет сложнее: =СУММПРОИЗВ(ПРОЦПЛАТ(ставка;СТРОКА(ДВССЫЛ(«1:»&кпер))-1;кпер;-ПС))
Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).
Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.
Как рассчитать платежи по кредиту в Excel
Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:
- Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
- При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.
Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.
Расчет аннуитетных платежей по кредиту в Excel
Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:
А = К * S
где:
- А – сумма платежа по кредиту;
- К – коэффициент аннуитетного платежа;
- S – величина займа.
Формула коэффициента аннуитета:
К = (i * (1 + i)^n) / ((1+i)^n-1)
- где i – процентная ставка за месяц, результат деления годовой ставки на 12;
- n – срок кредита в месяцах.
В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:
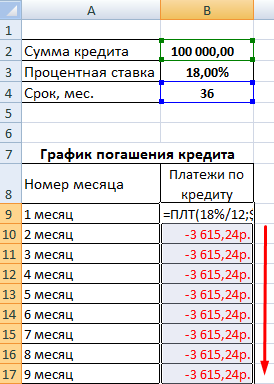
- Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
- Составим график погашения кредита. Пока пустой.
- В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).
Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.
Расчет платежей в Excel по дифференцированной схеме погашения
Дифференцированный способ оплаты предполагает, что:
- сумма основного долга распределена по периодам выплат равными долями;
- проценты по кредиту начисляются на остаток.
Формула расчета дифференцированного платежа:
ДП = ОСЗ / (ПП + ОСЗ * ПС)
где:
- ДП – ежемесячный платеж по кредиту;
- ОСЗ – остаток займа;
- ПП – число оставшихся до конца срока погашения периодов;
- ПС – процентная ставка за месяц (годовую ставку делим на 12).
Составим график погашения предыдущего кредита по дифференцированной схеме.
Входные данные те же:
Составим график погашения займа:
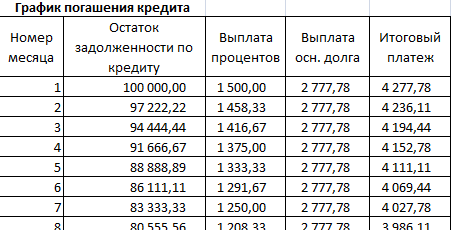
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.
Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).
Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).
Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.
Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.
Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:
Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.
Формула расчета процентов по кредиту в Excel
Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:
Рассчитаем ежемесячную процентную ставку и платежи по кредиту:
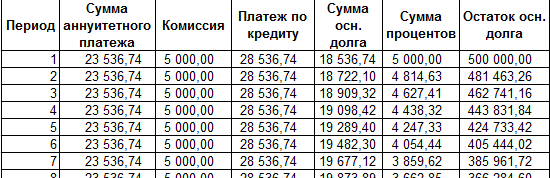
Заполним таблицу вида:
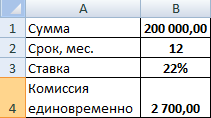
Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.
Сумма основного долга = аннуитетный платеж – проценты.
Сумма процентов = остаток долга * месячную процентную ставку.
Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.
Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:
- взяли кредит 500 000 руб.;
- вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
- переплата составила 184 881, 67 руб.;
- процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
- Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.
Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.
Расчет полной стоимости кредита в Excel
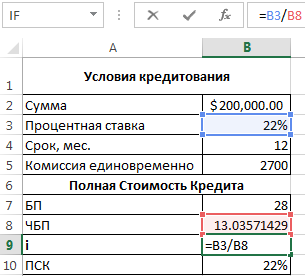
Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:
- ПСК = i * ЧБП * 100;
- где i – процентная ставка базового периода;
- ЧБП – число базовых периодов в календарном году.
Возьмем для примера следующие данные по кредиту:
Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).
Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.
Далее находим ЧБП: 365 / 28 = 13.
Теперь можно найти процентную ставку базового периода:
У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8
Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.
ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.
Скачать кредитный калькулятор в Excel
Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.
Автоматизировать процесс дифференцированного расчёта кредита можно при помощи кредитного калькулятора, разработанного в программе Microsoft Excel. В этой публикации мы вам расскажем и покажем, как это делается. Давайте приступим!
Содержание
- Где можно бесплатно скачать такой калькулятор
- Разрабатываем калькулятор дифференцированных платежей в Excel
Где можно бесплатно скачать такой калькулятор
Не удивляйтесь, друзья, но вначале вам действительно надо скачать готовый калькулятор дифференцированных платежей, который мы разработали в Excel. Именно его мы и будем «разбирать на запчасти». Также, при желании, вы сможете его доработать под свои требования.
На примере этого калькулятора вы немного познакомитесь с программой Microsoft Excel, а также автоматизируете расчёт дифференцированных платежей по кредиту. Бесплатно скачать калькулятор можно перейдя по ссылке ниже:
Получилось? Вот и отлично! Приступаем к «разбору полётов»!
Разрабатываем калькулятор дифференцированных платежей в Excel
Прежде всего давайте разберемся, по какому принципу работает наш калькулятор. Откройте скачанный «экселевкий» файл. В верхнем левом углу страницы вы увидите две таблицы. Они называются: «Укажите данные для расчёта» и «Результаты расчёта». Также сверху над всеми столбцами нашей страницы Excel есть буквы A, B, C, D, E, F и т.д., а слева напротив строк – цифры 1, 2, 3, 4, 5, 6 и т. д. Именно эти буквы и цифры определяют координаты каждой ячейки таблицы.
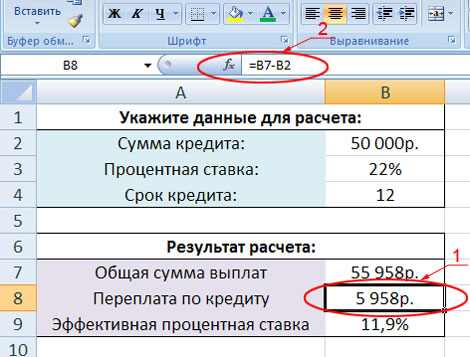
Кликните левой кнопкой мыши по ячейке со значением «5958р.», которое находится в результатах расчёта в строке «Переплата по кредиту». В нашем калькуляторе эта ячейка имеет координаты B8. Вот вам картинка для наглядности:
На изображении данную ячейку мы обвели красной линией и обозначили цифрой один. Обратите внимание ещё вот на что. Когда вы кликаете по какой-либо ячейке в таблице Excel, то эта ячейка выделяется чёрной жирной рамкой, а её буквенно-цифровые координаты сверху и слева окрашиваются другим фоном. Например, на нашем изображении буква B сверху и цифра 8 слева изменили цвет фона с серо-голубого на желтоватый. Также в верхней строке формул, слева от которой есть кнопка «fx» (на рисунке она обведена красным и обозначена цифрой два) указано значение или формула, по которой выполняется расчёт данных для выделенной ячейки. В нашем примере для ячейки с координатой B8 выполняется расчёт по следующей формуле: =B7-B2. В окне с координатой B7 указана общая сумма выплат по кредиту, которая в нашем примере равна 55 958 рублей, а B2 – это сам кредит, который равен 50 000 рублей. Выполнив простое математическое вычисление, наша программа занесла в ячейку B8 значение 5958 (55 958 – 50 000=5958).
Как видите, Microsoft Excel работает достаточно просто. По аналогичному принципу заданы формулы и значения для остальных ячеек нашего кредитного калькулятора дифференцированных платежей. Давайте рассмотрим, как они рассчитаны. Щёлкаем мышкой по изображению:
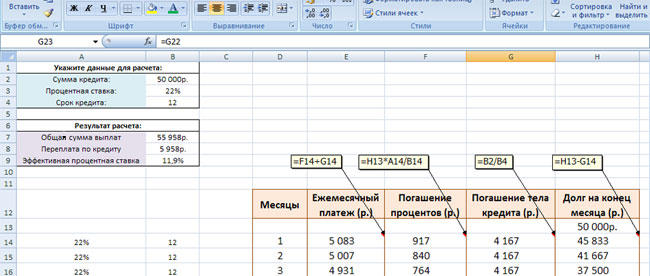
Итак, правее в оранжевой рамке вы видите график дифференцированных платежей по кредиту. Все значения в этой таблице рассчитываются автоматически по формулам, которые мы рассматривали в предыдущей публикации. Именно эти формулы и прописаны в ячейках нашего калькулятора. Давайте их детально рассмотрим на примере первой строки графика погашения кредита.
- «Ежемесячный платёж» – это ежемесячный дифференцированный платёж по займу. Он состоит из двух частей: суммы, идущей на погашение процентов (ячейка F14), и суммы, идущей на погашение тела кредита (ячейка G14). Именно потому ежемесячный платёж в первой строке рассчитан по формуле: =F14+ G14.
- «Погашение процентов» – здесь работает формула расчёта процентов по кредиту за данный период: остаток задолженности (в первом платеже он равен сумме кредита 50 000 руб., вынесенную в ячейку H13) умножить на годовую процентную ставку (она равна 22% и вынесена в ячейку A14) и разделить на 12 (мы вынесли это значение в ячейку B14). Собственно, эти условия и прописаны в формуле для ячейки F14: =H13*A14/B14. Кстати, вместо B14 можно просто указать фиксированную цифру – 12.
- «Погашение тела кредита» – это фиксированное значение, которое не меняется на протяжении всего срока кредитования. Рассчитывается этот показатель очень просто: сумма кредита (ячейка B2) делится на общий срок кредитования (ячейка B4). В итоге для ячейки G14 получаем такую формулу: = B2/B4.
- «Долг на конец месяца» – из суммы долга на конец предыдущего месяца (в первом платеже он у нас равен сумме кредита – 50 000 рублей и вынесен в ячейку H13) вычитаем выплату по телу кредита в текущем периоде (4167 рублей – ячейка G14). В результате, долг на конец месяца по первому платежу у нас равен 45 833 рубля (50 000 – 4167 = 45 833), что и записано в формуле для ячейки H14: = H13- G14.
Вот таким нехитрым способом разработан кредитный калькулятор дифференцированных платежей в Excel. Он рассчитан на кредиты сроком до 12 месяцев. При желании, вы можете его усовершенствовать и расширить данный диапазон до 24, 36 и более месяцев. В общем, теперь всё в ваших руках, друзья. Как говорится, мы вам дали удочку, а вы сами решайте, что с ней дальше делать.
Портал temabiz.com – ваш надёжный информационный помощник в вопросах кредитования. Оставайтесь с нами!
⇧
Время на прочтение: 6 минут(ы)
В большинстве случаев кредитные организации предлагают своим клиентам аннуитетную схему погашения долга, и лишь некоторые компании готовы предоставить собственным заемщикам возможность закрывать задолженность через дифференцированный платеж. О том, что собой представляет дифференцированный тип платежей и в чем его преимущество, мы сегодня и поговорим.
График дифференциального платежа на фото
Дифференцированный платеж – что это значит?
Дифференцированный тип погашения долга представляет собой способ выплаты кредита, при котором заемщик каждый месяц вносит платежи, состоящие из равных долей основного долга и процентов, начисленных на остаток задолженности.
Таким образом, сума каждого нового платежа будет отличаться от суммы предыдущего взноса. При этом неизменным останется только сумма основного платежа, с помощью которого погашается непосредственно «тело» кредита. Процентная составляющая формируется в каждом отчетном периоде по специальной схеме. Поэтому из-за уменьшения суммы основного долга сумма процентов также уменьшается, а значит, сокращаются и размеры обязательных выплат.
Внимание: При дифференцированном типе погашения долга возможно досрочное закрытие кредита.
Важно понимать, что лучше всего не сокращать общую сумму платежа, а стремиться к уменьшению срока кредитования, так как долговое бремя в любом случае будет смягчаться, но при этом сокращение периода кредитования позволит погасить кредит гораздо быстрее и сэкономить на процентах.
Необходимо отметить, что дифференцированный платеж не слишком популярен среди кредитных организаций, что объясняется сложностью понимания принципов работы заемщиками и относительной невыгодностью для кредитора.
Чем отличается аннуитетный платеж от дифференцированного?
Аннуитетный тип платежа представляет собой равные по размеру ежемесячные взносы, растянутые на весь период кредитования. В сумму каждого транша включены:
- часть основного долга;
- начисленные проценты;
- дополнительные комиссии и сборы организации.
При этом в первое время (месяцы, а порой и годы) заемщик по факту выплачивает в основном проценты за обслуживание кредита, а в счет погашения основного долга отправляется лишь малая часть платежей. Ближе к концу периода кредитования ситуация несколько меняется: большая часть взноса идет на погашение основного долга, а меньшая – на проценты. При этом общий размер платежа на протяжении всего срока кредитования остается одинаковым.
При этом дифференцированный платеж выражается в неравных между собой ежемесячных траншах, пропорционально уменьшающихся в течение всего периода кредитования. Наибольший размер платежей характерен первой четверти всего срока, наименьший – в последней.
При этом платежи в середине срока кредитования сопоставимы с аннуитетом.
Сумма транша изменяется от выплаты к выплате в связи с тем, что основная сумма задолженности по кредиту уменьшается с каждым платежом, а вместе с ней – и сумма процентов, рассчитываемая от «тела» кредита.
Что выгоднее заемщику?
Как показывает практика, во время оформления кредита практически все заемщики больше обеспокоены одобрением заявки, а не подбором схемы платежей.
Такой подход в корне не верен, так как неверно подобранный тип платежей может привести к достаточно серьезной переплате.
Важно понимать, что способ расчета ежемесячной суммы транша зависит и от суммы кредита, и от срока использования заемных средств.
Таким образом, для граждан, оформляющих кредит на пятнадцать и более лет, наиболее выгодным вариантом является дифференцированная система возврата долга, так как именно в таком случае сумма переплаты окажется существенно меньше, чем при аннуитетном погашении. При желании заемщик может внести сумму для полного погашения кредита, при этом он останется в плюсе и в начале, и в конце срока.
Для тех, кто оформляет ипотечный кредит на небольшой срок, наиболее выгодной является аннуитетная схема погашения задолженности. В таком случае заемщик будет выплачивать долг одинаковыми по размеру взносами, при этом его платежеспособность изменяться не будет (за исключением чрезвычайных и непредвиденных ситуаций). При таком способе погашения необходимо учитывать, что досрочное погашение кредита экономически выгодно только в первые годы погашения кредита.
Использование при расчете платежей по кредиту
Любой дифференцированный платеж включает в себя две основные составляющие:
- «тело» (основная сумма) кредита;
- проценты, ежемесячно начисляемые на фактический остаток долга.
Сумма делится на равные транши, количество которых зависит от периода кредитования. К примеру, оформив кредит на сумму в 240 тысяч рублей сроком на 12 месяцев, заемщик должен быть к тому, что сумма ежемесячных взносов, направленных на погашение «тела» кредита, составит около 20 тысяч рублей.
Сумма платежа для погашения основного долга будет оставаться неизменной на протяжении всего периода кредитования. Исключением может стать лишь:
- обращение заемщика к кредитору с просьбой продлить срок кредитования;
- частичное досрочное погашение задолженности.
В отношении начисляемых процентов ситуация выглядит несколько иначе. За счет постоянного снижения ежемесячной суммы на погашение процентов будет снижаться и общая сумма каждого последующего взноса.
Особенно выгодным в такой ситуации является частичное досрочное погашение долга. Достаточно одного внесения крупной суммы денег, существенно превышающей сумму обязательного платежа, для значительного снижения размера всех последующих взносов.
При повторном частичном погашении долга ситуация также изменится в пользу заемщика.
Все дифференцированные платежи по кредиту рассчитываются по определенной схеме.
Принцип расчета значительно отличается от принципа аннуитетного погашения задолженности, благодаря чему сумма ежемесячного взноса с каждым месяцев изменяется в меньшую сторону.
Для того чтобы рассчитать сумму дифференцированного платежа, необходимо всю сумму долга разделить на количество месяцев, указанных в качестве срока кредитования в договоре. После этого к каждому из платежей необходимо добавить проценты, которые начисляются на фактический остаток долга. Таким образом, с уменьшением суммы задолженности уменьшаются и начисляемые проценты.
Формула
Для расчета дифференцированного платежа необходимо отдельно рассчитать сумму основного платежа и сумму начисляемых процентов.
Для подсчета суммы основного платежа необходимо сумму задолженности разделить на количество месяцев, за которое планируется полное погашение кредита. Полученный результат и будет являться суммой основного платежа.
Формула для расчета основного платежа выглядит следующим образом:
b = S/N , где
b – сумма основного платежа;
S – общая сумма кредита;
N – количество месяцев, отведенных на погашение долга.
Для подсчета ежемесячно начисляемых процентов необходимо фактическую сумму задолженности на текущий момент времени умножить на годовую процентную ставку, и получившийся результат разделить на количество месяцев в году.
Формула для подсчета процентов будет выглядеть так:
p = Sn*P/12, где
p – сумма начисленных процентов;
Sn – фактический остаток задолженности на текущий период;
P – оговоренная сторонами годовая процентная ставка по кредиту.
Для расчета фактического остатка задолженности на определенную дату нужно из общей суммы задолженности вычесть размер основного платежа, умноженный на количество уже прошедших отчетных периодов, вследствие чего формула для расчета остатка приобретает следующий вид:
Sn = S–(b*n) , где
Sn – фактический остаток задолженности на определенный период;
S – общая сумма задолженности перед банком;
b – размер основного платежа;
n – количество прошедших периодов.
Расчет в Excel: пример
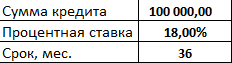
В качестве примера для расчета графика дифференцированных платежей по кредиту возьмем следующие данные:
- сумма кредита: 100 тысяч рублей;
- годовая процентная ставка: 10 процентов;
- предполагаемый срок погашения кредита: 6 месяцев.
Таким образом, сумма основного ежемесячного платежа составит: 100 тысяч рублей/ 6 месяцев = 16,666 тысяч рублей и 67 копеек.
Размер выплаты за каждый отчетный месяц составит:
- первый месяц: 16 666,67 рублей + (100 000 рублей – (16 666,67 рублей * 0 месяцев)) * 0,1 / 12 месяцев = 17 500 рублей;
- второй месяц: 16 666,67 рублей + (100 000 рублей – (16 666,67 рублей * 1 месяцев)) * 0,1 / 12 месяцев = 17 361,11 рублей;
- третий месяц: 16 666,67 рублей + (100 000 рублей – (16 666,67 рублей * 2 месяцев)) * 0,1 / 12 месяцев = 17 222,22 рублей;
- четвёртый месяц: 16 666,67 рублей + (100 000 рублей – (16 666,67 рублей * 3 месяцев)) * 0,1 / 12 месяцев = 17 083,33 рублей;
- пятый месяц: 16 666,67 рублей + (100 000 рублей – (16 666,67 рублей * 4 месяцев)) * 0,1 / 12 месяцев = 16 944,44 рублей;
- шестой месяц: 16 666,67 рублей + (100 000 рублей – (16 666,67 рублей * 5 месяцев)) * 0,1/12 месяцев = 16 805,56 рублей.
Таким образом, в течение всего срока кредитования заемщик выплатит кредитору 102 916,67 рублей, переплатив по кредиту всего лишь 2 619,67 рублей.
Расчет дифференцированных платежей по кредиту в Excel
Ознакомиться с другим примером графика дифференцированных платежей можно, скачав документ по ссылке: https://yadi.sk/i/MZm3Lnc03H8nVV.
Ипотека с дифференцированными платежами: список банков
В настоящее время подавляющее большинство банков предлагает собственным клиентам аннуитетную схему погашения задолженности, и лишь некоторые кредиторы готовы рассмотреть вопрос о дифференцированных выплатах. Обусловлено это тем, что кредитным организациям гораздо выгоднее именно аннуитетные выплаты, благодаря которым в первую очередь погашаются проценты, и лишь потом – основная сумма долга.
К числу самых популярных банков, выдающих ипотечные кредиты с возможностью дифференцированного погашения, относятся такие учреждения, как «Газпромбанк» и «Нордеа Банк». Клиенты данных организаций также могут выбрать аннуитетную схему выплат.
В то же время не менее известные учреждения в лице «Сбербанка», «ВТБ 24» и «Зенит» отказались от дифференцированных платежей и предоставляют жилищные кредиты только с возможностью аннуитетного погашения.
«Сбербанк»
Еще несколько лет назад клиенты самого известного финансового учреждения нашей страны имели возможность оформить ипотеку с возможностью дифференцированного погашения долга. Однако на данный момент все кредиты в «Сбербанке» выдаются только с аннуитетной схемой платежей. Дифференцированное погашение возможно только для клиентов, оформивших ипотеку до момента отмены такой схемы, и при условии, что в кредитном договоре предусмотрен именно дифференцированный способ выплат.
Таким образом, при грамотном подходе заемщик может сэкономить крупную сумму денег, лишь внимательно выбрав банк и тип погашения задолженности. Особенно актуален такой подход при оформлении ипотечного кредита – ведь в таком случае дифференцированная схема платежей позволит избежать переплаты в сотни тысяч (а в некоторых случаях и в миллионы) рублей.
Видео
Смотрите на видео ролике советы по выбору между аннуитетным или дифференциальным платежам:
Дифференцированный платеж по кредиту в разрезе большого промежутка времени намного выгоднее аннуитетного.
Предыдущая
Формулы и расчетыИнструкция как выполнить расчет пени по ставке рефинансирования
Следующая
Формулы и расчетыЧто такое маржа и инструкция как её рассчитать
Практическая
работа
«РАСЧёт
ПЛАТЕЖей ПО КРЕДИТУ В EXCEL»
Задача.
Допустим, что нам
нужно взять кредит в 2 млн. рублей на покупку квартиры под 10,2% годовых на 10
лет. Банк предлагает два вида платежей аннуитетный
платеж или дифференцированный платеж. Какой вид платежа выгоден клиенту и почему?
План работы:
1. Рассчитать
платежи по аннуитетной схеме погашения.
2. Рассчитать
платежи по дифференцированной схеме погашения.
3. Сравнить
переплату при аннуитетной и дифференцированной схеме погашения кредита.
4. Сделать
вывод (какой вид платежа выгоден клиенту, а какой банку).
Ежемесячные
выплаты зависят от схемы погашения кредита. Различают аннуитетные и
дифференцированные платежи:
1. Аннуитет
предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При
дифференцированной схеме погашения долга перед финансовой организацией проценты
начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут
уменьшаться.
1. Рассчитать
платежи по аннуитетной схеме погашения.
Ежемесячная сумма
аннуитетного платежа рассчитывается по формуле:
где:
·
А – сумма платежа по кредиту;
·
К – коэффициент аннуитетного платежа;
·
S – величина займа.
Формула коэффициента
аннуитета:
·
где i – процентная ставка за месяц, результат деления годовой
ставки на 12;
·
n – срок кредита в месяцах.
В программе Excel существует
специальная функция, которая считает аннуитетные платежи. Это =ПЛТ:
1. Заполним
входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа,
проценты и срок.
2. Составим
график погашения кредита. Пока пустой.
3. В первую
ячейку столбца «Платежи по кредиту» вводится формула расчета кредита аннуитетными
платежами: =ПЛТ($B$2/12; $B$3; $B$1). Чтобы закрепить ячейки, используем
абсолютные ссылки.
Ячейки окрасились в красный
цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать
банку, терять.
4. Подсчитаем
сумму выплат.
В ячейку столбца «Выплачено» вводится
формула суммирования выплат по кредиту: =СУММ(B7:B126)*(-1). Чтобы закрепить
ячейки, используем абсолютные ссылки.
Сумму переплат подсчитайте
самостоятельно.
2. Рассчитать
платежи по дифференцированной схеме погашения.
Дифференцированный способ
оплаты предполагает, что:
·
сумма основного долга распределена по периодам выплат равными
долями;
·
проценты по кредиту начисляются на остаток.
Формула расчета дифференцированного
платежа:
где:
·
ДП – ежемесячный платеж по кредиту;
·
ОСЗ – остаток займа;
·
ПП – число оставшихся до конца срока погашения периодов;
·
ПС – процентная ставка за месяц (годовую ставку делим на 12).
Составим график погашения
кредита по дифференцированной схеме.
Входные данные:
Составим график погашения
займа:
Остаток
задолженности по кредиту: в первый месяц равняется всей
сумме: =K2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(K9>$K$4;0;L8-N8).
Где K9 – номер текущего периода, K4 – срок кредита; L8 – остаток по кредиту в
предыдущем периоде; N8 – сумма основного долга в предыдущем периоде.
Выплата
процентов: остаток по кредиту в текущем периоде умножить
на месячную процентную ставку, которая разделена на 12 месяцев: =L8*($K$3/12).
Выплата
основного долга: сумму всего кредита разделить на
срок: = ЕСЛИ(K8<=$K$4;$K$2/$K$4;0).
Итоговый
платеж: сумма «процентов» и «основного долга» в
текущем периоде: =M8+N8
Внесем формулы в
соответствующие столбцы. Скопируем их на всю таблицу.
Сумму выплат и переплат
посчитайте самостоятельно.
3. Сравнить
переплату при аннуитетной и дифференцированной схеме погашения кредита.
Аннуитетный платёж:
___________________________
Дифференцированный платёж:
____________________________
4. Вывод
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________