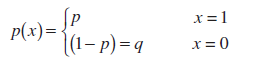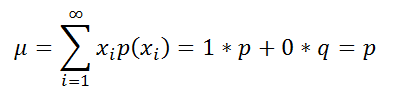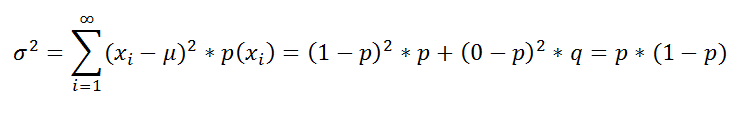Формуле бернулли в excel - Word и Excel - помощь в работе с программами

Формула Бернулли в Excel

В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!

Лучшее спасибо — порекомендовать эту страницу

Схема независимых испытаний

В общем виде схема повторных независимых испытаний записывается в виде задачи:

Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.

Эта вероятность вычисляется по формуле Бернулли:

$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k}=C_n^k cdot p^k cdot q^{n-k}. qquad(1)
$$

Здесь $C_n^k$ — число сочетаний из $n$ по $k$.

Еще: онлайн калькуляторы для формулы Бернулли.

Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:

Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.

Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.

Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.

Формула Бернулли в Эксель

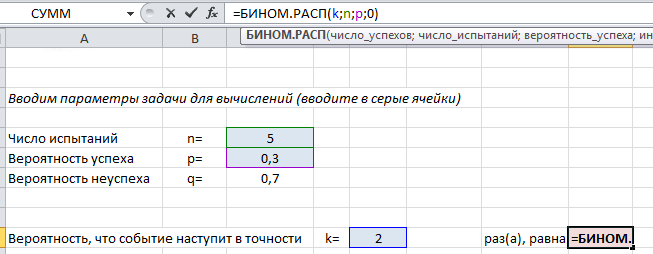
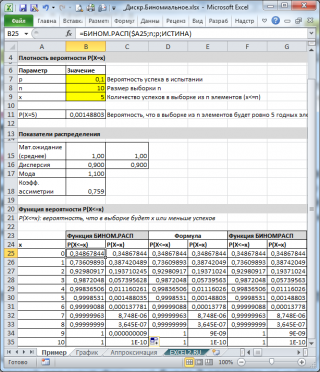
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП(), выдающая определенную вероятность биномиального распределения.

Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0).

Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).

Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:

Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):

Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^{n-k}$$
Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_{i=k_1}^{k_2} C_n^i cdot p^i cdot q^{n-i}$$
Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_{i=0}^{k_3} C_n^i cdot p^i cdot q^{n-i}$$
Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_{i=k_4}^{n} C_n^i cdot p^i cdot q^{n-i}$$
Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^{n}$$
Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$

Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.

Полезное: расчетный файл по формуле Бернулли

Нужна помощь в решении задач по теории вероятностей?

Примеры решений задач

Рассмотрим решение типовых задач.

Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.

Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:

$$
P_7(5)=C_{7}^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146.
$$

Для вероятности 6 или 7 попаданий суммируем:

$$
P_7(6)+P_7(7)=C_{7}^6 cdot 0,75^6 cdot 0,25^1+C_{7}^7 cdot 0,75^7 cdot 0,25^0= \
= 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495.
$$

А вот это решение в файле эксель:

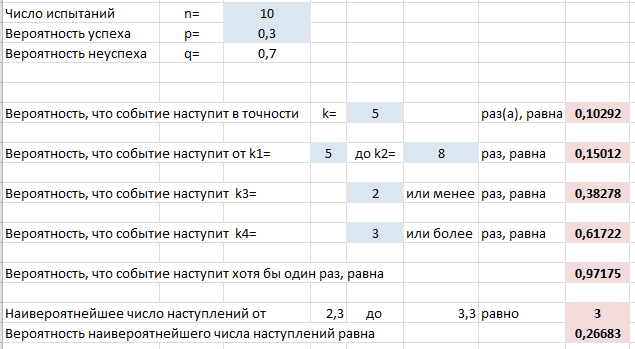
Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?

Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_{10}(k)=C_{10}^k cdot 0,5^kcdot 0,5^{10-k}=C_{10}^k cdot 0,5^{10}$$
Приступим к вычислениям:

$$1. P_{10}(2)=C_{10}^2 cdot 0,5^{10} = frac{10!}{2!8!}cdot 0,5^{10} approx 0,044.$$

$$2. P_{10}(4)+P_{10}(5)=C_{10}^4 cdot 0,5^{10} + C_{10}^5 cdot 0,5^{10}=left( frac{10!}{4!6!} + frac{10!}{5!5!} right)cdot 0,5^{10} approx 0,451.$$

$$3. P_{10}(0)+P_{10}(1)+P_{10}(2)=C_{10}^0 cdot 0,5^{10} + C_{10}^1 cdot 0,5^{10}+ C_{10}^2 cdot 0,5^{10}=left( 1+10+ frac{10!}{2!8!} right)cdot 0,5^{10} approx 0,055.$$

$$4. P_{10}(7)+P_{10}(8)+P_{10}(9)+P_{10}(10)=\ = C_{10}^7 cdot 0,5^{10} + C_{10}^8 cdot 0,5^{10}+ C_{10}^9 cdot 0,5^{10}+ C_{10}^10 cdot 0,5^{10} =\=left(frac{10!}{3!7!}+ frac{10!}{2!8!} + 10 +1right)cdot 0,5^{10} approx 0,172.$$

$$5. P_{10}(ge 1)=1-P_{10}(0)=1-C_{10}^0 cdot 0,5^{10} = 1- 0,5^{10} approx 0,999.$$

Наивероятнейшее число мальчиков найдем из неравенства:

$$
10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \
4,5 le m le 5,5,\
m=5.
$$

Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).

Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.

Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?

Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!

Понравилось? Добавьте в закладки

Полезные ссылки

Расчетный файл эксель для расчетов по формуле Бернулли

Калькуляторы на формулу Бернулли
Примеры решений задач

Как решать задачи по теории вероятностей?
Решение заданий на заказ

Решебник задач по вероятности

Источник

Рассмотрим Биномиальное распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL

БИНОМ.РАСП()

построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения p, математического ожидания распределения и стандартного отклонения. Также рассмотрим распределение Бернулли.

Определение

. Пусть проводятся

n

испытаний, в каждом из которых может произойти только 2 события: событие «успех» с вероятностью

p

или событие «неудача» с вероятностью

q

=1-p (так называемая

Схема Бернулли,

Bernoulli

trials

).

Вероятность получения ровно

x

успехов в этих

n

испытаниях равна:

Примечание

:

Порядок получения успехов значения не имеет. Если важен порядок, то см. статью

Отрицательное Биномиальное распределение

Количество успехов в выборке

x

является случайной величиной, которая имеет

Биномиальное распределение

(англ.

Binomial

distribution

)

p

и

n

–

являются параметрами этого распределения.

Примечание

: Запись

означает количество

сочетаний

из

n

элементов по

x

. Для сочетаний также используется запись

. Подробнее о сочетаниях см. статью

Сочетания без повторений: Комбинаторика в MS EXCEL

Напомним, что для применения

схемы Бернулли

и соответственно

Биномиального распределения,

должны быть выполнены следующие условия:

каждое испытание должно иметь ровно два исхода, условно называемых «успехом» и «неудачей».
результат каждого испытания не должен зависеть от результатов предыдущих испытаний (независимость испытаний).
вероятность успеха

p

должна быть постоянной для всех испытаний.

Биномиальное распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для

Биномиального распределения

имеется функция

БИНОМ.РАСП()

, английское название — BINOM.DIST(), которая позволяет вычислить вероятность того, что в выборке будет ровно

х

«успехов» (т.е.

функцию плотности вероятности

p(x), см. формулу выше), и

интегральную функцию распределения

(вероятность того, что в выборке будет

x

или меньше «успехов», включая 0).

СОВЕТ

: Подробнее о

Функции распределения

и

Плотности вероятности

см. статью

Функция распределения и плотность вероятности в MS EXCEL

До MS EXCEL 2010 в EXCEL была функция

БИНОМРАСП()

, которая также позволяет вычислить

функцию распределения

и

плотность вероятности

p(x).

БИНОМРАСП()

оставлена в MS EXCEL 2010 для совместимости.

В

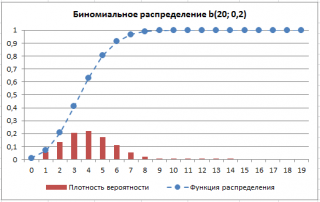
файле примера

приведены графики

плотности распределения вероятности

и

интегральной функции распределения

.

Биномиальное распределения

имеет обозначение

B

(

n

;

p

)

.

Примечание

: Для построения

интегральной функции распределения

идеально подходит диаграмма типа

График

, для

плотности распределения

–

Гистограмма с группировкой

. Подробнее о построении диаграмм читайте статью Основные типы диаграмм.

Примечание

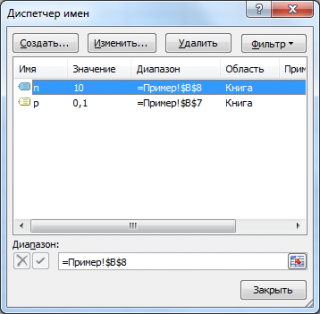
: Для удобства написания формул в

файле примера

созданы Имена для параметров

Биномиального распределения

: n и p.

В

файле примера

приведены различные расчеты вероятности с помощью функций MS EXCEL:

Как видно на картинке выше, предполагается, что:

В бесконечной совокупности, из которой делается выборка, содержится 10% (или 0,1) годных элементов (параметр

p

, третий аргумент функции =

БИНОМ.РАСП()

)
Чтобы вычислить вероятность, того что в выборке из 10 элементов (параметр

n

, второй аргумент функции) будет ровно 5 годных элементов (первый аргумент), нужно записать формулу:

=БИНОМ.РАСП(5; 10; 0,1; ЛОЖЬ)
Последний, четвертый элемент, установлен =ЛОЖЬ, т.е. возвращается значение функции

плотности распределения

.

Если значение четвертого аргумента =ИСТИНА, то функция

БИНОМ.РАСП()

возвращает значение

интегральной функции распределения

или просто

Функцию распределения

. В этом случае можно рассчитать вероятность того, что в выборке количество годных элементов будет из определенного диапазона, например, 2 или меньше (включая 0).

Для этого нужно записать формулу: =

БИНОМ.РАСП(2; 10; 0,1; ИСТИНА)

Примечание

: При нецелом значении х,

дробная часть отбрасывается

. Например, следующие формулы вернут одно и тоже значение:

=БИНОМ.РАСП(

2

; 10; 0,1; ИСТИНА)

=БИНОМ.РАСП(

2,9

; 10; 0,1; ИСТИНА)

Примечание

: В

файле примера

плотность вероятности

и

функция распределения

также вычислены с использованием определения и функции

ЧИСЛКОМБ()

.

Показатели распределения

В

файле примера на листе Пример

имеются формулы для расчета некоторых показателей распределения:

математического ожидания

=n*p;
дисперсии

(квадрата стандартного отклонения) = n*p*(1-p);
моды

= (n+1)*p;
коэффициента асимметрии

=(1-2*p)*КОРЕНЬ(n*p*(1-p)).

Выведем формулу

математического ожидания

Биномиального распределения

, используя

Схему Бернулли

.

По определению случайная величина Х в

схеме Бернулли

(Bernoulli random variable) имеет

функцию распределения

:

Это распределение называется

распределение Бернулли

.

Примечание

:

распределение Бернулли

– частный случай

Биномиального распределения

с параметром n=1.

Найдем

математическое ожидание

(

среднее,

mean

)

распределения Бернулли

(

x

принимает только 2 значения).

Предположим, что мы провели

n

последовательных

испытаний Бернулли

и у нас сформировалась

выборка

, состоящая из n элементов: x1, x2, …, xn (каждое из которых равно 0 или 1). Сумма этих случайных величин Y=X1+X2+…+Xn, в свою очередь, также является случайной величиной и, как мы помним, будет иметь

Биномиальное распределение

с параметрами

n

и

p

.

Учитывая, что

математическое ожидание

для каждого

x
_i
равно

p

, то для соответствующего

Биномиального распределения μ=p*n.

Аналогичным образом, можно вычислить

дисперсию

Биномиального распределения.

Для этого сначала найдем

дисперсию

(

второй момент, variance

)

распределения Бернулли

:

Соответственно, дисперсия для

Биномиального распределения

равна

σ
²
=n*p*(1-p)= n*p*q.

Генерация случайных чисел. Распределение Бернулли

С помощью надстройки

Пакет анализа

можно

сгенерировать случайные числа

, извлеченные из

распределения Бернулли

.

СОВЕТ

: О надстройке

Пакет анализа

можно прочитать в статье

Надстройка Пакет анализа MS EXCEL

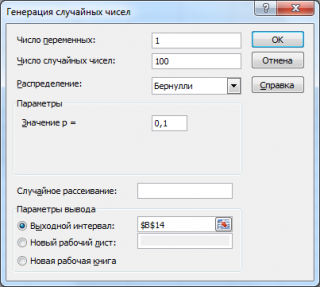
Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5 и 0,9. Для этого в окне

Генерация случайных чисел

установим следующие параметры для каждой вероятности p:

Примечание

: Если установить опцию

Случайное рассеивание

(

Random Seed

), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию =25 можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции

Случайное рассеивание

может запутать. Лучше было бы ее перевести как

Номер набора со случайными числами

.

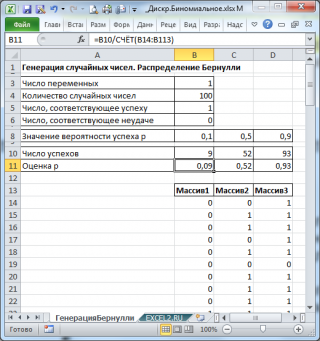
В итоге будем иметь 3 столбца по 100 чисел, на основании которых можно, например, оценить вероятность успеха

p

по формуле:

Число успехов/100

(см.

файл примера лист ГенерацияБернулли

).

Примечание

: Для

распределения Бернулли

с p=0,5 можно использовать формулу

=СЛУЧМЕЖДУ(0;1)

, которая соответствует

дискретному равномерному распределению

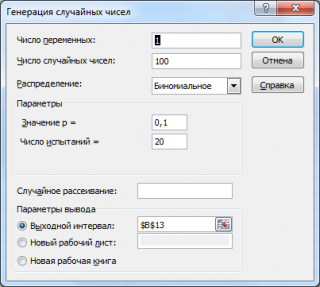
Генерация случайных чисел. Биномиальное распределение

С помощью надстройки

Пакет анализа

можно

сгенерировать случайные числа

, извлеченные из

Биномиального

распределения

.

Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5; 0,9. Количество испытаний n установим 20. Для этого в окне

Генерация случайных чисел

установим следующие параметры для каждой вероятности p:

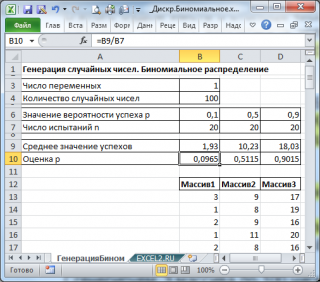
В итоге будем иметь 3 столбца чисел, на основании которых можно, например, оценить вероятность успеха

p

по формуле:

Среднее значение успехов/

n

(см.

файл примера лист ГенерацияБином

).

Примечание

: Для генерирования массива чисел, распределенных по

Биномиальному закону

, можно использовать формулу

=БИНОМ.ОБР(20; p; СЛЧИС())

, где p – вероятность успеха. Функция

СЛЧИС()

генерирует

непрерывное равномерное распределение

от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.

файл примера лист ГенерацияБином

).

Оценка параметра p

В

схеме Бернулли

оценить параметр распределения

p

можно по формуле

=СУММ(B14:B113)/СЧЁТ(B14:B113)

. В формуле предполагается, что массив случайных чисел находится в диапазоне

B14:B113

.

Оценить параметр

Биномиального распределения

p

можно по формуле

= СРЗНАЧ(B13:B112)/n

(предполагается, что случайные числа сгенерированы формулой

=БИНОМ.ОБР(n; p; СЛЧИС()

). Также в формуле предполагается, что массив случайных чисел находится в диапазоне

B13:B112

.

Обратная функция БИНОМ.ОБР()

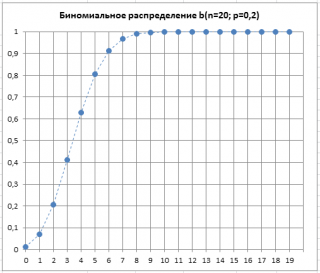
Вспомним график функции

Биномиального распределения

:

Решим задачу. Предположим, что для целей контроля качества нам требуется определить наибольшее допустимое количество дефектных изделий, которое еще позволяет обойтись без отбраковки всей партии.

Задана величина выборки из партии (

n

=20) и

р=

0,2 — доля дефектных изделий, которая обычно наблюдается в данном производственном процессе. Также пусть задана вероятность допустить

ошибку 1-го рода

(см.

статью про уровень доверия

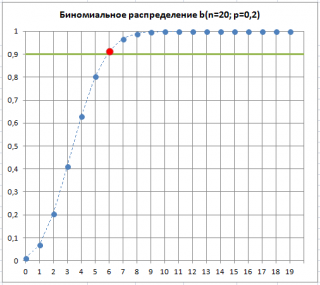
) равная 90%. Пороговый приемочный критерий можно вычислить по формуле

=БИНОМ.ОБР(20; 0,2; 90%)

. Формула вернет значение 6 — наибольшее количество дефектных изделий, допустимое в

выборке

.

Примечание

: Третий аргумент функции

БИНОМ.ОБР()

называется

Альфа

(

α error, type I error, риск производителя, альфа-риск

) и представляет собой вероятность допустить

ошибку 1-го рода

при

проверке статистической гипотезы

(см. статью

Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)

Предположим, что в выборке обнаружилось 7 дефектных изделий. Это означает, что «очень вероятна» ситуация, что изменилась доля дефектных изделий

p

, которая является характеристикой нашего производственного процесса. Хотя такая ситуация «очень вероятна», но существует вероятность (альфа-риск, ошибка 1-го рода, «ложная тревога»), что все же

p

осталась без изменений, а увеличенное количество дефектных изделий обусловлено случайностью выборки.

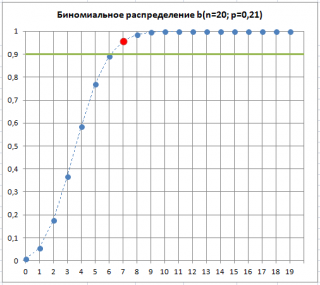
Как видно на рисунке ниже, 7 – количество дефектных изделий, которое допустимо для процесса с p=0,21 при том же значении

Альфа

. Это служит иллюстрацией, что при превышении порогового значения дефектных изделий в выборке,

p

«скорее всего» увеличилось. Фраза «скорее всего» означает, что существует всего лишь 10% вероятность (100%-90%) того, что отклонение доли дефектных изделий выше порогового вызвано только сучайными причинами.

Таким образом, превышение порогового количества дефектных изделий в выборке, может служить сигналом, что процесс расстроился и стал выпускать б

о

льший процент бракованных изделий.

Примечание

: До MS EXCEL 2010 в EXCEL была функция

КРИТБИНОМ()

, которая эквивалентна

БИНОМ.ОБР()

.

КРИТБИНОМ()

оставлена в MS EXCEL 2010 и выше для совместимости.

Связь Биномиального распределения с другими распределениями

Если параметр

n

Биномиального распределения

стремится к бесконечности, а

p

стремится к 0, то в этом случае

Биномиальное распределение

может быть аппроксимировано

Распределением Пуассона

. Можно сформулировать условия, когда приближение

распределением Пуассона

работает хорошо:

p
<0,1

(чем меньше

p

и больше

n

, тем приближение точнее);
p

>0,9

(учитывая, что

q

=1-

p

, вычисления в этом случае необходимо производить через

q

(а

х

нужно заменить на

n

—

x

). Следовательно, чем меньше

q

и больше

n

, тем приближение точнее).

При 0,1<=p<=0,9 и n*p>10

Биномиальное распределение

можно аппроксимировать

Нормальным распределением

В свою очередь,

Биномиальное распределение

может служить хорошим приближением

Гипергеометрического распределения

, когда размер совокупности N

Гипергеометрического распределения

гораздо больше размера выборки n (т.е., N>>n или n/N<<1).

Подробнее о связи вышеуказанных распределений, можно прочитать в статье

Взаимосвязь некоторых распределений друг с другом в MS EXCEL

. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

Источник

Лабораторная
работа №2. Повторные независимые
испытания.

Пусть один и тот
же эксперимент или испытание со случайным
исходом проводится многократно в одних
и тех же условиях. В каждом из испытаний
может наступить событие А с вероятностью
p,
не зависящей от наступления этого
события в других испытаниях. Говорят,
что в этом случае испытания проводятся
по схеме
Бернулли.

Формула Бернулли

Вероятность

того, что в n
испытаниях по схеме Бернулли событие
А наступит ровно m
раз можно вычислить по формуле

(1),

где р – вероятность
наступления события в одном испытании,
q=1-p.

В Excel’e
для вычисления вероятностей по формуле
Бернулли можно использовать статистическую
функцию

БИНОМРАСП(число_успехов;число_испытаний;вероятность_успеха ;интегральная)

Число_успехов —
количество успешных испытаний — m.

Число_испытаний
— число независимых испытаний — n.

Вероятность_успеха
— вероятность успеха каждого испытания
— p.

Интегральная
— логическое значение, определяющее
вид функции. Если аргумент «интегральная»
имеет значение ИСТИНА, функция БИНОМРАСП
возвращает интегральную функцию
распределения, то есть вероятность
того, что число успешных испытаний не
меньше значения аргумента «число_успехов»;
если этот аргумент имеет значение ЛОЖЬ,
то возвращается функция вероятностной
меры, то есть вероятность того, что число
успешных испытаний равно значению
аргумента «число_успехов».

Формула Пуассона

Формула Бернулли
позволяет всегда вычислить точное
значение вероятности
,
однако в случае большого числа
испытаний(n>15-20)
могут возникнуть вычислительные
трудности. В случае, когда n
достаточно велико, р – мало, а их
произведение
рекомендуется
использовать приближенную формулу
Пуассона:

(2)

В Excel’e
для вычисления вероятностей по формуле
Бернулли можно использовать статистическую
функцию

ПУАССОН(m;λ;интегральная)

m
— количество успешных событий;

— произведение
числа испытаний на вероятность успеха.

Интегральная
— логическое значение, определяющее
форму возвращаемого распределения
вероятностей. Если аргумент «интегральная»
имеет значение ИСТИНА, то функция ПУАССОН
возвращает интегральное распределение
Пуассона, то есть вероятность того, что
число случайных событий окажется в
диапазоне от 0 до m
включительно. Если этот аргумент имеет
значение ЛОЖЬ, то возвращается вероятность
точного равенства числа произошедших
событий значению m.

Теорема
Муавра-Лапласа

Еще одну приближенную
формулу для вычисления вероятности
дает
локальная теорема Муавра-Лапласа:

(3)

Функция f(x)
является четной и при
можно
полагать
.

В Excel’e
для вычисления вероятностей по этой
формуле следует использовать статистическую
функцию

НОРМРАСП(x;среднее;стандартное_откл;интегральная)

x
— значение, для которого строится
распределение(см. формулу 3).

Среднее
—
.

Стандартное_откл
—.

Интегральная
— логическое значение, определяющее
форму функции. Если аргумент «интегральная»
имеет значение ИСТИНА, функция НОРМРАСП
возвращает интегральную функцию
распределения; если этот аргумент имеет
значение ЛОЖЬ, возвращается функция
плотности распределения. Для формулы
необходимо этот параметр взять равным
ЛОЖЬ.

Для вычисления
вероятности, что число наступивших
событий А будет в пределах от m₁
до m₂,
следует воспользоваться интегральной
теоремой:

,
где (4)

Для вычисления в
Excel’e
следует каждое из значений
и
вычислить
с помощью функции НОРМРАСП,
указав в качестве последнего аргумента
значение ИСТИНА.

Наивероятнейшее
значение.

При испытаниях
по схеме Бернулли одно или два значения
m
– число успехов, будут иметь самую
высокую вероятность наступления. Это
число называется наивероятнейшим числом
наступления события А и обозначается
n₀.
Его можно вычислить, решив два неравенства:

(5)

Интервал, описываемый
этими неравенствами, в точности равен
единице, поэтому если выражения (np-p)
и (np+q)
– целые числа, то n₀
принимает два значения, иначе – одно.

Задание на
лабораторную работу 2.

1. Изучить образец
решения варианта 0.

2. Решить задачи
2.1-2,4 согласно варианту по образцу
решения, подставив данные из таблиц
2-1-2.4

3. Написать отчет
по лабораторной работе и защитить его.

Задача 2.1
Вероятность, что аудитор при проверке
документации фирмы найдет ошибку – p.
Аудитор проверяет n
фирм. Найти
вероятность того, что при проверке
аудитор найдет ошибку:

а) ровно в m
фирмах;

б) менее чем в k
фирмах:

в) не более чем в
l
фирмах;

Построить полигон
распределения. Найти наивероятнейшее
число фирм, при проверке которых
обнаружится ошибка.

Табл. 2.1

№ варианта	p	n	m	k	l
0	0.3	8	3	4	2
1	0.2	7	4	2	3
2	0.4	9	5	3	4
3	0.6	10	2	4	3
4	0.1	6	4	2	2
5	0.2	8	5	4	3
6	0.3	11	9	5	4
7	0.4	12	7	3	5
8	0.5	9	2	4	2
9	0.6	7	3	2	4
10	0.1	8	6	3	5
11	0.2	10	7	4	3
12	0.3	11	6	3	5

Задача 2.2 При
упаковке денежных купюр в пачки в банке
вероятность, что число купюр в пачке
окажется ошибочным – p.
Какова вероятность, что из n
пачек
ошибочное число купюр содержат

а) m
пачек

б) не более k
пачек

в) хотя бы l
пачек

Найти наивероятнейшее
число пачек, содержащих ошибочное число
купюр. Сколько пачек требуется взять,
чтобы наивероятнейшим числом пачек с
ошибочным числом купюр было u
пачек?

Табл. 2.3

№ варианта	p	n	m	k	l	u
0	0.002	4000	6	3	2	5
1	0.003	3000	7	4	1	3
2	0.001	5000	6	2	3	1
3	0.001	4000	3	3	2	4
4	0.002	3000	2	4	1	2
5	0.004	2000	7	2	4	3
6	0.002	3500	5	1	2	4
7	0.003	2500	4	2	3	2
8	0.001	7000	4	3	2	1
9	0.003	3500	7	4	2	3
10	0.001	8000	5	1	2	5
11	0.002	4500	3	2	1	4
12	0.002	2800	3	4	3	2

Задача 2.3
На факультете учатся n
студентов. Вероятность, что студент не
имеет задолженностей – p.
Найти вероятность, что задолженности
имеют

а) m
студентов

б) не более k
студентов

в) от l
до u
студентов

Табл. 2.2

№ варианта	p	n	m	k	l	u
0	0.8	600	15	110	100	120
1	0.7	500	160	120	105	135
2	0.5	600	320	400	300	370
3	0.6	400	150	175	140	160
4	0.75	700	190	180	160	170
5	0.55	500	235	260	220	240
6	0.65	600	235	250	255	275
7	0.8	700	150	160	120	135
8	0.85	600	100	115	65	80
9	0.7	600	195	200	165	185
10	0.6	500	185	215	190	205
11	0.65	400	115	145	130	155
12	0.4	500	285	315	300	325

Задача 2.4.

№ варианта	Текст задачи
1	1. Вероятность попадания в мишень при одном выстреле – 0,8. Какова вероятность, что при 9 выстрелах будет хотя бы 3 попадания? 2. Вероятность приживления саженца ели в условиях нашего города равна 0,75. Какова вероятность того, что из 192 высаженных саженцев погибнут ровно 44 саженца?
2	1. Вероятность, что пассажир опоздает на поезд – 0,002. Каково наивероятнейшее число опоздавших среди 4000 пассажиров? Чему равна вероятность этого числа? 2. В среднем 75% клиентов-заемщиков банка не допускают просрочки платежей. Какова вероятность, что просрочки не допускают не менее 150 клиентов из 200?
3	1. Вероятность встретить на улице своего преподавателя – 0,002. Какова вероятность, что среди 1000 прохожих вы встретите хотя бы одного своего преподавателя? 2. Доля изделий высшего сорта продукции составляет 80 %. Найти вероятность того, что в партии из 900 изделий высшего сорта будет не больше 600.
4	1. В течение семестра студент выполняет 10 контрольных работ. Вероятность, что он успешно выполнит каждую работу – 0,7. Какова вероятность, что он успешно выполнит хотя бы 8 контрольных работ? 2. Вероятность покупки при посещении клиентом магазина составляет 0,75. Найти вероятность того, что при 100 посещениях клиент совершит покупку ровно 80 раз.
5	1. Страховой агент заключает договор в 10% случаев при посещении потенциальных клиентов. Какова вероятность заключить хотя бы 1 договор при посещении 6 человек? 2. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получил меньше двух разбитых бутылок.

Образец решения.

Вариант 0.

Задача 2.1
Вероятность, что аудитор при проверке
документации фирмы найдет ошибку –
0.3. Аудитор проверяет 8
фирм. Найти
вероятность того, что при проверке
аудитор найдет ошибку:

а) ровно в 3
фирмах;

б) менее чем в 4
фирмах:

в) не более чем в
2 фирмах;

Построить полигон
распределения. Найти наивероятнейшее
число фирм, при проверке которых
обнаружится ошибка.

Решение:
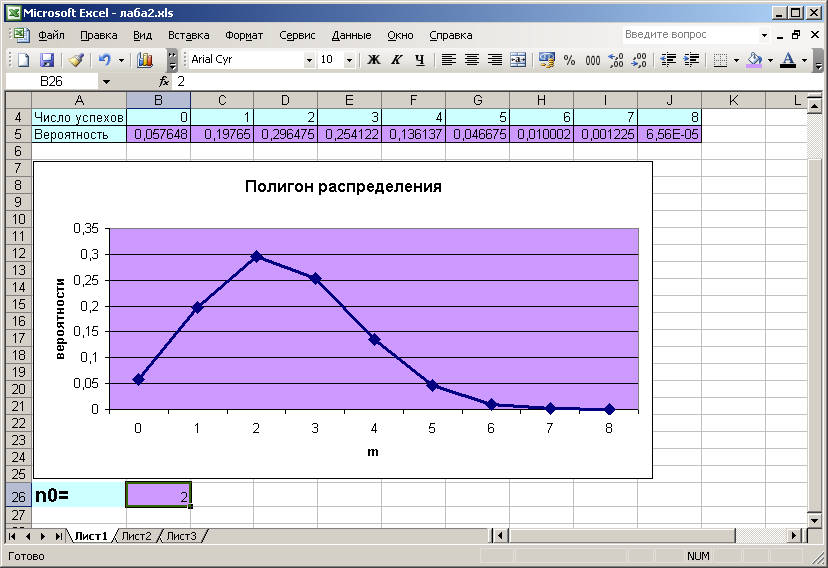
Запишем номер задачи и данные в ячейках
А1-F2.
В ячейке G2
наберем формулу БИНОМРАСП(D2;C2;B2;ЛОЖЬ) –
получим ответ на вопрос а). В ячейке H2
запишем формулу БИНОМРАСП(D2-1;C2;B2;ИСТИНА),
так как нам нужно менее чем k
фирм – первым аргументом будет значение
k-1
из ячейки D2,
последним аргументом будет ИСТИНА, так
как требуется просуммировать все
вероятности для значений от 0 до k-1,
полученный результат есть ответ на
вопрос б). В ячейке I2
запишем формулу 1-БИНОМРАСП(F2;C2;B2;ИСТИНА),
то есть мы вычисляем сначала вероятность
противоположного события – что ошибка
обнаружится в l
и менее чем l
фирмах
(поэтому последний аргумент = ИСТИНА),
затем вычитаем ее из единицы, результат
и есть ответ на вопрос в).

Для построения
полигона распределения запишем в ячейках
B4:J4
возможные значения числа наступивших
событий – от 0 до 8. Затем в ячейке B5
наберем формулу БИНОМРАСП(B4;$C$2;$B$2;ЛОЖЬ)
и выполним автозаполнение ячеек С5:J5
по ячейке B5.
После этого выделим ячейки B5:J5
и выберем значок «Диаграмма» на панели
инструментов или в меню «Вставка».
Выбираем далее 1)тип диаграммы – график,
2) в разделе «Ряд» выберем пункт «Подписи
по оси Х» — ячейки B4:J4
3)-4) можно добавить по желанию подписи
к осям и выбрать цвет и вид линий на
диаграмме.

Наивероятнейшее
число – это число, для которого вероятность
максимальна, в данной задаче это число
2 с вероятностью 0,296. Запишем это в ячейке
В26. Задача решена.

Задача 2.2 При
упаковке денежных купюр в пачки в банке
вероятность, что число купюр в пачке
окажется ошибочным – 0.002. Какова
вероятность, что из 4000
пачек
ошибочное число купюр содержат

а) 6 пачек

б) не более 3 пачек

в) хотя бы 2 пачек

г)Найти наивероятнейшее
число пачек, содержащих ошибочное число
купюр.

д) Сколько пачек
требуется взять, чтобы наивероятнейшим
числом пачек с ошибочным числом купюр
было 5 пачек?

Решение. В
данной задаче следует использовать
формулу Пуассона (2). Действительно, n
велико, p
мало и
.
Запишем обозначения и данные задачи в
ячейках A1:G2,
как показано на рисунке. В ячейке H2
набираем формулу ПУАССОН(D2;B2*C2;ЛОЖЬ),
первый параметр – число успехов, второй
значение λ=np,
третий параметр ЛОЖЬ, так как нас
интересует ровно m
успехов. Результат будет ответом на
вопрос а). В ячейке I2
задаем формулу ПУАССОН(E2;B2*C2;ИСТИНА),
получаем ответ на вопрос б) – третий
параметр выбираем ИСТИНА, так как нам
нужно 3 и менее успехов – 0,1,2. И в ячейке
J2
задаем формулу

1-ПУАССОН(F2;B2*C2;ИСТИНА),
ответ на вопрос в). Для ответа на вопрос
г) вычислим сначала величины np+p
и np-q
в ячейках K3
и K4
с помощью формул C2*B2+B2 и C2*B2-(1-B2). Так как
оба числа не целые, возьмем в качестве
ответа наибольшее из них, округленное
вниз до целого. Для этого записываем в
ячейке K2
формулу ОКРУГЛВНИЗ(K3;0). Получили ответ
на вопрос г). Для решения пункта д)
необходимо решить систему неравенств

,
выражая отсюда n
получим:
.Запишем
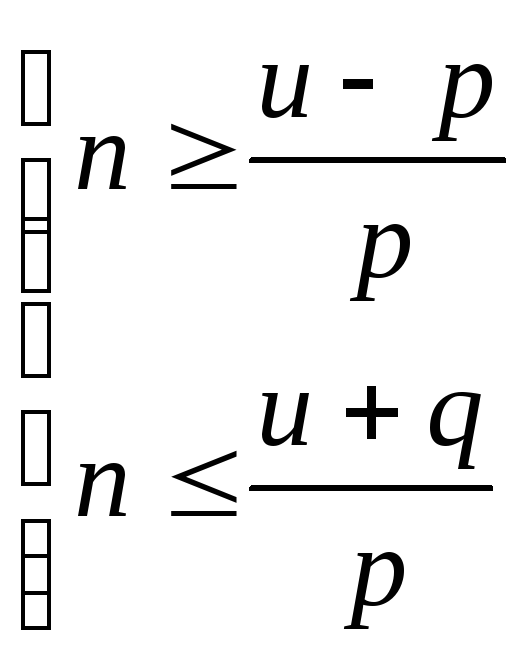
в ячейки L2
и L3
соответственно формулы (G2-B2)/B2 и
(G2+1-B2)/B2. Полученные два числа и будут
ответом – необходимо взять от 2499 до
2999 пачек, чтобы наивероятнейшим числом
ошибочных пачек было 5.

Задача 2.3
На факультете учатся 600 студентов.
Вероятность, что студент не имеет
задолженностей – 0.8. Найти вероятность,
что задолженности имеют

а) 150 студентов

б) не более 110
студентов

в) от 100 до 120
студентов

Решение.
В данной задаче будем использовать
формулы (3) и (4), так как число испытаний
велико, а вероятность не является
достаточно маленькой. Обратите внимание,
что в условии задачи дана вероятность
того, что студенты не
имеют
задолженностей, а далее спрашиваются
вероятности об имеющих
задолженности студентах, то есть работать
фактически надо с вероятностью 1-p=0.2,
ее и запишем сразу в таблицу. Запишем
обозначения и данные задачи в ячейках
A1:K2,
как показано на рисунке. Предварительно,
в ячейке H2 вычислим
величину
с
помощью формулы =КОРЕНЬ(B2*C2*(1-B2)), в
дальнейшем будем ее использовать там,
где требуется указать стандартное
отклонение. Для ответа на вопрос а)
набираем в ячейке I2
формулу НОРМРАСП(D2;B2*C2;H2;ЛОЖЬ). Первый
параметр здесь – число успехов, затем
следует указать величину np,
затем стандартное отклонение, и последний
параметр – ЛОЖЬ, так как нам требуется
вероятность только для 1 значения успеха.
Получившаяся маленькая величина не
должна смущать – событий вида «0 студентов
имеют задолженности», «1 студент имеет
задолженности» и т.д. – очень много, а
сумма всех их вероятностей вместе – 1.
Для ответа на вопрос б) набираем в ячейке
J2
формулу НОРМРАСП(E2;B2*C2;H2;ИСТИНА). Последний
параметр ИСТИНА –так, как нам требуется
сумма вероятностей для числа успехов
от 0 до 110. Для ответа на вопрос в) в ячейке
K2
набираем формулу
=НОРМРАСП(G2;B2*C2;H2;ИСТИНА)-НОРМРАСП(F2;B2*C2;H2;ИСТИНА).
Обратите внимание, в первой формуле
используем большее число – 120, во второй
меньшее – 100. Задача решена.

Задача 2.4.
Вероятность изготовления нестандартной
детали на станке-автомате равна 0,003 .
Найти вероятность того, что среди 1000
деталей окажется не более 2 нестандартных.

Решение.
В данной задаче число испытаний велико,
а вероятность мала. Проверим
λ=np=1000*0.003=3<10,
значит можно использовать формулу
Пуассона. Не более 2 – означает 0,1 или 2
детали, значит параметр Интегральная
будет равен ИСТИНА. Для ответа на вопрос
задачи запишем данные как показано на
рисунке и набираем формулу для ответа
=ПУАССОН(D2;B2*C2;ИСТИНА). Задача решена.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Комбинаторика и вероятность

Ниже вы найдете основные формулы Excel, которые могут применяться при решении вероятностных задач и задач по комбинаторике.

ФАКТР / FACT

СЛЧИС / RAND

Выдает случайное число в интервале от 0 до 1 (равномерно распределенное).

СЛУЧМЕЖДУ / RANDBETVEEN

Выдает случайное число в заданном интервале.

БИНОМРАСП / BINOMDIST

Вычисляет отдельное значение биномиального распределения.

ГИПЕРГЕОМЕТ / HYRGEOMDIST

Определяет гипергеометрическое распределение.

НОРМРАСП / NORMDIST

Вычисляет значение нормальной функции распределения.

НОРМОБР / NORMINV

Выдает обратное нормальное распределение.

НОРМСТРАСП / NORMSDIST

Выдает стандартное нормальное интегральное распределение.

НОРМСТОБР / NORMSINV

Выдает обратное значение стандартного нормального распределения.

ПЕРЕСТ / PERMUT

ВЕРОЯТНОСТЬ / PROB

Определяет вероятность того, что значение из диапазона находится внутри заданных пределов.

Математическая статистика

При решении задач по математической статистике можно использовать те формулы, что перечислены выше, а также следующие (сгруппированы для удобства: обработка выборки, разные распределения, остальные формулы):

Обработка выборки: формулы Excel

СРОТКЛ / AVEDEV

Вычисляет среднее абсолютных значений отклонений точек данных от среднего.

СРЗНАЧ / AVERAGE

Вычисляет среднее арифметическое аргументов.

СРГЕОМ / GEOMEAN

Вычисляет среднее геометрическое.

СРГАРМ / HARMEAN

Вычисляет среднее гармоническое.

ЭКСЦЕСС / KURT

Определяет эксцесс множества данных.

МЕДИАНА / MEDIAN

Находит медиану заданных чисел.

МОДА / MODE

Определяет значение моды множества данных.

КВАРТИЛЬ / QUARTILE

Определяет квартиль множества данных.

СКОС / SKEW

Определяет асимметрию распределения.

СТАНДОТКЛОН / STDEV

Оценивает стандартное отклонение по выборке.

ДИСП / VAR

Оценивает дисперсию по выборке.

Законы распределений: формулы Excel

БЕТАРАСП / BETADIST

Определяет интегральную функцию плотности бета-вероятности.

БЕТАОБР / BETAINV

Определяет обратную функцию к интегральной функции плотности бета-вероятности.

ХИ2РАСП / CHIDIST

Вычисляет одностороннюю вероятность распределения хи-квадрат.

ХИ2ОБР / CHIINV

Вычисляет обратное значение односторонней вероятности распределения хи-квадрат.

ЭКСПРАСП / EXPONDIST

Находит экспоненциальное распределение.

FРАСП / FDIST

Находит F-распределение вероятности.

FРАСПОБР / FINV

Определяет обратное значение для F-распределения вероятности.

ФИШЕР / FISHER

Находит преобразование Фишера.

ФИШЕРОБР / FISHERINV

Находит обратное преобразование Фишера.

ГАММАРАСП / GAMMADIST

ГАММАОБР / GAMMAINV

Находит обратное гамма-распределение.

ПУАССОН / POISSON

Выдает распределение Пуассона.

СТЬЮДРАСП / TDIST

Выдает t-распределение Стьюдента.

СТЬЮДРАСПОБР / TINV

Выдает обратное t-распределение Стьюдента.

ВЕЙБУЛЛ / WEIBULL

Выдает распределение Вейбулла.

Другое (корреляция, регрессия и т.п.)

ДОВЕРИТ / CONFIDENCE

Определяет доверительный интервал для среднего значения по генеральной совокупности.

КОРРЕЛ / CORREL

Находит коэффициент корреляции между двумя множествами данных.

СЧЁТ / COUNT

Подсчитывает количество чисел в списке аргументов.

СЧЁТЕСЛИ / COUNTIF

Подсчитывает количество непустых ячеек, удовлетворяющих заданному условию внутри диапазона.

КОВАР / COVAR

Определяет ковариацию, то есть среднее произведений отклонений для каждой пары точек.

ПРЕДСКАЗ / FORECAST

Вычисляет значение линейного тренда.

ЛИНЕЙН / LINEST

Находит параметры линейного тренда.

ПИРСОН / PEARSON

Определяет коэффициент корреляции Пирсона.

Справочный файл по формулам Excel

Нужна шпаргалка по функциям Excel под рукой? Скачивайте файл: Математические и статистические формулы Excel

Полезные ссылки

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике:

Пример 4.В партии 20 изделий, из них 5 бракованных. Найти вероятность того, что в выборке из 4 изделий ровно одно бракованное.

Решение. В данной задаче, прежде всего, определим значения параметров: число_успехов_ в_ выборке = 1; размер_ выборки = 4; число_ успехов_ в_ совокупности = 5; размер_ совокупности = 20.

Искомую вероятность можно рассчитать с помощью функции =ГИПЕРГЕОМЕТ(1; 4; 5; 20), которая дает значение 0,4696.

Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно событияА.

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 – р.

Вероятность того, что при n повторных независимых испытаниях событие А осуществится ровно k раз вычисляется по формуле Бернулли: .

Для нахождения наиболее вероятного числа успехов k по заданным n и р можно воспользоваться неравенствами np – q £ k£ np + p или правилом: если число np + p не целое, то k равно целой части этого числа.

В случае, если n велико, р мало, а 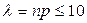, используют асимптотическую формулу Пуассона вычисления вероятности наступления события А ровно k раз при n повторных независимых испытаниях: .

Пример 5. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

Решение. Вероятность нормального расхода электроэнергии на протяжении каждых из 6 суток постоянна и равна p = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1— р = 1 — 0,75 = 0,25. Искомая вероятность по формуле Бернулли равна = 0,297. Для вычисления в Excel используем формулу =БИНОМРАСП(4; 6; 0,75; 0), которая дает значение 0,297. При этом определены следующие значения параметров: число_ успехов = 4; число_ испытаний = 6; вероятность_ успеха = 0,75; интегральная = 0. Подробно с синтаксисом функции БИНОМРАСП можно ознакомиться с помощью справки.

Пример 6. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность, что в течение часа ровно 5 абонентов позвонят на станцию.

Решение.Так как р = 0,01 мало и n = 400 велико, то будем пользоваться приближенной формулой Пуассона при l = 400 × 0,01 = 4. Тогда Р₄₀₀(5) » » 0,156293. Для вычисления в Excel используем формулу =ПУАССОН(5; 4; 0), которая дает значение 0,156293. При этом определены следующие значения параметров: количество_ событий = 5; среднее(λ) = 4; интегральная = 0. Подробно с синтаксисом функции ПУАССОН можно ознакомиться в справке.

В случае, когда число повторных испытаний большое и формула Бернулли неприменима, используют формулы Лапласа.

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции , где .

Имеются таблицы, в которых помещены значения функции .

Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в n испытаниях от k₁ до k₂ раз, приближенно равна определенному интегралу:

, где .

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами для интеграла , тогда .

Пример 7. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.

Решение. По условию n = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа: , , . Для вычисления в Excel используем формулу =НОРМРАСП(80; 80; 8; 0), которая дает значение 0,04986. При этом определены следующие значения параметров: k = 80; среднее= np = 80; стандартное_откл = = = 8, интегральная = 0. Подробно с синтаксисом функции НОРМРАСП можно ознакомиться с помощью справки.

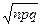
Пример 8. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.

Решение.Воспользуемся интегральной формулой Лапласа: n = 400; k₁= 70; k₂=100; р = 0,2; q = 0,8; . Так как функция является нечетной, то P₄₀₀(70; 100) = Ф(2,5)+ + Ф(1,25) = 0,4938 + 0,3944 = 0,8882.

Для вычисления в Excel используем формулу нормального распределения =НОРМРАСП(100; 80; 8; 1) — НОРМРАСП(70; 80; 8; 1), которая дает значение 0,8882. При этом параметр интегральная = 1, остальные значения параметров определяются аналогично примеру, рассмотренному выше.

В этой статье описаны синтаксис формулы и использование функции ВЕРОЯТНОСТЬ в Microsoft Excel.

Описание

Возвращает вероятность того, что значение из интервала находится внутри заданных пределов. Если верхний_предел не задан, то возвращается вероятность того, что значения в аргументе x_интервал равняются значению аргумента нижний_предел.

Синтаксис

Аргументы функции ВЕРОЯТНОСТЬ описаны ниже.

x_интервал Обязательный. Диапазон числовых значений x, с которыми связаны вероятности.

Интервал_вероятностей Обязательный. Множество вероятностей, соответствующих значениям в аргументе «x_интервал».

Нижний_предел Необязательный. Нижняя граница значения, для которого вычисляется вероятность.

Верхний_предел Необязательный. Верхняя граница значения, для которого вычисляется вероятность.

Замечания

Если любое значение в аргументе интервал_вероятностей меньше 0 или если какое-либо значение в аргументе интервал_вероятностей больше 1, то функция ВЕРОЯТНОСТЬ возвращает значение ошибки #ЧИСЛО!.

Если сумма значений в аргументе интервал_вероятностей не равна 1, функция ВЕРОЯТНОСТЬ возвращает значение ошибки #ЧИСЛО!.

Если верхний_предел опущен, то функция ВЕРОЯТНОСТЬ возвращает вероятность равенства значению аргумента нижний_предел.

Если x_интервал и интервал_вероятностей содержат различное количество точек данных, то функция ВЕРОЯТНОСТЬ возвращает значение ошибки #Н/Д.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Источник

Старая форма входа