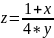Любой треугольник имеет шесть элементов: три стороны и три угла. На рисунке ниже показан прямоугольный треугольник, который имеет три угла (А, В и С), а также три стороны (гипотенузу, основание и высоту). Угол С всегда равен 90° (или π/2 радиан), поэтому, если известны два других элемента этого треугольника (исключая угол С), то с помощью определенных формул всегда можно вычислить остальные элементы.
Рабочую книгу, содержащую формулы расчета различных элементов прямоугольного треугольника по двум известным элементам, можно скачать с нашего сайта.
[lock]
скачать бесплатно
[/lock]
Рис. 1. Элементы прямоугольного треугольника
Вспомните, как выглядит теорема Пифагора: Высота^2+Основание^2=Гипотенуза^2. Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания: =КОРЕНЬ(Гипотенуза^2-Основание^2). В другой формуле, вычисляющей основание прямоугольного треугольника, используются
гипотенуза и высота: =КОРЕНЬ((Гипотенуза^2)-(Высота^2)). Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту: =КОРЕНЬ((Высота^2)+(Основание^2)).
Верны также приведенные ниже тригонометрические тождества:
- SIN(А) = Высота/Гипотенуза
- SIN(В) = Основание/Гипотенуза
- COS(А) = Основание/Гипотенуза
- COS(В) = Высота/Гипотенуза
- TAN(А) = Высота/Гипотенуза
Все тригонометрические функции Excel подразумевают, что угол, являющийся аргументом функции, представлен в радианах. Для преобразования градусов в радианы используйте функцию РАДИАНЫ. Для обратного преобразования радиан в градусы примените функцию ГРАДУСЫ.
Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А): =ATAN(Высота/Основание). Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу: =ГРАДУСЫ(ATAN(Высота/Основание)). Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В): =ПИ()/2-ATAN(Высота/Основание). Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу: =90-ГРАДУСЫ(ATAN(Высота/Основание).
На рис. 2 показана рабочая книга, которая содержит формулы для вычисления различных элементов прямоугольного треугольника.
Рис. 2. Данная рабочая книга пригодится для вычисления элементов прямоугольных треугольников
Резюме
Чтобы вычислить самую длинную сторону (гипотенузу) прямоугольного треугольника в Excel, вы можете использовать формулу, основанную на теореме Пифагора, адаптированную для использования математических операторов и функций Excel. В показанном примере формула в D5, скопированная ниже, имеет следующий вид:
=SQRT(B5^2+C5^2)
который возвращает длину гипотенузы с учетом длины стороны a и стороны b, указанной в столбцах B и C соответственно.
Объяснение
Теорема Пифагора — ключевой принцип евклидовой геометрии. В нем говорится, что квадрат самой длинной стороны прямоугольного треугольника (гипотенуза) равен сумме квадратов двух других сторон. Теорема записывается в виде следующего уравнения:
а 2 + Ь 2 = с 2
Когда известны любые две стороны, это уравнение можно использовать для решения третьей стороны. Когда a и b известны, длину гипотенузы можно вычислить с помощью:
Когда известны b и c, длину стороны a можно рассчитать с помощью:
Когда a и c известны, длину стороны b можно рассчитать с помощью:
Чтобы перевести приведенное выше в синтаксис формулы Excel, используйте оператор возведения в степень (^) и функцию КОРЕНЬ, как показано ниже. Теорема Пифагора может быть записана как:
=a^2+b^2=c^2 // pythagorean theorem
Приведенные ниже формулы можно использовать для решения каждой из трех сторон:
c=SQRT(a^2+b^2) // hypotenuse a=SQRT(c^2-b^2) // side a b=SQRT(c^2-a^2) // side b
Вместо оператора возведения в степень вы также можете использовать функцию POWER следующим образом:
c=SQRT(POWER(a,2)+POWER(b,2)) a=SQRT(POWER(c,2)-POWER(b,2)) b=SQRT(POWER(c,2)-POWER(a,2))
Приведенные выше формулы являются примером вложения одной функции в другую.
Как при помощи формул Excel решить теорему Пифагора для прямоугольных треугольников
Любой треугольник имеет шесть элементов: три стороны и три угла. На рисунке ниже показан прямоугольный треугольник, который имеет три угла (А, В и С), а также три стороны (гипотенузу, основание и высоту). Угол С всегда равен 90° (или π/2 радиан), поэтому, если известны два других элемента этого треугольника (исключая угол С), то с помощью определенных формул всегда можно вычислить остальные элементы.
Рабочую книгу, содержащую формулы расчета различных элементов прямоугольного треугольника по двум известным элементам, можно скачать с нашего сайта.
[lock] скачать бесплатно [/lock]
Рис. 1. Элементы прямоугольного треугольника
Вспомните, как выглядит теорема Пифагора: Высота^2+Основание^2=Гипотенуза^2. Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания: =КОРЕНЬ(Гипотенуза^2-Основание^2) . В другой формуле, вычисляющей основание прямоугольного треугольника, используются
гипотенуза и высота: =КОРЕНЬ((Гипотенуза^2)-(Высота^2)) . Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту: =КОРЕНЬ((Высота^2)+(Основание^2)) .
Верны также приведенные ниже тригонометрические тождества:
- SIN(А) = Высота/Гипотенуза
- SIN(В) = Основание/Гипотенуза
- COS(А) = Основание/Гипотенуза
- COS(В) = Высота/Гипотенуза
- TAN(А) = Высота/Гипотенуза
Все тригонометрические функции Excel подразумевают, что угол, являющийся аргументом функции, представлен в радианах. Для преобразования градусов в радианы используйте функцию РАДИАНЫ. Для обратного преобразования радиан в градусы примените функцию ГРАДУСЫ.
Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А): =ATAN(Высота/Основание) . Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу: =ГРАДУСЫ(ATAN(Высота/Основание)) . Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В): =ПИ()/2-ATAN(Высота/Основание) . Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу: =90-ГРАДУСЫ(ATAN(Высота/Основание) .
На рис. 2 показана рабочая книга, которая содержит формулы для вычисления различных элементов прямоугольного треугольника.
Рис. 2. Данная рабочая книга пригодится для вычисления элементов прямоугольных треугольников
Расчеты в Microsoft Excel: Решение и оформление задач
Лабораторная работа №5
1. Ознакомьтесь с задачей, представленной ниже.
Вычисление элементов треугольника.Даны три стороны треугольника a, b, c. Требуется вычислить его площадь по формуле Герона 



1. Создайте в Microsoft Excel «Чистую книгу». Переименуйте, как показано на картинке Лист1 в «Треугольник».
2. Для получения красивых заголовков используйте возможности меню Формат à Ячейки à Выравнивание.[1]Шапка таблицы получена путем объединения ячеек. Оформите границы таблицы (кнопка 
3. Постройте модель решения задачи в среде Microsoft Excel, максимально автоматизировав расчеты. Для этого в ячейке, где должен находиться результат вычислений, необходимо вести формулы. Ввод всегда начинается со знака =. Вам понадобятся стандартная функция Excel 

4. Сравните полученные Вами результаты с теми, которые представлены в задании. Если Вы наблюдаете некоторые расхождения, значит формулы в вашей электронной таблице записаны ошибочно. В этом случае Ваша модель нуждается в корректировке.
5. Задайте формат ячеек с результатами вычислений Числовойс четырьмя десятичными знаками после запятой (Формат à Ячейки à Число).
6. Исследование зависимостей. Выделите D8 и выберите в меню Сервис à Зависимости формулà Влияющие ячейки. На экране протянутся синие стрелки от ячеек, содержащих длины сторон к ячейке D8. Исследуйте зависимости и влияния для других ячеек. Уберите стрелки соответствующей командой меню.
1. 
Будем вычислять отдельно подкоренное выражение р*(р-а)*(р-b)*(р-c) и определять его знак. Если оно положительно, вычисляем S, R и r. Если же нет, то в ячейке D9 выведем текстовую строку «Это не треугольник!», а в ячейках D11 и D12 выведем пустые строки.
Скопируйте формулу из D9 в D10. Отредактируйте D10, убрав КОРЕНЬ. В ячейке останется формула =D8*(D8-B4)*(D8-B5)*(D8-B6)
В D9 разместите формулу =ЕСЛИ(D10>0;КОРЕНЬ(D10);»Это не треугольник!»)[2].
В D11 формулу =ЕСЛИ(D10>0; D9/D8;»»). Аналогично измените формулу в D12.
2. Ограничение ввода. Разрешите пользователю вводить только положительные длины сторон треугольника (меню Данные à Проверка à Параметры.
3. Предъявите работу преподавателю.
[1] Обратите внимание, в ячейках Excel буквенные значения всегда автоматически отформатированы по левому краю ячейки, а численные – по правому. Также, заметьте, разделителем десятичных разрядов в Microsoft Excel 2003 является запятая.
[2] Обратите внимание на синтаксис функции ЕСЛИ. Разделителем трех переменных является точка с запятой ;
Задание в Microsoft Excel. Вычисления с использованием стандартных функций
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Задание в Microsoft Excel . Вычисления с использованием стандартных функций
Создать таблицу по образцу:
3 . Высоту подсчитать по формуле:
4 . Медиану подсчитать по формулам:
5 . Биссектрису подсчитать по формулам:
6. Углы подсчитать по формулам:
При вычислении углов функция arccos дает ответ в радианах, нужно перевести ответ в градусы, например: САВ =ACOS((E2*E2+G2*G2-C2*C2)/(2*E2*G2))*180/ПИ()
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 964 человека из 79 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Курс добавлен 23.11.2021
- Сейчас обучается 56 человек из 28 регионов
Курс повышения квалификации
Авторская разработка онлайн-курса
- Курс добавлен 02.12.2021
- Сейчас обучается 78 человек из 38 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 520 514 материалов в базе
Другие материалы
- 07.04.2016
- 486
- 0
- 07.04.2016
- 364
- 0
- 07.04.2016
- 966
- 5
- 07.04.2016
- 913
- 9
- 07.04.2016
- 794
- 2
- 07.04.2016
- 680
- 1
- 07.04.2016
- 1582
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 07.04.2016 975
- DOCX 36.6 кбайт
- 3 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Гнездилова Людмила Алексеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 10360
- Всего материалов: 6
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Онлайн-тренинг о способах взаимодействия с разными категориями учащихся
Время чтения: 2 минуты
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Путин поручил обучать педагогов работе с девиантным поведением
Время чтения: 1 минута
Минобрнауки учредит стипендию для студентов — победителей международных олимпиад
Время чтения: 1 минута
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
источники:
http://mydocx.ru/10-2081.html
http://infourok.ru/zadanie-v-microsoft-ecel-vichisleniya-s-ispolzovaniem-standartnih-funkciy-1015391.html
теорема Пифагора
Чтобы вычислить самую длинную сторону (гипотенузу) прямоугольного треугольника в Excel, вы можете использовать формулу, основанную на теореме Пифагора, адаптированную для использования математических операторов и функций Excel. В показанном примере формула в D5, скопированная ниже, имеет следующий вид:
который возвращает длину гипотенузы с учетом длины стороны a и стороны b, указанной в столбцах B и C соответственно.
Объяснение
Теорема Пифагора — ключевой принцип евклидовой геометрии. В нем говорится, что квадрат самой длинной стороны прямоугольного треугольника (гипотенуза) равен сумме квадратов двух других сторон. Теорема записывается в виде следующего уравнения:
Когда известны любые две стороны, это уравнение можно использовать для решения третьей стороны. Когда a и b известны, длину гипотенузы можно вычислить с помощью:
Когда известны b и c, длину стороны a можно рассчитать с помощью:
Когда a и c известны, длину стороны b можно рассчитать с помощью:
Чтобы перевести приведенное выше в синтаксис формулы Excel, используйте оператор возведения в степень (^) и функцию КОРЕНЬ, как показано ниже. Теорема Пифагора может быть записана как:
Приведенные ниже формулы можно использовать для решения каждой из трех сторон:
Вместо оператора возведения в степень вы также можете использовать функцию POWER следующим образом:
Приведенные выше формулы являются примером вложения одной функции в другую.
Как сделать таблицу пифагора в excel одной формулой
Создать таблицу умножения чисел от 1 до 9 (9 строк, 9 столбцов). В ячейке, соответствующей произведению 1*1, должна быть записана формула, которая затем должна быть скопирована во все остальные 80 ячеек. Решение в двух вариантах:
1)с использованием смешанных ссылок;
2)с использованием формулы массивов.
Метод 1. С использованием смешанных ссылок.
Составим таблицу. Введем по столбцам цифры от 1 до 9 и по строкам.
В ячейку В2 введем формулу: =$A2*Bкопируем эту ячейку во все остальные ячейки диапазона В2:J10. Получим таблицу умножения:
Метод 2. С использованием формулы массивов.
В ячейки В2:J2 введем цифры от1 до 9 и в ячейки А14:А22.
Выделим ячейки В14:J22 и введем формулу =B13:J13*A14:A22. Нажмем Ctrl+shift+Enter, чтобы формула вставилась как формула массива. Получим:
Excel: Абсолютные и относительные ссылки. Таблица Пифагора
Сегодняшняя статья для новичков. Помнится, не так давно на глаза попалась «экселевская» шутка, про то, что если ты не знаешь, чем $A$1 отличается от A1, то нам не о чем с тобой разговаривать. Но нам всегда есть о чём поговорить с нашими читателями и тем более о таком базовом вопросе, как абсолютные и относительные ссылки в Excel.
Итак, чем же эти ссылки отличаются одна от другой? Относительная ссылка в формуле вида A1 – это адресация на ячейку, которая удалена от ячейки с формулой на определённое расстояние. Поэтому, при протягивании формулы в сторону, она будет ссылаться на то же самое расстояние, а не на определённую ячейку. Например, если формулу протянуть вправо на одну ячейку, то она уже будет ссылаться не на A1, а на B1. Если вместо этого мы протянем формулу вниз, то ссылка окажется не на A1, а на A2. Таким образом, ссылки собьются и формула выдаст неправильный результат.
Если же мы вместо ссылки на ячейку A1, проставим $A$1, то куда бы мы не сдвигали формулу и на какое бы количество ячеек, формула всё равно будет ссылаться именно на ячейку A1. Сделать такую ссылку можно во время выбора ячейки в формуле, нажав клавишу F4.
Кроме жёсткой привязки к определённой ячейке может быть смешанная ссылка вида $A1 (фиксация столбца) или A$1 (фиксация строки). Это также достигается нажатием клавиши F4 два или три раза, пока знак $ не появится в нужном месте. Что это значит? При фиксации столбца $A1 во время сдвига формулы в сторону не будет происходить изменений. Ссылка будет изменяться только при движении по столбцу, то есть при протягивании формулы вверх или вниз. Соответственно, с учётом того, что ссылка идёт на ячейку A1, то при протягивании вверх, будет выдаваться ошибка #ССЫЛКА! (потому что выше A1 ячеек нет), а при протягивании формулы вниз, ссылка на ячейку примет вид $A2.
При создании ссылки вида A$1, будет зафиксирована строка, в результате, при протягивании формулы вверх или вниз, изменений в адресации ячейки не будет. При протягивании формулы влево будет выдаваться ошибка #ССЫЛКА! (слева от A1 нет ячеек), при протягивании формулы вправо, ссылка примет вид B$1 и выдаст значение из этой ячейки. Наглядным примером использования разной адресации ячеек служит таблица Пифагора. Если кто-то не помнит – это таблица умножения в шахматном виде, где перекрёстно перемножаются цифры из верхней строки (от 1 до 10) и из левого столбца (от 1 до 10).
Соответственно, мы получаем значения от 1 до 100. Если мы в ячейку B2 введём формулу =A2*B1 и протянем строки и столбцы, то формула будет считать неправильно, или, верней сказать, выдаст не те значения, которые нам нужны, так как, если вы помните, формула будет перемножать данные на определённом расстоянии от себя.
Если мы поставим формулу с жёсткой фиксацией (абсолютная адресация), то также не получим нужный результат. Формула просто скопирует одно и то же значение.
Лишь вводя смешанную адресацию, фиксируя левый столбец и верхнюю строку, мы получим правильный результат.
Наглядно ещё раз этот пример нам поможет проиллюстрировать короткое видео.
Как при помощи формул Excel решить теорему Пифагора для прямоугольных треугольников
Любой треугольник имеет шесть элементов: три стороны и три угла. На рисунке ниже показан прямоугольный треугольник, который имеет три угла (А, В и С), а также три стороны (гипотенузу, основание и высоту). Угол С всегда равен 90° (или π/2 радиан), поэтому, если известны два других элемента этого треугольника (исключая угол С), то с помощью определенных формул всегда можно вычислить остальные элементы.
Рабочую книгу, содержащую формулы расчета различных элементов прямоугольного треугольника по двум известным элементам, можно скачать с нашего сайта.
[lock] скачать бесплатно [/lock]
Рис. 1. Элементы прямоугольного треугольника
Вспомните, как выглядит теорема Пифагора: Высота^2+Основание^2=Гипотенуза^2. Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания: =КОРЕНЬ(Гипотенуза^2-Основание^2) . В другой формуле, вычисляющей основание прямоугольного треугольника, используются
гипотенуза и высота: =КОРЕНЬ((Гипотенуза^2)-(Высота^2)) . Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту: =КОРЕНЬ((Высота^2)+(Основание^2)) .
Верны также приведенные ниже тригонометрические тождества:
- SIN(А) = Высота/Гипотенуза
- SIN(В) = Основание/Гипотенуза
- COS(А) = Основание/Гипотенуза
- COS(В) = Высота/Гипотенуза
- TAN(А) = Высота/Гипотенуза
Все тригонометрические функции Excel подразумевают, что угол, являющийся аргументом функции, представлен в радианах. Для преобразования градусов в радианы используйте функцию РАДИАНЫ. Для обратного преобразования радиан в градусы примените функцию ГРАДУСЫ.
Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А): =ATAN(Высота/Основание) . Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу: =ГРАДУСЫ(ATAN(Высота/Основание)) . Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В): =ПИ()/2-ATAN(Высота/Основание) . Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу: =90-ГРАДУСЫ(ATAN(Высота/Основание) .
На рис. 2 показана рабочая книга, которая содержит формулы для вычисления различных элементов прямоугольного треугольника.
Рис. 2. Данная рабочая книга пригодится для вычисления элементов прямоугольных треугольников
Любой треугольник имеет шесть элементов: три стороны и три угла. На рисунке показан прямоугольный треугольник, который имеет три угла (А, В и С), а также три стороны (гипотенузу, основание и высоту). Угол С всегда равен 90 гр. (или π/2 радиан), поэтому, если известны два других элемента этого треугольника (исключая угол С), то с помощью определенных формул всегда можно вычислить остальные элементы.
Вспомните, как выглядит теорема Пифагора:
Высота^2+Основание^2=Гипотенуза^2
Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания:
=КОРЕНЬ(Гипотенуза^2-Основание^2 )
В другой формуле, вычисляющей основание прямоугольного треугольника, используются гипотенуза и высота:
=КОРЕНЬ((Гипотенуза^2)-(Высота^2))
Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту:
=КОРЕНЬ((Высота^2)+(Основание^2))
Верны также приведенные ниже тригонометрические тождества.
SIN(А) = Высота/Гипотенуза
SIN(В) = Основание/Гипотенуза
COS(А) = Основание/Гипотенуза
COS(В) = Высота/Гипотенуза
TAN(А) = Высота/Гипотенуза
Примечание
Все тригонометрические функции Excel подразумевают, что угол, являющийся аргументом функции, представлен в радианах. Для преобразования градусов в радианы используйте функцию РАДИАНЫ. Для обратного преобразования радиан в градусы примените функцию ГРАДУСЫ.
Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А).
=ATAN(Высота/Основание)
Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу:
=ГРАДУСЫ(ATAN(Высота/Основание))
Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В):
=ПИ()/2-ATAN(Высота/Основание)
Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу:
=90-ГРАДУСЫ(ATAN(Высота/Основание)
В начало
Полезное
Задание
№ 1
В
данном задании предлагается ознакомиться
с интерфейсом программы MS
Excel.
Переключение
между листами в программе можно
осуществлять кликом левой кнопки мыши
по соответствующему листу, либо при
помощи сочетания клавиш <Ctrl>+<PageUp>
или <Ctrl>+<PageDown>.
Добавить новый лист можно сочетанием
клавиш <Shift>+<F11>.
Окно программы представлено на рисунке
19.

Рисунок
19 – Окно MS
Excel
Задание
№ 2
В
данном задании необходимо создать
таблицу, оформить шапку таблицы, выполнить
форматирование текста и таблицы.
Для
создания шапки объединяются ячейки
A1:A2,
B1:B2,
C1:G1,
H1:H2.
Далее данные заносятся в соответствии
с образцом. Направление текста можно
изменить в меню “Формат
ячеек”
(Рис. 20).

Рисунок
20 – Меню “Формат ячеек”
Результат
выполнения и заполнения таблицы данными
представлен на рисунке 21.

Рисунок
21 – Результат задания 2
Задание
№ 3
В
задании 3 нужно настроить вычисление
значения
.
Для
этого в ячейках A1,
A2,
A3
заноситься обозначение переменных
«X»,
«Y»,
«Z»
соответственно. В ячейку B3
вводится формула =(1+B1)/(4*B2).
Для получения значения Z
необходимо ввести числа в ячейки B1
для X
и B2
для Y.
После
этого по заданию предлагается составить
для данной формулы диапазон значений.
Для это заполняются некоторыми числами
некоторый диапазон ячеек, после чего
ему присваивается имя. Для этого данный
диапазон выделяется, щелчком правой
кнопкой мыши открывается выпадающее
меню и выбирается пункт “Присвоить
имя”. Результат представлен в виде
таблицы 3.
Таблица
3 – Результат задания 3
Задание
№ 4
В
задании 4 необходимо сделать таблицу
для расчёта размера возвращенной суммы
краткосрочной ссуды для трех вариантов
исходных данных.
Перед
занесением данных в таблицу необходимо
задать ячейкам столбцов B,
C,
D
нужный формат данных. Формат данных
задается в меню “Формат ячеек”, во
вкладке “Число”. Там выбирается
необходимый формат данных. Для ячеек 1
строки был задан формат “Общий”, для
2 –“Денежный” с обозначением “русский”,
для 3 и 4 – “Дата”, а для 5 – “Процентный”.
Далее в ячейку B6
была записана формула =B2*(1+B5)^((D4-D3)/365),
после чего была скопирована во весь
диапазон B6:D6.
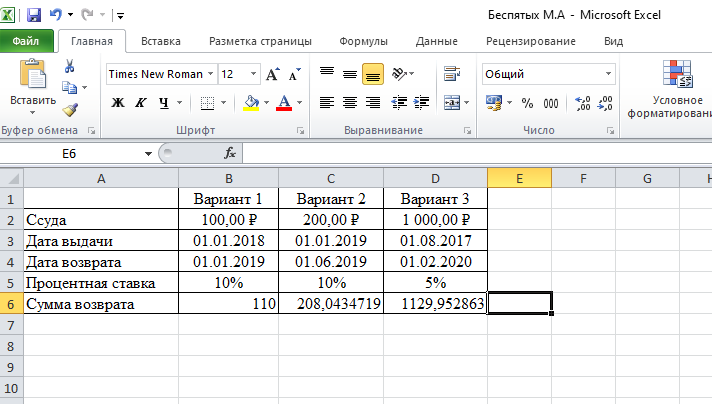
Рисунок
22 – Результат задания 4
Задание
№ 5
В
данном задании предлагается создать
таблицу для вычисления гипотенузы
прямоугольного треугольника, заданного
длинами своих катетов.
Для
этого в крайнем левом столбце и крайней
верхней строке записываются длины
катетов треугольника от 1 до 10. В ячейку
A2
записывается формула вычисления
гипотенузы. Для нахождения квадратного
корня использовалась функция “Корень”.
Для этого необходимо нажать “Вставить
функцию” на вкладке “Формулы”. Результат
представлен на рисунке 23.

Рисунок
23 – Результат задания 5
Лабораторная работа №6. Вычисления в среде ms Excel
Задание
№ 1
В
первом задании необходимо определить
точки пересечения графиков двух функций.
Для
этого создаем новый файл в MS
Excel
и заполняем первую строку значениями
в диапазоне [-10; 15] с шагом 0,5. После чего
заполняются значения для функций
и
.
Далее
строятся графики этих функций. Рассмотрим
на построении графика функции f(x).
Для этого выделяем диапазон значений
“f(x)”,
заходим в меню “Вставка” и выбираем
“график”. Далее необходимо заменить
значения по горизонтали на значения из
строки “x”.
Для этого нажимаем правой кнопкой мыши
на график и выбираем пункт “Выбрать
данные”. После в области “Подписи
горизонтальной оси” нажать кнопку
“Изменить” и выбрать диапазон со
значениями “x”.
Далее на этом же графике строится функция
s(x).
Для этого в окне области “Элементы
легенды (ряда)” нажать кнопку “Добавить”,
в строку “Значения” внести диапазон
s(x),
а в имя ряда “s(x)”.
Исходя
из построения графиков данных функций
видно, что они пересекаются в 3 точках
(рисунок 24).

Рисунок
24 – Графики функций f(x)
и s(x)
Задание
№ 2
Во
втором задании нужно отобразить
графически затухающие колебания.
Создается
новый файл или лист. В ячейки вносятся
значения А0,
δ, φ0
и ω0
.
На
свободном месте внести в строку значения
времени t.
В другую строку внести формулу вычисления
x(t).
После на основе полученных значений
построить график (рисунок 25).

Рисунок
25 – График затухающих колебаний
Задание
№ 3
В
задании 3 необходимо построить изображение
трехмерной функции.
Для
этого создается таблица значений x
и y
и результат функции при этих значениях.
Далее выделяются значения функции и на
их основе строиться изображение. Для
этого в меню “Вставка” во вкладке
“Диаграммы” выбрать “Другие”, затем
– “Поверхность”.
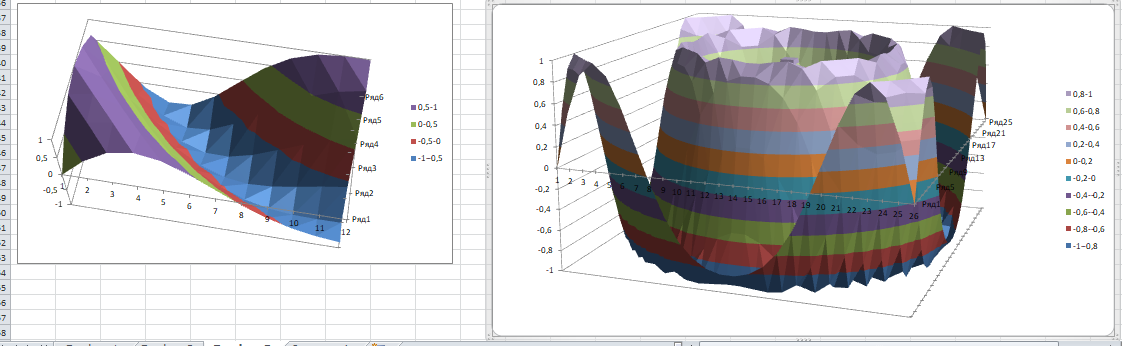
Рисунок
26 – Результат задания 3
Задание
№ 4
Выполнение
задания 4 подразумевает создание сводной
таблицы.
Для
этого создается таблица с данными,
например “Прайс-лист”. После необходимо
добавить фильтр. Для этого выделяются
все столбцы и в меню “Данные” выбирается
инструмент “Фильтр”. Далее на основе
этой таблицы создается сводная таблица.
Для этого полностью выделяется основная
таблица вместе с заголовками и в меню
“Вставка” выбирается инструмент
“Сводная таблица”. Сводная таблица
настраивается для отображения средней
стоимости каждого товара и суммарного
количества каждого товара во всех
магазинах. Чтобы добавить поле в сводную
таблицу, установите
флажок
рядом с именем поля в области “Поля
сводной таблицы”.
Чтобы
переместить поле из одной области в
другую, перетащите его левой кнопкой
мыши в целевую область. В область
“Названия строк” помещается поле “
Товар”, в область “Значения” – поля
“Количество” и ”Стоимость”. В параметрах
поля “Стоимость” выбрать операцию
“Среднее”, в “Пользовательское имя”
записать “Среднее”. Убрать “Общий
итог” в параметрах сводной таблицы.
Соседние файлы в папке Лабы 1 курс 1 семестр
- #
- #
- #
- #
- #
- #
Формулы Excel используют на порядок больше пользователей, чем все программисты C, C++, C#, Java и Python в мире вместе взятые. Несмотря на свой успех, Excel как язык программирования, имеет фундаментальные недостатки: (1) формулы Excel поддерживают только скалярные значения – числа, строки и логические значения; (2) Excel (без кода VBA) не позволяет определять новые функции. Ситуация изменилась с появлением в 2019 г. динамических массивов. С их помощью обычные формулы обрабатывают диапазон ячеек, а результаты также разливаются в диапазон ячеек. В декабре 2020 года Microsoft анонсировал функцию LAMBDA, которая позволяет определять новые функции, написанные на языке формул Excel. Функция LAMBDA поддерживает рекурсию, т.е. может вызывать сама себя. Это позволяет организовать циклы. В течение 2021 г. постепенно у всех пользователей Excel после плановых обновлений Office 365 появилась функция LAMBDA.
Рис. 1. Механизм создания пользовательских функций Excel без кода VBA
Скачать заметку в формате Word или pdf, примеры в формате Excel
Синтаксис функции LAMBDA
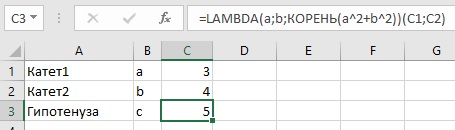
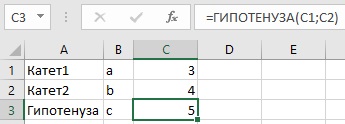
Начнем с простого примера. Создадим функцию для расчета гипотенузы по катетам.
Рис. 2. Формула расчета гипотенузы на основе функции LAMBDA
В общем виде синтаксис функции LAMBDA:
Рис. 3. Синтаксис функции LAMBDA
Последний аргумент функции LAMBDA – расчет (он же вычисление). Все предыдущие аргументы – параметры. Обязательный аргумент один. И это вычисление. Параметров может быть до 253.
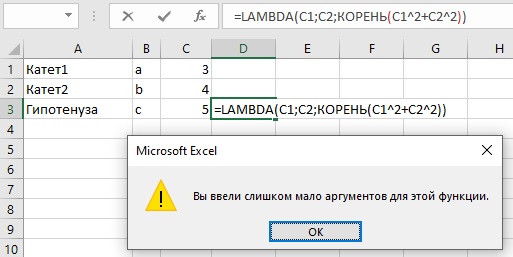
Любопытной особенностью функции LAMBDA является отсутствие ссылок на ячейки в ее синтаксисе (см. рис. 2). Вместо них используются условные обозначения – параметры. Попробуйте в ячейке D3 ввести функцию LAMBDA со ссылками (см. рис. 4). Нажмите Enter. Получите ошибку:
Рис. 4. Ссылки на ячейки не работают
Для того, чтобы можно было протестировать функцию в ячейке разработчики добавили в синтаксис вызов функции
|
= LAMBDA([параметр1; параметр2; ...];вычисление) (вызов функции) |
На рис. 2 вызов функции реализован через передачу ей значений двух параметров: а из ячейки С1 и b из ячейки С2.
|
=LAMBDA(a;b;КОРЕНЬ(a^2+b^2))(C1;C2) |
В вызове функции параметры разделяются точкой с запятой, даже если они находятся в соседних ячейках. Например, такой синтаксис…
|
=LAMBDA(a;b;КОРЕНЬ(a^2+b^2))(C1:C2) |
…вернет ошибку #ЗНАЧ!
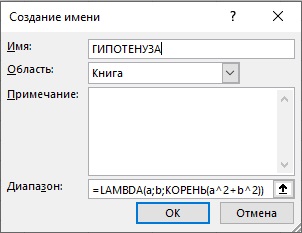
Естественно, такое использование весьма неудобно, поэтому разработчики MS предлагают присвоить функции имя. Пройдите Формулы –> Диспетчер имен, и введите следующие настройки в окне Создание имени:
Рис. 5. Присвоении функции имени
Рис. 6. Функция ГИПОТЕНУЗА принимает два аргумента в виде ссылок на ячейки
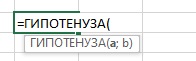
К сожалению, подсказка при вводе формулы выглядит не слишком информативно:
Рис. 7. Ввод формулы ГИПОТЕНУЗА
Если вас интересует, почему так происходит, см. дискуссию на эту тему. Преодолеть такое положение вещей пока невозможно.
Если формула основана на LAMBDA, сервис Формулы –> Вычислить формулу не позволяет увидеть шаги вычисления так, как вы ожидаете… И с этим тоже ничего нельзя поделать.
Вычисление расстояния между городами
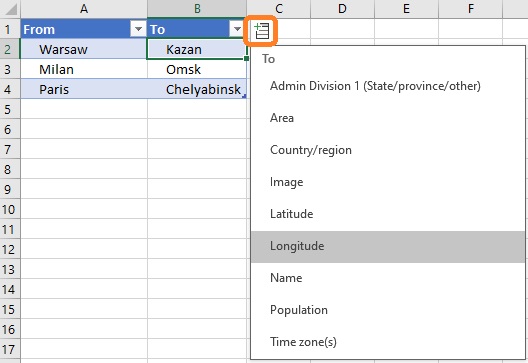
Команда разработчиков LAMBDA ранее создала географический тип данных и функцию LET. Так что LAMBDA отлично работает с географией. Допустим, у вас есть пары городов в столбцах A и B. Названия городов желательно ввести на английском языке, хотя часто Excel распознает и русское написание. Преобразуйте диапазон в умную таблицу. Для этого выделите диапазон и нажмите Ctrl+T (англ.). Выделите Таблицу и пройдите Данные –> Типы данных –> География. Если встать в любую ячейку Таблицы, появится значок полей данных. Кликните на него и раскроется список доступных полей:
Рис. 8. Географический тип данных
Если вы впервые сталкиваетесь с географическим типом данных, рекомендую изучить Николай Павлов. Новые типы данных в Excel 2016.
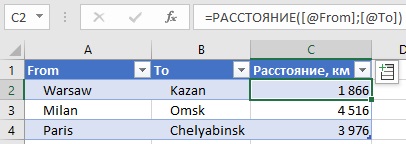
Рассчитаем расстояние между городами с использованием полей Широта (Latitude) и Долгота (Longitude). Для простоты будем считать, что наш земной шар – идеальная сфера с диаметром 12 742 км. Определим функцию РАССТОЯНИЕ(From; To):
=LAMBDA(From;To;(12742)*ASIN(КОРЕНЬ(0,5-COS((To.Latitude-From.Latitude)*ПИ()/180)/2+COS(From.Latitude*ПИ()/180)*COS(To.Latitude*ПИ()/180)*(1-COS((To.Longitude-From.Longitude)*ПИ()/180))/2)))
К сожалению, не по всем городам России имеются данные по широте и долготе. В частности, их нет по Москве и СПб…
В итоге получим:
Рис. 9. Расстояние между городами
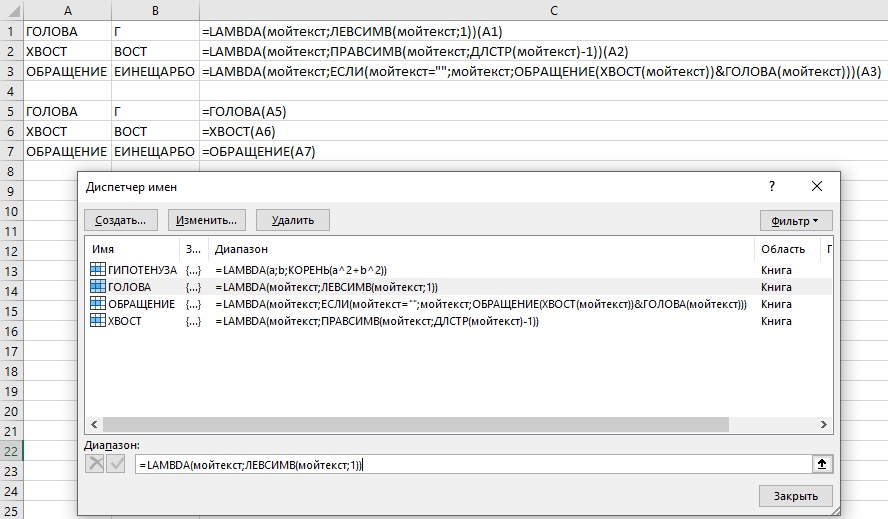
Обращение строки
Рассмотрим более сложный пример – использование рекурсии для обращения текста. Ранее встроенные функции Excel с этим не справлялись. Такое было возможно с помощью Visual Basic или JavaScript. Определим функцию ОБРАЩЕНИЕ(мойтекст), использующую рекурсию на основе LAMBDA. В формуле используются вспомогательные функции – ГОЛОВА и ХВОСТ для вычисления первого символа и остального текста.
Рис. 10. Обращение текста
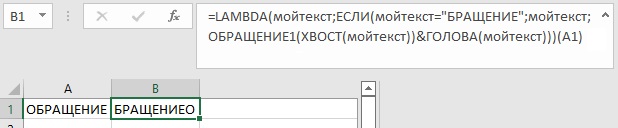
Разберем, как работает функция ОБРАЩЕНИЕ(). На первой итерации функция ГОЛОВА() возвращает букву О, а ХВОСТ() – БРАЩЕНИЕ. Чтобы показать только первую итерацию работы функции ОБРАЩЕНИЕ(), я создал функцию ОБРАЩЕНИЕ1():
Рис. 11. Первая итерация
Конструкция ЕСЛИ(мойтекст=»БРАЩЕНИЕ»;мойтекст;…) служит проверкой для выхода из рекурсии (цикла). Видно, что после одной итерации исходный текст потерял первую букву, поэтому проверка заканчивается успешно и возвращается текст ХВОСТ(мойтекст)&ГОЛОВА(мойтекст) = «БРАЩЕНИЕО». Первая буква ушла в конец текста. После каждой итерации первоначальный текст теряет по одной букве в начале. Когда выполнится условие мойтекст=»», цикл заканчивается, и возвращается обращенный текст.
Функции ГИПОТЕНУЗА() и РАССТОЯНИЕ() продемонстрировали использование LAMBDA для упрощения и повышения наглядности формул. В то же время функция ОБРАЩЕНИЕ() показала нетривиальное использование LAMBDA для организации цикла. Именно такое использование является серьезным шагом в развитии программирования в Excel. Рассмотрим еще один пример организации цикла.
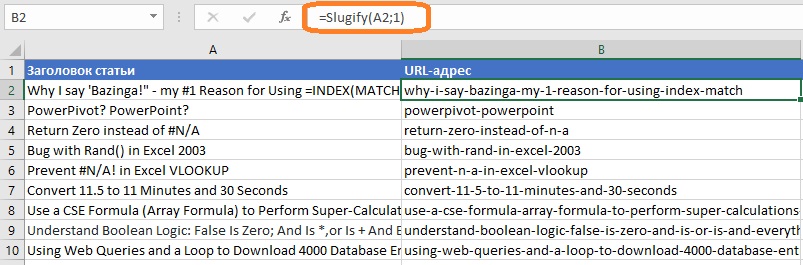
Преобразование заголовка заметки в URL-адрес
Я публикую заметки с помощью WordPress, который делает это преобразование автоматически. Например, недавно я опубликовал заметку Заключительный проект в Power Query: объединяем все вместе. WordPress дал ей адрес https://baguzin.ru/wp/zaklyuchitelnyj-proekt-v-power-query-obedinyaem-vse-vmeste/
Адрес содержит слова в английской транслитерации, разделенные тире. В URL-адресах используются строчные буквы от a до z, цифры и дефис. Все остальные знаки недопустимы. Преобразование заголовка в URL-адрес можно реализовать с помощью LAMBDA-функции Slugify с двумя аргументами.[1] Первый – это текст (phrase), а второй всегда будет равен 1 и будет сохранен в переменной «ndx». Такое имя выбрано потому, что оно напоминает слово «индекс».
Для программистов VBA: «ndx» – это наш счетчик циклов. В отличие от VBA, где можно создать переменную на лету, для LAMBDA мы должны передать 1 в качестве аргумента.
|
=LAMBDA(phrase;ndx; ЕСЛИ(ndx <= ДЛСТР(phrase); Slugify( LET( char; СТРОЧН(ПСТР(phrase; ndx; 1)); charcode; КОДСИМВ(char); ЛЕВСИМВ(phrase; ndx — 1) & ЕСЛИ(ИЛИ(И(charcode > 96; charcode < 123); И(charcode > 47; charcode < 58)); char; «-«) & ПРАВСИМВ(phrase; ДЛСТР(phrase) — ndx) ); ndx + 1); ПОДСТАВИТЬ(СЖПРОБЕЛЫ(ПОДСТАВИТЬ(phrase; «-«; » «));» «;«-«) ) ) |
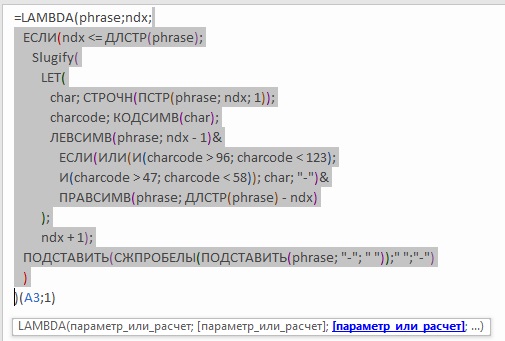
Очень удобно изучать формулы, увеличив строку формул, и кликая на аргументы функций:
Рис. 12. Формула, преобразующая заголовок заметки в URL-адрес; выделен третий аргумент функции LAMBDA – расчет
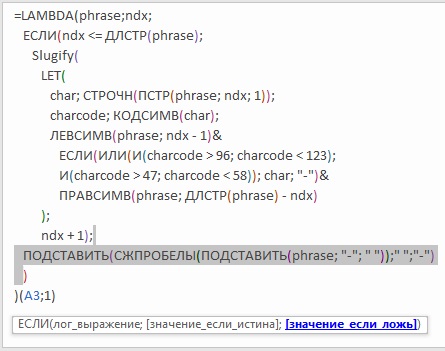
Далее можно кликнуть во второй строке после открывающей скобки, и изучить аргументы функции ЕСЛИ:
Рис. 13. Подсвечен аргумент значение_если_ложь функции ЕСЛИ
Итак, функция LAMBDA начинается с двух параметров: phrase и ndx (см. рис. 12). Остальная часть формулы – это третий аргумент функции LAMBDA. Далее функция ЕСЛИ проверяет, находится ли ndx в пределах фразы? Если проверка пройдена, выполняется блок со строки LET( до строки ); Если проверка завершилась неудачей, т.е., счетчик вышел за пределы фразы, формируется URL-адрес (см. подсвеченную строку на рис. 13).
Шесть строк внутри блока LET() создают phrase для следующего вызова Slugify. ПСТР() извлекает один символ из phrase, соответствующий номеру индекса ndx. Этот символ переводится в нижний регистр и присваивается переменной char:
|
char; СТРОЧН(ПСТР(phrase; ndx; 1)); |
Код символа char присваивается переменной charcode:
Если код символа буква или цифра…
|
ЕСЛИ(ИЛИ(И(charcode > 96; charcode < 123);И(charcode > 47; charcode < 58)); char; «-«) |
…используйте его (char), в противном случае используйте дефис («-«).
Фраза для следующей итерации будет состоять из части слева от исправленного символа…
|
ЛЕВСИМВ(phrase; ndx — 1) & |
…самого исправленного символа…
|
ЕСЛИ(ИЛИ(И(charcode > 96; charcode < 123);И(charcode > 47; charcode < 58)); char; «-«)& |
и правой части…
|
ПРАВСИМВ(phrase; ДЛСТР(phrase) — ndx) |
При первом вызове Slugify обрабатывает первый символ. Затем механизм вычислений Excel вызовет Slugify, чтобы исправить 2-й символ. Это будет продолжаться до тех пор, пока ndx не превысит длину phrase. Как только ndx превысит длину phrase формула вернет результат:
|
ПОДСТАВИТЬ(СЖПРОБЕЛЫ(ПОДСТАВИТЬ(phrase; «-«; » «));» «;«-«) |
Сначала мы заменим многочисленные дефисы, которыми в цикле LET() заменяли недопустимые символы, на пробелы – внутренняя функция ПОДСТАВИТЬ(). Затем удалим лишние пробелы – СЖПРОБЕЛЫ(). И наконец, заменим оставшиеся одиночные пробелы на дефисы – внешняя функция ПОДСТАВИТЬ().
Написание сложной формулы LAMBDA в ячейке Excel довольно сложное занятие. Использование окна Добавления имени еще хуже. Пожалуй, лучше всего писать формулу в блокноте или в текстовом поле в Excel (Вставка –> Текст –> Надпись). Нет хорошего способа проверить LAMBDA, использующую рекурсию. Пока вы не создадите имя, проверить формулу не получится. Но, если вы ошибетесь, формула с именем не будет работать, не сообщая почему. Хорошая новость заключается в том, что Microsoft работает над новым интерфейсом редактирования формул.
Теперь у вас есть функция SLUGIFY:
Рис. 14. Функция SLUGIFY за работой
Является ли число простым
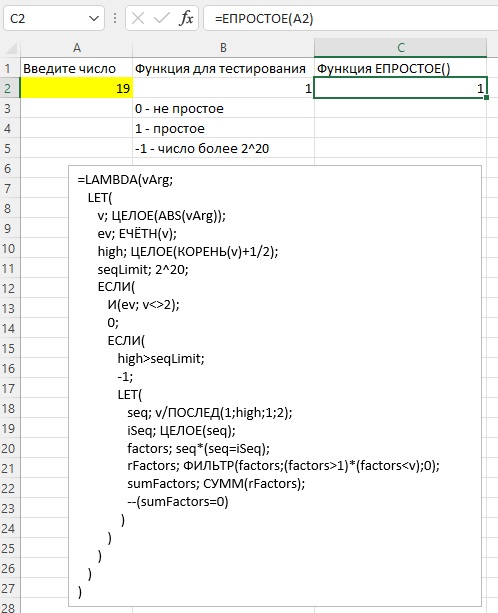
На просторах Инета нашел любопытную функцию (на основе LAMBDA и LET), которая проверяет, является ли число простым. Привожу её код, а как она работает предлагаю разобраться вам самим в качестве небольшого домашнего задания))
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
=LAMBDA(vArg; LET( v; ЦЕЛОЕ(ABS(vArg)); ev; ЕЧЁТН(v); high; ЦЕЛОЕ(КОРЕНЬ(v)+1/2); seqLimit; 2^20; ЕСЛИ( И(ev; v<>2); 0; ЕСЛИ( high>seqLimit; —1; LET( seq; v/ПОСЛЕД(1;high;1;2); iSeq; ЦЕЛОЕ(seq); factors; seq*(seq=iSeq); rFactors; ФИЛЬТР(factors;(factors>1)*(factors<v);0); sumFactors; СУММ(rFactors); —(sumFactors=0) ) ) ) ) ) |
Рис. 15. Является ли число простым
Использованные материалы
LAMBDA: The ultimate Excel worksheet function https://www.microsoft.com/en-us/research/blog/lambda-the-ultimatae-excel-worksheet-function/
Подсказки при вводе функции малоинформативны https://www.planetaexcel.ru/forum/index.php?PAGE_NAME=read&FID=1&TID=144443&TITLE_SEO=144443-voprosy-po-novoy-funktsii-_lambda_&FID_8=&tags=SQL
Билл Джелен. Срывая маску с Excel. Глава 89. LAMBDA-функция, как хранилище сложной логики вычислений (на англ. языке) https://www.mrexcel.com/products/mrexcel-2021-unmasking-excel/
Лямбда-функция Excel, которая проверяет, является ли число простым https://thefaq.ru/ljambda-funkcija-excel-kotoraja-proverjaet-javljaetsja-li-chislo-prostym/
Дополнительные материалы
С добавлением лямбда-функций язык программирования Excel стал полным по Тьюрингу https://habr.com/ru/news/t/540308/
LAMBDA — новая суперфункция Excel https://www.planetaexcel.ru/techniques/25/20915/
How to write recursive LAMBDA function in Excel with examples https://www.ablebits.com/office-addins-blog/write-recursive-lambda-function-excel/
Функция ЛЯМБДА в Excel https://ru.wiki-base.com/7773197-excel-lambda-function
Microsoft позволит создавать пользовательские функции в Excel https://infostart.ru/journal/news/tekhnologii/microsoft-pozvolit-sozdavat-polzovatelskie-funktsii-v-excel_1354120/
Jon Acampora. The LAMBDA Function Explained – How to Create Custom Functions in Excel https://www.excelcampus.com/functions/lambda-explained/
Разделение по столбцам https://www.youtube.com/watch?v=o9UNfjol_Ok&ab_channel=AbiolaDavid
Calculate Nice Axis Scales with LET and LAMBDA https://peltiertech.com/calculate-nice-axis-scales-with-let-and-lambda/
Справка Microsoft на русском языке: Функция ЛЯМБДА
[1] Это перевод части главы из книги Билла Джелена (см. в конце заметки Использованные материалы)