В этом учебном материале по Excel мы рассмотрим примеры того как рассчитать периметр круга
Основная формула
Описание
Чтобы вычислить длину окружности, вы можете использовать функцию ПИ().
В показанном примере формула в C5, имеет следующий вид:
формула вычисляет длину окружности с радиусом, указанным в столбце B.
Пояснение
В геометрии длина окружности радиуса (R) определяется по следующей формуле:
C = 2πr
Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π представлено в формуле с функцией ПИ, которая возвращает число 3,14159265358979 с точностью до 15 цифр.
|
=ПИ() ‘Результат: 3.14159265358979 |
Следовательно, формула для вычисления длины окружности с радиусом 3:
|
=2*ПИ()*3 ‘Результат: 18.85 |
А формула для вычисления длины окружности на основе значений радиуса в столбце B:
Длина окружности в excel
Формулы и функции
Мы подошли, пожалуй, к самой интересной и полезной особенности программы Excel. Именно формулы и функции делают Excel мощным вычислительным инструментом, который может освободить вас от рутинного вычисления различных данных. Приложение Excel не является узконаправленным, наоборот, оно универсально. Эта программа может пригодиться инженерам, бухгалтерам, аналитикам, студентам. Трудно представить род деятельности, где вычислительным способностям Excel было бы невозможно найти применение.
Смотрите главу «Программирование на рабочем листе. Формулы и имена», а также «Функции рабочего листа».
Работа с формулами
В ячейках таблицы Excel могут содержаться как данные, так и формулы. Формулы – не что иное, как набор математических и логических операторов и данных. В качестве данных в формулах могут выступать как постоянные значения, так и адреса ячеек (или диапазонов). При этом если формула использует адреса ячеек, то возвращает новый результат вычисления сразу, как только данные в этих ячейках меняются.
Создание простой формулы
Создадим первую формулу. Допустим, вы хотите вычислить площадь круга. Конечно, можно взять в руки калькулятор и сделать это. А если вам требуется вычислить площадь круга сто раз при разных значениях радиуса? Представляете, сколько раз вам нужно нажать кнопки калькулятора, при этом записывая куда-то все результаты? Программа Excel может сделать это быстрее.
Итак, всем известно, что площадь круга равняется ?r2, где r – это радиус круга, а ? – константа.
1. Создайте новую книгу Excel или перейдите на чистый лист.
2. В ячейку R1C1 введите текст Радиус, а в ячейку R1C2 – Площадь круга.
3. Щелкните кнопкой мыши на ячейке R2C2. В этой ячейке мы создадим формулу.
4. Введите знак =. Это сообщает программе Excel, что в этой ячейке создается формула.
5. Введите число 3,14. Это число ?, округленное до двух знаков после запятой.
6. Введите знак *. В программе Excel это – знак умножения.
7. Щелкните кнопкой мыши на ячейке R2C1.
Вокруг этой ячейки появится «муравьиная дорожка», а относительный адрес этой ячейки отобразится в создаваемой формуле.
8. Введите знак ^. Это знак возведения числа в степень.
9. Введите число 2. Это степень, в которую нужно возвести число (рис. 6.1).
Рис. 6.1. Создание формулы для вычисления площади круга
Текст в ячейках R1C1 и R1C2 нам нужен только в качестве заголовков столбцов для наглядности. В столбец 1 мы будем вводить значение радиуса круга, а в столбце 2 получать результат (площадь).
Программа Excel содержит функцию автоматического добавления числа ?, с точностью пятнадцать знаков после запятой. Но о функциях мы поговорим позже.
10. Нажмите клавишу Enter. Формула будет создана, а в ячейке R2C2 появится значение 0.
Мы создали формулу в ячейке R2C2. Щелкните кнопкой мыши на этой ячейке и посмотрите на строку формул. Вы должны увидеть следующую формулу: =3,14*RC[-1]^2. В нашей формуле число 3,14 (?) умножается на значение ячейки, стоящей слева (в этой ячейке мы позже укажем радиус), которое, в свою очередь, возводится в квадрат. В данный момент результат вычисления равен нулю, так как ячейка R2C1 пуста (формула воспринимает это как 0).
Проверим результаты вычисления.
1. В ячейку R2C1 введите 10 и нажмите клавишу Enter. В ячейке R2C2 появится число 314.
2. В ячейку R2C1 введите число 15 и нажмите клавишу Enter. В ячейке R2C2 появится число 706,5.
Как видите, результат вычисления в ячейке R2C2 автоматически обновляется, как только вы вводите новое значение в ячейку R2C1. Иными словами, вы указываете только радиус, все остальное делает Excel по созданной вами формуле. И это, пожалуй, самый простой пример.
В столбце 3 создадим формулу вычисления длины окружности, которая также будет использовать значение радиуса из столбца 1. Формула длины окружности – 2?r.
1. В ячейку R1C3 введите текст Длина окружности.
2. Щелкните кнопкой мыши на ячейке R2C3.
4. Введите цифру 2.
5. Введите знак умножения (*).
6. Введите число ? (3,14).
7. Введите знак умножения (*).
8. Щелкните кнопкой мыши на ячейке R2C1. В формуле появится относительный адрес первой ячейки, в которой мы указываем радиус. У вас должна получиться формула следующего вида: =2*3,14*RC[-2].
9. Нажмите клавишу Enter. Если в ячейке R2C1 указано какое-либо число, вы немедленно получите результат вычисления длины окружности в ячейке R2C3.
10. Введите новое значение радиуса в ячейку R2C1 и нажмите клавишу Enter. Обратите внимание, что в ячейках R2C2 и R2C3 значения изменились одновременно. Сколько бы вы ни создали формул, использующих значение ячейки R2C1, результат их вычисления будет обновляться при изменении значения в этой ячейке (рис. 6.2).
Рис. 6.2. Формулы в ячейках R2C2 и R2C3 используют значение ячейки R2C1
Приведу арифметические операторы, которые вы можете использовать при создании формул:
^ – оператор возведения в степень. Этот оператор ставится после числа (или переменной), которое возводится в степень. После этого оператора указывается значение степени, которое может быть как числом, так и переменной (переменной в данном случае мы считаем ссылку на ячейку со значением);
% – оператор вычисления процента.
Абсолютный и относительный адреса
Вы заметили, что при создании формул мы указывали ячейку R2C1, но в формулах появлялись значения RC[-1] и RC[-2]? Ранее упоминалось, что ячейка может иметь абсолютный и относительный адреса. Относительный адрес указывает путь к ячейке относительно ячейки с формулой. Так, в формуле вычисления площади круга значение RC[-1] показывает, что данные нужно взять из ячейки той же строки, но на один столбец левее. В формуле длины окружности значение RC[-2] сообщает, что данные необходимо взять из ячейки той же строки, но на два столбца левее. Конечно, вы можете в формулах указать и абсолютный адрес ячейки.
Что дает относительный адрес в формуле? Чтобы получить ответ, выполните следующие действия.
1. Выделите ячейку R2C2, то есть ячейку с формулой площади круга.
2. Установите указатель мыши на рамку выделения, чтобы он принял вид четырех противоположно направленных стрелок.
3. Нажав и удерживая кнопку мыши, перетащите рамку выделения в ячейку R6C3 и отпустите кнопку мыши. Результат вычисления площади круга появится в ячейке R6C3.
4. Попробуйте изменить значения радиуса круга в ячейке R2C2. В ячейке R6C3 обновится значение площади.
5. Выделите ячейку R6C3 и посмотрите на строку формул. Формула несколько изменилась, и теперь она выглядит так: =3,14*R[-4]C[-2]^2. Выражение R[-4]C[-2] означает, что данные (радиус) следует искать в ячейке, расположенной на четыре строки выше и два столбца левее.
Куда бы вы ни перетаскивали ячейку с формулой, относительный адрес ячейки радиуса будет меняться и указывать именно на ячейку R2C1. Точно такой же результат вы получите, изменив положение ячейки R2C1 (ячейки со значением радиуса). Куда бы вы ни переместили эту ячейку, формулы по-прежнему будут возвращать верный результат вычислений, но относительный адрес ячейки со значением радиуса в них будет меняться. Относительный адрес в формуле как бы «цепляется» к ячейке, на которую он ссылается, и не позволяет разорвать эту связь при любом перемещении ячейки формулы или ячеек данных.
Приведу пример, который наглядно покажет преимущества относительного адреса перед абсолютным. Мы создадим таблицу вычислений площади круга в зависимости от радиуса, чтобы увидеть несколько значений площади при разных радиусах.
1. Верните данные с радиусом и формулой на свои места (соответственно в ячейки R2C1 и R2C2).
2. Выделите ячейку R2C2.
3. Скопируйте ее содержимое в буфер обмена. Для этого нажмите кнопку Копировать на вкладке Главная или сочетание клавиш Ctrl+Insert.
4. Выделите ячейку R3C2.
5. Нажав и удерживая клавишу Shift, нажимайте клавишу Стрелка вниз, пока не выделите диапазон до ячейки R10C2.
6. Вставьте содержимое буфера обмена в выделенный диапазон – нажмите кнопку Вставить на вкладке Главная или сочетание клавиш Shift+Insert. В ячейках R3C2?R10C2 появятся нули.
7. Если вы щелкнете кнопкой мыши на любой из ячеек диапазона R3C2?R10C2 и посмотрите на строку формул, то увидите одну и ту же формулу =3,14*RC[-1]^2.
8. В ячейки R2C1?R10C1 введите различные числа, например от 1 до 9 (можете использовать инструмент автозаполнения).
В ячейках R2C2?R10C2 появились разные значения площади круга (рис. 6.3).
Рис. 6.3. В ячейках R2C2?R10C2 содержится одна и та же формула
Каждая формула возвращает результат вычисления в зависимости от радиуса, указанного в ячейке слева. Почему? Ответ прост: в формуле используется относительный адрес, который ссылается не на ячейку R2C1, а на ячейку RC[-1], то есть ячейку, расположенную в той же строке столбцом левее. Если бы в формулах диапазона R2C2?R10C2 использовался абсолютный адрес ячейки R2C1, мы бы получили одинаковые результаты во всех ячейках, поскольку значение радиуса для всех формул бралось бы из одной и той же ячейки. В то же время, если бы понадобилось «размножить» такие же формулы с прямым адресом на целый диапазон, вам пришлось бы в каждой формуле править абсолютный адрес, чтобы указать на ячейку слева.
Чтобы изменить относительный адрес в формуле на абсолютный, поместите курсор в конец адреса в строке формул и нажмите клавишу F4, затем клавишу Enter, чтобы записать изменения в формуле. Таким же образом вы можете поменять абсолютный адрес на относительный.
Порядок вычисления в формулах
Чтобы формула выдавала верный результат, необходимо учитывать порядок вычисления в ней. В этом нет ничего сложного, главное – проявлять внимательность при расстановке знаков в формуле.
Для следующего примера создайте таблицу, изображенную на рис. 6.4.
Рис. 6.4. Таблица для примера порядка вычисления
Допустим, нам нужно сумму содержимого ячеек R1C1 и R1C2 умножить на содержимое ячейки R1C3 и вывести результат в ячейку R2C4.
Для этого в ячейке R2C4 необходимо создать формулу.
1. Выделите ячейку R2C4.
3. Щелкните кнопкой мыши на ячейке R1C1, введите знак + и щелкните кнопкой мыши на ячейке R1C2.
4. Введите знак умножения (*) и щелкните кнопкой мыши на ячейке R1C3.
5. Нажмите клавишу Enter. Ячейка R2C4 выдаст вам результат 310. Это неверный результат.
Попробуем разобраться, почему так получилось. Тот, кто хорошо помнит математику со школы, поймет сразу. Дело в том, что программа Excel при совершении арифметических операций использует элементарные математические правила. В математике сначала производятся операции умножения и деления, а затем – сложения и вычитания. Наша формула сначала умножила содержимое ячейки R1C2 на значение ячейки R1C3, а затем сложила этот результат с содержимым ячейки R1C1, что и привело к неверному результату.
Чтобы наша формула считала правильно, необходимо сумму ячеек R1C1 и R1C2 заключить в скобки. Операции в скобках в математике имеют приоритет, то есть сначала выполняются вычисления в скобках, а потом – за их пределами.
1. Внесите коррективы в строку формул. Исправленная формула должна выглядеть следующим образом: =(R[-1]C[-3]+R[-1]C[-2])*R[-1]C[-1].
2. Нажмите клавишу Enter. Изменения в формуле будут применены, а ячейка R2C4 вернет результат 500, что соответствует нашей задаче и верному решению (рис. 6.5).
Рис. 6.5. В формуле определен верный порядок вычисления
Итак, мы изменили формулу, добавив в нее скобки. Теперь процесс вычисления формулы выглядит следующим образом: сначала происходит сложение содержимого ячеек R1C2 и R1C2, а уже затем полученный результат умножается на содержимое ячейки R1C3, что и требовалось условиями задачи.
Вот некоторые математические операторы, перечисленные в порядке приоритета выполнения: % (вычисление процента), ^ (возведение в степень), * и / (умножение и деление), + и – (сложение и вычитание). Иными словами, если в формуле производится возведение в степень какого-то числа или переменной, это делается раньше умножения или деления и тем более – сложения и вычитания. Если часть формулы заключена в скобки, то сначала производится вычисление в скобках. В свою очередь, если в скобках также присутствует несколько операторов, то они выполняются в порядке приоритета, о котором мы только что говорили.
«Формулы в формулах»
При создании формул вы используете в качестве данных константы и адреса ячеек с данными. Вы можете также указать адреса ячеек, содержащих формулы. Допустим, в вашей таблице есть формула, возвращающая результат какого-то вычисления. Назовем ее Формула1. Вы создаете новую формулу (Формула2), в которой вам нужно произвести какие-то операции над результатом вычисления Формулы1. В этом случае, вам следует в Формуле2 указать адрес ячейки Формулы1 и произвести с ней какие-либо операции. При этом в Формуле2 будет обрабатываться не Формула1, а результат, который она возвращает.
Для следующего примера используйте таблицу, которую мы создали в предыдущем разделе. В ячейке R2C4 содержится формула, возвращающая произведение ячейки R1C3 и суммы ячеек R1C1 и R1C2. Мы создадим формулу в ячейке R2C5, которая будет делить содержимое ячейки R2C4 на 2.
1. Щелкните кнопкой мыши на ячейке R2C4.
3. Щелкните кнопкой мыши на ячейке R2C4. В формуле появится относительный адрес этой ячейки.
4. Ведите знак деления (/) и затем цифру 2.
5. Нажмите Enter. В ячейке R2C5 появится результат вычисления 250.
6. Измените значение в любой из ячеек: R1C2 или R1C3. Результат вычисления изменится и в ячейке R2C5, и в ячейке R2C4.
При любом изменении исходных данных формула, расположенная в ячейке R2C4, возвращает результат вычисления, который, в свою очередь, влияет на результат вычисления формулы ячейки R2C5. Таким образом, вы можете создать любые формулы, которые будут использовать в том числе и результаты вычисления других формул. Старайтесь не перегружать таблицу такими сложноподчиненными формулами. В конце концов, можно просто запутаться, какая формула на что влияет, а любая ошибка в формуле приведет к неверному результату в остальных формулах, использующих результат ее вычисления.
В некоторых случаях в ячейке с формулой вы можете вместо результатов увидеть одно из следующих значений: ######, #ЗНАЧ! или #ДЕЛ/0!.
• ###### означает, что результат вычисления не умещается в видимой части ячейки. Чтобы увидеть результат вычисления, следует просто увеличить ширину столбца, содержащего ячейку с формулой.
• #ЗНАЧ! возникает при вводе некорректного значения в одну из ячеек, ссылка на которую присутствует в формуле. Например, если вы попытаетесь умножить число на текст, получите результат #ЗНАЧ!.
• #ДЕЛ/0! появляется при попытке деления на 0 или на пустое значение ячейки (которое программой Excel расценивается как 0).
Программа Excel содержит огромное количество функций: математических, статистических, инженерных, логических, текстовых, финансовых и т. д. Эти функции вы можете использовать для создания формул или обработки данных таблицы.
В данном разделе действие той или иной функции будет кратко описываться и показываться на примере.
Создайте чистую таблицу. Эту таблицу мы будем использовать для примеров использования функций.
Наиболее часто используемая функция в математических расчетах – это КОРЕНЬ.
1. Выделите ячейку R2C2. В эту ячейку мы будем вставлять функцию.
2. Нажмите кнопку Вставить функцию, расположенную в левой части строки формул. Появится диалоговое окно Мастер функций ? шаг 1 из 2 (рис. 6.6).
Рис. 6.6. Диалоговое окно Мастер функций – шаг 1 из 2
3. В раскрывающемся списке Категория выберите пункт Математические.
4. В списке Выберите функцию выберите пункт КОРЕНЬ. Обратите внимание, что в нижней части диалогового окна появляется краткое сообщение о назначении выбранной функции.
5. Нажмите кнопку ОК. Появится диалоговое окно Аргументы функции. В поле Число следует указать число или адрес ячейки, из значения которой следует извлечь корень (рис. 6.7).
Рис. 6.7. Диалоговое окно Аргументы функции
Вы также можете воспользоваться кнопкой, расположенной в правой части поля Число, чтобы указать ячейку R1C1 мышью.
Вы можете не пользоваться диалоговым окном Мастер функций – шаг 1 из 2, а просто ввести в ячейку R2C2 следующий текст: =КОРЕНЬ(R1C1). Со временем, скорее всего, вы запомните часто используемые функции и в некоторых случаях будете вводить их вручную.
6. Введите в поле Число адрес ячейки R1C1. В эту ячейку мы будем подставлять числовые значения, из которых следует извлечь корень.
7. Нажмите кнопку ОК. Диалоговое окно закроется, а в ячейке R2C2 появится значение 0. Функция вернула значение 0, потому что ячейка R1C1 пуста.
8. Введите число 81 в ячейку R1C1 и нажмите клавишу Enter. В ячейке R2C2 появится число 9, которое является корнем числа 81.
Какое бы число вы ни подставляли в ячейку R1C1, ячейка R2C2 вернет вам корень этого числа. Если вы введете отрицательное число в ячейку R1C1, получите результат #ЧИСЛО!. Корень не может быть извлечен из отрицательного числа. Кроме того, сообщение об ошибке (#ЗНАЧ!) вы получите при попытке извлечь корень из текста.
В следующем примере мы переведем величину угла из градусов в радианы.
1. Очистите ячейку R2C2.
2. Нажмите кнопку Вставить функцию. В появившемся диалоговом окне в списке Выберите функцию щелкните кнопкой мыши на пункте РАДИАНЫ и нажмите кнопку ОК (убедитесь, что в диалоговом окне выбрана категория Математические).
3. В поле Число появившегося диалогового окна укажите адрес ячейки R1C1.
4. Нажмите кнопку ОК. Диалоговое окно будет закрыто, а в ячейке R2C2 появится значение ячейки R1C1, переведенное в радианы.
5. Введите в ячейку R1C1 число 180 и нажмите Enter. В ячейке R2C2 появится число 3,141593. Это – число ?. 180 градусов равняются числу ?.
Теперь рассмотрим функцию, предназначенную для округления числа. Допустим, у вас возникла необходимость округлить десятичную дробь с некоторым количеством символов после запятой до целого или до определенного количества знаков после запятой.
1. Очистите ячейку R2C2.
2. Нажмите кнопку Вставить функцию и выберите функцию ОКРУГЛ.
3. Нажмите кнопку ОК. Обратите внимание, что диалоговое окно Аргументы функции на этот раз содержит два поля (рис. 6.8). В первом поле следует указать число, которое требуется округлить (или адрес ячейки), а во втором (Число_разрядов) – количество знаков после запятой, до которого нужно округлить число.
Рис. 6.8. Два аргумента в диалоговом окне Аргументы функции
Функция ГРАДУСЫ действует наоборот: переводит значение угла, указанное в радианах, в градусы.
4. В поле Число укажите адрес ячейки R1C1.
5. В поле Число_разрядов введите цифру 2. Мы округлим число до двух знаков после запятой.
6. Нажмите кнопку ОК. Диалоговое окно закроется.
7. В ячейку R1C1 введите число 3,151593 и нажмите клавишу Enter. В ячейке R2C2 появится число 3,15, то есть значение ячейки R1C1, округленное до двух знаков после запятой (рис. 6.9).
Рис. 6.9. Функция возвращает число ячейки R1C1, округленное до сотой доли
Вы можете править аргументы функции, не прибегая к диалоговому окну Мастер функций ? шаг 1 из 2. Изменим аргументы функции, чтобы она округляла значение ячейки R1C1 до четырех знаков после запятой.
1. Выделите ячейку R2C2 и посмотрите на строку формул. После адреса ячейки R1C1 (или ее относительного адреса) через точку с запятой указана цифра 2. Это и есть аргумент функции, указывающий количество знаков после запятой в результате округления.
2. Исправьте аргумент 2 в строке формул на 4 и нажмите клавишу Enter. В ячейке R2C2 появится значение 3,1516.
Таким образом, вы можете править аргументы функции прямо в строке формул.
Иногда возникает необходимость преобразовать арабские цифры и числа в римские. В программе Excel предусмотрена и такая функция.
1. Очистите ячейку R2C2.
2. Откройте диалоговое окно Мастер функций ? шаг 1 из 2 и выберите функцию РИМСКОЕ.
3. Нажмите клавишу Enter, в появившемся диалоговом окне укажите адрес ячейки R1C1 и нажмите кнопку ОК. В ячейке R2C2 появилась римская цифра III. Римские цифры не имеют дробной части, а поскольку в ячейке R1C1 было указано число 3,151593, функция вернула нам целую часть этого числа в римском формате.
4. В ячейку R1C1 введите число 15 и нажмите клавишу Enter. В ячейке R2C2 появится число XV.
5. Усложним задачу. Введите в ячейку R1C1 число 1145 и нажмите клавишу Enter. Как видите, функция справилась и с этой задачей и вернула число MCXLV.
Вы можете использовать функцию для получения случайного числа. Для этого следует указать два числа, и функция вернет вам случайное число в диапазоне этих чисел.
1. Очистите ячейку R2C2, откройте диалоговое окно Мастер функций ? шаг 1 из 2 и выберите функцию СЛУЧМЕЖДУ.
2. В диалоговом окне Аргументы функции следует указать нижнюю и верхнюю границу числа в соответствующих полях. В поле Нижн_граница укажите адрес ячейки R1C1, а в поле Верхн_граница – R1C2.
3. Закройте диалоговое окно и в ячейках R1C1 и R1C2 укажите два разных числа, например 1 и 6. В ячейке R2C2 появится случайное число от 1 до 6.
Вышеуказанная функция может заменить, например, игральные кубики.
Вы можете поэкспериментировать с остальными математическими функциями самостоятельно. Подсказка в диалоговом окне Мастер функций ? шаг 1 из 2 достаточно четко описывает назначение выбранной функции, а также вы можете воспользоваться ресурсами справочной системы программы, щелкнув кнопкой мыши на ссылке Справка по этой функции, расположенной в нижней части диалогового окна.
Логические функции могут найти применение при математических, инженерных вычислениях или при сравнительном анализе данных. Мы рассмотрим одну логическую функцию на примере функции ЕСЛИ.
С помощью функции ЕСЛИ вы можете создать логическое выражение и в нужную ячейку вывести результат этого выражения. Чтобы разобраться в этой функции, рассмотрим простой пример. Сравним числа в двух разных ячейках (R1C1 и R1C2) и результат сравнения выведем в ячейку R2C2.
1. Очистите ячейку R2C2.
2. Откройте диалоговое окно Мастер функций ? шаг 1 из 2, перейдите в категорию Логические и выберите функцию ЕСЛИ.
3. В диалоговом окне Аргументы функции вам предлагается ввести аргументы в три поля.
4. В поле Лог_выражение введите следующее выражение: R1C1>R1C2.
Таким образом, мы как бы утверждаем, что число в ячейке R1C1 больше числа R1C2.
В поле Значение_если_истина следует ввести число или текст, который будет возвращать ячейка R2C2 при справедливости указанного нами логического выражения.
1. В поле Значение_если_истина введите текст Да, это правда.
2. В поле Значение_если_ложь введите текст Нет, это неправда. Данный текст будет выводиться в ячейке R2C2, если логическое выражение окажется неверным, то есть число ячейки R1C1 на самом деле окажется меньше числа ячейки R2C2.
3. Нажмите кнопку ОК.
4. В ячейку R1C1 введите число 5, а в R1C2 – 10. Ячейка R2C2 выдаст сообщение Нет, это неправда. Действительно, число 5 не может быть больше числа 10 (рис. 6.10).
Рис. 6.10. Результат выполнения логической операции
5. В ячейку R1C1 введите число 10, а в R1C2 – 5. Ячейка R2C2 выдаст сообщение Да, это правда. Теперь условие логического выражения выполняется: первое число больше второго.
6. Введите одинаковые числа в обе ячейки, например 10 и 10. Вы получите сообщение Нет, это неправда. Действительно, если числа одинаковые, то одно из них не может быть больше другого.
Иными словами, результатом проверки логического выражения могут быть только два варианта – ИСТИНА и ЛОЖЬ, и в зависимости от этого результата ячейка с функцией возвращает вам заранее указанный результат.
Мы использовали текстовые сообщения в этом примере для наглядности, хотя в сложных инженерных или математических расчетах может понадобиться подставить числовые значения. Например, если какое-то условие выполняется, то ячейка возвращает число 5 (или, к примеру, синус угла), если не выполняется – другое число (или косинус угла). В свою очередь, другая формула может использовать данные ячейки R2C2 и производить вычисление в зависимости от результатов проверки логического выражения. Например, при расчете температуры подачи воды в систему центрального отопления: если температура воздуха меньше определенного значения – повысить температуру воды до такого-то значения, если температура воздуха выше – понизить температуру воды. Примеров использования функции ЕСЛИ можно привести множество. Вы сами найдете применение этой функции.
Программа Excel содержит функции для операций с датами и временем. Мы рассмотрим несколько таких функций на примерах.
Функция ГОД возвращает значение года из даты. К примеру, в какой-либо ячейке вашей таблицы указана дата (текущая или нет, неважно). При использовании функции ГОД, где в качестве аргумента указана ячейка с датой, из даты выделяется только значение года.
Проверим это на практике.
1. Очистите ячейку R1C1.
2. Вставьте в ячейку R2C2 функцию ГОД из категории Дата и время.
3. В качестве аргумента функции укажите ячейку R1C1.
4. В ячейку R1C1 введите какую-либо дату, например 12/01/2006, и нажмите клавишу Enter. В ячейке R2C2 появится значение 2006.
Функция ТДАТА возвращает текущую дату и время. Данная функция не имеет аргументов, вы просто вставляете эту функцию в ячейку, в которой появляется значение текущей даты и времени, например 08.01.2006 14:22. Позже (при помощи других функций категории Дата и время) вы можете выделить из этой ячейки отдельно дату или время.
Функция ДЕНЬНЕД возвращает порядковый номер дня недели из даты. Для изучения этой функции выполните следующие практические шаги.
1. Используя функцию ТДАТА, добавьте в ячейку R1C1 текущую дату.
2. Выделите ячейку R2C2 и добавьте в нее функцию ДЕНЬНЕД из категории Дата и время.
3. В диалоговом окне Аргументы функции в поле Дата_в_числовом_формате укажите абсолютный или относительный адрес ячейки R1C1.
4. В поле Тип необходимо указать одно из следующих значений.
• 1 – неделя будет начинаться с воскресенья (как в некоторых западных странах). При этом возвращенное значение 1 будет соответствовать воскресенью, а 7 – субботе.
• 2 – неделя будет начинаться с понедельника. Возвращенное значение 1 будет соответствовать понедельнику, а 7 – воскресенью.
• 3 – неделя также будет начинаться с понедельника, но отсчет дней недели будет вестись с нуля, то есть возвращенное значение 0 будет соответствовать понедельнику, а 6 – воскресенью.
Укажите значение 2.
5. Закройте диалоговое окно кнопкой ОК. В ячейке R1C1 будет указан порядковый номер текущего дня недели.
Функция НОМНЕДЕЛИ часто применяется в бухгалтерии и при составлении рабочих графиков. Она возвращает порядковый номер недели (с начала года) из даты. В качестве аргумента этой функции указывается дата или ячейка, содержащая информацию о дате. Результатом выполнения функции является число, означающее номер недели, на которую приходится указанная в качестве аргумента дата.
Текстовые функции также нередко применяются в таблицах Ecxel для преобразования различных текстовых данных.
Функция ЛЕВСИМВ возвращает заданное количество символов от начала текстовой строки, заданной в качестве аргумента. Рассмотрим действие этой функции на примере.
1. Очистите ячейку R1C1 и введите в нее текст Фрагмент текста.
2. Добавьте в ячейку R2C2 функцию ЛЕВСИМВ из категории Текстовые.
3. В поле Текст диалогового окна Аргументы функции укажите адрес ячейки R1C1.
4. В поле Количество_знаков диалогового окна Аргументы функции нужно ввести количество знаков от начала строки, которые следует возвратить. Мы возвратим слово Фрагмент, которое содержит восемь символов (букв), поэтому укажем в качестве аргумента Количество_символов цифру 8.
5. Закройте диалоговое окно. В ячейке R2C2 появится слово Фрагмент.
Функция СЦЕПИТЬ объединяет текст из нескольких ячеек в одну строку.
1. В ячейку R1C1 введите текст Фрагмент.
2. В ячейку R1C2 введите текст текста.
3. В ячейку R2C2 добавьте функцию СЦЕПИТЬ из категории Текстовые.
4. Откройте диалоговое окно Аргументы функции и в поле Текст1 укажите адрес ячейки R1C1, а в поле Текст2 – адрес ячейки R2C2.
5. Закройте диалоговое окно. В ячейке R2C2 появится текст Фрагменттекста (рис. 6.11). Обратите внимание, что оба слова были соединены без пробела. Если бы мы добавили пробел в конце текста ячейки R1C1 или в начале R1C2, мы бы получили текст Фрагмент текста.
Рис. 6.11. Результат выполнения функции СЦЕПИТЬ
Программа Excel содержит более 350 различных функций, и рамки этой книги не позволяют раскрыть все возможности их использования. Мы рассмотрели лишь несколько примеров использования функций различных категорий. Справочная система приложения Microsoft Excel достаточно подробно описывает работу с каждой функцией. Взгляните на рис. 6.12.
Рис. 6.12. Справка программы Excel по функции LOG
Каждое описание функции в справочной системе снабжено практическим примером, который вы можете скопировать прямо из окна справки и вставить в свою таблицу, чтобы поэкспериментировать с различными значениями аргументов функций.
Как мы уже говорили, функции могут существовать как самостоятельно, так и в составе формул. Например, если вы введете в ячейку формулу =R[-2]C-(КОРЕНЬ(R1C1)*КОРЕНЬ(R1C1)), то получите значение 0 при любом числовом значении ячейки R1C1 (кроме отрицательного). Как видите, в этой формуле используются как арифметические операторы (умножение и вычитание), так и функции (КОРЕНЬ). В процессе создания сложных таблиц вам часто придется использовать в формулах функции.
Обратите внимание, что по мере добавления аргументов в диалоговом окне Аргументы функции появляются новые поля (Текст3, Текст4 и т. д.). Это дает возможность объединять текст из большего количества ячеек.
Кроме того, функции в качестве аргумента могут использовать ячейки с другими функциями. При создании таких подчиненных функций будьте внимательны, так как ошибка в первой ячейке с функцией повлечет за собой ошибки во всех связанных с ней ячейках.
Чтобы проверить связи влияния ячеек друг на друга, необходимо выделить нужную ячейку и нажать кнопку Влияющие ячейки, расположенную в группе Зависимости формул вкладки Формулы. Между влияющими ячейками появятся стрелки, показывающие, какие ячейки влияют на результат других ячеек (рис. 6.13).
Рис. 6.13. Стрелками показаны пути влияния ячеек
На рис. 6.13 показано, что ячейка R1C2 влияет на результат ячейки R3C2 (по всей видимости, ячейка R3C2 использует данные ячейки R1C2), а ячейка R3C2 влияет на ячейку R5C1 (ячейка R5C1, в свою очередь, использует для расчетов данные ячейки R3C2). Таким образом, вы можете проследить пути влияния ячеек и быстро найти ошибку в формулах в случае неверного итогового результата.
Чтобы скрыть стрелки влияния, нужно просто нажать кнопку Убрать стрелки, расположенную в группе Зависимости формул.
Кроме того, добавить в ячейку функцию вы можете с помощью кнопок, находящихся в группе Библиотека функций на вкладке Формулы. Нажатие кнопки с названием категории функции приводит к появлению списка функций, расположенных в этой категории. Вслед за выбором нужной функции из списка сразу появляется диалоговое окно Аргументы функции.
Возможно, такой способ добавления функции вам покажется более удобным и быстрым, поскольку вы пропускаете процедуру открытия диалогового окна Мастер функций ? шаг 1 из 2 и выбора категории функции, что сокращает количество шагов при выполнении задачи.
Практическое использование средства «Подбор параметра» для решения простых математических задач
Приведенные в этой статье примеры и упражнения покажут, как применять средство Подбор параметра для решения следующих математических задач: вычисление скорости, времени и расстояния; вычисление диаметра, длины окружности и площади круга; нахождение корней алгебраических уравнений.
Вычисление скорости, времени и расстояния
Прежде чем приступать к решению объявленных задач, советую создать рабочий лист, показанный на рис. 1.6. О том как создать новый лист в книге Excel, вы можете узнать на странице http://www.cyberforum.ru/ms-excel/.
Рис. 1.6. Рабочий лист для решения задач вычисления скорости, времени и расстояния
С помощью средства Подбор параметра значения скорости, врени и расстояния будут вычисляться соответственно в столбцах А, D и G.
- Скорость вычисляется в ячейке А4 как произведение «километров» и результата деления 60 минут на заданное количество минут (записано в ячейке А5). Другими словами, в ячейке А4 записана формула =А6*(60/А5) .
- Время вычисляется в ячейке D5 как произведение «километров» и результата деления 60 минут на скорость (записана в ячейке D4), т.е. используется формула =D6*(60/D4) .
- Расстояние в ячейке G6 вычисляется по аналогичной формуле =G4*(G5/60) , т.е. как произведение скорости и результата деления 60 минут на заданное количество минут.
Подбор параметра для скорости
Задача: какое расстояние можно преодолеть за 12 минут при скорости 75 км в час? Ниже приведено решение задачи с помощью средства Подбор параметра.
- В ячейку А5 введите число 12.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А4 или щелкните на ячейке А4.
- В поле ввода Значение введите число 75.
- В поле ввода Изменяя значение ячейки введите А6 или щелкните на ячейке А6.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: за 12 минут при скорости 75 км в час можно преодолеть 15 км.
Подбор параметра для времени
Задача: с какой скоростью вы передвигаетесь, если 12 км преодолели за 8 минут? Ниже приведено решение задачи с помощью средства Подбор параметра.
- В ячейку D6 введите число 12.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите D5 или щелкните на ячейке D5.
- В поле ввода Значение введите число 8.
- В поле ввода Изменяя значение ячейки введите D4 или щелкните на ячейке D4.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если вы преодолели 12 км за 8 минут, то ваша скорость составляет 90 км в час.
Подбор параметра для расстояния
Задача: за какое время вы преодолеете 85 км при скорости 75 км в час? Решение задачи с помощью средства Подбор параметра приведено ниже.
- В ячейку G4 введите число 72.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите G6 или щелкните на ячейке G6.
- В поле ввода Значение введите число 85.
- В поле ввода Изменяя значение ячейки введите G5 или щелкните на ячейке G5.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке.
Ответ: 85 км при скорости 75 км в час вы преодолеете за 71 мин.
Вычисление диаметра, длины окружности и площади круга
Для решения этих задач создайте рабочий лист, показанный на рис. 1.7. На этом рабочем листе радиус в виде числового значения задается в ячейке А10, другие числовые характеристики вычисляются по следующим формулам.
- Диаметр как удвоенное значение радиуса вычисляется в ячейке Al 1 по формуле =А10*2 .
- Длина окружности в ячейке А12 вычисляется как число π, умноженное на диаметр, т.е. по формуле =ПИ()*А11 .
- Площадь круга в ячейке А13 вычисляется как число π, умноженное на квадрат радиуса, т.е. по формуле =ПИ()*СТЕПЕНЬ(А10;2) .
Рис. 1.7. Рабочий лист для решения задач вычисления диаметра, длины окружности и площади круга
В этих задачах единицы измерения не имеют значения, можете подставить километры, миллиметры или дюймы.
Подбор параметра для диаметра
Задача: какое значение имеет радиус круга, если его диаметр равен 6,25? Решение задачи с помощью средства Подбор параметра таково.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите A11 или щелкните на ячейке A11.
- В поле ввода Значение введите число 6,25.
- В поле ввода Изменяя значение ячейки введите А10 или щелкните на ячейке А10.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если диаметр круга равен 6,25, то радиус равен 3,125.
Подбор параметра для длины окружности
Задача: каково значение радиуса круга, если длина окружности равна 30? Решение задачи с помощью средства Подбор параметра приведено ниже.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А12 или щелкните на ячейке А12.
- В поле ввода Значение введите число 30.
- В поле ввода Изменяя значение ячейки введите А10 или щелкните на ячейке А10.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если длина окружности равна 30, то радиус равен 4,8.
Подбор параметра для площади круга
Задача: каково значение радиуса круга, если площадь круга равна 17? Ниже приведено решение задачи с помощью средства Подбор параметра.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А13 или щелкните на ячейке А13.
- В поле ввода Значение введите число 17.
- В поле ввода Изменяя значение ячейки введите А10 или щелкните на ячейке А10.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если площадь круга равна 17, то радиус равен 2,3.
Вычисление корней алгебраических уравнений
Для решения задач этого раздела подготовьте рабочий лист, показанный на рис. 1.8. Алгебраическое выражение ах + by + cz = d по значениям переменных а, b, с, х, у и z вычисляет значение переменной d. Имея значения любых шести переменных, с помощью средства Подбор параметра можно вычислить значение седьмой переменной.
Рис. 1.8. Рабочий лист для вычисления корней алгебраического уравнения
Подбор параметра для вычисления переменной с
Задача: зная значения переменных
- а = 1,
- b = 2,
- d = 12,
- х = 1,
- у = 2,
- z = 1,
необходимо найти значение переменной с.
- Введите следующие значения в указанные ячейки:
- ячейка А17:1,
- ячейка А18:2,
- ячейка С17:1,
- ячейка С18:2,
- ячейка С19:1.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А20 или щелкните на ячейке А20.
- В поле ввода Значение введите число 12.
- В поле ввода Изменяя значение ячейки введите А19 или щелкните на ячейке А19.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если а = 1, b = 2, d = 12, х = 1, у = 2, z = 1, то с = 7.
Подбор параметра для вычисления переменной z
Задача: зная значения переменных
- а = 2,
- b = 4,
- с = 3,
- d = 65,
- х = 5,
- y = 7,
необходимо найти значение переменной z.
- Введите следующие значения в указанные ячейки:
- ячейка А17:2,
- ячейка А18:4,
- ячейка А19:3,
- ячейка С17:5,
- ячейка С18:7.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А20 или щелкните на ячейке А20.
- В поле ввода Значение введите число 65.
- В поле ввода Изменяя значение ячейки введите С19 или щелкните на ячейке С19.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если а = 2, b = 4, с = 3, d = 65, х = 5, у = 7, то z = 9.
Подбор параметра для вычисления переменной а
Задача: зная значения переменных
- b = 6,
- с = 2,
- d = 84,
- х = 4,
- y = 7,
- z = 9,
необходимо найти значение переменной а.
- Введите следующие значения в указанные ячейки:
- ячейка А18:6,
- ячейка А19:2,
- ячейка С17:4,
- ячейка С18:2,
- ячейка С19:9.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А20 или щелкните на ячейке А20.
- В поле ввода Значение введите число 84.
- В поле ввода Изменяя значение ячейки введите А17 или щелкните на ячейке А17.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если b = 6, с = 2, d = 84, х = 4, у = 2, z = 9, то а = 13,5.
Теперь, когда вы знаете, как использовать средство Подбор параметра для решения математических задач, испытаем его на задачах экономического характера.
Как в Excel найти длину окружности
В этом учебном материале по Excel мы рассмотрим примеры того как рассчитать периметр круга
Основная формула
Описание
Чтобы вычислить длину окружности, вы можете использовать функцию ПИ().
В показанном примере формула в C5, имеет следующий вид:
формула вычисляет длину окружности с радиусом, указанным в столбце B.
Пояснение
В геометрии длина окружности радиуса (R) определяется по следующей формуле:
C = 2πr
Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π представлено в формуле с функцией ПИ, которая возвращает число 3,14159265358979 с точностью до 15 цифр.
Следовательно, формула для вычисления длины окружности с радиусом 3:
А формула для вычисления длины окружности на основе значений радиуса в столбце B:
источники:
http://excel2010.ru/prakticheskoe-ispolzovanie-sredstva-podbor-parametra-dlya-resheniya-prostyx-matematicheskix-zadach.html
http://itsteps.ru/excel-kak-najti-dlinu-okruzhnosti.html
Практическое использование средства «Подбор параметра» для решения простых математических задач
Приведенные в этой статье примеры и упражнения покажут, как применять средство Подбор параметра для решения следующих математических задач: вычисление скорости, времени и расстояния; вычисление диаметра, длины окружности и площади круга; нахождение корней алгебраических уравнений.
Вычисление скорости, времени и расстояния
Прежде чем приступать к решению объявленных задач, советую создать рабочий лист, показанный на рис. 1.6. О том как создать новый лист в книге Excel, вы можете узнать на странице http://www.cyberforum.ru/ms-excel/.
Рис. 1.6. Рабочий лист для решения задач вычисления скорости, времени и расстояния
С помощью средства Подбор параметра значения скорости, врени и расстояния будут вычисляться соответственно в столбцах А, D и G.
- Скорость вычисляется в ячейке А4 как произведение «километров» и результата деления 60 минут на заданное количество минут (записано в ячейке А5). Другими словами, в ячейке А4 записана формула
=А6*(60/А5). - Время вычисляется в ячейке D5 как произведение «километров» и результата деления 60 минут на скорость (записана в ячейке D4), т.е. используется формула
=D6*(60/D4). - Расстояние в ячейке G6 вычисляется по аналогичной формуле
=G4*(G5/60), т.е. как произведение скорости и результата деления 60 минут на заданное количество минут.
Подбор параметра для скорости
Задача: какое расстояние можно преодолеть за 12 минут при скорости 75 км в час? Ниже приведено решение задачи с помощью средства Подбор параметра.
- В ячейку А5 введите число 12.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А4 или щелкните на ячейке А4.
- В поле ввода Значение введите число 75.
- В поле ввода Изменяя значение ячейки введите А6 или щелкните на ячейке А6.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: за 12 минут при скорости 75 км в час можно преодолеть 15 км.
Подбор параметра для времени
Задача: с какой скоростью вы передвигаетесь, если 12 км преодолели за 8 минут? Ниже приведено решение задачи с помощью средства Подбор параметра.
- В ячейку D6 введите число 12.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите D5 или щелкните на ячейке D5.
- В поле ввода Значение введите число 8.
- В поле ввода Изменяя значение ячейки введите D4 или щелкните на ячейке D4.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если вы преодолели 12 км за 8 минут, то ваша скорость составляет 90 км в час.
Подбор параметра для расстояния
Задача: за какое время вы преодолеете 85 км при скорости 75 км в час? Решение задачи с помощью средства Подбор параметра приведено ниже.
- В ячейку G4 введите число 72.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите G6 или щелкните на ячейке G6.
- В поле ввода Значение введите число 85.
- В поле ввода Изменяя значение ячейки введите G5 или щелкните на ячейке G5.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке.
Ответ: 85 км при скорости 75 км в час вы преодолеете за 71 мин.
Вычисление диаметра, длины окружности и площади круга
Для решения этих задач создайте рабочий лист, показанный на рис. 1.7. На этом рабочем листе радиус в виде числового значения задается в ячейке А10, другие числовые характеристики вычисляются по следующим формулам.
- Диаметр как удвоенное значение радиуса вычисляется в ячейке Al 1 по формуле
=А10*2. - Длина окружности в ячейке А12 вычисляется как число π, умноженное на диаметр, т.е. по формуле
=ПИ()*А11. - Площадь круга в ячейке А13 вычисляется как число π, умноженное на квадрат радиуса, т.е. по формуле
=ПИ()*СТЕПЕНЬ(А10;2).
Рис. 1.7. Рабочий лист для решения задач вычисления диаметра, длины окружности и площади круга
В этих задачах единицы измерения не имеют значения, можете подставить километры, миллиметры или дюймы.
Подбор параметра для диаметра
Задача: какое значение имеет радиус круга, если его диаметр равен 6,25? Решение задачи с помощью средства Подбор параметра таково.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите A11 или щелкните на ячейке A11.
- В поле ввода Значение введите число 6,25.
- В поле ввода Изменяя значение ячейки введите А10 или щелкните на ячейке А10.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если диаметр круга равен 6,25, то радиус равен 3,125.
Подбор параметра для длины окружности
Задача: каково значение радиуса круга, если длина окружности равна 30? Решение задачи с помощью средства Подбор параметра приведено ниже.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А12 или щелкните на ячейке А12.
- В поле ввода Значение введите число 30.
- В поле ввода Изменяя значение ячейки введите А10 или щелкните на ячейке А10.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если длина окружности равна 30, то радиус равен 4,8.
Подбор параметра для площади круга
Задача: каково значение радиуса круга, если площадь круга равна 17? Ниже приведено решение задачи с помощью средства Подбор параметра.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А13 или щелкните на ячейке А13.
- В поле ввода Значение введите число 17.
- В поле ввода Изменяя значение ячейки введите А10 или щелкните на ячейке А10.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если площадь круга равна 17, то радиус равен 2,3.
Вычисление корней алгебраических уравнений
Для решения задач этого раздела подготовьте рабочий лист, показанный на рис. 1.8. Алгебраическое выражение ах + by + cz = d по значениям переменных а, b, с, х, у и z вычисляет значение переменной d. Имея значения любых шести переменных, с помощью средства Подбор параметра можно вычислить значение седьмой переменной.
Рис. 1.8. Рабочий лист для вычисления корней алгебраического уравнения
Подбор параметра для вычисления переменной с
Задача: зная значения переменных
- а = 1,
- b = 2,
- d = 12,
- х = 1,
- у = 2,
- z = 1,
необходимо найти значение переменной с.
- Введите следующие значения в указанные ячейки:
- ячейка А17:1,
- ячейка А18:2,
- ячейка С17:1,
- ячейка С18:2,
- ячейка С19:1.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А20 или щелкните на ячейке А20.
- В поле ввода Значение введите число 12.
- В поле ввода Изменяя значение ячейки введите А19 или щелкните на ячейке А19.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если а = 1, b = 2, d = 12, х = 1, у = 2, z = 1, то с = 7.
Подбор параметра для вычисления переменной z
Задача: зная значения переменных
- а = 2,
- b = 4,
- с = 3,
- d = 65,
- х = 5,
- y = 7,
необходимо найти значение переменной z.
- Введите следующие значения в указанные ячейки:
- ячейка А17:2,
- ячейка А18:4,
- ячейка А19:3,
- ячейка С17:5,
- ячейка С18:7.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А20 или щелкните на ячейке А20.
- В поле ввода Значение введите число 65.
- В поле ввода Изменяя значение ячейки введите С19 или щелкните на ячейке С19.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если а = 2, b = 4, с = 3, d = 65, х = 5, у = 7, то z = 9.
Подбор параметра для вычисления переменной а
Задача: зная значения переменных
- b = 6,
- с = 2,
- d = 84,
- х = 4,
- y = 7,
- z = 9,
необходимо найти значение переменной а.
- Введите следующие значения в указанные ячейки:
- ячейка А18:6,
- ячейка А19:2,
- ячейка С17:4,
- ячейка С18:2,
- ячейка С19:9.
- Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра.
- В поле ввода Установить в ячейке введите А20 или щелкните на ячейке А20.
- В поле ввода Значение введите число 84.
- В поле ввода Изменяя значение ячейки введите А17 или щелкните на ячейке А17.
- Щелкните на кнопке ОК.
- В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.
Ответ: если b = 6, с = 2, d = 84, х = 4, у = 2, z = 9, то а = 13,5.
Теперь, когда вы знаете, как использовать средство Подбор параметра для решения математических задач, испытаем его на задачах экономического характера.
ВикиЧтение
Excel. Мультимедийный курс
Мединов Олег
Создание простой формулы
Создание простой формулы
Создадим первую формулу. Допустим, вы хотите вычислить площадь круга. Конечно, можно взять в руки калькулятор и сделать это. А если вам требуется вычислить площадь круга сто раз при разных значениях радиуса? Представляете, сколько раз вам нужно нажать кнопки калькулятора, при этом записывая куда-то все результаты? Программа Excel может сделать это быстрее.
Итак, всем известно, что площадь круга равняется ?r2, где r – это радиус круга, а ? – константа.
1. Создайте новую книгу Excel или перейдите на чистый лист.
2. В ячейку R1C1 введите текст Радиус, а в ячейку R1C2 – Площадь круга.
3. Щелкните кнопкой мыши на ячейке R2C2. В этой ячейке мы создадим формулу.
4. Введите знак =. Это сообщает программе Excel, что в этой ячейке создается формула.
5. Введите число 3,14. Это число ?, округленное до двух знаков после запятой.
6. Введите знак *. В программе Excel это – знак умножения.
7. Щелкните кнопкой мыши на ячейке R2C1.
Вокруг этой ячейки появится «муравьиная дорожка», а относительный адрес этой ячейки отобразится в создаваемой формуле.
8. Введите знак ^. Это знак возведения числа в степень.
9. Введите число 2. Это степень, в которую нужно возвести число (рис. 6.1).
Рис. 6.1. Создание формулы для вычисления площади круга
ПРИМЕЧАНИЕ
Текст в ячейках R1C1 и R1C2 нам нужен только в качестве заголовков столбцов для наглядности. В столбец 1 мы будем вводить значение радиуса круга, а в столбце 2 получать результат (площадь).
ПРИМЕЧАНИЕ
Программа Excel содержит функцию автоматического добавления числа ?, с точностью пятнадцать знаков после запятой. Но о функциях мы поговорим позже.
10. Нажмите клавишу Enter. Формула будет создана, а в ячейке R2C2 появится значение 0.
Мы создали формулу в ячейке R2C2. Щелкните кнопкой мыши на этой ячейке и посмотрите на строку формул. Вы должны увидеть следующую формулу: =3,14*RC[-1]^2. В нашей формуле число 3,14 (?) умножается на значение ячейки, стоящей слева (в этой ячейке мы позже укажем радиус), которое, в свою очередь, возводится в квадрат. В данный момент результат вычисления равен нулю, так как ячейка R2C1 пуста (формула воспринимает это как 0).
Проверим результаты вычисления.
1. В ячейку R2C1 введите 10 и нажмите клавишу Enter. В ячейке R2C2 появится число 314.
2. В ячейку R2C1 введите число 15 и нажмите клавишу Enter. В ячейке R2C2 появится число 706,5.
Как видите, результат вычисления в ячейке R2C2 автоматически обновляется, как только вы вводите новое значение в ячейку R2C1. Иными словами, вы указываете только радиус, все остальное делает Excel по созданной вами формуле. И это, пожалуй, самый простой пример.
В столбце 3 создадим формулу вычисления длины окружности, которая также будет использовать значение радиуса из столбца 1. Формула длины окружности – 2?r.
1. В ячейку R1C3 введите текст Длина окружности.
2. Щелкните кнопкой мыши на ячейке R2C3.
3. Введите знак =.
4. Введите цифру 2.
5. Введите знак умножения (*).
6. Введите число ? (3,14).
7. Введите знак умножения (*).
8. Щелкните кнопкой мыши на ячейке R2C1. В формуле появится относительный адрес первой ячейки, в которой мы указываем радиус. У вас должна получиться формула следующего вида: =2*3,14*RC[-2].
9. Нажмите клавишу Enter. Если в ячейке R2C1 указано какое-либо число, вы немедленно получите результат вычисления длины окружности в ячейке R2C3.
10. Введите новое значение радиуса в ячейку R2C1 и нажмите клавишу Enter. Обратите внимание, что в ячейках R2C2 и R2C3 значения изменились одновременно. Сколько бы вы ни создали формул, использующих значение ячейки R2C1, результат их вычисления будет обновляться при изменении значения в этой ячейке (рис. 6.2).
Рис. 6.2. Формулы в ячейках R2C2 и R2C3 используют значение ячейки R2C1
Приведу арифметические операторы, которые вы можете использовать при создании формул:
+ – оператор сложения;
– – оператор вычитания;
* – оператор умножения;
/ – оператор деления;
^ – оператор возведения в степень. Этот оператор ставится после числа (или переменной), которое возводится в степень. После этого оператора указывается значение степени, которое может быть как числом, так и переменной (переменной в данном случае мы считаем ссылку на ячейку со значением);
% – оператор вычисления процента.
Данный текст является ознакомительным фрагментом.
Читайте также
Математические формулы
Математические формулы
Кирпичи просто создавать, использовать, они понятны и просты, но на протяжении столетий возникло и сформировалось более тонкое понимание систем упорядочения. Эти открытия и нововведения развивали наше понимание сеток. Обращаясь к математике,
Формулы
Формулы
Электронные таблицы не имели бы и сотой доли той популярности, которая есть у них на данный момент, если бы у них не было главного преимущества – возможности работать с формулами, на лету пересчитывая сотни и тысячи введенных значений, подводя промежуточные суммы
1.7. Формулы
1.7. Формулы
Формулой считают любую последовательность не менее чем двух символов, которая не является словом (названием, аббревиатурой) в русском или каком-либо другом языке. Например, «MATLAB» является словом, «/(л:(0))» – нет.Формулы также нумеруются внутри одного раздела.
4.1. Математические формулы
4.1. Математические формулы
В текстовом редакторе Word существует специальный инструмент для работы с формулами – редактор формул. С его помощью можно создавать сложные объекты, выбирая символы с панели инструментов и задавая переменные и числа. При этом размер шрифтов,
«Формулы в формулах»
«Формулы в формулах»
При создании формул вы используете в качестве данных константы и адреса ячеек с данными. Вы можете также указать адреса ячеек, содержащих формулы. Допустим, в вашей таблице есть формула, возвращающая результат какого-то вычисления. Назовем ее
Создание простой графики
Создание простой графики
Вы можете создавать простые графические объекты, используя простые геометрические фигуры, множество шаблонов которых представлено в галерее Фигуры. Можете изменять свойства каждой фигуры (форму, цвет, контур), а также добавлять к ним различные
Формулы
Формулы
Разбить лист на ячейки и разрешить пользователям заполнять их – дело нехитрое. Но возможности Excel этим не ограничиваются. Следующая ступень мастерства – связать отдельные клетки с цифрами невидимыми связями с помощью математических формул. А это значит, что при
16.3. Формулы
16.3. Формулы
Если вы никогда не работали в электронных таблицах с формулами, можете считать, что вы не использовали электронные таблицы вообще. Только хорошо освоив формулы, вы сможете понять всю гибкость и мощь электронных таблиц.Давайте разберемся с самыми простыми
1.7. Формулы
1.7. Формулы
Формулой считают любую последовательность не менее чем двух символов, которая не является словом (названием, аббревиатурой) в русском или каком-либо другом языке. Например, MATLAB является словом, f(x(0)) – нет.Формулы также нумеруются внутри одного раздела. Номер
2.4. Формулы
2.4. Формулы
2.4.1. Формулы в документе, если их более одной, нумеруются арабскими цифрами, номер ставят с правой стороны страницы, в скобках, на уровне формулы.В пределах всего документа или ею частей, в случае деления документа на части, формулы имеют сквозную
14.8. Формулы
14.8. Формулы
Ячейка может содержать не только статическое значение, но и формулу, т. е. значение ячейки будет вычисляться по заданной вами формуле. Давайте сразу перейдем к примерам формул — как говорится, лучше один раз увидеть, чем сто раз
5.2.6. Формулы
5.2.6. Формулы
Формулой называется математическое выражение, начинающееся со знака равенства, которое содержит адреса ячеек, соединенные знаками арифметических операций. Также формула может содержать различные функции, аргументами которых являются как адреса ячеек, так
Формулы
Формулы
Кроме тех типов данных, которые указаны в поле Числовые форматы диалогового окна Формат ячеек (см. рис. 4.23), существует еще один формат данных, который называется формулой и может храниться в ячейке. Этот формат указывает программе Excel, что прежде, чем поместить
Практическая работа 38. Создание простой таблицы
Практическая работа 38. Создание простой таблицы
Задание. Создать таблицу, показанную на рис. 5.70, ввести в ячейки текст и отформатировать его.
Рис. 5.70.Пример простой таблицыПоследовательность выполнения1. Создайте новый документ.2. Вставьте в документ таблицу 5 х 7 с помощью
Практическая работа 44. Создание простой таблицы с формулами
Практическая работа 44. Создание простой таблицы с формулами
Задание. Составить таблицу расчета заработной платы для работников отдела, имея следующие исходные данные: фамилии сотрудников, их часовые ставки и количество отработанных часов.В таблице требуется вычислить:
Вычисление формулы объема и площади в Excel
Программа Excel является лучшим калькулятором. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы. Все их возможности поддерживает программа Excel. Более того, он имеет неоспоримые преимущества.
В некоторых формулах можно выполнить только одно математическое вычисление при калькуляционных расчетах. В таких случаях, если меняются данные нужно изменить формулу. Но если все данные будут распределены по ячейкам, а формула будет только ссылаться на них, то при любых изменениях нет необходимости менять формулу. Одна формула может использоваться многократно. Чтобы понять, как это работает, лучше привести несколько практических примеров.
Как рассчитать объем и площадь в Excel
В ячейке A1 запишем формулу вычисления объема параллелепипеда: a = 6 см; b = 8 см; c = 12 см.
В ячейке A2 запишем формулу вычисления площади круга: r = 25 см.
В ячейке A3 формула содержит безаргументную функцию ПИ(), которая содержит в себе полное число ПИ (а не 3.14). Поэтому значения ячеек A2 и A3 немного отличаются.
Вычисление арифметических формул в Excel
Допустим нам нужно в Excel вычислить формулу:
Чтобы получить результат вычисления ее нужно просто записать в одну строку: =(125*(3+4,5)^2)/(12-3,7).
Данная формула содержит 5 арифметических действий: суммирование, вычитание, умножение, деление и поднесение к степени (^). Если мы записываем все в одно строку, то нужно соблюдать правила арифметической последовательности. Для этого нужно использовать скобки.
Формула для вычисления объема сферы в Excel
Например, нам нужно регулярно вычислить объемы сфер с разными радиусами.
Формула вычисления объема сферы выгладит так:
Предыдущие примеры плохо подходят для решения данной задачи, так как они не используют переменных значений в формулах, а только константы. Из-за этого при смене радиуса нужно переписывать формулу. Но Excel позволяет нам использовать эффективное решение:
- В ячейку B2 запишем формулу вычисления объема сферы в одну строку: =(4/3)*ПИ()*A2^3 (A2 – это ссылка на ячейку).
- В ячейке A2 будем вводить разные радиусы и после каждого ввода в ячейке B2 будем получать результат вычисления объема сфер соответствующих своим радиусам.
Примечание. Если вы используете в Excel многократные вычисления или формулы содержащие ссылки на ячейки в качестве переменных значений, то всегда подписывайте каждую ячейку с входящими данными и формулами. Это позволит избежать ошибок и легко читать значения или результаты вычисления формул.
Урок комбинированный по дисциплинам «Информатика» и «Математика». Вычисление площадей и объемов геометрических фигур в редакторе Excel
Цель урока: Усвоение новых знаний. Формирование знаний об использовании редактора электронных таблиц для решения задач математики. Вычисление площадей и объемов геометрических фигур. Освоение компетенций использования информационно-коммуникативных технологий.
ОКЗ. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.
ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности.
ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями
- формирование знаний об использовании редактора электронных таблиц для решения задач математики;
- вычисление площадей и объемов геометрических фигур.
- развивать логику мышления
- развивать положительные мотивы учебно-познавательной деятельности, интересов, творческой инициативы и активности.
- воспитывать интерес к изучаемой профессии.
- воспитывать такие качеств личности как дисциплины, самостоятельности, трудолюбия, и т.д.;
- воспитывать навыки организации рабочего места.
Оборудование: ПК, проектор, MS Excel 2010.
Тип урока: Комбинированный урок.
- Организационный момент (3 мин).
- Постановка темы и цели урока (3 мин).
- Систематизация знаний и умений по пройденному материалу.
- Опрос учащихся (18 мин).
- Изложение нового материала. Введение понятия математических функций в редакторе электронных таблиц. Вычисление площадей и объемов геометрических фигур. (25 мин.).
- Закрепление полученных знаний (15 мин.).
- Выполнение компьютерного теста (16 мин.)
- Постановка домашнего задания (5 мин.).
- Подведение итогов урока. Выставление оценок (5 мин.).
1. Организационный момент
Цель: Организовать группу, создать обстановку для естественного самовыражения студента.
Вместе с дежурным преподаватель проверяет готовность кабинета к занятию, отмечает отсутствующих.
2. Постановка темы и цели урока.
Цель: Ознакомление с темой урока, постановка проблемы, цели урока.
При постановке проблемы используется ПК для наглядности.
3. Систематизация знаний и умений по пройденному материалу.
Цель: Обобщение и систематизация знаний. Развитие логических умений: сравнивать, выделять главное.
Для подготовки студентов к усвоению нового материала повторяются и систематизируются их знания и умения в процессе устного опроса:
- Сформулируйте, как используется редактор электронных таблиц?
- Как построить таблицу?
- Как образуется адрес ячейки?
4. Изложение нового материала.
Цель: Усвоение новых знаний, создание положительного эмоционального настроя на работу всех студентов.
Преподаватель математики объясняет тему: Вычисление объемов и площадей геометрических фигур на примере цилиндра.
Расчет площади поверхности цилиндра
r- радиус основания
h- высота цилиндра
Формула площади боковой поверхности цилиндра, (Sбок):
Формула площади всей поверхности цилиндра:
Как вычислить объем цилиндра?
Объем цилиндра, (V):
- Создаем новый документ в редакторе электронных таблиц Excel.
- Создаем таблицу вычисления площади и объема цилиндра. Помним, что формула начинается со знака =
Не забываем, что программа использует адреса ячеек в формулах. - Формулы по столбцу распространяем автозаполнением.
- В столбцах D и E таблицы 2 раскрыты формулы редактора электронных таблиц Excel.
Задача. Заданы 3 цилиндра с высотой Н и радиусом основания R. Вычисляем объем фигуры V, площадь боковой поверхности Sб.п.
Таблица 1
Таблица 2
Задание 1: Самостоятельно заполнить столбец F, написать формулу для вычисления Sп.п.
Проверяется правильность выполнения задания с применением таблиц. Приложения 2.
Задание 2: Продолжить таблицу – добавить 3 строки: высота 10, а радиус равен номеру учащегося в журнале.
Задание для опережающих учащихся: по образцу на листе 3 в редакторе Excel создать таблицу вычисления объема и площади боковой поверхности шара (радиус 5 и 10условных единиц).
Закрепление полученных знаний.
Цель: Закрепление нового материала. Обобщение полученных знаний. Формирование умений. Освоение компетенций использования информационно-коммуникативных технологий. Развитие логического мышления. Формирование навыков самоконтроля. Воспитание воли, настойчивости и трудолюбия.
Для закрепления полученных знаний студенты выполняют тест в электронном виде на компьютере по теме “Редактор электронных таблиц Excel”. Приложение 1.
Фронтальным опросом вместе с учащимися подводятся итоги урока:
— сформулируйте, как вычислить объем цилиндра с помощью редактора электронных таблиц;
— сформулируйте, как вычислить площадь боковой поверхности цилиндра с помощью редактора электронных таблиц.
Постановка домашнего задания.
Цель: Закрепление знаний, применение знаний. Развитие умений и навыков. Воспитание воли, настойчивости, трудолюбия. Воспитание самоконтроля.
На дом задается прочитать объяснительный текст параграф 11.4 на странице 248. Учебник “Информатика” Е.В. Михеева. Составить таблицу для подсчета площадей геометрических фигур: треугольника и круга с выбранными произвольно размерами на плоскости в редакторе электронных таблиц, раскрыть формулы.
Подведение итогов урока.
Цель: Выставление оценок студентам, анализ ответов студентов, выяснить, что понравилось (не понравилось) и почему.
Обсудить с детьми, что узнали (чем овладели), что понравилось (не понравилось) и почему, что бы хотелось выполнить еще раз. Выставление оценок (поощрение) при опросе на уроке не только правильного ответа студента, но и анализ того, как студент рассуждал, какой способ использовал, почему и в чем ошибся. Отметка аргументируется по ряду параметров: правильности, самостоятельности, оригинальности.
Создание простой формулы
Создадим первую формулу. Допустим, вы хотите вычислить площадь круга. Конечно, можно взять в руки калькулятор и сделать это. А если вам требуется вычислить площадь круга сто раз при разных значениях радиуса? Представляете, сколько раз вам нужно нажать кнопки калькулятора, при этом записывая куда-то все результаты? Программа Excel может сделать это быстрее.
Итак, всем известно, что площадь круга равняется ?r2, где r – это радиус круга, а ? – константа.
1. Создайте новую книгу Excel или перейдите на чистый лист.
2. В ячейку R1C1 введите текст Радиус, а в ячейку R1C2 – Площадь круга.
3. Щелкните кнопкой мыши на ячейке R2C2. В этой ячейке мы создадим формулу.
4. Введите знак =. Это сообщает программе Excel, что в этой ячейке создается формула.
5. Введите число 3,14. Это число ?, округленное до двух знаков после запятой.
6. Введите знак *. В программе Excel это – знак умножения.
7. Щелкните кнопкой мыши на ячейке R2C1.
Вокруг этой ячейки появится «муравьиная дорожка», а относительный адрес этой ячейки отобразится в создаваемой формуле.
8. Введите знак ^. Это знак возведения числа в степень.
9. Введите число 2. Это степень, в которую нужно возвести число (рис. 6.1).
Рис. 6.1. Создание формулы для вычисления площади круга
ПРИМЕЧАНИЕ
Текст в ячейках R1C1 и R1C2 нам нужен только в качестве заголовков столбцов для наглядности. В столбец 1 мы будем вводить значение радиуса круга, а в столбце 2 получать результат (площадь).
ПРИМЕЧАНИЕ
Программа Excel содержит функцию автоматического добавления числа ?, с точностью пятнадцать знаков после запятой. Но о функциях мы поговорим позже.
10. Нажмите клавишу Enter. Формула будет создана, а в ячейке R2C2 появится значение 0.
Мы создали формулу в ячейке R2C2. Щелкните кнопкой мыши на этой ячейке и посмотрите на строку формул. Вы должны увидеть следующую формулу: =3,14*RC[-1]^2. В нашей формуле число 3,14 (?) умножается на значение ячейки, стоящей слева (в этой ячейке мы позже укажем радиус), которое, в свою очередь, возводится в квадрат. В данный момент результат вычисления равен нулю, так как ячейка R2C1 пуста (формула воспринимает это как 0).
Проверим результаты вычисления.
1. В ячейку R2C1 введите 10 и нажмите клавишу Enter. В ячейке R2C2 появится число 314.
2. В ячейку R2C1 введите число 15 и нажмите клавишу Enter. В ячейке R2C2 появится число 706,5.
Как видите, результат вычисления в ячейке R2C2 автоматически обновляется, как только вы вводите новое значение в ячейку R2C1. Иными словами, вы указываете только радиус, все остальное делает Excel по созданной вами формуле. И это, пожалуй, самый простой пример.
В столбце 3 создадим формулу вычисления длины окружности, которая также будет использовать значение радиуса из столбца 1. Формула длины окружности – 2?r.
1. В ячейку R1C3 введите текст Длина окружности.
2. Щелкните кнопкой мыши на ячейке R2C3.
4. Введите цифру 2.
5. Введите знак умножения (*).
6. Введите число ? (3,14).
7. Введите знак умножения (*).
8. Щелкните кнопкой мыши на ячейке R2C1. В формуле появится относительный адрес первой ячейки, в которой мы указываем радиус. У вас должна получиться формула следующего вида: =2*3,14*RC[-2].
9. Нажмите клавишу Enter. Если в ячейке R2C1 указано какое-либо число, вы немедленно получите результат вычисления длины окружности в ячейке R2C3.
10. Введите новое значение радиуса в ячейку R2C1 и нажмите клавишу Enter. Обратите внимание, что в ячейках R2C2 и R2C3 значения изменились одновременно. Сколько бы вы ни создали формул, использующих значение ячейки R2C1, результат их вычисления будет обновляться при изменении значения в этой ячейке (рис. 6.2).
Рис. 6.2. Формулы в ячейках R2C2 и R2C3 используют значение ячейки R2C1
Приведу арифметические операторы, которые вы можете использовать при создании формул:
+ – оператор сложения;
– – оператор вычитания;
* – оператор умножения;
/ – оператор деления;
^ – оператор возведения в степень. Этот оператор ставится после числа (или переменной), которое возводится в степень. После этого оператора указывается значение степени, которое может быть как числом, так и переменной (переменной в данном случае мы считаем ссылку на ячейку со значением);
% – оператор вычисления процента.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Математические формулы
Математические формулы Кирпичи просто создавать, использовать, они понятны и просты, но на протяжении столетий возникло и сформировалось более тонкое понимание систем упорядочения. Эти открытия и нововведения развивали наше понимание сеток. Обращаясь к математике,
Формулы
Формулы Электронные таблицы не имели бы и сотой доли той популярности, которая есть у них на данный момент, если бы у них не было главного преимущества – возможности работать с формулами, на лету пересчитывая сотни и тысячи введенных значений, подводя промежуточные суммы
1.7. Формулы
1.7. Формулы Формулой считают любую последовательность не менее чем двух символов, которая не является словом (названием, аббревиатурой) в русском или каком-либо другом языке. Например, «MATLAB» является словом, «/(л:(0))» – нет.Формулы также нумеруются внутри одного раздела.
4.1. Математические формулы
4.1. Математические формулы В текстовом редакторе Word существует специальный инструмент для работы с формулами – редактор формул. С его помощью можно создавать сложные объекты, выбирая символы с панели инструментов и задавая переменные и числа. При этом размер шрифтов,
«Формулы в формулах»
«Формулы в формулах» При создании формул вы используете в качестве данных константы и адреса ячеек с данными. Вы можете также указать адреса ячеек, содержащих формулы. Допустим, в вашей таблице есть формула, возвращающая результат какого-то вычисления. Назовем ее
Создание простой графики
Создание простой графики Вы можете создавать простые графические объекты, используя простые геометрические фигуры, множество шаблонов которых представлено в галерее Фигуры. Можете изменять свойства каждой фигуры (форму, цвет, контур), а также добавлять к ним различные
Формулы
Формулы Разбить лист на ячейки и разрешить пользователям заполнять их – дело нехитрое. Но возможности Excel этим не ограничиваются. Следующая ступень мастерства – связать отдельные клетки с цифрами невидимыми связями с помощью математических формул. А это значит, что при
16.3. Формулы
16.3. Формулы Если вы никогда не работали в электронных таблицах с формулами, можете считать, что вы не использовали электронные таблицы вообще. Только хорошо освоив формулы, вы сможете понять всю гибкость и мощь электронных таблиц.Давайте разберемся с самыми простыми
1.7. Формулы
1.7. Формулы Формулой считают любую последовательность не менее чем двух символов, которая не является словом (названием, аббревиатурой) в русском или каком-либо другом языке. Например, MATLAB является словом, f(x(0)) – нет.Формулы также нумеруются внутри одного раздела. Номер
2.4. Формулы
2.4. Формулы 2.4.1. Формулы в документе, если их более одной, нумеруются арабскими цифрами, номер ставят с правой стороны страницы, в скобках, на уровне формулы.В пределах всего документа или ею частей, в случае деления документа на части, формулы имеют сквозную
14.8. Формулы
14.8. Формулы Ячейка может содержать не только статическое значение, но и формулу, т. е. значение ячейки будет вычисляться по заданной вами формуле. Давайте сразу перейдем к примерам формул — как говорится, лучше один раз увидеть, чем сто раз
5.2.6. Формулы
5.2.6. Формулы Формулой называется математическое выражение, начинающееся со знака равенства, которое содержит адреса ячеек, соединенные знаками арифметических операций. Также формула может содержать различные функции, аргументами которых являются как адреса ячеек, так
Формулы
Формулы Кроме тех типов данных, которые указаны в поле Числовые форматы диалогового окна Формат ячеек (см. рис. 4.23), существует еще один формат данных, который называется формулой и может храниться в ячейке. Этот формат указывает программе Excel, что прежде, чем поместить
Практическая работа 38. Создание простой таблицы
Практическая работа 38. Создание простой таблицы Задание. Создать таблицу, показанную на рис. 5.70, ввести в ячейки текст и отформатировать его. Рис. 5.70.Пример простой таблицыПоследовательность выполнения1. Создайте новый документ.2. Вставьте в документ таблицу 5 х 7 с помощью
Практическая работа 44. Создание простой таблицы с формулами
Практическая работа 44. Создание простой таблицы с формулами Задание. Составить таблицу расчета заработной платы для работников отдела, имея следующие исходные данные: фамилии сотрудников, их часовые ставки и количество отработанных часов.В таблице требуется вычислить:
Общая формула
=2*PI()*A1
Резюме
Чтобы вычислить длину окружности круга, вы можете использовать функцию PI. В показанном примере формула в C5, скопированная, имеет следующий вид:
=PI()*B5^2
который вычисляет длину окружности с радиусом, указанным в столбце B.
Объяснение
В геометрии длина окружности радиуса (r) определяется по следующей формуле: = 2πr
Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π представлено в формуле с функцией PI, которая возвращает число 3,14159265358979 с точностью до 15 цифр.
=PI() // returns 3.14159265358979
Следовательно, формула для вычисления длины окружности с радиусом 3:
=2*PI()*3 // returns 18.85
А формула для вычисления длины окружности на основе значений радиуса в столбце B:
=2*PI()*B5
Вычисления на рабочем листе
Вычисление
– это процесс расчета формул с последующим
выводом результатов в виде значений в
ячейках, содержащих формулы. При изменении
значений в ячейках, на которые ссылаются
формулы, Excel обновляет
значения (выполняет повторное вычисление)
этих формул. Этот процесс называется
пересчетом, он затрагивает только те
ячейки, которые содержат ссылки на
изменившиеся ячейки.
Проектирование расчетов на рабочем
листе
Задание 1.
Вычисление элементов треугольника.
Даны
три стороны треугольника а, b,
с. Требуется вычислить по формуле
Герона площадь треугольника:

= p (p – a) (p – b) (p –
c),
где
полупериметр p равен:
|
p = |
a + b |
|
2 |
радиус
вписанной окружности r равен:
|
r = |
S |
|
p |
радиус
описанной окружности R равен:
|
R = |
abc |
|
4S |
-
Откройте
книгу Упражнения.xlsx. -
Добавьте
в книгу новый лист, переименуйте его в
Упр.11. -
В ячейки
В2, В3, В4 введите числа и присвойте им
соответствующие имена из левого столбца
(рис. 11.1).
Рис. 11.1. Исходные
данные
Обратите
внимание, какое имя получила ячейка
В4. Это связано с тем, что имена c и r
в Excel зарезервированы: c (column) –
столбец, r (row) – строка. Поэтому
Excel ввел в имя символ подчеркивания –
с_.
-
В ячейке
В8 вычислите площадь по предложенной
выше формуле. -
Задайте
длину стороны а, равную 10. В ячейках
с результатами появится сообщение об
ошибке – #ЧИСЛО! Дело в том, что стороны
10, 4, 5 не образуют треугольника. При
вычислении площади под корнем получается
отрицательное число. -
Необходимо
переделать формулы таким образом, чтобы
пользователь получал сообщение, почему
не могут быть вычислены значения S,
R и r, а в ячейках с результатами
вычислений R и r ничего не должно
выводиться. -
В ячейке
В7 отдельно вычислите подкоренное
выражение. Анализ подкоренного выражения
можно выполнить с помощью функции
ЕСЛИ(). Если подкоренное выражение
получится положительным, вычислите S,
R и r. Если же нет, то в ячейке В8 введите
текстовую строку «Это не треугольник!»,
а в ячейках В10 и В12 выведите пустые
строки (рис. 11.2).
Рис.11.2. Формулы с
учетом аналиа подкоренного выражения
Задание
2. Самостоятельно выполните следующие
примеры.
-
Вычислите
сторону треугольника а по
заданному R = 3. Используйте команду
Подбор параметра. -
Вычислите углы
треугольника А, В, С (по теореме
косинусов), используя функцию ACOS().
В результате углы будут вычислены
в радианах.A =
arccos
b2 + c2 – a2
2bc
-
Переведите
углы, вычисленные в радианах в
градусы, используя функцию ГРАДУСЫ().
Вычислите отдельно сумму углов для
углов треугольника, выраженных в
радианах и в градусах соответственно
(рис. 11.3).
Рис. 11.3. Вычсление
углов треугольника
-
Вычислите
длину и площадь окружности по
заданному радиусу R по следующим
формулам: R2
и 2R. -
Вычислите
расстояние между двумя точками на
плоскости, заданными своими
координатами (рис. 11.4) по следующей
формуле: (Х2-Х1)^2+(Y2-Y2)^2.
В формуле должны быть использованы
имена координат.
Рис. 11.4. Коордитаты
точек
-
Вычислите
общее сопротивление трех параллельных
сопротивлений по формуле
|
R = |
1 |
|||
|
1 |
+ |
1 |
+ |
1 |
|
R1 |
R2 |
R3 |
Лабораторная работа 6. Проектирование
расчетов
на рабочем листе
Откройте
книгу Лабораторные работы.xls и на
листе Лаб_6 выполните следующие
задания.
Задание
1. Дан прямоугольный параллелепипед
со сторонами a, b, c. Вычислить:
-
Объем
V = abc
-
Площадь
поверхности
S = 2(ab + bc + ac)
-
Длину
диагонали

= a2 + b2
+ c2
-
Угол
между диагональю и плоскостью основания
=arctg
(c
)
a2 + b2 -
Угол
между диагональю и боковым ребром =
—
2
-
Объем
шара, диаметром которого является
диагональ,
|
Vш |
d3 |
|
6 |
Задание
2. В правильной четырехугольной
пирамиде заданы: длина стороны основания
а и высота h. Вычислить:
-
Объем
|
V = |
a2h |
|
3 |
-
Угол
наклона бокового ребра к плоскости
основания =
arctg
h
2a
-
Радиус
описанного около пирамиды шараR =
2h2
+ a24h
-
Угол
наклона боковой грани к основанию =
arctg
2h
a
-
Радиус
вписанного в пирамиду шараr =
a
tg
2
2
-
Площадь
полной поверхности пирамиды
|
S = |
3 V |
|
r |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
Группа: Друзья Ранг: Старожил Сообщений: 1762
Замечаний: |
Даны диаметр D и длина хорды X. Найти длину дуги:
L = D arcsin(X/D) = 2*R*asin(X/(2*R))
Не забудьте проверить то, что длина хорды не превосходит диаметр.
Думаю, подставить ссылки в формулу вы способны…
Skype: andre.tm.007
Donate: Qiwi: 9517375010
Сообщение отредактировал AndreTM — Суббота, 06.06.2015, 07:12


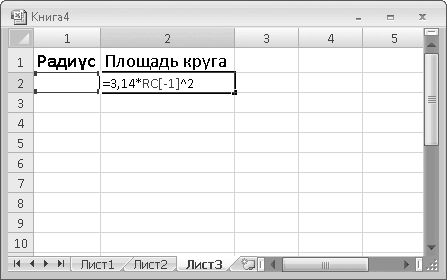
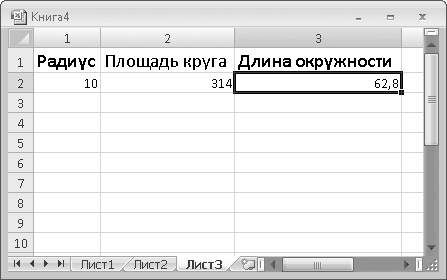
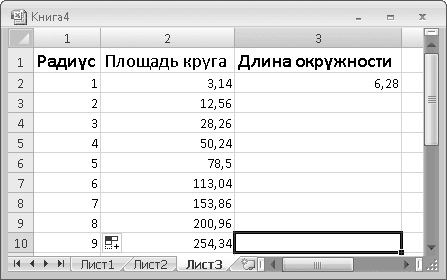
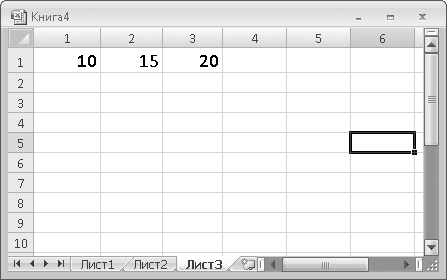

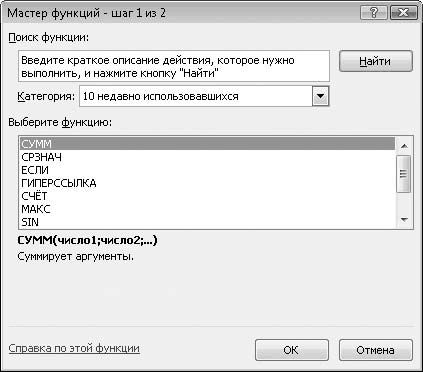
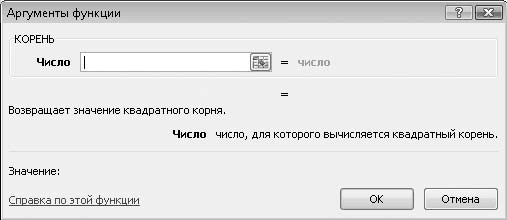
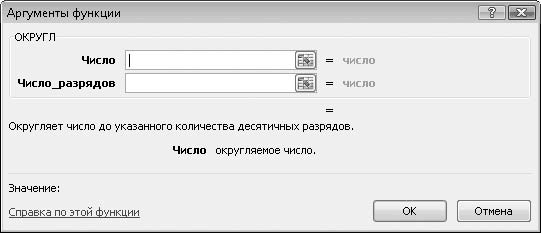
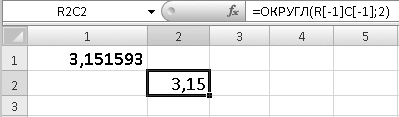



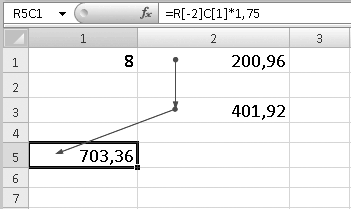



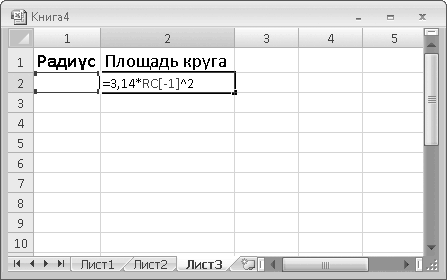
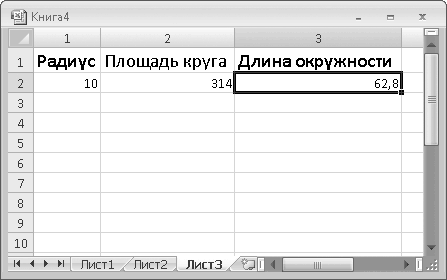
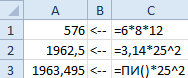
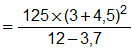
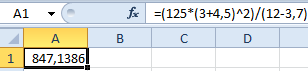
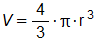





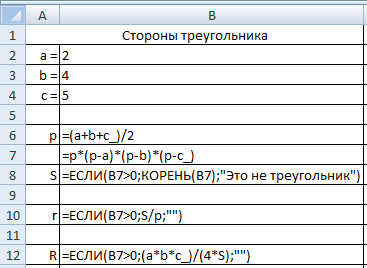
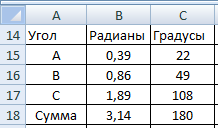
 Вычислите
Вычислите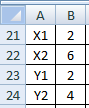

 Угол
Угол