производственными травмами, чем на заводе № 2, а число дней с временной утратой трудоспособности в связи с инфекциями кожи и подкожной клетчатки, гриппом, фарингитом и тонзиллитом выше на заводе № 2.
Исследователь не учел, что экстенсивный показатель характеризует состав только конкретной совокупности и различия в этих совокупностях могут быть обусловлены как разницей в общем абсолютном числе дней временной нетрудоспособности на этих заводах так и различными размерами (абсолютными величинами) каждого конкретного явления в каждой совокупности.
Для того чтобы сделать правильный вывод при сравнении структур временной нетрудоспособности на этих заводах необходимо отдельно проанализировать совокупность и описать ее, определив ранговое место каждого заболевания в структуре числа дней с временной утратой трудоспособности.
ВНИМАНИЕ! При сравнении 2-х и более совокупностей или одной в динамике по экстенсивному показателю выводы можно делать только по каждой конкретной совокупности, определив приоритетность составных частей данной совокупности по величине удельного веса.
Более детальный сравнительный анализ проводится при применении интенсивных показателей, характеризующих частоту конкретных явлений в конкретной среде.
В качестве примера рассмотрим расчет структуры первичной заболеваемости (в %) и первичной заболеваемости (на 1000 населения) сельского административного района в электронных таблицах Excel. после ввода первичных данных – абсолютного количества заболеваний (Рис. 1) – с помощью мыши выделяем ячейки С3:С21 и нажатием на правую кнопку мыши вызываем контекстное меню, в котором выбираем пункт «Формат ячеек» (Рис. 2).
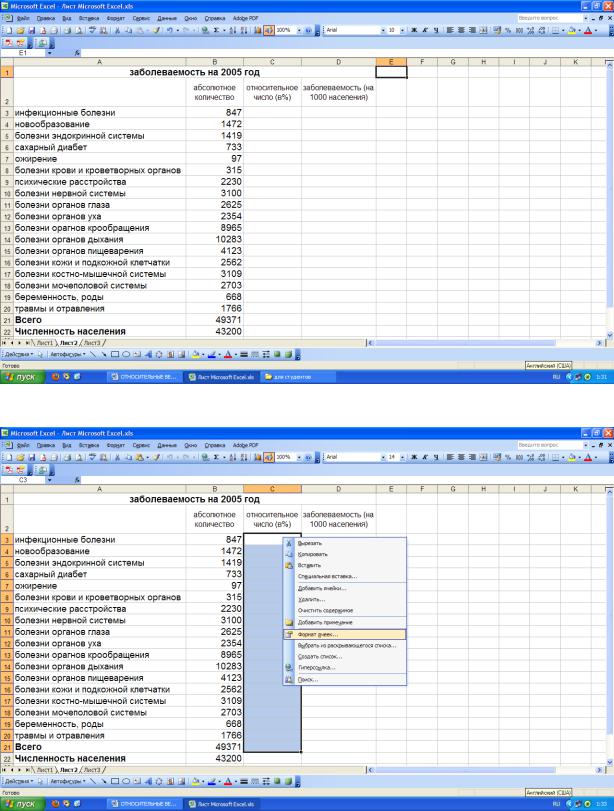
Рис. 1. Таблица с введенными данными количества первичных заболеваний
Рис. 2. Выбор пункта «Формат ячеек» в контекстном меню Далее в подразделе «Число» выбираем процентный формат ячеек и
устанавливаем необходимое количество знаков после запятой (Рис. 3), после чего нажимаем кнопку ОК.
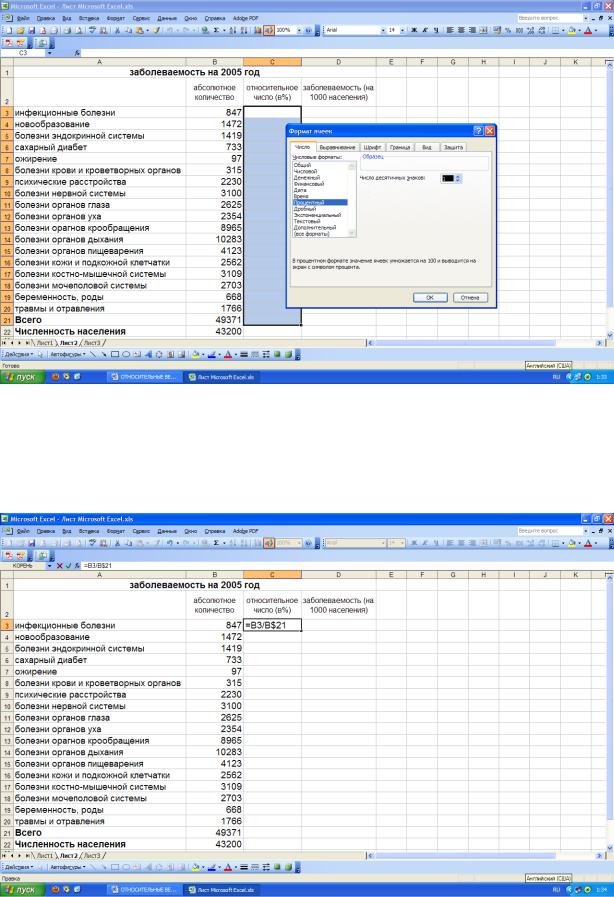
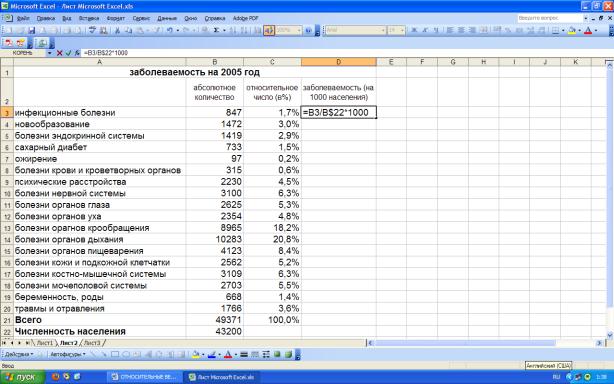
Рис. 3. Установка процентного формата ячеек В ячейку С3 вводим формулу деления количества инфекционных
болезней на обще количество заболеваний В3/В$21 (знак $ означает неизменный адрес строки) и нажимаем клавишу ввода. В ячейке появляется результат, представляющий процентную (%) долю инфекциооных заболеваний в общем количестве заболеваний (Рис.4).
Рис. 4. Ввод формулы в ячейку Далее устанавливаем курсор на ячейку С3 с формулой и копируем ее
содержимое, вызвав контекстное меню нажатием правой кнопки мыши и
выбрав соответствующий пункт. выделяем мышью ячейку С3:С21 и вводим в
них скопированную формулу, используя пункт «Вставить» главного меню или контекстного меню, вызванного нажатием правой кнопки мыши. после нажатия клавиши ввода получаем заполненный столбец таблицы с результатами расчета структуры заболеваемости (в %) (экстенсивные показатели).
Для расчета интенсивных показателей заболеваемости на 1000 населения выделяем и форматируем ячейки D3:D21 в числовом формате и вводим в ячейку D3 формулу расчета для инфекционных болезней деление абсолютного числа заболеваний на общее число жителей района,
умноженное на 1000 (В3/В$22*1000) (Рис. 5).
Рис. 5. Ввод формулы показателя заболеваемости на 1000 населения
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Цель:
- Обучающая: Формировать умение обработки
статистических данных с помощью информационных
технологий. - Развивающая: способствовать развитию
логического мышления, практических навыков
работы с ПК. - Воспитательная: способствовать
формированию уважительного отношения к
преподавателю, предмету, друг к другу;
воспитывать организованность, деловитость,
самостоятельность.
Вид урока: урок изучения нового
материала
Тип урока: комбинированный
Методы проведения урока:
- Методы организации и осуществления учебной
деятельности: словесные, наглядные,
практические. - Методы стимулирования и мотивации:
мотивационные установки, оценка.
Форма обучения: фронтальная,
индивидуальная.
Оборудование урока: мультимедийный
проектор, компьютеры, раздаточный материал на
каждого студента.
Ход урока
| № п/п | Структурные элементы урока |
Деятельность преподавателя |
Деятельность студентов |
| 1. | Организационный этап | Приветствие, проверка готовности группы к занятию, организация внимания |
Проверяют свою готовность к уроку |
| 2. | Целевая установка, мотивация | Сообщение темы.
Преподаватель Задаёт вопрос в каком случае лучше усваивается Разъяснение целей урока. |
Восприятие разъяснений преподавателя, отвечают на вопрос преподавателя |
| 3. | Этап повторения изученного материала |
Преподаватель проводит опрос студентов о видах статистических величин и формулах для их вычисления: Назовите виды Дать краткую характеристику статистическим Назовите формулы для вычисления величин Преподаватель акцентирует внимание на не |
Отвечают на вопросы преподавателя. |
| 4. | Актуализация | Преподаватель обращает внимание студентов на то, что большинство статистических данных обобщается с помощью MS Excel; данную программу также используют для графического представления статистических данных. Преподаватель организует проблемную |
Воспринимают разъяснение преподавателя. |
| 5. | Этап сообщения новых знаний | Статистические функции программы MS Excel Определение функции Excel Статистические функции: определение и значение Ввод функций и определение аргументов функции: Решение задачи с применением статистических |
студенты воспринимают разъяснение преподавателя и отвечают на вопросы по ходу рассказа |
| 4. | Этап закрепления | Преподаватель предлагает обобщить изученный материал и приступить к решению задачи в табличном редакторе. Преподаватель Преподаватель предлагает вспомнить этапы |
Студенты самостоятельно открывают табличный редактор и выполняют задания на закрепление пройденного материала Слушают |
| 5. | Подведение итогов | Диалог со студентами, выявление трудностей |
Студенты подводят итог работы, проводят самооценку |
| 6. | Оценка деятельности студентов |
Преподаватель делает выводы по уроку, комментирует и оценивает работу студентов. |
Студенты принимают участие в подведении итогов урока. |
Литература:
- Безручко В.Т. Практикум по курсу “Информатика”
М.2002-272с. - Златопольский Д.М. 1700 заданий по Microsoft Excel
СПб.2003-544с. - Могилёв А.В. и др. Практикум по информатике: Учеб.
Пособие для высш. учеб. Заведений. М. 2001-608с. - Практикум по технологии работы на компьютере
под ред. Макаровой Н.В. М. 2003-256С. - Сафронов И.К. Задачник-практикум по информатике
СПб. 2002-432с. - Кодле Я.К. Практикум по статистике. М.:Высшая
школа 1991. - Иванков В.И. Сборник лекций по статистике М.2001.
- Толстик Н.В., Матегорина Н.М. Статистика Ростов-
на Дону: Феникс 2001. - Годин А.М. Статистика М.: 2003.
План-конспект
Организационный момент (1-2мин)
Здравствуйте дети, уважаемые коллеги и гости.
Приготовим ручки и тетради, подготовим рабочее
место к занятию
Целевая установка (1-3 мин)
Тема сегодняшнего занятия “Статистические
функции в MS Excel”
Цель нашего занятия:
Формировать умение обработки статистических
данных с помощью информационных технологий.
Мотивация (5-7 мин)
Ответьте на вопрос (преподаватель читает очень
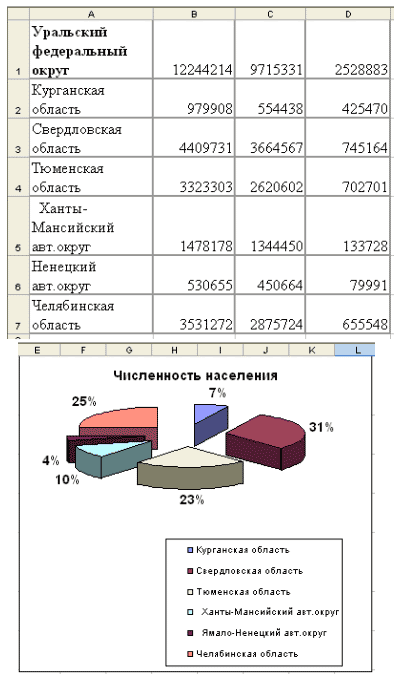
быстро): На территории Уральского федерального
округа проживает 12244214человек. Из них в
Курганской области 979908 человек, в Свердловской
области 4409731 человек, в Тюменской области
3323303человека, в Ханты-Мансийском округе 1478178
человек, в Ямала-Ненецком автономном округе 530655
человек, в Челябинской области3531272 человека.
Какая из областей наиболее многочисленна?
Посмотрите на экран, где представлены данные в
виде таблицы и диаграммы (Приложение
1).
В каком случае лучше усваивается информация и
почему?
Графическая информация усваивается лучше,
благодаря наглядности.
Цель нашего урока: научиться обрабатывать
статистические данные с помощью программы MS Excel.
Повторение изученного материала.
Давайте вспомним, какие виды статистических
величин вы знаете:
- Абсолютные величины.
- Относительные величины.
- Средние величины.
Дайте краткую характеристику данных величин.
Какие величины не были названы?
Какие ошибки были замечены в ответах?
Актуализация.
Ребята, я предлагаю вам решить задачу с помощью
компьютера. (Приложение 2), (Приложение 3), (Приложение
4).
Я попрошу трех человек быть помощниками –
консультантами. По ходу выполнения задания
консультанты будут помогать вам, а в конце работы
выставят оценки.
Ребята, вы посмотрели задачу, можете ли вы
приступить к решению?
Нет, поэтому сейчас я вам расскажу, как
выполнить решение.
Сообщение новых знании (Приложение
5).
Функция. В общем случае — это переменная
величина, значение которой зависит от
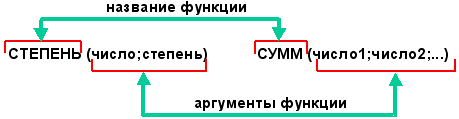
аргументов. Функция имеет имя (например, СТЕПЕНЬ,
СУММ) и, как правило, аргументы, которые записываются
в круглых скобках следом за именем функции.
Скобки — обязательная принадлежность функции,
даже если у нее нет аргументов. Если аргументов
несколько, один аргумент отделяется от другого
запятой. В качестве аргументов функции могут
использоваться числа, адреса ячеек, диапазоны
ячеек, арифметические выражения и функции.
Excel предлагает большой (несколько сотен) набор
стандартных (встроенных) функций, которые можно
использовать в формулах, например:
математические, финансовые, статистические,
текстовые, логические и многие другие.
Ввод функций можно осуществить несколькими
способами
Способ 1
Выбор функции из списка функций
использовавшихся последними (список появляется
при входе в режим ввода формул)
Имя функции выбирается из списка
Если в списке нет нужной функции, выберите
Другие функции, чтобы перейти в окно Мастер
функций
Способ 2
Для упрощения ввода функций в Excel предусмотрен
специальный Мастер функций, который можно
вызвать либо нажатием кнопки 
на панели инструментов
“Стандартная” или в строке формул, либо
командой Вставка, Функция…
Для поиска функции опишите действие, которое
она должна выполнить и нажмите Найти
Если функция известна, сначала выбирается
категория, затем имя функции
Можно просмотреть синтаксис выбранной функции
и прочитать её краткое описание
Способ 3
Непосредственный ввод функции вручную в строке
формул. Этот способ используется редко, т.к. это
достаточно трудно запомнить все имена функций
Если функция вводится не вручную, то для ввода
аргументов используется диалоговое окно
Аргументы функций, с помощью которого можно не
только ввести данные, но и увидеть значения
аргументов, результат вычисления значения
функции, краткое описание текущей функции и
текущего аргумента.
При обработке данных довольно часто возникает
необходимость определения различных
статистических характеристик. Поэтому в состав
Excel встроен ряд функций, применяемых при решении
задач статистического анализа. Сегодня на уроке
мы познакомимся с некоторыми статистическими
функциями, которые вам понадобятся для решения
задачи
СРЗНАЧ (число 1; число 2;…) соответствует
среднему значению в статистике – возвращает
среднее значение аргументов
МАКС (число 1; число 2;…) соответствует
максимальному значению в статистике –
возвращает наибольшее значение в списке
аргументов
МИН (число 1; число 2;…) соответствует
минимальному значению в статистике – возвращает
наименьшее значение в списке аргументов
РАНГ (число, ссылка, порядок) – возвращает ранг
числа в списке чисел: его порядковый номер
относительно других чисел в списке (есть
показатели, каждому из них присваивается место)
А сейчас я покажу использование данных функций
на практическом примере (Приложение 6).
Ваша задача внимательно слушать, наблюдать за
моими действиями (преподаватель показывает с
помощью проектора решение задачи, а студенты
смотрят). Также у вас на столах лежат опорные
конспекты (Приложение 7), и по ходу
рассказа я буду делать на них ссылки.
Посмотрите на задачу здесь представлены
названия стран, площадь страны, население,
плотность.
Первое что мы должны сделать это рассчитать
среднюю плотность населения. Для этого
используем первый способ ввода функции (схема 1).
В строке формул ставим знак =. Обратите внимание,
что вместо поля имени появляется поле функции и
из списка выбираем нужную нам функцию это СРЗНАЧ.
В появившееся окне в поле Число 1 необходимо
указать блок ячеек для подсчёта среднего в нашей
таблице и нажимаем ОК (схема 2).
Затем мы должны найти максимальную плотность.
Для этого используем второй способ ввода функции
(схема 3). Данный способ заключается в
использовании мастера функции. Выберете в окне
мастера функций в поле Категория Статистические.
В списке Функция выберите строку МАКС и щёлкните
ОК. В появившееся окне в поле Число 1 необходимо
указать блок ячеек для подсчёта максимального в
нашей таблице и нажимаем ОК (схема 4)
Дальше мы должны найти минимальную плотность.
Для этого мы используем третий способ (схема 5).
Необходимо в строке формул поставить знак = с
клавиатуры ввести имя функции МИН поставить (и
указать блок ячеек для подсчёта минимального
значения, закрыть ( и нажать ОК.
И последнее нам необходимо расставить страны
по местам, в зависимости от плотности населения.
Нажимаем кнопку вставка функций в строке формул.
Выберете в окне мастера функций в поле Категория
Статистические. В списке Функция выберите строку
РАНГ и щёлкните ОК. В появившееся окне в поле
Число необходимо указать значение для которого
определяется ранг это у нас число в ячейке Е2. В
поле Ссылка необходимо указать блок ячеек для
подсчёта максимального в нашей таблице и
нажимаем ОК (схема 6)
Закрепление
Мы рассмотрели статистические функции, которые
вам понадобятся для решения задач.
Вы можете приступать к работе, если у вас
возникнут трудности при решении задач, вы можете
воспользоваться помощью консультантов.
Студенты решают задачи.
При решении различных задач, подготовке
отчётов нередко возникает необходимость
графического представления числовых данных.
Основное достоинство такого представления –
наглядность.
Давайте вернёмся к нашей задаче (которую решали
при объяснении статистических функций) и
вспомним основные этапы построения диаграмм. Нам
необходимо будет построить диаграмму,
отражающую плотность населения каждой страны.
Для построения диаграммы обычно используется
Мастер диаграмм
Необходимо выделить ячейки, содержащие данные,
которые должны быть отражены в диаграмме
Необходимо выбрать команду меню
Вставка/Диаграмма или кнопку на панели
инструментов, а затем следовать инструкциям
мастера:
Шаг 1. Выбор типа диаграммы
Шаг 2. Выбор исходных данных для диаграммы: если
данные не выбраны перед шагом один, то выделите
столбцы и строки с необходимыми данными и
щелкните по кнопке Далее.
Шаг 3. Задание параметров диаграммы: выполните
необходимые настройки параметров, используя
вкладки Заголовки, Оси, Линии сетки, Легенда,
Подписи данных, Таблицы данных, затем щелкните на
кнопке Далее.
Шаг 4. Размещение диаграммы: определите место
для диаграммы и щелкните на кнопке Готово.
Ребята, вы можете приступить к построению
диаграмм для своей задачи, если возникают
трудности, то вы можете обратиться к блок –
схеме.
Оценка деятельности
Заканчиваем работу, студенты – консультанты,
прошу подвести итоги по решению задачи в
соответствии с критериями оценки (Приложение
8).
Прошу I консультанта предоставить отчет о
работе студентов, решавших первую задачу.
Посмотрим на лучшую работу, преподаватель
проводит оценку работы.
Прошу II консультанта предоставить отчет о
работе студентов, решавших вторую задачу.
Посмотрим на лучшую работу, консультант
проводит оценку работы, в соответствии с
критериями оценки первой работы.
Прошу III консультанта предоставить отчет о
работе студентов, решавших третью задачу.
Посмотрим на лучшую работу, консультант
проводит оценку работы; преподаватель
спрашивает консультанта другой группы, согласен
ли он с оценкой.
Подведение итогов
Ребята, вы решили задачу. Обратите внимание на
экран (Приложение 9), где
представлены статистические данные за 2007 год.
Можно сделать вывод, что почти 10% населения
города является не здоровыми. Наша с вами задача,
сделать так, чтобы данный процент с каждым годом
становился меньше. И в заключении мне бы хотелось
прочитать вам стихотворение
Что есть жизнь — это вечный вопрос,
Но решать его надо всерьез.
Жизнь прекрасна и бесконечна,
Если только она человечна!Посмотри! Как прекрасна земля!
Реки, горы, леса и поля
Это все – наша жизнь и вовек
Ты в ответе за жизнь человек!Но какая-то страшная сила
Человеческий разум затмила,
Краски радуги тьмой заменила,
И шагаем мы в бездну уныло.Мы забыли, зачем родились
Что перед нами прекрасная жизнь
Человек! Взрослый ты иль дитя,
Жизнь одна только есть у тебя,
Ты в ответе один за себя!Кто сказал, что все надо попробовать?
Кто сказал, что все надо познать?
Нужно верную выбрать дорогу,
Чтобы твердо по жизни шагать!
Оценка деятельности студентов
Преподаватель благодарит за работу, выставляет
оценки
Примеры формул для анализа инвестиционных проектов и расчета финансовых планов по показателям финансовой деятельности фирмы.
Формулы для финансового анализа данных
Строка формул в Excel ее настройки и предназначение.
Как использовать строку формул и какие преимущества предоставляет для ввода и редактирования данных в ячейках? Как включить или отключить строку формул в настройках программы.
Работа в Excel с формулами и таблицами для чайников.
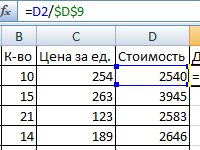
Формулы в Excel для чайников: правила введения, операторы, использование абсолютных и относительных ссылок. Как задать формулу для столбца? Автозаполнение таблиц.
Как посчитать процент от суммы чисел в Excel.
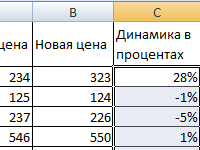
Как найти процент от числа, от суммы чисел, разницу в процентном отношении? Умножение, сложение и другие действия; расчет процентов по кредиту с помощью функций и формул.
Ссылка на ячейку в другом листе Excel.
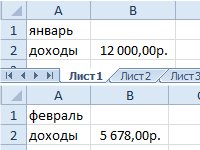
Ссылки в формулах сразу на несколько листов. Синтаксис ссылки на ячейку в другом файле xlsx. Разбор и описание сложных ссылок на другие листы и книги.
Вычисление формулы объема и площади в Excel.
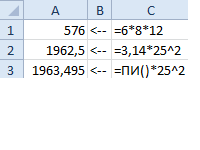
Быстрый и многократный расчет арифметических формул для вычисления объема или площади для разных геометрических фигур в большом количестве.
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Размах вариации
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Простая формула для расчета объема выборки
- Пример расчета объема выборки
- Задачи о генеральной доле
- По части судить о целом
- Как рассчитать объем выборки
- Как определить статистические выбросы и сделать выборку для их удаления в Excel
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- СРЗНАЧ()
- СРЗНАЧЕСЛИ()
- МАКС()
- МИН()
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.
Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;
p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = (1 – p);
e – допустимая ошибка, в долях.
Пример расчета объема выборки
Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A:
где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле
|
Гипотеза |
H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |  |
 |
| Статистика K |  |
 |
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет 
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле 
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. 
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка 
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет 
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности 
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку: 
где n=40, N = 365 (дней). Отсюда 
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193
Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства 
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при
достаточном числе наблюдений
. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:
С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.
Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.
Как рассчитать объем выборки
Достаточный размер выборки зависит от следующих составляющих:
- изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
- размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
- уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)
ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента
Формулы для расчета объема выборки:
Формулы расчета объема выборки
Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.
График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.
Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:
Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Способ 1: применение расширенного автофильтра
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
Источники
- https://lumpics.ru/descriptive-statistics-in-excel/
- https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
- https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
- http://galyautdinov.ru/post/formula-vyborki-prostaya
- https://math.semestr.ru/group/interval-estimation-share.php
- https://tidydata.ru/sample-size
- https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
- https://lumpics.ru/how-to-make-a-sample-in-excel/
- https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html
17 авг. 2022 г.
читать 2 мин
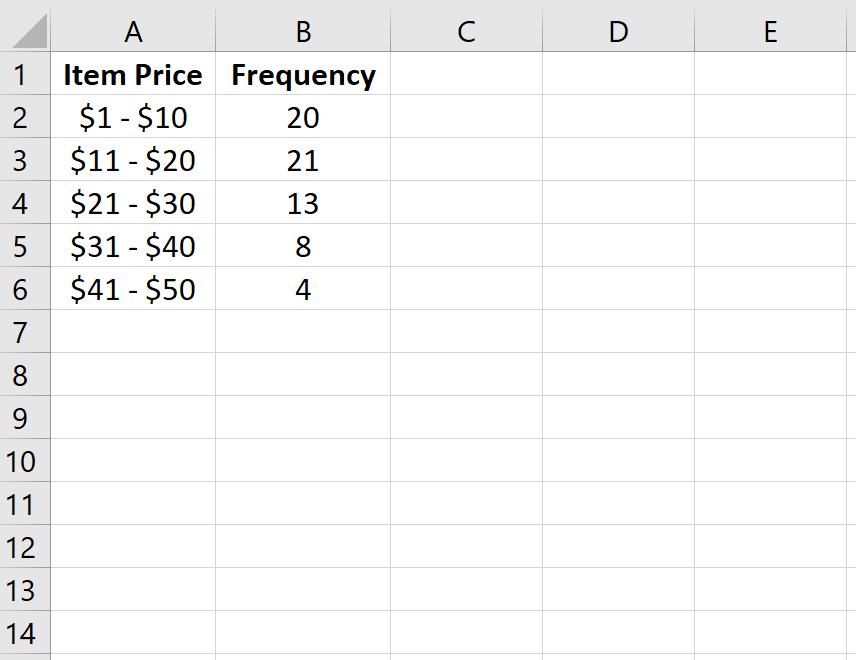
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например , в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
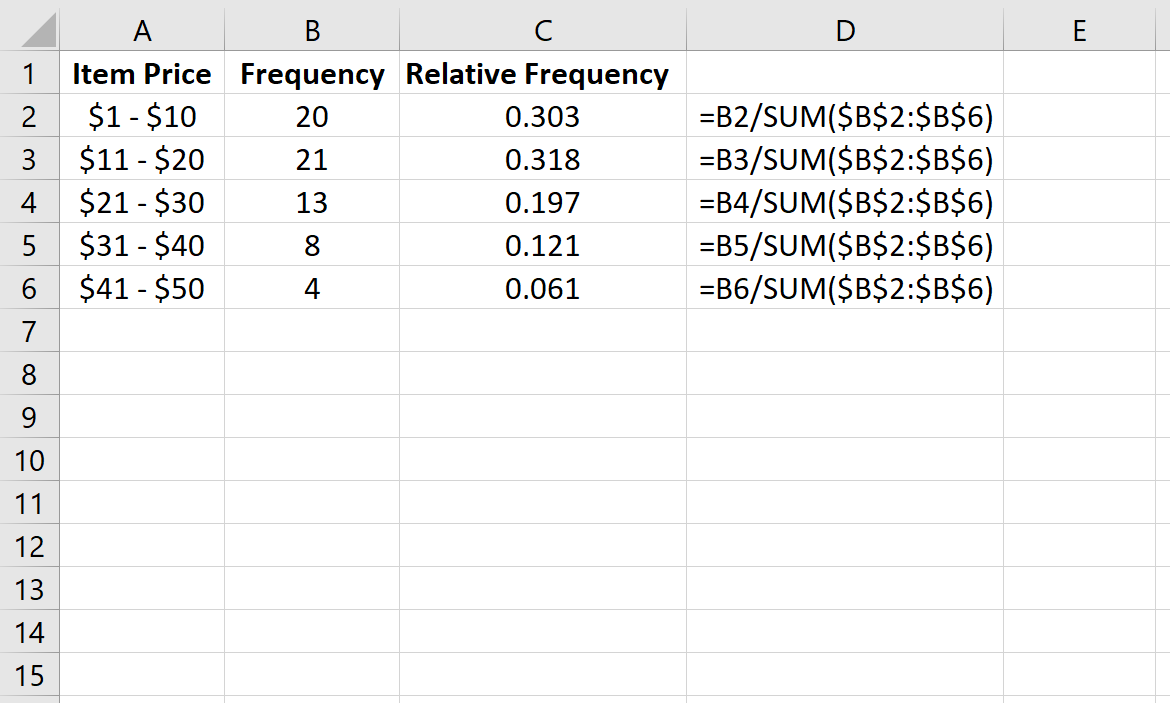
Также можно рассчитать относительную частоту для каждого класса, которая представляет собой просто частоту каждого класса в процентах от целого.
| Цена товара | Частота | Относительная частота | | — | — | — | | $1 – $10 | 20 | 0,303 | | $11 – $20 | 21 | 0,318 | | 21 – 30 долларов США | 13 | 0,197 | | $31 – $40 | 8 | 0,121 | | $41 — $50 | 4 | 0,061 |
Всего было продано 66 штук. Таким образом, мы нашли относительную частоту каждого класса, взяв частоту каждого класса и разделив ее на общее количество проданных товаров.
Например, было продано 20 товаров по цене от 1 до 10 долларов. Таким образом, относительная частота класса $1 – $10 составляет 20/66 = 0,303 .
Затем был продан 21 предмет в ценовом диапазоне от 11 до 20 долларов. Таким образом, относительная частота класса $11 – $20 составляет 21/66 = 0,318 .
В следующем примере показано, как найти относительные частоты в Excel.
Пример: относительные частоты в Excel
Сначала мы введем класс и частоту в столбцах A и B:
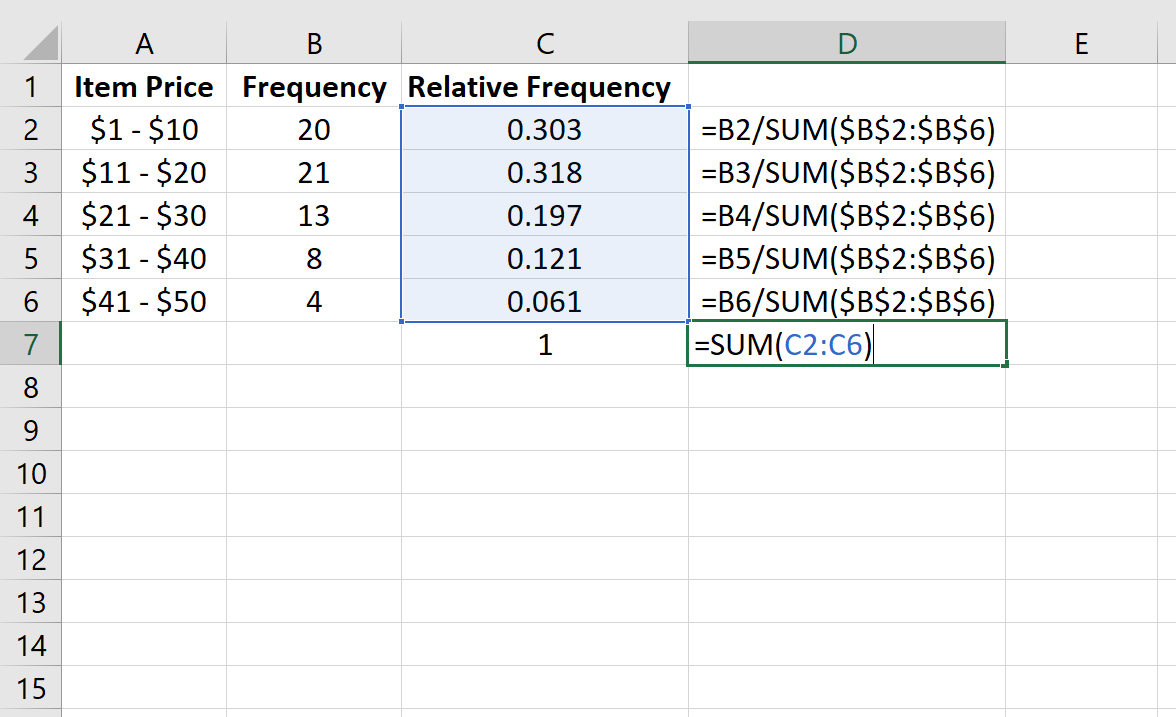
Далее мы рассчитаем относительную частоту каждого класса в столбце C. В столбце D показаны формулы, которые мы использовали:
Мы можем проверить правильность наших расчетов, убедившись, что сумма относительных частот равна 1:
Мы также можем создать гистограмму относительной частоты для визуализации относительных частот.
Просто выделите относительные частоты:
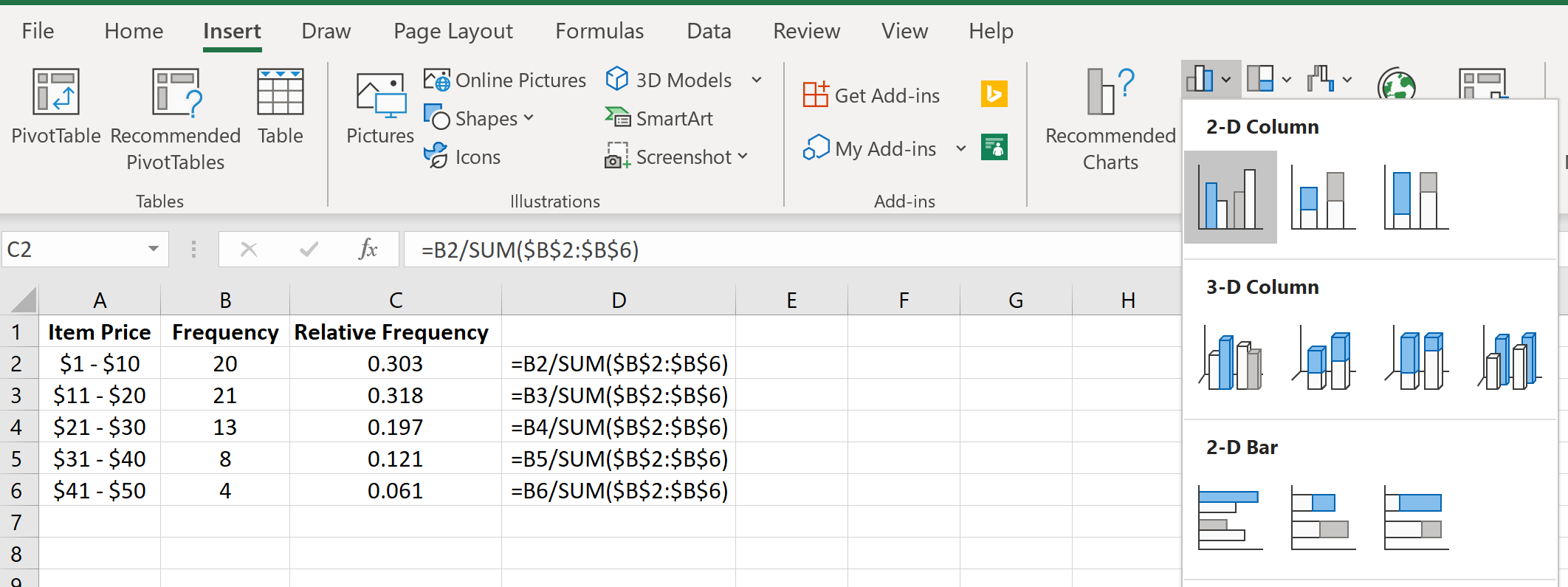
Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :
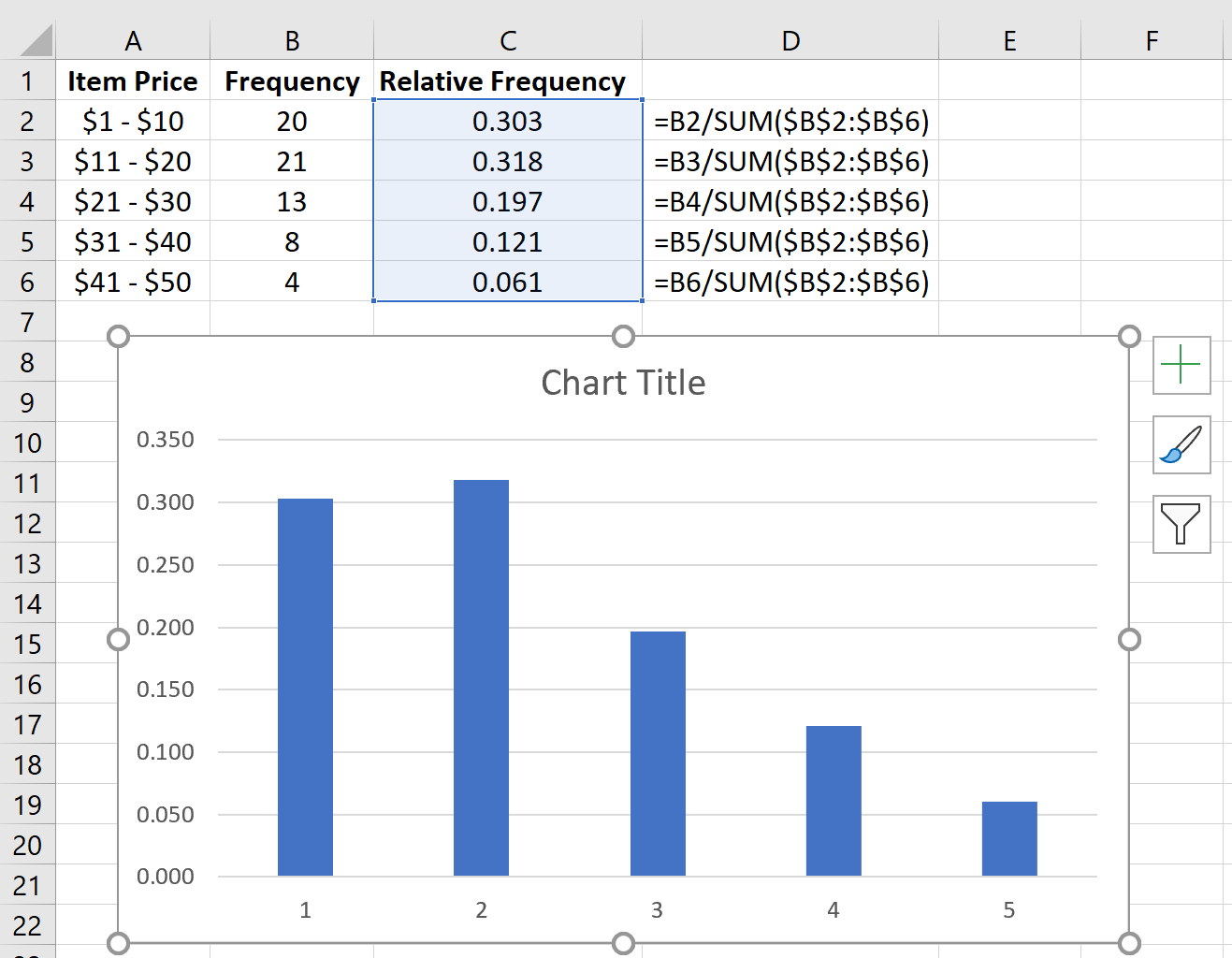
Автоматически появится гистограмма относительной частоты:
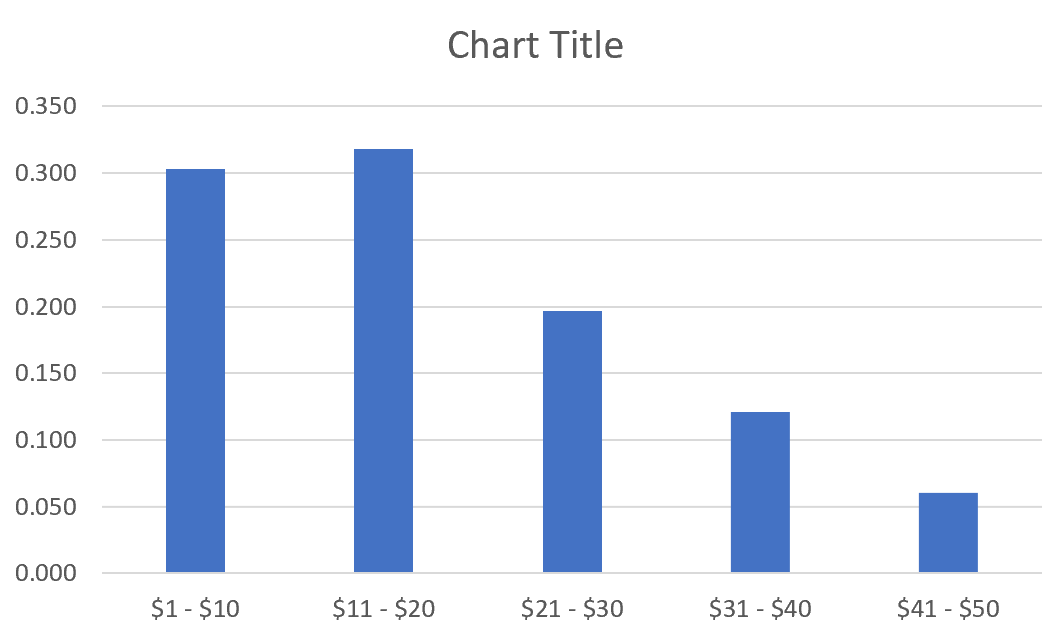
Измените метки оси X, щелкнув правой кнопкой мыши диаграмму и выбрав Выбрать данные.В разделе « Ярлыки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий цены на товары. Нажмите OK , и новые метки осей появятся автоматически:
Дополнительные ресурсы
Калькулятор относительной частоты
Гистограмма относительной частоты: определение + пример
Как работает стандартное отклонение в Excel
Добрый день!
В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику. А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается. В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.
В Excel используются несколько вариантов этой функции отклонения:
- Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
- Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
- Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
- Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.
Математическая теория
Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.
Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!
Для начала нам нужно определить «среднеквадратическое отклонение», что бы в дальнейшем произвести расчёт «стандартного отклонения», в этом нам поможет формула: 
Описать формулу возможно так: среднеквадратическое отклонение будет измеряться в тех же единицах что и измерения случайной величины и применяется при вычислении стандартной среднеарифметической ошибки, когда производятся построения доверительных интервалов, при проверке гипотез на статистику или же при анализе линейной взаимосвязи между независимыми величинами. Функцию определяют, как квадратный корень из дисперсии независимых величин.
Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так: 
Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.
Практическое воплощение в Excel
Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.
Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:
- Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.
Теперь создадим файл примера и на его основе рассмотрим работу этой функции. 
Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц. Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.
Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4). 
Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода. Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4). 
Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты. Получаем такую таблицу: 
Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно. Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:
С возрастом желание заработать переходит в желание сэкономить.
Михаил Жванецкий
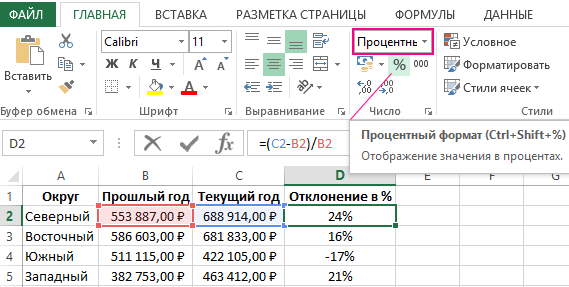
Как рассчитать процент отклонения факта от плана?
Как посчитать процент отклонения факта от плана?
Расчёт показателей, позволяющих определить, на сколько выполнен план, очень важен.
Если отклонение от плана слишком большое, то это может сильно повлиять на бюджет организации — возникнет необходимость принимать соответствующие меры.
Итак, как найти процент отклонения от плана?
Как известно, отклонение бывает двух видов — абсолютное и относительное.
Абсолютное отклонение представляет собой разницу между 2 показателями (плановым и фактическим, базовым и расчётным). Это числовая величина.
Относительное отклонение — это отношение между 2 показателями в процентах.
Так как речь идёт о проценте отклонения, то будем пользоваться формулой относительного отклонения.
Процент отклонения факта от плана рассчитывается для заданного отчётного периода — месяц, квартал, год.
1) Pi — плановые показатели по продукции / услуге / виду деятельности i.
2) Fi — фактические показатели.
В качестве базового показателя берём план, в качестве текущего показателя — факт.
Отклонение в процентах будет рассчитываться по формуле:
Oo = (Fi / Pi) * 100% — 100%
Другой вид формулы:
Oo = (Fi / Pi — 1) * 100%
Ещё можно воспользоваться такой формулой:
Oo = ((Fi — Pi) / Pi) * 100%
При этом возможны несколько ситуаций:
1) Oo > 0 — план перевыполнен.
2) Oo = 0 — плановые показатели были достигнуты.
Пример
Предприятие работает в целлюлозно-бумажной отрасли. Имеются плановые и фактические показатели по выпуску (в тоннах) различных видов бумаги за 1 квартал 2017 года.
Нужно найти процент отклонения факта от плана.
Для каждого вида продукции делим значения «факт» на значения «план», вычитаем единицу и переводим в проценты.
По 1 и 2 показателю план не выполнен. По 3 показателю план перевыполнен.
По сути, одно из основных направлений в работе экономиста — это планирование, сбор фактической информации и проведение сравнительного анализа для оптимизации расходов предприятия.
Отклонения принято рассчитывать, как абсолютные, так и относительные.
В формулировке вопроса имеется в виду расчёт относительных отклонений.
Относительное отклонение в результате даёт процент отклонения Факта от Плана.
Вообще, на своей практике встречался с двумя вариантами расчёта.
В первом варианте относительное отклонение рассчитывается, как
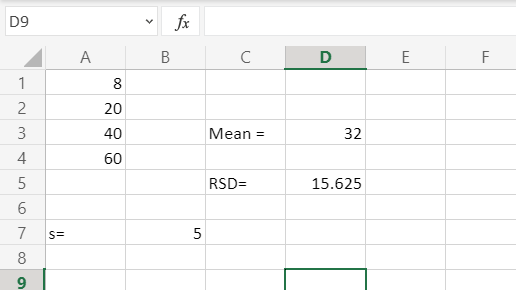
Результат расчёта можно наблюдать на рисунке ниже.
Полученное отклонение показывает на сколько процентов выполнен План, то есть 100% будет идеальным значением, когда фактические данные будут полностью соответствовать плановым. Если значение меньше 100%, то План недовыполнили, если больше — перевыполнили.
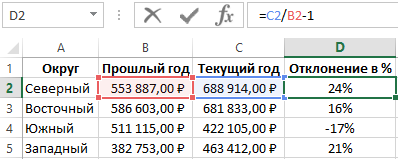
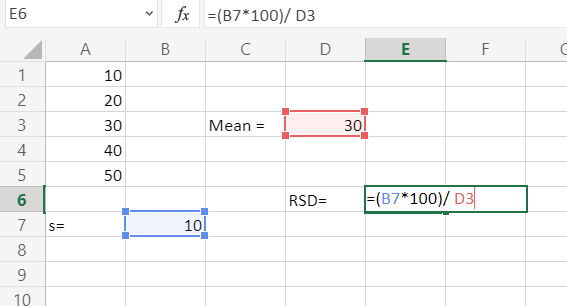
Второй способ расчёта практически отражает первый, только полученное значение вычитается из 100%, то есть формула расчёта относительного отклонения во втором случае будет следующей
100-(Факт/План)*100, либо (План-Факт)/План*100
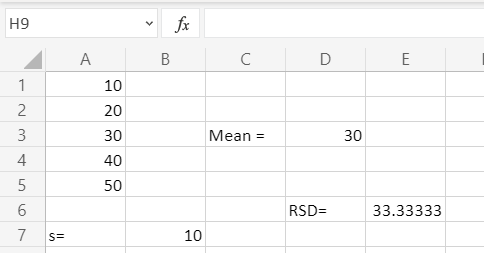
Результат данного расчёта можно наблюдать также на рисунке ниже.
При данном варианте расчёта мы видим на сколько процентов произошло отклонение от Плана. Таким образом 0% показывает соответствие Факта Плану, отрицательное значение говорит о перевыполнении Плна, а положительное — недовыполнении.
При расчёте Абсолютного отклонения всё гораздо проще.
Таким образом, мы сможем увидеть абсолютное отклонение Факта от Плана. Если значение равно 0, то Факт равен Плану, если получаем положительное значение, то произошло перевыполнение Плана, отрицательное — недовыполнение.
Бывает отставание фактических показателей от плановых, а бывает перевыполнение плана. В обоих случаях требуется рассчитать процент отклонения факта от плана.
Проще всего работать с конкретными цифрами. Например, завод должен был произвести 150 автомобилей, а выпустил 175 шт. На сколько процентов перевыполнен план?
Можно построить пропорцию:
х = 175*100/150 = 116,67%
Процент отклонения факта от нормы 116,67% — 100% = 16,67%
Или сначала посчитаем, что завод выпустил «лишние» 25 авто (175-150),
а потом составляем пропорцию:
у = 25*100 / 150 = 16,67%.
Ещё проще воспользоваться возможностями таблицы excel:
Часто требуется рассчитать процент отклонения факта от плана в excel.
Составляем таблицу, состоящую из 4-х столбиков:
Наименование показателя, план, факт и процент отклонения.
Формула для расчета процента отклонения факта от плана приведена на рисунке выше.
Можно записать как =ОКРУГЛ(B3/A3*100;2) или =ОКРУГЛ(B3/A3*100-10 0;2)
В зависимости от того, какие вам показатели нужны, абсолютные или относительные.
Если у нас есть таблица, в которой занесены все данные, т.е. прописан определенный показатель, и даны исходные данный (в виде план и факт), тогда высчитать процент отклонения не составит труда.
Не стоит забывать, что отклонение есть абсолютное и относительное.
Мы высчитывает относительное отклонение, подставляя данные в формулу
Факт :(делим) на План х(умножаем) 100%
Чтобы было более понятно приведем пример. Для этого найдем таблицу:
Высчитываем первый показатель «Товарная продукция»
936,5 : 982,1 х 100% = 0,95 х 100% = 95%
Получается, что план был не выполнен в полном объеме, так как показатель менее 100%.
Если после высчитывания получится 100%, значит план полностью выполнен.
А если будет более 100%, значит перевыполнен.
Так как вопрос о проценте отклонения, то речь идет об относительном отклонении факта от плана, но мы посчитаем в нашем примере и абсолютное отклонение.
Допустим, мы запланировали выпустить в 2018 году 120 единиц продукции, а выпустили фактически — 130 единиц. Процент отклонения факта от плана считается так: факт поделить на план, умножить на 100, и вычесть из полученного результата 100.
Считаем: 130 / 120 = 1,083, умножаем на 100, получается 108,3, вычитаем 100 = 8,3 %
Отклонение равно 8,3 %. Так как мы получили положительный результат, то речь идет о перевыполнении плана на 8,3 процентов, если бы результат был отрицательным, то план был бы недовыполнен. Абсолютное же отклонение считается вообще очень просто — от факта отнимается план, в нашем случае это 130-120 = 10 единиц продукции, план перевыполнен на 10 единиц продукции.
С этим вопросом сталкиваются экономисты многих предприятий, особенно когда нужно предоставить начальству расчет. Лучше всего рассмотреть на примере:
Например, нам нужно выпустить 1000 единиц продукции, но по факту предприятие выпустило 900 единиц продукции. Чтобы узнать насколько выполнен план, необходимо будет фактическое значение на планируемое значение и умножить на 100 процентов.
Итак, получаем 900/1000*100 = 90%. Значит план был выполнен только на девяносто процентов.
В данном примере, который представлен в ответе выше, предприятие не смогло выполнить план на десять процентов.
Такие задачки лучше всего решать в Экселе.
Для того, чтобы понимать на сколько процентов отличается факт от плана нужно воспользоваться простой формулой рассчёта, которая представлена ниже:
(Ф ÷ П) • 100, где в формуле
Рассмотрим на примере для большей наглядности.
Фабрика по пошиву одежды должна была сшить по плану 300 рабочих комбинезонов, но за отведенный срок сшили всего 250 комбинезонов. Производим рассчёт.
250 ÷ 300 = 0,83 • 100 = 83,33 %
Получается, что план не был выполнен на 100 %, а лишь 83,33 %.
Поменяем значения в задаче: П = 250, Ф = 300.
300 ÷ 250 = 1,2 • 100 = 120 %.
Получается, что план был перевыполнен на 20 %.
Посчитать процент отклонения не так и сложно.
Чтобы было проще можно объяснить на примере.
Производство должно было выпустить за одни месяц 200 000 книг, а выпустили только 180000.
Факт делим на план и умножаем на 100%.
Теперь высчитываем 100%-90%=10% — наш план не выполнили на 10%, это и есть показатель недовыполнения.
Теперь посчитаем, если мы план перевыполнили.
План составляет 200000 книжек, мы выпустили 210000.
Таким образом перевыполнение плана равняется 5%.
Почему-то проценты у многих вызывают сложности. Много раз наблюдал, как на уроках даже те, у кого с остальными темами все в порядке, столкнувшись с процентами и долями начинают «буксовать». И почему-то у учителей не получалось понять, из-за чего тема процентов вызывает такие проблемы и как её объяснять. Впрочем, непонимание процентов выражается хотя бы в распространенных выражениях типа «это гарантировано на 120%» или «я выложился на 200%». Прежде всего очень важно осознать, что 100% — это основа, норма. 100% — это всё, что есть или должно быть. То есть нельзя гарантировать что-то больше, чем на 100%, и нельзя усилий приложить на 200%, так как все ваши возможные усилия и гарантии составляют эту основу, эти 100%.
В примере про план и факт за план берется 100%. Это — наша основа, норма, и нам надо понять, насколько этот план выполнен. В случае с планом может быть и 98%, и 134%, так как технически можно выпустить больше продукции, чем запланировано.
Чтобы узнать, насколько выполнен план, нам необходимо знать цифры плана и факта и сравнить их. Из этих цирф делаем два простых и понятных уравнения:
Со школы в наших головах должно было отпечататься, что такие системы составляются в одно уравнение крест-накрест, то есть мы берем диагонали: (план) и (Х) и (факт) и (100%):
Посчитать отклонение в Excel
Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…) = СТАНДОТКЛОН.Г(Число1;Число2;…) = СТАНДОТКЛОН.В(Число1;Число2;…)
-
Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Урок: Формула среднего квадратичного отклонения в Excel
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция — СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
Урок: Как посчитать среднее значение в Excel
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
-
Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
-
Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Как посчитать проценты в Excel
Мы сталкиваемся с процентами не только на работе или учебе, но и в нашей повседневной жизни – скидки, чаевые, депозитные ставки, кредиты и прочее. Поэтому умение работать с процентами будет полезно в разных сферах жизни. В этой статье мы ближе познакомимся с процентами, и рассмотрим, как быстро посчитать проценты в Excel, а также на примерах разберем следующие вопросы:
- как посчитать проценты в Excel формула;
- как посчитать процент от числа в Excel;
- как посчитать проценты от суммы в Excel;
- посчитать разницу в процентах Excel;
Как посчитать проценты в Excel формула
Прежде чем перейти к вопросу подсчета процентов в Excel, давайте вспомним основные знания о процентах. Процент – это сотая часть единицы. Из школьной программы вы наверняка знаете, что для того чтобы посчитать проценты, необходимо разделить искомую часть на целое и умножить на 100. Таким образом формула расчёта процентов выглядит следующим образом:
Посчитать проценты в Excel намного проще, так как вычисление некоторых математических операций в Excel происходит автоматически. Поэтому формула расчета процентов в Excel преобразуется следующим образом:
Для того чтобы посчитать проценты в Excel нет необходимости умножать результат на 100, если для ячейки используется Процентный формат.
Рассмотрим наглядный пример, как посчитать процент выполнения плана в Excel. Пусть у нас есть таблица с данными о запланированном объеме реализации продукции и фактическом объеме.
Как посчитать проценты в Excel – Исходные данные для расчета процентов
Для того чтобы посчитать процент выполнения плана необходимо:
- В ячейке D2 ввести формулу =C2/B2 и скопировать ее в остальные ячейки с помощью маркера заполнения.
- На вкладке « Главная » в группе « Число » выбрать «Процентный формат» для отображения результатов в формате процентов.
В результате мы получаем значения, округленные до целых чисел, которые показывают процент выполнения плана:
Как посчитать проценты в Excel – Процент выполнения плана
Следует отметить, что универсальной формулы, как посчитать проценты нет. Все зависит от того, что вы хотите получить в результате. Поэтому в этой статье мы рассмотрим примеры формул вычисления процента от числа, от общей суммы, прироста в процентах и многое другое.
Как посчитать процент от числа в Excel
Для того, чтобы посчитать процент от числа, необходимо использовать следующую формулу:
Рассмотрим пример расчета процента от числа. У нас есть таблица со стоимостью товаров без НДС и ставкой НДС для каждого товара.
Как посчитать проценты в Excel – Исходные данные для расчета процента от числа
Примечание : если вы вручную вводите в ячейке числовое значение и после него ставите знак %, то Excel применяет к данной ячейке процентный формат и воспринимает это число как его сотую часть. Например, если в ячейку ввести 18%, то для расчётов Excel будет использовать значение 0,18.
Пусть нам необходимо рассчитать НДС и стоимость продуктов с налогом на добавленную стоимость.
- Для того чтобы посчитать НДС в денежном эквиваленте, т.е. посчитать процент от числа в ячейке D2 вводим формулу =B2*C2 и заполняем остальные ячейки.
- В ячейке E2 суммируем ячейки B2 и D2 , для того чтобы получить стоимость с НДС.
В результате получаем следующие данные расчета процента от числа:
Как посчитать проценты в Excel – Процент от числа в Excel
Как посчитать проценты от суммы в Excel
Рассмотрим пример, когда нам необходимо посчитать проценты от суммы по каждой позиции. Пусть у нас есть таблица продаж некоторых видов продуктов с итоговой суммой. Нам необходимо посчитать проценты от суммы по каждому виду товара, то есть посчитать в процентном соотношении сколько выручки приносит каждый товар от общей суммы.
Как посчитать проценты в Excel – Исходные данные для расчета процентов от суммы
Для этого проделываем следующее:
- В ячейке C2 вводим следующую формулу: =B2/$B$9 . Для ячейки B9 мы используем абсолютную ссылку (со знаками $), чтобы она была неизменной, а для ячейки B2 – относительную, чтобы она изменялась при копировании формулы в другие ячейки.
- Используя маркер заполнения копируем эту формулу расчета процентов от суммы для всех значений.
- Для отображения результатов в формате процентов, на вкладке « Главная » в группе « Число », задаем «Процентный формат» с двумя знаками после запятой.
В результате мы получаем следующие значения процентов от суммы:
Как посчитать проценты в Excel – Проценты от суммы в Excel
Посчитать разницу в процентах Excel
Для того чтобы посчитать разницу в процентах, необходимо использовать следующую формулу:
где А – старое значение, а B – новое.
Рассмотрим пример, как посчитать разницу в процентах. Пусть у нас есть данные о продажах за два года. Нам необходимо определить процентное изменение продаж в отчетном году, по сравнению с предыдущим.
Как посчитать проценты в Excel – Исходные данные для расчета разницы в процентах
Итак приступим к расчетам процентов:
- В ячейке D2 вводим формулу =(C2-B2)/B2 .
- Копируем формулу в остальные ячейки, используя маркер заполнения.
- Применяем процентный формат для результирующих ячеек.
В результате у нас получается следующая таблица:
Как посчитать проценты в Excel – Вычисление разницы в процентах
В нашем примере положительные данные показывают прирост в процентах, а отрицательные значения – уменьшение в процентах.
Теперь вы знаете, как посчитать проценты в Excel, например, как посчитать процент от числа, проценты от общей суммы и прирост в процентах.
Как посчитать процент отклонения в Excel по двум формулам
Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?
Как посчитать отклонение в процентах в Excel
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.
Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки.
Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.
Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.
Альтернативная формула для вычисления процента отклонения в Excel
В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.
Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.
Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.
Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Definition: Related standard deviation is also known as the relative percentage standard deviation form, the deviation measurement which tells us how different numbers are dispersed around the mean in a particular set of data. This format shows the percentage distribution of data.
If a relative standard deviation of the product is higher, that means that the numbers are very wide-ranging from the mean of that product. The RSD team sometimes needs certain data which is far removed from the Average RSD according to product requirement. Data that are well deviated from the RSD are taken into consideration in those cases.
In the event of the reverse situation, i.e. a lower relative default, the numbers are closer than the average and are also referred to as the coefficient of difference. In general, the idea of actual forecasts is given within the given data set.
Uses of Relative Standard Deviation:
- Relative standard deviation is used widely in the interpretation of statistical data relations in different segments.
- This is one of the primary tools indicating whether the stock price is changing the growth of the company.
- RSD is a sophisticated version of an analytical tool that assists the end-user in understanding trends, product demand, and customer preferences across various industries. RSD thus helps to detect the actual results of various options.
Formula:
RSD(Relative Standard Deviation)=s×100 / x¯
where,
RSD = Relative standard deviation
s = Standard deviation
x¯ = Mean of the data.
Example 1: Calculate RSD when numbers: 8,20,40,60 and the standard deviation is 5.
First calculating mean(x)
Then calculating RSD
Example 2: Calculate RSD when numbers: 10,20,30,40,50 and the standard deviation is 10.
First calculating mean(x)
Then calculating RSD
Like Article
Save Article