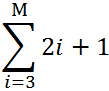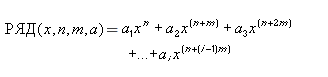Содержание
- Операции над натуральными числами
- Сколько нулей в числе
- Повторяем состав чисел
- Геометрические фигуры и задачи
- Поверья разных народов
- Магия чисел
- Изучение чисел от 1 до 100
- Разряды и классы натурального числа
- Подготовка к гаданию
- Таблица квадратов
- Случайное | рандомное число онлайн в 1 клик
- Натуральный ряд.
- Таблица натуральных чисел
- Сравнение натуральных чисел.
- Определяем верные и неверные равенства
Операции над натуральными числами
К замкнутым операциям над натуральными числами (операциям в результате, которых получается натуральных чисел) относятся следующие арифметические операции:
- Сложение
- Умножение
- Возведение в степень ab, где a — основание степени и b — показатель степени. Если основание и показатель – натуральные числа, то и результат будет являться натуральным числом.
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как их результат не всегда будет натуральным числом.
- Вычитание (При этом Уменьшаемое должно быть больше Вычитаемого)
- Деление
Сколько нулей в числе
Узнать количество нулей, и сколько десятков, сотен, тысяч, миллионов, миллиардов, триллионов содержится в любом числе.
Сколько нулей в числе
Повторяем состав чисел
Сова: Хорошо. Посмотрим, как ребята помнят состав чисел. Что такое состав чисел? Правильно. Это два числа, из которых состоит каждое число. А зачем нам нужно знать состав чисел? Чтобы быстро считать удобным способом.
Давайте вспомним, как мы это делали во втором классе. Например, нам нужно найти сумму чисел 23 и 50. Что мы с вами будем делать? Разложим число 27 на два слагаемых: 20 и 7. Теперь нам легче будет сложить десятки и к полученной сумме прибавить три единицы.
Вспомнили? Решите несколько примеров, используя свои знания о составе чисел.
Сова : Молодцы, ребята! О, черепашке Маше уже не терпится решать с вами задачи. Что ты ребятам сегодня приготовила?
Геометрические фигуры и задачи
Кошка Алиса: Мур, мур! Да, я люблю рисовать различные геометрические фигуры. А ребята помнят геометрические фигуры?
Назовите все геометрические фигуры, которые видите.
Сова: Ну что скажешь, Алиса, знают ребята геометрические фигуры?
Алиса :Мур, мур, знают. А вот,помнят они, как чертить отрезки, делить их и обозначать буквами?
Сова: А ты проверь. Дай им задачу и посмотри, помнят или забыли за лето?
Алиса: Хорошо. Вот вам геометрическая задача.
Начертите в тетради отрезок АВ длиной 1 дм 2 см. Разделите его точками на три равные части. Обозначьте буквами отмеченные точки. Запишите все полученные отрезки.
Ответ : АС, СD, DB..
Поверья разных народов
У различных древних народов есть дополнительные правила трактовки чисел. Одни уверенны, что счастливым знаком являются только нечетные. Мудрецы Востока считают девятку предвестником неудачи. Она предупреждает об изменениях в жизни, как о положительных, так и о негативных.
Считается, что гадание на время на часах предупреждает о недругах, если человеку постоянно попадаются четные комбинации. Избежать неприятностей можно, если снизить активность, занять выжидательную позицию.
Магия чисел
Каждый человек, как всем известно, является любопытным от природы существом, особенно если речь идет про его будущее. Даже те люди, которые не воспринимают эзотерику всерьез, все равно иногда невольно прислушиваются к ней. Особо восприимчивыми к таким практикам являются те люди, у которых в жизни появились некоторые проблемы.
С начала нашего рождения числа следуют за нами по пятам. Вы наверняка знаете, что дата рождения, количество букв в имени и фамилии человека имеют большое влияние на судьбу младенца. Это всё есть знаки судьбы, которые предсказывают наше будущее либо предупреждают о предстоящих опасностях.
Изучение чисел от 1 до 100
Это табличка для изучения чисел от 1 до 100. Пособие подходящее для детей старше 4 лет.
Те, кто знаком с Монтесори обучением, наверно уже такую табличку видел. У нее есть много приложений и сейчас мы с ними познакомимся.
Ребенок должен отлично знать числа до 10, прежде начать работу с таблицей, так как счет до 10 лежит в основе обучения чисел до 100 и выше.
При помощи этой таблице, ребенок выучит имена чисел до 100; считать до 100; последовательность чисел. Можно так же тренироватся считать через 2, 3, 5, и т.д.
Разряды и классы натурального числа
Рассмотрим натуральное число 783 502 197 048
| Название класса |
Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) |
7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
| Название класса |
Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) |
7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
C помощью таблицы разрядов прочитаем это число. Для этого надо слева направо по очереди называть количество единиц каждого класса и добавлять название класса.
Название класса единиц не произносят, также не произносят название класса, если все три цифры в его разрядах — нули.
Теперь прочтем число 783 502 197 048 из таблицы: 783 миллиарда 502 миллиона 197 тысяч 48.
Запомните!
Любое натуральное число можно записать в виде разрядных слагаемых.
Числа 1, 10, 100, 1000… называются разрядными единицами. С их помощью натуральное число записывается в виде разрядных слагаемых. Так, например, число 307 898 будет выглядеть в виде разрядных слагаемых.
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Проверить свои вычисления вы можете с помощью нашего калькулятора разложения числа на разряды онлайн.
Следующие за миллиардом классы названы в соответствии с латинскими наименованиями чисел. Каждая следующая единица содержит тысячу предыдущих.
- 1 000 миллиардов = 1 000 000 000 000 = 1 триллион («три» — по латыни «три»)
- 1 000 триллионов = 1 000 000 000 000 000 = 1 квадриллион («квадра» — по латыни «четыре»)
- 1 000 квадриллионов = 1 000 000 000 000 000 000 = 1 квинтиллион («квинта» — по латыни «пять»)
Все числа пересчитать невозможно, поскольку за каждым числом следует число на единицу большее, но очень большие числа в повседневной жизни не нужны.
Однако, физики нашли число, которое превосходит количество всех атомов (мельчайших частиц вещества) во всей Вселенной.
Это число получило специальное название — гугол. Гугол — число, у которого 100 нулей.
Подготовка к гаданию
Сперва вы должны решить, на кого станете гадать. Вам нужно будет представить человека в мельчайших подробностях, таких как его лицо, привычки, внешность и т. д. Проведите глубокую концентрацию на своём запросе, глубоко осознайте что вас именно интересует.
Для гадания «Сотня» вам понадобится: листок бумаги (чистый), а также пишущее средство. На листке заполняем в любом порядке цифры от 1 до 100 (цифры с нулями, как и нули, ставить не надо, а если хотите поставить цифру 30, вписываете число 3).
Прежде чем начать гадать, нужно обязательно поверить в эту практику, и тогда она приоткроет завесу в будущее.
Ряд первый заполняйте так, как вам вздумается. Доверьтесь своей судьбе и пишите любое количество цифр. В последующих рядах их должно быть то же количество символов, ни больше ни меньше. Внизу вы обязательно должны указать день, месяц, год, а также точное время ритуала.
Таблица квадратов
|
02=0 12=1 22=4 32=9 42=16 52=25 62=36 72=49 82=64 92=81 |
102=100 112=121 122=144 132=169 142=196 152=225 162=256 172=289 182=324 192=361 |
202=400 212=441 222=484 232=529 242=576 252=625 262=676 272=729 282=784 292=841 |
302=900 312=961 322=1024 332=1089 342=1156 352=1225 362=1296 372=1369 382=1444 392=1521 |
402=1600 412=1681 422=1764 432=1849 442=1936 452=2025 462=2116 472=2209 482=2304 492=2401 |
|
502=2500 512=2601 522=2704 532=2809 542=2916 552=3025 562=3136 572=3249 582=3364 592=3481 |
602=3600 612=3721 622=3844 632=3969 642=4096 652=4225 662=4356 672=4489 682=4624 692=4761 |
702=4900 712=5041 722=5184 732=5329 742=5476 752=5625 762=5776 772=5929 782=6084 792=6241 |
802=6400 812=6561 822=6724 832=6889 842=7056 852=7225 862=7396 872=7569 882=7744 892=7921 |
902=8100 912=8281 922=8464 932=8649 942=8836 952=9025 962=9216 972=9409 982=9604 992=9801 |
Случайное | рандомное число онлайн в 1 клик
Числа окружают нас с самого рождения и играют важную роль в жизни. У многих людей сама работа связана с числами, кто-то полагается на удачу, заполняя числами лотерейные билеты, а кто-то придает им и вовсе мистическое значение. Так или иначе, иногда нам не обойтись без того, чтобы воспользоваться такой программой, как генератор рандомных чисел.
К примеру, вам необходимо организовать розыгрыш призов среди подписчиков вашей группы. Быстро и честно выбрать призеров и поможет наш генератор случайных чисел онлайн. Вам просто нужно, например, задать нужное количество рандомных чисел (по числу призеров) и максимальный диапазон (по числу участников, если им присвоены номера). Подтасовка в таком случае полностью исключается.
Эта программа может также послужить как генератор случайных чисел для лото. К примеру, вы купили билет и хотите полностью полагаться на случайность и удачу в выборе чисел. Тогда наш рандомайзер чисел поможет заполнить ваш лотерейный билет.
Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Свойства натурального ряда:
- Наименьшее натуральное число – единица.
- У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
- Натуральный ряд не имеет наибольшего числа, он бесконечен.
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.
Таблица натуральных чисел
Таблица натуральных чисел от 1 (одного) до 120 (ста двадцати) представляет собой последовательность целых положительных чисел, которые в математике принято называть натуральными числами. Здесь вы можете скачать таблицу натуральных чисел бесплатно. В таблице представлен натуральный ряд чисел от 1 (единицы) до 120 (ста двадцати).
В таблице наглядно представлена последовательность натуральных чисел, образующих натуральный ряд чисел. Эту таблицу смело можно назвать Периодическая Система Натуральных Чисел Николая Хижняка))) Или периодическая таблица чисел натурального ряда – это уже не я придумал, это такой красивый поисковый запрос кто-то задал. По аналогии с периодической системой химических элементов. Почему мой ряд натуральных чисел заканчивается на числе 120? Просто мне было лень писать дальше. Если вам жизненно необходима таблица натуральных чисел больших размеров (ну, там, диванчик застелить), пишите в комментах заказ с размерами – выполню непременно. Первой блондинке – бесплатно)))
Таблица натуральных чисел поможет вам мастерски определять количество различных цифр в натуральных числах и удовлетворять другие математические нужды. Таблица натуральных чисел разработана в секретных лабораториях внеземных цивилизаций специально для блондинок, на случай жестоких допросов инквизиторами от математики))) В настоящее время рассматривается вопрос создания таблицы натуральных чисел для скачивания на мобильные телефоны (такой себе математический бронежилетик).
Когда числа путают с цифрами:
Скачать таблицу цифр от 1 до 20 – только здесь представлена таблица натуральных чисел, а не цифр. Циферок всего десять.
Цифры от 1 до 100 – штучки от 1 до 100 называются числами, ведь само число 100 состоит из трех цифр – одна единичка 1 и два нолика 0 и 0.
Натуральные цифры – цифры бывают арабские, римские и другие, а вот натуральными бывают числа.
Цифра 100 – сто является числом и это число 100 состоит из трех цифр – одна единичка 1 и два нолика 0 и 0. Все вместе эти три цифры образуют число 100 – сто.
Сравнение натуральных чисел.
Из 2-х натуральных чисел меньше то число, которое при счете называется ранее. Например, число 7 меньше 11 (записывают так: 7 < 11). Когда одно число больше второго, это записывают так: 386 > 99.
Определяем верные и неверные равенства
Сова : Продолжаем работать. Вспомним, что такое равенство и неравенство?
Равенство это когда левая часть выражения (примера) равна правой. Например, 12+4 = 16. В равенстве используют знак «=»
А неравенство – левая часть выражения больше или меньше правой. Например, 12+4 < 23. В неравенствах используют знаки < или >
Повторили? А теперь, закрепим. Вам нужно будет выписать только неверные неравенства.
Источники
- https://ru.onlinemschool.com/math/library/numbers/integers/
- https://www.calc.ru/Chisla-Naturalnyye-Chisla.html
- https://100urokov.ru/predmety/urok-1-chisla-ot-1-do-100
- https://maginarius.ru/gadaniya/gadanie-po-chasam.html
- https://www.webarbeit.ru/2015/09/chisla-ot-0-do-100.html
- http://math-prosto.ru/?page=pages/set-of-numbers/natural.php
- https://doza.pro/art/math/algebra/table-squares
- https://generator-online.com/numbers/
- https://TutoMath.ru/5-klass/naturalnye-chisla.html
- http://www.webstaratel.ru/2010/01/blog-post.html
|
VDM Пользователь Сообщений: 779 |
Здравствуйте уважаемые Форумчане! Возник (не прикладной пока) вопрос: |
|
Alex_ST Пользователь Сообщений: 2746 На лицо ужасный, добрый внутри |
На сколько я помню ещё школьную математику, проблема вычисления ряда простых чисел так и не решена вообще (формулы вычисления числового ряда нет). С уважением, Алексей (ИМХО: Excel-2003 — THE BEST!!!) |
|
VDM Пользователь Сообщений: 779 |
{quote}{login=Alex_ST}{date=17.08.2010 11:13}{thema=}{post}На сколько я помню ещё школьную математику, проблема вычисления ряда простых чисел так и не решена 99336 |
|
алгоритм простой |
|
|
А как это на примере будет выглядеть? |
|
|
VDM Пользователь Сообщений: 779 |
{quote}{login=Vlad}{date=17.08.2010 11:51}{thema=}{post}А как это на примере будет выглядеть?{/post}{/quote} Да, согласен — не очень понятен алгоритм и его практическая реализация. |
|
Option Base 1 |
|
|
Alex_ST Пользователь Сообщений: 2746 На лицо ужасный, добрый внутри |
Формулы ряда НЕ СУЩЕСТВУЕТ! Таким образом все составные числа будут просеяны, и останутся только простые числа 2, 3, 5, 7, 11, 13… http://www.wikiznanie.ru/ru-wz/index.php/Решето_Эратосфена ) С уважением, Алексей (ИМХО: Excel-2003 — THE BEST!!!) |
|
KuklP Пользователь Сообщений: 14868 E-mail и реквизиты в профиле. |
Так: Я сам — дурнее всякого примера! … |
|
Вот мой вариант… на основе алгоритма Alex_ST |
|
|
kim Пользователь Сообщений: 3139 Игорь |
{quote}{login=Alex_ST}{date=17.08.2010 11:13}{thema=}{post}На сколько я помню ещё школьную математику, проблема вычисления ряда простых чисел так и не решена вообще (формулы вычисления числового ряда нет). Зато формулой можно пометить простые числа… |
|
KuklP Пользователь Сообщений: 14868 E-mail и реквизиты в профиле. |
{quote}{login=Михаил}{date=17.08.2010 08:05}{thema=}{post}Вот мой вариант… на основе алгоритма Alex_ST у меня: Я сам — дурнее всякого примера! … |
|
MCH Пользователь Сообщений: 3875 |
{quote}{login=Михаил}{date=17.08.2010 08:05}{thema=}{post}Вот мой вариант… на основе алгоритма Alex_ST По алгоритму неизвестного от 17.08.2010, 11:44 на основании файла от Михаила post_146715.xls P.S.: мой первый макрос, сделал в QBASIC (учил когда-то в школе) и переложил в VBA |
|
KuklP Пользователь Сообщений: 14868 E-mail и реквизиты в профиле. |
Класс. Я сам — дурнее всякого примера! … |
|
Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел?) |
|
|
{quote}{login=Михаил}{date=17.08.2010 10:27}{thema=MCH}{post}Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел?){/post}{/quote} у меня 2003 поэтому ограничиваюсь результатом в 65536 найденых натуральных числел, на бОльших суммах не могу проверить, да и в VBA не силен |
|
|
kim Пользователь Сообщений: 3139 Игорь |
{quote}{login=Михаил}{date=17.08.2010 10:27}{thema=MCH}{post}Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел?){/post}{/quote} Может пересохранить файл в xlsx? |
|
{quote}{login=kim}{date=17.08.2010 10:42}{thema=Re: MCH}{post}{quote}{login=Михаил}{date=17.08.2010 10:27}{thema=MCH}{post}Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел?){/post}{/quote} Может пересохранить файл в xlsx?{/post}{/quote}Да я просто копирую макрос в книгу 2010.. до 800 000 считает, а выше 900 000 — Type mismatch |
|
|
MCH Пользователь Сообщений: 3875 |
<<Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел> Проблема в Range(Cells(1, 1), Cells(count, 1)) = Application.WorksheetFunction.Transpose(a) при попытке вывести более 65536 значений выдает ошибку 400. Заменив данную строчку на цыкл, через который выводятся данные, считает 1 000 000 — 8 секунд (3,9 секунды без вывода значений); 10 000 000 — менее 2х минут |
|
Для интересУ проверил скорость различных версий, на 10 000 000, вот результат: за 248,12с (19,42) в 2010 20204 |
|
|
MCH Пользователь Сообщений: 3875 |
<<Для интересУ проверил скорость различных версий, на 10 000 000, вот результат: за 248,12с (19,42) в 2010 считает одинаково, а выводит по разному. и судя по скорости машинка у Вас быстрая, значительно быстрее моей |
|
{quote}{login=MCH}{date=18.08.2010 02:06}{thema=Re: }{post} и судя по скорости машинка у Вас быстрая, значительно быстрее моей :({/post}{/quote} |
|
|
VDM Пользователь Сообщений: 779 |
#23 18.08.2010 12:00:18 Спасибо Всем — здорово и познавательно! И формулы и макросы! По последнему предложенному коду, 2003 экс: за 5,28с (0,88) 78499 чисел 1000000 |
Как найти сумму числового и функционального ряда
Числовой ряд является некой последовательностью, которая рассматривается совместно с другой последовательностью (ее еще называют последовательностью частичных сумм). Подобные понятия применяются в математическом и комплексном анализе.
Сумму числового ряда можно легко вычислить в Excel с помощью функции РЯД.СУММ. Рассмотрим на примере, как работает данная функция, а после построим график функций. Научимся применять числовой ряд на практике при подсчете роста капитала. Но для начала немного теории.
Сумма числового ряда
Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:
Здесь показана начальная последовательность чисел ряда и правило суммирования:
- ∑ — математический знак суммы;
- ai — общий аргумент;
- i — переменная, правило для изменения каждого последующего аргумента;
- ∞ — знак бесконечности, «предел», до которого проводится суммирование.
Запись 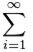
В соответствии с переменной i ряд можно записать развернуто:
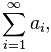
Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:
S1 = а1
S2 = а1 + а2
S3 = а1 + а2 + а3
S4 = а1 + а2 + а3 + а4
Сумма числового ряда – это предел частичных сумм Sn. Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».
Сначала найдем сумму числового ряда:
М = 10.
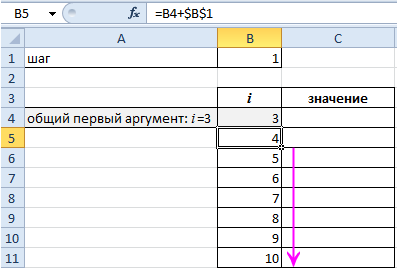
Теперь построим в Excel таблицу значений членов ряда:
Общий первый аргумент берем из формулы: i=3.
Все следующие значения i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.
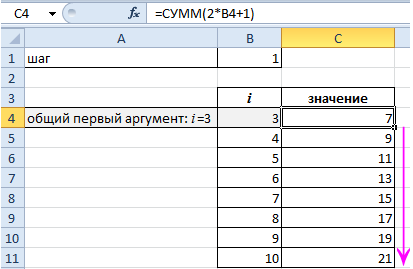
Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.
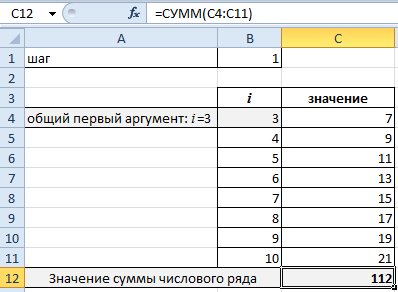
Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).
Функция РЯД.СУММ в Excel
Для нахождения суммы числового ряда в Excel применяется математическая функция РЯД.СУММ. Программой используется следующая формула:
Аргументы функции:
- х – значение переменной;
- n – степень для первого аргумента;
- m – шаг, на который увеличивается степень для каждого последующего члена;
- а – коэффициенты при соответствующих степенях х.
Важные условия для работоспособности функции:
- все аргументы обязательные (то есть все должны быть заполнены);
- все аргументы – ЧИСЛОвые значения;
- вектор коэффициентов имеет фиксированную длину (предел в «бесконечность» не подойдет);
- количество «коэффициентов» = числу аргументов.
Вычисление суммы ряда в Excel
Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.
Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.
Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:
S1 = a (1 + x).
На конец второго и последующих периодов – вид выражений следующий:
S2 = a (1 + x)2;
S3 = a (1 + x)2 и т.д.
Чтобы найти общую сумму:
Sn = a (1 + x) + a (1 + x)2 + a (1 + x)3 + … + a (1 + x)n
Частичные суммы в Excel можно найти с помощью функции БС().
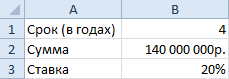
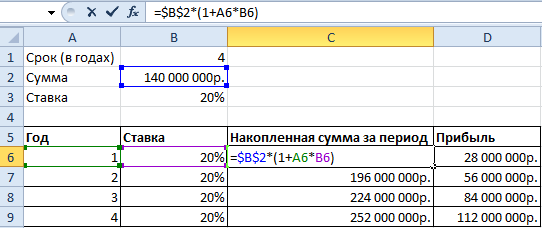
Исходные параметры для учебной задачи:
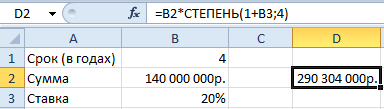
Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)
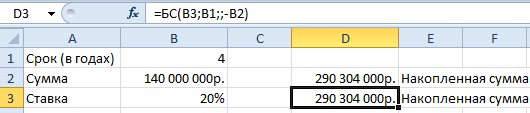
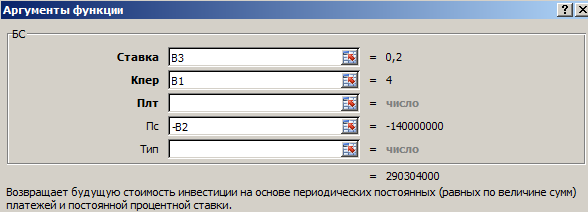
Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)
Результаты одинаковые, как и должно быть.
Как заполнить аргументы функции БС():
- «Ставка» — процентная ставка, под которую оформлен вклад. Так как в ячейке В3 установлен процентный формат, мы в поле аргумента просто указали ссылку на эту ячейку. Если было бы указано число, то прописывали бы его сотую долю (20/100).
- «Кпер» — число периодов для выплат процентов. В нашем примере – 4 года.
- «Плт» — периодические выплаты. В нашем случае их нет. Поэтому поле аргумента не заполняем.
- «Пс» — «приведенная стоимость», сумма вклада. Так как мы на время расстаемся с этими деньгами, параметр указываем со знаком «-».
Таким образом, функция БС помогла найти нам сумму функционального ряда.
В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.
Построение графика функций суммы числового ряда
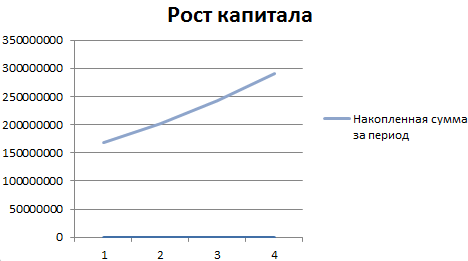
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:
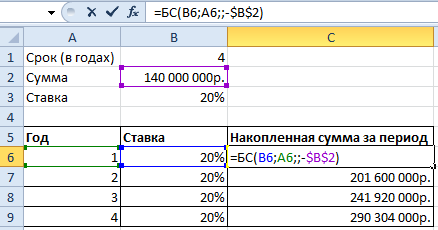
Дальше нам нужна функция для начисления сложных процентов — БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:
В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.
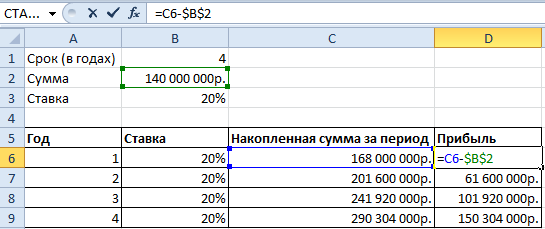
Сделаем еще один столбец, в котором отразим прибыль:
Как мы считали – в строке формул.
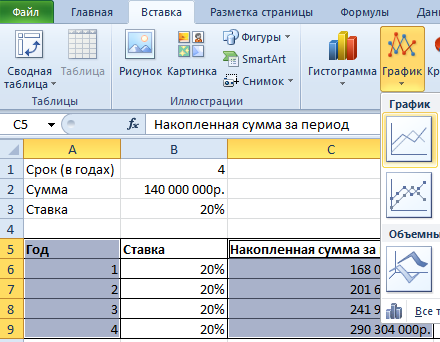
На основании полученных данных построим график функций.
Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» — инструмент «Диаграммы». Выбираем первый график:
Сделаем задачу еще более «прикладной». В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.
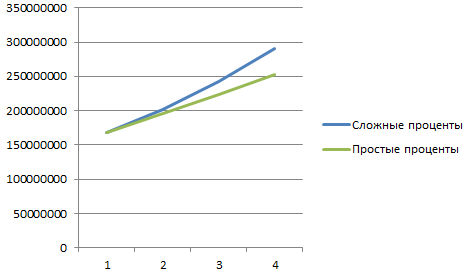
Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)
Добавим полученные значения в график «Рост капитала».
Какие именно выводы сделает инвестор – очевидно.
Математическая формула частичной суммы функционального ряда (с простыми процентами): Sn = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.
Содержание
- 1 Функция случайного числа в Excel
- 1.1 Выборка случайных чисел с помощью СЛЧИС
- 1.2 Функция СЛУЧМЕЖДУ
- 2 Как сделать генератор случайных чисел в Excel
- 3 Генератор случайных чисел нормального распределения
- 3.1 Про аргументы функции РЯД
- 3.2 Применение именованных диапазонов в функции РЯД
Перед многими пользователями встает задача оформить в табличном виде какую-либо последовательность данных, подчиняющихся стандартным правилам. Примером может служить нумерация строк (последовательность натуральных чисел), последовательность дат в графике работы, инвентарные номера в ведомости учета и так далее. Статья поможет вам использовать возможности Excel для автоматизации процесса создания таких последовательностей.
Ввод каких данных может быть автоматизирован?
- последовательность чисел;
- последовательность дат;
- последовательность текстовых данных;
- последовательность формул.
Справиться с поставленной задачей могут помочь:
- маркер заполнения;
- команда «Заполнить».
Рассмотрим решение задачи формирования последовательности чисел. Здесь возможно несколько вариантов:
- нужно получить ряд натуральных чисел (пронумеровать строки);
- нужно получить ряд чисел, в котором последующее число отличается от предыдущего на определенный шаг (четные, нечетные, арифметическая прогрессия);
Для создания таких последовательностей нужно:
- ввести первое и последующее значения (разница между значениями задает шаг изменения значений ряда);
- выделить обе ячейки;
- навести курсор мыши на маркер заполнения (правый нижний угол выделенного диапазона) и с нажатой левой кнопкой мыши протянуть маркер до формирования нужного количества значений (если тянуть маркер в направлении второго выделенного числа, то получаем ряд последующих чисел, если в направлении первого выделенного числа, то получаем ряд предыдущих чисел).
Вариант решения:
- ввести первое значение;
- в группе «Редактирование» на вкладке «Главная» открыть список у пункта «Заполнить» и выбрать вариант «Прогрессия» (обратите внимание, что при этом должна быть выделена ячейка с начальным значением);
- заполнить поля формы нужными данными (в рассматриваемом примере формируется ряд четных чисел, расположение сверху вниз (по столбцам), предельное значение 10, шаг 2).
Для создания последовательности дат (если нужны все даты определенного диапазона) достаточно ввести только начальное значение и воспользоваться маркером заполнения. Если нужны некоторые даты (в случае составления графика работы, например), то необходимо ввести начальную и последующую даты, далее выполнить такой же алгоритм, как для последовательности чисел. Команда
«Прогрессия» дает возможность выбрать варианты формирования ряда (например, нужны только рабочие дни).
Последовательность текстовых данных может быть получена для дней недели, месяцев, для любого текста с цифрой (цифрами) в конце (например, ИНВ01). Для ее формирования достаточно начального значения.
Можно создавать свои списки. На рисунке приведен пример списка сотрудников. Этот список необходимо импортировать с помощью команды
«Параметры» меню
«Файл».
Стоит отметить, что встроенные последовательности существуют и в более ранних версиях Excel.
У нас есть последовательность чисел, состоящая из практически независимых элементов, которые подчиняются заданному распределению. Как правило, равномерному распределению.
Сгенерировать случайные числа в Excel можно разными путями и способами. Рассмотрим только лучше из них.
- Функция СЛЧИС возвращает случайное равномерно распределенное вещественное число. Оно будет меньше 1, больше или равно 0.
- Функция СЛУЧМЕЖДУ возвращает случайное целое число.
Рассмотрим их использование на примерах.
Выборка случайных чисел с помощью СЛЧИС
Данная функция аргументов не требует (СЛЧИС()).
Чтобы сгенерировать случайное вещественное число в диапазоне от 1 до 5, например, применяем следующую формулу: =СЛЧИС()*(5-1)+1.
Возвращаемое случайное число распределено равномерно на интервале .
При каждом вычислении листа или при изменении значения в любой ячейке листа возвращается новое случайное число. Если нужно сохранить сгенерированную совокупность, можно заменить формулу на ее значение.
- Щелкаем по ячейке со случайным числом.
- В строке формул выделяем формулу.
- Нажимаем F9. И ВВОД.
Проверим равномерность распределения случайных чисел из первой выборки с помощью гистограммы распределения.
- Сформируем «карманы». Диапазоны, в пределах которых будут находиться значения. Первый такой диапазон – 0-0,1. Для следующих – формула =C2+$C$2.
- Определим частоту для случайных чисел в каждом диапазоне. Используем формулу массива {=ЧАСТОТА(A2:A201;C2:C11)}.
- Сформируем диапазоны с помощью знака «сцепления» (=»»).
- Строим гистограмму распределения 200 значений, полученных с помощью функции СЛЧИС ().
Диапазон вертикальных значений – частота. Горизонтальных – «карманы».
Функция СЛУЧМЕЖДУ
Синтаксис функции СЛУЧМЕЖДУ – (нижняя граница; верхняя граница). Первый аргумент должен быть меньше второго. В противном случае функция выдаст ошибку. Предполагается, что границы – целые числа. Дробную часть формула отбрасывает.
Пример использования функции:
Случайные числа с точностью 0,1 и 0,01:
Как сделать генератор случайных чисел в Excel
Сделаем генератор случайных чисел с генерацией значения из определенного диапазона. Используем формулу вида: =ИНДЕКС(A1:A10;ЦЕЛОЕ(СЛЧИС()*10)+1).
Сделаем генератор случайных чисел в диапазоне от 0 до 100 с шагом 10.
Из списка текстовых значений нужно выбрать 2 случайных. С помощью функции СЛЧИС сопоставим текстовые значения в диапазоне А1:А7 со случайными числами.
Воспользуемся функцией ИНДЕКС для выбора двух случайных текстовых значений из исходного списка.
Чтобы выбрать одно случайное значение из списка, применим такую формулу: =ИНДЕКС(A1:A7;СЛУЧМЕЖДУ(1;СЧЁТЗ(A1:A7))).
Генератор случайных чисел нормального распределения
Функции СЛЧИС и СЛУЧМЕЖДУ выдают случайные числа с единым распределением. Любое значение с одинаковой долей вероятности может попасть в нижнюю границу запрашиваемого диапазона и в верхнюю. Получается огромный разброс от целевого значения.
Нормальное распределение подразумевает близкое положение большей части сгенерированных чисел к целевому. Подкорректируем формулу СЛУЧМЕЖДУ и создадим массив данных с нормальным распределением.
Себестоимость товара Х – 100 рублей. Вся произведенная партия подчиняется нормальному распределению. Случайная переменная тоже подчиняется нормальному распределению вероятностей.
При таких условиях среднее значение диапазона – 100 рублей. Сгенерируем массив и построим график с нормальным распределением при стандартном отклонении 1,5 рубля.
Используем функцию: =НОРМОБР(СЛЧИС();100;1,5).
Программа Excel посчитала, какие значения находятся в диапазоне вероятностей. Так как вероятность производства товара с себестоимостью 100 рублей максимальная, формула показывает значения близкие к 100 чаще, чем остальные.
Перейдем к построению графика. Сначала нужно составить таблицу с категориями. Для этого разобьем массив на периоды:
- Определим минимальное и максимальное значение в диапазоне с помощью функций МИН и МАКС.
- Укажем величину каждого периода либо шаг. В нашем примере – 1.
- Количество категорий – 10.
- Нижняя граница таблицы с категориями – округленное вниз ближайшее кратное число. В ячейку Н1 вводим формулу =ОКРВНИЗ(E1;E5).
- В ячейке Н2 и последующих формула будет выглядеть следующим образом: =ЕСЛИ(G2;H1+$E$5;»»). То есть каждое последующее значение будет увеличено на величину шага.
- Посчитаем количество переменных в заданном промежутке. Используем функцию ЧАСТОТА. Формула будет выглядеть так:
На основе полученных данных сможем сформировать диаграмму с нормальным распределением. Ось значений – число переменных в промежутке, ось категорий – периоды.
График с нормальным распределением готов. Как и должно быть, по форме он напоминает колокол.
Сделать то же самое можно гораздо проще. С помощью пакета «Анализ данных». Выбираем «Генерацию случайных чисел».
О том как подключить стандартную настройку «Анализ данных» читайте здесь.
Заполняем параметры для генерации. Распределение – «нормальное».
Жмем ОК. Получаем набор случайных чисел. Снова вызываем инструмент «Анализ данных». Выбираем «Гистограмма». Настраиваем параметры. Обязательно ставим галочку «Вывод графика».
Получаем результат:
Скачать генератор случайных чисел в Excel
График с нормальным распределением в Excel построен.
Если вы выберите ряд данных какой-нибудь диаграммы и взгляните на строку формул, вы увидите, что ряд данных генерируется с помощью функции РЯД. РЯД – это специальный вид функции, который используется только в контексте создания диаграммы и определяет значения рядов данных. Вы не сможете использовать ее на рабочем листе Excel и не сможете включить стандартные функции в ее аргументы.
Про аргументы функции РЯД
Для всех видов диаграмм, кроме пузырьковой, функция РЯД имеет список аргументов, представленных ниже. Для пузырьковой диаграммы, требуется дополнительный аргумент, который определяет размер пузыря.
| АРГУМЕНТ | ОБЯЗАТЕЛЬНЫЙ/ НЕ ОБЯЗАТЕЛЬНЫЙ | ОПРЕДЕЛЕНИЕ |
| Имя | Не обязательный | Имя ряда данных, которое отображается в легенде |
| Подписи_категорий | Не обязательный | Подписи, которые появляются на оси категорий (если не указано, Excel использует последовательные целые числа в качестве меток) |
| Значения | Обязательный | Значения, используемые для построения диаграммы |
| Порядок | Обязательный | Порядок ряда данных |
Каждый из этих аргументов соответствует конкретным данным в полях диалогового окна Выбор источника данных (Правый щелчок мыши по ряду данных, во всплывающем меню выбрать Выбор данных).
В строке формул Excel вы можете увидеть примерно такую формулу:
=РЯД(Diag!$B$1;Diag!$A$2:$A$100;Diag!$B$2:$B$100;1)
Аргументами функции РЯД являются данные, которые можно найти в диалоговом окне Выбор источника данных:
Имя – аргумент Diag!$B$1 можно найти, если щелкнуть по кнопке Изменить, во вкладке Элементы легенды (ряды) диалогового окна Выбор источника данных. Так как ячейка B1 имеет подпись Значение, ряд данных будет называться соответственно.
Подпись_категорий – аргумент Diag!$A$2:$A$100 находится в поле Подписи горизонтальной оси (категории).
Значения – аргумент значений ряда данных Diag!$B$2:$B$100 находится там же, где мы указали имя ряда.
Порядок – так как наша диаграмма имеет всего один ряд данных, то и порядок будет равен 1. Порядок рядов данных отражается в списке поля Элементы легенды (ряды)
Применение именованных диапазонов в функции РЯД
Прелесть использования функции РЯД заключается в возможности использования именованных диапазонов в ее аргументах. Используя именованные диапазоны, вы можете легко переключаться между данными одного ряда данных. Что более важно, используя именованные диапазоны в качестве аргументов функции РЯД, можно создавать динамические диаграммы. Вообще, все диаграммы динамические, в том смысле, что при изменении данных, диаграммы меняют свой внешний вид. Но используя именованные диапазоны вы можете сделать так, чтобы график автоматически обновлялся при добавлении новых данных в книгу или выбирал какое-нибудь подмножество данных, например, последние 30 значений.
Методика создания динамических диаграмм на основе именованных диапазонов была описана мной в одной из предыдущих статей.
В программе Excel разработчиками заложено огромное количество различных функций, но, пользователи чаще всего пользуются математическими. Давайте рассмотрим их и подробнее остановимся на самых популярных.
-
Использование математических функций в программе
- СУММ
- СУММЕСЛИ
- ПРОИЗВЕД
- ЧАСТНОЕ
- СТЕПЕНЬ
- КОРЕНЬ
- ОКРУГЛ
- ABS
- LOG
- ОСТАТОК
- Заключение
Использование математических функций в программе
В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.
Вставить функцию в свободную ячейку таблицы можно по-разному:
- Жмем кнопку “Вставить функцию” (fx) слева от строки формул. Выполнить данное действие можно, находясь в любой вкладке.
- Переключаемся во вкладку “Формулы”. Здесь также представлена кнопка “Вставить функцию” – в левом углу ленты инструментов.
- Нажимаем комбинацию клавиш Shift+F3, чтобы вызвать Мастер функций.
Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.
Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK.
После этого откроется окно с аргументами для заполнения.
Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.
Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.
Теперь перейдем к детальному рассмотрению самых популярных функций.
СУММ
Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:
=СУММ(число1;число2;...)
В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.
Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.
СУММЕСЛИ
Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):
- больше (“>”)
- меньше (“<“)
- не равно (“<>”)
Аргумент “Диапазон_сумирования” заполнять не обязательно.
ПРОИЗВЕД
С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:
=ПРОИЗВЕД(число;число;…)
В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.
ЧАСТНОЕ
Чаще всего для деления используется формула со знаком “/” между делимым и делителем: =Число1/Число2.
Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:
=ЧАСТНОЕ(Числитель;Знаменатель)
Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).
СТЕПЕНЬ
Оператор позволяет возвести число в указанную степень. Формула выглядит так:
=СТЕПЕНЬ(число;степень)
В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.
КОРЕНЬ
С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:
=КОРЕНЬ(число)
Заполнить требуется только один аргумент – “Число”.
ОКРУГЛ
Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:
=ОКРУГЛ(число;число_разрядов)
В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.
Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).
ABS
Позволяет получить модуль числа. Формула функции представлена ниже:
=ABS(число)
Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.
LOG
С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:
=LOG(Число;Основание)
Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).
Также для десятичного логарифма предусмотрена отдельная функция – LOG10.
ОСТАТОК
Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:
=ОСТАТ(чило;делитель)
Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.
Заключение
Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.