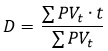Формула модифицированной дюрации в excel - Word и Excel

дюрации Маколея и используется для расчета изменения продолжительности облигации и цены на каждый процент изменения доходности к погашению.

Ключевые выводы

Формула модифицированной дюрации показывает изменение стоимости облигации по отношению к изменению ее доходности к погашению.
В Excel формула встроена в функцию MDURATION.
Следуйте этому пошаговому примеру, чтобы заполнить формулу.

Вы можете использовать Microsoft Excel для расчета модифицированной дюрации облигации с учетом следующих параметров: дата расчета, дата погашения, купонная ставка, доходность к погашению и частота.

Что вам говорит измененная продолжительность

Модифицированная дюрация определяет изменение стоимости ценной бумаги с фиксированным доходом по отношению к изменению доходности к погашению. Формула, используемая для расчета модифицированной дюрации облигации, представляет собой дюрацию Маколея, деленную на 1, плюс доходность облигации к погашению, деленную на количество купонных периодов в году.

В Excel формула, используемая для расчета модифицированной дюрации облигации, встроена в функцию MDURATION. Эта функция возвращает измененную продолжительность Маколея для ценной бумаги, предполагая, что номинальная стоимость составляет 100 долларов США.

Пример расчета модифицированной продолжительности в Excel

Например, вы хотите рассчитать модифицированную дюрацию Маколея 10-летней облигации с датой погашения 1 января 2020 г., датой погашения 1 января 2030 г., годовой купонной ставкой 5% и годовой доходность к погашению 7%. Купон выплачивается ежеквартально.

Чтобы узнать измененную продолжительность, выполните следующие действия в Excel:

Сначала щелкните правой кнопкой мыши столбцы A и B.
Затем щелкните левой кнопкой мыши по ширине столбца и измените значение на 32 для каждого из столбцов, затем нажмите кнопку ОК. Введите «Описание облигации» в ячейку A1, затем выберите ячейку A1 и нажмите клавиши CTRL и B вместе, чтобы выделить заголовок жирным шрифтом. Затем введите «Данные облигации» в ячейку B1, затем выберите ячейку B1 и нажмите клавиши CTRL и B вместе, чтобы выделить заголовок жирным шрифтом.
Введите «Дата погашения облигации» в ячейку A2 и «1 января 2020 года» в ячейку B2. Затем введите «Дата погашения облигации» в ячейку A3 и «1 января 2030 года» в ячейку B3. Затем введите «Годовая купонная ставка » в ячейку A4 и «5%» в ячейку B4. В ячейке A5 введите «Годовая доходность к погашению», а в ячейке B5 введите «7%». Поскольку купон выплачивается ежеквартально, частота составляет 4. Введите «Частота выплаты купона» в ячейку A6 и «4» в ячейку B6.
Затем введите «Основа» в ячейку A7 и «3» в ячейку B8. В Excel базис не является обязательным, и выбранное значение рассчитывает измененную продолжительность с использованием фактических календарных дней для периода начисления и предполагает, что в году 365 дней.
Теперь вы можете решить модифицированную дюрацию Маколея для облигации. Введите «Измененная продолжительность» в ячейку A8 и формулу «= MDURATION (B2, B3, B4, B5, B6, B7)» в ячейку B8. В результате модифицированная длительность составляет 7,59.

Формула, используемая для расчета процентного изменения цены облигации, представляет собой изменение доходности к погашению, умноженное на отрицательное значение модифицированной дюрации, умноженное на 100%. Следовательно, если процентные ставки увеличиваются на 1%, цена облигации, как ожидается, упадет на 7,59% = [0,01 * (-7,59) * 100%].

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование MDURATION
в Microsoft Excel.

Описание

Возвращает модифицированную продолжительность Макалея для ценных бумаг с предполагаемой номинальной стоимостью 100 р.

Синтаксис

МДЛИТ(дата_согл; дата_вступл_в_силу;купон;доход;частота;[базис])

Важно: Даты должны быть введены с использованием функции ДАТА или как результат вычисления других формул и функций. Например, для указания даты 23 мая 2008 г. воспользуйтесь выражением ДАТА(2008,5,23). Если ввести даты как текст, это может привести к возникновению проблем.

Аргументы функции МДЛИТ описаны ниже.

Дата_согл — обязательный аргумент. Дата расчета за ценные бумаги (дата продажи ценных бумаг покупателю, более поздняя, чем дата выпуска).
Дата_вступл_в_силу — обязательный аргумент. Срок погашения ценных бумаг. Эта дата определяет момент, когда истекает срок действия ценных бумаг.
Купон — обязательный аргумент. Годовая процентная ставка для купонов по ценным бумагам.
Доход — обязательный аргумент. Годовой доход по ценным бумагам.
Частота — обязательный аргумент. Количество выплат по купонам за год. Для ежегодных выплат частота равна 1, для полугодовых — 2, для ежеквартальных — 4.
Базис — необязательный аргумент. Используемый способ вычисления дня.

Базис	Способ вычисления дня
0 или опущен	Американский (NASD) 30/360
1	Фактический/фактический
2	Фактический/360
3	Фактический/365
4	Европейский 30/360

Замечания

В приложении Microsoft Excel даты хранятся в виде последовательных чисел, что позволяет использовать их в вычислениях. По умолчанию дате 1 января 1900 года соответствует номер 1, а 1 января 2008 года — 39448, так как интервал между этими датами составляет 39 448 дней.
Дата соглашения является датой продажи покупателю купона, например облигации. Срок платежа представляет собой дату истечения срока действия купона. Предположим, например, что облигация со сроком действия 30 лет выпущена 1 января 2008 г. и приобретена покупателем через шесть месяцев после выпуска. Датой выпуска будет 1 января 2008 г., датой расчета — 1 июля 2008 г., а срок погашения такой облигации наступит 1 января 2038 г., то есть через 30 лет после даты выпуска.
Дата_согл, дата_вступл_в_силу, частота и базис усекаются до целых чисел.
Если дата расчета или дата погашения не является допустимой датой, то MDURATION возвращает #VALUE! значение ошибки #ЗНАЧ!.
Если доход < 0 или купон < 0, то MDURATION возвращает #NUM! значение ошибки #ЗНАЧ!.
Если частота является любым числом, кроме 1, 2 или 4, то МДРАТ возвращает #NUM! значение ошибки #ЗНАЧ!.
Если базис < 0 или базис > 4, то МДРАТ возвращает #NUM! значение ошибки #ЗНАЧ!.
Если «≥», то МДРАТ возвращает #NUM! значение ошибки #ЗНАЧ!.
Модифицированная продолжительность определяется следующим образом:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
01.01.2008	Дата соглашения
01.01.2016	Дата вступления в силу
8 %	Процентная ставка по купонам
9 %	Процент прибыли
2	Частота полугодовая (см. выше)
1	Базис фактический/фактический (см. выше)
Формула	Описание	Результат
=МДЛИТ(A2;A3;A4;A5;A6;A7)	Модифицированная продолжительность Макалея для облигации в соответствии с условиями, указанными в ячейках A2:A5.	5,736

Нужна дополнительная помощь?

Источник

Содержание

Обзор функции MDURATION
Что такое MDURATION?
Что такое функция Excel MDURATION?
Дополнительные замечания
MDURATION в Google Таблицах
Примеры MDURATION в VBA

В этом руководстве показано, как использовать Функция Excel MDURATION в Excel для расчета модифицированной продолжительности безопасности Маколея.

Функция MDURATION Расчет годовой дюрации ценной бумаги.

Чтобы использовать функцию листа Excel MDURATION, выберите ячейку и введите:

(Обратите внимание, как появляются входные данные формулы)

Синтаксис и входные данные функции MDURATION:

= MDURATION (расчет, срок погашения, купон, год, частота, [базис])

поселок— Это дата расчетов по ценной бумаге или дата покупки ценной бумаги. Это дата, которая наступает после даты выпуска ценной бумаги.

зрелость— Это дата истечения срока действия залога или ценной бумаги, когда основная сумма возвращается держателю облигации или ценной бумаги.

купон— Годовая купонная ставка ценной бумаги.

yld— Это годовая доходность облигации или ценной бумаги.

частота— Это количество периодических купонных выплат в год. Значение частоты ежегодных, полугодовых и квартальных платежей составляет 1, 2 и 4 соответственно.

основа— ДОПОЛНИТЕЛЬНО: указывает тип подсчета дней, который будет использоваться ценной бумагой или облигацией. Возможные значения могут быть:

Основа	Счетчик дней
0	США (NASD) 30/360
1	Фактический / фактический
2	Acutal / 360
3	Acutal / 365
4	Европейский 30/360

Если аргумент основания опущен, он принимает значение по умолчанию, то есть US (NASD) 30/360.

Что такое MDURATION?

Модифицированная дюрация — это увеличение дюрации Маколея, которая измеряет чувствительность цены облигации к изменениям ее доходности. Модифицированная дюрация основана на концепции, согласно которой доходность и цена облигаций движутся в противоположных направлениях.

Модифицированная продолжительность рассчитывается с использованием следующего уравнения:

MDURATION = Продолжительность / (1+ (market_yield / coupon_payments_per_year))

Что такое функция Excel MDURATION?

Функция Excel MDURATION вычисляет модифицированную дюрацию Маколея для облигации или ценной бумаги, по которым периодически выплачиваются проценты, исходя из номинальной стоимости 100 долларов.

Модифицированная дюрация Маколея облигации

В этом примере мы хотим рассчитать модифицированную дюрацию Маколея с годовой купонной ставкой 7%. Прочая информация о облигации представлена в таблице выше.

Формула, используемая для расчета:

= MDURATION (C4, C5, C6, C7, C8, C9)

Функция Excel MDuration возвращает значение

МЕДУРАЦИЯ = 7,41 года

Модифицированная дюрация Маколея ценной бумаги с фиксированным доходом

Давайте посмотрим на другой пример, здесь мы собираемся узнать, сколько времени у ценных бумаг с фиксированным доходом до тех пор, пока они не будут возвращены. Другие детали ценной бумаги с фиксированным доходом упомянуты на приведенном выше рисунке.

Используемая формула:

= MDURATION (C4, C5, C6, C7, C8, C9)

Получаем следующий результат:

МЕДУРАЦИЯ = 3,98 года.

Дополнительные замечания

# ЧИСЛО! Ошибка возникает, если дата расчета больше или равна дате погашения; или значения аргументов rate, yld, redemption, frequency или [базис] не являются допустимыми числами (т. е. rate <0; или yld <0; или redemption ≤ 0; или частота — любое значение, кроме 1, 2 или 4 ; или [базовое] значение отличается от 0, 1, 2, 3 или 4)

#ЦЕНИТЬ! Ошибка возникает, если даты расчета или аргументы срока погашения не являются допустимыми датами Excel.

Рекомендуется вводить даты расчета и погашения в функцию DURATION как ссылки на ячейки, содержащие даты или даты, возвращаемые из формул.

Вернуться к списку всех функций в Excel

MDURATION в Google Таблицах

Все приведенные выше примеры работают в Google Таблицах точно так же, как и в Excel.

Примеры MDURATION в VBA

Вы также можете использовать функцию MDURATION в VBA. Тип:
application.worksheetfunction.mduration (расчет, срок погашения, купон, годовой доход, частота, основание)
Для аргументов функции (скорость и т. Д.) Вы можете либо ввести их непосредственно в функцию, либо определить переменные, которые будут использоваться вместо них.

Источник

Одной из важнейших характеристик, используемых в практических расчетах по денежным потокам, является дюрация, или продолжительность (duration). Дюрация представляет собой средневзвешенный срок по анализируемой последовательности платежей, где в качестве весов используется приведенная стоимость этих платежей (денежных потоков):

где PV_t — платеж, относящийся ко времени t.

Скачать заметку в формате Word или pdf, примеры в формате Excel

Одним из важнейших свойств дюрации является то, что она представляет собой интегральную характеристику денежных потоков, рассроченных во времени, — средний срок выплаты или получения причитающихся сумм. Например, если у компании много обязательств и выплаты по ним предполагаются в разные периоды времени, то средневзвешенная дюрация обязательств компании может быть принята как оценка среднего срока погашения обязательств.[1]

Таким образом, условно заменим множество рассроченных во времени обязательств всего одним платежом со сроком, равным дюрации.

Рассмотрим пример. Корпоративная облигация выпущена на 3 года с купоном 10% в год и выплатой купонов раз в год. По окончании 3-го года она будет погашена по 100%-ной номинальной стоимости. Ставка дисконтирования – 12% годовых. Какова дюрация облигации?

Решение. Облигация генерирует последовательность платежей (денежных потоков):

1-й год = 10%;

2-й год = 10%;

3-й год = 100% + 10% (купон + погашение) = 110%.

Дюрация D:

Иногда в целях упрощения в качестве весов в этой формуле используют сами платежи, а не их приведенные стоимости, т.е. в нашем примере 10; 10; 110 вместо 8,93; 7,97 и 78,3. Это может быть оправданно, если ставка дисконтирования мало отличается от купона, а ее точное определение вызывает сложности теоретического или практического характера.

В нашем примере, дюрация рассчитанная таким образом составит:

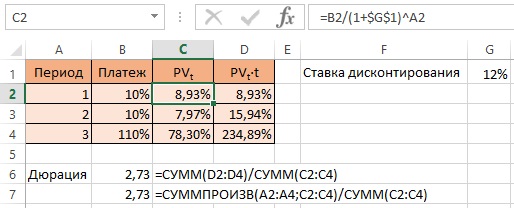
Шаблон для расчета дюрации в Excel можно найти в прикрепленном файле.

Рис. 1. Расчет дюрации в Excel

[1] Это фрагмент из книги Михаил Лимитовский. Инвестиционные проекты и реальные опционы на развивающихся рынках

Источник

Видео: Выборочные вычисления суммы, среднего и количества в Excel

Содержание

Ключевые выводы
О чем вам говорит измененная продолжительность
Пример расчета модифицированной продолжительности в Excel

Модифицированная дюрация облигации представляет собой скорректированную версию дюрации Маколея и используется для расчета изменений дюрации и цены облигации для каждого процентного изменения доходности к погашению.

Ключевые выводы

Формула модифицированной дюрации показывает изменение стоимости облигации по отношению к изменению ее доходности к погашению.
В Excel формула встроена в функцию MDURATION.
Следуйте этому пошаговому примеру, чтобы заполнить формулу.

Вы можете использовать Microsoft Excel для расчета модифицированной дюрации облигации с учетом следующих параметров: дата расчета, дата погашения, ставка купона, доходность к погашению и частота.

О чем вам говорит измененная продолжительность

В Excel формула, используемая для расчета модифицированной дюрации облигации, встроена в функцию MDURATION. Эта функция возвращает измененную продолжительность Маколея для ценной бумаги при условии, что номинальная стоимость составляет 100 долларов.

Пример расчета модифицированной продолжительности в Excel

Чтобы найти измененную продолжительность, выполните следующие действия в Excel:

Сначала щелкните правой кнопкой мыши столбцы A и B.
Затем щелкните левой кнопкой мыши по ширине столбца и измените значение на 32 для каждого из столбцов, затем нажмите кнопку ОК. Введите «Описание облигации» в ячейку A1, затем выберите ячейку A1 и нажмите клавиши CTRL и B вместе, чтобы выделить заголовок жирным шрифтом. Затем введите «Данные облигации» в ячейку B1, затем выберите ячейку B1 и нажмите клавиши CTRL и B вместе, чтобы выделить заголовок жирным шрифтом.
Введите «Дата погашения по облигации» в ячейку A2 и «1 января 2020 года» в ячейку B2. Затем введите «Дата погашения облигации» в ячейку A3 и «1 января 2030 года» в ячейку B3. Затем введите «Годовая купонная ставка» в ячейку A4 и «5%» в ячейку B4. В ячейке A5 введите «Годовая доходность к погашению», а в ячейке B5 введите «7%». Поскольку купон выплачивается ежеквартально, частота составляет 4. Введите «Частота выплаты купона» в ячейку A6 и «4» в ячейку B6.
Затем введите «Основа» в ячейку A7 и «3» в ячейку B8. В Excel базис не является обязательным, а выбранное значение рассчитывает измененную продолжительность с использованием фактических календарных дней для периода начисления и предполагает, что в году 365 дней.
Теперь вы можете решить модифицированную дюрацию Маколея для облигации. Введите «Измененная продолжительность» в ячейку A8 и формулу «= MDURATION (B2, B3, B4, B5, B6, B7)» в ячейку B8. В результате модифицированная длительность составляет 7,59.

Источник