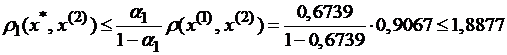Формула метода простых итераций в excel - Word и Excel - помощь в работе с программами

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х² + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.

Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.

После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

Значения элементов введем в ячейки Excel в виде таблицы.

Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.

Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.

Умножим обратную матрицу Ах^-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.

Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.

Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.

Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.

Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.

В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х³ + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

Х_n+1 = X_n– F (X_n) / M, n = 0, 1, 2, … .

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х³ – 1. М = 11.

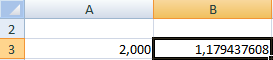
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Скачать решения уравнений в Excel

Корень на заданном промежутке один.

Источник

Решение СЛАУ методом простой итерации

Назначение сервиса . Онлайн-калькулятор предназначен для решения СЛАУ методом простой итерации в онлайн режиме (см. пример решения). Для проверки решения генерируется шаблон в Excel .

Шаг №1
Шаг №2
Видеоинструкция

Рассмотрим достаточные условия сходимости итерационной последовательности n>.
Практически, для применения метода итерации систему линейных уравнений удобно «погрузить» в одну из трёх следующих метрик:
(3.4)
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ₁: , т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по строкам, должна быть меньше единицы.
б) в пространстве с метрикой ρ₂: , т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по столбцам, должна быть меньше единицы.
в) в пространстве с метрикой ρ₃: , т. е. сумма квадратов при неизвестных в правой части системы (3.2) должна быть меньше единицы

Пример . Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x 0 =(0; 0; 0).

Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:

Последовательные приближения будем искать по формулам:

Получаем:
x 1 =(-1.9022; 0.4889; 2.1456), x 2 =(-1.1720; 0.6315; 1.2389).
Для оценки погрешности в метрике ρ₁ вычисляем коэффициент μ
.
Вычисляем погрешность:

При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В этом случае для решения СЛАУ иногда удобнее пользоваться методом простой итерации.

Метод итераций для системы уравнений в Excel

Для вычисления точности epsilon .
Итерация №1: =ABS(B7)-ABS(B6);=ABS(C7)-ABS(C6);=ABS(D7)-ABS(D6)
Итерация №2: =ABS(B8)-ABS(B7);=ABS(C8)-ABS(C7);=ABS(D8)-ABS(D7)
Скачать шаблон решения.

Решение уравнений в Excel методом итераций Крамера и Гаусса

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

Значения элементов введем в ячейки Excel в виде таблицы.
Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Excel. Использование циклических ссылок для решения уравнений итерационным способом

Ранее я описал, как найти и исправить циклическую ссылку. Напомню, что циклическая ссылка появляется, если в ячейку Excel введена формула, содержащая ссылку на саму эту ячейку (напрямую или через цепочку других ссылок). Например (рис. 1), в ячейке С2 находится формула, ссылающаяся на саму ячейку С2.

Рис. 1. Пример циклической ссылки

Но. Не всегда циклическая ссылка является бедствием. Циклическую ссылку можно использовать для решения уравнений итерационным способом. Для начала нужно позволить Excel вести вычисления, даже при наличии циклической ссылки. В обычном режиме Excel, обнаружив циклическую ссылку, выдаст сообщение об ошибке, и потребует ее устранения. В обычном режиме Excel не может провести вычисления, так как циклическая ссылка порождает бесконечный цикл вычислений. Можно, либо устранить циклическую ссылку, либо допустить вычисления по формуле с циклической ссылкой, но ограничив число повторений цикла. Для реализации второй возможности щелкните на кнопке «Office» (в левом верхнем углу), а затем на «Параметры Excel» (рис. 2).

Скачать заметку в формате Word, примеры в формате Excel

Рис. 2. Параметры Excel

В открывшемся окне «Параметры Excel» перейдите на вкладку Формулы и отметьте «Включить итеративные вычисления» (рис. 3). Помните, что эта опция включается для приложения Excel в целом (а не для одного файла), и будет действовать, пока вы ее не отключите.

Рис. 3. Включить итеративные вычисления

На этой же вкладе, можно выбрать, как будут вестись вычисления: автоматически или вручную. При автоматическом вычислении Excel сразу рассчитает конечный результат, при вычислениях, вручную, можно будет наблюдать результат каждой итерации (простым нажатием F9 запуская каждый новый цикл вычисления).

Решим уравнение третьей степени: х 3 – 4х 2 – 4х + 5 = 0 (рис. 4). Для решения этого уравнения (и любого другого уравнения совершенно произвольного вида) понадобится всего одна ячейка Excel.

Рис. 4. График функции f(x)

Для решения уравнения нам понадобится рекуррентная формула (то есть, формула, выражающая каждый член последовательности через один или несколько предыдущих членов):

(1) x = x – f(x)/f’(x), где

f(x) – функция, задающая уравнение, корни которого мы ищем; f(x) = х 3 – 4х 2 – 4х + 5

f’(x) – производная нашей функции f(x); f’(x) = 3х 2 – 8х – 4; производные основных элементарных функций можно посмотреть здесь.

Если вы заинтересовались, откуда взялась формула (1), можете почитать, например, здесь.

Итоговая рекуррентная формула имеет вид:

(2) х = x – (х 3 – 4х 2 – 4х + 5)/(3х 2 – 8х – 4)

Выберем любую ячейку на листе Excel (рис. 5; в нашем примере это ячейка G19), присвоим ей имя х, и введем в нее формулу:

Можно вместо х использовать адрес ячейки… но согласитесь, что имя х, смотрится привлекательнее; следующую формулу я ввел в ячейку G20:

Рис. 5. Рекуррентная формула: (а) для поименованной ячейки; (б) для обычного адреса ячейки

Как только мы введем формулу и нажмем Enter, в ячейке сразу же появится ответ – значение 0,77. Это значение соответствует одному из корней уравнения, а именно второму (см. график функции f(x) на рис. 4). Поскольку начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке х и равного нулю. Как же получить остальные корни уравнения?

Для изменения стартового значения, с которого рекуррентная формула начинает свои итерации, предлагается использовать функцию ЕСЛИ: [1]

Здесь значение «-5» – начальное значение для рекуррентной формулы. Изменяя его, можно выйти на все корни уравнения:

Начальное значение	Корень уравнения
1	0,77
-5	-1,40
8	4,63

[1] Идея подсмотрена здесь

7 комментариев для “Excel. Использование циклических ссылок для решения уравнений итерационным способом”

Офигенный сайт!
И как всегда когда не нужно все находишь!
Блин у меня по экономическому моделированию в Excell курсовик был в институте, вот время помню кучу потерял а тут все в одном флаконе:)
Все равно инфа пригодится, даже очень!

И нам зараза в этом гребанном институте мать их так этих учителей даже близко ничего подобного не рассказывали. Я не про этот пример говорю а про остальные..
«Вычисление стандартного отклонения для данных с тенденцией», «Нормальное распределение» и т.п.. даже объяснить не могли или не хотели как это все применять, а тут все наглядно и понятно! Огромное спасибо! Не зря я на этот сайт наткнулся, чую он мне еще окажет неплохую помощь))))

В упор не понимаю откуда берется предел для определения корней уравнения, если «Здесь значение «-5» – начальное значение для рекуррентной формулы. Изменяя его, можно выйти на все корни уравнения»

У меня график получается, который с осью Х не имеет вообще пересечений, мож где накосячила?
Пожалуйста подскажите, а то у меня взрыв мозга будет скоро…((((

Тамара, если Вы строите график на основе моих данных, откройте файл Excel; если Вы используете собственные данные, пришлите мне на mail Ваш файл, попробую помочь))

Спасибо заранее за беспокойство, вот такое уравнение у^3-20у^2-158у-420=0, если не трудно объясните пожалуйста как вы определяте предел в каких знчениях надо считать корни.

источники:

http://exceltable.com/otchety/reshenie-uravneniy

http://baguzin.ru/wp/excel-ispolzovanie-tsiklicheskih-ssylok-d/

Источник

Метод простой итерации

Метод основан на замене исходного
уравнения F(x)=0на эквивалентноеx=(x).
Функция(x)
выбирается таким образом, чтобы на обоих
концах отрезка [a,b]
выполнялось условие сходимости(x)< 1. В этом случае
в качестве начального приближения можно
выбрать любой из концов отрезка.
Итерационная формула имеет вид

Итерационный процесс продолжается до
тех пор, пока не будет выполнено условие
F(x)<,
где- заданная
точность.

2.6. Реализация в пакете Excel

В качестве примера рассмотрим уравнение
x²— 4x+ 3 = 0. Интервал поиска [0;3,3], шагh= 0,3. Решим его, используя различные
численные методы, а также специальные
возможности пакетаExcel-
«Подбор параметра» и «Поиск решения».

Последовательность действий (см. рис.
5):

Оформить заголовок в строке 1 «Численные
методы решения нелинейного уравнения».
Оформить заголовок в строке 3 «Шаговый
метод».
В ячейки B4 иC4
записать заголовки рядов — соответственноxиF(x).
В ячейки B5 иB6
ввести первые два значения аргумента
— 0 и 0,3.
Выделить ячейки B5-B6
и протащить ряд данных до конечного
значения (3,3), убедившись в правильном
выстраивании арифметической прогрессии.
В ячейку C5 ввести формулу
«=B5*B5-4*B5+3».
Скопировать формулу на остальные
элементы ряда, используя прием
протаскивания. В интервале C5:C16
получен ряд результатов вычисления
функцииF(x).
Видно, что функция дважды меняет знак.
Корни уравнения расположены на интервалах
[0,9;1,2] и [3;3,3].
Для построения графика зависимости
F(x)используем Мастер диаграмм (тип
«Точечная», маркеры соединяются гладкими
кривыми).
Оформить заголовок в строке 17 «Методы
уточнения».
Ввести в ячейку E18
заголовок «Метод половинного деления»
(выравнивание по центру).
Ввести в ячейку H18 текст
«е=», а в ячейкуI18 значение
точности «0,001».
В области C19:I19
оформить заголовок таблицы (рядC- левая граница отрезка «a»,
рядD- середина отрезка
«x», рядE- правая граница отрезка «b»,
рядF- значение функции
на левой границе отрезка «F(a)»,
рядG- значение функции
на середине отрезка «F(x)»,
рядH- произведение
«F(a)*F(x)»,
рядI- проверка достижения
точности «F(x)<е».
Ввести первоначальные значения концов
отрезка: в ячейку C20 «0,9»,
в ячейкуE20 «1,2».
Ввести в ячейку D20 формулу
«=(C20+E20)/2».

Рис. 5

Ввести в ячейку F20 формулу
«=C20*C20-4*C20+3».
Ввести в ячейку G20 формулу
«=D20*D20-4*D20+3».
Ввести в ячейку H20 формулу
«=F20*G20».
Ввести в ячейку I20 формулу
«=ЕСЛИ(ABS(G20)<$I$18;корень,)».
Ввести в ячейку C21 формулу
«=ЕСЛИ(H20<0;C20;D20)».
Ввести в ячейку E21 формулу
«=ЕСЛИ(H20<0;D20;E20)».
Скопировать ячейку D20 в
ячейкуD21, ячейкиF20:I20
в ячейкиF21:I21.
Выделить область C21:I21
и протащить ее по вертикали вплоть до
появления в рядуIсообщения
«корень» (ячейкаI27).
Ввести в ячейку C28
заголовок «Метод Ньютона» (выравнивание
по левому краю).
Ввести в ячейку C29 текст
«е=», а в ячейкуD29 значение
точности «0,000001».
Убедиться, что при x=0,9
значение функции и ее второй производной
имеют одинаковые знаки.
В области B30:E30
оформить заголовок таблицы (рядB- значение аргумента «x»,
рядC- значение функции
«F(x)», рядD- производная функции
«F(x)»,
рядE- проверка достижения
точности «F(x)<е».
В ячейку B31 ввести
первоначальное значение аргумента
«0,9».
Ввести в ячейку C31 формулу
«=B31*B31-4*B31+3».
Ввести в ячейку D31 формулу
«=2*B31-4».
Ввести в ячейку E31 формулу
«=ЕСЛИ(ABS(C31)<$D$29;корень,)».
Ввести в ячейку B32 формулу
«=B31-C31/D31».
Скопировать ячейки C31:E31
в ячейкиC32:E32.
Выделить область B32:E32
и протащить ее по вертикали вплоть до
появления в рядуEсообщения
«корень» (ячейкаE34).
Ввести в ячейку G28
заголовок «Метод простой итерации»
(выравнивание по левому краю).
Ввести в ячейку H29 текст
«е=», а в ячейкуI29 значение
точности «0,001».
Выбрать функцию (x),
удовлетворяющую условию сходимости.
В нашем случае такой функцией является
функцияS(x)=(x*x+3)/4.
В области G30:J30
оформить заголовок таблицы (рядG- значение аргумента «x»,
рядH- значение функции
«F(x)», рядI- значение вспомогательной
функции «S(x)»,
рядJ- проверка достижения
точности «F(x)<е».
В ячейку G31 ввести
первоначальное значение аргумента
«0,9».
Ввести в ячейку H31 формулу
«=G31*G31-4*G31+3».
Ввести в ячейку I31 формулу
«=(G31*G31
+3)/4».
Ввести в ячейку J31 формулу
«=ЕСЛИ(ABS(H31)<$I$29;корень,)».
Ввести в ячейку G32 формулу
«=I31».
Скопировать ячейки H31:J31
в ячейкиH32:J32.
Выделить область G32:J32
и протащить ее по вертикали вплоть до
появления в рядуJсообщения
«корень» (ячейкаJ39).
Выделить ряд x, полученный с помощью
метода половинного деления (ячейки
D20:D27). Используя Мастер диаграмм,
построить зависимость x от номера
итерации (тип диаграммы «График»).
Определить заголовок ряда «Метод
половинного деления».
Добавить на график еще два ряда: «Метод
Ньютона» — ячейки B31:B34 и «Метод простой
итерации» — ячейки G31:G39. Для каждого
ряда использовать сою маркировку.
График показывает, что наибольшую
скорость сходимости имеет метод Ньютона.
Ввести в ячейку C57 заголовок «Подбор
параметра» (выравнивание по левому
краю).
Ввести в ячейку C59 текст «x», а в ячейку
D59 — «F(x)».
Занести в ячейку C60 начальное значение
переменной (например, ноль).
Ввести в ячейку столбца D60 формулу
«=C60*C60-4*C60+3».
Дать команду «Сервис»
«Подбор параметра».
В поле «Установить в ячейке» указать
ячейку D60, в которой занесена формула,
в поле «Значение» задать 0 (ноль), в поле
«Изменяя значение ячейки» указать
ячейку C60, где занесено начальное
значение переменной.
Щелкнуть <ОК> и посмотреть на результат
подбора, отображенный в диалоговом
окне «Результаты подбора параметра».
Нажать <ОК>, чтобы сохранить полученные
значения.
Повторить расчет п.п. 49-54, задав другое
начальное значение в ячейке C60. Совпали
ли результаты вычисления?
Ввести в ячейку H57 заголовок «Поиск
решения» (выравнивание по левому краю).
Ввести в ячейку H59 текст «x», а в ячейку
I59 — «F(x)».
Занести в ячейку H60 начальное значение
переменной (например, ноль).
Ввести в ячейку столбца I60 формулу
«=H60*H60-4*H60+3».
Дать команду «Сервис»
«Поиск решения».
В поле «Установить целевую ячейку»
указать ячейку $I$60, в которой занесена
формула, в поле «Равной» установить
«значению 0», в поле «Изменяя ячейки»
указать ячейку $H$60, в поле «Ограничения»
установить два ограничения «$H$60>=0,9 и
$H$60<=1,2».
Нажать кнопку «Выполнить». Появится
сообщение, что решение найдено.
Нажать кнопку <ОК>, результат будет
помещен в рабочий лист.
Повторить расчет п.п. 58-63, задав другое
начальное значение в ячейке H60. Совпали
ли результаты вычисления?

Источник

Метод простой итерации даёт возможность получить последовательность приближённых значений, сходящуюся к точному решению системы.
Преобразуем систему (3.1) к нормальному виду:
. (3.2)
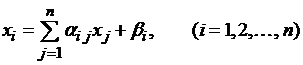
Правая часть системы (3.2) определяет отображение:
x=(x₁, x₂, …, x_n), преобразующее точку n-мерного метрического пространства в точку y=(y₁, y₂, …, y_n) того же пространства.
Выбрав начальную точку x⁰=(x⁰₁, x⁰₂, …, x⁰_n), можно построить итерационную последовательность точек n — мерного пространства: x⁰, x¹=F(x⁰), … , xⁿ⁺¹=F(xⁿ)
При определённых условиях данная последовательность сходится.
Так, для исследования сходимости таких последовательностей используется принцип сжимающих отображений, который состоит в следующем.
Если F– сжимающее отображение, определённое в полном метрическом пространстве с метрикой ρ(x,y), то существует единственная неподвижная точка x*, такая, что x*=F(x*). При этом итерационная последовательность, {x_n}, полученная с помощью отображения F с любым начальным членом х⁽⁰⁾, сходится к x*.
Оценка расстояния между неподвижной точкой x* отображения F и приближением х^(к) даётся формулами:
(3.3)
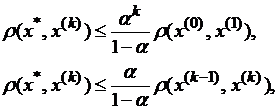
где α – множитель, определяемый достаточными условиями сжимаемости отображения F.
Значение множителя α, определяется выбором метрики, в которой проверяется сходимость последовательности значений x_i.

Рассмотрим достаточные условия сходимости итерационной последовательности {x_n}.
Практически, для применения метода итерации систему линейных уравнений удобно «погрузить» в одну из трёх следующих метрик:
(3.4)
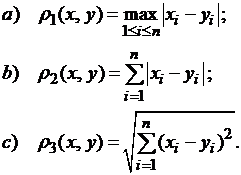
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ₁: 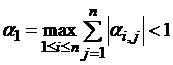, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по строкам, должна быть меньше единицы.
б) в пространстве с метрикой ρ₂: 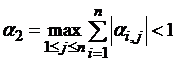, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по столбцам, должна быть меньше единицы.
в) в пространстве с метрикой ρ₃: 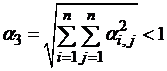, т. е. сумма квадратов при неизвестных в правой части системы (3.2) должна быть меньше единицы

ПРИМЕР. Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x⁰=(0; 0; 0).

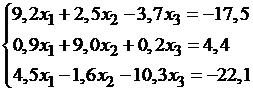
Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:

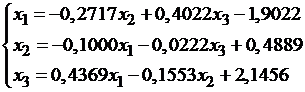
Последовательные приближения будем искать по формулам:

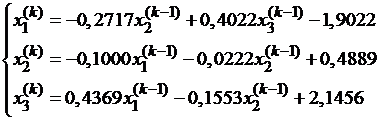
Получаем:
x¹=(-1.9022; 0.4889; 2.1456), x²=(-1.1720; 0.6315; 1.2389).
Для оценки погрешности в метрике ρ₁ вычисляем коэффициент μ
.
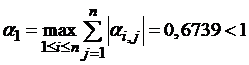
Вычисляем погрешность:

Метод итераций для системы уравнений в Excel

На листе Excel организуется таблица в три зоны: первая зона состоит из одного столбца (номер итерации), вторая зона определяет переменные x, третья зона под вычисления точности epsilon.
Во второй зоне по итерационной схеме организуется расчет переменных x (в примере для случая трех переменных):
Итерация №1:=$F$2/$B$2-C6*$C$2/$B$2-D6*$D$2/$B$2;=$F$3/$C$3-B6*$B$3/$C$3-D6*$D$3/$C$3;=$F$4/$D$4-B6*$B$4/$D$4-C6*$C$4/$D$4
Итерация №2:=$F$2/$B$2-C7*$C$2/$B$2-D7*$D$2/$B$2;=$F$3/$C$3-B7*$B$3/$C$3-D7*$D$3/$C$3;=$F$4/$D$4-B7*$B$4/$D$4-C7*$C$4/$D$4

Для вычисления точности epsilon.
Итерация №1:=ABS(B7)-ABS(B6);=ABS(C7)-ABS(C6);=ABS(D7)-ABS(D6)
Итерация №2:=ABS(B8)-ABS(B7);=ABS(C8)-ABS(C7);=ABS(D8)-ABS(D7)
Скачать шаблон решения.

ПРИМЕР. Методом итераций решить систему линейных алгебраических уравнений предварительно приведя ее к диагональному преобладанию.
Решение. Приведем матрицу к диагональному преобладанию.
Умножаем матрицы A^TA.

Умножаем матрицы A^Tb.

Приведем к виду:
x₁=7.25-1.5x₃
x₂=-0.8+0.24x₃
x₃=-3.67-0.5x₁+0.5x₂
Покажем вычисления на примере нескольких итераций.
N=1
x₁=7.25 — 0 • 0 — 0 • (-1.5)=7.25
x₂=-0.8 — 0 • 0 — 0 • 0.24=-0.8
x₃=-3.67 — 0 • (-0.5) — 0 • 0.5=-3.67
N=2
x₁=7.25 — (-0.8) • 0 — (-3.67) • (-1.5)=1.75
x₂=-0.8 — 7.25 • 0 — (-3.67) • 0.24=0.0588
x₃=-3.67 — 7.25 • (-0.5) — (-0.8) • 0.5=0.36
N=3
x₁=7.25 — 0.0588 • 0 — 0.36 • (-1.5)=7.79
x₂=-0.8 — 1.75 • 0 — 0.36 • 0.24=-0.89
x₃=-3.67 — 1.75 • (-0.5) — 0.0588 • 0.5=-2.82
Остальные расчеты сведем в таблицу.

N	x₁	x₂	x₃	e₁	e₂	e₃

	7.25	-0.8	-3.67	7.25	0.8	3.67
	1.75	0.0588	0.36	-5.5	-0.75	-3.31
	7.79	-0.89	-2.82	6.04	0.83	2.46
	3.02	-0.14	0.67	-4.77	-0.75	-2.15
	8.26	-0.96	-2.09	5.24	0.82	1.41
	4.12	-0.31	0.94	-4.14	-0.65	-1.14
	8.67	-1.03	-1.45	4.55	0.71	0.51
	5.07	-0.46	1.18	-3.59	-0.56	-0.27
	9.02	-1.08	-0.9	3.95	0.62	-0.28
	5.9	-0.59	1.38	-3.12	-0.49	0.49
	9.33	-1.13	-0.42	3.42	0.54	-0.96
	6.62	-0.71	1.56	-2.7	-0.42	1.14
	9.59	-1.17	-0.00351	2.97	0.47	-1.56
	7.24	-0.8	1.71	-2.35	-0.37	1.71
	9.82	-1.21	0.36	2.58	0.4	-1.36
	7.79	-0.89	1.85	-2.04	-0.32	1.49
	10.02	-1.24	0.67	2.24	0.35	-1.18
	8.26	-0.96	1.96	-1.77	-0.28	1.29

После N-ой итерации получаем: x₁ = 7.5, x₂ = -0.75, x₃ = 0.25

Источник

Тема: Решение систем линейных уравнений методом простой итерации.

Цель работы: изучить особенности различных методов решения систем линейных алгебраических уравнений (далее — СЛАУ), приобрести навыки решения СЛАУ с помощью средств MS Excel выполнения задания

Задание 1. Используя методы Гаусса, простых итераций и Зейделя, разработайте схемы соответствующих алгоритмов решения СЛАУ в среде MS Excel.

1.1. Метод Гаусса в среде MS Excel

1.1.1. В ячейки А2:Е5 введите расширенную матрицу системы (рис. 1.1), скопируйте ее в диапазоны ячеек А7:Е10.

a)предположите, что в ячейке А2 не ноль. Если это не так, то переставьте строки таким образом, чтобы число в ячейке А2 было отлично от нуля;

нажмите клавиши + + . В результате формула примет вид:

в) протянув за маркер автозаполнения, скопируйте формулу в ячейки А9:Е10. В результате этих операций коэффициенты при х₁ во всех уравнениях кроме первого обратятся в ноль;

г) выделите диапазон А7:Е10 и скопируйте значения, хранящиеся в нем в ячейки диапазонов А12:Е15. Для копирования значений нужно воспользоваться специальной вставкой. Ей соответствует пункт меню Правка-Специальная вставка. После выбора этого пункта появляется диалоговое окно Специальная вставка, в котором нужно выбрать Вставить-Значения и нажать ОК;

д) аналогичным образом обратите в ноль коэффициенты при х₂. В диапазон ячеек В14:Е14 введите формулу

е) протяните маркер автозаполнения этого диапазона так, чтобы заполнить ячейки диапазона В15:Е15. Это обратит в ноль коэффициенты при х₂ в последних двух уравнениях.

ж) далее содержимое (только значения!) диапазона A12:Е15 скопируйте в ячейки диапазона A17:Е20;

з) выделите диапазон С20:Е20, введите в него формулу

{=C15:E15–$C$14:$E$14*C15/$C$14},

что обратит в ноль коэффициент при х₃ в последнем уравнении;

и) в результате этих преобразований матрица системы примет треугольный вид.

1.1.3.Обратный ход метода Гаусса:

а)в ячейки G2, G3, G4 и G5 введите х4, x3, x2 и х1 соответственно, а в ячейки Н2:Н5 — формулы из таблицы 1.1;

Таблица 1.1 — Обратный ход метода Гаусса

Ячейка

Формула

Н2

= E20 / D20

Н3

= (E19 – D19 * H2) / C19

Н4

= (E18 – D18 * H2 – C18 * H3) / B18

Н5

= (E17 – D17*H2 – C17 * H3 – B17 * H4) / A17

б) в результате чего в диапазоне Н2:Н5 будет получено решение системы (рис. 1.1).

1.2. Метод простых итераций в среде MS Excel:

а) в ячейки А2:Е5 введите расширенную матрицу системы (рис. 1.2) и сделайте пояснительные записи;

б) приведите систему к нормальному виду, т. е. все коэффициенты первого уравнения разделите на а₁₁, все коэффициенты второго уравнения на а₂₂ и т. д. Для этого в диапазон ячеек А8:А11 введите надписи: х1=, х2=, х3=, х4=. Выделите блок ячеек В8:Е8, в строке формул введите формулу =$B$2:$E$2/$A$2 и нажмите клавиши + + (операция над матрицей);

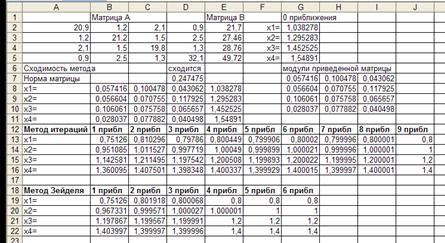
Рисунок 1.2 – Вид решения СЛАУ методом простых итераций и методом Зейделя в Excel

б) в ячейку В9 введите формулу =А3/В3. Далее выделите диапазон ячеек С9:Е9 и введите формулу =С3:Е3/В3, используя операцию над матрицей;

в) в блок ячеек В10:С10 внесите формулу =А4:В4/С4, а в блок D10:E10 — соответственно =D4:E4/C4, используя операцию над матрицами. Для блока В11:D11 введите формулу =А5:С5/D5, а в ячейку Е5 — формулу = E5/D5;

г) из полученной системы определите норму матрицы и признак сходимости метода. Для этого найдите модули полученных коэффициентов и в ячейку G7 введите формулу =ABS(B8), которую скопируйте на блок G7:I10. В ячейке D6 проверьте один из признаков сходимости и введите формулу =ЕСЛИ(МАКС (G7 + G8 + G9 + G10; H7 + H8 + H9 + H10; I7 + I8 + I9 + I10)

д) в ячейке D7 определите норму матрицы по формуле: =МАКС(G7 + H7 + I7; G8 + H8 + I8; G9 + H9 + I9; G10 + H10 + I10). Если полученный ответ меньше 1, то метод сходится при любых начальных приближениях. За начальное (нулевое) приближение возьмите полученные свободные члены и внесите их в ячейки G2:G5. Вычислим первые приближенные значения: х1(1), х2(1), х3(1), х4(1) по формулам (табл. 1.2);

Таблица 1.2 – Вычисление первых приближенных значений

Ячейка

Формула

В13

= E8 – B8*G3 – C8 * G4 – D8 * G5

В14

= E9 – B9 * G2 – C9 * G4 – D9 * G5

В15

= E10 – B10 * G2 – C10 * G3 – D10 * G5

В16

= E11 – B11 * G2 – C11 * G3 – D11 * G4

е) таким образом получите первые приближенные значения х1, х2, х3, х4. Далее в ячейки С13:С16 введите формулы, используя уже новые полученные приближения из В13:В16 (табл. 1.3).

Таблица 1.3 – Продолжение вычислений

Ячейка

Формула

С13

= $E$8 – $B$8 * B14 – $C$8 * B15 – $D$8 * B16

С14

= $E$9 – $B$9 * B13 – $C$9 * B15 – $D$9 * B16

С15

= $E$10 – $B$10 * B13 – $C$10 * B14 – $D$10 * B16

С16

= $E$11 – $B$11 * B13 – $C$11 * B14 – $D$11 * B15

ж) используя полученные вторые приближения, скопируйте формулы из ячеек С13:С16 на блок ячеек D13:D16. В результате получите новые приближенные значения корней. Продолжайте операцию копирования, получая новые приближения. Момент прекращения вычислений определите эмпирическим правилом.

1.3.Метод Зейделя в среде MS Excel:

а) в блоке ячеек В19:В22введите формулы вычисления корней уравнения по методу Зейделя (табл. 1.4).

Таблица 1.4 – Вычисление корней уравнения по методу Зейделя

Ячейка

Формула

В19

= $E$8 – $B$8 * G3 – $C$8 * G4 – $D$8 * G5

В20

= $E9 – $B$9 * B19 – $C$9 * G4 – $D$9 * G5

В21

= $E$10 – $B$10 * B19 –$C$10 * B20 – $D$10 * G5

В22

= $E$11 – $B$11 * B19 – $C$11 * B20 – $D$11 * B21

б) рассуждая аналогично, введите формулы в ячейки C19:C22, используя соответственно полученные данные из В19:В22 (табл. 1.5).

Таблица 1.5 – Продолжение вычислений

Ячейка

Формула

С19

=$E$8 – $B$8 * B20 – $C$8 * B21 – $D$8 * B22

С20

=$E$9 – $B$9 * C19 – $C$9 * B21 – $D$9 * B22

С21

=$E$10 – $B$10 * C19 – $C$10 * C20 – $D$10 * B22

С22

=$E$11 – $B$11 * C19 – $C$11 * C20 – $D$11 * C21

в) скопируйте формулы из ячеек С19:С22 на блоки: D19:D22, Е19:Е22 и т.д. Момент прекращения вычислений определяется, как и в методе простых итераций, эмпирическим правилом.

3. Выполненной задание прислать по эл.почте [email protected]

или в л/с ВК (Елена Ленина)

Источник

Ячейка	Формула
Н2	= E20 / D20
Н3	= (E19 – D19 * H2) / C19
Н4	= (E18 – D18 * H2 – C18 * H3) / B18
Н5	= (E17 – D17H2 – C17 H3 – B17 * H4) / A17

Ячейка	Формула
В13	= E8 – B8G3 – C8 G4 – D8 * G5
В14	= E9 – B9 * G2 – C9 * G4 – D9 * G5
В15	= E10 – B10 * G2 – C10 * G3 – D10 * G5
В16	= E11 – B11 * G2 – C11 * G3 – D11 * G4

Ячейка	Формула
С13	= $E$8 – $B$8 * B14 – $C$8 * B15 – $D$8 * B16
С14	= $E$9 – $B$9 * B13 – $C$9 * B15 – $D$9 * B16
С15	= $E$10 – $B$10 * B13 – $C$10 * B14 – $D$10 * B16
С16	= $E$11 – $B$11 * B13 – $C$11 * B14 – $D$11 * B15

Ячейка	Формула
В19	= $E$8 – $B$8 * G3 – $C$8 * G4 – $D$8 * G5
В20	= $E9 – $B$9 * B19 – $C$9 * G4 – $D$9 * G5
В21	= $E$10 – $B$10 * B19 –$C$10 * B20 – $D$10 * G5
В22	= $E$11 – $B$11 * B19 – $C$11 * B20 – $D$11 * B21

Ячейка	Формула
С19	=$E$8 – $B$8 * B20 – $C$8 * B21 – $D$8 * B22
С20	=$E$9 – $B$9 * C19 – $C$9 * B21 – $D$9 * B22
С21	=$E$10 – $B$10 * C19 – $C$10 * C20 – $D$10 * B22
С22	=$E$11 – $B$11 * C19 – $C$11 * C20 – $D$11 * C21